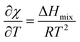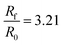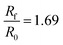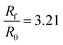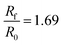Open Access Article
Open Access ArticleA refined mechanistic model for swelling kinetics of starch granules†
Botong
Li
 a,
Lanxin
Mo
b,
Vivek
Narsimhan
a,
Lanxin
Mo
b,
Vivek
Narsimhan
 *c,
Ganesan
Narsimhan
*c,
Ganesan
Narsimhan
 d and
John M.
Frostad
*be
d and
John M.
Frostad
*be
aSchool of Mathematics and Physics, University of Science and Technology Beijing, China
bFood Science, University of British Columbia, Canada. E-mail: john.frostad@ubc.ca
cDavidson School of Chemical Engineering, Purdue University, USA. E-mail: vnarsim@purdue.edu
dDepartment of Agricultural and Biological Engineering, Purdue University, USA
eDepartment of Chemical and Biological Engineering, University of British Columbia, Canada
First published on 18th February 2025
Abstract
This paper investigates the gelatinization of individual starch granules using numerical simulations, validated against experimental microscopy data from a ParCS apparatus. We show that the dynamics of starch-granule swelling can be captured by a diffusion equation for mass transfer of water into the granule, with the equilibrium water content captured by a Flory–Rehner theory of a cross-linked network in which the fraction of cross-linked chains is made to vary as an empirical function of temperature. Having the cross-link density vary with temperature is vital to capture the swelling behavior at large and small swelling extents (i.e., close to and far away from the gelatinization temperature). The theory produces excellent agreement with both equilibrium swelling data and dynamic swelling data for red bean starch. Further, we show that the model is able to reproduce a previous experimental finding that swelling data from different granules from red bean, chickpea, green lentil, and yellow pea starches can be collapsed onto a universal curve with only two empirical parameters. The simulations are then used to predict the relationship between the empirical parameters in the master curve and the true material properties. The modified theory presented here is a major step forward in the fundamental understanding of starch gelatinization and the ability to use predictive models for optimization of industrial manufacturing processes.
1 Introduction
Starch is the main source of carbohydrates for humans in their diet, and makes up a significant portion of their caloric intake.1 Starch is obtained from agricultural products such as rice, corn, potato, and legumes,2 and determines the texture, mouth-feel, shelf life and consistency of many foods.3 Starch naturally exists in the form of discrete, insoluble, semi-crystalline granules that differ in size and shape depending on the plant origin. These granules may range from around 1 μm to more than 100 μm,4 and the shape can be ovoid, disc-like, polyhedral or irregular.5 The granules themselves are mostly composed of unbranched amylose and highly branched amylopectin.1 The relative amounts of these two polymers and their molecular structure lead to fundamental variability in the physical properties of different starch varieties,1 and result in differences in how the different starches behave during processing, as well as the attributes of the final product.6One of the major changes that occurs during starch processing is gelatinization, which is the sudden intake of water into their granules above a critical temperature that occurs between 60 °C and 80 °C for most starch varieties.7,8 It is known that starch gelatinization is affected by many factors such as the heating rate, heating time, moisture, and presence of other ingredients.9–11 Experimentally, gelatinization is characterized by many methods. Rheometry is widely used to obtain bulk measurements of gelatinization temperature, while differential scanning calorimetry is used to obtain this quantity as well as the gelatinization enthalpy.12–16 To examine gelatinization at the individual granule level, optical microscopy can be used to monitor morphological changes during heating.17–19 Recent studies have suggested that there is considerable variability in gelatinization between granules from the same starch sample, causing the study of starch gelatinization to be a complex undertaking.19–21
Besides experimental analysis, theoretical analysis and quantitative prediction of starch gelatinization are in great demand and significant effort has been made in this area. For example, recently Desam et al. proposed a first-principles model for the swelling kinetics and gelatinization behavior of waxy maize starch.22 This model consists of three elements: (a) a Flory–Rehner theory23–27 for the equilibrium swelling of starch granules (treated as a polymer network), (b) a heat and mass transport model for water diffusion into granules to describe swelling kinetics towards equilibrium, and (c) a population balance model to describe how the granule size distribution evolves over time. Subsequently, these ideas have been used to describe the swelling of many other starches (potato, rice),17,22,28 as well as forecast the rheology of starch dispersions during the initial stages of swelling.28 In other work, Evans et al. used the Flory theory to explain the effect of solutions on the gelatinization temperature of potato starch.29
While these models are promising, more work is needed to validate them and improve them. For example, Flory theories of polymer swelling often assume reversible swelling, when in fact starch swelling is known to be irreversible. Additionally, Flory theories assume the granule is a loosely cross-linked polymer network, which is reasonable during the late stages of swelling but may not be the case during the early stages when the granule is tightly packed. Prior to the present work, it has not been clear if these considerations need to be taken into account to improve modeling.
With this motivation in mind, this study aims to make a systematic comparison between the theoretical Flory models of Desam et al.22 and recent experimental measurements from our group.19 The experimental study described in ref. 19 performed measurements of swelling kinetics for hundreds of individual granules during gelantinization from four different legume plants (red bean, chickpea, green lentil, and yellow pea). The data showed that all of the data from the hundreds of granules can be described by a single empirical function with only four free parameters, where two parameters correspond to the initial and final granule size. Because of this, the data obtained in that study present a highly convenient case for validation of theoretical models that can predict granule swelling. New experimental data were also gathered for the swelling of red bean, to be compared against existing models.
In this work, we will test the experimental data against the model from Desam et al.22 to see if the model can be validated. If necessary, the assumptions made in the model will be revisited and the model revised. We hypothesize that the theoretical model of Desam et al. can be non-dimensionalized in such a way that (with appropriate constraints) it will also result in a universal curve as found experimentally by Mo et al. in ref. 19. We further hypothesize that it will be possible to make a clear mathematical connection between the theoretical model parameters of Desam et al. (based on material properties) and the empirical model parameters of Mo et al.
2 Methods and materials
2.1 Materials
Starch from red bean (Vigna angularis) (President's Choice Canada) was isolated following a the method outlined in ref. 30 with some minor modifications. Briefly, 100 g of dried beans was soaked in 200 mL of 0.5 wt% sodium bisulfite solution for 20 h at 4 °C, then drained and blended with 500 mL of distilled water for 5 min. The mixture was filtered through a 125 μm sieve, then centrifuged at 1500g for 15 minutes. The supernatant was discarded and the starch was resuspended in distilled water for centrifuging again under the same conditions. The top non-white layer in the centrifuge tube was removed and discarded. Finally, the starch was dried at 40 °C for 24 h and gently broken into a powder using a mortar and pestle.2.2 Equilibrium granule swelling measurements
Starch samples with 20 ± 5 mg were dispersed in 17 mL of deionized water in a 20 mL vial. After shaking by hand, a small amount of solution was injected into the ParCS chamber (custom instrument described in ref. 31) using a syringe. The temperature was monitored and controlled by a platinum series universal benchtop PID controller (OMEGA Engineering, Norwalk, CT, USA) to achieve a sequence of increasing temperatures.The temperature was controlled according to the following steps. First, the chamber was equilibrated to 55 °C (328 K) and maintained for 4 h, after which we assumed that equilibrium was reached and the size of the granule was recorded. Then, the temperature was increased to 333 K, 338 K, 340.5 K, 343 K, 345.5 K, 353 K, 355.5 K, and 358 K in sequence. Each increment in the temperature was completed within 30 s and each temperature was maintained for 7 h before recording the size and then increasing the temperature.
The swelling process of the individual starch granules was captured by camera and image analysis was done using a custom Python script. Using the Python script, the boundaries of the granules were manually outlined and the projected area (A) was computed. The equivalent spherical diameter (d) of the starch granules was then calculated using the following formula:
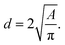 | (1) |
It was noted during method development that there was a fair amount of variation in the equilibrium granule size for starch granules with different swelling ratios. Therefore, when preparing the data for comparison to theory, granules were only included in the data set if the swelling ratio (ratio of swollen and unswollen granule diameters) was 2.15 ± 0.24 (approximately 10% variation about the mean). Due to the painstaking nature of making this measurement, data from only 12 granules were included in this manuscript due to the need to restrict the range of swelling ratios, and this was found to be sufficient for the present purpose.
3 Theory and numerical methods
3.1 Equilibrium granule swelling (Flory–Rehner theory)
The Flory–Rehner theory states that the free energy of a polymer network is determined by the competition between water–polymer mixing and the elastic stretching of the polymer chains. In this work, we will assume that a starch granule can be modeled as a polymer network that can be swollen in water, throughout the gelatinization process. We will also assume that the granule is neutral and the internal granule architecture is uniform. A number of more refined assumptions related to the actual structure of starch granules could be made based on previous theoretical work.32–45 However, incorporating these additional assumptions is not trivial in light of our specific objectives and hypotheses, and so will be reserved for future work.At equilibrium, the chemical potential of water within the granule (μ1) must be equal to its chemical potential outside the granule (μ1,b). In this work we assume that the expression for the chemical potential difference is given by the following equation:
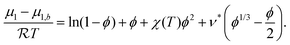 | (2) |
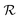 , T, χ(T), ν* denote the ideal gas constant, temperature, the Flory–Huggins parameter, and the fraction of cross-linked chains, respectively. The first two terms on the right hand side of eqn (2) are derived from mixing entropy, the third term from mixing enthalpy, and the fourth one from elastic entropy due to polymer stretching. In the elastic portion of the model, we have assumed that the reference state (unstretched state) corresponds to a fully dry granule (ϕ = 1), though other assumptions are possible and will be explored in future work.40
, T, χ(T), ν* denote the ideal gas constant, temperature, the Flory–Huggins parameter, and the fraction of cross-linked chains, respectively. The first two terms on the right hand side of eqn (2) are derived from mixing entropy, the third term from mixing enthalpy, and the fourth one from elastic entropy due to polymer stretching. In the elastic portion of the model, we have assumed that the reference state (unstretched state) corresponds to a fully dry granule (ϕ = 1), though other assumptions are possible and will be explored in future work.40
Since starch swelling occurs mainly above the gelatinization temperature Tg, the molar enthalpy of interaction with water, χ, will be assumed to be constant below Tg, and only dependent on temperature. Others have shown that under certain circumstances, χ is effectively independent of temperature.32 However, in this work we have elected to use the temperature dependence from the lattice model used in Flory–Huggins solution theory:46,47
Lastly, we also assume that χ is independent of composition, though we will revisit that assumption in future work. Thus, we can treat the Flory–Huggins parameter χ(T) as a piece-wise function as done in ref. 22:
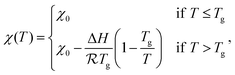 | (3) |
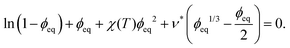 | (4) |
Further, the conservation of starch inside the granule requires that:
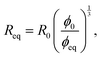 | (5) |
3.2 Kinetics of granule swelling (diffusion equation)
When a starch granule is heated, gelatinization occurs. During this process, the difference in water's chemical potential between the outside and inside of the granule leads to mass transfer of water into the granule. This process occurs until the granule reaches chemical equilibrium. The temporal evolution of chemical potential of water inside a spherical granule μ1 can be described by a diffusion equation:22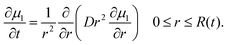 | (6) |
The chemical potential μ1 is related to the local starch volume fraction ϕ(r,t) through the Flory–Rehner equation (eqn (2)). The starch volume fraction is related to the granule size R(t) through conservation of mass:
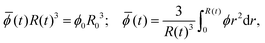 | (7) |
![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) is the average starch volume fraction in the granule. Lastly, the effective diffusivity D is assumed to have a dependence on temperature that follows the Arrenhius equation, as well as a dependence on the porosity and tortuosity45,48 as follows:
is the average starch volume fraction in the granule. Lastly, the effective diffusivity D is assumed to have a dependence on temperature that follows the Arrenhius equation, as well as a dependence on the porosity and tortuosity45,48 as follows: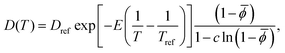 | (8) |
![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) = 0),44 and can be regarded as constants in the model. The effective diffusivity is taken to be proportional to the porosity (1 −
= 0),44 and can be regarded as constants in the model. The effective diffusivity is taken to be proportional to the porosity (1 − ![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) ) and inversely proportional to tortuosity as is commonly done in a Darcy model of a porous medium, and the tortuosity is related to porosity according to an empirical model proposed in ref. 45, and here we set c = 0.77 as done in that work.
) and inversely proportional to tortuosity as is commonly done in a Darcy model of a porous medium, and the tortuosity is related to porosity according to an empirical model proposed in ref. 45, and here we set c = 0.77 as done in that work.
We assume that the temperature inside the starch granule is uniform and equal to the outside water temperature. This assumption is reasonable when the Lewis number (ratio of thermal diffusivity to mass diffusivity) is very large, as is expected here. In other words, the timescale of heat transfer is much smaller than that of molecular diffusion of water. Thus, the temperature equation describing the heat conduction in the granule is neglected in this study, and thermal equilibrium is assumed throughout the process. In turn, this means that the kinetics of swelling (as opposed to the equilibrium effects) can only be governed by mass transfer.
The following dimensionless variables are adopted to re-write eqn (6)–(8):
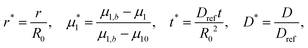 | (9) |
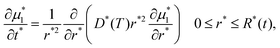 | (10) |
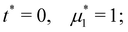 | (11) |
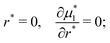 | (12) |
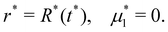 | (13) |
The chemical potential is related to the volume fraction through the Flory equation. In dimensionless form, we have:
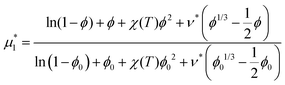 | (14) |
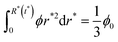 | (15) |
3.3 Simulation details
All the simulations are performed using Python on a laptop with Intel(R) Core(TM) i7-9750H CPU@2.60 GHz and 16.0 GB RAM. In the calculation, dimensionless eqn (10) subject to the conditions in eqn (11)–(13) are solved firstly by adopting an implicit finite difference method: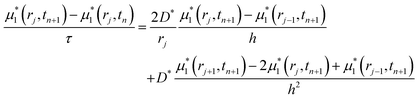 | (16) |
Given a radius R*(tn) and diffusion D*(tn) at time tn, we compute the chemical potential 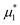 at time tn+1 using the implicit finite difference method in eqn (16). With the chemical potential
at time tn+1 using the implicit finite difference method in eqn (16). With the chemical potential 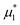 obtained from eqn (10), Flory–Rehner theory eqn (2) is utilized to obtain the starch volume fraction ϕ at time tn+1 by using the “root” function from the scipy module in Python. The average starch volume fraction
obtained from eqn (10), Flory–Rehner theory eqn (2) is utilized to obtain the starch volume fraction ϕ at time tn+1 by using the “root” function from the scipy module in Python. The average starch volume fraction ![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) (t*) at time tn+1 is calculated as:
(t*) at time tn+1 is calculated as:
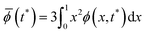 | (17) |
![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) (t*) into eqn (7), the starch granule size R*(tn+1) at time tn+1 is obtained. We compute D*(tn+1) using eqn (8), and replace the diffusion coefficient D*(tn) in eqn (10) and granule size R*(tn) in eqn (13) with the new D*(tn+1) and R*(tn+1). Having computed all quantities at tn+1 and updated all equations, we repeat the procedure to compute quantities at the next time step tn+2, and so on. Thus, an iteration is constructed until the size of starch granule at a set time is acquired. The parameter values that are not changed in any of the simulations are given in Table 1 and reflect the values in ref. 22. The default values for all other parameters, when not being varied for analysis, are given in Table 2.
(t*) into eqn (7), the starch granule size R*(tn+1) at time tn+1 is obtained. We compute D*(tn+1) using eqn (8), and replace the diffusion coefficient D*(tn) in eqn (10) and granule size R*(tn) in eqn (13) with the new D*(tn+1) and R*(tn+1). Having computed all quantities at tn+1 and updated all equations, we repeat the procedure to compute quantities at the next time step tn+2, and so on. Thus, an iteration is constructed until the size of starch granule at a set time is acquired. The parameter values that are not changed in any of the simulations are given in Table 1 and reflect the values in ref. 22. The default values for all other parameters, when not being varied for analysis, are given in Table 2.
| Parameter | Value |
|---|---|
| ϕ 0 | 0.586 |
| R 0 | 3 × 10−5 m |
| D ref | 3.98 × 10−9 m2 s−1 |
| T ref | 323 K |
| Parameter | Value |
|---|---|
| ν ∞ | 0.012 |
| a | 0.5 K−1 |
| T 0 | 323 K |
| T g | 339 K |
| ΔH | 1.35 × 104 J mol−1 |
| χ 0 | 0.497 |
| c | 0.9 |
4 Results and discussions
4.1 Missing physics in standard Flory–Rehner theory
In the process of validating the theory outlined in Section 3, we observed a non-physical result that stems from the Flory–Rehner portion of the model. In this section, we present the results of some of the simulations of granule swelling (radius vs. time) that illustrate the deficiency of the model. In each of the simulations in this section we examined a starch granule with the physical parameters listed in Table 1 and a gelatinization temperature of Tg = 339 K. The granule was exposed to a temperature profile that increased linearly in time as T = T0 + bt, with four different heating rates b, from an initial temperature T0 = 323 K to a final temperature Tf = 363 K where the temperature was then held steady.In Fig. 1(a), we see that the granule size undergoes two distinct stages. The first stage occurs when T < Tg and the granule swells rapidly to an intermediate size and then stops increasing. The second stage occurs when T > Tg and the granule swells again to its final size corresponding to the equilibrium size at T = Tf. In experiments, only the second stage is observed, and to our knowledge previous modeling efforts have also only shown the second stage (e.g., ref. 22). However, stage 1 shown here using the same physics as ref. 22, is inconsistent with experiments, as granule swelling should not occur appreciably below the gelatinization temperature.
To illustrate what is happening in stage 1 more clearly, we plot the average starch volume fraction ![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) (t*) vs. time in Fig. 1(b) for two of the heating rates. Fig. 1(b) reveals that the volume fraction will drop rapidly from the given initial value ϕ0 to a steady state value before the gelatinization temperature is reached. This suggests that the specified initial starch volume fraction of the granule does not correspond to the equilibrium value calculated from Flory–Rehner theory for temperatures below the gelatinization temperature.
(t*) vs. time in Fig. 1(b) for two of the heating rates. Fig. 1(b) reveals that the volume fraction will drop rapidly from the given initial value ϕ0 to a steady state value before the gelatinization temperature is reached. This suggests that the specified initial starch volume fraction of the granule does not correspond to the equilibrium value calculated from Flory–Rehner theory for temperatures below the gelatinization temperature.
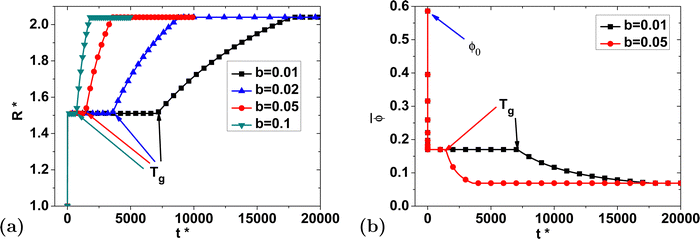
To verify that the initial volume fraction does not correspond to an equilibrium condition, we plot the equilibrium starch volume fraction ϕeq as a function of temperature in Fig. 2(a). The values of ϕeq in this plot are calculated from the Flory–Rehner theory using eqn (4). The data show that below the gelatinization temperature T < Tg the equilibrium starch volume fraction is constant at ϕeq ≈ 0.17, which is much smaller than typical initial conditions of ϕ0 > 0.5 (and ϕ0 = 0.586 in this case) and hence drives strong swelling. In actuality, the equilibrium volume fraction for T < Tg should be very close to ϕ0 so that no appreciable swelling will be observed.
Before jumping to the conclusion that this points to a flaw in the theory, it is important to determine if this discrepancy is simply the result of poorly chosen material parameters (e.g., Table 1). To check this, we examined the effect of the two material parameters that influence ϕeq at T0: the density of cross-links ν* and the starch–water interaction parameter χ0. Fig. 2(b) shows that ϕeq at T0 is rather insensitive to χ0, but quite sensitive to ν*. However, we found that if ν* is adjusted so that ϕeq = ϕ0 at T0, swelling is severely restricted and it is not possible to reach realistic values of the final volume fraction. Thus, we can conclude that there is a deeper problem with the use of Flory–Rehner theory for this application.
We propose that the problem with the standard Flory–Rehner model is that it is likely a missing piece of the underlying physics. Generally, Flory swelling theories assume constant material properties (e.g., ν* and χ0 are constant), while in reality the cross-link density in a starch granule, ν*, may decrease during swelling as some of the physical cross-links break, which break much more easily than chemical cross-links. In turn, the starch–water interaction parameter, χ0, could also change since more starch–water sites would be exposed as the cross-links break. We assume that from a microstructural viewpoint, the granule can be considered to appear initially as a tightly-packed polymer glass that undergoes a phase transition to become a loosely-packed polymer network as the degree of gelatinization increases.38,39
With this physical picture of a granule that undergoes a phase transition, it makes sense that a single cross-link density would be incapable of accurately describing the polymer network both before and after gelatinization as shown in Fig. 2. Specifically, if we fix χ0 = 0.497, the cross-link density that results in the correct initial volume fraction for T < Tg is ν* = 0.23. Similarly, the cross-link density that results in the correct final volume fraction after gelatinization at 363 K is ν* = 0.0042. Therefore, we hypothesize that a simple modification to the Flory–Rehner theory that allows for a variable value of the cross-link density will allow us to qualitatively capture granule swelling from the unswollen size to the final granule size.
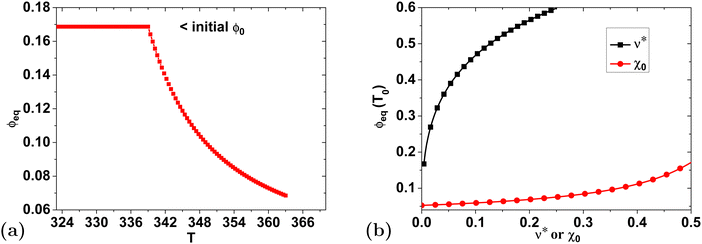
Here, we will test this hypothesis by examining four of the simplest possible dependencies of the cross-link density on temperature. These four functional relationships are depicted in Fig. 3(a) and given by:
(1) a step function
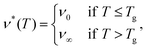 | (18) |
(2) a linear function
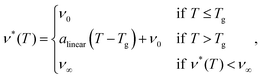 | (19) |
(3) a negative exponential function
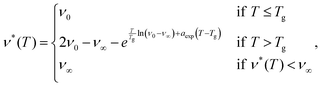 | (20) |
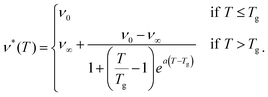 | (21) |
In these four empirical models Tg is the gelatinization temperature, ν0 is the cross-link density at T < Tg that sets the initial starch volume fraction ϕ0, ν∞ is the cross-linking density that sets the equilibrium swelling at the final temperature T = Tf, and alinear, aexp, and a are free parameters to be determined.
The advantage of these four models is that they have at most one free parameter that cannot be determined from material properties alone. The functions were chosen in such a way that they have increasing smoothness of the transition between different cross-link densities. Also, all of the models are designed to produce a relatively sharp transition in the cross-link density after T > Tg since prior work showed a reasonable agreement for the latter stages of granule swelling with a constant value of the cross-link density equal to ν∞.22Fig. 3(b) shows how each of these four models influences the equilibrium starch volume fraction ϕeq as a function of temperature.
4.2 Comparison of modified theory to experimental results
Next, we examined the ability of each of the four empirical models for cross-link density (eqn (18)–(21)) to improve the accuracy of the numerical simulations of granule swelling. In Fig. 4, we study how the four different models compare against granule swelling data from literature. In ref. 19, gelatinization of individual starch granules from four types of legume starches (chickpea, red bean, green lentil, and yellow pea) was observed, and it was shown that all of the data from hundreds of granules of each type could be described by a universal curve (after appropriate normalization). We will first attempt to validate our model against these dynamic swelling measurements.In the experiments, the heating was done via a quadratic function of time as follows:
| T = T0 + T1t − T2t2 | (22) |
 | (23) |
Based on the comparison between simulations and data in Fig. 4, we can conclude that, indeed, allowing for the cross-link density to vary with temperature results in a significant improvement in the ability of the simulations to capture the dynamics of granule swelling. However, Flory–Rehner is inherently an equilibrium theory and therefore it is important to also compare this modification against equilibrium granule swelling. To do this we measured the equilibrium granule size as a function of temperature for 12 individual red-bean, starch granules that all had a similar swelling ratio (see Section 2.2). Because we do not have a way of directly measuring the initial starch volume fraction, we assumed that all granules start with an equilibrium starch volume fraction of 0.586. We then calculated the equilibrium starch volume fraction as a function of temperature and the results of these measurements are shown in Fig. 5.
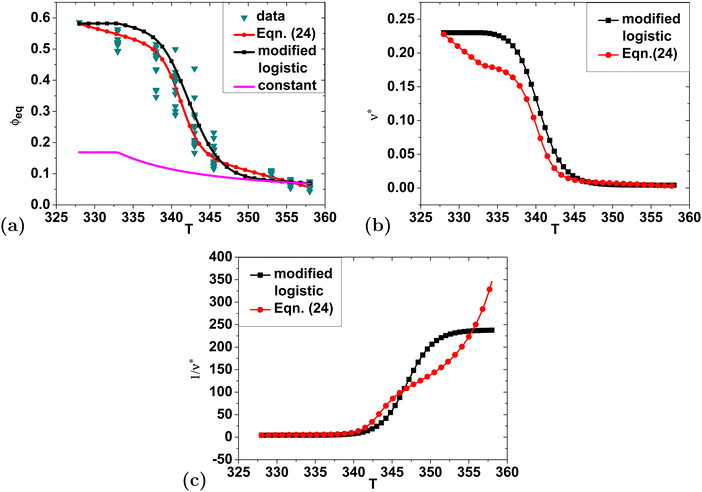 | ||
| Fig. 5 (a) Comparison between experimental values of the equilibrium volume fraction of red bean starch granules (labeled as “data” in the legend) and the prediction of three different models. The experimental data correspond to 12 different granules. (b) and (c) Comparison of ν*(T) and 1/ν*(T) from the modified logistic function and eqn (24) fit to the data. Note, the free parameters used in the modified logistic function shown here correspond to the best fit for a swelling ratio of 2.15 to match the data set. | ||
As with the dynamic data from simulations, it is clear from Fig. 5(a) that the Flory–Rehner theory with a constant cross-link density is unable to adequately describe the data. However, it is also evident that a modified logistic function for the cross-link density is not a perfect fit either. Therefore, we also proposed the following fitting function for describing the data with a relatively simple analytical expression:
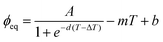 | (24) |
By substituting this fitting function (eqn (24)) into eqn (4), we can also back-calculate ν*(T) to compare it to the modified logistic function for the cross-link density as shown in Fig. 5(b) and (c). As with a comparison of ϕeq(T), the data do not agree perfectly with the modified logistic function and the inherent differences in the functional form cause large differences in cross-link density both at low and high temperature. However, the data do support the idea that the current Flory–Rehner theory is inadequate and that using a variable cross-link density that varies sigmoidally with temperature is a significant improvement. Interestingly, the degree of gelatinization for rice starch was also found to vary sigmoidally with temperature through DSC experiments,37 though in that work it is unclear if the sigmoidal character is related to the phase transition or due to intrasample variability (see ref. 19 for a discussion of intrasample variability).
Although, it would not be feasible as a general strategy, we also attempted to use eqn (24) directly for the simulations to see if this resulted in better predictions of the dynamics of swelling. To do this, we used the values of ν*(T) calculated from eqn (24) in the swelling simulations. Fig. 6 shows the results of this simulation and from this we learn the following. First, the swelling dynamics are extremely sensitive to minor variations in the value of ν* at later stages of swelling, as evidenced by the differences in the shape of the swelling curve for temperatures above 340 K where the differences in ν* are small between the data and the logistic function. We also learn that, in contrast to the effect at higher temperatures, very large differences in the value of ν* make only a small difference at lower temperatures when swelling is just beginning to occur.
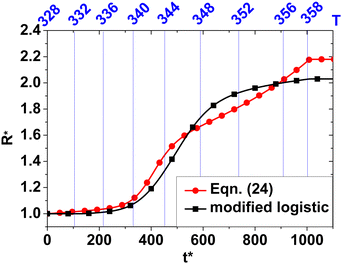 | ||
| Fig. 6 Comparison of the swelling process simulated using the modified logistic function for ν* with the swelling process simulated using eqn (24). | ||
In summary, we have considered multiple options for correcting the missing physics in the model. It is clear that a variable cross-link density is necessary and that the modified logistic function captures this in a way that produces realistic swelling dynamics. Therefore, we conclude that it is reasonable to proceed to perform simulations where ν* varies sigmoidally with temperature and in the remainder of this paper will use the modified logistic function in all simulations.
4.3 Relationship between modified Flory model and experimental master curve
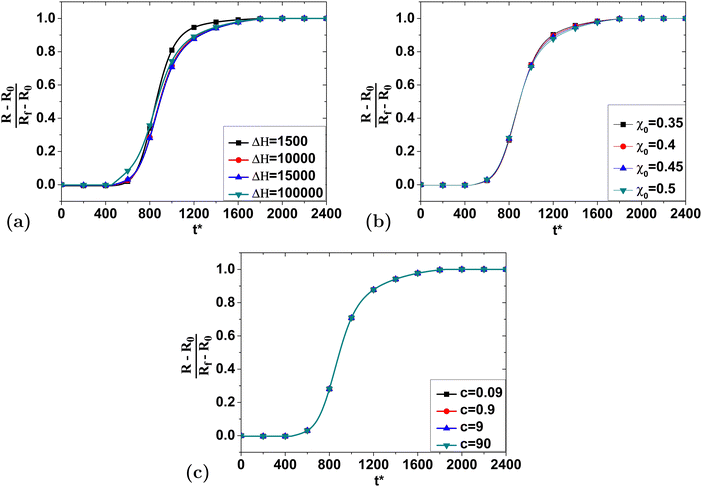
As discussed in the previous section, we determined that by using a modified logistic function for the cross-link density ν*(T) in the Flory–Rehner swelling model, one can reasonably predict dynamic experimental swelling data. In a previous paper, we also found that for a given heating profile (eqn (22)), the experimental swelling data for four types of starch granules follow a universal curve with only two empirical parameters: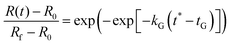 | (25) |
In the sections that follow, we will systematically vary the parameters, one at a time, and generate dynamic swelling curves. We will then attempt to collapse the resultant numerical data onto a master curve by shifting the time and/or rescaling the time according to eqn (25) in order to collapse the numerical data onto a master curve. Finally, we will examine the relationship between the empirical parameters and the theoretical parameters to determine what relationship may exist between them. Ideally, such relationships will be obtained as some specific, but as yet unknown, mathematical functions as follows:
| tG = f(a,ν∞,ϕ0,Tg,T0,ΔH,χ0,c) | (26) |
| kG = g(a,ν∞,ϕ0,Tg,T0,ΔH,χ0,c) | (27) |
The inability to collapse the curves can be interpreted in at least two ways. First, it may suggest that the empirical function obtained in ref. 19 may not be applicable to all starches. Second, it may suggest that there is only one value of a that is physically realistic. However, recall that a is not based on a known material property and instead only used to smoothly vary the cross-link density as a function of temperature. Therefore, we elect to proceed in our analysis by adopting the latter interpretation and assume that a must be selected such that the swelling curve has the same qualitative shape as eqn (25).
Next we recall that in Section 4.2 we found that the optimal value of a was different for different values of ν∞. From this we assume that a is a function of ν∞ alone and determine this relationship by obtaining the best fit for a at four different values of ν∞ as shown in Fig. 7(c). From the results in Fig. 7(c), we find that the relationship between the optimal value of a and ν∞ can be approximated by the following power-law function:
| a = 0.341ν∞−0.0750 | (28) |
To illustrate the impact of varying ν∞, we have replotted the data from Fig. 7(d), without rescaling the granule radius, in Fig. 8(a). As expected, we see that the final granule radius is directly controlled by the final cross-link density. Plotting the value of ν∞ as a function of the swelling ratio Rf/R0 in Fig. 8(b), we find that it is also possible to approximate their relationship using another power-law function:
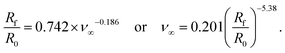 | (29) |
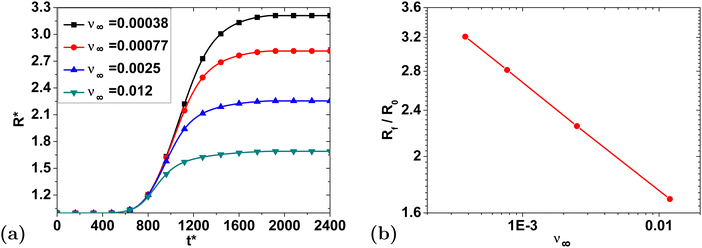 | ||
| Fig. 8 (a) Swelling curves from Fig. 7(d) replotted to show the impact of ν∞ on the dimensionless radius. (b) Swelling ratio vs. ν∞ on log–log axes. | ||
The final parameter that is involved in the cross-link density is the initial starch volume fraction ϕ0. Fig. 9(a) shows the swelling curves when ϕ0 changes from 0.5 to 0.65 when ν∞ = 0.012. The results show only slight differences, revealing that ϕ0 has little impact on the swelling process. Applying a time shift, these curves collapse very well, as presented in Fig. 9(b). When the same time shifting procedure is applied at different values of ν∞, Fig. 9(c) shows how the required time shift varies with ϕ0 in each case.
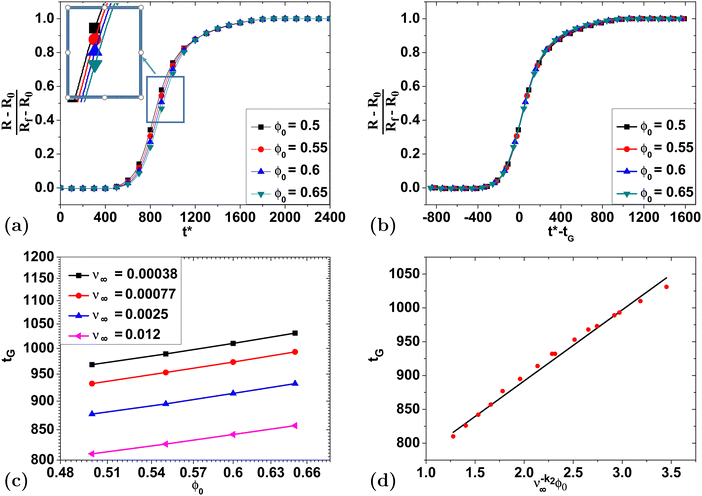 | ||
| Fig. 9 (a) Swelling curves simulated for various values of ϕ0 for a swelling ratio of 1.69 (ν∞ = 0.012). (b) Illustration of the collapse of the curves from (a) by changing tG. (c) Illustration of the optimal values of tG needed to collapse the swelling curves for different values of ϕ0 at different values of ν∞ on log–log axes. (d) Data in (c) collapsed onto a single curve given by eqn (31). | ||
From the data in Fig. 9(c), we find that tG appears to depend linearly on ϕ0 and, after examining the best fits to a line at different values of ν∞, we see that the dependence of both parameters is well approximated by the following type of function:
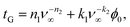 | (30) |
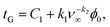 | (31) |
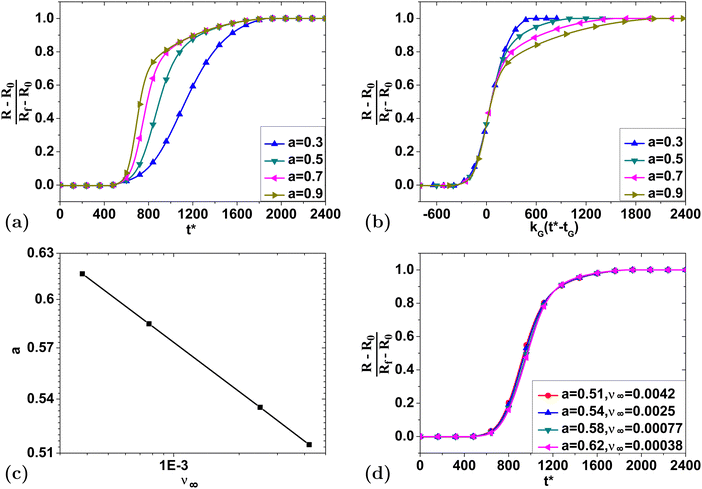
As in Section 4.3.1, we see that the time shift required to collapse the curves depends both on the gelatinization temperature and the cross-link density as shown in Fig. 10(c). Quantitatively, we find that the relation between tG and Tg can be well described by a second order polynomial where the prefactors each may depend on ν∞ as follows:
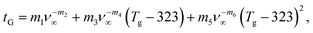 | (32) |
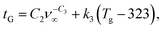 | (33) |
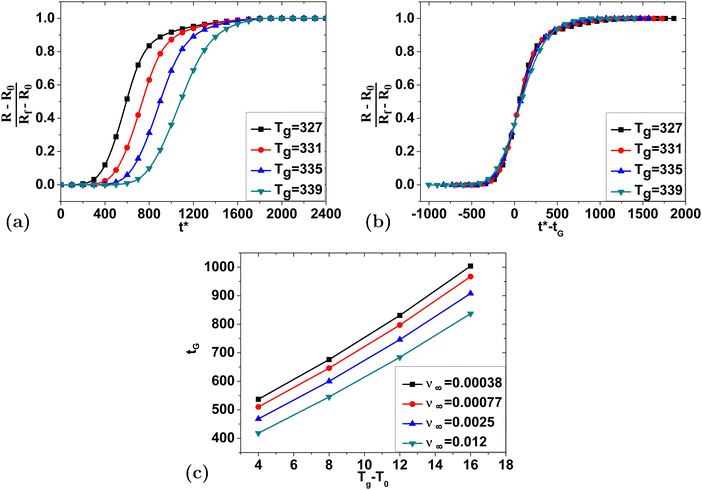
Next, we vary the initial temperature T0 while holding the gelatinization temperature at Tg = 339 K. Fig. 11(a) reveals the influence of initial temperature T0 on the swelling process. Similar to Tg, changes in T0 also only require time shifts to collapse onto a single curve in as shown in Fig. 11(b). Fig. 11(c) also reveals a very similar relationship between tG and Tg (refer to Fig. 10(c)).
Therefore, we again find that the same type of second order polynomial in eqn (34) fits the data very well:
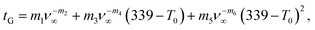 | (34) |
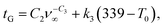 | (35) |
From the best fit parameters to eqn (33) and (35), we observe that the dependence of tG is very similar for the same difference between Tg and T0. For this reason, both Fig. 10(c) and 11(c) were plotted versus the temperature difference Tg − T0, even though in each case one of the two values was held constant. Given the high degree of similarity when varying the two parameters independently, we combined all of the data from both cases and fit them to the following function:
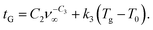 | (36) |
4.4 Summary of parametric analysis
In Section 4.3 we hypothesized that the empirical parameters that can be used to scale and shift the swelling data to produce a universal curve could be predicted from material properties and written as some function of the material parameters:| tG = f(ν∞,ϕ0,a,Tg,T0,ΔH,χ0,c) | (37) |
| kG = g(ν∞,ϕ0,a,Tg,T0,ΔH,χ0,c). | (38) |
Looking at the remaining parameters we see that none of them influence kG, suggesting that the timescale of gelatinization is entirely determined by the diffusive time scale. This is interesting, because it suggests that by fitting experimental data, one can obtain an estimate of the diffusion coefficient that is relevant to gelatinization. In turn, this will help determine if assumptions in our model about the diffusivity are correct. This will be the subject of future work.
Further, tG was found to be adequately described by a linear dependence on ϕ0 and (Tg − T0) with a slope and an intercept, respectively, that depend on ν∞, which in turn depends on the swelling ratio. Thus, we can now revise eqn (37) and (38) to be:
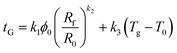 | (39) |
| kG = 1. | (40) |
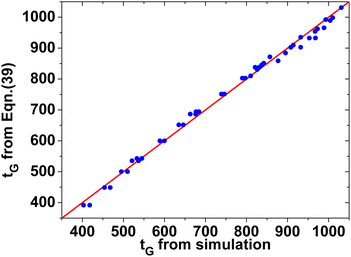 | ||
| Fig. 13 The accuracy of eqn (39) by comparing its prediction for tG with those from simulation. | ||
Finally, we return to the functional dependence of the cross-link density on temperature. We found that there appears to be a power-law dependence of the parameter a on ν∞ (eqn (28)), and hence on the swelling ratio. This means that we can rewrite the modified logistic function as follows:
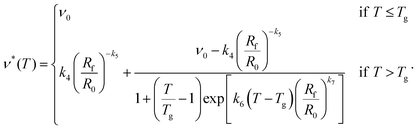 | (41) |
4.5 Influence of heating rate and heating function
As a final point of discussion, we wish to point out that the specific shape of the swelling curve must depend on the way in which the temperature of the system increases with time. This is a noteworthy point because our comparisons were done with experimental swelling data obtained where the temperature was increased quadratically with time, and other researchers might instead increase the temperature linearly with time. In Fig. 14, we have compared the swelling curves from simulations in which the temperature was increased linearly with time as T = 323 + bt at different rates, b in K s−1, against the original parabolic heating function used in ref. 19. In each case, two different values of the swelling ratio were used.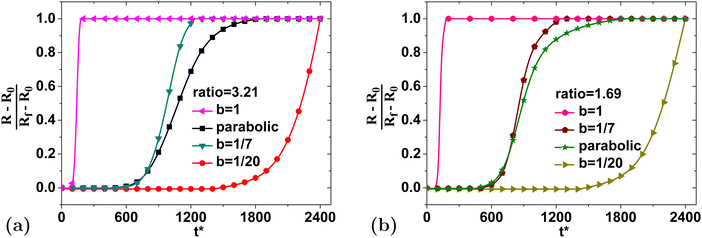 | ||
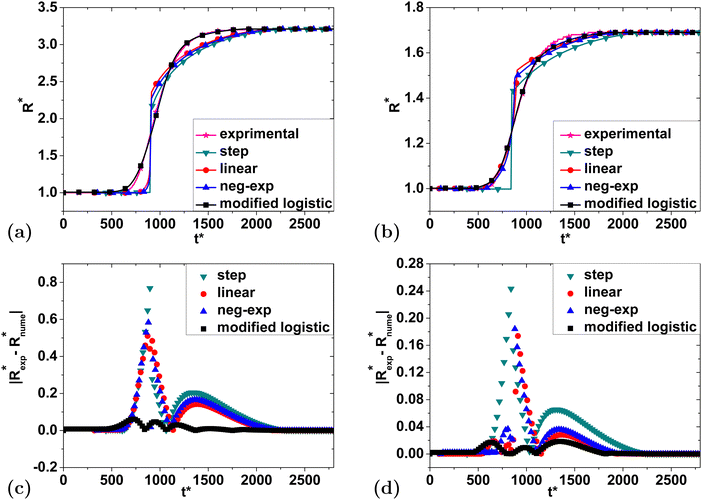
| Fig. 14 Comparison of the effect of the heating rate on the functional form of the swelling curve. Note that the parameter b corresponds to the linear heating ramp T = 323 + bt, while the parabolic profile refers to heating using eqn (22). The results from two different swelling ratios are shown: (a) Rf/R0 = 3.21 and (b) Rf/R0 = 1.69. | ||
As expected, using different heating functions and rates has a large impact on the shape of the swelling curve. Even a slight difference in the heating function will result in different shapes of the swelling curve and the ability to collapse the data onto the function found in ref. 19 is clearly a special case. Nevertheless, the convenience of the functional dependence found in ref. 19 has allowed us to make substantial progress in understanding which material properties will influence the swelling process. Further, if other researchers utilize the same heating function, the present analysis will likely enable them to extract material properties directly from swelling data.
5 Conclusion
In this work we used numerical simulations based on a first-principles model of the swelling of starch granules to help understand a previously published experimental result19 in which a universal curve was seen for the granule size as a function of time. While validating the governing equations for the simulations, we found that the standard Flory–Rehner theory used in previous work22 was ill-suited to simulating the initial stages of starch swelling near the gelatinization temperature. However, we concluded that with a minor modification, in which we allow the fraction of cross-linked chains in the granule to decrease as temperature increases, that the Flory–Rehner theory can be used to successfully predict the swelling process of legume-starch granules.Using the modified theory and systematically varying the model parameters, we found that the granule size as a function of time from numerical simulations can also be collapsed onto the same master curve found in experiments. We presented a simple relationship between the empirical scaling and shifting parameters used in experiments and the material properties used in the modified theory. Of particular note is that once the time is non-dimensionalized by the diffusion time scale, no further rescaling is needed to collapse the swelling data. Changes to all other model parameters only require a shift in the time, to collapse the swelling data.
In summary, this is the first study to demonstrate that the swelling of individual starch granules during gelatinization can be described by a universal function that is generated from first-principles. This will enable future experiments with granule swelling to extract material properties such as the diffusivity, gelatinization temperature, and initial starch volume fraction for individual starch granules. Further, the framework we developed will lend itself well to exploring the utility of using more sophisticated variants of the Flory theory in future work.32,34,36,40,41 Finally, this work will enable more accurate predictions of the behavior of starches during advanced processing operations, in which the gelatinization of starch is critical to the functional properties of the final product.
Author contributions
Botong Li: formal analysis; funding acquisition; software and validation; original draft. Lanxin Mo: experiment. Vivek Narsimhan: formal analysis; funding acquisition; methodology; review and editing. Ganesan Narsimhan: formal analysis; funding acquisition; methodology; review and editing. John M. Frostad: conceptualization; formal analysis; funding acquisition; methodology; project administration; original draft; review and editing.Data availability
The datasets supporting this article have been uploaded as part of ESI.†Conflicts of interest
The authors declare that they do not have any conflicts of interest.Acknowledgements
The author B. Li is grateful for the China Scholarship Council (202106465015). Authors G. Narsimhan, V. Narsimhan, and J. M. Frostad would like to acknowledge support from USDA-NIFA (grant 2024-67017-42557). J. M. Frostad is also grateful for support through funding from the Canada Foundation of Innovation John R. Evans Leaders Fund, the British Columbia Knowledge Development Fund, and the Discovery Grant Program of the Natural Sciences and Engineering Research Council of Canada (NSERC) (Grant No. RGPIN-2017-04466).References
- S. Wang and L. Copeland, Molecular disassembly of starch granules during gelatinization and its effect on starch digestibility: a review, Food Funct., 2013, 4(11), 1564–1580, 10.1039/C3FO60258C.
- L. Roy, Whistler and James N. BeMiller, Carbohydrate chemistry for food scientists, Eagan Press, 1997 Search PubMed.
- R. Hoover, The Impact of Heat-Moisture Treatment on Molecular Structures and Properties of Starches Isolated from Different Botanical Sources, Crit. Rev. Food Sci., 2010, 50(9), 835–847, DOI:10.1080/10408390903001735.
- S. Dhital, et al., Rice starch granule amylolysis – Differentiating effects of particle size, morphology, thermal properties and crystalline polymorph, Carbohydr. Polym., 2015, 115, 305–316, DOI:10.1016/j.carbpol.2014.08.091.
- P. Chen, et al., Morphology and Microstructure of Maize Starches with Different Amylose/Amylopectin Content, Starch-Stärke, 2006, 58(12), 611–615, DOI:10.1590/1981-6723.0516.
- N. Lindeboom, P. R. Chang and R. T. Tyler, Analytical, Biochemical and Physicochemical Aspects of Starch Granule Size, with Emphasis on Small Granule Starches: A Review, Starch-Stärke, 2004, 56(3–4), 89–99, DOI:10.1002/star.200300218.
- D. Lund and K. J. Lorenz, Influence of time, temperature, moisture, ingredients, and processing conditions on starch gelatinization, CRC Crit. Rev. Food Sci., 1984, 20(4), 249–273, DOI:10.1080/10408398409527391.
- Y. Liu, et al., Gelatinization behavior of starch: Reflecting beyond the endotherm measured by differential scanning calorimetry, Food Chem., 2019, 284, 53–59, DOI:10.1016/j.foodchem.2019.01.095.
- M. Beck, M. Jekle and T. Becker, Starch re-crystallization kinetics as a function of various cations, Starch-Stärke, 2011, 63(12), 792–800, DOI:10.1002/star.201100071.
- M. Schirmer, et al., Physicochemical and morphological characterization of different starches with variable amylose/amylopectin ratio, Food Hydrocolloids, 2013, 32(1), 52–63, DOI:10.1016/j.foodhyd.2012.11.032.
- M. Mariotti, et al., Effects of dispersing media and heating rates on pasting profiles of wheat and gluten-free samples in relation to their solvent retention capacities and mixing properties, LWT – Food Sci. Technol., 2016, 66, 201–210, DOI:10.1016/j.lwt.2015.09.041.
- M. Joshi, et al., Physicochemical and functional characteristics of lentil starch, Carbohydr. Polym., 2013, 92(2), 1484–1496, DOI:10.1016/j.carbpol.2012.10.035.
- M. S. Shang, et al., Effect of single and dual heat–moisture treatments on the gelatinization properties and crystalline structure of normal corn starch, Starch-Stärke, 2016, 68(11–12), 1196–1202, DOI:10.1002/star.201500350.
- T. J. Woodbury, et al., Mechanisms of the different effects of sucrose, glucose, fructose, and a glucose–fructose mixture on wheat starch gelatinization, pasting, and retrogradation, J. Food Sci., 2023, 88(1), 293–314, DOI:10.1111/1750-3841.16414.
- C. V. T. Rigueto, et al., Gelatin films from wastes: A review of production, characterization, and application trends in food preservation and agriculture, Food Res. Int., 2022, 162, 112114, DOI:10.1016/j.foodres.2022.112114.
- C. Li, Recent progress in understanding starch gelatinization – An important property determining food quality, Carbohydr. Polym., 2022, 293, 119735, DOI:10.1016/j.carbpol.2022.119735.
- G. P. Desam, et al., Prediction of swelling behavior of crosslinked maize starch suspensions, Carbohydr. Polym., 2018, 199, 331–340, DOI:10.1016/j.carbpol.2018.07.020.
- T. Zhang, et al., Gelatins as emulsifiers for oil-in-water emulsions: Extraction, chemical composition, molecular structure, and molecular modification, Trends Food Sci. Technol., 2020, 106, 113–131, DOI:10.1016/j.tifs.2020.10.005.
- L. Mo, J. Cheon and J. M. Frostad, Quantifying and modeling the gelatinization properties of individual pulse-starch granules by ParCS, Food Hydrocolloids, 2023, 135, 107896, DOI:10.1016/j.foodhyd.2022.107896.
- M. C. Allan, Q. D. Read and S. D. Johanningsmeier, Impact of sweetpotato starch structures, thermal properties, and granules sizes on sweetpotato fry textures, Food Hydrocolloids, 2023, 137, 108377, DOI:10.1016/j.foodhyd.2022.108377.
- A. Palanisamy, et al., Kinetic modelling of individual starch granules swelling, Food Struct., 2020, 26, 100150, DOI:10.1016/j.foostr.2020.100150.
- G. P. Desam, et al., A mechanistic model for swelling kinetics of waxy maize starch suspension, J. Food Eng., 2018, 222, 237–249, DOI:10.1016/j.jfoodeng.2017.11.017.
- P. J. Flory and J. Rehner, Statistical Mechanics of Cross-Linked Polymer Networks II. Swelling, J. Chem. Phys., 1943, 11(11), 521–526, DOI:10.1063/1.1723792.
- P. J. Flory, Statistical Mechanics of Swelling of Network Structures, J. Chem. Phys., 1950, 18(1), 108–111, DOI:10.1063/1.1747424.
- Y. Zhao and B. E. Eichinger, Study of solvent effects on the dilation modulus of poly(dimethylsiloxane), Macromolecules, 1992, 25(25), 6988–6995, DOI:10.1021/ma00051a041.
- Z.-Y. Lu and R. Hentschke, Swelling of model polymer networks with different crosslink densities: A computer simulation study, Phys. Rev. E:Stat., Nonlinear, Soft Matter Phys., 2002, 66(4), 041803, DOI:10.1103/PhysRevE.66.041803.
- C. Du and R. J. Hill, Swelling and Dissolution Transitions of DNA- and “Bis”-Cross-Linked Polyacrylamide, Macromolecules, 2020, 53(12), 4845–4854, DOI:10.1021/acs.macromol.0c00471.
- J. Li, et al., Methodology to predict the time-dependent storage modulus of starch suspensions during heating, Food Hydrocolloids, 2021, 113, 106463, DOI:10.1016/j.foodhyd.2020.106463.
- I. D. Evans and D. R. Haisman, The Effect of Solutes on the Gelatinization Temperature Range of Potato Starch, Starch-Stärke, 1982, 34(7), 224–231, DOI:10.1002/star.19820340704.
- M. Milene, et al., Physical and chemical properties of starch and flour from different common bean (Phaseolus vulgaris L.) cultivars, Braz. J. Food Technol., 2016, 19, e2016005 Search PubMed.
- D. T. Do, et al., A novel apparatus for time-lapse optical microscopy of gelatinisation and digestion of starch inside plant cells, Food Hydrocolloids, 2020, 104, 105551, DOI:10.1016/j.foodhyd.2019.105551.
- R. G. M. van der Sman and M. B. J. Meinders, Prediction of the state diagram of starch water mixtures using the Flory–Huggins free volume theory, Soft Matter, 2011, 7(2), 429–442, 10.1039/C0SM00280A.
- R. G. M. van der Sman and M. B. J. Meinders, Moisture diffusivity in food materials, Food Chem., 2013, 138(2), 1265–1274, DOI:10.1016/j.foodchem.2012.10.062.
- R. G. M. van der Sman, Predicting the solubility of mixtures of sugars and their replacers using the Flory–Huggins theory, Food Funct., 2017, 8(1), 360–371, 10.1039/C6FO01497F.
- R. G. M. van der Sman, Effects of viscoelasticity on moisture sorption of maltodextrins, Food Hydrocolloids, 2023, 139, 108481, DOI:10.1016/j.foodhyd.2023.108481.
- R. G. M. van der Sman, M. Curatolo and L. Teresi, Pore development in viscoelastic foods during drying, Soft Matter, 2024, 20(26), 5183–5194, 10.1039/D4SM00201F.
- A. Briffaz, et al., Modelling starch phase transitions and water uptake of rice kernels during cooking, J. Cereal Sci., 2013, 58(3), 387–392, DOI:10.1016/j.jcs.2013.08.001.
- M. Alan and R. W. Hausslein, Elastic factors controlling sorption and transport properties of polyethylene, J. Polym. Sci., Part C, 1965, 10(1), 61–86 CrossRef.
- M. Alan and R. W. Hausslein, Elastic constraints in solvent swollen polyethylene, J. Polym. Sci., Polym. Lett. Ed., 1965, 3(1), 61–62 CrossRef.
- R. G. M. van der Sman, Biopolymer gel swelling analysed with scaling laws and Flory–Rehner theory, Food Hydrocolloids, 2015, 48, 94–101, DOI:10.1016/j.foodhyd.2015.01.025.
- W. Hong, Z. Liu and Z. Suo, Inhomogeneous swelling of a gel in equilibrium with a solvent and mechanical load, Int. J. Solids Struct., 2009, 46(17), 3282–3289, DOI:10.1016/j.ijsolstr.2009.04.022.
- C. Cai and C. Wei, In situ observation of crystallinity disruption patterns during starch gelatinization, Carbohydr. Polym., 2013, 92(1), 469–478, DOI:10.1016/j.carbpol.2012.09.073.
- W. David, et al., Characterizing internal cavity modulation of corn starch microcapsules, Heliyon, 2020, 6(10), e05294 CrossRef PubMed.
- A. J. Easteal, W. E. Price and L. A. Woolf, Diaphragm cell for hightemperature diffusion measurements. Tracer Diffusion coefficients for water to 363 K, J. Chem. Soc., Faraday Trans. 1, 1989, 85(5), 1091–1097, 10.1039/F19898501091.
- M. Matyka, A. Khalili and Z. Koza, Tortuosity-porosity relation in porous media flow, Phys. Rev. E:Stat., Nonlinear, Soft Matter Phys., 2008, 78(2), 026306, DOI:10.1103/PhysRevE.78.026306.
- P. J. Flory, Principles of polymer chemistry, Cornell University Press, 1953 Search PubMed.
- M. Rubinstein and R. H. Colby, Polymer Physics, Oxford University Press, USA, 2003 Search PubMed.
- J. J. M. Swinkels, Composition and Properties of Commercial Native Starches, Starch-Stärke, 1985, 37(1), 1–5, DOI:10.1002/star.19850370102.
- J. A. Nelder and R. Mead, A Simplex Method for Function Minimization, Comput. J., 1965, 7(4), 308–313, DOI:10.1093/comjnl/7.4.308.
- M. Wright, Direct search methods: Once scorned, now respectable. English (US), in Numerical analysis, ed. D. F. Griffiths and G. A. Watson, Addison-Wesley, 1996, pp. 191–208 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sm00980k |
| This journal is © The Royal Society of Chemistry 2025 |