Mechano-diffusion of particles in stretchable hydrogels

Abstract

Precise control over particle diffusion is promising for diverse modern technologies. Traditionally, particle diffusion is governed by the inherent properties of a liquid medium, limiting versatility and controllability. Here, we report a mechano-diffusion mechanism that harnesses mechanical deformation to control particle diffusion in stretchable hydrogels with a significantly enlarged tuning ratio and a highly expanded tuning freedom. The working principle is to leverage the mechanical deformation of stretchable hydrogels for modulating the polymer network's geometric transformation and the polymer chain's energy modulation, which synergistically tunes the energy barrier for particle diffusion. Using a model particle-hydrogel material system and a customized mechano-diffusion characterization platform, we demonstrate that tension loads can enhance the diffusivity of gold nanoparticles up to 22 times, far exceeding that in traditional liquid medium and by external fields. Additionally, we show particle diffusion in hydrogels can be manipulated spatiotemporally by controlling the hydrogels’ stress state and loading rate. To further push the limit of the mechano-diffusion, we use experiment, theory, and simulation to explore particle diffusion in biaxially stretched hydrogels, simultaneously expanding the mesh size and reducing the energy barrier. The enlarged tuning ratio and expanded tuning freedom enable a model-guided drug delivery system for pressure-controlled release of drug molecules. Understanding this spatiotemporal mechano-diffusion mechanism will provide insights pertinent to a broad range of biological and synthetic soft materials.

---

1. Introduction

The movement of particles such as biomacromolecules, gold nanoparticles, and quantum dots from one location to another, broadly impacts many fundamental processes in life science and physical systems. On one hand, particle diffusion plays a critical role in maintaining the function and survival of living organisms with examples such as intracellular transport,^1,2 mucus clearance,³ and cytoplasmic streaming.^4,5 On the other hand, technologies that facilitate nanoparticle diffusion with high efficiency, specificity, and tunability have shown promising applications in drug delivery,^6,7 water treatment,^8,9 and in situ biosensing.^10,11

The diffusion of particles is typically characterized by their diffusivity (D), which describes the rate of particles moving from high–concentration regions to low–concentration regions within a liquid medium. Traditionally, the particle diffusivity is governed by the liquid medium's viscosity and temperature, following the Stokes–Einstein equation.^12,13 However, controlling particle diffusion in liquid media presents two main challenges. First, the temperature variation for a specific liquid medium is often narrow,¹⁴ limiting the range of achievable particle diffusivities. For example, in aqueous solutions of biomedical or environmental applications, the temperature range of 273 to 373 K results in only a 2.4-fold difference in diffusivity.¹⁵ Second, the spatially uniform viscosity and temperature across the liquid medium do not allow for precise manipulation of specific diffusion directions or complex diffusion patterns.

In contrast, solid materials such as polymers, elastomers, and hydrogels can sustain mechanical stress without flowing, allowing them to be deformed under mechanical load. Hydrogels, as polymer networks infiltrated with a large quantity of water molecules, are particularly effective for transporting particles in aqueous environments.^16–20 Different from the diffusion of particles in liquid medium, the diffusion of particles in hydrogels is dominated by the confinement from polymer networks.^19–21 Applying mechanical deformation to hydrogels offers unique capabilities for modulating particle diffusion, surpassing the limitation of liquid medium. These capabilities include a broader spectrum of diffusivities, directional movement of particles, and triggered release of particles in response to mechanical cues. In particular, recent developments of tough^22,23 and fatigue-resistant^24–26 hydrogels enable the potential to further push the limit of particle diffusion tuning by leveraging their superior mechanical properties. The ability to apply mechanical deformation to these hydrogels with varying magnitude, direction, and timing provides vast possibilities for engineering particle diffusion. Despite this promise, the effects of mechanical deformation on particle diffusion in hydrogels remain largely unexplored. The existing understanding of strain-dependent diffusivity in hydrogels is mainly attributed to strain-induced geometrical transformation^19,20,27,28 such as the size of polymer meshes, the connectivity of pores, and the tortuosity of diffusion pathways.

In this work, we report a mechano-diffusion mechanism that harnesses mechanical deformation to control particle diffusion in stretchable hydrogels via the synergy of geometrical transformation and energy modulation, achieving a significantly enlarged tuning ratio and a highly expanded tuning freedom. Using a model particle-hydrogel material system and a customized mechano-diffusion characterization platform, we systematically investigate the diffusion of gold nanoparticles (AuNPs) of various sizes in hydrogels under controlled stress states and loading rates. Our experiments demonstrate that tension loads can enhance AuNP diffusivity by up to 22 times, far surpassing that in traditional liquid medium (e.g., 2.43 times in water, 1.34 times in diluted polymer solution, 1.21 times in concentrated polymer solution) and by external fields (e.g., 3.86 times for light field, 0.99 times for magnetic field, 1.15 times for electrical field). Intriguingly, torsion loads slightly suppress AuNP diffusivity by 33%. We also observe that increasing the loading rate from 0 to 4.8 s⁻¹ reduces AuNP diffusivity by approximately 50%. To further push the limit of mechano-diffusion, we combine our mechano-transport theory with coarse-grained simulations to study particle diffusion in biaxially stretched polymer networks, which simultaneously expand the mesh size and reduce the energy barrier. This dual effect amplifies particle diffusivity by approximately 50 times due to the synergy of the polymer network's geometric transformation and the polymer chain's energy modulation. This work not only provides fundamental insights into the mechano-diffusion mechanism pertinent to a broad range of biological and synthetic soft materials, but also lays a theoretical foundation for developing previously inaccessible transport-based technologies.

2. Materials and methods

2.1. Synthesis of hydrogels

A 50 mL hydrogel precursor solution was prepared by mixing a 4 M lithium chloride (LiCl) aqueous solution, 3.5 g of Acrylamide (AAm), 30 mg of N,N′-methylenebis(acrylamide) (MBAA), 500 μL of a 10 wt% ammonium persulfate (APS) aqueous solution, and 50 μL of N,N,N′,N′-tetramethylethylenediamine (TEMED) using a centrifugal mixer (AR-100, THINKY). The introduction of the LiCl salt served the purpose of preventing significant dehydration during prolonged diffusion experiments. The mesh size of the polymer network under undeformed state can be estimated by eqn S1 (ESI,† eqn S1), which is around 3 nm. The hydrogel was cast in a mold measuring 20 mm × 20 mm × 20 mm (length × width × height). To create a reservoir of the AuNPs solution at the top center of the hydrogel, an acrylic cuboid measuring 3 mm × 3 mm × 8 mm (length × width × height) was affixed to the acrylic lid. The acrylic molds were cut using a laser cutter (Epilog Laser) and assembled using superglue (Krazy). The hydrogel precursor solution was then poured into the mold with the cuboid securely positioning at the top. The assembly was subsequently placed in an oven (CL-1000 Ultraviolet Crosslinker) and cured at 60 °C for 2 hours. Thereafter, the hydrogel sample was gently released from the mold, and the concentrated AuNPs were injected into the central reservoir for further measurement and analysis.

2.2. Synthesis of functionalized AuNPs

To synthesize AuNPs with precise control over their core and hydrodynamic diameters, we followed a modified protocol.^27,29 Specifically, a mixture of 20 mL deionized (DI) water, 0.25 mM HAuCl₄, and 0.25 mM tri-sodium citrate were stirred magnetically at 650 rpm for 15 minutes. Concurrently, we added 600 μL of ice-cold 0.1 M NaBH₄ solution into the mixture, which instantly transformed the initially colorless solution into a vivid red hue. The mixture was left undisturbed for 1 hour to allow the solution to reach reaction.³⁰ To enhance the compatibility between the hydrophobic AuNPs and the hydrophilic hydrogel, the AuNPs’ surfaces were functionalized with thiol-terminated PEG chains. Specifically, 50 mg of MPEG1000-SH was dissolved in 500 μL of DI water and then added dropwise to the 20 mL AuNPs solution while stirring at 650 rpm, resulting in a solution with deeper color. Subsequently, the mixture was stirred for 1 hour to ensure a thorough ligand exchange. The solution was then allowed to stand for 1 hour to stabilize. Afterward, 4 mL of the solution was transferred to a centrifugal filter and centrifuged at 4000 rpm for 10 minutes to eliminate any residual reagents. This centrifugation process was repeated three times, each time with the addition of 4 mL of DI water. After the final centrifugation, the concentrated AuNPs solution exhibited a dark purple color.³¹

2.3. Structural characterization of AuNPs

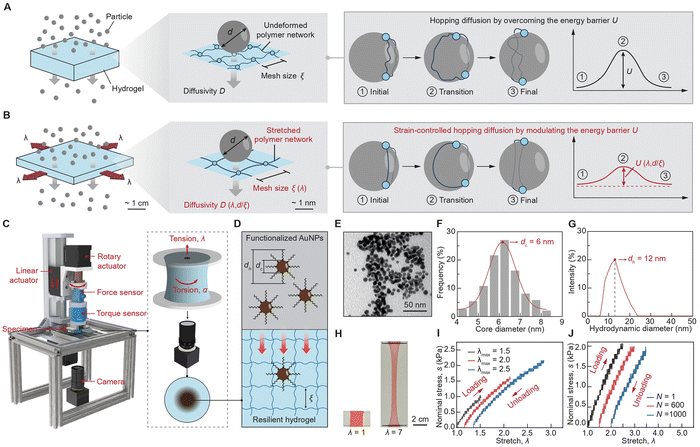
The core diameter and hydrodynamic diameter of the AuNPs were characterized by transmission electron microscopy (TEM) imaging and dynamic light scattering (DLS), respectively. Specifically, the TEM imaging was carried out using the JEOL 1400 Flash TEM equipment with a maximum accelerating voltage of 120 kV and a lattice resolution of 0.2 nm; and the DLS was performed using the Malvern Zetasizer Nano-ZS equipment. Given the measured distributions of AuNPs’ core diameter and hydrodynamic diameter, we can identify the mean values of core diameter and hydrodynamic diameter of the two kinds of AuNPs as d_c = 6 nm and 18 nm and d_h = 12 nm and 28 nm, respectively.

2.4. Mechano-diffusion characterization platform

The platform can be divided into the mechanical loading module, the force/torque measurement module, and the imaging module. In the mechanical loading module, a two-phase stepper motor drives a 1604-type ball screw with a linear guide to achieve static or dynamic uniaxial stretching of the hydrogel samples. Additionally, another two-phase stepper motor was used to apply torsion loads to the hydrogel samples. An Arduino UNO microcontroller controlled the movement of this module. The force/torque measurement module integrated a force sensor with a 9.8 N measurement range and a 1.9 mV V⁻¹ sensitivity, as well as a torque sensor with a 0.3 Nm measurement range and a 0.6 mV V⁻¹ sensitivity. Since the sensor outputs were at millivolt levels, an amplification circuit based on an INA128P instrumental amplifier amplified the signals to volt levels. These measured forces and torques were then calculated and recorded on a computer via an NI USB 6008 data acquisition board and LabVIEW software. In the imaging module, a high-resolution camera with a maximum resolution of 3264 × 2448 pixels and a video capture capability of 15 frames per second captured images. This setup measured the diffusion profiles of the AuNPs in the hydrogel. During experiments, the camera's spatial resolution was approximately 0.015 mm per pixel, which was sufficient for determining diffusivity, as the diffusion profiles were at the millimeter scale.

2.5. Coarse-grained molecular dynamics simulation

The coarse-grained (CG) molecular dynamics (MD) modeling was based on the molecular dynamic simulation software package LAMMPS. A 3D crosslinked network was constructed with 3546 sphere monomers that are modeled with CG beads. To model the influence of the solutions on the diffusion mechanism, solution CG beads were also constructed with an initial uniform interval along all directions. Using the Lennard-Jones (LJ) unit system, the diameter of the CG bead σ for the polymer chains was set as the length unit, while the diameter for the solution CG beads was set as 0.1σ. Along all three directions, the length of polymer chains was set as 36σ while the periodic boundary conditions (PBC) were applied. Cubic cells with a uniform side length of 6σ were considered, creating 8 polymer chains along each direction and a total of 125 cells in the whole system via the crosslinkers. More details on the simulation settings are provided in ESI.†

3. Results

3.1. Working principle

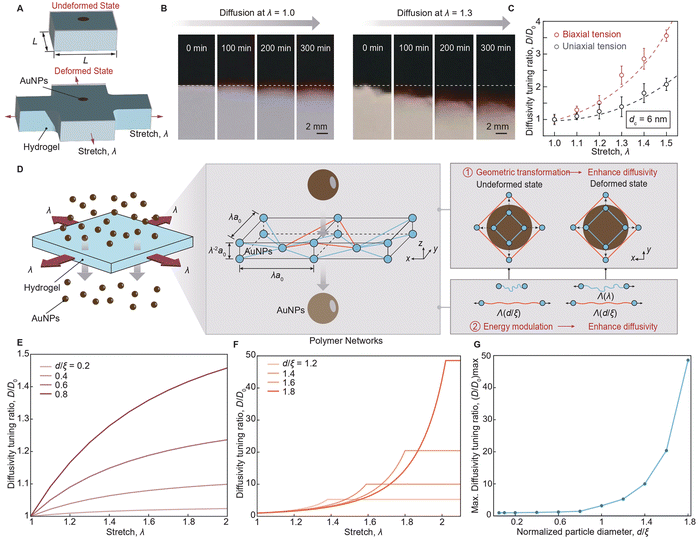
The working principle of the mechano-diffusion mechanism is to leverage the mechanical deformation of stretchable hydrogels for modulating the polymer network's geometric transformation and the polymer chain's energy modulation, which synergistically tunes the energy barrier for particle diffusion. As illustrated in Fig. 1(A), particles with controlled diameter d diffuse across a layer of undeformed hydrogel with controlled mesh size ξ, the particle diffusivity of which is governed by the elastic energy barrier U for deforming polymer chains, known as hopping diffusion.^32,33 As a tensile stretch λ is applied to the hydrogel (Fig. 1(B)), the hydrogel reduces in thickness and expands in area, enlarging the polymer mesh size ξ(λ) and reducing the energy barrier U(λ,d/ξ), enabling the strain-controlled and size-dependent particle diffusivity D(λ,d/ξ).

Fig. 1 Working principle of mechano-diffusion of particles in stretchable hydrogels. (A) Illustration of particles transport in undeformed hydrogel medium. The particles need to overcome a high energy barrier U when diffusing through the polymer networks. (B) Illustration of particles transport in deformed hydrogel medium. The particles need to overcome a lower energy barrier U(λ, d/ξ) due to the synergy of geometrical transformation and energy modulation. (C) Schematics of the mechano-diffusion characterization platform, which can apply tension and torsion to hydrogel samples. (D) Schematics of polyethylene glycol (PEG) functionalized gold nanoparticles (AuNPs) with core diameter d_c and hydrodynamic diameter D_h diffusing through hydrogels with controlled mesh size ξ. (E) Transmission electron microscopy (TEM) image of 6 nm AuNPs. (F) Statistical size distribution of 6 nm AuNPs based on TEM image. (G) Hydrodynamic diameter distribution of 6 nm AuNPs characterized by dynamic light scattering (DLS). (H) Optical image showing the stretchability of the hydrogel. (I) Single-cycle stress–stretch curves of the hydrogel at different stretch ratios, showing negligible mechanical hysteresis. (J) Multiple-cycle stress–stretch curves of the hydrogel under different cycle numbers, showing little stress shakedown. The scale bars in E and H are 50 nm and 2 cm, respectively.

3.2. Mechano-diffusion characterization

We develop a customized mechano-diffusion characterization platform and synthesize a model particle-hydrogel system to rigorously investigate the mechano-diffusion mechanism. As illustrated in Fig. 1(C) and ESI,† Fig. S1, the mechano-diffusion characterization platform integrates a mechanical system to apply controlled tension and torsion loads to hydrogels, and an imaging system to measure the spatiotemporal diffusion profiles of AuNPs.³⁴ For the mechanical system, we adopt two-phase stepper motors controlled by a microcontroller to independently drive linear and rotary motions. The mechanical system allows for the application and recording of controlled tension and torsion loads on hydrogel samples with adjustable linear and angular velocities, further enabling various loading stretching and torsion rates applied to hydrogel samples. For the imaging system, we employ a high-resolution camera with a maximum resolution of 3264 × 2448 pixels and a video capture rate of 15 frames per second to capture images, measuring the diffusion profiles of AuNPs in deformed hydrogels. In a typical mechano-diffusion experiment, the camera resolution is approximately 0.015 mm per pixel, which is sufficient for determining the diffusivity of AuNPs, since their diffusion profiles are on the millimeter scale.

As illustrated in Fig. 1(D), the particle-hydrogel system consists of a single-network hydrogel³⁵ made of polyacrylamide (PAAm) and functionalized AuNPs²⁹ modified with polyethylene (PEG) chains. The functionalized AuNPs are synthesized by surface-modifying pristine AuNPs with 1 kDa PEG shells, resulting in two critical dimensions: the core diameter d_c of the pristine AuNPs and the hydrodynamic diameter d_h of the overall AuNPs with PEG shells. We synthesized two types of functionalized AuNPs with average core diameters of 6 nm and 18 nm, detailed in ESI,† Fig. S2 and S3, respectively. The core diameter d_c and the hydrodynamic diameter d_h of the functionalized AuNPs were characterized using transmission electron microscopy (TEM, Fig. 1(E) and (F)) and dynamic light scattering (DLS, Fig. 1(G)), respectively. The zeta potentials of both functionalized AuNPs are nearly 0 mV, indicating their neutral surface electrokinetic potential and inert surface charge characteristics (ESI,† Fig. S4). The PAAm hydrogel was chosen for its superior resilience and high stretchability,³⁵ therefore, allowing us to exclude the effect of polymer-network evolution in this study. As shown in Fig. 1(H), the PAAm hydrogel achieves a high stretchability of more than five times its original length while maintaining negligible mechanical hysteresis (Fig. 1(I)) and minimal stress shakedown under cyclic loading (Fig. 1(J)). Additionally, we incorporate hygroscopic salts (i.e., 4 M lithium chloride) into the hydrogel to prevent dehydration during long-term mechano-diffusion experiments (ESI,† Fig. S5).

3.3. Effects of uniaxial tension and pure torsion

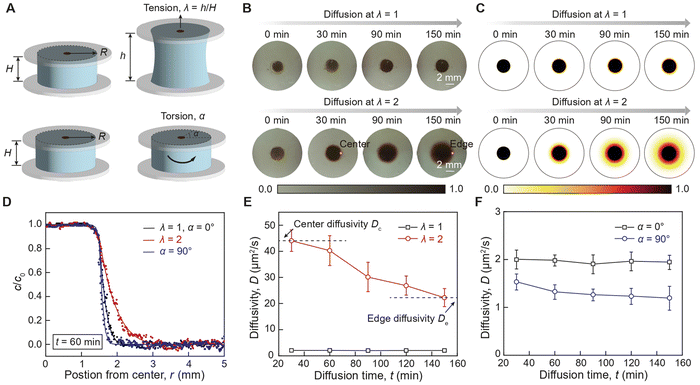
We first examine the impact of tension and torsion on the diffusion of AuNPs in hydrogels under static loading. As illustrated in Fig. 2(A), an aqueous AuNP solution is initially placed in the central reservoir of a cylindrical hydrogel sample with a radius R of 9 mm and a height H of 6 mm, which is then subjected to controlled tension and torsion. As illustrated in ESI,† Fig. S6, the hydrogel sample is covalently bonded between two glass substrates via silane chemistry³⁶ allowing the application of tension and torsion on the hydrogel sample by manipulating the glass substrates while preventing delamination between the hydrogel sample and the glass substrates. A typical measured diffusion profile sequence of AuNPs in the hydrogel sample is presented in Fig. 2(B). The AuNPs gradually diffuse along the radial direction, forming an increasingly larger circle. To extract the diffusivity D of AuNPs, we use the numerical finite difference method implemented in MATLAB to solve the diffusion governing equation in the cylindrical coordinate system, reading as ∂c/∂t = D(∂²c/∂r² + ∂c/(r∂r) + ∂²c/∂z²). In the simulation, the cylindrical sample occupies the domain where −9 mm < r < 9 mm and 0 < z < 6 mm, and the AuNP reservoir occupies the domain where −1.5 mm < r < 1.5 mm and 0 < z < 3 mm. The initial concentration of AuNPs in the reservoir is set as a constant c = c₀, while the initial concentration of AuNPs in the rest of the cylindrical sample is set as c = 0. A typical simulated diffusion profile sequence of AuNPs in the hydrogel sample is presented in Fig. 2(C). By fitting the simulated concentration profile to the measured concentration profile, we can extract the measured diffusivity D of AuNPs in hydrogels subjected to controlled stress states (ESI,† Fig. S7).

Fig. 2 Mechano-diffusion characterization of AuNPs in deformed hydrogels. (A) Illustration of the experiment setups of AuNPs diffusion in a cylindrical hydrogel with radius R and height H subjected to uniaxial tensile stretch λ or pure torsion angle α. (B) Optical images of 18 nm AuNPs diffusion in undeformed (λ = 1) and stretched (λ = 2) hydrogels at various diffusion times. The AuNPs diffusivity at the center of the sample is denoted as center diffusivity D_c, while the AuNPs diffusivity at the edge of the sample is denoted as edge diffusivity D_e. (C) Numerical simulations of 18 nm AuNPs diffusion in undeformed (λ = 1) and stretched (λ = 2) hydrogels at various diffusion times. (D) Concentration of 18 nm AuNPs along radius direction in undeformed (λ = 1), stretched (λ = 2), and twisted (α = 90°) hydrogels. The solid dots denote the measured experimental results, and the solid lines denote the fitted simulation results using the numerical finite difference method. (E) Comparison of the extracted diffusivity D as a function of diffusion time t in undeformed (λ = 1) and stretched (λ = 2) hydrogels. The short-term diffusivity corresponds to center diffusivity D_c, while the long-term diffusivity corresponds to center diffusivity D_e. (F), Comparison of the extracted diffusivity D as a function of diffusion time t in undeformed (α = 0°) and twisted (α = 90°) hydrogels. The error bars in E and F represent the standard deviation from at least three independent tests. The scale bar in B is 2 mm.

We first compare the diffusion concentration profile of both types of AuNPs in undeformed (λ = 1, α = 0⁰), stretched (λ = 2), and twisted (α = 90°) hydrogels after the same diffusion duration. As shown in Fig. 2(D), the 18 nm AuNPs in the stretched hydrogel (λ = 2) exhibit an extended diffusion front compared to the undeformed hydrogel (λ = 1), indicating enhanced diffusion due to tension. In contrast, the 18 nm AuNPs in the twisted hydrogel (α = 90°) exhibit a significantly suppressed diffusion front compared to the undeformed hydrogel (α = 0°), indicating a slight reduction in diffusion due to torsion. To further quantify the strain effect, we compare the diffusivity of AuNPs in undeformed and stretched hydrogels at various diffusion times. Traditionally, particle diffusivity in hydrogels is constant throughout the diffusion process,²⁷ consistent with our measurements of the diffusivity of AuNPs in the undeformed hydrogel (Fig. 2(E)). Intriguingly, the diffusivity of 18 nm AuNPs in the stretched hydrogel shows pronounced spatial dependence, suggesting that tensile strain plays a role in tuning particle diffusivity due to the nonuniform stress state along the radial direction in the cylindrical hydrogel sample.³⁷ As shown in Fig. 2(E), the diffusivity decreases from 44.1 ± 3.98 μm² s⁻¹ to 22.3 ± 3.47 μm² s⁻¹ as the 18 nm AuNPs diffuse from the center to the edge of the sample. In contrast, the diffusivity of 18 nm AuNPs in the twisted hydrogel (α = 90°) shows a slight spatial dependence from 1.53 ± 0.16 μm² s⁻¹ to 1.19 ± 0.25 μm² s⁻¹, suggesting that shear strain slightly reduces particle diffusivity as the AuNPs diffuse from the center to the edge of the sample (Fig. 2(F)). Compared to the 18 nm AuNPs, the 6 nm AuNPs exhibit enhanced diffusivity but less pronounced spatial-dependent particle diffusivity (ESI,† Fig. S8, Movie S1–S2, ESI†). This discrepancy is primarily due to the variation in AuNP core diameters, as larger AuNPs require higher energy barriers for particle diffusion compared to smaller AuNPs.

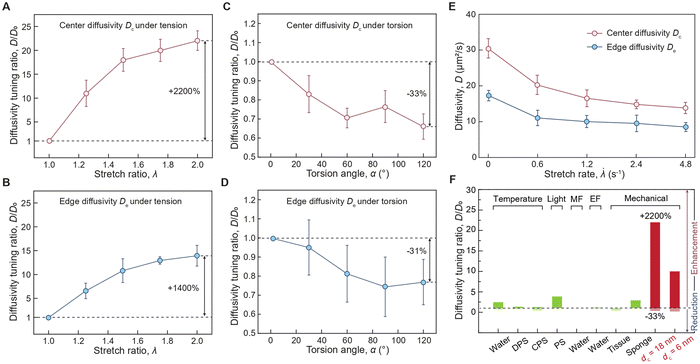
To further quantify the spatial-dependent diffusivity of AuNPs in the deformed cylindrical hydrogel sample, we take the measured AuNPs diffusivity at the center of the sample as center difficulty D_c, while defining the measured AuNPs diffusivity at the edge of the sample as edge diffusivity D_e. As shown in Fig. 3(A) and (B), when the hydrogel is under tension, the center diffusivity and the edge diffusivity of the 18 nm AuNPs increases by 22 times and 14 times, respectively, as the tensile stretch reaches 2. In contrast, when the hydrogel is under torsion, the center diffusivity and the edge diffusivity of the 18 nm AuNPs decreases by 33% and 31%, respectively, as the torsion angle reaches 120 degrees (Fig. 3(C) and (D)). Notably, the center diffusivity and the edge diffusivity of the 6 nm AuNPs increase by 7.5 times and 4.6 times at the same tensile stretch of 2 (ESI,† Fig. S9) and decreases by 14% and 29% at the same torsion angle of 120 degrees (ESI,† Fig. S10). We compare our strain-controlled particle diffusion with existing particle diffusion tuning approaches. As summarized in Fig. 3(F) and Table S1 (ESI†), the particle diffusivity tuning by temperature variation from 273 K to 333 K in water, diluted polymer solution, and concentrated polymer solution achieves tuning ratios around 2.43,¹⁴ 1.34,³⁸ and 1.21,^39–41 respectively, which are governed by the temperature-dependent viscosity of the liquid medium (ESI,† Fig. S11a). The particle diffusivity tuning by external fields such as light field, magnetic field, and electrical field achieves tuning ratios of around 3.86,⁴² 0.99,⁴³ and 1.15,⁴⁴ respectively. Furthermore, the particle diffusivity tuning by mechanical deformation to biological porous tissues (e.g., meniscus) and synthetic porous materials attain tuning ratios of approximately 0.45⁴⁵ and 5⁴⁶ respectively, which are mainly attributed to the deformation-induced changes in porosity (ESI,† Fig. S11b). In contrast, our strain-controlled particle diffusion achieves a diffusivity tuning ratio of up to 22, thanks to the substantial reduction in the energy barrier encountered by particles (ESI,† Fig. S11c). We further examine the effect of loading rate on center diffusivity D_c and edge diffusivity D_e. As shown in Fig. 3(E), both D_c and D_e decrease as the stretch rate increases. Generally, the loading rate modulates the mode of diffusion, depending on the interplay among three critical time scales: the time scale associated with loading rate τ₁ on the order of a few seconds, the time scale associated with relaxation of polymer chains τ₂ measured to be around 19. 4 seconds,³⁴ and the time scale associated with particle diffusion τ₃ that varies significantly depending on its travel distance. At a low loading rate (τ₁ ≫ τ₂, τ₃), the diffusion system has sufficient time to reach its equilibrium state, and the diffusion process is primarily governed by the inherent particle diffusivity without interference from loading rate. At a high loading rate (τ₁ ≪ τ₂, τ₃), the polymer chains do not have enough time to relax during the loading, leading to a non-equilibrium state where polymer chain relaxation and particle hopping diffusion are coupled. The reduced diffusivity of AuNPs in a dynamically stretched hydrogel indicates a non-equilibrium hopping diffusion process. To summarize, the reduction in diffusivity under dynamic load is mainly attributed to the interplay among the time for particle hopping, the time for mechanical loading, and the time for polymer relaxation, which will be thoroughly investigated in future studies.

Fig. 3 Effects of stress states and loading rates on mechano-diffusion of AuNPs in hydrogels. (A) Center diffusivity tuning ratio D_c/D₀versus stretch ratio λ of 18 nm AuNPs in hydrogels under uniaxial tension. (B) Edge diffusivity tuning ratio D_e/D₀versus stretch ratio λ of 18 nm AuNPs in hydrogels under uniaxial tension. (C) Center diffusivity tuning ratio D_c/D₀versus torsion angle α of 18 nm AuNPs in hydrogels under pure torsion. (D) Edge diffusivity tuning ratio D_e/D₀versus torsion angle α of 18 nm AuNPs in hydrogels under pure torsion. (E) Center diffusivity D_c and edge diffusivity D_eversus stretch rates [small lambda, Greek, dot above] torsion angle α of 18 nm AuNPs in hydrogels under uniaxial tension. (F) Summarized diffusivity tuning ratio D/D₀ of existing particle diffusivity tuning approaches (green columns) and mechano-diffusion approach in this work (red columns). The existing particle diffusion tuning approaches include the particle diffusivity tuning by temperature variation from 273 K to 333 K in water, diluted polymer solution (DPS), and concentrated polymer solution (CPS), by external fields such as light, magnetic field (MF), and electrical field (EF), and by mechanical deformations. The error bars in A to E represent the standard deviation from at least three independent tests.

3.4. Effects of biaxial tension

Despite the high diffusivity tuning ratio under uniaxial tensile loading, the potential of strain-controlled particle diffusivity tuning has not been achieved. According to our mechano-diffusion theory,³⁷ particle diffusivity in uniaxially stretched hydrogels is controlled by the combined effects of geometric transformation of the deformed polymer networks and energy modulation of the stretched polymer chains. While the stretched polymer chains reduce the energy barrier to enhance particle diffusivity, the deformed polymer networks contract significantly perpendicular to the stretch direction, leading to either enhanced or suppressed particle diffusivity depending on the stretch ratio. In contrast to uniaxial tension, biaxial tension causes elongation in both in-plane directions, which can collectively enhance particle diffusivity. In this section, we use experiment, theory, and simulation to uncover the potential of harnessing mechanical deformation to control particle diffusion in biaxially stretched hydrogels.

We first develop a customized experimental setup to measure the AuNP diffusivity in hydrogels subjected to controlled biaxial tensile stretch λ. As illustrated in ESI,† Fig. S12, the experimental setup consists of a mechanical system for applying x–y plane biaxial tensile deformation and an imaging system for recording the diffusion process of AuNPs along the z direction. The four arms of the hydrogel are stretched in x and y directions by manipulating the glass slides covalently bonded to the arms. We measure the out-of-plane diffusivity of AuNPs in the hydrogel subject to in-plane equal biaxial tensile stretch λ_x = λ_y = λ (Fig. 4(A)). The penetration depth of the 6 nm AuNPs in the undeformed hydrogel (λ = 1) is less than 2 mm after a 300-minute duration; in contrast, the penetration depth of the AuNPs in the deformed hydrogel (λ = 1.3) increases significantly to 5 mm (Fig. 4(B) and Movie S3, ESI†). Compared to uniaxial tension, the 6 nm AuNPs exhibit higher diffusivity in hydrogels under biaxial tensile load at the same stretch level (Fig. 4(C)).

Fig. 4 Effect of biaxial tension on mechano-diffusion of particles in hydrogels. (A) Schematic illustration of the experimental setup for mechano-diffusion of AuNPs in hydrogels under biaxial tension. (B) Optical images of 6 nm AuNPs diffusion in undeformed (λ = 1) and biaxially stretched (λ = 2) hydrogels at various diffusion times. (C) Comparison of diffusivity tuning ratio D/D₀ as a function of stretch ratio λ for 6 nm AuNPs diffusion in uniaxially and biaxially stretched hydrogels. (D) Schematic illustration of particle diffusion in a polymer network under biaxial tension. The unit-cell polymer network expands its area to λa₀ × λa₀ and reduces its thickness to λ⁻²a₀, where a₀ is the length of the unit cell at its undeformed state. Biaxial tension induces geometric transformation and energy modulation that collectively enhance the particle diffusivity. (E) Calculated diffusivity tuning ratio D/D₀versus stretch ratio λ for particles with small diameters (d/ξ < 1) governed by the obstruction model. (F) Calculated diffusivity tuning ratio D/D₀versus stretch ratio λ for particles with small diameters (d/ξ > 1) governed by the hopping diffusion model. (G) Maximum diffusivity tuning ratio (D/D₀)_maxversus normalized particle diameters d/ξ. The error bars in C represent the standard deviation from at least three independent tests.

To maximize the potential of biaxial tension in facilitating mechano-diffusion of particles, we next formulate a cross-scale mechano-diffusion theory to establish the relationship between biaxial tensile stretch λ and particle diffusivity D with various diameters d. The key idea of the mechano-diffusion theory is to establish the relationship between the macroscopic deformation of soft materials and the microscopic diffusion of particles. As illustrated in ESI,† Fig. S14, the mechano-transport theory combines three models: (1) the eight-chain model,⁴⁷ which connects the bulk deformation of soft materials to the stretch state of individual polymer chains, (2) the ideal chain model,⁴⁸ which correlates the free energy of an individual polymer chain with its specified stretch state, and (3) the particle diffusion models, which quantify the diffusivity of particles with various diameters. Specifically, for particles larger than the mesh size of polymer networks, we adopt the hopping diffusion model³² to determine particle diffusivity, which depends on the energy barrier encountered during particle movements; while for particles smaller than the mesh size of polymer networks, we adopt the obstruction model⁴⁹ to determine particle diffusivity, which depends on the probability of the particle encountering neighboring polymer chains. The mechano-diffusion theory is adopted to capture the mechano-diffusion of particles in uniaxially stretched polymer networks.³⁷

Here, we use the theory to study the mechano-diffusion of particles in polymer networks subjected to equal biaxial tension. As schematically illustrated in Fig. 4(D), as a hydrogel is subjected to an equal biaxial tension stretch λ, the unit-cell polymer network of the hydrogel expands its area to λa₀ × λa₀ and reduces its thickness to λ⁻²a₀, where a₀ is the length of the unit cell at an undeformed state. The biaxial tension induces two effects that collectively enhance the particle diffusivity: (1) geometric transformation that enhances particle diffusivity via enlarged mesh size regardless of particle diameters, and (2) energy modulation that enhances particle diffusivity via reduced energy barrier dependent on particle diameters. We plot the calculated particle diffusivity normalized by its corresponding value at an undeformed state. As shown in Fig. 4(E), for particles with small diameters (d/ξ < 1), the normalized particle diffusivity increases drastically at small deformation and gradually reaches a plateau at large deformation. The particle diffusivity tuning ratio for small particles is low (e.g., 1.21 for d/ξ = 0.5), because the diffusion of small particles in polymer networks is governed by the obstruction model⁴⁹ that is predominately influenced by geometric transformation instead of energy modulation. In contrast, for particles with large diameters (d/ξ > 1), the particle diffusivity tuning ratio significantly increases (e.g., 48 for d/ξ = 1.8), because the diffusion of large particles in polymer networks is governed by the hopping diffusion model³² that is impacted by both geometric transformations and energy modulations (Fig. 4(F)). As summarized in Fig. 4(G), the maximum particle diffusivity tuning ratio reaches up to ∼ 50 as particle diameter increases. Notably, as the stretch reaches a critical value, the diffusivity tuning ratio reaches a plateau, indicating a transition in the diffusion mode from hopping diffusion to Brownian diffusion within the polymer network. This shift occurs due to the reduction of mesh size in the biaxially stretched polymer network. The significantly enhanced particle diffusivity tuning ratio suggests the potential for achieving on and off tuning of particle diffusion,⁵⁰ a key mechanism essential for on-demand and real-time control of particle diffusion in practical applications such as drug delivery and biomarker detection.

We then conducted coarse-grained molecular dynamics (CGMD) to investigate the effect of particle size on mechano-diffusion in polymer networks under biaxial tension. CGMD simplifies complex molecular systems, enabling the study of particle diffusion within cross-linked polymer networks. For example, recent studies have employed CGMD to investigate the transport behavior of penetrants by revealing the interplay between penetrant size, polymer relaxation, and mesh confinement.^51,52 By modeling large-scale dynamics, CGMD highlights the critical role of cross-link density, temperature, and penetrant characteristics.⁵³ Additionally, CGMD has been applied to nanoparticle diffusion in biological systems, focusing on how the structure of the extracellular matrix modulates the nanoparticle transport efficiency.⁵⁴

We start with the simulation of a single particle diffusion in an aqueous medium with and without polymer networks (Fig. 5(A) and Movie S4, ESI†), where the polymer chain in the polymer network is simulated based on a coarse-grained bead-spring-chain model^55,56 (Fig. 5(B)). We employ a uniform mesh size that simplifies the real structural complexity of hydrogels, which offers the advantage of reducing computational resource demands while providing a foundational understanding of the mechano-diffusion of particles in a model polymer network. As shown in Fig. 5(C), the mean square displacement (MSD) of particles diffusing in an aqueous medium with polymer networks is slightly lower than that of particles diffusing in an aqueous medium without polymer networks, suggesting the role of polymer network in suppressing particle diffusion. We further simulate the diffusion of particles with various diameters in undeformed polymer networks, calculating the diffusivity of particles with polymer networks D₀ normalized by that without polymer networks D_Sol as a function of normalized particle size d/ξ. As shown in Fig. 5(D), the simulated particle diffusivity decreases significantly with increasing particle diameter, aligning qualitatively with our mechano-diffusion theory. However, quantitatively, the simulated diffusivity of particles with diameters slightly smaller than mesh size is lower than the theoretical prediction. This discrepancy may arise from the polymer network in MD simulation imposing constraints on the particle diffusion, which are not fully captured by the obstruction model. For example, a previous study showed that the diffusivity of water molecules (much smaller than mesh size) decreases with an increase in the polymer volume fraction,⁵⁷ indicating that the polymer hinders the diffusivity of particles (i.e., ∼ 0.3 nm for water molecules) even smaller than monomer radius (∼ 0.5 nm for polyethylene hydrogels).

Fig. 5 MD simulation of mechano-diffusion of particles in polymer networks under biaxial tension. (A) Coarse-grained molecular dynamics simulation model of single-particle diffusion in polymer networks at undeformed state. (B) Force in the unit of mσ/τ²versus stretch λ curve of a single polymer chain in the simulation model, where m is the mass of the coarse-grained beads. (C) Normalized mean-square displacement (MSD) versus diffusion time t for particle diffusion in an aqueous medium with and without polymer networks. The MSD is normalized by the MSD of particle diffusion in an aqueous medium without polymer networks at the diffusion time t = 10⁵τ. (D) Diffusivity of particles with polymer networks D₀ normalized by that without polymer networks D_sol as a function of normalized particle size d/ξ. (E) Coarse-grained molecular dynamics simulation model of single-particle diffusion in polymer networks under biaxial tension. (F) Diffusivity tuning ratio D/D₀versus stretch ratio λ for particles with diameters smaller than mesh size (e.g., d = 0.5ξ). (G) Diffusivity tuning ratio D/D₀versus stretch ratio λ for particles with diameters slightly larger than mesh size (e.g., d = 4ξ). (H) Diffusivity tuning ratio D/D₀versus stretch ratio λ for particles with diameters much larger than mesh size (e.g., d = 6ξ). (I) Zoom-in visualization of the process of a single particle passing through the polymer network in the MD simulation. (J), Energy barrier overcome by a particle when passing through polymer networks with and without biaxial tension.

We next simulate the single-particle diffusion in polymer networks subject to equal biaxial tensile stretch λ (Fig. 5(E) and Movie S4, ESI†). As shown in Fig. 5(F), for particles with diameters smaller than mesh size (e.g., d = 0.5ξ), the biaxial tension has a minimal impact on particle diffusivity tuning, because the diffusion of smaller particles is primarily governed by strain-induced geometrical transformation, with little influence from strain-induced energy modulation. In contrast, for particles with diameters slightly larger than mesh size (e.g., d = 4ξ), there exists a critical stretch λ_c, below which the equal biaxial tensile load effectively promotes hopping diffusion of particles due to a significant reduction in the energy barrier experienced by particles, and beyond which the equal biaxial tensile load has little effect on particle diffusivity since the energy barrier is completely diminished. As shown in Fig. 5(G), biaxial tension dramatically increases particle diffusivity at large deformation, by approximately 40 times in simulation, due to the combined effects of strain-induced geometrical transformation and energy modulation. For particles much larger than mesh size (e.g., d = 6ξ), particle diffusion does not occur due to the ultra-high energy barrier encountered by the particles, even when individual chains in the polymer network are stretched to their breaking point, resulting in no strain effect. The comparisons between simulation and theory are presented in ESI,† Fig. S17, qualitatively matching well with each. We also simulate the energy barrier when a particle is passing the mesh cage. As shown in Fig. 5(J), the polymer networks without tension build up a higher energy barrier, the total energy consisting of both potential energy and kinetic energy, for particles passing through than the polymer networks with tension-induced deformation. The simulation and theoretical results underscore the critical role of particle size in determining the particle diffusivity tuning ratio.

3.5. Model-guided drug delivery system

The mechano-diffusion of particles holds promise as a model-guided drug delivery system for pressure-controlled release of drug molecules. To demonstrate the potential, we develop a pressure-triggered drug delivery system, which consists of a closed-loop pneumatic actuator and a drug-load hydrogel membrane (Fig. 6(A) and Fig. S18, S19, ESI†). As the inflation pressure p increases, the hydrogel membrane is subjected to an approximately biaxial tensile deformation (Fig. 6(D)), controlling the release rate of drug molecules from the hydrogel into the surrounding environment (i.e. deionized water bath). To harness the potential of model-guided drug release, we first carry out finite element simulation to correlate the inflated pressure p with the average effective stretch λ_eff applied on the hydrogel membrane (Fig. 6(B) and Fig. S20, Movie S5, ESI†). We further perform a comparison experiment to quantify the impact of biaxial tensile deformation on the enhanced drug release rate. The comparison of drug release profiles from deformed and undeformed hydrogel membranes indicates that a compressive stress of 10 kPa (equivalently biaxial tensile load) effectively increases the concentration of released drug molecules by around 1.5 times (Fig. 6(C)). Given the simulated stress distribution and the particle mechano-diffusion in the hydrogel membrane, we quantitatively predict the concentration of drug molecules released into the water bath, matching the experimental results (Fig. 6(D)). The model-guided drug delivery system has the potential to revolutionize drug delivery in biomedical applications such as closed-loop glucose control, scar-free wound healing, and ophthalmic drug delivery, which require drug delivery that responds to mechanical forces in the surrounding environment.

Fig. 6 Model-guided drug delivery system. (A) Design of pressure-triggered drug delivery system, which consists of a pneumatic actuator and a drug-loaded hydrogel membrane. As the inflation pressure p increases, the hydrogel membrane is subjected to an approximately biaxial tensile deformation, controlling the release rate of drug molecules from the hydrogel into the surrounding environment (i.e. deionized water bath). (B) Finite element simulation (left panel) to correlate the inflated pressure p with the average effective stretch λ_eff applied on the hydrogel membrane (right panel). (C) A comparison experiment (left panel) to quantify the impact of biaxial tensile deformation on the enhanced drug release rate (right panel). (D) A comparison of drug release profile C/C₀ (bottom right panel) of inflated and uninflated drug delivery systems (left panel) subject to controlled inflation pressure p (top right panel), where C is the drug concentration released into the environment and C₀ is the initial drug concentration in the hydrogel membrane. The triangle dots in the bottom right panel are the theoretical predictions based on the simulated stress distribution and the mechano-diffusion of particles in the hydrogel membrane.

4. Conclusions

Building a mechano-diffusion characterization platform and a model particle-hydrogel system, we experimentally studied the diffusion of AuNPs in hydrogels subjected to the controlled stress state and loading rate. Our experiments demonstrate that tension loads can enhance AuNP diffusivity by up to 22 times, far surpassing traditional particle diffusivity tuning approaches. Further empowered by mechano-diffusion theory and coarse-grained simulation, we push the limit of mechano-diffusion of particles in biaxially stretched polymer networks, which simultaneously expand the mesh size and reduce the energy barrier. This dual effect amplifies particle diffusivity by approximately 30 times due to the synergy of the polymer network's geometric transformation and the polymer chain's energy modulation. The geometric transformation of polymer networks affects the dynamics of particles, primarily following the obstruction model, a continuous process where particles diffuse through the aqueous medium; while the energy modulation of polymer chains impacts the dynamics of particles following the hopping diffusion model, a discrete process where particles escape from one polymer cage to another. This work will not only advance new knowledge of mechano-diffusion mechanisms pertinent to a broad range of biological and synthetic soft materials, but also lay a foundation for developing transport-based technologies that were previously inaccessible including but not limited to high-specific electrochemical biosensors with selective transport of biomarker,⁵⁸ force-sensitive cargo for on-demand drug delivery,⁵⁹ nanoparticle-induced biopolymer hydrogel toughening,⁶⁰ and strain-programmable tissue adhesive for prolonged tissue repair.⁶¹

Author contributions

S. L. conceived the idea. C. Y., C. W., J. L., and T. W. performed the experiments and analysed the data. C. Y., C. W., J. L., T. W., and S. L. wrote the manuscript with inputs from all the authors. C. Y., C. W., J. L., T. W., X. L., Z. S., C. W., Z. L., and S. L. analysed and interpreted the results. S. L., Z. L., and C. W. supervised the research.

Data availability

The data supporting this article have been included as part of the ESI.†

Conflicts of interest

The authors declare no conflict of interest.

Acknowledgements

The authors thank A. Withrow for help with TEM imaging and W. Zhang and R. Benedict for help with DLS characterization. The authors thank Dr J. Laaser for helpful discussion on AuNP diffusion characterization in hydrogels. S. L. thank the support of National Science Foundation grant NSF-CMMI-2338747 and National Science Foundation grant NSF-CBET-2320716. C. W. thank the support of National Science Foundation grant NSF-CBET-2414719.

Notes and references

1. S. Patel, N. Ashwanikumar, E. Robinson, Y. Xia, C. Mihai, J. P. Griffith, S. 3rd Hou, A. A. Esposito, T. Ketova, K. Welsher, J. L. Joyal, O. Almarsson and G. Sahay, Naturally-occurring cholesterol analogues in lipid nanoparticles induce polymorphic shape and enhance intracellular delivery of mRNA, Nat. Commun., 2020, 11(1), 983.
2. M. Liu, Q. Li, L. Liang, J. Li, K. Wang, J. Li, M. Lv, N. Chen, H. Song, J. Lee, J. Shi, L. Wang, R. Lal and C. Fan, Real-time visualization of clustering and intracellular transport of gold nanoparticles by correlative imaging, Nat. Commun., 2017, 8, 15646.
3. M. I. Pino-Argumedo, A. J. Fischer, B. M. Hilkin, N. D. Gansemer, P. D. Allen, E. A. Hoffman, D. A. Stoltz, M. J. Welsh and M. H. Abou Alaiwa, Elastic mucus strands impair mucociliary clearance in cystic fibrosis pigs, Proc. Natl. Acad. Sci. U. S. A., 2022, 119(13), e2121731119.
4. H. Gu, E. Hanedan, Q. Boehler, T.-Y. Huang, A. J. T. M. Mathijssen and B. J. Nelson, Artificial microtubules for rapid and collective transport of magnetic microcargoes, Nat. Mach. Intell., 2022, 4(8), 678–684.
5. A. Mateu-Regue, J. Christiansen, F. O. Bagger, O. Winther, C. Hellriegel and F. C. Nielsen, Single mRNP Analysis Reveals that Small Cytoplasmic mRNP Granules Represent mRNA Singletons, Cell Rep., 2019, 29(3), 736–748.
6. S. Hu, X. Pei, L. Duan, Z. Zhu, Y. Liu, J. Chen, T. Chen, P. Ji, Q. Wan and J. Wang, A mussel-inspired film for adhesion to wet buccal tissue and efficient buccal drug delivery, Nat. Commun., 2021, 12(1), 1689.
7. S. Basu, L. T. Holbrook, K. Kudlaty, O. Fasanmade, J. Wu, A. Burke, B. W. Langworthy, Z. Farzal, M. Mamdani, W. D. Bennett, J. P. Fine, B. A. Senior, A. M. Zanation, C. S. Ebert Jr., A. J. Kimple, B. D. Thorp, D. O. Frank-Ito, G. J. M. Garcia and J. S. Kimbell, Numerical evaluation of spray position for improved nasal drug delivery, Sci. Rep., 2020, 10(1), 10568.
8. S. Raju, M. Carbery, A. Kuttykattil, K. Senthirajah, A. Lundmark, Z. Rogers, S. Scb, G. Evans and T. Palanisami, Improved methodology to determine the fate and transport of microplastics in a secondary wastewater treatment plant, Water Res., 2020, 173, 115549.
9. S. Freeman, A. M. Booth, I. Sabbah, R. Tiller, J. Dierking, K. Klun, A. Rotter, E. Ben-David, J. Javidpour and D. L. Angel, Between source and sea: The role of wastewater treatment in reducing marine microplastics, J. Environ. Manage., 2020, 266, 110642.
10. H. Zhang, Z. Wang, F. Wang, Y. Zhang, H. Wang and Y. Liu, In Situ Formation of Gold Nanoparticles Decorated Ti(3)C(2) MXenes Nanoprobe for Highly Sensitive Electrogenerated Chemiluminescence Detection of Exosomes and Their Surface Proteins, Anal. Chem., 2020, 92(7), 5546–5553.
11. S. Lin, B. Wang, Y. Zhao, R. Shih, X. Cheng, W. Yu, H. Hojaiji, H. Lin, C. Hoffman, D. Ly, J. Tan, Y. Chen, D. Di Carlo, C. Milla and S. Emaminejad, Natural Perspiration Sampling and in Situ Electrochemical Analysis with Hydrogel Micropatches for User-Identifiable and Wireless Chemo/Biosensing, ACS Sens., 2020, 5(1), 93–102.
12. C. C. Miller, The Stokes–Einstein law for diffusion in solution, Proc. R. Soc. London, Ser. A, 1924, 106(740), 724–749.
13. Q. Liu, S. Huang and Z. Suo, Brownian Motion of Molecular Probes in Supercooled Liquids, Phys. Rev. Lett., 2015, 114(22), 224301.
14. B. E. Poling; J. M. Prausnitz and J. P. O’connell, Properties of gases and liquids, McGraw-Hill Education, 2001.
15. A. Carruthers and D. Melchior, Study of the relationship between bilayer water permeability and bilayer physical state, Biochemistry, 1983, 22(25), 5797–5807.
16. Y. Hu, X. Zhao, J. J. Vlassak and Z. Suo, Using indentation to characterize the poroelasticity of gels, Appl. Phys. Lett., 2010, 96(12), 121904.
17. T. Baumberger, C. Caroli and D. Martina, Solvent control of crack dynamics in a reversible hydrogel, Nat. Mater., 2006, 5(7), 552–555.
18. X. Zhao, X. Chen, H. Yuk, S. Lin, X. Liu and G. Parada, Soft materials by design: unconventional polymer networks give extreme properties, Chem. Rev., 2021, 121(8), 4309–4372.
19. C. H. Lee, A. J. Crosby, T. Emrick and R. C. Hayward, Characterization of heterogeneous polyacrylamide hydrogels by tracking of single quantum dots, Macromolecules, 2014, 47(2), 741–749.
20. E. Parrish, M. A. Caporizzo and R. J. Composto, Network confinement and heterogeneity slows nanoparticle diffusion in polymer gels, J. Chem. Phys., 2017, 146(20), 203318.
21. C. M. Hartquist, B. Li, J. H. Zhang, Z. Yu, G. Lv, J. Shin, S. V. Boriskina, G. Chen, X. Zhao and S. Lin, Reversible two-way tuning of thermal conductivity in an end-linked star-shaped thermoset, Nat. Commun., 2024, 15(1), 5590.
22. J. P. Gong, Y. Katsuyama, T. Kurokawa and Y. Osada, Double-network hydrogels with extremely high mechanical strength, Adv. Mater., 2003, 15(14), 1155–1158.
23. J.-Y. Sun, X. Zhao, W. R. Illeperuma, O. Chaudhuri, K. H. Oh, D. J. Mooney, J. J. Vlassak and Z. Suo, Highly stretchable and tough hydrogels, Nature, 2012, 489(7414), 133–136.
24. S. Lin, X. Liu, J. Liu, H. Yuk, H.-C. Loh, G. A. Parada, C. Settens, J. Song, A. Masic and G. H. McKinley, Anti-fatigue-fracture hydrogels, Sci. Adv., 2019, 5(1), eaau8528.
25. M. Hua, S. Wu, Y. Ma, Y. Zhao, Z. Chen, I. Frenkel, J. Strzalka, H. Zhou, X. Zhu and X. He, Strong tough hydrogels via the synergy of freeze-casting and salting out, Nature, 2021, 590(7847), 594–599.
26. J. Steck, J. Kim, Y. Kutsovsky and Z. Suo, Multiscale stress deconcentration amplifies fatigue resistance of rubber, Nature, 2023, 624(7991), 303–308.
27. P. J. Moncure, Z. C. Simon, J. E. Millstone and J. E. Laaser, Relationship between gel mesh and particle size in determining nanoparticle diffusion in hydrogel nanocomposites, J. Phys. Chem. B, 2022, 126(22), 4132–4142.
28. E. Axpe, D. Chan, G. S. Offeddu, Y. Chang, D. Merida, H. L. Hernandez and E. A. Appel, A multiscale model for solute diffusion in hydrogels, Macromolecules, 2019, 52(18), 6889–6897.
29. A. Gole and C. J. Murphy, Seed-mediated synthesis of gold nanorods: role of the size and nature of the seed, Chem. Mater., 2004, 16(19), 3633–3640.
30. C. J. Murphy, Seed-Mediated Synthesis of Gold Nanorods: Role of the Size and Nature of the Seed, Chem. Mater., 2004, 16(19), 3633–3640.
31. P. J. Moncure, Z. C. Simon, J. E. Millstone and J. E. Laaser, Relationship between Gel Mesh and Particle Size in Determining Nanoparticle Diffusion in Hydrogel Nanocomposites, J. Phys. Chem. B, 2022, 126(22), 4132–4142.
32. L.-H. Cai, S. Panyukov and M. Rubinstein, Hopping diffusion of nanoparticles in polymer matrices, Macromolecules, 2015, 48(3), 847–862.
33. Z. Xu, X. Dai, X. Bu, Y. Yang, X. Zhang, X. Man, X. Zhang, M. Doi and L.-T. Yan, Enhanced heterogeneous diffusion of nanoparticles in semiflexible networks, ACS Nano, 2021, 15(3), 4608–4616.
34. C. Ye and S. Lin, A mechano-diffusion characterization platform for probing strain-programmable nanoparticle diffusion in hydrogels, MRS Commun., 2024, 1–8.
35. J. Kim, G. Zhang, M. Shi and Z. Suo, Fracture, fatigue, and friction of polymers in which entanglements greatly outnumber cross-links, Science, 2021, 374(6564), 212–216.
36. H. Yuk, T. Zhang, S. Lin, G. A. Parada and X. Zhao, Tough bonding of hydrogels to diverse non-porous surfaces, Nat. Mater., 2016, 15(2), 190–196.
37. J. Liu and S. Lin, Strain-Engineered Particle Diffusion in Uniaxially Deformed Polymer Networks, J. Mech. Phys. Solids, 2024, 105732.
38. W. W. Graessley, Polymeric liquids & networks: structure and properties, Garland Science, 2003.
39. P.-G. De Gennes, Scaling concepts in polymer physics, Cornell University Press: 1979.
40. P. J. Flory, Principles of polymer chemistry, Cornell University Press, 1953.
41. D. E. Dunstan, The viscosity-radius relationship for concentrated polymer solutions, Sci. Rep., 2019, 9(1), 543.
42. M. Moniruzzaman, J. M. Bellerby and N. Mai, The effect of light on the viscosity and molecular mass of nitrocellulose, Polym. Degrad. Stab., 2011, 96(5), 929–935.
43. S. Ghauri and M. Ansari, Increase of water viscosity under the influence of magnetic field, J. Appl. Phys., 2006, 100, 6.
44. D. Zong, H. Hu, Y. Duan and Y. Sun, Viscosity of water under electric field: Anisotropy induced by redistribution of hydrogen bonds, J. Phys. Chem. B, 2016, 120(21), 4818–4827.
45. G. Schwartz, A. Morejon, T. M. Best, A. R. Jackson and F. Travascio, Strain-dependent diffusivity of small and large molecules in meniscus, J. Biomech. Eng., 2022, 144(11), 111010.
46. H. Wu, W.-Z. Fang, Q. Kang, W.-Q. Tao and R. Qiao, Predicting effective diffusivity of porous media from images by deep learning, Sci. Rep., 2019, 9(1), 20387.
47. E. M. Arruda and M. C. Boyce, A three-dimensional constitutive model for the large stretch behavior of rubber elastic materials, J. Mech. Phys. Solids, 1993, 41(2), 389–412.
48. W. Kuhn and F. Grün, Beziehungen zwischen elastischen Konstanten und Dehnungsdoppelbrechung hochelastischer Stoffe, Kolloid-Z., 1942, 101, 248–271.
49. B. Amsden, An obstruction-scaling model for diffusion in homogeneous hydrogels, Macromolecules, 1999, 32(3), 874–879.
50. C. Alvarez-Lorenzo and A. Concheiro, Intelligent drug delivery systems: polymeric micelles and hydrogels, Mini-Rev. Med. Chem., 2008, 8(11), 1065–1074.
51. B. Mei, T.-W. Lin, G. S. Sheridan, C. M. Evans, C. E. Sing and K. S. Schweizer, How segmental dynamics and mesh confinement determine the selective diffusivity of molecules in cross-linked dense polymer networks, ACS Cent. Sci., 2023, 9(3), 508–518.
52. T.-W. Lin, B. Mei, K. S. Schweizer and C. E. Sing, Simulation study of the effects of polymer network dynamics and mesh confinement on the diffusion and structural relaxation of penetrants, J. Chem. Phys., 2023, 159(1), 014904.
53. B. Mei, T.-W. Lin, C. E. Sing and K. S. Schweizer, Self-consistent hopping theory of activated relaxation and diffusion of dilute penetrants in dense crosslinked polymer networks, J. Chem. Phys., 2023, 158(18), 184901.
54. X. He, Y. Yang, Y. Han, C. Cao, Z. Zhang, L. Li, C. Xiao, H. Guo, L. Wang and L. Han, Extracellular matrix physical properties govern the diffusion of nanoparticles in tumor microenvironment, Proc. Natl. Acad. Sci. U. S. A., 2023, 120(1), e2209260120.
55. B.-R. Zhao and B. Li, Molecular simulation of hopping mechanisms of nanoparticles in regular cross-linked polymer networks, J. Chem. Phys., 2022, 157(10), 104901.
56. C. P. Goodrich, M. P. Brenner and K. Ribbeck, Enhanced diffusion by binding to the crosslinks of a polymer gel, Nat. Commun., 2018, 9(1), 4348.
57. T. Fujiyabu, X. Li, U.-I. Chung and T. Sakai, Diffusion behavior of water molecules in hydrogels with controlled network structure, Macromolecules, 2019, 52(5), 1923–1929.
58. X. Jia, S. Dong and E. Wang, Engineering the bioelectrochemical interface using functional nanomaterials and microchip technique toward sensitive and portable electrochemical biosensors, Biosens. Bioelectron., 2016, 76, 80–90.
59. X. Zhao, J. Kim, C. A. Cezar, N. Huebsch, K. Lee, K. Bouhadir and D. J. Mooney, Active scaffolds for on-demand drug and cell delivery, Proc. Natl. Acad. Sci. U. S. A., 2011, 108(1), 67–72.
60. O. Ronsin, I. Naassaoui, A. Marcellan and T. Baumberger, Environmental Nanoparticle-Induced Toughening and Pinning of a Growing Crack in a Biopolymer Hydrogel, Phys. Rev. Lett., 2019, 123(15), 158002.
61. Z. Ma, G. Bao and J. Li, Multifaceted design and emerging applications of tissue adhesives, Adv. Mater., 2021, 33(24), 2007663.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sm01522c

‡ These authors contribute equally to this work.

---