A magnetorheological study of an uncoated nanoparticle-dispersed magnetic ionic liquid

Abstract

Magnetic ionic liquids (MILs) are a new class of materials that embody intrinsic paramagnetic properties due to the presence of transition metals. They have rudimentary characteristics like high ionic conductivity, extreme thermal stability, and unique magnetic response. The present research deals with a solution of an imidazolium-based MIL, 1-butyl-3-methylimidazolium tetrachloroferrate, and uncoated iron oxide nanoparticles. First, the homogeneous dispersion of these nanoparticles in the MIL has been investigated, followed by the characterization of the magneto-rheological shear rate vs. shear stress hysteresis without and with an applied magnetic field. Even in the absence of any steric repulsion among them, these uncoated particles are found to distribute uniformly in the solution. The magnetorheological properties of this solution have been explored by stress–strain analysis and by quantifying the viscoelastic response to an oscillatory shear. It shows a shear thinning behaviour, which diminishes systematically with the applied field. Under an applied magnetic field, the viscosity increases to a saturation value beyond which it remains unaltered. The relaxation time of the fluid drops down considerably due to the applied field, indicating a transformation from viscous to elastic nature. These observations may help in easy synthesis and widening the applications of magnetofluids in various biomedical and engineering fields.

---

1. Introduction

An important turning point in the quest for better substitutes for conventional organic solvents was reached more than a century ago with the introduction of ionic liquids (ILs). ILs are liquids with the melting point below 100 °C and consist of an organic cation and either an organic or an inorganic anion in a liquid state.^1,2 These ILs are distinguished by their outstanding physical and chemical properties, including very low vapor pressure, strong chemical and thermal stability and efficient solvation interactions with a wide spectrum of compounds, covering organic, inorganic and polymeric substances.^1–6 The manipulation of ion combinations within these ILs enables the fine-tuning of properties like solubility, density and viscosity to achieve a specific property for a particular application.^7–11 The unique characteristics as well as the intended uses of ILs determine their classification as room-temperature ILs (RTILs),¹² task-specific ILs (TSILs),^13,14 protic and aprotic ILs (PILs and APILs)^15–17 and magnetic ILs (MILs).^8,18 Among these, MILs have garnered a lot of attention due to their versatility and effectiveness in multiple applications.^19,20

MILs share the fundamental properties with traditional ILs, such as recyclability,^21,22 along with a unique property of response to the applied magnetic field.^23,24 MILs are distinguished by the incorporation of transition metal or lanthanide complexes, which endows them with an inherent paramagnetic nature.^25–29 Therefore, MILs are single-component liquid systems that combine the characteristics of both metallic substances and liquids, offering a notable advantage by standing apart from common two-component systems like ferrofluids and magnetorheological fluids (MRFs).^8,26,30,31 The ferrofluids and magnetorheological fluids have the base liquids that are not as stable as ionic liquids. Because of extreme thermal stability, MILs can extend their applications to those driven by their ability to respond to an external magnetic field. MILs have potential applications in various technologies including robotics, artificial hearts, microsatellite thrusters and air pollution control. They possess additional advantages such as optical transparency and high colour purity, making them more pertinent for many applications compared to traditional magnetic fluids.²⁶ Furthermore, MILs provide a streamlined solution to most of the applications requiring a lower magnetic response exhibited by a paramagnetic liquid, such as water treatment, lubrication, controlled drug delivery and high-performance lithium-ion batteries.³²

In 2004, Hayashi and Hamaguchi introduced MILs, specifically 1-butyl-3-methylimidazolium tetrachloroferrate(III) [BMIM-FeCl₄] and 1-butyl-3-methylimidazolium tetrabromoferrate(III) [BMIM-FeBr₄], exhibiting exclusive paramagnetic properties.^8,32,33 These particular MILs have emerged as versatile materials, finding applications in advanced electrochemical systems, cutting-edge sensor technologies, desulfurization, analytical chemistry and novel magnetic innovations.^18,25,34,35 Furthermore, these fluids are excellent candidates for magnetic hyperthermia, where magnetic particles generate heat due to an external alternating magnetic field, which holds promise for targeted cancer therapy.

Since the pure MILs have very low magnetic sustainability, they are weakly responsive to the external magnetic field. Hence, researchers have focused on ferrofluids and MRFs, which exhibit rapid and reversible transitions from liquid to almost solid states within milliseconds when exposed to external magnetic fields.^34–36 The macron-sized magnetic particles in MRFs and nano-sized magnetic particles in ferrofluids allow modulated rheological properties, including viscosity and relaxation time.^36,37 These fluids incorporate coated nanoparticles, with coatings applied using various substances such as surfactants,³⁸ thixotropic agents,³⁹ and polymers.⁴⁰ These coatings are essential for the synthesis of uniform and homogeneous solutions. In a study, Yu Tong et al. discovered that carbonyl iron powder dispersed in an IL exhibits a pronounced rheological effect and a greater shear yield strength.⁴¹ Another work conducted by Jan Novak and Melanie M. Britton observed non-Newtonian shear thickening in 1-butyl-3-methylimidazolium tetrafluoroborate ([BMIM-BF₄]) with silica nanoparticles, while tetradecyl(trihexyl)phosphonium bistriflamide ([P6,6,6,14][NTf2]) displayed complex shear banding confirmed by the magnetic resonance velocity imaging (MRI) technique.⁴² Several factors influence the rheological properties of these fluids, such as the concentration and size of dispersed nanoparticles, magnetic field strength, types of micro- and nanoscale particles and the carrier fluid. Guerrero-Sanchez et al. reported an IL-based MRF, emphasizing the influence of IL type and particle concentration.⁴³ By assessing the magnetorheological characteristics of an IL-based fluid, Pramith et al. revealed shear-thinning behaviour, which is important for applications like lubrication and electro-spraying.⁴⁴

A multitude of research works have examined the stability and dispersion of coated nanoparticles in diverse carrier fluids, delving into their rheological properties using both experimental and theoretical investigations. Remarkably, there has been no exploration into utilizing inherently magnetic carrier fluids to probe rheological behaviour with uncoated magnetic nanoparticles. In the present system, the use of uncoated nanoparticles simplifies the preparation process and reduces the complexity of manufacturing compared to traditional magnetofluids where surface coatings are required. Additionally, the MIL used as the carrier fluid inherently provides both ionic and magnetic properties. This dual functionality enhances the nanoparticles' responsiveness to external magnetic fields, resulting in a more efficient and controllable magnetorheological effect with improved tuning of mechanical properties. This study investigates the stability of the intriguing dispersions and demonstrates their distinct magnetorheological behaviours. This study includes the stress–strain characterization of the fluid in the absence and presence of an external magnetic field. Furthermore, the rheological response in terms of storage and loss moduli has been quantified under oscillatory shear.

2. Materials and methods

2.1. Materials

The magnetic ionic liquid (MIL) 1-butyl-3-methylimidazolium tetrachloroferrate [BMIM-FeCl₄] with molecular weight 336.87 g mol⁻¹ and purity ≥98.0% was obtained from TCI, Japan and was used without any further purification. The non-magnetic ionic liquid (NMIL) 1-butyl-3-methylimidazolium tetrafluoroborate [BMIM-BF4] was purchased from Sigma Aldrich, USA. The chemical structures of these ILs are shown in Fig. 1(A). Iron oxide magnetic nanoparticles (MNPs) of type Fe₂O₃ with a size of <50 nm and type Fe₃O₄ with a size of 50–100 nm were used in this study and purchased from Sigma Aldrich, USA. The MNPs with a smaller size are termed as small magnetic nanoparticles (S-MNPs), while the larger ones are termed as large magnetic nanoparticles (L-MNPs). This particle-size distribution has also been characterized by atomic force microscopy (AFM) (see Section S1 and Fig. S1 in the ESI†). Different weight percentages (wt%) of both these particles were added into the MIL. The prepared solution was then vortexed for 5 minutes, followed by two cycles of ultrasonication for 15 minutes. Each sample was stored for 3 days at room temperature to achieve a homogenous solution for measurement.

Fig. 1 (A) Chemical structures of the non-magnetic ionic liquid (NMIL) 1-butyl-3-methylimidazolium tetrafluoroborate ([BMIM-BF₄]) and the magnetic ionic liquid (MIL) 1-butyl-3-methylimidazolium tetrachloroferrate ([BMIM-FeCl₄]). (B) Schematic diagram of magnetic arrangement within a parallel-plate geometry setup utilized in the rheometer. (C) Sample shows the sedimentation of the magnetic nanoparticles (MNPs) from the NMIL. (D) Sample shows homogenous dissolution of MNPs in the MIL.

2.2. Methods

2.2.1. Vibration sample magnetometer (VSM) measurement. A vibrating sample magnetometer (VSM) is a device used to measure the magnetic moment of a sample by vibrating it perpendicular to a uniform magnetic field. The magnetic properties of the pure MIL and the dispersion of L-MNPs in MIL samples were measured using a vibrating sample magnetometer (VSM) (Quantum Design PPMS Dyna Cool Instrument). The field sequence was −1000 Oe to 1000 Oe with a rate of 200 Oe s⁻¹ with 10 steps. The measurement was performed at a temperature of 27 °C.

2.2.2. Rheology. Rheological measurements of pure MIL, S-MNP/MIL and L-MNP/MIL dispersions were carried out in the MRD70/1T configuration using a stress-controlled rheometer (MCR-302e, Anton Paar, USA). All experiments were performed at 25 °C. For these magnetorheological measurements, a parallel plate geometry made of titanium with a diameter of 20 mm was used. The gap between the base plate and the measuring parallel plate was 1 mm. In this setup, the magnetic field was applied perpendicular to the direction of flow, with the field strength ranging from 0 to 1 Tesla in terms of coil current from 0.02 to 5 A. The shear rate was varied in the range of 0.01 to 1000 s⁻¹.

In magneto-oscillatory measurement, all samples were initially subjected to a constant shear rate of 30 s⁻¹ for 60 seconds and then magneto-oscillatory sweep tests were performed. Many complex fluids, such as gels, colloidal suspensions and dispersions, can possess an initial structure or exhibit history effects due to phenomena like shear banding, aggregation, thixotropy and aging. Therefore, pre-shearing is necessary to eliminate deformation history and to establish a reproducible initial state of the sample's microstructure. In oscillatory measurements, the viscoelastic moduli are particularly sensitive to this initial state. Therefore, pre-shearing is necessary prior to frequency sweep measurements to eliminate deformation history and establish a reproducible microstructure. Before performing frequency sweep measurements, the amplitude sweep measurements were performed to recognize the linear viscoelastic region (see Section S2 and Fig. S2 in ESI†). All the frequency sweep measurements have been performed at 0.1% shear strain. Finally, the frequency sweep measurements were carried out within this linear viscoelastic region. Fig. 1(B) shows a schematic of the experimental setup used in the study.

3. Results and discussion

3.1. Homogeneous dispersion of uncoated nanoparticles in a magnetic ionic liquid

As shown in Fig. 1(C), the process of dissolving MNPs in the nonmagnetic ionic liquid [BMIM-BF4] results in sedimentation, which is consistent with the findings reported in the literature.^45,46 Here, since the used nanoparticles are not coated with any organic macromolecules, the absence of any steric repulsion leads to the formation of aggregates due to interparticle attraction. The present study addresses this challenge by employing an MIL for the dispersion of the MNPs. As of now, there is no report exploring the solubility of uncoated iron nanoparticles in MILs. As observed in Fig. 1(D), the utilization of MILs prevents MNPs from settling down in the solution. It ensures a homogeneous distribution of the MNPs, providing stability to the solution. Therefore, it is possible to produce a uniform dispersion of uncoated nanoparticles in a solvent. Although there is no stabilizing steric repulsion among the nanoparticles, the interesting observation of uniform MNP/MIL solution led to a further investigation to comprehend the solubility phenomena. For this purpose, VSM measurements were conducted on both the pristine MIL and L-MNP/MIL samples. The MIL used in the present study is reported to be a weak paramagnetic liquid with the molar susceptibility value of 4.11 emu K mol⁻¹.³³ In general, a paramagnetic material exhibits weak magnetization in the presence of an external magnetic field, losing its magnetization upon the removal of the field without exhibiting a hysteresis loop. As evident in the inset of Fig. 2(A), the MIL shows a very little magnetization in the range of the applied magnetic field exhibiting no hysteresis loop. However, the introduction of 12 wt% L-MNPs into the MIL induces a hysteresis loop, indicating the preservation of magnetic ordering even at a zero magnetic field at which, normally, the thermal fluctuations overpower the spatial ordering created by aligning the magnetic domain along the magnetic field. This is mainly due to the ferromagnetic nature of the added MNPs in the MIL. This nature of the MNPs generates a magnetic dipole interaction between the MIL and the single domain nanoparticles. Such an interaction may stabilize the nanoparticles in the solution. Looking at the stabilization of these uncoated MNPs in only magnetic ionic liquids and not in a similarly chemically active nonmagnetic ionic liquid, coupled with the behaviour shown in the hysteresis, this is the most feasible explanation. However, this explanation requires an in-depth investigation. It is worth mentioning that over the course of a month, no phase separation occurs in the homogenous solution of the MNPs and the MIL.

Fig. 2 (A) Hysteresis loop of the solution of 12 wt% large-size magnetic nanoparticles (L-MNPs). Inset shows the effect of magnetic field on a pure magnetic ionic liquid (MIL). (B) Magneto-rheological shear rate vs. shear stress hysteresis curve of L-MNPs/MIL in the absence and presence of magnetic field (B) of 1 T. The dashed arrows indicate the forward and backward directions of a cycle.

In the magnetorheological measurement, the shear stress is plotted as a function of shear rate for the pure MIL and the mixed L-MNP/MIL system without and with an applied magnetic field of 1 T (Fig. 2(B)). A very similar hysteresis loop is observed for a pure MIL in the absence and presence of external magnetic field. Therefore, a very weak effect of the external magnetic field on the pure MIL is evident. However, the MIL with MNPs behaves quite differently. Upon the application of a magnetic field, the MNP/MIL system show a hysteresis loop with a much higher value of shear stress. In the absence of a magnetic field, there are random collisions between the MNPs within the MIL during the process of shear. In the presence of a magnetic field, the MNPs are aligned into chains, which introduces further resistance to flow under shear. Note that here in the present experimental geometry, the direction of the applied magnetic field and the direction of flow are perpendicular to each other. Of course, the nondeformable nature of individual MNPs contributes to this friction, as this nature inherently creates additional frictional force.

3.2. Field-enhanced viscosity

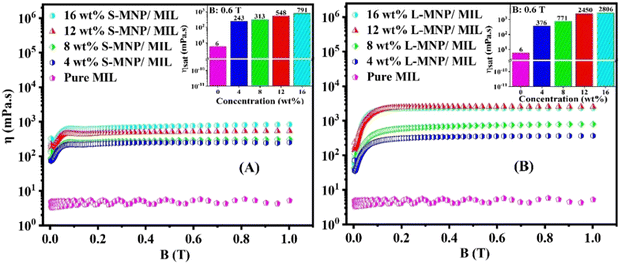
As mentioned in the Introduction section, MILs stand out as a unique entity in the realm of ILs, having been utilized in magneto-responsive materials for a range of applications including targeted drug delivery,³¹ controlled release,⁴⁷ protein separation,^47,48 cellulose dissolution⁴⁹ and cancer treatment.^50,51 Understanding the rheological nature of MILs with dispersed uncoated MNPs may widen these applications. As shown in Fig. 3, the viscosity (η) of MILs shows enhanced values with increasing concentrations of both S-MNPs and L-MNPs even without the applied magnetic field (B (T) = 0). The value of η increases from 5 mPa for the pure MIL to ∼160 and ∼172 mPa s for the 12 wt% added S-MNPs and L-MNPs in the MIL, respectively. This observation is readily recognizable due to the nondeformable nature of individual MNPs, which provides additional frictional force during the flow of the fluid. When subjected to the magnetic field, a significant and systematic increase in η is recorded in the range of B (T) from 0 to 0.1 T, beyond which, no significant change is noticed. Thus, this 0.1 T is identified as the required value of magnetic field to achieve the maximum value of η, which is the saturation value of viscosity (η_sat). This observation is in line with the findings reported by Guerrero-Sanchez et al. emphasizing that the viscosity of the magnetic fluid remains unchanged with variations of high magnetic field.⁴³ As shown in the respective insets of Fig. 3, the value of η_sat is higher for the L-MNPs/MIL system compared to the S-MNPs/MIL system. For example, while the value is ∼2500 mPa s for the L-MNPs/MIL system, it drops to ∼550 mPa s for the S-MNPs/MIL system at the applied magnetic field of 0.6 T with 12 wt% added nanoparticles. In the absence of a magnetic field, these systems are characterized by a random distribution of MNPs. However, in the presence of a magnetic field, the particles may align along the field direction, forming chain or layer structures. As the applied field is perpendicular to the flow direction, when the magnetic field strength increases, both systems become more resistant to flow, showing a higher viscosity. As shown in the inset of Fig. 3, the saturated viscosity (η_sat) is higher for the L-MNP system compared to the S-MNP system at an applied field of 0.6 T for all concentrations of the added nanoparticles. Under this field, each MNP is magnetized. Because of their larger size, L-MNPs are expected to have a larger magnetic domain. As a result, they generate a stronger local magnetic field compared to S-MNPs. This stronger field leads to enhanced interparticle interaction. Furthermore, compared to the smaller nanoparticles, the bigger particles have less thermal randomization. Therefore, the value of η_sat is higher for the L-MNPs/MIL system compared to the S-MNPs/MIL system. Furthermore, a higher concentration of MNPs results in increased particle–particle interactions under the magnetic field, which increases resistance to flow. This leads to a higher value of η_sat at a higher concentration as observed from the data provided in the insets of Fig. 3(A) and (B).

Fig. 3 Viscosity (η) of a magnetic ionic liquid (MIL) with various concentrations of (A) small-size magnetic nanoparticles (S-MNPs) and (B) large-size magnetic nanoparticles (L-MNPs) at different magnetic fields (B (T)). Inset: histograms illustrating the variation of saturated viscosity with concentrations of respective MNPs at a constant magnetic field of 0.6 T.

3.3. Stress–strain characteristics

Magnetorheological fluids and ferrofluids exhibit swift response to magnetic fields, which makes them valuable materials for controlled engineering applications. The static yield stress of these fluids is influenced by both the external magnetic fields and the particle content. Therefore, it is worth unravelling the rheological behaviour of MIL in the presence of the uncoated MNPs by stress–strain characterisation. The concentration dependent shear stress against the shear rate for the samples of MILs in the presence of varying concentration of MNPs in the absence of any magnetic field is shown in Fig. 4(A) and (B). It reveals the significant differences in the viscoelastic nature of pure MIL and MIL-containing MNP systems. The pure MIL exhibits Newtonian behaviour, characterized by a linear increase in shear stress with the shear rate. Upon addition of MNPs, the behaviour becomes non-Newtonian. This non-Newtonian behaviour is also described in Section S3 of the ESI† by the viscosity vs. shear rate flow curve. As observed in Fig. 4(A) and (B), there is a difference in the shear stress between MILs with small-sized MNPs (S-MNPs) and large-sized MNPs (L-MNPs). The difference can be attributed to the particle size and number density. Since S-MNPs are smaller, they may yield a higher number density at the same mass concentration of 8 wt%. This higher number density could lead to more particle–particle and particle–fluid interactions, resulting in higher shear stress for S-MNPs compared to L-MNPs.

Fig. 4 Shear rate versus shear stress curves of magnetic ionic liquids (MILs) in the presence of different concentrations of (A) small-size magnetic nanoparticles (S-MNPs) and (B) large-size magnetic nanoparticles (L-MNPs) without a magnetic field. Respective data at a constant magnetic field of 1T are shown in (C) and (D). (E) and (F) are the respective curves of MILs with 8 wt% added MNPs with varying magnetic fields.

Many rheological models, including the Bingham fluid model,^52–54 Herschel–Bulkley (HB) model,^52–55 and Cho–Choi–Jhon model (CCJ)^52,55–57 have been employed to scrutinize the flow curve of magnetofluids when a magnetic field is applied. Notably, J. Zhang and collaborators explored the rheological properties of silicon-oil-based ferrofluids, emphasizing shear stress and viscosity using the HB model.⁵⁸ In another study, G. Morales pioneered the development of electro-sensitive eco-lubricants based on nano-cellulose and nano-silicates in castor oil. The electrorheological effects were evaluated by determining the yield stress magnitude. The CCJ model played a crucial role in optimizing this parameter for these applications.⁵⁹ All previous investigations have consistently highlighted the shear stress in the high shear rate region, leaving a gap in the low shear rate region. The introduction of a new model by Y. Zhang et al. addresses this issue, enabling the fitting of the data in both regimes.⁶⁰ This modified model is tailored to fit the flow curve obtained in the present study of the MIL system with MNPs under the influence of a magnetic field. As shown in Fig. 4(C)–(F), the shear stress (τ)–strain rate ([small gamma, Greek, dot above]) curves are fitted by this modified model utilizing the expression,⁶⁰, where τ_s represents the static yield stress, which is the amount of stress needed to initiate the flow. Here, d is the correlation index, η_H is the viscosity when the fluid starts flow and m is the exponent parameter. t₁ and t₂ are the characteristic times. In this model, m > 0 and m < 0 indicate the shear-thickening and shear-thinning behaviours, respectively. For a Newtonian fluid, m is expected to be zero. The first term of the equation addresses the region of the lower shear rate where the impact of magnetic field is significant. In contrast, the second term emphasizes the higher shear rate region, where the effect of the shear rate is pronounced compared to the field. This equation is not used for the data shown in Fig. 4(A) and (B) as no magnetic field is applied on the samples.

As evident in Fig. 4(C) and (D), the pure MIL exhibits closely the Newtonian behaviour characterized by a linear increase in stress (τ) with the shear rate ([small gamma, Greek, dot above]) with a constant value of viscosity at an applied magnetic field of 1 T. The value of the exponent parameter m is found to be very low (Table 1). However, the addition of S-MNPs and L-MNPs in the MIL shows a non-Newtonian behaviour where shear stress increases non-linearly with the shear rate. The value of m < 0 explains the shear-thinning behaviour of the MNP/MIL mixed system (Table 1). The modified model fit also shows a clear increase in the static yield stress (τ_s) with increasing concentrations of the nanoparticles. As the concentration of nanoparticles increases, the number density increases leading to a higher viscous solution. Consequently, it demands more stress to initiate the flow. These MNPs, under the applied magnetic field, align into chains along the field direction. The increase in MNP concentration results in higher number density, which leads to a greater number of chains. This, in turn, requires additional force to break the increased number of chains. Note that while the value of τ_s for a pure MIL is 0.005 Pa, it jumps to 1695 and 3199 Pa for 4 and 16 wt% of added S-MNPs in the MIL. The shear-thinning occurs as the chain structures align forming layers, which can slide on top of each other, facilitating easy flow with increasing shear rate. However, the nature of this shear thinning behaviour reduces with the increase of the particle wt%, which is evident from the less negative value of m from −1.109 to −0.920 for the 4 and 16 wt% L-MNPs (Table 1). With an increase in the concentration of MNPs, greater particle density and a higher number of chains result in heightened friction. This hinders the smooth sliding of the chain or layer, contrasting with the smoother sliding observed at lower concentrations. The subsequent increase of η_H from 0.201 mPa s to 0.218 and 0.497 mPa s for the 4 and 12 wt% S-MNPs indicates the increased resistivity as predicted. It is to be noted that the qualitative behaviour of the fluid in the presence of both the S-MNPs and the L-NMPs is the same although the effects are much enhanced for the larger particles as explained in the previous section and evident from the fitting parameters given in Table 1.

Table 1 Modified model fitting parameters of the shear stress vs. shear rate curves shown in Fig. 4(C) and (D). Data shown for the pure magnetic ionic liquid (MIL) and the MIL in the presence of varying weight percentage (wt%) of small-size magnetic nanoparticles (S-MNPs) and large-size magnetic nanoparticles (L-MNPs). Here, τ_s is the static yield stress, t₁ and t₂ are the characteristic times, η_H is the viscosity at the high shear rate region, d is the correlation index and m is the exponent parameter. The constant magnetic field applied is 1 T

Fitted parameters		τ s (Pa)	t 1 (s)	H (mPa s)	t 2 (s)	d	m
Pure MIL		0.0057	5.3 × 10^−3	0.201	0	0.008	0.016
4 wt%	S-MNPs	1695.24	1.5 × 10^−7	0.218	0.911	−0.424	−1.105
	L-MNPs	1698.01	3.1 × 10^−8	0.286	0.129	−0.378	−1.109
8 wt%	S-MNPs	2000.00	5.4 × 10^−7	0.329	0.019	−0.535	−0.983
	L-MNPs	2238.26	4.0 × 10^−6	2.798	0.091	−0.585	−0.980
12 wt%	S-MNPs	3037.94	1.8 × 10^−6	0.497	0.012	−0.596	−0.946
	L-MNPs	3584.00	1.0 × 10^−5	2.990	0.036	−0.674	−0.930
16 wt%	S-MNPs	3199.00	2.1 × 10^−5	1.075	0.012	−0.964	−0.939
	L-MNPs	3892.00	4.0 × 10^−5	3.220	0.017	−0.925	−0.920

---

Fig. 4(E) and (F) show the effect of the varying magnetic field on the stress–strain curve of the MIL at a fixed amount of added MNPs (8 wt%). The feature of the curves is like the ones shown in Fig. 4(C) and (D), where the wt% of added MNPs has been varied at a fixed applied magnetic field. Hence, enhancing the magnetic field is equivalent to enhancing the nanoparticle concentration, at least qualitatively. As mentioned earlier, the applied magnetic field direction is perpendicular to the shear stress. Therefore, viscous stress and magnetic stress are not in cooperation. While the magnetic stress tries to align the particles along the magnetic field direction, the shear stress tries to break the particle chain to flow the fluid along the direction of the stress. As the magnetic field strength increases, the magnetic stress intensifies, which consequently reinforces the interparticle interaction within the chain structure. Therefore, the system requires more shear stress to initiate flow, leading to an increase in the values of τ_s (Table 2). While the value of τ_s is ∼600 Pa at the magnetic field of 0.05 T, it rises to ∼2000 Pa at the field of 1 T for the S-MNPs/MIL system. The η_H is the viscosity shown in the second term of the used equation under the modified model. The decreasing value of this η_H with the applied magnetic field is the signature of the shear thinning behavior of the fluid. At higher magnetic fields, there are more particle chains along the field, which change their orientation along the shear stress at higher stress regimes to exhibit this shear-thinning behavior. This shear thinning tendency is also evident through the negative values of the exponent parameters m shown in Table 2.

Table 2 Modified model fitting parameters of the shear stress vs. shear rate curves shown in Fig. 4(E) and (F). Data shown for the MIL in the presence of 8 wt% of small-size magnetic nanoparticles (S-MNPs) and large-size magnetic nanoparticles (L-MNPs) of varying magnetic field (B). Here, τ_s is the static yield stress, t₁ and t₂ are the characteristic times, η_H is the viscosity at a high shear rate regime, d is the correlation index and m is the exponent parameter

Fitted parameters		τ s (Pa)	t 1 (s)	η H (mPa s)	t 2 (s)	d	m
B: 0.05 T	S-MNPs	600.67	2.4 × 10^−6	0.461	0.221	−0.490	−1.058
	L-MNPs	790.00	3.9 × 10^−7	2.950	1.629	−0.450	−1.090
B: 0.1 T	S-MNPs	979.00	4.3 × 10^−6	0.430	0.102	−0.514	−1.050
	L-MNPs	1090	4.1 × 10^−6	2.820	0.340	−0.480	−1.000
B: 1 T	S-MNPs	2000.00	5.4 × 10^−7	0.329	0.019	−0.535	−0.983
	L-MNPs	2238.26	4.0 × 10^−6	2.798	0.091	−0.585	−0.980

---

As evident from Table 1, the data with the pure MIL show a negligible value of t₂. With the addition of the MNPs, the value becomes high, which decreases with increasing concentration of the particle and magnetic field. This suggests that t₂ is related to the recovery time of the elongated MNP chain after it is broken due to application of shear. For this high concentration of particles and field, the MNP chain will recover to the initial chain structures after being destroyed due to applied shear, which is evident from the nature of t₂. The parameter t₁ has a significant value only when the pure ionic liquid data are fitted. After the introduction of MNPs, the value falls by many orders of magnitude. This parameter imparts correction to the static yield stress, which can be possible only due to conformational changes in self-interaction between the MIL molecules. Introduction of the MNPs changes the nature of the MIL, and interaction between the MIL and MNPs becomes the dominant interaction, so the weightage of MIL molecular interaction becomes quite small leading the t₁ to decrease drastically.

It is to be noted that for a given magnetic field, the viscosity of the nanoparticle dispersed MIL solution follows the Einstein viscosity expression that relates the viscosity of the pure MIL with the solution. As detailed in Section S4 of the ESI,† the viscosity of the solution increases linearly with the concentration of the MNP in the solution.

3.4. Viscoelastic response to oscillatory shear

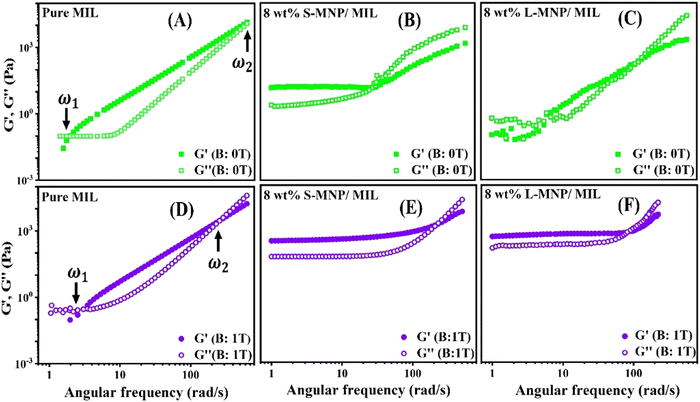
To study the viscoelastic properties of the pure MIL system and the MIL with 12 wt% of added S-MNP and L-MNP systems, the frequency sweep measurements were performed with the results presented in Fig. 5. At the cross-over frequency, G′ = G′′ gives rise to the relaxation time, . As evident for the pure MIL, there are two frequencies, ω₁ and ω₂, at which the storage modulus (G′) and loss modulus (G′′) cross each other. As shown in Fig. 5(A), the behaviour of the pure MIL is delineated by these two distinct relaxation times, which divide the entire region into three segments: a Newtonian region (ω < ω₁), an intermediate region (ω₁ < ω < ω₂) and a transitional region (ω > ω₂).⁶¹ Below the lower cross-over frequency (ω₁), G′′ > G′, showing the MIL to behave like a liquid, where the viscous property dominates over the elastic property. In the intermediate region, the elastic nature dominates. Interestingly, the sample of the MIL with added S-MNPs shows different nature (Fig. 5(B)). Due to the higher number density of S-MNPs, their dispersion in the MIL exhibits a much thicker texture compared to the L-MNPs/MIL system. The high number density of S-MNPs fosters an internally ordered arrangement of MNPs. This structure arises due to the strong interactions among the higher number of S-MNPs and between the S-MNPs and the MIL matrix. These interactions may result in a stable, interconnected network of particles that resists deformation and maintains its structure over a wide range of frequencies. Consequently, both the G′ and the G′′ remain relatively constant across the wide range of frequencies, indicating a well-maintained balance between the elastic and viscous responses of the system. Over the measured frequency range, only one crossover frequency is observed for the S-MNPs/MIL system as it maintains its solid-like behaviour (G′ > G′′) over a broad range of frequencies before transitioning to a more fluid-like behaviour (G′′ > G′).

Fig. 5 Frequency sweep variation of the storage modulus (G′) and loss modulus (G′′) of (A) a pure magnetic ionic liquid (MIL), (B) a MIL with 8 wt% small-size magnetic nanoparticles (S-MNPs) and (C) a MIL with 8 wt% large-size magnetic nanoparticles (L-MNPs) without any applied magnetic field (B = 0 T). Lower panels (D), (E) and (F) show the respective samples in the presence of the 1 T magnetic field.

For L-MNPs/MIL, two crossover frequencies are observed. As the number density of the L-MNPs is lower in the case of this dispersion, the interaction was not able to impart any kind of structural arrangement of the L-MNPs within the MIL matrix. However, the dispersed particle provides a more friction compared to the pure MIL, which is manifested by the higher first cross-over frequency (ω₁), thereby showing a lower relaxation time. The lower relaxation time (τ₁) for the pure MIL is calculated to be 522 ms, which drops to 175 ms for the L-MNPs/MIL. The second relaxation time (τ₂) of the pure MIL system (1.52 ms) was found to be lower compared to the L-MNPs/MIL system (10 ms). A higher value of the ratio of the two relaxation times (τ₁/τ₂) indicates the extension of frequency over which the system shows an elastic-like behaviour.⁶² As visible in Fig. 5, the range of this frequency is less for the case of the L-MNPs/MIL system compared to the pure MIL. It is important to explore the detailed assembly of nanoparticles in the MIL to understand this behaviour. After τ₂, both pure MIL and L-MNPs/MIL systems transition back to their viscous behaviour with G′′ becoming dominant over G′.

The lower section of Fig. 5 illustrates the system's response to a magnetic field of 1 T. Although the pure MILs have low susceptibility, they demonstrate a reduction in the frequency range, where they exhibit elastic behaviour. This is evident from the shift of the second crossover frequency (ω₂) from 613 to 258 rad s⁻¹ in the absence and presence of the magnetic field, respectively. Also, at this frequency, both G′ and G′′ values are higher (Fig. 5(D)). Under this field, in the presence of MNPs in the MIL, the particles themselves align in the field direction, forming aggregated structures as discussed in the previous section. This leads to a rigid and elastic-like dispersion, characterized by a higher value of G′. For example, at the frequency (ω) of 100 rad s⁻¹, the respective values of G′ for pure MIL, S-MNPs/MIL and L-MNPs/MIL are 449 Pa, 699 Pa and 828 Pa. Another notable observation is that both the S-MNPs/MIL and L-MNPs/MIL systems produce qualitatively similar curves explaining the intensified elastic nature in both the systems under the applied magnetic field.

4. Limitations

As mentioned earlier, ferrofluids and magnetorheological fluids have a wide range of applications. However, synthesizing these versatile fluids needs the incorporation of nanoparticles into the carrier fluids. Research to date indicates that this synthesis process is often hindered by the poor solubility of uncoated nanoparticles. In the present study, no coating was required in synthesizing a homogeneous magnetofluid because of the magnetic interaction between the matrix fluid and the nanoparticles. To extend the application of this fluid, more careful investigations are needed. Although the current study provides insights into the rheological behaviour, the limitation still lies in the direct evidence of structural assembly of the particles in the fluid. Chain-like structures of arrangement of nanoparticles along the field direction have been predicted earlier by computer simulation.⁶³ M. Chand et al. have demonstrated the formation of these chain-like structures in the presence of a magnetic field in ferrofluid-based magnetorheological fluids (F-MRFs).⁶¹ Mousav et al. have also reported such an arrangement of magnetite nanoparticles in water using cryo-TEM images.⁶⁴ Even though the base fluid is different in our present study, a similar arrangement of nanoparticles may be observed here, which is in the scope of future studies. Therefore, the system demands electron microscopy studies to visualize this arrangement. Additionally, rheo-small angle neutron scattering (Rheo-SANS) and rheo-small angle X-ray scattering (Rheo-SAXS) experiments could be useful for this purpose. In this study, we have explored the rheological behaviour using different number densities of both MNPs. In the future, one could further investigate by keeping a constant number density.

In the present study only spherical nanoparticles with different sizes have been utilized. The work could be extended to the anisotropic particles, such as cylinders or discs, as well as different types of particles, such as diamagnetic ones, which may exhibit different properties. Furthermore, the assembly of such particles in a two-dimensional system could be very fascinating. For example, a long hydrocarbon chain magnetic ionic liquid could be synthesized, which is expected to be surface active. Such amphiphilic molecules will form a mono-molecular layer at the air–water interface. The assembly of the nanoparticle in such an environment could lead to enriching science. In this paper, we used a phenomenological equation to fit the stress–strain curves. In the future, we can develop a theoretical model to better understand the stress–strain behaviour and other mechanical properties.

5. Conclusions

In this work, the rheological properties of a magnetic ionic liquid containing magnetic nanoparticles have been investigated as a function of magnetic field and particle concentration with varying shear rate and frequency of oscillatory shear. The striking result of this study is the stability of the uncoated particles in the ionic liquid due to the particle–liquid interaction. A pure ionic liquid displays Newtonian behaviour, whereas the liquid with the dispersed nanoparticles exhibits a shear-thinning behaviour, which diminishes under an applied magnetic field. Increasing the concentration of the particles leads to a significant increase in viscosity due to the enhanced metallic nature of the sample. Although the qualitative effects of the magnetic field on the properties are the same in the presence of small and large size nanoparticles, quantitatively the effect is more prominent with the large ones. The frequency sweep measurement suggests that the small particle-based fluid shows elastic nature over viscous nature over a wider range of frequencies.

Data availibility

All the data are included as figures and tables in the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

All the authors acknowledge the financial support from the Shiv Nadar Foundation for conducting this research.

References

1. G. Sharma, S. Mitra, S. M. Kamil and S. K. Ghosh, J. Chem. Phys., 2023, 158, 094904.
2. S. Mitra, R. Das, A. Singh, M. K. Mukhopadhyay, G. Roy and S. K. Ghosh, Langmuir, 2020, 36, 328–339.
3. T. Welton, Biophys. Rev., 2018, 10, 691–706.
4. S. Santhosh Kumar and S. Ramesh Kumar, Mater. Today: Proc., 2021, 37, 2121–2125.
5. M. J. Earle and K. R. Seddon, Pure Appl. Chem., 2000, 72, 1391–1398.
6. C. Capello, U. Fischer and K. Hungerbühler, Green Chem., 2007, 9, 927.
7. A. Shakeel, H. Mahmood, U. Farooq, Z. Ullah, S. Yasin, T. Iqbal, C. Chassagne and M. Moniruzzaman, ACS Sustainable Chem. Eng., 2019, 7, 13586–13626.
8. K. D. Clark, O. Nacham, J. A. Purslow, S. A. Pierson and J. L. Anderson, Anal. Chim. Acta, 2016, 934, 9–21.
9. S. De Sarkar, S. Mitra and S. K. Ghosh, Eur. Phys. J. E:Soft Matter Biol. Phys., 2020, 43, 55.
10. N. Gathergood and P. J. Scammells, Aust. J. Chem., 2002, 55, 557.
11. I. Mitrofanov, S. Sansonetti, J. Abildskov, G. Sin and R. Gani, Computer Aided Chemical Engineering, Elsevier, 2012, vol. 30, pp. 762–766.
12. H. Tokuda, S. Tsuzuki, Md. A. B. H. Susan, K. Hayamizu and M. Watanabe, J. Phys. Chem. B, 2006, 110, 19593–19600.
13. J. H. Davis, Jr., Chem. Lett., 2004, 33, 1072–1077.
14. J. Palomar, M. Gonzalez-Miquel, J. Bedia, F. Rodriguez and J. J. Rodriguez, Sep. Purif. Technol., 2011, 82, 43–52.
15. T. L. Greaves and C. J. Drummond, Chem. Rev., 2008, 108, 206–237.
16. C. A. Angell, N. Byrne and J.-P. Belieres, Acc. Chem. Res., 2007, 40, 1228–1236.
17. J. E. S. J. Reid, R. J. Gammons, J. M. Slattery, A. J. Walker and S. Shimizu, J. Phys. Chem. B, 2017, 121, 599–609.
18. E. Santos, J. Albo and A. Irabien, RSC Adv., 2014, 4, 40008–40018.
19. C. Zhu, M. Varona and J. L. Anderson, ACS Omega, 2020, 5, 11151–11159.
20. K. D. Clark, O. Nacham, H. Yu, T. Li, M. M. Yamsek, D. R. Ronning and J. L. Anderson, Anal. Chem., 2015, 87, 1552–1559.
21. T. Chatzimitakos, P. Anagnostou, I. Constantinou, K. Dakidi and C. Stalikas, Separations, 2021, 8, 153.
22. L. Li, Y. Huang, G. Yan, F. Liu, Z. Huang and Z. Ma, Mater. Lett., 2009, 63, 8–10.
23. M. Sajid, TrAC, Trends Anal. Chem., 2019, 113, 210–223.
24. S. Sadjadi, J. Mol. Liq., 2021, 323, 114994.
25. N. M. Figueiredo, I. V. Voroshylova, E. S. C. Ferreira, J. M. C. Marques and M. N. D. S. Cordeiro, Chem. Rev., 2024, 124, 3392–3415.
26. A. Joseph, G. Żyła, V. I. Thomas, P. R. Nair, A. S. Padmanabhan and S. Mathew, J. Mol. Liq., 2016, 218, 319–331.
27. R. E. Del Sesto, T. M. McCleskey, A. K. Burrell, G. A. Baker, J. D. Thompson, B. L. Scott, J. S. Wilkes and P. Williams, Chem. Commun., 2008, 447–449.
28. P. Nockemann, B. Thijs, N. Postelmans, K. Van Hecke, L. Van Meervelt and K. Binnemans, J. Am. Chem. Soc., 2006, 128, 13658–13659.
29. B. Mallick, B. Balke, C. Felser and A. Mudring, Angew. Chem., Int. Ed., 2008, 47, 7635–7638.
30. S. H. Lee, S. H. Ha, C.-Y. You and Y.-M. Koo, Korean J. Chem. Eng., 2007, 24, 436–437.
31. A. Kulshrestha, P. S. Gehlot and A. Kumar, Mater. Today Chem., 2021, 21, 100522.
32. M. S. Sitze, E. R. Schreiter, E. V. Patterson and R. G. Freeman, Inorg. Chem., 2001, 40, 2298–2304.
33. S. Hayashi and H. Hamaguchi, Chem. Lett., 2004, 33, 1590–1591.
34. M. Ashtiani, S. H. Hashemabadi and A. Ghaffari, J. Magn. Magn. Mater., 2015, 374, 716–730.
35. M. T. López-López, P. Kuzhir, S. Lacis, G. Bossis, F. González-Caballero and J. D. G. Durán, J. Phys.: Condens. Matter, 2006, 18, S2803–S2813.
36. S. Elizabeth Premalatha, R. Chokkalingam and M. Mahendran, Am. J. Polit. Sci., 2012, 2, 50–55.
37. G. Bossis, S. Lacis, A. Meunier and O. Volkova, J. Magn. Magn. Mater., 2002, 252, 224–228.
38. C. Fei, L. Haopeng, H. Mengmeng, T. Zuzhi and L. Aimin, Mater. Manuf. Processes, 2020, 35, 1077–1083.
39. Z.-D. Xu and B.-B. Chen, J. Mater. Civ. Eng., 2016, 28, 04015198.
40. S. V. Ganachari, V. B. Patil, N. R. Banapurmath, M. E. M. Soudagar, K. Shahapurkar, A. Elfasakhany, M. Alsehli, A. Yavagal, P. Mogre, V. M. Hiremath and S. A. Hallad, Adv. Mater. Sci. Eng., 2021, 1–11.
41. Y. Tong, X. Li, P. Zhao, X. Dong, Z. Wu and M. Qi, Front. Mater., 2021, 8, 659998.
42. J. Novak and M. M. Britton, Soft Matter, 2013, 9, 2730.
43. C. Guerrero-Sanchez, T. Lara-Ceniceros, E. Jimenez-Regalado, M. Raşa and U. S. Schubert, Adv. Mater., 2007, 19, 1740–1747.
44. P. Priyananda, H. Sabouri, N. Jain and B. S. Hawkett, Langmuir, 2018, 34, 3068–3075.
45. K. Ueno, A. Inaba, M. Kondoh and M. Watanabe, Langmuir, 2008, 24, 5253–5259.
46. V. Khare, A. Kraupner, A. Mantion, A. Jeličić, A. F. Thünemann, C. Giordano and A. Taubert, Langmuir, 2010, 26, 10600–10605.
47. A. M. Curreri, S. Mitragotri and E. E. L. Tanner, Adv. Sci., 2021, 8, 2004819.
48. K. D. Clark, M. J. Trujillo-Rodríguez and J. L. Anderson, Anal. Bioanal. Chem., 2018, 410, 4567–4573.
49. J. Muraoka, N. Kamiya and Y. Ito, J. Mol. Liq., 2013, 182, 76–78.
50. A. Fallah Shojaei, K. Tabatabaeian, S. Shakeri and F. Karimi, Sens. Actuators, B, 2016, 230, 607–614.
51. I. Ali, M. Hozaifa, S. Ali, A. Malik and M. Locatelli, J. Mol. Liq., 2023, 388, 122823.
52. P. Pei, Y. Peng and C. Qiu, J. Intell. Mater. Syst. Struct., 2022, 33, 1271–1291.
53. P. Pei and Y. Peng, J. Magn. Magn. Mater., 2022, 550, 169076.
54. M. Osial, A. Pregowska, M. Warczak and M. Giersig, J. Intell. Mater. Syst. Struct., 2023, 34, 1864–1884.
55. J. Y. Jeong, S. Kim, E. Baek, C. Y. You and H. J. Choi, Colloids Surf., A, 2023, 656, 130438.
56. H. M. Kim, J. Y. Jeong, S. H. Kang, H.-J. Jin and H. J. Choi, Materials, 2022, 15, 2677.
57. Y. Seo and H. J. Choi, J. Korean Ceram. Soc., 2020, 57, 608–631.
58. J. Zhang, H. Cui, S. Han, Z. Li and J. Lu, Korea-Aust. Rheol. J., 2023, 35, 179–190.
59. M. García-Morales, S. D. Fernández-Silva, C. Roman, M. A. Olariu, M. T. Cidade and M. A. Delgado, Processes, 2020, 8, 1060.
60. Y. Zhang, D. Li, H. Cui and J. Yang, J. Magn. Magn. Mater., 2020, 500, 166377.
61. M. Chand, A. Shankar, N. Ali, K. Jain and R. P. Pant, RSC Adv., 2014, 4, 53960–53966.
62. P. Tapadia and S.-Q. Wang, Macromolecules, 2004, 37, 9083–9095.
63. A. Satoh and R. W. Chantrell, Mol. Phys., 2006, 104, 3287–3302.
64. N. S. S. Mousavi, S. D. Khapli and S. Kumar, J. Appl. Phys., 2015, 117, 103907.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5sm00193e

‡ Present address: Biological Physics Group, Department of Physics, Carnegie Mellon University, Pittsburgh, PA 15213, USA.

---