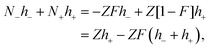DOI:
10.1039/D5SM00319A
(Paper)
Soft Matter, 2025,
21, 4498-4516
Temperature induced migration of interacting charged colloidal particles: an irreversible thermodynamics approach
Received
27th March 2025
, Accepted 30th April 2025
First published on 5th May 2025
Abstract
The migration of particles induced by spatial gradients in temperature is commonly referred to as thermophoresis, thermodiffusion, thermal diffusion, or the (Ludwig-)Soret effect. The force on colloidal particles that drives such a migration depends on the response to variations in temperature, both of single particles and of interactions between particles. A distinction can thus be made between single-particle and collective contributions to the thermophoretic force experienced by a colloidal particle. There is as yet no systematic theory for thermophoresis of charged colloids that accounts for the collective contribution due to interactions between charged colloids. In a previous study, we developed an irreversible thermodynamics approach for uncharged colloids [J. K. G. Dhont and W. J. Briels, J. Colloid Interface Sci., 2024, 666, 457]. In the present study we extend this approach to account for interactions between charged colloids, which includes additional fluxes of ions. Enslavement of ion fluxes to the relatively slowly evolving concentration profile of the colloids, and an approximate evaluation of the heat-of-transfer, leads to microscopic, particle-based expressions for the thermodiffusion coefficient and the Soret coefficient. In addition, an explicit expression for the macroscopic thermoelectric field is derived, which gives rise to a thermoelectrophoretic force. A comparison to existing experimental thermophoresis experiments is presented.
1 Introduction
The very first study on temperature-gradient induced mass transport stems from Ludwig in 1856, who referred to the phenomenon as “hydrodiffusion”. In a one-page report (in German), a single measurement is performed on a sodium sulphate solution.1 About two decades later, quite extensive and systematic studies were published by Soret (in French) on various types of salts.2–4 Since then, many experiments have been performed on other types of molecular systems. With the advent of microfluidics, single-particle imaging, and several different types of optical techniques, thermodiffusion of macromolecular systems gained scientific interest over the last few decades. Overviews of these techniques and/or experimental results on many different macromolecular systems can be found, for example, in ref. 5–11.
Accompanying these experimental developments, a large body of theoretical work specifically aiming at colloidal suspensions has been put forward. The main focus of this previous theoretical research is concerned with thermodiffusion of single colloidal particles, in which case the concentration of colloids is sufficiently low to neglect contributions arising from interactions between the colloids. Single-particle theories and experiments include the contribution of an electric double layer of charged colloids to thermodiffusion,12–21 of Marangoni-related interfacial forces,22–24 and of solvated uncharged colloids.25,26
As yet, there is no systematic theory that accounts for the contribution to thermodiffusion due to interactions between charged colloids. There are only a few theoretical studies of the effect of inter-colloidal interactions on thermodiffusion. In ref. 27 and 28, the force between charged colloids is assumed to be given by the spatial gradient of a temperature dependent mean-field potential. As will be discussed later, however, the force due to interactions is non-conservative. In ref. 8, 24 and 29–31, the force of a colloid is related to the spatial derivative of the equation-of-state pressure (which is referred to in these references as the osmotic pressure). As will be shown, this expression omits the contribution from the heat-of-transfer.
The only published experimental thermophoresis data for charged colloids where interaction effects are probed are on micellar sodium dodecyl sulphate (SDS) systems12,30–32 and charged silica spheres.33 As for the uncharged sticky-sphere colloids,34 a strong concentration and temperature dependence due to colloid–colloid interactions is found. Due to the lack of full characterization of these systems, an accurate quantitative comparison to the present theory is not possible. The experiments on micellar SDS systems can only be compared to some extent to the present theory.
In all of the abovementioned experiments and theories, a prescribed and time independent externally imposed temperature gradient is applied. In the irreversible thermodynamics approach described in this paper we will also consider the situation where such an externally imposed temperature is present.
The present study is solely concerned with the effects of colloid–colloid interactions on thermophoresis. For single-colloidal particle thermophoresis, interactions between solvent and solute molecules with a colloidal particle surface are highly significant. The corresponding interfacial thermophoretic phenomenon renders the irreversible thermodynamics approach discussed in the present study not meaningful for single-particle thermophoresis. We do, however, include single-particle thermophoretic forces in our theory as an unspecified additional contribution to those resulting from colloid–colloid interactions. In a comparison of our theory to experiments, the single-particle contribution must be obtained from either a specific theory for single-particle thermophoresis (see the references above), or from an extrapolation of experimental data to zero colloid concentration.
Fig. 1 is an overview of the content of this study. The thermophoretic force on a charged colloid particle due to colloid–colloid interactions is derived in Section 2. As indicated in Fig. 1, the derivation consists of several consecutive steps, starting from Onsager's irreversible thermodynamics flux–force relations, which are formulated in Section 2.1. In the first step 2.2 the fluxes of solvent molecules and small ions are related to that of the colloid flux. These so-called enslavement relations are used in the subsequent step 2.3 to eliminate the solvent and salt fluxes to arrive at an effective one-component flux–force relation for the double-layer-dressed colloids. In the next step 2.4, the thermophoretic force is expressed in terms of gradients of the colloid pressure (not to be confused with the osmotic pressure) and the colloid heat-of-transfer. Separating out the mechanical forces due to pressure variations allows us to derive an explicit expression for the colloid heat-of-transfer in the subsequent step 2.5. We find a contribution to the thermophoretic force on a charged colloid due to colloid–colloid interactions that has not been considered before, which we refer to as the thermophoretic interaction force. There is also an electrophoretic force due to a macroscopic electric field generated by the spatially varying temperature and colloid concentration, commonly referred to as thermoelectricity. The origin of this electric field and an expression for it is derived in Section 3. Microscopic expressions for the Soret coefficient and thermodiffusion coefficient in terms of the pair-correlation function and the pair-interaction potential are then given in Section 4, which in principle allow for a microscopic, particle-based comparison of our theory with experiments. Finally, Section 5 conducts a comparison with experiments, and Section 6 contains a summary and conclusion.
 |
| | Fig. 1 An overview of the steps taken to arrive at an expression for the thermophoretic force due to colloid–colloid interactions, and subsequent sections in this paper. | |
2 The forces acting on a colloid in concentration and temperature gradients
In this section we calculate the contribution to the thermophoretic force on a charged colloidal particle in a salt solution that originates from its interactions with other colloids. Single-particle contributions, which are due to the response of degrees of freedom of the electric double layer (and possibly a solvation layer, a grafted polymer brush, adsorbed surfactants, …) to the temperature gradient are not explicitly specified.
For simplicity, we consider two types of ions being present: mono-valent positive ions which dissociated from the surfaces of the colloids and those resulting from added salt, while the mono-valent negatively charged ions originate solely from added salt. For many types of charged colloids the positive ions are H+-ions. In an electro-neutral homogeneous suspension the ±-ion number concentrations ρ± are thus equal to,
| |  | (1) |
where
ρ0 is the number concentration of added salt,
Z > 0 is the number of negatively charged colloid surface groups, and
ρc is the number concentration of colloids.
In classic irreversible thermodynamics, the system is subdivided into volume elements which are sufficiently large to be considered as thermodynamic systems by themselves, but small enough so that concentrations and temperatures do not substantially vary within the volume elements. These homogeneous volume elements are assumed to be in internal equilibrium. Hereafter, we shall refer to these volume elements as “irreversible thermodynamics volume elements”.
2.1 Irreversible thermodynamics approach
As a first step, as indicated in Fig. 1, the basic irreversible thermodynamics flux–force relations are introduced, and the approximations made in the further development of the theory are specified.
In order to quantify the thermophoretic force on a colloid that is due to interactions between the colloids we start from the fundamental Onsager flux–force relations,35–39
| |  | (2) |
where
Jc is the particle-number flux of colloidal particles,
Js of solvent molecules,
J± are the number fluxes of ±-ions, and
JU is the flux of internal energy. The fundamental forces are equal to,
| |  | (3) |
with
μc,s,± the chemical potentials of the colloids, solvent and ions, respectively, and where
T is the temperature. The flux–force relations are valid for linear order in local spatial gradients. These relations remain valid, however, in the presence of large global variations, in which case the Onsager coefficients
Lij are functions of the local thermodynamic variables.
40 Furthermore,
E is the macroscopic electric field that is due to colloid concentration and temperature gradients. As will be discussed in Section 3, the origin of this electric field is solely due to the spatial variation of the Donnan potential, to within the approximations set out in the classic Poisson–Boltzmann approach.
The Onsager flux–force relations in eqn (2) and (3) relates to a mixture of ions, solvent molecules, and bare colloids (without the presence of an electric double layer, but just a core which carries charges), and therefore has the same standing as for simple mixtures. In particular, the Onsager coefficients satisfy the symmetry relations Lij = Lji.
The approximations that we will make concerning the behaviour of the solvent and the salt ions are much the same as those made in the classic Poisson–Boltzmann theory for charged colloids.41 Apart from excluded volume interactions, which prevent solvent molecules (and salt ions) to penetrate the cores of the colloids, solvent molecules do not interact with the colloids in any other way. Salt ions do not occupy volume, and do not interact with the solvent molecules. In addition, salt ions behave as an ideal gas in a homogeneous solution that is everywhere electro-neutral. The ions only interact with each other through the electric field that they generate due to locally unequal concentrations of ±-ions leading to a violation of local electroneutrality. The solvent is assumed to be incompressible and therefore is fully packed in the sense that each solvent molecule occupies a fixed volume vs, independent of salt and colloid concentration, which will be referred to as “the volume of a solvent molecule”. In thermodynamic terms this means that the partial molar volume of solvent is assumed constant. The number concentration of solvent molecules within bulk salt solution is thus equal to 1/vs, which is of course different from the thermodynamic concentration Ns/V of solvent in a suspension (with Ns the number of solvent molecules and V the volume of the system). The difference between the two concentrations is due to the volume that is occupied by the colloids. The cores of the colloids are assumed incompressible, and the volume vc of the core is constant, similar to the solvent molecules.
The difference in the relatively slow dynamics of the large colloids in comparison to the fast dynamics of the much smaller ions and solvent molecules will be shown below to enable the reduction of the Onsager flux–force relations(2) to an effective two-component system, involving only the colloid flux and the heat flux, evidently with forces that differ from those in eqn (3).
These assumptions constitute a minimal (Poisson–Boltzmann type) model which allows us to derive an explicit expression for the thermophoretic force on charged colloids resulting from interactions between them.
2.2 Enslavement of solvent and ion fluxes
In the next step in the derivation of the thermophoretic force as indicated in Fig. 1, we discuss how the solvent flux and ion fluxes instantaneously adapt to the relatively slowly evolving colloid concentration profile. The solvent flux  defined in eqn (4) and the ion fluxes
defined in eqn (4) and the ion fluxes  defined in eqn (15) will be argued as vanishing due to enslavement. This sets the relation between the solvent and ion fluxes, and the colloid flux.
defined in eqn (15) will be argued as vanishing due to enslavement. This sets the relation between the solvent and ion fluxes, and the colloid flux.
As discussed in ref. 42, the displacement of a colloid is accompanied by an opposite displacement of vc/vs solvent molecules. The corresponding trivial contribution −(vc/vs)Jc to the solvent flux is accounted for by introducing an effective solvent flux,
| |  | (4) |
Fluxes are defined relative to the volume-fixed frame, for which,
For the incompressible system under consideration, fluxes are thus measured relative to a position fixed to that of a closed sample cell. It thus follows that

is zero. This implies that the solvent flux responsible for the relaxation of the corresponding pressure gradients relaxes to zero instantaneously. We note that this results in zero fluxes only for closed systems, where the system boundary is impenetrable for solvent molecules.
Due to the fast dynamics of the ions relative to that of the much larger colloids, the macroscopic concentration profiles of the ions (quasi) instantaneously adapt to the slowly changing concentration profile of the colloids. The ion concentrations are therefore enslaved, and henceforth referred to as ρens±. The superscript “ens” is used to indicate that this is the ion concentration profile under the assumption that the ion concentration profiles fully adapt to the colloid's concentration profiles.
To obtain the two ion fluxes in terms of the colloid flux, two equations are needed that connect the concentration of the ions to that of the colloids.
First, the stationary state that the ions (quasi) instantaneously attain in a closed system for a given configuration of the colloids corresponds to zero ion fluxes. As for the solvent, ion fluxes vanish in their stationary state in a closed system, since the system boundaries are impenetrable for the ions. A zero flux implies a vanishing total force on the ions, which is the result of two counter-acting forces. There is a force due to the variation in the equation-of-state pressure of the ions. Since within a Poisson–Boltzmann approach the pressure of the ions is that of an ideal gas, the corresponding force per unit volume on the ±-ions is equal to −∇[ρ±kBT/(1 − φ)], where ρ± is the thermodynamic concentration of ions (number of ions per unit volume of suspension), and kB is the Boltzmann constant. Note that this equation holds on length scales comparable to the dimensions of irreversible thermodynamics volume elements. Furthermore,
is the volume fraction of colloids. Note that
ρ±/(1 −
φ) is the concentration of ions within the solvent surrounding the colloids, which is the concentration that determines the ion-pressure. There is also an electrostatic force per unit volume equal to ±
ρ±eE, with
e > 0 the elementary charge, and
E the thermoelectric field (see Section 3 for a detailed discussion concerning the thermoelectric field). The total force vanishes, and hence,
| |  | (7) |
As mentioned before,
ρens± denotes the ion concentrations that are instantaneously adapted to the colloid concentration profile (hence the superscript “ens” referring to enslavement). The thermophoretic force experienced by the ions is included in the temperature derivative that is implicit on the left hand-side: in the absence of colloids and a vanishing electric field, the above equation implies ion-Soret coefficients equal to
SionT = 1/
T, which complies with the ideal gas behavior of the ions within a Poisson–Boltzmann approximation.
41
The second equation needed to connect the concentration of the ions to that of the colloids is the Poisson equation on length scales larger than the size of the irreversible thermodynamics volume elements,
| | | ∇·[εsE] = −eZρc + ρense, | (8) |
with
ρense =
e(
ρens+ −
ρens−) the charge density due to unequal concentrations of ions, and where, as before,
Z > 0 is the number of negative surface charges carried by a single colloid, and where
ρc is the spatially varying number concentration of colloids. Furthermore,
εs is the dielectric constant of the solvent, which is kept inside the divergence operator to account for its temperature-gradient induced spatial variation.
As will be shown in Appendix A, the two eqn (7) and (8) imply local electro neutrality within each irreversible thermodynamics volume elements, that is,
The divergence of the electric field on the left hand-side of
eqn (8) is shown in Appendix A to be relevant only at the walls of the sample container.
It is furthermore shown in Appendix A that eqn (7) and (8) imply the following enslavements relations,
| | 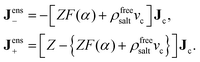 | (10) |
For brevity, the function
F is introduced,
| |  | (11) |
where the parameter
α > 0 is defined as,
| |  | (12) |
which is the ratio of the number of positive ions
Ncoll+ that dissociated from the colloid's surfaces, and the number of positive ions
Nsalt+ originating from added salt, within the corresponding irreversible thermodynamics volume element. Provided that the global variation of
ρc and
ρ0 are small, the concentrations
ρc and
ρ0 on the right hand-side in
eqn (12) can be obtained from are their ambient values, that is, in that case
ρc =
Nc/
V and
ρ0 =
Nsalt/
V, with
Nc and
Nsalt the total number of colloids and dissolved salt molecules in the volume
V of the sample container. Furthermore,
| |  | (13) |
As will be shown below, this is the concentration of salt within the solvent surrounding the colloids.
The interpretation of eqn (10) for the enslaved ion fluxes is as follows. The contribution −ρfreesaltvcJc accounts for the trivial displacement of salt in the opposite direction of the colloids, just like for the solvent molecules in eqn (4). If there is no salt added, in which case α → ∞ and ρ0 → 0, the above results in eqn (10) reduce to Jens− = 0, which complies with the fact that there are no negatively charged ions present, and Jens+ = ZJc, which implies that a colloid drags all its counter ions along with it. In the opposite situation when α ≪ 1, we have the leading order Jens± = [±(1/2)Z − ρfreesaltvc]Jc. The first contribution ±(1/2)Z is in accordance with colloids that drag along their electric double layer as predicted by standard linear Poisson–Boltzmann theory for a single spherical colloid. As already mentioned, the second term −ρfreesaltvcJc accounts for the displacement of salt contained in a volume vc in the opposite direction of a colloid. No linearization with respect to the potential within the double layer around the colloids has been made, so that the result in eqn (10) is valid within the realm of a non-linear Poisson–Boltzmann approach. In addition, the above relations are valid also for non-spherical colloids.
That ρfreesalt in eqn (13) is the salt concentration that does not involve the ions within the double layers that are dragged along with the colloids can be seen as follows: According to eqn (10), the expression between square brackets is equal to the number N± of ±-ions that is displaced along with a single colloid,
| | 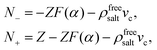 | (14) |
where a minus sign indicates displacement in the opposite direction of the colloids. The concentrations
ρfree± of ions that do not involve such colloid-enslaved ions are therefore equal to
ρfree± =
ρ± −
N±ρc. From
ρ− =
ρ0,
ρ+ =
ρ0 +
Zρc, and
eqn (12)–(14) it is found that
ρfree+ =
ρfree−, both being equal to the right hand-side of
eqn (13), which is therefore the salt concentration
ρfreesalt of free salt within the solvent outside the cores of the colloids.
Since we are interested in fluxes on time scales larger than relaxation times of ions, there are no ion fluxes other than those enslaved by the colloids. It follows that the fluxes,
| |  | (15) |
vanish. These definitions of the primed fluxes will be needed in the subsequent subsection to eliminate the solvent and ion fluxes from the original Onsager
relations (2), in order to reduce the number of flux–force relations to an effective one-component system.
2.3 Reduction of the Onsager flux–force relations
In this subsection, corresponding to the next step in our derivation in Fig. 1 vanishing of the fluxes in eqn (4) and (15) due to enslavement is used to derive an effective one-component colloid flux–force relation (see eqn (22)), which contains the as yet unknown modified Onsager coefficients ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) . This allows (as for any one-component system) to express the total force F in eqn (25) in terms of the effective chemical potential ν in eqn (20), the effective partial molar enthalpy in eqn (21), and the heat-of-transfer
. This allows (as for any one-component system) to express the total force F in eqn (25) in terms of the effective chemical potential ν in eqn (20), the effective partial molar enthalpy in eqn (21), and the heat-of-transfer 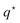 in eqn (26). The latter is the as yet unknown quantity. This total force is due to spatial gradients in temperature and colloid concentration, and also contains single-particle thermophoretic forces.
in eqn (26). The latter is the as yet unknown quantity. This total force is due to spatial gradients in temperature and colloid concentration, and also contains single-particle thermophoretic forces.
The flux–force relations (2) are reformulated in terms of the fluxes  in eqn (4) and (15), without yet setting these equal to zero, and the heat flux,
in eqn (4) and (15), without yet setting these equal to zero, and the heat flux,
| | | Jq = JU − h+J+ − h−J− − hsJs − hcJc, | (16) |
where the partial molar enthalpies of the ions are defined as,
| |  | (17) |
and similarly for the partial molar enthalpies
hs and
hc for the solvent and colloids, respectively. In terms of these fluxes, the Onsager
relations (2) become,
| |  | (18) |
with Onsager coefficients that differ from those in
eqn (2). By construction, the new Onsager coefficients are symmetric.
37,38 The new forces are equal to,
| | 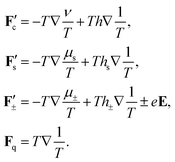 | (19) |
The “effective chemical potential”
ν is defined as,
| |  | (20) |
and the “effective partial molar enthalpy”
h is equal to,
| |  | (21) |
This new set of Onsager relations is completely equivalent to the original Onsager relations and therefore describes the same physical phenomena. In this respect we mention that although the electric field has disappeared from the force

, it is still in principle present in the colloid flux through the contribution

.
As discussed in the previous subsection, we set 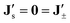 , which is a consequence of enslavement. This allows elimination of the forces
, which is a consequence of enslavement. This allows elimination of the forces  from the above Onsager relations (18) to arrive at an effective one-component flux–force relation,
from the above Onsager relations (18) to arrive at an effective one-component flux–force relation,
| |  | (22) |
The new Onsager coefficients can be expressed, with some effort, in terms of the symmetric Onsager coefficients in the flux–force
relations (18). These rather lengthy expressions show that symmetry is preserved, that is,
![[script L]](https://www.rsc.org/images/entities/char_e144.gif) cq
cq =
![[script L]](https://www.rsc.org/images/entities/char_e144.gif) qc
qc.
In the force  on the colloids, the macroscopic electric field is absent, which can be understood as follows. The total charge carried by the ions within a double layer is equal to e(N+ − N−) = Ze and therefore compensates the surface charge −Ze of a colloid. This confirms the well-known fact that a dressed colloid, including its electric double layer, is uncharged. The simultaneous displacement of the colloid together with its double layer does not lead to a change of the electrostatic energy, which is the reason for the absence of the electric field in the force
on the colloids, the macroscopic electric field is absent, which can be understood as follows. The total charge carried by the ions within a double layer is equal to e(N+ − N−) = Ze and therefore compensates the surface charge −Ze of a colloid. This confirms the well-known fact that a dressed colloid, including its electric double layer, is uncharged. The simultaneous displacement of the colloid together with its double layer does not lead to a change of the electrostatic energy, which is the reason for the absence of the electric field in the force 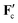 .
.
The interpretation of eqn (21) being an effective one-component partial molar enthalpy is as follows. As mentioned before, the contribution −ρfreesaltvc(h− + h+) accounts for the opposite displacement of a volume vc of dissociated salt solution. A similar opposite displacement of solvent is accounted for by the contribution −(vc/vs)hs. Furthermore, according to eqn (14), the number of positive ions contained within the electric double layer that is dragged along with the colloid is equal to N+ = Z[1 − F], while the number of enslaved negative ions is equal to N− = −ZF (as before, the minus sign indicates that the number of negative ions decreases upon displacement of the colloid). The electric double layer thus contributes
to the effective partial molar enthalpy, in accordance with
eqn (21).
Within the Onsager irreversible thermodynamics approach the temperature gradient and electric field induced deformation of the electric double layer is not accounted for. The enslavement relations (7) and (8) apply on length scales larger than the size of the irreversible thermodynamics volume elements, and therefore do not resolve the double layer structure around single colloids. The double layer deformation due to temperature gradients gives rise to a single-particle thermophoretic force, while the electric field induced double layer deformation gives rise to an electrophoretic force. The electrophoretic force in the present context will hereafter be referred to as the thermoelectrophoretic force. Both the resulting single-particle force and the thermoelectrophoretic force will be added by hand: our interest here is in the effect of inter-colloidal interactions on the electrophoretic force. The thermoelectrophoretic force Fel is proportional to the electric field up to leading order in spatial gradients, and can be written as,
where
μf is related to the electrophoretic mobility. The relation of
μf to the electrophoretic mobility will be discussed in Section 4. The origin of the macroscopic electric field will be discussed, and an explicit expression for the electric field will be derived, in Section 3. We note that the temperature-gradient induced deformation of the electric double layer of a colloid contributes to the single-particle thermophoretic force. The total deformation of the double layer is the sum of the deformation due to the macroscopic electric field (thermoelectricity) and the temperature gradient (single-particle thermodiffusion).
The colloid flux is driven by the total force F on a single colloidal particle,
| | Jc = ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) ccF, ccF, | (24) |
for which the following expression is found from
eqn (22) for the colloid number flux and
eqn (19) for the forces,
| | 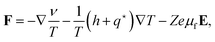 | (25) |
where the so-called heat-of-transfer is given by,
| |  | (26) |
The name “heat-of-transfer” refers to its contribution to the heat flux
Jq. From
eqn (22) it is readily seen that

for constant temperature (excluding mere heat conduction), which leads to the well-known interpretation of

being equal to the heat that is transported per colloidal particle.
37–39,42 The heat-of-transfer in the present case includes the solvent molecules and ions that are enslaved and dragged along with the colloid.
In ref. 27 and 28, the force on a colloid, including the thermophoretic force, is assumed to be given by the spatial gradient of a temperature dependent mean-field colloid–colloid interaction potential. Eqn (25), however, shows that the force contains several additional contributions, and in particular is non-conservative. Depending on the type of colloid under consideration, the temperature dependent part of the pair-interaction potential consists of an electrostatic contribution, van der Waals attractions, depletion attractions, and possible interactions between molecules grafted or adsorbed to the surfaces of the colloids.
Eqn (25) for the force is formally the same as for uncharged colloids as found in ref. 42, but now with additional contributions to ν from the ions, and with an additional thermoelectrophoretic force.
2.4 The force in terms of the colloid pressure pc
For the derivation of an expression for the heat-of-transfer, the force in eqn (25) on a colloid is first expressed in terms of gradients of the colloid pressure pc instead of the chemical potential ν, which is the subsequent step in our derivation as presented in Fig. 1. The resulting expression for the force is given in eqn (34). The colloid pressure, which is related to the osmotic pressure, is the contribution of the colloids to the total pressure, as will be discussed below.
The starting point is the Gibbs–Duhem relation for the suspension, which reads,43
| | 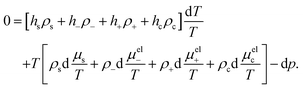 | (27) |
where, as before,
hs,±,c are the partial molar enthalpies,
ρs,±,c =
Ns,±,c/
V are the thermodynamic number concentrations of the solvent, the ions, and the colloids, respectively, and
p is the (total) pressure. Furthermore
μel±,c are the electro-chemical potentials,
| |  | (28) |
where, as before,
μ±,c are the purely chemical contributions and
Φ the electric potential corresponding to the macroscopic electric field
E. We note that, on the level of the above Gibbs–Duhem relation, the colloid electro-chemical potential pertains to the bare colloids, not including the enslaved ions or solvent molecules. The macroscopic electric field will be discussed in more detail in Section 3.
The fundamental difference between colloids and mixtures of simple fluids is that for the latter the total pressure cannot be written as a sum of the equations-of-state pressures for the otherwise pure species. For such systems, there are contributions to the pressure due to interactions between the various species in the mixture. Within the present approach, the system can be considered to consist of three independent subsystems. First, we have the colloids, including their electric double layers, which interact only amongst each other. Secondly, we have solvent molecules interacting with each other, while being confined to the volume outside the colloids. Finally, the excess (dissociated) salt molecules, with concentration ρfreesalt, that do not interact with the solvent, and similarly to the solvent have the same limited accessible volume.
As a consequence, the total pressure is a sum of three equation-of-state pressures, ps of pure bulk solvent, psalt of (dissociated) salt molecules, and the equation-of-state pressure pc resulting from the colloids. The latter pressure includes the interactions between the colloids due to enslaved ions present within the electric double layers. For spherical colloids, the equation-of-state pressure pc can be expressed in terms of an integral of the pair-correlation function and pair-interaction potential, as will be discussed in Section 4. Since within the Poisson–Boltzmann approximation the (dissociated) salt molecules behave as an ideal gas, as discussed before, their equation of state reads psalt = 2ρfreesaltkBT. That the total pressure can be written as such a sum of three independent equation-of-state pressures, can be shown similarly to that for uncharged colloids in Appendix B in ref. 42 based on the virial theorem, considering that the colloids with their double layers behave as a single species due to enslavement. Hence,
As in ref.
42, we will henceforth refer to
pc as the colloid pressure, which now includes the interactions between the colloids
via their electric double layers.
An effective one-component Gibbs–Duhem relation for the colloids can now be derived as follows. Within the Poisson–Boltzmann approximation, the ions do not occupy any volume, so that ρcvc + ρsvs = 1. Furthermore using eqn (1) and (9), imposing ion-enslavement, it follows that ρ+ − Zρc = ρ0 and ρ− = ρ0, with ρ0 the spatially varying salt concentration that would have existed in the absence of the colloids. In addition,
| | | ρ0 + ρcZF + ρcvcρfreesalt = ρfreesalt, | (30) |
which follows from the definition of
ρfreesalt in
eqn (13), as well as
F = 1/(2 +
α) with
α =
Zρc/
ρ0. Using these relations, together with
eqn (20) and (21) in order to eliminate d(
νc/
T) and
hc in favour of d(
ν/
T) and
h, it is found, with some effort, that the suspension Gibbs–Duhem relation
(27) can be rewritten as,
| | 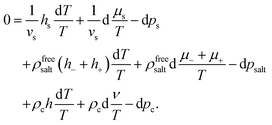 | (31) |
As mentioned earlier, each irreversible thermodynamics volume element is in internal equilibrium, and the solvent molecules and salt do not interact with each other nor with the colloids (except for exclusion of volume). The relation between variations of temperature, chemical potential, and the pressure for the solvent and the salt between the volume elements are therefore given by their corresponding Gibbs–Duhem relations. The first two lines in the suspension Gibbs–Duhem relation (31) therefore vanish (note that 1/vs is the solvent number concentration in bulk, outside the cores of the colloids). We thus arrive at the following effective one-component Gibbs–Duhem relation for the colloids,
| |  | (32) |
Since the infinitesimal differences can be related to the differences between the irreversible thermodynamics volume elements, the above Gibbs–Duhem relation implies that,
| | 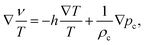 | (33) |
from which
eqn (25) for the force can be rewritten as,
| |  | (34) |
Except for the thermoelectrophoretic force, this expression for the force is formally identical to that for uncharged colloids.
42 However, both the colloid pressure and the heat-of-transfer now include the enslaved ions, that is, the electric double layer that is dragged along with the colloid. The earlier proposed expressions for the force in ref.
8,
24 and
29–31 do not include the contribution arising from the heat-of-transfer, while
pc is referred to as the osmotic pressure (although the correct equation-of-state pressure is used in these references in its virial expression, as will be further discussed in Section 5).
It is important to realize that the colloid pressure pc is not the osmotic pressure Π, which is commonly defined as the excess pressure of the suspension with respect to a salt reservoir with a separating membrane that is permeable for solvent molecules and salt ions. For example, for low colloid concentrations and for ideal salt solutions pc = ρckBT, while Π = [ρc + ρ− + ρ+ − 2ρRsalt]kBT, with ρ± the ion concentrations within the suspension and ρRsalt the number concentration of salt in the reservoir.44,45
Note that the heat-of-transfer 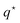 is responsible for the Dufour effect, where transport of particles gives rise to a temperature gradient.
is responsible for the Dufour effect, where transport of particles gives rise to a temperature gradient.
2.5 Expression for the heat-of-transfer and the total thermophoretic force
As the last step in Fig. 1 to arrive at an explicit expression for the thermophoretic force, the remaining unknown quantity needed to fully specify the total force in eqn (34) is the heat-of-transfer  . In this subsection, an explicit expression for the heat-of-transfer is derived. The expression for
. In this subsection, an explicit expression for the heat-of-transfer is derived. The expression for  in eqn (37) contains the internal energy u per colloidal particle, which is an additive contribution uint due to colloid–colloid interactions and usingle from single colloids. This finally leads to eqn (39), where fint and fsingle are defined in eqn (38).
in eqn (37) contains the internal energy u per colloidal particle, which is an additive contribution uint due to colloid–colloid interactions and usingle from single colloids. This finally leads to eqn (39), where fint and fsingle are defined in eqn (38).
The derivation of an expression for the heat-of-transfer follows the same lines of reasoning as for uncharged colloids in ref. 42. First, the force on a colloid due to mere heat conduction (without particle transport) is neglected. The motivation for this approximation is that microstructural ordering of the colloids, contrary to simple liquids, is not affected by mere heat conduction (heat conduction in the absence of particle transport) since colloids behave in that respect as macroscopic objects. Secondly, the forces on the colloids due to pressure gradients as a result of gradients in concentration and temperature need not be considered in the calculation of the heat-of-transfer, since these forces are already included in the first term on the right hand-side in eqn (34) for the force. In fact, the force has been expressed in terms of the pressure in favour of the chemical potential to render the calculation of the heat-of-transfer feasible.
As in ref. 42 we consider two irreversible thermodynamics volume elements which are thermally isolated from their surroundings and from each other. We next pull, by means of an external force balancing the force in eqn (34) a colloid from one volume element to the other. By isolation of the volume elements, we have excluded the possibility of mere heat conduction. The work done by the external force then consists of work against pressure gradients and work needed to change the thermodynamic internal energy u per colloid. Therefore,
| |  | (35) |
where Δ
FT denotes the thermophoretic force responsible for the changing internal energy. As before, displacing a single colloid implies displacing enslaved solvent and ions, so that
| | 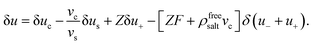 | (36) |
The interpretation of each of the terms on the right hand-side is the same as that discussed for the effective molar enthalpy in Section 2.3. It thus follows that,
| |  | (37) |
The variation of the effective partial molar internal energy comprises an additive contribution δ
uint from interactions between neighbouring colloids and a single-particle contribution δ
usingle, that is, δ
u = δ
uint + δ
usingle. The single-particle contribution is understood to include the internal energy involving the earlier discussed opposite displacement of a volume
vc of solvent molecules and salt.
For convenience we introduce the abbreviations,
| | 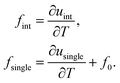 | (38) |
In addition to the contribution to the single-particle thermophoretic force that follows from
eqn (37) for

, we introduced
f0 in the above expression for
fsingle. This additional contribution accounts for effects such as solvent flow induced by the interface between the solvent and the solid core of the colloids.
22 For charged colloids, for example, it is well-known that electro-osmotic flow plays a role in addition to the temperature dependence of the internal thermodynamic energy
usingle of the electric double layer. To leading order in spatial gradients, such phenomena do not give rise to additional colloid–colloid interaction forces.
We thus find,
| | 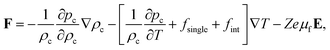 | (39) |
where both
pc and
fint are functions of just two variables
ρc and
T, as is evident from the effective one-component Gibbs–Duhem relation in
eqn (32).
In the comparison to experiments, fsingle is determined from thermophoretic data extrapolated to zero concentration. In addition to the purely thermodynamic contribution to fsingle in eqn (38), there are in general contributions that cannot be described on the basis of thermodynamics alone, due to temperature-gradient induced solvent flow.19,37,46–49
The above expression for the force is formally identical to that for uncharged colloids.42 The new aspect of the current discussion is that the ions which are dragged along with the colloids, which give rise to additional interactions between the colloids, are fully accounted for through the colloid pressure and the thermophoretic interaction force. Eqn (39) is more general than just for uncharged colloids.
In the following section an explicit expression for the macroscopic electric field is derived, which then specifies the thermoelectrophoretic force in eqn (39).
3 The macroscopic electric field: Donnan and Seebeck contributions to thermoelectricity
The phenomenon in which an electric field arises as a result of a temperature gradient is commonly referred to as thermoelectricity. There are two mechanisms for colloidal suspensions giving rise to thermoelectricity. One mechanism arises from concentration gradients of the colloids (also in the absence of a temperature gradient) and one from temperature gradients (also in the absence of colloid concentration gradients). Both mechanisms will be discussed below.
First, the local Donnan electric potential within an irreversible thermodynamics volume element is defined as the volume averaged electric potential of a unit charge. That potential depends on the concentration of the colloids, and thus varies between volume elements, giving rise to a Donnan electric field. In a closed system, there are oppositely charged layers formed at the opposite (uncharged) walls of the sample container. These thin charged layers on either side of the container lead to the Donnan electric field, even though the bulk system is locally electro-neutral (see also the discussion at the end of Appendix A). This is very similar to the electric field that exists in an isothermal diffusion-sedimentation equilibrium of charged colloids.50,51
The second contribution to the macroscopic electric field is due to the disproportional accumulation of different species of ions at the walls of the sample container as a result of their different thermophoretic mobilities.31,52–57 This mechanism is similar to the Seebeck effect in solid state physics, where electrons accumulate at the walls of a conducting material (see, for example, ref. 58). That contribution to the electric field is therefore referred to as the Seebeck electric field. Within the Poisson–Boltzmann approximation used in the present approach, the ±-ions have identical Soret coefficients being equal to 1/T so that the Seebeck electric field in our approach is absent.
We note that within the present approach, an additional external electric field will not give rise to an additional electrophoretic force. Enslavement implies complete electrode polarization: double layers are present at the walls of the sample container which compensate the externally applied charge, leading to a zero additional macroscopic field within the bulk of the suspension. In electrophoresis experiments, enslavement of the ion concentration profiles must therefore be avoided. This is accomplished by using a large distance between the electrodes (which enhances the time to establish electrode polarization), and switching the direction of the external field before electrode polarization kicks in (see, for example, ref. 59 and references therein).
An expression for the macroscopic Donnan electric field can be obtained by subtraction of the two eqn (7) for the ±-ions, and using that ∇ρ+ = ∇ρ− + Z∇ρc which follows from local electro-neutrality as discussed in Section 2.2, leading to,
| |  | (40) |
where, as before,
α =
Zρc/
ρ0, with
ρ0 =
ρ− is the spatially varying local thermodynamic number concentration of negative salt ions (see
eqn (1)), and
φ is the volume fraction of colloids.
Eqn (40) for the Donnan electric field in the presence of a temperature gradient has not been derived before. The contribution ∼∇
T to the Donnan electric field stems from the temperature dependent structure of the electric double layers of the colloids.
The thermoelectrophoretic force in eqn (23) is thus equal to,
where,
| | 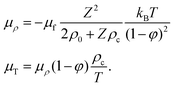 | (42) |
where it is used that
α =
Zρc/
ρ0 (see
eqn (12)).
The response to a given temperature gradient in terms of the resulting colloid concentration gradient in the stationary state, which is often probed in experiments, is quantified by the Soret coefficient ST, which is defined as,
| |  | (43) |
The Donnan electric field in
eqn (40) in the stationary state can be rewritten as,
| |  | (44) |
Although this is the Donnan electric field, one can formally define the Seebeck coefficient
Se in the stationary state as
E =
Se∇
T. From the above expression for the electric field, the following relation between the Soret coefficient and the Seebeck coefficient is obtained as
| |  | (45) |
For non-interacting colloids and without colloid-internal degrees of freedom contributing to single-particle thermophoresis, we have
ST = 1/
T, and hence
Se ∼
φ/(1 −
φ)
2. For very dilute suspensions, the Seebeck coefficient is therefore, as expected, solely due to single-particle contributions to the colloid's Soret coefficient.
An expression for the macroscopic electric field in the stationary state is proposed in ref. 57 on the basis of a Nernst–Planck approach. In this approach the variation of the Donnan potential as a consequence of the varying colloid concentration and temperature is not included. In addition, the heat-of-transfer for the colloids is not accounted for. A relatively large increase of the Seebeck coefficient is experimentally observed in ref. 60 upon adding colloids to an electrolyte solution, which might be due to the Donnan electric field in eqn (40).
There are some studies on thermoelectricity of suspensions of colloids with added salt which indicate that once colloids accumulate at the container walls, specific interactions with the wall lead to a significant chance of the thermoelectric potential.61,62 The details of such electrode-specific interactions are as yet unclear.
4 The Soret and thermodiffusion coefficient
Here, microscopic expressions for the Soret coefficient ST (defined in eqn (43)) and the thermodiffusion coefficient DT (see eqn (49)) will be discussed. This allows in principle for a particle-based evaluation of ST and DT as far as the collective contributions are concerned. The single-particle contribution fsingle in eqn (39) for the force requires a separate theoretical approach for each different type of colloid particles.
In typical closed systems, like for example in cells with thermalized boundaries, as well as in thermodiffusion forced Rayleigh scattering (TDFRS) experiments,63,64 the colloid flux vanishes in the stationary state. A vanishing flux implies a vanishing force on the colloidal particles. It thus follows from eqn (39) and (41)–(43) that
| |  | (46) |
The coefficients
μρ and
μT will be specified in terms of the electrophoretic mobility
μel below (see
eqn (53)).
Eqn (39) for the force, and hence the above expression for the Soret coefficient, is valid for any type of geometry of the core of the colloids, spherical, rod-like, plate-like, or otherwise. For spherical colloids, for which the theory will compared to experiments below, a particle-based approach is feasible, based on the expressions,42,65
| |  | (47) |
where
V(
R) is the pair-interaction potential between the colloids, and
geq(
R) is the equilibrium pair-correlation function which specifies the probability to find two colloids a distance
R apart. The pair-correlation is understood to be evaluated at a local temperature and colloid concentration.
The transient dynamics in reaching the stationary state is governed by the phenomenological diffusion equation,
| | 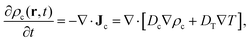 | (48) |
where
Dc is collective diffusion coefficient, and
DT is the thermodiffusion coefficient.
Eqn (24) and (39) lead to the following expressions for these diffusion coefficients,
| |  | (49) |
From the well-known expression for the collective diffusion coefficient of spherical colloids in the absence of thermoelectricity,
66–69 it immediately follows that the mobility
![[script L]](https://www.rsc.org/images/entities/char_e144.gif) cc
cc is equal to
| | ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) cc = D0ρcβH0, cc = D0ρcβH0, | (50) |
where
D0 =
kBT/6π
ηsa is the Stokes–Einstein–Sutherland diffusion coefficient for non-interacting colloids (
ηs is the solvent shear-viscosity),
β = 1/
kBT, and the hydrodynamic mobility function is defined as (with
![[k with combining circumflex]](https://www.rsc.org/images/entities/b_char_006b_0302.gif)
=
k/
k the unit vector in the direction of the wave vector
k),
| |  | (51) |
Here, 〈·〉
0 denotes the equilibrium average with respect to the position coordinates {
ri|
i = 1, 2, …
Nc} of the colloids, and the tensors
Dij specify hydrodynamic interactions between the colloids.
66–69 Note that
H0 is a function of the local colloid concentration and temperature through the probability density function with respect to which the average 〈·〉
0 in
eqn (51) is taken. We note that a non-zero wave vector
k has a significance in light, X-ray, and neutron scattering experiments, being related to the wave length and scattering angle.
66–69
We note that the expression for the collective diffusion coefficient is the short-time coefficient, whereas the diffusion coefficient in eqn (49) is the long-time diffusion coefficient. It is well-known, however, that the zero-wavevector limit of the short-time collective diffusion coefficient is essentially equal to the long-time diffusion coefficient.70–72
The relation between μf in eqn (23) and the electrophoretic mobility μel is as follows. By definition, v = μelE, v being the field-induced velocity of a colloid. The colloid flux due to that velocity is Jel = ρcv = ρcμelE. On the other hand, from eqn (23) and (24), Jel = ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) ccFel = −
ccFel = −![[script L]](https://www.rsc.org/images/entities/char_e144.gif) ccZeμfE, and hence,
ccZeμfE, and hence,
| |  | (52) |
The relation between the coefficients
μρ and
μT in
eqn (46) for the Soret coefficient, according to
eqn (42) and (52), thus reads (using that
β = 1/
kBT),
| |  | (53) |
Well-known expressions for the electrophoretic mobility
μel on the single-particle level in terms of the surface charge
Z and the salt concentration
ρ0 exist. It should be noted, however, that colloid–colloid interactions give rise to a concentration dependence of the electrophoretic mobility, for which simulation data are available for particular system parameters (see ref.
73–76 and references therein).
The above expressions for the Soret coefficient and the thermodiffusion coefficient allow in principle for a microscopic, particle-based test of the validity of the theory for spherically shaped colloids.
5 Comparison with experiments
For a detailed comparison of the theory with experiments, a set of thermophoretic data as a function of the colloid concentration, temperature, and salt concentration is required, preferably with a characterization of the temperature and salt-concentration dependence of the pair-interaction potential (similar to the uncharged colloids in ref. 42). Such data are unfortunately not available for charged colloids. The most complete set of thermophoretic data of charged colloids that allow a comparison to the theory to some extent concerns micellar sodium dodecyl sulfate (SDS) suspensions.
It is stated in ref. 31 that for the micellar SDS suspensions under consideration no significant thermoelectric contributions to experimental Soret coefficients are found, which is in accordance with the present theory, as shown in Appendix B.
In ref. 12, 30 and 31 the Soret coefficient for SDS micelles is reported as a function of the NaCl concentration at a fixed temperature. Here, it is found that 1/ST varies linearly with the micellar concentration for various NaCl salt concentrations, up to micellar concentrations of about 20 g dm−3. The slope of these curves can be determined from eqn (46) for the Soret coefficient.
First, it follows from eqn (46), by neglecting thermoelectricity,31 that the single-particle Soret coefficient S0T is equal to
| |  | (54) |
so that the Soret coefficient can also be written as,
| |  | (55) |
Expanding both the numerator and the denominator to leading order in concentration, using that
pc =
kBTρc[1 +
B2ρc], where
| |  | (56) |
is the second virial coefficient, leads to,
| | 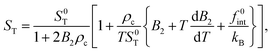 | (57) |
with (see
eqn (47)),
| |  | (58) |
considering
geq(
R) = exp{−
V(
R)/
kBT} at low concentrations. The linear dependence of 1/
ST on the micellar SDS concentration that is found in ref.
12,
30, and
31 suggests that the term in the numerator involving the curly brackets in
eqn (57) is small compared to unity. Expanding the corresponding term in the expression for 1/
ST up to leading terms in concentration leads to
| |  | (59) |
where,
| |  | (60) |
The coefficient
k is not to be confused with the wave vector in
eqn (51).
The term in the curly brackets has not been included in the data interpretation in ref. 12, 30 and 31. In ref. 12 and 30 a typical ratio k/2B2 was approximately equal to 2, while in ref. 31 a typical ratio close to 1 was reported.
To obtain numerical values for k, we need values for S0T, B2, dB2/dT, and f0int. Values for S0T can be directly obtained from extrapolation of data in ref. 12 and 30 for 1/ST to zero micellar SDS concentration. The results are given in Fig. 2, for 25 °C at which the thermophoretic experiments were performed. Values for B2 and dB2/dT can be obtained from independent light scattering data in ref. 77–79, albeit for a single NaCl concentration of 100 mM. How to obtain the second viral coefficients B2 in units of nm3 from those reported in ref. 77–79 is discussed in Appendix C. The resulting second virial coefficient B2 in units of nm3 is given in Fig. 3 as a function of temperature for a salt concentration of 100 mM. Independent values for f0int are not available. However, the amplitude f0int can be expressed in terms of the second virial coefficient up to leading order in Vel/kBT (with Vel the electric contribution to the pair-interaction potential), which leads to f0int/kB = B2 + TdB2/dT, and hence,
Accepting this estimate, the numerical value of
k for 25 °C and an NaCl concentration of 100 mM can be obtained from
Fig. 2 and 3, although numerical errors are quite substantial. From
Fig. 2 it is found, for
T = 298 K, that 1/(
TS0T) = 0.071 ± 0.015, and from
Fig. 3,
Td
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
ln
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) B2
B2/d
T = −(6.3 ± 2.7). It thus follows that Δ
k/2
B2 = 0.38 ± 0.30. In ref.
12 and
30 it was reported that Δ
k/2
B2 = 1, with an equally large experimental error, while in ref.
31 a smaller value was found. The above theoretical estimate is therefore in agreement with those experiments, although error margins are quite substantial.
 |
| | Fig. 2
TS
0T as a function of the salt concentration in moles NaCl per dm3. These data are obtained from Fig. 1 in ref. 30 by linear extrapolation. The ambient temperature is 25 °C. The solid line is a guide to the eye. | |
 |
| | Fig. 3 The second virial coefficient as a function of temperature at a NaCl concentration of 100 mM obtained from data in ref. 78 (◇), ref. 77 (■), and ref. 79 (●). The solid line is a guide to the eye. | |
In ref. 32 the Soret coefficient for the same micellar SDS system is reported as a function of temperature for two NaCl concentrations (10 and 20 mM), and for two surfactant concentrations (10 and 20 g dm−3). As discussed in the Appendix C, this allows in principle for the determination of numerical values for k in eqn (60) as a function of temperature for the two salt concentrations from eqn (59). The necessary independent information for the temperature- and salt-concentration dependence of the micellar molar mass and critical micellar concentration (cmc) can be found in ref. 77–80. As discussed in Appendix C, the substantial variation of reported values for the molar mass and cmc as a function of temperature does not allow for a (semi-) quantitative comparison. Note the quite substantial variation of reported data on micellar systems is also reflected in the variation between B2's taken from ref. 77–79 as plotted in Fig. 3.
As mentioned above, there are at present no experimental thermophoresis data available where the colloid concentration, temperature, and ionic strength are systematically varied, together with a characterization of the colloids concerning their size and effective surface charge. Such data would allow for a quantitative comparison to our theory, similar to that for uncharged colloids in ref. 42.
6 Summary and conclusions
We present an irreversible thermodynamics analysis of the thermodiffusion of charged colloids, focussing on the effect of colloid–colloid interactions. This is an extension of our earlier work on uncharged colloids.42 The starting points are the irreversible thermodynamics flux–force relations in eqn (2) and (3) for the colloids, solvent molecules, and ions. Due to the relatively fast dynamics of the solvent molecules and ions as compared to the colloids, the spatially varying solvent and ion concentrations quasi instantaneously adjust to the relatively slowly varying colloid's concentration profile. This allows us to derive enslavement relations, where the fluxes of solvent molecules and ions are proportional to the colloid flux (see eqn (4) and (15)), with vanishing  ). This in turn allows reducing the flux–force relations to the effective one-component colloid flux–force relation in eqn (19) and (22). Subsequently this leads to the expression (25) for the force on a single colloid, which contains the still unknown heat-of-transfer. The Onsager irreversible thermodynamics approach does not account for deformation of the electric double layers of the colloids due to the macroscopic electric field. The corresponding thermoelectrophoretic force in eqn (23) is therefore added by hand in eqn (25) for the total force. After expressing the force on a colloidal particle in terms of spatial gradients of the colloid pressure (see eqn (34), an approximate expression for the heat-of-transfer is derived (see eqn (37)), which contains both single-particle and collective contributions. The approximation involves neglecting pure heat conduction (that is, heat conduction in the absence of colloid migration), which is argued to be a good approximation due to the relatively large size of the colloids. The total force in eqn (39) is valid for arbitrary core geometries (spherical, rod-like, plate-like, etc.) and arbitrary surface charge density. It consists of a single-particle thermophoretic force, a term proportional to the spatial gradient of the colloid pressure, a thermoelectrophoretic force, and a thermophoretic force that we refer to as the thermophoretic interaction force. In a closed system, the stationary state implies a zero flux and hence a zero force, which leads to the explicit expression (46) for the Soret coefficient. An expression for the mobility, valid for spherical colloids, is then derived, which leads to an explicit expression for the thermodiffusion coefficient (see eqn (49)–(51)). The coefficients μρ and μT in the expression (46) for the Soret coefficient and eqn (49)–(51) for the diffusion coefficients, which account for the thermoelectrophoretic force, are expressed in terms of the electrophoretic mobility in eqn (53), for the derivation of which the expression (44) for the macroscopic electric field is essential. The colloid–colloid interaction contributions to the Soret and thermodiffusion coefficients can be expressed in terms of integrals of the pair-interaction potential and the pair-interaction function (see eqn (47)), which are valid for spherical colloids). This allows in principle a particle-based, microscopic comparison of the theory with experiments.
). This in turn allows reducing the flux–force relations to the effective one-component colloid flux–force relation in eqn (19) and (22). Subsequently this leads to the expression (25) for the force on a single colloid, which contains the still unknown heat-of-transfer. The Onsager irreversible thermodynamics approach does not account for deformation of the electric double layers of the colloids due to the macroscopic electric field. The corresponding thermoelectrophoretic force in eqn (23) is therefore added by hand in eqn (25) for the total force. After expressing the force on a colloidal particle in terms of spatial gradients of the colloid pressure (see eqn (34), an approximate expression for the heat-of-transfer is derived (see eqn (37)), which contains both single-particle and collective contributions. The approximation involves neglecting pure heat conduction (that is, heat conduction in the absence of colloid migration), which is argued to be a good approximation due to the relatively large size of the colloids. The total force in eqn (39) is valid for arbitrary core geometries (spherical, rod-like, plate-like, etc.) and arbitrary surface charge density. It consists of a single-particle thermophoretic force, a term proportional to the spatial gradient of the colloid pressure, a thermoelectrophoretic force, and a thermophoretic force that we refer to as the thermophoretic interaction force. In a closed system, the stationary state implies a zero flux and hence a zero force, which leads to the explicit expression (46) for the Soret coefficient. An expression for the mobility, valid for spherical colloids, is then derived, which leads to an explicit expression for the thermodiffusion coefficient (see eqn (49)–(51)). The coefficients μρ and μT in the expression (46) for the Soret coefficient and eqn (49)–(51) for the diffusion coefficients, which account for the thermoelectrophoretic force, are expressed in terms of the electrophoretic mobility in eqn (53), for the derivation of which the expression (44) for the macroscopic electric field is essential. The colloid–colloid interaction contributions to the Soret and thermodiffusion coefficients can be expressed in terms of integrals of the pair-interaction potential and the pair-interaction function (see eqn (47)), which are valid for spherical colloids). This allows in principle a particle-based, microscopic comparison of the theory with experiments.
The main results are summarized in Section 4: the Soret coefficient is given in eqn (46) (where μρ and μT specify the contributions from electrophoresis, which are given in eqn (53)), and the collective and thermodiffusion coefficients are given in eqn (49) and (50) (where H0 is the hydrodynamic mobility function, which is defined in eqn (51)).
To within the Poisson–Boltzmann approximations that were made, and assuming enslavement of the ion concentrations, there is a macroscopic electric field that is given in eqn (44). This expression for the macroscopic electric field is a necessary input to quantify the thermoelectrophoretic force in eqn (23). The electric field is solely due to the spatial variations of the Donnan potential, which is very similar to the field that exists in an isothermal diffusion–sedimentation equilibrium for charged colloids.50,51
That the force on a colloid in a temperature gradient is proportional to spatial gradients of the colloid pressure has been suggested before in ref. 8, 24 and 29–31, albeit without further justification and without inclusion of the thermophoretic interaction force. The force on a colloid is argued in ref. 27 and 28 to be proportional to gradients of the mean-field colloid–colloid interaction potential, which resembles the present thermophoretic interaction force that originates from the heat-of-transfer. Forces due to gradients of the colloid pressure are not included in these latter papers. Moreover, a term proportional to the concentration derivative of the colloid–colloid interaction potential appears in ref. 27 and 28 that is absent within our theory. The theory presented here provides a systematic approach that leads to the force in eqn (39) that contains contributions resulting from gradients of the colloid pressure (like in ref. 8, 24 and 29–31), as well as the gradient of the colloid–colloid interaction potential as far as its temperature dependence is concerned (like in ref. 27 and 28, except that there the concentration derivative of the colloid–colloid interaction energy should be omitted).
The colloid pressure pc in eqn (47) should not be confused with the osmotic pressure Π. The colloid pressure is the contribution to the total suspension pressure originating from the presence of the colloids in a closed system. The osmotic pressure on the contrary is the excess pressure of the suspension with respect to an osmotic reservoir, with a membrane that is permeable for both solvent molecules and ions. This is most explicitly seen from the expression Π = (ρc + ρ− + ρ+ − 2ρR±)kBT for the osmotic pressure at low colloid concentrations,44,45 for which pc = ρckBT.
A comparison of the theory with experiments for uncharged colloids requires data where the concentration and temperature are systematically varied ref. 34 and 42. For charged colloids, where also the ionic strength is varied, are not available. The only experiments that allow for a comparison to some extent are those conducted on a micellar sodium dodecyl sulphate (SDS) system.12,30–32 In these references the inverse Soret coefficient (without the contribution from the thermophoretic interaction force) is expanded to leading order in concentration. In that case, apart from the single-particle contribution, the only unknown parameter that is left is the second-order virial coefficient originating from the colloid pressure. For such micellar SDS systems additional information is necessary, such as the temperature and concentration dependence of the molar mass and the critical micellar concentration. The limited available data and the variation of such data between different publications77–80 unfortunately renders a conclusive quantitative comparison not feasible. We presented a comparison that indicates that the thermophoretic interaction force could explain differences between second-virial coefficients obtained from thermophoresis experiments as described above12,30–32 and those obtained by independent light scattering experiments.77–80
Experiments on well-defined charged colloids where the colloid concentration, ionic strength, temperature, and possibly the colloid's charge are systematically varied are required for a conclusive comparison with the theory. A particle-based comparison would also provide access to knowledge of the pair-interaction potential and the pair-correlation function.
The results obtained here for charged colloids are applicable to other types of colloids as well. The analysis is equally valid in case there are additional colloid–colloid direct interactions, on top of the excluded-volume and double-layer interactions, due to for example, van der Waals attractions and/or an uncharged polymer brush grafted to the surface of the colloids. Furthermore, for the additional presence of relatively small solutes, their enslavement can be assumed just as for ions.
The main assumption in our treatment of the ions is conform those made in the classic Poisson–Boltzmann approach of charged colloids.41 The ions are assumed to behave as an ideal gas, and only respond to the (mean) electric field that is generated by the colloid's surface charges and the unequal ±-ion concentrations within the double layers. This is a crucial assumption for the formulation of eqn (7), which is one of the equations to obtain the ion-enslavement relations. This equation is also at the origin of the expression (40) for the macroscopic electric field. Including interactions between the ions would be an important generalization of the theory towards very high salt concentrations.
Data availability
All data are displayed within the paper.
Conflicts of interest
There are no conflicts to declare.
Appendices
A: Derivation of the enslavement relations
First, we rewrite eqn (7), as,| |  | (61) |
Adding the equation for the ± ions eliminates the electric field, and leads to| |  | (62) |
Performing the differentiation gives,| |  | (63) |
and hence,| | ∇![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ρens+ + ∇ ρens+ + ∇![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ρens− + ∇ ρens− + ∇![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) T2 − ∇ T2 − ∇![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(1 − φ)2 = 0. ln(1 − φ)2 = 0. | (64) |
It thus follows that,| | 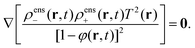 | (65) |
As before, the superscript “ens” refers to enslavement. Note that we consider throughout this paper a time independent, externally imposed temperature gradient, so that T ≡ T(r) is independent of time. Since eqn (65) holds for all times, we also have,| |  | (66) |
where δt is an infinitesimally change of the time. During the time interval (t,t + δt), the colloid concentration profile changes from ρc(r,t) to ρc(r,t) + δρc(r,t) and the ion concentrations change from ρens±(r,t) to ρens±(r,t) + δρens±(r,t). Subtracting eqn (65) and (66) this leads to, up to leading order in the changes of the concentrations (not denoting the position and time dependencies for brevity),| |  | (67) |
Since linear irreversible thermodynamics assumes from the outset small spatial gradients, and δρens± and δφ are by definition infinitesimally small differences, products of gradients with either δρens± or δφ can be neglected, so that eqn (67) leads to| |  | (68) |
The combination within the square brackets is thus a function of time only. Dividing by ρens−ρens+ and using that φ = vcρc thus gives,| | 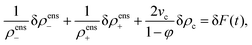 | (69) |
where δF(t) is the infinitesimally small change of the as yet unknown function F(t) during the time interval δt. That δF(t) = 0 can be shown as follows. Since δρens± = δt(∂ρens±/∂t) = −δt∇·Jens± and similarly δρc = −δt∇·Jc, while the fluxes are linear in gradients, eqn (69) can be written as,| |  | (70) |
up to linear order in gradients, where products of two gradients are neglected. Due to the impermeability of the boundary of the system (the wall of the sample container) for ions and colloids, the components of fluxes normal to the boundary vanish. Therefore, according to Gauss' integral theorem, the integral over the volume of the system of the left hand-side of eqn (70) vanishes. The integral on the right hand-side is equal to (δF(t)/δt) × V, with V as the volume of the system. It thus follows F is independent of time, so that δF in eqn (69) vanishes, and hence,| |  | (71) |
The number-concentration increments δρ±,c are directly correlated with their corresponding fluxes. Enslavement implies that each colloid drags along with it, in the same direction, a proportional amount of positive and negative ions. These amounts of ±-ions that are dragged along with a single colloid correspond to are specified by eqn (71) as δρens±/δρc = −ρens±[2vc/(1 − φ)]. Since the ions are dragged along with the colloids, it follows directly from eqn (71) that
| |  | (72) |
In order to obtain the second enslavement relation, we calculate ∇·[εsE] from eqn (7) and compare the result to eqn (8). Subtraction of the eqn (7) for ρens+ and ρens− leads to the following expression for the electric field,
| | 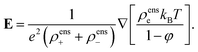 | (73) |
Within linear irreversible thermodynamics, products of two gradients are neglected. Multiplication of
eqn (73) with
εs then leads to
| |  | (74) |
where
κ−1 is the Debye screening length,
| | 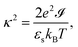 | (75) |
with
![[scr I, script letter I]](https://www.rsc.org/images/entities/char_e143.gif)
the ionic strength,
| |  | (76) |
Within the present setting, contrary to the classic Poisson–Boltzmann theory for single charged colloids, both the Debye length and the ionic strength are position dependent quantities that vary between irreversible thermodynamics volumes and are thus related to the macroscopically varying ion concentrations. Each term on the right hand-side of
eqn (74) is of the form
κ−2∇
2(·), which is the second order gradient contribution in a Taylor expansion of (·) over a distance equal to the Debye length
κ−1. Since the Debye length is of the order of the size of a colloid, these terms constitute the spatial variation of (·) within irreversible thermodynamics volume elements. The Onsager irreversible thermodynamics approach, (·) is assumed constant within irreversible thermodynamics volume elements which contain many colloids. The terms on the right hand-side of
eqn (74) are therefore of no significance within the present irreversible thermodynamics approach. In other words, the variation of (·) over distances comparable to the size of a single colloid is negligible as compared to the change of (·) over distances comparable to the size of irreversible thermodynamics volume elements. Within the bulk of the system, we thus find that
which implies local electro neutrality to leading order in spatial gradients. A small change δ
ρc thus leads to changes δ
ρens± equal to
| | | δρens+ − δρens− = Zδρc, | (78) |
and hence, similarly as discussed just below
eqn (71),
Combining eqn (72) and (79) it is found that,
| | 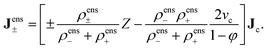 | (80) |
According to
eqn (1) for the (position dependent) concentration profiles
ρens± that exists under enslavement and the corresponding position dependent concentration
ρ0, together with the definitions in
eqn (11)–(13); this can be rewritten in the final form given in
eqn (10).
We note that the right hand-side of eqn (74) cannot be neglected in the Poisson equation to describe sample container wall effects. In an isothermal sedimentation–diffusion equilibrium, for example, similar contributions lead to thin charged layers of ions at the sample container walls with an extent of the order of the Debye length, within which κ−1∇(·) cannot be neglected.50 No approximation is made, however, neglecting these wall effects to correctly describe the electric field within the bulk of the system (see also the discussion section in ref. 51).
B: The significance of thermoelectrophoretic forces
An estimate of the significance of thermoelectrophoretic forces can be made on the basis of data provided in ref. 31 and 77–80: a ≈ 2.5 nm, Z ≈ 17 (less than the number of monomers due to physical adsorption of ions), B2 ≈ 8.2 × 10−25 m3, and the dimensionless electrophoretic mobility ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) el = (6πηsa/e)μel = 3Z/[2(1 + κa)] is equal to 7 (where κa = 2.6). Furthermore, dB2/dT ≈ −14 × 10−27 m3 K, and fsingle/kB = 13 (see eqn (54) and Fig. 2 for 100 mM salt). To within the second virial approximation it follows that, for T = 298 K, (1/kBT)(∂pc/∂ρc) ≈ 1 + 24φ, and (1/ρckB)(∂pc/∂T) + fsingle/kB ≈ 14 − 52φ. In addition, H0 ≈ 1, so that, ρcμρ/kBT ≈ μT/kB ≈ 290φ/(2ρ0vc + 17φ). For the 100 mM salt solution ρ0vc ≈ 4, so that it follows that, (∂pc/∂ρc)/(ρcμρ) ≈ (1 + 24φ)(8 + 17φ)/290φ and (∂pc/∂T + ρcfsingle)/(ρcμT) ≈ (14 − 52φ)(8 + 17φ)/290φ. The micellar SDS concentrations correspond to volume fractions 0.002 < φ < 0.02, so that 6 < (∂pc/∂ρc)/(ρcμρ) < 37 (the 6 for φ = 0.02 and 37 for φ = 0.002), and 46 < (∂pc/∂T + ρcfsingle)/(ρcμT) < 460 (the 460 for φ = 0.02 and 46 for φ = 0.002). The above lower limit of 6 is most probably about a factor 2 larger, since the μel decreases with increasing concentration. Thermoelectric contributions can thus be safely neglected against those from pressure gradients and single-particle forces for the micellar SDS system under consideration.
el = (6πηsa/e)μel = 3Z/[2(1 + κa)] is equal to 7 (where κa = 2.6). Furthermore, dB2/dT ≈ −14 × 10−27 m3 K, and fsingle/kB = 13 (see eqn (54) and Fig. 2 for 100 mM salt). To within the second virial approximation it follows that, for T = 298 K, (1/kBT)(∂pc/∂ρc) ≈ 1 + 24φ, and (1/ρckB)(∂pc/∂T) + fsingle/kB ≈ 14 − 52φ. In addition, H0 ≈ 1, so that, ρcμρ/kBT ≈ μT/kB ≈ 290φ/(2ρ0vc + 17φ). For the 100 mM salt solution ρ0vc ≈ 4, so that it follows that, (∂pc/∂ρc)/(ρcμρ) ≈ (1 + 24φ)(8 + 17φ)/290φ and (∂pc/∂T + ρcfsingle)/(ρcμT) ≈ (14 − 52φ)(8 + 17φ)/290φ. The micellar SDS concentrations correspond to volume fractions 0.002 < φ < 0.02, so that 6 < (∂pc/∂ρc)/(ρcμρ) < 37 (the 6 for φ = 0.02 and 37 for φ = 0.002), and 46 < (∂pc/∂T + ρcfsingle)/(ρcμT) < 460 (the 460 for φ = 0.02 and 46 for φ = 0.002). The above lower limit of 6 is most probably about a factor 2 larger, since the μel decreases with increasing concentration. Thermoelectric contributions can thus be safely neglected against those from pressure gradients and single-particle forces for the micellar SDS system under consideration.
C: Converting experimental second virial coefficients to B2
The experimental determination of the second virial coefficient and the molar mass M of colloids by means of static light scattering experiments is based on the following relation involving the (inverse) Rayleigh ratio R(k → 0), which goes back to Debye,81| |  | (81) |
where K is a constant, c is the colloid concentration in units g ml−1. Furthermore, B is the second virial coefficient in units ml mol g−2, which is proportional to the second virial coefficient B2 in eqn (56). To obtain the proportionality constant between B and B2, it is noted that (see, for example, ref. 69, Section 3.5),| |  | (82) |
Comparing the two expressions above, and using that ρc[#colloids per m3] = (NAv/M)106c [g ml−1], leads to,where B2 is understood to have the unit m3, M is expressed in units g mol−1, and the unit of B is already mentioned above. Experimental light scattering data for B are given in Fig. 4.77–79 The necessary temperature and salt-concentration dependence of the molar mass of SDS micelles, required to convert experimental values for B into B2, are given in Fig. 5 and 6, respectively, where the data are taken from the same references. These plots are used to generate Fig. 3 for B2versus temperature for cs = 100 mM in the main text.
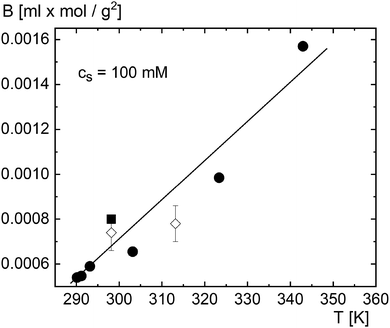 |
| | Fig. 4 The second virial coefficient B as defined in eqn (81) in units of ml mol g−2 for a NaCl concentration of cs = 100 mM, as a function of temperature. The data points ● are taken from ref. 79, the points are from ref. 78, and the point ■ is taken from ref. 77. Note that the definition of the second virial coefficient kI in eqn (3a) in ref. 78 differs by a factor of 2 M from the definition of the second virial coefficient B in ref. 77 and 79. | |
 |
| | Fig. 5 The molar mass of SDS micelles as a function of temperature at a salt concentration of 100 mM. The data points ● are taken from ref. 79, the two points ◇ from ref. 78, and the single point ■ from ref. 77. | |
 |
| | Fig. 6 The molar mass as a function of NaCl concentration for two temperatures. The data points ● and ○ are taken from ref. 78, for 25 and 40 °C, respectively. The points ■ for 25 °C are taken from ref. 77. The two points ◇ are obtained by interpolation of the data in Fig. 5 from ref. 79 to 25 and 40 °C. The points △ for 25 °C are from ref. 82. The solid lines are guides to the eye. | |
Also note that relation (3a) in ref. 78 implies that the numerical values for kI in Tables I and II in that reference (for 25 and 40 °C, respectively) are related to B as kI = 2MB. Alternatively, B2 can also be obtained from ref. 78 without the use of their eqn (3a), using the values for kI and the aggregation numbers m in Tables I and II (with the molecular weight of a single surfactant equal to M1 = 288 g mol−1), together with the relation  . The specific volume
. The specific volume ![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) of a micelle is obtained from the data for the radii in Tables III and IV in ref. 78, using that
of a micelle is obtained from the data for the radii in Tables III and IV in ref. 78, using that ![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) = [NAv/(mM1)]vc. The thus obtained numerical values for B2 are the two data points ⋄ in Fig. 3.
= [NAv/(mM1)]vc. The thus obtained numerical values for B2 are the two data points ⋄ in Fig. 3.
For a given temperature and salt concentration, eqn (59) predicts that,
| |  | (84) |
where the superscripts refer to two different micellar concentrations. Fig. 2 in ref.
32 allows in principle to obtain
k as a function of temperature for the two salt concentrations 10 and 20 mM. To this end, however, the concentration in units g dm
−3 must be converted to the number of colloids
ρc per unit volume, for which the molar mass is needed for the two salt concentrations as a function of temperature. Furthermore, the total surfactant concentration in terms of which Fig. 2 in ref.
32 is plotted, should be corrected for the cmc to obtain the concentration of the surfactant in the micellar form.
Without salt, the cmc is equal to (2.30 ± 0.15) mg ml−1 within the temperature range of 15–30 °C.83 In ref. 79, for a NaCl concentration of 100 mM, the cmc concentration of (0.41 ± 0.01) mg ml−1 is also found to be independent of the temperature within the temperature range of 17–30 °C. One can therefore safely assume that the cmc is independent of temperature within the temperature range of interest. For 25 °C the cmc is equal to 1.50 mg ml−1 for a NaCl concentration of 10 mM, and 0.43 mg ml−1 for 100 mM,82 and is found to vary from 2.65 to 0.53 mg ml−1 for salt concentrations varying from 10 to 100 mM in ref. 77. These data are plotted in Fig. 7, and are thus taken to be independent of temperature. For the salt concentrations of 10 and 20 mM it is found from Fig. 7 that cmc = (1.57 ± 0.10) mg ml−1 and (1.35 ± 0.10) mg ml−1, respectively. The molar mass on the contrary is a function of temperature, as shown in Fig. 5 and 6. For a salt concentration of 100 mM, the data for the molar mass in Fig. 6 are in quite good agreement between the varies reported values. For the salt concentrations of 10 and 20 mM used in the temperature dependent thermophoretic measurements in ref. 32, however, there is quite a significant variation between the reported values for the molar mass. It turns out that this variation leads to quite large errors in the expression (84) for k, and thus prevents us from a comparison of the experimental data in ref. 32 with theory.
 |
| | Fig. 7 The cmc, which is essentially constant within the temperature range 15–30 °C, as a function of NaCl concentration. The data points ■ are taken from ref. 77, the points ◇ from ref. 83, □ from ref. 79, and the points ○ from ref. 82. The solid line is a guide to the eye. | |
Notes and references
- C. Ludwig, Diffusion zwischen ungleich erwärmten Orten gleich zusammengesetzter Lösungen, Sitzungsber. Akad. Wiss. Wien, Math.-Naturwiss. Kl., 1856, 20, 539 Search PubMed.
- C. Soret, Sur l’état d’équilibre que prend au point de vue de sa concencentration une dissolution saline primitivement homogène dont deux parties sont portées à des températures différentes, Arch. Sci. Phys. Nat., 1879, 3, 48 Search PubMed.
- C. Soret, Influence de la température sur la distribution des sels dans leurs solutions, C. R. Hebd. Seances Acad. Sci., 1880, 91, 289 Search PubMed.
- C. Soret, Sur l’etat d’équilibre que prend, au point de vue de sa concentration, une dissolution saline primitivement homogène dont deux parties sont portées a des températures différentes, Ann. Chim. Phys., 1881, 22, 293 Search PubMed.
-
Thermal nonequilibrium phenomena in fluid mixtures, ed. W. Köhler and S. Wiegand, Springer-Verlag, Berlin, 2001 Search PubMed.
-
Thermodiffusion: Basics and application, ed. M. M. Bou-Ali and J. K. Platten, Mondragon Unibertsitatea, 2006 Search PubMed.
- M. A. Rahman and M. Z. Saghir, Thermodiffusion or Soret effect: Historical review, Int. J. Heat Mass Transfer, 2014, 73, 693 CrossRef.
- R. Piazza and A. Parola, Thermophoresis in colloidal suspensions, J. Phys.: Condens. Matter, 2008, 20, 153102 CrossRef.
- A. Würger, Thermal non-equilibrium transport in colloids, Rep. Prog. Phys., 2010, 73, 126601 CrossRef.
- W. Köhler and K. I. Morozov, The Soret effect in liquid mixtures-A review, J. Non-Equilib. Thermodyn., 2016, 41, 151 Search PubMed.
- S. Wiegand, Thermal diffusion in liquid mixtures and polymer solutions, J. Phys.: Condens. Matter, 2004, 16, 357 CrossRef.
- R. Piazza, Thermal diffusion in ionic micellar solutions, Philos. Mag., 2003, 83, 2067 CrossRef CAS.
- S. A. Putnam and D. G. Cahill, Transport of nanoscale latex spheres in a temperature gradient, Langmuir, 2005, 21, 5317 CrossRef CAS.
- K. I. Morozov, Thermal diffusion in disperse systems, J. Exp. Theor. Phys., 1999, 88, 944 CrossRef CAS.
- K. I. Morozov, Thermodiffusion in magnetic colloids, J. Magn. Magn. Mater., 1999, 201, 248 CrossRef CAS.
- S. Fayolle, T. Bickel and A. Würger, Thermophoresis of charged colloidal particles, Phys. Rev. E:Stat., Nonlinear, Soft Matter Phys., 2008, 77, 041404 CrossRef.
- S. N. Rasuli and R. Golestanian, Soret motion of a charged spherical colloid, Phys. Rev. Lett., 2008, 101, 108301 CrossRef PubMed.
- A. Würger, Transport in charged colloids driven by thermoelectricity, Phys. Rev. Lett., 2008, 101, 108302 CrossRef.
- J. K. G. Dhont and W. J. Briels, Single-particle thermal diffusion of charged colloids: Double-layer theory in a temperature gradient, Eur. Phys. J. E:Soft Matter Biol. Phys., 2008, 25, 61 CrossRef CAS PubMed.
- M. Yang, Y. Zhou, W. Chen, W. Wang and C. Yang, Thermal conductivity effect on thermophoresis of charged spheroidal colloids in aqueous media, Electrophoresis, 2023, 44, 1868 CrossRef CAS.
- Y. Zhou, Y. Yang, C. Zhu, M. Yang and Y. Hu, Numerical analysis of thermophoresis of a charged spheroidal colloid in aqueous media, Micromachines, 2021, 12, 224 CrossRef PubMed.
- J. L. Anderson, Colloid transport by interfacial forces, Annu. Rev. Fluid Mech., 1989, 21, 61 CrossRef.
- S. Iacopini and R. Piazza, Thermophoresis in protein solutions, Europhys. Lett., 2003, 63, 247 CrossRef CAS.
- A. Würger, Thermophoresis in colloidal suspensions Driven by Marangoni forces, Phys. Rev. Lett., 2007, 98, 138301 CrossRef CAS PubMed; P. Pulyala, M. Jing, W. Gao and X. Cheng, Solution composition dependent Soret coefficient using commercial micro scale thermophoresis instrument, RSC Adv., 2023, 13, 15901 RSC.
- K. I. Morozov and W. Köhler, Can the thermophoretic mobility of uncharged colloids be predicted?, Langmuir, 2022, 38, 2478 CrossRef CAS PubMed.
- A. Parola and R. Piazza, Particle thermophoresis in liquids, Eur. Phys. J. E:Soft Matter Biol. Phys., 2004, 15, 255 CrossRef CAS PubMed.
- E. Bringuier, A. Bourdon, Colloid transport in nonuniform temperature, Phys. Rev. E:Stat., Nonlinear, Soft Matter Phys., 2003, 67, 011404 CrossRef CAS PubMed.
- S. Fayolle, T. Bickel, S. Le Boiteux and A. Würger, Thermodiffusion of charged micelles, Phys. Rev. Lett., 2005, 95, 208301 CrossRef.
- A. Würger, Heat capacity-driven inverse Soret effect of colloidal nanoparticles, Europhys. Lett., 2006, 74, 658 CrossRef.
- R. Piazza and A. Guarino, Soret effect in interacting micellar solutions, Phys. Rev. Lett., 2002, 88, 208302 CrossRef.
- D. Vigolo, S. Buzzaccaro and R. Piazza, Thermophoresis and thermoelectricity in surfactant solutions, Langmuir, 2010, 26, 7792 CrossRef CAS.
- S. Iacopini, R. Rusconi and R. Piazza, The “macromolecular tourist”: Universal temperature dependence of thermal diffusion in aqueous colloidal suspensions, Eur. Phys. J. E:Soft Matter Biol. Phys., 2006, 19, 59 CrossRef CAS PubMed.
- N. Ghofraniha, G. Ruocco and C. Conti, Collective thermal diffusion of silica colloids studied by nonlinear optics, Langmuir, 2009, 25, 12495 CrossRef CAS.
- H. Ning, J. Buitenhuis, J. K. G. Dhont and S. Wiegand, Thermal diffusion behavior of hard-sphere suspensions, J. Chem. Phys., 2006, 125, 204911 CrossRef PubMed.
- L. Onsager, Reciprocal relations in irreversible processes. I, Phys. Rev., 1931, 37, 405–426 CrossRef CAS.
- L. Onsager, Reciprocal relations in irreversible processes. II, Phys. Rev., 1931, 38, 2265–2279 CrossRef CAS.
-
S. R. de Groot, Thermodynamics of irreversible processes, North-Holland Publishing Company, Amsterdam, 1966 Search PubMed.
-
S. R. de Groot and P. Mazur, Non-equilibrium thermodynamics, Dover Publications, New York, 1984 Search PubMed.
-
S. Kjelstrup and D. Bedeaux, Non-equilibrium thermodynamics of heterogeneous systems, World Scientific, New Jersey, 2008 Search PubMed.
- N. G. van Kampen, Onsager relations for transport in inhomogeneous media, J. Stat. Phys., 1991, 63, 1019 CrossRef.
-
R. Blossey, The Poisson-Boltzmann equation: an introduction, SpringerBriefs in Physics, Springer, 2022 Search PubMed.
- J. K. G. Dhont and W. J. Briels, Temperature-induced migration of electro-neutral interacting colloidal particles, J. Colloid Interface Sci., 2024, 666, 457 CrossRef CAS PubMed.
- The usual formulation of the (one-component) Gibbs–Duhem relation, 0 = −(1/ρ)dp + dμ + sdT, with s the partial molar entropy, is rewritten here as 0 = −(1/ρ)dp + Td(μ/T) + (h/T)dT, where it is used that μ = h − Ts.
- F. G. Donnan, Theorie der Membrangleichgewichte und Membran potentiale bei vorhandensein von nicht dialysierenden Elektrolyten. Ein Beitrag zur physikalisch-chemischen Physiologie, Z. Elektrochem. Angew. Phys. Chem., 1911, 17, 572 CrossRef CAS.
- A. P. Philipse and A. Vrij, The Donnan equilibrium: I. On the thermodynamic foundation of the Donnan equation of state, J. Phys.: Condens. Matter, 2011, 23, 194106 CrossRef CAS.
- J. Burelbach, D. Frenkel, I. Pagonabarraga and E. Eiser, A unified description of colloidal thermophoresis, Eur. Phys. J. E:Soft Matter Biol. Phys., 2018, 41, 7 CrossRef.
- J. Burelbach, D. B. Brückner, D. Frenkel and E. Eiser, Thermophoretic forces on a mesoscopic scale, Soft Matter, 2018, 14, 7446 RSC.
- M. Hartung and W. Köhler, Reversible mass exchange between two multicomponent systems of different temperatures, Eur. Phys. J. E:Soft Matter Biol. Phys., 2009, 29, 117 CrossRef CAS.
- A. Würger, Is Soret equilibrium a non-equilibrium effect?, C. R. Mec., 2013, 341, 438 CrossRef.
- R. van Roij, Defying gravity with entropy and electrostatics: sedimentation of charged colloids, J. Phys.: Condens. Matter, 2003, 15, 3569 CrossRef.
- A. P. Philipse, Remarks on the Donnan condenser in the sedimentation diffusion equilibrium of charged colloids, J. Phys.: Condens. Matter, 2004, 16, 4051–4062 CrossRef.
- J. R. Vinograd and J. W. McBain, Diffusion of Electrolytes and of the Ions in their Mixtures, J. Am. Chem. Soc., 1941, 63, 2008 CrossRef CAS.
- G. Guthrie, J. N. Wilson and V. Schomaker, Theory of the thermal diffusion of electrolytes in a Clusius column, J. Chem. Phys., 1949, 17, 310 CrossRef CAS.
- H. J. V. Tyrrell, D. A. Taylor and C. M. Williams, The ‘Seebeck effect’ in a purely ionic system, Nature, 1956, 177, 668 CrossRef CAS PubMed.
- D. Zhao, A. Würger and X. Crispin, Ionic thermoelectric materials and devices, J. Energy Chem., 2021, 61, 88 CrossRef CAS.
- L. J. Morthomas and A. Würger, Thermoelectric effect on charged colloids in the Hückel limit, Eur. Phys. J. E: Soft Matter Biol. Phys., 2008, 27, 425 CrossRef.
- A. Majee and A. Würger, Collective thermoelectrophoresis of charged colloids, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 83, 061403 CrossRef PubMed.
- M. Massetti, F. Jiao, A. J. Ferguson, D. Zhao, K. Wijeratne, A. Würger, J. L. Blackburn, X. Crispin and S. Fabiano, Unconventional thermoelectric materials for energy harvesting and sensing applications, Chem. Rev., 2021, 121, 12465 CrossRef CAS.
- P. S. Mohanty, S. Nöjd, M. J. Bergman, G. Nägele, S. Arrese-Igor, A. Alegria, R. Roa, P. Schurtenberger and J. K. G. Dhont, Dielectric spectroscopy of ionic microgel suspensions, Soft Matter, 2016, 2, 9705 RSC . Here it is shown that electrode polarization can be neglected when the dimensionless number ωL/Dκ is larger than about 10 (ω is the frequency of the AC field, L the distance between the electrodes, D the diffusion coefficient of ions, and κ−1 the Debye length. It shows that, in order to avoid electrode polarization, smaller frequencies can be used when the distance between the electrodes is larger.
- B. T. Huang, M. Roger, M. Bonetti, T. J. Salez, C. Wiertel-Gasquet, E. Dubois, R. Cabreira Gomes, G. Demouchy, G. Mériguet, V. Peyre, M. Kouyaté, C. L. Filomeno, J. Depeyrot, F. A. Tourinho, R. Perzynski and S. Nakamae, Thermoelectricity and thermodiffusion in charged colloids, J. Chem. Phys., 2015, 143, 054902 CrossRef CAS PubMed.
- I. Chikina and V. Shikin, Seebeck effect in colloidal electrolytes, Russ. J. Electrochem., 2021, 57, 930–937 CrossRef CAS.
- I. Chikina, S. Nakamae, V. Shikin and A. Varlamov, Two-Stage Seebeck Effect in Charged Colloidal Suspensions, Entropy, 2021, 23, 150 CrossRef PubMed.
- S. Wiegand, Thermal diffusion in liquid mixtures and polymer solutions, J. Phys.: Condens. Matter, 2004, 16, R357 CrossRef CAS.
- S. Wiegand, H. Ning and H. Kriegs, Thermal diffusion forced Rayleigh scattering setup optimized for aqueous mixtures, J. Phys. Chem. B, 2007, 111, 14169 CrossRef CAS.
-
D. A. McQuarrie, Statistical mechanics, Harper & Row, New York, 1976 Search PubMed.
- B. J. Ackerson, Correlations for interacting Brownian particles, J. Chem. Phys., 1976, 64, 242 CrossRef CAS.
-
P. N. Pusey, Course 10, Colloidal suspensions in Colloidal suspensions in liquids, freezing and the glass transition, Elsevier Science Publishers, Les Houches, 1991 Search PubMed.
- G. Nägele, On the dynamics and structure of charge-stabilized suspensions, Phys. Rep., 1996, 272, 215 CrossRef.
-
J. K. G. Dhont, An introduction to dynamics of colloids, in Studies in Interface Science, ed. D. Möbius and R. Miller, Elsevier, Amsterdam, 1996 Search PubMed.
- B. U. Felderhof and J. Vogel, Long-time collective diffusion coefficient of semidilute suspensions of spherical Brownian particles, J. Chem. Phys., 1992, 96, 6978 CrossRef CAS.
- E. Wajnryb, P. Szymczak and B. Cichocki, Brownian dynamics: divergence of mobility tensor, Phys. A, 2004, 335, 339 CrossRef.
- A. J. Bianchio and G. Nägele, Short-time transport properties in dense suspensions: From neutral to charge-stabilized colloidal spheres, J. Chem. Phys., 2008, 128, 104903 CrossRef PubMed.
- C. Felix, A. Yaroshchuk, S. Pasupathi, B. G. Pollet, M. P. Bondarenko, V. I. Kovalchuk and E. K. Zholkovskiy, Electrophoresis and stability of nano-colloids: History, theory and experimental examples, Adv. Colloid Interface Sci., 2014, 211, 77 CrossRef CAS.
- K. Kang, Y. Nakayama and R. Yamamoto, Direct Numerical Simulations of Electrophoresis of Charged Colloids, Phys. Rev. Lett., 2006, 96, 208302 CrossRef PubMed.
- G. Giupponi and I. Pagonabarraga, Colloid electrophoresis for strong and weak ion diffusivity, Phys. Rev. Lett., 2011, 106, 248304 CrossRef PubMed.
- B. Dünweg, V. Lobaskin, K. Seethalakshmy-Hariharan and C. Holm, Colloidal electrophoresis: scaling analysis, Green-Kubo relation, and numerical results, J. Phys.: Condens. Matter, 2008, 20, 404214 Search PubMed.
- C. Thévenot, B. Grassl, G. Bastiat and W. Binana, Aggregation number and critical micellar concentration of surfactant determined by time-dependent static light scattering (TDSLS) and conductivity, Colloids Surf., A, 2005, 252, 105 CrossRef.
- M. Corti and V. Degiorgio, Quasi-elastic light scattering study of intermicellar interactions in aqueous sodium dodecyl sulfate solutions, J. Phys. Chem., 1981, 85, 711 Search PubMed.
- K. Kuriyama, Temperature dependence of micellar weight of non-ionic surfactant in the presence of various additives, Kolloid-Z. Z. Polym., 1961, 180, 55 CrossRef . Data in this reference are also given for ionic SDS micelles, contrary what is suggested by the title.
- S. Bucci, C. Fagotti, V. Degiorgio and R. Piazza, Small-angle neutron-scattering study of ionic-nonionic mixed micelles, Langmuir, 1991, 7, 824 CrossRef CAS.
- J. P. Debye, Molecular-weight determination by light scattering, J. Phys. Colloid Chem., 1947, 51, 18 Search PubMed.
- S. Ikada, S. Ozeki and S. Hayashi, Size and shape of charged micelles of ionic surfactants in aqueous salt solutions, Biophys. Chem., 1980, 11, 417 CrossRef PubMed.
- A. Chatterjee, S. P. Moulik, S. K. Sanyal, B. K. Mishra and P. M. Puri, Thermodynamics of micelle formation of ionic surfactants: A critical assessment for sodium dodecyl sulfate, cetyl pyridinium chloride and dioctyl sulfosuccinate (Na Salt) by microcalorimetric, conductometric, and tensiometric measurements, J. Phys. Chem. B, 2001, 105, 12823 CrossRef CAS.
|
| This journal is © The Royal Society of Chemistry 2025 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *a and
W. J.
Briels
*ab
*a and
W. J.
Briels
*ab




 defined in eqn (4) and the ion fluxes
defined in eqn (4) and the ion fluxes  defined in eqn (15) will be argued as vanishing due to enslavement. This sets the relation between the solvent and ion fluxes, and the colloid flux.
defined in eqn (15) will be argued as vanishing due to enslavement. This sets the relation between the solvent and ion fluxes, and the colloid flux.

 is zero. This implies that the solvent flux responsible for the relaxation of the corresponding pressure gradients relaxes to zero instantaneously. We note that this results in zero fluxes only for closed systems, where the system boundary is impenetrable for solvent molecules.
is zero. This implies that the solvent flux responsible for the relaxation of the corresponding pressure gradients relaxes to zero instantaneously. We note that this results in zero fluxes only for closed systems, where the system boundary is impenetrable for solvent molecules.

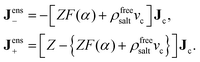



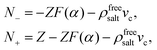

![[script L]](https://www.rsc.org/images/entities/char_e144.gif) . This allows (as for any one-component system) to express the total force F in eqn (25) in terms of the effective chemical potential ν in eqn (20), the effective partial molar enthalpy in eqn (21), and the heat-of-transfer
. This allows (as for any one-component system) to express the total force F in eqn (25) in terms of the effective chemical potential ν in eqn (20), the effective partial molar enthalpy in eqn (21), and the heat-of-transfer  in eqn (26). The latter is the as yet unknown quantity. This total force is due to spatial gradients in temperature and colloid concentration, and also contains single-particle thermophoretic forces.
in eqn (26). The latter is the as yet unknown quantity. This total force is due to spatial gradients in temperature and colloid concentration, and also contains single-particle thermophoretic forces.
 in eqn (4) and (15), without yet setting these equal to zero, and the heat flux,
in eqn (4) and (15), without yet setting these equal to zero, and the heat flux,

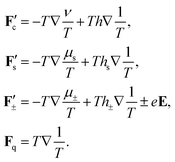


 , it is still in principle present in the colloid flux through the contribution
, it is still in principle present in the colloid flux through the contribution  .
.
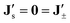 , which is a consequence of enslavement. This allows elimination of the forces
, which is a consequence of enslavement. This allows elimination of the forces  from the above Onsager relations (18) to arrive at an effective one-component flux–force relation,
from the above Onsager relations (18) to arrive at an effective one-component flux–force relation,
![[script L]](https://www.rsc.org/images/entities/char_e144.gif) cq =
cq = ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) qc.
qc.
 on the colloids, the macroscopic electric field is absent, which can be understood as follows. The total charge carried by the ions within a double layer is equal to e(N+ − N−) = Ze and therefore compensates the surface charge −Ze of a colloid. This confirms the well-known fact that a dressed colloid, including its electric double layer, is uncharged. The simultaneous displacement of the colloid together with its double layer does not lead to a change of the electrostatic energy, which is the reason for the absence of the electric field in the force
on the colloids, the macroscopic electric field is absent, which can be understood as follows. The total charge carried by the ions within a double layer is equal to e(N+ − N−) = Ze and therefore compensates the surface charge −Ze of a colloid. This confirms the well-known fact that a dressed colloid, including its electric double layer, is uncharged. The simultaneous displacement of the colloid together with its double layer does not lead to a change of the electrostatic energy, which is the reason for the absence of the electric field in the force 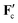 .
.![[script L]](https://www.rsc.org/images/entities/char_e144.gif) ccF,
ccF,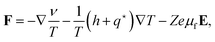

 for constant temperature (excluding mere heat conduction), which leads to the well-known interpretation of
for constant temperature (excluding mere heat conduction), which leads to the well-known interpretation of  being equal to the heat that is transported per colloidal particle.37–39,42 The heat-of-transfer in the present case includes the solvent molecules and ions that are enslaved and dragged along with the colloid.
being equal to the heat that is transported per colloidal particle.37–39,42 The heat-of-transfer in the present case includes the solvent molecules and ions that are enslaved and dragged along with the colloid.
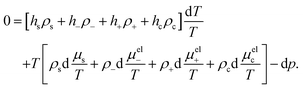

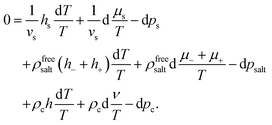

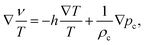

 is responsible for the Dufour effect, where transport of particles gives rise to a temperature gradient.
is responsible for the Dufour effect, where transport of particles gives rise to a temperature gradient. . In this subsection, an explicit expression for the heat-of-transfer is derived. The expression for
. In this subsection, an explicit expression for the heat-of-transfer is derived. The expression for  in eqn (37) contains the internal energy u per colloidal particle, which is an additive contribution uint due to colloid–colloid interactions and usingle from single colloids. This finally leads to eqn (39), where fint and fsingle are defined in eqn (38).
in eqn (37) contains the internal energy u per colloidal particle, which is an additive contribution uint due to colloid–colloid interactions and usingle from single colloids. This finally leads to eqn (39), where fint and fsingle are defined in eqn (38).

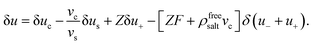

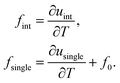
 , we introduced f0 in the above expression for fsingle. This additional contribution accounts for effects such as solvent flow induced by the interface between the solvent and the solid core of the colloids.22 For charged colloids, for example, it is well-known that electro-osmotic flow plays a role in addition to the temperature dependence of the internal thermodynamic energy usingle of the electric double layer. To leading order in spatial gradients, such phenomena do not give rise to additional colloid–colloid interaction forces.
, we introduced f0 in the above expression for fsingle. This additional contribution accounts for effects such as solvent flow induced by the interface between the solvent and the solid core of the colloids.22 For charged colloids, for example, it is well-known that electro-osmotic flow plays a role in addition to the temperature dependence of the internal thermodynamic energy usingle of the electric double layer. To leading order in spatial gradients, such phenomena do not give rise to additional colloid–colloid interaction forces.
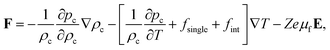

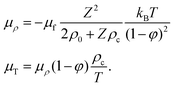





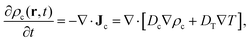

![[script L]](https://www.rsc.org/images/entities/char_e144.gif) cc is equal to
cc is equal to![[script L]](https://www.rsc.org/images/entities/char_e144.gif) cc = D0ρcβH0,
cc = D0ρcβH0,![[k with combining circumflex]](https://www.rsc.org/images/entities/b_char_006b_0302.gif) = k/k the unit vector in the direction of the wave vector k),
= k/k the unit vector in the direction of the wave vector k),
![[script L]](https://www.rsc.org/images/entities/char_e144.gif) ccFel = −
ccFel = −![[script L]](https://www.rsc.org/images/entities/char_e144.gif) ccZeμfE, and hence,
ccZeμfE, and hence,




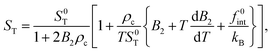



![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) B2/dT = −(6.3 ± 2.7). It thus follows that Δk/2B2 = 0.38 ± 0.30. In ref. 12 and 30 it was reported that Δk/2B2 = 1, with an equally large experimental error, while in ref. 31 a smaller value was found. The above theoretical estimate is therefore in agreement with those experiments, although error margins are quite substantial.
B2/dT = −(6.3 ± 2.7). It thus follows that Δk/2B2 = 0.38 ± 0.30. In ref. 12 and 30 it was reported that Δk/2B2 = 1, with an equally large experimental error, while in ref. 31 a smaller value was found. The above theoretical estimate is therefore in agreement with those experiments, although error margins are quite substantial.


 ). This in turn allows reducing the flux–force relations to the effective one-component colloid flux–force relation in eqn (19) and (22). Subsequently this leads to the expression (25) for the force on a single colloid, which contains the still unknown heat-of-transfer. The Onsager irreversible thermodynamics approach does not account for deformation of the electric double layers of the colloids due to the macroscopic electric field. The corresponding thermoelectrophoretic force in eqn (23) is therefore added by hand in eqn (25) for the total force. After expressing the force on a colloidal particle in terms of spatial gradients of the colloid pressure (see eqn (34), an approximate expression for the heat-of-transfer is derived (see eqn (37)), which contains both single-particle and collective contributions. The approximation involves neglecting pure heat conduction (that is, heat conduction in the absence of colloid migration), which is argued to be a good approximation due to the relatively large size of the colloids. The total force in eqn (39) is valid for arbitrary core geometries (spherical, rod-like, plate-like, etc.) and arbitrary surface charge density. It consists of a single-particle thermophoretic force, a term proportional to the spatial gradient of the colloid pressure, a thermoelectrophoretic force, and a thermophoretic force that we refer to as the thermophoretic interaction force. In a closed system, the stationary state implies a zero flux and hence a zero force, which leads to the explicit expression (46) for the Soret coefficient. An expression for the mobility, valid for spherical colloids, is then derived, which leads to an explicit expression for the thermodiffusion coefficient (see eqn (49)–(51)). The coefficients μρ and μT in the expression (46) for the Soret coefficient and eqn (49)–(51) for the diffusion coefficients, which account for the thermoelectrophoretic force, are expressed in terms of the electrophoretic mobility in eqn (53), for the derivation of which the expression (44) for the macroscopic electric field is essential. The colloid–colloid interaction contributions to the Soret and thermodiffusion coefficients can be expressed in terms of integrals of the pair-interaction potential and the pair-interaction function (see eqn (47)), which are valid for spherical colloids). This allows in principle a particle-based, microscopic comparison of the theory with experiments.
). This in turn allows reducing the flux–force relations to the effective one-component colloid flux–force relation in eqn (19) and (22). Subsequently this leads to the expression (25) for the force on a single colloid, which contains the still unknown heat-of-transfer. The Onsager irreversible thermodynamics approach does not account for deformation of the electric double layers of the colloids due to the macroscopic electric field. The corresponding thermoelectrophoretic force in eqn (23) is therefore added by hand in eqn (25) for the total force. After expressing the force on a colloidal particle in terms of spatial gradients of the colloid pressure (see eqn (34), an approximate expression for the heat-of-transfer is derived (see eqn (37)), which contains both single-particle and collective contributions. The approximation involves neglecting pure heat conduction (that is, heat conduction in the absence of colloid migration), which is argued to be a good approximation due to the relatively large size of the colloids. The total force in eqn (39) is valid for arbitrary core geometries (spherical, rod-like, plate-like, etc.) and arbitrary surface charge density. It consists of a single-particle thermophoretic force, a term proportional to the spatial gradient of the colloid pressure, a thermoelectrophoretic force, and a thermophoretic force that we refer to as the thermophoretic interaction force. In a closed system, the stationary state implies a zero flux and hence a zero force, which leads to the explicit expression (46) for the Soret coefficient. An expression for the mobility, valid for spherical colloids, is then derived, which leads to an explicit expression for the thermodiffusion coefficient (see eqn (49)–(51)). The coefficients μρ and μT in the expression (46) for the Soret coefficient and eqn (49)–(51) for the diffusion coefficients, which account for the thermoelectrophoretic force, are expressed in terms of the electrophoretic mobility in eqn (53), for the derivation of which the expression (44) for the macroscopic electric field is essential. The colloid–colloid interaction contributions to the Soret and thermodiffusion coefficients can be expressed in terms of integrals of the pair-interaction potential and the pair-interaction function (see eqn (47)), which are valid for spherical colloids). This allows in principle a particle-based, microscopic comparison of the theory with experiments.



![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ρens+ + ∇
ρens+ + ∇![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ρens− + ∇
ρens− + ∇![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) T2 − ∇
T2 − ∇![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(1 − φ)2 = 0.
ln(1 − φ)2 = 0.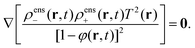



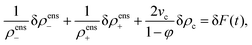



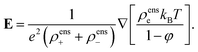

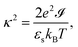
![[scr I, script letter I]](https://www.rsc.org/images/entities/char_e143.gif) the ionic strength,
the ionic strength,
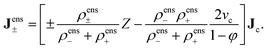
![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) el = (6πηsa/e)μel = 3Z/[2(1 + κa)] is equal to 7 (where κa = 2.6). Furthermore, dB2/dT ≈ −14 × 10−27 m3 K, and fsingle/kB = 13 (see eqn (54) and Fig. 2 for 100 mM salt). To within the second virial approximation it follows that, for T = 298 K, (1/kBT)(∂pc/∂ρc) ≈ 1 + 24φ, and (1/ρckB)(∂pc/∂T) + fsingle/kB ≈ 14 − 52φ. In addition, H0 ≈ 1, so that, ρcμρ/kBT ≈ μT/kB ≈ 290φ/(2ρ0vc + 17φ). For the 100 mM salt solution ρ0vc ≈ 4, so that it follows that, (∂pc/∂ρc)/(ρcμρ) ≈ (1 + 24φ)(8 + 17φ)/290φ and (∂pc/∂T + ρcfsingle)/(ρcμT) ≈ (14 − 52φ)(8 + 17φ)/290φ. The micellar SDS concentrations correspond to volume fractions 0.002 < φ < 0.02, so that 6 < (∂pc/∂ρc)/(ρcμρ) < 37 (the 6 for φ = 0.02 and 37 for φ = 0.002), and 46 < (∂pc/∂T + ρcfsingle)/(ρcμT) < 460 (the 460 for φ = 0.02 and 46 for φ = 0.002). The above lower limit of 6 is most probably about a factor 2 larger, since the μel decreases with increasing concentration. Thermoelectric contributions can thus be safely neglected against those from pressure gradients and single-particle forces for the micellar SDS system under consideration.
el = (6πηsa/e)μel = 3Z/[2(1 + κa)] is equal to 7 (where κa = 2.6). Furthermore, dB2/dT ≈ −14 × 10−27 m3 K, and fsingle/kB = 13 (see eqn (54) and Fig. 2 for 100 mM salt). To within the second virial approximation it follows that, for T = 298 K, (1/kBT)(∂pc/∂ρc) ≈ 1 + 24φ, and (1/ρckB)(∂pc/∂T) + fsingle/kB ≈ 14 − 52φ. In addition, H0 ≈ 1, so that, ρcμρ/kBT ≈ μT/kB ≈ 290φ/(2ρ0vc + 17φ). For the 100 mM salt solution ρ0vc ≈ 4, so that it follows that, (∂pc/∂ρc)/(ρcμρ) ≈ (1 + 24φ)(8 + 17φ)/290φ and (∂pc/∂T + ρcfsingle)/(ρcμT) ≈ (14 − 52φ)(8 + 17φ)/290φ. The micellar SDS concentrations correspond to volume fractions 0.002 < φ < 0.02, so that 6 < (∂pc/∂ρc)/(ρcμρ) < 37 (the 6 for φ = 0.02 and 37 for φ = 0.002), and 46 < (∂pc/∂T + ρcfsingle)/(ρcμT) < 460 (the 460 for φ = 0.02 and 46 for φ = 0.002). The above lower limit of 6 is most probably about a factor 2 larger, since the μel decreases with increasing concentration. Thermoelectric contributions can thus be safely neglected against those from pressure gradients and single-particle forces for the micellar SDS system under consideration.





 . The specific volume
. The specific volume ![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) of a micelle is obtained from the data for the radii in Tables III and IV in ref. 78, using that
of a micelle is obtained from the data for the radii in Tables III and IV in ref. 78, using that ![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) = [NAv/(mM1)]vc. The thus obtained numerical values for B2 are the two data points ⋄ in Fig. 3.
= [NAv/(mM1)]vc. The thus obtained numerical values for B2 are the two data points ⋄ in Fig. 3.