Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Pressure effects on the nanostructure of bicontinuous propane microemulsions with extended surfactants: a SANS study†
Maximilian
Krappel
 a,
Christian
Bittner
b,
Ralf
Schweins
c and
Thomas
Sottmann
a,
Christian
Bittner
b,
Ralf
Schweins
c and
Thomas
Sottmann
 *a
*a
aInstitute of Physical Chemistry, University of Stuttgart, Pfaffenwaldring 55, 70569 Stuttgart, Germany. E-mail: thomas.sottmann@ipc.uni-stuttgart.de; Tel: +49 (0)711 685-64494
bBASF SE, Carl-Bosch-Strasse 38, 67056 Ludwigshafen am Rhein, Germany
cInstitut Laue-Langevin, 71 Avenue des Martyrs, CS 20156, 38042 Grenoble CEDEX 9, France
First published on 22nd May 2025
Abstract
In our recent work, we investigated the influence of pressure on the temperature-dependent phase behavior of symmetric, application-relevant microemulsions containing propane, stabilized by an extended surfactant mixture. By means of high-pressure small-angle neutron scattering, the present study provides further insights by unraveling the impact of pressure and propane on the nanostructure of these microemulsions near their optimum point. Despite the obvious presence of multiple scattering, all recorded scattering curves show the typical characteristics of symmetric bicontinuous microemulsions. Analysis of the scattering data using the Teubner–Strey model and Porod's law for diffuse interfaces provided the periodicity dTS, the correlation length ξTS, and the specific interface S/V, as well as the amphiphilicity factor fa and the effective bending rigidity κeff of the amphiphilic film. The overall structural order of pure propane microemulsions was found to be markedly lower compared to the n-decane microemulsions. While the structure of n-decane-rich microemulsions only shows a weak pressure dependence, propane-rich formulations exhibit a significant increase of ξTS with pressure due to an increasing surfactant monolayer rigidity, caused by enhanced interactions of the compressible propane with the surfactant tails. Microemulsions containing mixtures of the two hydrocarbons behave accordingly, demonstrating that the presence of the short-chain alkane gradually amplifies the sensitivity of the amphiphilic film to pressure changes. Interestingly, the geometric prefactor a of bicontinuous structure models increases from slightly above 7 for n-decane microemulsions to a > 8 for propane formulations, owing to the increasing disorder.
1 Introduction
Microemulsions are thermodynamically stable mixtures of water and oil, stabilized by a surfactant monolayer separating polar and non-polar nanodomains. Adsorption of surfactant molecules at the oil/water interface enables to achieve ultra-low interfacial tensions between the immiscible liquids.1–4 While microemulsions are optically homogeneous, they exhibit a wide range of nanostructures, including droplet-like, lamellar, or bicontinuous structures.5,6 Owing to their unique properties, conveniently adjustable via composition, temperature, or pressure, microemulsions have found their way into many applications such as cleaning, cosmetics, pharmaceutics and enhanced oil recovery.7–11Studies on the properties of microemulsions containing gaseous components, such as short-chain alkanes, are scarce, although such formulations can play a central role for instance in chemical-enhanced oil recovery, where the use of microemulsions can improve the exploitation of existing crude oil reservoirs instead of having to explore new oil fields. Reasons for the under-representation of such investigations on microemulsions containing volatile components – which have to be carried out at high pressures in order to solubilize these (liquefied) components and to match reservoir conditions, such as pressures in the range of a few hundred bar – are the necessity for special setups and the experimentally more demanding and time-consuming measurements compared to investigations at ambient pressure.
Just recently, we systematically studied the pressure-dependent phase behavior of application-relevant brine/butyldiglycol – n-decane/propane – alkyl alkoxy sulfate/alkyl sulfonate microemulsions containing equal amounts of water and oil for temperatures up to 80 °C and pressures up to 350 bar, which covers reservoir depths of several thousand meters when using pressure gradients of approximately 0.1 bar per meter (depends on fluid density).12 Due to their long alkyl chains and ionic nature, the surfactants used in our current work exhibit negligible monomeric solubilities in both water and oil, preventing extraction effects. Extended surfactants such as alkyl alkoxy sulfates, which feature groups of intermediate polarity between the hydrophobic tail and hydrophobic head, are characterized by high solubilization capacities and may offer an even stronger reduction of the oil/water interfacial tension compared to conventional surfactants, making them particularly attractive for the recovery of oil trapped within rock pores.13,14 We found that the influence of pressure depends on the oil used in the microemulsion: While in n-decane-rich microemulsions, pressure moves the system from water-in-oil (w/o) to oil-in-water (o/w) structures, the phase sequence inverts from o/w to w/o in propane-rich formulations, with a bicontinuous structure found during the structural transition.15,16 This was explained by the competing effects of headgroup hydration and oil penetration and is thus related to the strength of interactions between surfactant and oil. The first effect outweighs the second in n-decane rich formulations, whereas a facilitated oil penetration and a stronger pressure dependence of propane–surfactant interactions result in the opposite behavior in propane-rich formulations.
Motivated by this oil-dependent influence of pressure on the phase behavior of symmetrical microemulsions, the aim of the present study was to systematically investigate the effect of pressure on the nanostructure of these systems. Considering the need for even more specialized setups to perform such investigations, it is not surprising that even fewer publications exist that use methods such as small-angle neutron scattering (SANS), neutron spin echo (NSE) or dynamic light scattering (DLS). In the following, a brief overview of relevant studies is given.
Starting with liquid oils, three studies conducted by Kawabata et al., who utilized a combination of SANS, NSE and DLS, revealed a nearly pressure-independent droplet radius for water-in-decane microemulsions stabilized by different ionic and non-ionic surfactants.17–19 The authors report a pressure-induced increase of the bending rigidity, κ, of the surfactant monolayer which is one of the two elastic moduli (alongside the saddle splay modulus ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) ) in Helfrich's description of the elastic energy of a membrane,20 whereas higher temperatures led to a less rigid amphiphilic film.
) in Helfrich's description of the elastic energy of a membrane,20 whereas higher temperatures led to a less rigid amphiphilic film.
Interestingly, almost no pressure dependence of the droplet radii was likewise found in most studies on water-in-oil microemulsions containing more volatile hydrocarbons, revealing no influence of alkane chain length or density.21–23 Similar findings were obtained for water-in-CO2 and CO2-in-water microemulsions, which are typically solubilized by fluorinated surfactants owing to the stronger affinity to CO2 compared to conventional hydrocarbon-based surfactants.24–27 One of these studies reported a pressure-induced change of the shape of the nanostructure due to a pressure-induced shift of phase behavior, in particular the emulsification failure boundary.26 More notable deviations of the droplet radius under pressure were only observed for water-in-propane droplets stabilized by the non-ionic surfactant C12E5, which was explained by its pressure-dependent monomeric solubility.21
Just a handful of studies have been conducted on the pressure dependence of the nanostructure of bicontinuous microemulsions.28–31 In two works on supercritical CO2 microemulsions stabilized by a mixture of technical non-ionic fluorinated surfactants,29,30 a stiffening of the surfactant monolayer under pressure was found, allowing for a higher structural order, which is in agreement with the works on water-in-decane droplet microemulsions. Minor changes in the periodicity under pressure were again attributed to the monomeric solubility of the surfactant.30 Apart from the SANS study by Pütz et al. with a CO2/cyclohexane mixture,27 systematic investigations on the influence of a varying ratio of volatile and non-volatile oils on the impact of pressure on microemulsion nanostructure are still missing. Equally scarce are high-pressure nanostructure investigations of microemulsions stabilized by application-relevant extended surfactants.
This brief literature review emphasizes the scarcity of insights into the nanostructure of microemulsions containing volatile alkanes, which is even more noticeable when it comes to bicontinuous structures and the use of extended surfactants. Having just recently studied the phase behavior of such microemulsion formulations,15,16 this work therefore aims to elucidate the influence of pressure on the nanostructure of balanced microemulsions of the type brine/butyldiglycol – n-decane/propane – C16–18-7PO-0.1EO-SO4Na/C14–17-SO3Na via high-pressure small-angle neutron scattering studies. To the best of our knowledge, no high-pressure SANS studies on extended surfactant microemulsions have been reported in literature to date. We thus conducted bulk contrast SANS experiments to study the influence of pressure and oil composition, systematically adjusted via the propane-to-n-decane ratio, on microemulsions prepared near their respective optimum point. To quantify the influence of propane and pressure on microemulsion nanostructure, all recorded scattering curves were analyzed using the Teubner–Strey model32 and Porod's law for diffuse interfaces.33,34 We demonstrate that propane and pressure significantly and systematically influence the ordering of the nanostructure, quantified via the amphiphilicity factor fa, which depends on the width of scattering peak (∝ correlation length ξTS) and is related to a systematically changing bending rigidity of the amphiphilic film.
2 Experimental
2.1 Reagents
H2O was double-distilled, D2O (Deutero, 99.9%) was used as obtained. Sodium chloride (NaCl, Carl Roth, 99.5%) was used as salt. n-Decane (Acros Organics, 99%) and propane (Air Liquide, 99.95%) were used as oils. BASF SE provided the co-solvent butyldiglycol (99%) and aqueous solutions of the anionic surfactants C16–18-7PO-0.1EO-SO4Na (47–54 wt% active content), an alkyl alkoxy sulfate (“extended surfactant”), and C14–17-SO3Na (30–32 wt% active content), a secondary alkyl sulfonate. All chemicals were used without further purification, but surfactant homogeneity was ensured before sample preparation.2.2 High-pressure SANS cell
SANS experiments were performed with a high-pressure setup developed by Strey and coworkers.30 The cell is equipped with two customized sapphire windows (dsapphire = 12 mm) with a sample thickness of dsample = 2 mm (transmission at measurement conditions is Tcell = 0.89), allowing for sufficient miscibility and homogeneity of the samples when studying phase behavior via visual determination. Regulating pressure mechanically with a piston, thereby adjusting a sample volume of approximately 17 mL, instead of via pressurization with gas circumvents changes in the sample composition during measurements. Pressure is measured using a pressure transducer (Burster 81530) connected to a measurement amplifier with an accuracy of ±3 bar. Calibration is performed with a dead weight tester (WIKA CPB5800) up to a pressure of pmax,cal = 400 bar, with the experimental highest pressure being pmax,exp ≈ 350 bar. The cell is temperature-controlled by a liquid flowing through tubes in the thermal coating around the stainless steel centerpiece of the setup, with temperature regulation taking place with a thermostat connected to the tubing. Temperature can be read off a thermometer in the steel cylinder, offering a precision of ±0.1 K after temperature equilibration.2.3 Sample preparation
All investigated microemulsion are pseudo-ternary A–B–C systems recorded in bulk contrast. Here, A = H2O/D2O/NaCl/butyldiglycol, with a fixed salinity of 4.37 wt% to set the target temperature range. In our previous D2O-free phase behavior study,15 the salinity was 4.70 wt%. This change is required to keep the molar salt concentration of the brine constant. With the surfactants containing H2O by default, we set the highest possible D2O/H2O ratio of 73/27 (w/w). Despite its amphiphilic nature, butyldiglycol, used at 5 wt% of A to facilitate phase behavior studies, is treated as a co-solvent due to its high hydrophilicity. From electrical conductivity measurements, we know that its impact on the phase inversion temperature![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) and therefore on the curvature of the amphiphilic film is marginal at the concentration used here.15 B is n-decane and/or propane, C is the surfactant mixture of C16–18-7PO-0.1EO-SO4Na/C14–17-SO3Na, which were used in a 3
and therefore on the curvature of the amphiphilic film is marginal at the concentration used here.15 B is n-decane and/or propane, C is the surfactant mixture of C16–18-7PO-0.1EO-SO4Na/C14–17-SO3Na, which were used in a 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (w/w) ratio (based on active content) to set the desired temperature range. Stock solutions with surfactant (= stock C) and without (= stock A) were used to adjust the desired surfactant concentration. Samples were prepared with equal volumes of hydrophilic and hydrophobic component (VA = VB) to obtain symmetric microemulsions, using the propane density at filling pressure and temperature.35 Given the different densities of H2O and D2O, surfactant mass fractions (as used in our previous work)15,16 were converted to the respective amphiphilic volume ratio, with ϕC = VC/Vtotal (referring to filling conditions), while keeping the equivolumetric oil-to-water ratio. Samples were prepared in proximity to the respective optimum points
1 (w/w) ratio (based on active content) to set the desired temperature range. Stock solutions with surfactant (= stock C) and without (= stock A) were used to adjust the desired surfactant concentration. Samples were prepared with equal volumes of hydrophilic and hydrophobic component (VA = VB) to obtain symmetric microemulsions, using the propane density at filling pressure and temperature.35 Given the different densities of H2O and D2O, surfactant mass fractions (as used in our previous work)15,16 were converted to the respective amphiphilic volume ratio, with ϕC = VC/Vtotal (referring to filling conditions), while keeping the equivolumetric oil-to-water ratio. Samples were prepared in proximity to the respective optimum points ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) of each microemulsion system to adjust the bicontinuous structure while maintaining a sufficient width of the one-phase region to allow for pressure variations.
of each microemulsion system to adjust the bicontinuous structure while maintaining a sufficient width of the one-phase region to allow for pressure variations. ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) is characterized by
is characterized by ![[small phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e2.gif) C, the minimum surfactant volume fraction required to fully solubilize water and oil, as well as the phase inversion (or optimum) temperature
C, the minimum surfactant volume fraction required to fully solubilize water and oil, as well as the phase inversion (or optimum) temperature ![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) .
.
Samples were prepared directly in the high-pressure cell. Liquid components were added in the order stock C, n-decane, stock A. Liquefied propane was inserted subsequently via a filling station with a diaphragm accumulator. Since weighing the heavy HP-SANS cell with sufficient precision to account for the small amounts of added propane is not feasible, piston height was calibrated against sample volume. Densities were determined beforehand using an Anton Paar DMA 5000 M density meter. After filling in the liquids, piston height was adjusted to fill in the target amount of propane. Temperature of the HP cell was regulated as describe above. Homogeneity of the sample was achieved under continuous stirring using a special magnetic stirring bar until the temperature equilibrium was reached. The SANS cell was additionally rotated perpendicular to the z axis to avoid phase separation above or below the visible scattering volume. Once a measurement was finished, the cell was emptied and cleaned thoroughly with water, acetone and CO2. New samples were prepared for each compositional change after air-drying the cell.
2.4 Phase behavior
Phase behavior studies in our previous work were performed as T(γ) cuts (“fish cuts”) with H2O.15 Given the use of D2O in the present SANS study, mass fractions were converted to volume fractions (ϕC, see above). Phase transition temperatures of the D2O-containing samples investigated here were checked via visual determination in the HP-SANS cell before each measurement, considering that the switch from H2O to D2O typically produces a small temperature shift of the phase boundaries.34,36,372.5 Small-angle neutron scattering
SANS measurements were conducted during three days of beam time at the D22 diffractometer of the Institut Laue-Langevin (ILL) in Grenoble, France, with a wavelength of λ = 6 Å (Δλ/λ = 0.1). Experiments were performed at a collimation/detector distance of 17.6/17.6 m, providing a q range of 0.0032 < q (Å−1) < 0.62 with further use of the side detector of D22. Samples were prepared in the HP-SANS cell (dsample = 2 mm) as discussed above, ensuring sample homogeneity via visual inspection before mounting the cell into the beam line. A reference measurement at 1 bar was done in a 1 mm Hellma quartz cuvette. In the ESI,† the impact of sample thickness on absolute scattering intensities as well as the influence of multiple scattering are addressed in more detail.3 Reduction and analysis of SANS data
Raw scattering data, obtainable from the ILL,38 were converted to absolute scattering intensities using direct beam measurements. The GRASP software39 was utilized for data reduction, considering empty cell and background scattering as well as transmission. Unless stated otherwise, data were radially averaged.3.1 Teubner–Strey model and Porod's law
The peak region of all scattering profiles was analyzed with the Teubner–Strey model by treating the bicontinuous domains as non-rigid domains characterized by their periodicity dTS and correlation length ξTS.32 The Teubner–Strey model is derived from Landau theory, for which the Landau free energy, obtained from an order parameter expansion of the free energy density using gradient terms, provides the scattering intensity distribution I(q) under consideration of the free energy change resulting from fluctuations of the order parameter. The typical correlation peak of well-structured microemulsions occurs when the order parameter expansion coefficient c1 < 0 (with a2 > 0 and c2 > 0). Details on the analysis are presented in the ESI.† Expressing these coefficients and thus I(q) with more descriptive fit parameters provides the fitting function used for the scattering data analysis, with | (1) |
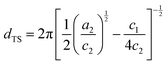 | (2) |
 | (3) |
The value of the periodicity, dTS, of the structure predominantly depends on the position of the peak (i.e., qmax). In a symmetric bicontinuous microemulsion with equal volumes of water and oil, the size, dTS/2, of water and oil domains is therefore equal. The sharpness of the correlation peak characterizes the order of the bicontinuous structure via the correlation length ξTS, which is a measure for the length at which the order of the structure persists. Given that microemulsions do not exhibit long-range order, ξTS is typically small, roughly of the order of the domain size.32,36,40
In Fig. 3–6, the Teubner–Strey fit is shown as a solid red line. The fit almost quantitatively describes the data around the peak, but it deviates from the scattering data at higher q due to multiple scattering. Even though the q−4 decay is mathematically incorporated in the Teubner–Strey fit, the fact that Teubner and Strey's publication explicitly focuses on the origin of the scattering peak32 and to avoid inconsistencies due to multiple scattering contributions (as discussed in the ESI†), it was considered more adequate to limit the analysis to just the peak region. The entire q range could be described by models such as a fractal scattering-based Beaucage model41 or the clipped random wave model,42 both of which introduce a third length scale (radius of gyration and surface roughness parameter, respectively), or by trying to consider multiple scattering by simply combining multiple Teubner–Strey fits.43
Instead, we analyzed the high q data using Porod's law for diffuse interfaces
 | (4) |
3.2 Bending rigidity and amphiphilicity factor
Following Gompper et al.'s modification of the random interface model developed by Pieruschka and Safran, dTS and ξTS can be utilized to determine the bending rigidity κ (cf.Fig. 1), which is one of the two elastic moduli employed to describe the elastic properties of amphiphilic membranes alongside the saddle splay modulus![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) .20,44–46 A higher κ corresponds to a more rigid interfacial film, whose thermal fluctuations lead to its softening and the concomitant decrease of κ. These thermal fluctuations range from small molecular length scales to the order of dTS, which causes a renormalization of κ. Furthermore, they increase the consumption of interface, which affects the domain spacing, i.e., dTS.47 Monte Carlo simulations and experimental neutron spin echo (NSE) and small-angle neutron scattering experiments have indicated that κ determined via the Teubner–Strey analysis of SANS data is perhaps better understood as a mixture of the actual bending rigidity and the saddle splay modulus.48,49 Given that NSE was not available within the scope of this work and an estimation would only be possible using a theoretical value, κ is therefore conceived as an effective bending rigidity, labelled κeff, as done by other authors.43,50–52 This effective bending rigidity of the amphiphilic film is given as
.20,44–46 A higher κ corresponds to a more rigid interfacial film, whose thermal fluctuations lead to its softening and the concomitant decrease of κ. These thermal fluctuations range from small molecular length scales to the order of dTS, which causes a renormalization of κ. Furthermore, they increase the consumption of interface, which affects the domain spacing, i.e., dTS.47 Monte Carlo simulations and experimental neutron spin echo (NSE) and small-angle neutron scattering experiments have indicated that κ determined via the Teubner–Strey analysis of SANS data is perhaps better understood as a mixture of the actual bending rigidity and the saddle splay modulus.48,49 Given that NSE was not available within the scope of this work and an estimation would only be possible using a theoretical value, κ is therefore conceived as an effective bending rigidity, labelled κeff, as done by other authors.43,50–52 This effective bending rigidity of the amphiphilic film is given as | (5) |
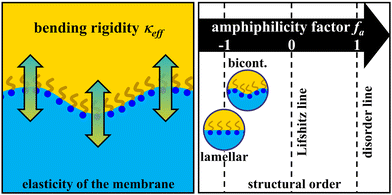 | ||
| Fig. 1 Left: Schematic illustration of the (effective) bending rigidity κeff of the surfactant membrane (amphiphilic film). The higher κeff, the stiffer the membrane. Right: Scale of the amphiphilicity factor between −1 and 1. Well-structured microemulsions are located at fa < −0.6.53 | ||
A higher value of κeff therefore enables the formation of a bicontinuous microemulsion with higher structural order, characterized by a sharper scattering peak and thus a higher ratio of ξTS/dTS. In this context, a suitable measure for quantifying the influence of propane and pressure on the structural order of the investigated microemulsions is the so-called amphiphilicity factor32,53,54
 | (6) |
4 Results and analysis
In the following, we briefly present the most important features of the phase behavior of the investigated extended surfactant microemulsions, serving as the foundation of the subsequent HP-SANS studies. Afterwards, we showcase the scattering profiles obtained from measurements near the respective optimum points. Initial SANS investigations with the microemulsion containing only n-decane were performed at the respective pressure-dependent phase inversion temperature. A further set of scattering curves was recorded isothermally as a function of pressure, which was likewise done in the subsequent experiments of the pure propane microemulsion and for two microemulsions containing oil mixtures at different propane-to-n-decane ratios. A quantitative analysis utilizing the Teubner–Strey model,32 shown as solid red lines in Fig. 3–6, and Porod's law for diffuse interfaces,33,34 represented as dashed blue lines, is provided afterwards. Theoretical foundations are illustrated above and in the ESI.† The analysis is followed by a comprehensive discussion of the high-pressure data, in which the influence of pressure and propane on the structural order is addressed by the so-called amphiphilicity factor fa53,54 and their impact on the bending rigidity κeff of the surfactant monolayer discussed by applying the model of random interfaces.44–464.1 Phase behavior
A prerequisite for meaningful studies on the influence of pressure and oil composition on the nanostructure of symmetrical microemulsions is the knowledge of their phase behavior. Detailed T(γ) cuts of the D2O-free microemulsions were measured at constant oil-to-water ratio in one of our recent works,15 in which we confirmed bicontinuity near the phase inversion temperature through electrical conductivity measurements. Fig. 2 shows the pressure-dependent fish cuts for the microemulsions containing n-decane or propane, respectively. The red arrows emphasize the opposite pressure-induced shift of the phase boundaries and the optimum point![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) . As expected, propane-containing formulations are located at much lower temperatures due to its significantly shorter chain length compared to n-decane, although it should be mentioned that the temperature shift for volatile hydrocarbons has been found to be less pronounced than anticipated.15,16,55 The value of γ at the
. As expected, propane-containing formulations are located at much lower temperatures due to its significantly shorter chain length compared to n-decane, although it should be mentioned that the temperature shift for volatile hydrocarbons has been found to be less pronounced than anticipated.15,16,55 The value of γ at the ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) point denotes the minimum surfactant concentration required to form a one-phase microemulsion and thus represents the efficiency of the surfactant mixture to fully solubilize water and oil. As opposed to the pure n-decane microemulsions, formulations with propane show a pressure-dependent efficiency, explained by the higher compressibility of propane and the related pressure-dependent strength of interactions between propane and the alkyl chains of the surfactant.15,56 Considering those weak interactions at low pressures, the limited active content of the commercial surfactants, and that preliminary phase behavior tests indicated a very low solubility of the surfactant mixture in propane at lower pressures, a rather high starting pressure had to be chosen for the propane microemulsion.15
point denotes the minimum surfactant concentration required to form a one-phase microemulsion and thus represents the efficiency of the surfactant mixture to fully solubilize water and oil. As opposed to the pure n-decane microemulsions, formulations with propane show a pressure-dependent efficiency, explained by the higher compressibility of propane and the related pressure-dependent strength of interactions between propane and the alkyl chains of the surfactant.15,56 Considering those weak interactions at low pressures, the limited active content of the commercial surfactants, and that preliminary phase behavior tests indicated a very low solubility of the surfactant mixture in propane at lower pressures, a rather high starting pressure had to be chosen for the propane microemulsion.15
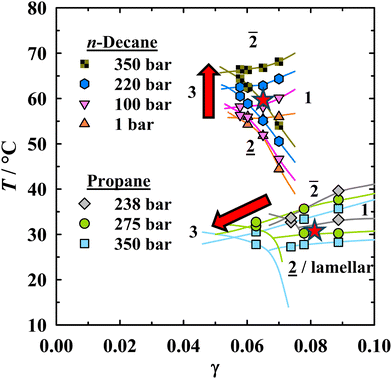 | ||
Fig. 2 Influence of pressure on the phase behavior of the microemulsion H2O/NaCl/BDG – n-alkane – C16–18-7PO-0.1EO-SO4Na/C14–17-SO3Na containing either n-decane or propane. Equal volumes of brine/BDG (salinity of 4.70 wt%) and oil were used. The surfactant ratio is 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (w/w) based on active content. Phase transition temperatures were taken from our previous study.15 The red arrows indicate the opposite pressure-induced shift of the phase boundaries and 1 (w/w) based on active content. Phase transition temperatures were taken from our previous study.15 The red arrows indicate the opposite pressure-induced shift of the phase boundaries and ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) for n-decane and propane-rich formulations. Red stars denote the measurement temperature for the isothermal HP-SANS experiments (salinity of 4.37 wt%). for n-decane and propane-rich formulations. Red stars denote the measurement temperature for the isothermal HP-SANS experiments (salinity of 4.37 wt%). | ||
For the SANS studies, surfactant mass fractions were converted to volume fractions, given that the switch from H2O to D2O would otherwise change the volumetric oil-to-water ratio owing to their different densities. All phase transition temperatures with D2O are compiled in the ESI† (Tables S1–S4). By and large, the influence of pressure and propane on the phase behavior of the D2O-containing microemulsions corroborates the findings for the D2O-free systems: pressure shifts phase boundaries upwards for the n-decane-rich microemulsions containing 0 and 30 wt% propane. A decrease of the phase transition temperatures is observed for the propane-rich systems with 60 and 100 wt% in the oil phase. The pressure-induced phase boundary shift is less pronounced for the oil mixtures than for the pure alkanes. Furthermore, good agreement between D2O and H2O microemulsions regarding the overall temperature range of the phase boundaries is found, with the red stars in Fig. 2 denoting the measurement temperature for the respective isothermal measurements. Small temperature shifts upon deuteration have also been noted by other authors.34,36
4.2 Small-angle neutron scattering
Small-angle neutron scattering was chosen as a powerful, non-destructive technique to obtain information on the length scales of water/oil domains and insights into the impact of pressure and propane on microemulsion nanostructure. SANS experiments discussed in the following were conducted in bulk contrast, setting the highest possible deuteration degree in the hydrophilic component, which was kept constant for all samples. Since all pressure-dependent bulk contrast scattering curves (with one exception discussed later) recorded exhibited isotropic scattering patterns, they were radially averaged over the full azimuthal range to obtain I(q) data. Irrespective of pressure, these scattering curves, which are shown in Fig. 3–6, exhibit certain similar features and trends commonly reported for bicontinuous microemulsions containing comparable amounts of water and oil. | ||
| Fig. 3 Pressure-dependent bulk contrast SANS curves for the microemulsion system containing 100 wt% n-decane, recorded at ϕC = 0.058 at the respective phase inversion temperature of each pressure. Curves are displaced by a factor of 10 (1 bar unscaled). Peak region analyzed via the Teubner–Strey model32 (red solid lines); high q analyzed with Porod's law, taking into account the diffuseness of the amphiphilic film33,34 (blue dashed lines). Inset: Unscaled close-up of the peak region with linear I axis. Fits are omitted for better visibility. | ||
 | ||
| Fig. 4 Pressure-dependent bulk contrast SANS curves for the microemulsion system containing 100 wt% n-decane, recorded isothermally at T = 60.6 °C and ϕC = 0.058. Curves are displaced by a factor of 10 (101 bar unscaled). Peak region analyzed via the Teubner–Strey model32 (red solid lines); high q analyzed with Porod's law, taking into account the diffuseness of the amphiphilic film33,34 (blue dashed lines). Inset: Unscaled close-up of the peak region with linear I axis. Fits are omitted for better visibility. | ||
 | ||
| Fig. 5 Pressure-dependent bulk contrast SANS curves for the microemulsion system containing 100 wt% propane, recorded isothermally at T = 30.5 °C and ϕC = 0.064. Curves are displaced by a factor of 10 (243 bar unscaled). Peak region analyzed via the Teubner–Strey model32 (red solid lines); high q analyzed with Porod's law, taking into account the diffuseness of the amphiphilic film33,34 (blue dashed lines). The measurement at 200 bar, measured outside of the one-phase region, no longer exhibits the typical features of bicontinuous microemulsions (cf. Fig. S5 and S6, ESI†). Inset: Unscaled close-up of the peak region with linear I axis. Fits are omitted for better visibility. | ||
 | ||
| Fig. 6 Pressure-dependent bulk contrast SANS curves for the microemulsion system containing (top) 30 wt% propane, recorded isothermally at T = 34.9 °C and ϕC = 0.042, and (bottom) 60 wt% propane, recorded isothermally at T = 27.0 °C and ϕC = 0.039. Curves are displaced by a factor of 10 (lowest pressure unscaled). Peak region analyzed via the Teubner–Strey model32 (red solid lines); high q analyzed with Porod's law, taking into account the diffuseness of the amphiphilic film33,34 (blue dashed lines). Inset: Unscaled close-up of the peak region with linear I axis. Fits are omitted for better visibility. | ||
![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) point, where countless studies have confirmed that the structure is indeed bicontinuous, bicontinuity can be presumed for all experiments, even if there might be slight deviations from a state of zero mean curvature.
point, where countless studies have confirmed that the structure is indeed bicontinuous, bicontinuity can be presumed for all experiments, even if there might be slight deviations from a state of zero mean curvature.
![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) , which was found to increase with increasing pressure by approximately 3 K per 100 bar, as visible from Fig. 2.15
, which was found to increase with increasing pressure by approximately 3 K per 100 bar, as visible from Fig. 2.15
Fig. 3 reveals only negligible changes in the scattering data when pressure is increased from 101 bar to 353 bar at the respective ![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) , with minor differences compared to the 1 bar measurement performed in a Hellma cuvette. For all pressures, the peak position remains nearly unchanged, indicating that pressure does not significantly affect the size of the water and oil domains. Within experimental and analytical error, the periodicity dTS, obtained from the analysis with eqn (2), is constant with dTS = (571 ± 6) Å (cf.Table 1). This observation is readily explained by the weak compressibility of water and n-decane, illustrated in Fig. S1 (ESI†). Similarly, a nearly pressure-independent radius was reported for water-in-decane droplet microemulsions.17,18 A close-up of the peak region, shown in the inset of Fig. 3, demonstrates that the SANS data are almost in quantitative agreement with regard to their forward and maximum scattering intensity, I0 and Imax. Consequently, the sharpness of the correlation peak is likewise unaffected by pressure, as is thus the correlation length ξTS.
, with minor differences compared to the 1 bar measurement performed in a Hellma cuvette. For all pressures, the peak position remains nearly unchanged, indicating that pressure does not significantly affect the size of the water and oil domains. Within experimental and analytical error, the periodicity dTS, obtained from the analysis with eqn (2), is constant with dTS = (571 ± 6) Å (cf.Table 1). This observation is readily explained by the weak compressibility of water and n-decane, illustrated in Fig. S1 (ESI†). Similarly, a nearly pressure-independent radius was reported for water-in-decane droplet microemulsions.17,18 A close-up of the peak region, shown in the inset of Fig. 3, demonstrates that the SANS data are almost in quantitative agreement with regard to their forward and maximum scattering intensity, I0 and Imax. Consequently, the sharpness of the correlation peak is likewise unaffected by pressure, as is thus the correlation length ξTS.
| Oil composition | ϕ C | p/bar | T/°C | d TS/Å | ξ TS/Å | f a | κ eff/kBT | S/V/10−3 Å−1 | t/Å | a |
|---|---|---|---|---|---|---|---|---|---|---|
| a 1 bar measurement recorded in a Hellma cuvette. | ||||||||||
| 100 wt% n-decane | 0.058 | 1a | 56.1 | 565 | 295 | −0.83 | 0.44 | 5.3 | 4.0 | 6.0 |
| 101 | 57.0 | 576 | 279 | −0.80 | 0.41 | 6.3 | 5.0 | 7.2 | ||
| 221 | 61.9 | 571 | 278 | −0.81 | 0.41 | 6.3 | 5.2 | 7.2 | ||
| 353 | 65.1 | 570 | 273 | −0.80 | 0.41 | 6.3 | 5.3 | 7.2 | ||
| 100 wt% n-decane | 0.058 | 101 | 60.6 | 577 | 284 | −0.81 | 0.42 | 6.0 | 5.5 | 6.9 |
| 141 | 60.6 | 568 | 278 | −0.81 | 0.42 | 6.2 | 5.5 | 7.0 | ||
| 180 | 60.6 | 569 | 280 | −0.81 | 0.42 | 6.3 | 5.8 | 7.2 | ||
| 221 | 60.6 | 571 | 278 | −0.81 | 0.41 | 6.3 | 5.5 | 7.2 | ||
| 260 | 60.6 | 574 | 269 | −0.80 | 0.40 | 6.4 | 6.0 | 7.3 | ||
| 300 | 60.6 | 577 | 255 | −0.77 | 0.38 | 6.4 | 6.0 | 7.4 | ||
| 353 | 60.6 | 592 | 246 | −0.74 | 0.35 | 6.5 | 6.0 | 7.7 | ||
| 30 wt% propane, 70 wt% n-decane | 0.042 | 200 | 34.9 | 758 | 325 | −0.76 | 0.36 | 5.0 | 4.5 | 7.6 |
| 240 | 34.9 | 754 | 328 | −0.76 | 0.37 | 5.0 | 5.5 | 7.5 | ||
| 290 | 34.9 | 753 | 322 | −0.76 | 0.36 | 5.2 | 5.5 | 7.8 | ||
| 351 | 34.9 | 754 | 303 | −0.73 | 0.34 | 5.1 | 5.0 | 7.7 | ||
| 60 wt% propane, 40 wt% n-decane | 0.039 | 101 | 27.0 | 839 | 318 | −0.70 | 0.32 | 4.6 | 4.5 | 7.7 |
| 175 | 27.0 | 828 | 316 | −0.70 | 0.32 | 4.7 | 4.5 | 7.8 | ||
| 240 | 27.0 | 820 | 320 | −0.71 | 0.33 | 4.7 | 4.0 | 7.7 | ||
| 291 | 27.0 | 810 | 318 | −0.72 | 0.33 | 4.8 | 4.5 | 7.8 | ||
| 350 | 27.0 | 803 | 326 | −0.73 | 0.35 | 4.8 | 4.5 | 7.7 | ||
| 100 wt% propane | 0.064 | 243 | 30.5 | 527 | 162 | −0.58 | 0.26 | 8.0 | 5.5 | 8.4 |
| 260 | 30.5 | 530 | 170 | −0.61 | 0.27 | 8.0 | 5.0 | 8.5 | ||
| 275 | 30.5 | 534 | 176 | −0.62 | 0.28 | 7.8 | 5.0 | 8.3 | ||
| 294 | 30.5 | 529 | 181 | −0.64 | 0.29 | 7.8 | 4.8 | 8.3 | ||
| 312 | 30.5 | 516 | 185 | −0.67 | 0.30 | 7.8 | 4.8 | 8.1 | ||
| 351 | 30.5 | 518 | 197 | −0.70 | 0.32 | 7.8 | 5.0 | 8.1 | ||
The somewhat higher I0 and Imax at elevated pressures, which lead to a broader peak than for the 1 bar measurement, are explained by stronger multiple scattering contributions due to the higher sample thickness of the high-pressure SANS cell (2 mm) compared to the Hellma cell (1 mm). This is also visible in the more pronounced shoulder at q ≈ 2qmax, which affects the intensity of the high q data. Thus, the differences in the value of the specific internal interface, which is S/V = (5.3 ± 0.5) × 10−3 Å−1 for the 1 bar measurement but S/V = (6.3 ± 0.6) × 10−3 Å−1 for all higher pressures, indicate that the obtained absolute values of S/V should be taken with caution. This is further addressed in the ESI,† including a quantitative analysis via the MuScatt software, which could make the “true” absolute value of S/V accessible. Especially the 2 mm sample thickness could render a correction essential given that the low sample transmission (Tsample between 0.19 and 0.32); nonetheless, in the main part of the manuscript, we decided to analyze the original 1D scattering curves obtained via GRASP from the raw detector data in order to avoid systematic errors. In principle, multiple scattering corrections can be highly useful to maintain comparability under different conditions (sample thickness, wavelength, instrument) and to generate “real” values by eliminating the impact of multiple scattering, which in our case particularly affects I0 – and thus ξTS, κeff and fa – as well as S/V (cf. discussion in the ESI†). Nevertheless, it is crucial but arguably difficult to ensure that treated data are entirely free of multiple scattering contributions; otherwise, data integrity may be compromised if the fine line between methodical data treatment and questionable data manipulation blurs.
The previous SANS measurements show that the nanostructure of the bicontinuous n-decane microemulsion remains almost unchanged near the respective ![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) , regardless of pressure. In the second set of experiments, a constant temperature of 60.6 °C was set, corresponding to
, regardless of pressure. In the second set of experiments, a constant temperature of 60.6 °C was set, corresponding to ![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) of an intermediate pressure (roughly 180 bar) and conveniently allows to study the impact of pressure isothermally without leaving the one-phase region. The scattering curves shown in Fig. 4 reveal that the peak position and therefore dTS are once more nearly unaffected by pressurization. However, quantitative differences are observed in the low q region, where the forward scattering intensity I0 and maximum scattering intensity Imax are pressure-dependent. Initially, I0 decreases with pressure before it increases again, whereas Imax consistently decreases. Thus, a similar peak sharpness is observed for the lower pressures, while higher pressures exhibit a broader peak. Accordingly, the correlation length ξTS remains almost constant up to a pressure of 221 bar, i.e., close to where the set temperature corresponds to
of an intermediate pressure (roughly 180 bar) and conveniently allows to study the impact of pressure isothermally without leaving the one-phase region. The scattering curves shown in Fig. 4 reveal that the peak position and therefore dTS are once more nearly unaffected by pressurization. However, quantitative differences are observed in the low q region, where the forward scattering intensity I0 and maximum scattering intensity Imax are pressure-dependent. Initially, I0 decreases with pressure before it increases again, whereas Imax consistently decreases. Thus, a similar peak sharpness is observed for the lower pressures, while higher pressures exhibit a broader peak. Accordingly, the correlation length ξTS remains almost constant up to a pressure of 221 bar, i.e., close to where the set temperature corresponds to ![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) , and further decreases considerably with increasing pressure. For these isothermal measurements, a pressure-induced shift away from the phase inversion temperature and thus to a slightly curved structure leads to a less pronounced correlation peak, characterized by a decreasing correlation length. From the analysis of the high q data, a pressure-independent specific internal interface of S/V = (6.3 ± 0.9) × 10−3 Å−1 is found within measurement uncertainty, the same as when studied at the respective phase inversion temperature.
, and further decreases considerably with increasing pressure. For these isothermal measurements, a pressure-induced shift away from the phase inversion temperature and thus to a slightly curved structure leads to a less pronounced correlation peak, characterized by a decreasing correlation length. From the analysis of the high q data, a pressure-independent specific internal interface of S/V = (6.3 ± 0.9) × 10−3 Å−1 is found within measurement uncertainty, the same as when studied at the respective phase inversion temperature.
![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) .
.
As shown in Fig. 5, the SANS profiles qualitatively resemble those of the n-decane microemulsion. Due to the limited surfactant active content, the low solubility of the surfactant mixture in propane at low pressures, as well as their concomitant weak interactions,56 243 bar was chosen as the starting pressure, as done in the phase behavior studies (cf.Fig. 2).15 Intriguingly, the peak position is again almost unaffected by pressure, with the periodicity dTS remaining constant at approximately (526 ± 10) Å – albeit with a slight decrease toward higher pressures. The exact values are listed in Table 1. Given that the volatile propane is more compressible than n-decane, this finding appears somewhat counterintuitive. However, the overall density changes in the investigated temperature and pressure range only lead to minor deviations of the actual volumetric water-to-oil ratio of the specimen (cf. Fig. S1, ESI†); consequently, there is no strong trend in the periodicity. For other compressible oils, Eastoe et al. likewise report an almost pressure-independent radius of water-in-propane,21,23 water-in-n-butane,22 and water-in-CO2 droplets.24 In contrast, a change in the water content of these w/o structures unsurprisingly affects the droplet size.22,24 More notable variations of the droplet radius under applied pressure were only observed for water-in-propane droplets stabilized by the non-ionic surfactant C12E5 as well as balanced CO2 microemulsions stabilized by fluorinated surfactants, which was in both cases explained by the pressure-dependent monomeric solubility of the surfactant.21,30 For the ionic surfactants used in this work, only a very small monomeric solubility in propane is expected, irrespective of pressure.
In the low q part, a rising pressure leads to a lower forward scattering intensity as well as a higher maximum scattering intensity and therefore a sharper peak. As a consequence, the correlation length systematically increases by roughly 20% from ξTS = 162 Å to 197 Å within just a little more than 100 bar, in contrast to the trend observed for n-decane microemulsions.
In our previous phase behavior studies with propane, we observed demixing when moving to lower pressures, even at higher surfactant concentrations,15 which could be confirmed when recording phase boundaries for the HP-SANS investigations presented here. We hypothesized that there might be a coexistence of a lamellar phase together with another phase below the lower phase boundary. Therefore, we recorded an additional SANS measurement at 200 bar, shown in Fig. S5 (ESI†). This dataset was excluded from the analysis because its scattering profile no longer exhibits the typical correlation peak at qmax, instead showing an increasing forward scattering intensity towards q → 0 and two smaller local peaks at intermediate q. Even though those peaks are only weakly pronounced, scattering pattern, shown in Fig. S6 (ESI†), and scattering curve give rise to the assumption that a transition towards a lamellar phase has indeed taken place. The presence of such a lamellar phase below the lower phase boundary in gas-rich microemulsions with non-ionic behavior has also been proposed by different authors.64 In the ESI,† a detailed discussion of the anisotropic scattering pattern at 200 bar as well as the isotropic scattering patterns of two higher pressures is provided in Fig. S6 (ESI†) by means of an azimuth-dependent analysis of the scattering intensities (I(χ)). To briefly summarize the most important findings, we found that the scattering intensity of the isotropic scattering patterns is unsurprisingly χ-independent, whereas the anisotropic scattering pattern reveals two intensity peaks in close proximity to 90° and 270° (cf. Table S6, ESI†), proving the presence of lamellar sheets stacked perpendicular to the plane defined by neutron path and z axis. Given that lower pressures limit the solubilization capacity of propane, we assume that this lamellar phase coexists with some oil-rich phase. Consequently, our observations can be attributed to demixing of the sample due to a pressure-induced phase behavior shift outside the one-phase region, whose width was shown to be pressure-dependent for propane-rich microemulsions even at a constant surfactant concentration.15
As anticipated, observing an almost unchanged peak position highlights that the periodicity is nearly unaffected by pressure, albeit with a slight decrease of dTS in the propane-rich mixture. Note that in our previous work, we found a higher solubilization efficiency for the microemulsions containing oil mixtures compared to those with the pure oils.15 While it is known that the solubilization efficiency of surfactants generally decreases with increasing (non-gaseous) oil chain length,62,65,66 the pressure-dependent propane–surfactant tail interactions limit the solubilization potential and yield an efficiency drawback at low pressures. Therefore, the optimum point is located at different surfactant concentrations and we thus need to adjust the surfactant volume fraction ϕC to stay in proximity to it. Due to the lower ϕC set for the two oil mixtures compared to the pure n-decane and propane formulations, the domain sizes are therefore significantly larger, with dTS close to (30 wt% propane) or even above (60 wt% propane) 800 Å. The influence of pressure on peak sharpness and forward scattering intensity is likewise weak and, as expected, somewhat stronger for the formulation with a higher proportion of propane in the oil mixture, which exhibits an increasing peak sharpness under pressurization, as was previously observed for the pure propane microemulsion. The fact that the shoulder at q ≈ 2qmax appears more prominent for the mixtures confirms an increased multiple scattering contribution due to the stronger scattering caused by larger water/oil domains.
5 Discussion
In this chapter, the influence of propane on the pressure-dependent nanostructure of the investigated microemulsions is discussed in a more general context. We begin by examining whether the prefactor of geometric models of the bicontinuous structure67,68 depends on pressure and the propane-to-n-decane ratio. Subsequently, we discuss the impact of the aforementioned parameters on the effective bending rigidity κeff of the surfactant monolayer and on the amphiphilicity factor fa, which characterizes the structural order of the microemulsion.5.1 Geometric prefactor of bicontinuous structures
As expected for bicontinuously structured microemulsions, our data analysis clearly shows the inverse proportionality of periodicity and surfactant volume fraction (dTS ∝ ϕC−1). In the ESI,† this is addressed quantitatively by introducing a normalized periodicity, with Fig. S4 (ESI†) proving that changes in dTS can be fully explained by a variation of ϕC, further highlighting the low monomeric solubility of the surfactant mixture in both oil and water.Geometric models of the bicontinuous structure67,68 predict that its periodicity dTS is inversely proportional to the specific internal interface S/V according to
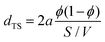 | (7) |
In Fig. 7, the determined geometric factors are plotted as a function of pressure for the bicontinuous microemulsions containing different propane-to-n-decane ratios. All values are compiled in Table 1. Interestingly, pressure has a minor effect on a for each of the studied microemulsions, which can be explained by the small pressure-induced volume contraction, even for propane-rich specimens. Therefore, the values obtained for the n-decane microemulsion are close to the value of a = 7.16 (red long dashes) determined for bicontinuous non-ionic model microemulsions.36 With an increasing amount of propane in the sample, the value of the geometric prefactor a increases, with a > 8 for the microemulsion containing only propane as the oil. One reason for this interesting systematic trend could be the increasing disorder observed with increasing propane content, which will be further addressed in terms of the amphiphilicity factor later. In Fig. 7, we omitted the value for the n-decane microemulsion at 1 bar because the impact of multiple scattering in the Hellma cuvette (d = 1 mm) is distinctly lower than for the measurements in the high-pressure cell (d = 2 mm), even though it exactly matches a = 6 as predicted by de Gennes. Utilizing the MuScatt software to mitigate the impact of multiple scattering, we still observe an increase of the prefactor with increasing propane concentration, albeit somewhat less pronounced. As listed in Table S5 in the ESI,† the values of a are around 20% lower, ranging between 5.0 and 6.4.
 | ||
| Fig. 7 Geometric prefactor a = 2dTSS/V as a function of pressure for the studied symmetric bicontinuous microemulsions. The black short dashes denote a = 6, as theoretically predicted by de Gennes and Taupin.68 Red long dashes denote a = 7.16, as experimentally determined by Sottmann et al.36 The 1 bar measurement is omitted due to a non-comparable impact of multiple scattering in the 1 mm Hellma cuvette. | ||
5.2 Bending rigidity and amphiphilicity factor
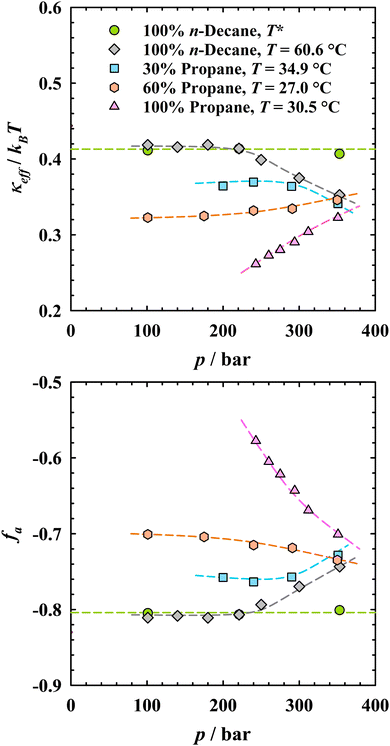
The trends observed for the nanostructure of bicontinuous microemulsions as a function of pressure and the propane-to-n-decane ratio should be attributable, at least qualitatively, to the influence of these two parameters on the amphiphilic film. Thus, we utilize Gompper et al.'s modification of the random interface model developed by Pieruschka and Safran44–46 to determine the effective bending rigidity κeffviaeqn (5) and further quantify the amphiphilicity factor viaeqn (6) as a measure for the order of the bicontinuous structure (see SANS analysis chapter and Fig. 1 for details). All values of κeff and fa are compiled in Table 1 and visualized in Fig. 8 as a function of pressure.Starting with the n-decane microemulsions studied at the respective phase inversion temperatures, the pressure independence of dTS and ξTS leads to a pressure-independent κeff ≈ 0.41kBT, shown in Fig. 8 as green circles. Note that for many well-structured bicontinuous microemulsions, dTS/ξTS ≈ 2, and similar values of κeff are thus found at their respective ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) point, independent of the oil and the alkyl chain length of the surfactant.36,62 This is because the higher rigidity of monolayers formed by longer-chain surfactants is compensated by the stronger thermal fluctuations inherent in the larger structures.36,44,70 The amphiphilicity factor of fa ≈ −0.81 (cf. bottom plot in Fig. 8) indicates a well-structured microemulsion according to the notion of Schubert et al.53 This pressure independence is explained by the small temperature changes and the weak compressibility of n-decane, and can likewise be anticipated when considering the counteracting influences of temperature and pressure on the bending rigidity as well as macroscopic phase behavior (cf.Fig. 2). Similar findings have been reported in literature, independent on the nature of the surfactant.17–19
point, independent of the oil and the alkyl chain length of the surfactant.36,62 This is because the higher rigidity of monolayers formed by longer-chain surfactants is compensated by the stronger thermal fluctuations inherent in the larger structures.36,44,70 The amphiphilicity factor of fa ≈ −0.81 (cf. bottom plot in Fig. 8) indicates a well-structured microemulsion according to the notion of Schubert et al.53 This pressure independence is explained by the small temperature changes and the weak compressibility of n-decane, and can likewise be anticipated when considering the counteracting influences of temperature and pressure on the bending rigidity as well as macroscopic phase behavior (cf.Fig. 2). Similar findings have been reported in literature, independent on the nature of the surfactant.17–19
Moving to the isothermal measurements at 60.6 °C (gray diamonds in Fig. 8), κeff and fa for all pressures up to 221 bar match the values determined from the analysis at the respective pressure-dependent phase inversion temperature (green circles). As pressure is increased further, κeff decreases slightly, accompanied by a slightly less negative value of fa, which could be due to the formation of less ordered, elongated structures that are typically present when moving slightly away from ![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) .
.
For the bicontinuous propane microemulsions, the effective bending rigidity systematically increases from κeff = 0.26 to 0.32kBT within just a little more than 100 bar (pink triangles in Fig. 8). Even at the highest pressure, κeff is clearly lower than in the n-decane microemulsions. A possible explanation for the generally smaller κeff values and their pressure trend could be related to the lower density of propane, which however noticeably increases with pressure and thus results in stronger pressure-dependent interactions between propane molecules and the alkyl chains of the surfactant. Similarly, a slight increase of the bending rigidity with pressure was found in bicontinuous water/CO2 microemulsions stabilized by a commercial fluorinated non-ionic surfactant.29,30 In line with these results, the amphiphilicity factor fa becomes increasingly negative with rising pressure, from −0.58 at 243 bar to −0.70 at 351 bar. In summary, the impact of pressure on the properties of the amphiphilic film in propane microemulsions is considerably stronger than for formulations with the incompressible n-decane, whose structural order can no longer be reached, even at the highest investigated pressure.
Attempting a deeper physicochemical understanding of the influence of propane on κeff based on these observations, we propose that the small and more diffusive propane molecules can interpenetrate the surfactant tails more easily compared to n-decane, which increases the local disorder and disrupts tail–tail interactions, leading to a softening of the surfactant monolayer and a reduction of κeff. Considering further the entropic effect, the vastly different number of molecules per volume unit could offer more degrees of freedom and hence explain stronger fluctuations of the amphiphilic film in the presence of propane.20,71
For the two microemulsions containing mixtures of n-decane and propane, Fig. 8 demonstrates that amphiphilicity factors as well as effective bending rigidities lie in between those of the pure alkane microemulsions. For the n-decane-rich mixture (blue squares), κeff remains almost constant at low and intermediate pressures. However, as in the case of the n-decane microemulsion, a decrease in κeff is observed at the highest pressure, which can again be explained by the increasing distance from ![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) . This trend is corroborated by the pressure dependence of fa. Increasing the propane content to 60 wt% (coral hexagons) leads to a further softening of the surfactant monolayer. With increasing pressure, κeff now consistently increases, as found for the pure propane microemulsion. The reason for the weaker increase compared to the pure propane formulation is that the microemulsion with the oil mixture is less compressible, which leads to a lower pressure dependence of the oil–surfactant tail interactions and thus to a smaller change in the nanostructural properties.56
. This trend is corroborated by the pressure dependence of fa. Increasing the propane content to 60 wt% (coral hexagons) leads to a further softening of the surfactant monolayer. With increasing pressure, κeff now consistently increases, as found for the pure propane microemulsion. The reason for the weaker increase compared to the pure propane formulation is that the microemulsion with the oil mixture is less compressible, which leads to a lower pressure dependence of the oil–surfactant tail interactions and thus to a smaller change in the nanostructural properties.56
5.3 Generalizing the influence of pressure and propane on microemulsion nanostructure
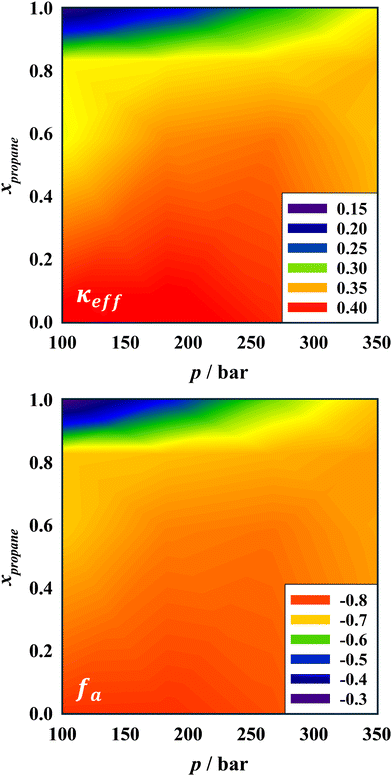
The findings discussed above show how the pressure and the propane-to-n-decane ratio systematically affect the bending rigidity of the surfactant film and the order of the bicontinuous nanostructure. It shall be emphasized that these are no run-of-the-mill SANS experiments, but instead rely on time-consuming procedures that allow only for limited experiments during the allocated beam time. We thus summarize the insights into the influence of pressure and propane by interpolating and extrapolating bending rigidity and amphiphilicity factor for currently non-explored measurement conditions, visualized as heat maps. These were calculated via second-order polynomials using the isothermal measurement data (cf.Table 1). Thus, the trends of κeff and fa illustrated by the heat maps correspond to bicontinuous microemulsions having their respective phase inversion temperature at an intermediate pressure for a given oil ratio.Fig. 9 (top) demonstrates that κeff systematically reduces when n-decane is replaced by the more compressible propane. With an increasing amount of propane, the sensitivity of the amphiphilic film to pressure changes is significantly enhanced. Similar observations can be made for the amphiphilicity factor fa, shown in the bottom part of Fig. 9. The structural order decreases in propane-rich formulations; however, pressure becomes more decisive and can lead to a significantly higher structural order. Higher pressures could not be investigated due to limitations of the experimental setup, but it stands to reason that the impact of the nature of the oil on the structural order of the microemulsion becomes less crucial when pressure is elevated further. On the other hand, Fig. 9 demonstrates that a combination of low pressures and high propane proportions leads to weakly structured mixtures, although one should keep in mind the uncertainty of extrapolations outside the measurement range toward experimentally inaccessible pressures and temperatures.
The similarity of the heat maps emphasizes that the rigidity of the amphiphilic monolayer is governed by the same factors as the overall structural order of the microemulsion. Expressed from a different perspective, a more rigid monolayer is able to form a well-structured microemulsion. Increasing the proportion of propane in the oil mixture hence always leads to a softening of the amphiphilic film and a loss of structural order. However, the exact impact strongly depends on pressure. At high pressures, the influence of the propane concentration is smaller because the interaction strength between surfactant tails and the compressible propane is significantly enhanced56 and thus only moderately weaker compared to the surfactant tail–n-decane interactions. At low pressures, these interactions are essentially unchanged for the incompressible n-decane but substantially weakened for propane. As discussed in our recent work, it was postulated that these altered interactions and their relative magnitude explain changes in curvature as well as the pressure-(in)dependent solubilization capacity of propane (n-decane) microemulsions.15 The high-pressure SANS studies strongly corroborate that this further holds true for the nanostructure of these microemulsions.
6 Conclusions
Even though microemulsions containing volatile alkanes play a central role for instance in chemical-enhanced oil recovery, where the use of microemulsions can improve the exploitation of existing crude oil reservoirs, studies of their properties are scarce. Just recently, we found that the pressure-dependent phase behavior of application-relevant microemulsions of the type H2O/NaCl/butyldiglycol – n-decane/propane – C16–18-7PO-0.1EO-SO4Na/C14–17-SO3Na strongly depends on the oil used in the microemulsion.15 Motivated by this intriguing result and the lack of studies on the pressure dependence of the nanostructure of bicontinuous microemulsions containing short-chain alkanes, we performed pressure-dependent bulk contrast small-angle neutron scattering experiments on this type of microemulsions near the respective![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) points.
points.
Scattering curves obtained by radial averaging of the recorded isotropic scattering signals showed a pronounced correlation peak, followed by a q−4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−q2t2) decay according to Porod's law for diffuse interfaces, from which the specific internal interface S/V could be obtained. Despite the noticeable impact of multiple scattering, they exhibit the typical features of symmetrical microemulsions with equal amounts of water and oil being studied close to the phase inversion, where a bicontinuous structure can be expected. Accordingly, the correlation peak was analyzed by means of the Teubner–Strey model, from which two length scales, periodicity dTS and correlation length ξTS, were obtained, further enabling the determination of the amphiphilicity factor fa and the effective bending rigidity κeff of the amphiphilic film.
exp(−q2t2) decay according to Porod's law for diffuse interfaces, from which the specific internal interface S/V could be obtained. Despite the noticeable impact of multiple scattering, they exhibit the typical features of symmetrical microemulsions with equal amounts of water and oil being studied close to the phase inversion, where a bicontinuous structure can be expected. Accordingly, the correlation peak was analyzed by means of the Teubner–Strey model, from which two length scales, periodicity dTS and correlation length ξTS, were obtained, further enabling the determination of the amphiphilicity factor fa and the effective bending rigidity κeff of the amphiphilic film.
Studying n-decane microemulsions at the respective pressure-dependent phase inversion temperature revealed that the bicontinuous nanostructure is virtually unaffected by pressure due to the weak compressibility of n-decane and its nearly pressure-independent interactions with the surfactant. Instead, isothermal measurements showed that a pressure-induced shift away from the phase inversion and thus to a structure with small curvature around water or oil leads to a slightly less pronounced correlation peak, characterized by a decreasing correlation length.
For the pure propane microemulsion investigated at constant temperature, the overall structural order was found to be markedly lower compared to the n-decane microemulsion. While the periodicity turned out to be nearly pressure-independent, the correlation length significantly increased with pressure. Concomitantly, the increase of κeff indicates a more rigid amphiphilic film due to amplified interactions of the compressible propane with the surfactant tails under pressure. Mixtures of n-decane and propane showed intermediate behavior with fa and κeff in between those obtained for the pure microemulsions, proving that an increasing concentration of the volatile alkane leads to a reduction of the structural order of the bicontinuous microemulsions, while the pressure dependence steadily increases.
Despite confirming the inverse relationship between periodicity and surfactant volume fraction irrespective of the propane-to-n-decane ratio and pressure, it was found by using the dTS and S/V values obtained from the SANS data analysis that the geometric prefactor a of models describing the bicontinuous structure increases from slightly above 7 for n-decane microemulsions, matching the experimentally determined a for non-ionic bicontinuous microemulsions,36 to a > 8 for propane microemulsions, which is most likely due to the increased consumption of amphiphilic film owing to the increasing disorder.
Utilizing the MuScatt software, it was quantified in the ESI† that the values of ξTS, S/V, a and fa are systematically influenced due to multiple scattering. While such a correction could help maintaining comparability under different conditions, original data analysis was prioritized to ensure methodical data reduction in order to guarantee data integrity. In order to elucidate in detail how absolute intensities and the shoulder are affected by multiple scattering, thermal fluctuations, domain size and sample thickness, future systematic studies at high and constant transmission using adjustable sample thickness could be envisioned.
Thus, the findings obtained from our high-pressure SANS experiments proved that the impact of pressure-dependent interactions between (non-)volatile hydrocarbons and surfactant tails is not limited to changes of the macroscopic phase behavior, but likewise affects the nanostructure of the microemulsion. Future studies could target the highly compressible ethane or methane. Expecting weaker interaction strengths with the surfactant tails, it is assumed that such microemulsions would exhibit an even stronger influence of pressure on their nanostructure.
Author contributions
Maximilian Krappel: formal analysis, investigation, visualization, writing – original draft. Christian Bittner: conceptualization, resources. Ralf Schweins: methodology, resources. Thomas Sottmann: conceptualization, investigation, methodology, resources, writing – original draft.Data availability
Raw scattering data are available under https://doi.org/10.5291/ILL-DATA.9-10-1745.38 Further data supporting this article have been included as part of the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge BASF SE for financial support and permission to publish these results and thank Nicole Lichterfeld-Weber for providing the BASF chemicals. The authors appreciate the electrical and technical workshop of the Institute of Physical Chemistry for their work on the high-pressure setup. We acknowledge the ILL for beamtime at D22 (proposal 9-10-1745) and thank Julian Fischer, Nadine Schnabel, Diana Sottmann and Florian Trummer for their assistance with the SANS experiments.Notes and references
- K. Shinoda and S. Friberg, Adv. Colloid Interface Sci., 1975, 4, 281–300 Search PubMed.
- C. Huh, J. Colloid Interface Sci., 1979, 71, 408–426 Search PubMed.
- R. Aveyard, B. P. Binks, S. Clark and J. Mead, J. Chem. Soc., Faraday Trans., 1986, 82, 125 RSC.
- T. Sottmann and R. Strey, J. Chem. Phys., 1997, 106, 8606–8615 Search PubMed.
- W. Jahn and R. Strey, J. Phys. Chem., 1988, 92, 2294–2301 CrossRef CAS.
- R. Strey, Colloid Polym. Sci., 1994, 272, 1005–1019 CrossRef CAS.
- Improved Oil Recovery by Surfactant and Polymer Flooding, ed. D. O. Shah and R. S. Schechter, Academic Press, New York, 1977 Search PubMed.
- B. K. Paul and S. P. Moulik, Curr. Sci., 2001, 80, 990–1001 Search PubMed.
- M. Schwarze, T. Pogrzeba, I. Volovych and R. Schomäcker, Catal. Sci. Technol., 2015, 5, 24–33 Search PubMed.
- E. J. Acosta, J. H. Harwell, J. F. Scamehorn and D. A. Sabatini, Handbook for Cleaning/Decontamination of Surfaces, Elsevier, 2007, pp. 831–884 Search PubMed.
- F. Garavand, M. Jalai-Jivan, E. Assadpour and S. M. Jafari, Food Chem., 2021, 364, 130376 Search PubMed.
- Exploring for oil and gas traps, ed. E. O. Beaumont and N. H. Foster, American Association of Petroleum Geologists, Tulsa, OK, 1999 Search PubMed.
- M. Miñana-Perez, A. Graciaa, J. Lachaise and J.-L. Salager, Colloids Surf., A, 1995, 100, 217–224 Search PubMed.
- T. Sottmann and C. Stubenrauch, Microemulsions, Wiley, Chichester, West Sussex, U.K. and Ames, Iowa, 2009, pp. 1–47 Search PubMed.
- M. Krappel, J. Hippele, C. Bittner and T. Sottmann, Ind. Eng. Chem. Res., 2024, 63, 10041–10053 Search PubMed.
- M. Krappel, J. Hippele, S. Kolin, N. Lichterfeld-Weber, R. Schweins, C. Bittner and T. Sottmann, 85th EAGE Annual Conference & Exhibition, 2024.
- Y. Kawabata, M. Nagao, H. Seto, S. Komura, T. Takeda, D. Schwahn, N. L. Yamada and H. Nobutou, Phys. Rev. Lett., 2004, 92, 056103 Search PubMed.
- Y. Kawabata, H. Seto, M. Nagao and T. Takeda, J. Chem. Phys., 2007, 127, 044705 Search PubMed.
- H. Seto, M. Nagao and Y. Kawabata, Colloids Surf., A, 2006, 284–285, 430–433 Search PubMed.
- W. Helfrich, Z. Naturforsch., C, 1973, 28, 693–703 CrossRef CAS PubMed.
- J. Eastoe, D. C. Steytler, B. H. Robinson and R. K. Heenan, J. Chem. Soc., Faraday Trans., 1994, 90, 3121 Search PubMed.
- J. Eastoe, W. K. Young, B. H. Robinson and D. C. Steytler, J. Chem. Soc., Faraday Trans., 1990, 86, 2883 Search PubMed.
- E. W. Kaler, J. F. Billman, J. L. Fulton and R. D. Smith, J. Phys. Chem., 1991, 95, 458–462 Search PubMed.
- J. Eastoe, B. M. H. Cazelles, D. C. Steytler, J. D. Holmes, A. R. Pitt, T. J. Wear and R. K. Heenan, Langmuir, 1997, 13, 6980–6984 Search PubMed.
- M. Klostermann, T. Foster, R. Schweins, P. Lindner, O. Glatter, R. Strey and T. Sottmann, Phys. Chem. Chem. Phys., 2011, 13, 20289–20301 RSC.
- A. Müller, Y. Pütz, R. Oberhoffer, N. Becker, R. Strey, A. Wiedenmann and T. Sottmann, Phys. Chem. Chem. Phys., 2014, 16, 18092–18097 Search PubMed.
- Y. Pütz, L. Grassberger, P. Lindner, R. Schweins, R. Strey and T. Sottmann, Phys. Chem. Chem. Phys., 2015, 17, 6122–6134 Search PubMed.
- M. Nagao, H. Seto, S. Komura, T. Takeda and M. Hikosaka, Formation and Dynamics of Self-Organized Structures in Surfactants and Polymer Solutions, Steinkopff, Darmstadt, 1997, vol. 106, pp. 86–90 Search PubMed.
- O. Holderer, M. Klostermann, M. Monkenbusch, R. Schweins, P. Lindner, R. Strey, D. Richter and T. Sottmann, Phys. Chem. Chem. Phys., 2011, 13, 3022–3025 RSC.
- M. Klostermann, R. Strey, T. Sottmann, R. Schweins, P. Lindner, O. Holderer, M. Monkenbusch and D. Richter, Soft Matter, 2012, 8, 797–807 Search PubMed.
- M. Berghaus, M. Paulus, P. Salmen, S. Al-Ayoubi, M. Tolan and R. Winter, J. Phys. Chem. B, 2016, 120, 7148–7153 CrossRef CAS PubMed.
- M. Teubner and R. Strey, J. Chem. Phys., 1987, 87, 3195–3200 Search PubMed.
- G. Porod, Small Angle X-ray Scattering, Academic Press, London, 1982 Search PubMed.
- R. Strey, J. Winkler and L. Magid, J. Phys. Chem., 1991, 95, 7502–7507 Search PubMed.
- E. W. Lemmon, I. H. Bell, M. L. Huber and M. O. McLinden, NIST Chemistry WebBook, NIST Standard Reference Database 69, National Institute of Standards and Technology, Gaithersburg, MD, 2023 Search PubMed.
- T. Sottmann, R. Strey and S.-H. Chen, J. Chem. Phys., 1997, 106, 6483–6491 CrossRef CAS.
- M. Laupheimer, T. Sottmann, R. Schweins and C. Stubenrauch, Soft Matter, 2014, 10, 8744–8757 Search PubMed.
- T. Sottmann, C. Bittner, J. Fischer, M. Krappel, N. Schnabel, R. Schweins, F. Trummer and D. Sottmann, Influence of Pressure on the Microstructure of Bicontinuous Propane Microemulsions, Institut Laue-Langevin (ILL), 2023 DOI:10.5291/ILL-DATA.9-10-1745.
- C. D. Dewhurst, J. Appl. Crystallogr., 2023, 56, 1595–1609 Search PubMed.
- D. Langevin, Acc. Chem. Res., 1988, 21, 255–260 CrossRef CAS.
- C. Frank, H. Frielinghaus, J. Allgaier and H. Prast, Langmuir, 2007, 23, 6526–6535 Search PubMed.
- S. M. Choi, S. H. Chen, T. Sottmann and R. Strey, Phys. A, 2002, 304, 85–92 Search PubMed.
- K. Schneider, P. Verkoyen, M. Krappel, C. Gardiner, R. Schweins, H. Frey and T. Sottmann, Langmuir, 2020, 36, 9849–9866 Search PubMed.
- G. Gompper, H. Endo, M. Mihailescu, J. Allgaier, M. Monkenbusch, D. Richter, B. Jakobs, T. Sottmann and R. Strey, EPL, 2001, 56, 683–689 Search PubMed.
- P. Pieruschka and S. A. Safran, EPL, 1993, 22, 625–630 Search PubMed.
- P. Pieruschka and S. A. Safran, EPL, 1995, 31, 207–212 Search PubMed.
- D. Byelov, H. Frielinghaus, O. Holderer, J. Allgaier and D. Richter, Langmuir, 2004, 20, 10433–10443 Search PubMed.
- M. Peltomäki, G. Gompper and D. M. Kroll, J. Chem. Phys., 2012, 136, 134708 CrossRef PubMed.
- O. Holderer, H. Frielinghaus, M. Monkenbusch, M. Klostermann, T. Sottmann and D. Richter, Soft Matter, 2013, 9, 2308 Search PubMed.
- B. Jakobs, Amphiphile Blockcopolymere als Efficiency Booster für Tenside: Entdeckung und Aufklärung des Effekts, Cuvillier, Göttingen, 2002 Search PubMed.
- H. F. M. Klemmer, J. Allgaier, H. Frielinghaus, O. Holderer and M. Ohl, Colloid Polym. Sci., 2017, 295, 911–923 Search PubMed.
- J. Fischer, L. Porcar, J. T. Cabral and T. Sottmann, J. Colloid Interface Sci., 2023, 635, 588–597 Search PubMed.
- K.-V. Schubert, R. Strey, S. R. Kline and E. W. Kaler, J. Chem. Phys., 1994, 101, 5343–5355 CrossRef CAS.
- K.-V. Schubert and R. Strey, J. Chem. Phys., 1991, 95, 8532–8545 Search PubMed.
- M. C. Puerto and R. L. Reed, Soc. Pet. Eng. J., 1983, 23, 669–682 Search PubMed.
- D. G. Peck and K. P. Johnston, J. Phys. Chem., 1991, 95, 9549–9556 Search PubMed.
- J. A. Silas and E. W. Kaler, J. Colloid Interface Sci., 2003, 257, 291–298 Search PubMed.
- H. Frielinghaus, Nucl. Instrum. Methods Phys. Res., Sect. A, 2018, 904, 9–14 Search PubMed.
- S. Jaksch, V. Pipich and H. Frielinghaus, J. Appl. Crystallogr., 2021, 54, 1580–1593 Search PubMed.
- M. Nagao, H. Seto, T. Takeda and Y. Kawabata, J. Chem. Phys., 2001, 115, 10036–10044 CrossRef CAS.
- H. Endo, M. Mihailescu, M. Monkenbusch, J. Allgaier, G. Gompper, D. Richter, B. Jakobs, T. Sottmann, R. Strey and I. Grillo, J. Chem. Phys., 2001, 115, 580–600 Search PubMed.
- K. Schneider, T. M. Ott, R. Schweins, H. Frielinghaus, O. Lade and T. Sottmann, Ind. Eng. Chem. Res., 2019, 58, 2583–2595 Search PubMed.
- N. Freiberger, C. Moitzi, L. de Campo and O. Glatter, J. Colloid Interface Sci., 2007, 312, 59–67 Search PubMed.
- M. Schwan, L. G. A. Kramer, T. Sottmann and R. Strey, Phys. Chem. Chem. Phys., 2010, 12, 6247–6252 RSC.
- M. Kahlweit, R. Strey, P. Firman, D. Haase, J. Jen and R. Schomaecker, Langmuir, 1988, 4, 499–511 CrossRef CAS.
- S. Queste, J. L. Salager, R. Strey and J. M. Aubry, J. Colloid Interface Sci., 2007, 312, 98–107 CrossRef CAS PubMed.
- Y. Talmon and S. Prager, J. Chem. Phys., 1978, 69, 2984–2991 Search PubMed.
- P. G. de Gennes and C. Taupin, J. Phys. Chem., 1982, 86, 2294–2304 Search PubMed.
- P. Debye, H. R. Anderson and H. Brumberger, J. Appl. Phys., 1957, 28, 679–683 CrossRef CAS.
- D. C. Morse, Curr. Opin. Colloid Interface Sci., 1997, 2, 365–372 Search PubMed.
- G. Porte and C. Ligoure, J. Chem. Phys., 1995, 102, 4290–4298 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Phase transition temperatures, discussion and illustration of multiple scattering corrections using MuScatt, fundamentals of the Teubner–Strey model, dependence of periodicity on surfactant volume fraction, azimuthal analysis of scattering patterns. See DOI: https://doi.org/10.1039/d5sm00343a |
| This journal is © The Royal Society of Chemistry 2025 |