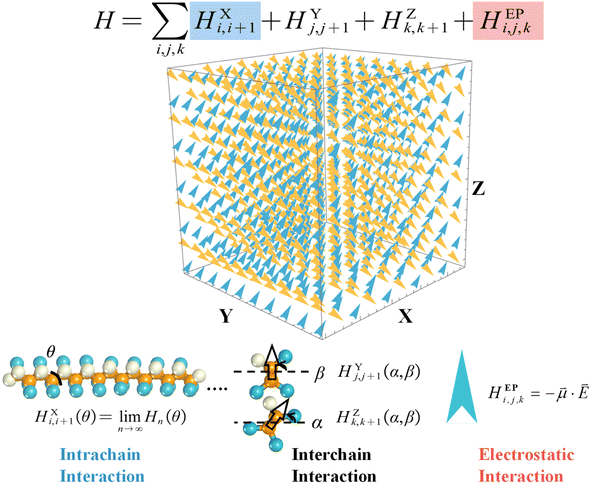
Monte Carlo simulations of the temperature-dependent microstructure evolution of relaxor ferroelectric polymers†
Tong
Guan
a,
Quan-Ao
He
b and
Shuang
Chen
 *ac
*ac
aKuang Yaming Honors School, Nanjing University, Nanjing, Jiangsu 210023, China. E-mail: chenshuang@nju.edu.cn
bSchool of Chemistry and Chemical Engineering, Nanjing University, Nanjing, Jiangsu 210023, China
cNational Laboratory of Solid State Microstructures, Nanjing University, Nanjing 210093, China
First published on 13th November 2024
Abstract
Poly(vinylidene fluoride-trifluoroethylene) [P(VDF-TrFE)] relaxor ferroelectrics are drawing significant attention nowadays owing to their excellent multifunctionality and extensive applications. However, microstructures responsible for their relaxor behaviors have not been well understood to tailor their application-oriented properties. Monte Carlo (MC) modeling has been developed to successfully reproduce the relaxor ferroelectricity versus normal ferroelectricity of regiodefect-tuned P(VDF-TrFE) polymers. A series of MC simulations was conducted to understand the temperature-dependent microstructure evolutions of both P(VDF-TrFE) relaxor and normal ferroelectrics and further estimate their dielectric permittivity and hysteresis loops. In P(VDF-TrFE) relaxors, their microstructure evolution follows the slush model, involving various nanoscale domains. Significantly, a new phase, a large nanodomain with strongly correlated and randomly oriented dipoles, was found for the first time and is different from the traditional paraelectric phase. Our study not only provides a computational paradigm for ferroelectric polymers but also provides guidance for the design and synthesis of new relaxor polymers by tuning regiodefects.
1. Introduction
The poly(vinylidene fluoride) [P(VDF)] family enables versatile device applications because of the exceptional ferroelectricity,1 piezoelectricity,2 electrocaloricity,3 and dielectricity.4 Specific synthesis methods, such as thermal annealing,5 electron irradiation,6 or introduction of other monomers,7 can significantly enhance its piezoelectric and electrocaloric properties and even facilitate the formation of relaxor ferroelectrics.8 Relaxor ferroelectric polymers have aroused considerable research interest owing to their unexplained diffused phase transition, dielectric dispersion, polarization residue at high temperatures beyond the Curie temperature (TC), slim ferroelectric hysteresis (P–E) loops, and other characteristic behaviors.1,2,4 Among these property characterizations, on-the-fly microstructure characterization is difficult when experimentally conducted. However, it can be easily realized by virtue of computational simulations.9 Furthermore, the microstructure evolution information on relaxor ferroelectric polymers is very helpful in understanding their chemical-composition-dependent relaxor behaviors. Thus, it should be well investigated to establish manipulation strategies to obtain P(VDF)-family-based relaxor ferroelectric polymers.Drawing on insights from inorganic perovskite ferroelectrics, a conventional explanation for relaxor ferroelectric behaviors can be attributed to the formation of polar nanoregions (PNRs) embedded inside a nonpolar matrix.10–13 In addition, their reorientation energy barriers are comparable to thermal motions.10–13 In this model, dipoles are randomly aligned in ferroelectrics when temperature is higher than the Burns temperature (TB).12,13 These randomly aligned dipoles correspond to the paraelectric phase (PEP) of each studied system. During annealing, PNRs emerge and grow to interact with each other.12,13 As the temperature falls down to intermediate temperature (T*), static local distortions within the PNRs are found to contribute to their further growth.12,13 These PNRs cannot reorient anymore and transform into a frozen phase as the studied system is further cooled down to the freezing temperature (Tf).12,13 This PNR model has been widely accepted to describe the phase transition of inorganic perovskite solid solutions.10–13 However, the absence of direct experimental and computational evidences supporting the existence of PNRs hinders our capacity to utilize this model for further prediction of the properties of unexplored systems, e.g., relaxor polymers with low crystallinity.8 Fortunately, the polar slush model9 established in 2017 solves this problem, providing a dynamic evolution picture of domains in Pb-based perovskite relaxor ferroelectrics. In the slush model, the relaxor ferroelectric behaviors result from the size and polarization fluctuations of the domains on the nanoscale.9 When T < Tf, the size of each domain is frozen. Meanwhile, the polarization of each domain undergoes slow rotation on approximately 1 nanosecond timescales.9 For Tf < T < T*, the domain size and polarization fluctuate slowly but the size of correlated regions almost remains constant at about 6 nm.9 For T* < T < TB, the domain size and polarization both vary rapidly. The dipole correlation within domains is weakened.9 When T > TB, only the paraelectric phase remains.9 Noticeably, no nonpolar matrix is found in the bulk below TB owing to the local dynamics.9 Unlike the PNRs model, T* and Tf are regarded as the critical points below which domain sizes and polar directions would be respectively frozen.9 The slush model is successfully applied to describe the phase transition of complex Pb-containing perovskite solid solutions.14,15 However, a satisfactory understanding of the relaxor ferroelectric behaviors exhibited by P(VDF) and its copolymers remains elusive.
In this study, Monte Carlo (MC) modeling was developed in Subsection 2.1 by further modifying our previously formulated coarse-grained force field16 to both well treat with poly(vinylidene fluoride-trifluoroethylene), P(VDF-TrFE), relaxor ferroelectrics and normal ferroelectrics. Based on this modeling, a series of coarse-grained MC simulations, whose details can be found in Subsection 2.2, on P(VDF-TrFE) ferroelectrics was conducted to establish dynamic microstructure evolution pictures during phase transition. By performing statistical analysis (see Section 3) on temperature-dependent total energy, polarization, heat capacity, dipole orientation angle difference, and domain size of P(VDF-TrFE) ferroelectric polymers, their underlying relaxor ferroelectric behaviors have been well understood. The total energy, polarization, and heat capacity information of P(VDF-TrFE) relaxor ferroelectrics can be found in Subsection 4.1. Our microstructure evolution findings in Subsection 4.2 prove that the slush model can be used to properly describe the P(VDF)-based relaxor ferroelectric polymers, enhancing its concept. Remarkably, a new nanometer-sized phase with strongly correlated but randomly orientated dipoles was located before the paraelectric phase appears, which signifies the advancement of the slush model. The domain size-dependent free energy changes in Subsection 4.3 for P(VDF-TrFE) relaxor ferroelectrics under different temperatures were estimated based on our MC simulations to understand the temperature-dependent microstructure evolution in these relaxor ferroelectrics. Additionally, the characteristic phenomena for P(VDF-TrFE) relaxor ferroelectrics are reproduced in our MC simulations in Subsection 4.4, such as slim E–P loops, high-temperature polarization residual, and dielectric dispersion. In Section 5, the specific phase transition model for P(VDF-TrFE) relaxor ferroelectrics was proposed. Finally, we find that it is an effective way to realize P(VDF-TrFE) relaxor ferroelectrics or normal ferroelectrics through regiodefect tuning in Section 6. Our MC modeling successfully reproduces temperature-dependent relaxor ferroelectric or normal ferroelectric behaviors for the P(VDF) family and further establishes its dynamic microstructure evolution picture. Hence, our study lastly supplies defect-engineering strategies to realize P(VDF)-based relaxor ferroelectrics or normal ferroelectrics.
2. Monte Carlo modeling
2.1 Construction of coarse-grained force fields
The MC simulations conducted here were based on the coarse-grained force field developed in our previous study16 to deal with the responsive behaviors of P(VDF-TrFE) ferroelectric polymers under light/electric fields. Here, in order to well describe the molecular motions of P(VDF-TrFE) ferroelectric polymer chains under the temperature field, each VDF-TrFE monomer was taken as a dipole unit in the three-dimensional (3D) Ising model in Fig. 1 to construct the MC model Hamiltonian. In our previous study, each VDF-TrFE tetramer was taken as a coarse-grained dipole to generate the model Hamiltonian and 3D Ising model.16 As shown in Fig. 1, the model Hamiltonian is decomposed into three key components, namely, the intrachain interaction term (HXi,i+1), the interchain interaction terms (HYj,j+1 and HZk,k+1), and the term exerted by external field (HEPi,j,k), according to the structural characteristics and responsive behaviors of P(VDF-TrFE) chains. The intrachain interaction can be treated as the function of the dihedral angle (θ) between two VDF-TrFE monomers, and its contribution to the Hamiltonian can be extrapolated from the VDF-TrFE dimer, trimer, and tetramer to the infinite P(VDF-TrFE) chain based on the quantum chemistry (QM) calculations we did before16 as follows.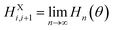 | (1) |
For the P(VDF-TrFE) bulk, the interchain interaction plays the most important role in determining its properties and responsive behaviors. In the previous study, we found a VDF-TrFE tetramer that can be regarded as a unit dipole to represent P(VDF-TrFE) bulk in the coarse-grained way.16 Hence, the angle difference (α − β) between two interchain dipoles can be used to describe the relative rotation of two neighboring chains.16 The interchain interaction term was fitted from the first-principles calculations on two chains with different configurations.16 Here, referring to our previous Hamiltonian,16 the interchain interaction term has been more accurately treated to well reproduce the temperature-dependent relaxor ferroelectric behaviors of P(VDF-TrFE) chains. The previous univariate (α − β) approximation was not adopted. Remarkably, the interchain interaction term is regarded as a two-variable function dependent on orientation angles α and β of the nearest unit dipoles, i.e.,
| HYj,j+1 = HYj,j+1(α,β) | (2) |
| HZk,k+1 = HZk,k+1(α,β). | (3) |
Noticeably, the correlation length, corresponding to the sizes of polar or nonpolar domains, in poly(vinylidene fluoride-trifluoroethylene-1,1-chlorofluoroethylene), P(VDF-TrFE-CFE), relaxor ferroelectric is smaller than 4.7 nm.7 The chain length of the VDF-TrFE tetramer is about 2 nm,16 comparable to this correlation length of the similar ferroelectric polymer system. The previous coarse-grained unit dipole (VDF-TrFE tetramer)16 is too large to reproduce the relaxor ferroelectric behaviors of P(VDF-TrFE) bulk. Therefore, the VDF-TrFE monomer with its size of about 0.5 nm × 0.5 nm × 0.5 nm is used as the unit dipole here to generate the initial advanced 3D dipole Ising model. We should emphasize that this used dipole unit corresponds to a VDF-TrFE monomer in the trans configuration, which would be always fixed in the following simulations. However, it does not mean that no trans–gauche effect is taken into account in our MC modeling. Actually, the coarse-grained dipoles can rotate freely around the X axis (chain extension direction) in MC simulations. The trans or gauche configuration between two adjacent dipoles can be considered in our MC simulations. This conformational change can be partially introduced in our MC modeling to influence polarization variation of the studied ferroelectric polymers. In order to estimate dielectric constant and ferroelectric hysteresis loop of the studied P(VDF-TrFE) bulk through MC simulations, the external electric field would be applied in our MC modeling. The external field effect can be well considered as a classical electrostatic force between the external field and VDF-TrFE dipoles as
HEPi,j,k = −![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) × × ![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) . . | (4) |
The exact eqn (2) and (3) were also obtained from the first-principles calculations in the Dmol3 module of Material Studio, regarded as the asymmetric interchain interaction terms. The PBE-D2 functional was used to well describe the van der Waals interactions in the P(VDF-TrFE) bulk, and the double numerical basis set plus polarization (DNP) was adopted. A two-P(VDF-TrFE)-chain unit cell was used similar to that in our previous study.16 In order to precisely depict the interchain interactions, a two-chain slab model was built with a volume of 20 Å × 50 Å × 50 Å. These two infinite P(VDF-TrFE) polymer chains still extend along the X axis, and their interchain distance refers to the optimized crystalline packing.16 Then, this slab model was sampled with a Monkhorst–Pack k-point mesh of 2 × 1 × 1. The constrained optimization for this two-chain model was performed with their dipole orientation angles α and β changing from 0°, 30°, 60°, … to 360° respectively to relax other degrees of freedoms, such as bond lengths, bond angles, dihedrals, and interchain distance. Noticeably, the interchain distance for these two chains remained almost unchanged in geometry optimization, which is about 5 Å in average. The convergence tolerance for the total energy, the residual forces on all atoms, and the atomic displacement were set to be 2.0 × 10−5 Ha, 4.0 × 10−3 Ha Å−1, and 5.0 × 10−3 Å, respectively.
We know that the external field responsive behaviors of P(VDF-TrFE) chains completely depend on the rotation of VDF-TrFE monomers. Here, each VDF-TrFE monomer is treated as a single dipole. Actually, these monomers connect with each other along the X axis, which finally determines that the X component of each dipole never changes to respond to the applied external field and its Y and Z components can freely rotate to reflect the external field influence. We know that the molecular dipoles of VDF-TrFE monomers are related to the spatial distribution of fluorine and hydrogen atoms in each monomer. In addition, there are the head-to-head (–CF2–CF2–) or head-to-end (–CH2–CF2–) connections between VDF and TrFE units, also named as head-to-head and head-to-end defects, during the experimental synthesis8,17 to bring local compositional disorder (i.e., regiodefects) for the P(VDF-TrFE) bulk. Significantly, this effect finally determines the phase transition behaviors of P(VDF-TrFE). Therefore, it is really important to take the VDF-TrFE monomer as the coarse-grained unit dipole to construct the interchain interaction term in our model Hamiltonian, unlike the previous VDF-TrFE tetramer dipole unit.16 To date, the regiodefects have been not considered in our 3D Ising model. Each P(VDF-TrFE) chain is treated as the perfect head-to-end (–CF2–CH2–CF2–CHF–) connection. Correspondingly, the asymmetry force field was formulated (see Data availability) to express the intrachain term in eqn (1) and the interchain terms in eqn (2) and (3). Here without rebuilding the model P(VDF-TrFE) bulks in consideration of the regiodefects and with reference to the asymmetric force field, a fully symmetric force field was developed to mimic randomly distributed regiodefects as
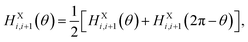 | (5) |
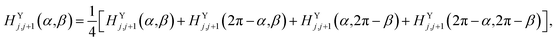 | (6) |
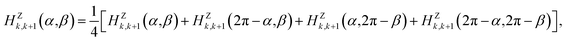 | (7) |
2.2 MC simulations
Based on our developed MC modeling, a series of Metropolis MC simulations in NVT ensemble was conducted to well illustrate the phase transition behaviors of P(VDF-TrFE) relaxor ferroelectrics (see Fig. S1–S4†) versus normal ferroelectric (see Fig. S5–S8†). First, we should emphasize that the reason for adopting the coarse-graining modeling rather over full-atom molecular dynamics (MD) simulations for P(VDF-TrFE) bulks stems from their phase transition picture that we are targeting. We know that the ferroelectric/relaxor ferroelectric–paraelectric phase transitions of P(VDF-TrFE) bulks involve the evolution of nanosized domains.1,6,17–19 Simulations on such processes need to cover tens of nanometer in size and more than nanoseconds in time length. The traditional full-atom MD simulations have been used to investigate the electrocaloric properties of P(VDF)-based copolymers20 and regiodefected P(VDF-TrFE) polymers.21 However, such simulations are surely constrained to 5–13 nm in length and not more 10 ns in time.20,21 In addition, the coercive field (about 10–102 MV m−1) is not small to switch the polarization of the P(VDF-TrFE) thin films,1,6 indicating that it is not easy to realize polarization reversal of the P(VDF-TrFE) bulk in full-atom MD simulations even by virtue of increasing temperatures and introducing large electric fields. Therefore, MC simulations are a good choice to quickly fulfill the polarization reversal of ferroelectric polymers here by treating with dipole rotation as an MC event. Secondly, the real polymer systems are complicated. For P(VDF)-based copolymers, they are semicrystalline.8 It is believed that the interactions between crystalline and amorphous regions or so-called interphase play a non-negligible role in tuning the ferroelectric and piezoelectric properties.8 Based on the semicrystalline picture, a three-phase model with an additional phase, the oriented phase, between the crystalline and amorphous regions was also proposed to understand enhanced ferroelectric and electrostrictive properties and even relaxor ferroelectric structures of P(VDF)-based copolymers.22,23 These all point to large-scale structural models that can well deal with semicrystalline or three-phase ferroelectric polymers rather than full-atom structural models in this case. The next challenge for us is to illustrate the microstructure evolution and properties of the P(VDF) family by considering their semicrystalline or three-phase structures. Still, MC simulations based on the coarse-grained force fields have great potential to achieve this challenge. Noticeably, the comprehensive structural characterization and theoretical insight support that the emerging relaxor phase occurs in the crystalline regions of P(VDF-TrFE) bulks.1,24,25 Hence, it is also generally believed that the relaxor phase is inherent to crystalline structures rather than amorphous regions.8 For example, real perovskite relaxor ferroelectrics may be non-crystalline phases. The crystal model combined with full-atom MD simulations can be employed to present their relaxor behaviors.9 Here, it is plausible and advisable to take the ideal P(VDF-TrFE) crystal with a VDF content (CVDF) of 50 mol% as the model system to investigate possible ferroelectric/relaxor ferroelectric–paraelectric phase transitions, surely considering computational consumption. We should emphasize that first, it is convenient to use this VDF/TrFE molar ratio of 50/50 to build the model system, and secondly, the P(VDF-TrFE) bulk behaves like a relaxor at this VDF content.1,6,8 The P(VDF-TrFE) (50/50 mol%) bulks can transform from normal ferroelectrics to relaxor ferroelectrics under electron irradiation.6 The relaxor behaviors appear within the P(VDF-TrFE) bulks when CVDF decreases to 55 mol% with the coexistence and competition of relaxor and ferroelectric order (49 mol% ≤ VDF ≤ 55 mol%).1 In the following, this ideal crystal model was employed to demonstrate the microstructure evolution of the P(VDF-TrFE) relaxor or normal ferroelectrics.A 50 × 50 × 50 supercell (equivalent to a 24.8 nm × 29.9 nm × 29.8 nm bulk) was generated based on the optimized single-chain P(VDF-TrFE) crystal, whose unit cell contains a VDF-TrFE monomer with perfect head-to-tail connection, to conduct the following MC simulations. In this supercell, 2500 P(VDF-TrFE) chains are parallel to each other. Each chain contains 50 VDF-TrFE monomers along the X direction. This initial state corresponds to the most ordered ferroelectric phase with all the dipoles pointing to the Z direction. One more 100 × 100 × 100 supercell (equivalent to a 49.3 nm × 59.8 nm × 59.6 nm bulk) was also built to discuss the size effect of our MC modeling. First, a preequilibrium with 106 MC steps was conducted at 100–2000 K, which was increased by 100 K each time to allow the P(VDF-TrFE) bulk to relax to its temperature-dependent equilibrium state. Subsequently, for each system, an additional sampling with 106 MC steps was conducted for further statistical analysis. Noticeably, we should emphasize that we did not scale the MC simulation temperatures here referring to the experimental phase transition temperatures. Hence, these simulation temperature values are not consistent with the real ones. In the following, the temperatures correspond to MC simulation ones if without a special illustration.
In order to compare the dielectric properties of the P(VDF-TrFE) ferroelectric state versus the relaxor state, a series of small-step-length MC simulations on these two states at 200–800 K that increased by 100 K each time was performed based on symmetric and asymmetric force fields to estimate their dielectric spectra under an alternating current (AC) field with a frequency of 1 kHz. Noticeably, the introduction of symmetric force field indicates that the studied P(VDF-TrFE) bulk possesses disorder resulting from head-to-head or head-to-end connections between the VDF and TrFE units. Because of this structural disorder generated in polymer synthesis, the developed symmetric force field was developed to deal with this uncontrollable defect distribution within P(VDF-TrFE) bulks.
Additionally, polarization-electric field (P–E) loops were generated to exhibit difference between the P(VDF-TrFE) ferroelectric and relaxor states. Here, the P(VDF-TrFE) ferroelectric state at 100 K was taken as an example to illustrate how to estimate its hysteresis loop. First, we should emphasize that the symmetric force field was used to conduct MC simulations on P(VDF-TrFE) ferroelectric states here. The first MC simulation starts from a non-polarized equilibrium structure at 100 K. Then, it was polarized under a direct current (DC) field as large as 1012 V m−1. After a relaxation as long as 4 × 105 steps, sampling was conducted in another 4 × 105 steps to calculate the averaged polarization under this electric field. Then, the last snapshot of this finished MC simulation was taken as the initial polarized configuration to perform the next-round MC simulation under a decreased DC field of 8 × 1011 V m−1. Continuous MC simulations were carried out for every 2 × 1011 V m−1 decrease/increase within the range of −1012–1012 V m−1. Finally, the polarization for each MC simulation under a certain DC field was collected to plot the E–P loops as follows.
3. Statistical analysis for estimation of characteristic parameters
3.1 Total energy, polarization, and heat capacity
Based on MC simulations, the total energy, polarization, and heat capacity of P(VDF-TrFE) bulk can be estimated to depict its phase transition process. As our MC modeling was developed utilizing the Metropolis algorithm to ensure the evenly spaced sampling, the averaged physical quantities are equivalent to the arithmetic mean of the sampling data. The total energy (U) and polarization (P) of P(VDF-TrFE) bulk can be obtained as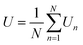 | (8) |
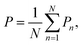 | (9) |
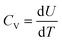 | (10) |
3.2 Orientation angle difference of dipoles
Based on our MC simulations, the orientation angle differences between two nearest monomers along the X, Y, and Z directions, especially for interchain Y and Z directions, were calculated in Fig. S1 and S6 (ESI)† to analyze the ordering of dipoles within the P(VDF-TrFE) bulk and further reveal detailed temperature-dependent microstructure evolution, which is helpful to locate the phase transition mechanism of the P(VDF-TrFE) bulk. The orientation angle difference distribution function, f(Δθ), along a certain direction is defined as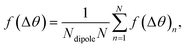 | (11) |
3.3 Domain size
A general algorithm was utilized as followed to define the domain size in the P(VDF-TrFE) bulk. The quantification of domain size is useful to demonstrate microstructure evolution during temperature-triggered phase transition of the P(VDF-TrFE) bulk. The domains in ferroelectrics can be conventionally defined as regions that have a uniform direction of electric polarization contributed by dipoles with the same orientation. These domains can spontaneously form in the specific ferroelectric materials under certain conditions, and they play a crucial role to determine the unique properties and applications of ferroelectric materials.By virtue of our MC simulations combined with statistical analysis, domains here can be easily located according to the simple recognition of a group of neighboring dipoles almost aligned in the same direction. Hence, a domain could be located by two steps: first find the domain core and then ascertain the domain boundary. Now, we start to test every dipole whether it is a potential domain core. The potential core dipole of a domain is defined to satisfy the following criterion
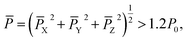 | (12) |
![[P with combining macron]](https://www.rsc.org/images/entities/i_char_0050_0304.gif) is the averaged polarization of the tested dipole at the specific site,
is the averaged polarization of the tested dipole at the specific site, ![[P with combining macron]](https://www.rsc.org/images/entities/i_char_0050_0304.gif) X,
X, ![[P with combining macron]](https://www.rsc.org/images/entities/i_char_0050_0304.gif) Y, and
Y, and ![[P with combining macron]](https://www.rsc.org/images/entities/i_char_0050_0304.gif) Z are the polarization components along the X, Y, and Z directions, respectively, and P0 (= 13 μC cm−2) is the polarization of a unit dipole used in our 3D Ising model. The polarization components along the Y and Z directions are defined as
Z are the polarization components along the X, Y, and Z directions, respectively, and P0 (= 13 μC cm−2) is the polarization of a unit dipole used in our 3D Ising model. The polarization components along the Y and Z directions are defined as![[P with combining macron]](https://www.rsc.org/images/entities/i_char_0050_0304.gif) Y = P0(sin Y = P0(sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ0 + 0.4∑sin θ0 + 0.4∑sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ1 + 0.2∑sin θ1 + 0.2∑sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ2 + 0.1∑sin θ2 + 0.1∑sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ3)Y θ3)Y | (13) |
![[P with combining macron]](https://www.rsc.org/images/entities/i_char_0050_0304.gif) Z = P0(cos Z = P0(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ0 + 0.4∑cos θ0 + 0.4∑cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ1 + 0.2∑cos θ1 + 0.2∑cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ2 + 0.1∑cos θ2 + 0.1∑cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ3)Z, θ3)Z, | (14) |
![[P with combining macron]](https://www.rsc.org/images/entities/i_char_0050_0304.gif) X) does not have to be taken into consideration.
X) does not have to be taken into consideration.
If the tested dipole can be regarded as the domain core, it will be used to locate its boundary next. Then, its first and second von Neumann neighbors will be checked whether they are in the same direction as the core dipole or not in order to determine whether they belong to this newly-found domain or not. The domain boundary criterion is
| |θneigh − θcore| < θcutoff, | (15) |
After this domain location, we can approximately measure the size (r) of the located irregular domain according to the spherical approximation as
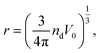 | (16) |
3.4 Nucleation-related free energy change
In order to follow the law of energy change for temperature-dependent domain growth in the P(VDF-TrFE) bulk, the free energies of the nucleation processes can be estimated under different temperatures according to the domain size information illustrated above. According to the Gibbs nucleation theory,26 the Gibbs free energy change of a nucleation process (ΔG) can be expressed as a function of the domain size (r), i.e., ΔG = ΔG(r). In equilibrium, the probability distribution function of the domain size, D(r), should follow the Boltzmann distribution to be related to the nucleation free energy as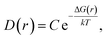 | (17) |
ΔG(r) = −kT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D(r) + ΔG0 D(r) + ΔG0 | (18) |
ΔG0 = kT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C. C. | (19) |
ΔG(r) = −kT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D(r) D(r) | (20) |
3.5 Dielectric permittivity
According to the previous study,27,28 the dielectric permittivity χ under an AC field with a frequency (ω) and at a temperature (T) can be obtained from the Fourier transformation of the autocorrelation function of polarization ϕ(t), that is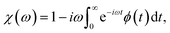 | (21) |
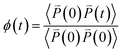 | (22) |
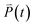 is the polarization of P(VDF-TrFE) bulk at time t.
is the polarization of P(VDF-TrFE) bulk at time t.
In our study, the dielectric permittivity under an AC field with its frequency of 1 kHz and at a certain temperature was estimated based on the MC simulations. The polarization of P(VDF-TrFE) bulk at each MC step should be printed in these MC simulations. When calculating the dielectric permittivity based on eqn (21) and (22), the MC step should be converted into real time by a linear relationship as
| t = αnMC, | (23) |
4. Temperature-dependent relaxor ferroelectric behaviors
4.1 Total energy, heat capacity, and polarizations
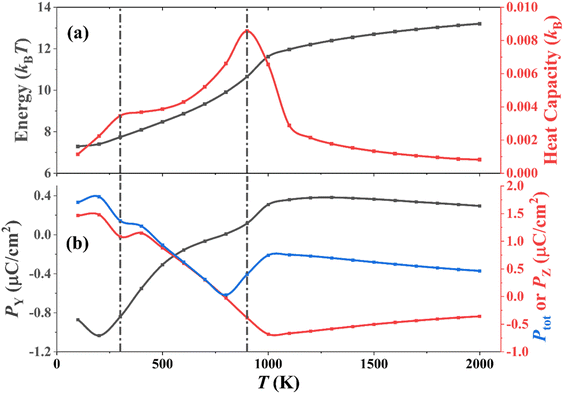
A series of MC simulations on ordered versus disorder P(VDF-TrFE) (50/50 mol%) bulks in the temperature range of 100–2000 K was conducted to demonstrate their temperature-dependent phase transition behaviors and microstructure evolution. Noticeably, the P(VDF-TrFE) bulk was generated by connecting VDF and TrFE monomers one-by-one and keeping their head-to-end connection way. In fact, this bulk corresponds to the ordered one, and the VDF-TrFE monomer was employed as the unit dipole to finally generate the 3D Ising model used in our MC simulations. However, VDF and TrFE monomers can connect with each other in the head-to-head way in real polymer synthesis to result in disorder or regiodefects within the P(VDF-TrFE) bulk. We did not generate one more 3D Ising model for disordered P(VDF-TrFE) (50/50 mol%) bulk through the introduction of regiodefects. Remarkably, the structurally ordered and disordered P(VDF-TrFE) bulks were realized in our MC simulations by adopting asymmetric and symmetric force fields, respectively, as demonstrated above in Subsection 2.1. Based on our MC simulations and statistical analysis, we know that the orderly/disordered structures of P(VDF-TrFE) bulks ensure the realization of relaxor ferroelectric/ferroelectric states, agreeing with the experimental observation that high-content head-to-head defects contribute to the easy formation of all-trans conformation of the polymer chain for the realization of normal ferroelectric states.8 Therefore, we directly name the ordered/disordered P(VDF-TrFE) bulks as P(VDF-TrFE) relaxor ferroelectrics (relaxor states) and ferroelectrics (ferroelectric states), respectively.Based on the MC simulations that utilized the asymmetric force field, the temperature-dependent total energy, heat capacity, and polarizations of P(VDF-TrFE) relaxor ferroelectric are present in Fig. 2 to reveal its phase transition behaviors. As shown in Fig. 2a, the total energy continuously increases as the temperature increases. There are two steps on this increasing energy–temperature (U–T) curve. The first step may be not so obvious. However, the heat capacity–temperature (CV–T) curve exhibits two peaks at 300 K and 900 K, completely corresponding to these two steps on the U–T curve. These two peak values also signify two phase-transition points for the P(VDF-TrFE) bulk. Two transition points (25–60 °C and 65–90 °C) were observed in the P(VDF-TrFE-CFE) terpolymer, corresponding to well-ordered and less-order polar phases (i.e., relaxor ferroelectric phases), which are different from normal ferroelectric phases.7 We should emphasize again that our MC simulation temperatures here do not match the real experimental temperatures since we cannot find the completely consistent experimental system to scale our MC simulation temperatures. Our simulation model is the P(VDF-TrFE) single crystal. In real P(VDF-TrFE) bulk, there are amorphous regions.8 We should say that the ordered P(VDF-TrFE) (50/50 mol%) bulk behaves like a relaxor ferroelectric in the MC temperature ranges (100–2000 K) employing asymmetric force field in MC simulations, which can be further confirmed by our statistical analysis of microstructure evolution with temperature in the P(VDF-TrFE) bulk in Fig. 3 and 4 later.
The variations of polarizations along the Y and Z directions with temperature in Fig. 2b also provide more details to support the phase transition behaviors mentioned above. The Y polarization ranges from −1.03 μC cm−2 to 0.38 μC cm−2, and it starts to decline slightly, then rises continuously, and finally continues to decrease slightly after passing 1100 K as the temperature increases. The Z polarization ranges from −0.68 μC cm−2 to 1.48 μC cm−2, and it continues to decrease, especially showing a local minimum at 300 K but starts to rise slightly after passing 1100 K as the temperature increases. The maximum Y and Z polarizations both appear at 200 K. The characteristic transition temperatures for polarizations here well match the temperatures of the transition points shown in the U–T and CV–T curves. Because PZ dominates among three polarization components, the total polarization (Ptot) is comparable to PZ in Fig. 2b, ranging from 0.03 and 1.80 μC cm−2. It is worth noting that the computational polarization values are smaller than both the experimentally-measured P(VDF-TrFE) (50/50 mol%) ferroelectrics (±10 μC cm−2) and relaxor ferroelectrics (±5 μC cm−2).6 Maybe, this smaller polarization results from the structural difference between our computational bulk and real polymer bulks. But we still believe that our computational polarization values here in the temperature range of 100–2000 K correspond to the relaxor ferroelectric phases for the P(VDF-TrFE) bulk.
The changes in total energy, heat capacity, and polarizations of P(VDF-TrFE) relaxor ferroelectric with temperature can be all attributed to the microstructure evolution within this bulk, as discussed below.
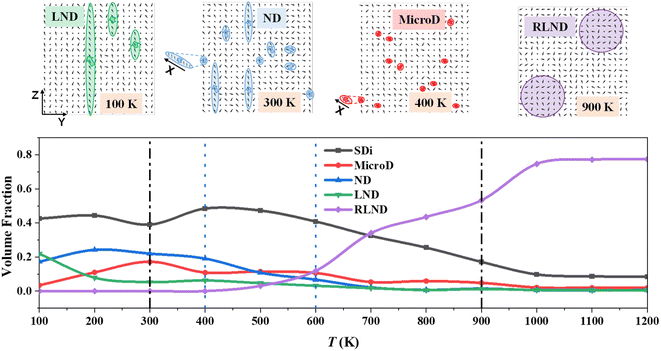
4.2 Microstructure evolution
As mentioned above, the P(VDF-TrFE) bulk undergoes phase transition from the orderly polar phase to the disordered polar phase (i.e., dynamic evolution of relaxor ferroelectric state) in the whole temperature range of 100–2000 K. As shown in Fig. 3, the temperature-dependent dynamic evolution of the nanostructures (i.e., domain reorganization) within the P(VDF-TrFE) relaxor ferroelectric has been well illustrated. This nanostructure evolution follows two phase transition points (300 K and 900 K, marked by black dotted lines in Fig. 3), as revealed by the U–T, CV–T, and PY/PZ–T curves in Fig. 2. Additionally, two more transition points (marked by blue dotted lines in Fig. 3) are also located here through nanostructure analysis. Now, we illustrate this microstructure evolution and related property change of P(VDF-TrFE) relaxor ferroelectric in detail.First, the nanostructures inside the P(VDF-TrFE) bulk are not uniform. According to our domain size analysis, four typical nanostructures are located in the P(VDF-TrFE) bulk, involving randomly distributed microdomains (MicroDs), nanodomains (NDs), large nanodomains (LNDs), and large nanodomains with randomly oriented dipoles (RLNDs), following the tendency of increasing domain size. Additionally, single dipoles (SDis) are also taken into account to highlight the degree of disorder within the P(VDF-TrFE) bulks. SDis indicate free dipoles without nucleation, and their size is about 0.5 nm. They exist in the whole temperature range as nonpolar matrices. The appearance of different types of domains in the P(VDF-TrFE) bulk corresponds to the nucleation of dipoles. The microdomains are the smallest domains with the size of 1.0–2.5 nm among the located ones in Fig. 3. The nanodomains possess a larger size (2.5–5.0 nm). This polar nanodomain with a correlation length of about of 4.7 nm has been also observed in the P(VDF-TrFE-CFE) relaxor ferroelectric.7 The characteristic crystalline region is also about 5 nm in P(VDF)-based ferroelectric polymers.29 Both strongly support the domain division criterion in Fig. 3. The further larger nanodomains (LNMs) have a correlation length of 5.0–8.0 nm. From microdomains, nanodomains, to large nanodomains, dipoles within them are strongly correlated and all aligned, and they nucleate and continuously grow more easily along the X direction than those along the Y or Z directions due to their chemical bonding along the X direction. The RLNDs with the size larger than 8 nm are really a particular type of nanostructures, beyond our chemical intuition. Their correlation length is the largest among all the studied nanostructures, but the dipoles inside are relatively randomly aligned. Unlike three smaller domains mentioned above, RLDNs here do not display a preferential direction for domain growth. The identification of different nanostructures and their evolution (see Fig. 3) generally agrees with the slush model proposed from inorganic perovskite relaxor ferroelectrics.9 Remarkably, RLDNs are a completely new discovery beyond the slush model.9 The existence of RLDNs may be attributed to the particularity of ferroelectric polymers, unlike the traditional inorganic perovskite relaxors.
As shown in Fig. 3, LNDs have the largest volume fraction among different domains at 100 K, indicating its domination in the P(VDF-TrFE) bulk as ordered polar regions. Surprisingly, single dipoles have the largest volume fraction at 100 K, and they are greatly distributed inside. There are still different kinds of nanodomains distributed inside. This situation seems like a slurry-like mixture of small ice crystals and liquid water proposed by the slush model.9 The dispersive and randomly aligned single dipoles cannot be treated as nonpolar regions, which are chemically imbalanced, large, disordered regions found in inorganic perovskite ferroelectrics.9 They can be regarded as a paraelectric matrix, and they have the largest volume fraction until the P(VDF-TrFE) bulk is heated to 700 K. All of these align with our chemical intuition since this relaxor state evolves from the lower-temperature ferroelectric state. In addition, this relaxor state of the P(VDF-TrFE) bulk possesses less-orderly structures than the ferroelectric state. Noticeably, LNDs at 100 K (see Fig. 3) almost contain dipoles with consistent orientation nearly pointing towards the 11 o'clock direction in the Y–O–Z plane, ensuring nearly the largest polarizations along the Y and Z directions in Fig. 2b. The large number of NDs and LNDs at 100 K also contribute to quite large polarization components along the Y and Z directions.
As the temperature increases from 100 K to 300 K, the system undergoes the first phase transition at 300 K. In this temperature range, the volume fractions of single dipoles and nanodomains change a little. The nanodomains dominate as ordered polar regions in the P(VDF-TrFE) bulk. At 200 K, the volume fraction of single dipoles reaches the first peak value (about 0.44), and the volume fraction of nanodomains attains its maximum (about 0.24) in the whole temperature range. Both are conductive to the realization of PY/PZ maxima at 200 K in Fig. 2b. For the snapshot shown in Fig. 3, the needle-like nanodomains form at 300 K, nearly keeping the same orientation as LNDs at 100 K. These needle-like nanodomains were also observed in hybrid organic–inorganic perovskites30 and doped inorganic perovskite.31 Noticeably, other nanodomains with various sizes and polarization orientations also appear. The volume fraction of LNDs steadily decreases to about 0.05. The microdomains appear, and their volume fraction linearly increases to about 0.17. We can imagine that LNDs dissolve and turn into quite small microdomains to switch the phase transition. The systematic energy in Fig. 2a increases to cause the microstructure evolution from LNDs to microdomains, and a location minimum appears in the PY–T curve in Fig. 2b. The dominant nanodomains may contribute to the first peak heat capacity in Fig. 2a. The state at 300 K exhibits a more disordered structure than the state at 100 K.
For the temperature ranging in 300–400 K, it is particular because the maximal volume fraction are always for disperse single dipoles in Fig. 3. Although the volume fraction of nanodomains is larger than that of microdomains, both of them decrease compared to those at 300 K. However, the contents of microdomains and nanodomains in P(VDF-TrFE) bulk are still high. All of these indicate their potential interconversion between microdomains, nanodomains, and single dipoles. We think the needle-like nanodomains disintegrate at 400 K, which would contribute to the formation of LNDs or RLNDs at the next stage. This abnormal volume fraction increase of LNDs indicates an exceptional domain reorganization in the P(VDF-TrFE) bulk. Hence, the state at 400 K is more disordered than that at 300 K, also proved by the continuously decreasing PY/PZ values after 200 K in Fig. 2b. As the temperature increases, the thermal energy brings more randomly-oriented single dipoles and less polar regions. 400 K is such an important transition point here that an extremely special nanostructure, RLND, starts to emerge at this temperature.
As the temperature increases from 400 K to 600 K, the single dipoles, nanodomains, and LNDs persistently reduce. The microdomains hold a stable volume percentage of about 0.11, and its volume fraction is larger for the first time than that of the nanodomains. The volume fraction of RLNDs increases continually and surpasses that of ordered nanostructures for the first time at 600 K, indicating the continuous growth of RLNDs from other orderly domains. When the temperature is higher than 600 K, the volume fraction of RLNDs rapidly exceeds that of single dipoles and persistently increases. Except for RLNDs, the volume fractions of all the other types of nanostructures further decrease. Because RLNDs dominate in the P(VDF-TrFE) bulk, the polarization reversal for PY and PZ happens at 800 K, as shown in Fig. 2b. At 900 K, other ordered nanodomains become negligible, and only a few microdomains remain with the volume fraction of about 0.05. In the temperature range of 900–1200 K, RLNDs still dominate in the P(VDF-TrFE) bulk, and just a small portion (about 0.08) of single dipoles remains. This indicates that randomly oriented dipoles in RLNDs are different from single dipoles for the paraelectric phase and correlated with each other. We should emphasize again that a new phase RLND is located during the phase transition of the P(VDF-TrFE) relaxor ferroelectric. As shown in Fig. 2a, the dominating RLNDs causes the peak heat capacity at 900 K, and the formation of RLNDs consumes thermal energy. Within RLNDs at 900 K, a large number of dipoles with random orientations emerge, resulting in nearly zero polarization (Ptot) for the P(VDF-TrFE) bulk in Fig. 2b. Importantly, it does not indicate the appearance of a paraelectric state at this stage. In addition, the degree of ordering of dipoles along the polymer chain direction (i.e., X direction) almost vanishes at 900 K in Fig. S1a.† After 1000 K, the total energy (see Fig. 2a) and PY/PZ/Ptot values (see Fig. 2b) of the P(VDF-TrFE) bulk change a little. This formation of dominating RLNDs would contribute to the emergence of the paraelectric state for the next stage.
After a series of MC simulations on the large-size P(VDF-TrFE) relaxor ferroelectric with its volume of 49.3 nm × 59.8 nm × 59.6 nm (100 × 100 × 100 supercell) at different temperatures (100–1200 K), its microstructure evolution was also estimated (Fig. S3†) to compare with that of the small-size P(VDF-TrFE) relaxor ferroelectric, whose volume is as large as 24.8 nm × 29.9 nm × 29.8 nm (50 × 50 × 50 supercell), to discuss their size effect on temperature-dependent microstructure evolution. Noticeably, the volume fraction of microdomains (1.0–2.5 nm), nanodomains (2.5–5.0 nm), and large nanodomains (5.0–8.0) are gathered together to estimate their total volume fraction for simple and clear comparison between simulated systems with various sizes. The size change of simulated systems does not affect the sizes of the observed nanoscale domains but causes a change in the relative magnitudes of volume fractions of typical domains. Especially, the volume fraction (about 0.81) of LNDs + NDs + MicroDs largely increases in the large-size P(VDF-TrFE) bulk when T = 100 K compared to that (0.43) in the small-size bulk. When the large-size simulated system is adopted, the content of LNDs greatly increases at low temperature. It can be well understood that these high-content LNDs evolve from the low-temperature ferroelectric phase. Noticeably, the peak values and the temperature ranges at which these peaks appear, for single dipoles, RLNDs, and LNDs + NDs + MicroDs, remain unchanged. This indicates that the whole phase transition pictures for both the systems remain identical.
4.3 Variation of free energy with temperature
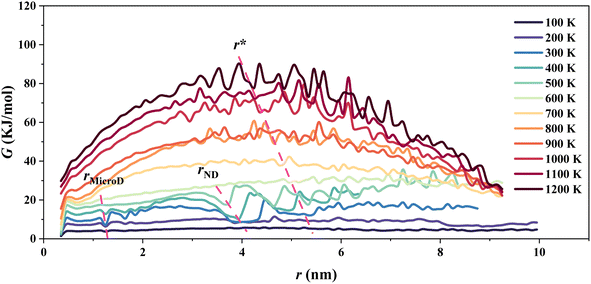
Based on the Gibbs nucleation theory26 and our MC simulations, the Gibbs free change was estimated as a function of domain size of the P(VDF-TrFE) relaxor ferroelectric (Fig. 4). Below 600 K, three local minima highlighted by rose-red dashed lines can be located in each G–r curve, and they appear at about 1.7 nm, 3.8–4.0 nm, and 5–5.3 nm, respectively. Differently, there is one local minimum left above 700 K located at 4.7–5 nm. According to these characteristic domain sizes, we know that these local minima correspond to the microdomains, nanodomains, and large nanodomains, respectively. According to the Gibbs nucleation theory,26 the critical nucleation size (r*) corresponds to the maximum of each G–r curve. Below 600 K, two more peak values appear, indicating possible formations of ordered microdomain and nanodomains at the low temperature. As the temperature increases, the peak values of these G–r curves shift towards the side with smaller values, indicating a reduction of the critical nucleation size. From 100 K to 1200 K, the critical nucleation size varies from 5.4 nm to 4.0 nm. This is completely consistent with the continuous decrease of the critical correlation length in relaxor ferroelectrics as the temperature increases.7,29 Surely, the corresponding nucleation energy barrier climbs with the increase in temperature. The increasing energy barrier would slow down and eventually prohibit the polarization nucleation in the P(VDF-TrFE) bulk. Even though the nucleation centers form in the P(VDF-TrFE) bulk as the temperature increases, their size becomes small. Above 600 K, the nanodomains and large nanodomains vanish, and even the microdomains are also difficult to be found in this bulk. The particular nanostructures, large nanodomains with randomly oriented dipoles, emerge and they would dominate this system.4.4 Dielectric permittivity and P–E hysteresis loops
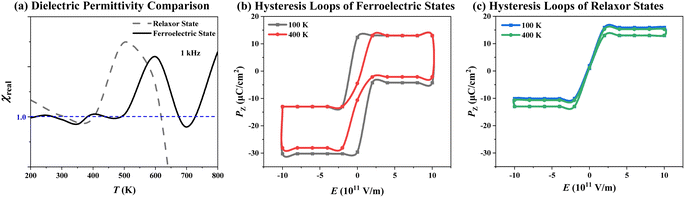
In order to confirm our developed MC modeling, which can well describe the temperature-dependent phase transition behaviors of the P(VDF-TrFE) bulk, the macroscopic properties, dielectric permittivity and hysteresis loops, have been also calculated in Fig. 5 based on our MC simulations on P(VDF-TrFE) ferroelectric and relaxor ferroelectric, respectively. Although the experiments cannot monitor the microstructure evolution on-the-fly for polymer ferroelectrics or relaxor ferroelectrics, these macroscopic properties can be experimentally measured to exhibit property differences between polymer ferroelectrics and relaxor ferroelectrics.As shown in Fig. 5a, the dielectric spectra of P(VDF-TrFE) ferroelectric and relaxor ferroelectric states are displayed in the varied temperature range from 200 K to 800 K under 1 kHz AC electric field. The permittivity curve of P(VDF-TrFE) relaxor ferroelectric shows a broad peak from 400 K to 640 K and its peak value is located at 500 K, while that of P(VDF-TrFE) the ferroelectric exhibits a slimmer and lower peak from 500 K to 660 K and its peak value emerges at 600 K. The broader permittivity peak at lower temperature, named as “dielectric dispersion”, is regarded as a characteristic feature of relaxor ferroelectrics in comparison with normal ferroelectrics.7 The corresponding temperature (500 K here) to the peak value is a critical point for domain fluctuations in P(VDF-TrFE) relaxor ferroelectrics. At this temperature, the large nanodomains with randomly oriented dipoles emerge and other orderly domains, including microdomains and nanodomains, and single dipoles fluctuate fiercely and convert into each other. All of these contribute to the largest dielectric response to the AC field. As shown in Fig. S4,† the frequency-dependent dielectric spectra were further estimated to highlight the important signature of relaxor behaviors in dielectric response. As the AC frequency increases from 1 kHz to 1.78 kHz, the wide dielectric peaks under different frequencies shift toward higher temperatures for P(VDF-TrFE) relaxor ferroelectrics. In contrast to P(VDF-TrFE) normal ferroelectrics, their dielectric peaks do not shift as the AC frequency increases, exhibiting frequency-independent dielectric anomaly.
The other important evidence to support our MC modeling for the P(VDF-TrFE) bulk is different P–E hysteresis loops between ferroelectric and relaxor ferroelectric states under different MC temperatures. As shown in Fig. 5b, the normal P(VDF-TrFE) ferroelectric shows wide P–E loops switching between −1012 V m−1 and 1012 V m−1, and its polarization changes between −30 μC cm−2 and 13 μC cm−2, agreeing with the experimentally measured polarization values of the P(VDF-TrFE) ferroelectrics.1,6 The polarization measured at lower temperature would be larger. As shown in Fig. 5c, the P(VDF-TrFE) relaxor ferroelectric exhibits quite slim hysteresis loops driven by the same magnitude of the electric field. In addition, its polarization switches between −13 μC cm−2 and 15.3 μC cm−2, much smaller than that of normal P(VDF-TrFE) ferroelectric, consistent with the experimental observation of P(VDF-TrFE) relaxor ferroelectrics.1,6 As the temperature rises, even this slim hysteresis loop disappears. The slim hysteresis loops of P(VDF-TrFE) bulk, which might result from the percolation and growth of nanoscale domains induced by a DC field as large as 1011 V m−1 in our MC simulations, are still characteristic features of relaxor ferroelectrics to distinguish them from the normal ferroelectrics.32 In the previous P(VDF-TrFE) (50/50 mol%) bulks, the transformation from normal ferroelectrics to relaxor ferroelectrics was realized through electron irradiation.6 We think that the VDF content is not the most important factor for relaxor formation. The irradiation brings much free volume in these P(VDF-TrFE) bulks to allow the polymer chains to freely rotate, which significantly contributes to relaxor formation. On the basis of our MC modeling, its additional advantage compared to full-atom MD simulations is that each monomer, i.e., each coarse-grained dipole, can more easily rotate to quickly respond to external electric or temperature fields. This indicates that our MC modeling can accelerate the simulations on temperature-dependent phase transitions, unlike the full-atom MD simulations that tend to trap simulated systems into specific localized states. The previous measurement on temperature-dependence dielectric constant confirms that the P(VDF-TrFE) (CVDF = 50 mol%) bulk shows relaxor behaviors.1 Once again, we can address that CVDF is not the decisive factor to drive this system to form a relaxor. Noticeably, the regiodefects are unavoidable and uncontrollable in P(VDF-TrFE) synthesis. This effect is introduced using symmetric force field in our MC simulations. We follow the real experiments and grasp the structural characteristics of P(VDF-TrFE) bulks to build both asymmetric and symmetric force fields to reproduce their relaxor ferroelectric and normal ferroelectric behaviors. These treatments approach to real conditions well. The previous effective Hamiltonian was built based on the first-principles calculations combined with the soft mode approximation to grasp the structural characteristics of inorganic perovskite relaxor ferroelectrics during phase transition.33,34 The MC simulations based on this effective Hamiltonian can well reproduce the relaxor behaviors of inorganic ferroelectrics.33,34 The studied P(VDF-TrFE) ferroelectric polymers are a more complicated case. The chosen MC modeling balances both computational efficiency and accuracy.
5. Phase transition model
By virtue of MC simulations based on asymmetric force field and 3D Ising model, the phase transition process of the P(VDF-TrFE) relaxor ferroelectric in the MC temperature range of 100–1200 K has been well illustrated. This phase transition process well agrees with the reported slush model in inorganic perovskite relaxor ferroelectrics.9 The relaxor-like behaviors and properties of P(VDF-TrFE) ferroelectrics are predominantly attributed to the presence of nanoscale domains with their size ranging from 1.0 nm to 10.5 nm and their interconversion with disperse single dipoles in the bulks, as described by the slush model.9 The size (2.5–5 nm) of nanodomains found in the P(VDF-TrFE) bulk aligns with the correlation length (4.7 nm) of polar nanodomains in the P(VDF-TrFE-CFE) relaxor ferroelectric,7 confirming our proposed nanodomains-predominant phase transition model. A new discovery of our model here is that a completely new type of nanodomain, large nanodomain with randomly oriented dipoles (RLND), is found to exist stably even at high temperature. The RLNDs are different from and more orderly than the paraelectric phases in polymer bulks. The existence of RLNDs can be used to well understand residual polarization of relaxor ferroelectrics to counteract the increase in temperature. Both the polar nanoregion model10,11 and the slush model9 originated from inorganic perovskite relaxor ferroelectrics argue whether there is only the paraelectric phase with randomly oriented dipoles in the bulks as the temperature exceeds the Curie temperature (TC). Noticeably, the initial emergence and later depolarization of macrodomains were observed near the secondary phase transition of P(VDF-TrFE-CFE) relaxor ferroelectrics.7 In addition, these domains are proposed to finally convert into the paraelectric phases.7 This microstructure information was obtained through the limited time resolution of X-ray diffraction (XRD).7 It is obvious that the previous researchers ignored the potential degree of order in the high-temperature involving randomly disrupted structures. These observed domains behave similar to our proposed RLNDs. Our newly developed phase transition model not only confirms the existence of a series of ordered nanostructures with high conversion rates but also provides a probable domain evolution picture driven by thermal energy.Actually, the similar phase transition phenomena were observed by piezoresponse force microscopy (PFM) in the (PbMg1/3Nb2/3O3)0.75(PbTiO3)0.25 (PMN-25PT) relaxor ferroelectric.35 This PMN-25PT single crystal experiences two phase transitions at 90 °C and 120 °C, respectively.35 At 90 °C, a ferroelectric phase-microdomain phase transition happens, corresponding to the first transition in the studied P(VDF-TrFE) bulk at 300 K involving the conversion of large nanodomains into microdomains and nanodomains. In the PMN-25PT bulk, the small speckle domains grow from the original ferroelectric stripe-like domain matrices,35 indicating the emergence of a new type of domains aligning in different directions from the ferroelectric ones. This growth direction preference of newly-grown domains35 is identical to the growth pattern observed in microdomains and nanodomains in the studied P(VDF-TrFE) bulk. As the temperature rises to 110 °C, the stripe domains gradually disappear, while the speckle domains grow further.35 These correspond to the fierce domain fluctuation and percolation and the appearance of RLNDs observed in our MC simulations. The secondary phase transition happens at 120 °C with the domain walls further blurred, corresponding to the 900 K phase transition of the P(VDF-TrFE) bulk in our MC simulations for the continuous growth of RLNDs. A number of residual polar nanoregions can be found as high as 140 °C,35 providing compelling evidence to support the existence of RLNDs predicted by our phase transition model. The comparability between inorganic perovskite and ferroelectric polymer relaxors mentioned above also proves that our phase transition model can be applied to other sophisticated relaxor ferroelectric systems.
6. Regiodefect-switched ferroelectric versus relaxor ferroelectric states
As mentioned above, the asymmetric force field for the P(VDF-TrFE) bulk was developed based on the highly orderly P(VDF-TrFE) single crystal. In this polymer crystal, VDF-TrFE monomers follow the head-to-end connection to form an ordered P(VDF-TrFE) single chain, and each P(VDF-TrFE) chain is even aligned in the same direction. In fact, this orderly structure of the P(VDF-TrFE) bulk ensures its potential relaxor ferroelectric behaviors. In order to further confirm this order structure-determined relaxor behaviors, a symmetric force field was developed with reference to the asymmetric force field by adding the terms involving the symmetrical treatment of orientation angles α or β with respect to the X–O–Z plane in eqn (5)–(7) to consider the regiodefects in the P(VDF-TrFE) bulk due to random head-to-head or head-to-end connections between the VDF and TrFE monomers during polymer synthesis. Based on this symmetric force field, we find that the relatively disordered structure of the P(VDF-TrFE) bulk ensures its ferroelectric behaviors and not relaxor behaviors. The disordered P(VDF-TrFE) bulk undergoes ferroelectric–paraelectric phase transition. The introduction of the degree of disorder may hinder the free rotation of coarse-grained dipoles, finally contributing to the formation of normal ferroelectrics. One more series of MC simulations on P(VDF-TrFE) ferroelectrics was also performed based on the symmetric force field under different temperatures following the procedure in Subsection 2.2 to illustrate the difference between P(VDF-TrFE) ferroelectrics and relaxor ferroelectrics well studied above.Unlike the tendencies of total energy and heat capacity (see Fig. 2a) and polarizations (see Fig. 2b) of the P(VDF-TrFE) relaxor ferroelectric, the P(VDF-TrFE) normal ferroelectric possesses continuously increasing E–T curve in Fig. S5a (ESI†) and consistently decreasing/increasing/decreasing PY/PZ/Ptot–T curves in Fig. S5b (ESI†), all indicating the typical characteristics of ferroelectric–paraelectric phase transition. Although the phase transition temperature predicted by our MC simulations is much higher than the experimental one of the P(VDF-TrFE) ferroelectric, the predicted polarizations along the Y and Z directions with values of 9 μC cm−2 and −9 μC cm−2, respectively, align with the experimental ones (±10 μC cm−2) of P(VDF-TrFE) (50/50 mol%) ferroelectrics.6 All these results strongly support that our developed symmetric force field excellently reproduces the ferroelectric–paraelectric phase transition of the P(VDF-TrFE) ferroelectric. Therefore, we believe the domain evolution of the P(VDF-TrFE) ferroelectric can be well reproduced by virtue of our MC simulations. As shown in Fig. S6–S8 (ESI),† the temperature-dependent microstructure evolution of the P(VDF-TrFE) ferroelectric is obviously different from that of the P(VDF-TrFE) relaxor ferroelectric [see Fig. 3, 4 and S1–S3 (ESI)†]. The P(VDF-TrFE) ferroelectric only contains disperse single dipoles and ferroelectric domains. No polar microdomains and nanodomains that exist in the P(VDF-TrFE) relaxor ferroelectric are found here. As the temperature increases, the ferroelectric domains largely reduce and their size decreases at the same time to become randomly-oriented single dipoles. The needle-like ferroelectric domains emerge at 300 K. The ferroelectric domains eventually vanished at about 1000 K, corresponding to the phase transition point, to finally turn into the paraelectric phase.
As discussed above, we find that it is significant to manipulate the degree of orderly of P(VDF-TrFE) bulks for switching between polymer ferroelectrics and polymer relaxor ferroelectrics. For ferroelectric copolymers, it is convenient to control their structural degree of order by subtly manipulating the connection ways between monomers. We believe that our study can supply an important clue for experimental specialists to preciously manipulate polymer synthesis condition to realize the ferroelectrics versus relaxor ferroelectrics.
Surely, the introduction of a third component such as CFE (1,1-chlorofluoroethylene) significantly contributes to the relaxor formation of P(VDF)-based copolymers.8 We hope that our developed MC modeling can be transferable to deal with more complex ferroelectric polymers. Taking P(VDF-TrFE-CFE) as an example, our MC modeling can indeed be applied to this polymer system. Using the first-principles calculations, the model Hamiltonian can be obtained in the same way as illustrated to describe its intrachain, interchain, and dipole-external field interactions. One noteworthy point is that the uncontrollable regiodefects are much more complicated. One possible way to depict such sophisticated defects precisely is to conduct first-principles calculations in consideration of such complicated cases and fit the corresponding intrachain and interchain terms separately. For example, the intrachain interactions between VDF monomers can be calculated by scanning the rotational energy profile of the VDF–VDF dimer. VDF, TrFE, and CFE monomers can be randomly distributed in the periodical lattice. MC simulations based on this model Hamiltonian and the random lattice model can be employed to investigate the relaxor behaviors of the P(VDF-TrFE-CFE) bulk in the future.
7. Conclusions
Sufficiently considering the molecular characteristics (even structural order-related monomer connection ways) and responsive behaviors under external stimuli (temperature field or electric field), our Metropolis MC modeling was developed upon the coarse-grained 3D Ising model and asymmetric/symmetric force fields on the basis of high-accuracy QM and first-principles calculations. Therefore, our MC simulations reproduce temperature-dependent phase transitions and experimentally consistent dielectric permittivity and hysteresis loops of P(VDF-TrFE) relaxor ferroelectrics versus normal ferroelectrics. By virtue of these MC simulations, their dynamic microstructure evolution pictures are successfully established with the increase in temperature. The domain evolution of P(VDF-TrFE) relaxors agrees with the slush model.9 Remarkably, a new type of large nanodomains with randomly oriented dipoles was found for the first time. These RLNDs appear at high temperatures, but they are different from the traditional paraelectric phases. Within these RLNDs, dipoles still correlate with each other, but their orientations are relatively random. In addition, we find a type of needle-like nanodomains that both contribute to the formation of polar nanoregions in P(VDF-TrFE) relaxor ferroelectrics or ferroelectric domains in P(VDF-TrFE) ferroelectrics. We find that a high degree of structural order for P(VDF-TrFE) bulks, resulting from perfectly head-to-end connected VDF and TrFE monomers, significantly contributes to the formation of P(VDF-TrFE) relaxor ferroelectrics, while a low degree of structural order resulting from head-to-head regiodefects contributes to the formation of normal ferroelectrics. Further analyzing the domain evolution information, the P(VDF-TrFE) relaxor ferroelectrics versus normal ferroelectrics can be well distinguished from each other by judging whether the microdomains or nanodomains emerge or not upon the increase in temperature from the initial low-temperature ferroelectric phases. In the normal ferroelectrics, they only contain disperse single dipoles or ferroelectric domains. Our MC modeling provides a paradigm for the method development of complex relaxor ferroelectric or ferroelectric polymers, and our MC simulations demonstrate the regiodefect manipulation strategy to experimental specialists for further exploration to realize polymer relaxor ferroelectrics or ferroelectrics.Data availability
The codes for both asymmetry/symmetry force fields can be accessed on the GitHub repository (https://github.com/echocreater/P-VDF-TrFE--nanodomains-/). The other data is available from the corresponding author upon reasonable request.Author contributions
T. G.: data curation, formal analysis, investigation, software, validation, visualization, and writing_original draft. Q. A. H.: validation and visualization. S. C.: conceptualization, data curation, funding acquisition, methodology, project administration, resources, supervision, validation, visualization, and writing_review and editing.Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
S. C. was supported by the National Key Research and Development Program of China (Grant No. 2023YFB3813001), the National Natural Science Foundation of China (Grant No. 22073044), and the Fundamental Research Funds for the Central Universities. The computation was performed in the High Performance Computing Center (HPCC) and the High-Performance Computing Center of Collaborative Innovation Center of Advanced Microstructures in Nanjing University.References
- Y. Liu, H. Aziguli, B. Zhang, W. Xu, W. Lu, J. Bernholc and Q. Wang, Nature, 2018, 562, 96–100 CrossRef CAS.
- H. Xu, Z. Y. Cheng, D. Olson, T. Mai, Q. M. Zhang and G. Kavarnos, Appl. Phys. Lett., 2001, 78, 2360–2362 CrossRef CAS.
- B. Neese, B. Chu, S. G. Lu, Y. Wang, E. Furman and Q. M. Zhang, Science, 2008, 321, 821–823 CrossRef CAS PubMed.
- L. Yang, B. A. Tyburski, F. D. Dos Santos, M. K. Endoh, T. Koga, D. Huang, Y. Wang and L. Zhu, Macromolecules, 2014, 47, 8119–8125 CrossRef CAS.
- S. Nayak, H. T. Ng and A. Pramanick, Appl. Phys. Lett., 2020, 117, 232903 CrossRef CAS.
- Q. M. Zhang, V. V. Bharti and X. Zhao, Science, 1998, 280, 2101–2104 CrossRef CAS.
- H. M. Bao, J. F. Song, J. Zhang, Q. D. Shen, C. Z. Yang and Q. M. Zhang, Macromolecules, 2007, 40, 2371–2379 CrossRef CAS.
- Y. Liu, X. Chen, Z. Han, H. Zhou and Q. Wang, Appl. Phys. Rev., 2022, 9, 031306 CAS.
- H. Takenaka, I. Grinberg, S. Liu and A. M. Rappe, Nature, 2017, 546, 391–395 CrossRef CAS PubMed.
- K. Hirota, Z. G. Ye, S. Wakimoto, P. M. Gehring and G. Shirane, Phys. Rev. B, 2002, 65, 104105 CrossRef.
- I. K. Jeong, T. W. Darling, J. K. Lee, T. Proffen, R. H. Heffner, J. S. Park, K. S. Hong, W. Dmowski and T. Egami, Phys. Rev. Lett., 2005, 94, 147602 CrossRef PubMed.
- G. Xu, Z. Zhong, Y. Bing, Z. G. Ye and G. Shirane, Nat. Mater., 2006, 5, 134–140 CrossRef CAS.
- F. Li, S. Zhang, T. Yang, Z. Xu, N. Zhang, G. Liu, J. Wang, J. Wang, Z. Cheng, Z. G. Ye, J. Luo, T. R. Shrout and L. Q. Chen, Nat. Commun., 2016, 7, 13807 CrossRef CAS.
- J. Kim, H. Takenaka, Y. Qi, A. R. Damodaran, A. Fernandez, R. Gao, M. R. McCarter, S. Saremi, L. Chung, A. M. Rappe and L. W. Martin, Adv. Mater., 2019, 31, e1901060 CrossRef PubMed.
- A. Kumar, J. N. Baker, P. C. Bowes, M. J. Cabral, S. Zhang, E. C. Dickey, D. L. Irving and J. M. LeBeau, Nat. Mater., 2021, 20, 62–67 CrossRef CAS PubMed.
- T. Guan and S. Chen, J. Phys. Chem. B, 2023, 127, 6385–6394 CrossRef CAS.
- H.-M. Bao, C.-L. Jia, C.-C. Wang, Q.-D. Shen, C.-Z. Yang and Q. M. Zhang, Appl. Phys. Lett., 2008, 92, 042903 CrossRef.
- Y. Liu, B. Zhang, W. Xu, A. Haibibu, Z. Han, W. Lu, J. Bernholc and Q. Wang, Nat. Mater., 2020, 19, 1169–1174 CrossRef CAS PubMed.
- S. Nayak, H. T. Ng and A. Pramanick, Appl. Phys. Lett., 2020, 117, 232903 CrossRef CAS.
- V. I. Sultanov, V. V. Atrazhev, D. V. Dmitriev, N. S. Erikhman, D. U. Furrer and S. F. Burlatsky, Macromolecules, 2021, 54, 3744–3754 CrossRef CAS.
- V. I. Sultanov, V. V. Atrazhev and D. V. Dmitriev, J. Phys. Chem. B, 2024, 128, 6376–6386 CrossRef CAS.
- G. Rui, Y. Huang, X. Chen, R. Li, D. Wang, T. Miyoshi and L. Zhu, J. Mater. Chem. C, 2021, 9, 894–907 RSC.
- Z. Zhu, G. Rui, R. Li, H. He and L. Zhu, ACS Appl. Mater. Interfaces, 2021, 13, 42063–42073 CrossRef CAS.
- Y. Liu, Z. Han, W. Xu, A. Haibibu and Q. Wang, Macromolecules, 2019, 52, 6741–6747 CrossRef CAS.
- Y. Liu, Y.-T. Lin, A. Haibibu, W. Xu, Y. Zhou, L. Li, S. H. Kim and Q. Wang, Small Sci., 2021, 1, 2000061 CrossRef CAS.
- J. W. Gibbs, Am. J. Sci. Arts, 1878, s3–16, 441–458 CrossRef.
- E. Saiz, E. Riande and R. Díaz-Calleja, J. Phys. Chem. A, 1997, 101, 7324–7329 CrossRef CAS.
- S. Eker, S. Bozdemir and M. Özdemir, J. Non-Cryst. Solids, 2005, 351, 2905–2910 CrossRef CAS.
- C. Welter, L. O. Faria and R. L. Moreira, Phys. Rev. B, 2003, 67, 144103 CrossRef.
- Y. M. You, W. Q. Liao, D. Zhao, H. Y. Ye, Y. Zhang, Q. Zhou, X. Niu, J. Wang, P. F. Li, D. W. Fu, Z. Wang, S. Gao, K. Yang, J. M. Liu, J. Li, Y. Yan and R. G. Xiong, Science, 2017, 357, 306–309 CrossRef CAS.
- C. J. Lu, C. J. Nie, X. F. Duan, J. Q. Li, H. J. Zhang and J. Y. Wang, Appl. Phys. Lett., 2006, 88, 201906 CrossRef.
- L. E. Cross, Ferroelectrics, 1987, 76, 241–267 CrossRef CAS.
- A. R. Akbarzadeh, S. Prosandeev, E. J. Walter, A. Al-Barakaty and L. Bellaiche, Phys. Rev. Lett., 2012, 108, 257601 CrossRef CAS PubMed.
- A. Al-Barakaty, S. Prosandeev, D. Wang, B. Dkhil and L. Bellaiche, Phys. Rev. B, 2015, 91, 214117 CrossRef.
- X. Zhao, J. Y. Dai, J. Wang, H. L. W. Chan, C. L. Choy, X. M. Wan and H. S. Luo, Phys. Rev. B, 2005, 72, 064114 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: orientation angle differences in Fig. S1 and S5, domain size distribution in Fig. S2 and S6 for both P(VDF-TrFE) relaxor ferroelectrics and ferroelectrics, respectively, variations in the volume fraction of typical nanostructures with temperature involved in small-/large-size P(VDF-TrFE) relaxor ferroelectrics in Fig. S3, frequency-dependent dielectric permittivity comparison in Fig. S4, and energy/heat capacity/polarization–temperature curves (Fig. S7) and a free energy-domain size curve (Fig. S8) of P(VDF-TrFE) ferroelectrics. See DOI: https://doi.org/10.1039/d4ta06242f |
| This journal is © The Royal Society of Chemistry 2025 |