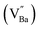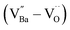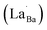Enhanced colossal permittivity in mono-doped BaTiO3via particle hydroxylation-induced defect dipoles†
Seung Yong
Lee
a,
Jung Hwan
Song
a,
Jiseop
Oh
b and
Do Kyung
Kim
 *a
*a
aDepartment of Materials Science and Engineering, Korea Advanced Institute of Science and Technology (KAIST), Daejeon 34141, Republic of Korea. E-mail: dkkim@kaist.ac.kr
bCorporate R&D Institute, Samsung Electro-Mechanics Co., Suwon 16674, Republic of Korea
First published on 26th November 2024
Abstract
Hydroxyl defects in oxide particles are often avoided in the development of high-capacity energy storage devices, as they produce structural defects such as intragranular pores and delamination. However, the discovery of electron-pinning defect dipoles has highlighted the significance of a tailored defect distribution in the oxide lattice, wherein oxygen vacancies and Ti3+ polarons bind free electrons to defect dipoles and lead to quasi-intrinsic colossal permittivity and low dielectric loss. Inspired by this observation, herein, excess hydroxyl defects are intentionally introduced into BaTiO3 nanoparticles to induce the formation of electron-pinning sites within the polycrystalline grains. A substantial number of oxygen vacancies are formed during the early stage of sintering. The addition of La3+ increases the permittivity by two orders of magnitude (εr ≈ 3.5 × 105 at 1 kHz) with moderate dielectric loss (tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ ≈ 0.06). The high defect concentration inhibits long-range hopping, thereby paving the way for the potential commercialization of ultrafine particles with defects. The present work emphasizes that the proper adjustment of defects, rather than complete elimination, in nanocrystal synthesis is a key approach for manipulating defect dipoles in ferroelectric oxides for high-performance ceramic capacitors and energy storage applications.
δ ≈ 0.06). The high defect concentration inhibits long-range hopping, thereby paving the way for the potential commercialization of ultrafine particles with defects. The present work emphasizes that the proper adjustment of defects, rather than complete elimination, in nanocrystal synthesis is a key approach for manipulating defect dipoles in ferroelectric oxides for high-performance ceramic capacitors and energy storage applications.
1 Introduction
Colossal permittivity (CP) (εr > 104) materials are a promising class of dielectrics with significant potential for applications in sensors, energy storage, and ceramic capacitors.1–4 The CP characteristics depend on multiple factors, and hence, the mechanisms underlying giant polarization remain unclear. Furthermore, their low insulation resistance leads to poor reliability, which, in turn, hinders their practical applications. Surface barrier layer capacitance (SBLC) and internal barrier layer capacitance (IBLC) are commonly observed in most CP systems and are less desirable as they require long-range charge hopping to reach the interfaces. In this context, electron-pinned defect dipoles (EPDDs) have emerged as promising alternatives that may help in the commercialization of CP materials. Free electrons in rutile TiO2 are localized by defect clusters introduced via donor–acceptor co-doping, which allows for both giant permittivity (εr > 104) and low dielectric loss (tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ < 0.05).5 Acceptor-driven oxygen vacancies
δ < 0.05).5 Acceptor-driven oxygen vacancies 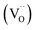 are the key component of ionized defect clusters, critically governing the motion of charge carriers.
are the key component of ionized defect clusters, critically governing the motion of charge carriers.
This discovery has spurred extensive research on TiO2 (ref. 6 and 7) and other crystal structures, such as BaTiO3 (BT),8–11 SrTiO3 (STO),12–15 NiO,16–18 and ZnO,19–22 exploring various donor–acceptor dopant combinations. Colossal permittivity with low dielectric loss in BaTiO3 was first demonstrated in B-site modified (Nb + Mg),23 (Nb + Ga),24 and (Nb + In)25 ceramics. Li et al. revealed that the ratio of donor to acceptor also has a significant impact on the activation energy of charge transition.23 More recently, high-performance CP ceramics have also been reported in mono-doped BaTiO3 systems. For example, Ta5+-doped BaTiO3 ceramics, when annealed in an N2 atmosphere, achieved exceptional colossal permittivity (εr > 2.6 × 105) with low dielectric loss (tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ < 0.04), which could be clearly distinguished from the BLC (tan
δ < 0.04), which could be clearly distinguished from the BLC (tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ > 0.10).26,27 However, the oxygen vacancies induced by the annealing process are highly unstable and prone to being eliminated upon re-oxidation, which poses a challenge for long-term stability in practical applications. Furthermore, optimizing sintering conditions (i.e. temperature, PO2) represents another effective strategy for engineering defect dipoles to enhance CP performance. A physical model describing the electronic motion in (Ta + Al) co-doped BaTiO3 ceramics sintered under different atmospheres has been proposed.28 Additionally, Wang et al. demonstrated exceptional CP performance, achieving high insulation resistivity (ρv ≈ 1011 Ω cm) in BaTiO3–Na0.5Bi0.5TiO3 ceramics by carefully controlling hydrogen content during the sintering process.29 Hence, these findings underscore the significance of optimal defect concentration in tailoring CP ceramics for high-performance capacitors.
δ > 0.10).26,27 However, the oxygen vacancies induced by the annealing process are highly unstable and prone to being eliminated upon re-oxidation, which poses a challenge for long-term stability in practical applications. Furthermore, optimizing sintering conditions (i.e. temperature, PO2) represents another effective strategy for engineering defect dipoles to enhance CP performance. A physical model describing the electronic motion in (Ta + Al) co-doped BaTiO3 ceramics sintered under different atmospheres has been proposed.28 Additionally, Wang et al. demonstrated exceptional CP performance, achieving high insulation resistivity (ρv ≈ 1011 Ω cm) in BaTiO3–Na0.5Bi0.5TiO3 ceramics by carefully controlling hydrogen content during the sintering process.29 Hence, these findings underscore the significance of optimal defect concentration in tailoring CP ceramics for high-performance capacitors.
Ultrafine particles have been used to improve volumetric efficiency and achieve superior dielectric performance in layered capacitors. Wet chemical methods, such as the hydrothermal and sol–gel techniques, are commonly favored for synthesizing submicron particles because they allow for exceptional control over particle size, homogeneity, and composition. However, size effects30,31 and internal defects32–35 at subcritical dimensions adversely affect the dielectric properties of the sintered ceramics, thereby hindering their practical applications. Notably, hydroxyl defects inevitably arise during hydrothermal reactions and are often prevented because they tend to introduce structural flaws at the interfaces.36 However, completely eliminating hydroxyl defects in nanocrystals is challenging. Therefore, leveraging these defects is considered to be the most viable approach for achieving high capacitance with ultrafine particles.
In contrast to previously reported co-doped CP ceramics fabricated via solid-state methods, we designed BT nanoparticles (NPs) using a facile hydrothermal method to manipulate an electron-pinning ceramic matrix. A large number of hydroxyl defects were deliberately introduced into the BT NPs as a source of defect clusters. The formation and evolution of defects from synthesis to sintering were thoroughly examined. Furthermore, we focused on a mechanism that elucidates the origin of defect dipoles in monodoped BT ceramics and highlights the critical role of hydroxyl ions in influencing CP performance. Raman maps of the de-hydroxylated ceramics were obtained to visualize the defect concentration in the micron-scale microstructures.
2 Experimental
2.1 Material preparation
Hydroxylated BaTiO3 nanocrystals were synthesized via a conventional hydrothermal method by the hydrolysis of an alkoxide precursor. Titanium butoxide (Ti(OBu)4, Sigma-Aldrich, 97%) was dispersed in 60 °C ethanol. A white precipitate was obtained after adding NH4OH (Sigma-Aldrich, ACS reagent, 28.0–30.0%) to the Ti-solution. Ba(OH)2·H2O (Sigma-Aldrich, 98%) was dissolved in 80 °C distilled water. Each solution was vigorously stirred for a sufficient period. The Ba solution was then poured into the Ti solution while ensuring a stoichiometric molar ratio of (Ba + La) to Ti of 1.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. For partially hydroxylated (PH0) particles, 30 ml of distilled water was added to dilute the alkaline solution; the same amount of 10 M NaOH solution was added for fabricating fully hydroxylated (FH0) particles. For La3+ doped PH1 and FH1 particles, 1 mol% La(NO3)3·6H2O (Sigma-Aldrich, 99.99%) was additionally dissolved in Ba2+ solution. Finally, the mixtures were transferred to a Teflon-lined stainless steel autoclave. Hydrothermal reaction was performed in a 200 °C oven for 48 h. The powder was washed several times with distilled water and dried at 80 °C. The as-prepared BaTiO3 powders were individually mixed with 0.35 wt% SiO2 through ball milling for 24 h to improve their sinterability. The powders were then homogenized using a 200-mesh sieve and pelletized using a uniaxial press. The green compacts were sintered at 1350 °C for 3 h in a N2 + 0.07% H2 atmosphere at a heating rate of 10 °C min−1. After the dielectric measurements, printed electrodes were removed and a re-oxidation process was conducted at 1150 °C for 12 h. The de-hydroxylated ceramics were polished and thermally etched for microstructural observation.
1. For partially hydroxylated (PH0) particles, 30 ml of distilled water was added to dilute the alkaline solution; the same amount of 10 M NaOH solution was added for fabricating fully hydroxylated (FH0) particles. For La3+ doped PH1 and FH1 particles, 1 mol% La(NO3)3·6H2O (Sigma-Aldrich, 99.99%) was additionally dissolved in Ba2+ solution. Finally, the mixtures were transferred to a Teflon-lined stainless steel autoclave. Hydrothermal reaction was performed in a 200 °C oven for 48 h. The powder was washed several times with distilled water and dried at 80 °C. The as-prepared BaTiO3 powders were individually mixed with 0.35 wt% SiO2 through ball milling for 24 h to improve their sinterability. The powders were then homogenized using a 200-mesh sieve and pelletized using a uniaxial press. The green compacts were sintered at 1350 °C for 3 h in a N2 + 0.07% H2 atmosphere at a heating rate of 10 °C min−1. After the dielectric measurements, printed electrodes were removed and a re-oxidation process was conducted at 1150 °C for 12 h. The de-hydroxylated ceramics were polished and thermally etched for microstructural observation.
2.2 Characterization
The morphologies of the particles and intragranular pores were examined with scanning electron microscopy (SU-8230, Hitachi) and transmission electron microscopy at 300 kV (Tecnai G2F30 S-TWIN, FEI). The phase and crystallinity were characterized using a conventional powder X-ray diffractometer (XRD, Smartlab, Rigaku) with CuKα radiation between 20° and 70°. The hydroxylation was quantified via TGA (TGA 92-18, Setaram) conducted from room temperature to 800 °C in air at a heating rate of 10 °C min−1. The O–H groups were further characterized via FT-IR (Nicolet iS50, Thermo Fisher). The BaTiO3 NPs (1 wt%) were pelletized with KBr powder and dried overnight to eliminate surface-absorbed –OH before the measurement. The symmetry deformations due to the defects in the BaTiO3 nanocrystals were investigated via Raman spectroscopy (LabRAM, Horiba) with a 514 nm excitation source. For dielectric properties, Pt paste was screen-printed on the polished surface as an electrode and annealed at 850 °C for 30 min to remove organic binder. The frequency-dependent capacitance was measured using an LCR meter (E4990A, Keysight) from 100 Hz to 1 MHz at an applied voltage of 0.5 Vrms. For the 2D Raman maps, polished BT was placed on a SiO2 substrate with epoxy resin and dried at 80 °C overnight. The specimen was loaded onto the piezo-stage, which enabled precise positioning at the nanoscale level. A 20 × 20 μm area was scanned via the point-by-point method; the distance between the points was 0.5 μm. The obtained Raman spectra were converted into color maps after removing the background using a polynomial function.3 Results and discussion
3.1 Hydroxylated Ba1−xLaxTiO3OH nanoparticles
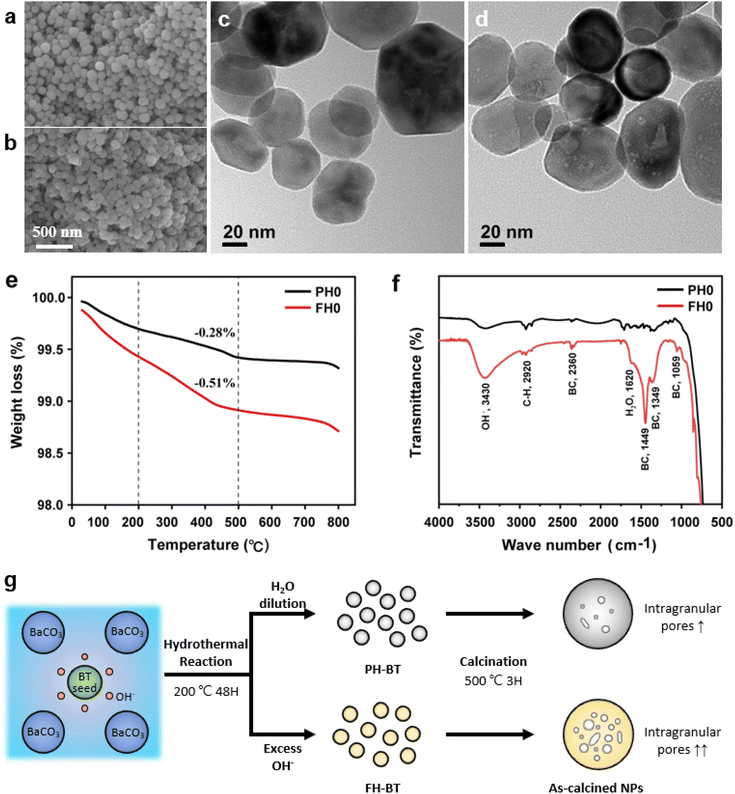
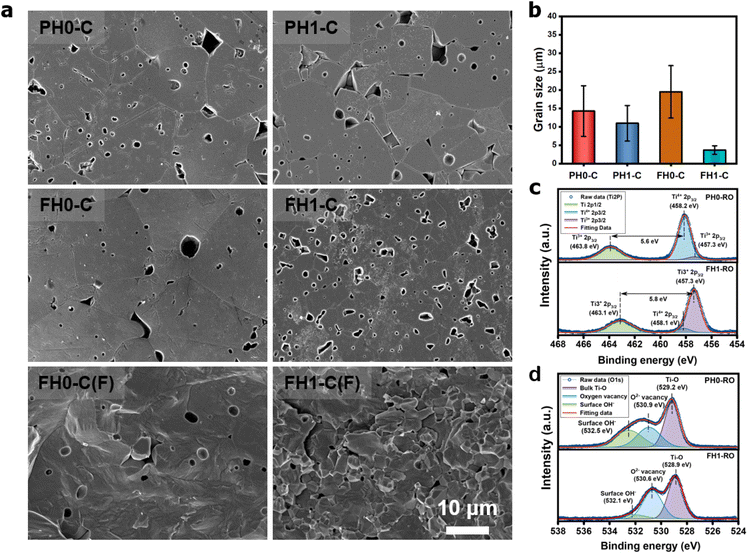
Fig. 1a and b show the surface morphologies of the hydroxylated BT NPs synthesized under different pH conditions. The partially and fully hydroxylated BT NPs are denoted PH0 and FH0, respectively. A strongly alkaline environment promotes nucleation, resulting in a reduction in particle size.37 However, to prevent additional crystal distortion due to the size effect, similarly sized particles were fabricated at different alkalinity by prolonging the reaction time (48 h). Hydroxyl defects in the BT lattice are known to accumulate and form intercrystallite pores when exposed to elevated temperatures.35 Accordingly, the PH0 and FH0 NPs were annealed to examine the concentration of OH− lattice defects. HRTEM images indicated pore-free particles with clear lattice fringes for both NPs (Fig. S1†); however, a large number of pores appeared in the nanocrystals when exposed to 500 °C (Fig. 1c and d). A large number of intragranular pores were formed in BT in the OH− excess environment, indicating that the concentration of defects in PH0 and FH0 NPs was significantly different.The presence of hydroxyl lattice defects was further confirmed via thermogravimetric analysis (TGA) and infrared spectroscopy (Fig. 1e and f). De-hydroxylation occurs during heating, resulting in the release of H2O vapor and the creation of oxygen vacancies in the crystal.32
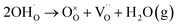 | (1) |
The amount of vapor released is proportional to the number of hydroxyl defects within the lattice, which is the primary reason for mass reduction in the low-temperature region. A significant disparity in the mass reduction is evident at temperatures below 500 °C: FH0 exhibits a twofold increase in loss (1.09%) compared to PH0 (0.58%); the theoretical values of the corresponding OH− concentrations are 13.4 and 7.4 mol% respectively.38 In addition, lattice O–H vibrational bands (bending: 1620 cm−1; stretching: 2800–3650 cm−1) were observed in the FT-IR spectra.39 FH0 exhibited a stronger integral intensity of the O–H bands, consistent with the TGA results. The bands at 1059, 1349, 1449, and 2360 cm−1 in the FH0 spectra were attributed to the vibration motions from –CO3, indicating that there is a high concentration of secondary phase (BaCO3) along with hydroxyl defects.40–42 The evolution of the internal defects during hydroxylation and de-hydroxylation in the PH0 and FH0 NPs is shown in Fig. 1g.
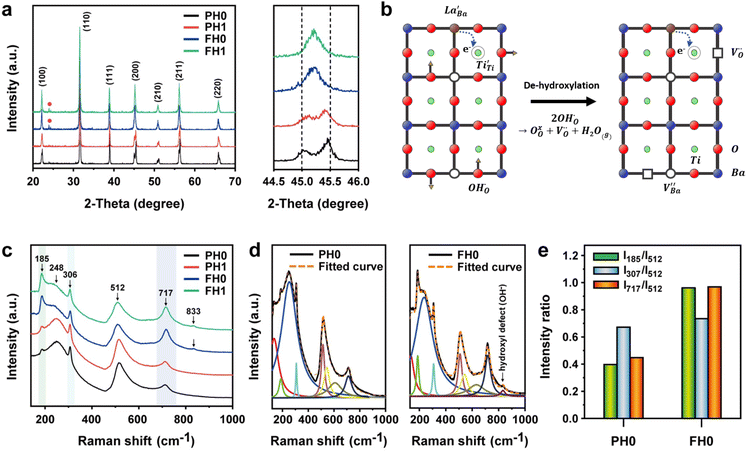
Highly crystalline BaTiO3 NPs are crucial to achieve high-performance dielectric properties. However, defects (i.e.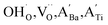 ) often cause the short-range order to deteriorate and induce stresses that contribute to local tetragonal–cubic transition.32,33 The effect of defects on the crystallinity of the hydroxylated BT NPs was characterized via XRD (Fig. 2a). PH0 exhibited a highly asymmetric TiO6 octahedral structure, whereas defective FH0 exhibited a pseudo-cubic phase with a broad (200) peak. Because the particle sizes of PH0 and FH0 were comparable, size effects on the nanocrystals were expected to be similar. Therefore, we attribute the poor tetragonality of FH0 to the introduction of highly concentrated lattice defects during the hydrothermal reaction. Furthermore, the introduction of lattice defects can be controlled by adjusting the synthesis parameters, as the tetragonality gradually decreases with increasing solution pH (Fig. S2†). Although the effect of La3+ (1 mol%) on the tetragonality of PH1 and FH1 is limited, La-related compounds were not detected, indicating a complete solid solution. Fine particles with highly concentrated defects create complexities in discriminating the doping effects on the nanocrystals.23,25,43 The presence of La3+ in BaTiO3 NPs was further confirmed via TEM elemental analysis (Fig. S3†).
) often cause the short-range order to deteriorate and induce stresses that contribute to local tetragonal–cubic transition.32,33 The effect of defects on the crystallinity of the hydroxylated BT NPs was characterized via XRD (Fig. 2a). PH0 exhibited a highly asymmetric TiO6 octahedral structure, whereas defective FH0 exhibited a pseudo-cubic phase with a broad (200) peak. Because the particle sizes of PH0 and FH0 were comparable, size effects on the nanocrystals were expected to be similar. Therefore, we attribute the poor tetragonality of FH0 to the introduction of highly concentrated lattice defects during the hydrothermal reaction. Furthermore, the introduction of lattice defects can be controlled by adjusting the synthesis parameters, as the tetragonality gradually decreases with increasing solution pH (Fig. S2†). Although the effect of La3+ (1 mol%) on the tetragonality of PH1 and FH1 is limited, La-related compounds were not detected, indicating a complete solid solution. Fine particles with highly concentrated defects create complexities in discriminating the doping effects on the nanocrystals.23,25,43 The presence of La3+ in BaTiO3 NPs was further confirmed via TEM elemental analysis (Fig. S3†).
The hydroxylation of oxides inevitably introduces negatively charged defects to maintain charge neutrality. The lattice stress due to the OH− ions is generally relieved via ionic compensation rather than electronic compensation:38,44 either 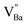 or
or 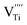 is formed when OH− defects are introduced into the BT crystals. However, the formation of
is formed when OH− defects are introduced into the BT crystals. However, the formation of 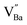 is more likely because Ba-deficient particles are frequently reported in cubic hydrothermal BT NPs.45 In line with the FTIR spectra, crystalline BaCO3 was observed only in FH0 and FH1 (red circles), which implies that a substantial amount of Ba2+ in the hydrothermal solution did not participate in the reaction (Fig. 2a). Because a strong alkalinity promotes the nucleation of BT nanocrystals, such large amounts of BaCO3 can only be obtained when a substantial amount of
is more likely because Ba-deficient particles are frequently reported in cubic hydrothermal BT NPs.45 In line with the FTIR spectra, crystalline BaCO3 was observed only in FH0 and FH1 (red circles), which implies that a substantial amount of Ba2+ in the hydrothermal solution did not participate in the reaction (Fig. 2a). Because a strong alkalinity promotes the nucleation of BT nanocrystals, such large amounts of BaCO3 can only be obtained when a substantial amount of 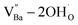 is formed in BT NPs.
is formed in BT NPs.
X-ray fluorescence and inductively coupled plasma spectroscopy are widely used to determine the Ba/Ti molar ratio in the synthesized BT NPs. However, the reliability of these techniques is severely limited because of impurities. In contrast, Raman spectroscopy can be used to detect changes in the crystal symmetry and the vibrational bands in BaTiO3 are not disturbed by BaCO3. Fig. 2c shows the Raman spectra of the hydroxylated BT NPs. Despite the cubic-like crystallography of FH0 and FH1, typical tetragonal BT Raman bands at 185, 248, 306, 512, and 717 cm−1 were observed, thereby affirming the local preservation of strong anisotropic symmetry.46,47 These bands were assigned to diverse physical factors for quantitative characterization after normalizing each scattering intensity with the broad band centered at 512 cm−1 (I512). I185/I512 was attributed to the internal stresses in the BT NPs; I307/I512 was attributed to the distortion of the TiO6 octahedra; and I717/I512 was attributed to the symmetry change due to Ba-vacancies.39,48 The Raman spectra of the PH0 and FH0 NPs were deconvoluted to first order Raman bands, and the corresponding intensity ratios are shown in Fig. 2d and e. The intensity ratios I717/I512 of PH0 and FH0 indicate that a large number of Ba-vacancies are generated during hydrothermal synthesis to compensate for the hydroxyl defects 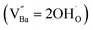 . The significant increase in I185/I512 indicates that the defects induce a considerable amount of stress in the nanocrystals. This further supports the presence of inactive Ba2+ ions during the hydrothermal reaction. Despite the structural stress in the lattice, TiO6 distortion (I307/I512) remained constant, suggesting that the effect of
. The significant increase in I185/I512 indicates that the defects induce a considerable amount of stress in the nanocrystals. This further supports the presence of inactive Ba2+ ions during the hydrothermal reaction. Despite the structural stress in the lattice, TiO6 distortion (I307/I512) remained constant, suggesting that the effect of 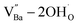 on the t–c transition is physically localized.
on the t–c transition is physically localized.
The Raman spectrum of tetragonal BaTiO3 comprised the five bands mentioned above. However, several previous studies have reported a newly activated band in the vicinity of 830 cm−1. This band has been assigned to complex perovskites, where the symmetry of the TiO6 octahedron is directly disordered due to B-site substitution (MTiO6) or vacancy formation 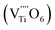 .48–50 La3+, with an ionic size of 1.15 Å, is a highly preferred dopant for Ba-site (1.35 Å) substitution; therefore, the formation of the
.48–50 La3+, with an ionic size of 1.15 Å, is a highly preferred dopant for Ba-site (1.35 Å) substitution; therefore, the formation of the 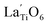 symmetry is unlikely.51 As shown in Fig. 2c, small peaks centered at 833 cm−1 (I833) were observed only for highly hydroxylated compounds, including the La-free composition. Thus, the possibility of
symmetry is unlikely.51 As shown in Fig. 2c, small peaks centered at 833 cm−1 (I833) were observed only for highly hydroxylated compounds, including the La-free composition. Thus, the possibility of 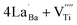 was excluded because the band is not associated with the deformation from La3+ introduction. Wada et al. assigned the 830 cm−1 band in pure BT NPs to hydroxyl lattice defects because the band gradually disappeared with increasing annealing temperature.40 A similar phenomenon was observed for FH0 and FH1 wherein I833 disappeared in the sintered ceramics. The 833 cm−1 scattering intensity remains weak despite the high hydroxyl concentrations owing to the poor sensitivity of –OH vibrations in Raman spectroscopy. The defect status of La3+ and OH− in FH1 NPs is summarized in Fig. 2b.
was excluded because the band is not associated with the deformation from La3+ introduction. Wada et al. assigned the 830 cm−1 band in pure BT NPs to hydroxyl lattice defects because the band gradually disappeared with increasing annealing temperature.40 A similar phenomenon was observed for FH0 and FH1 wherein I833 disappeared in the sintered ceramics. The 833 cm−1 scattering intensity remains weak despite the high hydroxyl concentrations owing to the poor sensitivity of –OH vibrations in Raman spectroscopy. The defect status of La3+ and OH− in FH1 NPs is summarized in Fig. 2b.
3.2 Colossal permittivity in de-hydroxylated Ba1−xLaxTiO3OH ceramics
The frequency characteristics of the dielectric constant and dielectric loss of the ceramics fabricated with hydroxylated BLT (La = 0, 1 mol%) powders are presented in Fig. 3a. PH0-C exhibited CP (εr > 3.0 × 105), whereas the dielectric constant of FH0-C was ∼103. The giant permittivity with relatively high dielectric loss (tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ ≈ 0.10) in PH0-C is expected; this is often observed in reduced-BT, wherein long-range charge hopping induces strong dipoles at the interfaces.52 FH0-C was not reduced under the sintering conditions used in this study and exhibited electrically insulating characteristics, wherein spontaneous polarization governs the dielectric properties. The reduction resistance of perovskite oxides can be improved using acceptor dopants. Undoubtedly, FH0-C is free of acceptors in either the Ba or Ti sites, and the difference with PH0-C lies in the hydroxyl defects in the synthesized particles. Therefore, we conclude that the difference in reducibility is strongly related to the OH− defects in the BT NPs.
δ ≈ 0.10) in PH0-C is expected; this is often observed in reduced-BT, wherein long-range charge hopping induces strong dipoles at the interfaces.52 FH0-C was not reduced under the sintering conditions used in this study and exhibited electrically insulating characteristics, wherein spontaneous polarization governs the dielectric properties. The reduction resistance of perovskite oxides can be improved using acceptor dopants. Undoubtedly, FH0-C is free of acceptors in either the Ba or Ti sites, and the difference with PH0-C lies in the hydroxyl defects in the synthesized particles. Therefore, we conclude that the difference in reducibility is strongly related to the OH− defects in the BT NPs.
The reduction of oxygen atoms in Ti-based perovskite oxides requires a high temperature (>600 °C) environment with low oxygen partial pressure, whereas hydroxyl defects can be effectively removed at low temperatures (<600 °C) (Fig. 1d). As these reactions occur sequentially, the pre-formed oxygen vacancies from the de-hydroxylation 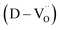 lower the driving force for thermal reduction at elevated temperatures (depletion of oxygen reactant in eqn (2) and (3)), and play a similar role to oxygen vacancies induced by acceptors. Thus, the non-reducible feature in FH0-C is significantly more pronounced than in PH0-C. In contrast, delocalized electrons compensated for by thermal vacancies
lower the driving force for thermal reduction at elevated temperatures (depletion of oxygen reactant in eqn (2) and (3)), and play a similar role to oxygen vacancies induced by acceptors. Thus, the non-reducible feature in FH0-C is significantly more pronounced than in PH0-C. In contrast, delocalized electrons compensated for by thermal vacancies 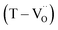 in reduced PH0-C accumulate at the interfaces providing strong BLC.
in reduced PH0-C accumulate at the interfaces providing strong BLC.
| BaTiO3 + xH2 → BaTi1−2x4+Ti2x3+O3−x + xH2O | (2) |
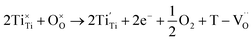 | (3) |
Therefore, PH1-C and FH1-C represent A-site donor effects on two distinct BT ceramics with different defect characteristics. In contrast to the marginal increase in permittivity of PH1-C, FH1-C exhibited a substantial increase in permittivity (εr > 3.5 × 105) upon La3+ addition with moderate dielectric loss (tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ ≈ 0.06 at 1 kHz). Moreover, the significant decrease in dielectric loss at low frequency suggests that the long-range charge conduction is effectively inhibited and the reduction is more significant in FH1-C. This is attributed to the activation of a new polarization mechanism beyond spontaneous polarization.
δ ≈ 0.06 at 1 kHz). Moreover, the significant decrease in dielectric loss at low frequency suggests that the long-range charge conduction is effectively inhibited and the reduction is more significant in FH1-C. This is attributed to the activation of a new polarization mechanism beyond spontaneous polarization.
Various evaluation methods, including multiple electrode assessment,53 surface polishing,54 re-oxidation,24 and modeling of charge hopping,55–57 have been proposed to distinguish between the multiple dipoles that contribute to CP performance. Among these, re-oxidation is a simple technique for screening the contribution of space charges. Fig. 3b and c show the frequency dependence of dielectric response after re-oxidation and the variation in the permittivity at 1 kHz, respectively. PH0-RO exhibited a significant decrease in permittivity (εr ≈ 1500) and loss (tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ ≈ 0.02), resulting in the loss of giant dielectricity. Because oxidation and reduction are reversible, the large decrease in the permittivity confirms that the CP originated from the accumulation of space charges at the interfaces and the recombination of Ti polarons (Ti3+ + e− → Ti4+) takes place during re-oxidation. As expected, the insulating FH0-RO maintained its spontaneous polarization before and after heat treatment. Surprisingly, the La3+-doped system maintained its CP performance over a wide frequency range, and the effect of re-oxidation on FH1-RO was negligible. Compared to
δ ≈ 0.02), resulting in the loss of giant dielectricity. Because oxidation and reduction are reversible, the large decrease in the permittivity confirms that the CP originated from the accumulation of space charges at the interfaces and the recombination of Ti polarons (Ti3+ + e− → Ti4+) takes place during re-oxidation. As expected, the insulating FH0-RO maintained its spontaneous polarization before and after heat treatment. Surprisingly, the La3+-doped system maintained its CP performance over a wide frequency range, and the effect of re-oxidation on FH1-RO was negligible. Compared to 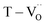 , the removal of
, the removal of 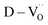 through re-oxidation can be challenging because they are ionically coupled with Ba vacancies. Thus, the conditions for defect dipoles were satisfied as large numbers of
through re-oxidation can be challenging because they are ionically coupled with Ba vacancies. Thus, the conditions for defect dipoles were satisfied as large numbers of 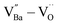 and
and 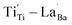 were distributed within the grains, which can lead to the formation of either
were distributed within the grains, which can lead to the formation of either 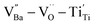 or
or 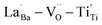 defect clusters. In addition, the difference in re-oxidation behavior was prominently reflected in the temperature characteristics of the dielectric constant. While PH0-RO, having lost its colossal dielectric properties, exhibited the typical temperature characteristics of barium titanate ceramics with a Curie temperature of around 130 °C, FH1-RO maintained stable colossal dielectric properties up to 250 °C (Δεr/ε25 < 15%). Dielectric loss also remained low and stable, exceeding 10% only above 200 °C. This suggests that a significant number of electrons associated with defect clusters are retained even in high-temperature environments (Fig. S4†).
defect clusters. In addition, the difference in re-oxidation behavior was prominently reflected in the temperature characteristics of the dielectric constant. While PH0-RO, having lost its colossal dielectric properties, exhibited the typical temperature characteristics of barium titanate ceramics with a Curie temperature of around 130 °C, FH1-RO maintained stable colossal dielectric properties up to 250 °C (Δεr/ε25 < 15%). Dielectric loss also remained low and stable, exceeding 10% only above 200 °C. This suggests that a significant number of electrons associated with defect clusters are retained even in high-temperature environments (Fig. S4†).
Quantifying the polarization mechanisms that contribute to the measured capacitance is crucial; however, this remains a subject of considerable debate. Han et al. categorized the CP of reduced BT into 15% SBLC, 20% IBLC, and 65% e-hopping by applying the universal dielectric response model.57 We assumed that all space charges are eliminated after re-oxidation and approximated the contribution of the defect dipole to the total capacitance by simply calculating the reduction in permittivity before and after re-oxidation:
| PDefect(%) = [1 − (εRed − εRO)/εRed] × 100 | (4) |
The dielectric permittivities and loss tangents of PH1-RO and FH1-RO at 1 kHz were compared with those of previously reported BT ceramics with CPs (Fig. 3e). BaTiO3 with BLC (Pinterface) is positioned in the region with high permittivity and dielectric loss due to long-range charge hopping.58–60 In contrast, defects such as Ti3+ polarons and/or divacancies provide short-range hopping sites; however, in such cases, the electron mobility is compromised, which leads to a decrease in the dielectric loss. In both cases, thermally activated defects can be easily eliminated after re-oxidation, as was the case for PH0-RO. Thus, particle hydroxylation-driven defect polarization is superior to conventional CP mechanisms. The minimal change in the dielectric loss of PH1-RO and FH1-RO further suggests that charge conduction is not a major cause of such loss. Instead, it is inferred that the high concentration of 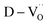 and the suboptimal La3+/OH− (or
and the suboptimal La3+/OH− (or 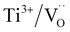 ) ratio may contribute to the increase in dielectric loss at high frequency.
) ratio may contribute to the increase in dielectric loss at high frequency.
The effective permittivity of IBLC depends strongly on the crystallite size (εeff = εgbtg/tgb).1 Therefore, microstructural analysis of CP ceramics is essential for determining the polarization mechanism. Fig. 4a shows the unique microstructures of de-hydroxylated BLT ceramics. Micron-sized crystallites with pores from de-hydroxylation trapped in the grains and grain boundaries were observed. Similar sized pores observed in the fracture surfaces prove that neither the mechanical polishing nor the etching process have caused these defective microstructures. The inhibition of grain growth due to the addition of rare-earth elements was observed in both PH1-C and FH1-C; the effect was more pronounced in particles with higher hydroxyl content (Fig. 4b).51 If interfacial polarization dominated the CP characteristics of all BT ceramics regardless of de-hydroxylation, a lower permittivity should have been observed in fine-grained FH1-C.27 However, the permittivities were similar, and this observation further indicates the presence of strong dipoles other than Maxwell–Wagner polarization.
Charged defects in the hydroxylated BT NPs must be retained in the microstructures to limit the movement of delocalized electrons. Because the sintering parameters (i.e., temperature and PO2) determine the equilibrium defect concentration, their effect on the CP performance should be considered. Defect annihilation 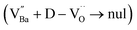 that may occur during re-oxidation decreases the concentration of oxygen vacancies, thereby eliminating electron-pinning sites. The XPS spectra of Ti and O in the re-oxidized PH0 and FH1 ceramics are shown in Fig. 4c and d, respectively. The Ti 2P3/2 peaks at 458.2 and 457.3 eV correspond to the binding energies of Ti4+ and Ti3+, respectively.61 The intensity of Ti4+ was stronger in PH0-RO, whereas that of Ti3+ was dominant in FH1-RO. In addition, the spin–orbit splitting increased up to 5.8 eV for Ti3+, which is marginally higher than the splitting energy reported for Ti4+ systems (5.7 eV).29 This demonstrates that loosely bound electrons are widely distributed in the Ti orbitals, which are considered the most critical components for defect dipole formation. The asymmetric O 1s peak near 529.0 eV corresponds to bulk Ti4+–O2− bonds in the lattice. The shoulder peak around 530.6 eV is attributed to the sub-coordinated oxygen atoms, and the tail above 531.5 eV corresponds to the binding energy of the chemisorbed –OH on the surface.61 The peak centered at ∼530.6 eV was sharp and shows an intensity comparable to that of the bulk Ti4+–O2− bond in FH1-RO, whereas a broad peak was observed in PH0-RO. It can be concluded that defects from thermal reduction are mostly removed after the 12 h re-oxidation process whereas defects from de-hydroxylation
that may occur during re-oxidation decreases the concentration of oxygen vacancies, thereby eliminating electron-pinning sites. The XPS spectra of Ti and O in the re-oxidized PH0 and FH1 ceramics are shown in Fig. 4c and d, respectively. The Ti 2P3/2 peaks at 458.2 and 457.3 eV correspond to the binding energies of Ti4+ and Ti3+, respectively.61 The intensity of Ti4+ was stronger in PH0-RO, whereas that of Ti3+ was dominant in FH1-RO. In addition, the spin–orbit splitting increased up to 5.8 eV for Ti3+, which is marginally higher than the splitting energy reported for Ti4+ systems (5.7 eV).29 This demonstrates that loosely bound electrons are widely distributed in the Ti orbitals, which are considered the most critical components for defect dipole formation. The asymmetric O 1s peak near 529.0 eV corresponds to bulk Ti4+–O2− bonds in the lattice. The shoulder peak around 530.6 eV is attributed to the sub-coordinated oxygen atoms, and the tail above 531.5 eV corresponds to the binding energy of the chemisorbed –OH on the surface.61 The peak centered at ∼530.6 eV was sharp and shows an intensity comparable to that of the bulk Ti4+–O2− bond in FH1-RO, whereas a broad peak was observed in PH0-RO. It can be concluded that defects from thermal reduction are mostly removed after the 12 h re-oxidation process whereas defects from de-hydroxylation 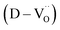 were preserved.
were preserved.
The existence of defect dipoles in CP ceramics has been analyzed by XPS, EPR, and XANES.6,54,62 Although these techniques are highly sensitive to changes in the chemical composition and electronic structures, their detection depth is limited to the outermost few nanometers and they require ultra-high-vacuum or cryogenic temperatures. Furthermore, the techniques cannot distinguish between intrinsic and extrinsic oxygen vacancies (i.e.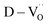 ,
, 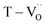 ) in de-hydroxylated ceramics. In contrast,
) in de-hydroxylated ceramics. In contrast, 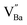 remains an intrinsic defect throughout the sintering process, shifting its compensating counterpart from OH− to
remains an intrinsic defect throughout the sintering process, shifting its compensating counterpart from OH− to 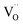 . Moreover, Ba-vacancies have a higher effective mass than
. Moreover, Ba-vacancies have a higher effective mass than 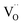 , hence making it easier to detect with vibrational spectroscopy. Therefore, identifying Ba vacancies can reveal well-sustained defect clusters in polycrystalline grains after sintering.
, hence making it easier to detect with vibrational spectroscopy. Therefore, identifying Ba vacancies can reveal well-sustained defect clusters in polycrystalline grains after sintering.
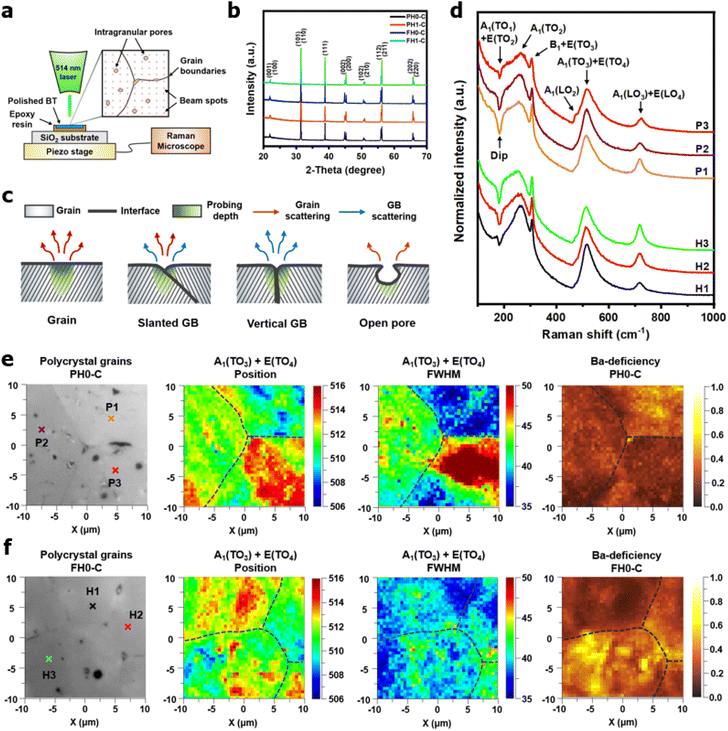
In powders, the incident beam of a laser interacts with randomly oriented grains. In contrast, crystal orientation and microstructural defects play a significant role in polycrystalline Raman spectroscopy. Therefore, spectra are collected from multiple regions, including the grains, interfaces, and voids (Fig. 5a). In addition, X-ray diffraction analysis was conducted to identify any residual phases that could affect the lattice vibrations. Single-phase tetragonal BaTiO3 ceramics were obtained, indicating that the BaCO3 in the FH NPs was completely decomposed and that La3+ remained in the solid solution after sintering (Fig. 5b). For microstructural defects, it is reasonable to assume that three-dimensional grain boundary configurations influence Raman scattering (Fig. 5c). Interfacial scattering was evident when the grain boundaries were perpendicular to the surface (Fig. S5†). However, this may not be a critical problem because the average grain size of de-hydroxylated BT was larger than the Raman probing area. The scattering intensities at the macropores were weak because of defocusing; however, the effects of submicron-sized pores on the spectrum are minimal. In conclusion, structural defects are less significant in coarse ceramics; instead, the angular dependency of the incident beam should be carefully considered.
Fig. 5d shows representative Raman spectra of the grains in PH0-C and FH0-C. The corresponding spots are marked with cross signs (×) in the optical micrographs shown in Fig. 5e and f. Although the relative intensities of the crystallites were different, first-order Raman scattering of tetragonal BaTiO3 (P4mm–C4v) was observed for all grains. According to the Raman selection rule, the A1(TO) and A1(LO) phonons cannot be strongly activated within the same crystallographic orientation.63 Therefore, the A1(TO) bands centered at 180, 260, and 520 cm−1 can serve as crucial metrics for determining the angular effect on the A1(LO3) intensity. The negative dip near 180 cm−1 represents the coupling behavior of A1(TO1) modes; the dip turns shallow when this phonon propagation is hindered.46 Provided that no external factors other than crystal orientation influence A1(TO1) propagation, its spectral shape can provide evidence for identifying the angular configuration of the specific grains in polycrystal ceramics. Hence, the P1/H3, P2/H2, and P3/H1 grains can be grouped based on their unique 180 cm−1 dips. The pronounced dip observed for both the P1/H3 and P2/H2 grains indicates solid A1(TO) coupling. However, in both groups, strong A1(LO3) phonon vibration is observed simultaneously and its intensity was higher for the FH0-C. If the higher intensity of A1(LO3) was solely due to angular dependency, the A1(TO) coupling would have been suppressed, resulting in a shallower dip. In contrast, the distinct A1(LO2) near 480 cm−1 in P3 and the sharp A1(TO2) in H1 suggest that P3/H1 has a different orientation, irrespective of the dip.
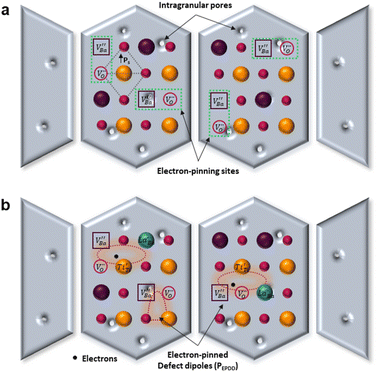
The A1(TO3) + E(TO4) band is used to normalize the other bands in the BT Raman spectrum. Therefore, in addition to the coupling behavior, the crystallographic effect on the phonon parameters of the reference band should also be carefully considered. The optical micrographs of the polished grains and the corresponding A1(TO3) band features are shown in Fig. 5e and f, respectively. The peak position and FWHM for PH0-C were discrete with respect to the adjacent grains, whereas more uniform band features were observed in FH0-C. This indicates that the selected grains in FH0-C were more aligned in terms of the A1(TO3) vibration. The mapping regions for band position and FWHM in P3 are distinctly different from those in FH0-C. Because the stress concentration on the P3 crystallite alone is unlikely, the abnormal shift and broadening band characteristics in P3 suggest that the crystal is more compatible with the in-plane E mode than the ferroelectric polar axis (A mode). Moreover, the FWHM of the crystallites in FH0-C is positioned in between that of P1 and P2. The strong compositional inhomogeneity in FH0-C broadens the band, thereby making the FWHM feature in FH0-C grains more similar to that of P1. Considering all band parameters of the A1 phonons in BaTiO3, the grains P1 and H3 share a similar scattering configuration, and the strong A1(LO) intensity originates from the symmetry changes due to structural irregularities. Therefore, the concentrations of the Ba vacancies in PH0-C and FH0-C are mapped with the ratio of the integrated areas of A1(LO3) + E(LO4) and A1(TO3) + E(TO4) in Fig. 5e and f. In addition, the ratios corresponding to points in P1 and H3 are shown as histograms for a statistical comparison (Fig. S6†). Although P1 exhibited a Gaussian distribution, H3 showed an asymmetric profile with pronounced shoulders. The average ratios of P1 and H3 were 0.368 and 0.424, respectively. D90, which represents the value of the top 90% of the overall population, was 16% higher in the H3 grains of fully hydroxylated BT. In addition, considering the angular dependence of the maximum and minimum intensities of the A1 phonon in polycrystalline BaTiO3 varied by 20%, the difference is statistically significant.64 Combined with the results of the XPS analysis, Raman areal scanning indicates that 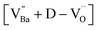 annihilation did not occur during sintering. The defects originating from the hydrothermally treated particles remained within the porous microstructures and acted as hosts for defect dipoles (Fig. 6). We believe that the proposed powder design is a universal approach for introducing hydrothermal defects in other oxide-based CP materials (CCTO, TiO2, ZnO, and NiO). Thus, fine ceramics can be fabricated by adopting appropriate sintering techniques along with defect engineering. Hence, our approach can help improve the potential of defect-derived NPs for applications in high-density energy storage and high-capacity capacitors.
annihilation did not occur during sintering. The defects originating from the hydrothermally treated particles remained within the porous microstructures and acted as hosts for defect dipoles (Fig. 6). We believe that the proposed powder design is a universal approach for introducing hydrothermal defects in other oxide-based CP materials (CCTO, TiO2, ZnO, and NiO). Thus, fine ceramics can be fabricated by adopting appropriate sintering techniques along with defect engineering. Hence, our approach can help improve the potential of defect-derived NPs for applications in high-density energy storage and high-capacity capacitors.
4 Conclusions
A significant number of hydroxyl defects were introduced into BaTiO3 NPs via conventional hydrothermal synthesis. Hydroxyl defects play a role similar to that of acceptors in CP materials fabricated via solid-state methods. Intrinsic oxygen vacancies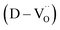 were formed during the early stage of heating and preserved throughout the sintering. When aliovalent La3+ was introduced (FH1-C), the permittivity increased by two orders of magnitude (εr ≈ 3.5 × 105 at 1 kHz) with moderate dielectric loss (tan
were formed during the early stage of heating and preserved throughout the sintering. When aliovalent La3+ was introduced (FH1-C), the permittivity increased by two orders of magnitude (εr ≈ 3.5 × 105 at 1 kHz) with moderate dielectric loss (tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ ≈ 0.06) across a wide frequency range. The high defect concentration inhibited long-range hopping, leading to the formation of defect dipoles in the polycrystalline grains. Furthermore, these dipoles remained active even after the re-oxidation process, indicating that their dielectric features were distinct from those observed in reduced ceramics. In conjunction with XPS analysis, micron-scale Raman maps revealed that ionically coupled
δ ≈ 0.06) across a wide frequency range. The high defect concentration inhibited long-range hopping, leading to the formation of defect dipoles in the polycrystalline grains. Furthermore, these dipoles remained active even after the re-oxidation process, indicating that their dielectric features were distinct from those observed in reduced ceramics. In conjunction with XPS analysis, micron-scale Raman maps revealed that ionically coupled 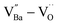 provides electron-pinning sites and leads to the development of
provides electron-pinning sites and leads to the development of 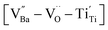 and/or
and/or 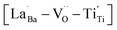 types of giant defect dipoles. Defects in BT nanocrystals may help achieve ultrahigh capacitance. Hence, the appropriate modification of defects rather than their complete elimination is key for synthesizing nanocrystals. The novel powder approach proposed in this study offers a new perspective for regulating the CPs of ferroelectric oxides for high-performance ceramic capacitors.
types of giant defect dipoles. Defects in BT nanocrystals may help achieve ultrahigh capacitance. Hence, the appropriate modification of defects rather than their complete elimination is key for synthesizing nanocrystals. The novel powder approach proposed in this study offers a new perspective for regulating the CPs of ferroelectric oxides for high-performance ceramic capacitors.
Data availability
The data supporting this article have been included as part of the ESI.†Author contributions
Seung Yong Lee: conceptualization, methodology, formal analysis, investigation, writing – original draft. Jung Hwan Song: methodology, data curation, validation. Jiseop Oh: investigation, resources, project administration. Do Kyung Kim: writing – review and editing, validation, supervision, funding acquisition.Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
This work was supported by Samsung Electro-Mechanics Co. (G01220232 and G01230534). The authors gratefully acknowledge the technical support from the staff at the spectroscopy lab at the KAIST Analysis Center for Research Advancement.References
- Y. Wang, W. Jie, C. Yang, X. Wei and J. Hao, Adv. Funct. Mater., 2019, 29, 1808118 CrossRef.
- S. Krohns, P. Lunkenheimer, S. Meissner, A. Reller, B. Gleich, A. Rathgeber, T. Gaugler, H. U. Buhl, D. C. Sinclair and A. Loidl, Nat. Mater., 2011, 10, 899–901 CrossRef CAS PubMed.
- R. Lo Nigro, R. G. Toro, G. Malandrino, M. Bettinelli, A. Speghini and I. L. Fragalà, Adv. Mater., 2004, 16, 891–895 CrossRef CAS.
- C. C. Homes, T. Vogt, S. M. Shapiro, S. Wakimoto and A. P. Ramirez, Science, 2001, 293, 673–676 CrossRef CAS PubMed.
- W. Hu, Y. Liu, R. L. Withers, T. J. Frankcombe, L. Norén, A. Snashall, M. Kitchin, P. Smith, B. Gong, H. Chen, J. Schiemer, F. Brink and J. Wong-Leung, Nat. Mater., 2013, 12, 821–826 CrossRef CAS PubMed.
- X. Cheng, Z. Li and J. Wu, J. Mater. Chem. A, 2015, 3, 5805 RSC.
- W. Dong, W. Hu, T. J. Frankcombe, D. Chen, C. Zhou, Z. Fu, L. Candido, G. Hai, H. Chen, Y. Li, R. L. Withers and Y. Liu, J. Mater. Chem. A, 2017, 5, 5436 RSC.
- P. Ren, J. He, X. Wang, M. Sun, H. Zhang and G. Zhao, Scr. Mater., 2018, 146, 110–114 CrossRef CAS.
- L. Li, Z. Cai, N. Zhang and J. Li, Ceram. Int., 2017, 43, 7271 CrossRef CAS.
- L. Li, R. Wang, S. Yu, Z. Sun and H. Zheng, Mater. Lett., 2018, 220, 119–121 CrossRef CAS.
- Y. Meng, K. Liu, X. Zhang, X. Lei, J. Chen, Z. Yang, B. Peng, C. Long, L. Liu and C. Li, J. Am. Ceram. Soc., 2022, 105, 5725–5737 CrossRef CAS.
- Y. Qiao, J. Li, W. Li, C. Gao, H. Ding, W. Cao and X. Tan, Ceram. Int., 2024, 50, 6358–6364 CrossRef CAS.
- Y. Qiao, W. Li, Y. Zhang, L. Jing, C. Gao, W. Cao, D. Xu and W. Fei, J. Mater. Sci. Technol., 2020, 44, 54–61 CrossRef CAS.
- X. Guo, Y. Pu, W. Wang, L. Zhang, J. Ji, R. Shi, Y. Shi, M. Yang and J. Li, ACS Sustain. Chem. Eng., 2019, 7, 13041–13052 CrossRef CAS.
- X. Zhang, J. Zhang, Y. Zhou, Z. Yue and L. Li, J. Alloys Compd., 2018, 767, 424–431 CrossRef CAS.
- S. Tangwancharoen, P. Thongbai, T. Yamwong and S. Maensiri, Mater. Chem. Phys., 2009, 115, 585–589 CrossRef CAS.
- Y. Li, L. Fang, L. Liu, Y. Huang and C. Hu, Mater. Sci. Eng. B, 2012, 177, 673–677 CrossRef CAS.
- V. S. Puli, C. Orozco, R. Picchini and C. V. Ramana, Mater. Chem. Phys., 2016, 184, 82–90 CrossRef CAS.
- D. Huang, Z. Liu, Y. Li and Y. Liu, J. Alloys Compd., 2017, 698, 200–206 CrossRef CAS.
- H. V. S. Pessoni, P. Banerjee and A. Franco, Phys. Chem. Chem. Phys., 2018, 20, 28712–28719 RSC.
- Y. Wu, J. Li, H. Bai, S. He, Y. Hong, K. Shi and Z. Zhou, Phys. Status Solidi RRL, 2018, 12, 1–5 Search PubMed.
- D. Huang, W. L. Li, Z. F. Liu, Y. X. Li, C. Ton-That, J. Cheng, W. C. H. Choy and F. C. C. Ling, J. Mater. Chem. A, 2020, 8, 4764–4774 RSC.
- L. Li, J. Xie, M. Wang and K. Zhang, Ceram. Int., 2021, 47, 10072–10078 CrossRef CAS.
- Y. Wu, J. Miao, Z. Liu and Y. Li, Ceram. Int., 2015, 41, S846–S850 CrossRef CAS.
- J. Sun, S. T. Wang, L. Tong, Q. J. Li, Y. Yu, Y. D. Li, S. G. Huang, Y. M. Guo and C. C. Wang, Mater. Lett., 2017, 200, 51–54 CrossRef CAS.
- C. Huang, Y. Meng, C. Li, D. Wang, X. Chen, L. Sun, B. Peng, X. Lei, Y. Shen and L. Liu, J. Mater. Sci.: Mater. Electron., 2023, 34, 2231 CrossRef CAS.
- R. Zuo, L. Feng, Y. Yan, B. Chen and G. Cao, Solid State Commun., 2006, 138, 91–94 CrossRef CAS.
- J. Fan, G. He, Z. Long and Z. Hu, J. Am. Ceram. Soc., 2024, 107, 4854–4863 CrossRef CAS.
- W. Wang, L. Li, T. Lu, R. Wang, N. Zhang, W. Luo and B. Zhang, J. Eur. Ceram. Soc., 2019, 39, 4168–4176 CrossRef CAS.
- M. Frey and D. Payne, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 3158–3168 CrossRef CAS PubMed.
- M. Yashima, T. Hoshina, D. Ishimura, S. Kobayashi, W. Nakamura, T. Tsurumi and S. Wada, J. Appl. Phys., 2005, 98, 014313 CrossRef.
- D. F. K. Hennings, C. Metzmacher and B. S. Schreinemacher, J. Am. Ceram. Soc., 2001, 84, 179–182 CrossRef CAS.
- H. W. Lee, S. Moon, C. H. Choi and D. K. Kim, J. Am. Ceram. Soc., 2012, 95, 2429–2434 CrossRef CAS.
- S. Moon, H. W. Lee, C. H. Choi and D. K. Kim, J. Am. Ceram. Soc., 2012, 95, 2248–2253 CrossRef CAS.
- C. Baek, J. E. Wang, S. Moon, C. H. Choi and D. K. Kim, J. Am. Ceram. Soc., 2016, 99, 3802–3808 CrossRef CAS.
- D. H. Yoon, J. Ceram. Process. Res., 2006, 7, 343–354 Search PubMed.
- A. Testino, M. T. Buscaglia, V. Buscaglia, M. Viviani, C. Bottino and P. Nanni, Chem. Mater., 2004, 16, 1536–1543 CrossRef CAS.
- D. Hennings and S. Schreinemacher, J. Eur. Ceram. Soc., 1992, 9, 41–46 CrossRef CAS.
- C. Zhu, Q. Zhao, Z. Cai, L. Guo, L. Li and X. Wang, J. Alloys Compd., 2020, 829, 154496 CrossRef CAS.
- T. Noma, S. Wada, M. Yano and T. Suzuki, J. Appl. Phys., 1996, 80, 5223–5233 CrossRef CAS.
- S. Wada, T. Suzuki and T. Noma, Jpn. J. Appl. Phys., 1995, 34, 5368–5379 CrossRef CAS.
- J. Adam, G. Klein and T. Lehnert, J. Am. Ceram. Soc., 2013, 96, 2987–2993 CrossRef CAS.
- S. Liu, Q. Xie, L. Zhang, Y. Zhao, X. Wang, P. Mao, J. Wang and X. Lou, J. Eur. Ceram. Soc., 2018, 38, 4664–4669 CrossRef CAS.
- C. Pithan, D. Hennings and R. Waser, Int. J. Appl. Ceram. Technol., 2005, 2, 1–14 CrossRef CAS.
- J. W. Arblaster, Platin. Met. Rev., 1997, 41, 12–21 CrossRef CAS.
- Z. Meić, M. Žinić, S. Miljanić, L. Frkanec and T. Biljan, J. Raman Spectrosc., 2007, 38, 1538–1553 CrossRef.
- F. A. Rabuffetti and R. L. Brutchey, J. Am. Chem. Soc., 2012, 134, 9475–9487 CrossRef CAS.
- J. Pokorńy, U. M. Pasha, L. Ben, O. P. Thakur, D. C. Sinclair and I. M. Reaney, J. Appl. Phys., 2011, 109, 1–5 CrossRef.
- H. Zheng, I. M. Reaney, G. D. C. C. de Györgyfalva, R. Ubic, J. Yarwood, M. P. Seabra and V. M. Ferreira, J. Mater. Res., 2004, 19, 488–495 CrossRef CAS.
- V. K. Veerapandiyan, S. Khosravi H, G. Canu, A. Feteira, V. Buscaglia, K. Reichmann and M. Deluca, J. Eur. Ceram. Soc., 2020, 40, 4684–4688 CrossRef CAS.
- Y. Wang, K. Miao, W. Wang and Y. Qin, J. Eur. Ceram. Soc., 2017, 37, 2385–2390 CrossRef.
- S. Guillemet-Fritsch, Z. Valdez-Nava, C. Tenailleau, T. Lebey, B. Durand and J. Y. Chane-Ching, Adv. Mater., 2008, 20, 551–555 CrossRef CAS.
- J. Fan, S. Leng, Z. Cao, W. He, Y. Gao, J. Liu and G. Li, Ceram. Int., 2019, 45, 1001–1010 CrossRef CAS.
- T. Nachaithong, P. Kidkhunthod, P. Thongbai and S. Maensiri, J. Am. Ceram. Soc., 2017, 100, 1452–1459 CrossRef CAS.
- H. Han, C. Davis and J. C. Nino, J. Phys. Chem. C, 2014, 118, 9137–9142 CrossRef CAS.
- S. Sulekar, J. H. Kim, H. Han, P. Dufour, C. Tenailleau, J. C. Nino, E. Cordoncillo, H. Beltran-Mir, S. Dupuis and S. Guillemet-Fritsch, J. Mater. Sci., 2016, 51, 7440–7450 CrossRef CAS.
- H. Han, C. Voisin, S. Guillemet-Fritsch, P. Dufour, C. Tenailleau, C. Turner and J. C. Nino, J. Appl. Phys., 2013, 113, 024102 CrossRef.
- S. Yan, C. Mao, G. Wang, C. Yao, F. Cao, X. Dong and X. Meng, Mater. Res. Express, 2016, 3, 0–9 CAS.
- B. Luo, X. Wang, E. Tian, H. Song, Q. Zhao, Z. Cai, W. Feng and L. Li, J. Eur. Ceram. Soc., 2018, 38, 1562–1568 CrossRef CAS.
- K. Xu, G. Zhu, H. Xu, Y. Zhao, K. Jiang, X. Zhang, H. Yin, M. Shangguan, L. Wan and T. Huang, Appl. Phys. A: Mater. Sci. Process., 2022, 128, 1–10 CrossRef.
- B. Wang, Y. Pu, Y. Shi, X. Guo, L. Zhang, L. Chang, J. Li, R. Li, J. Ji and T. Wei, J. Am. Ceram. Soc., 2020, 103, 6811–6821 CrossRef CAS.
- Q. Sun, Q. Gu, K. Zhu, R. Jin, J. Liu, J. Wang and J. Qiu, Sci. Rep., 2017, 7, 1–8 CrossRef.
- M. D. Fontana, N. Kokanyan and T. H. Kauffmann, J. Phys. Condens. Matter, 2020, 32, 285403 CrossRef CAS PubMed.
- T. Sakashita, H. Chazono and G. Pezzotti, J. Appl. Phys., 2007, 102, 124106 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ta04895d |
| This journal is © The Royal Society of Chemistry 2025 |