Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Pseudo-lithium vacancies in hydrogen rich Li3OCl†
Benjamin A. D.
Williamson
 *,
Kristoffer
Eggestad
*,
Kristoffer
Eggestad
 and
Sverre M.
Selbach
and
Sverre M.
Selbach

Department of Materials Science and Engineering, NTNU Norwegian University of Science and Technology, Trondheim, Norway. E-mail: benjamin.williamson@ntnu.no
First published on 18th February 2025
Abstract
The antiperovskite Li3OCl is reported as a superionic conductor, however, reproducibility has been poor due to its hygroscopic nature, suggesting that reports are in fact on Li3−xOHxCl. Most experimental and computational studies in the literature focus on pure Li3OCl however, and do not take into account the role of hydrogen in the material. Here, we develop a full defect model of H-doped Li3OCl, showing that the nominal Schottky disorder diminishes with hydrogen incorporation. Additionally, H helps to facilitate Li-ion mobility in Li3OCl by firstly introducing rotatable OH species as well as forming HLi which relaxes off site to form what we define as a “pseudo-VLi” enhancing the ionic conductivity in line with experimentally observed values. Intentional hydrogen doping of hygroscopic materials constitute an underexplored strategy for enhancing ionic transport properties.
1. Introduction
Electrochemical energy storage has become an increasingly vital component of modern society ever present in both portable electronics and transportation, as well as becoming important in the realisation of a full renewable energy grid. The dominating type of rechargeable battery rely on Li-ions which intercalate into an anode upon charging, typically graphitic,1 migrate back to a cathode (for example: LiCoO2,2 LiFePO4 (ref. 3 and 4) (LFP), or LiNixMnyCo1−x−yO2 (NMC)5) upon discharging, and a liquid/polymer electrolyte such as LiTFSI.6 These electrolytes typically possess desirable conductivities7 of the order of 10−2 S cm−1. However, they present significant safety risks due to their flammable nature. Further disadvantages are formation of potentially rate limiting solid-electrolyte interphases, simultaneous anion diffusion,8 lower operating voltages,9 and (dendrite formation causing incompatibility with Li-metal anodes with ∼10× the capacity of current graphitic anodes10).11 The use of a solid-state electrolyte (SSE) is therefore desirable as it fixes many of these problems simultaneously.Current solid electrolyte materials include e.g. the Li-rich garnets such as Li7La3Zr2O12 (LLZO),12–14 the Argyrodites Li6MS5X (M = S, Se, X = Cl, Br, I),15–17 Li10GeP2S12 (LGPS),18–20 as well as LixPyOzN (LiPON).21,22 Unfortunately, these materials possess a tradeoff between stability and conductivity. LiPON, for example, possesses excellent electrochemical stability and resistance towards dendrite formation,23 (yet poor/mediocre conductivities of the order of 10−6 S cm−1 are typically observed21), making it suitable for small scale devices or as a protective layer in conventional lithium battery cells.24 Whilst a lower conductivity would intuitively be expected in the solid state compared to the liquid state, competitively high conductivities (>10−3 S cm−1) are observed for some solid state materials.25 However, some expected issues do arise with respect to stability and synthesis of these materials.8,26
Within the past decade, Li-rich anti-perovskites, such as Li3OCl have gained a lot of interest due to their initial high reported ionic conductivities at ambient conditions (10−3 S cm−1) as reported by Zhao and Daemen.27 Subsequent experimental and density functional theory (DFT) studies, however, have placed the conductivity to be much lower with a higher migration barrier (∼0.6 eV and 10−6 S cm−1 (ref. 28 and 29)). Both nominally Li3OCl and Li3OBr have been shown to possess wide electrochemical stability windows even if they are metastable and not in a global ground state. This has been attributed to not possessing additional cations that may be reduced by Li-metal, yet may form Li2O and LiCl/Br at the anode.30 Additional antiperovskite ionic conductor compositions have been reported including, Na3OCl/Br,31,32 Na3SI33 and Na3HS34 to name a few.
Despite promising electrochemical stability and sometimes promising ionic conductivities, Li3OCl is a hygroscopic and air sensitive material.29 This has raised numerous questions on the legitimacy of Li3OCl as the true composition, with consensus trending towards the fact that Li3OCl being a hydrated form (Li3−xOHxCl) or even Li2OHCl.29,35 In a critical review by Rettenwander and coworkers,35 they point out the fact that typical syntheses of Li3OCl uses LiH, H2O, or LiOH within the synthesis, thus it is inevitable that H/OH will be present in “Li3OCl”. All may not be lost, however, after several experimental and computational studies show that a hydrated composition may be to the advantage of the ionic conductivity, as rotatable OH units enhance the mobility of Li-species in the bulk and at grain boundaries.36–38 Ultimately this may come at a cost, as the conductivity has been shown to be highly correlated with the proton and lithium vacancy concentration,36 and controlling the amount of hydrogen in a hygroscopic material is difficult at best.35 Whilst computational studies exist on the intrinsic defects of Li3OCl,30,33,39–42 including a full defect model by Squires et al.,43 hydrogen has not previously been included in these. Squires et al. show that purely undoped Li3OCl is an extended Schottky disordered material ([VLi + VCl + OCl]), similar to what is seen in previously calculated models [VLi + VCl],43 which Mouta et al. showed to enhance the ionic conductivity of Li3OCl.42 Squires also showed that undoped Li3OCl could expect equilibrium ionic conductivities of ∼10−10 S cm−1, significantly below experimental observations.29
Here, we present full intrinsic and extrinsic (H) defect models for metastable Li3OCl, calculated with the hybrid functional HSE06. Using the quasi-harmonic approximation (QHA), the chemical potential stability region of Li3OCl is shown to exist from ∼750 K and shows that when undoped, Li3OCl displays two types of Schottky disorder: full disorder under Li-rich conditions, and Li2O disorder under Li-poor conditions. Hydrogen is shown to incorporate very easily, in line with the hygroscopic nature of Li3OCl, and suppresses these Schottky defect clusters. Additionally, lithium substituted hydrogen is likely to relaxe offsite to form OH groups and induce a “pseudo-VLi”. Accounting for this defect in a conductivity model reproduces experimentally observed values.
2. Computational methods
Ab initio calculations were performed using DFT implemented within the plane-wave periodic code, VASP.44–47 The projector-augmented wave method (PAW)48,49 was used to describe the interaction between the core electrons and the valence electrons. All electrons were treated explicitly for Li, while for O, Cl, and H the standard pseudopotentials supplied with VASP were used. The hybrid functional HSE06 (Heyd–Scuseria–Ernzerhof)50 was used in order to address the self-interaction error thus allowing for an accurate description of the band gap and electronic properties of Li3OCl.Hybrid functionals have consistently displayed improved geometry and electronic properties of semiconductors.13,51–53 The band gap calculated herein is ∼6.6 eV which aligns well with previous HSE06 studies (∼6.4–6.6 eV).43,53,54 To date, however, there is no experimental band gap with which to compare.
Determination of the bulk electronic and structural properties were performed on the cubic form (5 atom primitive cell) of Li3OCl (space group: Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m). To this end, a full geometric relaxation using a Γ-centred k-point grid of 6 × 6 × 6 and a plane wave energy cutoff of 500 eV was carried until the largest force on any atom was below the force criterion of 0.01 eV Å−1. The intrinsic defects were simulated using a 3 × 3 × 3 supercell expansion of the conventional cell containing 135 atoms. Spin-polarised geometry relaxations (to the same convergence criteria as the conventional cell) of each defect cell and its respective charge states were performed using a Γ-centred 2 × 2 × 2 k-point mesh and 500 eV plane wave energy cutoff. A Γ-centred k-point 2 × 2 × 2 mesh was chosen in order to capture the M-point in the 1st Brillouin zone, which is the valence band maximum (VBM) and conduction band minimum (CBM) (ESI Fig. S1†), which was not captured in a Monkhorst–Pack 2 × 2 × 2 grid. The bulk electronic and structural properties are given in the ESI (Sections ESI 2 and ESI 1).†
m). To this end, a full geometric relaxation using a Γ-centred k-point grid of 6 × 6 × 6 and a plane wave energy cutoff of 500 eV was carried until the largest force on any atom was below the force criterion of 0.01 eV Å−1. The intrinsic defects were simulated using a 3 × 3 × 3 supercell expansion of the conventional cell containing 135 atoms. Spin-polarised geometry relaxations (to the same convergence criteria as the conventional cell) of each defect cell and its respective charge states were performed using a Γ-centred 2 × 2 × 2 k-point mesh and 500 eV plane wave energy cutoff. A Γ-centred k-point 2 × 2 × 2 mesh was chosen in order to capture the M-point in the 1st Brillouin zone, which is the valence band maximum (VBM) and conduction band minimum (CBM) (ESI Fig. S1†), which was not captured in a Monkhorst–Pack 2 × 2 × 2 grid. The bulk electronic and structural properties are given in the ESI (Sections ESI 2 and ESI 1).†
2.1. Defect formalism
Eqn (1) describes the enthalpy of formation of a defect in charge state q: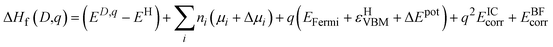 | (1) |
Where EH is the total energy of the host supercell, ED,q is the total energy of the defective supercell in charge state q. Chemical potentials denoted by μi of each atomic species, i (Li(s), Cl2(g), O2(g), H2(g)), are added to or removed from an external reservoir55 by an amount n. In this work, the Fermi level ranges from the valence band maximum (VBM) at 0 eV (where εHVBM denotes the eigenvalue of the VBM in the host material) to the conduction band minimum (CBM) which occurs at 6.38 eV. The potential of the defect supercell bar the immediate vicinity of the defect is averaged and aligned to the host supercell and is described by ΔEpot.56
To account for the finite size effects of the defect supercells, two post-processing corrections are applied, EICcorr and EBFcorr. The first correction term corresponds to the image-charge correction which minimises the long ranged nature of the Coulomb interaction57,58 of the charged defect and its periodic images. The implementation used herein uses a formalism based upon the Lany and Zunger correction56 with a ‘non-cubic’ adaptation as implemented by Hine and Murphy.58,59 Lastly a band-filling correction is applied to shallow and resonant defects to account for the high carrier concentrations present in supercell calculations so as to regain the ‘dilute limit’.56,60
2.2. Equilibrium concentrations
Equilibrium concentrations of defects in both Li3OCl can be calculated self-consistently as implemented in the code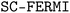 .61 By determining the Fermi energy self-consistently the concentration of a defect D in charge state q can be evaluated through:
.61 By determining the Fermi energy self-consistently the concentration of a defect D in charge state q can be evaluated through: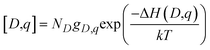 | (2) |
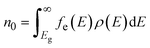 | (3) |
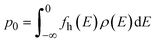 | (4) |
where ρ(E) is the density of states (DOS), Eg is the band gap and fe is the Fermi–Dirac distribution function given by 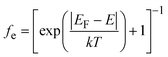 and fh = 1 − fe(E). This approach has successful been applied to Li7La3Zr2O12 (ref. 13) (LLZO) and elsewhere.51,62
and fh = 1 − fe(E). This approach has successful been applied to Li7La3Zr2O12 (ref. 13) (LLZO) and elsewhere.51,62
3. Results
3.1. Defining a chemical potential stability region for metastable Li3OCl
Determination of the formation energies of defects in materials requires knowledge of the individual elemental chemical potentials (eqn (1)) which are typically constrained by the thermodynamic stability of the host material relative to competing phases. As Li3OCl is metastable and not globally stable, calculating the chemical potentials requires either prior experimental knowledge about phase stability,43 or calculation of host and competing phases at finite temperatures.63 As the structure and composition of Li3OCl is not widely acknowledged, the latter is chosen in this instance, however it is important to note that studies exist showing Li3OCl to possess kinetic stability relative to LiCl and Li2O,30,64 proposed to be due to the sluggish anion transport in Li3OCl.65 In this study, the chemical potential limits analysis program (CPLAP66) is combined with the quasi-harmonic approximation (QHA) to determine the temperature dependent stability region of Li3OCl and thus unveil suitable chemical potentials without a priori knowledge. This approach, whilst not widely used due to its increased computational expense, has shown recent success in determining the stability of Na2Ti3O7.63 From our results, Li3OCl becomes the dominant phase at 750 K/476.85 °C (HSE06 functional), which agrees well with the expected experimental synthesis temperature from nominally non-hydrogen containing precursors, Li2O and LiCl at (773 K/500 °C):35 | (5) |
Typically, however, Li3OCl is often formed via a solid state synthesis from a combination of LiCl and LiOH at lower temperatures:27
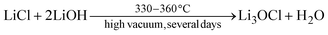 | (6) |
An overview of the common synthesis routes is given in ESI Section 6† together with their calculated Gibbs free energy of reaction (ΔGreac). Rettenwander and coworkers35 showed that LiCl is still present after following the synthesis outlined in eqn (6) suggesting that Li3OCl is Cl-poor. This indicates that OH− is likely present in the samples due to an excess of LiOH.35
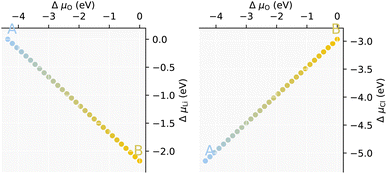
Nevertheless, a calculated stability region can be formed and is given in Fig. 1. What is seen is a very narrow region (straight line) between Li-rich/anion-poor (μLi = −2.17 eV, μO = 0 eV, μCl = −2.97 eV) designated point A, and Li-poor/anion-rich ((μLi = 0 eV, μO = −4.35 eV, μCl = −5.14 eV)) designated point B. Whilst the results obtained from this method are somewhat strict, a larger region may be realised due to anion partial pressures. Anhydrous Li3OCl can therefore be said to be stable over a more modest range of μLi than the larger μO and μCl, anion deficiency or substitution in Li3OCl is much more tolerated compared to Li deficiency, which could lead to thermodynamic instability towards other phases.
At point A, Li3OCl is calculated to be in equilibrium with Li2O, Li, and LiCl. At point B, Li3OCl is in equilibrium with LiCl, Li2O, and O2.
3.2. Defect thermodynamics
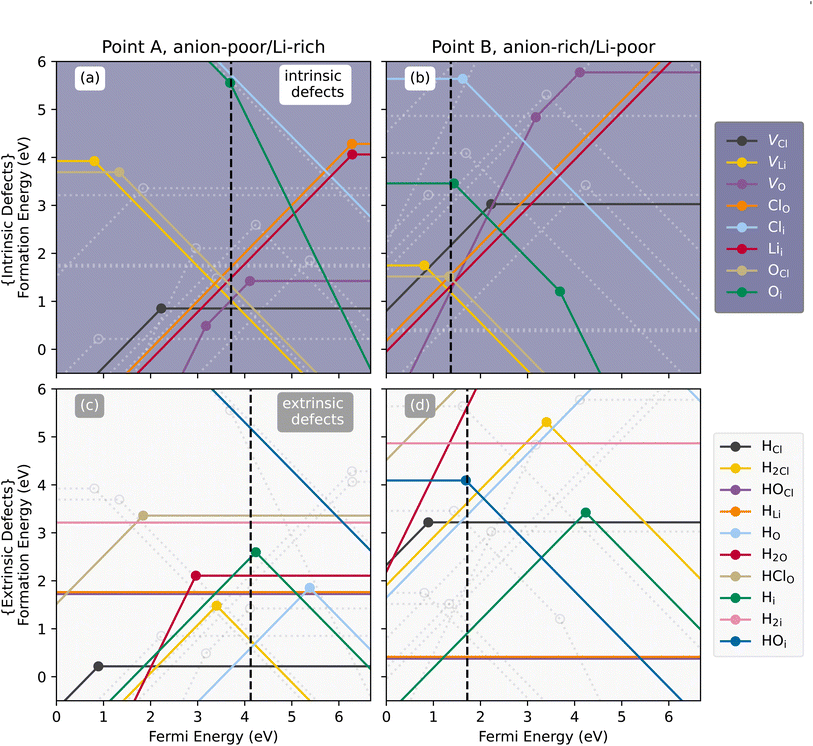
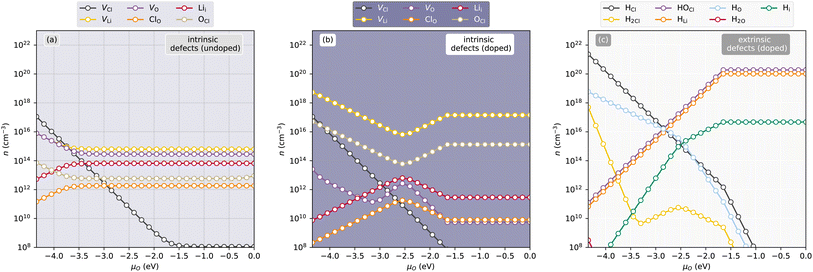
The thermodynamic transition levels as calculated with the HSE06 functional for Li3OCl are plotted in Fig. 2 showing both intrinsic (upper panels (a) and (b)) and extrinsic hydrogen defects (lower panels (c) and (d)) at anion-poor/Li-rich conditions (point A, in Fig. 1) and anion-rich/Li-poor conditions (point B in Fig. 1) respectively. Additionally, the equilibrium concentrations of the dominant defects (≥1 × 108 cm−3) are given in Fig. 3 as a function of oxygen chemical potential (μO) as one travels from point A to point B. Even though hydrogen incorporation is typically unavoidable in Li3OCl we will still refer to it as “doping” for the case of simplicity in this work.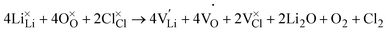 | (7) |
Partial charge densities are provided in ESI Fig. S5–S7† for VLi, VO, and VCl and their corresponding charge states, respectively. What results are localised electrons within the anion vacancies and a localised hole on an adjacent O 2p orbital for VLi. Such localizations induce slight local structure distortions around the defect, which can enhance the mobility of Li.12 As observed in the undoped concentrations in Fig. 3(a), [VCl] decreases rapidly between point A (anion poor) and point B (anion rich), and is not wholly influenced by H. This is in contrast to what is seen in Squires et al. where they show that the LiCl Schottky defect (VLi + VCl) is predicted.
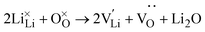 | (8) |
Counterintuitively, equilibrium [VLi] under Li-rich conditions are higher than those under Li-poor conditions (∼8 × 1015 cm−3vs. ∼6 × 1014 cm−3) despite the existence of neutral VCl under Li-rich conditions. Incidentally, interstitial Li (Lii) will not be the dominant charge carrier over the entirety of the chemical potential range, which is echoed by previous literature,29 despite its lower migration barrier.30 ESI Fig. S8† shows the partial charge density of Lii showing distinct local distortion due to sterics, but delocalised electron density allowing for reduced coulombic repulsion which likely supports the lower migration barrier. Despite this, it is expected that Lii will be present, albeit in small quantities in undoped Li3OCl (∼7 × 1013 cm−3) in a combined Schottky–Frenkel defect:
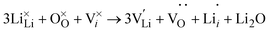 | (9) |
Upon H-doping, however, Lii and VO become suppressed as evident in Fig. 3(b) severely reducing both Li2O Schottky and Schottky–Frenkel disorder under Li-poor conditions in Li3OCl.
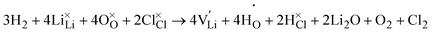 | (10) |
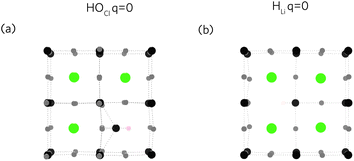
Fig. 4(a) and (b) show the relaxed defect supercells of HOCl (at q = 0), and HLi (at q = 0) respectively. HOCl, warps the structure shifting adjacent Li away from its preferred site (Wyckoff: 3c) towards the neutral cluster. As this defect is nominally neutral, the displacement arises due to the smaller OH− radii (110 pm) compared to Cl− radii (181 pm) and may aid in improving Li-ion transport by increasing “accessible space” and weakening the Li–O bonds. In HLi (Fig. 4(b)), H shifts off its Li site (3c) towards an adjacent O forming a neutral OH. This defect can therefore be seen as a “pseudo-VLi” or as suggested by Song et al.67 a Frenkel-type defect as any moving Li into this space technically becomes an interstitial. Experimentally, Schwering et al.68 suggested HLi as the dominant defect, remarking also that HLi provides rotatable OH that facilitates Li transport. Work carried out by Eilbracht et al.69 using single crystal data on Li2OHCl also suggest Li site occupation. Similar evaluations of the role of rotatable OH groups have been suggested in the literature.36,67,70 Dawson et al.36 using molecular dynamics simulations (MD) combined with 2H NMR spectroscopy, observe that both highly rotatable OH groups exist alongside fixed OH groups. Further investigation shows that OH rotations are more free when O is coordinated to fewer lithiums.
4. Discussion
In this study, we have performed hybrid functional charged defect calculations on H-doped Li3OCl. This is in order to determine the influence of hydrogen on intrinsic defect chemistry of Li3OCl and its influence on structure and ionic conductivity. In this model we have considered all vacancies, interstitials, antisites and varying H-related extrinsic species such as singular H, H2, OH and HCl. A self-consistent model such as this is highly important for getting a holistic overview of the mechanisms for ionic conductivity as well unravelling the thermodynamics of Li3OCl as given in experimental and computational studies in previous literature.30,33,36,39–42,67,70Taking undoped Li3OCl, we find that across the range of synthesis conditions, (Li-poor to Li-rich), VLi is the dominant charge carrying defect whilst Lii exists in much lower concentrations, thus ruling out an interstitial or interstitialcy mechanism within Li3OCl consistent with other reports,30,42,43,71 despite the lower migration energy barrier of 0.17 eV (compared to 0.34 eV for VLi).30 Under the most Li-rich/anion-poor conditions, the full Schottky defect exists, (VLi + VO + VCl), however with VCl existing in the neutral charge state. This is somewhat contrary to previous reports of Li3OCl being LiCl ([VLi + VCl]) Schottky disordered.30,40,43,72,73 It is important to note, however, that with the exception of the work in ref. 43, the other studies only consider neutral defects and assume full charge neutrality from VLi and VCl, yet we find that the positive compensating defect for VLi are oxygen vacancies (VO). This changes to a Li2O Schottky defect (VLi + VO) under Li-poor conditions. Equally, whilst antisites are expected to form in small quantities (∼1012–1013 cm−3) in undoped Li3OCl, our results do not point towards significant anion disorder.18 Consensus in the literature is that anion disorder is beneficial to increasing the conductivity of Li-ion solid electrolytes. This is attributed to significant anion disorder opening up percolating three-dimensional pathways previously inaccessible to anion ordered systems.15 In a paper by Li et al.74 they stated that due to the size mismatch between O and Cl, anion antisite defects would cause a strong structural distortion and an electrostatic penalty for mobile lithium defects thus reducing the conductivity.
The inconsistency between this work and previous calculations is likely down to both the choice of functional, as well as from the calculation of the chemical potential stability region for Li3OCl of which the defect formation energies are highly sensitive to. Hybrid functionals typically give a much better description of electron localisation for defects, as well as favourable description of the band gap of a material relative to experiment.12,52,75,76 Both of these are crucial when determining charged defect calculations in order to correctly describe the thermodynamic defect quantities of solid electrolytes.12,13,18,43 In this work, the chemical potential region was determined “temperature-dependently” through calculating the free energies of competing phases using QHA (Section 3 3.1), which has shown success previously in Na2Ti3O7.63 Confidence in this result arises from the fact that Li3OCl becomes “stable” around ∼750 K, in excellent agreement with the experimental synthesis temperature (without H) of ∼773 K.35
The unfortunate reality of Li3OCl is that it is highly unlikely to be purely Li3OCl, but a hydrated form Li3−xOHxCl.35,36 Even when attempting to create dehydrated forms of Li3OCl, Li et al.77 acknowledged that some form of OH is observable from FTIR. This work shows that hydrogen defects are omnipresent in the structure of Li3OCl and high defect concentrations of at least ≥1020 cm−3 are to be expected. Our results indicate a baseline equilibrium which is likely to be higher based on both synthesis conditions and local atmosphere indeed forming Li2OHCl. Nevertheless, our results do not rule out the formation of cubic anti-perovskite Li3OCl without forming full Li2OHCl compositions. Dawson et al. showed that hydrogen does not diffuse in Li3OCl due to the large jump distances of 3.91 Å.36
Under Li-rich conditions, it is expected that neutral HCl forms as the dominant defect which pushes EF higher in energy towards the CBM thereby reducing the formation energy of VLi within the crystal structure. Additionally in work carried out by Gao et al.,37,78 they showed that in M3HCh (M = Li, Na; Ch = S, Se, Te), that the influence of H− reduced the energy barrier of migration due to its large polarizability, thus a similar effect may be present here with HCl. At the same time, H-incorporation suppresses the Schottky disorder as seen in purely undoped Li3OCl. This is also the case under Li-poor conditions, whereby the Li2O Schottky disorder is cancelled by the neutral hydrogen defects: HLi and OHCl. HLi is seen to relax off its nominal Li site towards an adjacent oxygen forming an “OHO” which can also be seen as a “pseudo-VLi”. Work by Schwering et al.68 on Li3OCl and Eilbracht et al.69 on Li2OHCl agree with this conclusion. This “pseudo-VLi” can also be seen as a Frenkel defect, where the mobile Li becomes effectively an interstitial upon rotation of the OH species.67 Additionally, OHCl, whilst neutral, acts to distort the structure slightly due to its smaller radii compared to Cl which may also aid Li mobility.
Squires et al.43 calculated the conductivity of Li3OCl within their full defect model through:
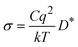 | (11) |
Fig. 5 displays the ionic conductivity as a function of μO calculated with the same strategy using our defect model for undoped and H-doped Li3OCl. Our results align well with Squires et al.43 where low conductivities of ∼10−10 S cm−1 are observed. Upon incorporation of hydrogen, the VLi conductivity increases from ∼3.75 × 10−11 S cm−1 under Li-poor conditions to ∼3.35 × 10−10 S cm−1 under Li-rich conditions. By including the “pseudo-VLi” into our model, before considering potential enhancements to the mobility due to OH rotations the ionic conductivity of H-doped Li3OCl lie in the region of ∼10−6 S cm−1 in better agreement with experiment. Work by Dawson et al.36 showed that lower concentrations of H within Li3OCl resulted in lower migration energy barriers ∼0.30 eV whilst Song et al.67 predicted values of ∼0.24/0.26 eV. Whilst OHCl has an increased Li-coordination to HLi, it is likely that OHCl may lower the barrier for migration in a similar way that Br does in Li3OCl1−nBrn.80
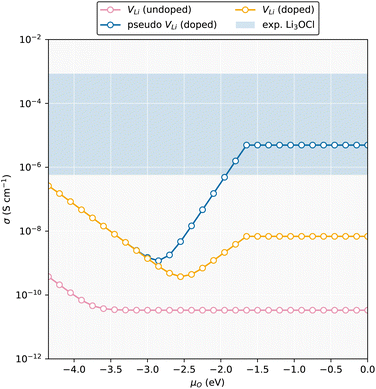 | ||
| Fig. 5 Room temperature ionic conductivity as a function of oxygen chemical potential taking into account the sum of VLi and Lii. Included is also the “pseudo” VLi whereby HLi is treated as a VLi using the same migration barrier. The blue shaded region corresponds to experimental conductivities taken from ref. 27 and 79. | ||
5. Conclusions
In this work we illustrate the need for consideration of hydrogen as both a compositional changing opportunistic dopant, as well as a strategy for enhancing the ionic conductivity, not only in Li3OCl but other hygroscopic solid electrolytes as well. A full defect model combined with a temperature dependent defined chemical potential stability region is necessary in order to outline doping strategies, killer defects, as well as structural changes in a given material. Our results highlight that, when undoped, Li3OCl can expect a degree of Schottky disorder, both full and Li2O-Schottky, in line with other computational predictions. Such a disorder, particularly anion disorder, can give rise to favourable ionic mobility of Li-species within the structure, similar to that in other solid electrolytes. Upon inevitable hydrogen incorporation, the Schottky disorder disappears, instead favouring the formation of neutral H species such as OHCl and HLi. HLi is shown to relax off site towards an adjacent oxygen forming an effective (OHO + VLi) defect pair, or a “pseudo-VLi”. Considering only purely VLi results in low ionic conductivities, however, upon consideration of a “pseudo-VLi”, our calculated ionic conductivities are more in line with experimentally observed values. Whilst Li3OCl remains a controversial and challenging material, our results show that H may be a source of enhancement in Li3OCl, increasing both the ionic mobility due to OH rotations, as well as increasing the effective carrier concentration.Data availability
The data for this article have been included as part of the ESI.†Author contributions
BADW provided the idea for this study and performed the calculations and analysis, with help from KE. BADW wrote the manuscript, and all authors contributed to the reviewing and editing of the final manuscript and have given approval to the final version of the manuscript. SMS provided funding for this project.Conflicts of interest
There are no conflicts of interest in this work.Acknowledgements
This work was supported by the Research Council of Norway through Projects no. 275810 and 302506. Computational resources were provided by UNINETT Sigma2 through Projects NN9264K and ntnu243. B.A.D.W would like to acknowledge Nora S. Løndal and Caren R. Zeiger for useful discussions.References
- T. Kim, W. Song, D.-Y. Son, L. K. Ono and Y. Qi, J. Mater. Chem. A, 2019, 7, 2942 RSC.
- K. Mizushima, P. C. Jones, P. J. Wiseman and J. B. Goodenough, Mater. Res. Bull., 1980, 15, 783 CrossRef CAS.
- S. Geller and J. L. Durand, Acta Crystallogr., 1960, 13, 325 CrossRef CAS.
- J. Li and Z.-F. Ma, Chem, 2019, 5, 3 CAS.
- H.-J. Noh, S. Youn, C. S. Yoon and Y.-K. Sun, J. Power Sources, 2013, 233, 121 CrossRef CAS.
- Z. Huang, Z. Xiao, R. Jin, Z. Li, C. Shu, R. Shi, X. Wang, Z. Tang, W. Tang and Y. Wu, Energy Environ. Sci., 2024, 17, 5365 RSC.
- D. Lu, Y. Shao, T. Lozano, W. D. Bennett, G. L. Graff, B. Polzin, J. Zhang, M. H. Engelhard, N. T. Saenz, W. A. Henderson, P. Bhattacharya, J. Liu and J. Xiao, Adv. Energy Mater., 2015, 5, 1400993 CrossRef.
- J. Janek and W. G. Zeier, Nat. Energy, 2016, 1, 1 Search PubMed.
- X. Fan and C. Wang, Chem. Soc. Rev., 2021, 50, 10486 RSC.
- S. S. Park, S. A. Han, R. Chaudhary, J. H. Suh, J. Moon, M.-S. Park and J. H. Kim, Adv. Energy Sustainability Res., 2023, 4, 2300074 CrossRef CAS.
- I. T. Røe, S. M. Selbach and S. K. Schnell, J. Phys. Chem. Lett., 2020, 11, 2891 CrossRef PubMed.
- K. Eggestad, S. M. Selbach and B. A. D. Williamson, J. Mater. Chem. A, 2024, 12, 15666–15675 RSC.
- A. G. Squires, D. O. Scanlon and B. J. Morgan, Chem. Mater., 2020, 32, 1876 CrossRef CAS.
- A. G. Squires, D. W. Davies, S. Kim, D. O. Scanlon, A. Walsh and B. J. Morgan, Phys. Rev. Mater., 2022, 6, 085401 CrossRef CAS.
- B. J. Morgan, Chem. Mater., 2021, 33, 2004 CrossRef CAS PubMed.
- M. A. Kraft, S. P. Culver, M. Calderon, F. Böcher, T. Krauskopf, A. Senyshyn, C. Dietrich, A. Zevalkink, J. Janek and W. G. Zeier, J. Am. Chem. Soc., 2017, 139, 10909 CrossRef CAS PubMed.
- C. Yu, F. Zhao, J. Luo, L. Zhang and X. Sun, Nano Energy, 2021, 83, 105858 CrossRef CAS.
- P. Gorai, H. Long, E. Jones, S. Santhanagopalan and V. Stevanović, J. Mater. Chem. A, 2020, 8, 3851 RSC.
- S. P. Ong, Y. Mo, W. D. Richards, L. Miara, H. S. Lee and G. Ceder, Energy Environ. Sci., 2012, 6, 148 RSC.
- N. Kamaya, K. Homma, Y. Yamakawa, M. Hirayama, R. Kanno, M. Yonemura, T. Kamiyama, Y. Kato, S. Hama, K. Kawamoto and A. Mitsui, Nat. Mater., 2011, 10, 682 CrossRef CAS PubMed.
- V. Lacivita, A. S. Westover, A. Kercher, N. D. Phillip, G. Yang, G. Veith, G. Ceder and N. J. Dudney, J. Am. Chem. Soc., 2018, 140, 11029 CrossRef CAS PubMed.
- P. López-Aranguren, M. Reynaud, P. Głuchowski, A. Bustinza, M. Galceran, J. M. López del Amo, M. Armand and M. Casas-Cabanas, ACS Energy Lett., 2021, 6, 445 CrossRef.
- F. Han, A. S. Westover, J. Yue, X. Fan, F. Wang, M. Chi, D. N. Leonard, N. J. Dudney, H. Wang and C. Wang, Nat. Energy, 2019, 4, 187 CrossRef CAS.
- S. Nowak, F. Berkemeier and G. Schmitz, J. Power Sources, 2015, 275, 144 CrossRef CAS.
- Z. Zhang, Y. Shao, B. Lotsch, Y.-S. Hu, H. Li, J. Janek, L. F. Nazar, C.-W. Nan, J. Maier, M. Armand and L. Chen, Energy Environ. Sci., 2018, 11, 1945 RSC.
- S. Zhang, J. Ma, S. Dong and G. Cui, Electrochem. Energy Rev., 2023, 6, 4 CrossRef.
- Y. Zhao and L. L. Daemen, J. Am. Chem. Soc., 2012, 134, 15042 CrossRef CAS PubMed.
- X. Lü, J. W. Howard, A. Chen, J. Zhu, S. Li, G. Wu, P. Dowden, H. Xu, Y. Zhao and Q. Jia, Adv. Sci., 2016, 3, 1500359 CrossRef PubMed.
- J. A. Dawson, T. Famprikis and K. E. Johnston, J. Mater. Chem. A, 2021, 9, 18746 RSC.
- A. Emly, E. Kioupakis and A. Van der Ven, Chem. Mater., 2013, 25, 4663 CrossRef CAS.
- T. H. Wan, Z. Lu and F. Ciucci, J. Power Sources, 2018, 390, 61 CrossRef CAS.
- K. Hippler, S. Sitta, P. Vogt and H. Sabrowsky, Acta Crystallogr., Sect. C, 1990, 46, 736 CrossRef.
- Z. Wang and G. Shao, J. Mater. Chem. A, 2017, 5, 21846 RSC.
- S. Gao, T. Broux, S. Fujii, C. Tassel, K. Yamamoto, Y. Xiao, I. Oikawa, H. Takamura, H. Ubukata, Y. Watanabe, K. Fujii, M. Yashima, A. Kuwabara, Y. Uchimoto and H. Kageyama, Nat. Commun., 2021, 12, 201 CrossRef CAS PubMed.
- I. Hanghofer, G. J. Redhammer, S. Rohde, I. Hanzu, A. Senyshyn, H. M. R. Wilkening and D. Rettenwander, Chem. Mater., 2018, 30, 8134 CrossRef CAS.
- J. A. Dawson, T. S. Attari, H. Chen, S. P. Emge, K. E. Johnston and M. S. Islam, Energy Environ. Sci., 2018, 11, 2993 RSC.
- A. C. C. Dutra and J. A. Dawson, J. Phys. Chem. C, 2023, 127, 18256 CrossRef CAS PubMed.
- J. A. Quirk and J. A. Dawson, Adv. Energy Mater., 2023, 13, 2301114 CrossRef CAS.
- Z. Lu, C. Chen, Z. M. Baiyee, X. Chen, C. Niu and F. Ciucci, Phys. Chem. Chem. Phys., 2015, 17, 32547 RSC.
- A. Baktash, B. Demir, Q. Yuan and D. J. Searles, Energy Storage Mater., 2021, 41, 614 CrossRef.
- Z. Zhang, Z. Ma and Y. Pei, Phys. Chem. Chem. Phys., 2023, 25, 13297 RSC.
- R. Mouta, M. A. B. Melo, E. M. Diniz and C. W. A. Paschoal, Chem. Mater., 2014, 26, 7137 CrossRef CAS.
- A. G. Squires, J. M. Dean and B. J. Morgan, Chemrxiv, 2021, preprint, DOI:10.26434/chemrxiv-2021-hzrls.
- G. Kresse and J. Hafner, Phys. Rev. B:Condens. Matter Mater. Phys., 1994, 49, 14251 CrossRef CAS PubMed.
- G. Kresse and J. Hafner, Phys. Rev. B:Condens. Matter Mater. Phys., 1993, 47, 558 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B:Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS PubMed.
- P. E. Blöchl, Phys. Rev. B:Condens. Matter Mater. Phys., 1994, 50, 17953 CrossRef PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B:Condens. Matter Mater. Phys., 1999, 59, 1758 CrossRef CAS.
- A. V. Krukau, O. A. Vydrov, A. F. Izmaylov and G. E. Scuseria, J. Chem. Phys., 2006, 125, 224106 CrossRef PubMed.
- B. A. D. Williamson, J. Buckeridge, N. P. Chadwick, S. Sathasivam, C. J. Carmalt, I. P. Parkin and D. O. Scanlon, Chem. Mater., 2019, 31, 2577 CrossRef CAS PubMed.
- B. A. D. Williamson, T. J. Featherstone, S. S. Sathasivam, J. E. N. Swallow, H. Shiel, L. A. H. Jones, M. J. Smiles, A. Regoutz, T.-L. Lee, X. Xia, C. Blackman, P. K. Thakur, C. J. Carmalt, I. P. Parkin, T. D. Veal and D. O. Scanlon, Chem. Mater., 2020, 32, 1964 CrossRef CAS PubMed.
- M. Wu, B. Xu, X. Lei, K. Huang and C. Ouyang, J. Mater. Chem. A, 2018, 6, 1150 RSC.
- Y. Zhang, Y. Zhao and C. Chen, Phys. Rev. B:Condens. Matter Mater. Phys., 2013, 87, 134303 CrossRef.
- C. G. Van de Walle and J. Neugebauer, J. Appl. Phys., 2004, 95, 3851 CrossRef CAS.
- S. Lany and A. Zunger, Phys. Rev. B:Condens. Matter Mater. Phys., 2008, 78, 235104 CrossRef.
- R. M. Nieminen, Model. Simul. Mater. Sci. Eng., 2009, 17, 084001 CrossRef.
- N. D. M. Hine, K. Frensch, W. M. C. Foulkes and M. W. Finnis, Phys. Rev. B:Condens. Matter Mater. Phys., 2009, 79, 024112 CrossRef.
- S. T. Murphy and N. D. M. Hine, Phys. Rev. B:Condens. Matter Mater. Phys., 2013, 87, 094111 CrossRef.
- C. Persson, Y.-J. Zhao, S. Lany and A. Zunger, Phys. Rev. B:Condens. Matter Mater. Phys., 2005, 72, 035211 CrossRef.
- J. Buckeridge, Comput. Phys. Commun., 2019, 244, 329 CrossRef CAS.
- F. H. Taylor, J. Buckeridge and C. R. A. Catlow, Chem. Mater., 2016, 28, 8210 CrossRef CAS.
- Y.-S. Choi, S. I. R. Costa, N. Tapia-Ruiz and D. O. Scanlon, ACS Appl. Energy Mater., 2023, 6, 484 CrossRef CAS PubMed.
- M.-H. Chen, A. Emly and A. Van der Ven, Phys. Rev. B:Condens. Matter Mater. Phys., 2015, 91, 214306 CrossRef.
- J. a. S. Serejo, J. S. Pereira, R. Mouta and L. G. C. Rego, Phys. Chem. Chem. Phys., 2021, 23, 6964 RSC.
- J. Buckeridge, D. O. Scanlon, A. Walsh and C. R. A. Catlow, Comput. Phys. Commun., 2014, 185, 330 CrossRef CAS.
- A.-Y. Song, Y. Xiao, K. Turcheniuk, P. Upadhya, A. Ramanujapuram, J. Benson, A. Magasinski, M. Olguin, L. Meda, O. Borodin and G. Yushin, Adv. Energy Mater., 2018, 8, 1700971 CrossRef.
- G. Schwering, A. Hönnerscheid, L. van Wüllen and M. Jansen, ChemPhysChem, 2003, 4, 343 CrossRef CAS PubMed.
- C. Eilbracht, W. Kockelmann, D. Hohlwein and H. Jacobs, Physica B, 1997, 234, 48 CrossRef.
- F. Wang, H. A. Evans, K. Kim, L. Yin, Y. Li, P.-C. Tsai, J. Liu, S. H. Lapidus, C. M. Brown, D. J. Siegel and Y.-M. Chiang, Chem. Mater., 2020, 32, 8481 CrossRef CAS PubMed.
- X. Lü, J. W. Howard, A. Chen, J. Zhu, S. Li, G. Wu, P. Dowden, H. Xu, Y. Zhao and Q. Jia, Adv. Sci., 2016, 3, 1500359 CrossRef PubMed.
- Y. Zhang, X. He, Z. Chen, Q. Bai, A. M. Nolan, C. A. Roberts, D. Banerjee, T. Matsunaga, Y. Mo and C. Ling, Nat. Commun., 2019, 10, 5260 CrossRef PubMed.
- J. A. Dawson, H. Chen and M. S. Islam, J. Phys. Chem. C, 2018, 122, 23978 CrossRef CAS.
- P. Li, F. Hussain, P. Cui, Z. Li and J. Yang, Phys. Rev. Mater., 2019, 3, 115402 CrossRef CAS.
- D. Broberg, K. Bystrom, S. Srivastava, D. Dahliah, B. A. D. Williamson, L. Weston, D. O. Scanlon, G.-M. Rignanese, S. Dwaraknath, J. Varley, K. A. Persson, M. Asta and G. Hautier, npj Comput. Mater., 2023, 9, 1 CrossRef.
- M. Quesada-Gonzalez, B. A. D. Williamson, C. Sotelo-Vazquez, A. Kafizas, N. D. Boscher, R. Quesada-Cabrera, D. O. Scanlon, C. J. Carmalt and I. P. Parkin, J. Phys. Chem. C, 2018, 122, 714 CrossRef CAS.
- Y. Li, W. Zhou, S. Xin, S. Li, J. Zhu, X. Lü, Z. Cui, Q. Jia, J. Zhou, Y. Zhao and J. B. Goodenough, Angew. Chem., Int. Ed., 2016, 55, 9965 CrossRef CAS PubMed.
- S. Gao, T. Broux, S. Fujii, C. Tassel, K. Yamamoto, Y. Xiao, I. Oikawa, H. Takamura, H. Ubukata, Y. Watanabe, K. Fujii, M. Yashima, A. Kuwabara, Y. Uchimoto and H. Kageyama, Nat. Commun., 2021, 12, 201 CrossRef CAS PubMed.
- X. Lu, G. Wu, J. W. Howard, A. Chen, Y. Zhao, L. L. Daemen and Q. Jia, Chem. Commun., 2014, 50, 11520 RSC.
- Z. Deng, B. Radhakrishnan and S. P. Ong, Chem. Mater., 2015, 27, 3749 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ta08352k |
| This journal is © The Royal Society of Chemistry 2025 |