Open Access Article
Open Access ArticleInterlayer pillaring influences the octahedral tilting and electrochemical capacity of tungsten oxides†
Ran
Ding
 ,
Michael A.
Spencer
,
Noah P.
Holzapfel
,
Michael A.
Spencer
,
Noah P.
Holzapfel
 ,
Matthew
Chagnot
and
Veronica
Augustyn
,
Matthew
Chagnot
and
Veronica
Augustyn
 *
*
Department of Materials Science and Engineering, North Carolina State University, Raleigh, NC 27695, USA. E-mail: vaugust@ncsu.edu
First published on 26th February 2025
Abstract
One strategy to tune the electrochemical properties of layered inorganic materials for energy storage and conversion is to introduce molecular organic pillars. We investigated how pillaring tungsten oxides with alkylammonium cations influences their physical and electrochemical properties relative to the non-pillared host. While the presence of alkylammonium increased the interlayer spacing, we found that the electrochemical capacity of the materials decreased in non-aqueous electrolytes. In aqueous acidic electrolytes, replacement of the interlayer alkylammonium pillars with water molecules led to the recovery of the electrochemical capacity. We rationalize these results based on the influence of interlayer pillars on the degree of octahedral tilting within the inorganic tungsten oxide layers. The presence of alkylammonium in the interlayer leads to an increase in octahedral tilting relative to interlayer water. In turn, this leads to an increase in the band gap and corresponding decrease in the electrochemical capacity. Our findings emphasize the correlation between the chemical nature of the interlayer molecular pillars and the electronic structure, which in turn affects the electrochemical capacity.
1. Introduction
One strategy for influencing the electrochemical reactivity of layered inorganic materials is through the introduction of organic molecules within the interlayer void space to yield layered hybrid organic–inorganic materials. This is particularly interesting for electrochemical ion-insertion reactions, where the presence of organic molecule “spacers” in the interlayer can influence the electrochemical microenvironment. For example, organic molecules that increase the interlayer spacing relative to the unmodified host could facilitate the insertion of species that are difficult to accommodate within the interlayer of many inorganic materials, such as anions, multivalent cations, solvent molecules, and dissolved gas molecules. The electrochemical behavior of several classes of layered hybrid organic–inorganic materials has been reported, such as graphene oxides,1–3 transition metal sulfides,4,5 and transition metal oxides.6,7 The primary focus of these studies was to understand the relationships between the size of the organic molecule and interlayer space, and the accessibility of ions and solvent molecules to the interlayer.8,9 Banda et al. synthesized reduced graphene oxide pillared with different length alkyl diamines, and found a correlation between the interplanar d-spacing and size of electrolyte desolvated ions: electrolyte ions could access the interlayer when their desolvated ion size was less than the d-spacing.1 The capacitance of the alkyl diamine pillared reduced graphene oxides was comparable to the non-pillared material but electrochemical impedance spectroscopy (EIS) results showed increased resistance to ion transport. This was attributed to steric hindrance of the ion transport within the interlayer, which was hypothesized to be too crowded to facilitate efficient ion movement.2 In a separate study, the same authors reported the importance of controlling the density of the interlayer pillaring molecules in reduced graphene oxide.3 Reduced graphene oxide “sparsely” pillared by 1,6-diaminohexane showed higher gravimetric and volumetric capacitances than the non-pillared material, which was again attributed to reduced steric hindrance.There are also reports of utilizing interlayer pillaring in transition metal oxides to influence their electrochemical ion insertion behavior. Layered transition metal oxides can be pillared by chemical insertion of metal cations, as has been shown for MnO2 and vanadium oxides.10–13 This approach is hypothesized to influence electrochemical ion insertion by weakening the interactions between the oxide and subsequently electrochemically inserted ions, thus facilitating solid state ion transport, and ultimately leading to better cyclability and rate capability.14,15 Organic molecules can also be used to pillar layered transition metal oxides. The acidic early transition metal oxides (e.g., MoO3, WO3, TiO2, V2O5) can react with organic bases such as alkylamines to form layered hybrid organic–inorganic oxide materials.16–22 Pomerantseva et al. reported the electrochemical behavior of alkylammonium–pillared bilayered vanadium oxide in non-aqueous electrolytes.23,24 The interlayer distance of the resulting hybrid material was controlled by the chain length of the alkyl group. They found that the pillared vanadium oxides showed a higher cycling stability, but lower capacity, for both Li+ and Na+ intercalation, as compared to the pristine bilayered vanadium oxides. Recently, our lab reported that octylammonium–pillared tungsten oxide showed lower capacities than its parent phase, WO3·H2O, towards proton, Li+, and tetrabutylammonium [NBu4]+ insertion.25 Therefore, it is a fairly common observation that upon pillaring the interlayer with organic molecules (and in the absence of exfoliation), the capacity towards ion insertion decreases relative to the parent oxide. The most common explanation for this phenomenon is that the capacity decline occurs from the restriction of ion insertion sites in an interlayer saturated with organic molecules.23
In this work, we provide an additional explanation for reduced electrochemical ion insertion into layered hybrid organic–inorganic oxides by investigating the structure and electrochemical properties of alkylammonium–pillared layered tungsten oxides. We prepared a series of layered hybrid tungsten oxides, where the organic pillaring molecules were propylammonium (PA), butylammonium (BA), or octylammonium (OA), and performed electrochemical characterization in a series of non-aqueous electrolytes containing alkali cations (Li+, Na+, Cs+) or [NBu4]+ as well as in aqueous sulfuric acid. We found that in all investigated electrolytes, the hybrid oxides showed smaller capacities than the parent layered oxide, WO3·2H2O. In other words, the capacities were smaller not only with Li+, but also with larger cations like Cs+ and [NBu4]+. We hypothesize that this decrease in the capacity occurs not only from the saturation of the interlayer and blocking of ion insertion, but rather from the influence of the organic pillaring molecules on the octahedral tilting of the inorganic WO6 layers which controls the electronic properties of the hybrid materials. During extended electrochemical cycling of the layered hybrid tungsten oxides in an acidic electrolyte, the intercalated organic molecules are progressively replaced with water, which leads to a continuous shift in the onset potential and capacity associated with H+ insertion. This study provides insight into the various factors that influence the electrochemical behavior of layered hybrid oxides.
2. Experimental methods
2.1 Chemicals
All chemicals were used as received. Sodium tungsten oxide dihydrate (Na2WO4·2H2O; 99%), lithium perchlorate (LiClO4; electrochemical grade), cesium perchlorate (CsClO4; reagent grade), propylene carbonate (PC; anhydrous, 99.7%), lithium (99.9%), and ferrocene (Fc; 98%) were purchased from Millipore Sigma. Hydrochloric acid (36.5–38.0%, certified ACS Plus), ethanol (EtOH; anhydrous), acetylene black (100% compressed), stainless steel mesh (400 mesh woven from 0.028 mm dia.), tetrabutylammonium perchlorate ([NBu]4ClO4; 99%), sulfuric acid (H2SO4; certified ACS Plus) were purchased from Fisher Scientific. Octylamine (99%), butylamine (99%), and propylamine (99%) were purchased from Acros Organics. Latex-PVDF solution (20 wt% aqueous dispersion) was purchased from MTI Corp. Carbon paper (AvCarb MGL 190) was purchased from Fuel Cell Earth.2.2 Materials synthesis
WO3·2H2O was synthesized via an acid precipitation reaction.26 Typically, 50 mL of 1 M Na2WO4·2H2O was added dropwise to 450 mL of 4 M HCl while stirring at 300 rpm overnight. The precipitates were collected and washed with DI water under vacuum filtration until the rinsed solution reached neutral pH. The filtered WO3·2H2O was then dried at 60 °C overnight and ground into a fine powder. xBA–WO3 (xOA–WO3, xPA–WO3) was synthesized by a dissolution–reorganization reaction using WO3·2H2O as the precursor.27 300 mg of WO3·2H2O was added to a solution of butylamine (octylamine, propylamine) in 2 mL EtOH with molar ratio of 0.5–2 BA (OA, PA) to 1 WO3·2H2O. This mixture was stirred rigorously in a round-bottom flask for 2 days. After completion, the powder was collected via centrifugation and washed by redispersing the powder in EtOH and centrifuging three times. The product was dried at 60 °C under vacuum and ground to a fine powder. The products were denoted as xBA–WO3 (xOA–WO3, xPA–WO3), where x = 0.5, 1 or 2, representing the molar ratio between butylamine (octylamine, propylamine) and WO3·2H2O during the synthesis.2.3 Materials characterization
XRD measurements were conducted on a PANalytical X'Pert diffractometer in the Bragg–Brentano geometry with Cu Kα radiation (λ1/λ2 = 1.5406/1.5444 Å). Raman spectroscopy was performed using a WiTEC alpha 300R confocal Raman spectrometer with a laser wavelength of 532 nm and a 100× objective lens. TGA was performed on a Seiko Exstar TG/DTA6200 instrument. SEM was performed using a field emission FEI Verios 460L microscope. Ex situ XRD and Raman were performed using slurry electrodes coated on stainless steel mesh substrates. Diffuse reflectance spectroscopy (DRS) data of the various pillared tungsten oxides were collected on a Shimadzu UV-vis-NIR spectrophotometer (UV-3600) equipped with a deuterium–halogen lamp and an integrating sphere detector with a wavelength range of 200–1100 nm. A flat BaSO4 (Alfa Aesar, 99%) surface served as the background reference. The analyte was evenly spread then pressed onto the background reference. Reflectance of the analyte was recorded then transformed using the Kubelka–Munk remission function.2.4 Electrode preparation
Electrodes were prepared by mixing the active material with acetylene black and latex-PVDF solution in a weight ratio of 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 in EtOH. Typically, 24 mg of tungsten oxide materials and 3 mg of acetylene black were dispersed in 500 μL EtOH. After stirring 1 hour, 33 μL of 20 wt% latex-PVDF was added into the solution, followed by a short vortex (30 s). Then, 50 μL of the slurry solution was dropcast onto a carbon paper (Fuel Cell Earth) or stainless-steel mesh (Fisher Scientific) current collector with an area of 2 × 1 cm2. The electrode was ready to use after drying at 60 °C overnight.
1 in EtOH. Typically, 24 mg of tungsten oxide materials and 3 mg of acetylene black were dispersed in 500 μL EtOH. After stirring 1 hour, 33 μL of 20 wt% latex-PVDF was added into the solution, followed by a short vortex (30 s). Then, 50 μL of the slurry solution was dropcast onto a carbon paper (Fuel Cell Earth) or stainless-steel mesh (Fisher Scientific) current collector with an area of 2 × 1 cm2. The electrode was ready to use after drying at 60 °C overnight.
2.5 Electrochemical characterization
Electrochemical characterization was performed in three-electrode cells using a potentiostat (bio-logic MPG2, VMP3, or SP50). Non-aqueous electrochemistry was performed in an argon-filled glovebox (MBraun LABstar pro, <1 ppm O2 and H2O). Li+ insertion was studied in a 0.1 M LiClO4 in PC electrolyte with Li metal counter and reference electrodes. Potentials were converted to the standard hydrogen electrode (SHE) scale using the following equation: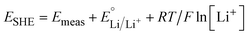 | (1) |
Cs+ and [NBu]4+ insertion were studied from 0.1 M CsClO4 and [NBu4]ClO4 in PC electrolytes, respectively, with a Pt coil counter electrode (99.99%, Pine Research Instrumentation) and a Ag wire pseudo-reference electrode (99.999%, Fisher Scientific). To determine the potential vs. SHE in these electrolytes, 5 mM Fc was added to the electrolytes upon completion of the electrochemical tests to serve as an internal standard. As shown in Fig. S1,†E1/2 of ferrocene is ∼0.80 V vs. Ag/Ag+ in 0.1 M CsClO4 and ∼0.72 V vs. Ag/Ag+ in 0.1 M [NBu4]ClO4, respectively. Thus, we have the following equations to convert the potential to SHE scale:
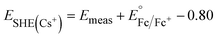 | (2) |
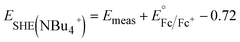 | (3) |
Electrochemical cycling of 2BA–WO3 was carried out in 1 M H2SO4 with a graphite rod counter electrode (Pine Research Instrumentation) and a Ag/AgCl in 4 M KCl reference electrode (Pine Research Instrumentation). All reported current densities were based on the geometric surface area. Potentials were converted to the standard hydrogen electrode (SHE) scale using the following equation:
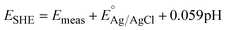 | (4) |
2.6 Electrochemical simulation
We performed an electrochemical simulation following the model described by Fabregat-Santiago et al.28 This simulation models capacitive voltammetry using an equation of the form: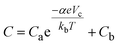 | (5) |
2.7 Ex situ Raman sample preparation
0.5BA–WO3 was coated on carbon paper via the above protocol. Cyclic voltammetry was performed to 1.9 V vs. Li/Li+ in 0.1 M LiClO4 in PC, followed by chronoamperometry at 1.9 V for 2 min. After being rinsed with DMC and dried in the glovebox, the electrode was transferred into an operando electrochemical Raman cell (EL-Cell ECC-Opto-10) to protect it from air (but without applying a potential during Raman spectroscopy).2.8 Ex situ XRD sample preparation
0.5BA–WO3 was coated on stainless steel mesh via the above protocol. Cyclic voltammetry was performed to 1.9 V vs. Li/Li+ in 0.1 M LiClO4 in PC, followed by chronoamperometry at 1.9 V for 2 min. After being rinsed with DMC and dried in the glovebox, the electrode was wrapped with Kapton tape (Thorlabs Inc.) and sealed in a polyethylene bag.2.9 Operando electrochemical XRD
Operando synchrotron XRD was conducted at the Stanford Synchrotron Radiation Lightsource (SSRL) using beamline 2–1 in Bragg–Brentano geometry with an incident energy of 17 keV. A Pilatus 100 K area detector was used to collect the area diffraction patterns. The 2D diffraction patterns were compiled and integrated using a Python script developed at SSRL beam line 2–1. The measurement was performed in an in situ cell following previously described protocols.29,30 The cell was composed of a 5.0 mm thick PEEK electrode holder with a 1/32′′ thick fluorosilicone rubber gasket (McMaster-Carr) for preventing electrolyte leaks and a polyimide (Kapton) film to provide a low background window suitable for X-ray transmission. The in situ cell was assembled in an Ar-filled glovebox and transferred out, where it was then placed in a sealed helium (He) chamber. The full assembly was mounted onto the diffractometer. Helium flowed through the chamber throughout the experiment. Cyclic voltammetry was performed in the in situ cell at a scan rate of 2 mV s−1 for three cycles from 3.8 V to 1.9 V (vs. Li/Li+) using a BioLogic SP150 potentiostat in a two-electrode configuration, with Li metal serving as the counter electrode and 1.0 M LiClO4 in PC as the electrolyte. 2D diffraction patterns were collected with a fixed incident angle (θ) of 2° and fixed detector angle (2θ) of 5° providing an angular range ±3.4° 2θ. The data acquisition time was 3 seconds per scan.2.10 Electronic structure calculations
Density functional theory (DFT) was used to calculate the electronic band structures of a model structure of H2WO4 as implemented with the Quantum ESPRESSO (version 6.1) freeware in combination with the BURAI (version 1.3.1) GUI.31–33 These calculations were performed using projector augmented wave potentials based on the PBE exchange–correlation functional.34 Hubbard U parameters35–38 of 6.20 eV and 9.00 eV were used for W and O, respectively, to account for localization of the W 5d and O 2p orbitals. Cut off energies of 6.466 keV and a 2 × 2 × 3 k-point grid were used for the calculations.393. Results and discussion
3.1 Electrochemical behavior of layered hybrid organic-tungsten oxides in non-aqueous and aqueous electrolytes
WO3·2H2O was used as the precursor for the synthesis of hybrid organic–pillared tungsten oxides. Stirring WO3·2H2O in a solution containing the alkylamine of interest (butylamine, propylamine, or octylamine) and ethanol leads to a dissolution–precipitation reaction and the formation of hybrid layered tungsten oxides pillared with alkylammonium cations.25,27 These products are designated as BA–WO3, PA–WO3 and OA–WO3, where BA indicates butylammonium, PA is propylammonium, and OA is octylammonium. XRD shows that the presence of alkylammonium cations increases the interlayer distance relative to WO3·2H2O (Fig. S2†), from 0.70 nm to 1.28 nm (PA–WO3), 1.40 nm (BA–WO3), and 2.60 nm (OA–WO3). The bond length of CH3NH3+ is estimated to be 0.248 nm, and each additional –CH2– unit of the alkyl chain increases the chain length by 0.127 nm.27 Therefore, the length of alkylammonium chains all with trans conformation are estimated to be 0.502 nm for PA, 0.629 nm for BA, and 1.137 nm for OA. To accommodate the interlayer expansion observed from XRD analysis, the alkylammonium chains must be in a bilayer arrangement in the interlayer with a non-negligible van der Waals gap between each layer of the alkylammonium bilayer. The tilt angle of the alkylammonium chains with respect to the basal plane can be estimated by considering the measured d-spacing, the thickness of the inorganic layer, and the calculated chain lengths using the following relationship:27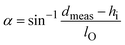 | (6) |
We further synthesized a series of BA–pillared tungsten oxides by varying the ratio of butylamine to WO3. These products are denoted as xBA–WO3, where x = 0.5, 1 or 2, representing the molar ratio of butylamine to WO3 during synthesis. XRD shows that 1BA–WO3 and 2BA–WO3 (Fig. 1a) are phase-pure layered hybrid materials, with no peaks associated with the precursor, WO3·2H2O. We designate these materials as “fully pillared”. The interlayer space expands from 0.70 nm in the precursor to 1.40 nm. In contrast, 0.5BA–WO3 shows the presence of both the organic hybrid phase and the parent WO3·2H2O phase. Thus, the product of 0.5BA–WO3 reaction is a mixture of the fully pillared phase and the hydrated tungsten oxide precursor. The XRD results are in accordance with the color differences between the samples (Fig. S3†), which ranged from yellow for WO3·2H2O to white for both 1BA–WO3 and 2BA–WO3. Similar results were observed in OA–pillared tungsten oxides, except 1OA–WO3 was not phase pure and contained small amounts of WO3·2H2O (Fig. S4†).
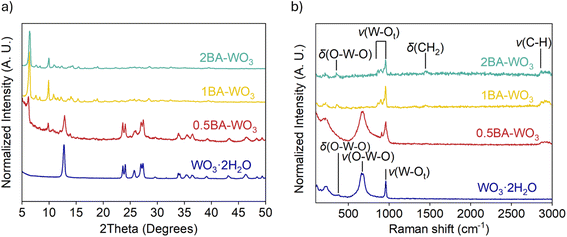 | ||
| Fig. 1 (a) XRD and (b) Raman spectroscopy of WO3·2H2O and BA–pillared WO3 obtained from syntheses using different ratios of butylamine to WO3·2H2O. | ||
We used Raman spectroscopy to investigate changes in W–O bonding between WO3·2H2O and the BA pillared materials, 0.5BA–WO3, 1BA–WO3 and 2BA–WO3 (Fig. 1b and Table S1†). WO3·2H2O has three characteristic peaks below 1000 cm−1: at 950 cm−1, between 600 and 700 cm−1, and at 330 cm−1.42,43 The 950 cm−1 peak is assigned to the W–terminal oxygen stretching (ν) mode, ν(W–Ot). This peak is indicative of water in the structure, present as a long W–OH2 bond that in turn leads to a shorter W–Ot bond. In all the pillared tungsten oxides, the presence of BA leads to new peaks of ν(W–Ot) at lower wavenumbers (860 and 890 cm−1), indicating a longer W–Ot bond relative to WO3·2H2O. The broad peak between 600 cm−1 to 700 cm−1 is assigned to the in-plane ν(O–W–O) stretching mode, which is absent in the fully pillared oxides, 1BA–WO3 and 2BA–WO3.44 The small peak at 330 cm−1 shown in all samples is attributed to the δ(O–W–O) bending mode. The pillared tungsten oxides also show two additional peaks at 1470 cm−1 and 2800–2900 cm−1, which are attributed to the δ(CH2) twisting and ν(C–H) stretching of the alkyl group of the organic molecules.45,46
We performed thermogravimetric analysis (TGA) in air to understand the temperature stability and interlayer composition of each oxide (Fig. S5†). Both WO3·H2O and WO3·2H2O show a distinct mass loss step from 150 to 250 °C, and WO3·2H2O shows an additional mass loss step at 80 °C. One molar equivalent of H2O was removed during each step, confirming the composition of both WO3·H2O and WO3·2H2O. The 0.5BA–WO3 shows a minor mass loss step at 80 °C, corresponding to the removal of unbound interlayer water from the unreacted WO3·2H2O. The broad mass loss step between 100 and 450 °C is attributed to the removal of BA from the pillared phase and bound water molecules from unreacted WO3·2H2O (which is assumed to be equal to the mass loss at 80 °C). The ratio of BA to WO3 is 0.53, which is in line with that expected from the synthesis conditions. The TGA results are also in agreement with the XRD and Raman results, shown in Fig. 1, that 0.5BA–WO3 is a mixture of organically pillared and hydrated oxides. 1BA–WO3 and 2BA–WO3 share similar overall mass loss features, with only slight differences in the low temperature region. Compared to 0.5BA–WO3, 1BA–WO3 and 2BA–WO3 show almost no mass loss at 80 °C, suggesting that WO3·2H2O fully reacted with BA under these conditions. The ratio of BA to WO3 in the reaction product is 1 for both, indicating they are fully pillared, and that excess BA does not lead to more pillar insertion between the layers. Like 2BA–WO3, 2OA–WO3 is also fully pillared, and the ratio of OA to WO3 is 1.
Scanning electron microscopy (SEM) was used to determine the microstructure of WO3·2H2O and BA pillared tungsten oxides (Fig. 2). The particle size increases significantly upon pillaring: for WO3·2H2O and 0.5BA–WO3, the particle size is ∼0.5 μm, whereas in fully pillared 1BA–WO3 and 2BA–WO3, the particle size increases to 2–10 μm. This change in microstructure is proof of the dissolution–precipitation reaction mechanism, which gives rise to completely different particle sizes and morphologies compared to the pristine hydrates. Importantly, it shows that the alkylammonium cations do not undergo an exchange mechanism with the interlayer water molecules in WO3·2H2O.
 | ||
| Fig. 2 SEM of the precursor WO3·2H2O (a) and BA–pillared tungsten oxides obtained from syntheses with various ratios of butylamine: (b) 0.5BA–WO3, (c) 1BA–WO3, and (d) 2BA–WO3. | ||
3.2 Electrochemical behavior of pillared tungsten oxides in non-aqueous electrolytes
We first investigated the electrochemical behavior of BA–pillared tungsten oxides in 0.1 M LiClO4 in PC through cyclic voltammetry (Fig. 3a). In the case of the parent material, WO3·2H2O, our previous studies show that it will dehydrate upon exposure to the non-aqueous electrolyte and transform to the related layered hydrate, WO3·H2O. Therefore, the parent tungsten oxide hydrate will be referred to as WO3·nH2O (1 ≤ n < 2) when cycled in non-aqueous electrolytes for the remainder of the study. Electrochemical insertion of Li+ into WO3·nH2O was studied previously,47 and can be described as:| WO3·nH2O + xLi+ + xe− ↔ LixWO3·nH2O, with 0 ≤ x ≤ 1 | (7) |
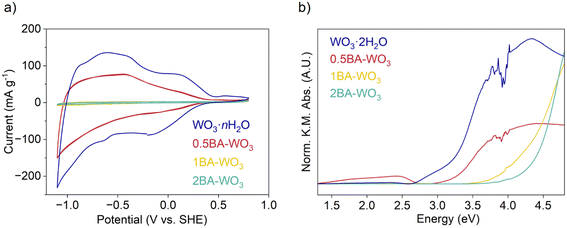
The cyclic voltammogram (CV) of WO3·nH2O at 1 mV s−1 is nearly symmetrical, and the current, which is entirely associated with Li+ insertion, is reversible. The cathodic capacity was 40 mA h g−1 while the anodic capacity was 38 mA h g−1, corresponding to 0.39 Li+ e− per W. The presence of BA led to a decrease in the current and thus capacity, with the trend WO3·nH2O > 0.5BA–WO3 > 1BA–WO3 – 2BA–WO3. The capacity of the fully pillared 2BA–WO3 is less than 1 mA h g−1 (0.01 Li+ e− per W). Therefore, as has been observed with some other layered materials, the presence of organic molecules in the interlayer suppresses electrochemical Li+ insertion.25
The capacity decrease upon pillaring layered materials with organic molecules has been described previously and is usually attributed to restricted mass transport for ion insertion due to occupancy of the interlayer by densely packed organic pillars.1–3,8,23,25 However, we propose an additional consideration related to distortions in the inorganic layers for the case of layered hybrid tungsten oxides. Whether the pillaring molecules are water or alkylammonium cations, the tungsten oxide layers consist of corner-sharing octahedra that can be expressed using Niggli-type connectivity formulas as WO4/2O2/1 or [WO4/2O1/1(OH2)1/1] octahedra.48 In general, the conduction bandwidth of layered perovskite-like oxide materials containing d0 transition metal cations is maximized when the M–O–M bonds have a linear (180°) configuration because this allows for the greatest overlap between transition metal d orbitals and oxygen 2p orbitals.49 Introducing organic cations between the tungsten oxide layers can distort the inorganic framework via rotations of the octahedral units (i.e. tilting) which decreases the W–O–W bond angles. This structural change often leads to narrower conduction band widths and larger optical band gaps. This change in electronic structure upon octahedral tilting has been reported in a variety of transition metal oxides including layered perovskites, bilayered vanadium oxides, layered molybdenum oxides, and tungsten oxides.11,22,50 According to the DRS results shown in Fig. 3b, the band gap increases in the trend of WO3·2H2O (3.15 eV) < 0.5BA–WO3 (3.19 eV) < 1BA–WO3 (4.16 eV) < 2BA–WO3 (4.36 eV), which is in accordance with the shift of the onset potential to more negative values in the CVs shown in Fig. 3a. We attribute this shift in optical absorbance and potential to increasing degrees of octahedral tilting within the inorganic layer upon introduction of alkylammonium cations into the interlayer. CVs in Fig. S6† show that OA has a similar effect to BA on the Li+ insertion behavior with a suppression of the insertion capacity from ∼40 to 1 mA h g−1 (0.40 to 0.01 Li+ e− per W). We note that the increase in particle size from WO3·2H2O to the layered hybrid tungsten oxides is also expected to play a role in determining the ion insertion capacity, especially at fast rates. However, the mixed phase 0.5BA–WO3 has a similar particle size as WO3·2H2O yet shows a lower Li+ insertion capacity. Therefore, we attribute the change in electronic structure due to increased octahedral tilting of the tungsten oxide layers as the primary reason for the capacity decline.
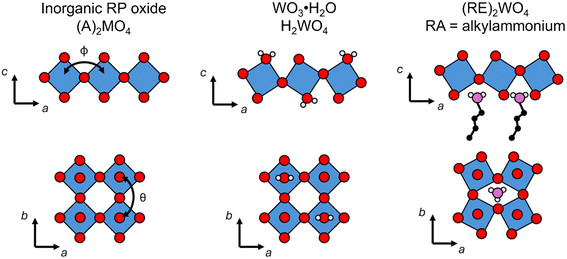
The effects of octahedral tilting on the electronic structure of perovskite-related materials containing d0 transition metals has been studied quite extensively.49 As discussed previously by Eng et al.,49 fully inorganic layered derivatives of oxide perovskite structures such as Ruddlesden–Popper (RP) phases should not have significantly different band gaps from their 3D counterparts in cases where the M–O bond distances and M–O–M bond angles remain similar. In the case of hybrid layered halide perovskites, previous work by Liu et al. showed that the incorporation of hydrocarbon ammonium groups almost always leads to octahedral tilting.50 This work further shows that the most common forms of tilts seen in layered perovskite derivatives are out-of-phase tilts (φ-tilts) along the lateral directions of the inorganic layer and θ-tilts perpendicular to the layer plane. The most commonly observed tilting patterns in the halide perovskite examples were found to be φφθ/φφθ and 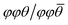 which produce unit cells with Pbca and P21/c space group symmetry, respectively. The formation of these two tilting schemes is driven by the optimization of hydrogen-bonding interactions between the ammonium group and the inorganic layer. Both WO3·H2O and WO3·2H2O are structurally similar to these layered perovskite derivatives and we can assign tilting patterns using the same notation. For WO3·H2O, the structure reported by Szymanski et al.40 has Pmnb space group symmetry with the pattern of octahedral tilting described as φφ0/φφ0. From the report by Liu, this pattern of tilting would correspond to a structure with Cmce space group symmetry. However, the symmetry is lowered from Cmce to Pmnb by the second order Jahn–Teller distortion of W6+ (5d0) within the octahedral coordination environment. For WO3·2H2O, the structure reported by Li et al.51 has a complex pattern of octahedral tilting involving varying degrees of φ-, θ-, and in-phase (ψ-) tilts. The increased complexity of the tilting scheme with the presence of the interlayer water suggests hydrogen bond doners (either H2O or alkylammonium pillars) can drastically alter the tilting of the inorganic layer. A pictorial representation of the structural relationships between an all-inorganic RP oxide, WO3·H2O, and a hybrid RP oxide is given in Fig. 4.
which produce unit cells with Pbca and P21/c space group symmetry, respectively. The formation of these two tilting schemes is driven by the optimization of hydrogen-bonding interactions between the ammonium group and the inorganic layer. Both WO3·H2O and WO3·2H2O are structurally similar to these layered perovskite derivatives and we can assign tilting patterns using the same notation. For WO3·H2O, the structure reported by Szymanski et al.40 has Pmnb space group symmetry with the pattern of octahedral tilting described as φφ0/φφ0. From the report by Liu, this pattern of tilting would correspond to a structure with Cmce space group symmetry. However, the symmetry is lowered from Cmce to Pmnb by the second order Jahn–Teller distortion of W6+ (5d0) within the octahedral coordination environment. For WO3·2H2O, the structure reported by Li et al.51 has a complex pattern of octahedral tilting involving varying degrees of φ-, θ-, and in-phase (ψ-) tilts. The increased complexity of the tilting scheme with the presence of the interlayer water suggests hydrogen bond doners (either H2O or alkylammonium pillars) can drastically alter the tilting of the inorganic layer. A pictorial representation of the structural relationships between an all-inorganic RP oxide, WO3·H2O, and a hybrid RP oxide is given in Fig. 4.
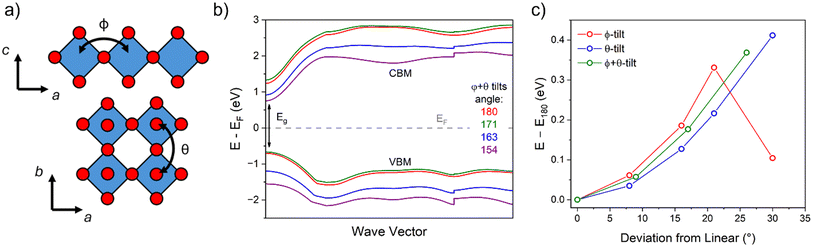
For hybrid layered oxide perovskites, we may expect that the hydrogen bonding interactions are stronger than the related halide phases, suggesting more optimal patterns of tilting. From the DRS measurements, we observe a significant shift in absorbance onset (∼+1 eV) upon replacing the water groups with organic ammonium cations. While we are not able to obtain crystal structures from the laboratory XRD data, we may still expect significant changes in the degree and patterns of octahedral tilting of the inorganic tungsten oxide layers. We utilized DFT electronic structure calculations of an idealized unit cell of H2WO4 with the parent RP-phase structure (I4/mmm) to show how octahedral tilting can influence the band gap. We lowered the space group symmetry to P21/c to allow for the 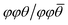 pattern of tilting using the ISODISTORT program52 following the previous report by Liu.50 With ISODISTORT, we could then vary the individual tilting angles (φ and θ) by adjusting the magnitude of the related distortion parameters while keeping the equatorial bond lengths relatively similar. Using this program, we produced 11 structures with increasing degrees of φ-tilts, θ-tilts, and combined φ + θ-tilts. We then calculated the band structures of all 12 structures under identical conditions to determine how the band gap energy (Eg) changes as the tilting angle deviates from linear (180°). Fig. 5 shows the results of these calculations with φ + θ-tilts showing a 0.4 eV band gap increase when the tilting angle is 25–30° from linear. While these calculations do not fully account for the 1 eV band gap shift observed experimentally, we found that octahedral tilting alone can account for almost half of this observed shift. More in-depth calculations from a solved crystal structure would provide further insight on the change in absorbance.
pattern of tilting using the ISODISTORT program52 following the previous report by Liu.50 With ISODISTORT, we could then vary the individual tilting angles (φ and θ) by adjusting the magnitude of the related distortion parameters while keeping the equatorial bond lengths relatively similar. Using this program, we produced 11 structures with increasing degrees of φ-tilts, θ-tilts, and combined φ + θ-tilts. We then calculated the band structures of all 12 structures under identical conditions to determine how the band gap energy (Eg) changes as the tilting angle deviates from linear (180°). Fig. 5 shows the results of these calculations with φ + θ-tilts showing a 0.4 eV band gap increase when the tilting angle is 25–30° from linear. While these calculations do not fully account for the 1 eV band gap shift observed experimentally, we found that octahedral tilting alone can account for almost half of this observed shift. More in-depth calculations from a solved crystal structure would provide further insight on the change in absorbance.
Next, we consider why a change in the band gap should affect the cyclic voltammetry current. Bisquert et al. proposed a cyclic voltammetry model to quantify the effect of the semiconductor electronic properties on the cyclic voltammetry current and electrochemical capacitance.28 The capacitive current for a semiconductor electrode can be calculated from the capacitance C:
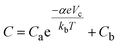 | (8) |
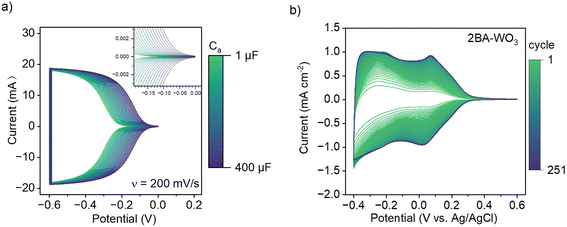 | ||
| Fig. 6 (a) Simulated CV based on the chemical capacitance model reported by ref. 28 with Cb = 0 mF and Ca varying between 1 μF and 400 μF. The depicted trend shows potential-dependent filling of the conduction band at all values of Ca in the absence of additional phase transformations. (b) CV of 2BA–WO3 at 50 mV s−1 in 1 M H2SO4 for 251 cycles, showing how exchange of BA with H2O and simultaneous decrease in the degree of octahedral tilting and band gap leads to a progressive increase in the current associated with H+ insertion. | ||
Since the pillaring molecules play an important role in determining the band gap and thus the electrochemical capacity of tungsten oxides, we determined how gradually replacing the interlayer organic molecules with water affects the cyclic voltammetry current. We previously found that exposing layered hybrid OA–WO3 to aqueous acid solutions led to the exchange of OA with H2O.25 Therefore, we performed cyclic voltammetry of 2BA–WO3 in 1 M H2SO4 for 250 cycles at 10 mV s−1 (Fig. 6b) and found that the current progressively increased upon cycling, the capacity increased from 0.04 to 0.17 H+ e− per W, and the onset potential (at 0.1 mA cm−2) increased from 0.18 V vs. Ag/AgCl to 0.30 V. Ex situ Raman spectroscopy showed that 2BA–WO3 transformed to WO3·2H2O within 250 cycles (Fig. S7†). The conversion of 2BA–WO3 to WO3·2H2O leads to a decrease in the band gap (Fig. 3b). Therefore, changes in the CV current are directly correlated to changes in the electronic structure of the oxide: the band gap of 2BA–WO3 in the 1st cycle is the largest (corresponding to low values of Ca in the simulation in Fig. 6a) while the band gap of WO3·2H2O in the last cycle is the smallest (corresponding to high values of Ca in the simulation). The simple CV simulation in Fig. 6a does not account for any insertion-induced structural phase transformations, so it does not capture the finer features of the experimental CV shown in Fig. 6b where the peaks are associated with structural transitions in various HxWO3·2H2O phases.29 However, the simulation results clearly show how modification of the electronic structure leads to the types of changes observed during electrochemical cycling of water or organic pillar-containing tungsten oxides in aqueous and non-aqueous electrolytes.
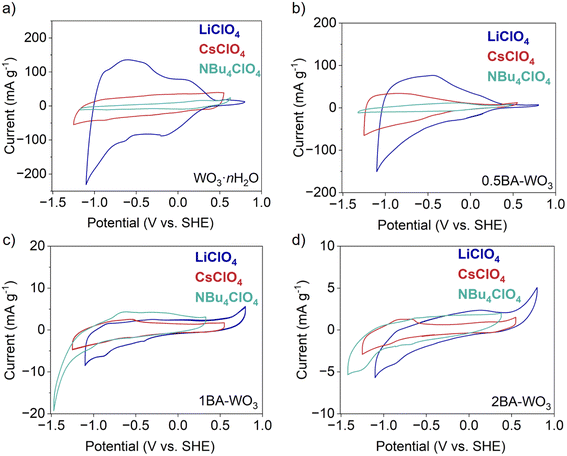
To further investigate the electrochemical behavior of the layered hybrid tungsten oxides, we performed cyclic voltammetry in three non-aqueous electrolytes while the concentration (0.1 M) and solvent (PC) were held constant: LiClO4, CsClO4, and [NBu4]ClO4. Given that all the materials are in their fully oxidized state, we focused on their behavior when applying reducing potentials, where the expected charge-compensating species from the electrolyte are cations. Fig. 7a shows that the capacity of WO3·nH2O decreased from 40 mA h g−1 with Li+ to 12 mA h g−1 with Cs+ and 4 mA h g−1 with [NBu4]+. The small capacities observed in Cs+ and [NBu4]+-containing electrolytes indicate that the larger cations do not insert into WO3·nH2O and only participate in charge compensation in the electric double layer, at the outer surface. CVs of BA–WO3 with various butylamine ratios in the above three electrolytes are shown in Fig. 7b–d. The capacity of partially pillared 0.5BA–WO3 (Fig. 7b) decreases from 21 mA h g−1 with Li+ to 11 mA h g−1 with Cs+ and 3 mA h g−1 with [NBu4]+. Compared with WO3·nH2O and in the Li+-containing electrolyte, the capacity of 0.5BA–WO3 decreases from 40 mA h g−1 to 21 mA h g−1. This indicates that the electrochemical response of 0.5BA–WO3 in Li+ consists of both ion insertion and outer surface adsorption, whereas the capacity with Cs+ and [NBu4]+ is attributed to only outer surface adsorption. For the fully pillared 1BA–WO3 and 2BA–WO3, the capacity is less than 1 mA h g−1 in all three electrolytes. The lack of ion specificity on the capacity means that only outer surface adsorption contributes to the capacity of the fully pillared oxides, even in the case of Li+.
We observed similar phenomena in OA–WO3, shown in Fig. S8.† For partially pillared 0.5OA–WO3, the ion size effect is still significant as the capacity decreased from 20 mA h g−1 (0.24 Li+ e− per W) with Li+ to 10 mA h g−1 (0.12 Cs+ e− per W) with Cs+ and 3 mA h g−1 (0.04 [NBu4]+ e− per W) with [NBu4]+. For partially pillared 1OA–WO3, the ion size effect became less significant as the capacity decreased from 12 mA h g−1 (0.14 Li+ e− per W) with Li+ to 6.5 mA h g−1 (0.076 Cs+ e− per W) with Cs+ and 2 mA h g−1 (0.02 [NBu4]+ e− per W) with [NBu4]+. For the fully pillared 2OA–WO3, the ion size effect disappeared completely as the capacity in all electrolytes was 1 mA h g−1 (0.01 e− per W).
In summary, the capacity decreased as the organic molecule ratio increased in different electrolytes and the ion size plays different roles (Fig. 8 for BA–WO3 and Fig. S9† for OA–WO3). The significance of the ion size effect decreases in the trend WO3·nH2O > 0.5A–WO3 > 1A–WO3 ∼ 2A–WO3(A represents BA or OA). The large capacity of WO3·nH2O with Li+ over Cs+ and [NBu4]+ indicates that small cations like Li+ can insert into the hydrated tungsten oxide whereas bulky cations can only be adsorbed onto the outer surface. By contrast, in fully pillared tungsten oxides (1BA–WO3, 2BA–WO3, and 2OA–WO3) the capacity is comparable among different ions. In this case, no ion insertion took place. The mixed phase tungsten oxides (0.5BA–WO3, 0.5OA–WO3, and 1OA–WO3) are more ambiguous. While their ion size effect is less significant than in WO3·nH2O, it remains likely due to the presence of residual WO3·2H2O. Thus, we assume the capacity of mixed phase tungsten oxides is from both ion insertion and surface adsorption. Interestingly, in electrolytes with the bulky cations Cs+ and [NBu4]+, the capacity still follows the trend of WO3·nH2O > 0.5BA–WO3 > 1BA–WO3 – 2BA–WO3, which could not be explained by the accessibility of ions into the interlayer region of BA–WO3. Since those bulky cations are not expected to be intercalated into the structure of tungsten oxides, the change of capacity is attributed to the modification of band structures by tilting.
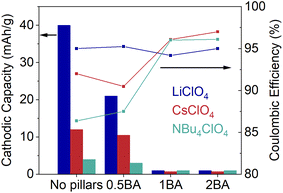 | ||
| Fig. 8 Cathodic capacity and coulombic efficiency of WO3·nH2O, pillared tungsten oxides 0.5BA–WO3, 1BA–WO3 and 2BA–WO3 in different non-aqueous electrolytes. | ||
Since the highest capacities for the layered hybrid tungsten oxides were obtained with the partially pillared 0.5BA–WO3 in 0.1 M LiClO4 in PC, we performed Raman spectroscopy and XRD characterization to understand if any structural changes took place during electrochemical cycling. Ex situ Raman spectroscopy of a 0.5BA–WO3 electrode at a reduction potential of 2 V vs. Li/Li+ (Fig. S10†) contains two peaks associated with the inorganic tungsten oxide layers (950 cm−1 and ∼650 cm−1). These are W–terminal oxygen stretching modes, ν(W–Ot), and in-plane ν(O–W–O) stretching mode, as shown in Fig. 1b. The peaks at 1345 cm−1 and 1590 cm−1 are typical peaks for activated carbon, which is used as the conductive material in the assembly of the working electrode. The last two broad peaks at ∼2700 cm−1 and ∼2900 cm−1 are assigned to the δ(CH2) twisting and ν(C–H) stretching of the alkyl group of the organic molecules and activated carbon. We observed no significant changes in all the above peaks after cycling to 2 V vs. Li/Li+, indicating the structural integrity of 0.5BA–WO3 during cycling. We also performed ex situ XRD (Fig. S11†) and in situ XRD (Fig. S12†) of 0.5BA–WO3. The ex situ XRD of 0.5BA–WO3 was performed with running cyclic voltammetry at potential between 2 to 3.9 V and at a scan rate of 2 mV s−1 in 0.1 M LiClO4 in PC, presenting several peaks: two peaks at 6° and 10° are assigned to the BA pillars in the interlayer of WO3; two peaks at 13° and 17° are assigned to the (020) peak of WO3·2H2O and WO3·H2O, respectively; three peaks at 24°, 26° and 27° are peaks of WO3·2H2O. The electrode was sealed in a polyethylene (PE) bag to prevent possible reoxidation in the air, which led to the strong peaks between 22° to 23° (see controlled experiment in the black curve in Fig. S11†). After reduction of 0.5BA–WO3 to 2 V, peaks at low angles are too poor to be compared, while peaks higher than 15° are unchanged. We also performed in situ XRD focusing on the low angle region, which showed one peak at 2.6° (corresponding to the peak at 5.5° with Cu Kα1 X-rays) that was unchanged during several cycles between 3.9 V and 2 V. The ex situ and in situ XRD results both show that in the case of 0.5BA–WO3 in 0.1 M LiClO4 in PC, there were no structural changes during cycling. Given that 0.5BA–WO3 contains some unreacted hydrate, this means that the phase fraction of hydrate phase was insufficient to observe structural changes due to Li+ insertion.
4. Conclusions
We investigated the influence of organic interlayer pillaring molecules on the electrochemical properties of tungsten oxides. An increased ratio of pillaring molecules (BA or OA) led to an increase of the band gap as well as reduction of the electrochemical capacity relative to the non-pillared host in non-aqueous electrolytes. A common hypothesis for this decrease in electrochemical capacity is that it occurs from the dense packing and/or hydrophobic nature of the interlayer alkylammonium cations, which disfavor electrochemical ion insertion. On the other hand, cycling of fully pillared 2BA–WO3 in aqueous solution of 1 M H2SO4 led to gradual removal of BA pillars, with simultaneous increase in the onset potential and electrochemical capacity. We rationalize these results based on the influence of interlayer organic molecules on the electronic band structure of inorganic layered materials that exhibit octahedral tilting (i.e., contain networks of corner-sharing octahedra). Relative to interlayer water, alkylammonium increases the degree of octahedral tilting within the tungsten oxide layer which increases the band gap. The increase in band gap leads to a decrease in the electrochemical capacity, which we also demonstrated via a cyclic voltammetry model. This work shows that molecular pillaring of inorganic materials containing corner-sharing octahedra can tune their electrochemical behavior by modifying their band structures, and as a result, the increased interlayer spacing in such systems does not facilitate electrochemical ion insertion.Data availability
Data from this work is openly available at https://doi.org/10.5281/zenodo.14259834.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank Seongbak Moon for performing SEM and Dr Saeed Saeed for performing in situ XRD. This work was supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences Early Career Research Program, under Award No. DE-SC0020234. This work was performed in part at the Analytical Instrumentation Facility (AIF), North Carolina State University, which is supported by the State of North Carolina and the National Science Foundation (Award No. ECCS-2025064). The AIF is a member of the North Carolina Research Triangle Nanotechnology Network (RTNN), a site in the National Nanotechnology Coordinated Infrastructure (NNCI). Use of the Stanford Synchrotron Radiation Lightsource, SLAC National Accelerator Laboratory, is supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences under Contract No. DE-AC02-76SF00515.References
- H. Banda, B. Daffos, S. Périé, Y. Chenavier, L. Dubois, D. Aradilla, S. Pouget, P. Simon, O. Crosnier, P. L. Taberna and F. Duclairoir, Ion Sieving Effects in Chemically Tuned Pillared Graphene Materials for Electrochemical Capacitors, Chem. Mater., 2018, 30(9), 3040–3047, DOI:10.1021/acs.chemmater.8b00759.
- H. Banda, S. Périé, B. Daffos, L. Dubois, O. Crosnier, P. Simon, P. L. Taberna and F. Duclairoir, Investigation of Ion Transport in Chemically Tuned Pillared Graphene Materials through Electrochemical Impedance Analysis, Electrochim. Acta, 2019, 296, 882–890, DOI:10.1016/j.electacta.2018.11.122.
- H. Banda, S. Périé, B. Daffos, P. L. Taberna, L. Dubois, O. Crosnier, P. Simon, D. Lee, G. De Paëpe and F. Duclairoir, Sparsely Pillared Graphene Materials for High–Performance Supercapacitors: Improving Ion Transport and Storage Capacity, ACS Nano, 2019, 13(2), 1443–1453, DOI:10.1021/acsnano.8b07102.
- R. Bissessur, J. Heising and W. Hirpo, Toward Pillared Layered Metal Sulfides. Intercalation of the Chalcogenide Clusters Co6Q8(PR3)6 (Q = S, Se, and Te and R = Alkyl) into MoS2, Chem. Mater., 1996, 8(2), 318–320, DOI:10.1021/cm950378+.
- S. Zhang, H. Ying, P. Huang, J. Wang, Z. Zhang, T. Yang and W. Q. Han, Rational Design of Pillared SnS/Ti3C2Tx MXene for Superior Lithium-Ion Storage, ACS Nano, 2020, 14(12), 17665–17674, DOI:10.1021/acsnano.0c08770.
- Y. Cho, P. Oh and J. Cho, A New Type of Protective Surface Layer for High–Capacity Ni–Based Cathode Materials: Nanoscaled Surface Pillaring Layer, Nano Lett., 2013, 13(3), 1145–1152, DOI:10.1021/nl304558t.
- Y. Li, S. Zhang, S. Wang, Z. Xiao, F. Meng, Q. Li, X. Zhang, Z. Zhang, L. Zhi and Z. Tang, Layered Structure Regulation for Zinc–Ion Batteries: Rate Capability and Cyclability Enhancement by Rotatable Pillars, Adv. Energy Mater., 2023, 13(16), 2203810, DOI:10.1002/aenm.202203810.
- S. Fleischmann, M. A. Spencer and V. Augustyn, Electrochemical Reactivity under Confinement Enabled by Molecularly Pillared 2D and Layered Materials, Chem. Mater., 2020, 32(8), 3325–3334, DOI:10.1021/acs.chemmater.0c00648.
- Y. Zhang, E. H. Ang, Y. Yang, M. Ye, W. Du and C. C. Li, Interlayer Chemistry of Layered Electrode Materials in Energy Storage Devices, Adv. Funct. Mater., 2021, 31, 2007358, DOI:10.1002/adfm.202007358.
- L. Liu, Y. C. Wu, L. Huang, K. Liu, B. Duployer, P. Rozier, P. L. Taberna and P. Simon, Alkali Ions Pre-Intercalated Layered MnO2 Nanosheet for Zinc-Ions Storage, Adv. Energy Mater., 2021, 11(31), 2101287, DOI:10.1002/aenm.202101287.
- M. Clites and E. Pomerantseva, Bilayered Vanadium Oxides by Chemical Pre–Intercalation of Alkali and Alkali–Earth Ions as Battery Electrodes, Energy Storage Mater., 2018, 11, 30–37, DOI:10.1016/j.ensm.2017.09.005.
- M. Clites, J. L. Hart, M. L. Taheri and E. Pomerantseva, Chemically Preintercalated Bilayered KxV2O5·nH2O Nanobelts as a High-Performing Cathode Material for K-Ion Batteries, ACS Energy Lett., 2018, 3(3), 562–567, DOI:10.1021/acsenergylett.7b01278.
- Y. Zhao, C. Han, J. Yang, J. Su, X. Xu, S. Li, L. Xu, R. Fang, H. Jiang, X. Zou, B. Song, L. Mai and Q. Zhang, Stable Alkali Metal Ion Intercalation Compounds as Optimized Metal Oxide Nanowire Cathodes for Lithium Batteries, Nano Lett., 2015, 15(3), 2180–2185, DOI:10.1021/acs.nanolett.5b00284.
- S. Fleischmann, Y. Zhang, X. Wang, P. T. Cummings, J. Wu, P. Simon, Y. Gogotsi, V. Presser and V. Augustyn, Continuous Transition from Double–Layer to Faradaic Charge Storage in Confined Electrolytes, Nat. Energy, 2022, 7(3), 222–228, DOI:10.1038/s41560–022–00993–z.
- E. Pomerantseva and Y. Gogotsi, Two–Dimensional Heterostructures for Energy Storage, Nat. Energy, 2017, 2(7), 17089, DOI:10.1038/nenergy.2017.89.
- G. Lagaly, Interaction of Alkylamines with Different Types of Layered Compounds, Solid State Ionics, 1986, 22(1), 43–51, DOI:10.1016/0167–2738(86)90057–3.
- S. Ayyappan, G. N. Subbanna and C. N. R. Rao, Novel Metastable Structures of WO3, MoO3 and W1- xM xO3 Obtained by the Deintercalation of Layered Amine Adducts, Chem.–Eur. J., 1995, 1(3), 165–170, DOI:10.1002/chem.19950010305.
- B. Wang, X. Dong, Q. Pan, Z. Cheng and Y. Yang, Intercalation Behavior of N-Alkylamines into an A-Site Defective Layered Perovskite H2W2O7, J. Solid State Chem., 2007, 180(3), 1125–1129, DOI:10.1016/j.jssc.2007.01.009.
- B. Ingham, S. V. Chong and J. L. Tallon, Novel Materials Based on Organic–Tungsten Oxide Hybrid Systems, MRS Proc., 2003, 775, 31, DOI:10.1557/PROC–775–P6.31.
- A. F. Walte, R. Torres-Cadena, W. L. N. Dayaratne and A. Jaffe, Mixed–Metal Alloying in Hybrid Bronzes, J. Am. Chem. Soc., 2024, 146(34), 23699–23703, DOI:10.1021/jacs.4c08960.
- S. Wan, N. Musielak, A. G. Oliver and A. Jaffe, Controlling Electron Delocalization in Vanadium-Based Hybrid Bronzes through Molecular Templation, Angew. Chem., Int. Ed., 2023, 62(51), e202314523, DOI:10.1002/anie.202314523.
- W. L. N. Dayaratne, R. Torres-Cadena, B. P. Schmitt, E. M. Westrick and A. Jaffe, Hybrid Bronzes: Mixed–Valence Organic–Inorganic Metal Oxides as a Tunable Material Platform, Chem. Sci., 2023, 14(39), 10756–10767, 10.1039/D3SC03828A.
- X. Zhang, R. Andris, T. Averianov, M. J. Zachman and E. Pomerantseva, Hybrid Bilayered Vanadium Oxide Electrodes with Large and Tunable Interlayer Distances in Lithium–Ion Batteries, J. Colloid Interface Sci., 2024, 674, 612–623, DOI:10.1016/j.jcis.2024.06.164.
- M. Clites and E. Pomerantseva, Synthesis of Hybrid Layered Electrode Materials via Chemical Pre–Intercalation of Linear Organic Molecules, in Low–Dimensional Materials and Devices 2018, ed. N. P. Kobayashi, A. A. Talin, A. V. Davydov, and M. S. Islam, SPIE: San Diego, United States, 2018, p. 27, DOI:10.1117/12.2321263.
- M. A. Spencer, J. Fortunato and V. Augustyn, Electrochemical Proton Insertion Modulates the Hydrogen Evolution Reaction on Tungsten Oxides, J. Chem. Phys., 2022, 156(6), 064704, DOI:10.1063/5.0082459.
- M. L. Freedman, The Tungstic Acids, J. Am. Chem. Soc., 1959, 81(15), 3834–3839, DOI:10.1021/ja01524a009.
- D. Chen, T. Li, L. Yin, X. Hou, X. Yu, Y. Zhang, B. Fan, H. Wang, X. Li, R. Zhang, T. Hou, H. Lu, H. Xu, J. Sun and L. Gao, A Comparative Study on Reactions of N–Alkylamines with Tungstic Acids with Various W–O Octahedral Layers: Novel Evidence for the “Dissolution–Reorganization” Mechanism, Mater. Chem. Phys., 2011, 125(3), 838–845, DOI:10.1016/j.matchemphys.2010.09.039.
- F. Fabregat-Santiago, I. Mora-Seró, G. Garcia-Belmonte and J. Bisquert, Cyclic Voltammetry Studies of Nanoporous Semiconductors. Capacitive and Reactive Properties of Nanocrystalline TiO2 Electrodes in Aqueous Electrolyte, J. Phys. Chem. B, 2003, 107(3), 758–768, DOI:10.1021/jp0265182.
- M. A. Spencer, N. P. Holzapfel, K. E. You, G. Mpourmpakis and V. Augustyn, Participation of Electrochemically Inserted Protons in the Hydrogen Evolution Reaction on Tungsten Oxides, Chem. Sci., 2024, 15(14), 5385–5402, 10.1039/D4SC00102H.
- C. Cao, H. G. Steinrück, B. Shyam, K. H. Stone and M. F. Toney, In Situ Study of Silicon Electrode Lithiation with X–Ray Reflectivity, Nano Lett., 2016, 16(12), 7394–7401, DOI:10.1021/acs.nanolett.6b02926.
- P. Giannozzi, et al., QUANTUM ESPRESSO: a modular and open–source software project for quantum simulations of materials, J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef.
- P. Giannozzi, et al., Advanced capabilities for materials modelling with Quantum ESPRESSO, J. Phys.: Condens. Matter, 2017, 29, 465901 CrossRef CAS.
- Satomichi Nishihara, BURAI 1.3, A GUI of Quantum ESPRESSO Search PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS.
- O. Hurtado-Aular, R. Anez and A. Sierraalta, DFT+ U study of the electronic structure changes of WO3 monoclinic and hexagonal surfaces upon Cu, Ag, and Au adsorption. Applications for CO adsorption, Surf. Sci., 2021, 714, 121907 CrossRef CAS.
- M. Cococcioni and S. De Gironcoli, Linear Response Approach to the Calculation of the Effective Interaction Parameters in the LDA + U Method, Phys. Rev. B, 2005, 71(3), 035105, DOI:10.1103/PhysRevB.71.035105.
- N. Bondarenko, O. Eriksson and N. V. Skorodumova, Polaron Mobility in Oxygen–Deficient and Lithium–Doped Tungsten Trioxide, Phys. Rev. B:Condens. Matter Mater. Phys., 2015, 92(16), 165119, DOI:10.1103/PhysRevB.92.165119.
- L. Zhang, B. Wen, Y. N. Zhu, Z. Chai, X. Chen and M. Chen, First–Principles Calculations of Water Adsorption on Perfect and Defect WO3(0 0 1), Comput. Mater. Sci., 2018, 150, 484–490, DOI:10.1016/j.commatsci.2018.04.056.
- J. D. Pack and H. J. Monkhorst, “Special points for Brillouin–zone integrations”—a reply, Phys. Rev. B, 1977, 16, 1748 CrossRef.
- J. T. Szymanski and A. C. Roberts, The crystal structure of tungstite,WO3·H2O, Can. Mineral., 1984, 22, 681–688 CAS.
- S. V. Chong, B. Ingham and J. L. Tallon, Novel Materials Based on Organic–Tungsten Oxide Hybrid Systems I: Synthesis and Characterisation, Curr. Appl. Phys., 2004, 4(2–4), 197–201, DOI:10.1016/j.cap.2003.11.008.
- H. Sun, F. Song, C. Zhou, X. Wan, Y. Jin, Y. Dai, J. Zheng, S. Yao and Y. Yang, Lattice–Water–Induced Acid Sites in Tungsten Oxide Hydrate for Catalyzing Fructose Dehydration, Catal. Commun., 2021, 149, 106254, DOI:10.1016/j.catcom.2020.106254.
- D. Y. Lu, J. Chen, J. Zhou, S. Z. Deng, N. S. Xu and J. B. Xu, Raman Spectroscopic Study of Oxidation and Phase Transition in W18O49 Nanowires, J. Raman Spectrosc., 2007, 38(2), 176–180, DOI:10.1002/jrs.1620.
- H. Suzuki, O. Tomita, M. Higashi and R. Abe, Tungstic Acids H2WO4 and H4WO5 as Stable Photocatalysts for Water Oxidation under Visible Light, J. Mater. Chem. A, 2017, 5(21), 10280–10288, 10.1039/C7TA01228D.
- A. M. A. Da Costa, C. F. G. C. Geraldes and J. J. C. Teixeira-Dias, A Raman Spectroscopic Study of Molecular Interaction in Long-chain Primary Amines Systems, J. Raman Spectrosc., 1982, 13(1), 56–62, DOI:10.1002/jrs.1250130111.
- A. M. Rich, S. Bhattacharyya, V. R. Aldilla, J. E. Beves, M. Bhadbhade, N. Kumar, E. T. Luis and C. E. Marjo, Quantifying Alkyl Chain Disorder in Crystalline Models of Lipid Bilayers Using Raman Spectroscopy, J. Raman Spectrosc., 2019, 50(1), 63–73, DOI:10.1002/jrs.5501.
- J. B. Mitchell, R. Wang, J. S. Ko, J. W. Long and V. Augustyn, Critical Role of Structural Water for Enhanced Li+ Insertion Kinetics in Crystalline Tungsten Oxides, J. Electrochem. Soc., 2022, 169(3), 030534, DOI:10.1149/1945–7111/ac58c8.
- U. Müller, in Niggli Notation Described, Inorganic Structural Chemistry, J. Wiley, Chichester, 2nd edn, 2007, p. 7 Search PubMed.
- H. W. Eng, P. W. Barnes, B. M. Auer and P. M. Woodward, Investigations of the Electronic Structure of D0 Transition Metal Oxides Belonging to the Perovskite Family, J. Solid State Chem., 2003, 175(1), 94–109, DOI:10.1016/S0022–4596(03)00289–5.
- T. Liu, N. P. Holzapfel and P. M. Woodward, Understanding Structural Distortions in Hybrid Layered Perovskites with the n = 1 Ruddlesden–Popper Structure, IUCrJ, 2023, 10(4), 385–396, DOI:10.1107/S2052252523003743.
- Y. M. Li, M. Hibino, M. Miyayania and T. Kudo, Proton Conductivity of Tungsten Trioxide Hydrates at Intermediate Temperature, Solid State Ionics, 2000, 134(3–4), 271–279, DOI:10.1016/S0167–2738(00)00759–1.
- B. J. Campbell, H. T. Stokes, D. E. Tanner and D. M. Hatch, ISODISPLACE: A Web–Based Tool for Exploring Structural Distortions, J. Appl. Crystallogr., 2006, 39(4), 607–614, DOI:10.1107/S0021889806014075.
Footnote |
| † Electronic supplementary information (ESI) available: Additional experimental details and electrochemical and spectroscopic information about materials. See DOI: https://doi.org/10.1039/d4ta08647c |
| This journal is © The Royal Society of Chemistry 2025 |