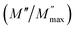Achieved excellent energy storage performance under moderate electric field in BaTiO₃-modified Bi_0.5Na_0.5TiO₃-based lead-free ceramics via multiple synergistic design

Abstract

Dielectric capacitors show great potential for use in pulse power devices due to their high power density. However, achieving ultrahigh recoverable energy density (W_rec) and efficiency (η) remains a challenge, limiting their applications. To address this, Na_0.5Bi_0.5TiO₃–BaTiO₃ (NBT-BT) ceramics were optimized for energy storage devices operating at a relatively low electric field (E). This study introduces a synergistic optimization strategy by incorporating Ca(Hf_0.7Zr_0.3)O₃ (CHZ) into 0.93NBT–0.07BT (BNBT) ceramics. The addition of CHZ, in concentrations ranging from x = 0.00 to 0.18, significantly enhances the differences between saturation and remnant polarization from 15.6 μC cm⁻² to 42.5 μC cm⁻², while reducing the grain size from 2.44 μm to 620 nm. An optimal W_rec of ∼5.09 J cm⁻³ with η of ∼77% was achieved in BNBT–0.14CHZ ceramics at a moderate electric field (283 kV cm⁻¹). Moreover, the energy storage density and efficiency exhibited good frequency stability (10–1000 Hz), temperature stability (25–150 °C) and fatigue resistance (1–10⁴ cycles). A fast discharge time (∼72 ns) was concurrently realized at x = 0.14 ceramics. These results suggest that the eco-friendly BNBT–0.14CHZ ceramic is a promising candidate for application in dielectric energy storage capacitors under moderate electric field.

---

1. Introduction

Dielectric ceramic capacitors, as potential high-power energy storage devices, have attracted increasing attention due to their advantages of high power density, fast charging and discharging speed, good stability, and low cost.¹ However, the low energy storage density remains a major bottleneck that needs to be addressed, significantly limiting their applications. Generally, the energy storage performance (ESP) of dielectric capacitors is determined by three parameters:² total energy storage density (W_tol), recoverable energy storage density (W_rec) and energy storage efficiency (η). These parameters are typically derived from the hysteresis loop of the polarized-electric field and are defined by the following equations:³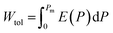, 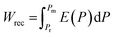and 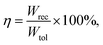where P_m, P_r and E denote maximum polarization value, remnant polarization value and the applied electric field, respectively. A large polarization discrepancy ΔP (ΔP = P_m − P_r) and a high breakdown strength (BDS) are beneficial for achieving high ESP. Among all reported dielectric systems, relaxor ferroelectrics (RFE) have shown great promise as energy storage materials due to their relatively large P_m, decent electric field, and narrow hysteresis loops. For instance, Chen et al. reported a great W_rec of ∼11.2 J cm⁻³ with a ΔP of ∼49 μC cm⁻² at 400 kV cm⁻¹ in (Pb_0.94Sm_0.04)(Zr_0.6Sn_0.4)O₃ ceramic.⁴ Zhou et al. revealed a W_rec of ∼3.74 J cm⁻³ with a ΔP of ∼35.5 μC cm⁻² under 273 kV cm⁻¹ at a BaTiO₃-based ceramic.⁵ Despite these promising results, the inherent inversion correlation between polarization and BDS in relaxor ferroelectrics remains a limiting factor for achieving further improvements in ESP. To address this challenge, novel structure designs such as core–shell structures and multi-layered ceramics have been widely explored. For example, Huang et al. achieved an excellent W_rec of ∼5.92 J cm⁻³ and a η of ∼81.7% at 552.3 kV cm⁻¹ in the core–shell Ba_0.55Sr_0.39Zn_0.06TiO₃–BiMg_2/3Nb_1/3O₃ ceramics.⁶ Ma et al. designed 0.65Bi_0.5Na_0.5TiO₃–0.35SrTiO₃–0.15La(Mg_1/2Zr_1/2)O₃ multilayered ceramics with an ultrahigh W_rec of ∼13.5 J cm⁻³ at 1050 kV cm⁻¹.⁷

Recently, environmentally friendly lead-free RFE ceramics, such as BaTiO₃ (BT), Na_0.5Bi_0.5TiO₃ (NBT) and BiFeO₃ (BF) have also attracted great attention. For instance, Dai et al. reported a W_rec of ∼3.81 J cm⁻³ and a η of ∼90.5% at 405 kV cm⁻¹ in Ba_0.85Ca_0.15Zr_0.1Ti_0.9O₃–0.075BiMg_2/3Nb_1/3O₃ ceramics.⁸ Luo et al. achieved an extraordinary W_rec of 6.02 J cm⁻³ and a superior η of 94.5% at 450 kV cm⁻¹ in a new type of lead-free 0.94Bi_0.47Na_0.47Ba_0.06TiO₃–0.06CaHfO₃–0.45Bi_0.2Sr_0.7TiO₃ relaxor ferroelectric ceramics.⁹ Zhao et al. also obtained a large W_rec ∼ 6 J cm⁻³ along with superior η of ∼90% at 520 kV cm⁻¹ by incorporating BaTiO₃–Bi(Li_1/3Hf_2/3)O₃ into BiFeO₃.¹⁰ Although significant progress has been made, the majority of these results are obtained at high electric fields (>500 kV cm⁻¹). However, high E limits the applicability due to environmental concerns and increased losses during long-term operation.¹¹ Therefore, developing new lead-free ceramics with excellent W_rec at relatively low E remains a critical challenge.

It is noted that a high ΔP is a prerequisite for achieving high ESP under a low electric field. Among traditional ferroelectric materials, the lead-free NBT-BT system with a morphotropic phase boundary (MPB) is a promising candidate for energy storage applications due to its good ferroelectricity (P_m > ∼40 μC cm⁻²)¹² and high Curie temperature (>320 °C).¹³ Unfortunately, high remnant polarization severely limits the energy storage density and efficiency. To address this issue, ion doping and the construction of new solid solutions have been employed. For instance, a high W_rec of ∼4.60 J cm⁻³ with a η of ∼82% at 260 kV cm⁻¹ was reported in Na_0.5Bi_0.5TiO₃–Sr_0.7Bi_0.2TiO₃–0.04Ag_0.9Ca_0.05NbO₃ ceramic.¹⁴ Nie et al. revealed a W_rec of ∼3.14 J cm⁻³ and a η of ∼71.3% at 250 kV cm⁻¹ for Na_0.5Bi_0.5TiO₃–BaTiO₃–BiFeO₃–0.15CaTiO₃ ceramic.¹⁵ Although some progress has been made in NBT-BT-based ceramics, a high ESP with a large W_rec (>5 J cm⁻³) and large η (>70%) is still hard to obtain at a relatively low electric field (<300 kV cm⁻¹).

To address the challenges and further enhance the ESP of NBT-BT-based ceramics, the primary method involves regulating the compositional disorder of A/B sites. This is achieved by enhancing relaxor behavior, employing nanodomain engineering, and refining grain size, as illustrated in Fig. 1. To design NBT-BT-based ceramics for energy storage devices with high ESP at relatively low electric fields, a multiscale optimization strategy is proposed by introducing CHZ into BNBT ceramics. The rationale for selecting CHZ as the chemical modifier is as follows: (1) Hf elements, known for their wide bandgap and superior quality, contribute effectively to grain refinement. For example, Luo et al. introduced Hf⁴⁺ into Bi_0.47Na_0.47Ba_0.06TiO₃, achieving a fine grain size of ∼0.59 μm.¹³ (2) The introduction of weakly polar ions Ca²⁺ and Zr⁴⁺ induces local random field effects, disrupting the long-range ferroelectric (FE) sequence and generating polar nanoregions (PNRs), thereby improving ESP. Acosta et al. incorporated CaZrO₃ into Bi_0.5Na_0.5TiO₃–BaTiO₃, which contributed to non-uniform domain structures, further enhancing ESP.¹⁶ By utilizing this synergistic optimization strategy, a high ESP at moderate electric fields can be achieved.

Fig. 1 Schematic diagram of the strategy for achieving excellent energy storage properties under a relatively low electric field via synergistic optimization design.

Motivated by this approach, (Bi_0.5Na_0.5)_0.93Ba_0.07TiO₃–xCa(Hf_0.7Zr_0.3)O₃ (x = 0.00, 0.10, 0.12, 0.14, 0.16, and 0.18) lead-free ceramics were synthesized using a conventional solid-state sintering method. Remarkably, a giant W_rec of ∼5.09 J cm⁻³ and a η of ∼77% were obtained at a moderate of ∼283 kV cm⁻¹ for BNBT–0.14CHZ ceramics, along with an ultrahigh ΔP of ∼42.5 μC cm⁻². Furthermore, the optimal ceramics have good frequency stability (10–1000 Hz), good temperature stability (25–150 °C), superior fatigue resistance (1–10⁴ cycles), and a rapid discharge time (∼72 ns). The mechanism for improving ESP will be explored.

2. Experimental methods

The (Bi_0.5Na_0.5)_0.93Ba_0.07TiO₃–xCa(Hf_0.7Zr_0.3)O₃ (x = 0.00, 0.10, 0.12, 0.14, 0.16, and 0.18) lead-free ceramics were synthesized via a conventional solid-state sintering method. The raw materials, including Bi₂O₃ (99.99%), Na₂CO₃ (99.8%), BaCO₃ (99.95%), TiO₂ (99.99%), CaCO₃ (99.99%), HfO₂ (99.9%), and ZrO₂ (99.99%) were weighed according to their stoichiometric formula and ball-milled for 24 h in ethanol. The collected powders were pre-sintered at 800 °C for 2 h, mixed with 5% PVA, and then pressed into discs with a diameter of approximately 13 mm and a thickness of about 1 mm at a pressure of 10 MPa. Prior to sintering, the samples were heated to 600 °C and held for 120 minutes to discharge the PVA. Finally, all samples were sintered at 1100–1200 °C for 3 h.

X-ray diffraction (XRD) using a PANalytical X'Pert PRO diffractometer was employed to investigate the crystal structure. Raman spectroscopy was conducted using a Raman scattering spectrometer (inVia, RENISHAW, UK). Microstructure analysis was performed using a scanning electron microscope (SEM, ZEISS Ultra 500, Germany). The polished discs were thermally etched at 950 °C for 10 minutes before SEM examination. Dielectric behavior was characterized using an LCR meter (E4980A, Agilent). Ferroelectric properties were measured by recording P–E loops with a ferroelectric analyzer (Radiant Technology). Ultraviolet-visible absorbance spectra was characterized by a UV-vis spectrophotometer (UV2600, Shimadzu, Kyoto, Japan), and the domain morphologies were observed with a transmission electron microscope (TEM, JEM-2100HR, JEOL, Japan).

3. Results and discussion

The XRD patterns of the BNBT–xCHZ (x = 0.00, 0.10, 0.12, 0.14, 0.16, and 0.18) ceramics are presented in Fig. 2(a). Each sample shows a typical cubic perovskite structure without any impure peak, indicating that CHZ is well incorporated into the BNBT matrix. A detailed analysis of the (200) diffraction peak, as shown in Fig. 2(b), reveals a gradual shift towards a lower angle with increasing CHZ doping content (x), suggesting lattice expansion. This shift is attributed to the substitution of Ti⁴⁺ (CN6, 0.605 Å) at the B-site by Hf⁴⁺ (CN6, 0.71 Å) and Zr⁴⁺ (CN6, 0.84 Å), which have larger ionic radii. Raman spectra was used to measure their vibration modes and local structure. As exhibited in Fig. 2(c), the active mode below 200⁻¹ related to the A-site vibration, remains almost unchanged across all CHZ doping levels, suggesting that the high polarization can be primarily maintained through Bi ion activity.^17,18 In contrast, the Raman active mode between 500–600 cm⁻¹ weakens and diffuses toward higher wave numbers as CHZ content increases. This phenomenon is due to the more disordered lattice structures induced by CHZ, which contribute to the improvement of relaxor behavior.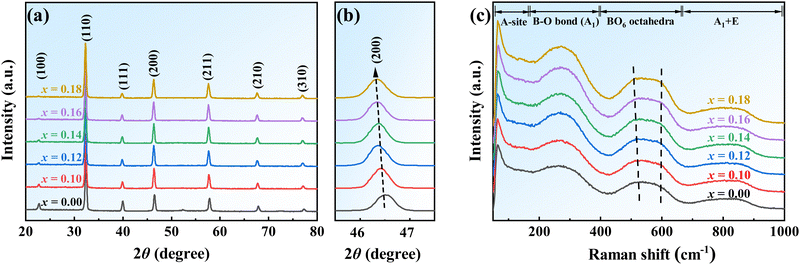

Fig. 2 (a) XRD patterns of BNBT–xCHZ ceramics and (b) The enlarged (200) peaks. (c) Room-temperature Raman spectra for BNBT–xCHZ ceramics.

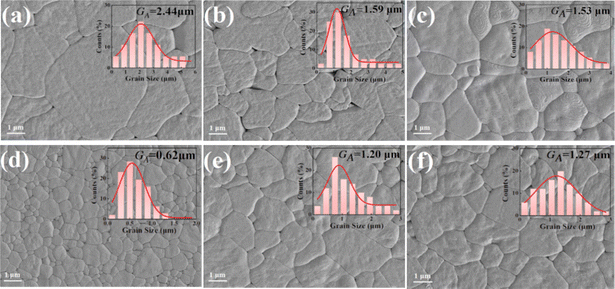
Fig. 3(a)–(f) display the SEM micro-images of the thermally-etched BNBT–xCHZ ceramics. All ceramics exhibit a dense microstructure with low porosity and well-defined grain boundaries. The corresponding insets in Fig. 3(a)–(f) exhibit their grain size distributions. Upon increasing x, the average grain size (G_A) first gradually decreases and then slightly increases. The reduced G_A can be attributed to the doping of CHZ, in which the larger ionic radius and the heavier atomic mass could hinder the ion-diffusion rates in sintering, retarding grain growth. When x > 0.14, a slight increase in G_A can be seen, possibly indicating that excessive doping leads to crystal lattice defects and abnormal grain growth.¹⁹ The smallest G_A of ∼0.62 μm is obtained at x = 0.14 ceramics. Based on the relationship: 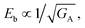²⁰ it is expected that smaller grains will improve the BDS.

Fig. 3 The SEM images of the BNBT–xCHZ ceramics: (a) x = 0.00, (b) x = 0.10, (c) x = 0.12, (d) x = 0.14, (e) x = 0.16, and (f) x = 0.18. The insets in (a)–(f) are the corresponding distribution of grain size.

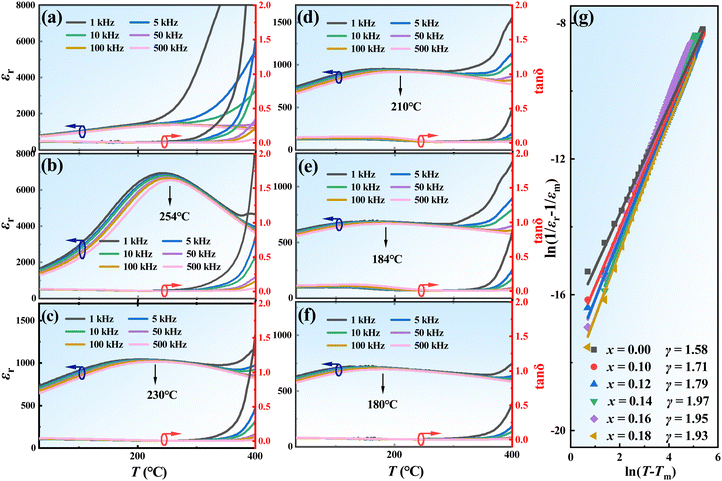
Fig. 4(a)–(f) present the dielectric properties of BNBT–xCHZ ceramics at different temperatures (T). For the ceramics with x = 0.00, the dielectric peak exists above 400 °C making it undetectable due to the experimental range (T ∈ (−50 °C, 400 °C)). Upon the introduction of CHZ, a relaxor-like peak, exhibiting frequency dependence, emerges, signifying a transition from ferroelectric to relaxor characteristics.¹⁸ As the CHZ content increases further, the relaxor dielectric peak becomes gradually suppressed, broadened, and shifts towards lower T, indicating enhanced relaxor behavior.²¹ To accurately explore the relaxation behavior of ceramics, the modified Curie–Weiss method²² was employed to evaluate the relaxation degree (γ) by the equation: 1/ε − 1/ε_m = (T − T_m)^γ/C, at T > T_m, where ε_m and T_m is the maximum dielectric constant and the corresponding T, respectively, and C is the constant. The curves of log(1/ε − 1/ε_m) and log(T − T_m) at 500 kHz are plotted in Fig. 4(g). The parameter γ is defined between 1 and 2, where 1 corresponds to an ideal ferroelectric and 2 corresponds to an ideal relaxor ferroelectric.²⁰ Compared to pure BNBT (x = 0.00) ceramics (γ = 1.58), the γ value increases almost linearly with CHZ content, further confirming the enhancement of relaxor behavior,^19,23 which is consistent with the Raman results shown in Fig. 2(c).

Fig. 4 Temperature-dependence of dielectric constant (ε_r) and loss (tan δ) of the BNBT–xCHZ ceramics measured from 1 kHz to 500 kHz: (a) x = 0.00, (b) x = 0.10, (c) x = 0.12, (d) x = 0.14, (e) x = 0.16, and (f) x = 0.18. (g) ln(1/ε − 1/ε_m) as a function of ln(T − T_m) of the BNBT–xCHZ ceramics at 500 kHz.

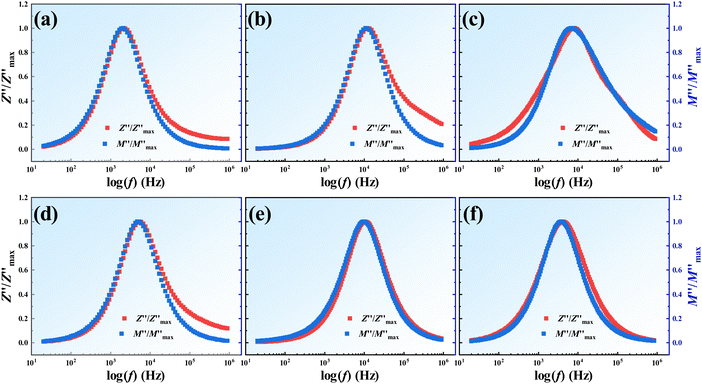
To investigate the influence of grains, grain boundaries, and electrode interfaces on the conductivity behavior, the complex impedance plots (Z′ − Z′′) of BNBT–xCHZ ceramics from 370 °C to 450 °C were measured and signified in Fig. 5(a)–(f). All samples exhibit a single semicircular arc, indicating a single relaxation mechanism caused by the grains of the ceramic, which is classified as a bulk response.²¹ This is because the grain boundary and electrode responses are not observed within the tested temperature and frequency ranges. For all samples, as the temperature increases, the intercept of the curve on the x-axis decreases, which is attributed to the oxygen vacancies generated at higher temperatures.¹² With increasing doping content (x), the impedance initially increases and then decreases, reaching its maximum value in BNBT–0.14CHZ ceramics. This behavior is related to the refinement of grain size, as shown in Fig. 3, while the subsequent decrease with excessive doping is likely due to defects between the grain boundaries.²⁴ Moreover, grains and grain boundaries in ceramics generally correspond to different electroactive regions, each having distinct time constants, characteristic frequencies, and activation energies. The electroactive regions of ceramics are further explored using Z′′ and M′′, measured at 410 °C, as a function of frequency and normalized in Fig. 6(a)–(f).²⁵M* represents electric modulus, which can be expressed in terms of Z* through the following equations: M* = M′ + jM′′ = jωC₀Z* = ωC₀Z′′ + jωC₀Z′. Notably, for all samples, the two curves nearly overlap, suggesting that the electroactive properties of the ceramic grains and grain boundaries are similar, indicating good electrical homogeneity in the ceramics. This homogeneity helps to reduce the likelihood of local electrical breakdown.

Fig. 5 The complex impedance spectra of the BNBT–xCHZ ceramics from 370 °C to 450 °C: (a) x = 0.00, (b) x = 0.10, (c) x = 0.12, (d) x = 0.14, (e) x = 0.16, and (f) x = 0.18.

Fig. 6 Plots of normalized imaginary of part complex impedance and imaginary part of complex electric modulus at 410 °C: (a) x = 0.00, (b) x = 0.10, (c) x = 0.12, (d) x = 0.14, (e) x = 0.16, and (f) x = 0.18.

At 410 °C, Z-view software was used to fit the arcs of complex impedance. The corresponding R-CPE component was selected to match the shape of the curve, as shown in Fig. 7(a) [see Table S2 for the fitted parameters, ESI†]. Moreover, based on the Arrhenius fitting: σ = σ₀ exp(E_a/k_BT), where σ is conductivity, σ₀ is the constant and k_B is the Boltzmann constant, the activation energy (E_a) are calculated. This energy reflects the barrier that must be overcome for carrier injection into the dielectric. As shown in Fig. 7(b), the maximum E_a is obtained at BNBT–0.14CHZ ceramics for 1.741 eV. A high E_a also indicates that the ceramic has a strong resistance to electrical breakdown.

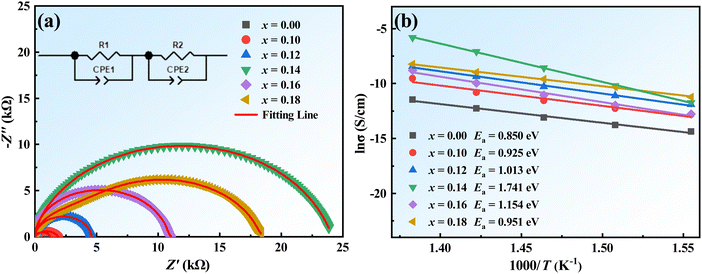Fig. 7 (a) Equivalent model and fitting results of BNBT–xCHZ ceramics at 410 °C and (b) relationship between ln(σ) and 1000/T for BNBT–xCHZ ceramics.

To evaluate the average E_b values of BNBT–xCHZ ceramics, a Weibull distribution analysis was conducted. As shown in Fig. 8(a), the large slope value (β > 14) demonstrated good reliability.²⁰ The average E_b increases steadily from 119 to 286 kV cm⁻¹. This enhancement in E_b is not only related to grain refinement but also to the reduced dielectric loss (see Fig. 4) and leakage current (see Fig. S2, ESI†). Next, the unipolar P–E loops tested at the average E_b and 100 Hz are presented in Fig. 8(b). For the ceramics with x = 0.00, a well-saturated P–E loop with large hysteresis is exhibited, illustrating a typical ferroelectric behavior.²⁶ The maximum polarization P_m is up to ∼58.6 μC cm⁻², which is consistent with the reports.^21,22 Upon increasing CHZ doping content, the shape of P–E loops become slimmer, indicating the transformation from FE to RFE. Notably, an ultrahigh ΔP of up to ∼42.5 μC cm⁻² is achieved in BNBT–0.14CHZ ceramics, which is higher than most reported NBT-based ceramics,^{13–15,27–31} as summarized in Fig. 8(d). The ultrahigh ΔP value should be owing to the large lattice distortions in the perovskite structure.¹² Consider that the ferroelectric polarization in NBT-based ceramics is mainly attributed to the hybridizations between 6p electrons of Bi³⁺ and 2p electrons of O²⁻ orbitals. In this work, the substitutions of Bi³⁺ by Na⁺, Ba²⁺ and Ca²⁺ on A-sites, and Ti⁴⁺ by Hf⁴⁺ and Zr⁴⁺ on B-sites could further enhance the lattice distortion. It was also widely reported that doping can enhance the polarization of NBT-based ceramics.¹¹ According to these P–E data, the corresponding W_rec and η can be evaluated, and shown in Fig. 8(c) as a function of doping CHZ content, x. It can be found that an a giant W_rec of ∼5.09 J cm⁻³ and a η of ∼77% are achieved in BNBT–0.14CHZ. A comparison of W_rec and η between our BNBT–0.14CHZ ceramics and previously reported lead-free dielectric ceramics^{5,8–10,13,26,27,30–50} is summarized in Fig. 8(e). It can be seen that the achievement of a giant W_rec (>5 J cm⁻³) usually requires a large E (>400 kV cm⁻¹), while our BNBT–0.14CHZ ceramics receive an excellent W_rec of ∼5.09 J cm⁻³ at a moderate E of 283 kV cm⁻¹, indicating great potential for applications at moderate electric field.

Fig. 8 (a) Weibull distribution of dielectric breakdown strengths of BNBT–xCHZ ceramics. (b) Unipolar P–E loops of BNBT–xCHZ ceramics with various electric fields at 100 Hz and (c) the corresponding ESP values as a function of the doping content of CHZ. (d) A comparison of ΔP and E between BNBT–0.14CHZ ceramic and previously reported NBT-based ceramics. (e) A comparison of W_rec and E between BNBT–0.14CHZ ceramic and previously reported ceramics.

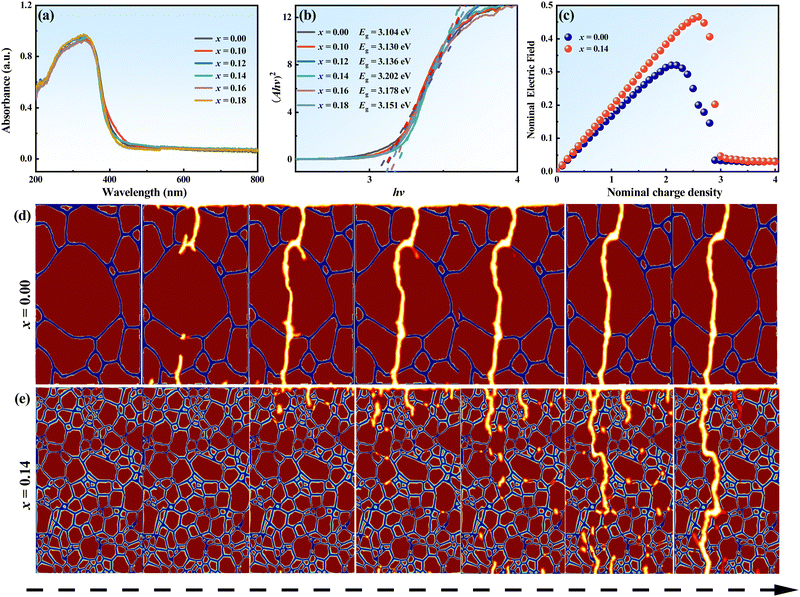
To explore the intrinsic mechanism of the enhanced BDS in BNBT–xCHZ ceramics, their UV spectrophotometer were measured and results are displayed in Fig. 9(a). From Fig. 9(a), the band gap width (E_g) could be calculated by the Tauc equation:¹³ (hv)² = A(hv − E_g), where h, A, α, and v are the Planck constant, the constant, the absorption coefficient, and the frequency, respectively. The detailed derivation of E_g is enlarged in Fig. 9(b), and the value of E_g is listed in the insert in Fig. 9(b). It can be seen that E_g gradually increases from 3.104 eV @ x = 0.00 to 3.202 eV @ x = 0.14 ceramics. The increased E_g indicates that it becomes more difficult for electrons in the valence band to transition to the conduction band,⁹ which contributes significantly to the enhanced BDS and the consequent improvement in ESP. However, excessive doping creates a disproportionate relationship between E_g and E_b, likely due to the appearance of small pores, as shown in Fig. 3(e) and (f).

Fig. 9 (a) The UV absorption spectra, and (b) the E_g of BNBT–xCHZ ceramics. (c) Corresponding nominal electric field vs. charge density curves. Breakdown paths at different moments of the BNBT–xCHZ ceramics: (d) x = 0.00 and (e) x = 0.14.

To further explore the effect of grain size on the BDS, COMSOL Multiphysics Software was used to analyze the breakdown behavior of the BNBT–xCHZ ceramics with x = 0.00 and x = 0.14. The breakdown path diagrams at different moments are shown in Fig. 9(d) and (e), respectively. It is evident that the breakdown path initiates from a point at the top of the intensified field and gradually spreads throughout the ceramic. In contrast, the ceramics with x = 0.14 exhibit a longer breakdown time along the breakdown path at the grain boundary, indicating that CHZ could run as a “strengthened grain boundary” in the ceramic, contributing to the refined grain size and improved E_b. As exhibited in Fig. 9(c), the nominal electric field of BNBT–0.14CHZ ceramic is significantly higher compared to the BNBT–xCHZ ceramic with x = 0.00, demonstrating the substantial enhancement in breakdown strength due to the introduction of CHZ.

The optimal BNBT–0.14CHZ ceramics were further studied with TEM to investigate the relationship between the ESP and microstructure. The low-resolution TEM in Fig. 10(a) reveals a well-organized grain structure with tightly connected grain boundaries. Fig. 10(b) further confirms the tightly bonded grain boundaries, free of voids. These dense grain boundaries not only inhibit the diffusion of defects under external stress and electric fields but also provide high resistance, which contributes to the improvement in BDS of the ceramics.⁵¹Fig. 10(c) displays the existence of the short-range ordered nanoscale fringe domains, which also can be confirmed by the P–E loops in Fig. 8(b). The existence of PNRs is attributed to the introduction of CHZ in BNBT ceramics, which destroys the long-range ferroelectric domain by the displacement of Hf⁴⁺ and Zr⁴⁺ for Ti⁴⁺ at B-site.¹¹ These PNRs can be interconnected to form long-range ferroelectric domains under the applied electric field, resulting in a large P_max, and then restore to the state of PNRs to attain a low P_r when the applied electric field is removed, consequently, improving the ESP.¹⁸Fig. 10(d) exhibits the HR-TEM images of lattice fringes and the corresponding selected area electron diffraction (SAED) pattern along the [110] zone axis, revealing an excellent grain structure.³¹

Fig. 10 TEM images of (a) grains and (b) grain boundary. (c) HR-TEM images of domain morphology, and (d) lattice fringes (inset is the corresponding SAED pattern along [110] c) of BNBT–0.14CHZ ceramic.

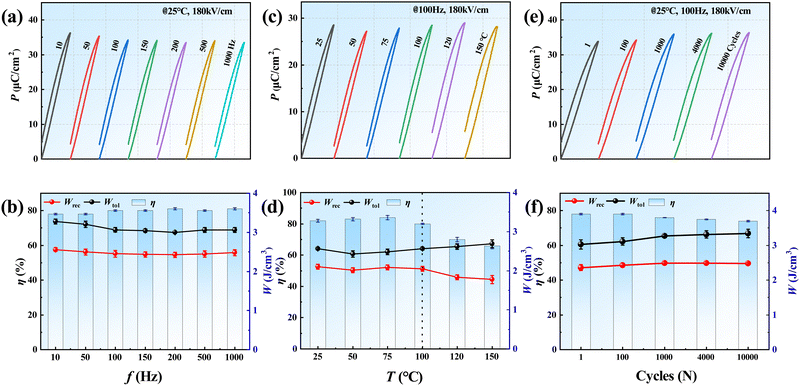
In practical applications of dielectric energy storage capacitors, good frequency and temperature stabilities, and fatigue resistance are critical. Thus, it is necessary to further explore these characteristics. Fig. 11(a) displays the unipolar P–E loops of BNBT–0.14CHZ ceramics from 10 Hz to 1000 Hz at RT and 180 kV cm⁻¹. The curves clearly maintain a slim shape. The corresponding W_rec and η shown in Fig. 11(b), exhibit only slight fluctuation (<4%), indicating good frequency stability. Fig. 11(c) displays the unipolar P–E loops of BNBT–0.14CHZ ceramics from 25 °C to 150 °C at 180 kV cm⁻¹ and 100 Hz. Fig. 11(d) shows good temperature stability with a variation of W_rec < 2.3% at T ≤ 100 °C, while they are degraded at T > 100 °C, which might be attributed to the enhanced domain switching polarization as well as increased the conduction loss at high temperature.⁵²Fig. 11(e) displays the unipolar P–E loops of BNBT–0.14CHZ ceramics from 1 to 10⁴ cycles at 180 kV cm⁻¹ and 100 Hz. With the rise of cycle numbers, P_m increases slightly, while the fluctuations of W_rec and η are less than ∼5.1% and ∼2.3%, respectively, as shown in Fig. 11(f), suggesting a good fatigue resistance.

Fig. 11 (a) Unipolar P–E loops and (b) ESP for the BNBT–0.14CHZ ceramics as a function of frequency from 10 Hz to 1000 Hz under 180 kV cm⁻¹ at room temperature. (c) Unipolar P–E loops and (d) ESP as a function of temperature from 25 °C to 150 °C for the BNBT–0.14CHZ ceramics under 180 kV cm⁻¹ at 100 Hz. (e) Unipolar P–E loops and (f) ESP for the BNBT–0.14CHZ ceramic with different fatigue cycles under 180 kV cm⁻¹ at 100 Hz.

The underdamped pulsed discharge electric current–time curves as a function of electric field were investigated to reveal the actual energy discharge behavior of BNBT–0.14CHZ, as depicted in Fig. 12(a). The corresponding current density (C_D = I_max/S, where S is the effective electrode area) and power density (P_D = EI_max/2S) under various E are illustrated in Fig. 12(b). C_D and P_D are ∼499.6 A cm⁻² and ∼25.0 MW cm⁻³ at 100 kV cm⁻¹, respectively. The overdamped discharge curves under various E are shown in Fig. 12(c), and the corresponding discharge energy density can be calculated by the equation: where I, t, R (100 Ω in this paper), and V are the current value, time, load resistance, and volume, respectively, as plotted in Fig. 12(d). Note that under the same E, W_dis is smaller than W_rec, which is attributed to domain clamping caused by the more energy loss during charge and discharge testing. Moreover, the discharge time t_0.9 (corresponding to the time of 90% energy releasing) is ∼72 ns. The fast discharge rate should be mainly ascribed to the existence of highly dynamic nanodomains featuring a fast polarization response to the applied electric field. The high P_D, W_dis values and a short t_0.9 indicate that the BNBT–0.14CHZ ceramics are promising candidates for pulsed power system applications.

Fig. 12 (a) Underdamped discharge current curves of the x = 0.14 ceramics at room temperature. (b) Variation of C_D and P_D at different electric fields. (c) Overdamped discharge current curves of the x = 0.14 ceramics at room temperature. (d) The discharge energy density (W_dis) of the x = 0.14 ceramics at different electric fields.

4. Conclusion

In summary, BNBT–xCHZ ceramics were successfully designed by a synergistic optimization strategy. The incorporation of BT into NBT to construct MPB was helpful to sustain a high P_m, while the addition of CHZ optimized the microstructure, refined the grain size, reduced P_r, narrowed the hysteresis loops, and formed PNRs. Consequently, a giant W_rec of ∼5.09 J cm⁻³ and a large ΔP of ∼42.5 μC cm⁻² were obtained simultaneously in BNBT–0.14CHZ ceramics at 283 kV cm⁻¹. In addition, good frequency stability from 10 Hz to 1000 Hz, good temperature stability from 25 °C to 150 °C, excellent fatigue resistance among 1–10⁴ cycles and a fast discharge time of ∼72 ns were achieved. These results suggested that the BNBT–0.14CHZ ceramics could be a promising material to use in high-energy storage dielectric capacitors applications.

Data availability

All data is presented in the form of charts in the paper.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the Funding by Science and Technology Projects in Guangzhou (202201000008), the Natural Science Foundation of Guangdong Province of China (2024A1515012484), the Guangdong Provincial Key Laboratory (2020B1212060066), the Young Innovative Talent Project in Higher Education of Guangdong Province (2023KQNCX162), Guangdong Basic and Applied Basic Research Foundation (2022A1515110515), the Applied Basic Research Foundation of Guangdong Province (Grant No. 2022A1515011530), and the Shenzhen Natural Science Fund (Stable Support Plan Program, Grant No. GXWD20220818165637002).

References

1. H. B. Zhang, T. Wei, Q. Zhang, W. G. Ma, P. Y. Fan, D. Salamon, S. T. Zhang, B. Nan, H. Tan and Z. G. Ye, A review on the development of lead-free ferroelectric energy-storage ceramics and multilayer capacitors, J. Mater. Chem. C, 2020, 8, 16648–16667.
2. G. Wang, Z. L. Lu, Y. Li, L. H. Li, H. F. Ji, A. Feteira, D. Zhou, D. W. Wang, S. J. Zhang and L. M. Reaney, Electroceramics for High-Energy Density Capacitors: Current Status and Future Perspectives, Chem. Rev., 2021, 121, 6124–6172.
3. Y. Lin, D. Li, M. Zhang and H. B. Yang, (Na_0.5Bi_0.5)_0.7Sr_0.3TiO₃ modified by Bi(Mg_2/3Nb_1/3)O3 ceramics with high energy-storage properties and an ultrafast discharge rate, J. Mater. Chem. C, 2020, 8, 2258–2264.
4. L. M. Chen, J. Zhou, L. Z. Xu, J. X. Ding, Z. M. Sun, Q. H. Bao and X. H. Hao, Achieving ultra-short discharge time and high energy density in lead-based antiferroelectric ceramics by A-site substitution, Chem. Eng. J., 2022, 447, 137367.
5. S. Y. Zhou, Y. P. Pu, X. Q. Zhang, Y. Shi, Z. Y. Gao, Y. Feng, G. D. Shen, X. Y. Wang and D. W. Wang, High energy density, temperature stable lead-free ceramics by introducing high entropy perovskite oxide, Chem. Eng. J., 2022, 427, 131684.
6. W. Huang, Y. Chen, X. Li, G. S. Wang, J. K. Xia and X. L. Dong, Superior energy storage performances achieved in (Ba,Sr)TiO₃-based bulk ceramics through composition design and Core-shell structure engineering, Chem. Eng. J., 2022, 444, 135523.
7. Z. Y. Ma, Y. Li, Y. Zhao, N. N. Sun, C. X. Lu, P. Han, D. W. Wang, Y. H. Hu, X. J. Lou and X. H. Hao, High-performance energy-storage ferroelectric multilayer ceramic capacitors via nano-micro engineering, J. Mater. Chem. A, 2023, 11, 7184–7192.
8. Z. H. Dai, J. L. Xie, Z. B. Chen, S. Zhou, J. J. Liu, W. G. Liu, Z. Z. Xi and X. B. Ren, Improved energy storage density and efficiency of (1 − x)Ba_0.85Ca_0.15Zr_0.1Ti_0.9O_3−xBiMg_2/3Nb_1/3O₃ lead-free ceramics, Chem. Eng. J., 2021, 410, 128341.
9. C. Y. Luo, Y. Z. Wei, Q. Feng, M. Wang, N. N. Luo, C. L. Yuan, C. R. Zhou, T. Fujita and J. W. Xu, Significantly enhanced energy-storage properties of Bi_0.47Na_0.47Ba_0.06TiO₃–CaHfO₃ ceramics by introducing Sr_0.7Bi_0.2TiO₃ for pulse capacitor application, Chem. Eng. J., 2022, 429, 132165.
10. J. H. Zhao, Z. B. Pan, L. M. Tang, Y. H. Shen, X. Q. Chen, H. H. Li, P. Li, Y. Zhang, J. J. Liu and J. W. Zhai, Greatly enhanced discharged energy density and efficiency of BiFeO₃-based ceramics by regulating insulation performance, Mater. Today Phys., 2022, 27, 100821.
11. X. B. Zhang, G. S. Chen, Z. X. Liu, X. L. Miao, Z. H. Zhang, D. Y. Chen, K. H. Lam, M. Zeng, X. S. Gao and J. M. Liu, Achieving ultrahigh energy storage density under low electric field in (Na_0.5Bi_0.5)TiO₃-based relaxor ferroelectric ceramics via a synergistic optimization strategy, Chem. Eng. J., 2024, 480, 147973.
12. X. S. Qiao, D. Wu, F. D. Zhang, B. Chen, X. D. Ren, P. F. Liang, H. L. Du, X. L. Chao and Z. P. Yang, Bi_0.5Na_0.5TiO₃-based relaxor ferroelectric ceramic with large energy density and high efficiency under a moderate electric field, J. Mater. Chem. C, 2019, 7, 10514–10520.
13. C. Y. Luo, Q. Feng, N. N. Luo, C. L. Yuan, C. R. Zhou, Y. Z. Wei, T. Fujita, J. W. Xu and G. H. Chen, Effect of Ca²⁺/Hf⁴⁺ modification at A/B sites on energy-storage density of Bi_0.47Na_0.47Ba_0.06TiO₃ ceramics, Chem. Eng. J., 2021, 420, 129861.
14. W. J. Cao, L. Li, H. Y. Zhao, C. Y. Wang, C. Liang, F. Li, X. C. Huang and C. C. Wang, Outstanding energy storage performance of NBT-based ceramics under moderate electric field achieved via antiferroelectric engineering, ACS Appl. Mater. Interfaces, 2023, 15, 38633–38643.
15. H. H. Nie, L. M. Ruan, L. Hu, X. R. Wang, F. K. Chen, S. Zhou, Y. Y. Wang, T. T. Ai, Y. Yan and G. Liu, Enhanced dielectric energy storage performance of A-site Ca²⁺-doped Na_0.5Bi_0.5TiO₃–BaTiO₃–BiFeO₃ Pb-free ceramics, Ceram. Int., 2022, 48, 21061–21070.
16. M. Acosta, J. D. Zang, W. Jo and J. Roedel, High-temperature dielectrics in CaZrO₃-modified Bi_1/2Na_1/2TiO₃-based lead-free ceramics, J. Eur. Ceram. Soc., 2012, 32, 4327–4334.
17. L. Zhang, Y. P. Pu, M. Chen, F. P. Zhuo, C. Dietz and T. Froemling, Decreasing polar-structure size: achieving superior energy storage properties and temperature stability in Na_0.5Bi_0.5TiO₃-based ceramics for low electric field and high-temperature applications, J. Eur. Ceram. Soc., 2021, 41, 5890–5899.
18. Z. X. Liu, C. A. Wang, X. B. Zhang, G. S. Chen, A. H. Zhang, M. Zeng, D. Y. Chen, Z. P. Hou, Z. Fan, M. H. Qin, X. B. Lu, X. S. Gao and J. M. Liu, Ultrahigh polarization response along large energy storage properties in BiFeO₃–BaTiO₃-based relaxor ferroelectric ceramics under low electric field, ACS Appl. Mater. Interfaces, 2022, 14, 53690–53701.
19. X. S. Qiao, D. Wu, F. D. Zhang, M. S. Niu, B. Chen, X. M. Zhao, P. F. Liang, L. L. Wei, X. L. Chao and Z. P. Yang, Enhanced energy density and thermal stability in relaxor ferroelectric Bi_0.5Na_0.5TiO₃–Sr_0.7Bi_0.2TiO₃ ceramics, J. Eur. Ceram. Soc., 2019, 39, 4778–4784.
20. D. Hu, Z. B. Pan, X. Zhang, H. R. Ye, Z. Y. He, M. K. Wang, S. Xing, J. W. Zhai, Q. Fu and J. J. Liu, Greatly enhanced discharge energy density and efficiency of novel relaxation ferroelectric BNT-BKT-based ceramics, J. Mater. Chem. C, 2020, 8, 591–601.
21. L. Zheng, P. C. Sun, P. Zheng, W. F. Bai, L. L. Li, F. Wen, J. J. Zhang, N. N. Wang and Y. Zhang, Significantly tailored energy-storage performances in Bi_0.5Na_0.5TiO₃–SrTiO₃-based relaxor ferroelectric ceramics by introducing bismuth layer-structured relaxor BaBi₂Nb₂O₉ for capacitor application, J. Mater. Chem. C, 2021, 9, 5234–5243.
22. Y. C. Wu, Y. Z. Fan, N. T. Liu, P. Peng, M. X. Zhou, S. G. Yan, F. Cao, X. L. Dong and G. S. Wang, Enhanced energy storage properties in sodium bismuth titanate-based ceramics for dielectric capacitor applications, J. Mater. Chem. C, 2019, 7, 6222–6230.
23. J. H. Wang, Y. Li, N. N. Sun, J. H. Du, Q. W. Zhang and X. H. Hao, Bi(Mg_0.5Ti_0.5)O₃ addition induced high recoverable energy-storage density and excellent electrical properties in lead-free Na_0.5Bi_0.5TiO₃-based thick films, J. Eur. Ceram. Soc., 2019, 39, 255–263.
24. D. D. Wang, J. Y. Zhu, Z. X. Liu, A. H. Zhang, C. A. Wang, C. M. Leung, X. S. Gao, X. B. Lu and M. Zeng, Enhanced energy storage performance in (1 − x)Bi_0.85Sm_0.15FeO_3−xCa_0.5Sr_0.5Ti_0.9Zr_0.1O3 relaxor ceramics, J. Alloys Compd., 2022, 903, 163888.
25. Y. Li, G. C. Wang, A. Gong, S. Zhang, J. Liu, N. N. Sun and X. H. Hao, High-Performance Ferroelectric Electromagnetic Attenuation Materials with Multiple Polar Units Based on Nanodomain Engineering, Small, 2022, 18, 2106302.
26. B. K. Chu, J. G. Hao, P. Li, Y. C. Li, W. Li, L. M. Zheng and H. R. Zeng, High-energy storage properties over a broad temperature range in La-modified BNT-based lead-free ceramics, ACS Appl. Mater. Interfaces, 2022, 14, 19683–19696.
27. B. Yan, K. P. Chen and L. A. An, Design and preparation of lead-free (Bi_0.4Na_0.2K_0.2Ba_0.2)TiO₃–Sr(Mg_1/3Nb_2/3)O₃ high-entropy relaxor ceramics for dielectric energy storage, Chem. Eng. J., 2023, 453, 139921.
28. L. N. Shi, Y. G. Wang, Z. H. Ren, A. Jain, S. S. Jiang and F. G. Chen, Significant improvement in electrical characteristics and energy storage performance of NBT-based ceramics, Ceram. Int., 2022, 48, 37494.
29. L. N. Shi, Z. H. Ren, A. Jain, R. H. Jin, S. S. Jiang, H. Z. Zhou, F. G. Chen and Y. G. Wang, Enhanced energy storage performance achieved in Na_0.5Bi_0.5TiO₃–Sr_0.7Bi_0.2TiO₃ ceramics via domain structure and bandgap width tuning, Ceram. Int., 2023, 49, 12822–12831.
30. W. J. Shi, Y. L. Yang, L. Y. Zhang, R. Y. Jing, Q. Y. Hu, D. O. Alikin, V. Y. Shur, J. H. Gao, X. Y. Wei and L. Jin, Enhanced energy storage performance of eco-friendly BNT-based relaxor ferroelectric ceramics via polarization mismatch-reestablishment and viscous polymer process, Ceram. Int., 2022, 48, 6512–6519.
31. X. Li, X. Y. Dong, F. Wang, Z. Tan, Q. M. Zhang, H. Chen, J. W. Xi, J. Xing, H. F. Zhou and J. G. Zhu, Realizing excellent energy storage properties in Na_0.5Bi_0.5TiO₃-based lead-free relaxor ferroelectrics, J. Eur. Ceram. Soc., 2022, 42, 2221–2229.
32. B. Yang, J. Y. Zhang, X. J. Lou, Y. F. Gao, P. Shi, Y. D. Yang, M. Yang, J. Cui, L. L. Wei and S. D. Sun, Enhancing comprehensive energy storage properties in tungsten bronze Sr_0.53Ba_0.47Nb₂O₆-based lead-free ceramics by B-site doping and relaxor tuning, ACS Appl. Mater. Interfaces, 2022, 30, 34855–34866.
33. B. Yang, Y. F. Gao, X. J. Lou, Y. D. Yang, Y. H. Hu, G. J. Zhang and S. D. Sun, Remarkable energy storage performances of tungsten bronze Sr_0.53Ba_0.47Nb₂O₆-based lead-free relaxor ferroelectric for high-temperature capacitors application, Energy Storage Mater., 2023, 55, 763–772.
34. D. Li, Y. Lin, M. Zhang and H. B. Yang, Achieved ultrahigh energy storage properties and outstanding charge–discharge performances in (Na_0.5Bi_0.5)_0.7Sr_0.3TiO₃-based ceramics by introducing a linear additive, Chem. Eng. J., 2020, 392, 123729.
35. F. Yan, Y. J. Shi, X. F. Zhou, K. Zhu, B. Shen and J. W. Zhai, Optimization of polarization and electric field of bismuth ferrite-based ceramics for capacitor applications, Chem. Eng. J., 2021, 417, 127945.
36. G. Liu, Y. Li, B. Guo, M. Y. Tang, Q. Li, J. Dong, L. J. Yu, K. Yu, Y. Yan and D. W. Wang, Ultrahigh dielectric breakdown strength and excellent energy storage performance in lead-free barium titanate-based relaxor ferroelectric ceramics via a combined strategy of composition modification, viscous polymer processing, and liquid-phase sintering, Chem. Eng. J., 2020, 398, 125625.
37. G. F. Liu, L. Chen, H. F. Yu, Z. F. Zhang, J. Wu, C. Zhou, H. Qi and J. Chen, High energy-storage performance in multiple roles modified NaNbO₃–Ba(Fe_0.5Nb_0.5)O₃ lead-free relaxors, Chem. Eng. J., 2023, 474, 145705.
38. H. B. Yang, J. H. Tian, Y. Lin and J. Q. Ma, Realizing ultra-high energy storage density of lead-free 0.76Bi_0.5Na_0.5TiO₃–0.24SrTiO₃–Bi(Ni_2/3Nb_1/3)O₃ ceramics under low electric fields, Chem. Eng. J., 2021, 418, 129337.
39. J. F. Lin, G. L. Ge, K. Zhu, H. R. Bai, B. S. Sa, F. Yan, G. H. Li, C. Shi, J. W. Zhai, X. Wu and Q. W. Zhang, Simultaneously achieving high performance of energy storage and transparency via A-site non-stoichiometric defect engineering in KNN-based ceramics, Chem. Eng. J., 2022, 444, 136538.
40. K. Wei, J. H. Duan, X. F. Zhou, G. S. Li, D. Zhang and H. Li, Achieving ultrahigh energy storage performance for NaNbO₃-based lead-free antiferroelectric ceramics via the coupling of the stable antiferroelectric R phase and nanodomain engineering, ACS Appl. Mater. Interfaces, 2023, 15, 48354–48364.
41. M. S. Wang, A. W. Xie, J. Fu and R. Z. Zuo, Energy storage properties under moderate electric fields in BiFeO₃-based lead-free relaxor ferroelectric ceramics, Chem. Eng. J., 2022, 440, 135789.
42. P. Shi, X. P. Zhu, X. J. Lou, B. Yang, Q. D. Liu, C. C. Kong, S. Yang, L. Q. He, R. R. Kang and J. T. Zhao, Tailoring ferroelectric polarization and relaxation of BNT-based lead-free relaxors for superior energy storage properties, Chem. Eng. J., 2022, 428, 132612.
43. Q. F. Chen, T. T. Gao, R. Lang, Z. Tan, J. Xing and J. G. Zhu, Achieving outstanding temperature stability in KNN-based lead-free ceramics for energy storage behavior, J. Eur. Ceram. Soc., 2023, 43, 2442–2451.
44. Q. J. Li, S. S. Ji, D. D. Wang, J. Y. Zhu, L. Y. Li, W. Wang, M. Zeng, Z. P. Hou, X. S. Gao, X. B. Lu, Q. L. Li and J. M. Liu, Simultaneously enhanced energy storage density and efficiency in novel BiFeO₃-based lead-free ceramic capacitors, J. Eur. Ceram. Soc., 2021, 41, 387–393.
45. S. Li, T. F. Hu, H. C. Nie, Z. Q. Fu, C. H. Xu, F. F. Xu, G. S. Wang and X. L. Dong, Giant energy density and high efficiency achieved in silver niobate-based lead-free antiferroelectric ceramic capacitors via domain engineering, Energy Storage Mater., 2021, 34, 417–426.
46. S. Liu, W. W. Feng, J. H. Li, B. He, M. T. Liu, Z. D. Bao, D. J. Luo and C. C. Zhao, Realizing excellent energy storage performance and fatigue endurance in Sr_0.7Sm_0.2TiO₃ modified 0.67BiFeO₃–0.33BaTiO₃ lead-free relaxor ceramics, J. Eur. Ceram. Soc., 2022, 42, 7430–7440.
47. S. Liu, W. W. Feng, J. H. Li, C. C. Zhao, C. Hu, B. He, Z. D. Bao and X. Z. Luan, Achieving high energy storage density and efficiency simultaneously in Sr(Nb_0.5Al_0.5)O₃ modified BiFeO₃ based lead-free ceramics, Chem. Eng. J., 2023, 451, 138916.
48. T. Y. Li, P. F. Chen, F. Li and C. C. Wang, Energy storage performance of Na_0.5Bi_0.5TiO₃–SrTiO₃ lead-free relaxors modified by AgNb_0.85Ta_0.15O₃, Chem. Eng. J., 2021, 406, 127151.
49. Y. Pan, X. Wang, Q. P. Dong, J. M. Wang, H. Y. Chen, X. Y. Dong, L. Deng, H. L. Zhang, X. L. Chen and H. F. Zhou, Enhanced energy storage properties of Bi(Ni_2/3Nb_1/6Ta_1/6)O₃–NaNbO₃ solid solution lead-free ceramics, Ceram. Int., 2022, 48, 26466–26475.
50. Z. P. Wang, R. R. Kang, W. Y. Liu, L. X. Zhang, L. Q. He, S. Y. Zhao, H. X. Duan, Z. H. Yu, F. Kang, Q. Z. Sun, T. R. Zhang, P. Mao, J. P. Wang and L. Zhang, (Bi_0.5Na_0.5)TiO₃-based relaxor ferroelectrics with medium permittivity featuring enhanced energy-storage density and excellent thermal stability, Chem. Eng. J., 2022, 427, 131989.
51. L. Chen, F. X. Long, H. Qi, H. Liu, S. Q. Deng and J. Chen, Outstanding energy storage performance in high-hardness (Bi_0.5K_0.5)TiO₃-based lead-free relaxors via multi-scale synergistic design, Adv. Funct. Mater., 2022, 32, 2110478.
52. N. N. Sun, J. H. Du, Y. Zhao, C. X. Lu, P. Han, Y. Li, Q. W. Zhang and X. H. Hao, Flexible multilayer lead-free film capacitor with high energy storage performances via heterostructure engineering, J. Materiomics, 2022, 8, 772–780.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4tc03558e

---