The isovalent alloying assisted anomalous valley Hall effect in a hexagonal antiferromagnetic monolayer

Abstract

Exploring the combination of antiferromagnetic (AFM) spintronics and the anomalous valley Hall effect (AVHE) is one of the most important aspects for developing valleytronic applications. The key to address this issue is to achieve spin splitting around the valleys in AFM systems. Here, we propose a possible way for achieving the AVHE in a hexagonal AFM monolayer, which involves the isovalent alloying. This can break the combined symmetry (PT symmetry) of spatial inversion (P) and time reversal (T), giving rise to spin splitting. More specifically, the large spin splitting around the Fermi energy level is attributed to d orbital mismatch among the different transition metal ions. Based on first-principles calculations, the proposed way can be verified in an out-of-plane AFM CrMoC₂S₆ monolayer, which possesses spontaneous valley polarization and spitting, providing possibility to realize the AVHE. It is also proved that tensile strain can strengthen the valley splitting and maintain the out-of-plane AFM ordering. Our work provides an experimentally feasible way for developing AFM valleytronic devices.

---

I. Introduction

Valleys, as an additional degree of freedom of electrons besides charge and spin, lay the foundation for developing information encoding and processing applications.^1–4 The discovery and successful preparation of rich two-dimensional (2D) materials promote the development of the valley concept due to the large separation in momentum space. 2D transition metal dichalcogenides (TMDs) possess intrinsic broken inversion symmetry and large spin-orbital coupling (SOC), and they are widely recognized as the most representative valleytronic materials with a pair of degenerate but inequivalent −K and K valleys in the reciprocal space.^5–10 However, there is a lack of spontaneous valley polarization in these nonmagnetic TMD monolayers, and some external methods can achieve valley polarization, such as applying external magnetic field, proximity effects, magnetic doping and light excitation.^9–12 Although these methods can achieve valley polarization, they have many shortcomings, such as small valley splitting, destruction of the crystal structure and limited carrier life.

Compared with external methods, the intrinsic valley polarization is highly desirable. Fortunately, a ferrovalley semiconductor was proposed,¹³ which possessed intrinsic valley polarization and can exhibit the anomalous valley Hall effect (AVHE). For the AVHE, additional charge Hall current is realized by the spontaneous valley polarization caused by the combination of magnetic properties and SOC, which is similar to that of the anomalous Hall effect in ferromagnetic materials.¹³ Ferrovalley materials are generally built on ferromagnetic (FM) hexagonal symmetric systems with broken spatial inversion symmetry.^13–22 Compared to FM materials, antiferromagnetic (AFM) materials possess high storage density and robustness against external magnetic field, as well as ultrafast writing speed.²³ Therefore, realizing valley polarization and the AVHE in AFM materials is more meaningful for valleytronic applications. However, 2D AFM valleytronic materials with intrinsic valley polarization and a realizable AVHE are still scarce. Only a few candidate systems have been proposed, such as a MnPSe₃/Sc₂CO₂ or a Cr₂CH₂/Sc₂CO₂ heterojunction^24,25 and Janus Mn₂P₂X₃Y₃ (X, Y = S, Se Te; X ≠ Y) monolayers.²⁶

In particular, the presence of spin degeneracy poses a significant obstacle to realize the AVHE in AFM systems. The out-of-plane external electric field has been used to induce spin splitting in AFM systems, such as A-type AFM hexagonal monolayer Cr₂CH₂ and tetragonal monolayer Fe₂BrMgP.^27,28 This can be explained by the introduction of layer-dependent electrostatic potential caused by out-of-plane external electric field, and the spin order of spin splitting can be reversed by flipping the direction of electric field. In fact, the AVHE can be achieved by electric-potential-difference antiferromagnetism (EPD-AFM) without external electric field,^27,28 which can be equivalently replaced by a built-in electric field caused by a Janus structure.

Here, we propose a way to achieve spin splitting by isovalent alloying, and then realize the AVHE in a hexagonal AFM monolayer. The proposed way can produce large spin splitting around the Fermi energy level, which is due to d orbital mismatch among the magnetic atoms. Using first-principles calculations, we translate our proposed way into the CrMoC₂S₆ monolayer and clarify the isovalent alloying assisted AVHE in the hexagonal AFM monolayer.

II. Ways to achieve the AVHE

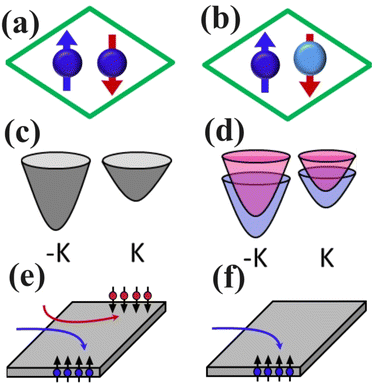
The isovalent alloying assisted AVHE in a hexagonal AFM monolayer is schematically illustrated in Fig. 1. Fig. 1(a) shows that the two magnetic atoms of a hexagonal AFM monolayer per unit cell are the same 3d elements, and its energy extrema of conduction/valence bands is at a high symmetry −K/K point. We assume that the lattice of the hexagonal AFM monolayer has spatial inversion symmetry, but the AFM ordering leads to the simultaneously broken inversion (P) symmetry and time reversal (T) symmetry, which produce spontaneous valley polarization (Fig. 1(c)). However, the system possesses PT symmetry, which gives rise to spin degeneracy, prohibiting the realization of the AVHE. PT symmetry is an antiunitary symmetry, which leads to (PT)²= −1. Under PT symmetry, arbitrary k is invariant, because both P and T map k to −k. For a system with PT symmetry, the Hamiltonian H(k) should meet [H(k), PT] = 0. The energy eigenvalue of an arbitrary eigenstate |ψ(k)〉 of H(k) is E(k), and its PT pair |ϕ(k)〉 = PT|ψ(k)〉 is also an eigenstate with k and E(k). For a PT symmetry system, every band must be doubly degenerate with spin-up and spin-down, even in the presence of SOC (for details, see ref. 29). By breaking the PT symmetry, for example breaking the P symmetry by isovalent alloying, the spin splitting can be achieved.

Fig. 1 (a) and (c) A hexagonal 3d-AFM monolayer with PT symmetry possesses spin degeneracy but nonequivalent −K and K valleys; (b) and (d) via isovalent alloying, (a) becomes 3d- and 4d-AFM monolayer with removed spin degeneracy, and the −K and K valleys still are unequal; in the presence of a longitudinal in-plane electric field, an appropriate electron doping for two cases produces a valley-spin Hall effect (e) and AVHE (f). In (a) and (b), the blue and red arrows indicate spin-up and spin-down, and the small and large balls mean the 3d and 4d atoms. In (d), the spin-up and spin-down channels are depicted in blue and red. In (e) and (f), the blue and red balls mean the carriers of spin-up and spin-down, and the arrows show the directions of spin.

Due to PT symmetry, the zero berry curvature (Ω(k)) everywhere in the momentum space can be observed. However, the Berry curvatures for the spin-up and spin-down channels are nonzero, and they are equal in magnitude and opposite in sign. In the presence of a longitudinal in-plane electric field, an appropriate electron doping produces a valley-spin Hall effect (Fig. 1(e)). For the valley-spin Hall effect, the Berry curvatures make the Bloch carriers of spin-up and spin-down form the same −K valley acquiring opposite anomalous transverse velocity, which leads to the accumulation of spin-up and spin-down carriers at the two edges of the sample, respectively.

Here, substituting elements via isovalent alloying (one of the two magnetic atoms is replaced by a 4d element with the same outer electrons) can be applied to break the PT symmetry (Fig. 1(b)), and the spin degeneracy of −K and K valleys can be removed. Our proposed system can be called an asymmetric AFM semiconductor (AAFMS).³⁰ Although the two magnetic atoms (3d and 4d elements) have the same surrounding atomic arrangement, the energy level of 4d electrons is higher than that of 3d ones (d orbital mismatch), producing spin splitting. Due to the broken PT symmetry, the spin splitting of the −K and K valleys can be observed (Fig. 1(d)), resulting in the AVHE (Fig. 1(f)).

Among bulk materials, the AAFMS property has been predicted in a family of double perovskites A₂CrMO₆ (A = Ca, Sr, and Ba, and M = Ru, Os).³⁰ The large spin polarization around the Fermi energy level has been observed due to d orbital mismatch among these magnetic ions. Among 2D materials, CrMoA₂S₆ (A = C, Si, or Ge) monolayers are AAFMSs, of which CrMoC₂S₆ has the highest Néel temperature of 556 K with robust magnetism against carrier doping and external in-plane strain.³¹ Next, we take the CrMoC₂S₆ monolayer as an example to illustrate our proposal.

III. Computational details

We perform spin-polarized first-principles calculations within density functional theory (DFT)^32,33 by using the projector augmented-wave (PAW) method, as implemented in the Vienna ab initio Simulation Package (VASP).^34–36 We use the generalized gradient approximation of Perdew–Burke–Ernzerhof (PBE-GGA)³⁷ as the exchange–correlation functional. A kinetic energy cutoff of 500 eV, a total energy convergence criterion of 10⁻⁸ eV, and a force convergence criterion of 0.0001 eV Å⁻¹ are set to obtain accurate results. To describe the strong correlation interaction of 3d and 4d electrons in CrMoC₂S₆, a Hubbard correction U_eff = 3.0 eV (ref. 31) is used for the rotationally invariant approach proposed by Dudarev et al.³⁸ The SOC is incorporated for investigation of valley splitting and magnetic anisotropy energy (MAE). To avoid the interaction between adjacent layers, a vacuum space of more than 20 Å along the z direction is adopted. A 12 × 12 × 1 Γ-centered Monkhorst–Pack grid is used to sample the Brillouin zone (BZ). Based on the finite displacement method, the interatomic force constants (IFCs) are calculated by employing a 3 × 3 × 1 supercell, and the phonon dispersion spectrum is obtained using the Phonopy code.³⁹ The elastic stiffness tensors C_ij are calculated by using the strain–stress relationship (SSR) method. C^2D_ij has been renormalized by C^2D_ij = L_zC^3D_ij, where L_z is the length of the unit cell along the z direction. The Berry curvatures are calculated directly from the calculated wave functions based on Fukui's method,⁴⁰ as implemented in the VASPBERRY code.^41–43

IV. Crystal and electronic structures

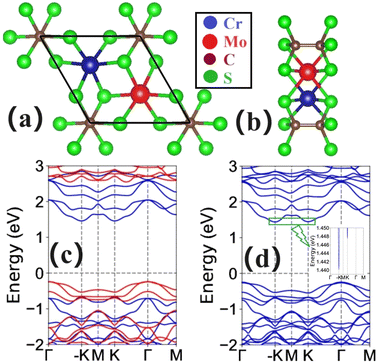
It has been proved that the CrMoC₂S₆ monolayer possesses dynamical and thermal stabilities, and the experimental possibility is also confirmed by the formation energy.³¹ Here, we also calculate two independent elastic constants: C₁₁ = 91.69 N m⁻¹ and C₁₂ = 34.57 N m⁻¹, which satisfy the Born criteria of mechanical stability:⁴⁴C₁₁ > 0 and C₁₁–C₁₂ > 0, confirming its mechanical stability. The crystal structures of CrMoC₂S₆ are shown in Fig. 2(a) and (b), which crystallizes in the P312 space group (no. 149), lacking spatial inversion symmetry. CrMoC₂S₆ can be obtained by substituting one Cr of Cr₂C₂S₆ with Mo via isovalent alloying. Cr and Mo are surrounded by six S atoms, forming a honeycomb lattice. Two CS₃ moieties are connected by two C atoms, forming a dumbbell-like structure. The optimized equilibrium lattice constants of CrMoC₂S₆ are a = b = 5.714 Å according to the GGA+U method. To determine the magnetic ground state of CrMoC₂S₆, the FM and three AFM configurations (AFM1, AFM2 and AFM3) are constructed (Fig. S1, ESI†), and the AFM1 is called the Néel AFM state. The energy of AFM1 per unit cell is 580 meV, 365 meV and 191 meV lower than those of FM, AFM2 and AFM3 cases, respectively, confirming that CrMoC₂S₆ possesses the AFM1 ground state.

Fig. 2 For monolayer CrMoC₂S₆, (a) and (b) the top and side views of crystal structures; (c) and (d) the energy band structures without SOC and with SOC. (c) The spin-up and spin-down channels are depicted in blue and red. (d), The inset shows the enlarged portion of conduction bands near the Fermi energy level.

The energy band structures of CrMoC₂S₆ and Cr₂C₂S₆ without SOC are plotted in Fig. 2(c) and Fig. S2 (ESI†), respectively. The lattice of Cr₂C₂S₆ has spatial inversion symmetry, but the inversion symmetry will disappear with AFM1 ordering. However, a combination of inversion symmetry P and time-reversal symmetry T (PT) exist, which leads to disappeared spin splitting. For CrMoC₂S₆, a large spin splitting around the Fermi energy level can be observed. The symmetry of spin splitting of CrMoC₂S₆ is s-wave, which is different from the symmetry of spin splitting of altermagnetism,^45,46i.e., d-wave, g-wave or i-wave. In other words, the altermagnets exhibit momentum-dependent spin splitting, while a spin splitting occurs throughout the whole BZ for CrMoC₂S₆. The total magnetic moment of the system is equal to the number of spin-up electrons minus the number of spin-down electrons. For CrMoC₂S₆, both spin channels have energy band gaps, so the numbers of electrons of both spin channels are integers. Therefore, the total magnetic moment of CrMoC₂S₆ per unit cell is strictly equal to 0μ_B and does not deviate from 0μ_B slightly. Strictly speaking, this CrMoC₂S₆ should be called a fully compensated ferrimagnet. For altermagnetism, the absolute values of the magnetic moments of two magnetic atoms with opposite spins are strictly equal because they are connected together by rotational symmetry.^45,46 For our discussed case CrMoC₂S₆, the absolute values of the magnetic moments of two magnetic atoms with opposite spins are not strictly equal because they are not symmetrically connected. It is clearly seen that CrMoC₂S₆ is an indirect gap semiconductor with a conduction band bottom (CBM)/valence band maximum (VBM) at the K/Γ point, and the energies of −K and K valleys in the conduction bands are degenerate. Monolayer CrMoC₂S₆ is a bipolar AFM semiconductor with the VBM and CBM in different spin channels.

When including SOC, the magnetic orientation of CrMoC₂S₆ should be determined by MAE, and only the out-of-plane case can produce spontaneous valley polarization.²⁷ The MAE can be calculated using E_MAE = E^‖_SOC − E^⊥_SOC, where ‖ and ⊥ mean that spins lie in the plane and out-of-plane. The positive MAE means out-of-plane magnetic anisotropy, while the negative value indicates in-plane one. The predicted MAE is 148 meV per unit cell, which means the out-of-plane easy magnetization axis of CrMoC₂S₆. The energy band structures of CrMoC₂S₆ with SOC are plotted in Fig. 2(d), which shows the valley polarization with the valley splitting of only 7.4 meV (ΔE_C = E^C_K − E^C_−K), and the energy of the K valley is higher than that of the −K valley. In order to strengthen valley splitting, strain engineering may be an effective and feasible method.⁴⁷ In the next section, we will study the strain effects on the magnetic and electronic properties of CrMoC₂S₆.

V. Strain effects

Here, a/a₀ (0.94–1.06) is used to simulate the biaxial strain, where a and a₀ are the strained and unstrained lattice constants, respectively. a/a₀ < 1/> 1 means the compressive/tensile strain. Firstly, we determine the magnetic ground state of strained CrMoC₂S₆ by the energy difference between FM/AFM2/AFM3 and AFM1 configurations, which is shown in Fig. 3(a). Within the considered a/a₀ range, the AFM1 ordering is always the ground state. With increasing strain, the strength of the magnetic interaction is reduced. To maintain spontaneous valley polarization, the direction of magnetization is another key factor. The MAE vs. a/a₀ is plotted in Fig. 3(b), which shows a transition of the magnetization direction. Compressive strain can make the magnetization direction of CrMoC₂S₆ change from the out-of-plane case to the in-plane case, and this critical strain point is about 0.98. Fortunately, tensile strain can enhance the MAE of CrMoC₂S₆, thereby promoting the spontaneous valley polarization.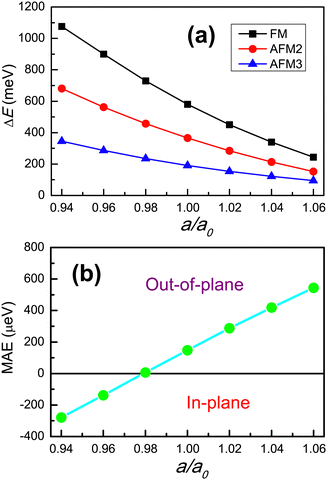

Fig. 3 For CrMoC₂S₆, (a) the energy difference between FM/AFM2/AFM3 and AFM1 orderings as a function of a/a₀; (b) the MAE vs. a/a₀.

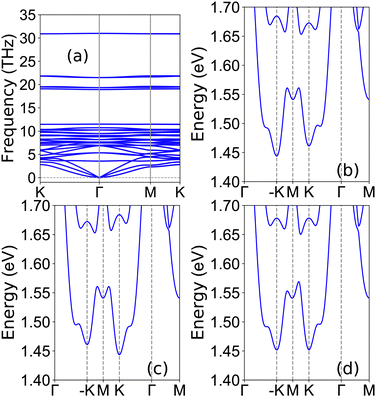
The energy band structures of CrMoC₂S₆ at representative a/a₀ by using both GGA and GGA + SOC are plotted in Fig. S3 (ESI†), and the enlarged figures of SOC energy band structures near the Fermi energy level for the conduction band are plotted in Fig. 4. The valley splitting with assumed out-of-plane and intrinsic magnetization directions for the conduction band as a function of a/a₀ is plotted in Fig. 5. Based on Fig. S3 (ESI†), CrMoC₂S₆ is always a bipolar AFM semiconductor. Near the Fermi energy level, the conduction bands come from the spin-up channel, while the valence band is dominated by the spin-down channel. With assumed out-of-plane magnetization, the compressive strain can induce K valley polarization, while the tensile strain maintains −K valley polarization. Both increasing compressive and tensile strains can enhance the absolute size of valley splitting |ΔE_C|. From this perspective, strain can be considered analogous to a pseudomagnetic field. Stain-driven valley polarization transition can also be observed in the Janus GdClF monolayer.⁴⁸ When considering intrinsic magnetic anisotropy, the spontaneous valley polarization appears with a/a₀ being larger than 0.98. At a/a₀ = 1.06, the corresponding valley splitting is about 19.5 meV.

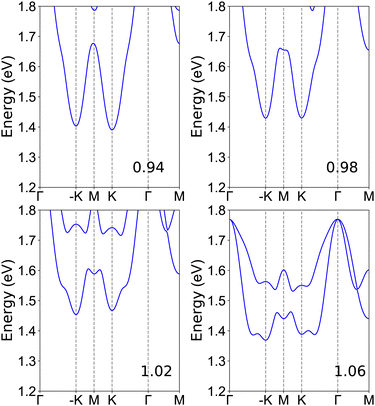Fig. 4 For CrMoC₂S₆, the energy band structures of conduction bands near the Fermi energy level with SOC at representative a/a₀ (0.94, 0.98, 1.02, and 1.06).

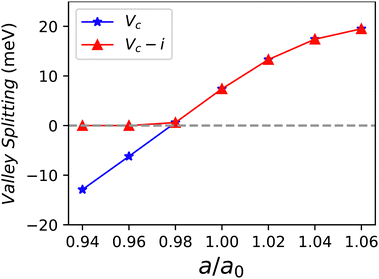Fig. 5 For CrMoC₂S₆, the valley splitting with assumed out-of-plane and intrinsic magnetization directions (V_c and V_c–i) for the conduction band as a function of a/a₀.

Finally, taking typical a/a₀ = 1.04, the physical properties of CrMoC₂S₆ are detailedly investigated. The calculated phonon spectrum of CrMoC₂S₆ with a/a₀ = 1.04 is shown in Fig. 6(a), which shows no obvious imaginary frequencies, indicating its dynamic stability. The energy band structures of conduction bands near the Fermi energy level with SOC for the magnetization direction along the positive z, negative z, and positive x directions are plotted in Fig. 6 (b)–(d). Fig. 6(b) shows the valley polarization with a valley splitting of 17.4 meV, and the energy of the K valley is higher than that of the −K valley. Fig. 6(c) indicates that the valley polarization can be switched by reversing the magnetization direction. When the magnetization direction of CrMoC₂S₆ is in-plane (see Fig. 6(d)), no valley polarization can be observed.

Fig. 6 For CrMoC₂S₆ with a/a₀ = 1.04, the phonon dispersion curves (a); the energy band structures of conduction bands near the Fermi energy level with SOC (b)–(d) for the magnetization direction along the positive z, negative z, and positive x directions, respectively.

For CrMoC₂S₆ at a/a₀ = 1.04, the distributions of Berry curvatures of total, spin-up and spin-down are plotted in Fig. 7. For purposes of comparison, the related distribution of the Berry curvatures of Cr₂C₂S₆ is also shown in Fig. S4 (ESI†). Due to PT symmetry, the total Berry curvatures of Cr₂C₂S₆ are zero, but the berry curvatures are opposite for the same valley at different spin channels and different valleys at the same spin channel. However, for CrMoC₂S₆, the total Berry curvatures are nonzero at −K and K valleys due to the broken PT symmetry. The Berry curvatures of the −K and K valleys have opposite signs for the same spin channel, and the Berry curvatures are also opposite for the same valley at different spin channels. With an applied longitudinal in-plane electric field, the Bloch carriers will acquire an anomalous transverse velocity v_⊥ ∼ E_‖ × Ω(k).⁴ When the Fermi energy level is shifted between the −K and K valleys in the conduction band, the spin-up carriers from the −K valley will accumulate along one edge of the sample, resulting in the AVHE (Fig. 1(f)).

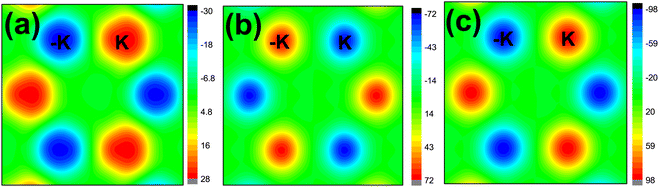Fig. 7 For CrMoC₂S₆ with a/a₀ = 1.04, the distribution of Berry curvatures of total (a), spin-up (b) and spin-down (c).

In general, 3d electrons have a stronger electron correlation than 4d electrons. For monolayer CrMoC₂S₆ at a/a₀ = 1.04, the different U (Cr, Mo) values are also considered to confirm the reliability of our results. From U (3, 2) to U (3, 3) to U (4, 3), the magnetic interaction energy and MAE of CrMoC₂S₆ become weak, but it always possesses out-of-plane AFM1 ordering. At different U (Cr, Mo) values, the energy band structures of conduction bands near the Fermi energy level with SOC for the magnetization direction along the positive z direction are plotted in Fig. S5 (ESI†). They all show −K valley polarization, and the valley splitting increases with increasing U (Cr, Mo). The related data are summarized in Table 1.

Table 1 The energies of FM, AFM1, AFM2 and AFM3 ordering (meV); the MAE/unit cell in meV; and the valley splitting (V_c) for the conduction band (meV) of monolayer CrMoC₂S₆ with a/a₀ = 1.04 at different U values

U (Cr, Mo)	E FM	E AFM1	E AFM2	E AFM3	MAE	V c
(3, 2)	371	0	231	128	478	16.5
(3, 3)	339	0	214	122	419	17.4
(4, 3)	292	0	181	107	416	18.2

---

To elucidate the mechanical performance of CrMoC₂S₆, an isotropic in-plane Young's modulus C_2D of 78.66 N m⁻¹ is predicted. This is weaker than those of graphene (∼340 ± 40 N m⁻¹) and MoS₂ (∼126.2 N m⁻¹),^49,50 indicating the better mechanical flexibility of monolayer CrMoC₂S₆, which is in favour of experimentally enhancing valley splitting by strain. For the MoS₂ monolayer, the strain with as large as 5.6% has been achieved experimentally.⁵¹ Therefore, 1.04 (4%) strain in CrMoC₂S₆ can be realized experimentally due to small C_2D.

VI. Conclusion

In summary, we present a way to induce the AVHE in a hexagonal AFM monolayer by isovalent alloying. Using first-principles calculations, we confirm the validity of our proposed way by an extensive study of the CrMoC₂S₆ monolayer. Due to broken P and T symmetries in CrMoC₂S₆, there is a spontaneous valley polarization. Moreover, the spin splitting can occur due to broken PT symmetry, which can also be explained by the d orbital mismatch of different magnetic atoms. Strain engineering can be used to tune valley splitting, and the calculated results show that tensile strain can enhance the valley splitting of CrMoC₂S₆ with the out-of-plane AFM1 ordering. With an applied longitudinal in-plane electric field, the Berry curvature can produce the AVHE. Our work is expected to speed up the realization of the AVHE in AFM monolayers, and provide a route for constructing energy-efficient and ultrafast valleytronic devices.

Data availability

The magnetic configurations and the related energy band structures and Berry curvature distributions have been included as part of the ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work is supported by the Natural Science Basis Research Plan in Shaanxi Province of China (2021JM-456). We are grateful to Shanxi Supercomputing Center of China, and the calculations were performed on TianHe-2.

References

1. J. R. Schaibley, H. Yu, G. Clark, P. Rivera, J. S. Ross, K. L. Seyler, W. Yao and X. Xu, Nat. Rev. Mater., 2016, 1, 16055.
2. G. Pacchioni, Nat. Rev. Mater., 2020, 5, 480.
3. S. A. Vitale, D. Nezich, J. O. Varghese, P. Kim, N. Gedik, P. Jarillo-Herrero, D. Xiao and M. Rothschild, Small, 2018, 14, 1801483.
4. D. Xiao, M. C. Chang and Q. Niu, Rev. Mod. Phys., 2010, 82, 1959.
5. A. Srivastava, M. Sidler, A. V. Allain, D. S. Lembke, A. Kis and A. Imamoglu, Nat. Phys., 2015, 11, 141.
6. K. F. Mak, K. He, J. Shan and T. F. Heinz, Nat. Nanotechnol., 2012, 7, 494.
7. H. Zeng, J. Dai, W. Yao, D. Xiao and X. Cui, Nat. Nanotechnol., 2012, 7, 490.
8. M. Zeng, Y. Xiao, J. Liu, K. Yang and L. Fu, Chem. Rev., 2018, 118, 6236.
9. C. Zhao, T. Norden, P. Zhang, P. Zhao, Y. Cheng, F. Sun, J. P. Parry, P. Taheri, J. Wang, Y. Yang, T. Scrace, K. Kang, S. Yang, G. Miao, R. Sabirianov, G. Kioseoglou, W. Huang, A. Petrou and H. Zeng, Nat. Nanotechnol., 2017, 12, 757.
10. D. MacNeill, C. Heikes, K. F. Mak, Z. Anderson, A. Kormanyos, V. Zolyomi, J. Park and D. C. Ralph, Phys. Rev. Lett., 2015, 114, 037401.
11. X. X. Zhang, Y. Lai, E. Dohner, S. Moon, T. Taniguchi, K. Watanabe, D. Smirnov and T. F. Heinz, Phys. Rev. Lett., 2019, 122, 127401.
12. T. Cao, G. Wang, W. Han, H. Ye, C. Zhu, J. Shi, Q. Niu, P. Tan, E. Wang, B. Liu and J. Feng, Nat. Commun., 2012, 3, 887.
13. W. Y. Tong, S. J. Gong, X. Wan and C. G. Duan, Nat. Commun., 2016, 7, 13612.
14. Y. B. Liu, T. Zhang, K. Y. Dou, W. H. Du, R. Peng, Y. Dai, B. B. Huang and Y. D. Ma, J. Phys. Chem. Lett., 2021, 12, 8341.
15. Z. Song, X. Sun, J. Zheng, F. Pan, Y. Hou, M.-H. Yung, J. Yang and J. Lu, Nanoscale, 2018, 10, 13986.
16. J. Zhou, Y. P. Feng and L. Shen, Phys. Rev. B, 2020, 102, 180407.
17. P. Zhao, Y. Ma, C. Lei, H. Wang, B. Huang and Y. Dai, Appl. Phys. Lett., 2019, 115, 261605.
18. X. Y. Feng, X. L. Xu, Z. L. He, R. Peng, Y. Dai, B. B. Huang and Y. D. Ma, Phys. Rev. B, 2021, 104, 075421.
19. Y. Zang, Y. Ma, R. Peng, H. Wang, B. Huang and Y. Dai, Nano Res., 2021, 14, 834.
20. R. Peng, Y. Ma, X. Xu, Z. He, B. Huang and Y. Dai, Phys. Rev. B, 2020, 102, 035412.
21. W. Du, Y. Ma, R. Peng, H. Wang, B. Huang and Y. Dai, J. Mater. Chem. C, 2020, 8, 13220.
22. R. Li, J. W. Jiang, W. B. Mi and H. L. Bai, Nanoscale, 2021, 13, 14807.
23. T. Jungwirth, J. Sinova, A. Manchon, X. Marti, J. Wunderlich and C. Felser, Nat. Phys., 2018, 14, 200.
24. T. Zhao, S. Xing, J. Zhou, N. Miao and Z. Sun, J. Mater., 2024, 10, 269.
25. W. Du, R. Peng, Z. He, Y. Dai, B. Huang and Y. Ma, npj 2D Mater. Appl., 2022, 6, 11.
26. Y. Xu, H. Liu, Y. Dai, B. Huang and W. Wei, Appl. Phys. Lett., 2023, 122, 242404.
27. S. D. Guo, Y. L. Tao, Z. Y. Zhuo, G. Zhu and Y. S. Ang, Phys. Rev. B, 2024, 109, 134402.
28. S. D. Guo, W. Xu, Y. Xue, G. Zhu and Y. S. Ang, Phys. Rev. B, 2024, 109, 134426.
29. Y. Xue, W. Xu, B. Zhao, J. Zhang and Z. Yang, Phys. Rev. B, 2023, 108, 075138.
30. X. Li, X. Wu, Z. Li and J. Yang, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 125202.
31. P. Wang, D. X. Wu, K. Zhang and X. J. Wu, J. Phys. Chem. Lett., 2022, 13, 3850.
32. P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864.
33. W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133.
34. G. Kresse, J. Non-Cryst. Solids, 1995, 193, 222.
35. G. Kresse and J. Furthmuller, Comput. Mater. Sci., 1996, 6, 15.
36. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758.
37. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
38. S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505.
39. A. Togo, F. Oba and I. Tanaka, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 134106.
40. T. Fukui, Y. Hatsugai and H. Suzuki, J. Phys. Soc. Jpn., 2005, 74, 1674.
41. H. J. Kim, 2018, https://github.com/Infant83/VASPBERRY.
42. H. J. Kim, C. Li, J. Feng, J.-H. Cho and Z. Zhang, Phys. Rev. B, 2016, 93, 041404.
43. S. W. Kim, H. J. Kim, S. Cheon and T. H. Kim, Phys. Rev. Lett., 2022, 128, 046401.
44. R. C. Andrew, R. E. Mapasha, A. M. Ukpong and N. Chetty, Phys. Rev. B, 2012, 85, 125428.
45. L. Smejkal, J. Sinova and T. Jungwirth, Phys. Rev. X, 2022, 12, 031042.
46. I. Mazin, Phys. Rev. X, 2022, 12, 040002.
47. H. X. Cheng, J. Zhou, W. Ji, Y. N. Zhang and Y. P. Feng, Phys. Rev. B, 2021, 103, 125121.
48. S. D. Guo, X. S. Guo, X. X. Cai and B. G. Liu, Phys. Chem. Chem. Phys., 2022, 24, 715.
49. K. N. Duerloo, M. T. Ong and E. J. Reed, J. Phys. Chem. Lett., 2012, 3, 2871.
50. C. Lee, X. g Wei, J. W. Kysar and J. Hone, Science, 2008, 321, 385.
51. D. Lloyd, X. H. Liu and J. W. Christopher, et al. , Nano Lett., 2016, 16, 5836.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4tc03700f

---