Experimental evidence of the excited-state mixing in the blue emitter for organic light-emitting diodes

Abstract

High hopes have been placed on organic emitters, which are supposed to solve the problem of low stability of blue OLEDs. A peculiar phenomenon of thermally activated delayed fluorescence (TADF), which brought such emitters to the range of the top-studied materials for organic optoelectronics within the last decade, remains poorly understood. Here, we report the results of comprehensive photophysical studies of one of the most successful candidates for blue TADF OLEDs, the TMCz-BO emitter (9-(5,9-dioxa-13b-boranaphtho[3,2,1-de]anthracen-7-yl)-1,3,6,8-tetramethyl-9H-carbazole) characterised by outstanding triplet-harvesting properties. One of the main aims of this work is to understand the reason for these unique properties. Steady-state and time-resolved spectroscopic investigations in media of various polarity, viscosity, and temperature reveal that at least five excited states of different characters and multiplicity are responsible for the emissive and spin–flip transitions in the TMCz-BO molecular systems. First of all, in contrast to typical donor–acceptor TADF emitters, the S₁ state of TMCz-BO does not have a pure charge-transfer character but shows a considerable contribution of the locally-excited state of the acceptor fragment, which provides a fast radiative rate. The T₁ state is a superposition of two locally excited and one charge-transfer states, providing reasonable spin–orbit coupling. Regarding the TADF mechanism in various media, reverse intersystem crossing follows the T₁ → S₁ model, considering the excited-state mixing, a notion introduced here to explain the triple and dual nature of the respective states. Such a mixing is dynamic in low-viscosity solutions due to low barriers for molecular vibrations. In films with a host matrix, a static excited-state mixing occurs, assisted by the low-amplitude vibrations within the local energetic minimum of the emitting species. The high efficiency of the excited-state mixing in TMCz-BO is explained by the rigid structure of its donor and acceptor fragments and their limited but still active mutual rotations. This provides negligible structural differences between various electronic states, enabling low reorganisation energies favourable for radiative and spin–flip processes while maintaining vibrational activation of spin–orbit coupling. Despite a lower reverse intersystem crossing rate in media of high viscosity, TMCz-BO shows rare near-UV TADF in films with the non-polar host. Our results thus highlight the unique and intriguing properties of TMCz-BO, opening up new perspectives for further research and potential improvements in OLED applications.

---

Introduction

Organic light-emitting diodes, commonly known as OLEDs, represent a cutting-edge technology that has revolutionised the display and lighting industries. OLEDs are a type of light-emitting diode (LED) in which most of the layers, including the emissive one, are composed of organic compounds. Unlike traditional LEDs or liquid crystal displays (LCDs), OLEDs are characterised by their self-emissive nature, allowing each pixel to emit light independently. The fundamental principle behind OLEDs lies in the emissive nature of the organic material used. The parameters of such organic compounds can be adjusted to emit light of different colours when an electric current is applied. This unique property enables OLED displays to achieve deeper blacks, higher contrast ratios, and a wider range of vibrant colours as compared to conventional display technologies.

Despite the accent on “organic” in the title, commercial OLEDs still rely on heavy metals as crucial components of the light-emitting layers. Heavy-metal organic complexes, or so-called OLED emitters of the second generation, apply the phosphorescence principle to convert triplet exciton energy from electric excitation to light, thus achieving quantitative internal quantum efficiency. Despite the high efficiency and stability of such emitters of different colours, environmental issues and especially low stability in the blue region stimulated great efforts in the research of all-organic emitters, specifically blue ones.

The key problem of all-organic emitters that should be solved is triplet harvesting. In the context of OLEDs and organic semiconductors, triplet excitons or states refer to a specific electronic configuration of the excited species. In organic materials, when a photon is absorbed, it can create an exciton, which is essentially an electron–hole pair bound together. This exciton can exist in the two spin states: singlet and triplet. Singlet excitons can pair electron and hole spins that are antiparallel. They are characterised by a total spin angular momentum of 0. On the other hand, triplet excitons have paired electron and hole spins that are parallel, giving a total spin angular momentum of 1. Typically, triplet excitons, or analogously triplet states of molecules, have longer lifetimes than singlet ones as their deactivation to the ground state requires spin change. Such long lifetimes above tens of microseconds cause a decrease in the efficiency and stability of OLED devices. Efficient harvesting and utilisation of both singlet and triplet states thus contribute to improved device performance, including enhanced external quantum efficiency and lower power consumption.

Thermally activated delayed fluorescence (TADF)¹ is one of the most promising solutions for the triplet harvesting problem, enabling 100% of internal quantum efficiency (IQE) and up to 40% of external quantum efficiency (EQE) in the TADF OLED devices.^2,3 The latter feature brought organic emitters closer to their second-generation analogues and paved the way for their commercial applications. TADF is based on the reverse intersystem crossing (rISC) process, the “return” of excitons from T₁ to S₁ and further fluorescence. TADF molecules emit light in two regimes: prompt fluorescence (PF) and delayed fluorescence (DF). PF occurs from the S₁ state excited directly by photo- or electroexcitation. Delayed fluorescence also occurs from the S₁ state but is derived from T₁ produced by electroexcitation or photoexcitation to S₁ and further intersystem crossing (ISC). In TADF emitters, the rISC rate parameter is the most important for triplet harvesting. When other parameters are unchanged, the faster the rISC rate and the shorter the DF lifetime, the higher the TADF efficiency and – as a result – the OLED stability.⁴

The mechanism of rISC has been investigated extensively within the last decade. In general terms, rISC is a spin–forbidden process that occurs in the (milli)second-time domain, which is too slow for OLED applications. To achieve fast rISC in the sub-microsecond domain, efficient TADF emitters have to meet the criteria of a minor (<0.2 eV) energy gap between S₁ and T₁ (ΔE_ST) and reasonable spin–orbital coupling (SOC). Several molecular design strategies developed recently enable rISC in micro- and even sub-microsecond time domains.^5–8 The most efficient and reliable method combines strong donor (D) and strong acceptor (A) fragments that are connected orthogonally. Such strategy leads to (i) spatial separation of highest occupied and lowest unoccupied molecular orbitals (HOMO and LUMO, respectively), (ii) formation of singlet and triplet states of charge transfer character, ¹CT and ³CT, respectively, and (iii) decrease in the exchange energy and thus reduction of the energy gap (ΔE_ST).

The origin of relatively high SOC in such organic D–A molecules is still debated. In the frames of the classic quantum physical approach, usually applied to describe electronic properties of molecules (referred further as a static quantum model), the excited states are regarded as single-configurational systems or, in other words, of fixed electronic character and energy values. The transition between two excited states with the same multiplicity, but different character occurs via internal conversion (IC). Due to the spin selection rule, the transition between two states with the same character but different multiplicity is forbidden. Therefore, in D–A emitters, SOC between ¹CT and ³CT states of the same character should be zero. With the assumption that ³CT → ¹CT is forbidden, the three-state rISC model was developed. It relies on the presence of another energetically proximate triplet state of a different CT nature or, more often – a locally excited state involving a donor (³LE_D) or acceptor (³LE_A) fragment. According to this model, the highest rISC rate is achieved when the ³LE state aligns energetically^9,10 and vibronically¹¹ with the ³CT or ¹CT states. The distinguishing difference between the CT and LE states is the dipole moment. Significant dipole moments of the CT states cause high sensitivity to the polarity of the medium, which is not the case for weakly polarised LE states. Within the static quantum model, this means that the energy gaps ΔE_CT–LE can be altered by polarity. CT and LE states also have different geometry, affecting another important parameter – reorganisation energy (λ). Regarding Marcus's theory, the smaller the λ, the faster the electronic transition.

Molecular vibrations are crucial for SOC in D–A emitters and are the basis of another, two-state rISC model. It was shown that in the emitters with strongly stabilised CT states, the ³CT → ¹CT transition is, in fact, not forbidden and can be highly efficient, playing a crucial role in the rISC process. In this case, the molecular motions activate SOC, which changes the dihedral angle (θ) between the D and A fragments. Together with the ΔE_¹CT–³CT and λ_¹CT–³CT values of a few meV, this affords fast rISC up to the sub-microsecond domain in polar media¹² and/or in strong D–A emitters.¹³ In the media of low polarity or when ΔE_¹CT–³CT is increased by weakened A and/or D, the ³LE–¹CT transition can compete with ³CT–¹CT, affording a usually slower multichannel mechanism for rISC. The decrease of the rISC rate in weak DA systems is the main reason for the continuous lack of fast-rISC deep-blue emitter and has been a persistent challenge in the field of organic electronics.

Some examples of the extensive studies on blue emitters are discussed briefly below. In the work¹⁴ authors report two deep-blue emitters based on the 2,12-di-tert-butyl-5-oxa-9-thia-13b-boranaphtho[3,2,1-de]anthracene acceptor and two weak donors for blue emission: carbazole (PhCz-TOSBA) and triphenylamine (TPA-TOSBA). The emitters showed PL_max of 454 and 467 nm, lifetimes of DF (τ_DF) of 47 μs and 140 μs and k_rISC values of 4 × 10⁴ s⁻¹ and 1.9 × 10⁴ s⁻¹, respectively, in the doped films. The EQE_max values for OLED devices did not exceed 17% in both cases. In the work of Niu et al.,¹⁵ authors combined a relatively weak but sterically hindered 1-methylcarbazol donor with a triphenyl-s-triazine acceptor. The resulting 1-MeCz-TRZ emitter in 10 wt% DPEPO doped film showed PL_max of 449 nm and τ_DF value of 24.8 μs. OLED devices showed EQE_max of 13.1%. In the work,¹⁶ authors introduced a series of indenocarbazole derivatives, featuring substitutions at the 2,3 and 3,4 positions on the carbazole moiety with various groups, and such donors were coupled with a triphenyl-s-triazine acceptor. The InCz34DPhTz emitter bearing diphenyl (DPh) groups performed best with a PL_max of 475 nm and high PLQY of 97.9% in 10 wt% DPEPO doped film. The τ_DF time was equal to 70.3 μs and k_rISC value of 1.6 × 10⁴ s⁻¹. In OLED devices, the InCz34DPhTz emitter enabled EQE_max of 25.9% with strong roll-off at 1000 cd m⁻² reaching 20.6%. Such examples illustrate the general problem mentioned above of blue TADF emitters: the decreased CT strength required for deep-blue emission causes long DF lifetime, low EQE and/or low operational stability of OLED due to slow rISC.

According to the photophysical and electroluminescent characteristics, the TMCz-BO (Fig. 1) molecule, consisting of 1,3,6,8-tetramethyl-9H-carbazole (TMCz) donor and 5,9-dioxa-13b-boranaphtho[3,2,1-de]anthracene (BO) acceptor (Fig. 1) described in ref. 17 by Adachi and coworkers remains one of the best deep-blue emitters up to date. Authors reported a short τ_DF lifetime of 0.75 μs, a high k_rISC value of 1.9 × 10⁻⁶ s⁻¹ and EQE_max of 20.7%. The key parameter is the low-efficiency roll-off of the OLED device below 3.5%, measured at a high luminance of 1000 cd m⁻². Such a small roll-off indicates high stability and potential for commercialisation in blue OLEDs. Excellent exciton dynamics in 30 wt% PPF films were explained by the small activation energy of rISC (13.4 meV) and an energetical proximity of the LE_A state localised on the BO acceptor. The latter attributed to a much larger SOC value for the 3LE → 1CT transition, reaching 0.12 cm⁻¹, than the ³CT → ¹CT one, equal to 0.001 cm⁻¹. The authors thus suggested the three-state rISC in TMCz-BO: ³CT → ³LE → ¹CT.

Fig. 1 Structure of the TMCz-BO molecule.

Taking into account the outstanding TADF features of the TMCz-BO emitter and the importance of understanding the mechanism of enhanced rISC for further progress in the blue OLED technology, we took a deeper look at the photophysics of this emitter in various media. Our results indicate that in TMCz-BO, the rISC rate can be increased substantially with the increase of polarity both in liquid and amorphous solid state. Moreover, a strong dependence on medium viscosity was also observed. The complex photophysical behaviour of this emitter is accomplished by the coexistence of the two singlets and three triplet excited states, which distinguish TMCz-BO from other D–A emitters with three or two key excited states. Our findings indicate that, in TMCz-BO, the TADF mechanism lies far beyond the three-state rISC model, and even the well-known bases of the static quantum model should be upgraded to explain the intense mixing of the excited states at room temperature.

Experimental and computational methods

Reagents and materials

TMCz-BO was synthesised according to the synthesis route described in ref. 17. A comparison of the results of the analyses confirmed the structural identity and purity of the above compound. Solvents of spectroscopic grade were used for all solvatochromic measurements. Solvents mentioned below were selected to enable gradual change of photoluminescence maximum of TMCz-BO. All reagents were purchased and used without further purification.

Sample preparation

Films were prepared on quartz glass using a solution-processing technique, applying the spin-coating method from the CHCl₃ solutions of the emitter and appropriate host. A ULTRON ultrasonic bath (TME Electronic Components, Poland) was used before spin-coating to facilitate the solubility of compounds.

Apparatus

UV-vis absorption spectra were recorded using a Shimadzu UV-1900 spectrophotometer. Steady-state photoluminescence (PL) spectra were recorded employing the FS5 spectrofluorometer (Edinburgh Instruments, UK) using front-face excitation geometry with a 1 nm spectral resolution. Absolute PL quantum yields (PLQYs) for films were measured using an integrating sphere included in the Quantaurus-QY Absolute PL quantum yield spectrometer. PLQYs for solutions were measured using the FS5 spectrofluorometer. Steady-state phosphorescence spectra in solvents were measured in liquid nitrogen (77 K) quartz dewar using a Varian spectrofluorometer with a 50 ms delay time and 0.5 s time gate. Time-resolved measurements were performed using a customised system consisting of a pulsed YAG:Nd laser (PL2251A, EKSPLA) coupled with an optical parametric generator (PG 401/SH) as the excitation light source and 2501S grating spectrometer (Bruker Optics) combined with a streak camera system (C4334-01 Hamamatsu) as (the detection unit).¹⁸ The system was equipped with a double-stage high vacuum pump (T-Station 85 Edwards). To reduce scattering, reflections and secondary order artefacts, a set of various high-performance optical bandpass (BP) and longpass (LP) filters were used in the excitation path 325/50BP, together with LP filter 375LP (Edmund Optics). Streak camera images were integrated over a constant specified wavelength interval to build PL intensity decay profiles. Phosphorescence measurements in films were recorded using a closed-cycle helium cryostat (APD DE-202) and a temperature controller (LakeShore 336). Photophysical constant rates k_r, k_ISC and k_rISC were calculated according to equations described in ESI,† Section 1. Fityk¹⁹ and Origin²⁰ programs were used for the plot building and fitting.

Quantum-chemical calculations

Quantum chemical calculations were conducted at the DFT/TD-DFT level of theory using the Gaussian 16 program package.²¹ The B3LYP,²² CamB3LYP,²³ M06,²⁴ M062X,²² PBE0²⁵ functionals were used with cc-pVDZ²⁶ basis set for geometry optimizations in various electronic states. Spin–orbit coupling (SOC) constants were computed using the ORCA 4.2 software package²⁷ with B3LYP functional and DEF2-TZVP²⁸ basis set with included relativistic zero-order regular approximation (ZORA).²⁹

Results and discussion

Steady-state absorption and PL in liquid solutions

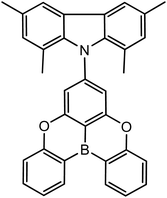
We start the discussion of electronic properties with the absorption spectra analysis, which provides information on the properties of molecules in the ground state geometry. In nonpolar methylcyclohexane (MCH), the long-wavelength absorption of TMCz-BO is represented by a narrow and intense band (Fig. 2A) with the molar extinction coefficient ε of 15 100 L mol⁻¹ cm⁻¹ at the peak maximum of 378 nm. This feature is somewhat unusual for the D–A type TADF emitters, whose long-wavelength absorption band is broad, structureless, and has much lower ε below 2000 L mol⁻¹ cm⁻¹.³⁰ Such a low-intensity absorption is typically ascribed to the charge-transfer (CT) band. It evidences the formation of the CT state, which has crucial importance for TADF, as was mentioned above. On the contrary, TMCz-BO shows absorption similar to that of the isolated BO acceptor unit. This indicates the locally excited nature of its S₀ → S₁ transition, which involves the electronic density on the BO fragment: the S₀ → ¹LE_A transition. Slightly broadened absorption of TMCz-BO in the blue edge indicates that the S₀ → ¹CT transition is characterised by higher energy and strongly overlaps with more intense S₀ → ¹LE_A. Moreover, absorption spectra of TMCz-BO are identical in nonpolar methylcyclohexane (MCH) and other solvents, including polar dimethyl sulfoxide (DMSO). The lack of solvatochromism led us to the conclusion that independently of the polarity of the medium in the ground state geometry, the S₀ → S₁ transition in TMCz-BO leads to the formation of the singlet locally-excited state ¹LE_A localised on the acceptor fragment.

Fig. 2 Absorption spectra of TMCz-BO and the isolated acceptor (BO) in MCH (A). Emission spectra of TMCz-BO in various solvents: PL at 77 K (B), phosphorescence at 77 K (C), and fluorescence at room temperature (D). Films: time-resolved emission spectra at 15 K (E) and stationary PL spectra at RT (F).

On the other hand, strong changes are observed in the photoluminescence (PL) spectra under the solvent change. In nonpolar MCH, fluorescence and absorption spectra follow the mirror image rule, preserving vibrational structure in liquid solution at room temperature (RT, Fig. 2D) and in frozen glass at 77 K (Fig. 2B), where solvent relaxation is blocked due to high viscosity. Absorption and PL spectra overlap substantially (Fig. S1, ESI†), showing a small Stokes shift value of 0.06 eV (77 K) and 0.20 eV (RT). Under such conditions, the emission of TMCz-BO is very similar to that of the isolated acceptor molecule (Fig. S2, ESI†), revealing its ¹LE_A-state origin. At 77 K, when moving from MCH to more polar benzene, the fluorescence maximum shifts from 385 nm to 416 nm, whilst its band shape maintains the narrow shape and vibronic structure of the ¹LE_A fluorescence (Fig. 2B and 3A). With further growing polarity in frozen chlorobenzene, 1,2-dichloroethane (DCE), and especially DMSO, the fluorescence band gradually becomes broad and structureless, and its maximum wavelength reaches 445 nm in DMSO. Thus, one can suggest that the ¹CT character plays an important role in the S₁ state under the increase of polarity and becomes dominant in DMSO.

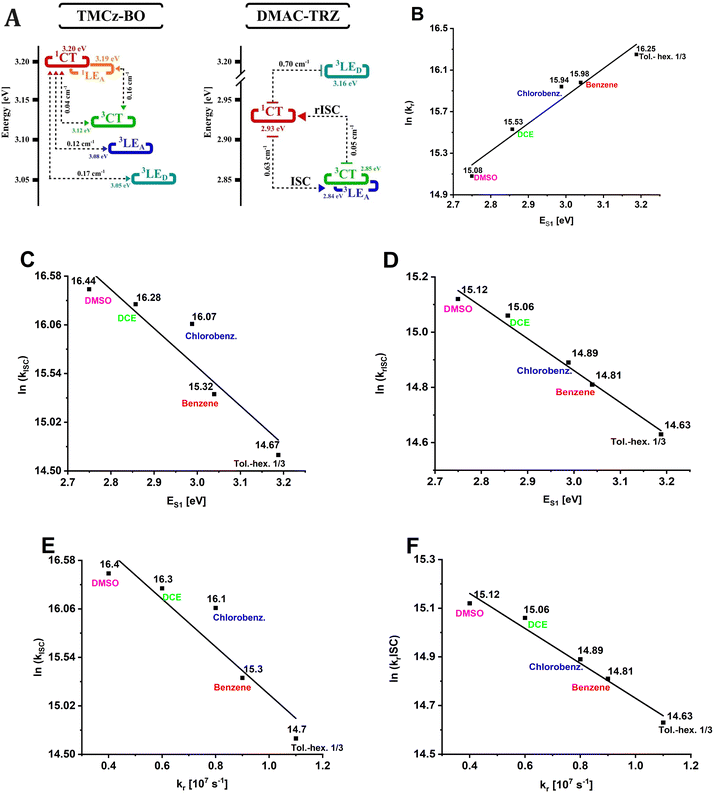Fig. 3 An illustrative energy diagram of the lowest excited states of TMCz-BO at 77 K with the TDDFT-predicted SOC values showed (A). The dependencies of the natural logarithm of k_r (B), k_ISC (C), and k_rISC (D) on the energy of S₁ state (E_S1) in solutions. The dependencies of ln(k_rISC) (E) and k_ISC (F) on k_r in solutions. For fitted equations and R² parameters see Table S1 (ESI†).

At room temperature, the polarity effect is much more pronounced (Fig. 2D): the fluorescence maximum shifts from 403 nm (MCH) to 557 nm (DMSO), while the PL band becomes broad and structureless. Such a strong positive solvatofluorochromism and shape changes indicate that the ¹CT state is dominant in most of the discussed solvents, except for MCH. The observed temperature effect indicates the importance of solvent relaxation in the formation and stabilisation of the ¹CT state. For example, according to the comparison of fluorescence maxima at 77 K and RT in DMSO, solvent relaxation is responsible for more than 0.55 eV decrease of the S₁-state energy, most likely via efficient ¹CT stabilisation.

The discussed temperature-dependent solvatofluorochromic investigations led us to conclude that, at room temperature, the S₁ state of TMCz-BO has a dual nature. Depending on the medium, ¹LE_A or ¹CT characters can dominate, or both can contribute. In this context, the radiative rate constant (k_r) can serve as an adequate measure of the contribution of the ¹LE_A character. The ¹LE_A → S₀ transition in BO analogues is usually more intense³¹ than the ¹CT → S₀ one, which is “forbidden” by the selection rule due to non-overlapping transition molecular orbitals. In fact in MCH, where the ¹LE_A character dominates, the k_r value is the highest reaching 1.7 × 10⁷ s⁻¹, and decreases to 3.5 × 10⁶ s⁻¹ in the most polar DMSO where ¹CT dominates (Table 1). The k_r value shows strong logarithmic dependence on the energy of the S₁ state (E_S1), an effective internal measure of medium polarity in D–A emitters (Fig. 3B). This illustrates the effect of increasing contribution of the CT character in the S₁ state with the increasing polarity due to more efficient separation of frontier molecular orbitals, reduction of the oscillator strength and consequent decrease of k_r.

Table 1 Photophysical properties in liquid solutions and amorphous films

Medium	λ abs [nm]	PLmax [nm]	PLonset/ES1 [nm]/[eV]	PLQY [%]	τ PF [ns]	τ DF [μs]	k r	k nr	k ISC	k rISC
							[10^6 s^−1]
a Average PF and DF lifetimes. For details see ESI, Section 1.
Solutions
MCH	378	405	386/3.21	12	7	—	17	—	—	—
Tol.-hex. 1/3 (v/v)		424	389/3.19	20	17	0.46	11	46	2.4	2.3
Benzene		450	408/3.04	37	36	0.44	8.7	15	4.5	2.7
Chlorobenzene		482	415/2.99	66	45	0.60	8.4	4.3	9.5	2.9
DCE		519	434/2.86	57	46	0.64	5.5	4.2	12	3.5
DMSO		557	451/2.75	45	46	0.75	3.5	4.3	14	3.7
Films
ZNX	378	411	377/3.31	50	8.6	149	14	29	73	1.8 × 10^−2
PMMA		430	381/3.25	53	19	52	14	15	21	3.1 × 10^−2
DPEPO		459	411/3.02	69	21	9.0	22	11	10	0.14

---

Next, the nature of the triplet excited state was analysed based on phosphorescence spectra at 77 K. In MCH, the phosphorescence spectra of TMCZ-BO and BO are very similar (Fig. S3, ESI†), indicating the ³LE_A character of T₁. In the row benzene, chlorobenzene, and DCE, the increase of polarity causes bathochromic shift and broadening of the spectra, which may indicate the growing contribution of ³CT (Fig. 2C and Fig. S4, ESI†). A peculiar behaviour is observed for DMSO, where TMCz-BO unexpectedly exhibits phosphorescence similar to the donor fragment TMCz (Fig. S5, ESI†). This may indicate the effect of specific intermolecular interactions on the triplet state character: DMSO has high basicity and nucleophilicity, which causes selective stabilisation of the triplet state localised on the donor fragment (³LE_D).

Following a so-called static quantum model, which assumes the lack of electronic state mixing, a qualitative alignment of the lowest excited states at 77 K is presented in Fig. 3A. The energies of ¹CT and ¹LE_A states were estimated by deconvolution of fluorescence spectra in benzene solution of TMCz-BO at 77 K, respective values for triplets E_³LEA, E_³CT, and E_³LED estimated from the phosphorescence spectra in MCH, benzene, and DMSO solutions, respectively. At room temperature, under polarity variations, solvent relaxation and specific medium effects, the alignment of states can be different. However, it is important to notice that there are at least five excited states of close energy: ¹LE_A, ¹CT, ³LE_A, ³CT, and ³LE_D, which can participate in photophysical processes.

Calculations on various levels of theory support these experimental findings. Whilst the predicted energy of a selected state differs depending on the computational method, the analysis of the transition molecular orbitals confirms the coexistence of the five lowest excited states ¹LE_A, ¹CT, ³LE_A, ³CT, and ³LE_D (Fig. S6, ESI†). The excited singlet localised on the TMCz donor, ¹LE_D, has sufficiently higher energy above 3.8 eV and is relatively inactive in terms of optical and photophysical properties.

PL in films

As was reported previously,¹⁷ TMCz-BO has a specific potential in OLED applications, where it can be used as a dopant dispersed in a solid host material. For this reason, we further analysed the electronic states in films of different hosts: nonpolar Zeonex® (ZNX), polar bis[2-(diphenylphosphino)phenyl]ether oxide (DPEPO), and medium polarity polymethyl methacrylate (PMMA), which helps to differentiate the emitting species.³⁰

As depicted in Fig. 1E and F, in ZNX at both 15 K and RT, TMCz-BO shows blue-UV emission with PL_max at 411 nm and full width at half maximum (FWHM) of 40 nm (0.29 eV). Time-resolved emission spectra (TRES) at RT evidence a 7 nm red-shift within the first 10 ns of prompt fluorescence and reverse blue-shift after the 10 μs of the delayed fluorescence (Fig. S7, ESI†). In polar DPEPO films, the PL spectrum is sufficiently red-shifted and broader with PL_max at 459 nm and FWHM of 70 nm (0.40 eV); at 15 K, TRES show negligible changes in time, whilst at RT, a relatively small 7 nm (40 meV) red-shift is observed within the first 10 ns of prompt fluorescence, with further stable PL_max of the delayed fluorescence at >200 ns (Fig. S8, ESI†). In films of D–A TADF emitters, strong spectral dependence on the delay time after excitation is usually caused by the rotational isomerism of the emitter involving the dihedral angle θ between the donor and acceptor fragment.^13,32 For example, under the same conditions, the DPEPO film of popular TADF emitter, DMAC-TRZ, shows more than twice as much shift of 35 nm (160 meV), indicating much higher conformational disorder and inhomogeneity of the emitting species as compared to TMCz-BO.

On the other hand, in a medium-polar PMMA at 15 K, TMCz-BO exhibits dual fluorescence resembling the bands observed in both ZNX and DPEPO. The transformation of two spectral bands is well distinguished in TRES: within the first few nanoseconds, the 410 nm band transforms into the broad 450 nm band (Fig. 2E). At higher temperatures, such spectral changes are faster and more intense. During the first 50 ns, the PL_max shifts from 420 nm to 455 nm, and the reverse shift occurs in the delayed fluorescence region from 1 μs to 1 ms (Fig. S9, ESI†). As was concluded from absorption spectra, excitation provides the ¹LE_A state. Thus, the observed spectral changes indicate its transformation to the ¹CT one. Considering the conclusions made for the liquid solutions, we suggest that the contributions of ¹LE_A and ¹CT characters are decisive in the S₁ state in ZNX and DPEPO films, respectively, but in PMMA, their contributions are comparable.

At 15 K, the phosphorescence spectra in films differ from those in frozen solutions by their almost identical shape and maximum in all types of studied solid hosts (Fig. S10, ESI†). This indicates that under such conditions, the nature and energy of the T₁ state are negligibly affected by medium parameters. There is no reliable information on the contribution of ³LE_A, ³LE_D, or ³CT characters, but the complex and broad shape of the phosphorescence spectra indicates that these characters can be strongly mixed. At this point, we assume that when moving from liquid solutions to solid matrices, the high viscosity of the medium plays a key role in the nature of triplet states.

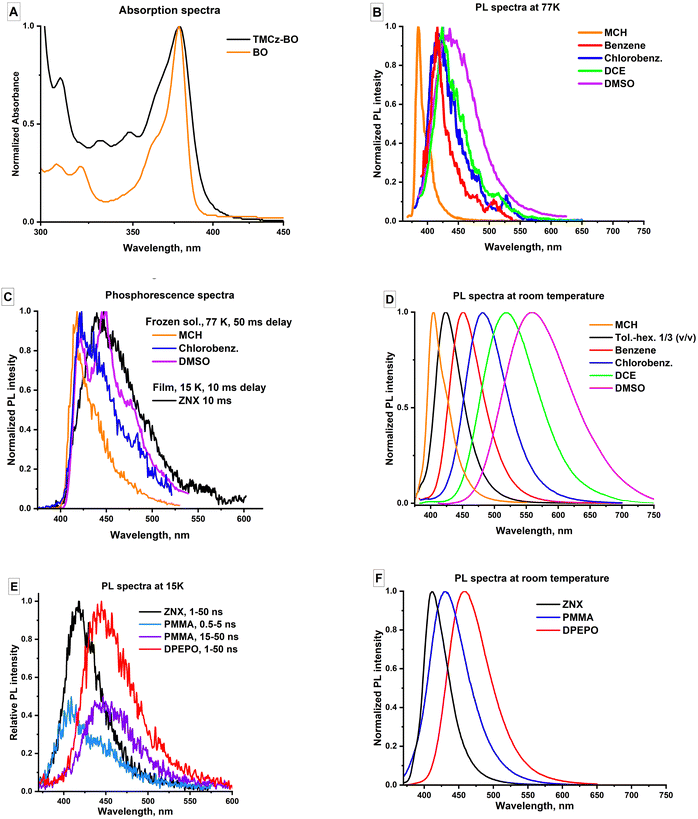
PL kinetics

In all the investigated media except for MCH solutions, TMCz-BO shows TADF. In the PL decay profile, there are well-defined regions of PF until 100 ns and DF up to 10 μs in solutions (Fig. 4A) and up to 10 ms in films (Fig. 4B). The polarity increase leads to the elongation of the PF lifetime rise of the DF plateau (in solutions) and/or shortening of the DF lifetime (in films).

Fig. 4 PL decay curves in solutions (A) and films (B) at room temperature, vacuum.

The gradual change of polarity in liquid solvents without strong specific intermolecular interactions enables the analysis of the trends of ISC and rISC change. According to the correlations in Fig. 3C and D, natural logarithms of the ISC (k_ISC) and rISC (k_rISC) rate constants grow linearly with the increase of polarity described by the decrease of E_S1. This indicates the acceleration of the spin–flip transitions: in the most polar DMSO solution, k_ISC and k_rISC reach 1.4 × 10⁷ s⁻¹ and 3.7 × 10⁶ s⁻¹, respectively (Table 1). Moreover, both ISC and rISC rate constants rise linearly with the decrease of k_r, which, as was mentioned above, indicates the reduction of the ¹LE_A character in favour of the ¹CT one (Fig. 3E and F).

Together with a strong solvatofluorochromic effect, the decrease of k_r with E_S1 (Fig. 3B) indicates (i) stabilisation of the ¹CT character, (ii) decrease of the ¹LE_A contribution to S₁, and (iii) more efficient separation of HOMO and LUMO. On the other hand, such a separation of the frontier molecular orbitals decreases the exchange energy and the energy gap between the S₁ and T₁ states. This explains the correlations observed for the rISC rate (Fig. 3D) following the exponential dependence on ΔE_S1–T1 (eq. 1) and also provides a meaningful conclusion on the two-state T₁–S₁ mechanism of rISC in TMCz-BO because (i) rISC increases with the decrease of E_S1 (ΔE_S1–T1) and (ii) these correlations are linear without any local maxima, which indicates that rISC is not mediated by a higher-energy triplet state of different sensitivity to medium polarity.

In films, TMCz-BO shows several differences in the PL kinetics. Most importantly, whilst the τ_PF, k_r, and k_ISC remain in a similar range as in solutions, DF lifetimes are two orders longer, and the k_rISC values are two orders smaller. Regarding the polarity effect, the τ_DF is shortened, and k_rISC is increased with the growing polarity (decreasing E_S1) in the row ZNX–PMMA–DPEPO, similar to the liquid phase. This is in agreement with the decrease of the ΔE_S1–T1 in polar media, as was mentioned above, but according to much slower rISC, the energy gap value should be much larger than in solutions. Another difference is that the k_ISC dependence on polarity is inversed in films: k_ISC decreases with E_S1, indicating different ISC mechanisms. Considering that the most crucial difference between solutions and films is viscosity, we suggest that the change in rotational freedom is the reason for the lower rISC rate and different ISC mechanisms in films.

The largest difference between the liquid and solid hosts for TMCz-BO is observed in the MCH solution and ZNX film. In spite of very similar polarity, in ZNX, both S₁ and T₁ emissions are broader (Table S2, ESI†) and red-shifted (Fig. S12, ESI†). Specifically, phosphorescence in ZNX at 15 K, differs strongly from that in MCH frozen glass, showing similar onset value, but no longer resembling pure ³LE_A emission by shape. What is more, despite similar E_S1 values, only in the MCH solution, TMCz-BO lacks TADF. Under such low-viscosity, low-polarity conditions, TMCz-BO thus behaves like a LE emitter, but not a CT one. We suggest that considerable role of ¹LE_A character in the S₁ state is the reason of slow ISC which occur via the ¹LE_A → T_n mechanism. When ¹CT is stabilised in more polar media, the ¹CT → T_n mechanism affords higher ISC rates (Fig. 3C).

To explain the inversed k_ISC(E_S1) dependence in films vs. solutions (Table 1) and the k_ISC(k_r) dependence in general (Fig. 3E), it is useful to compare TMCz-BO with another blue TADF emitter, DMAC-TRZ and its analogues, whose S₁ states are of pure ¹CT character.^12,33 In the solutions of such CT-emitters, the ISC rate, remains relatively constant, because the ΔE_S1–T1 value as well as its change with polarity is small. In films, where the statistical ΔE_S1–T1 value and its change with E_S1 are larger, k_ISC decreases with E_S1 just like in films doped with TMCz-BO (Table 1). In fact, in terms of Marcus theory, the decrease of the ΔE_S1–T1 energy gap is equal to the decrease of the driving force of ISC. Hence, if SOC of the S₁ → T_n transition remains constant, which is the case when S₁ has pure character (like ¹CT as in DMAC-TRZ), the ISC rate should either (1) remain relatively constant, if the change of ΔE_S1–T1 is small (as in DMAC-TRZ solutions)¹² or (2) decrease, if the reduction of ΔE_S1–T1 is substantial (as for DMAC-TRZ emitters in films).³³ The latter case correlates very well with the ISC rate of TMCz-BO in films. Therefore, in high-viscosity media regardless of polarity, TMCzBO behaves more as a CT emitter.

Last but not least experimental peculiarity is the following. In ZNX, TMCz-BO represents one of very rare examples of UV-blue TADF with a reasonable rISC rate and microsecond DF lifetime. In such a medium, the large portion of the ¹LE state enables narrow-band emission. On the other hand, thanks to the discussed viscosity effect, both S₁ and T₁ states bear a considerable portion of the CT character thus serving as mediators for rISC. One can consider this as an atypical case of inversed three-state rISC model via³LE_i ⇄ ³CT ⇄ ¹CT ⇄ ¹LE_A. In contrast, D–A emitters usually take advantage of the ³LE state as a mediator for the ³CT ⇄ ¹CT transition, via the ³CT ⇄ ³LE_i ⇄ ¹CT model.¹¹

The role of rotational isomerism and excited-state mixing. Whilst the effect of medium polarity on the CT states of DA emitters is well-known, the described effects of medium viscosity is rather unexpected and needs to be explained. To do so, we rely on the key role of molecular vibrations for the photophysical properties.

As was mentioned above, from the point of view of the TADF mechanism, the molecular vibrations which change the dihedral angle θ between D and A are of key importance for TADF. Such θ-rotations have the strongest effect on the ¹CT ⇄ ³CT transition in TMCz-BO (Fig. S5A, ESI†) affording SOC increase from zero (θ = 90°) to 0.12 (θ = 60°). With other triplet states, the ¹CT state shows comparable SOC constants: 0.12 cm⁻¹ for ¹CT ⇄ ³LE_A and 0.17 cm⁻¹ for ¹CT ⇄ ³LE_D, but these transitions are weakly affected by the change of θ. Regarding the spin–flip transitions involving another excited singlet state, ¹LE_A, only ¹LE_A ⇄ ³CT shows nonzero SOC constant of 0.16 cm⁻¹ and weak θ-rotational activation (Fig. 5A). Other transitions, namely ¹LE_A ⇄ ³LE_A and ¹LE_A ⇄ ³LE_D, are almost completely forbidden (Fig. 5A). This leads to an important conclusion that the contribution of ¹LE_A should thus decrease total SOC constant of the S₁ ⇄ T₁ transitions.

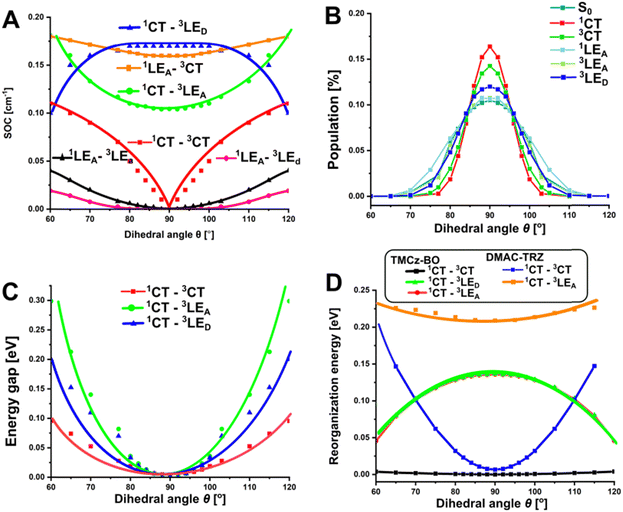Fig. 5 Dependences of SOC (A), θ-rotamer distribution at room temperature (B), relative singlet–triplet energy gaps (C) reorganisation energy (D) on the θ value.

As the experimental data support the two-state rISC mechanism, we calculated the rotationally enhanced rISC rate for the ³CT → ¹CT transition, because only in this case the triplet–singlet energy gap should decrease with the increase of medium polarity due to stabilisation of charge transfer. Following the procedure described previously,¹² for various E_S1 corresponding to each solvent the ΔE_³CT→¹CT values were estimated from the k_r(E_S1) dependence and the k_³CT→¹CT rate constants were calculated for all θ-rotamers available at room temperature using Marcus–Hush equation (for details see ESI,† Section 4 and Tables S3–S8). In this case, the DFT-predicted SOC constants for the ³CT → ¹CT transition (V_T1→S1 = V_³CT→¹CT) were used (Approach 1 in Section 4, ESI†). The obtained statistically weighted k_³CT→¹CT follow the experimental linear dependence of the k_rISC value on E_S1 (Fig. 6): rISC rate increases gradually with polarity as the ³CT and ¹CT states become energetically closer indicating that in fact the ³CT → ¹CT channel is realized in TMCz-BO. However, the calculated values of k_³CT→¹CT are 3–5 times lower than the experimental k_rISC, which means that the applied SOC of pure ³CT → ¹CT transition is too low.

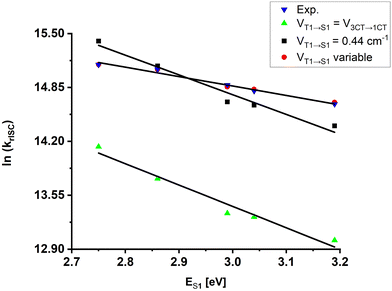Fig. 6 Summary of k_rISC calculations using various approaches and comparison with experimental values; V values for the “V_T1→S1 variable” set are given in Table S9 (ESI†).

Apparently, rISC in TMCz-BO can be described by the two-state T₁ → S₁ model with the key role of CT states. On the other hand, SOC of the real system is substantially higher than that of the ¹CT ⇄ ³CT transition itself. In fact, under the assumption that SOC is constant, the predicted rISC rates become close to the experimental ones when the statistically weighted V_T1→S1 exceeds twice that predicted for V_³CT→¹CT and reaches 0.044 cm⁻¹ (Fig. 6, and Approach 2 in Section 4, ESI†). However, even in this case, the experimental k_rISC(E_S1) dependence is not described properly due to different slopes of fitted linear equations. Finally, the numerical solution of the system of k_rISC equations using ΔE_³CT→¹CT yielded different SOC constants for each solution (Fig. 6 and Approach 3 in Section 4, ESI†) varying from 0.051 cm⁻¹ (the toluene–hexane mixture) to 0.038 cm⁻¹ (DMSO) (Table S3, ESI†). This provides a conclusion that SOC is a function of the excited state energy. Importantly, this means that the nature of S₁ and T₁ changes with medium polarity.

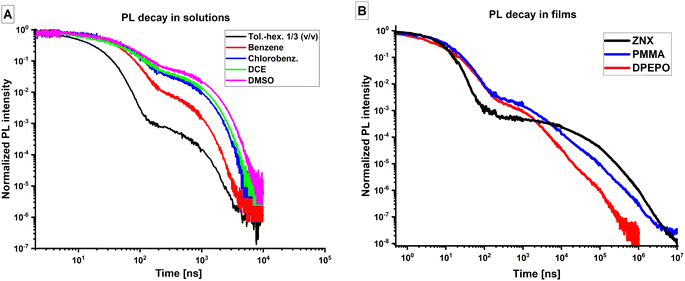
What is more, as was mentioned above, high k_r values indicate the decreasing contribution of the ¹LE character in S₁ with growing polarity, and the phosphorescence spectra differentiate various triplet-state characters ³LE_A, ³LE_D, and ³CT which prevail or coexist in T₁ depending on the medium features. All these observations cannot be explained within the static quantum model which assumes different polarity dependence of the CT and LE states’ energies. Namely, in polar media at room temperature, as the energy gaps between LE and CT states should be too high to afford thermally activated internal conversion (IC) (Fig. S12, ESI†). To explain such contradictions, we suggest the occurrence of vibrationally assisted excited-state mixing (Fig. 7A) which is required to modify the notion of IC typically used for the description of the interaction of the excited states of the same multiplicity. The excited-state mixing will be further used as a basis of a semiempirical model beyond the θ-rotamer model to explain complex deviation of the real TMCz-BO system from the Born–Oppenheimer approximation.

Fig. 7 Illustration of the vibrationally-assisted excited state mixing (A) with the qualitative distribution of θ angle in solutions and films (B). The resulting dual and triple characters of S₁ and T₁ states (C) and contributions of various electronic transitions in rISC in various solutions estimated from empirical SOC (D).

With this in mind and taking into account the bases of the θ-rotamer model, we suggest the following. In solutions of low viscosity, molecular vibrations, specifically θ-rotations, occur barrierlessly within the amplitudes accessible at given temperature (Fig. 7B). The emitter can thus be described as a single individual with averaged electronic parameters of all contributing species with varying portions of different characters of the S₁ and T₁ states. That is in accordance with the monoexponential decays and identical TRES of PF and DF in solutions at RT. One can thus consider such a system as a dynamic mixture of coexisting species with various θ values which contribute collectively to the emissive and spin–flip processes via averaged single channel. Taking into account the observations of multiple nature of S₁ and T₁ states for TMCz-BO in low-viscosity media at room temperature, we introduce the notion of dynamic excited-state mixing (DESM), an electronic effect which affords dual ¹CT–¹LE_A nature of S₁ state and triple ³CT–³LE_A–³LE_D nature of T₁ state (Fig. 7C). DESM is activated by the vibrations within the energetic minima of S₁ or T₁ and is affected mostly by the θ-rotations, solvation (polarity/polarizability of the medium) and solvent relaxation.

In an attempt to understand the scale of DESM and its evolution with solvent, we estimated the contribution of each of the spin–flip transition by fitting empirical SOC constants with the TD-DFT predicted V_Tn→Si (Fig. 7D). It was taken into account that the contribution of LE characters decreases with polarity, and assumed that contributions of transitions involving ³LE_A and ³LE_D states is equal. According to such estimations, the rotationally-activated ³CT → ¹CT channel dominates in all media, with its contribution growing from 50% to over 85% with the increasing polarity. The transitions involving the ¹LE_A state have noticeable contributions in low to medium polarity solvents up to chlorobenzene, where E_S1 < 3.0 eV. In more polar media, ³LE_A → ¹CT and ³LE_D → ¹CT contribute from 20% to 15% in rISC. Note that such contributions are estimated using the ΔE_³CT→¹CT energy gaps and may vary if actual ΔE_T1–S1 is higher.

In amorphous films, the excited-state relaxation and solvent reorganisation are strongly inhibited. The species with various θ are formed during the film preparation and remain trapped in their non-equilibrium geometries with θ as in the S₀ state due to high energetic barrier for rotation of large molecular fragments A and D caused by high viscosity of the medium. Such θ-rotamers should be thus regarded as individual species with different electronic and spectral features. Under such conditions, emitter represents highly heterogeneous mixture of species with different characters of S₁ and T₁ coexisting within the same sample. This is supported by the above-mentioned spectral shifts in TRES, especially in PMMA, and polyexponential PL decays in films. To describe the electronic properties of such a system, we introduce the notion of static excited-state mixing (SESM) (Fig. 7B). Vibrations which enable SESM occur within a local energetic minima corresponding to each individuum, namely a θ-rotamer. In this case, in a group of rotamers with the same θ value, emission, ISC, and rISC can occur via its own unique mechanism. However, as such group coexists in a macroscopic system with the respective measurable values of k_r, k_ISC, and k_rISC appear as averaged complex functions. With the θ value being constrained, regarding actual state-mixing, SESM is much less effective than DESM, and thus S₁ and T₁ states have more defined characters.

The differences in the θ-rotamer distribution and occurrence of DESM or SESM explain different behavior of TMCz-BO in film and solutions. According to the (TD)DFT calculations, the energy of θ-rotamers differs for various electronic states of TMCz-BO (Fig. S13 and Table S4, ESI†). For this reason the distribution of rotamers in the ground and LE states, is substantially broader than in the excited CT states (Fig. 5B and Table S5, ESI†): in S₀, the deviation of the θ angle can reach ±30°, whilst in T₁(³CT), and especially S₁(¹CT), it can hardly exceed ±15°. Such a variation of rotamer distribution in S₀ and CT states explains global effect of medium viscosity. Specifically, the singlet–triplet energy gaps increase with the θ-deviation (Fig. 5C). In films, where the θ-distribution remains as in the S₀-state geometry at the moment of sample preparation, considerable contribution of the rotamers with large θ-deviation results in larger ΔE_S1–T1 and insufficiently higher SOC. On the example of the rotationally activated ³CT → ¹CT transition, the statistically weighted ΔE_¹CT–³CT and SOC for S₀ geometry, reach 10.4 meV and 0.027 cm⁻¹, respectively, causing faster ISC and slower rISC in films. The respective values predicted for S₁ and T₁ (CT) geometries and attributed to solutions are 7.8 meV and 0.021 cm⁻¹. As was mentioned above, at similar E_S1 in solutions (benzene, toluene–hexane mixture) SOC reaches 0.051 cm⁻¹, thus such an increase of SOC is rather negligible.

One should take into account that due to SESM, contribution of LE states should be considerable in all types of solid hosts, what causes much larger average energy gaps in films, where the portion of rotamers with pure CT states is low. On the other hand, constrained geometry in films, affords reasonable CT contribution to S₁ and T₁ states even at low polarities and enhances reasonable SOC via SESM. This affords rISC even at very low polarities, but the limiting factor is still large ΔE_S1–T1. In solutions, sufficient stabilisation of the CT states with polarity narrows the distribution of θ-rotamers, causing the decrease of the ΔE_S1–T1 energy gap, whilst efficient DESM maintains high SOC values. All together, these factors result in fast ISC and rISC rates in media with low viscosity and medium-high polarity, whilst relatively fast emission from S₁ is facilitated by the ¹LE_A-S₀ contribution via DESM.

Conclusions and outlook

TMCz-BO is an example of a complex polyelectronic molecular system with five strongly interacting excited states of different nature and multiplicity. Its fluorescent, phosphorescent, and triplet-harvesting properties strongly depend on the polarity and/or viscosity of medium due to its rich rotational isomerism and vibronic activation of spin–orbit coupling.

According to the experimental evidence, rISC is described by the two-state T₁ → S₁ model, where S₁ and T₁ states are represented by a superposition of two and three states, respectively, of different nature: charge-transfer states and locally-excited states localised on the acceptor and donor fragments.

Due to the efficient dynamic excited-state mixing and free θ-rotations under the conditions of low-viscosity, TMCz-BO achieves its highest rISC rates in liquid solutions. In low polarity solutions, the LE_A character dominates in T₁ and specifically S₁, which is less favourable for the spin–flip transitions (Fig. 5A). The increase of polarity stabilises CT states via solvent reorganisation, thus growing portion of ¹CT in S₁ favours the spin–flip channels with relatively high SOC, which yields higher rates of ISC and rISC.

Under the conditions of high-viscosity, in films, the θ-rotamer distribution is fixed during the film preparation and is negligibly affected by external or internal factors. The CT-state formation and static excited-state mixing are ensured by such a fixed θ-distribution. For this reason, CT character is present in S₁ and T₁ even in the ZNX films of the lowest polarity, enabling near-UV TADF. Such a static θ-rotamer distribution has favourable effect on SOC what is confirmed by the increased ISC rates. On the other hand, the species with large deviation of θ from 90° have increased ΔE_S1–T1 which results in long DF lifetimes and overall decrease of rISC rate. In the case of solid hosts, the enriched distribution of the ΔE_S1–T1 energy gap has bigger influence on TADF than the SOC activation via state-mixing.

The obtained results of relatively simple experiments with changing polarity and viscosity show how complex a single-molecular emissive system can be. Whilst the conclusions on the static and dynamic excited-state mixing were drawn mainly on the basis of the experimental data and only partly supported by DFT calculations, these findings indicate sharp need in more advanced theoretical approaches beyond the vibronic models developed recently to explain deviations from the Born–Oppenheimer approximation.

From the point of view of molecular design principles for deep-blue emitters we can confirm that:

– The control of the distribution of θ-rotamers in various electronic states is important, as was mentioned previously in ref. 13. Small θ-deviations observed for S₁ and T₁ states of TMCz-BO in solutions enable fast rISC, but larger θ-deviations in films are unfavourable for rISC.

– Low S₁–T₁ energy gap and reorganisation energy are very important. In TMCz-BO, the λ values between the LE, and CT states are below 0.13 eV, which is almost twice smaller that in DMAC-TRZ (Fig. 5D) and other blue DA emitters like DMAC-DPS.¹³ In the case of ³CT–¹CT transition, internal λ is negligibly small. Another favourable factor in TMCz-BO, is that λ decreases with the increase of θ-deviation. These factors facilitate the excited-state mixing.

– Evidence of strong CT–LE mixing in the excited states of TMCz-BO even in polar media indicate that the energy gap between the states of the same multiplicity, but different characters is not that important as assumed by static quantum model. In the case of TMCz-BO, the ¹CT–¹LE_A mixing occurs even in the S₁ state, but it is not favourable for spin–flip transitions. Most likely efficient mixing of three characters occurs in the T₁ state even when IC should be blocked by high energy barrier inaccessible by thermal activation at RT. We assume that the above-mentioned low reorganisation energy between LE and CT states achieved by the rigidification of donor and acceptor structure is the key to efficient excited-state mixing.

Data availability

The data supporting this article have been included as part of the ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

Financial support within the National Science Centre, Poland for financial support within the Sonata 16 project No. UMO-2020/39/D/ST5/03094 is gratefully acknowledged. Quantum chemical calculations were performed on the computers of the Wroclaw Centre for Networking and Supercomputing (WCSS), Poland.

References

1. H. Uoyama, K. Goushi, K. Shizu, H. Nomura and C. Adachi, Nature, 2012, 492, 234.
2. Z. Yang, Z. Mao, Z. Xie, Y. Zhang, S. Liu, J. Zhao, J. Xu, Z. Chi and M. P. Aldred, Chem. Soc. Rev., 2017, 46, 915–1016.
3. Y. Liu, C. Li, Z. Ren, S. Yan and M. R. Bryce, Nat. Rev. Mater., 2018, 3, 18020.
4. S. Diesing, L. Zhang and E. Zysman-Colman, et al. , Nature, 2024, 627, 747–753.
5. Y. X. Hu, J. Miao, T. Hua, Z. Huang, Y. Qi, Y. Zou, Y. Qui, H. Xia, H. Liu and X. Cao, et al. , Nat. Photonics, 2022, 16, 803–810.
6. L. S. Cui, A. J. Gillett, S. F. Zhang, H. Ye, Y. Liu, X. K. Chen, Z. S. Lin, E. W. Evans, W. K. Myers and T. K. Ronson Hajime, et al. , Nat. Photonics, 2020, 14, 636–642.
7. Y. Wada, H. Nakagawa, S. Matsumoto, Y. Wakisaka and H. Kaji, Nat. Photonics, 2020, 14, 643–649.
8. Y. Yu, S. Mallick, M. Wang and K. Börjesson, Nat. Commun., 2021, 12, 3255.
9. A. Endo, M. Ogasawara, A. Takahashi, D. Yokoyama, Y. Kato and C. Adachi, Adv. Mater., 2009, 21, 4802–4806.
10. A. Endo, K. Sato, K. Yoshimura, T. Kai, A. Kawada, H. Miyazak and C. Adachi, Appl. Phys. Lett., 2011, 98, 083302.
11. T. Penfold, F. Dias and A. Monkman, Chem. Commun., 2018, 54(32), 3926–3935.
12. I. E. Serdiuk, M. Monka, K. Kozakiewicz, B. Liberek, P. Bojarski and S. Y. Park, J. Phys. Chem. B, 2021, 125(10), 2696–2706.
13. C. H. Ryoo, J. Han, J.-H. Yang, K. Yang, I. Cho, S. Jung, S. Kim, H. Jeong, C. Lee and J. E. Kwon, et al. , Adv. Opt. Mater., 2022, 10, 2201622.
14. H. Gao, S. Shen, Y. Qin, G. Liu, T. Gao, X. Dong, Z. Pang, X. Xie, P. Wang and Y. Wang, J. Phys. Chem. Lett., 2022, 13(32), 7561–7567.
15. R. Niu, J. Li, D. Liu, R. Dong, W. Wei, H. Tian and C. Shi, Dyes Pigm., 2021, 194, 109581.
16. X. Lv, R. Huang, S. Sun, Q. Zhang, S. Xiang, S. Ye, P. Leng, F. B. Dias and L. Wang, ACS Appl. Mater. Interfaces, 2019, 11, 10758–10767.
17. J. U. Kim, I. S. Park, C.-Y. Chan, M. Tanaka, Y. Tsuchiya, H. Nakanotani and C. Adachi, Nat. Commun., 2020, 1765.
18. A. A. Kubicki, P. Bojarski, M. Grinberg, M. Sadownik and B. Kukliński, Opt. Commun., 2006, 269, 275–280.
19. M. Wojdyr, J. Appl. Crystallogr., 2010, 43, 1126–1128.
20. Origin. Origin 7.5, OriginLab Corp., Northampton, MA, 2003.
21. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson and H. Nakatsuji, et al., Gaussian 16, Revision C.01, Gaussian, Inc., Wallingford, CT, 2016.
22. A. D. Becke, J. Chem. Phys., 1993, 98, 1372–1377.
23. T. Yanai, D. Tew and N. Handy, Chem. Phys. Lett., 2004, 393, 51–57.
24. Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241.
25. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78, 1396.
26. T. H. Dunning Jr., J. Chem. Phys., 1989, 90, 1007–1023.
27. F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78.
28. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
29. E. van Lenthe, J. G. Snijders and E. J. Baerends, J. Chem. Phys., 1996, 105.
30. I. E. Serdiuk, C. H. Ryoo, K. Kozakiewicz, M. Mońka, B. Liberek and S. Y. Park, J. Mater. Chem. C, 2020, 8, 6052–6062.
31. J. Ochi, Y. Yamasaki, K. Tanaka, Y. Kondo, K. Isayama, S. Oda, M. Kondo and T. Hatakeyama, Nat. Commun., 2024, 15, 2361.
32. K. Stavrou, L. G. Franca and A. P. Monkman, ASC Appl. Electron. Mater., 2020, 2, 2868–2881.
33. M. Mońka, I. E. Serdiuk, K. Kozakiewicz, E. Hoffman, J. Szumilas, A. Kubicki, S. Y. Park and P. Bojarski, J. Mater. Chem. C, 2022, 10, 7925–7934.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4tc03925d

---