Open Access Article
Open Access ArticleReservoir computing determined by nonlinear weight dynamics in Gd-doped CeO2/CeO2 bi-layered oxide memristors†
Sola
Moon
 a,
Cheolhong
Park
b,
Yunyoung
Jung
c,
Kyeong-Sik
Min
d,
Hyunhyub
Ko
a,
Cheolhong
Park
b,
Yunyoung
Jung
c,
Kyeong-Sik
Min
d,
Hyunhyub
Ko
 *b and
Tae-Sik
Yoon
*b and
Tae-Sik
Yoon
 *a
*a
aGraduate School of Semiconductor Materials and Devices Engineering, Ulsan National Institute of Science and Technology, Ulsan 44919, Republic of Korea. E-mail: tsyoon@unist.ac.kr
bSchool of Energy and Chemical Engineering, Ulsan National Institute of Science and Technology, Ulsan 44919, Republic of Korea. E-mail: hyunhko@unist.ac.kr
cSecurity Technology Laboratory, Pentasecurity Inc, Seoul 07241, Republic of Korea
dSchool of Electrical Engineering, Kookmin University, Seoul 02707, Republic of Korea
First published on 20th February 2025
Abstract
Reservoir computing (RC) is an effective framework for processing spatiotemporal signals. Memristors are well-suited for physical reservoirs in hardware-based RC systems due to their nonlinear functions and memory characteristics. This study experimentally demonstrates an RC system using Pt/Gd-doped CeO2(GDC)/CeO2/Pt memristors. These devices exhibit time-dependent weight updates and decay characteristics, which are critical for extracting spatial and temporal features in RC applications. While previous research has explored implementing RC systems by exploiting the nonlinearity of memristors, there is a lack of systematic research on factors affecting the nonlinearity of memristors and analyzing the reservoir states. Using the time-dependent dynamics of Pt/GDC/CeO2/Pt memristors, this study extracts reservoir states under different pulse conditions and systematically analyzes the factors affecting the extraction of these states. Our findings demonstrate that nonlinearly mapped reservoir states can be linearly separated to achieve high-performance recognition and prediction in complex spatiotemporal tasks in RC systems. Finally, the RC performance of the memristor shows up to 90.5% accuracy in 4-bit pattern verification using the Modified National Institute of Standards and Technology (MNIST) database.
1. Introduction
Recently, artificial neural networks (ANNs) have enabled remarkable progress in the fields of artificial intelligence,1 information security,2 big data,3 and cloud computing.4 Among them, reservoir computing (RC), a subset of recurrent neural networks (RNNs), is particularly effective in handling complex data such as pattern recognition,5 speech recognition,6 time series analysis,7 and natural language processing.8 Unlike deep neural networks (DNNs), which require extensive weight training, RCs offer faster learning by updating only the output layer's weight while keeping the rest of the network fixed.9,10 In addition, the simplicity in training the output layer, such as linear regression in RC, avoids exploding and vanishing gradient problems that occur in traditional RNNs.11 The reservoir layer, which is the most important component of an RC system, dynamically extracts features from temporal input data by nonlinearly mapping low-dimensional inputs into a high-dimensional feature space. Reservoir computing then reprojects this high-dimensional space back to fit training signals. The key requirement for a reservoir layer is nonlinear recurrent network dynamics, ensuring that input signals decay over time while preserving historical dependencies for efficient training.Recent research trends in RC can be summarized and applied in solving real-world problems with actual data, modification of RC models to improve their performance, and physical implementation of RC models.12 Among them, physical implementation of RC models has received considerable attention, and it is important to investigate physical systems that can serve as reservoirs. In particular, physical implementation of RC systems in non-von Neumann architecture, including emerging neuromorphic architecture, is currently being extensively researched to mitigate the problems of limited performance of von Neumann architecture coming from its separation of processing and memory units.13,14 Memristors,15,16 oscillators,17 spintronics,18–20 and photonic devices21,22 have been explored as reservoir components. Among them, memristors offer unique advantages due to their short-term memory and nonlinear dynamic behavior, making them ideal for RC systems. Memristor-based RC systems have shown excellent performance in tasks such as pattern recognition, time-series forecasting tasks,23 signal processing24 and disease detection.25 However, optimizing nonlinearity of memristors is essential for achieving diverse and distinguishable reservoir states.15,26,27 Therefore, it is crucial to analyze time-dependent weight dynamics of memristors to extract various spatial and temporal characteristics of the reservoir in performing spatiotemporal operations for optimizing the RC systems. These features include high dimensionality of the reservoir, nonlinearity with respect to weight update, paired-pulse facilitation (PPF), nonlinear short-term plasticity (STP), and class separation properties. However, there is a lack of systematic research on the factors influencing the nonlinearity of memristors. Also, the analysis of reservoir states determined by the factors affecting this nonlinearity has not been thoroughly studied. Therefore, in order to achieve high-performance recognition and prediction in complex spatiotemporal tasks in RC systems, this study aims to extract reservoir states under various voltage application conditions and analyze the factors that influence the extraction of these reservoir states. Through this, the dominant factors that affect the performance of memristor-based RC systems and their optimized conditions can be identified.
Current research on artificial synapses with memristors focuses primarily on the non-volatile aspects of the memristors. It includes the enhanced transition from short-term memory (STM) to long-term memory (LTM),28 and improved retention for DNN computations and switching performance with low power and high speed.29 However, for the application to RC, it is essential to realize and control the time-dependent conductance decay behaviors of the memristors as STM functionality. In this work, we experimentally demonstrate a memristor-based RC system with Pt/Gd-doped CeO2 (GDC)/CeO2/Pt interfacial-type analog memristors. It exhibits time-dependent weight update and decay characteristics, which are beneficial for realizing an RC system. In the RC system, the weight update of memristors should be precisely controlled in an analog way with respect to the input conditions such as voltage pulse amplitude, pulse width, number of pulses, interval between pulses, and its decay with time. Memristors with oxide-based RRAM exhibit two resistance switching characteristics: digital and analog switching. Digital switching is achieved typically by the formation and rupture of conductive filaments in the insulating oxide. The alignment of defects or metal cations induced by external bias can form conductive filaments and cause consequent resistance changes. However, the formation and rupture of filaments is difficult to represent in multi-level resistance states, making it difficult to achieve analog synaptic weights. In contrast, analog switching employs a non-filamentary resistance change through the modification of the interface by external bias, causing a gradual change in resistance state. This gradual and analog change in the conductance is advantageous for implementing RC systems. As aforementioned, there have been many memristors with various single-layered and bi-layered oxides, such as CeO2,30 HfO2,31 TiOx/Al2O3,32 ZnO/TaOx,33 and ZrO2/IGZO.34 In this study, the bi-layered oxide memristors based on the same CeO2 matrix, i.e., GDC/CeO2, are employed to have more stable and controllable redistribution of oxygen vacancies between the CeO2 and GDC layers under the electric field.35
CeO2 has desirable properties for resistive switching such as the presence of abundant oxygen vacancies, high oxygen ion conductivity, and variable valence states of Ce cations (Ce3+ and Ce4+), which makes it favorable to exhibit a gradual analog resistance change.36–38 While CeO2 exhibits a gradual resistance change characteristic, the synaptic properties of Pt/CeO2/Pt memristor devices with a single CeO2 switching layer showed significantly asymmetric synaptic weight update behaviors (potentiation and depression), as reported in previous studies.39 They also suffered from the inconsistent dynamic range of resistance change during repeated operation. The GDC has also been reported to have increased oxygen ion conductivity via increased oxygen vacancy concentration as a result of Gd doped in CeO2.40,41 In our previous study, however, devices with a Pt/GDC/Pt structure consisting of a GDC single layer did not exhibit reliable analog weight updates.35 On the other hand, the proposed GDC/CeO2 bi-layered oxide memristor has been demonstrated to have analogous synaptic weight update, PPF, STP characteristics and their adjustment could be improved compared to the single-layered CeO2 or GDC memristors.35 For RC systems, the weights need to be adjusted analogically to subsequently separate the reservoir states based on the predictable decay characteristics. A memristor with a bi-layered oxide structure, where a GDC layer is stacked on top of the CeO2, is advantageous for exhibiting gradual analog resistance change states via the exchange of oxygen vacancies between two layers, compared to a single-layered device with limited controllable variables. Therefore, a bi-layered oxide memristor produces more precise and predictable synaptic weights updates in RC. This study demonstrated performing RC using the GDC/CeO2 bi-layered oxide memristors by storing reservoir states with controllable weight update and decay characteristics that effectively separate complex sequential information without superimposing the states. The RC performance of the memristor was evaluated via 4-bit pattern verification by applying various pulse signals to the memristor, where a Modified National Institute of Standards and Technology (MNIST) handwriting digit database was used to train and test the RC system. Although RC systems with various memristors have been researched previously,15,26,27 there has been a lack of systematic investigation on the relationship between memristor performance and RC operation. The efficient RC operation for discrimination of reservoir states is hard to achieve due to the overlap of states determined by multiple factors including the magnitude of weight update depending on the input strength, PPF, time-dependent decay of updated weight, and interval between input signals. Therefore, a systematic examination of the effect of these variables on RC performance was carried out to provide guidelines for the implementation of efficient RC systems with memristors.
2. Results and discussion
2.1 Requirements for memristor-based reservoir computing systems
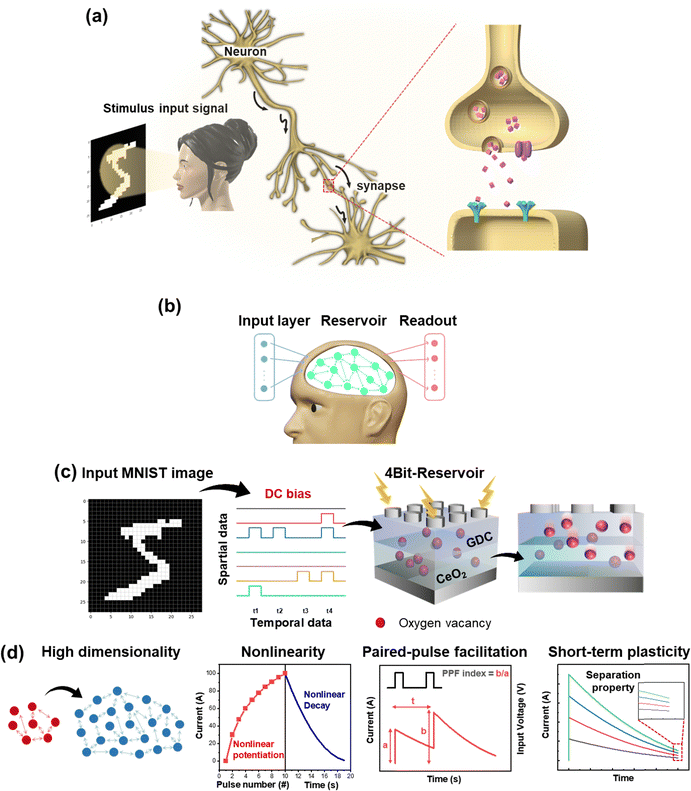
As shown in Fig. 1(a), the human brain processes input signal stimuli through connections called neurons and synapses. By mimicking the biological nervous system, which is capable of performing highly cognitive functions with low energy, a memristor can be a good candidate to produce the abundance of physical reservoir states for an RC system. The RC system consists of an input layer receiving the input signal, a reservoir layer processing the spatiotemporal input signal in high-dimensional space, and a trainable readout layer used to generate the output (Fig. 1(b)). In a memristor-based RC system, as shown in Fig. 1(c), when a spatiotemporal input signal stimulates a memristor, the modified conductance (or resistance) is stored in the memristor and constitutes a reservoir state. Then, it becomes the input to a subsequent readout layer, processing spatial and temporal tasks in parallel.As described earlier, it is of paramount importance that the reservoirs in an RC system have sufficient nonlinear recurrent network dynamics. There are four main requirements for such a physical reservoir (Fig. 1(d)). First, it must have high dimensionality, which means that a sequence of events can be linked together to express spatiotemporal dependencies. The problem with memristors in conventional RC systems is that each input signal to an individual memristor is processed independently, making it difficult to represent the spatial relationship between time-domain inputs.42 Instead, if the input signals are implicitly stored as historical information to map them to a higher dimension, spatiotemporal dependencies can be represented and generate enriched reservoir states. Second, strong nonlinearity of memristors is required. Memristors have an inherent nonlinear behavior that makes them very suitable for implementing RC systems.43 It has been reported that such nonlinearities in memristors can result from complex physico-chemical coupling processes such as ion drift, which involves redox or composition changes to maintain charge neutrality.44–46 The nonlinearity of memristors during the weights update and their decay is necessary to multiply the richness of physical reservoirs.26,27 The change in conductance of each memristor, controlled by nonlinear dynamics, facilitates the mapping of the input signal to various separated reservoir states in a high-dimensional space. Therefore, nonlinearly mapped reservoir states can be linearly separated, allowing RC systems to be implemented using only a simple linear network layer.15 In addition, PPF characteristics are one of the factors that contribute to the nonlinearity of the memristor and affect the separation capability of reservoir states. The output signal of each memristor is obtained through the excitatory post-synaptic current (EPSC) as a result of a series of temporal input stimuli. The EPSC is determined by the number, amplitude, and interval of input pulses as well as its gradual decay with time. This characteristic can be quantified by the PPF, expressed as the ratio of the first output signal to the second output signal for two consecutive input signals. The PPF illustration in Fig. 1(d) shows the change in current in a memristor measured between two consecutive pulses. Applying two consecutive pulses with the same amplitude results in a larger increase in the second output signal than that in the first output signal (a < b). Third, it must have short-term plasticity. Short-term plasticity features conductance that returns to its initial state on a timescale of seconds in general when the applied voltage is removed.47 Because the reservoir in the RC system needs to store the processed output from the relatively recent inputs, it is required to have a suitable STP that does not drop the processed conductance too fast or too slow. Finally, it should be easy to separate the implied output signals into different classes. The implied output signal is evaluated as conductance. The greater the difference between the respective conductance values, the easier it is to classify. To facilitate classification, the nonlinearly decaying dynamics of memristors should be well characterized. Also, the timing of applying the read voltage must be well determined accordingly, so that the nonlinearly mapped reservoir states can be linearly separated.
2.2 Electrical characteristics of Pt/GDC/CeO2/Pt memristors
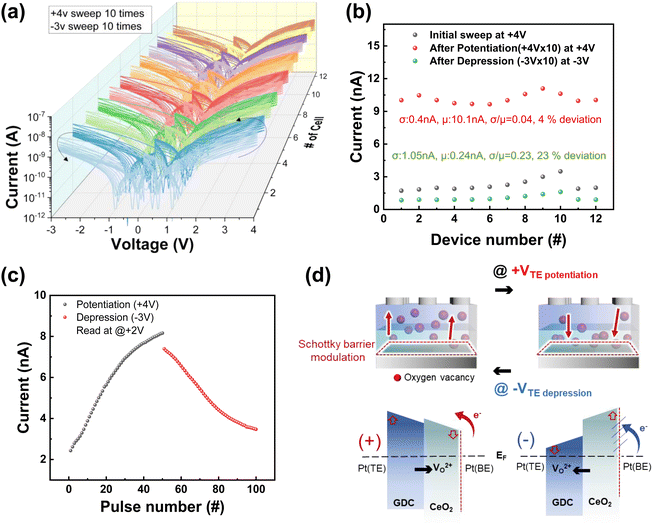
The current–voltage (I–V) hysteresis curves from 12 cells of Pt/GDC/CeO2/Pt memristors were obtained by repeating DC voltage sweeps, as shown in Fig. 2(a). First, positive voltage sweeps of 0 → +4 → 0 V were repeated ten times, then the same number of negative sweeps of 0 → −3 → 0 V were conducted. As repeating positive voltage sweeps, the current of the cell #1 increased consecutively within the range from 1.75 to 10.21 nA. Then, it decreased sequentially back to about 4.17 nA by repeating negative voltage sweeps. This confirms the voltage polarity-dependent analog resistance change in the memristors with the GDC/CeO2 bi-layer. To evaluate the cell-to-cell variation, the current values at the initial sweep, after potentiation sweeping ten times and subsequently 10 depression sweeps of 12 cells from the I–V curves in Fig. 2(a) are presented in Fig. 2(b). The black dots represent the current values, measured at +4 V after the initial +4 V double sweep as potentiation. The red dots indicate the current values measured at +4 V after 10 times of the +4 V double sweep as depression. The green dots correspond to the current values measured at −3 V after the subsequent 10 times of −3 V double sweeps. The mean value (μ) of potentiation was 10.1 nA, and the standard deviation (σ) was 0.4 nA; thus, the σ/μ value was about 0.04, which implies the deviation of 4% from the mean value. The μ after depression was 1.05 nA, and its σ was 0.24 nA; thus, the σ/μ value was about 0.23, which implies the deviation of 23% from the mean value. In this device, because the CeO2 layer was deposited by atomic layer deposition (ALD), it turns out that the resistance change is more stable and uniform than that of the device using sputtering for the layers.35 Fig. S1 (ESI†) shows the cell-to-cell distribution of the potentiation in the device using sputter-deposited bilayers and the device using sputter-GDC/ALD-CeO2 (ESI†). For potentiation, 30 pulses of +4 V and with a width of 0.64 ms were applied to 12 randomly selected cells and the current ratio before and after potentiation, i.e., degree of potentiation, was read at the readout voltage. Its distribution in the device using sputter-deposited bilayers, which is quantitatively defined as the percentage ratio of standard deviation (σ) to the mean value (μ), was calculated to be 25%, while the percentage ratio of σ/μ of the device using sputter-GDC/ALD-CeO2 was about 7%. This confirms a significant improvement in the uniformity by using ALD-deposited CeO2 in the bi-layered memristor. In addition, the I–V curves are highly asymmetric between positive and negative voltage sweeps, which can be attributed to the different Schottky barrier height at CeO2/Pt and Pt/GDC interfaces.48,49 The Schottky barrier height at the CeO2/Pt interface was measured to be approximately 0.3 eV, which is notably lowerthan ∼0.55 eV at the Pt/GDC interface (Fig. S2 in the ESI†). The different barrier heights between both interfaces construct an asymmetric band structure as shown in Fig. 2(d).Fig. 2(c) shows the weight update for potentiation and depression of the GDC/CeO2 bi-layered memristors. The measurement was conducted by applying 50 consecutive voltage pulses with +4 V and −3 V amplitudes for potentiation and depression, respectively, at a fixed pulse width of 0.64 ms. The current was read at +2 V after each pulse. It shows an analog change in resistance with respect to the voltage polarity, consistent with the polarity dependence in I–V sweep results. It is noteworthy that the resistance level can be tuned simply by repeating pulse application because the current changed sequentially proportional to the pulse number. Updating weights in an analog manner is important in RC systems because it can represent a variety of states to meet the high dimensionality of RC. Unlike the digital-type resistance change memristor, an analog-type resistance change memristor can represent various states with one device. Thus, it enables increases in the integration capacity and operation speed with reduced power consumption and hardware fabrication cost.
The analog resistance change is thought to come from the redistribution of oxygen vacancies, which modulates the energy barrier at the electrode/oxide interface and changes the resistance, as schematically illustrated in Fig. 2(d).35 When a positive voltage is applied to the Pt top electrode (TE), while the Pt bottom electrode (BE) was grounded in the Pt/GDC/CeO2/Pt memristor, the positively charged oxygen vacancies migrate from the GDC to the CeO2 layer, and oxygen ions move to the GDC layer in an opposite direction. Then, the added oxygen vacancies, as n-type dopants in CeO2, provide more electrons to the interface, which fill the interface traps and lift up the Fermi-level. As a result, the Schottky barrier height at the CeO2/Pt bottom interface is lowered and the resistance read at a positive voltage decreases gradually (potentiation). Conversely, applying a negative voltage to the Pt TE causes positively charged oxygen vacancies to migrate from the CeO2 to the GDC layer, increasing the Schottky barrier at the CeO2/Pt bottom interface. Therefore, the resistance read at +3 V increases gradually (depression).
In RC systems, the previous input influences the next response via storing information and organizing the state of the physical reservoir, characterized by a recurrent connection. A recurrent connection can be implemented with the decay characteristics having short-term plasticity and nonlinearity to ensure that past inputs influence temporally the current reservoir state and output. The behavior of current decay with time in the memristor is presented in Fig. 3. It shows that the current decay as a retention loss resembles the dynamics of human memory loss. In human memory, short-term memory (STM) remains typically for a few seconds to tens of minutes, while long-term memory (LTM) remains for hours to weeks, or even a lifetime.50 Although it is also pursued to intentionally switch from STM to LTM by strengthening input stimulating conditions for the application to nonvolatile memory,51 it is more desirable to have STM or STP characteristics for the use of a memristor as a reservoir to process spatiotemporal signals in RC systems.
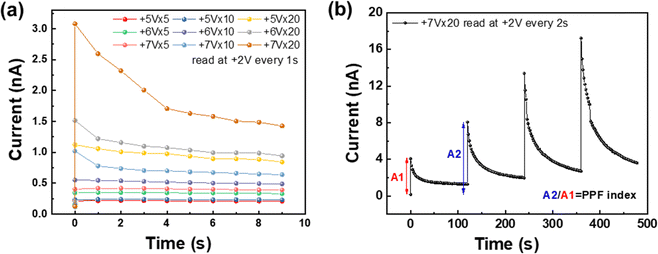
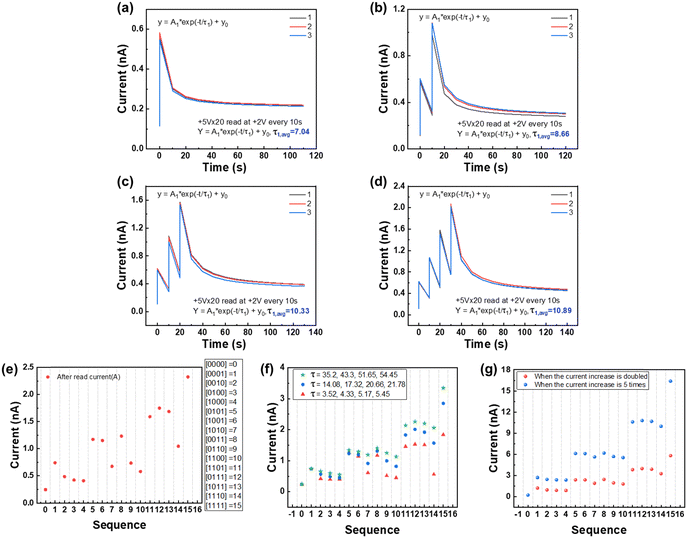
The retention loss characteristics with respect to the amplitudes and the number of pulses applied to the memristors are shown in Fig. 3(a). Here, the current was measured at +2 V every 1 s after applying the stimulus pulse under different conditions. Obviously, the current increased higher upon applying the pulses with higher amplitude of voltage and more times. When +5 V pulses were applied 5, 10, and 20 times, the current increased from 0.15 to 0.21 nA, 0.14 to 0.23 nA, and 0.34 to 1.12 nA, respectively. The current then decayed to 0.21, 0.23, and 0.84 nA after 9 s. Similarly, at +6 V pulses with the same pulse number conditions, the current increased from 0.15 to 0.34 nA, 0.14 to 0.55 nA, and 0.14 to 1.52 nA, and then decayed to 0.33, 0.48, and 0.94 nA after 9 s, respectively. Also at +7 V pulses, the current increased from 0.12 to 0.40 nA, 0.12 to 1.02 nA, and 0.12 to 3.08 nA, then decayed to 0.38, 0.64, and 1.43 nA after 9 s, respectively. It is also clearly observed that the fast initial decay as the STM is followed by a long and slow decay as the LTM, mimicking the human memory loss.52
The dependence of retention on the amplitude and number of pulses in Fig. 3(a) provides several notable characteristics for the RC applications. First, under the condition of a small number of pulse applications, e.g., 5 and 10 times, the change of current (conductance as a synaptic weight) was not significant but retained long with negligible decay with time, irrespective of the pulse amplitude. In this weak stimulation condition, it is thought that only a small number of oxygen vacancies are redistributed; thereby making a low oxygen vacancy concentration gradient. As a result, the driving force for oxygen vacancies to return back to the initial state is small, so long retention is achieved. Even though longer retention could be achieved in the weaker stimulus condition, the change of current is not sufficient, which limits the available weight levels. Memory is closely linked to synaptic weight, which is the strength of synaptic connections.53–55 In biological systems, the synaptic weight is strengthened or weakened by the change in ionic concentrations that determine the activation of receptors and the release of neurotransmitters (e.g. Ca2+, Na+, Mg2+, K+).56 In order to remember complex information or large amounts of data for a long time, stimuli should be strong enough to make the significant change in ionic concentrations to achieve strong synaptic weights. Nevertheless, it should be noted that the complex biological and molecular mechanisms for memory stability are still being investigated.57 Moreover, simply enhancing synaptic efficacy is not enough to store complex memories, as the response of a synapse in a long-term process is not simply determined by its own activity history.58,59 Second, the current increased proportionally to the amplitude of pulse in the order of +5, +6 and +7 V. Furthermore, the retention after 9 s was 64, 56, and 44% respectively. It is rational that the final current after decay is higher at the higher pulse amplitude condition. However, it is noticeable that the application of the higher amplitude pulse led to the greater initial current change but also resulted in the faster decay of current. This implies that the pulse application with the higher amplitude led to the higher conductance change, while causing further decay due to the higher driving force for the restoration to the initial state as discussed earlier. Therefore, the percentile retention loss is the highest at the highest pulse amplitude condition, although the absolute current value after decay is the highest. Even with the decay, the current at each condition could be distinguished from each other. For the RC application, both the sufficient conductance change and its discernable short-term decay are essential to differentiate the reservoir states. Thus, it is concluded that increasing the number and amplitude of pulses is preferred to achieve distinguishable reservoir states in response to temporal stimuli for RC applications.
Fig. 3(b) shows PPF characteristics of Pt/GDC/CeO2/Pt memristors. Since RC processes the temporal information, the responsive weight update to successive pulses with time interval as also involving short-term decay is one of the decisive factors to determine final reservoir states. The weight update for successive input signals with interval can be assessed by PPF characteristics. Twenty pulses with an amplitude of +7 V and 0.64 ms were applied and the current was read at +2 V every 2 s for 2 min, and it was repeated four times in total. After consecutive pulses, the initial current increased from 0.16 to 4.08 nA and decreased to 1.28 nA after 2 min. Application of another set of pulses further increased the current to 8.05 nA, then decreased it to 1.97 nA after 2 min. Apparently, the peak value of the EPSC by the second set of pulses is larger than that by the first set. The PPF index, defined as the ratio of the second EPSC (A2) to the first EPSC (A1), corresponds to 202%. The ratio of the third and fourth EPSCs to the first EPSC is 337% and 436%, respectively, verifying the continuously increasing EPSC upon repeating pulse application even with its decay with time. The enhanced PPF indices upon repeating pulse application are also explained with accumulative oxygen ion redistribution. Oxygen vacancies move from the GDC toward the CeO2/Pt interface under positive bias, then lower the Schottky barrier height at the CeO2/Pt bottom interface and consequently increase the conductance. These oxygen vacancies (and oxygen ions) tend to return back to the initial locations due to the driving force to minimize the concentration gradient, thereby causing retention loss when the voltage is removed. Nevertheless, repeated application of pulses causes more vacancies to be stuck near at CeO2/Pt interface stronger. Partially remained oxygen vacancies are responding to the consecutively applied pulse before they have fully returned to their original position. As a result, the current level after decay keeps increasing to exhibit PPF characteristics.
2.3 Memristor-based RC for 4-bit input discrimination
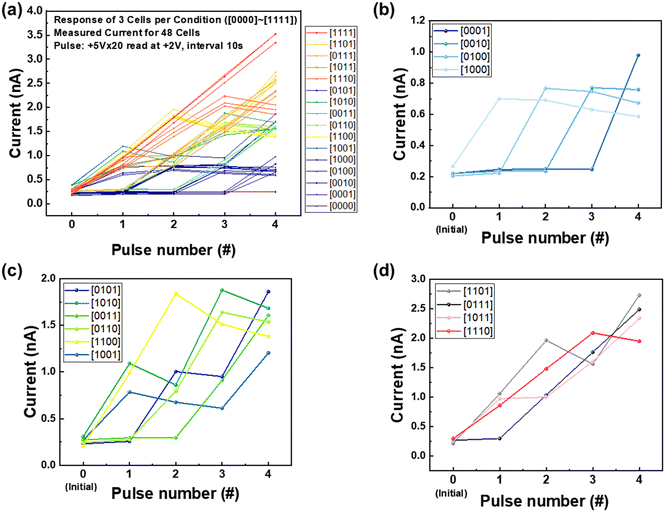
Using the characteristics of analog and time-dependent resistance change dynamics with its short-term decay in Pt/GDC/CeO2/Pt memristors, the RC operation for 4-bit input discrimination was demonstrated. In order to discriminate multi-bit input, the distinguishable reservoir states should be stored through analog weight update by a controllable change in conductance and its decay with time. In particular, nonlinearities in STP and PPF play a crucial role in representing different and distinguishable reservoir states. As shown in Fig. 2 and 3, the Pt/GDC/CeO2/Pt memristor has unique nonlinear STP and PPF characteristics with respect to the pulse condition.Fig. 4 shows the experimental results of binary 4-bit input data discrimination processing. The binary 4-bit data from [0000] to [1111] were processed by applying a pulse train consisting of a set pulse (+5 V, 0.64 ms, twenty times) for “1” and ground (0 V) for “0”, respectively. The current after pulsing was read at +2 V. Between each pulse, the interval time was set to be 10 s for utilizing the decay of conductance depending on conductance state. Fig. 4(a) shows the results from 48 cells measured by repeatedly applying a binary 4-bit pulse train with a total of 16 states ([0000] to [1111]) three times for each case. The current change is found to be consistent at each pulse train, discriminating input data according to the pulse train. To analyze the current change for the input data in detail, the results were divided into three groups with respect to the number of “1” bits. Then, one of the three repeated measurement results for each train was randomly selected and are presented in Fig. 4(b)–(d). The total results of three repeated measurements are shown in Fig. S4a–e (ESI†). Fig. 4(b) shows the simplest case of the current for the four states with one “1” bit, i.e., [1000], [0100], [0010], and [0001]. The measured currents for those states are shown to be in the order of I[1000] < I[0100] < I[0010] < I[0001]. Apparently, the [1000] state has the lowest final current due to the longest decay time, whereas the [0001] state has the highest current due to the shortest decay time. Due to the decrease in current with time, the four states from [1000] to [0001] with “1” input pulse at different time could be discriminated accordingly.
Compared to the case of one “1” input pulse train, the states with two and three “1” input pulse trains are more complicated. The discrimination of states is not determined only by the behavior of current decay with time, but also by the nonlinearity in PPF and weight update characteristics. In this measurement, the effect of nonlinearity of the current change on the state discrimination could be analyzed from PPF characteristics upon applying the first pulse (+5 V, 0.64 ms, twenty times) and the second pulse (+5 V, 0.64 ms, twenty times) with an interval time. Fig. 4(c) shows the currents in the case of six states with two “1” input trains, i.e., [0101], [1010], [0011], [0110], [1100], and [1001]. Pulses of the same sequence of “11”, i.e., [0011], [0110], and [1100] will have the same interval time between “1”. Therefore, the length of decaying time after input of “11” determines the final current. Similarly, the currents for [0101] and [1010] states having the same sequence of “101” are determined by the decaying time. As expected, the final current was measured to be I[0011] > I[0110] > I[1100], and I[0101] > I[1010]. On the other hand, it is not a simple matter to discriminate the states with different pulse sequences. This is because nonlinearities in decay, PPF, and the weight update as a function of pulse number are all involved at the same time. In order to examine the effect of nonlinearity in PPF as a function of interval time on the final current, the current for the [0101] state was compared with that for [0011], where the interval times between pulses were not the same as each other. The current for the [0101] state associates with the PPF with a longer interval time, whereas that for the [0011] state associates only consecutive pulsing with a much smaller interval time between pulses than the [0101] state. The result of I[0101] > I[0011] indicates that the increase in current via PPF surpasses the current change in consecutive pulses. As previously described, PPF can be enhanced during an appropriate interval time (presynaptic inhibition) between consecutive pulses. Therefore, it can be seen that the interval time of 10 s between the second pulse “1” and the fourth pulse “1” of the [0101] pulse resulted in a higher final current due to the enhanced PPF characteristics than the [0011] pulse. Nevertheless, caution is needed as the difference is minimal and could be changed depending on the interval, number of pulses for each train, and other factors. For example, the current for the [1001] state with the longer interval time of 20 s turned out to be the smallest. This means if the interval time is too long, the next synaptic response is inhibited because oxygen vacancies would return back to the equilibrium position given enough interval time. It can be summarized in the states with two “1” bits that the current in consecutive pulses without interval time was smaller than the current in pulses with an interval time of 10 s and larger than the current in pulses with a longer interval time of 20 s. This implies that there is an optimum condition in the interval time to enhance the PPF to discriminate the states due to the nonlinear decay characteristics of PPF. The nonlinearity of memristors can be tuned by appropriately modulating presynaptic inhibition and the final current levels for each state are the interwoven results with the effects of several nonlinear factors.
Fig. 4(d) shows the currents upon applying three “1” input trains, [1101], [0111], [1011], and [1110]. It is obvious that the current for the [0111] state is measured to be higher than that for [1110] because the former state has a shorter decay time. The following is a comparison between [1011], [1101] and [0111], where the first two states have an interval between pulses and the last has no interval between pulses. The first two cases with the interval between pulses associates both the PPF and decay with time depending on conductance. On the other hand, the last case without interval associates only the decay behavior. The final current was found to be in the order of I[1101] > I[0111] > I[1011]. The I[0111] by consecutive pulses without an interval was higher than I[1011] by the pulses with the interval time after the input pulse once. However, it is lower than I[1101] with the interval after input pulse twice. The result of I[1101] > I[0111] > I[1011] implies that PPF after input twice enhanced the current most, whose effect was even stronger than the current increase by consecutive pulsing (i.e., [0111] state). The PPF after input once (i.e., [1011]) was not as effective as that after input twice. This indicates again that the PPF and decay characteristic depending on its conductance level and the interval step is one of the decisive factors. The result of I[0111] > I[1011] implies that PPF is not so effective at a low current regime after one input pulse compared to the consecutive pulsing. However, the result of I[1101] > I[0111] indicates that PPF at a high current regime increases the current further than that of consecutive pulsing. As shown in the results, the discrimination of [1011] and [1101] states is correlated to the decay characteristics depending on its conductance level. Aforementioned, the conductance change and its decay are determined by the redistribution of oxygen vacancy. In the [1011] pulse, the amount of migrated oxygen vacancies after the first pulse application is less than that after the application of the first and second pulses in the [1101] pulse. When the applied voltage is removed, the oxygen vacancies return to equilibrium due to the concentration gradient during the interval time. Based on the interval time, for the pulse [1101], where more oxygen vacancies moved by “11” pulses, the current dropped more sharply during the interval due to the larger concentration gradient. The sharper decrease in current is consistent with that shown in Fig. 3via the rapid return of a large amount of oxygen vacancies that were moved as the number of stimuli increased. Then, the next pulse led to a higher final current than that for the [1011] pulse due to the enhanced PPF behavior. It is concluded from this result that PPF plays a crucial role to increase the nonlinearity of current increment during weight updates and determines the decay rate depending on the conductance level. Therefore, the effect of enhanced PPF by the number of pulses or interval time on discrimination of reservoir states needs to be precisely controlled.
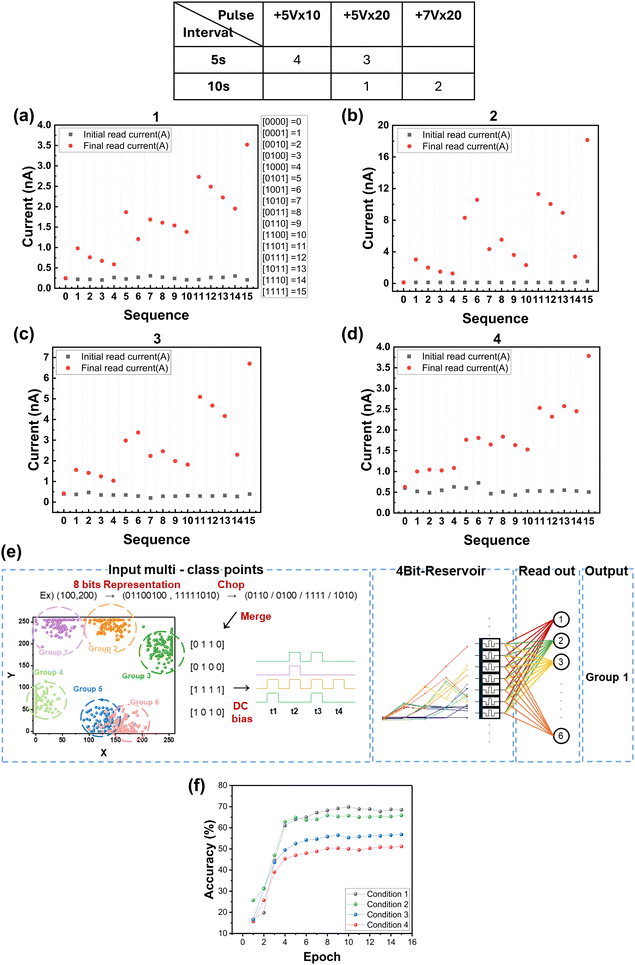
Fig. 5(a)–(d) show the final currents corresponding to a binary 4-bit pulse along with its initial values at four different conditions shown in the table. The final currents corresponding to 4-bit reservoir states are plotted, where the states with one “1” are referred to sequence 1–4 (Section 1), and the states with two “1”s are sequence 5–10 (Section 2), and the states for three “1”s are sequence 11–14 (Section 3), respectively. Depending on the pulse conditions of pulse amplitude, pulse number, and the interval time between pulses, the reservoir states were differentiated by a combination of the decrease in current with time and the nonlinearity of the PPF. Four different pulse conditions are summarized in the table in Fig. 5, with the application of +5 V twenty times and reading at +2 V with an interval of 10 s (Fig. 5(a), condition 1), +7 V twenty times with an interval of 10 s (Fig. 5(b), condition 2), +5 V twenty times with an interval of 5 s (Fig. 5(c), condition 3), and +5 V ten times with an interval of 5 s (Fig. 5(d), condition 4). Comparing the results for condition 1 and 2 with the different pulse amplitude of +5 and +7 V at the same number and interval time, the final current is higher at the higher amplitude of +7 V (i.e., the stronger stimulus condition). However, the final current values between sections becomes more overlapped due to the faster decay after the stronger stimulus. Comparing the results in condition 1 and 3 explains the effect of interval time of 10 and 5 s on the differentiation of states. At the shorter interval time of 5 s in condition 3, the overall current level is higher because there is less decay of the current during the interval step. However, the overlap of states could not be avoided either, e.g., the overlap between sequence 7 in Section 2 and sequence 14 in Section 3. Finally, when the number of applied pulses and the interval time between pulses are reduced compared to condition 1 (in Fig. 5(d)), the time-dependent decay characteristic does not appear clearly due to insufficient stimulus, which leads to the overlap of current levels within the section. These comparative results in Fig. 5 suggest that optimization of pulse conditions is essential to construct the distinguishable reservoir states because the pulse amplitude, number of pulses, and interval time between pulses are all comprehensively involved in this.
The multi-class classification test was performed by learning and testing the input pulse signal for a 4-bit pattern to assess its performance in the RC system with respect to the pulse conditions from condition 1 to 4. Fig. 5(e) illustrates the process of separating multi-class points into each group in the RC system. The data consists of 100 points in each of the six groups, where each point is randomly distributed along a normal distribution from a randomly selected center point. Each point lies on a two-dimensional plane with a range of 0 to 255 per axis. Each axis (x, y) can be represented by 8 bits binary, so a point can be represented by a total of 16 bits (x + y) and encoded as a pulse sequence. This pulse sequence is rearranged into 4 × 4 bits using a memristor with a separation capacity of 4 bits. Each of the four pulse sequences of 4 bits is then converted into one of 16 current values, each of which is a state identified in the 4-bit reservoir, for training and classification. The 16 current values, as the states that are identified in the 4-bit reservoir, are converted by the software through a normalization process between 0 and 1. The maximum number of iterations for training is set to 15 epochs. The simulation results of multi-class classification are shown in Fig. 5(f). The reservoir state constructed by pulse condition 1 showed the highest classification accuracy, followed by pulse conditions 2, 3, and 4. Compared to condition 1, the reservoir states in condition 2 with the higher pulse amplitude and the reservoir state in condition 3 with the shorter interval time had relatively lower accuracy due to overlap of the final currents. This was caused by the increased decay rate as the amplitude increased (condition 2) and the negligible decay of current for insufficient interval time (condition 3). In pulse condition 4 with reduced pulse number and interval time, the reservoir states were too overlapped to be discriminated, thus leading to the lowest accuracy. Since the reservoir states are normalized to be the values between 0 and 1 by the software, it is crucial to ensure that each of the 16 reservoir states is linearly distinguishable from one another. The relatively low accuracy in the multi-class classification task is thought to be due to the small dataset size and the inherent ambiguity within the data itself. Nevertheless, the dependence of accuracy on bit discrimination efficacy verifies that nonlinear decay characteristics play a crucial role in the multi-class classification task of RC operation.
As discussed earlier, the decay characteristic is one of the decisive factors and is determined by the amplitude and number of pulses and the interval time between pulses. In general, the current decays rapidly in the early stage and gradually afterward. Because RC utilizes these STP properties of decay to store information, its effect on the discrimination of 4-bit reservoir states was examined by quantitatively analyzing the decay curve. Numerous mathematical models have been proposed to quantitatively describe the decay curves.51,60 Among them, an exponential decay function was employed in this study with a form of61
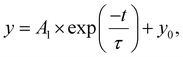 | (1) |
First, the configured reservoir states are constructed as shown in Fig. 6(f) by varying the relaxation time τ from the measured ones in Fig. 6(a)–(d). The three cases of reservoir states were constructed by setting τ values to be 0.5 times (3.52, 4.33, 5.17 and 5.45), 2 times (14.08, 17.32, 20.66 and 21.78), and 5 times (35.2, 43.3, 51.65 and 54.45) the measured ones (7.04, 8.66, 10.33 and 10.89). In the case of 0.5 times τ values, the current drops rapidly during interval time. Thus, the current is likely to be bisected. For example, the current bisection occurs at 5, 6, 8 and 7, 9, 10 in Section 2 with respect to whether the pulse was applied or not before the final current measurement. In Section 2, sequences at 5, 6, and 8 have “1” bit at the final input, so they exhibited a higher current at nearly the same level. However, since sequences at 7, 9, and 10 do not have the final “1” pulse, the currents remained to be the decayed ones. Therefore, it is found that a too small τ value is not desirable to enrich the reservoir state. In this case, it is suggested to reduce the interval time, then the currents can be read as distinct states before they are substantially decayed. Reducing interval time gives an advantage to reduce the time required for the RC system to train, so allows it to learn large amounts of data quickly. There is also a way to read by increasing the interval time nonlinearly. Actually, the current decays nonlinearly, falling rapidly at the early stage and then slowing down. In order to clearly distinguish between the currents, it is necessary to read higher-level currents quickly at the early stage when the current drops quickly or read lower-level currents slowly at the end when the current decays slowly.
Next is the cases where τ values are doubled and quintupled from the original τ values. In Fig. 6(f), when τ values are doubled, the dynamic range of the overall current distribution increases, so it avoids the overlap of current between each section. Moreover, in Fig. 6(f), when τ values are quintupled, the decay becomes much more gradual, resulting in a wider overall current distribution range. This prevents overlap between the current levels of different sections. However, because the current decays slowly, there is significant overlap of the current levels within each section. Therefore, it is concluded that appropriate τ values are required to achieve an overall distinguishable current range for each reservoir state without their overlap within and between the sections. For example, the case with double τ values is found to be better to discriminate the states than the case with quintupled τ values suffering significant overlaps between the states even with the wider overall current distribution.
Second, the reservoir states were constructed by doubling and quintupling ΔI as shown in Fig. 6(g). The two reservoir states of 4 bits by doubling ΔI (9.86 × 10−10, 1.49 × 10−9, 2.02 × 10−9, and 2.56 × 10−9 A) and quintupling ΔI (2.47 × 10−9, 3.73 × 10−9, 5.05 × 10−9, and 6.4 × 10−9 A) are presented in red and blue color, respectively. As ΔI increases, the overall current dynamic range increases, resulting in a larger difference in current level between sections. The difference in current level between sections is even much greater in the 5 times case, but the current level within sections becomes more overlapped compared to the original case. Final currents for 5 through 10 in Section 2 are mostly overlapped and 11 through 14 in Section 3 are also overlapped. Therefore, the value of τ should also be increased in order to avoid the overlap between the states because of enhanced decay at a high current level.
The RC system creates a single reservoir state with spatiotemporal information. In order to learn the generated reservoir states, the reservoir states must be distinguishable from each other. Through the examination of the dependence of discrimination capability of reservoir states on several parameters, the relaxation time constant τ and the current increment ΔI were found to be decisive factors. For a Pt/GDC/CeO2/Pt memristor under the same current increment condition, the case with doubled τ values made separable reservoir states. On the other hand, as the current increment increased under the same τ condition, the current tended to overlap within each section, leading to an indistinguishable reservoir state. Even if it is applied specifically in this device, it provides the quantitative guideline that the conditions with doubled τ while keeping ΔI are appropriate to achieve distinguishable reservoir states. Increasing ΔI via a strong stimulus pulse would require the increased τ values to separate the states. These guidelines are available by analyzing the effect of the current levels, ΔI, and τ values of the given memristors on the discrimination of reservoir states; thereby the optimized conditions would vary depending on the properties of the devices.
2.4 Pattern recognition through RC operation
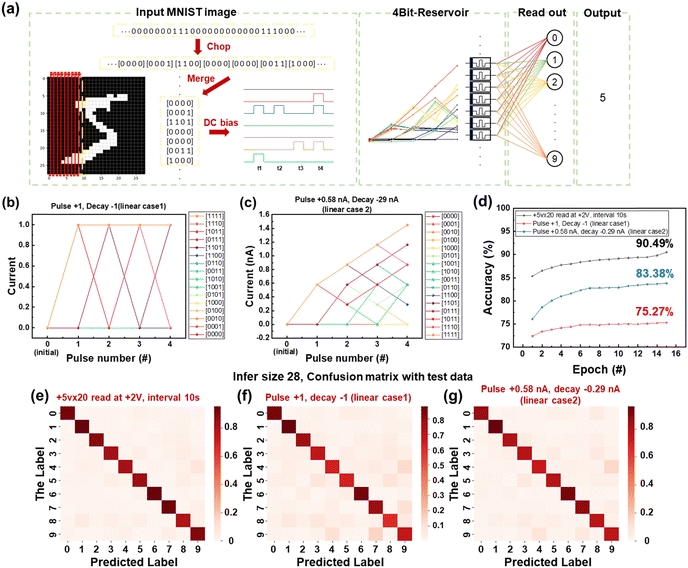
The RC system consists of an input layer, a reservoir layer, and an output layer. In this system, only the connection weights of a single linear output layer are trained to reduce the complexity of training RNNs. To benchmark the efficiency and performance of these RC frameworks using a Pt/GDC/CeO2/Pt memristor as a reservoir, a handwritten digit recognition test was performed by training and testing the input pulse signal for a 4-bit pattern.
Fig. 7(a) shows the process of recognizing a handwritten digit image in the RC system. The MNIST dataset from Kaggle's Digit Recognizer competition is utilized for training and evaluating the model. The training set consists of 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 handwritten digit images collected from the MNIST handwriting digit database and 4000 samples to be used for testing. First, the input image of 28 × 28 pixels is converted to a binary image and encoded as a pulse sequence. This pulse sequence is rearranged to 196 × 4 bits since it uses a memristor with a separation capacity of 4. The 196 pulse sequences of 4 bits are then trained and classified by converting each into one of the 16 current values, which are the states identified in the 4-bit reservoir. The 16 current values, which are the states identified in the 4-bit reservoir, are converted by software through a normalization process between 0 and 1. The maximum number of iterations for training is set to 15 epochs.
000 handwritten digit images collected from the MNIST handwriting digit database and 4000 samples to be used for testing. First, the input image of 28 × 28 pixels is converted to a binary image and encoded as a pulse sequence. This pulse sequence is rearranged to 196 × 4 bits since it uses a memristor with a separation capacity of 4. The 196 pulse sequences of 4 bits are then trained and classified by converting each into one of the 16 current values, which are the states identified in the 4-bit reservoir. The 16 current values, which are the states identified in the 4-bit reservoir, are converted by software through a normalization process between 0 and 1. The maximum number of iterations for training is set to 15 epochs.
To investigate the importance of nonlinear characteristics in RC, we compared the performance of the nonlinear reservoir model with STM characteristics and that with linear current change. The results of condition 1 in Fig. 5 were used for the simulation of image recognition in the nonlinear reservoir model. The simulation results for the other three conditions in Fig. 5 are shown in Fig. S7 (ESI†). The 16 different 4-bit input signals are well classified in this condition and represent the implied historical information. For comparison, the discrimination results of reservoir states for two cases assumed to have linear decay are presented in Fig. 7(b) and (c). The first case in Fig. 7(b) shows the discrimination of the reservoir state that was obtained under the condition of identical increase and decay of current, i.e., the current increases by +1 when the pulse is applied and decreases by −1 during the decay. In this case, the final current turns out to be either 0 or 1, because the current decreases completely during the interval time even if the current increases when a voltage is applied. As a result, 16 different 4-bit input signals are finally fixed to be only 0 and 1, which is not enough to reflect the richness of the reservoir state. The other is the case of larger current increase than current decrease, as shown in Fig. 7(c). In this case, the current does not return to the initial value via its decay during interval time. Therefore, the final currents can be discriminated with respect to the pulse input to some extent even with the linear decay of current. Nevertheless, it has a certain level of overlap between the states, which leads to less capability of discriminating the states compared to the nonlinear condition shown in Fig. 7(a). In Fig. 7(c), the current increase was assumed to be 0.58 nA, which is the average increase in current measured when applying a pulse corresponding to “1” in Fig. 4(b). The current decrease was 0.29 nA, assumed to be the 50% decrease in current in 10 s after applying +5 V voltage 20 times. Then, the final current became to have 6 states, ranging from 0 to 1.45 nA with an identical interval of 0.29 nA. Both cases have much lower discrimination capabilities compared to the nonlinear case showing 16 distinguished states. This verifies that the nonlinear and asymmetry of current change is highly desirable for digit discrimination in RC systems. This superior capability of discriminating 16 states in the nonlinear case than linear ones enabled the highest digit recognition accuracy of 90.49%, as shown in Fig. 7(d). As expected, the linear but asymmetric case exhibited the higher accuracy of 83.38% than the 75.27% of the linear and identical increase and decrease of current case. Considering that RC trains only the connection weights of a simple linear output layer, the accuracy of 90.49% in the nonlinear case is recognized to be quite high. It also has a negligible overlap of reservoir states. Thus, it is concluded that nonlinear decay benefits achieving the richness of the reservoir. The results of relatively fair accuracy >75% even in the linear cases are thought to be because classifying the MNIST handwritten digit is a simple task. If more complex problems were tested, there would be larger difference in the accuracy between nonlinear and linear cases. Fig. 7(e)–(g) show the confusion matrix, which is a table to compare the experimentally predicted labels of the RC system with the actual label in each condition. In this table, the dark red square indicates greater, and lighter red one represents lower probability of classifying the actual label. Apparently, the nonlinear case in Fig. 7(e) is found to have the greatest probability of classifying the actual label with the best accuracy.
The RC operation for 4-bit input discrimination was demonstrated in this study, focusing on the relationship between memristor dynamics and RC performance. It would be more beneficial to expand this analysis to higher bit discrimination to generalize the effect of these parameters on the efficacy of bit discrimination. Indeed, the RC operation for higher bit discrimination requires more sophisticated models and more precisely controlled weight update and decay dynamics. For this, achieving more accurate and optimized conditions of memristor characteristics, such as PPF, decay dynamics, and weight updates, should be further pursued.
3. Conclusion
An interfacial-type Pt/GDC/CeO2/Pt memristor was proposed for use as a physical reservoir in RC, and its weight update dynamics as a function of time with respect to pulse conditions were systematically investigated. The more rapid decay characteristics were obtained under the condition of the higher amplitudes and the larger number of pulses, along with the higher currents. RC operation for 4-bit input discrimination was demonstrated using different current responses and decay characteristics. The pulse amplitude, number of pulses, and interval time between pulses were all comprehensively related to determine a discriminable reservoir state. From the analysis of the current change under repeated 4-bit pulse application, it was verified that the nonlinearity of PPF and decay characteristics during weight update played an important role in representing distinguishable reservoir states. The PPF characteristic determined the rate of increase based on the previous conductance level after the weight update. And the decay characteristic determined the rate of current decrease based on the current increment. Considering the influence of the PPF on the decay response of the 4-bit pulse, the input pulse sequence could be optimized by adjusting the pulse conditions to obtain distinguishable reservoir states. Decay curves were also analyzed quantitatively to investigate their impact on the discrimination of 4-bit reservoir states. It was confirmed that the relaxation time constant and current increment in the exponential decay function are important variables to determine the discrimination capability of the reservoir states. The interval time between pulses was associated with the relaxation time and PPF depending on conductance in the construction of multi-bit reservoir states being linearly separated. The quantitative analysis of the time-dependent decay curves of memristors is crucial because it allows for the prediction of distinguishable reservoir states in advance. Finally, it was demonstrated that a 4-bit RC system could be utilized to solve the complex problems associated with the MNIST pattern recognition task with the accuracy of 90.5% and multi-class classification with 69.5% accuracy. Evaluation of MNIST pattern recognition performance with regard to the nonlinearity of current change and its decay confirmed that higher accuracy was achieved when the current change and its decay were nonlinear rather than linear. This study explored the optimized nonlinear characteristics of memristors required for use as the reservoir in the RC system for hardware and demonstrated the potential of the proposed bi-layered oxide memristor as the reservoir in energy-efficient RC systems.4. Experimental
Device fabrication
The GDC/CeO2 bi-layered oxide memristor with a simple MIM structure was fabricated as shown in Fig. 1(c). A 70 nm-thick Pt bottom electrode (BE) was deposited on a 10 nm-thick Ti adhesion layer on a SiO2/Si substrate via e-beam evaporation (FC-2000, Temescal). Then, a resistance changing layer of 20 nm-thick CeO2 film was deposited by thermal ALD (NCD D-200) at 240 °C using Ce(iPrCp)2(N-iPr-amd) as a cerium precursor and water vapor as an oxidant gas. A sequential precursor pulsing method was adopted to achieve sufficient vapor pressure of the cerium precursor.62 A total of 10 cerium precursor pulses of 1 s each with an interval of 2.5 s were dosed into the chamber, followed by a purge with nitrogen gas for 40 s. Subsequently, a single H2O pulse was dosed for 0.4 s, followed by a 15 s purge with nitrogen. On top of the CeO2 layer, a 30 nm-thick GDC layer was deposited by RF magnetron sputtering using a GDC target with a composition of CeO2/Gd2O3 (80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20 mol%) in an Ar environment, followed by annealing at 400 °C for 1 h in an air environment. Last, a 30 nm-thick Pt top electrode (TE) was deposited by e-beam evaporation using a shadow mask with a diameter of 100 μm.
20 mol%) in an Ar environment, followed by annealing at 400 °C for 1 h in an air environment. Last, a 30 nm-thick Pt top electrode (TE) was deposited by e-beam evaporation using a shadow mask with a diameter of 100 μm.
Electrical measurements
The DC current–voltage (I–V), potentiation and depression, PPF, and time-dependent current decay characteristics of the memristor were examined using a semiconductor parameter analyzer (Agilent 4156B). Also, for the digit recognition experiment, the input pulses were converted into digitized square pulse signals and applied to the memristor. The binary 4-bit data from [0000] to [1111] were processed by applying voltage pulses of amplitude (+5, +7 V) with a pulse width of 0.64 ms and a different number of applications. Based on the behavior of the current decay with time, the interval time between pulses was set to 5 and 10 s. The conductance of the device was read at +2 V. In the measurement setup, the voltage was applied to the TE while the BE was grounded.Reservoir computing simulation for multi-class classification
To compare the performance of RC with regard to various parameters, 4-bit reservoir states were constructed with memristors and the simulation of discriminating the separated groups was performed. The training dataset consists of 100 points in each of six groups, which are randomly distributed along a normal distribution from a randomly chosen center point on a two-dimensional plane from 0 to 255 per each axis. Each axis (x, y) can be represented by 8 bits of binary and one point can be represented by a total of 16 bits (x + y). To represent the reservoir state with 4 bits of separation capacity, the 16 bits of data representing one point were made into a matrix of size with 4 × 4 bits. The 4 × 4 bit pulses were used as input pulses to the memristor and converted into one conductance state. The conductance output from the resistors was fed into a single layer perceptron, passed through a softmax function, and finally output was obtained as a probability of which group it belongs to. The hyperparameters used for testing were the batch size of 1, running rate of 0.001, Adam as the optimizer, and cross entropy loss as the loss function. A total of 600 training sets were trained and tested for 15 epochs.Reservoir computing simulation for digit recognition tasks
A 4-bit reservoir state was constructed with memristors and the modeling of the RC system for the digit recognition task was performed in the order of preprocessing, training, and actual inference. As a preprocessing of the training dataset, the training dataset with 28 × 28 pixels of a black and white image based on MNIST as.jpg provided by Kaggle was preprocessed for 4-bit reservoir computing. To represent the reservoir state with a separation capacity of 4 bits, the data were binarized after reshaping the image into 4-pixel units, resulting in a matrix with a size of 196 × 4 bits. The 196 × 4 bits pulses were used as input pulses to the memristors to obtain one implied conductance value of each memristor, which was fed into and trained on a readout layer consisting of a single layer perceptron. After preprocessing the provided training dataset, the model was trained and tested for inference accuracy by inputting the test dataset with the trained model. The readout layer was composed of the pytorch module, which used softmax as the activation function and was trained by supervised learning. The Adam optimizer with a learning rate of 0.001 was utilized to minimize the categorical cross-entropy loss through mini-batch gradient descent, with a batch size of 100. After passing through one input layer consisting of 196 nodes, a batch normalization layer was used to optimize the training. The accuracy of the trained model was then obtained using the testset at each epoch. The confusion matrix for the testset was also plotted to show the accuracy of the trained model and the bias of the output.Author contributions
Conceptualization: S. M. Methodology: S. M., C. P., and Y. J. Supervision: T.-S. Y. Writing – original draft: S. M. Writing – review and editing: K.-S. M., H. K. and T.-S. Y.Data availability
The data supporting this article have been included as part of the ESI.†Conflicts of interest
The authors declare that they have no competing interests.Acknowledgements
This research was supported by the National Research Foundation of Korea (NRF) funded by the Korean government (MSIT) (no. RS-2024-00401234, no. RS-2024-00406006).References
- R. Gupta, D. Srivastava, M. Sahu, S. Tiwari, R. K. Ambasta and P. Kumar, Mol. Diversity, 2021, 25, 1315–1360 CrossRef CAS PubMed
.
- M.-J. Kang and J.-W. Kang, PLoS One, 2016, 11, e0155781 CrossRef PubMed
.
- W. Höpken, T. Eberle, M. Fuchs and M. Lexhagen, J. Travel Res., 2021, 60, 998–1017 CrossRef
.
- V. Lahoura, H. Singh, A. Aggarwal, B. Sharma, M. A. Mohammed, R. Damaševičius, S. Kadry and K. Cengiz, Diagnostics, 2021, 11, 241 CrossRef PubMed
.
- P. Jacobson, M. Shirao, K. Yu, G.-L. Su and M. C. Wu, J. Light Technol., 2021, 40, 692–699 Search PubMed
.
- D. Verstraeten, B. Schrauwen and D. Stroobandt, 2006.
- J. Pathak, B. Hunt, M. Girvan, Z. Lu and E. Ott, Phys. Rev. Lett., 2018, 120, 024102 CrossRef CAS PubMed
.
- L. Deng, J. Li, J.-T. Huang, K. Yao, D. Yu, F. Seide, M. Seltzer, G. Zweig, X. He and J. Williams, 2013.
- C. Sun, M. Song, D. Cai, B. Zhang, S. Hong and H. Li, IEEE Trans. Artif. Intell., 2022, 5, 23–37 Search PubMed
.
- J. Schmidhuber, Neural Netw., 2015, 61, 85–117 CrossRef PubMed
.
- M. Cucchi, S. Abreu, G. Ciccone, D. Brunner and H. Kleemann, Neuromorph. Comput. Eng., 2022, 2, 032002 CrossRef
.
- G. Tanaka, T. Yamane, J. B. Héroux, R. Nakane, N. Kanazawa, S. Takeda, H. Numata, D. Nakano and A. Hirose, Neural Netw., 2019, 115, 100–123 CrossRef PubMed
.
- S. Ambrogio, P. Narayanan, H. Tsai, R. M. Shelby, I. Boybat, C. Di Nolfo, S. Sidler, M. Giordano, M. Bodini and N. C. Farinha, Nature, 2018, 558, 60–67 CrossRef CAS PubMed
.
- T. Sugie, T. Akamatsu, T. Nishitsuji, R. Hirayama, N. Masuda, H. Nakayama, Y. Ichihashi, A. Shiraki, M. Oikawa and N. Takada, Nat. Electron., 2018, 1, 254–259 CrossRef
.
- J. Moon, W. Ma, J. H. Shin, F. Cai, C. Du, S. H. Lee and W. D. Lu, Nat. Electron., 2019, 2, 480–487 CrossRef
.
- R. Midya, Z. Wang, S. Asapu, X. Zhang, M. Rao, W. Song, Y. Zhuo, N. Upadhyay, Q. Xia and J. J. Yang, Adv. Intell. Syst., 2019, 1, 1900084 CrossRef
.
- J. C. Coulombe, M. C. York and J. Sylvestre, PLoS One, 2017, 12, e0178663 CrossRef PubMed
.
- J. Torrejon, M. Riou, F. A. Araujo, S. Tsunegi, G. Khalsa, D. Querlioz, P. Bortolotti, V. Cros, K. Yakushiji and A. Fukushima, Nature, 2017, 547, 428–431 CrossRef CAS PubMed
.
- R. Nakane, G. Tanaka and A. Hirose, IEEE Access, 2018, 6, 4462–4469 Search PubMed
.
- W. Jiang, L. Chen, K. Zhou, L. Li, Q. Fu, Y. Du and R. Liu, Appl. Phys. Lett., 2019, 115, 19 Search PubMed
.
- P. Antonik, F. Duport, M. Hermans, A. Smerieri, M. Haelterman and S. Massar, IEEE Trans. Neural Netw. Learn. Syst., 2016, 28, 2686–2698 Search PubMed
.
- L. Larger, M. C. Soriano, D. Brunner, L. Appeltant, J. M. Gutiérrez, L. Pesquera, C. R. Mirasso and I. Fischer, Opt. Express, 2012, 20, 3241–3249 CrossRef CAS PubMed
.
- R. Sacchi, M. C. Ozturk, J. C. Principe, A. A. Carneiro and I. N. da Silva, 2007.
- D. Kudithipudi, Q. Saleh, C. Merkel, J. Thesing and B. Wysocki, Front. Neurosci., 2016, 9, 166603 Search PubMed
.
- C. Merkel, Q. Saleh, C. Donahue and D. Kudithipudi, Procedia Comput. Sci., 2014, 41, 249–254 CrossRef
.
- L. Sun, Z. Wang, J. Jiang, Y. Kim, B. Joo, S. Zheng, S. Lee, W. J. Yu, B.-S. Kong and H. Yang, Sci. Adv., 2021, 7, eabg1455 CrossRef CAS PubMed
.
- K. Yang, J. Joshua Yang, R. Huang and Y. Yang, Small Sci., 2022, 2, 2100049 CrossRef CAS
.
- J. Tao, D. Sarkar, S. Kale, P. K. Singh and R. Kapadia, Nano Lett., 2020, 20, 7793–7801 CrossRef CAS PubMed
.
- S. Menzel, M. Von Witzleben, V. Havel and U. Böttger, Faraday Discuss., 2019, 213, 197–213 RSC
.
- S. Ali, M. A. Ullah, A. Raza, M. W. Iqbal, M. F. Khan, M. Rasheed, M. Ismail and S. Kim, Nanomaterials, 2023, 13, 2443 CrossRef CAS PubMed
.
- H. Jiang, L. Han, P. Lin, Z. Wang, M. H. Jang, Q. Wu, M. Barnell, J. J. Yang, H. L. Xin and Q. Xia, Sci. Rep., 2016, 6, 28525 CrossRef PubMed
.
- F. Wu, P. Cao, Z. Peng, S. Ke, G. Cheng, G. Cao, B. Jiang and C. Ye, IEEE Trans. Electron Devices, 2021, 69, 375–379 Search PubMed
.
- D. Kumar, L. B. Keong, N. El-Atab and T.-Y. Tseng, IEEE Electron Device Lett., 2022, 43, 2093–2096 CAS
.
- X. Chen, Y. Jin, Z. Tao, L. Jiang, X. Wu, Y. Xiao, B. Jiang, X. Wen, J. Zhang and M. Zhu, IEEE Trans. Electron Devices, 2023, 70, 1001–1005 CAS
.
- S. Moon, K. Park, P. H. Chung, D. P. Sahu and T.-S. Yoon, J. Alloys Compd., 2023, 963, 171211 CrossRef CAS
.
- Z. Li, D. Jia, W. Zhang, Y. Li, M. Wang and D. Zhang, Front. Chem. Sci. Eng., 2024, 18, 31 CrossRef CAS
.
- L. Huang, D. Bao, X. Jiang, J. Li, L. Zhang and X. Sun, J. Colloid Interface Sci., 2021, 588, 713–724 CrossRef CAS PubMed
.
- X. Liu, K. Zhou, L. Wang, B. Wang and Y. Li, J. Am. Chem. Soc., 2009, 131, 3140–3141 CrossRef CAS PubMed
.
- K. Park, P. H. Chung, D. P. Sahu and T.-S. Yoon, Mater. Sci. Semicond. Process., 2022, 147, 106718 CrossRef CAS
.
- S. Das, R. Bhaskar and K. B. Narayanan, J. Rare Earths, 2024, 1817–1834 CrossRef CAS
.
- R. Schmitt, J. Spring, R. Korobko and J. L. Rupp, ACS Nano, 2017, 11, 8881–8891 CrossRef CAS PubMed
.
- Y. H. Jang, S. H. Lee, J. Han, W. Kim, S. K. Shim, S. Cheong, K. S. Woo, J. K. Han and C. S. Hwang, Adv. Mater., 2024, 36, 2309314 CrossRef CAS PubMed
.
- Z. Wang, S. Joshi, S. E. Savel’ev, H. Jiang, R. Midya, P. Lin, M. Hu, N. Ge, J. P. Strachan and Z. Li, Nat. Mater., 2017, 16, 101–108 CrossRef CAS PubMed
.
- Y. Yang, P. Gao, S. Gaba, T. Chang, X. Pan and W. Lu, Nat. Commun., 2012, 3, 732 CrossRef PubMed
.
- Y. Yang, P. Gao, L. Li, X. Pan, S. Tappertzhofen, S. Choi, R. Waser, I. Valov and W. D. Lu, Nat. Commun., 2014, 5, 4232 CrossRef CAS PubMed
.
- S. H. Jo, T. Chang, I. Ebong, B. B. Bhadviya, P. Mazumder and W. Lu, Nano Lett., 2010, 10, 1297–1301 CrossRef CAS PubMed
.
- R. Wang, J.-Q. Yang, J.-Y. Mao, Z.-P. Wang, S. Wu, M. Zhou, T. Chen, Y. Zhou and S.-T. Han, Adv. Intell. Syst., 2020, 2, 2000055 CrossRef
.
- A. A. Bessonov, M. N. Kirikova, D. I. Petukhov, M. Allen, T. Ryhänen and M. J. Bailey, Nat. Mater., 2015, 14, 199–204 CrossRef CAS PubMed
.
- W. S. Choi, J. T. Jang, D. Kim, T. J. Yang, C. Kim, H. Kim and D. H. Kim, Chaos, Solitons Fractals, 2022, 156, 111813 CrossRef
.
- R. M. Shiffrin and R. C. Atkinson, Psychol. Rev., 1969, 76, 179 Search PubMed
.
- T. Chang, S.-H. Jo and W. Lu, ACS Nano, 2011, 5, 7669–7676 CrossRef CAS PubMed
.
- J. T. Wixted and E. B. Ebbesen, Psychol. Sci., 1991, 2, 409–415 CrossRef
.
- S. J. Martin, P. D. Grimwood and R. G. Morris, Annu. Rev. Neurosci., 2000, 23, 649–711 CrossRef CAS PubMed
.
- R. S. Zucker and W. G. Regehr, Annu. Rev. Physiol., 2002, 64, 355–405 CrossRef CAS PubMed
.
- N. Caporale and Y. Dan, Annu. Rev. Neurosci., 2008, 31, 25–46 CrossRef CAS PubMed
.
- G.-q Bi and M.-m Poo, J. Neurosci., 1998, 18, 10464–10472 CrossRef CAS PubMed
.
- M. Mayford, S. A. Siegelbaum and E. R. Kandel, Cold Spring Harbor Perspect. Biol., 2012, 4, a005751 Search PubMed
.
- E. R. Kandel, Science, 2001, 294, 1030–1038 CrossRef CAS PubMed
.
- J. Hawkins and S. Ahmad, Front. Neural Circuits, 2016, 10, 23 Search PubMed
.
- T. Ohno, T. Hasegawa, T. Tsuruoka, K. Terabe, J. K. Gimzewski and M. Aono, Nat. Mater., 2011, 10, 591–595 CrossRef CAS PubMed
.
- Z. Q. Wang, H. Y. Xu, X. H. Li, H. Yu, Y. C. Liu and X. J. Zhu, Adv. Funct. Mater., 2012, 22, 2759–2765 CrossRef CAS
.
- U. Kumar, C. Feit, S. N. Berriel, A. Arunachalam, T. S. Sakthivel, K. Basu, P. Banerjee and S. Seal, J. Vac. Sci. Technol., A, 2021, 39, 060405 CrossRef CAS
.
Footnote |
| † Electronic supplementary information (ESI) available: Supplementary Fig. S1–S8. See DOI: https://doi.org/10.1039/d4tc05041j |
| This journal is © The Royal Society of Chemistry 2025 |