Open Access Article
Open Access ArticleSoft carbon electrodes in capacitive energy extraction: exploring geometry and operational parameters in capacitive mixing systems†
Ana
Collazo-Castiñeira
 a,
Sergio
Orozco-Barrera
a,
Sergio
Orozco-Barrera
 a,
Guillermo R.
Iglesias
a,
Guillermo R.
Iglesias
 abc,
Ángel V.
Delgado
abc,
Ángel V.
Delgado
 abc and
Silvia
Ahualli
abc and
Silvia
Ahualli
 *a
*a
aDepartment of Applied Physics, University of Granada, 18071, Granada, Spain. E-mail: sahualli@ugr.es
bNanoMag Laboratory, University of Granada, Granada, Spain
cInstituto de Investigación Biosanitaria ibs, Granada, Spain
First published on 30th April 2025
Abstract
The global challenge of water scarcity, intensified by a growing population, climate change, and increased demand for fresh water, requires immediate investigation of innovative and sustainable technologies. Capacitive deionization (CDI) and capacitive mixing (CapMix) have emerged as promising solutions, leveraging the electric double layer (EDL) formed at the interface of charged surfaces and electrolytic solutions. The initial technique represents a promising approach to water desalination and ionic separation, as CapMix is a reciprocal technique for energy obtention from exchanging solutions with varying salinity. This study focuses on the use of carbon electrodes with polyelectrolyte (PE) coatings for capacitive energy extraction based on Donnan potential (CDP) in CapMix systems. This investigation considers the impact of applied current, volumetric charge densities of the PEs, and geometric parameters, such as electrode separation distance, on the efficiency and scalability of these systems. The findings provide valuable insights for enhancing energy extraction performance and overcoming challenges associated with electrode use in these applications.
1. Introduction
The global challenges of water scarcity and climate change affect millions of individuals across the globe. The combination of a growing population, the consequences of climate change, the increasing demand for fresh water, and the shrinking supply of this essential resource highlights the need to investigate innovative and sustainable technologies.1,2 These should provide clean water and generate energy in a sustainable and renewable manner. In some of these technologies, the capacitive properties of the interface between a solid charged surface and an electrolyte solution can serve as the foundation for significant advancements.3–5 This is due to the fact that the ionic arrangement surrounding the charged interface (electrical double layer or EDL) is distinguished by a considerable electrical capacitance, which can be regulated by the ionic composition of the liquid and the accessible surface area.6Specifically, capacitive deionization (CDI) and capacitive mixing (CapMix) have emerged as promising technologies offering complementary solutions to tackle both challenges, clean water production and sustainable energy harvesting.7,8 As it is well known, the EDL resembles a capacitor, with charged plates represented by the surface and the diffuse charge neutralizing it, respectively. If a porous, conducting surface is used, the associated large area/volume ratio provides extremely high capacitance values (up to hundreds of Farads per gram6). The fact that the thickness of the EDL decreases when the ionic contents of the solution in contact is increased produces a subsequent elevation of the capacitance.9,10
This behaviour of the EDL is taken advantage of in the CapMix methods for extracting energy from salinity gradients,11–15 which involves charging a pair of electrodes while in contact with a salty solution and discharging them after exchanging the solution with fresh water. This process generates electrical energy through the exchange of ions between two saline solutions with varying concentrations, leading to the expansion of the EDL. In turn, the arrangement of ions in the EDL means that they are withdrawn from the solution, and this is the basis of CDI technologies, capable of removing salt and impurities from brackish water, wherein salt ions are extracted under the influence of an electric field.16
For all the electrochemical techniques mentioned, the choice of materials is pivotal: porosity, electrical conductivity, and available surface area of the electrodes play a crucial role in their performance. Carbon-based materials, owing to their high surface area and pore size distribution, are commonly employed as electrodes for these techniques.14,15,17–21 Although activated carbon is frequently employed due to its elevated specific surface area, price and availability, alternative options include graphene,22,23 carbon nanotubes,24,25 templated (through, for instance, zeolites) carbon,26,27 or composite structures.28 Furthermore, the potential for exploiting pseudocapacitance associated with specific surface groups or with the intrinsic structure of the material can also be considered.29 In this study, we will focus on activated carbon with a sufficiently high specific surface area and high electrical conductivity. It should be noted that the selection of the material also involves the selection of structural properties, such as the average pore size and pore hierarchy. These are essential factors in the performance of Capmix methods, as has been repeatedly demonstrated. It is also pertinent to consider the hydrophobic/hydrophilic balance of the material, which determines the ease and extent of wetting and exchange of salt and fresh solutions.
It should be noted that other parameters may also have an impact on the performance of the energy production process. One particularly significant factor is the cell architecture itself. In this study, the focus will be on the flat, parallel electrode geometry and flow-by solution contact. However, flow-through30 and even cylindrical-electrode31 configurations have also been investigated. In the case of plane-parallel electrodes, the distance between the electrodes represents a fundamental magnitude that is expected to influence the internal resistance of the system, while leaving the capacitance unaffected. This is due to the fact that the capacitance is linked to the structure of the EDL at the pore size scale.
Although the Capmix method was originally employed with electrodes comprising uncoated carbon particles, subsequent research demonstrated that the utilisation of ion exchange membranes of appropriate polarity covering the electrodes led to a significant enhancement in efficiency. These membranes generate a natural potential difference between electrodes due to the Donnan equilibrium, eliminating the need for an external power source and transforming the method into capacitive energy extraction based on Donnan potential (CDP).32,33
In a different approach, the Donnan potential differences are obtained by coating the electrodes with oppositely charged polyelectrolytes (PEs), instead of using membranes. The coating produces a deformable and permeable interface, hence the designation soft electrodes (SE) given to the resulting structure, and, by extension, to the method.12,34 The selected PEs are poly(styrene sulfonate) (PSS, anionic) and Poly(diallyldimethylammonium chloride) (PDADMAC, cationic). These polymers are strong PEs, easy to work with, commercially available, and with strong affinity for the carbon surface. Other authors use the same PE combination for electrode preparation,35,36 although studies have also been carried out in which the cationic polymer poly(allylamine hydrochloride) (PAH) is used instead of PDADMAC.37,38 It has been found that this approach enhances electrode lifetime, adsorption capacity, and ion transport for various applications by increasing surface charge density, offering cost savings and simpler preparation compared to IEMs. Even a synergistic approach where SEs act as a more than suitable support for IEMs has also been studied previously.39 These coated electrodes will be the ones used in this work. Having made this selection, it is possible to make the charge transfer between electrodes in the different stages of the Capmix cycle occur in a ‘natural’ way, i.e. not externally forced, or by applying external currents to control the rate and amount of charge transfer. This is the choice in this work and therefore the value of the applied current appears as another fundamental variable to be studied.
This study examines the use of carbon electrodes with polyelectrolyte coatings (SE) for energy generation by Donnan potential difference, with a particular focus on experimental parameters that can be controllable, such as applied current and cell arrangement. The findings are expected to offer valuable insights for optimising these systems to enhance energy extraction performance, addressing some of the challenges associated with the use of these techniques in achieving the desired objectives.
2. Experimental section
2.1. Materials
For the energy extraction process, NaCl solutions of different concentrations were used, one of 20 mM, simulating fresh water from rivers, and another of 500 mM, representing salty water from the sea. The sodium chloride used was acquired from Merck Sigma-Aldrich (Spain), and the water used was previously deionized and filtered with a Milli-Q Academic System (Millipore, Molsheim, France). YP-80F activated carbon powder was supplied by Kuraray Co. Ltd (Japan). The manufacturers give information about the geometrical characteristics of this carbon: a pore size distribution that peaks at ∼1 nm and a surface area equal to 2271 m2 g−1. Przygocki et al.40 found that this carbon is characterized by 0.80 cm3 g−1 of micropores and 0.23 cm3 g−1 of mesopores, with an average micropore diameter of 1.01 nm. Carbon Black (Alfa Aesar, Termo Fisher, Germany) has also been used as additive for electric conductivity boost.41 Poly(diallyldimethyl-ammonium chloride) (PDADMAC, with a molecular weight 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 g mol−1) and poly(sodium 4-styrenesulfonate) (PSS, with a molecular weight of ∼70
000 g mol−1) and poly(sodium 4-styrenesulfonate) (PSS, with a molecular weight of ∼70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 g mol−1) were used as cationic and anionic polyelectrolyte for coating the electrodes, respectively, and both were obtained from Sigma-Aldrich.
000 g mol−1) were used as cationic and anionic polyelectrolyte for coating the electrodes, respectively, and both were obtained from Sigma-Aldrich.
2.2. Cell fabrication
The electrodes were composed of graphite discs of (1.87 ± 0.01) cm in diameter, on which a thin layer of polymer-coated YP-80F activated carbon was deposited. The polymer coating of the carbon particles was obtained by preparing 100 mM solutions of PDADMAC and PSS as positive and negative PEs, respectively. The carbon powder samples were immersed in each of the solutions and left under stirring for 24 hours. In order to separate the carbon from the polyelectrolyte excess, the samples were repeatedly subjected to cycles of centrifugation 500 rpm and redispersion in deionized water. The water excess was removed, and the sample was then left to dry overnight at 60 °C.After drying, polymer-coated YP-80F carbon powder was mixed with carbon black (CB) (95![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 ratio by mass). A 33 g L−1 solution of poly(vinylidene-fluoride) (PVDF, manufactured by Arkema, Colombes, France, as Kynar HSV 900, with molecular weight approximately 1
5 ratio by mass). A 33 g L−1 solution of poly(vinylidene-fluoride) (PVDF, manufactured by Arkema, Colombes, France, as Kynar HSV 900, with molecular weight approximately 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000
000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000) was prepared in 1-methyl 2-pyrrolidone (Sigma Aldrich). A slurry was prepared by mixing the YP-80F + CB ensemble with the PVDF solution in a mass ratio of 3
000) was prepared in 1-methyl 2-pyrrolidone (Sigma Aldrich). A slurry was prepared by mixing the YP-80F + CB ensemble with the PVDF solution in a mass ratio of 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10. The final carbon suspension was deposited onto the graphite collectors as a layer via thin casting, then left at 60 °C overnight for proper fixation. Finally, the electrodes were placed facing each other and separated by a (446 ± 1) μm mesh spacer (Fig. 1a) inside a methacrylate structure, properly connected and mounted for the upcoming measurements (Fig. 1b). The deposited amount of active material (YP80F + CB + PVDF) was 0.76 mg cm−2, and the thickness of the deposit was 105 ± 26 μm, determined with a Leica DM IL LED (Germany) microscope.
10. The final carbon suspension was deposited onto the graphite collectors as a layer via thin casting, then left at 60 °C overnight for proper fixation. Finally, the electrodes were placed facing each other and separated by a (446 ± 1) μm mesh spacer (Fig. 1a) inside a methacrylate structure, properly connected and mounted for the upcoming measurements (Fig. 1b). The deposited amount of active material (YP80F + CB + PVDF) was 0.76 mg cm−2, and the thickness of the deposit was 105 ± 26 μm, determined with a Leica DM IL LED (Germany) microscope.
2.3. Capacitive energy extraction setup and method
The setup used for capacitive energy extraction based on Donnan potential (CDP) measurements is based on the above-described cell. Salty and fresh solutions were stored in different vessels and were pumped when necessary. The flow rate was fixed at 0.8 mL s−1 in all experiments. The cell was connected to an IviumStat.h Potentiostat (Ivium Technologies, The Netherlands), which was used to set the different stages of the measurement cycles and apply currents or potential differences between the electrodes as needed. The digital outputs of the potentiostat were used to control the pumps of the two solutions. All measurements were performed at room temperature. The solution conductivities were determined with a WTW Multi920 IDS (Xylem Analytics, Germany) instrument, using a four electrode probe with cell constant 475.5 m−1. The complete experimental setup was prepared as illustrated in Fig. 2a.CDP in CapMix is based on the steps described elsewhere,42 and summarized as follows. These are graphically shown in Fig. 2b:
(1) Initially, uncharged functionalized electrodes are immersed in a saline solution, giving rise to Donnan potentials. Since the electrodes lack a charge, there is an absence of EDL potential, and the surface potential of each electrode aligns with the Donnan potential. In the case of symmetrical electrodes, the potential difference between them will be twice the Donnan potential.
(2) Both electrodes are externally connected to facilitate the transfer of charge from one to the other (positive charge transfer), leading to the formation of EDLs in the proximity of the surfaces. The EDL potential counteracts the Donnan potential, causing both electrodes to become equipotential and bringing the charge transfer to a halt. In this phase, a positive current is applied until the measured potential reaches 0 V.
(3) The external circuit is disconnected, and freshwater is introduced, resulting in an elevation in the absolute values of both Donnan and EDL potentials. This occurs due to the lower concentration of the bathing solution and the expansion of the double layer at a fixed charge on the surface. The increase in the Donnan potential is more pronounced, leading to an overall augmentation in both surface potentials.
(4) The electrodes are reconnected, initiating a negative charge flow through the application of a negative current, until equipotentiality is reestablished, and the potential at the surface returns to zero, owing to the system's symmetry.
(5) Finally, the circuit is reopened, and the freshwater is substituted with salty water. This step mirrors stage 1, and the process advances to stage 2 by reclosing the circuit and applying a positive current.
The applied current, I, took a constant value during the charge transfer to ensure that the potential drop process occurs in a controlled manner. The same procedure was followed for the negative charge transfer, in which the current applied was −I. The potentiostat was also used for measuring time, electric potential and applied current through the cell.
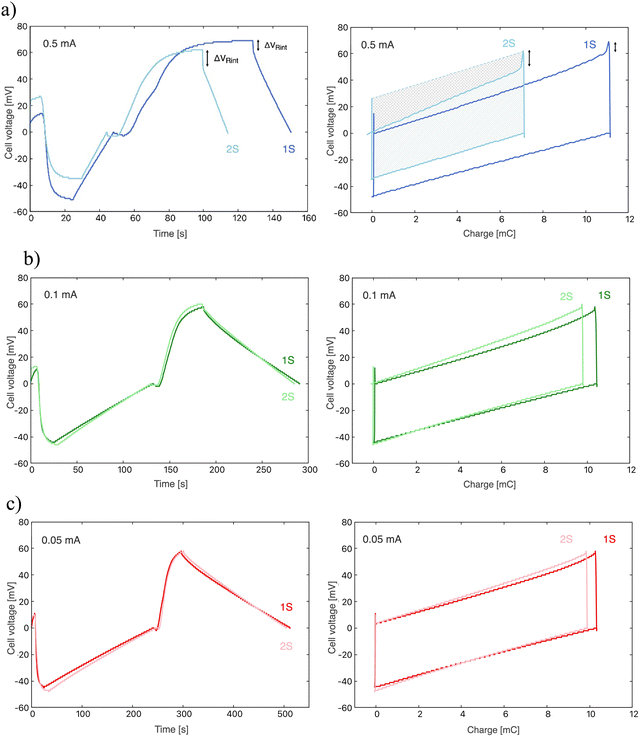
From the process described above, energy extraction cycles typically appear as shown in Fig. 3. As can be seen in Fig. 3a, in the first ∼25 seconds of the cycle (corresponding to stage 1 in Fig. 3b) there is a drop in potential, caused by the decrease in Donnan potential and the contraction of the EDL when exchanging fresh water for salt water while keeping the charge constant as the circuit is open. When the circuit is closed and a positive current is applied, leading to stage 2, charge transfer begins until the potential difference between the electrodes reaches 0 V. At this point, moving to stage 3, an increase in potential at constant charge is obtained, corresponding to the increase in Donnan potential and the expansion of the EDL after exchanging the salty water for fresh water while the circuit is open. Finally, in stage 4, the circuit is closed again while a current of the same magnitude but of opposite sign is applied, with a charge transfer in the opposite direction until the potential drops again to 0 V.
The potential difference between the electrodes depends on the charge density of the PE-coatings, as well as the concentration difference between salty and fresh water solutions.
On the other hand, the accumulated charge during the process is calculated from the applied current:
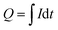 | (1) |
As represented graphically in Fig. 3b, the energy extracted from the cycle is given by the area enclosed by the measured potential difference Δψ ≡ V as a function of the charge, Q.32,42 Thus:
 | (2) |
If the complete cycle duration is Δt, then the power generated, P, can be calculated as:
 | (3) |
The greater the area enclosed by the potential vs. accumulated charge curves, the greater the energy extraction in each cycle. Thus, an increase in the energy obtained would be given by an extension of the transferred charge, leading to wider cycles, or by increasing of the potential difference obtained by salinity exchange. In order to extend the charge transfer stages it would be necessary to keep a low slope of the potential with respect to the charge. This is possible by increasing the capacitance of the system while maximizing the available area of the electrodes. Considering that this process can be described as charging and discharging of a system of two capacitors facing each other at constant current during the stages 2 and 4, the total capacitance of the EDLs, C, can be obtained from the variation of the measured potential difference with respect to time.
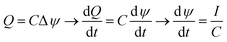 | (4) |
 | (5) |
3. Results and discussion
With the aim of maximizing the energy harvesting, the effects of varying different parameters such as the applied current during the charge transfer process, and the electrode spacing have been studied. These variations are expected to be reflected in characteristic parameters like the EDL capacity and the global internal resistance that would affect the energy and potential extraction in these processes.3.1. Potential difference using PE-coated electrodes
To determine the equilibrium potential profile as a function of the distance r from the center of a PE-coated particle (assume that it is spherical with radius a), three distinct regions have been defined for the Poisson equation:34,43,44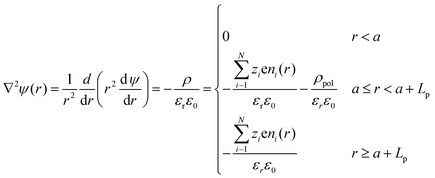 | (6) |
 | (7) |
It is of interest to determine the variation of the surface potential when the salt concentration is changed, ΔΨ, and the dependence of this variation with the polymer charge density ρp. It is possible to find the theoretical limit of ΔΨ when the electrode is coated with a polyelectrolyte. For this purpose, the value of ΔΨ for different polymer densities has been obtained by numerically solving the eqn (6) and (7) using a Matlab® routine, and the results are shown in Fig. 4a. It can be observed that the potential difference reaches a limit when the polymer charge density reaches around 4 × 106 C m−3. Beyond this value, even with a significant increase, the potential difference obtained between the two concentrations will barely change. This phenomenon is depicted in Fig. 4b, where the evolution of the potential for each solution is shown as a function of the distance to the electrode surface. The elevation of the Donnan potential when the ionic concentration is reduced from 500 mM NaCl (sea water) to 20 mM (fresh water) is clearly observed.
Different polymer charge densities, ρp, of 3.7 × 106 C m−3 and 5.6 × 106 C m−3 were considered for Fig. 4b. When moving from the first case (left graph) to the second (right graph), with a 50% increase in the value of ρp, we can observe that the potential difference has only increased by 2.5%, indicating that ΔΨ is close to reaching its limiting value. Therefore, in the case of electrodes coated with polymer, a maximum value of the potential with respect to the bulk solution of ΔΨmax ≈ 82 mV has been estimated for each electrode. So, according to our given scenarios, and considering two electrodes of different charge signs, the maximum achievable potential difference between electrodes is approximately ΔVmax ≈ 164 mV.
3.2. Effect of the applied current during charge transfer stages
To study the influence of the applied current during the charge transfer, three current values were used: 0.5 mA, 0.1 mA, and 0.05 mA (respectively, 0.16, 0.032, and 0.016 mA cm−2). Fig. 5 shows the cycles obtained experimentally: in Fig. 5a the time evolution of the potential difference between the two electrodes of the cell is depicted for the three current values. Fig. S1 (ESI† file) shows a number of successive cycles, demonstrating the stability of the behaviour. In these and all cases considered in the rest of the work, the solutions exchanged are NaCl 20 mM and 500 mM. The four steps previously described for each cycle are observable here: (0) the electrodes are short-circuited in fresh water; (1) the circuit is open and salt water enters the cell, leading to a decrease of the potential difference; (2) the current selected is applied to the cell until a zero potential difference is reached again; (3) fresh water is pumped into the cell, and the potential rises; (4) an inverse current is applied to discharge the electrodes and bring the cell to zero potential difference. Fig. 5b shows the corresponding values of potential difference between electrodes vs. charge transferred. Note the sharp potential decrease when the circuit is closed for discharging, consequence of the internal resistance of the cell. This will be discussed in the next section.The quantitative values obtained from these cycles are contained in Table 1. The potential difference between electrodes, ΔV, can be expected to be independent of the current applied, as it is generated from the salinity exchange when keeping the circuit open. This is in fact observed for 0.05 and 0.1 mA, which can be observed for the cases of 0.1 and 0.05 mA. However, the value measured for 0.5 mA is about 16% higher. This is attributed to the lack of time optimization that made the cycle last longer than the others. This is also evident in Fig. 5b, where a wider range of charge is explored compared with the 0.05 and 0.1 mA.
| I (±0.01 mA) | ΔVmax (±1 V) | Q (±0.02 mC) | t (±0.1 s) | t optim (±0.1 s) |
|---|---|---|---|---|
| 0.05 | 103 | 10.39 | 510.4 | 500.0 |
| 0.10 | 103 | 10.47 | 289.6 | 276.8 |
| 0.50 | 120 | 11.08 | 150.2 | 118.4 |
The maximum values of cell potential are, according to our calculations shown in Fig. 4, around 150 mV, if the polymer charge densities are as indicated in the figure. Previously reported data on a similar system showed that ρp = 6 × 106, ρp = −3.8 × 106C m−1 for PDADMAC and PSS coatings, respectively,34i.e., almost identical to the values used in Fig. 4. It is only possible to achieve these values if the polymer is in complete contact with the entire surface of the electrode. The maximum potential difference observed in the present experimental results, as detailed in Table 1, has been found to be approximately 120 mV, which is slightly lower than the predicted value. This discrepancy is likely a consequence of the tortuosity of the pores, which makes it challenging for the polymer to penetrate the entirety of the pores, thus preventing complete contact between the deposited polymer and the electrode surface. For the same reasons, it is not possible to guarantee the complete replacement of the saline solution with fresh water across the entire surface area of the pores.
Elapsed cycle times are shown in Table 1, as well as the optimized times for the electric potential stabilization in open circuit stages (stages 1 and 3). The duration of these steps was been chosen during the experimental process, aiming to find an optimal relationship between potential difference and cycle duration, as they mark the energy and power generation, respectively. The higher the potential difference, the higher the energy obtained; the shorter the cycle duration, the larger the power generated. As observed from eqn (4), the slopes of the potential vs. time curves during the charging and discharging processes (stages 2 and 4, respectively) are proportional to the applied current. Therefore, the most significant difference in the obtained results is the duration of each cycle, as depicted in Fig. 5a, as the cycle has a shorter duration when the current is increased.
Energy and power values per unit area have been obtained as explained above, and they are presented in Table 2. The extracted energy per cycle results almost constant for all three current values, with a slight increase in the 0.5 mA case, associated to the already mentioned higher charge exchanged. On the other hand, it is observed how power generation increases with the intensity of the applied current, due to the reduction in cycle duration (Table 1).
| I (±0.01 mA) | E (J m−2) | P (mW m−2) |
|---|---|---|
| 0.05 | 1.87 ± 0.04 | 3.73 ± 0.19 |
| 0.10 | 1.79 ± 0.04 | 6.46 ± 0.18 |
| 0.50 | 2.10 ± 0.05 | 17.71 ± 0.21 |
These values must be compared to published results using similar systems. Thus, Zhou et al.45 reported up to 9.5 mJ m−2 employing the CDLE technique, while Zou et al.46 have carried out a comparative study of the Capmix performance in CDLE and CDP modes using YP50F carbon (also from Kuraray). These authors found that the maximum power density achieved with CDLE was 15 mW m−2, whereas CDP (with ion exchange membranes, instead of SEs as in the present work) allowed to reach up to 22 mW m−2 if natural charge–discharge transfer stages were implemented. This value raised to 55 mW m−2 when a forced charging of 360 mC was accumulated on the electrodes. Improvements on the CDP technique were described by Liu et al.,32 who found that if the charge accumulated by controlling the applied current was up to 6 C, the power density produced was 205 mW m−2, probably the best performance reported using ion exchange membranes.
It is also observed from eqn (4) hat the slope of the electric potential vs. time is inversely proportional to the system capacitance, C, during the charge transfer stages. Since C only depends on geometrical parameters, and on salt concentration, it should remain constant for the different applied currents as the medium stays the same. By fitting the curves depicted in Fig. 5a in stage 2 with a straight line, the capacitance can be estimated. The obtained values are shown in Table 3, confirming that changes in the current do not affect the capacity of the system. Since the electrodes are disks 2 cm in diameter, we obtain an average value of (763 ± 3) F m−2 indicating the large capacitance value arising from the huge porous surface area and the small thickness of the EDL. This value corresponds to 100 F g−1, considering the amount of carbon deposited (2.4 mg) and the area of the electrode (3.14 cm2). This value is in agreement with those reported in the literature. Thus, Zhang and Zhao47 reported a specific capacitance <200 F g−1 for commercial electrodes with surface areas between 1000 and 3500 m2 g−1, and Ji et al.23 carried out an extensive review on the capacitance for surface areas between 200 and 3500 m2 g−1 both at the point of zero charge and for a wide potential range. For a carbon with a surface area similar to the one used in this work, the capacitances reported were 90 and 140 F g−1, respectively.
| I (±0.01 mA) | C (mF) |
|---|---|
| 0.05 | 243 ± 5 |
| 0.10 | 242 ± 2 |
| 0.50 | 233.8 ± 0.5 |
3.3. Effect of the separation between electrodes
Combinations of one and two mesh separators of thickness s = (446.3 ± 0.1) μm were used to study the influence of the separation between electrodes in these processes. The reference used for each of the combinations is 1S and 2S, respectively. These separations affect the global resistance of the cell, therefore altering the amount of energy obtained and the power generated. Considering the cylindrical geometry of the cell, the resistance, Rsp, of the solution filling the inter-electrode volume (the spacer) will be given by the classical expression Rsp = d/KA, being d the distance between the electrodes, A the effective area of each electrode, and K the solution conductivity (SI units will be used throughout the manuscript). In the present study, the two solutions with different salinities that are used have conductivities of K20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) mM = (0.2775 ± 0.0001) S m−1 and K500
mM = (0.2775 ± 0.0001) S m−1 and K500![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) mM = (5.6170 ± 0.0001) S m−1, respectively. Additionally, the resistance generated at the electrode/solution interface must be also considered, as schematically depicted in Fig. 6.48–50
mM = (5.6170 ± 0.0001) S m−1, respectively. Additionally, the resistance generated at the electrode/solution interface must be also considered, as schematically depicted in Fig. 6.48–50
 | ||
| Fig. 6 Circuit-EDL analogy, represented by two capacitors in series with their internal resistance Re, in series with the channel resistance Rsp. | ||
Two situations can be distinguished to calculate the voltage of the cell (ΔV), one corresponds to open circuit and the other, to electrodes externally connected:
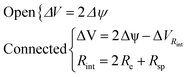 | (8) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) int is the potential drop due to internal resistance of the electrode and it is perceived when the circuit is closed and current flows for the circuit. Rsp is the resistance of the spacer and changes when the separation between electrodes is altered, affecting the global internal resistance. The latter can be calculated from the potential drop observed when transitioning from stage 1 to stage 2, or from 3 to 4. This potential drop becomes more evident at higher currents and amplified when there is an increase in the electrode separation, as can be observed in Fig. 7a. For estimating Rint, the potential drop in fresh water (stage 3 to stage 4) has been selected as it is even more noticeable due to the higher resistance of the solution. Therefore:
int is the potential drop due to internal resistance of the electrode and it is perceived when the circuit is closed and current flows for the circuit. Rsp is the resistance of the spacer and changes when the separation between electrodes is altered, affecting the global internal resistance. The latter can be calculated from the potential drop observed when transitioning from stage 1 to stage 2, or from 3 to 4. This potential drop becomes more evident at higher currents and amplified when there is an increase in the electrode separation, as can be observed in Fig. 7a. For estimating Rint, the potential drop in fresh water (stage 3 to stage 4) has been selected as it is even more noticeable due to the higher resistance of the solution. Therefore: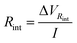 | (9) |
Table 4 contains the internal resistance values calculated as a function of the separation between electrodes for each of the applied current values. The internal resistance should remain constant for the different applied currents, while it should increase with larger electrode spacing. However, we can see that the lower the applied current is, the less its impact on the potential drop and more difficult to quantify. This could be justified by the accuracy of the potentiostat, as the measurements have been recorded at a 0.2 s rate and the potential drop is almost instantaneous.
| I (±0.01mA) | Separation | R int (Ω) |
|---|---|---|
| 0.05 | 1S | 25.00 ± 0.02 |
| 2S | 26.60 ± 0.02 | |
| 0.10 | 1S | 20.00 ± 0.01 |
| 2S | 26.00 ± 0.01 | |
| 0.50 | 1S | 14.50 ± 0.01 |
| 2S | 25.00 ± 0.01 |
Consequently, in order to continue with the analysis of the influence of the spacing on the internal resistance independently of the applied currents, the values obtained for the three cases have been averaged. By knowing the global internal resistance value and estimating the contribution of Rsp from eqn (8), each electrode resistance, Re, can be calculated. The goal is to verify whether the difference in Rint obtained when changing from 1S to 2S is accurate, based on the analog of the EDL with the circuit diagram shown in Fig. 6. To achieve this, while Rsp value should be doubled when increasing the space between the electrodes, Re should remain constant. These results are contained in Table 5.
| Separation | R int [Ω] (±0.01) | R sp [Ω] | R e [Ω] |
|---|---|---|---|
| 1S | 19.83 | 5.88 ± 0.18 | 6.98 ± 0.18 |
| 2S | 25.86 | 11.8 ± 0.3 | 7.03 ± 0.3 |
The percent variation obtained for Re is 0.8% when the separation between electrodes is doubled. Therefore, it can be confirmed that the EDL-circuit analogy proposed above is appropriate when the circuit is closed, and Rint = 2Re + Resp. The observed variation in the internal resistance with respect to the applied current, discussed above, is also reflected in the cycles shown in Fig. 7. For 0.5 mA, the voltage drop is more drastic when fresh water is flowing. Additionally, for this current value, the separation of the electrodes is more influential, and the enclosed area in the potential vs. charge curve for a separation of 2S is way smaller than for 1S under the same operating conditions.
The energy obtained and the power generated per unit area in these cycles are summarized in Table 6 and displayed in Fig. 8. For both 0.05mA and 0.1 mA, the extracted energy and the power generated do not change noticeably when increasing the electrode separation. On the other hand, performing such increase when 0.5 mA is applied leads to the generation of lower energy and power, which corresponds to the observed reduction of the enclosed area of the potential vs. charge curve caused by a larger potential drop in the internal resistance.
| I (±0.01 mA) | Separation | E (J m−2) | P (mW m−2) |
|---|---|---|---|
| 0.05 | 1S | 1.87 ± 0.04 | 3.73 ± 0.19 |
| 2S | 1.86 ± 0.04 | 3.78 ± 0.19 | |
| 0.10 | 1S | 1.79 ± 0.04 | 6.46 ± 0.18 |
| 2S | 1.78 ± 0.04 | 6.61 ± 0.18 | |
| 0.50 | 1S | 2.10 ± 0.05 | 17.71 ± 0.21 |
| 2S | 1.11 ± 0.03 | 11.48 ± 0.11 |
 | ||
| Fig. 8 Energy per cycle and per unit area (a) and power generated per unit area (b) as a function of the applied current for each spacer separation used: 1S (darker colour) and 2S (lighter colour). | ||
4. Conclusions
In this study, a CDP-suitable system has been developed through the application of PE-coatings (SEs) to the surface of bare activated carbon. This results in the generation of natural Donnan potentials, obviating the necessity for prior external charging or the utilisation of ion exchange membranes. Two solutions were prepared: one containing 500 mM NaCl and the other containing 20 mM NaCl. Theoretical calculations have been conducted to ascertain the electric potential differences (between the surface and the bulk solution) resulting from salinity exchange, as a function of the volumetric charge density (ρp) of the polymer coating. The potential differences with respect to the bulk increased with the polymer charge density, reaching a plateau of approximately 82 mV for each of the electrodes when ρp was higher than 5 × 106 C m−3, thus establishing a theoretical maximum in the energy generation by this method. The rate of charge transfer of the CDP cycles was controlled using three distinct applied currents: 0.05, 0.1 and 0.5 mA. The extracted energy results exhibited a high degree of consistency across all three current values, with a mean value of approximately 2 J m−2. Conversely, the power generation increased with the current due to the acceleration of the charge transfer stages, reaching a maximum of (17.71 ± 0.21) mW m−2. To investigate the influence of the separation between electrodes in these processes, a series of experiments were conducted using combinations of one and two mesh separators between the PE-coated electrodes. As a consequence of the rise in the internal resistance of the system, an increase in this geometrical parameter exerts a considerable influence on the measured ohmic voltage drop. However, for currents of 0.05 mA and 0.1 mA, the extracted energy and the power generated remained largely unaltered when the electrode separation was increased. Conversely, for 0.5 mA, the observed voltage drop exhibits a more pronounced change when the distance between electrodes is doubled, resulting in a direct reduction in the energy and power that can be achieved. This means that the electrode distance is a crucial experimental parameter for optimizing the energy and power generated.The system's future improvement will face several challenges, the first of which is scaling it up beyond the laboratory frame. This can be achieved by increasing the electrode area and connecting several cells in parallel. An increase in the total transferred charge will consequently result in an increase in total energy. An additional avenue for improvement would be to enhance the charge transfer rate, i.e., the current, which would result in an increased extracted power. Nevertheless, our findings indicate that maintaining a minimal distance between electrode pairs is crucial for optimal performance. Additionally, increasing the charge density of the polymer can enhance the system's performance by elevating the voltage rise during solution exchange. Our calculations suggest that the PEs employed in this study already exhibit a Donnan potential difference that approaches the maximum theoretical value.
Data availability
The data that support the findings of this study are included in it.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Financial support of this investigation by the grants TED2021-131855BI00 and PID2023-151881OB-I00 (AEI/10.13039/501100011033/Unión Europea Next Generation EU/PRTR) is gratefully acknowledged.References
- V. Krey, Wiley Interdiscip. Rev.:Energy Environ., 2014, 3, 363–383 Search PubMed.
- J. Liu, H. Yang, S. Gosling, M. Kummu, M. Flörke, S. Pfister, N. Hanasaki, Y. Wada, X. Zhang, C. Zheng, J. Alcamo and T. Oki, Earths Future, 2017, 5, 545–559 CrossRef PubMed.
- M. A. Alkhadra, X. Su, M. E. Suss, H. H. Tian, E. N. Guyes, A. N. Shocron, K. M. Conforti, J. P. De Souza, N. Kim, M. Tedesco, K. Khoiruddin, I. G. Wenten, J. G. Santiago, T. A. Hatton and M. Z. Bazant, Chem. Rev., 2022, 122, 13547–13635 CrossRef CAS PubMed.
- G. Folaranmi, M. Bechelany, P. Sistat, M. Cretin and F. Zaviska, Membranes, 2020, 10, 96 CrossRef CAS PubMed.
- P. Srimuk, X. Su, J. Yoon, D. Aurbach and V. Presser, Nat. Rev. Mater., 2020, 5, 517–538 CrossRef CAS.
- Z. N. Yu, L. Tetard, L. Zhai and J. Thomas, Energy Environ. Sci., 2015, 8, 702–730 RSC.
- B. P. Jia and W. Zhang, Nanoscale Res. Lett., 2016, 11, 140 CrossRef PubMed.
- M. Bijmans, O. Burnheim, M. Bryak, A. V. Delgado, P. Hack, F. Mantegazza, S. Tennison and B. Hamelers, Energy Procedia, 2012, 20, 108–115 CrossRef CAS.
- A. V. Delgado, M. L. Jimenez, G. R. Iglesias and S. Ahualli, Curr. Opin. Colloid Interface Sci., 2019, 44, 72–84 CrossRef CAS.
- Á. V. Delgado, Interfacial electrokinetics and electrophoresis, CRC Press, 2001 Search PubMed.
- N. Y. Yip, D. Brogioli, H. V. M. Hamelers and K. Nijmeijer, Environ. Sci. Technol., 2016, 50, 12072–12094 CrossRef CAS PubMed.
- M. M. Fernandez, R. M. Wagterveld, S. Ahualli, F. Liu, A. V. Delgado and H. V. M. Hamelers, J. Power Sources, 2016, 302, 387–393 CrossRef CAS.
- D. Brogioli, Phys. Rev. Lett., 2009, 103, 058501 CrossRef PubMed.
- D. Brogioli, R. Zhao and P. M. Biesheuvel, Energy Environ. Sci., 2011, 4, 772–777 RSC.
- S. Ahualli and Á. V. Delgado, Charge and Energy Storage in Electrical Double Layers, Academic Press, 2018 Search PubMed.
- S. Ahualli, G. R. Iglesias and Á. V. Delgado, in Interface Science and Technology, Elsevier, 2018, vol. 24, pp. 169–192 Search PubMed.
- S. Porada, R. Zhao, A. van der Wal, V. Presser and P. M. Biesheuvel, Prog. Mater. Sci., 2013, 58, 1388–1442 CrossRef CAS.
- B. P. Jia and L. D. Zou, Carbon, 2012, 50, 2315–2321 CrossRef CAS.
- G. Rasines, P. Lavela, C. Macias, M. C. Zafra, J. L. Tirado, J. B. Parra and C. O. Ania, Carbon, 2015, 83, 262–274 CrossRef CAS.
- J. Ma, L. Wang and F. Yu, Electrochim. Acta, 2018, 263, 40–46 CrossRef CAS.
- P. Zhang, J. Li and M. B. Chan-Park, ACS Sustainable Chem. Eng., 2020, 8, 9291–9300 CrossRef CAS.
- A. V. Delgado, S. Ahualli, M. M. Fernandez, M. A. Gonzalez, G. R. Iglesias, J. F. Vivo-Vilches and M. L. Jimenez, Environ. Chem., 2017, 14, 279–287 CrossRef CAS.
- H. Ji, X. Zhao, Z. Qiao, J. Jung, Y. Zhu, Y. Lu, L. Zhang, A. MacDonald and R. Ruoff, Nat. Commun., 2014, 5, 3317 CrossRef PubMed.
- T. Bordjiba, M. Mohamedi and L. Dao, Adv. Mater., 2008, 20, 815 CrossRef CAS.
- S. Lehtimaki, S. Tuukkanen, J. Porhonen, P. Moilanen, J. Virtanen, M. Honkanen and D. Lupo, Appl. Phys. A:Mater. Sci. Process., 2014, 117, 1329–1334 CrossRef CAS.
- C. Ania, V. Khomenko, E. Raymundo-Piñero, J. Parra and F. Béguin, Adv. Funct. Mater., 2007, 17, 1828–1836 CrossRef CAS.
- S. Orozco-Barrera, K. Wakabayashi, T. Yoshii, H. Nishihara, G. Iglesias, A. Delgado and S. Ahualli, Sep. Purif. Technol., 2025, 354, 129314 CrossRef CAS.
- H. Zhang, G. Cao, Z. Wang, Y. Yang, Z. Shi and Z. Gu, Nano Lett., 2008, 8, 2664–2668 CrossRef CAS PubMed.
- J. Cherusseri, K. S. Kumar, N. Choudhary, N. Nagaiah, Y. Jung, T. Roy and J. Thomas, Nanotechnology, 2019, 30, 202001 CrossRef CAS PubMed.
- E. M. Remillard, A. N. Shocron, J. Rahill, M. E. Suss and C. D. Vecitis, Desalination, 2018, 444, 169–177 CrossRef CAS.
- B. B. Sales, O. S. Burheim, F. Liu, O. Schaetzle, C. J. N. Buisman and H. V. M. Hamelers, Environ. Sci. Technol., 2012, 46, 12203–12208 CrossRef CAS PubMed.
- F. Liu, O. Schaetzle, B. B. Sales, M. Saakes, C. J. N. Buisman and H. V. M. Hamelers, Energy Environ. Sci., 2012, 5, 8642–8650 RSC.
- S. Ahualli, M. M. Fernández, Á. V. Delgado and G. R. Iglesias, in Interface Science and Technology, Elsevier, 2018, vol. 24, pp. 143–166 Search PubMed.
- S. Ahualli, M. L. Jimenez, M. M. Fernandez, G. Iglesias, D. Brogioli and A. V. Delgado, Phys. Chem. Chem. Phys., 2014, 16, 25241–25246 RSC.
- A. Bhat, E. Reale, M. del Cerro, K. Smith and R. Cusick, Water Res.:X, 2019, 3, 10027 Search PubMed.
- P. A. Fritz, R. M. Boom and K. Schroen, Sep. Purif. Technol., 2019, 220, 145–151 CrossRef CAS.
- S. Sahin, J. Dykstra, H. Zuilhof, R. Zornitta and L. de Smet, ACS Appl. Mater. Interfaces, 2020, 12, 34746–34754 CrossRef CAS PubMed.
- F. Gao, W. Shi, R. Dai and Z. Wang, ACS ES&T Water, 2022, 2, 237–246 Search PubMed.
- G. R. Iglesias, S. Ahualli, A. V. Delgado, P. M. Arenas-Fernandez and M. M. Fernandez, J. Power Sources, 2020, 453, 227840 CrossRef CAS.
- P. Przygocki, Q. Abbas and F. Béguin, Electrochim. Acta, 2018, 269, 640–648 CrossRef CAS.
- S. Nadakatti, M. Tendulkar and M. Kadam, Desalination, 2011, 268, 182–188 CrossRef CAS.
- S. Ahualli, M. L. Jimenez, Z. Amador, M. M. Fernandez, G. R. Iglesias and A. V. Delgado, Sustainable Energy Fuels, 2021, 5, 3321–3329 RSC.
- S. Ahualli, G. R. Iglesias, M. M. Fernandez, M. L. Jimenez and A. V. Delgado, Environ. Sci. Technol., 2017, 51, 5326–5333 CrossRef CAS PubMed.
- S. Orozco-Barrera, G. R. Iglesias, A. V. Delgado, S. Garcia-Larios and S. Ahualli, Phys. Chem. Chem. Phys., 2023, 25, 9482–9491 RSC.
- J. Zhou, G. Jing, J. Xie, W. Tang, X. Xu and S. Zhao, ACS Appl. Energy Mater., 2024, 7, 3635–3644 CrossRef.
- Z. Zou, L. Liu, S. Meng and X. Bian, Energy Rep., 2022, 8, 7325–7335 CrossRef.
- L. Zhang and X. Zhao, Chem. Soc. Rev., 2009, 38, 2520–2531 RSC.
- M. Bijmans, O. Burheim, M. Bryjak, A. Delgado, P. Hack, F. Mantegazza, S. Tenisson and H. Hamelers, Energy Procedia, 2012, 20, 108–115 CrossRef CAS.
- O. Burheim, B. Sales, O. Schaetzle, F. Liu and H. Hamelers, J. Energy Resour. Technol., 2013, 135, 011601 CrossRef.
- P. Biesheuvel and M. Bazant, Phys. Rev. E:Stat., Nonlinear, Soft Matter Phys., 2010, 81, 031502 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ya00605d |
| This journal is © The Royal Society of Chemistry 2025 |