Open Access Article
Open Access ArticleWhy is sodium-intercalated graphite unstable?
Hiroki
Moriwake
 *,
Akihide
Kuwabara
,
Craig A. J.
Fisher
and
Yuichi
Ikuhara
*,
Akihide
Kuwabara
,
Craig A. J.
Fisher
and
Yuichi
Ikuhara
Nanostructures Research Laboratory, Japan Fine Ceramics Center, 2-4-1 Mutsuno, Atsuta-ku, Nagoya, 456-8587 Japan
First published on 24th July 2017
Abstract
Na-ion batteries offer an attractive low-cost alternative to Li-ion batteries. Although graphite is used as the negative electrode in conventional Li-ion batteries, attempts to use it in Na-ion batteries have been hampered by the inability of Na to form graphite intercalation compounds (GICs) under moderate conditions. It is generally considered that this is due to the size mismatch between Na and the graphite interlayer spacings, but here we show with detailed first-principles calculations of Li, Na, K, Rb, and Cs GICs that the major reason is the change in chemical bonding between alkali metal (AM) ion and C atoms. van der Waals correction terms are introduced to better reproduce the layered graphite structure, and calculated formation energies of GICs AMC6, where AM = Li, Na, K, Rb, and Cs, are found to become less negative (less stable) as ion size decreases from Cs to Na as a result of weakening ionic bonding, until the formation energy of NaC6 becomes positive. The much smaller Li ion represents an exception to this trend, as its bonds with C atoms contain a covalent component, resulting in a negative formation energy. These subtle differences in staging for the different alkali metals explain why graphite is a good intercalation material for Li and K but not for Na.
Introduction
As demand for sustainable energy sources continues to grow, so does the need for cost-effective, high-efficiency, environmentally benign, and durable energy storage devices. Lithium-ion batteries (LIBs), widely used as power sources in mobile electronics (e.g., cell phones, laptops, and PCs) because of their high energy densities and good durability, are today being scaled up or connected in series to power electric vehicles, as well as serving as energy storage systems for intermittent power generators such as wind turbines and solar panels. For these large-scale applications, however, limited lithium reserves are a serious concern, and in recent years efforts to develop practical sodium-ion batteries (SIBs) have increased rapidly because of sodium's much greater crustal abundance.1–6 Compared to the range of sodium-intercalating materials proposed for use as positive electrodes,1–8 the materials known to be suitable for use as the negative electrode are considerably fewer in number.1–6,9In conventional LIBs, graphite is commonly used as the negative electrode because of its ability to reversibly intercalate Li ions, forming a series of binary graphite intercalation compounds (GICs) as it does so. With the notable exception of Na, the other alkali metals (AMs) are also known to form stable GICs.10
Graphite is a layered material with sp2 hybridized carbon–carbon bonds within the graphene layers and weak van der Waals (vdW) interactions between the graphene layers. Graphite intercalated with electron donors such as alkali metals display a rich variety of phases with different compositions and crystal structures. LiC6 and KC8 are examples of stage-1 GICs with the metal intercalated between all the graphite layers. The staging index refers to the number of graphene layers between two successive layers of intercalated alkali metal atoms. A low stage index Na-GIC has never been observed; only higher stage compounds such as NaC48, NaC64, NaC80, in which some Na is intercalated in every eighth layer or less, have ever been reported.11–13
Recent theoretical studies by Nobuhara et al.,14 Wang et al.,15 Okamoto,16 and Liu et al.17 using vdW functionals reported similar results. Both confirmed that lower-stage Na-GICs are unstable. Strategies to overcome this limitation based on the formation of ternary GICs have been proposed, for example, the intercalation of solvated Na ions (“co-intercalation”).18,19 Wen et al.20 have also reported that expanded graphite, in which the spacing between layers is increased by introducing functional groups, accepts a larger amount of Na intercalation, and the intercalation process was examined using first-principles calculations by Kang et al.21 In the case of graphite under normal conditions, however, the underlying mechanisms inhibiting Na intercalation remain poorly understood. To uncover the underlying reasons why only Na out of the alkali metals cannot be intercalated into graphite, we have carried out systematic first-principles calculations of the five AM-GIC systems using a vdW functional to reproduce the correct structure of the graphite crystal.
Methodology
First-principles calculations were performed using the projector-augmented wave (PAW) method22 within the framework of density functional theory (DFT),23 as implemented in the VASP code.24,25 Exchange-correlation interactions were treated by the generalized gradient approximation (GGA-PBE)26 with five different van der Waals (vdW) functionals,27,28 namely vdW-revPBE,27 vdW-optPBE,29 vdW-optB88,29 vdW-optB86b,30 and vdW-D2,31 implemented using the algorithm of Román-Pérez and Soler.32In the case of vdW-optB88, vdW-optB86b, and vdW-D2 functionals, default values were used for the input parameters. Calculations using standard functionals GGA-PBE and GGA-PBE_sol33 were also carried out for comparison. For the PAW potentials, 1s and 2s for La, 2p and 3s for Na, 3p and 4s for K, 4p and 5s for Rb, 5p and 6s for Cs, and 2s and 2p for C were explicitly treated as valence electrons. Planewave expansion was performed up to 500 eV with k-point spacings of the Brillouin zone of 0.25 A−1 using a Γ-point centered Monkhorst–Pack scheme.34 Lattice constants and internal atomic coordinates were considered fully optimized when residual Hellmann–Feynman forces were smaller than 10−3 eV Å−1.
The stabilities of AM-GICs were evaluated by calculating their formation energies (ΔE) according to
| ΔE = EAM-GIC − Egraphite − EAM, | (1) |
Results and discussion
Comparison of van der Waals functionals
Previous studies have shown the importance of van der Waal's forces in holding the 2D graphite structure together.14–17,35 It is also well known that the conventional GGA functional is unable to reproduce the layered structure of graphite, while the LDA functional can.15,36 Neither functional explicitly includes transient polar interactions, so the different results likely stem from the fact the LDA functional overestimates binding between atoms. Recently, many types of functionals have been developed to reproduce dispersive van der Waals interactions in weakly bonded systems. In this study, five types of van der Waals functionals were tested to assess how well they reproduce the structures and energetics of pure graphite and AM-GICs. Structural parameters obtained from the different functionals are compared in Tables 1 and 2 for pure graphite and LiC6, respectively. Most functionals apart from conventional GGA predict the graphite structure to be stable, but the vdW-D2 functional underestimates the c parameter by over 4%, while the GGA-PBEsol and GGA + vdW-revPBE functionals overestimate it by more than 5%. In contrast, in the case of LiC6, all functionals, including the conventional GGA-PBE and GGA-PBE_sol functionals, reproduced the structure reasonably well, consistent with previous studies.14–17 This is because the intercalated Li atoms bond with C to hold the graphene sheets together. Of the functionals examined, the vdW-optPBE functional produced the smallest deviations from experiment for both the graphite and LiC6 structures, so this was chosen for further calculations.| Functional | Parameter (Å) | Deviationa (%) | |
|---|---|---|---|
| a Relative to experimental values a = 2.464 Å, c = 6.711 Å (ref. 37). | |||
| GGA-PBE | a | — | — |
| c | — | — | |
| GGA-PBEsol | a | 2.461 | −0.11 |
| c | 7.063 | +5.25 | |
| vdW-D2 | a | 2.464 | −0.01 |
| c | 6.417 | −4.38 | |
| vdW-optB86b | a | 2.468 | +0.15 |
| c | 6.601 | −1.64 | |
| vdW-optB88 | a | 2.466 | +0.10 |
| c | 6.695 | −0.24 | |
| vdW-optPBE | a | 2.473 | +0.35 |
| c | 6.841 | +1.93 | |
| vdW-revPBE | a | 2.479 | +0.60 |
| c | 7.095 | +5.72 | |
| Functional | Parameter (Å) | Deviationa (%) | |
|---|---|---|---|
| a Relative to experimental values a = 4.316 Å, c = 3.700 Å (ref. 38). | |||
| GGA-PBE | a | 4.327 | +0.25 |
| c | 3.761 | +1.64 | |
| GGA-PBEsol | a | 4.314 | −0.06 |
| c | 3.683 | −0.46 | |
| vdW-D2 | a | 4.321 | +0.12 |
| c | 3.655 | −1.22 | |
| vdW-optB86b | a | 4.327 | +0.24 |
| c | 3.636 | −1.72 | |
| vdW-optB88 | a | 4.325 | +0.21 |
| c | 3.648 | −1.39 | |
| vdW-optPBE | a | 4.336 | +0.45 |
| c | 3.684 | −0.43 | |
| vdW-revPBE | a | 4.348 | +0.73 |
| c | 3.756 | +1.52 | |
Stability of alkali-metal graphite intercalation compounds
Formation energies were calculated for different alkali metal concentrations in the graphite layers. Similar to previous reports,14,15 energy differences between different stacking sequences of the graphite layers for the same alkali metal content were relatively small, so for the purpose of comparison, AA stacking of graphite sheets was assumed hereafter. Using the above assumptions, formation energies of the AMC6 series (AMC6, AMC12, AMC24, AMC36, AMC48, AMC72) and AMC8 series (AMC8, AMC16, AMC32, AMC64, AMC80) for AM = Li, Na, and K were calculated. The results for Li–C, K–C, and Na–C systems are summarized in Fig. 1(a)–(c), respectively. In Fig. 1(a), Li-GICs are stable even for low-stage structures (high Li concentrations). In fact, the stability increases with increasing Li content down to stage 2, before decreasing slightly for stage 1 for both LiC6 and LiC8 series. As shown in Fig. 1(b), despite the large ionic radius of K, K-GIC is more stable than Li-GIC for the same stage and series, and unlike the Li-GIC system, K-GICs are stable over the entire range of stages considered. Perhaps surprisingly, the change in stabilities with staging level follows the same trend as for Li-GICs. In contrast, Fig. 1(c) shows that the formation energies of Na-GICs are positive over the entire range of stages examined, indicating that Na-GIC is thermodynamically unstable for all compositions. Apart from this, however, the same trend is followed as for Li-GICs and K-GICs. These trends are in good agreement not only with previous experimental results11–13 but with theoretical reports14–16 as well.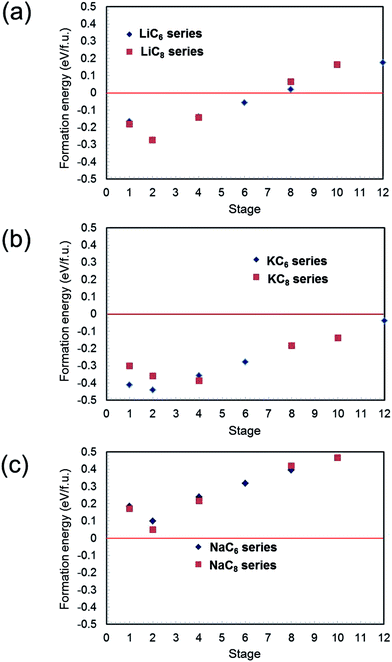 | ||
| Fig. 1 Calculated formation energies of AM-GICs (AM = Li, Na and K) as a function of stage number for AMC6 and AMC8 series: (a) Li-GIC, (b) K-GIC and (c) Na-GIC. | ||
As expressed by eqn (1), the formation energies of AM-GICs are a function of the total energy of the intercalated compound, the total energy of graphite, and the total energy of the pure metal. When comparing the different systems, the total energy of graphite is constant, so the trends in AM-GIC formation energies must be due to changes in the stabilities of the alkali metals or changes in the intercalated system energies. It would be easy to rationalize the instability of Na-GICs if Na metal were exceptionally stable, for example. However, of these three alkaline metals, Li metal is most stable (lowest energy), decreasing as the atomic radius increases. The reason for the deviation in linearity for the formation energies must lie in the nature of the AM-GICs themselves.
Origin of the instability of Na-GICs
Of the AM-GICs examined in the previous section, only Na-GIC is unstable for all intercalation stages. Extending these calculations to a wider range of alkali metals suggests that it is actually Li-GICs that deviate from the trend rather than Na-GIC. For example, Fig. 2 shows calculated formation energies of AMC6 structures where AM = Li, Na, K, Rb and Cs. Of the five alkali metals, only NaC6 has a positive formation energy. For cations larger than Na+, the formation energy becomes more negative (more stable) as the ion radius increases.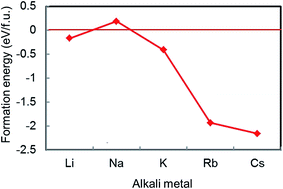 | ||
| Fig. 2 Calculated formation energies of AMC6 for AM = Li, Na, K, Rb, and Cs in order of increasing atomic number. | ||
The electronegativity of alkali metal atoms decreases down the period, meaning that the larger the ion radius, the greater the iconicity of the bond between metal and C atoms. Conversely, as the ion radius decreases, the metal–carbon bond becomes progressively weaker, with formation energies becoming more positive until for Na-GIC the formation energy is positive (i.e., NaC6 is unstable). For the smallest alkali metal, Li, the formation energy of the intercalated compound breaks from this trend, becoming negative again, consistent with Li-GICs being observed to be stable by experiment.
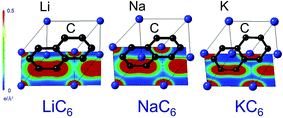
The reason for this apparent anomaly is that the binding energies of the GICs consist not only of an ionic component but also of a covalent component between the metal and carbon atoms.36 Maps of electron densities through the centers of AM and C atoms in AMC6 compounds for AM = Li, Na, and K, plotted to the same scale, are shown in Fig. 3. In the case of KC6 and NaC6, the electron density between C and AM is negligibly small. In the case of LiC6, the bond length is shorter and the electron density between C and Li atoms is greater. This indicates that in Li–C bonds there is a certain amount of sharing of electrons between atom species, in other words, a non-negligible covalent bond component. In contrast to Na-GIC and K-GIC, the increased covalent bonding in Li-GICs is sufficiently large to overcome the decrease in the ionic component, so that Li-GICs are more stable than Na-GICs. In other words, it is the balance between the proportion of iconicity and covalency in the metal–carbon bond that determines the shape of the formation energy versus ionic radius plot. Without the contribution from covalent bonding between C and Li atoms, Li-GICs would be even less stable than Na-GICs.
Conclusions
Density functional theory calculations incorporating van der Waals functionals to reproduce accurately the graphite layer structure were performed to evaluate the stabilities of alkali-metal graphite intercalation compounds. The main findings can be summarized as follows: Na-GIC was found to be thermodynamically unstable for all Na concentrations examined (stages 1 to 12). Li-, Na-, and K-GICs exhibit similar changes in formation energy as a function of stage number, although the absolute energies are very different. Of the wide range of staged structures examined, stage-2 AM-GICs, rather than stage-1 AM-GICs, were found to be the most stable (lowest energy) for Li, Na, and K. Of the five alkali metals examined, only Na-GICs were found to be unstable for all intercalation stages. Comparison of the formation energies of stage-1 AM-GICs revealed that Na actually conforms to the expected intercalation behavior extrapolated from the behavior of the larger alkali metals. Rather than Na, it is Li that is the exception to the trend obeyed by the alkali metals because, unlike the larger alkali metals, Li–C bonds contain a non-negligible covalent component that helps stabilize the intercalated layered material.Acknowledgements
This work was partially supported by the Research and Development Initiative for Scientific Innovation of New Generation Batteries II (RISING II) project from the New Energy and Industrial Technology Development Organization (NEDO), Japan. The authors acknowledge to Dr Masafumi Nose, Dr Hideki Nakayama, Dr Shinji Nakanishi, Dr Hideki Iba (Toyota Motor Corporation), for their fruitful discussion and support.References
- M. D. Slater, D. Kim, E. Lee and C. S. Johnson, Adv. Funct. Mater., 2013, 23, 947–958 CrossRef CAS
.
- V. Palomares, M. Casas-Cabanas, E. Castillo-Martínez, M. H. Han and T. Rojo, Energy Environ. Sci., 2013, 6, 2312–2337 CAS
.
- H. Pan, Y.-S. Hu and L. Chen, Energy Environ. Sci., 2013, 6, 2338–2360 CAS
.
- N. Yabuuchi, K. Kubota, M. Dahbi and S. Komaba, Chem. Rev., 2014, 114, 11636–11682 CrossRef CAS PubMed
.
- S.-W. Kim, D.-H. Seo, X. Ma, G. Ceder and K. Kang, Adv. Energy Mater., 2012, 2, 710–721 CrossRef CAS
.
- L. P. Wang, L. Yu, X. Wang, M. Srinivasan and Z. J. Xu, J. Mater. Chem. A, 2015, 3, 9353–9378 CAS
.
- M. H. Han, E. Gonzalo, G. Singh and T. Rojo, Energy Environ. Sci., 2015, 8, 81–102 CAS
.
- X. Liu, X. Wang, A. Iyo, H. Yu, D. Lia and H. Zhou, J. Mater. Chem. A, 2014, 2, 14822–14826 CAS
.
- G. Hasegawa, K. Kanamori, T. Kiyomura, H. Kurata, K. Nakanishi and T. Abe, Adv. Energy Mater., 2015, 5, 1400730 CrossRef
.
- M. S. Drusselhaus and G. Dresselhaus, Adv. Phys., 2002, 51, 1–186 CrossRef
.
- A. Metrot, D. Guerard, D. Billaud and A. Herold, Synth. Met., 1979/80, 1, 363–369 Search PubMed
.
- N. Adhouma, J. Bouteillon, D. Dumas and J. C. Poignet, Electrochim. Acta, 2006, 51, 5402–5406 CrossRef
.
- P. Ge and M. Fouletier, Solid State Ionics, 1988, 28–30, 1172–1175 CrossRef
.
- K. Nobuhara, H. Nakayama, M. Nose, S. Nakanishi and H. Iba, J. Power Sources, 2013, 243, 585–587 CrossRef CAS
.
- Z. Wang, S. M. Selbach and T. Grande, RSC Adv., 2014, 4, 4069–4079 CAS
.
- Y. Okamoto, J. Phys. Chem. C, 2014, 118, 16–19 CAS
.
- Y. Liu, B. V. Merinova and W. A. Goddard III, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 3735–3739 CrossRef CAS PubMed
.
- B. Jache and P. Adelhelm, Angew. Chem., Int. Ed., 2014, 53, 10169–10173 CrossRef CAS PubMed
.
- G. Yoon, H. Kim, I. Park and K. Kang, Adv. Energy Mater., 2017, 7, 1601519 CrossRef
.
- Y. Wen, K. He, Y. Zhu, F. Han, Y. Xu, I. Matsuda, Y. Ishii, J. Cumings and C. Wang, Nat. Commun., 2014, 5, 4033 CAS
.
- Y.-J. Kang, S. C. Jung, J. W. Choi and Y.-K. Han, Chem. Mater., 2015, 27, 5402–5406 CrossRef CAS
.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17975 CrossRef
.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133–A1138 CrossRef
.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS
.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS
.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed
.
- M. Dion, H. Rydberg, E. Schröder, D. C. Langreth and B. I. Lundqvist, Phys. Rev. Lett., 2004, 92, 246401 CrossRef CAS PubMed
.
- T. Thonhauser, V. R. Cooper, L. Shen, A. Puzder, P. Hyldgaard and D. C. Langreth, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 125112 CrossRef
.
- J. Klimeš, D. R. Bowler and A. Michaelides, J. Phys.: Condens. Matter, 2010, 22, 022201 CrossRef PubMed
.
- J. Klimeš, D. R. Bowler and A. Michaelides, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 195131 CrossRef
.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS PubMed
.
- G. Román-Pérez and J. M. Soler, Phys. Rev. Lett., 2009, 103, 096102 CrossRef PubMed
.
- J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Phys. Rev. Lett., 2008, 100, 136406 CrossRef PubMed
.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192 CrossRef
.
- Y. Ma, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 075419 CrossRef
.
- C. Hartwigsen, W. Witschel and E. Spohr, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 55, 4953–4959 CrossRef CAS
.
- P. Trucano and R. Chen, Nature, 1975, 258, 136–137 CrossRef CAS
.
- O. Dolotkoa, A. Senyshyn, M. J. Mühlbauer, K. Nikolowski and H. Ehrenberg, J. Power Sources, 2014, 255, 197–203 CrossRef
.
| This journal is © The Royal Society of Chemistry 2017 |