Open Access Article
Open Access ArticleProline bulky substituents consecutively act as steric hindrances and directing groups in a Michael/Conia-ene cascade reaction under synergistic catalysis†
Salil
Putatunda‡
 a,
Juan V.
Alegre-Requena‡
a,
Juan V.
Alegre-Requena‡
 b,
Marta
Meazza
b,
Marta
Meazza
 c,
Michael
Franc
c,
Michael
Franc
 a,
Dominika
Rohal'ová
a,
Pooja
Vemuri
c,
Ivana
Císařová
a,
Dominika
Rohal'ová
a,
Pooja
Vemuri
c,
Ivana
Císařová
 d,
Raquel P.
Herrera
d,
Raquel P.
Herrera
 *b,
Ramon
Rios
*b,
Ramon
Rios
 *c and
Jan
Veselý
*c and
Jan
Veselý
 *a
*a
aDepartment of Organic Chemistry, Faculty of Science, Charles University, Hlavova 2030, 128 43 Praha 2, Czech Republic. E-mail: jxvesely@natur.cuni.cz
bLaboratorio de Organocatálisis Asimétrica, Departamento de Química Orgánica, Instituto de Síntesis Química y Catálisis Homogénea (ISQCH), CSIC-Universidad de Zaragoza, C/Pedro Cerbuna 12, 50009 Zaragoza, Spain. E-mail: raquelph@unizar.es
cUniversity of Southampton, School of Chemistry, Highfield Campus, Southampton, SO17 1BJ, UK. E-mail: rrt1f11@soton.ac.uk
dDepartment of Inorganic Chemistry, Faculty of Science, Charles University, Hlavova 2030, 128 43 Praha 2, Czech Republic
First published on 4th March 2019
Abstract
In this study, we report a highly stereoselective and versatile synthesis of spiro pyrazolones, promising motifs that are being employed as pharmacophores. The new synthetic strategy merges organocatalysis and metal catalysis to create a synergistic catalysis using proline derivatives and Pd catalysts. This protocol is suitable for late-stage functionalization, which is very important in drug discovery. Additionally, a thorough computational study proved to be very useful to elucidate the function of the different catalysts along the reaction, showing a peculiar feature: the –CPh2OSiMe3 group of the proline catalyst switches its role during the reaction. In the initial Michael reaction, this group plays its commonly-assumed role of bulky blocking group, but the same group generates π–Pd interactions and acts as a directing group in the subsequent Pd-catalyzed Conia-ene reaction. This finding might be very relevant especially for processes with many steps, such as cascade reactions, in which functional groups are assumed to play the same role during all reaction steps.
Introduction
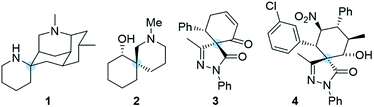
The synthesis of highly complex scaffolds has long generated considerable research interest among organic chemists. Some of the most challenging organic structures to synthesize are spiro compounds (formally bicyclic organic compounds with rings connected through a quaternary atom centre).1–8 Spirocycles have unique structural properties due to their rigidity, and they are present in several natural products such as spongistatins, fredericamycin, the fused tetracyclic lycopodium alkaloid nankakurine A (1) and alkaloid (−)-sibirine (2), and in pharmaceuticals (Fig. 1).9,10 However, libraries of spiro compounds are still underrepresented in medicinal chemistry despite their usefulness as rigid conformations that reduce conformational entropy penalty when binding to pharmaceutical targets.9,10 Recent advances in synthetic methods have provided access to spiro building blocks, thereby slightly expanding their use in drug discovery. However, further synthetic work is clearly still needed because spirocycles are difficult to prepare. Their synthesis involves the formation of a quaternary center, which is a challenging task in synthetic organic chemistry.Recently, we have focused our efforts on developing enantioselective methods for the synthesis of spiro compounds through organocatalytic cascade reactions,11,12 using a synergistic approach.13 It is remarkable that synergistic catalysis has opened an exciting gate for the development of new reactions due to the possibility to activate two unreactive compounds at the same time.14,15
Pyrazolones are a key class of five-membered ring nitrogen heterocycles, which have been used as pharmaceutical agents, agrochemicals, and chelating agents, among others.16,17 Pyrazole units are found in many natural products such as withasonine, pyrazofurin and formicin. Moreover, their use in pharmaceutical chemistry has increased due to their properties as p38 inhibitors and HIV integrase inhibitors.18 More specifically, spiro pyrazolones have been used as promising pharmacophores, showing potential as antitumor (3) and anti-inflammatory (4) agents (Fig. 1).19–22 In our research group, we have investigated the synthesis of spiropyrazolones by organocatalytic procedures (Scheme 1)23,24 and very recently by a synergistic approach.25
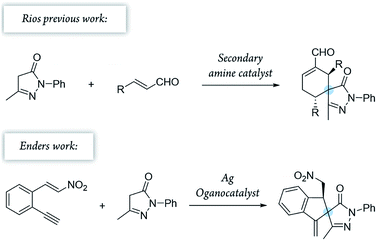
To combine spiropyrazolone synthesis with synergistic catalysis, we focused on the venerable Conia-ene reaction as a viable synthetic tool to build five-membered (hetero) carbocycles.26,27 Previously, the Cordova's group developed a Conia-ene reaction to prepare spirooxindoles with excellent results28,29 and, more recently, Enders and colleagues reported the synthesis of spiropyrazolones by sequential organo- and silver catalysis.30,31 The latter involves a Michael/Conia-ene cascade reaction between pyrazolones and nitroalkenes bearing an alkyne (Scheme 1).
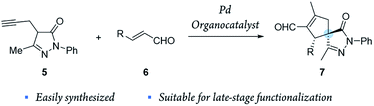
Inspired by these results, we envisioned a completely new strategy involving alkyne tethered pyrazolones 5 and enals 6 (Scheme 2). First, proline derived catalysts would be used to achieve a highly stereoselective activation of enals. Another reason to use this type of catalyst is that they preserve their catalytic activity even when metal Lewis acids, such as Pd, In and Ag, are also present in the reaction media.32–34 Moreover, we considered that this method could be easily applied to generate broad libraries of spiro compounds because enals 6 and pyrazolones 5 are easily synthesized and functionalized, and the compounds generated 7 contain several reactive groups (aldehydes, double bonds), thus enabling late-stage functionalization.
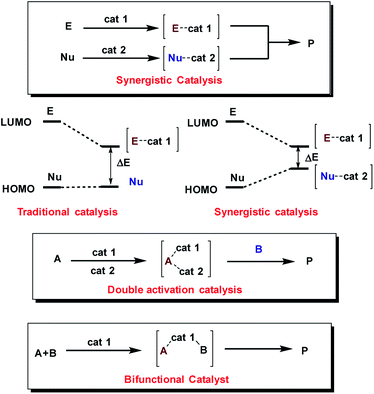
Moreover, the concurrent activation of both reactants through a synergistic catalysis allows a major reactivity scope and, at the same time, the use of simple catalysts that are not interconnected (in opposition to bifunctional catalysts35–37) (Fig. 2). Additionally, these processes require less synthetic effort in the reaction optimization process because each catalyst can be individually optimized.
Results and discussion
Synthetic results
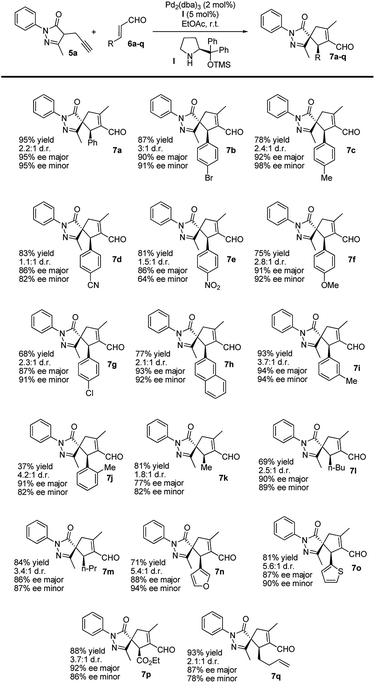
After optimizing the model reaction, we achieved our best results when using ethyl acetate as the solvent, at room temperature, in the presence of 5 mol% TMS-protected diphenyl prolinol (I), acting as the secondary amine catalyst, and 2 mol% Pd2(dba)3 (see the ESI† for more details about the optimization process). Remarkably, the reaction is catalyzed with a low organocatalyst loading (5 mol%), in contrast to similar organocatalytic reactions normally requiring 20 mol% of (I). Moreover, without adding Pd, no cyclization reaction is detected, highlighting the importance of this synergistic cascade.Thus, we studied the scope of this reaction using several enals 6 to demonstrate the general applicability of this synergistic cascade reaction (Scheme 3).
In general, good-to-excellent yields of spiro compounds 7 with excellent enantioselectivities and moderate-to-good diastereoselectivities were assessed with different enals. The reaction is compatible with aliphatic enals (7k, 7l and 7m), with the glyoxylate derivative (7p), with dienals (7q), with aromatic enals with electron withdrawing groups (7d, 7e) and with electron donating groups (7c, 7f) in a para position on the aromatic ring. Moreover, meta-substituted aromatic enal (7i) and heteroaromatic enals (7n and 7o) were prepared in excellent yields. As a general trend, heteroaromatics render final compounds 7 in higher diastereoselectivities (up to 5.6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 dr) whereas spiro compound 7j was formed in low yields when using the ortho-substituted cinnamic-type enal, most likely for steric reasons.
1 dr) whereas spiro compound 7j was formed in low yields when using the ortho-substituted cinnamic-type enal, most likely for steric reasons.
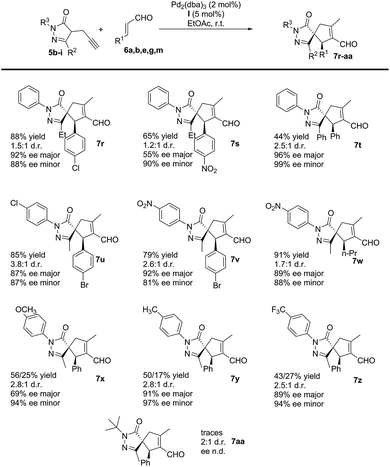
Subsequently, we studied the process using substituted pyrazolones 5b–i (Scheme 4). The reaction is sensitive to steric effects of the pyrazolones. When the initial Me group on the pyrazolone moiety was changed to a Ph group, the reaction rate significantly decreased. No full conversion was observed, even after a prolonged time (7 days), thus forming the corresponding product 7t in low yields. In contrast, when Et substituted pyrazolones were used, the results were similar to previously reported values when using their Me-substituted analogues (7rvs.7g and 7svs.7e). We finally studied the effect of different R3 substituents: the reaction works well with EWG, EDG and halogen as 4-substituent of the aromatic ring (7u–z), while negligible conversion was observed when R3 is an aliphatic substituent (7aa).
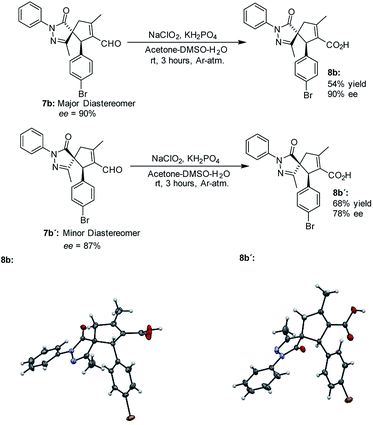
The absolute configuration of the final products was determined by X-ray diffraction analysis of compounds 8b and 8b' resulting from the oxidation of the separated diastereoisomers of 7b (Fig. 3).38 Based on the absolute configuration of the major diastereomer 8b, intermediate Int-Ald contains two stereocenters that will be referred to as (S,R) in the computational study.
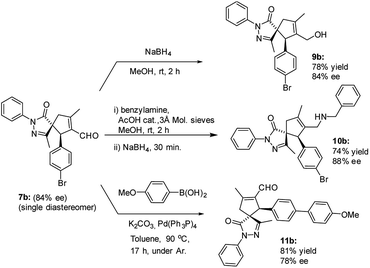
The versatility of the developed reaction has been demonstrated by late-stage derivatization of spiro compound 7b (Scheme 5). Reduction and reductive amination of 7b, used as a single diastereomer, afforded the corresponding alcohol 9b and amine 10b, respectively, in good yields, without losing enantiomeric purity. Similar result was found in Suzuki coupling with 4-methoxy phenyl boronic acid, affording spiro compound 11b, containing a biphenyl motif.
Mechanistic studies
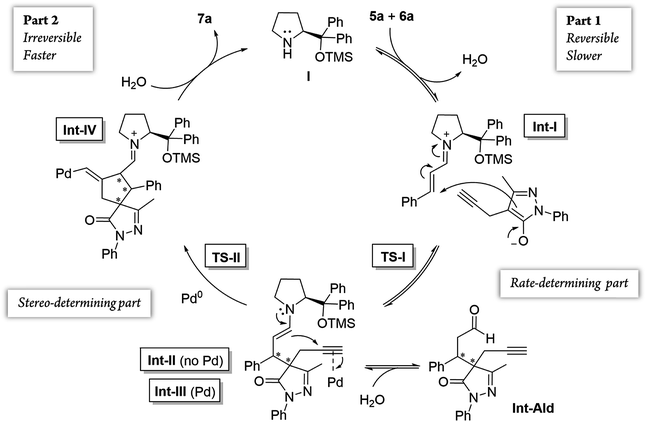
Additionally, we analyzed whether different parts of the reaction were reversible. The reaction was divided in two parts based on the two different C–C bond forming reactions (TS-I and TS-II) that occur during the whole process: part 1, including the Michael addition reaction that produces intermediate Int-Ald; and part 2, including the final Conia-ene reaction that generates product 7a (Scheme 6).
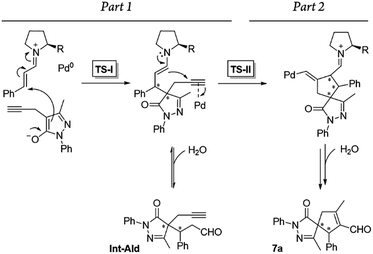 | ||
| Scheme 6 Summary of the reaction steps of this cascade reaction divided into two parts based on the different C–C bond-forming reactions. | ||
To study the reversibility of the different parts of the reaction, several variable temperature NMR experiments were conducted. In the first experiment, the reaction was performed without adding the Pd catalyst, and the Michael reaction (part 1) stopped before the initial reagents were completely consumed. When the reaction stopped (at 62% of cinnamaldehyde conversion, entry 1), we changed the temperature of the reaction mixture and analyzed how temperature variations affected the conversion (percentage) and diastereomeric ratio (dr) of intermediate Int-Ald (Table 1, entries 1–5 and Fig. S3†).
| Entrya | Substrate | T (K) | dr | Conversion (%) |
|---|---|---|---|---|
| a See the ESI for the reaction conditions of the kinetic experiments. b After cooling down the reaction from 328 K to 298 K. c Using pyrrolidine as the catalyst. | ||||
| 1 | Int-Ald | 298 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3.4 3.4 |
62 |
| 2 | Int-Ald | 308 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3.3 3.3 |
55 |
| 3 | Int-Ald | 318 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3.1 3.1 |
46 |
| 4 | Int-Ald | 328 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.9 2.9 |
40 |
| 5b | Int-Ald | 298 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3.4 3.4 |
62 |
| 6c | Int-Ald | 298 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3.4 3.4 |
— |
| 7 | 7a | 298 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6.1 6.1 |
100 |
| 8 | 7a | 308 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6.0 6.0 |
100 |
| 9 | 7a | 318 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6.1 6.1 |
100 |
| 10 | 7a | 328 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6.0 6.0 |
100 |
| 11c | 7a | 298 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.5 1.5 |
— |
The results indicated that changes in temperature affected both conversion and dr. Interestingly, the variations in these parameters were reversible because, when the reaction was cooled down from 328 K to rt, the initial conversion and dr were observed again within 5–10 minutes (Table 1, entry 5). Furthermore, when pyrrolidine was used as the catalyst, the same dr was observed at rt although this catalyst is not chiral (Table 1, entries 1 and 6). These results suggest that this Michael reaction is reversible and that the conversion and dr are primarily determined by the energy of the different diastereomers of Int-Ald (thermodynamically controlled stereoselectivity)41 rather than the energy of the transition states of C–C bond formation (TS-I, kinetically controlled stereoselectivity).
Similarly, we performed variable temperature NMR experiments using reactions containing both catalysts (I and Pd) and, therefore, leading to product 7a (Table 1, entries 7–10). In contrast to the previous experiments, we observed no retro-Conia-ene reaction or variations in the dr of product 7a at any temperature tested (Table 1 and Fig. S4†). Moreover, when pyrrolidine was used as the catalyst at rt, the dr of the product showed a significant change in comparison with the corresponding chiral reaction (Table 1, entries 7 and 11). These two findings suggest that the second part of the overall process is irreversible at the range of temperatures tested, thus indicating a Curtin–Hammett scenario (kinetically controlled stereoselectivity).42
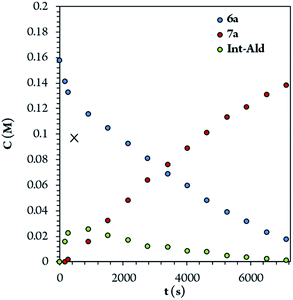
To identify the rate- and enantio-determining steps, we analyzed the concentration profiles of the different reaction components. As previously observed, when the equilibrium of part 1 is reached, cinnamaldehyde (6a) conversion is 62%, and intermediate Int-Ald has an equilibrium concentration of 0.098 M (marked with an “X” next to the Y axis). Fig. 4 shows that intermediate Int-Ald reacts quickly and generates product 7a before reaching the equilibrium concentration. This suggests that the slowest part of the reaction is part 1.
Although the stereocenters of the reactions are formed in part 1, diastereoselectivity changes from the intermediate Int-Ald, formed in part 1, to the final product 7a, formed in part 2. The results from the kinetic studies suggest that (1) part 1 is slower than part 2 and that (2) the diastereoselectivity of the final product is determined in part 2. Thus, although part 1 contains the rate-limiting step (or steps), part 2 contains the stereo-determining step because the reactions of part 1 are reversible whereas at least one reaction of part 2 is irreversible. Accordingly, we designed a catalytic cycle based on all the data gathered in the kinetic studies (Scheme 7).
Computational study43
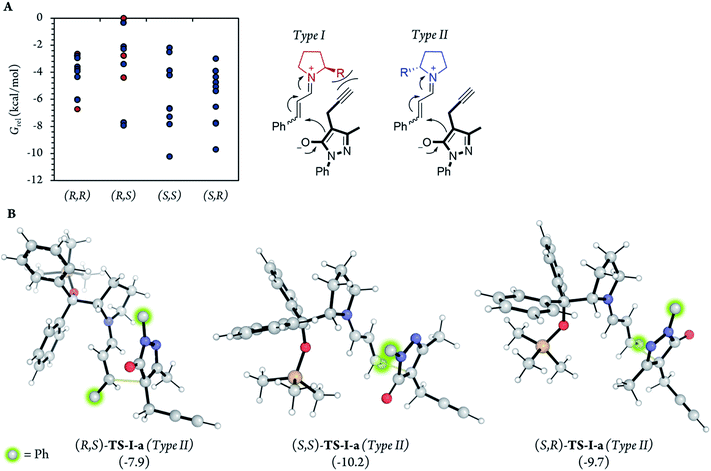
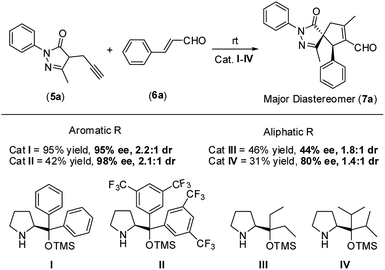
After the initial kinetic experiments, the reaction mechanism was computationally studied. All the calculations were performed at the ωB97X-D/Def2-QZVPP(SMD)(UFgrid)//ωB97X-D/6-311G(d)(SMD)(UF grid) level (using the Def2-TZVP basis set for Pd atoms instead of the 6-311G(d) basis set in geometry optimizations). ωB97X-D is a highly reliable functional in similar reactions with many noncovalent interactions.44–46 Moreover, we tested the validity of this computational approach in generating reliable structures by optimizing, using ωB97X-D/6-311G(d)(SMD)(UF grid), the geometry of a X-ray structure of the condensation product of proline (I) and cinnamaldehyde (6a).47 In this analysis, we found no significant structural differences between the computationally optimized structure and its corresponding crystal structure (see the ESI† for more information). First, the energies of the first C–C bond forming step (TS-I) were calculated (Fig. 5). As explained above, even though the stereocenters are formed in this step (TS-I), this transition state does not determine the final stereoselectivity (S,R) of product 7a. From the previous experiments, three important aspects of part 1 can be remarked: this part proceeds even when Pd is not added to the reaction; there is much more proline (I) in the reaction media than Pd; and the reaction rate does not vary in a great extent when Pd is added. Therefore, we can assume that most of the reaction pathways of part 1 and, therefore, most of the TS-I steps probably proceed without the Pd atom.Although no information on the stereoselectivity of final product 7a can be extracted from this study, a few common trends were observed among the most favorable TS-I steps of all diastereomers. Most importantly, the most stable TS-I steps lead to Michael reactions that occur on the opposite side of the proline substituent (–CPh2OTMS), as previously proposed by other authors (Fig. 5A, Type II attack).48 Furthermore, no significant noncovalent interactions occur between this group of the catalyst and the attacking pyrazolone group (5a). Therefore, the –CPh2OTMS group of the proline sterically hinders the approach of 5a to the side of the proline in which this blocking group is located.47
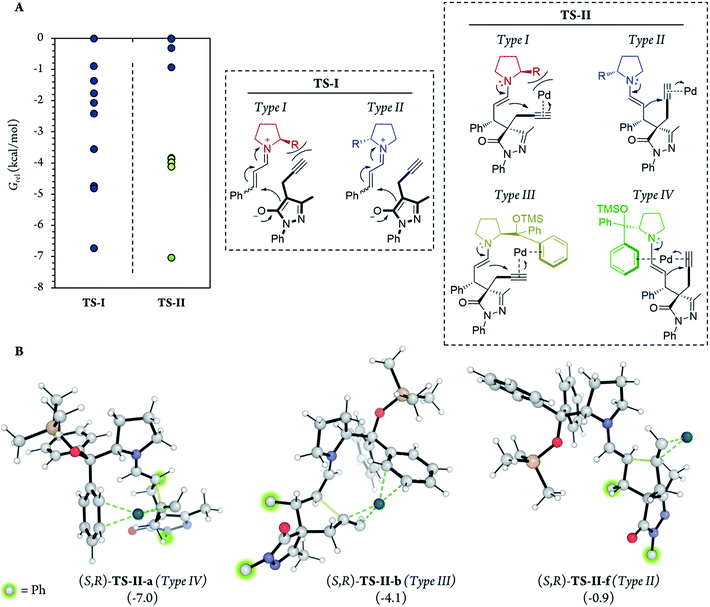
In addition, for further insight into the two C–C bond forming reactions (Fig. 6), we calculated Boltzmann averaged energies of the Int-I, Int-II, Int-III, TS-II and Int-IV systems of the (S,R) diastereomer, the major diastereomer of product 7a observed experimentally. Using Boltzmann averaged energies of the different reaction coordinates is a useful strategy that has been previously applied to study the global mechanism of systems with multiple possible conformations.49
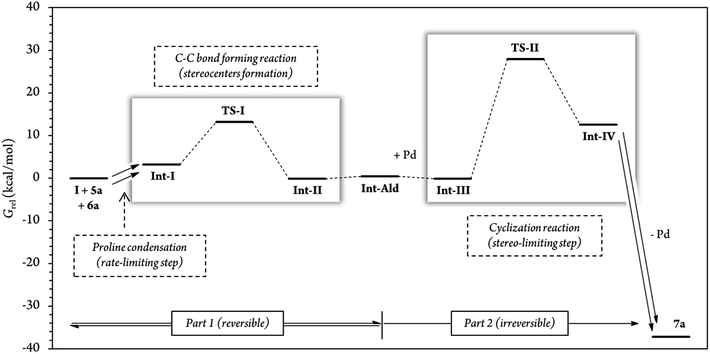 | ||
| Fig. 6 Relative Gibbs free energies along the (S,R) reaction coordinate (for more information see section G of the Calculations of the ESI†). For this energy profile, we used Boltzmann average G of the 10 most stable conformations of each reaction step. A total of 54 different conformations were analyzed for steps Int-I, TS-I and Int-II, and 62 conformations for steps Int-III, TS-II and Int-IV. | ||
The calculations predicted that the G necessary to promote the retro-Michael reaction of part 1 (from aldehyde Int-Ald to TS-I) is much lower than that required for the retro-Conia-ene reaction of part 2 (from final product 7a to TS-II). In fact, the retro-Conia-ene reaction shows an activation G of 65.2 kcal mol−1, which suggests that this retro-cyclization process is extremely slow at rt. This is in line with the initial experimental findings suggesting that part 1 is reversible, whereas part 2 is irreversible.
The experimental results showed that the rate-limiting step was enclosed in part 1 of the mechanism; however, the reaction coordinates from the computational study indicated that step TS-II (cyclization step), from part 2, had a much higher energy than TS-I (Michael addition). This difference suggests that the rate-limiting step is included in the initial iminium formation prior to the Michael reaction which agrees with the study conducted by Moliner, Luk and colleagues. These authors showed a relatively high G activation barrier of approximately 28 kcal mol−1 in the iminium formation between a proline derivative and cinnamaldehyde of a Henry reaction in various solvents.50 Additionally, when we followed the reaction by 1H-NMR experiments, we could not detect condensation products from catalyst (I) and cinnamaldehyde 6a, that is, iminium ion intermediate is neither accumulated nor detected before the Michael addition (Fig. S5 and S6†). This strongly suggests that the subsequent step, the Michael addition reaction, is faster than the initial proline condensation with cinnamaldehyde 6a. Thus, the in situ generated iminium ion intermediate would be rapidly consumed in the next step and consequently, not detected by NMR. Therefore, the NMR results from this study (Fig. 4 and S5, S6†) are in line with the computational energy profile calculated and indicate that the initial prolinol condensation with cinnamaldehyde 6a is the rate-limiting step of the process.
Notably, in the most favorable TS-II step, the CPh2OTMS group of proline (I) acts as a directing group due to a favorable π–Pd interaction (Fig. 7, Type III and IV), whereas this substituent acted as a blocking group in TS-I. This is an interesting example of a reaction in which one of the groups of the catalyst acts as a sterically hindered substituent in one part of the mechanism and as a directing group in the subsequent part. Hence, this finding highlights the importance of computational mechanistic studies, especially in multi-step reactions since researchers often assume that a specific functional group always plays the same role during the whole reaction.
Therefore, based on the computational results of TS-II, the stereoselective-limiting step, if the catalyst does not contain any aromatic group to coordinate with Pd the stereoselectivity obtained should change in a great extent. As expected, modifications of the aromatic ring of the catalyst led to similar enantioselectivities and diastereoselectivity (Scheme 8, (I) and (II)). In contrast, when the aromatic rings are replaced for aliphatic chains, the stereoselectivity dropped considerably (Scheme 8, (III) and (IV)). These experimental results are in line with the computational outcomes and support that the aromatic rings are coordinated to Pd during the cyclization step. On the other hand, the reactivity observed with each catalyst is intrinsic to each structure and directly related only with their structure-reactivity profile shown in part 1 of the mechanism (the rate-limiting step).
Finally, to further validate the method by comparing more experimental and theoretical results, we calculated the G of both syn- and anti-Int-Ald, the compound that controls the selectivity of part 1. Experimentally, we observed 38% cinnamaldehyde and 62% Int-Ald in the equilibrium at rt, which corresponds to a difference in G (ΔG) of −1.7 kcal mol−1 between the G of the initial products and the G of Int-Ald. Computationally, the ΔG between diastereomer Int-Ald and the initial reagents is −0.4 kcal mol−1, which shows a very low margin of error (1.3 kcal mol−1) in comparison with the experimental result (see Calculation of the dr in the Equilibrium of Part 1 section in ESI† for more information).
Conflicts of interest
There are no conflicts to declare.Acknowledgements
R. P. H. and J. V. A.-R. thank Ministerio de Economía, Industria y Competitividad (CTQ2017-88091-P) and Gobierno de Aragón Fondo Social Europeo (E07_17R) for funding their research. All calculations were performed at the Trueno cluster facility, SGAI-CSIC. J. V. A.-R. thanks Dr R. Paton for his help with the script to generate the PyMol style and GoodVibes. S. P. and J. V. thank the Czech Science Foundation (No 18-20645S) for funding the study, Dr Hybelbauerová and Dr Tošner for providing the NMR service, Dr Štícha for providing the MS analysis and Dr Carlos V. Melo for proofreading the manuscript. M. M. and R. R. are grateful for EPSRC Core Capability Funding (EP/K039466/1). R. R. thanks Alessandra Carnero for initial studies.Notes and references
- R. Rios, Chem. Soc. Rev., 2012, 41, 1060 RSC
.
- D. Cheng, Y. Ishihara, B. Tan and C. F. Barbas III, ACS Catal., 2014, 4, 743 CrossRef CAS
.
- Z.-Y. Cao and J. Zhou, Org. Chem. Front., 2015, 2, 849 RSC
.
- L.-J. Yan and Y.-C. Wang, ChemistrySelect, 2016, 1, 6948 CrossRef CAS
.
- S. Kotha, N. R. Panguluri and R. Ali, Eur. J. Org. Chem., 2017, 5316 CrossRef CAS
.
- X. Xie, W. Huang, C. Peng and B. Han, Adv. Synth. Catal., 2018, 360, 194 CrossRef CAS
.
- J. Guang-Mei and F. Shi, Chem. Commun., 2018, 54, 6607 RSC
.
- X. Fang and C.-J. Wang, Org. Biomol. Chem., 2018, 16, 2591 RSC
.
- Y. Zheng, C. M. Tice and S. B. Singh, Bioorg. Med. Chem. Lett., 2014, 24, 3673 CrossRef CAS PubMed
.
- T. L. Pavlovska, R. G. Redkin, V. V. Lipson and D. V. Atamanuk, Mol. Diversity, 2016, 20, 299 CrossRef CAS PubMed
.
- P.-Y. Géant, M. Urban, M. Remeš, I. Císařová and J. Veselý, Eur. J. Org. Chem., 2013, 7979 CrossRef
.
- X. Companyó, A. Zea, A.-N. R. Alba, A. Mazzanti, A. Moyano and R. Rios, Chem. Commun., 2010, 46, 6953 RSC
.
- M. Meazza and R. Rios, Chem.–Eur. J., 2016, 22, 9923 CrossRef CAS PubMed
.
- A. E. Allen and D. W. C. MacMillan, Chem. Sci., 2012, 3, 633 RSC
.
-
(a) M. Meazza and R. Rios, Synthesis, 2016, 48, 960 CrossRef CAS
; (b) S. Afewerki and A. Cordova, Chem. Rev., 2016, 116, 13512 CrossRef CAS PubMed
.
-
G. Varvounis, Pyrazol-3-ones. Part IV: Synthesis and Applications, Adv. Heterocyclic Chem., ed. A. R. Katritzky, Academic Press, 2009, vol. 98, p. 143 Search PubMed
.
- P. Chauhan, S. Mahajan and D. Enders, Chem. Commun., 2015, 51, 12890 RSC
.
- V. Hadi, Y. Koh, T. W. Sanchez, D. Barrios, N. Neamati and K. W. Jumg, Bioorg. Med. Chem. Lett., 2010, 20, 6854 CrossRef CAS PubMed
.
- Y. L. Janin, Bioorg. Med. Chem., 2007, 15, 2479 CrossRef CAS PubMed
.
- M.-T. Gutierrez-Lugo and C. Bewley, J. Med. Chem., 2008, 51, 2606 CrossRef CAS PubMed
.
-
I. R. Matthews, PCT Int. Appl. WO 46679, 2005
.
- A. Kimata, H. Nakagawa, R. Ohyama, T. Fukuuchi, S. Ohta, T. Suzuki and N. Miyata, J. Med. Chem., 2007, 50, 5053 CrossRef CAS PubMed
.
- A. Zea, A.-N. R. Alba, A. Mazzanti, A. Moyano and R. Rios, Org. Biomol. Chem., 2011, 9, 6519 RSC
.
- A. Zea, A.-N. R. Alba, G. Valero, T. Calbet, M. Font-Bardia, A. Moyano and R. Rios, Eur. J. Org. Chem., 2011, 2053 Search PubMed
.
- M. Meazza, M. Kamlar, L. Jašíková, B. Formánek, A. Mazzanti, J. Roithová, J. Veselý and R. Rios, Chem. Sci., 2018, 9, 6368 RSC
.
- For an excellent recent review regarding Conia-ene reactions, see: D. Hack, M. Blumel, P. Chauhan, A. R. Phillips and D. Enders, Chem. Soc. Rev., 2015, 44, 6059 RSC
.
- For an example of cooperative catalysis to develop this reaction, see: T. Yang, A. Ferrali, F. Sladojevich, L. Campbell and D. J. Dixon, J. Am. Chem. Soc., 2009, 131, 9140 CrossRef CAS PubMed
.
-
(a) C. Xu, L. Deiana, S. Afewerki, C. Incerti-Pradillos, O. Cordova, P. Guo, A. Cordova and N. Hedin, Adv. Synth. Catal., 2015, 357, 2150 CrossRef CAS
; (b) L. Deiana, Y. Jiang, C. Palo-Nieto, S. Afewerki, C. A. Incerti-Pradillos, O. Verho, C.-W. Tai, E. V. Johnston and A. Cordova, Angew. Chem., Int. Ed., 2014, 53, 3447 CrossRef CAS PubMed
.
- L. Deiana, L. Ghisu, S. Afewerki, O. Verho, E. V. Johnston, N. Hedin, Z. Bacsik and A. Cordova, Adv. Synth. Catal., 2014, 56, 2485 CrossRef
.
- D. Hack, P. Chauhan, K. Deckers, M. Yusuke, G. Raabe and D. Enders, Chem. Commun., 2015, 51, 2266 RSC
.
- D. Hack, K. Deckers, P. Chauhan, N. Selling, L. Rue-benach, L. Mertens, F. Schoenebeck and D. Enders, Angew. Chem., Int. Ed., 2016, 55, 1797 CrossRef CAS PubMed
.
- M. Meazza, M. E. Light, A. Mazzanti and R. Rios, Chem. Sci., 2016, 7, 984 RSC
.
- M. Meazza, V. Ceban, M. B. Pitak, S. J. Coles and R. Rios, Chem.–Eur. J., 2014, 20, 16853 CrossRef CAS PubMed
.
- V. Ceban, P. Putaj, M. Meazza, M. B. Pitak, S. J. Coles, J. Veselý and R. Rios, Chem. Commun., 2014, 50, 7447 RSC
.
- H. Miyabe and Y. Takemoto, Bull. Chem. Soc. Jpn., 2008, 81, 785 CrossRef CAS
.
- S. J. Connon, Chem. Commun., 2008, 2499 RSC
.
- I. G. Sonsona, E. Marqués-López and R. P. Herrera, Beilstein J. Org. Chem., 2016, 12, 505 CrossRef CAS PubMed
.
- Crystallographic data have been deposited with Cambridge Crystallographic Data Centre: deposit number: CCDC 1859005 and 1859006 for 8b and 8b′, respectively.
- F. Sladojevich, A. L. Fuentes de Arriba, I. Ortín, T. Yang, A. Ferrali, R. S. Paton and D. J. Dixon, Chem.–Eur. J., 2013, 19, 14286 CrossRef CAS PubMed
.
- S. Santoro, L. Deiana, G.-L. Zhao, S. Lin, F. Himo and A. Córdova, ACS Catal., 2014, 4, 4474 CrossRef CAS
and references therein.
- For other mechanistic studies using proline (I), see also: K. S. Halskov, B. S. Donslund, B. M. Paz and K. A. Jørgensen, Acc. Chem. Res., 2016, 49, 974 CrossRef CAS PubMed
.
- Q. Peng, F. Duarte and R. S. Paton, Chem. Soc. Rev., 2016, 45, 6093 RSC
.
-
M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision D.01, Gaussian, Inc., Wallingford CT, 2016 Search PubMed
.
- A. D. Becke, J. Chem. Phys., 1997, 107, 8554 CrossRef CAS
.
- J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615 RSC
.
- L. Goerigk and S. A. Grimme, Phys. Chem. Chem. Phys., 2011, 13, 6670 RSC
.
- U. Grošelj, D. Seebach, D. M. Badine, W. B. Schweizer, A. K. Beck, I. Krossing, P. Klose, Y. Hayashi and T. Uchimaru, Helv. Chim. Acta, 2009, 92, 1225 CrossRef
.
- E. Marqués-López and R. P. Herrera, Curr. Org. Chem., 2011, 15, 2311 CrossRef
and references therein.
- E. Lyngvi, J. W. Bode and F. A. Schoenebeck, Chem. Sci., 2012, 3, 2346 RSC
.
- K. Świderek, A. R. Nödling, Y.-H. Tsai, L. Y. P. Luk and V. Moliner, J. Phys. Chem. A, 2018, 44, 451 CrossRef PubMed
.
Footnotes |
| † Electronic supplementary information (ESI) available. CCDC 1859005 and 1859006. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c8sc05258a |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2019 |