Dynamical and electronic properties of anion-pillared metal–organic frameworks for natural gas separation†
Sabrina
Grigoletto
,
Arthur Gomes
dos Santos
,
Guilherme Ferreira
de Lima
and
Heitor Avelino
De Abreu
 *
*
Departamento de Química, ICEx, Universidade Federal de Minas Gerais, Belo Horizonte, MG 31270-901, Brazil. E-mail: heitorabreu@ufmg.br
First published on 2nd October 2023
Abstract
The increasing demand for natural gas as a clean energy source has emphasized the need for efficient gas separation technologies. Metal–organic frameworks (MOFs) have emerged as a promising class of materials for gas separation, with anion-pillared MOFs (APMOFs) gaining attention for their fine-tuned pore design and shape/size selectivity. In this study, we investigate the dynamical and electronic properties of three APMOFs, SIFSIX-3-Cu, SIFSIX-2-Cu-i, and SIFSIX-2-Cu, for the separation of methane from ethane, ethene, propane, propene, and N using computational simulations. Our simulations employ Grand Canonical Monte Carlo (GCMC) and Molecular Dynamics (MD) techniques combined with Density Functional Theory (DFT) calculations. We find that that all three APMOFs exhibit promising separation capabilities for methane from propane and propene based on both thermodynamics and kinetics parameters. In addition, we use Noncovalent Interaction (NCI) analysis to investigate intermolecular interactions and find that the fluorine atoms in the MOF can polarize gas molecules and establish electrostatic interactions with hydrogen atoms in the molecule. Finally, we show that SIFSIX-2-Cu-i is a potential candidate for separating N2/CH4 due to its interpenetration.
1 Introduction
The drastic climate change and the rising global demand for energy motivate the search for a more sustainable energy matrix.1–3 Natural gas plays an important role in this energetic transition.4 It emits less CO2 than the others fossil fuels, coal and gas, and also has a high energy conversion effiency.2 Natural gas is found in reserves around the world and is mainly composed by methane, light hydrocarbons, such as C and C3 fractions, and other impurities, including N2, CO2, and sulphur compounds.4,5 To avoid pipeline corrosion and enhance energetic potential of this fuel, those fractions are separated through cryogenic distillation.1 This process employs high pressures and under boiling point temperatures resulting in a high cost and power demanding process.6,7 To overcome this, adsorption processes using metal–organic frameworks (MOFs) are pointed out as a promissory alternative to separate methane from other light hydrocarbons8–10 and N2.11,12This novel class of materials stand out due to their composition, consisting of multifunctional organic linkers and inorganic clusters or metallic nodes.13 These components result in outstanding properties such as remarkable tunability, large surface area, and distinctive chemical environments as a result of the presence of electron donors and acceptors within the same cavity.14 In gas separation, the high selectivity of these materials stems from the pore aperture and the diverse functional groups, enabling size exclusion and selective binding, respectively.7,15–17 In this regard, anion-pillared metal–organic frameworks (APMOFs) are particularly noteworthy, as they feature anions, such as SiF62−, CrO72− and MO42− (M = Cr, Mo, W, etc.), in addition to organic spacers and metallic nodes. The inclusion of these anions can enhance the performance in separation processes by contributing to a synergistic effect with the existing functional groups and enable a more fine-tuned design of the pores, leading to greater shape/size selectivity.18 In the work of Zhang and coworkers, the new synthesized GeFSIX-3-M (M = Ni2+, Co2+) showed great potential to separate C3H8/C3H6 and C2H6/C2H4 mixtures. The change of the metal cation led to distinctive pore sizes and a greater selectivity for the Ni2+ material. The narrow cavities, combined with the hydrogen-bonding fluorine atoms from the GeF62− anion, result in large uptakes of propene and ethene while hindering the uptake of propane and ethane, respectively.19
The SIFSIX MOFs comprise a isoreticular series of anion-pilared metal–organic frameworks. These hybrid materials consist of a divalent metal cation, the SiF62− anion, and N-donors organic ligands that determine the pore size. The first SIFSIX MOFs synthesized, namely SIFSIX-1-Cu, SIFSIX-2-Cu, SIFSIX-2-Cu-i, SIFSIX-3-Cu, and SIFSIX-3-Zn, were reported as outstanding for their large uptakes of carbon dioxide and great selectivity for CO2 in CH4 and N2 mixtures.20–22 Moreover, these materials and also SIFSIX-3-Ni, have demonstrated potential for acetylene capture from ethylene.23 More recently, the doubly interpenetrated SIFSIX-2-Cu-i has been identified as a promising candidate for the separation of C3 fractions separation.24,25 The MOFs from the SIFSIX series have been extensively studied for their gas separation properties, and their remarkable selectivity has been attributed to their adsorption sites and pore tunability. In a study by Skarmoutsos et al., it was found that the dynamic behavior of CH4 and CO2 in SIFSIX-2-Cu-i is primarily governed by interactions with the nitrogen and fluorine atoms of the MOF.26 While the organic linker determines the pore size, the fluorine atoms from the anion pillars are responsible for fine-tuning the pore window to narrower apertures. In addition to the interactions for selectivity, the pore aperture and accessible pore volume also play crucial roles in enabling a molecular sieving effect. In another study by Skarmoutsos et al., the superior performance of SIFSIX-2-Cu-i over SIFSIX-2-Cu in separating N2 from SF6 was attributed to the smaller pores of the doubly interpenetrated MOF.27
To complement experimental investigations, computational simulations are an important tool in the study of gas separation process.28–30 The MOF components and the large number of experiments can result in high research costs. However, simulations are an alternative to address this issue. In this scenario, both quantum chemical calculations and classical mechanics can be employed.17 Quantum calculations employing Density Functional Theory (DFT) have high accuracy in predicting adsorption mechanisms and energies. The SIFSIX materials have been largely studied through DFT methods, reveling that the adsorption process often occur due to SiF62− anion potential to polarize the guest molecules.31–35 On the other hand, in classical mechanics calculations, Molecular Dynamics (MD) and Monte Carlo (MC) simulations allow us to obtain properties analogous to the experimental ones, such as self-diffusive coefficients, adsorption isotherms and to analyze molecules trajectory.36–40 The lower computational cost of the classical calculations allows the simulation of thousands of atoms and the evaluation of thousands of MOFs. An example is the high-throughput screening work of Gu and coworkers, when they evaluated almost 1000 anion-pillared MOFs through MC simulations. The results indicated that SIFSIX-2-i-Ni-i, SIFSIX-6-Cd-i, InFFIVE-5-Zn-i, and GaFFIVE-5-Cd-i are promising for separation of C3H6/C3H8, C2H6/CH4, C3H6/C2H4, and C3H8/C2H4 mixtures.41 Each computational simulation approach provides distinct kind of information as results, which can be combined to conduct a more comprehensive and effective analysis of the studied system.
Despite the large amount of reports about SIFSIX materials as efficient for light hydrocarbon separations, to the best of our knowledge, those materials have not been studied to separate the CH4 from the other light hydrocarbon fractions and N2 present in natural gas. Furthermore, studies about the dynamic of those gases in APMOFs are scarce as well as the electronic analysis of the interactions of these MOFs and these small molecules. This kind of study enables to understand the behavior of those gases in these hybrid materials and may lead to a design improvement so they can perform more efficiently. In this work, we have investigated three isoreticular MOFs: SIFSIX-3-Cu, SIFSIX-2-Cu, and SIFSIX-2-Cu-i aiming the separation of light hydrocarbons present in natural gas, methane, ethane, ethene, propane, propene and also N2. The classical methods Molecular Dynamics and Grand Canonical Monte Carlo (GCMC) were used to obtain self-diffusion coefficients, adsorption isotherms, and ideal adsorption solution theory (IAST) selectivity's. Furthermore, DFT calculations combined with Noncovalent interaction analysis (NCI) were performed to obtain structural, thermodynamics and electronic properties of the adsorption of those gases to better understand the molecules dynamics in these materials.
2 Methodology
The MOF structures were collected from crystallographic information files available in the literature.20,21 Both SIFSIX-3-Cu and SIFSIX-2-Cu belong to the P/4mmm space group, whereas the interpenetrated one belongs to the I4/mmm space group. Solvent molecules were removed, and in cases of atom disorder, one position was defined and the structure was fully optimized, both atoms positions and unit cell parameters. The optimization was performed using Density Functional Theory calculations with periodic boundary conditions and plane waves as basis functions, utilizing the QUANTUM ESPRESSO software.42 The Perdew–Burke–Ernzerhof (PBE) parametrization of the generalized gradient approximation (GGA) exchange–correlation functional was employed in combination with ultrasoft pseudopotentials to describe core electrons. The plane waves and electronic density cutoff energy and k-point mesh used were as defined in the work of Guimarães and de Lima.31 The cell parameters and bond lengths for the optimized MOFs can be found in Tables S1 and S2 (ESI†).For classical calculations, the optimized unit cells of SIFSIX-3-Cu were replicated in a 4 × 4 × 4 supercell, while SIFSIX-2-Cu-i and SIFSIX-2-Cu were replicated in a 2 × 2 × 3 supercell. Molecular dynamics and Grand Canonical Monte Carlo simulations were performed using the RASPA software.43 The combination of the Universal Force Field (UFF) and DREIDING force fields was employed to define the Lennard-Jones parameters of the MOFs and can be found in Table S3 (ESI†). This combination has been previously validated for studying gas adsorption processes in SIFSIX series MOFs.26,27,44 Additionally, we obtained the variation of adsorption energy values (Table S5, ESI†) through MC calculations in NVT ensemble, which demonstrated good agreement with the values obtained through DFT calculations discussed in Section 3.4. Atomic charges for the MOF atoms were calculated using the charge equilibration method45 with Ewald summation. The hydrocarbon molecules were modeled using a carbon-hydrogen united-atom scheme, while N2 was modeled as a three-site molecule, with two sites for the atoms and one for the triple bond. LJ parameters for the guest molecules were obtained from the TraPPE force field and are listed in Table S4 (ESI†). The potential energy (U) of the intermolecular interactions was described as sum of van der Waals and electrostatic interactions, considering a Lennard-Jones potential (ULJ) for the dispersion and classical Coulombic potential for electrostatic (UCoul.), as described in eqn (1) and (2):
| U = ULJ + UCoul. | (1) |
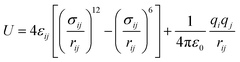 | (2) |
For the calculation of adsorption energies, DFT calculations were performed using the same unit cells that were optimized for classical calculations, except for SIFSIX-2-Cu-i, for which a reduced primitive cell was used to minimize the number of atoms.31 Optimization of the isolated guest molecules and of the adsorbed molecules MOF systems were carried out at the same theory level of the isolated MOFs, previously described. Isolated molecules were simulated in the centre of a cubic box of 15 Å axis. The adsorption energy (ΔEads) was calculated according to eqn (3), where EMOF+molecule, EMOF and Emolecule are the energy of the MOF with the adsorbed molecule, the isolated MOF energy and the isolated molecule energy, respectively:
| ΔEads = EMOF+molecule − (EMOF + Emolecule) | (3) |
3 Results and discussion
3.1 Structural properties of SIFSIX MOFs
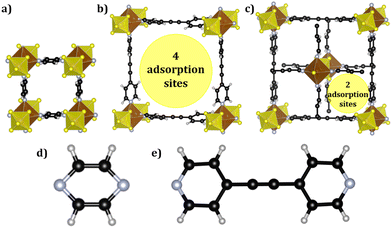
SIFSIX-3-Cu is synthesized using pyrazine as a ligand, resulting in small pores that measure 3.5 Å. On the other hand, SIFSIX-2-Cu-i and SIFSIX-2-Cu are synthesized using 4,4′-dipyridylacetylene as an organic linker. SIFSIX-2-Cu-i is distinguished by its interpenetrated structure, which reduces the pore size from 13.05 Å to 5.2 Å, consequently decreasing the surface area. Moreover, the interpenetration also affects the distribution of adsorption sites. In the case of the catenating MOF, there are only two adsorption sites in each pore, while SIFSIX-2-Cu and SIFSIX-3-Cu have four adsorption sites in each pore, as illustrated in Fig. 1.In the present work, the structure of these materials was characterized by computing the helium void fraction and accessible pore volume using helium as a probe atom. Additionally, the amount of CH4 adsorbed at 300 K and 1 × 105 Pa was calculated. The corresponding data can be found in Table 1.
| MOF | Helium void fraction | Accessible pore volume (cm3 g−1) | Adsorption (mmol g−1) |
|---|---|---|---|
| SIFSIX-3-Cu | 0.32 | 0.199 | 1.561 |
| SIFSIX-2-Cu-i | 0.39 | 0.323 | 3.860 |
| SIFSIX-2-Cu | 0.69 | 1.11 | 0.467 |
The relationship between pore size and both helium void fraction and accessible pore volume is evident, with larger pores resulting in higher values for both properties. SIFSIX-3-Cu and SIFSIX-2-Cu-i have small pores that can accommodate methane with a kinetic diameter of 3.8 Å, leading to interactions with all pore walls and higher uptakes. SIFSIX-2-Cu, however, has excessively large channels relative to the size of methane molecules, potentially resulting in poor host–guest interactions and a lower loading capacity. As a result, SIFSIX-2-Cu-i exhibits a higher methane adsorption capacity than SIFSIX-2-Cu.
3.2 GCMC calculations
Grand Canonical Monte Carlo simulations were performed to predict the adsorption of molecules in the MOFs SIFSIX-3-Cu, SIFSIX-2-Cu-i, and SIFSIX-2-Cu. The simulations consisted of 5.0 × 104 cycles of initialization and 1.0 × 106 cycles of simulation at 300 K. Fig. 2 displays the adsorption isotherms for each MOF, and the fitting parameters for the isotherms can be found in Tables S4–S6 (ESI†). Additionally, GCMC simulations of binary mixtures of methane and the other gases were performed to estimate IAST selectivity at 1.0 × 105 Pa. The calculated selectivities can be found in Fig. S1 (ESI†).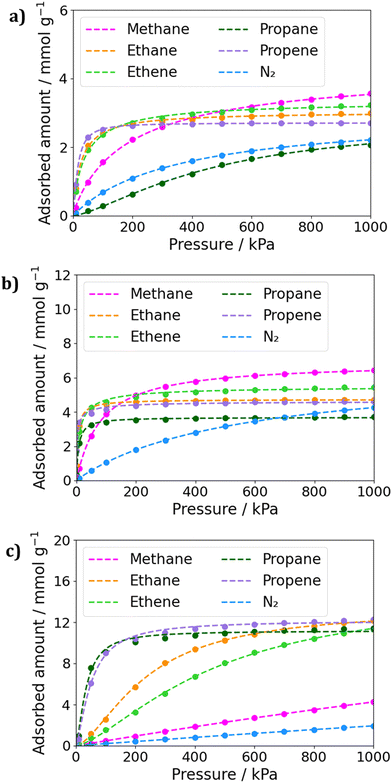 | ||
| Fig. 2 Fitted adsorption isotherms for gases in (a) SIFSIX-3-Cu, (b) SIFSIX-2-Cu-i and (c) SIFSIX-2-Cu. The dots corresponds to the calculated uptakes and the dashed lines to the fitting. | ||
It's interesting to note that SIFSIX-2-Cu shows the most promising behavior for methane separation from other hydrocarbons(Fig. 2c). From low to high loading's, we notice the larges uptakes of C3 fraction. In this MOF, the IAST selectivity of C3H8/CH4 mixtures reached expressive values of 38.5 and 39.0 for low concentrations of CH4 and for equal molar fraction mixtures, respectively. Even at high concentrations of methane, the selectivities for the APMOFs remain significant remarkable, with selectivity values of 29.5 and 17.0 for mixtures containing 0.75 and 0.99 molar fractions of methane, respectively. However, the selectivity tends to decrease as the methane concentration in the mixture increases, as the framework demonstrates better performance in adsorbing propane. For instance, in a 50/50 mixture, the adsorbed amount was 7.5 mmol g−1 for propane and only 0.19 mmol g−1 for methane. A similar trend is observed for propene mixtures in SIFSIX-2-Cu, with high uptakes though with slightly lower selectivity values.
It's worth noting that in SIFSIX-3-Cu and SIFSIX-2-Cu-i, mixtures containing propane exhibited the highest selectivities, with selectivity values around 8.0 for the smaller pore MOF and ranging from 9.3 to 21.0 in the interpenetrated MOF (Fig. S1, ESI†). However, the isotherms reveal that in the smaller pore MOFs, methane has larger uptakes than propane and propene at medium to high pressures, whereas in SIFSIX-2-Cu, the opposite behavior is observed. This can be explained by the kinetic diameters of propane and propene (5.1 Å and 4.7 Å, respectively), which do not fit well into the window aperture size of SIFSIX-3-Cu (3.5 Å) and SIFSIX-2-Cu-i (5.2 Å). On the other hand, methane, with a kinetic diameter of 3.8 Å, fits better in the pore size. The stronger dispersion interactions of the larger molecules in the larger pore sizes in SIFSIX-2-Cu may also contribute to the greater adsorbed amounts of C3 hydrocarbons. However, the interaction between methane and this framework appears to be too weak, which can be attributed to the smaller size of methane and its inability to form strong interactions with the MOF.
When considering smaller pore MOFs, we observe that they exhibit larger uptakes of C2 fractions compared to C3 fractions, with values more similar to methane uptake. In this sense, the selectivity of SIFSIX-3-Cu was low, varying from 3.0 to 4.0 for different molar fractions of ethane or ethene. In contrast, SIFSIX-2-Cu-i exhibited larger selectivity values ranging from 7.7 to 9.8 for ethane mixtures and 5.0 to 6.8 for ethene mixtures. The interpenetrated MOF showed the largest differences in the adsorbed amount when comparing ethane with ethene and propane with propene. This is in concordance with experimental results, as interpenetrated MOFs have already been reported as promisor for propane/propene and ethane/ethene separations.19,24,25 Additionally, this MOF exhibited the largest differences in IAST selectivity values of CH4/C3H8 with CH4/C3H6 and CH4/C2H6 with CH4/C2H4 when comparing different studied frameworks. At SIFSIX-2-Cu, IAST selectivity values for CH4/C2H4 mixtures were around 3.0, and for CH4/C2H6 mixtures were 4.5 to 5.0, as binary mixtures simulations were performed at low pressure. However, based on the isotherms, it appears that this MOF could be more promising for these types of separation at high pressures.
In Fig. 2, it is evident that SIFSIX-2-Cu-i has significant potential for gas separation when comparing the amount of methane and nitrogen adsorbed. This MOF shows a greater difference in adsorption even at low loadings. The calculated selectivity for CH4/N2 mixtures reaches 6.0 in a 0.25/0.75 mixture, and this behavior is maintained, reaching 6.5 in a 0.99/0.01 mixture. In contrast, SIFSIX-3-Cu has an IAST selectivity of approximately 3.0, and SIFSIX-2-Cu exhibits even lower values. In this sense, in the case of SIFSIX-2-Cu-i, the selectivity for this type of mixture is noteworthy, given that in the literature, the MOFs with the highest selectivity are a Ni-MOF reported by Kivi and coworkers,12 with S = 7.0, and the Zr-fum67-mes33-fcu-MOF membrane, which holds the record of 15.5.11
3.3 Molecular dynamics
To elucidate the trajectory of molecules within the solids, two dynamic properties were assessed: the mean square displacement (MSD) and the velocity auto-correlation function (VACF). In a plot of the MSD versus time, which are available in Fig. S2 (ESI†), the linearization of the initial points in the diffusive regime enables the determination of the self-diffusion coefficient (Ds),48 as shown in Table 2. The coefficients were calculated using the Einstein equation (eqn (4)) to derive these results, where t is the total time of diffusion, and r(t) and r(0) represent the positions of the particles n at times t and 0, respectively.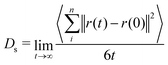 | (4) |
| MOF | Number of molecules | Diffusion × 10−9 (m2 s−1) | |||||
|---|---|---|---|---|---|---|---|
| Methane | Ethane | Ethene | Propane | Propene | N2 | ||
| SIFSIX-3-Cu | 8 | 1.66 | 6.03 | 6.30 | — | — | 1.06 |
| 16 | 2.98 | 2.91 | 5.03 | — | — | 1.80 | |
| 32 | 1.71 | 0.65 | 3.67 | — | — | 1.03 | |
| SIFSIX-2-i-Cu | 8 | 6.17 | 15.8 | 7.70 | 1.10 | 6.27 | 2.85 |
| 16 | 8.77 | 13.8 | 7.68 | 0.88 | 5.30 | 3.05 | |
| 32 | 3.62 | 9.07 | 5.97 | 0.72 | 4.07 | 2.20 | |
| SIFSIX-2-Cu | 8 | 33.9 | 19.4 | 22.5 | 15.2 | 16.9 | 28.2 |
| 16 | 30.3 | 17.5 | 19.8 | 12.8 | 13.8 | 26.2 | |
| 32 | 20.3 | 11.5 | 12.8 | 8.33 | 8.58 | 18.6 | |
To perform, molecular dynamics simulations, we employed the NVT ensemble with 5 × 105 equilibration cycles and 1 × 107 sampling cycles, using a timestep of 0.0005 ps at 298 K. We conducted simulations for loadings of 8, 16, and 32 molecules to assess the effects of loading on the system.
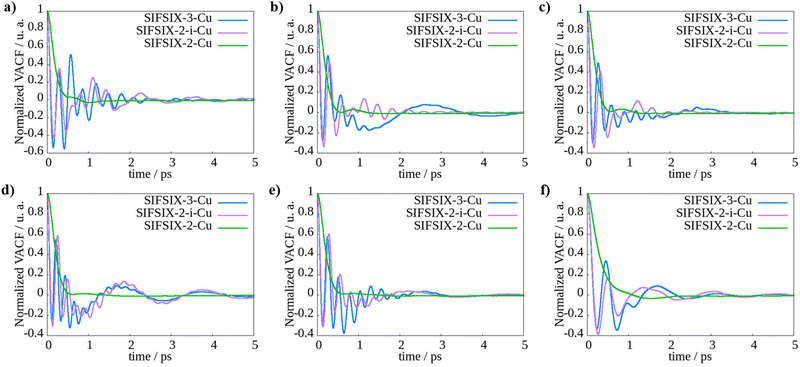
The observations on the diffusion behavior of SIFSIX-2-Cu, SIFSIX-2-Cu-i, and SIFSIX-3-Cu in different pore sizes are consistent with the general trend that larger channels allow for more unhindered molecular movement and faster diffusion rates. The VACF provides insights into the behavior of molecule velocities during diffusion. As shown in Fig. 3 and Fig. S3, S4 (ESI†), negative values in VACF indicate reversal of velocity vectors. In the case of MOFs, where molecules are confined, this change in velocity is primarily attributed to collisions with both other molecules and the framework walls. In addition, we calculated the self-diffusion coefficients by integrating the VACF curves. The results, available in Table S8 (ESI†), exhibit strong agreement with the values obtained through linear regression of the MSD.
The VACF plots support the trend of slower diffusion with smaller pore size and more collisions with the framework atoms, as observed in SIFSIX-2-Cu-i and SIFSIX-3-Cu, compared to SIFSIX-2-Cu with larger pores. In SIFSIX-2-Cu, all the molecules exhibit similar behavior and do not reach negative values, indicating a more uniform and unimpeded diffusion process. However, in SIFSIX-2-Cu-i and SIFSIX-3-Cu, the VACF plots show intense oscillations between positive and negative values, suggesting a higher incidence of collisions between the molecules and the framework atoms, hindering their movement. This can be attributed to the fact that in larger pores, molecules have more space to move without frequent collisions with the framework atoms, leading to smoother diffusion pathways. Furthermore, in the case of the smaller pore MOFs, SIFSIX-3-Cu and SIFSIX-2-Cu-i, we observed an intriguing phenomenon. Despite methane's smaller size, it exhibited slower diffusion compared to ethane and ethene. This behavior can be attributed to the more frequent collisions occurring due to methane's spherical shape, as opposed to the elongated shapes of ethane and ethene.44 The elongated molecules experience hindered limited rotations and translations, while methane undergoes more extensive rotations and translations, leading to increased collisions, particularly with the fluorine atoms from the anions of the MOF. These collisions contribute to the slower diffusion of methane within the smaller pore MOFs.
In summary, the trend of slower diffusion with smaller pore size and more collisions with the framework atoms, as observed in SIFSIX-2-Cu-i and SIFSIX-3-Cu, compared to SIFSIX-2-Cu with larger pores, is consistent with the general understanding of diffusion behavior in porous materials. Larger pore sizes generally allow for more unhindered molecular movement and faster diffusion rates. The insights gained from this study can aid in the rational design of MOFs for efficient gas separation and storage applications.
In SIFSIX-3-Cu, the movement of propane and propene within the solid is limited, while methane diffusion is superior to that of the C3 fraction. The normalized VACF of propane and propene stays mostly below zero, indicating restricted mobility. As discussed at the GCMC section, this can be attributed to the larger kinetic diameters of C3 fraction, which may be incompatible with the window aperture size of the MOF. On the other hand, methane, due to its smaller kinetic diameter, exhibits more favorable diffusion behavior. These observations suggest that the separation of CH4/C3H8 and CH4/C3H6 mixtures could be kinetically feasible through a size exclusion mechanism in this MOF. This suggests that this separation could be both thermodynamically and kinetically promising, as demonstrated by the self-diffusion and isotherms adsorption measurements.
The increase in pore size of SIFSIX-2-Cu-i compared to SIFSIX-3-Cu results in faster diffusion, particularly for propane and ethane, as evident from the analysis of VACF plots. These two MOFs exhibit significant differences in VACF behavior for these molecules; however, the diameter of propane and the cavity aperture still act as limiting factors in the intermediate channel size MOF, resulting in very low self-diffusion for propane, while propene demonstrates diffusion coefficients comparable to methane. This suggests that the 5.2 Å pore size allows for the diffusion of smaller C3 hydrocarbons, but not propane, indicating selective behavior. This observation is consistent with the discussed adsorption differences and also with previous reports on SIFSIX-2-Cu-i and GeFSIX-2-Cu-i, which exhibited selectivity values of 5.0 and 4.0, respectively, in 50/50 binary mixtures at 298 K and 1 bar.19 Therefore, SIFSIX-2-Cu-i shows promise for CH4/C3H8 separation in the context of natural gas valorization. Interestingly, in the case of ethane, its diffusion increases significantly in SIFSIX-2-Cu-i, surpassing values for ethene. This observation may be associated with different diffusion mechanisms of these molecules, which could be related to their distinct shapes and sizes, leading to faster diffusion of ethane.
Compared to the other two MOFs, SIFSIX-2-Cu exhibits higher diffusion rates for N2 and CH4. This can be attributed to their smaller size, which results in weaker intermolecular interactions compared to the larger chained hydrocarbons, allowing them to flow more rapidly through the channels. In contrast, larger hydrocarbons establish more interactions with the framework atoms, resulting in slower diffusions. Based on the self-diffusion data, it is evident that SIFSIX-2-Cu has the potential to selectively separate methane from other hydrocarbons, particularly propane and propene. This is because the diffusion coefficients for methane are higher than those for the C3 fraction. Therefore, SIFSIX-2-Cu shows promise as a potential candidate for the selective separation of methane from other hydrocarbons.
Comparing the dynamical properties of methane with other molecules, we have identified that N2 is the most challenging molecule for methane purification. In SIFSIX-3-Cu and SIFSIX-2-Cu, these molecules have shown similar self-diffusion, with methane being slightly faster. The separation of these molecules is challenging due to their very similar kinetic diameters, with CH4 and N2 having values of 3.8 Å and 3.6 Å, respectively. However, in SIFSIX-2-Cu-i, we observed a greater difference in the diffusion coefficients, suggesting that it is the most suitable MOF for separating this mixture. This could be attributed to the interpenetration of the MOF, as it has fewer adsorption sites in each channel. As widely reported in literature, the fluorine atoms of the SiF62− anions in the MOF can polarize the guest molecules.31–35 Since methane has a higher polarizability than N2, reducing the number of anion sites also decreases the number and strength of interactions between the MOF and methane, leading to increased diffusion. On the other hand, nitrogen, due to its higher electronegativity and lower polarizability, tends to experience repulsion with the fluorine atoms from the anions. Therefore, reducing the number of sites may have less influence on the increase in diffusion rate for nitrogen. This theory is supported by the self-diffusion results, as we observed a larger increase in methane diffusion from SIFSIX-3-Cu to SIFSIX-2-Cu-i compared to N2 in these MOFs. We did not observe the same proportionate increase in N2 diffusion coefficient. The slightly slower diffusion of N2 compared to methane can be attributed to the diffusion mechanism influenced by the kind of interactions established between the molecules and the framework. In the case of N2, it experiences significant repulsion with the fluorine atoms from SiF62− anions, which leads to the avoidance of these atoms during diffusion and establishing more interactions with the organic ligands, leading to a slower diffusion. Furthermore, these molecules displayed an interesting behavior while diffusing in SIFSIX-3-Cu and SIFSIX-2-Cu-i MOFs. As the loading increased from 8 to 16, the diffusion rates also increased, contrary to the results observed for other molecules. This phenomenon could be attributed to the fact that the pore sizes of these MOFs are small and so the diffusing molecules are in closer proximity. This proximity may lead to more favorable interactions and facilitate diffusion at higher loadings.
3.4 DFT calculations
We conducted DFT calculations to investigate the adsorption of gas molecules in SIFSIX-3-Cu, SIFSIX-2-Cu-i, and SIFSIX-2-Cu. Our objective was to gain insight into the diffusion behavior based on the adsorption mechanism and the nature of the interactions. To explore this, we proposed several starting structures in which the molecules were positioned at different locations, including along the organic ligands, closer to the metal, and to the SiF62− anion. The converged structures that yielded the most favorable ΔEads are presented in Fig. S5–S7 (ESI†), and the corresponding calculated ΔEads values are reported in Table 3.| MOF | Molecule | ΔEadsa (kcal mol−1) | X–F distanceb (Å) |
|---|---|---|---|
| a Calculated as eqn (3). b X–F distance corresponds to the distance between fluorine atom from the framework and the nearest hydrogen from the hydrocarbons. In case of N2, the distance from the nearest nitrogen atom. | |||
| SIFSIX-3-Cu | Methane | −8.5 | 2.6 |
| Ethane | −11.4 | 2.6 | |
| Ethene | −12.1 | 2.7 | |
| Propane | −14.4 | 2.5 | |
| Propene | −14.6 | 2.3 | |
| N2 | −7.5 | 3.2 | |
| SIFSIX-2-Cu-i | Methane | −7.3 | 2.4 |
| Ethane | −11.3 | 2.5 | |
| Ethene | −12.1 | 2.4 | |
| Propane | −13.3 | 2.5 | |
| Propene | −14.1 | 2.5 | |
| N2 | −6.3 | 3.1 | |
| SIFSIX-2-Cu | Methane | −4.4 | 2.3 |
| Ethane | −6.2 | 2.4 | |
| Ethene | −6.6 | 2.5 | |
| Propane | −7.9 | 2.6 | |
| Propene | −8.8 | 2.4 | |
| N2 | −3.9 | 3.1 | |
Analyzing the converged structures, we found a common trend in gas molecule the adsorption behavior in MOF frameworks. Specifically, gas molecules tend to interact with fluorine atoms of the anions of the framework, resulting in shorter distances between the hydrogen atoms of the gas molecules and the fluorine atoms from the MOF as shown in Table 3. The largest distances were found between the fluorine atoms and the nitrogen atoms of N2, suggesting that the orientation of the N2 triple bond toward fluorine atoms of the framework may prevent repulsion between the two electronegative atoms. We also observed a slight increase in adsorption energies for alkenes compared to alkanes, attributed to the higher acidity of unsaturated molecules allowing for stronger interactions with the fluorine atoms of the SiF62− anions. NCI results in Fig. S8–S10 (ESI†) showed well-oriented electrostatic interactions between the hydrogen atoms of the hydrocarbons and the fluorine atoms of the anions of the framework. These results further support the significance of the SiF62− anions in the adsorption process, indicating that they polarize adsorbed molecules and electrostatic interactions play a crucial role in stabilizing the adsorbed gas molecules within the MOF structure.
Upon analyzing the structures of gas molecules adsorbed in SIFSIX-3-Cu, we observed a dynamic behavior of the SiF62− anions. In the isolated MOF, the equatorial fluorine atoms of the anions face the center of the pore. However, we found that the anions rotate depending on the size and shape of the adsorbed molecules. For example, the largest rotation (≈45°) was observed for propane, which aligns with the pyrazine ligands and increases the size of the pore window. Methane, N2, and ethene, on the other hand, did not induce any anion rotation. Ethane and propene, being intermediate-sized molecules, induced small rotations of the anion. Notably, propane and propene showed the smallest F–H distances despite the anion rotation. Methane and N2 also exhibited a ring twist, which was attributed to optimizing the host–guest interactions, as reported by Elsaidi and coworkers.34 Interestingly, alkenes adsorption showed smaller rotations of the anions. As the fluorine atoms are more electronegative, the anion rotation can be attributed to repulsive interactions, whereas ring rotation is related to better accommodation of the adsorbed molecules in the framework. This dynamic behaviour of MOF SIFSIX-3-Cu indicates the importance of conducting further studies of adsorption isotherms and diffusion considering those effects.
The NCI colormaps (Fig. S11 and S12, ESI†) showed that propane and propene adsorption in SIFSIX-3-Cu and SIFSIX resulted in repulsion interactions with the largest areas in positive values of the sign(λ2)ρ. This quantitative analysis supports the observation that the diffusion of C3 is hindered due to spatial effects. As expected, in SIFSIX-2-Cu, with larger pore space, we did not identify any anion rotation. However, in SIFSIX-2-Cu-i, we identified a small anion rotation for ethane and N2 adsorption, which may help reduce repulsive interactions.
Overall, the dynamic behavior of SiF62− anions in response to the size and shape of the adsorbed molecules in SIFSIX-3-Cu is a fascinating phenomenon that highlights the importance of considering the flexibility and adaptability of MOFs in gas adsorption studies.
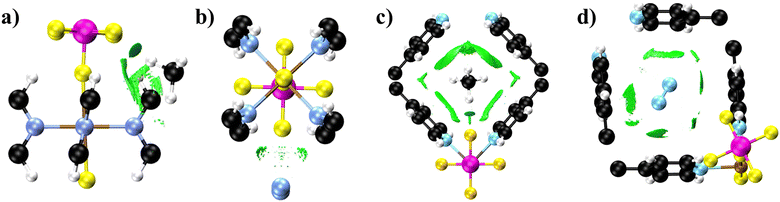
In the case of N2 and methane separation, both molecules show very similar adsorption energies in all three MOFs, with methane being slightly more favorable adsorption. The NCI results of methane adsorption reveal a similar behavior in SIFSIX-3-Cu and SIFSIX-2-Cu-i. In Fig. 4 and at the NCI colormaps in Fig. S8 and S9 (ESI†), we observe that the methane establishing van der Waals interactions with the N-donor ligands and electrostatic interactions between the methane hydrogen atom and the fluorine from the framework anions. However, the N2 interactions with these MOFs reveals distinct patterns, particularly in the NCI colormaps available in Fig. S11 and S12 (ESI†). For N2 adsorption, SIFSIX-3-Cu shows values of sign(λ2)ρ only around zero, indicating the presence of van der Waals interactions with ligand atoms (Fig. 4b), whereas SIFSIX-2-Cu-i displays a broader range of values of sign(λ2)ρ, indicating the presence of electrostatic interactions and steric clashes. The NCI plots in (Fig. 4d) illustrate that these interactions are oriented towards the carbon atoms of the ligand and, in particular, to the hydrogen atoms from the rings. This supports the argument that there is a larger increase in methane diffusion when moving from SIFSIX-3-Cu to SIFSIX-2-Cu-i due to interpenetration. Interpenetration reduces the number of fluorine sites in the pore. methane strongly interacts with fluorine atoms of the SiF62− anions, whereas nitrogen does not. Therefore, reducing the sites can make methane diffuse faster, as F–H interactions decrease in each channel. On the other hand, the reduction of anion sites appears to increase the possibilities of N2 establishing interactions with the ligands, as fewer fluorine atoms would reduce repulsion between nitrogen and fluorine atoms. We can also relate these results to the normalized VACF plots. Methane strongly interacts with the framework atoms, experiencing more collisions during the diffusion path, leading to the presence of more oscillations in the VACF plot compared to N2 behavior during diffusion.
4 Conclusions
We evaluated the dynamical, adsorption, and electronic properties of three anion-pillared metal–organic frameworks, namely SIFSIX-3-Cu, SIFSIX-2-Cu-i, and SIFSIX-2-Cu, for the separation of natural gas. Our analysis showed that the accessible volume of these materials is consistent with their respective pore sizes, following the order SIFSIX-3-Cu < SIFSIX-2-Cu-i < SIFSIX-2-Cu. In terms of adsorption and selectivity, all three MOFs showed high potential for separating CH4/C3 mixtures, with intermediate selectivity values for CH4/C2 mixtures. Additionally, we found that SIFSIX-2-Cu-i was the most promising material for N2/CH4 separation.Through our analysis of the dynamical, electronic, and thermodynamic properties of these materials, we gained better understanding of their adsorption and selectivity behavior. Our results indicate that the diffusion coefficients followed the trend of pore volumes, with values of SIFSIX-2-Cu > SIFSIX-2-Cu-i > SIFSIX-3-Cu. Furthermore, we observed that the self-diffusion of molecules was influenced by both the thermodynamics of adsorption and the compatibility between pore and molecule sizes. In this sense, the separation of methane and C3 fraction is both feasible due to thermodynamics and kinetic effects.
Our electronic characterization of intermolecular interactions revealed that the hydrogen atoms from hydrocarbons interacted with fluorine atoms from the SiF62− anions, which played an important role in the adsorption process. In contrast, N2 interacts with the ligand rings. Consequently, interpenetration, which reduces the number of fluorine sites in the MOF channels, increases the selectivity of SIFSIX-2-Cu-i for CH4/N2 mixtures.
Author contributions
Sabrina Grigoletto: investigation, methodology, visualization, writing – original draft, writing – review & editing. Arthur Gomes dos Santos: investigation, methodology, visualization. Guilherme Ferreira de Lima: conceptualization, data curation, funding acquisition, project administration, resources, supervision, writing – review & editing. Heitor Avelino De Abreu: conceptualization, data curation, funding acquisition, project administration, resources, supervision, writing – review & editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The following institutions are gratefully acknowledged by the financial support: Coordenação de Aperfeiçoamento de Pessoal de Nível Superior (CAPES), Fundação de Amparo à Pesquisa do Estado de Minas Gerais (FAPEMIG) grants APQ-00519-21 and RED-00102-16, Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq) grants 311402/2021-6, and the Brazilian National Institute of Science and Technology (INCT-Acqua).Notes and references
-
B. Shimekit and H. Mukhtar, in Advances in Natural Gas Technology, ed. H. A. Al-Megren, IntechOpen, Rijeka, 2012, ch. 9 Search PubMed
.
- M. J. Economides and D. A. Wood, J. Nat. Gas Sci. Eng., 2009, 1, 1–13 CrossRef
.
- bp, bp Statistical Review of World Energy, bp technical report, 2022.
- S. Faramawy, T. Zaki and A.-E. Sakr, J. Nat. Gas Sci. Eng., 2016, 34, 34–54 CrossRef CAS
.
- D. Saha, H. A. Grappe, A. Chakraborty and G. Orkoulas, Chem. Rev., 2016, 116, 11436–11499 CrossRef CAS PubMed
.
- D. S. Sholl and R. P. Lively, Nature, 2016, 532, 435–437 CrossRef PubMed
.
- R. Sahoo and M. C. Das, Coord. Chem. Rev., 2021, 442, 213998 CrossRef CAS
.
- C. Altintas and S. Keskin, RSC Adv., 2017, 7, 52283–52295 RSC
.
- L.-Z. Qin, X.-H. Xiong, S.-H. Wang, L. Zhang, L.-L. Meng, L. Yan, Y.-N. Fan, T.-A. Yan, D.-H. Liu, Z.-W. Wei and C.-Y. Su, ACS Appl. Mater. Interfaces, 2022, 14, 45444–45450 CrossRef CAS PubMed
.
- A. A. Lysova, K. A. Kovalenko, A. S. Nizovtsev, D. N. Dybtsev and V. P. Fedin, Chem. Eng. J., 2023, 453, 139642 CrossRef CAS
.
- S. Zhou, O. Shekhah, A. Ramírez, P. Lyu, E. Abou-Hamad, J. Jia, J. Li, P. M. Bhatt, Z. Huang, H. Jiang, T. Jin, G. Maurin, J. Gascon and M. Eddaoudi, Nature, 2022, 606, 706–712 CrossRef CAS PubMed
.
- C. E. Kivi, B. S. Gelfand, H. Dureckova, H. T. K. Ho, C. Ma, G. K. H. Shimizu, T. K. Woo and D. Song, Chem. Commun., 2018, 54, 14104–14107 RSC
.
- J. L. Rowsell and O. M. Yaghi, Microporous Mesoporous Mater., 2004, 73, 3–14 CrossRef CAS
.
- H. Furukawa, K. E. Cordova, M. OKeeffe and O. M. Yaghi, Science, 2013, 341, 1230444 CrossRef PubMed
.
- Z. Bao, G. Chang, H. Xing, R. Krishna, Q. Ren and B. Chen, Energy Environ. Sci., 2016, 9, 3612–3641 RSC
.
- Y. He, W. Zhou, R. Krishna and B. Chen, Chem. Commun., 2012, 48, 11813–11831 RSC
.
- Y. Wu and B. M. Weckhuysen, Angew. Chem., Int. Ed., 2021, 60, 18930–18949 CrossRef CAS PubMed
.
- X. Li, H. Bian, W. Huang, B. Yan, X. Wang and B. Zhu, Coord. Chem. Rev., 2022, 470, 214714 CrossRef CAS
.
- Z. Zhang, Q. Ding, X. Cui, X.-M. Jiang and H. Xing, ACS Appl. Mater. Interfaces, 2020, 12, 40229–40235 CrossRef CAS PubMed
.
- S. D. Burd, S. Ma, J. A. Perman, B. J. Sikora, R. Q. Snurr, P. K. T. J. Tian, L. Wojtas and M. J. Zaworotko, J. Am. Chem. Soc., 2012, 134, 3663–3666 CrossRef CAS PubMed
.
- P. Nugent, Y. Belmabkhout, S. D. Burd, A. J. Cairns, R. Luebke, K. Forrest, T. Phan, S. Ma, B. Space, L. Wojtas, M. Eddaoudi and M. J. Zaworotko, Nature, 2013, 495, 80–84 CrossRef CAS PubMed
.
- O. Shekhah, Y. Belmabkhout, Z. Chen, A. C. Vincent Guillerm, K. Adil and M. Eddaoudi, Nat. Commun., 2014, 5, 4228 CrossRef CAS PubMed
.
- X. Cui, K. Chen, H. Xing, Q. Yang, R. Krishna, Z. Bao, H. Wu, W. Zhou, X. Dong and Y. Han,
et al.
, Science, 2016, 353, 141–144 CrossRef CAS PubMed
.
- L. Yang, X. Cui, Z. Zhang, Q. Yang, Z. Bao, Q. Ren and H. Xing, Angew. Chem., 2018, 130, 13329–13333 CrossRef
.
- X. Wang, P. Zhang, Z. Zhang, L. Yang, Q. Ding, X. Cui, J. Wang and H. Xing, Ind. Eng. Chem. Res., 2020, 59, 3531–3537 CrossRef CAS
.
- I. Skarmoutsos, Y. Belmabkhout, K. Adil, M. Eddaoudi and G. Maurin, J. Phys. Chem. C, 2017, 121, 27462–27472 CrossRef CAS
.
- I. Skarmoutsos, M. Eddaoudi and G. Maurin, Microporous Mesoporous Mater., 2019, 281, 44–49 CrossRef CAS
.
- S. Rives, H. Jobic, F. Ragon, T. Devic, C. Serre, G. Férey, J. Ollivier and G. Maurin, Microporous Mesoporous Mater., 2012, 164, 259–265 CrossRef CAS
.
- Y. Zhang, B. E. Lucier, M. Fischer, Z. Gan, P. D. Boyle, B. Desveaux and Y. Huang, Chem. – Eur. J., 2018, 24, 7866–7881 CrossRef CAS PubMed
.
- D.-Y. Kang, J. S. Lee and L.-C. Lin, Langmuir, 2022, 38, 9441–9453 CrossRef CAS PubMed
.
- W. G. Guimarães and G. F. de Lima, J. Mol. Model., 2020, 26, 1–11 CrossRef PubMed
.
- K. A. Forrest, T. Pham and B. Space, CrystEngComm, 2017, 19, 3338–3347 RSC
.
- K. A. Forrest, T. Pham, S. K. Elsaidi, M. H. Mohamed, P. K. Thallapally, M. J. Zaworotko and B. Space, Cryst. Growth Des., 2019, 19, 3732–3743 CrossRef CAS
.
- S. K. Elsaidi, M. H. Mohamed, C. M. Simon, E. Braun, T. Pham, K. A. Forrest, W. Xu, D. Banerjee, B. Space, M. J. Zaworotko and P. K. Thallapally, Chem. Sci., 2017, 8, 2373–2380 RSC
.
- A. Ziaee, D. Chovan, M. Lusi, J. J. I. Perry, M. J. Zaworotko and S. A. M. Tofail, Cryst. Growth Des., 2016, 16, 3890–3897 CrossRef CAS
.
- S. Grubišić, R. Dahmani, I. Djordjević, M. Sentić and M. Hochlaf, Phys. Chem. Chem. Phys., 2023, 25, 954–965 RSC
.
- A. Luna-Triguero, J. M. Vicent-Luna, P. Gómez-Álvarez and S. Calero, J. Phys. Chem. C, 2017, 121, 3126–3132 CrossRef CAS
.
- A. Luna-Triguero, J. M. Vicent-Luna, R. M. Madero-Castro, P. Gómez-Álvarez and S. Calero, ACS Appl. Mater. Interfaces, 2019, 11, 31499–31507 CrossRef CAS PubMed
.
- N. Farzi, N. Salehi and A. Mahboubi, Microporous Mesoporous Mater., 2017, 248, 246–255 CrossRef CAS
.
- A. Liu, X. Peng, Q. Jin, S. K. Jain, J. M. Vicent-Luna, S. Calero and D. Zhao, ACS Appl. Mater. Interfaces, 2019, 11, 4686–4700 CrossRef CAS PubMed
.
- C. Gu, J. Liu and D. S. Sholl, J. Phys. Chem. C, 2021, 125, 20076–20086 CrossRef CAS
.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. D. Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef PubMed
.
- D. Dubbeldam, S. Calero, D. E. Ellis and R. Q. Snurr, Mol. Simul., 2016, 42, 81–101 CrossRef CAS
.
- I. Skarmoutsos, M. Eddaoudi and G. Maurin, J. Phys. Chem. Lett., 2018, 9, 3014–3020 CrossRef CAS PubMed
.
- C. E. Wilmer, K. C. Kim and R. Q. Snurr, J. Phys. Chem. Lett., 2012, 3, 2506–2511 CrossRef CAS PubMed
.
- A. O. de-la Roza, M. Blanco, A. M. Pendás and V. Luaña, Comput. Phys. Commun., 2009, 180, 157–166 CrossRef
.
- A. O. de-la Roza, E. R. Johnson and V. Luaña, Comput. Phys. Commun., 2014, 185, 1007–1018 CrossRef
.
-
G. Rothenberg, Handbook of Porous Materials, World scientific, 2021 Search PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp02368k |
| This journal is © the Owner Societies 2023 |