Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Triplet states in the reaction center of Photosystem II†
Sinjini
Bhattacharjee
 ,
Frank
Neese
,
Frank
Neese
 and
Dimitrios A.
Pantazis
and
Dimitrios A.
Pantazis
 *
*
Max-Planck-Institut für Kohlenforschung, Kaiser-Wilhelm-Platz 1, 45470 Mülheim an der Ruhr, Germany. E-mail: dimitrios.pantazis@kofo.mpg.de
First published on 17th August 2023
Abstract
In oxygenic photosynthesis sunlight is harvested and funneled as excitation energy into the reaction center (RC) of Photosystem II (PSII), the site of primary charge separation that initiates the photosynthetic electron transfer chain. The chlorophyll ChlD1 pigment of the RC is the primary electron donor, forming a charge-separated radical pair with the vicinal pheophytin PheoD1 (ChlD1+PheoD1−). To avert charge recombination, the electron is further transferred to plastoquinone QA, whereas the hole relaxes to a central pair of chlorophylls (PD1PD2), subsequently driving water oxidation. Spin-triplet states can form within the RC when forward electron transfer is inhibited or back reactions are favored. This can lead to formation of singlet dioxygen, with potential deleterious effects. Here we investigate the nature and properties of triplet states within the PSII RC using a multiscale quantum-mechanics/molecular-mechanics (QM/MM) approach. The low-energy spectrum of excited singlet and triplet states, of both local and charge-transfer nature, is compared using range-separated time-dependent density functional theory (TD-DFT). We further compute electron paramagnetic resonance properties (zero-field splitting parameters and hyperfine coupling constants) of relaxed triplet states and compare them with available experimental data. Moreover, the electrostatic modulation of excited state energetics and redox properties of RC pigments by the semiquinone QA− is described. The results provide a detailed electronic-level understanding of triplet states within the PSII RC and form a refined basis for discussing primary and secondary electron transfer, charge recombination pathways, and possible photoprotection mechanisms in PSII.
1. Introduction
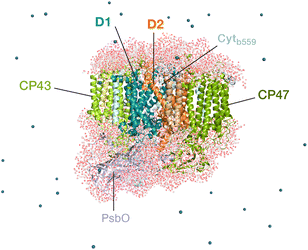
Oxygenic photosynthesis involves a series of light-dependent electron transfer reactions which are carried out by membrane-bound pigment–protein complexes.1 The reactions at these energy-converting enzymes generate a transmembrane electrochemical potential gradient to drive the synthesis of ATP. The first enzyme in the photosynthetic chain is Photosystem II (PSII), a dimeric multi-subunit protein–pigment complex responsible for the four-electron oxidation of water into molecular oxygen and two-electron reduction of a mobile plastoquinone acceptor (QB).2–7 The light-driven charge separation and the initial electron transfer events occur at the reaction center (RC) of PSII. This comprises four chlorophyll molecules, namely the PD1 and PD2 central pair flanked by the “accessory” chlorophylls ChlD1 and ChlD2, and two pheophytin molecules, PheoD1 and PheoD2. The RC pigments are arranged pseudo-symmetrically along the D1 and D2 heterodimeric subunits of PSII (Fig. 1) that are highly conserved across photosynthetic organisms.8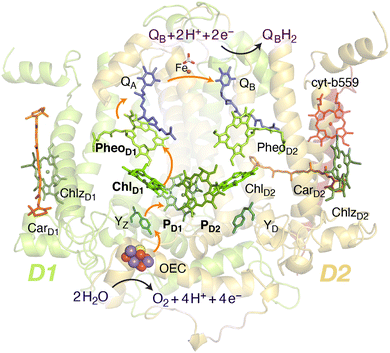 | ||
| Fig. 1 Reaction center pigments and other important cofactors, with schematic representation of electron flow along the active branch of Photosystem II. | ||
The excitation energy transfer from external light harvesting complexes and the internal antennae CP43 and CP47 initiates the electron transfer process along the D1 branch of the RC (Fig. 1). Charge-transfer excited states of mostly ChlD1δ+PheoD1δ− character are created, leading to formation of the primary charge separated radical pair ChlD1+PheoD1− (ref. 6 and 9–18) and the cationic charge is then distributed over the PD1PD2 pair (often referred to as P680+).10,19–21 This highly oxidizing radical cation (estimated Em of 1.1–1.3 V) is the strongest known oxidant in biology and drives water oxidation at the oxygen-evolving complex.3,22,23 Under normal conditions, charge recombination of the initially formed radical pairs [ChlD1+PheoD1−]4,11,16 (or possibly [PD1+PheoD1−] in some reaction centers)24 is prevented by forward electron transfer from PheoD1 to the primary plastoquinone acceptor QA within a few hundred ps. This leads to formation of the “closed RC” state with a reduced QA.5,25–29 If the plastoquinone pool remains reduced, electron transfer from QA− to the mobile acceptor QB is inhibited, thus preventing further electron transfer from PheoD1 to QA. This can facilitate charge recombination30–35 within the RC and enable formation of chlorophyll triplet states prior to relaxation to the ground state.14,30–33,36–46 Triplet states are detrimental as they can readily generate chemically active singlet oxygen (1O2) that reacts with the protein causing oxidative stress.47,48 The D1 protein embeds most crucial redox cofactors in PSII, including the oxygen-evolving complex (OEC), and thus photodamage can lead to a disruption of the entire photosynthetic machinery. Correlation has been reported between 1O2 production and the extent of photodamage of the D1 protein on exposure to excess light.49–51 All photosynthetic organisms therefore naturally adopt intrinsic strategies of photoprotection by efficiently quenching chlorophyll triplet states either by redox active cofactors (e.g. QA− in the RC)29,32,52 or carotenoids53–55 (e.g. in the bacterial RC or antenna complexes), but the exact molecular mechanisms of these phenomena are not fully understood. Therefore, it is useful to have a reliable description of the nature and localization of triplet states, as an essential basis for understanding photoprotection mechanisms in PSII.
Chlorophyll triplet states, in addition to being highly reactive, serve as chemical probes to investigate primary electron transfer pathways and characterize the chemical environment of photosynthetic reaction center pigments.44 Electron paramagnetic resonance (EPR) and electron–nuclear double resonance (ENDOR) spectroscopies29,37,39,44,56–69 and other spectroscopic approaches including Fourier-transform infrared (FTIR) and optically detected magnetic resonance (ODMR)36,38,39,51,54,70–76 suggest that the “primary donor” triplet is located on an individual accessory chlorophyll (ChlD1 or ChlD2) at cryogenic temperatures.30,56–58,61,77 It has also been suggested that the triplet is partially shared with other chlorophylls at the RC at higher temperatures, but this has not been well characterized.33,62 It is important to note that many studies report varying observations depending on the type of preparation and conditions used, as in the case of D1D2Cytb559 samples60,62,78,79 or samples with chemically reduced quinone (QA−/QA2−).25,29,46,52
Various chemical and photo-physical properties of pigments such as site energies and redox potentials10,22,43,80,81 are directly or indirectly controlled by the surrounding protein matrix,82–84 as already established in the case of charge transfer states involving the RC pigments.12,24 From a methodological perspective, this establishes the need for multilayer approaches to provide an accurate quantitative description of how inter-pigment and pigment–protein interactions determine spectroscopic properties. Previous excited state calculations based on time-dependent density functional theory (TD-DFT) and quantum-mechanics/molecular-mechanics (QM/MM) simulations on pigment assemblies have shown that the lowest singlet excitations in the RC are characterized by a mixture of excitonic and [ChlD1δ+PheoD1δ−] or [PD1δ+PheoD1δ−] charge-transfer (CT) character.12,24,85,86 However, a coherent description of excited and ground triplet states is lacking. The excitation profiles of all RC pigments in their triplet states are important elements for establishing possible routes of triplet delocalization87,88 and triplet–triplet energy transfer (T-TET) onto other pigments within the PSII core complex.89
In this work, we use a membrane-bound model of an entire PSII monomer as the basis for multiscale quantum-mechanics/molecular-mechanics (QM/MM) modelling to study singlet–triplet excitations as well as relaxed triplet states within the RC pigments. The quantum chemical descriptions of both local and charge-transfer excitations in oligomeric assemblies are obtained by range-separated time-dependent density functional theory (TD-DFT). We employ our QM/MM approach to also compute EPR properties of all triplet states localized on each chromophore, and compare the results with available spectroscopic data.37,39,65 Finally, we study how charge transfer pathways and triplet formation at the RC depend on the redox state of the primary quinone (QA) acceptor and of the OEC.61,90 Overall, the present work contributes to a more complete understanding of the nature of triplet states within the RC of PSII, of their electronic and spectroscopic properties, and of the electrostatic control exerted by the PSII protein matrix.
2. Methodology
2.1. QM/MM setup
The classical membrane-embedded MM setup was built using the 1.9 Å resolution crystal structure of PSII from the thermophilic cyanobacterium T. vulcanus (PDB ID: 3WU2).8 In the current study we chose a snapshot that resembles the X-ray structure configuration8,12 from an initial MD equilibration in the work by Sirohiwal et al.24 For the QM/MM calculations we retained the complete PSII monomer and all waters around the protein (7 Å bulk-region, in total 8000 water molecules including internal cavity waters). The final atom count for this QM/MM setup was 76![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 056 atoms (Fig. 2). The oxidation states of the Mn ions of the OEC were assumed to correspond to the dark-stable S1 state of its catalytic cycle. In order to model the “closed” reaction center in the S2QA− state, the AMBER parameter file was modified with the electrostatic charges for both cofactors (QA− and OEC) based on the standard MK-RESP (Merz–Kollman Restrained Electrostatic Potential) methodology.91–93 For the semiquinone, geometry optimization was first performed at the B3LYP/def2-SVP level94,95 and then single-point calculations were performed at the HF/6-31G* level of theory in ORCA.96 In order to compute the charges on the OEC (Mn4CaO5) a small cluster model was taken including the amino acid side chains directly coordinated to each metal site. The OEC was then modelled in the S2 state of the Kok–Joliot cycle, i.e. with formal oxidation states Mn1(III)–Mn2(IV)–Mn3(IV)–Mn4(IV); associated ligands are Asp170, Glu354, Ala344, Asp342, Glu189, His332, Glu333, and four H2O molecules.2,3 The corresponding RESP charges are derived from B3LYP/6-31G*.94,95 The RESP fitting of the charges was performed using Multiwfn.97 The charge on backbone atoms of the coordinated residues on the OEC is carefully restrained on the link atoms, according to the standard residue charges of the original AMBER force field.93
056 atoms (Fig. 2). The oxidation states of the Mn ions of the OEC were assumed to correspond to the dark-stable S1 state of its catalytic cycle. In order to model the “closed” reaction center in the S2QA− state, the AMBER parameter file was modified with the electrostatic charges for both cofactors (QA− and OEC) based on the standard MK-RESP (Merz–Kollman Restrained Electrostatic Potential) methodology.91–93 For the semiquinone, geometry optimization was first performed at the B3LYP/def2-SVP level94,95 and then single-point calculations were performed at the HF/6-31G* level of theory in ORCA.96 In order to compute the charges on the OEC (Mn4CaO5) a small cluster model was taken including the amino acid side chains directly coordinated to each metal site. The OEC was then modelled in the S2 state of the Kok–Joliot cycle, i.e. with formal oxidation states Mn1(III)–Mn2(IV)–Mn3(IV)–Mn4(IV); associated ligands are Asp170, Glu354, Ala344, Asp342, Glu189, His332, Glu333, and four H2O molecules.2,3 The corresponding RESP charges are derived from B3LYP/6-31G*.94,95 The RESP fitting of the charges was performed using Multiwfn.97 The charge on backbone atoms of the coordinated residues on the OEC is carefully restrained on the link atoms, according to the standard residue charges of the original AMBER force field.93
All QM/MM calculations were performed using the multiscale module of the ORCA 5.0 suite, which incorporates the electrostatic embedding technique.96,98,99 The hydrogen link atom approach was employed to cut through C–C covalent bonds and the charge-shift (CS) scheme was used to avoid over polarization of the QM region. Along with the chlorin macrocycles, the axially coordinated ligands to Mg2+ were also treated at the QM level. For ChlD1 and ChlD2, the water molecule hydrogen bonded to the axially ligated water and ester group attached to the 132-carbon position on ring E is also included in the QM region. Similarly, the axial histidines (His198 and His197) in case of PD1 and PD2 were also treated at the QM level. The phytyl chains were included in the QM region up to C17 (truncated as a methyl group) and the rest of the chain was treated in the MM region.
2.2. Geometry optimization
For geometry optimizations in the QM/MM framework, the complete system was further subdivided into two parts: active and static. The active region consists of atoms within the QM and MM regions that are flexible during the optimization, whereas the remaining MM atoms are fixed and only contribute to the electrostatics. The original pair-optimized QM geometries (i.e., ChlD1–PheoD1, ChlD2–PheoD2 and PD1–PD2), for the ground state singlet states (S = 0) were used as starting structures.24 The ground triplet states (S = 1) of all RC pigments were optimized individually except for the central pair (PD1PD2), which is considered as a single dimeric unit. For individual pigments, complete amino acid residues and waters within 10 Å around the QM region were included in the active region, whereas a larger active region was chosen around the PD1PD2 pair (∼10 Å around each of PD1 and PD2). The Perdew–Burke–Ernzerhof (PBE) functional100 was used to optimize the QM regions using the def2-TZVP basis set,101 along with D3(BJ) dispersion corrections.102,103 Dense DFT integration grids (DefGrid2 in ORCA convention) were used in all optimizations. The resolution of identity approximation (RI) was used to speed up the calculation of Coulomb integrals with the corresponding auxiliary basis set (def2/J).104,105 All QM/MM geometry optimizations were performed using the L-BFGS optimizer.1062.3. Excitation energies
Vertical triplet excitation energies were computed on the pair-optimized ground state singlet geometries (i.e. spin-restricted DFT reference), employing the Tamm-Dancoff approximation (TDA) to TD-DFT. It has been shown that the “triplet instability” problem of spuriously low-lying excitations for complex systems can be overcome to a large extent by using the TDA approach.107 In this work, we also considered the effect of this approximation on the singlet excitation energies of photosynthetic pigments, which remains a challenging problem for approximate TD-DFT.108,109 All TD-DFT calculations were performed using the range-separated ωB97X-D3(BJ) functional (modified version of ωB97X-V110 with D3BJ correction) along with def2-TZVP basis sets. The long-range-corrected functional has a fixed exact (Hartree–Fock) exchange of 16.7% (short-range) that increases to 100% at long range with a range-separation parameter of 0.30 a0−1. The performance of this functional towards the efficient treatment of excited states and electrochromic shifts using TD-DFT has already been confirmed in the past via direct comparisons with similarity transformed equation of motion coupled cluster theory (STEOM-CCSD).84,111 The RIJCOSX approximation104 was used to speed up the calculations and the corresponding auxiliary basis sets were used throughout. VeryTightSCF convergence criteria were applied throughout, along with dense integration grids (DefGrid2). The first 10 singlet (S = 0) and triplet (S = 1) excited states were computed for individual RC pigments as well as for oligomeric assemblies. This approach effectively describes the entire Q-band range and all low-lying excited states with local excitation (LE), charge-transfer (CT), and mixed LE/CT characters. The excited states for isolated pigments were computed using gas phase TD-DFT whereas in the case of the reaction center the electrostatic effects of the protein environment on the excited states were included through MM point charges of the entire PSII monomer. We further obtained the low-energy triplet (S = 1) excited states for pigment assemblies along the D1 [PD1PD2ChlD1PheoD1] and D2 [PD1PD2ChlD2PheoD2] branches (see Fig. 1). It is noted that specific pigment pairs at the RC are structurally uncoupled and that the geometries obtained by directly optimizing a tetramer are essentially identical compared to the combination of pairwise-optimized structures.24 The inclusion of tetramers in QM optimizations do not obviously alter the excited state energetics and provide the same qualitative picture of low-lying CT states and local excitons as the pair-optimized structures.2.4. EPR parameters
The isotropic hyperfine coupling constants of all the hydrogen atoms are computed on the localized triplet states of individual pigments incorporating the effect of the protein via the QM/MM approach. All EPR parameters were computed within the framework of a DFT-based coupled-perturbed self-consistent field approach (CP-SCF)112 on the QM/MM optimized geometries of the triplet (S = 1) states with separate QM regions defined for each RC chromophore. For the hyperfine coupling constants and g-tensors, we used the TPSSh functional113 with Barone's EPR-II basis set114 on hydrogen atoms and def2-TZVP on the remaining atoms in the QM region. The RIJCOSX approximation and VeryTightSCF convergence criteria were used along with the highest DefGrid3 integration grids.104 The triplet g-tensors were computed in conjunction with the spin–orbit mean-field (SOMF) approximation for the spin–orbit coupling.112,115 The spin–spin contribution to the zero field splitting (ZFS) tensors116 (D and E) were computed using the restricted open shell Kohn–Sham (ROKS) framework, as this approach was shown to yield better agreement with experimental results than unrestricted (UKS) for triplet states of several organic molecules involving π electrons.1173. Results and discussion
3.1. Singlet–triplet excitations in individual pigments
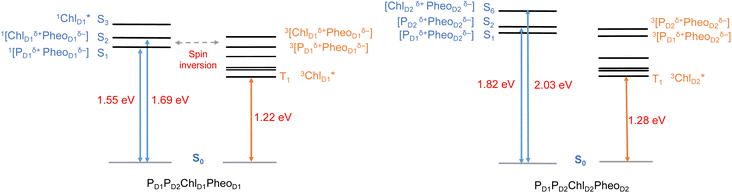
The electrostatic effects of the protein matrix are known to modulate the excited state properties of reaction center pigments.84 Previous work identified that the protein matrix is exclusively responsible for creating transverse and lateral excitonic asymmetry among the pigments within the PSII RC.12,82,83 This asymmetry leads to trapping of the excitation energy and initiation of primary charge-separation in the D1 branch. In the presence of the protein matrix the pigment with the lowest site energy is computed to be ChlD1.12 Detailed work on pigment assemblies additionally showed that the lowest singlet excited state is localized on the ChlD1–PheoD1 pair and that this is usually a mixture of excitonic and charge-transfer (CT) ChlD1δ+PheoD1δ− character.24 The corresponding CT state involving the ChlD2–PheoD2 pair on the inactive D2 is higher in energy, thus elucidating the excitonic asymmetry of the RC, where the protein matrix stabilizes excited CT states on the D1 branch. However, the explicit role of the protein electrostatics in controlling the excited state energetics of the triplet states has never been studied. It is also not clear if asymmetry exists at all in the case of triplet excitations. This information would be useful for understanding triplet-state formation and subsequently establish the role of protein matrix in photoprotection.As a first step, we computed the singlet and triplet excitation energies of individual RC pigments using TD-DFT in the QM/MM framework. The Q and B bands of the absorption spectra of porphyrin-like macrocyclic compounds are described according to the Gouterman model,118 which involves excitations within the four frontier molecular orbitals HOMO−1, HOMO, LUMO, and LUMO+1, delocalized over the chlorin ring.111 For instance, the fundamental singlet excitation of the chlorophylls is the Qy band (S1), corresponding to HOMO → LUMO and secondarily to HOMO−1 → LUMO+1 excitation. Based on the TD-DFT calculations, the lowest triplet excitations consist of two unpaired electrons, ferromagnetically coupled to each other in two singly occupied orbitals (SOMO 1, SOMO 2), also delocalized over the chlorophyll macrocycle.119,120 Our TDA-TDDFT results (see Tables S1–S5†) show that the two lowest energy triplet excited states (T1, T2) of RC chlorophylls are characterized by HOMO → LUMO (in the range of 1.22–1.30 eV) and HOMO−1 → LUMO (range of 1.73–1.78 eV) transitions. Furthermore, in all four central chlorophylls (i.e., ChlD1, PD1, PD2, ChlD2) the two lowest triplet excited states (T1 and T2) are energetically lower than the corresponding singlet excitations (S1 and S2). This observation suggests that the lowest triplet local excitations are likely to result from spin–orbit induced inter system crossing (ISC) from the corresponding first singlet excited state (S1) of each chlorophyll.84
The computation of singlet excitation energies without protein electrostatics demonstrates that both ChlD1 and ChlD2 pigments have similar site energy in the gas phase (1.88 eV and 1.90 eV, respectively, see Table 1). Moreover, the nature of excitations and participating orbitals for the chlorophyll triplet remains consistent even in the absence of the explicit PSII protein environment. On the other hand, calculations done with full inclusion of protein electrostatics red-shifts the first excited state for both pigments. This effect is more pronounced for 1ChlD1 (1.82 eV) compared to 1ChlD2 (1.88 eV). Interestingly, similar spectral shifts are obtained for the lowest triplet state (T1), where we observed protein-induced red shifts highest for 3ChlD1 (70 meV) followed by 3ChlD2 (31 meV), 3PD1 (18 meV) and 3PD2 (23 meV). The excitation energy of 3PheoD1 was found to be 17 meV higher than 3ChlD1, and about 10 meV higher than the T1 states of PD1, PD2 and ChlD2. Clearly, the signature of transverse excitonic asymmetry within the RC is preserved for the lowest localized triplet excitations. Nevertheless, it will be interesting to see how the absolute S1 and T1 excitation energies and S1–T1 gap are modulated by the protein matrix as these states should be involved in S–T intersystem crossing. The vertical excitation energies of the lowest singlet and triplet state along with the respective S–T gaps, in the presence and absence of the protein, are listed in Table 1. It is important to note that the protein matrix induces an asymmetry in tuning the S1–T1 gap for the accessory chlorophylls ChlD1 and ChlD2. In the case of ChlD1, both S1 and T1 are red-shifted by ca. 70 meV in the presence of the protein compared to the gas phase. In the case of ChlD2 the S1–T1 gap is 0.59 eV in the presence of the protein, similar to the gas phase (0.58 eV).
| Method | ΔE | TD-DFT (in protein) | TD-DFT (gas-phase) | |||||
|---|---|---|---|---|---|---|---|---|
| RC pigment | T1–S0 (opt) | ΔT1 (opt) | S1 | T1 | S1–T1 | S1 | T1 | S1–T1 |
| ChlD1 | 0.920 | 0.300 | 1.818 | 1.220 | 0.598 | 1.884 | 1.290 | 0.594 |
| PD1 | 0.994 | 0.311 | 1.859 | 1.305 | 0.554 | 1.898 | 1.323 | 0.575 |
| PD2 | 0.978 | 0.313 | 1.859 | 1.291 | 0.568 | 1.897 | 1.314 | 0.583 |
| ChlD2 | 0.970 | 0.318 | 1.878 | 1.288 | 0.590 | 1.900 | 1.319 | 0.581 |
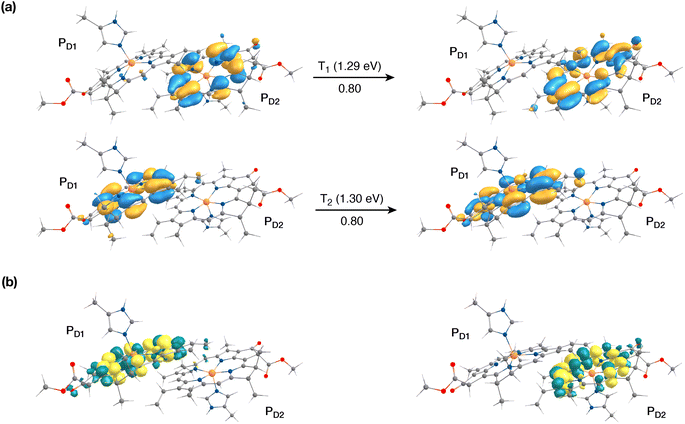
The singlet excited states on the central pair PD1PD2 in the presence of the protein point charges show that the lowest singlet excited states at 1.86 eV and 1.88 eV are a superposition of local excitons on PD1 and PD2, respectively (Table S6†). The lowest CT state involving the central pair (PD1δ+PD2δ−) is significantly higher (ca. 3.2 eV) than the S0. On the other hand, in the case of triplet excitations, the two lowest triplet states are isoenergetic and correspond to triplet excitons localized on PD2 (T1, 1.29 eV) and PD1 (T2, 1.30 eV) respectively (see Fig. 3a and b). Our results do not show any low-energy triplet state of the same character as the 1[PD1δ+PD2δ−] CT state mentioned above. Moreover, each triplet excitation spanning a range of 1.40–1.50 eV is attributed to individual pigments (see Table S6†), suggesting that the triplet excitons are entirely localized on either of the two chlorophyll molecules (PD1 or PD2) and therefore there is no superposition, in contrast to the singlet excitons. The absence of a low-lying triplet state with CT character is also indicative of the fact that a radical-pair charge recombination may not be favorable to form 3[PD1PD2] states in the RC. However, it cannot be excluded that delocalized triplet excited states exist at higher energies, similar to the singlet CT excitations.12,24
3.2. Singlet–triplet excitations in pigment assemblies
In photosynthetic RCs the excitation profiles of individual pigments are far from complete, and a thorough understanding of the initial charge-separation and charge recombination events requires insights from excitation energetics of multiple pigments. For instance, 1[PD1δ+PheoD1δ−] and 1[ChlD1δ+PheoD1δ−] charge-transfer (CT) excitations were found significantly stabilized, lower than the local excitons, due to the differential effect of the protein matrix.18,24 Moreover, the lowest (Qy) excitation of ChlD1 was found to be mixed significantly with the 1[ChlD1δ+PheoD1δ−] CT state.18 A number of experimental studies suggest that based on the characteristic spin polarization pattern of the EPR spectra, the observable triplet state should be formed from a charge recombination of the primary radical pair.37,56,58,61,64,66 This further necessitates a quantitative description of the excitation profiles of groups of pigment assemblies, in order to establish a connection between the singlet-triplet CT excitations and the experimentally observable triplet state. Towards this objective, we first computed the low energy singlet and triplet excited states for the tetrameric pigment assemblies along the D1 [PD1PD2ChlD1PheoD1] and D2 [PD1PD2ChlD2PheoD2] branches.The most common mechanism of triplet formation in organic chromophores involves a spin–orbit-induced intersystem crossing (ISC) but singlet fission, radical pair ISC, or spin–orbit charge-transfer ISC can result in triplet formation, particularly in systems with donor–acceptor pigment pairs.54,89,121,122 Similar studies on biomimetic assemblies have reported that low-lying CT states can promote triplet formation through a charge recombination of donor–acceptor radical pairs followed by ISC.123,124 Our TD-DFT results show that the lowest singlet excitations in the [PD1PD2ChlD1PheoD1] branch correspond to 1[PD1δ+PheoD1δ−] (1.548 eV) and 1[ChlD1δ+PheoD1δ−] (1.693 eV) CT states, respectively (Table 2). These results are further in line with recent QM/MM and TDDFT studies.18,24
| Roots | E S | f osc | Transition | E T | Transition |
|---|---|---|---|---|---|
| 1 | 1.548 | 0.00 | CT (PD1 →PheoD1) | 1.215 | LE (ChlD1) |
| 2 | 1.693 | 0.06 | CT (ChlD1 → PheoD1) | 1.291 | LE (PD2) |
| 3 | 1.801 | 0.32 | LE (ChlD1) | 1.303 | LE (PD1) |
| 4 | 1.807 | 0.02 | CT (PD2 → PheoD1) | 1.386 | LE (PheoD1) |
| 5 | 1.855 | 0.39 | LE (PD1) + LE (PD2) | 1.548 | CT (PD1 → PheoD1) |
| 6 | 1.882 | 0.05 | LE (PD1) + LE (PD2) | 1.681 | LE (PheoD1) |
| 7 | 2.023 | 0.00 | CT (PD1 → PheoD1) | 1.708 | CT (ChlD1 → PheoD1) |
| 8 | 2.033 | 0.17 | LE (PheoD1) | 1.731 | LE (ChlD1) |
| 9 | 2.251 | 0.00 | CT (ChlD1 → PheoD1) | 1.773 | LE (PD2) |
| 10 | 2.340 | 0.00 | CT (PD2 → PheoD1) | 1.778 | LE (PD1) |
| 11 | 2.385 | 0.04 | LE (ChlD1) | 1.807 | CT (PD2 → PheoD1) |
| 12 | 2.409 | 0.03 | LE (PD2) | 2.023 | CT (PD1 → PheoD1) |
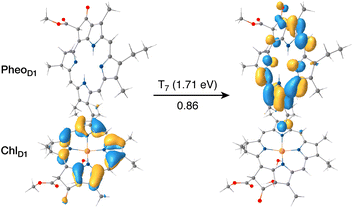
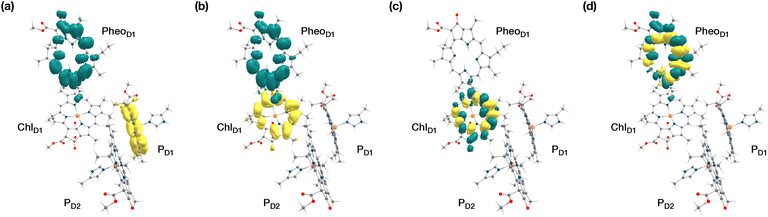
The results presented and analyzed in terms of natural transition orbital (NTO) compositions (see Table 2) and (TDA)-TDDFT difference densities show that the lowest triplet excited state of the D1 tetramer (T1 at 1.215 eV) is fully localized on ChlD1, which also exhibits the lowest site energy (S1 at 1.801 eV) among all RC pigments. The second and third triplet states (T2 at 1.291 eV and T3 at 1.303 eV) are localized excitations on PD2 and PD1 respectively. These results are in line with those obtained for the pigment monomers and dimers. Most importantly, we identified the “spin-flipped” triplet states 3[PD1δ+PheoD1δ−] (1.548 eV) and 3[ChlD1δ+PheoD1δ−] (1.708 eV, Fig. 4) that are isoenergetic with the lowest singlet CT states (see Table 2). The corresponding TD-DFT difference densities for the low-energy CT triplet excitations 3[PD1δ+PheoD1δ−] and 3[ChlD1δ+PheoD1δ−] are depicted in Fig. 5. It is noteworthy that all the RC pigments exhibit a triplet exciton lower than the above donor–acceptor CT states.
All the low-energy triplet states are dominated by local excitations on ChlD1, PD1, PD2 and PheoD1, all lower in energy than the lowest triplet CT states. This is in contrast to singlet excitations wherein the low-energy profile is dominated by mixed local excitons and CT excitations or states with pure CT character. Furthermore, most local excitons are blue-shifted compared to the donor–acceptor CT states. Overall, our results clearly demonstrate that low-energy singlet and triplet excited state manifolds differ significantly for primary donor–acceptor pairs in the RC. A detailed schematic representation comparing the complete low-energy spectrum (singlet and triplet excitations) of the RC is provided in Fig. 6. Based on our calculations one would expect that the observable triplet state in the RC can be formed from recombination of either of these radical pairs that subsequently decays to the neutral ground-state chlorophyll triplet 3ChlD1. This mechanism is different from the formation of other triplet states (e.g. in light-harvesting antennae) where 3Chl formation is mediated by triplet–triplet energy transfer (T-TET)54,55,70 or direct intersystem crossing from a singlet excited state.54 The singlet-triplet excitation spectra of the D2 tetramer [PD1PD2ChlD2PheoD2] (see Fig. S1 and Table S7†) are also comprised of CT triplet excitations corresponding to 3[PD2δ+PheoD2δ−] (1.706 eV), 3[PD2δ+PheoD2δ−] (1.816 eV) and 3[ChlD2δ+PheoD2δ−] (2.032 eV) respectively. The lowest triplet exciton in the D2 side is localized on ChlD2 at 1.279 eV.
3.3. Relaxed triplet states
In the previous section we explored the influence of the protein matrix on the excitonic asymmetry for singlets and triplets, where the lowest energy excitons were found to be localized on ChlD1. Interestingly, while singlet excitation energy transfer (EET) within the RC seems unlikely due to rapid charge separation, the protein matrix tends to delocalize triplet states over the four chlorophyll pigments. Understanding this phenomenon of triplet delocalization among RC pigments is crucial for comprehending the mechanisms of photo-quenching and photoprotection in PSII.51,87 Moreover, obtaining accurate estimates of the triplet energy gaps among individual pigments is necessary to determine the actual rates of photo-quenching. To address this, we conducted further QM/MM geometry optimizations of the individual pigments (ChlD1, ChlD2, PD1, and PD2) in their singlet and triplet states, enabling us to estimate the adiabatic T1–S0 energy gaps for each chlorophyll.Previous site-directed mutagenesis experiments on D1-H198G, combined with low-temperature optical difference spectroscopy, conducted by Diner et al.,9 reported shifts in the difference spectra of PD1+/PD1 and YZ˙/YZ, as well as displacements in the midpoint potential of PD1+/PD1. However, the mutation had no effect on the difference spectra or EPR properties corresponding to 3P680. Schlodder et al.125 performed similar studies on D1-T179H mutants, which involve the ligand H-bonded to the axially bound water of ChlD1, and observed shifts in the Qy band and EPR signals upon triplet formation. The T–S absorption spectra of photosynthetic pigments in D1D2Cytb559 complexes were also investigated by Renger et al.,15,42 and more recent phosphorescence measurements73,74 supported the notion that the triplet state is localized on an RC chlorophyll different from the one accommodating the stable positive charge. FTIR measurements indicated that the triplet is localized on a chlorophyll distinct from the primary cation-stabilizing chlorophyll, based on the vibrational peak of the 131-keto C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O keto arising from differences in H-bonding interactions.20 These experimental observations, combined with the latest experimental and theoretical descriptions of the primary events at the RC of PSII that identify ChlD1 as the primary donor, consistently support the idea that the accessory chlorophyll ChlD1 is the site of the most stable triplet state.
O keto arising from differences in H-bonding interactions.20 These experimental observations, combined with the latest experimental and theoretical descriptions of the primary events at the RC of PSII that identify ChlD1 as the primary donor, consistently support the idea that the accessory chlorophyll ChlD1 is the site of the most stable triplet state.
Here, we determined the TD-DFT vertical excitation energies for 3[PD1PD2] and 3ChlD2 to be 1.29 eV and 1.28 eV, respectively (see Table 1). Consequently, the lowest energy triplet excitation was found to be localized on ChlD1, consistent with the above findings. Additionally, we observed that the QM/MM geometry relaxation had a similar effect of approximately 0.3 eV on the triplet state for each chlorophyll in the reaction center (Table 1). The EPR/ENDOR and FTIR spectra obtained from temperature-dependent studies estimated energy differences between 3ChlD1 and 3PD1 of 8–13 meV from isolated RCs and 11 meV from core complexes.9,62,74,126 Our computational results align with these experimental observations, indicating that the triplet state on ChlD1 is also the lowest in energy among all pigments at the reaction center.15,42 However, given the close spacing of energy levels, it is expected that at higher temperatures, an equilibrium would exist among the triplet states of PD1, PD2, ChlD1, and ChlD2, resulting in the delocalization of the observable triplet state over more than one chlorophyll molecule. These conclusions are consistent with recent FTIR studies conducted by Noguchi and co-workers.87 Therefore, our findings support both the localization of the triplet on the specific chlorophyll center (ChlD1) at low temperatures and the decrease in triplet intensities due to delocalization at ambient temperatures.
3.4. EPR parameters of triplet chlorophylls
Magnetic resonance studies coupled with photoexcitation, especially time-resolved electron paramagnetic resonance (EPR) spectroscopy, have been widely applied to characterize the triplet states and organic radicals involving photosynthetic pigments.36,38,40,54,55,71,75,76,127 The triplet states involving RC, antenna chlorophylls as well as carotenoids have been characterized using transient and pulse ENDOR spectroscopy,37,39,66,126,128,129 however a number of these studies led to varying observations depending on the type of preparation and conditions used, as in the case of D1D2Cytb559 particles or PSII core complexes. DFT methods have also been used to quantify EPR properties of photosynthetic pigments but they have excluded so far the effect of protein electrostatics.127,128 Therefore, in order to obtain reliable quantitative insights regarding the influence of the local protein environment on the localisation site of the triplet states, here we compute for the first time the EPR properties of each RC pigment in their triplet (S = 1) geometries using the present QM/MM setup.The accurate determination of zero field splitting (ZFS) parameters D and E is important to characterize the spatial extent and specific location of the triplet-state spin densities. From a methodological perspective, the accuracy of the spin–spin contribution of the D-tensors (Dss) for organic radicals is significantly affected by spin contamination, and ROKS approaches show better performance than UKS approaches for predicting the correct sign and the ZFS tensor orientation in organic triplets.117 Based on our calculations (see Table S9†) we observe good agreement despite a small systematic underestimation of the magnitude of the ZFS for the RC triplets, as also reported in the past for isolated Chl a triplets.117 Our calculations nevertheless confirm that the lowest triplet state is localized on a monomeric chlorophyll at the RC, as can be concluded from the corresponding ZFS parameters and comparison with those of isolated Chl a. This appears to rule out the possibility that the observed triplet is delocalized at low temperatures. From the first series of EPR studies on chlorophyll triplets in photosynthetic RCs, Rutherford et al.56,61 and Van Mieghem et al.58 proposed that the observable triplet is localized on a pigment whose ring plane is tilted at an angle of 30° with respect to the membrane plane. Following on the 1.9 Å crystal structure of PSII,8 this was assumed to be either of the accessory chlorophylls, ChlD1 or ChlD2. Based on our QM/MM model and EPR calculations, we estimated an angle of about 37° between the chlorophyll plane and the approximate membrane plane, the z-axis of the ZFS tensor and the molecular z-axis (perpendicular to the porphyrin ring plane) being approximately collinear. However, one still cannot assign the triplet state of the RC to a specific pigment only based on the ZFS parameters.
A more sensitive tool that offer insights into the electronic nature of the triplet states is the electron-nuclear hyperfine coupling (HFC) for protons and heavier nuclei strongly interacting with it. We computed the 1H HFC constants for each of the chlorophyll triplet states explicitly accounting for the protein electrostatics. From our calculations, we can assign the EPR coupling constants to each proton corresponding to the chlorophyll triplet state (Table 3). It has been argued based on experiments that 3P680 is localized on ChlD1 or ChlD2, based on the low number of contacts of the three methyl groups (2, 7 and 12). We also conclude that the peak corresponding to the highest positive HFC should be assigned to the freely rotating methyl group at position 12, followed by that of 2, and this is consistent for all the RC pigments. Our assignment of the hyperfine coupling constants is also consistent with DFT computed Mulliken spin populations of the neighboring carbon atoms of the chlorin macrocycle (see Fig. S2†). Overall, C12 has the highest spin population (0.293 in ChlD1) in the chlorin ring, which consequently leads to a large proton hyperfine coupling in the C12 methyl protons. The spin population at C2 and C7 are comparatively lower. The assignment of the HFC constants at position 2 is also interesting, because the signal corresponding to these protons is not clearly assigned in ENDOR studies of isolated RC (D1D2Cytb559) samples.39 Interestingly, the largest contribution for each chlorophyll is seen to arise for the methyl protons oriented towards the perpendicular z-axis of the molecule. The negative values of the HFCs are assigned to the methine (CH) protons on the plane of the chlorin macrocycle (5, 10 and 20) because their isotropic couplings arise from spin polarization effects. Among these methine (CH) protons the carbon with highest spin density leads to more a negative value of 1H HFC due to a higher spin polarization and this trend is consistent among all the four RC pigments. In the recent work by Niklas and coworkers,37 the hyperfine coupling constants for the protons at C17 and C18 were not clearly determined for 3P680. From our calculations, we observe that for all the chlorophylls the proton at position 18 has a higher isotropic 1H HFC than position 17. Also, the corresponding spin population analysis of the macrocyclic carbon atoms indicate a higher spin density at C19 than C16. This trend is also consistent among all the RC chlorophylls (ChlD1, ChlD2, PD1 and PD2), and therefore our QM/MM calculations indicate the experimentally observed HFC of 2.99 in 3P680 likely arises from position 18.
| Triplet state | 10 (CH) | 20 (CH) | 5 (CH) | 7 (CH3) | 12 (CH3) | 2 (CH3) | 18 (CH) | 17 (CH) | 3′ (CH) | 3′′ (CH2) | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| ENDOR37,39,127 | 3P680 | −10.03 | −7.88 | −4.79 | 0.62 | 10.35 | 4.80 | 2.99 | n.d. | 0.91 | −1.30 |
| 3Chl a (WSCP) | −10.20 | −7.70 | −5.70 | 1.10 | 10.70 | 4.70 | 2.60 | n.d. | |||
| 3Chl a (MTHF) | −11.44 | −7.20 | −6.20 | n.d. | 7.40 | n.d. | |||||
| DFT | 3Chl a (gas-phase) | −5.12 | −5.21 | −3.32 | 0.97 | 10.77 | 5.61 | 4.81 | 3.96 | 0.69 | −1.64 |
| 3Chl a (MTHF) | −7.20 | −7.32 | −4.96 | 0.39 | 10.61 | 5.69 | 3.14 | 2.46 | 0.16 | −1.65 | |
| 3ChlD1 (gas-phase) | −6.63 | −6.77 | −5.61 | 0.61 | 10.95 | 5.35 | 2.90 | 1.78 | 0.39 | −2.04 | |
| QM/MM | 3ChlD1 | −6.98 | −6.18 | −5.64 | 1.25 | 12.27 | 5.68 | 2.59 | 1.28 | 0.52 | −2.80 |
| 3ChlD2 | −7.41 | −6.42 | −5.63 | 0.71 | 12.41 | 5.31 | 3.06 | 1.58 | 0.64 | −2.19 | |
| 3PD1 | −6.02 | −5.17 | −5.59 | 1.05 | 10.86 | 4.78 | 2.47 | 1.19 | 0.58 | −2.42 | |
| 3PD2 | −1.82 | −4.13 | −1.08 | 1.07 | 11.67 | 5.93 | 4.18 | 4.69 | 3.59 | −1.76 | |
We have also identified contributions from the vinyl group (3′, 3′′), the peaks of which were not clearly assigned in previous spectroscopic studies. The negative HFC at 3′′ is likely due to spin polarization from C3′′, and the magnitude is consistent with the corresponding spin populations. However, the orientation of the vinyl group of PD2 is particularly noteworthy here. It is known that in PD2 the vinyl CH2 is slightly out of plane from the chlorin macrocycle, and our results indicate that this significantly affects the spin density distribution of the vinyl carbons. This clearly explains why the 1H HFC of the vinyl protons in PD2 differ significantly from the other RC chlorophylls.
Our QM/MM methodology therefore not only reproduces the experimental EPR/ENDOR results obtained from intact PSII core samples but also accounts for local perturbations that might affect EPR signals from isolated RC samples. Overall, the triplet spin distribution of individual chlorophylls (Fig. 7b) remain unchanged for isolated RC samples.87 The EPR parameters however, are not sufficiently sensitive to the protein environment to enable confident differentiation between the chlorophylls of the RC and it is not possible to assign the spectroscopically observable triplet state to a single RC chlorophyll based on EPR parameters alone. Nevertheless, the lowest triplet excitations and the energetically most stable triplet state are found on ChlD1 and, hence, the combined results of all our calculations show a clear preference to assign this state to a triplet state localized on the accessory chlorophyll ChlD1.
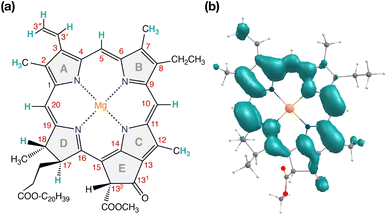 | ||
| Fig. 7 (a) Structure of Chl a with carbon atom numbering and spectroscopically important hydrogen positions indicated. (b) Computed spin density distribution of triplet (S = 1) Chl a. | ||
3.5. Electrostatic effects by plastoquinone QA and the OEC
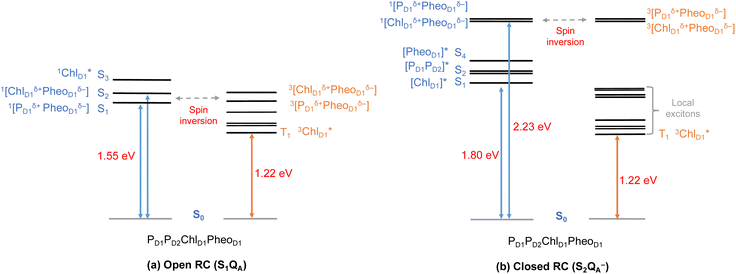
Until now, we discussed the optical properties of primary electron transfer processes in PSII, where the OEC is in its dark-stable state (S1) and QA is a neutral plastoquinone. Under normal conditions, the charge recombination of the primary charge separated states [ChlD1+PheoD1−]4,11,16 (or [PD1+PheoD1−])24 is prevented by forward electron transfer from PheoD1 to QA (within a few hundred ps). The oxidation of YZ (the redox-active tyrosine residue that interfaces the OEC with the RC) by PD1+ occurs instead within 25 ns to 50 μs.5 Both processes contribute to formation and modulation of an electrostatic gradient across the transmembrane region, which, coupled with intrinsic protein matrix effects, tunes the thermodynamics and kinetics of electron transfer pathways. Based on reported timescales, the oxidation of OEC by the YZ (50 μs to 4 ms), and electron transfer from QA to QB (0.2–0.8 ms) are the two main rate-limiting steps in PSII. These electron transfer processes thus eventually create the next stable intermediate of the RC with an oxidized OEC and reduced QA (S2QA−). On the other hand, in extreme conditions such as prolonged light exposure the plastoquinone (PQ) pool in thylakoid membranes can remain reduced, abolishing electron transfer from QA to QB and allowing QA− to accumulate. This can further drive competing secondary electron transfer pathways leading to triplet formation in the RC.In view of the above, as a next step we performed TD-DFT calculations on the “closed” RC, where the OEC is modelled in the S2 state of the Kok–Joliot cycle and QA is reduced, i.e., the S2QA− state. Our excited state calculations on the [PD1PD2ChlD1PheoD1] assembly (Table S8†) reveal interesting results. The low-energy spectrum (see Fig. 8) in the presence of the semiquinone QA− is dominated by local excitations both for singlets and triplets, in stark contrast to the case when QA is neutral and available to accept electrons. The relative stability of site energies (ChlD1, PD1, PD2 and PheoD1) also explains the longer lifetime of chlorophyll excited states and high fluorescence yields observed in closed RCs.26,45 Moreover, the 1[ChlD1δ+PheoD1δ−] CT state is 2.23 eV higher than the ground state and thus considerably blue-shifted compared to the open RC (1.69 eV). This is in line with previous experimental hypotheses regarding reduced charge separation due to the electrostatic repulsion of QA−.26,32,79 Interestingly, we also find that the two low-energy CT states 1[ChlD1δ+PheoD1δ−] (2.231 eV) and 1[PD1δ+PheoD1δ−] (2.276 eV) are almost isoenergetic for the closed RC (Table S8†). This is clearly an effect of the differential influence of oxidized OEC and QA− on the primary donor–acceptor pairs, with PheoD1− and PD1+ being more destabilized than ChlD1+ due to their spatial proximity to QA− and/or the oxidized OEC respectively (Fig. S4;† PheoD1 is the closest pigment to QA with an edge-to-edge distance of 8.8 Å, and a center-to-center distance of 13.2 Å, while PD1 is closest to OEC with a distance of about 17.2 Å).
Studies on charge recombination reactions have shown that formation of RC triplet states can be influenced not only by the presence of the semiquinone (QA−) but also by the complete absence of QA (e.g., isolated D1D2Cytb559 samples) or the double reduction of QA.45,46 In some experiments conducted at cryogenic temperatures the spin-polarized triplet state was only detected when QA was doubly reduced (QA2− or QAH2) and not when it was singly reduced, which led to controversies about whether or not primary charge separation can occur in the presence of QA−. Studies that monitored the light-induced triplet signals with different redox states of QA using EPR spectroscopy, reported higher triplet yields but shorter life times (t1/2 < 20 μs) with QA− (closed RC).29,32,33 On the other hand, Feikema et al. based on time-resolved EPR measurements on PSII core samples reported that the yield of the triplet state with a singly reduced QA− did not differ significantly from those with QAH2.29 In the case of QAH2 however, the chlorophyll triplet was reported to have a much extended lifetime (t1/2 ∼ 1–2 ms) and this has been attributed to the absence of QA− to quench chlorophyll triplet states in PSII. Moreover, flash-induced PSII activity measurements showed the extent of D1-photodamage due to 1O2 to be most pronounced in the S2 and S3 states of the OEC, and this also has been correlated to other competing back reactions.47,50 Hence, the pathway of triplet formation and the dependence of the singlet–triplet excitations on the redox state of the QA and OEC remain unclear, yet they are crucial to understand both the control of primary processes by the transmembrane electrostatic gradient and the photoprotection mechanisms of PSII.
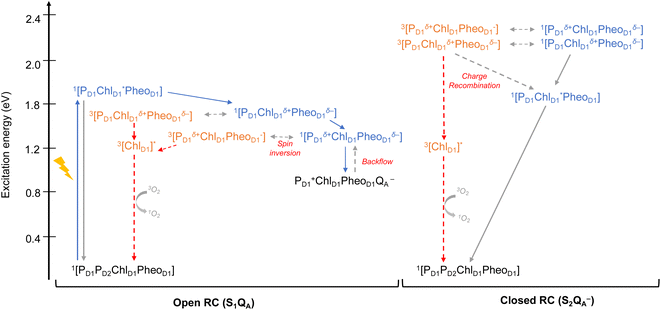
As seen from the excitation energy profiles (Fig. 8), the energetics of the singlet and triplet charge transfer excitations can be directly influenced by the redox state of surrounding cofactors, particularly QA. A more comprehensive overview of the singlet and triplet excitation energies, charge transfer pathways, charge recombination and triplet forming routes, is provided in Fig. 9. Based on our results, it can be suggested that formation of triplet states at the RC should be preceded by charge recombination of the primary radical pair [ChlD1+PheoD1−] or [PD1+PheoD1−] formed from the corresponding CT states. Subsequently, a very important aspect when discussing molecular mechanisms of photoprotection involves the acceptor side of PSII. PheoD1 is the site of the primary anion radical PheoD1−, following charge separation.4,11,12,15,79 In normal physiological conditions the electron is rapidly transferred to QA (PheoD1−QA → PheoD1QA−). The thermodynamic driving force for this step is governed by the relative midpoint potentials of PheoD1/PheoD1− and QA/QA− and is controlled by local pigment–protein interactions.32 However, the reduction of QA to QA− can lead to the following alternate possibilities: (a) direct charge recombination with P680+ to 1P680* and finally the ground state, (b) backward electron transfer onto PheoD1 to form 1[P680+PheoD1−] or (c) formation of the charge recombination triplet 3[P680+PheoD1−] which finally localizes on ChlD1i.e., the triplet route. Calculation of the PheoD1 electron affinity suggests that PheoD1− formation is disfavored by ca. 0.5–1 eV in the presence of a reduced QA−. The electrostatic repulsion of QA− destabilizes the primary radical pair [P680+PheoD1−], but also inhibits forward electron transfer. This might cause spin inversion from 1[P680+PheoD1−] to 3[P680+PheoD1−], the excess excitation energy dissipated through the non-radiative triplet route (Fig. 9). Experiments suggest that the observable triplet in the closed RC has an extremely short lifetime (t1/2 < 20 μs), and it has been proposed that this is because QA− quenches RC triplet states through 3PheoD1.32 However, this mechanism of triplet quenching involving the semiquinone (QA−) and 3PheoD1 is not well understood. Based on our computed excitation profile of the closed RC (Fig. 9), we find numerous thermodynamically accessible triplet states that are localized on the individual pigments (ChlD1, PD1, PD2 and PheoD1). All these local excitations are in fact lower in energy than the CT 3[ChlD1δ+PheoD1δ−] and 3[PD1δ+PheoD1δ+] excitations, which is in contrast to the triplet energy profile of open RC [S1QA] (see Fig. 8). Specifically, all D1 pigments in the closed RC possess at least two triplet excitations (T1 to T8) energetically lower than the first CT state. Thus, non-radiative energy dissipation involving multiple RC pigments might be a possibility in the closed RC, in line with arguments regarding triplet delocalization pathways discussed in recent FTIR studies.87 When QA is doubly reduced as QAH2, the PheoD1− anion is expected to be more stable in the absence of a negative charge in its vicinity.25,45,46,130 This can stabilize 1[P680+PheoD1−] and a subsequent spin inversion to 3[P680+PheoD1−] may again lead to more centers favoring the triplet route as opposed to a direct charge recombination to the singlet state.
It is known that formation of triplet states is detrimental to photosynthetic organisms as long-lived triplets in the RC can accelerate the formation of reactive oxygen species and subsequent photodamage.43,49,51 In this respect, we provided a quantitative explanation of how the PSII protein matrix and redox active cofactors may work in tandem to tune the energetics of primary charge separation and triplet formation in photosynthetic reaction centers. Our results have implications for photoprotection mechanisms in both the open and the closed states of active PSII. The next line of photoprotection in the RC may involve the delocalization of triplet states away from ChlD1 onto other pigments at ambient temperatures to avoid the selective damage of the D1 protein. However, if this still leads to photoinactivation, the D1 protein is selectively degraded and regenerated, thereby allowing photosynthetic organisms to preserve functionality even under extreme conditions.48,131,132
4. Conclusions
This work provides a detailed overview of the low-energy excitation spectrum of the PSII-RC, explaining the asymmetry of singlet-triplet excitations and charge transfer states along the D1 and D2 branches. The PSII protein environment explicitly controls the excitonic asymmetry of the RC, leading to low-energy charge-transfer excitations and triplet formation on the D1 side. Based on our calculations we may speculate that the observable triplet state at the RC is unlikely to be formed by usual inter-system crossing (ISC), but through a radical-pair charge recombination preceding ISC. However, this cannot yet be concluded with confidence given that the kinetics of triplet formation and the factors/processes that determine them are not addressed in the present work. We identified all low-lying charge transfer excitations in the pigment assemblies, and find that the lowest triplet exciton is localized on ChlD1. With supporting insights from EPR calculations we confirm the localization of the most stable triplet state on ChlD1. Furthermore, we present the first theoretical description of the excited state properties of the “closed RC” (S2QA−), explicitly quantifying the electrostatic effect of semiquinone (QA−) and how it influences excited state properties of RC pigments. Overall, this work provides a refined basis for the electronic-level understanding of primary and secondary electron transfer pathways, offering detailed electronic structure information as a foundation for discussing possible photoprotection mechanisms in oxygenic photosynthesis.Author contributions
S. B.: methodology, investigation, analysis, writing – original draft; F. N.: resources, supervision; D. A. P.: conceptualization, methodology, supervision, writing – review and editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors gratefully acknowledge support by the Max Planck Society. S. B. thanks the International Max Planck Research School on Reactive Structure Analysis for Chemical Reactions (IMPRS-RECHARGE) for support. The authors thank Krishna Siwakoti for preliminary calculations of redox properties of the reaction center pigments. Open Access funding provided by the Max Planck Society.References
-
R. E. Blankenship, Molecular mechanisms of photosynthesis, John Wiley & Sons, 2021 Search PubMed
.
- J.-R. Shen, Annu. Rev. Plant Biol., 2015, 66, 23–48 CrossRef CAS PubMed
.
- N. Cox, D. A. Pantazis and W. Lubitz, Annu. Rev. Biochem., 2020, 89, 795–820 CrossRef CAS
.
- T. Cardona, A. Sedoud, N. Cox and A. W. Rutherford, Biochim. Biophys. Acta, Bioenerg., 2012, 1817, 26–43 CrossRef CAS
.
- F. Muh, C. Glockner, J. Hellmich and A. Zouni, Biochim. Biophys. Acta, 2012, 1817, 44–65 CrossRef
.
- Y. Takahashi, Ö. Hansson, P. Mathis and K. Satoh, Biochim. Biophys. Acta, Bioenerg., 1987, 893, 49–59 CrossRef CAS
.
- D. J. Vinyard, G. M. Ananyev and G. Charles Dismukes, Annu. Rev. Biochem., 2013, 82, 577–606 CrossRef CAS
.
- Y. Umena, K. Kawakami, J.-R. Shen and N. Kamiya, Nature, 2011, 473, 55–60 CrossRef CAS PubMed
.
- B. A. Diner, E. Schlodder, P. J. Nixon, W. J. Coleman, F. Rappaport, J. Lavergne, W. F. J. Vermaas and D. A. Chisholm, Biochemistry, 2001, 40, 9265–9281 CrossRef CAS PubMed
.
- K. Saito, T. Ishida, M. Sugiura, K. Kawakami, Y. Umena, N. Kamiya, J.-R. Shen and H. Ishikita, J. Am. Chem. Soc., 2011, 133, 14379–14388 CrossRef CAS PubMed
.
- Y. Yoneda, E. A. Arsenault, S. Yang, Jr., K. Orcutt, M. Iwai and G. R. Fleming, Nat. Commun., 2022, 13, 2275 CrossRef CAS PubMed
.
- A. Sirohiwal, F. Neese and D. A. Pantazis, J. Am. Chem. Soc., 2020, 142, 18174–18190 CrossRef CAS PubMed
.
- V. A. Nadtochenko, I. V. Shelaev, M. D. Mamedov, A. Y. Shkuropatov, A. Y. Semenov and V. A. Shuvalov, Biochemistry (Moscow), 2014, 79, 197–204 CrossRef CAS
.
- W. Lubitz, F. Lendzian and R. Bittl, Acc. Chem. Res., 2002, 35, 313–320 CrossRef CAS
.
- T. Renger and E. Schlodder, ChemPhysChem, 2010, 11, 1141–1153 CrossRef CAS
.
- E. Romero, I. H. M. Van Stokkum, V. I. Novoderezhkin, J. P. Dekker and R. Van Grondelle, Biochemistry, 2010, 49, 4300–4307 CrossRef CAS
.
- N. P. Pawlowicz, M. L. Groot, I. H. M. Van Stokkum, J. Breton and R. Van Grondelle, Biophys. J., 2007, 93, 2732–2742 CrossRef CAS PubMed
.
- M. Capone, A. Sirohiwal, M. Aschi, D. A. Pantazis and I. Daidone, Angew. Chem., Int. Ed., 2023, 62, e202216276 CrossRef CAS PubMed
.
- P. J. O'Malley, J. Phys. Chem. B, 2000, 104, 2176–2182 CrossRef
.
- T. Noguchi, T. Tomo and Y. Inoue, Biochemistry, 1998, 37, 13614–13625 CrossRef CAS PubMed
.
- H. Tamura, K. Saito and H. Ishikita, Chem. Sci., 2021, 12, 8131–8140 RSC
.
- R. Takahashi, K. Hasegawa and T. Noguchi, Biochemistry, 2008, 47, 6289–6291 CrossRef CAS PubMed
.
- H. Tamura, K. Saito and H. Ishikita, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 16373–16382 CrossRef CAS
.
- A. Sirohiwal and D. A. Pantazis, Angew. Chem., Int. Ed., 2022, 61, e202200356 CrossRef CAS
.
- I. Vass, G. Gatzen and A. R. Holzwarth, Biochim. Biophys. Acta, Bioenerg., 1993, 1183, 388–396 CrossRef CAS
.
- M. Szczepaniak, J. Sander, M. Nowaczyk, M. G. Müller, M. Rögner and A. R. Holzwarth, Biophys. J., 2009, 96, 621–631 CrossRef CAS PubMed
.
- V. Martínez-Junza, M. Szczepaniak, S. E. Braslavsky, J. Sander, M. Nowaczyk, M. Rögner and A. R. Holzwarth, Photochem. Photobiol. Sci., 2008, 7, 1337 CrossRef
.
- G. Sipka, M. Magyar, A. Mezzetti, P. Akhtar, Q. Zhu, Y. Xiao, G. Han, S. Santabarbara, J.-R. Shen, P. H. Lambrev and G. Garab, Plant Cell, 2021, 33, 1286–1302 CrossRef
.
- W. O. Feikema, P. Gast, I. B. Klenina and I. I. Proskuryakov, Biochim. Biophys. Acta, Bioenerg., 2005, 1709, 105–112 CrossRef CAS
.
- Y. Takegawa, M. Nakamura, S. Nakamura, T. Noguchi, J. Selles, A. W. Rutherford, A. Boussac and M. Sugiura, Biochim. Biophys. Acta, Bioenerg., 2019, 1860, 297–309 CrossRef CAS PubMed
.
- S. Katagiri and Y. Kobori, Appl. Magn. Reson., 2010, 37, 177–189 CrossRef
.
- F. Van Mieghem, K. Brettel, B. Hillman, A. Kamlowski, A. W. Rutherford and E. Schlodder, Biochemistry, 1995, 34, 4798–4813 CrossRef CAS PubMed
.
- B. Hillmann, K. Brettel, F. Van Mieghem, A. Kamlowski, A. W. Rutherford and E. Schlodder, Biochemistry, 1995, 34, 4814–4827 CrossRef CAS PubMed
.
- D. Kleinfeld, M. Y. Okamura and G. Feher, Biochim. Biophys. Acta, Bioenerg., 1984, 766, 126–140 CrossRef CAS PubMed
.
- R. de Wijn and H. J. van Gorkom, Biochim. Biophys. Acta, Bioenerg., 2002, 1553, 302–308 CrossRef CAS
.
- D. Carbonera, M. Di Valentin, G. Giacometti and G. Agostini, Biochim. Biophys. Acta, Bioenerg., 1994, 1185, 167–176 CrossRef CAS
.
- J. Niklas, A. Agostini, D. Carbonera, M. Di Valentin and W. Lubitz, Photosynth. Res., 2022, 152, 213–234 CrossRef CAS
.
- S. Santabarbara, G. Agostini, A. P. Casazza, C. D. Syme, P. Heathcote, F. Böhles, M. C. W. Evans, R. C. Jennings and D. Carbonera, Biochim. Biophys. Acta, Bioenerg., 2007, 1767, 88–105 CrossRef CAS
.
- F. Lendzian, R. Bittl, A. Telfer and W. Lubitz, Biochim. Biophys. Acta, Bioenerg., 2003, 1605, 35–46 CrossRef CAS PubMed
.
- S. Santabarbara, E. Bordignon, R. C. Jennings and D. Carbonera, Biochemistry, 2002, 41, 8184–8194 CrossRef CAS PubMed
.
- M. Volk, M. Gilbert, G. Rousseau, M. Richter, A. Ogrodnik and M.-E. Michel-Beyerle, FEBS Lett., 1993, 336, 357–362 CrossRef CAS PubMed
.
- G. Raszewski, W. Saenger and T. Renger, Biophys. J., 2005, 88, 986–998 CrossRef CAS PubMed
.
- A. W. Rutherford, A. Osyczka and F. Rappaport, FEBS Lett., 2012, 586, 603–616 CrossRef CAS PubMed
.
- A. R. McIntosh and J. R. Bolton, Nature, 1976, 263, 443–445 CrossRef CAS
.
- I. Vass and S. Styring, Biochemistry, 1992, 31, 5957–5963 CrossRef CAS PubMed
.
- I. Vass, S. Styring, T. Hundal, A. Koivuniemi, E. Aro and B. Andersson, Proc. Natl. Acad. Sci. U. S. A., 1992, 89, 1408–1412 CrossRef CAS PubMed
.
- H. Mattila, S. Mishra, T. Tyystjärvi and E. Tyystjärvi, New Phytol., 2023, 237, 113–125 CrossRef CAS PubMed
.
- E.-M. Aro, I. Virgin and B. Andersson, Biochim. Biophys. Acta, Bioenerg., 1993, 1143, 113–134 CrossRef CAS PubMed
.
- I. Vass, Biochim. Biophys. Acta, Bioenerg., 2012, 1817, 209–217 CrossRef CAS
.
- I. Vass, Physiol. Plant., 2011, 142, 6–16 CrossRef CAS PubMed
.
- T. Noguchi, Plant Cell Physiol., 2002, 43, 1112–1116 CrossRef CAS PubMed
.
-
E. Schlodder, B. Hillmann, K. Brettel and F. Mallwitz, in Photosynthesis: Mechanisms and Effects: Volume I–V: Proceedings of the XIth International Congress on Photosynthesis, Budapest, Hungary, August 17–22, 1998, ed. G. Garab, Springer Netherlands, Dordrecht, 1998, pp. 1069–1072 Search PubMed
.
- J. Feng, C.-W. Tseng, T. Chen, X. Leng, H. Yin, Y.-C. Cheng, M. Rohlfing and Y. Ma, Nat. Commun., 2017, 8, 71 CrossRef PubMed
.
- S. Santabarbara, A. Agostini, A. P. Casazza, G. Zucchelli and D. Carbonera, Biochim. Biophys. Acta, Bioenerg., 2015, 1847, 262–275 CrossRef CAS PubMed
.
- S. Santabarbara and D. Carbonera, J. Phys. Chem. B, 2005, 109, 986–991 CrossRef CAS
.
- A. W. Rutherford, D. R. Paterson and J. E. Mullet, Biochim. Biophys. Acta, Bioenerg., 1981, 635, 205–214 CrossRef CAS PubMed
.
- A. W. Rutherford and J. E. Mullet, Biochim. Biophys. Acta, Bioenerg., 1981, 635, 225–235 CrossRef CAS PubMed
.
- F. J. E. Van Mieghem, K. Satoh and A. W. Rutherford, Biochim. Biophys. Acta, Bioenerg., 1991, 1058, 379–385 CrossRef CAS
.
- G. Chen, Y. Allahverdiyeva, E.-M. Aro, S. Styring and F. Mamedov, Biochim. Biophys. Acta, Bioenerg., 2011, 1807, 205–215 CrossRef CAS PubMed
.
- F. Mamedov, R. Danielsson, R. Gadjieva, P.-Å. Albertsson and S. Styring, Biochemistry, 2008, 47, 3883–3891 CrossRef CAS
.
- A. W. Rutherford, Biochim. Biophys. Acta, Bioenerg., 1985, 807, 189–201 CrossRef CAS
.
- M. K. Bosch, I. I. Proskuryakov, P. Gast and A. J. Hoff, J. Phys. Chem., 1996, 100, 2384–2390 CrossRef CAS
.
- A. Kawamori, T. A. Ono, A. Ishii, S. Nakazawa, H. Hara, T. Tomo, J. Minagawa, R. Bittl and S. A. Dzuba, Photosynth. Res., 2005, 84, 187–192 CrossRef CAS PubMed
.
- M. Kammel, J. Kern, W. Lubitz and R. Bittl, Biochim. Biophys. Acta, Bioenerg., 2003, 1605, 47–54 CrossRef CAS PubMed
.
- S. V. Pashenko, I. I. Proskuryakov, M. Germano, H. J. Van Gorkom and P. Gast, Chem. Phys., 2003, 294, 439–449 CrossRef CAS
.
- W. Lubitz, Phys. Chem. Chem. Phys., 2002, 4, 5539–5545 RSC
.
- A.-F. Miller and G. W. Brudvig, Biochim. Biophys. Acta, Bioenerg., 1991, 1056, 1–18 CrossRef CAS
.
- G. F. W. Searle, A. Telfer, J. Barber and T. J. Schaafsma, Biochim. Biophys. Acta, Bioenerg., 1990, 1016, 235–243 CrossRef CAS
.
-
M. Okamura, K. Satoh, R. Isaacson and G. Feher, Progress in Photosynthesis Research, 1987, vol. 1, pp. 379–381 Search PubMed
.
- A. Agostini, L. Nicol, N. Da Roit, M. Bortolus, R. Croce and D. Carbonera, Biochim. Biophys. Acta, Bioenerg., 2021, 1862, 148481 CrossRef CAS PubMed
.
- D. Carbonera, Photosynth. Res., 2009, 102, 403–414 CrossRef CAS PubMed
.
- T. Noguchi, T. Tomo and C. Kato, Biochemistry, 2001, 40, 2176–2185 CrossRef CAS PubMed
.
- A. A. Zabelin, K. V. Neverov, A. A. Krasnovsky, V. A. Shkuropatova, V. A. Shuvalov and A. Y. Shkuropatov, Biochim. Biophys. Acta, Bioenerg., 2016, 1857, 782–788 CrossRef CAS PubMed
.
- K. V. Neverov, A. A. Krasnovsky, A. A. Zabelin, V. A. Shuvalov and A. Y. Shkuropatov, Photosynth. Res., 2015, 125, 43–49 CrossRef CAS PubMed
.
- A. Agostini, D. M. Palm, H. Paulsen and D. Carbonera, J. Phys. Chem. B, 2018, 122, 6156–6163 CrossRef CAS PubMed
.
- S. Santabarbara, R. C. Jennings and D. Carbonera, Chem. Phys., 2003, 294, 257–266 CrossRef CAS
.
- D. E. Budil and M. C. Thurnauer, Biochim. Biophys. Acta, Bioenerg., 1991, 1057, 1–41 CrossRef CAS PubMed
.
- T. Noguchi, Y. Inoue and K. Satoh, Biochemistry, 1993, 32, 7186–7195 CrossRef CAS PubMed
.
- A. R. Holzwarth, M. G. Muller, M. Reus, M. Nowaczyk, J. Sander and M. Rogner, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 6895–6900 CrossRef CAS PubMed
.
- H. Ishikita, B. Loll, J. Biesiadka, W. Saenger and E.-W. Knapp, Biochemistry, 2005, 44, 4118–4124 CrossRef CAS PubMed
.
- F. Müh, F. Lendzian, M. Roy, J. C. Williams, J. P. Allen and W. Lubitz, J. Phys. Chem. B, 2002, 106, 3226–3236 CrossRef
.
- L. Zhang, D.-A. Silva, H. Zhang, A. Yue, Y. Yan and X. Huang, Nat. Commun., 2014, 5, 4170 CrossRef CAS PubMed
.
- F. Müh, M. Plöckinger and T. Renger, J. Phys. Chem. Lett., 2017, 8, 850–858 CrossRef PubMed
.
- A. Sirohiwal, F. Neese and D. A. Pantazis, J. Chem. Theory Comput., 2021, 17, 1858–1873 CrossRef CAS PubMed
.
- V. I. Novoderezhkin, J. P. Dekker and R. van Grondelle, Biophys. J., 2007, 93, 1293–1311 CrossRef CAS PubMed
.
- E. J. G. Peterman, H. van Amerongen, R. van Grondelle and J. P. Dekker, Proc. Natl. Acad. Sci. U. S. A., 1998, 95, 6128–6133 CrossRef CAS PubMed
.
- T. Hayase, Y. Shimada, T. Mitomi, R. Nagao and T. Noguchi, J. Phys. Chem. B, 2023, 127, 1758–1770 CrossRef CAS PubMed
.
- A. Kamlowski, L. Frankemöller, A. Van Der Est, D. Stehlik and A. R. Holzwart, Ber. Bunsen-Ges. Phys. Chem., 1996, 100, 2045–2051 CrossRef CAS
.
- J. Ho, E. Kish, D. D. Méndez-Hernández, K. Wongcarter, S. Pillai, G. Kodis, J. Niklas, O. G. Poluektov, D. Gust, T. A. Moore, A. L. Moore, V. S. Batista and B. Robert, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, E5513–E5521 CAS
.
- Y. Kato and T. Noguchi, Photosynth. Res., 2022, 152, 135–151 CrossRef CAS
.
- C. I. Bayly, P. Cieplak, W. Cornell and P. A. Kollman, J. Phys. Chem., 1993, 97, 10269–10280 CrossRef CAS
.
- E. Sigfridsson and U. Ryde, J. Comput. Chem., 1998, 19, 377–395 CrossRef CAS
.
- W. D. Cornell, P. Cieplak, C. I. Bayly, I. R. Gould, K. M. Merz, D. M. Ferguson, D. C. Spellmeyer, T. Fox, J. W. Caldwell and P. A. Kollman, J. Am. Chem. Soc., 1995, 117, 5179–5197 CrossRef CAS
.
- A. D. Becke, J. Chem. Phys., 1993, 98, 1372–1377 CrossRef CAS
.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS
.
- F. Neese, WIREs Comput. Mol. Sci., 2022, 12, e1606 CrossRef
.
- T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed
.
- F. Neese, F. Wennmohs, U. Becker and C. Riplinger, J. Chem. Phys., 2020, 152, 224108 CrossRef CAS PubMed
.
- S. J. Fox, C. Pittock, T. Fox, C. S. Tautermann, N. Malcolm and C.-K. Skylaris, J. Chem. Phys., 2011, 135, 224107 CrossRef PubMed
.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed
.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC
.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed
.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed
.
- F. Neese, F. Wennmohs, A. Hansen and U. Becker, Chem. Phys., 2009, 356, 98–109 CrossRef CAS
.
- K. Eichkorn, O. Treutler, H. Öhm, M. Häser and R. Ahlrichs, Chem. Phys. Lett., 1995, 240, 283–290 CrossRef CAS
.
- D. C. Liu and J. Nocedal, Math. Program., 1989, 45, 503–528 CrossRef
.
- M. J. G. Peach, M. J. Williamson and D. J. Tozer, J. Chem. Theory Comput., 2011, 7, 3578–3585 CrossRef CAS PubMed
.
- D. Jacquemin, E. A. Perpète, I. Ciofini and C. Adamo, J. Chem. Theory Comput., 2010, 6, 1532–1537 CrossRef CAS PubMed
.
- D. Hait, T. Zhu, D. P. McMahon and T. Van Voorhis, J. Chem. Theory Comput., 2016, 12, 3353–3359 CrossRef CAS PubMed
.
- N. Mardirossian and M. Head-Gordon, Phys. Chem. Chem. Phys., 2014, 16, 9904 RSC
.
- A. Sirohiwal, R. Berraud-Pache, F. Neese, R. Izsak and D. A. Pantazis, J. Phys. Chem. B, 2020, 124, 8761–8771 CrossRef CAS PubMed
.
- F. Neese, J. Chem. Phys., 2001, 115, 11080–11096 CrossRef CAS
.
- V. N. Staroverov, G. E. Scuseria, J. Tao and J. P. Perdew, J. Chem. Phys., 2003, 119, 12129–12137 CrossRef CAS
.
-
V. Barone, in Recent Advances in Density Functional Methods, World Scientific, 1995, vol. 1, pp. 287–334 Search PubMed
.
- F. Neese, J. Chem. Phys., 2005, 122, 034107 CrossRef PubMed
.
- F. Neese, J. Chem. Phys., 2007, 127, 164112 CrossRef PubMed
.
- S. Sinnecker and F. Neese, J. Phys. Chem. A, 2006, 110, 12267–12275 CrossRef CAS PubMed
.
- A. Ceulemans, W. Oldenhof, C. Gorller-Walrand and L. G. Vanquickenborne, J. Am. Chem. Soc., 1986, 108, 1155–1163 CrossRef CAS
.
- D. A. Hartzler, D. M. Niedzwiedzki, D. A. Bryant, R. E. Blankenship, Y. Pushkar and S. Savikhin, J. Phys. Chem. B, 2014, 118, 7221–7232 CrossRef CAS
.
- D. M. Niedzwiedzki and R. E. Blankenship, Photosynth. Res., 2010, 106, 227–238 CrossRef CAS PubMed
.
- P. D. Frischmann, K. Mahata and F. Würthner, Chem. Soc. Rev., 2013, 42, 1847–1870 RSC
.
- Y. Kobori, S. Yamauchi, K. Akiyama, S. Tero-Kubota, H. Imahori, S. Fukuzumi and J. R. Norris, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 10017–10022 CrossRef CAS PubMed
.
- M. L. Williams, I. Schlesinger, R. M. Jacobberger and M. R. Wasielewski, J. Am. Chem. Soc., 2022, 144, 18607–18618 CrossRef CAS PubMed
.
- S. M. Harvey and M. R. Wasielewski, J. Am. Chem. Soc., 2021, 143, 15508–15529 CrossRef CAS PubMed
.
- E. Schlodder, W. J. Coleman, P. J. Nixon, R. O. Cohen, T. Renger and B. A. Diner, Philos. Trans. R. Soc., B, 2008, 363, 1197–1202 CrossRef CAS PubMed
.
- M. Di Valentin, C. W. M. Kay, G. Giacometti and K. Möbius, Chem. Phys. Lett., 1996, 248, 434–441 CrossRef CAS
.
- A. Agostini, D. M. Palm, F.-J. Schmitt, M. Albertini, M. D. Valentin, H. Paulsen and D. Carbonera, Sci. Rep., 2017, 7 CAS
.
- A. Agostini, M. G. Dal Farra, H. Paulsen, A. Polimeno, L. Orian, M. Di Valentin and D. Carbonera, J. Phys. Chem. B, 2019, 123, 8232–8239 CrossRef CAS PubMed
.
- A. Marchanka, W. Lubitz and M. Van Gastel, J. Phys. Chem. B, 2009, 113, 6917–6927 CrossRef CAS PubMed
.
- F. Mokvist, J. Sjöholm, F. Mamedov and S. Styring, Biochemistry, 2014, 53, 4228–4238 CrossRef CAS PubMed
.
- P. Mulo, I. Sakurai and E.-M. Aro, Biochim. Biophys. Acta, Bioenerg., 2012, 1817, 247–257 CrossRef CAS PubMed
.
- A. K. Clarke, A. Soitamo, P. Gustafsson and G. Oquist, Proc. Natl. Acad. Sci. U. S. A., 1993, 90, 9973–9977 CrossRef CAS PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available: Tables S1–S9 and Fig. S1–S4. See DOI: https://doi.org/10.1039/d3sc02985a |
| This journal is © The Royal Society of Chemistry 2023 |