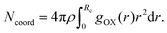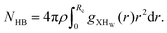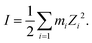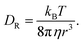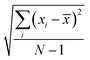Structure and dynamics of aqueous VOSO4 solutions in conventional flow through cell design: a molecular dynamics simulation study†
Received
24th July 2024
, Accepted 1st November 2024
First published on 12th November 2024
Abstract
A theoretical model has been proposed to study the structure and dynamics of aqueous vanadyl sulfate (VOSO4) solution used in the conventional flow (CF) through cell design operating under varying thermodynamic conditions. Classical molecular dynamics simulations have been carried out for aqueous solutions of vanadyl sulfate (VOSO4) and sulfuric acid (H2SO4) at two different concentrations and temperatures considering the temperature dependent degree of dissociation of sulfuric acid. The MD trajectories are used to study the equilibrium structural, dynamical properties such as viscosity, diffusivity and surface tension of the aqueous solution of vanadyl sulfate (VOSO4). According to the new model, the cation–cation and cation–anion interaction should be low in order to have a good current density in the conventional flow through cell design and further explains the importance of considering mass transport when designing high energy density redox flow batteries. The model is further validated by calculating the viscosity of each system, individual diffusion coefficient of each ion and by comparing them with the experimental data wherever they are available.
1 Introduction
Flow batteries are highly popular storage devices and can store large amounts of charge in stationary applications.1–36 Lithium batteries are very prone to igniting. They also offer a reduced cycle life (ca. 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cycles) in comparison to other devices (RFBs 20
000 cycles) in comparison to other devices (RFBs 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cycle) when used for grid scale applications. The efficiency of a flow battery depends on the power and energy density, which directly depends on the redox potential and solubility of ions in aqueous solution. In second generation redox flow batteries, these two parameters can be implemented individually. One can increase the efficiency of a flow cell by increasing the energy density without affecting the power density by directly increasing the solubility of redox active species. A significant number of experimental and theoretical studies have been done to increase the efficiency of all vanadium redox flow batteries and their optimization. However, very few theoretical studies32–39 have been carried out to understand the chemical physics behind the solubility of the redox active species in complex solution currently found in the field of aqueous vanadium redox flow batteries. Most theoretical32–39 models created in this field contain one vanadium ion in water and are for a binary mixture solution. The effect on the structural dynamical properties due to the presence of other ions has not been mentioned in these theoretical models. The real system shows a very strong regular solution behavior. To understand how the redox flow battery works, it is absolutely necessary to understand the dynamics of the electrolyte, solvent and additive roles at varying compositions and at different thermodynamic states using the principles of statistical mechanics. In 2020, the work published in the journal of power sources31 shows that the increasing polarization of the cell decreases the cell voltage in a conventional redox flow battery. Therefore, the polarization losses through charge transfer, ohmic resistance and mass transport limitation should be controlled to increase the energy density of the redox flow cell. All these factors responsible for the polarization loss depend on the cell material. One of the most important factors in this field is electrolyte resistance which is influenced by the electrolyte thickness and ionic conductivity of the aqueous solution. It is known that reducing electrolyte thickness and increasing ionic conductivity is a more efficient way to lower the electrolyte resistance, to control the cell polarization and to increase the voltage efficiency of the flow battery. The electrolyte thickness depends on the viscosity and surface tension of the medium. According to the study, the electrolyte conductivity for the positive and negative electrolyte of the VRFB increases with increasing the concentration of sulfuric acid and decreasing the concentration of vanadium. It was shown that reducing the surface tension of the electrolyte reduces the electrolyte leakage and thus increases the stack lifetime and its maintenance cost. The low concentration of vanadium ions with a high concentration of sulfuric acid at the high temperature can contribute to the enhanced energy density in the conventional VRFB. However, these experimental findings have not been explained from the microscopic point of view. What are the driving forces at the molecular level and how do they influence all these chemical and physical properties at the macro-scale? It is known that ion-pair or ion-cluster formation may occur in concentrated aqueous solution and this may increase the electrostatic interactions in the solution with respect to the dilute solution of ∼1 M strength.40,41 The diffusion of the active species and how it influences the overall solvation mechanism and affects the other transport properties of the aqueous ionic solution are important factors to be understood in the field of the redox flow batteries. During the dissolution process, the diffusion plays a very important role according to the Noyes–Whitney equation42 however, it is not the sole governing factor of the solubility and affects the dissolution rate, viscosity and, ionic conductivity of the media. Hence, it is necessary to understand the transport behavior of the aqueous solution and investigating the role of ion-pair and ion-cluster formation at the molecular level for the systematic design of a redox flow battery. Sulfuric acid used in all vanadium redox flow batteries undergoes a temperature dependent dissociation process. Thus, it plays an important role in the solubility of redox active species in VRFB operating over varying thermodynamic conditions. The role of the acid on the dynamical properties of redox active species needs to be understood from the microscopic point of view.
000 cycle) when used for grid scale applications. The efficiency of a flow battery depends on the power and energy density, which directly depends on the redox potential and solubility of ions in aqueous solution. In second generation redox flow batteries, these two parameters can be implemented individually. One can increase the efficiency of a flow cell by increasing the energy density without affecting the power density by directly increasing the solubility of redox active species. A significant number of experimental and theoretical studies have been done to increase the efficiency of all vanadium redox flow batteries and their optimization. However, very few theoretical studies32–39 have been carried out to understand the chemical physics behind the solubility of the redox active species in complex solution currently found in the field of aqueous vanadium redox flow batteries. Most theoretical32–39 models created in this field contain one vanadium ion in water and are for a binary mixture solution. The effect on the structural dynamical properties due to the presence of other ions has not been mentioned in these theoretical models. The real system shows a very strong regular solution behavior. To understand how the redox flow battery works, it is absolutely necessary to understand the dynamics of the electrolyte, solvent and additive roles at varying compositions and at different thermodynamic states using the principles of statistical mechanics. In 2020, the work published in the journal of power sources31 shows that the increasing polarization of the cell decreases the cell voltage in a conventional redox flow battery. Therefore, the polarization losses through charge transfer, ohmic resistance and mass transport limitation should be controlled to increase the energy density of the redox flow cell. All these factors responsible for the polarization loss depend on the cell material. One of the most important factors in this field is electrolyte resistance which is influenced by the electrolyte thickness and ionic conductivity of the aqueous solution. It is known that reducing electrolyte thickness and increasing ionic conductivity is a more efficient way to lower the electrolyte resistance, to control the cell polarization and to increase the voltage efficiency of the flow battery. The electrolyte thickness depends on the viscosity and surface tension of the medium. According to the study, the electrolyte conductivity for the positive and negative electrolyte of the VRFB increases with increasing the concentration of sulfuric acid and decreasing the concentration of vanadium. It was shown that reducing the surface tension of the electrolyte reduces the electrolyte leakage and thus increases the stack lifetime and its maintenance cost. The low concentration of vanadium ions with a high concentration of sulfuric acid at the high temperature can contribute to the enhanced energy density in the conventional VRFB. However, these experimental findings have not been explained from the microscopic point of view. What are the driving forces at the molecular level and how do they influence all these chemical and physical properties at the macro-scale? It is known that ion-pair or ion-cluster formation may occur in concentrated aqueous solution and this may increase the electrostatic interactions in the solution with respect to the dilute solution of ∼1 M strength.40,41 The diffusion of the active species and how it influences the overall solvation mechanism and affects the other transport properties of the aqueous ionic solution are important factors to be understood in the field of the redox flow batteries. During the dissolution process, the diffusion plays a very important role according to the Noyes–Whitney equation42 however, it is not the sole governing factor of the solubility and affects the dissolution rate, viscosity and, ionic conductivity of the media. Hence, it is necessary to understand the transport behavior of the aqueous solution and investigating the role of ion-pair and ion-cluster formation at the molecular level for the systematic design of a redox flow battery. Sulfuric acid used in all vanadium redox flow batteries undergoes a temperature dependent dissociation process. Thus, it plays an important role in the solubility of redox active species in VRFB operating over varying thermodynamic conditions. The role of the acid on the dynamical properties of redox active species needs to be understood from the microscopic point of view.
In this paper, we have set up a molecular dynamics simulation to study the chemical physical properties of the systems mentioned in ref. 31. Here, we are interested in revealing the structural and dynamical features of the redox active species at varying thermodynamic conditions and to find the underlying principles behind them. In the experimental paper,31 the conventional flow through battery was composed of vanadyl sulfate (VOSO4) solution in the positive and negative compartment of the redox flow battery with twice the volume used on the positive side. Therefore, the catholyte or posolyte was 0.5 M VOSO4 + 3.5 M H2SO4 and the anolyte or negolyte was 1.7 M VOSO4 + 3 M H2SO4, respectively. The conventional flow battery was constructed at two different temperatures such as 25 °C and 50 °C, respectively. In the molecular dynamics simulation, the same catholyte and anolyte have been modeled using the GROMACS molecular dynamics simulation package. The classical molecular dynamics simulation generated trajectories are then used for the study of different equilibrium structural and dynamical properties of the solutions. The structural properties have been thoroughly investigated by computing the radial distribution functions between the important sites. The other specific properties which have been looked at in this theoretical study are: (i) diffusivity of the individual ionic species, (ii) viscosity and, (iii) surface tension of the solutions. All theoretical studies have been carried out for two different temperatures and for varying concentrations of VOSO4 and sulfuric acid (H2SO4). The diffusivity of each ionic species has been computed using Fick's Law of diffusion.43 The shear viscosities are estimated using the Green–Kubo relationship.43 The static surface tension (SFT) has been computed from the diagonal components of the pressure tensors.43,44 The calculated results for all these solutions have been compared with the experimental results already available in this field.
The remaining paper has been organized in the following way. In Section 2, the details of the classical molecular dynamics simulation including the computational strategy of diffusivity, viscosity and surface tension have been given. In Section 3 the results on the density, radial distribution functions, hydrogen bond and ionic strength, diffusion coefficient of each ionic species, viscosity and surface tension of the solution have been discussed. Concluding remarks have been made in Section 4.
2 Computational details
The computational details have been divided into three sections. In the first section, a description about the systems and their set up have been given with the strategy to estimate the experimental density of the systems of interest. The inclusion of the degree of sulfuric acid dissociation and the approach to incorporate this in the molecular dynamics simulation have been given in the next section. In the third section, the computational technique for the diffusivity, viscosity and surface tension of the aqueous solution has been given.
2.1 Simulation
The molecular dynamics simulation was set up for the following systems: (1) 0.5 M VOSO4 in 3.5 M H2SO4 at 25 °C, (2) 0.5 M VOSO4 in 3.5 M H2SO4 at 50 °C, (3) 1.7 M VOSO4 in 3 M H2SO4 at 25 °C, (4) 1.7 M VOSO4 in 3 M H2SO4 at 50 °C and (5) 1 VO2+ in 1000 water molecules at 25 °C. We also set up the additional MD simulations for 3 M and 3.5 M H2SO4 at 25 °C and 50 °C without VOSO4 to study the effect of it on the structure of the liquid. The details of the MD simulations are given in Table 1. The additional MD simulations are named (6) 3.5 M H2SO4 at 25 °C, (7) 3.5 M H2SO4 at 50 °C, (8) 3 M H2SO4 at 25 °C, and (9) 3 M H2SO4 at 50 °C in Table 1. The box length of each simulation has been decided from their experimental densities. The experimental density of sulfuric acid (H2SO4) and water at a particular temperature has been calculated using the formula used in the work of Novotný et al. for the binary mixture.45 During the calculation of the box length, the degree of dissociation of sulfuric acid is included implicitly in terms of the number of individual species using the methodology described in the work of Myhre et al.46 From the binary mixture, the ternary mixture solution containing vanadyl sulfate (VOSO4), sulfuric acid (H2SO4) and water (H2O) is made. The density of that ternary mixture has been calculated following the strategy mentioned in ref. 4, 29 and 30. The working formula for the density of water at different temperature is| | | dH2O = 999.65 + 2.0438 × 10−1t − 6.1744 × 10−2t3/2, | (1) |
where t is the temperature of the solution. The density of the sulfuric acid solution can be found below| | | d = dH2O + Ac + Bct + Cct2 + Dc3/2 + Ec3/2t + Fc3/2t2. | (2) |
Table 1 The fitting parameters for eqn (2)
|
A
|
B
|
C
|
D
|
E
|
F
|
| 70.6 |
−0.2367 |
0.0017 |
−4.903 |
0.05698 |
−0.0003985 |
The parameters of the above equation are given in Table 1. Where, c is the concentration of sulfuric acid solution and t is the temperature of the solution. The density of the ternary solution in terms of VOSO4, H2SO4 and water has been calculated by using the following equation4,29,30
| | | dV = dH2SO4 + C1M1 + C2M2. | (3) |
where,
dV is the density of aqueous VOSO
4 solution in g cm
−3,
dH2SO4 is the density of sulfuric acid solution in g cm
−3,
M1 is the concentration of sulfuric acid in the molarity unit,
M2 is the concentration of the V in the molarity unit, and
C1 and
C2 are the adjustable parameters in the above equation at 20 °C. The parameters
C1 and
C2 have been given in
Table 2. We noticed that this above formula has been proposed in ref.
4,
29 and
30 for calculating the experimental density of vanadium(
V) ion solutions. It is noteworthy in this regard that in all vanadium redox flow batteries, in the catholyte compartment vanadium ion presents in both +IV and +V oxidation states and at a 1
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
:
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
1 molar ratio. Therefore, the same expression for the density calculation of aqueous vanadyl solution has been adapted here.
Table 2 The fitting parameters for eqn (3)
2.2 Dissociation of the sulfuric acid
The dissociation process of sulfuric acid (H2SO4) is given below| |  | (4) |
| |  | (5) |
where, α1 and α2 are the first and second degree of dissociation of sulfuric acid, respectively. It is known from the various experimental studies that the first step is completely dissociated i.e., α1 = 1.0, while the second step (α2) involves partial dissociation of the acid at different concentrations and at different temperatures.46,47 Therefore, the aqueous solution of sulfuric acid is composed of four different molecular species: H3O+, HSO4−, SO42−, and H2O depending on the concentration and temperature. According to ref. 46 the concentration of HSO4−, SO42−, H3O+ and H2O are given as| | | [HSO4−] = CO,SA × (1 − α2); [SO42−] = CO,SA × α2; [H3O+] = CO,SA × (1 + α2); | (6) |
| | 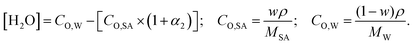 | (7) |
where, w is the sulfuric acid weight fraction and ρ is the density. The ionic concentrations are related as [H3O+] = [HSO4−] + 2 × [SO42−]. The degree of dissociation of sulfuric acid at a particular concentration and temperature has been calculated using the polynomial equation:46| | 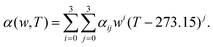 | (8) |
where, the first term at the right hand side is the degree of dissociation, w is the acid weight fraction and T is the temperature. The parameters have been taken from ref. 46 and can be found in Table 3. The temperature, calculated degree of dissociation, the density of sulfuric acid solution, the density of the solution containing VOSO4 in sulfuric acid solution, concentration of H2SO4 acid in the molarity and the molality scale are given in Table 4. The force field parameters for SO42− and HSO4− have been taken from the work in ref. 48 and 49, respectively. The same for H3O+ and H2O has been modeled using the SPC/E model for water.50 The ternary solution is composed of five different molecular entities: VO2+, H3O+, HSO4−, SO42− and H2O. Therefore, our all MD simulation systems are quinary in terms of the species present in the aqueous solutions. The force field parameters for vanadyl ion (VO2+) have been taken from ref. 33 and 34. All MD simulations have been run using GROMACS-2022 software version.51–55 The MD systems have been setup using PACKMOL Software56,57 for any random initial configuration. The all MD simulations have been performed within the periodic boundary condition to compute the structural and dynamical properties of all nine systems. The simulation box length has been calculated from the experimental densities for all systems. The simulation has been performed by following MD steps: (i) energy minimization has been performed to remove any hard contact between the species followed by (ii) the equilibration in the NVT ensemble followed by (iii) the equilibration in NPT ensemble followed by (iv) a production run in NVT ensemble to compute the various structural and dynamical properties for all systems. The details of the MD simulation set up have been given in Tables 5, 7 and in the ESI.† The force field parameters are given in Tables S1 and S2 in the ESI.† The geometrical shape and atom type nomenclature of each species have been given in Fig. S1–S5 in the ESI.† The experimental and calculated concentration of H3O+, HSO4− and SO42− using eqn (6) and (7) have been shown in Table 6 for systems 1–9. The concentration calculation has been done with the molality information provided in Table 4. The number of VOSO4 is obtained from the experimental density at a given box length in Table 5.
Table 3 The fitting parameters for eqn (8)
|
α
ij
|
j = 0 |
j = 1 |
j = 2 |
j = 3 |
|
i = 0 |
0.3933176 |
−0.0064027 |
−0.000026295 |
0.000000197 |
|
i = 1 |
1.2261331 |
−0.0128949 |
— |
— |
|
i = 2 |
−2.9175425 |
0.030305 |
0.0001422 |
— |
|
i = 3 |
1.1260874 |
— |
— |
— |
Table 4 The details of system density, temperature, degree of dissociation and concentration of sulfuric acid
| Systems |
Temperature (°C) |
α
w,T H2SO4 |
d
H2SO4 (kg m−3) |
d
VOSO4 (kg m−3) |
wt (%) H2SO4 |
Molarity H2SO4 (M) |
Molality H2SO4 (m) |
| 1 |
25 |
0.34 |
1202.68 |
1221.0 |
28.54 |
3.5 |
4.07 |
| 2 |
50 |
0.14 |
1188.39 |
1208.0 |
28.87 |
3.5 |
4.14 |
| 3 |
25 |
0.33 |
1174.86 |
1298.1 |
25.00 |
3.0 |
3.40 |
| 4 |
50 |
0.13 |
1161.04 |
1284.3 |
25.33 |
3.0 |
3.46 |
Table 5 The number of ions and water molecules for system 1–9
| Systems |
VO2+ |
H3O+ |
HSO4− |
SO42− |
H2O |
Box length (nm) |
Total species |
| 1 |
16 |
393 |
193 |
116 |
3607 |
5.20 |
4325 |
| 2 |
15 |
342 |
252 |
60 |
3658 |
5.22 |
4284 |
| 3 |
73 |
326 |
164 |
154 |
3674 |
5.17 |
4364 |
| 4 |
77 |
261 |
197 |
109 |
3739 |
5.17 |
4383 |
| 5 |
1 |
— |
— |
— |
1000 |
3.18 |
1001 |
| 6 |
— |
393 |
193 |
100 |
3607 |
5.18 |
4293 |
| 7 |
— |
342 |
252 |
45 |
3658 |
5.21 |
4254 |
| 8 |
— |
326 |
164 |
81 |
3674 |
5.14 |
4218 |
| 9 |
— |
261 |
197 |
32 |
3739 |
5.13 |
4229 |
Table 6 The calculated and experimental concentration of H3O+, HSO4− and, SO42− for systems 1–9 except for system 5 according to eqn (6) and (7)
| System |
Molality (m) |
H3O+ |
HSO4− |
SO42− |
| 1, 6 |
Exp. |
5.45 |
2.70 |
1.38 |
| Cal. |
5.46 |
2.68 |
1.39 |
|
|
| 2, 7 |
Exp. |
4.72 |
3.56 |
0.58 |
| Cal. |
4.75 |
3.50 |
0.63 |
|
|
| 3, 8 |
Exp. |
4.52 |
2.31 |
1.12 |
| Cal. |
4.53 |
2.28 |
1.13 |
|
|
| 4, 9 |
Exp. |
4.00 |
3.01 |
0.45 |
| Cal. |
3.63 |
2.74 |
0.44 |
Table 7 The molecular dynamics simulation run lengths for systems 1–9
| Systems |
Equilibrium (ns) |
Production (ns) |
| NVT |
NPT |
NVT |
Total |
| 1 |
10 |
20 |
50 |
80 |
| 2 |
10 |
20 |
50 |
80 |
| 3 |
10 |
30 |
50 |
90 |
| 4 |
5 |
30 |
50 |
85 |
| 5 |
2 |
10 |
25 |
37 |
| 6 |
10 |
20 |
50 |
80 |
| 7 |
10 |
20 |
50 |
80 |
| 8 |
10 |
20 |
50 |
80 |
| 9 |
10 |
20 |
50 |
80 |
2.3 Computation of dynamical properties
2.3.1 Diffusion.
The Fickian diffusion coefficient is calculated using the Einstein relationship43,58| | 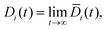 | (9) |
| | 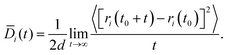 | (10) |
where, Di(t) is the self-diffusion constant for species i, d is the dimension of a system and the numerator is the mean square displacement (MSD). The self diffusion coefficient calculated in this study has been corrected using the Yeh Hummer (YH)59 correction factor to eliminate error due to the finite simulation box size (with periodic boundary conditions). The Yeh Hummer factor was| | 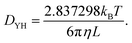 | (11) |
where, DYH is the correction term, kB is the Boltzmann's constant, T is the absolute temperature, η is the viscosity and L is the box size. The calculated diffusion coefficient will be read following this equation Dcal = DPBC + DYH. All diffusion calculations have been performed from the single 50 ns MD trajectory run in the NVT ensemble for each system by fitting the MSD vs. t plot from 2 ns to 10–20 ns. To check the convergence of the diffusion data, we also calculated the β term following the definition and characteristic feature of it.60 It is known that dense ionic solution has a tendency to show a ballistic region at short times (MSDβt, β = 2), followed by a plateau region (MSDβt, β < 1) then the diffusive region (MSDβt, β = 1) at long times. Being disturbed by the heavy noise, it is suggested to use the region for which the β = 1 of the MSDβt to obtain the diffusion coefficient. The β(t) can be used to identify the diffusive region of the MSD following this60| | 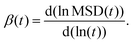 | (12) |
The ln (![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ) stands for the natural logarithm and MSD (t) is the mean square displacement at time t. As a guide for the eyes, we also plotted the log–log plot to see any noticeable changes in the diffusion behaviors of the ions and water molecules. The log–log plot shows the three regions of the MSD which is missing from the linear plot. The plots related to the diffusive motion of the species are shown in the Fig. S6–S8 in the ESI.†
) stands for the natural logarithm and MSD (t) is the mean square displacement at time t. As a guide for the eyes, we also plotted the log–log plot to see any noticeable changes in the diffusion behaviors of the ions and water molecules. The log–log plot shows the three regions of the MSD which is missing from the linear plot. The plots related to the diffusive motion of the species are shown in the Fig. S6–S8 in the ESI.†
2.3.2 Viscosity.
The dynamic (shear) viscosity of a fluid expresses its resistance to shearing flows, where adjacent layers move parallel to each other with different speeds. The equilibrium shear viscosity in molecular dynamics simulations has been computed using auto-correlation of the pressure tensor component43| | 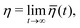 | (13) |
| | 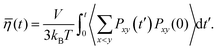 | (14) |
where, Pxy(t′) is the pressure tensor at time t = t′ and Pxy(0) is the pressure tensor at time t = 0. During an MD simulation run, it is very difficult to converge the pressure auto correlation which often suffers due to the rapid fluctuations. Therefore, the noise accumulated over a long time makes it difficult to converge for a reliable viscosity value. Hence, averaging over the multiple independent runs is required to obtain a better convergence than a single long trajectory. We have run for each system 10 independent MD simulations in the NVT ensemble to compute the viscosity using the last gro file generated after the equilibration in the NPT and NVT ensemble for each systems. At room temperature, each MD run length is 6 ns for the dilute solution of VOSO4 while the same is 10 ns for the concentrated solution. This is adapted for the better convergence of the viscosity data at room temperature. We also assumed that the high viscosity value needs a much longer run for converging to a reliable data. At higher temperature, each MD run length is 4 ns for the dilute and concentrated solution. This has been done because the dynamics will be fast at the high temperature with respect to the ambient condition. The viscosity of the medium will be low at the high temperature because it depends on the strength of the molecular interactions which will be low at the high temperature. The total MD simulation run length for each system is 100 ns for system 3, 60 ns for system 1, 40 ns for system 2 and 4, and 30 ns for system 5, respectively. Since viscosity depends on the intermolecular interaction between the molecules of a system, to study that effect, we computed the same using our in-house code for each system presented in this work and compared the results with the structural properties of the aqueous solution in the results and discussions section.
2.3.3 Surface tension.
The static surface tension (SFT) or interfacial tension is calculated from the diagonal components of the pressure tensor Pii where lz is the length of the simulation box in the direction parallel to the interface normal, here the z-axis.44| | 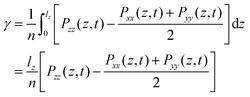 | (15) |
where, n is the number of surfaces. Pxx, Pyy and Pzz are the pressure tensor along the x, y and z axis, respectively. To compute the surface tension, we simulate the vapor–liquid system for 10 ns in NVT ensemble for systems 1 and 2 and calculate the surface tension from the last 8 ns MD trajectories. First 2 ns has been left for the equilibration of the systems. To simulate the vapor–liquid interface, the box length along the z axis is increased by 4 times with respect to the box length along the x and y axis for all systems. To generate the files for the surface tension calculation, the last gro file generated after 50 ns MD simulation in NVT ensemble is used for system 1 and 2 only. The calculated SFT corresponds to the value of surface tension in the thermodynamic equilibrium independent of time. The obtained surface tension in this study is for the top and bottom interface due to the periodic boundary condition. Therefore, to obtain the surface tension of one interface it is necessary to divide this value by 2 times the surface area. To check the noise present in the surface tension calculation, we generated 5 independent trajectories of 10 ns each after a 50 ns MD run in the NVT ensemble in the production phase for system 1 only. The Piivs. t plot has been shown in Fig. S10 (ESI†) for each run and the corresponding calculated pressure tensor along the x, y and z axis has been given beside each plot. The uncertainty present in the computed result has been calculated using the standard error of the mean27| |  | (16) |
and| |  | (17) |
where, σE is the standard deviation, N is the sample size, xi is the ith value of a property and ![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) is the mean and δE is the standard error of mean (SEM). The error %δE has been calculated by dividing δE by
is the mean and δE is the standard error of mean (SEM). The error %δE has been calculated by dividing δE by ![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) multiplied by 100. The calculated average surface tension for system 1 is 65.39 N m−1 (±0.21). We noticed that the error percentage present in the SFT simulation is ∼0.32%. The computed surface tensions for each run and relevant error analysis are shown in Table 8. The experimental surface tension was not reported for system 1 in ref. 31. However, one will know that the presence of the ionic species in solution will increase the cohesive energy of the system and thus, the surface tension of it. Cohesive forces are affected by the hydrogen bonding and van der Waals interaction. It will depend on the ionic strength of the medium. We have extracted a relationship between the surface tension and the predicted ionic strength of the medium for which experimental SFT values were reported in ref. 31. In the experimental paper, 2.6 M H2SO4 was used to dissolve VOSO4 at varying temperature to obtain the experimental SFT values. For any particular temperature, the SFT shows a linear relationship with the concentration of dissolved VOSO4 as the concentration of H2SO4 is constant. The SFT will directly depend on the ionic strength of the medium because it depends on the concentration of the ionic species. Therefore, a SFT value for an unknown system was predicted by following the relationship γi/γj = Ii/Ij for the aqueous vandium redox flow battery in this study. Where, γi and γj are the experimental SFT and Ii and Ij are the ionic strength of the ith and jth system, respectively. According to the above relationship, the predicted experimental surface tension for system 1 and 2 would be 57.55 and 45.39 N m−1 at 25 °C and 50 °C, respectively. Hence, the computed surface tension is within 14% and 16% in error with respect to the predicted experimental SFT for system 1 and 2, respectively.
multiplied by 100. The calculated average surface tension for system 1 is 65.39 N m−1 (±0.21). We noticed that the error percentage present in the SFT simulation is ∼0.32%. The computed surface tensions for each run and relevant error analysis are shown in Table 8. The experimental surface tension was not reported for system 1 in ref. 31. However, one will know that the presence of the ionic species in solution will increase the cohesive energy of the system and thus, the surface tension of it. Cohesive forces are affected by the hydrogen bonding and van der Waals interaction. It will depend on the ionic strength of the medium. We have extracted a relationship between the surface tension and the predicted ionic strength of the medium for which experimental SFT values were reported in ref. 31. In the experimental paper, 2.6 M H2SO4 was used to dissolve VOSO4 at varying temperature to obtain the experimental SFT values. For any particular temperature, the SFT shows a linear relationship with the concentration of dissolved VOSO4 as the concentration of H2SO4 is constant. The SFT will directly depend on the ionic strength of the medium because it depends on the concentration of the ionic species. Therefore, a SFT value for an unknown system was predicted by following the relationship γi/γj = Ii/Ij for the aqueous vandium redox flow battery in this study. Where, γi and γj are the experimental SFT and Ii and Ij are the ionic strength of the ith and jth system, respectively. According to the above relationship, the predicted experimental surface tension for system 1 and 2 would be 57.55 and 45.39 N m−1 at 25 °C and 50 °C, respectively. Hence, the computed surface tension is within 14% and 16% in error with respect to the predicted experimental SFT for system 1 and 2, respectively.
Table 8 Computed surface tension for system 1 and relevant analysis
3 Results and discussions
3.1 Density
At the NPT MD simulation step, the density of all the systems have been checked and the box length for each MD simulation at the production phase run has been adjusted according to the result obtained in the NPT simulation. The density convergence for all four systems is shown in Fig. 1 for system 1–4 and in Fig. 2(a) for system 5. The all experimental densities of aqueous VOSO4 solution have been calculated by using the empirical eqn (3). In Table 9, the lists of experimental densities, the computed densities from the MD simulation and the calculated error percentages have been shown for all systems. For system 5, the density of pure water at 25 °C has been used. In Fig. 2(b), a correlation between experimental and calculated density has been shown and are found to be in good agreement with a correlation coefficient value R2 = 0.99. The calculated % error is found to be within the 2.4% for the given set of the force field parameter used in this work. This error is within the range of error reported in ref. 61 and 62. The experimental densities predicted using empirical eqn (3) are found to be in good agreement with the results reported in ref. 63 for all vanadium redox flow batteries.
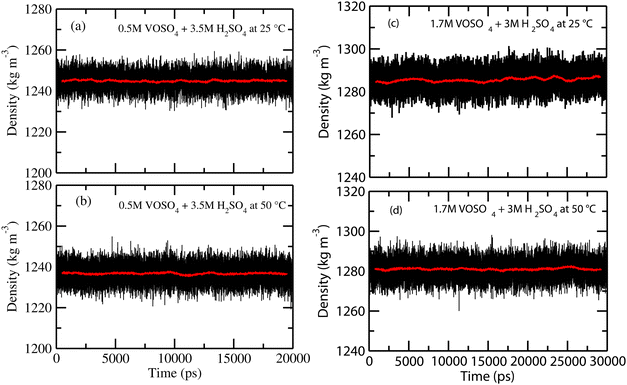 |
| | Fig. 1 The calculated density for systems 1–4. | |
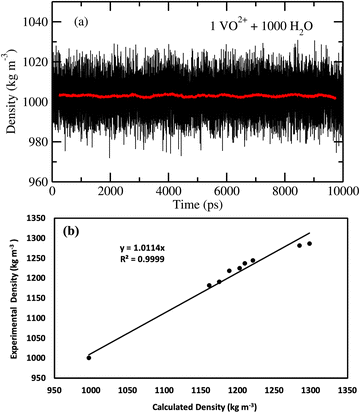 |
| | Fig. 2 (a) The fluctuation in density of system 5. (b) The experimental density versus the calculated density. | |
Table 9 The computed density versus the experimental density with % error for each system
| Systems |
Exp. density (kg m−3) |
Cal. density (kg m−3) |
Error (%) |
| 1 |
1221.00 |
1244.0 |
−1.88 |
| 2 |
1208.00 |
1236.5 |
−2.36 |
| 3 |
1298.10 |
1286.0 |
0.93 |
| 4 |
1284.30 |
1281.0 |
0.26 |
| 5 |
997.00 |
1000.0 |
−0.30 |
| 6 |
1202.70 |
1216.2 |
−1.10 |
| 7 |
1188.39 |
1210.8 |
−1.88 |
| 8 |
1174.86 |
1190.6 |
−1.34 |
| 9 |
1161.04 |
1181.3 |
−1.74 |
3.2 Radial distribution function
The structural properties have been looked at by computing the radial distribution functions between the important interacting sites. The radial distribution function (rdf) between the vanadium atom of the VO2+ ion and the oxygen atom of the water molecule and the vanadyl ion is shown in Fig. 3(a) and the rdf between the oxygen atom and vanadium atom of the vanadyl ion is shown in Fig. 3(b). From the radial distribution function, it is known that the vanadium ion is surrounded by the five oxygen atoms of the water molecules through the coordinate or dative bond formation between vanadium and oxygen atoms of the water molecule. One oxygen atom covalently bonded with the vanadium atom and that is reflected from the very strong first peak in the RDFs between the vanadium and oxygen atom shown in Fig. 3(a) and (b). The corresponding running coordination numbers have been shown by using the dashed solid line in all rdfs. We computed the coordination number using the following equation:| | 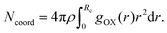 | (18) |
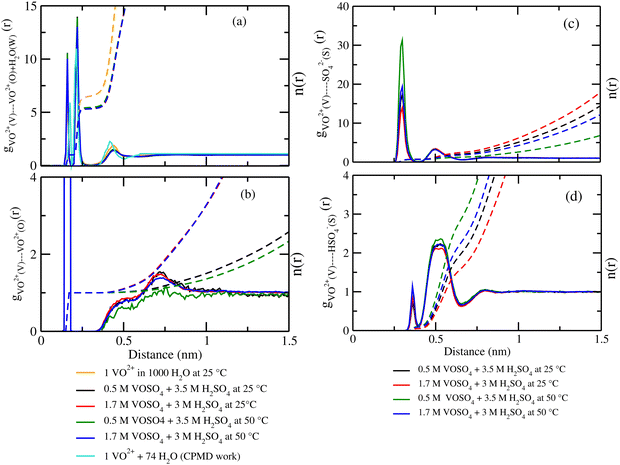
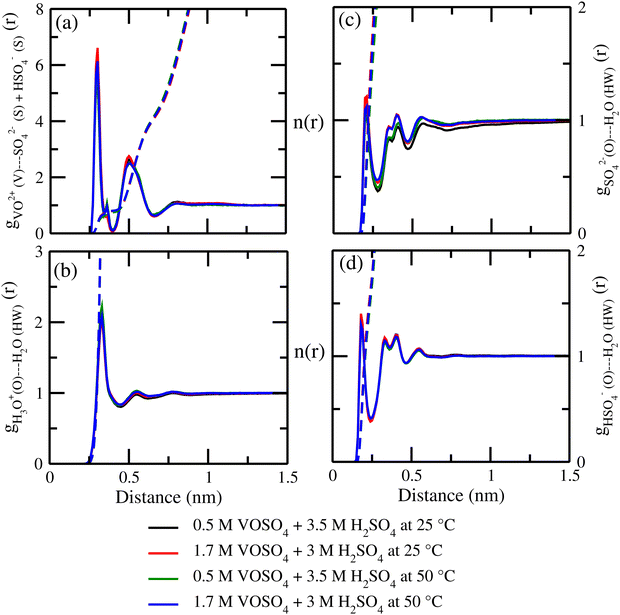
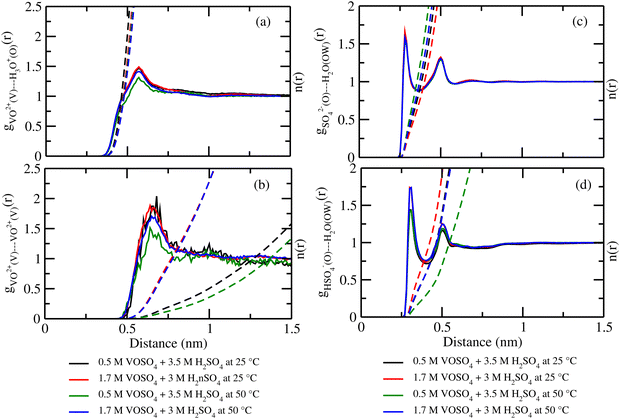
where, X = VO2+ and ρ is the average number density and Rc is the cut-off distance corresponding to the location of the first minimum of the VO2+⋯O correlation shown in Fig. 3(a). The calculated coordination number around the central vanadium ion is found to be equal to 6 in all systems. The result in Fig. 3(a) has been further supported by the rdf results reported in ref. 35. In Fig. 3(c) and (d), SO42− and HSO4− ions are found to present in the second coordination shell of the vanadyl ion and this is in good agreement with the work reported in ref. 35. A significant change in the peak height of the radial distribution functions has been noticed in Fig. 3(b) and (c). In Fig. 3(b), the peak height of the rdfs between the vanadium and oxygen atom of the vanadyl ion is found to decrease with increasing temperature and decreasing concentration of VOSO4 in the solution. This is indicative towards the decreasing intermolecular interaction between vanadyl ions in the solution at the high temperature. This decreasing cation–cation interaction is responsible for the high ionic conductivity reported in ref. 31 of the solution. In Fig. 3(c), the peak height of the rdf between the vanadium ion of the vanadyl ion and the sulfur atom of the sulfate anion is found to increase with increasing temperature and decreasing concentration of VOSO4 in the solution. The increasing cation–anion interaction will correspond to the peak height in that case. However, the same is not observed in the case of bisulfate anion. Therefore, the net effect due to these sulfur atoms on the vanadium of the vanadyl ion will be different and this is shown in Fig. 4(a). The decreasing peak height of the radial distribution function between sulfur of SO42− + HSO4− and the vanadium of the vanadyl ion indicates towards the decreasing viscosity of the system at the high temperature. Such observation corresponds to the overall net lowering of vanadyl and SO42− + HSO4− ion interaction in the solution. This also indicates the formation of more free VO2+ ions in the solution and thus is responsible for the increasing ionic conductivity of it at the low concentration of VOSO4 and at high temperature. In Fig. 5(a), the rdf between the vanadium of the vanadyl ion and oxygen of the hydronium ion is shown. It is clear from the figure that hydronium ion present in the second coordination shell of vanadyl ion and the interaction between them is found to decrease with increasing temperature and decreasing VOSO4 concentration. The intermolecular interaction between the two vanadium of a vanadyl ion is shown in Fig. 5(b) and this result has similarity with the result reported in Fig. 3(b). Both rdfs are indicative towards the decreasing cation–cation interaction at the high temperature and at the low concentration of VOSO4. In Fig. 5(c) and (d), the interaction between the oxygen atom of the water molecule and sulfur atom of sulfate and bisulfate anion is shown for all systems. This interaction becomes predominant after the first coordination shell of vanadium of the vanadyl ion and further confirmed that there was no presence of sulfate and bisulfate anion in the first coordination shell of the vanadyl ion. The first coordination shell of the vanadyl ion is found to complete ∼2.5 Å according to Fig. 3(a). This result of VO2+ is in good agreement with the CPMD work in ref. 36 and the experimental result reported in ref. 63. The CPMD result is shown in Fig. 3(a) for the comparison. In Fig. 6(a) and (b), the two important rdfs have been shown. They are an oxygen atom of water and sulfur atom of sulfate and bisulfate anion in Fig. 6(a) and an oxygen atom of hydronium anion and sulfur atom of sulfate and bisulfate anion in Fig. 6(b). The rdfs shown in Fig. 5(c) and 6(a) are the same, however, in Fig. 5(c) only a sulfur atom coming from sulfate ion and in Fig. 6(a) a sulfur atom coming from sulfate and bisulfate ion are shown. From individual rdfs shown in Fig. 5(c) and (d), it is known that these two ions interact with the vanadium of the vanadyl ion in a different way and present in the second coordination shell of the vanadyl ion. In Fig. 6(c) and (d), the interaction between oxygen and hydrogen atom and oxygen–oxygen atom interaction in liquid water have been shown to understand the modification of the 3-D hydrogen bonded network in the presence of the foreign solutes in water. The radial distribution functions between SO42− (O)⋯H2O (HW), HSO4− (O)⋯H2O (HW) and H3O+ (O)⋯H2O (HW) are shown in Fig. 4. According to the work in ref. 35, the octahedral structure of vanadium(IV) species is stable up to the concentration of 3 M and between 240–340 K temperature. We also calculated the coordination number around SO42− and HSO4− using eqn (18) considering X = OS. The calculated coordination number is found to be ∼6 for SO42− and ∼5 for HSO4− which are within the range of the coordination number reported in ref. 64 and 65 for infinite dilute aqueous solutions of sulfate and bisulfate ion, and63 for varying concentration of aqueous vanadyl sulfate solution. The predicted theoretical result is found to be in good agreement with the result for VO2+ ion reported in ref. 35.
 |
| | Fig. 3 The radial distribution function for (a) vanadium of the VO2+ ion and oxygen of the H2O molecule, (b) vanadium of the VO2+ ion and oxygen of the VO2+ ion, (c) vanadium of the VO2+ ion and sulfur of the SO42− ion and (d) vanadium of the VO2+ ion and sulfur of the HSO4− ion interaction for system 1–4. The CPMD result has been taken from ref. 36. | |
 |
| | Fig. 4 The radial distribution function for (a) vanadium of the VO2+ ion and sulfur of the HSO4− + SO42− ion, (b) oxygen of H3O+ and hydrogen of the H2O molecule, (c) sulfur of the SO42− ion and hydrogen of the H2O molecule, and (d) sulfur of the HSO4− ion and hydrogen of the H2O molecule for systems 1–4. | |
 |
| | Fig. 5 The radial distribution function for (a) vanadium of the VO2+ ion and oxygen of the H3O+ ion, (b) vanadium of the two VO2+ ions, (c) oxygen of SO42− and oxygen of the H2O molecule and, (d) oxygen of HSO4− and oxygen of the H2O interaction for systems 1–4. | |
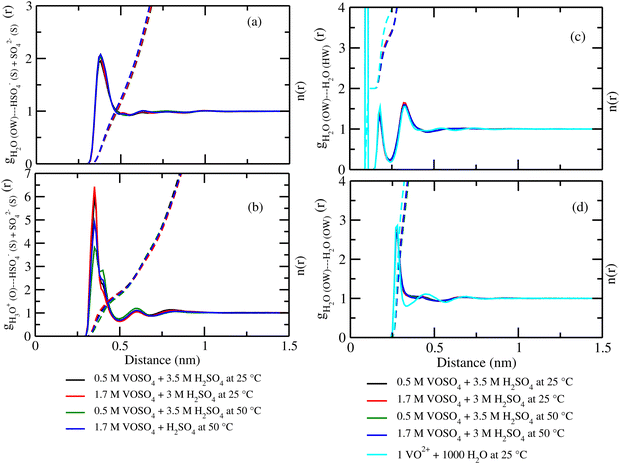 |
| | Fig. 6 The radial distribution function for (a) oxygen of H2O and sulfur of HSO4− + SO42− ion, (b) oxygen of H3O+ and sulfur of HSO4− + SO42− ion, (c) oxygen of H2O and hydrogen of the H2O molecule, and (d) oxygen of H2O and oxygen of the H2O interaction for systems 1–4. | |
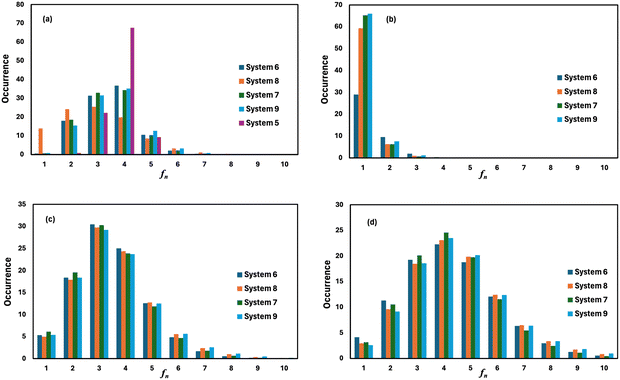
3.3 Hydrogen bond and ionic strength
We also computed the hydrogen bond (HB) number for the molecules of interest by integrating the X⋯HW radial distribution function around the first solvation shell for all systems following the relationship between the hydrogen bond number and the radial distribution function| | 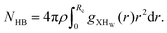 | (19) |
where, X is equal to OW, SO42− (O), HSO4− (O) and H3O+ (O). ρ is the average number density and Rc is the cut-off distance corresponding to the location of the first minimum of the X⋯HW correlation. In this work, all hydrogen bonds for the hydronium ion were calculated for the H2O(OW)⋯H3O+(H) interaction using the above equation. The hydrogen bond has been defined following the geometric criteria. According to the geometric criteria, if the distance between the O and X (= O, H) atom of two species of interest is less than the first minimum in the respective radial distribution functions, they will be known as a hydrogen bonded system. The bulk hydrogen bond numbers are found to be affected in the concentrated solution because with increasing the concentration of the ions in the aqueous solution the ionic strength of the medium will increase. This will affect the hydrogen bond number since more water molecules will prefer bonding with the ions present in the solution. A direct relationship between hydrogen bond number and ionic strength of the medium has been reported in ref. 66 and 67 for the aqueous halide ion solutions. In ref. 66 and 67, the authors showed that the water–water hydrogen bond lifetime will decrease with increasing ion concentration. Furthermore, the formation of the hydrogen bond or the hydrogen bond type of interaction depends on the presence and accessibility of the atom of a molecule participating in hydrogen bonding.28 All these are applicable in the case of I to IV type of interactions mentioned later in this section. The hydrogen bond number and ionic strength are shown in Table 10 for systems 1–9. The ionic strength (I) of the medium has been calculated following the equation68| | 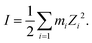 | (20) |
where, mi is the concentration of the ith species in the molality unit and Zi is the charge of the ith species, respectively. Therefore, the ionic strength of the medium is directly proportional to the concentration of the ionic species and its charge in the aqueous solution. We are interested at looking at the fraction of the water molecule forming ‘n’ number of hydrogen bonds for (i) H2O⋯H2O; (ii) H3O+⋯H2O; (iii) HSO4−⋯H2O; and (iv) SO42−⋯H2O interactions. The results are shown in Fig. 7 in the presence of VOSO4 and in Fig. 8 in the absence of VOSO4. The theoretical values of fraction of forming ‘n’ number of hydrogen bonds and the associated mean hydrogen bonds are given in Tables S3–S6 in the ESI.† The hydrogen bond number 〈nHB〉 ∼ 4 for the type I interaction is found to form by 67.6% water molecules for the dilute solution (system 5). The calculated average hydrogen bond number for system 5 is in good agreement with the same for pure water.69,70 The fraction of forming this number of hydrogen bonds by the water molecules is found to decrease with increasing concentration of VOSO4 and increasing temperature. This implies that with increasing the concentration of ions, the water–water hydrogen bond will be affected more in the presence of the ions because the water molecules will prefer interacting with ions with increasing ion concentration. This trend will be followed for the decreasing VOSO4 concentration and for the increasing temperature according to Table S3 (ESI†). The fraction of water molecules forming ‘n’ number of hydrogen bonds with the H3O+ ion is found to increase with increasing H3O+ concentration, decreasing VOSO4 concentration and with increasing temperature. The hydrogen bond between HSO4− and H2O is found to show a maximum for fn = 3 for the dilute solution in the absence of VOSO4 and fn = 4 in the presence of VOSO4. For the type II interaction, the average hydrogen bond 〈nHB〉 ∼ 1 and the fraction of water molecule with ‘n’ number of hydrogen bonds was maximum for system 2 and increases with temperature. The increasing acid–water interaction with temperature is found to promote the ion diffusion at high temperature while this trend is found to show a different behavior at room temperature. In all cases, we noticed a decrease in the fraction of water molecules forming ‘n’ number of hydrogen bonds with increasing temperature except for the hydrogen bond between the H3O+ ion and H2O molecule. We also performed similar calculations for systems 6–9 to study the effect of the VO2+ ion on sulfuric acid and water. In Fig. 8, we notice that the fraction of water molecules pass through a maximum at fn ∼ 4 for type I interaction. This observation is found not to change in the presence of VO2+ ion, however, the fraction of water molecules forming 4 HBs is found to increase significantly with increasing the concentration of VOSO4. This observation is indicative towards the formation of more water–water hydrogen bonds in presence of hexa-coordinated VO2+ ion. The fraction of water molecules forming H3O+⋯H2O HBs was found to be unaltered. For type III HBs, bisulfate anion is always found to form ∼4–5 hydrogen bonds64 and SO42− anion is found to form ∼5–6 HBs in the presence and absence of VOSO4. These numbers are slightly different in comparison to the mean hydrogen bond numbers reported in the ESI.† It is noteworthy in this regard that a typical water molecule can act as two HB acceptors and two HB donors for the hydrogen bond formation. Therefore, the hydrogen bond number of a water molecule should be ∼4.70 The HSO4− and SO42− anion has the ability to form a higher number of hydrogen bonds through the oxygen atom as the HB acceptor and through the hydrogen atom as the HB donor in the case of HSO4− anion.64,65 The HB numbers are captured in the calculation by using eqn (19) for the I to IV type of interaction considering the individual X⋯HW interaction and adding them for a particular category. The hydrogen bond numbers are shown in Table 8 for the H2O molecule, H3O+, HSO4− and SO42+ ion for the systems 6–9. The hydronium ion can also form 4 HBs through the three hydrogen atoms as HB donors and through the oxygen atom as the HB acceptor. In the hydrogen bond definition, we considered the first definition only i.e. hydrogen atom as the HB donor. The hydrogen bond number calculated using eqn (19) is found to be different than the mean hydrogen bond number reported in Table S3 (ESI†) because the former was calculated for individual H3O+(H)⋯H2O (OW) using eqn (19) and then added together. However, the fraction of water molecules forming ‘n’ number of hydrogen bonds has been calculated averaging over all configurations and over all hydrogen atoms attached to the oxygen atom. Following the same procedure, the mean hydrogen bond number of other interactions have been calculated for all systems. Based on the methods of calculation, these numbers differ slightly from each other. However, the overall results based on the structure of the solutions are in good agreement with the available experimental results.
Table 10 The hydrogen bond number calculated using eqn (19). The ionic strength has been calculated using the concentration in the molality unit
| Hydrogen bond no. |
| Systems |
H2O⋯H2O |
H3O+⋯H2O |
HSO4−⋯H2O |
SO42−⋯H2O |
Ionic strength (I) |
| 1 |
4.2 |
2.4 |
4.5 |
5.4 |
9.0 |
| 2 |
4.0 |
2.8 |
4.3 |
5.4 |
7.1 |
| 3 |
4.0 |
2.3 |
4.6 |
6.3 |
12.8 |
| 4 |
4.0 |
2.5 |
4.4 |
5.5 |
11.0 |
| 5 |
3.9 |
— |
— |
— |
— |
| 6 |
4.2 |
2.5 |
4.6 |
5.6 |
7.2 |
| 7 |
4.2 |
2.9 |
4.4 |
5.4 |
5.3 |
| 8 |
4.0 |
2.6 |
4.6 |
5.8 |
5.6 |
| 9 |
4.0 |
3.0 |
4.4 |
6.2 |
4.4 |
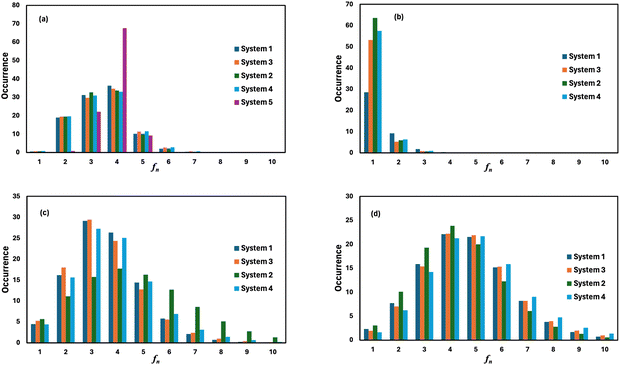 |
| | Fig. 7 The fraction of water molecules forming ‘n’ number of hydrogen bonds of (a) H2O⋯H2O, (b) H3O+⋯H2O, (c) HSO4−⋯H2O, and (d) SO42−⋯H2O type in the presence of VOSO4. | |
 |
| | Fig. 8 The fraction of water molecules forming ‘n’ number of hydrogen bonds of (a) H2O⋯H2O, (b) H3O+⋯H2O, (c) HSO4−⋯H2O, and (d) SO42−⋯H2O type in the absence of VOSO4. | |
3.4 Diffusion, viscosity and surface tension
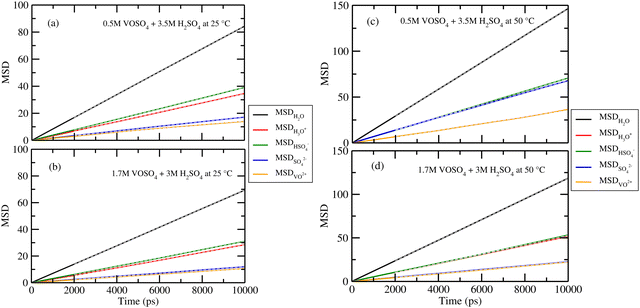
According to Fick's law of diffusion, flux is proportional to the negative concentration gradient. The results of the diffusion coefficient of each species for all systems are shown in Fig. 9. The values are given in Table 11. The gray dashed lines are for the fitted data from 2 ns to 10 ns for the systems 1–4. For system 5, the diffusion data is fitted from 2 ns to 20 ns. The result is shown in Fig. S8 in the ESI.† The diffusion coefficient of vanadyl (VO2+) and sulfate (SO42−) ions is found to increase at low concentration of VOSO4 and at high temperature. However, in system 1, 3 and 4, they are found to show similar diffusional motion that means these two ions have a tendency to form an ion-pair in the solution at low temperature and high concentration. The diffusion coefficient of all ions is found to increase with increasing temperature and decreasing concentration of vandyl sulfate. The increasing order of the diffusion coefficient is DH2O > DHSO4− ≳ DH3O+ > DSO42− ≳ DVO2+ for all systems. This order is according to the trend notice in the work of ref. 71 and 72 for sulfuric acid and the ions coming from its dissociation. With respect to vanadyl (VO2+) and sulfate (SO42−) ion, the diffusion coefficient of other ions is found to increase with temperature and decrease with concentration of VOSO4. To test our model we also computed the diffusivity of the vanadyl ion and water molecule for system 5 at room temperature. The calculated diffusivity of the ions and water molecule was in good agreement with the available theoretical and experimental data.36,73 Overall, the diffusion coefficient of the vanadyl ion is found to decrease with increasing concentration of VOSO4 and H2SO4. In Table 8, we noticed that the diffusion coefficient of VO2+ is the highest in system 2 whose experimental ionic conductivity is also highest among the other four systems. In all systems except system 2, the diffusion coefficient of H3O+ and bisulfate ion is on the same scale while the same is true for the VO2+ ion and sulfate ion. The diffusion coefficient of the water molecule is highest in all cases and it decreases from low to high concentration of VO2+ ions. This indicates the increasing ionic strength of the medium because in the high ionic strength medium, water molecules will prefer interacting more with ions and thus, their diffusional motion will be retarded.66,67 In system 2, the diffusion coefficient of the SO42− ion is almost twice that of the VO2+ ion. This implies that VOSO4 is completely dissociated and formed solvent separated ions in the solution for the lower concentration of VO2+ ion at the high temperature. The difference between the diffusion coefficient of VO2+ and SO42− is found to decrease in the given order i.e.; system 2 > system 1 > system 3 > system 4. The corresponding values are 0.51 for system 2, 0.06 for system 1, 0.02 for system 3 and 0.0005 for system 4, respectively. In system 2 and 4, the diffusion coefficient of H3O+ and HSO4− ions is also high with respect to the same for system 1 and 3. The higher diffusion coefficient of the individual species is responsible for the high ionic conductivity in those systems. The motion of SO42− and VO2+ ions is uncorrelated at the low concentration and high temperature condition and thus causes the formation of free VO2+ and SO42− ion at the high temperature. The formation of more free ions affects the ion conductance of the medium at that particular condition and thus results in high ionic conductivity in the system.
 |
| | Fig. 9 The diffusion coefficient of the ions and water molecule for systems 1–4. The grey dashed lines are the fitted data. | |
Table 11 The calculated and experimental diffusion coefficient of the ions and water molecules with the Yeh Hummer correction factor (shown in the bracket) for systems 1–4. The same is shown for the sulfuric acid without the Yeh Hummer correction factor for systems 6–9. In the last row, the diffusion coefficient of VO2+ taken from ref. 36 and the experimental diffusion coefficient of H2O from ref. 73 are shown
|
D × 1e−5 cm2 s−1 |
| Systems |
(DH2O)(DYH) |
(DH3O+)(DYH) |
(DHSO4−)(DYH) |
(DSO42−)(DYH) |
(DVO2+)(DYH) |
| 1 |
1.41(0.04) |
0.58(0.04) |
0.65(0.04) |
0.28(0.04) |
0.23(0.04) |
| 2 |
2.44(0.08) |
1.12(0.08) |
1.19(0.08) |
1.12(0.08) |
0.61(0.08) |
| 3 |
1.16(0.03) |
0.48(0.03) |
0.52(0.03) |
0.20(0.03) |
0.18(0.03) |
| 4 |
2.00(0.05) |
0.86(0.05) |
0.89(0.05) |
0.37(0.05) |
0.37(0.05) |
| 5 |
2.41(0.20) |
— |
— |
— |
0.55(0.20) |
| 6 |
1.53(—) |
0.63(—) |
0.69(—) |
0.34(—) |
— |
| 7 |
2.50(—) |
1.30(—) |
1.30(—) |
0.67(—) |
— |
| 8 |
1.71(—) |
0.76(—) |
0.85(—) |
0.37(—) |
— |
| 9 |
2.81(—) |
1.45(—) |
1.36(—) |
0.75(—) |
— |
| 10 |
2.30 |
— |
— |
— |
0.42 |
According to the Walden plot, there is a strong connection between diffusion, viscosity and ionic conductivity of the media. The computed viscosity is shown in Fig. 10(a)–(d) for systems 1–4 and in Table 12 for system 1–5. The calculated viscosity for system 5 is shown in Fig. S9(a) in the ESI.† We observed that the viscosity of VOSO4 solution is found to be the lowest for system 2 with respect to the other systems. The order of the computed viscosity is in good agreement with the experimental viscosity results and is found to follow the order reported in ref. 31. A correlation between the experimental versus calculated viscosity is shown in Fig. 10(e). The two data sets were found to be in correlation with a correlation coefficient value R2 = 0.9902. It is noteworthy in this regard that the first peak height of the radial distribution function of the VO2+ (V)⋯HSO4− (S) + SO42− (S) interaction decreases from the concentrated to the dilute solution. This structural feature has the resemblance with the decreasing order (i.e., system 3 > system 1 > system 4 > system 2) of viscosity of the medium and increasing order of diffusivity of the redox active species in ref. 31. This finding is indicative to the decreasing cation–anion interaction for the system showing the highest ionic conductivity. In order to understand the individual motion of ions, we have also plotted the diffusivity (D) against the inverse of the viscosity (1/ηexp) of the medium for VO2+ ions at the ambient condition for systems 1, 3 and 5. A linear correlation between the diffusion coefficient (D) and inverse of the viscosity (1/ηexp) was obtained with a correlation coefficient R2 = 0.9968. The result is shown in Fig. S9(b) in the ESI.† Assuming a spherical shape of the VO2+ ion, the Stokes–Einstein equation was applied to calculate the hydrodynamic radius of the VO2+ ion from the slope in Fig. S9(b) (ESI†) and the calculated Stokes radius is 0.25 nm which is equal to the minimum of the rdfs of the VO2+ (O)⋯H2O (OW) interaction in Fig. 3(a). This result further strengthens the fact of the presence of VO2+ ion as a hexa-coordinated complex species in the aqueous solution of it. The theoretical value of the SR of the VO2+ ion is found to be in good agreement with the result reported in ref. 63. We were interested to know about the effect of the sulfuric acid on the Stokes radius of the VO(H2O)52+ and therefore, correlate the Stokes radius to the rotational diffusion using the Stokes–Einstein–Debye (SED) equation74
| |  | (21) |
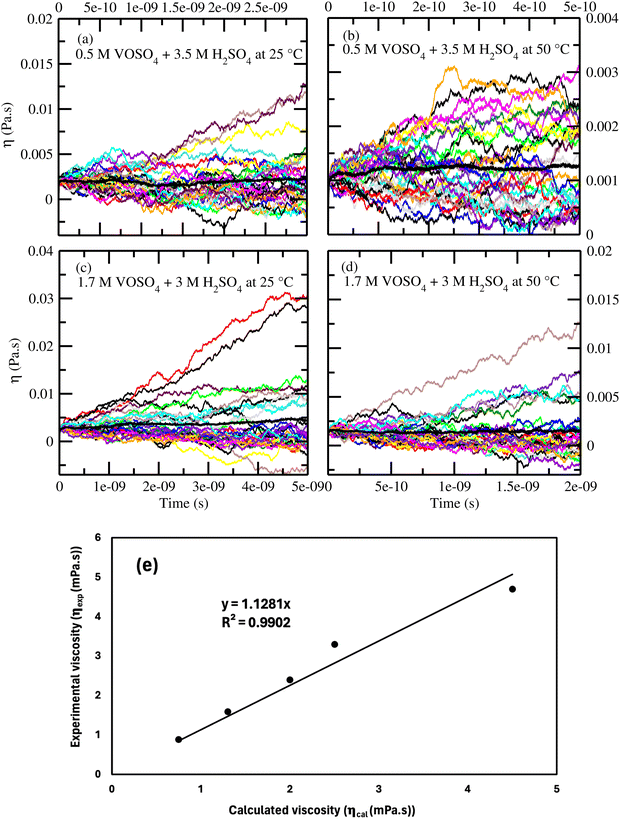 |
| | Fig. 10 (a)–(d) The computed viscosity for systems 1–4. (e) The correlation between the calculated and experimental31 viscosity. | |
Table 12 The calculated and experimental viscosity, Stokes–Einstein radius of VO2+ and SO42− and the rotational diffusion constant of VO2+ with the % error in viscosity for systems 1–4. The experimental viscosity of water for system 5 at 25 °C is taken from ref. 75. The viscosity unit is in mPa s
| Systems |
Viscosity (Exp.) |
Viscosity (Cal.) |
Error (%) |
SE (nm) (VO2+) |
SE (nm) (SO42−) |
D
R × 109 (s−1) (VO2+) |
| 1 |
3.30 |
2.50 |
24.24 |
0.25 |
0.21 |
3.24 |
| 2 |
1.60 |
1.30 |
18.75 |
0.20 |
0.13 |
12.94 |
| 3 |
4.70 |
4.50 |
4.25 |
0.22 |
0.20 |
3.25 |
| 4 |
2.40 |
2.00 |
16.67 |
0.24 |
0.24 |
5.47 |
| 5 |
0.89 |
0.75 |
15.70 |
0.36 |
— |
4.34 |
The Stokes radius and rotational diffusion are related to the translational diffusion through Stokes–Einstein (SE) diffusion following
| | 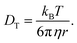 | (22) |
The SED and SE are both related to each other following
| | 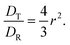 | (23) |
The calculated SE of VO(H2O)52+ is found to decrease with increasing temperature at high concentration of sulfuric acid and low concentration of VOSO4. The SE and SED values are given in Table 12. The increasing SR of VO2+ with increasing sulfuric acid concentration is seen in this study and is in accordance with the observation stated in ref. 63 at room temperature. To achieve high energy density in a redox flow battery, the translational and rotational diffusion constant of VO2+ ion should be high due to the presence of free ions in place of the formation of an ion-pair. Our theoretical study shows that not only the high concentration of the redox active species but the motion of it in media and how this motion affects the ionic conductivity of it will be the governing factor for high energy density in a redox flow battery.
In a flow battery, the low surface tension of the redox active species is an important criteria to prevent the leakage of the electrolyte in the battery to prolong the life span of it.31 The computed surface tensions are 65.39 and 62.0 Nm−1 for system 1 and 2, respectively. The bulk density for vapor–liquid interface, fluctuation of the surface tension for system 1 and 2 are shown in Fig. S11 (ESI†). The surface tension of aqueous vanadium solution decreases with decreasing concentration of VOSO4 and at high temperature according to ref. 31.
4 Conclusion
A theoretical model has been proposed to study the structure and dynamics of aqueous vanadium redox flow battery under varying thermodynamic conditions. The benchmark calculations have been done for the five systems: (i) 0.5 M VOSO4 in 3.5 M H2SO4 at 25 °C, (ii) 0.5 M VOSO4 in 3.5 M H2SO4 at 25 °C, (iii) 1.7 M VOSO4 in 3 M H2SO4 at 25 °C, (iv) 1.7 M VOSO4 in 3 M H2SO4 at 50 °C and (V) 1 VO2+ in 1000 water molecules at 25 °C. Using the proposed technique, we were able to successfully simulate the concentrated multi-component (quinary) solution of aqueous VOSO4 solution at different temperatures. The role of sulfuric acid in aq. VRFB is investigated including the temperature dependent dissociation of it implicitly in the MD simulation. The model is further validated by computing various structural and dynamical properties and by comparing them with the available experimental results for the same. The computed density, surface tension and viscosity are found to be in good agreement with the available experimental data in ref. 31. The structural properties of the aqueous solutions provide physical insight into the dynamical properties reported in ref. 31. According to the theoretical study, uncorrelated motion of the cation–cation and cation–anion coming from the redox active species is the main governing factor for the high ionic conductivity and hence for the high energy density in the conventional redox flow battery at the low concentration of VOSO4 and at high temperature. The theoretical study also reveals that the presence of the free ions in the solution will affect the translational and rotational diffusion of the redox active species in a different way than the ion-pair existence (which is very common in the concentrated solution) of the same in the aqueous solutions. Also, the size and shape of the ions will play a significant role in its motion through the electrolyte solvent and thus will influence the magnitude of ionic conductivity and energy density of the aqueous vanadium redox flow battery.
Data availability
All data presented in this work are available in the manuscript and in the ESI.†
Conflicts of interest
There are no conflicts of interest to declare.
Acknowledgements
The author gratefully acknowledges the funding support through the teaching and research position in the Department of Chemistry and Physics of the University of Akron, USA and SERB – DST NPDF grant no. PDF/2021/003347 from India. The author would also like to thank the Indian Institute of Technology Hyderabad, Telangana for the high performance computational facility.
References
-
L. H. Thaller, Electrically rechargeable redox flow cells, 1974.
-
L. H. Thaller, Redox flow cell development and demonstration project, 1979.
-
M. Skyllas-Kazacos, M. Rychick and R. Robins, US Pat., US4786567A, 1988.
-
F. Rahman, Stability and properties of supersaturated vanadium electrolytes for high energy density vanadium redox battery, PhD thesis, The University of New South Wales, Australia, 1998.
- Z. Yang, J. Zhang, M. C. W. Kintner-Meyer, X. Lu, D. Choi, J. P. Lemmon and J. Liu, Chem. Rev., 2011, 111, 3577–3613 CrossRef.
- B. Dunn, H. Kamath and J. M. Tarascon, Science, 2011, 334, 928–935 CrossRef.
- G. L. Soloveichik, Annu. Rev. Chem. Biomol. Eng., 2011, 2, 503–527 CrossRef.
- L. Li, S. Kim, W. Wang, M. Vijayakumar, Z. Nie, B. Chen, J. Zhang, G. Xia, J. Hu, G. Graff, J. Liu and Z. Yang, Adv. Energy Mater., 2011, 1, 394–400 CrossRef CAS.
- V. Murugesan, Z. Nie, X. Zhang, P. Gao, Z. Zhu, Q. Huang, L. Yan, D. Reed and W. Wang, Cell Rep. Phys. Sci., 2021, 2, 100323 CrossRef CAS.
-
Y. A. Gandomi, Electrochemical Engineering of All-Vanadium Redox Flow Batteries for Reduced Ionic and Water Crossover via Experimental Diagnostics and Multiscale Modeling, PhD thesis, University of Tennessee, 2019.
- B. K. Chakrabarti, E. Kalamaras, A. K. Singh, A. Bertei, J. Rubio-Garcia, V. Yufit, K. M. Tenny, B. Wu, F. Tariq, Y. S. Hajimolana, N. P. Brandon, C. T. J. Low, E. P. L. Roberts, Y.-M. Chiang and F. R. Brushett, Sustainable Energy Fuels, 2020, 4, 5433–5468 RSC.
- I. Aramendia, U. Fernandez-Gamiz, A. Martinez-San-Vicente, E. Zulueta and J. M. Lopez-Guede, Energies, 2020, 14, 176 CrossRef.
- R. E. Hage, F. Chauvet, B. Biscans, L. Cassayre, L. Maurice and T. Tzedakis, Chem. Eng. Sci., 2019, 199, 123–136 CrossRef.
- S. Tsushima and T. Suzuki, J. Electrochem. Soc., 2020, 167, 020553 CrossRef.
- M. Skyllas-Kazacos, L. Cao, M. Kazacos, N. Kausar and A. Mousa, ChemSusChem, 2016, 9, 1521–1543 CrossRef PubMed.
- L. Cao, M. Skyllas-Kazacos, C. Menictas and J. Noack, J. Energy Chem., 2018, 27, 1269–1291 CrossRef.
- K. J. Kim, M.-S. Park, Y.-J. Kim, J. H. Kim, S. X. Dou and M. Skyllas-Kazacos, J. Mater. Chem. A, 2015, 3, 16913 RSC.
- M. Skyllas-Kazacos, N. Milne and G. C. Kazacos, Mater. Forum, 2007, 32, 72–77 Search PubMed.
- A. Parasuraman, T. M. Lima, C. Menictas and M. Skyllas-Kazacos, Electrochim. Acta, 2013, 101, 27–40 CrossRef.
- K. Gong, Q. Fang, S. Gu, S. F. Y. Li and Y. Yan, Energy Environ. Sci., 2015, 8, 3515 RSC.
- Z. Zhao, B. Zhang, B. R. Schrage, C. J. Ziegler and A. Boika, ACS Appl. Energy Mater., 2020, 3, 10270–10277 CrossRef.
- Q. Chen, Y. Li, D. Y. Liu, P. Sun, Z. Yang and T. Xu, ChemSusChem, 2020, 14, 1295–1301 CrossRef PubMed.
- J. Yu, M. Salla, H. Zhang, Y. Ji, F. Zhang, M. Zhou and Q. Wang, Energy Storage Mater., 2020, 19, 216–222 CrossRef.
- B. Hu, C. DeBruler, Z. Rhodes and T. L. Liu, J. Am. Chem. Soc., 2017, 139, 1207–1214 CrossRef.
- S. Sharma, G. A. Andrade, S. Maurya, I. A. Popov, E. R. Batista, B. L. Davis, R. Mukundan, N. C. Smythe, A. M. Tondreau, P. Yang and J. C. Gordon, Energy Storage Mater., 2021, 37, 576–596 CrossRef.
- J. F. Kucharyson, L. Cheng, S. O. Tung, L. A. Curtiss and L. T. Thompson, J. Mater. Chem. A, 2017, 5, 13700 RSC.
- A. Karmakar, R. Mukundan, P. Yang and E. R. Batista, RSC Adv., 2019, 9, 18506 RSC.
- A. Karmakar, R. Mukundan, P. Yang and E. R. Batista, Phys. Chem. Chem. Phys., 2021, 23, 21106–21129 RSC.
- F. Rahman and M. Skyllas-Kazacos, J. Power Sources, 1998, 72, 105–110 CrossRef CAS.
- F. Rahmana and M. Skyllas-Kazacos, J. Power Sources, 2009, 189, 1212–1219 CrossRef.
- Y. Song, X. Li, C. Yan and A. Tang, J. Power Sources, 2020, 480, 229141 CrossRef CAS.
- S. Gupta, T. M. Lim and S. H. Mushrif, Electrochim. Acta, 2018, 270, 471–479 CrossRef CAS.
- S. Gupta, N. Wai, T. M. Lim and S. H. Mushrif, J. Mol. Liq., 2016, 215, 596–602 CrossRef CAS.
- S. Gupta, N. Wai, T. M. Lim and S. H. Mushrif, J. Mol. Liq., 2016, 219, 1180 CrossRef CAS.
- M. Vijayakumara, S. D. Burtona, C. Huanga, L. Lia, Z. Yanga, G. L. Graffa, J. Liua, J. Hua and M. Skyllas-Kazacos, J. Power Sources, 2010, 195, 7709–7717 CrossRef.
- Z. Jiang, K. Klyukin and V. Alexandrov, J. Chem. Phys., 2016, 145, 114303 CrossRef.
- F. Sepehr and S. J. Paddison, J. Phys. Chem. A, 2015, 119, 5749–5761 CrossRef.
- M. Bon, T. Laino, A. Curioni and M. Parrinello, J. Phys. Chem. C, 2016, 120, 10791–10798 CrossRef.
- C. F. Schwenk, H. H. Loeffler and B. M. Rode, J. Am. Chem. Soc., 2003, 125, 1618–1624 CrossRef.
- P. Walden and E. J. Birr, Z. Phys. Chem., 1932, A160, 57–68 CrossRef.
- K. R. Harris, J. Phys. Chem. B, 2019, 123, 7014–7023 CrossRef.
- A. A. Noyes and W. R. Whitney, J. Am. Chem. Soc., 1897, 19, 930–934 CrossRef.
-
M. P. Allen, Computer Simulation of Liquids, Oxford University Press, 1st edn, 1987 Search PubMed.
- E. A. Muller, Å. Ervik and A. Mejía, Living J. Comput. Mol. Sci., 2021, 2, 21385 Search PubMed.
- P. Novotný and O. Sóhnel, J. Chem. Eng. Data, 1988, 33, 49–55 CrossRef.
- C. E. L. Myhre, D. H. Christensen, F. M. Nicolaisen and C. J. Nielsen, J. Phys. Chem. A, 2003, 107, 1979–1991 CrossRef.
- D. A. Knopf, B. P. Luo, U. K. Krieger and T. Koop, J. Phys. Chem. B, 2003, 107, 4322–4332 CrossRef.
- C. Williams and P. Carbone, J. Chem. Phys., 2015, 143, 174502 CrossRef PubMed.
- B. Schwenzer, S. Kerisit and M. Vijayakumar, RSC Adv., 2014, 4, 5457–5464 RSC.
- H. J. C. Berendsen, J. R. Grigera and T. P. Straatsma, J. Phys. Chem., 1987, 91, 6269–6271 CrossRef.
-
H. Bekker, H. J. C. Berendsen, E. Dijkstra, S. Achterop, R. Vondrumen, D. Vanderspoel, A. SijbersI, H. Keegstra and M. K. R. Renardus, GROMACS – A parallel computer for molecular dynamics simulations, World Scientific Publishing, 1993, pp. 252–256 Search PubMed.
- B. Hess, C. Kutzner, D. van der Spoel and E. Lindahl, J. Chem. Theory Comput., 2008, 4, 435–447 CrossRef.
- B. Hess, J. Chem. Theory Comput., 2008, 4, 116–122 CrossRef.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1–19 CrossRef.
- M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, SoftwareX, 2015, 1, 19–25 CrossRef.
- L. Martínez, R. Andrade, E. G. Birgin and J. M. Martínez, J. Comput. Chem., 2009, 30, 2157–2164 CrossRef PubMed.
- J. M. Martínez and L. Martínez, J. Comput. Chem., 2003, 24, 819–825 CrossRef PubMed.
-
D. Frenkel and B. Smith, Understanding Molecular Simulation, Academic Press, 2nd edn, 1996 Search PubMed.
- I.-C. Yeh and G. Hummer, J. Phys. Chem. B, 2004, 108, 15873–15879 CrossRef.
- N. V. S. Avula, A. Karmakar, R. Kumar and S. Balasubramanian, J. Chem. Theory Comput., 2021, 17, 4274–4290 CrossRef PubMed.
- W. L. Jorgensen, D. S. Maxwell and J. Tirado-Rives, J. Am. Chem. Soc., 1996, 118, 11225–11236 CrossRef.
- G. Kaminski and W. L. Jorgensen, J. Phys. Chem., 1996, 100, 18010–18013 CrossRef.
- G. Oriji, Y. Katayama and T. Miura, Electrochim. Acta, 2008, 49, 3091–3095 CrossRef.
- V. Vchirawongkwin, B. M. Rode and I. Persson, J. Phys. Chem. B, 2007, 111, 4150–4155 CrossRef.
- V. Vchirawongkwin, B. M. Rode and I. Persson, J. Phys. Chem. B, 2010, 114, 11561–11569 CrossRef PubMed.
- A. Karmakar, J. R. Choudhuri, V. K. Yadav, B. S. Mallik and A. Chandra, Chem. Phys., 2013, 412, 13–21 CrossRef.
- A. Karmakar and A. Chandra, J. Phys. Chem. B, 2015, 119, 8561–8572 CrossRef.
-
P. Atkins and J. de Paula, Physical Chemistry, Oxford University Press, 11th edn, 2018 Search PubMed.
- A. Chandra, Phys. Rev. Lett., 2000, 85, 768–771 CrossRef PubMed.
- A. Bankura, A. Karmakar, V. Carnevale, A. Chandra and M. L. Klein, J. Phys. Chem. C, 2014, 118, 29401–29411 CrossRef.
- M. Canales and E. Guárdia, J. Mol. Liq., 2019, 293, 111463 CrossRef.
- M. Canales and E. Guárdia, J. Mol. Liq., 2022, 347, 118351 CrossRef.
- M. Holz, S. R. Heila and A. Sacco, Phys. Chem. Chem. Phys., 2000, 2, 4740–4742 RSC.
- J. S. Lawton, S. M. Tiano, D. J. Donnelly, S. P. Flanagan and T. M. Arruda, Batteries, 2018, 4, 40–54 CrossRef.
- J. Kestin, M. Sokolov and W. A. Wakeham, J. Chem. Phys., 1978, 7, 941–948 Search PubMed.
|
| This journal is © the Owner Societies 2024 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cycles) in comparison to other devices (RFBs 20
000 cycles) in comparison to other devices (RFBs 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cycle) when used for grid scale applications. The efficiency of a flow battery depends on the power and energy density, which directly depends on the redox potential and solubility of ions in aqueous solution. In second generation redox flow batteries, these two parameters can be implemented individually. One can increase the efficiency of a flow cell by increasing the energy density without affecting the power density by directly increasing the solubility of redox active species. A significant number of experimental and theoretical studies have been done to increase the efficiency of all vanadium redox flow batteries and their optimization. However, very few theoretical studies32–39 have been carried out to understand the chemical physics behind the solubility of the redox active species in complex solution currently found in the field of aqueous vanadium redox flow batteries. Most theoretical32–39 models created in this field contain one vanadium ion in water and are for a binary mixture solution. The effect on the structural dynamical properties due to the presence of other ions has not been mentioned in these theoretical models. The real system shows a very strong regular solution behavior. To understand how the redox flow battery works, it is absolutely necessary to understand the dynamics of the electrolyte, solvent and additive roles at varying compositions and at different thermodynamic states using the principles of statistical mechanics. In 2020, the work published in the journal of power sources31 shows that the increasing polarization of the cell decreases the cell voltage in a conventional redox flow battery. Therefore, the polarization losses through charge transfer, ohmic resistance and mass transport limitation should be controlled to increase the energy density of the redox flow cell. All these factors responsible for the polarization loss depend on the cell material. One of the most important factors in this field is electrolyte resistance which is influenced by the electrolyte thickness and ionic conductivity of the aqueous solution. It is known that reducing electrolyte thickness and increasing ionic conductivity is a more efficient way to lower the electrolyte resistance, to control the cell polarization and to increase the voltage efficiency of the flow battery. The electrolyte thickness depends on the viscosity and surface tension of the medium. According to the study, the electrolyte conductivity for the positive and negative electrolyte of the VRFB increases with increasing the concentration of sulfuric acid and decreasing the concentration of vanadium. It was shown that reducing the surface tension of the electrolyte reduces the electrolyte leakage and thus increases the stack lifetime and its maintenance cost. The low concentration of vanadium ions with a high concentration of sulfuric acid at the high temperature can contribute to the enhanced energy density in the conventional VRFB. However, these experimental findings have not been explained from the microscopic point of view. What are the driving forces at the molecular level and how do they influence all these chemical and physical properties at the macro-scale? It is known that ion-pair or ion-cluster formation may occur in concentrated aqueous solution and this may increase the electrostatic interactions in the solution with respect to the dilute solution of ∼1 M strength.40,41 The diffusion of the active species and how it influences the overall solvation mechanism and affects the other transport properties of the aqueous ionic solution are important factors to be understood in the field of the redox flow batteries. During the dissolution process, the diffusion plays a very important role according to the Noyes–Whitney equation42 however, it is not the sole governing factor of the solubility and affects the dissolution rate, viscosity and, ionic conductivity of the media. Hence, it is necessary to understand the transport behavior of the aqueous solution and investigating the role of ion-pair and ion-cluster formation at the molecular level for the systematic design of a redox flow battery. Sulfuric acid used in all vanadium redox flow batteries undergoes a temperature dependent dissociation process. Thus, it plays an important role in the solubility of redox active species in VRFB operating over varying thermodynamic conditions. The role of the acid on the dynamical properties of redox active species needs to be understood from the microscopic point of view.
000 cycle) when used for grid scale applications. The efficiency of a flow battery depends on the power and energy density, which directly depends on the redox potential and solubility of ions in aqueous solution. In second generation redox flow batteries, these two parameters can be implemented individually. One can increase the efficiency of a flow cell by increasing the energy density without affecting the power density by directly increasing the solubility of redox active species. A significant number of experimental and theoretical studies have been done to increase the efficiency of all vanadium redox flow batteries and their optimization. However, very few theoretical studies32–39 have been carried out to understand the chemical physics behind the solubility of the redox active species in complex solution currently found in the field of aqueous vanadium redox flow batteries. Most theoretical32–39 models created in this field contain one vanadium ion in water and are for a binary mixture solution. The effect on the structural dynamical properties due to the presence of other ions has not been mentioned in these theoretical models. The real system shows a very strong regular solution behavior. To understand how the redox flow battery works, it is absolutely necessary to understand the dynamics of the electrolyte, solvent and additive roles at varying compositions and at different thermodynamic states using the principles of statistical mechanics. In 2020, the work published in the journal of power sources31 shows that the increasing polarization of the cell decreases the cell voltage in a conventional redox flow battery. Therefore, the polarization losses through charge transfer, ohmic resistance and mass transport limitation should be controlled to increase the energy density of the redox flow cell. All these factors responsible for the polarization loss depend on the cell material. One of the most important factors in this field is electrolyte resistance which is influenced by the electrolyte thickness and ionic conductivity of the aqueous solution. It is known that reducing electrolyte thickness and increasing ionic conductivity is a more efficient way to lower the electrolyte resistance, to control the cell polarization and to increase the voltage efficiency of the flow battery. The electrolyte thickness depends on the viscosity and surface tension of the medium. According to the study, the electrolyte conductivity for the positive and negative electrolyte of the VRFB increases with increasing the concentration of sulfuric acid and decreasing the concentration of vanadium. It was shown that reducing the surface tension of the electrolyte reduces the electrolyte leakage and thus increases the stack lifetime and its maintenance cost. The low concentration of vanadium ions with a high concentration of sulfuric acid at the high temperature can contribute to the enhanced energy density in the conventional VRFB. However, these experimental findings have not been explained from the microscopic point of view. What are the driving forces at the molecular level and how do they influence all these chemical and physical properties at the macro-scale? It is known that ion-pair or ion-cluster formation may occur in concentrated aqueous solution and this may increase the electrostatic interactions in the solution with respect to the dilute solution of ∼1 M strength.40,41 The diffusion of the active species and how it influences the overall solvation mechanism and affects the other transport properties of the aqueous ionic solution are important factors to be understood in the field of the redox flow batteries. During the dissolution process, the diffusion plays a very important role according to the Noyes–Whitney equation42 however, it is not the sole governing factor of the solubility and affects the dissolution rate, viscosity and, ionic conductivity of the media. Hence, it is necessary to understand the transport behavior of the aqueous solution and investigating the role of ion-pair and ion-cluster formation at the molecular level for the systematic design of a redox flow battery. Sulfuric acid used in all vanadium redox flow batteries undergoes a temperature dependent dissociation process. Thus, it plays an important role in the solubility of redox active species in VRFB operating over varying thermodynamic conditions. The role of the acid on the dynamical properties of redox active species needs to be understood from the microscopic point of view.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 molar ratio. Therefore, the same expression for the density calculation of aqueous vanadyl solution has been adapted here.
1 molar ratio. Therefore, the same expression for the density calculation of aqueous vanadyl solution has been adapted here.


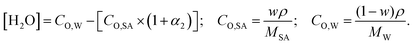
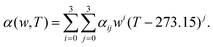
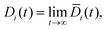
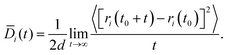
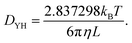
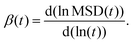
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ) stands for the natural logarithm and MSD (t) is the mean square displacement at time t. As a guide for the eyes, we also plotted the log–log plot to see any noticeable changes in the diffusion behaviors of the ions and water molecules. The log–log plot shows the three regions of the MSD which is missing from the linear plot. The plots related to the diffusive motion of the species are shown in the Fig. S6–S8 in the ESI.†
) stands for the natural logarithm and MSD (t) is the mean square displacement at time t. As a guide for the eyes, we also plotted the log–log plot to see any noticeable changes in the diffusion behaviors of the ions and water molecules. The log–log plot shows the three regions of the MSD which is missing from the linear plot. The plots related to the diffusive motion of the species are shown in the Fig. S6–S8 in the ESI.†
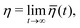
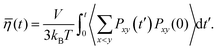
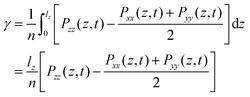
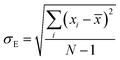
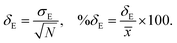
![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) is the mean and δE is the standard error of mean (SEM). The error %δE has been calculated by dividing δE by
is the mean and δE is the standard error of mean (SEM). The error %δE has been calculated by dividing δE by ![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) multiplied by 100. The calculated average surface tension for system 1 is 65.39 N m−1 (±0.21). We noticed that the error percentage present in the SFT simulation is ∼0.32%. The computed surface tensions for each run and relevant error analysis are shown in Table 8. The experimental surface tension was not reported for system 1 in ref. 31. However, one will know that the presence of the ionic species in solution will increase the cohesive energy of the system and thus, the surface tension of it. Cohesive forces are affected by the hydrogen bonding and van der Waals interaction. It will depend on the ionic strength of the medium. We have extracted a relationship between the surface tension and the predicted ionic strength of the medium for which experimental SFT values were reported in ref. 31. In the experimental paper, 2.6 M H2SO4 was used to dissolve VOSO4 at varying temperature to obtain the experimental SFT values. For any particular temperature, the SFT shows a linear relationship with the concentration of dissolved VOSO4 as the concentration of H2SO4 is constant. The SFT will directly depend on the ionic strength of the medium because it depends on the concentration of the ionic species. Therefore, a SFT value for an unknown system was predicted by following the relationship γi/γj = Ii/Ij for the aqueous vandium redox flow battery in this study. Where, γi and γj are the experimental SFT and Ii and Ij are the ionic strength of the ith and jth system, respectively. According to the above relationship, the predicted experimental surface tension for system 1 and 2 would be 57.55 and 45.39 N m−1 at 25 °C and 50 °C, respectively. Hence, the computed surface tension is within 14% and 16% in error with respect to the predicted experimental SFT for system 1 and 2, respectively.
multiplied by 100. The calculated average surface tension for system 1 is 65.39 N m−1 (±0.21). We noticed that the error percentage present in the SFT simulation is ∼0.32%. The computed surface tensions for each run and relevant error analysis are shown in Table 8. The experimental surface tension was not reported for system 1 in ref. 31. However, one will know that the presence of the ionic species in solution will increase the cohesive energy of the system and thus, the surface tension of it. Cohesive forces are affected by the hydrogen bonding and van der Waals interaction. It will depend on the ionic strength of the medium. We have extracted a relationship between the surface tension and the predicted ionic strength of the medium for which experimental SFT values were reported in ref. 31. In the experimental paper, 2.6 M H2SO4 was used to dissolve VOSO4 at varying temperature to obtain the experimental SFT values. For any particular temperature, the SFT shows a linear relationship with the concentration of dissolved VOSO4 as the concentration of H2SO4 is constant. The SFT will directly depend on the ionic strength of the medium because it depends on the concentration of the ionic species. Therefore, a SFT value for an unknown system was predicted by following the relationship γi/γj = Ii/Ij for the aqueous vandium redox flow battery in this study. Where, γi and γj are the experimental SFT and Ii and Ij are the ionic strength of the ith and jth system, respectively. According to the above relationship, the predicted experimental surface tension for system 1 and 2 would be 57.55 and 45.39 N m−1 at 25 °C and 50 °C, respectively. Hence, the computed surface tension is within 14% and 16% in error with respect to the predicted experimental SFT for system 1 and 2, respectively.