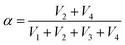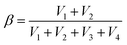Empowering soft conductive elastomers with self-reinforcement and remarkable resilience via phase-locking ions†
Kai
Lu
a,
Zaizheng
Sun
a,
Jinming
Liu
a,
Chengyi
Huang
abc,
Dongsheng
Mao
 a and
Haiming
Chen
a and
Haiming
Chen
 *abc
*abc
aKey Laboratory of Advanced Marine Materials, Ningbo Institute of Materials Technology and Engineering, Chinese Academy of Sciences, Ningbo, 315201, China. E-mail: chenhaiming@nimte.ac.cn
bLaboratory of Polymers and Composites, Ningbo Institute of Materials Technology and Engineering, Chinese Academy of Sciences, Ningbo, 315201, China
cNingbo Key Laboratory of High-Performance Polymers and Composites, Ningbo, 315201, China
First published on 16th October 2024
Abstract
Endowing soft and long-range stretchable elastomers with exceptional strength, resilience, and ion-conductivity is crucial for high-performance flexible sensors. However, achieving this entails significant challenges due to intrinsic yet mutually exclusive structural factors. In this work, a series of self-reinforcing ion-conductive elastomers (SRICEs) is thus designed to meet the advanced but challenging requirements. The SRICEs behave like a soft/hard dual-phase separated micro-structure, which is optimized through a straightforward preferential assembly strategy (PAS) to ensure that the subsequently introduced ions are locked in the soft phase. Meanwhile, the interaction between ions and soft segments is meticulously tailored to achieve self-reinforcement through strain-induced crystallization. Consequently, an outstanding ultimate strength of approximately ∼51.0 MPa and an exceptional instant resilient efficiency of ∼92.9% are attained. To the best knowledge of the authors, these are the record-high values achieved simultaneously in one ion-conductive elastomer. Furthermore, the resultant toughness of ∼202.4 MJ m−3 is significantly higher, while the modulus of ∼5.0 MPa is lower than that of most reported robust ion-conductive elastomers. This unique combination of properties makes it suitable for advanced flexible applications, e.g. grid-free position recognition sensors. This work provides guidance for designing soft yet robust ion-conductive elastomers and optimizing their mechanical properties.
New conceptsSwelling a polymeric network with ionic liquids or ionic salts has emerged as a popular strategy for developing flexible sensors, actuators, artificial muscles, and ionotronics owing to their high ionic conductivity, ease of fabrication, non-volatility, non-freezing properties, and transparency. However, creating soft yet robust ion-conductive elastomers with long-range stretchability and exceptional resilience remains challenging due to their inherent yet mutually exclusive structural factors. For example, softness, indicative of a low modulus typically induced by increased viscosity, is often accompanied by poor strength and substantial plastic residue in a non-chemical crosslinked system. In contrast, a denser covalently crosslinked network offers tremendous strength and modulus but sacrifices long-range stretchability. Besides, supramolecular crosslinked ion-conductive elastomers exhibit long-range deformation due to the dynamics of their reversible crosslinking points. However, the interaction between ions and strong polar sites in supramolecular ion-conductive elastomers disrupts chain packing and prevents polar segments from aggregating, causing significant chain slippage during deformation. Consequently, most reported supramolecular ion-conductive elastomers demonstrate weak strength (<1 MPa), poor toughness (<5 MJ m−3), and low resilient efficiency (<80%). Developing a simple preferential assembly strategy (PAS) is essential to optimize microphase-separated structures, ensuring that the subsequently introduced ions are locked in the soft phase. Simultaneously, instead of pursuing excessively strong interactions, it aims at appropriate interactions between ions and soft segments that would facilitate self-reinforcement through strain-induced crystallization. As a result, a series of self-reinforcing ion-conductive elastomers with an exceptional ultimate strength of ∼51.0 MPa and an outstanding instant resilient efficiency of ∼92.9% are achieved. It is worth noting that no liquid leakage occurs during both storage and deformation when the ionic liquid content is less than 20%; such exceptional strength and instant resilient efficiency set record highs that were achieved simultaneously in one ion-conductive elastomer. Moreover, the soft phase-locked ions contribute to lowering rigidity, resulting in a modulus of ∼5.0 MPa and a toughness of ∼202.4 MJ m−3. This unique combination of properties makes it suitable for advanced flexible applications. Thereby, a grid-free position recognition sensor based on a triboresistive touch sensing mechanism is finally demonstrated. |
1. Introduction
Swelling a polymeric network with ionic liquids or ionic salts has emerged as a popular strategy for developing flexible sensors, actuators, artificial muscles, and ionotronics owing to their high ionic conductivity, ease of fabrication, non-volatility, non-freezing, and transparency.1 However, creating soft yet robust ion-conductive elastomers with long-range stretchability and exceptional resilience remains challenging due to their inherent yet mutually exclusive structural factors. Softness, indicative of a low modulus typically induced by increased viscosity, is often accompanied by poor strength and substantial plastic residue in a non-chemical crosslinked system.2 In contrast, a denser covalently crosslinked network offers tremendous strength and modulus but sacrifices long-range stretchability.3 Supramolecular crosslinked ion-conductive elastomers exhibit long-range deformation due to the dynamics of their reversible crosslinking points.4 However, the interaction between ions and strong polar sites in supramolecular ion-conductive elastomers disrupts chain packing and prevents polar segments from aggregating,5 causing significant chain slippage during deformation. Consequently, most reported supramolecular ion-conductive elastomers demonstrate low strength (<1 MPa), toughness (<5 MJ m−3), and resilient efficiency (<80%).6The rational design that prevents large-scale chain slippage plasticized by ionic additives is thus necessary for strengthening and toughening supramolecular ion-conductive elastomers. Several ingenious design strategies, including construction of micro/nanocomposites,7 topological networks,8 and multiscale structures,9 have been proved in a homogeneous network. Also, increasing the density of supramolecular interaction sites within and between molecules enhances robustness and rigidity significantly.10 However, in the case of high-quality flexible sensors intended to mimic animal skin and respond to minor perturbations, a lower modulus combined with higher strength is appreciated.11 The typical positive association between strength and modulus, stemming from similar structural factors, presents a fundamental conflict between modulus, strength, and sensing. Additionally, interactions between ions and strong polar sites consume considerable conformational energy during load–unloading cycles, resulting in significant strain residue that must be addressed in long-range stretchable sensing applications.12 Moreover, while strain-induced crystallization is usually an effective method for reinforcing soft polymers such as hydrogels,13 rubbers,14 and thermoplastic elastomers,15 the strong supramolecular interaction between ions and polymeric chains makes the strain-induced crystallization problematic.
Constructing an isotropic hard-soft dual-phase structure to decouple strength and modulus while maintaining resilience has been successfully demonstrated in thermoplastic elastomers, thanks to their flexible soft-segment and rigid hard-phase. Thereby, Bao et al.5a introduced lithium ions (Li+) into phase-separated polyurethane (PU) elastomers, resulting in an optimized strength of 11.9 MPa and a modulus of 0.87 MPa. Ding et al.16 developed a dynamic supramolecular Li+-conductive elastomer by incorporating multiple hydrogen bonds, achieving an ultimate strength of 27.8 MPa. However, the strong supramolecular interaction between ions and hard segment has a negative effect on the strength and resilient efficiency due to the disturbed chain packing. Therefore, the key to effectively protecting the hard segment from interference is to lock the ions in the soft phase. However, achieving this goal still presents challenges in terms of molecular design and coupling techniques.
Therefore, a simple preferential assembly strategy (PAS) was developed in this work to optimize microphase-separated structures, ensuring that the subsequently introduced ions are locked in the soft phase. Simultaneously, instead of pursuing excessively strong interactions, it aimed at appropriate interactions between ions and soft segment that would facilitate self-reinforcement through strain-induced crystallization.17 As a result, a series of self-reinforcing ion-conductive elastomers (SRICEs) with an exceptional ultimate strength of ∼51.0 MPa and an outstanding instant resilient efficiency of ∼92.9% are achieved. It is worth noting that no liquid leakage occurs during both storage and deformation when the ionic liquid content is less than 20%. To the best knowledge of the authors, such exceptional strength and instant resilient efficiency set record highs that were achieved simultaneously in one ion-conductive elastomer. Moreover, the soft phase-locked ions contribute to lowering rigidity, resulting in a modulus of ∼5.0 MPa and a toughness of ∼202.4 MJ m−3. This unique combination of properties makes it suitable for advanced flexible applications. Thereby, a grid-free position recognition sensor based on a triboresistive touch sensing mechanism is finally demonstrated.
2. Results and discussion
2.1 Molecular design and preparation
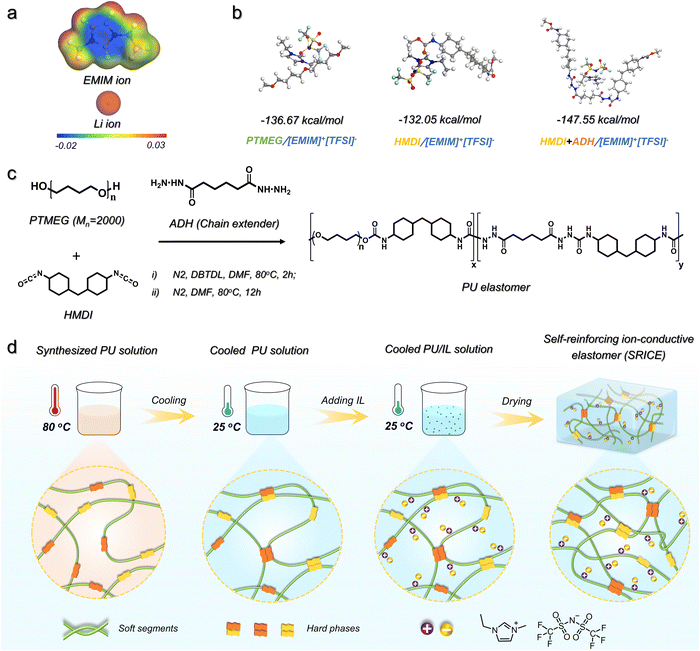
One of the most difficult aspects of developing SRICEs is determining the optimal intermolecular interaction between the soft segment and the ionic liquid. Here, the 1-ethyl-3-methylimidazolium bis(trifluoromethylsulfonyl)imide ([EMIM]+[TFSI]−) is selected as the mobile phase instead of LiTFSI because the volume of [EMIM]+ is calculated to be 252.67 Å3, which is 3.2 times bigger than that of Li+ (78.40 Å3), as exhibited in Fig. 1a. The larger volume is expected to be more easily trapped in the soft phase. Then, four common soft segments—polytetramethylene ether glycol (PTMEG), polyethylene glycol (PEG), polypropylene glycol (PPG), and polydimethylsiloxane (PDMS)—are evaluated as candidates. The binding energy between [EMIM]+[TFSI]− and each soft segment was calculated (Fig. S1, ESI†), revealing that the PTMEG/[EMIM]+[TFSI]− couple exhibits an appropriate binding energy of −136.67 kJ mol−1 (Fig. 1b). This value is lower than that of PEG/[EMIM]+[TFSI]− but higher than that of PPG/[EMIM]+[TFSI]− and PDMS/[EMIM]+[TFSI]−. Considering that PPG and PDMS are amorphous, and PEG undergoes crystallization in ambient environments, PTMEG was selected as the soft segment in this work. Regarding hard segments, their structural regularity is crucial as it facilitates the formation of hydrogen bond aggregates and promotes the strain-induced crystallization of soft segments. Isophorone diisocyanate (IPDI), with its irregular spatial configuration, is not conducive to PTMEG crystallize and exhibits weak intermolecular interaction.18 Therefore, dicyclohexylmethane 4,4′-diisocyanate (HMDI), with a more regular configuration, was chosen to react with PTMEG diol owing to its lower binding energy of HMDI/[EMIM]+[TFSI]− (−132.05 kJ mol−1, Fig. 1b). However, only HMDI contained in a hard segment is insufficient to maintain its strength, resulting in a viscous mechanical performance (Fig. S2, ESI†). The adipic acid dihydrazide (ADH) with a regular structure is thus chosen as a chain extender to further improve the binding force among hard segments. Fortunately, the binding energy of hard segment (HMDI+ADH)/[EMIM]+[TFSI]− (−147.55 kJ mol−1) is slightly higher than that of PTMEG/[EMIM]+[TFSI]−. Therefore, a series of PU elastomers are achieved according to the synthesis route as shown in Fig. 1c.However, an increase in the amount of chain extender leads to a notable increase in rigidity. The Young's modulus of such elastomers increases from 1.69 MPa to 4.28 MPa, 15.4 MPa, and 66.4 MPa as the molar ratio of PTMEG to ADH varies as 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 to 1
0 to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.5, 1
0.5, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, and 1
1, and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, respectively (Fig. S2, ESI†). Similarly, the strength also increases from 5.74 MPa to 50.3 MPa, 43.8 MPa, and 54.8 MPa, respectively. Hence, a PTMEG/ADH molar ratio of 1
2, respectively (Fig. S2, ESI†). Similarly, the strength also increases from 5.74 MPa to 50.3 MPa, 43.8 MPa, and 54.8 MPa, respectively. Hence, a PTMEG/ADH molar ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.5 was settled upon to synthesize a SRICE based on two considerations: (1) maintaining the modulus at a relatively low level; and (2) minimizing the binding energy between ions and the hard segment by using a lower ADH content. The weight-average molecular weight (Mw) of the resultant elastomer is approximately 12.7 × 104 with a dispersion index of 2.62. The thermal decomposition temperature surpassing 320 °C suggests good thermal stability (Fig. S3, ESI†).
0.5 was settled upon to synthesize a SRICE based on two considerations: (1) maintaining the modulus at a relatively low level; and (2) minimizing the binding energy between ions and the hard segment by using a lower ADH content. The weight-average molecular weight (Mw) of the resultant elastomer is approximately 12.7 × 104 with a dispersion index of 2.62. The thermal decomposition temperature surpassing 320 °C suggests good thermal stability (Fig. S3, ESI†).
The coupling process of the synthesized PU and [EMIM]+[TFSI]− is schematically illustrated in Fig. 1d. Due to the comparable binding energy between the soft/hard segments and [EMIM]+[TFSI]−, the synthesized PU solution was initially cooled to 25 °C from 80 °C to facilitate hard segmental assembly through the formation of hydrogen bonds. This process, termed preferential assembly strategy (PAS) in this work, ensures effective packing of the hard segments. Subsequently, the [EMIM]+[TFSI]− with a preset ratio was added. The mass ratio of [EMIM]+[TFSI]− to the polymer was set to 5 wt%, 10 wt%, and 20 wt%, respectively. The resulting specimens are named SRICE-x, where x represents the mass ratio of [EMIM]+[TFSI]−. To verify the validity of PAS, the corresponding specimens prepared without utilizing PAS are compared. They exhibit a significantly decreased strength from 49.3 MPa to 28.6 MPa at the same [EMIM]+[TFSI]− content of 20 wt% (Fig. S4, ESI†), which is consistent with that in literature reports,5a,17 suggesting the soft/hard dual-phase separated micro-structure is significantly optimized by using the PAS procedure.
2.2 Structural investigation
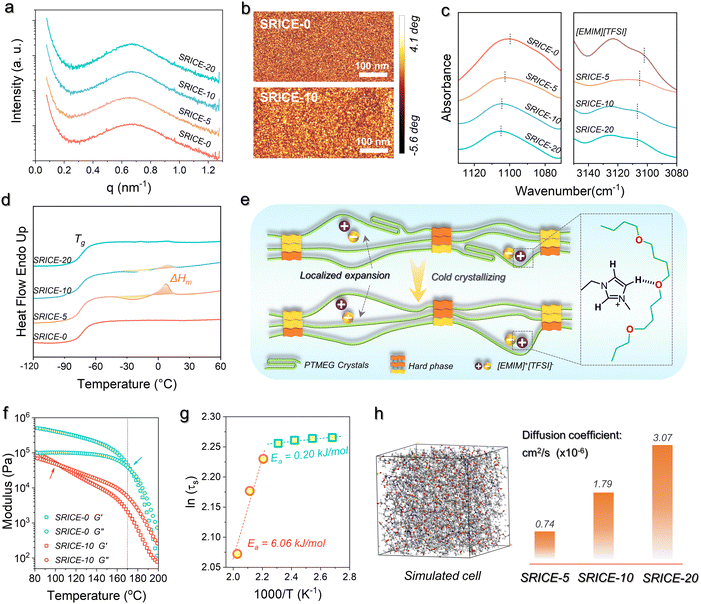
The isotropic scattering rings observed in the 2D small-angle X-ray scattering (SAXS) pattern confirms the soft/hard dual-phase separated micro-structure (Fig. S5, ESI†), the average distance between scattering centers is approximately 9.2–9.4 nm according to Bragg's law (L = 2π/q) (Fig. 2a). This morphology is further supported by phase images obtained from atomic force microscopy (AFM), where bright spots represent the hard phase with a high modulus, while dark areas represent the soft phase with a low modulus (Fig. 2b). Besides, the transmittance of SRICEs across the entire visible range exceeds 80% (Fig. S6, ESI†). The transparent and colorless appearance of SRICEs indicates the excellent compatibility between [EMIM]+[TFSI]− and PTMEG-based PU elastomers. Moreover, energy dispersive X-ray spectroscopy (EDS) reveals well-distributed F and S elements throughout the material (Fig. S7, ESI†), suggesting no significant aggregation of [EMIM]+[TFSI]− owing to the considerable affinity between [EMIM]+[TFSI]− and the PTMEG chain. This affinity is confirmed by the FTIR spectra (Fig. 2c), where the bands at 1100 cm−1 and 3102 cm−1 correspond to the C–O–C stretching vibration of the soft segment and the C–H stretching vibration of the imidazolium ring, respectively. Both bands exhibit a blue shift to 1105 cm−1 and 3107 cm−1 respectively, indicating the formation of a hydrogen bond between the ether bond and the imidazolium ring.19 Furthermore, all SRICEs exhibit similar positions for the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching bands and total amounts of hydrogen bonding20 (Fig. S8, ESI†), suggesting that ions do not impede hard segmental packing.
O stretching bands and total amounts of hydrogen bonding20 (Fig. S8, ESI†), suggesting that ions do not impede hard segmental packing.
More intriguingly, noticeable exothermic (approx. −24 °C) and the corresponding endothermic (∼8 °C) peaks are observed in DSC heating scans of SRICE-5 and SRICE-10, attributed to the cold crystallization and crystal melting of PTMEG segments, respectively (Fig. 2d). However, these peaks are absent in SRICE-0 and SRICE-20. The crystallinity (Xc = 100% × ΔHm/ΔH0m, where ΔH0m refers to the enthalpy of fusion of completely crystalline PTMEG, 172.2 J g−1 (ref. 21)) of SRICE-5 and SRICE-10 is calculated to be 2.91% and 0.38%, respectively. It is proposed that such lower crystallinity results from the competition between the affinity of PTMEG/ions and the expansion effect of [EMIM]+[TFSI]− on the packing of PTMEG segments. Considering that each PTMEG segment (Mn ∼ 2000 kg mol−1) contains approximately 27 oxygen atoms, and the molar ratio of oxygen atoms on soft segments to [EMIM]+[TFSI]− is as high as 91![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 45
1, 45![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, and 22.5
1, and 22.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 in SRICE-5, SRICE-10, and SRICE-20 respectively. The average packing distance among chains characterized by Bragg's equation is 4.4–4.5 Å for all SRICEs (Fig. S9, ESI†). It is thus thought that the PTMEG segments experience localized expansion induced by [EMIM]+[TFSI]− (with sizes of 18.1 Å × 10.3 Å × 6.5 Å), as depicted in Fig. 2e. Such local expansion facilitates the PTMEG conformational adjustment, thereby promoting crystallization when the ion interaction sites are few. However, as the concentration of [EMIM]+[TFSI]− increases, the ions interact with PTMEG at more sites, which is detrimental to PTMEG crystallization due to the enhanced affinity between ions and the PTMEG segments. The promoted crystallization of PTMEG in turn proved that the [EMIM]+[TFSI]− are distributed in the soft phase.
1 in SRICE-5, SRICE-10, and SRICE-20 respectively. The average packing distance among chains characterized by Bragg's equation is 4.4–4.5 Å for all SRICEs (Fig. S9, ESI†). It is thus thought that the PTMEG segments experience localized expansion induced by [EMIM]+[TFSI]− (with sizes of 18.1 Å × 10.3 Å × 6.5 Å), as depicted in Fig. 2e. Such local expansion facilitates the PTMEG conformational adjustment, thereby promoting crystallization when the ion interaction sites are few. However, as the concentration of [EMIM]+[TFSI]− increases, the ions interact with PTMEG at more sites, which is detrimental to PTMEG crystallization due to the enhanced affinity between ions and the PTMEG segments. The promoted crystallization of PTMEG in turn proved that the [EMIM]+[TFSI]− are distributed in the soft phase.
The good assembly of hard segments is further confirmed by temperature-dependent rheological properties (Fig. 2f). The intersection of storage and loss moduli is typically regarded as the critical point marking the transition from elasticity to viscosity dominance.22 Here, it gradually shifts from 173.3 °C (SRICE-0) to 136.9 °C (SRICE-5), 98.6 °C (SRICE-10), and 102.8 °C (SRICE-20) respectively, demonstrating enhanced viscous characteristics with ions. However, a significant decline in both moduli and complex viscosity occurs until 170 °C regardless of [EMIM]+[TFSI]− content (Fig. 2f and Fig. S10, ESI†). This transition is directly related to the dynamic dissociation of the hard phase; then they reach the viscous state. The consistency of such transition suggests that the assembly of hard segments remains unaffected by ions. The activation energies of segmental relaxation are calculated using the Arrhenius equation, as depicted in Fig. 2g and Fig. S11 in the ESI.† Taking SRICE-0 and SRICE-10 as examples, the activation energies (Ea) above 170 °C are 6.58 kJ mol−1 (SRICE-0) and 6.06 kJ mol−1 (SRICE-10), with a difference of only 7.9%, further indicating that the assembly of hard segments is unaffected by ions. However, once the temperature drops below 170 °C, the Ea decreases to 0.86 kJ mol−1 (SRICE-0) and 0.20 kJ mol−1 (SRICE-10), with the difference increasing to 76.7%. This observation confirms that the soft phase-locked ions facilitate segmental relaxation.
The reversible dynamics of supramolecular interactions between the ether bond and the imidazolium ring impart SRICEs with remarkable temperature-dependent conductivity. At 20 °C, the conductivity of SRICE-10 measures 12.3 μS m−1, increasing to 37.2 μS m−1 at 50 °C (Fig. S12a, ESI†). This suggests faster ion movement at higher temperatures, attributed to the weaker supramolecular interactions. Therefore, SRICEs can function as temperature-sensitive switches, powering bulbs at elevated temperatures and extinguishing them at lower temperatures (Video S1, ESI†). Electrochemical impedance spectroscopy (EIS) is also used to characterize the resistance of SRICE, the semicircle observed at high frequencies can be attributed to the charge transfer resistance (Rct), while the slope at low frequencies corresponds to the Warburg impedance (Zw), which is associated with the ion diffusion process. The Rct of SRICE-0 is too high to be measured at experimental frequencies, whereas the Rct values of SRICE-5, SRICE-10 and SRICE-20 decrease to 2028 kΩ, 441 kΩ, and 171 kΩ, respectively, demonstrating the good conductivity of the SRICE. Additionally, the diffusion coefficient of [EMIM]+[TFSI]− in the PU elastomer is calculated using molecular dynamics (MD) with a forcite module, with results illustrated in Fig. 2h. Notably, a higher content of [EMIM]+[TFSI]− correlates with a faster diffusion rate.
2.3 Mechanical performance
Fig. 3a depicts the typical engineering stress–strain curves of SRICEs, with the corresponding strength and Young's modulus detailed in Fig. 3b. Notably, all SRICEs exhibit similar mechanical behavior, particularly during initial deformation, with Young's modulus values of 5.47 ± 0.45 MPa (SRICE-0), 5.23 ± 0.35 MPa (SRICE-5), 5.00 ± 0.50 MPa (SRICE-10), and 4.98 ± 0.51 MPa (SRICE-20) respectively. Upon exceeding a strain of 400%, significant strain-reinforcing behavior is observed for all SRICEs. In situ wide-angle X-ray scattering (WAXS) confirms that the strain-reinforcement arises from strain-induced crystallization of PTMEG, evidenced by the appearance of a diffraction peak corresponding to the (020) crystal plane of PTMEG (Fig. 3c, d and Fig. S13, ESI†). Remarkably, the resultant strengths of 53.3 ± 3.21 MPa (SRICE-5), 51.0 ± 3.04 MPa (SRICE-10), and 49.3 ± 1.92 MPa (SRICE-20) are comparable to that of SRICE-0 (50.3 ± 0.56 MPa), indicating significant self-reinforcement irrespective of the addition of [EMIM]+[TFSI]−, a phenomenon divergent from cases where hard segments are interfered with by ions.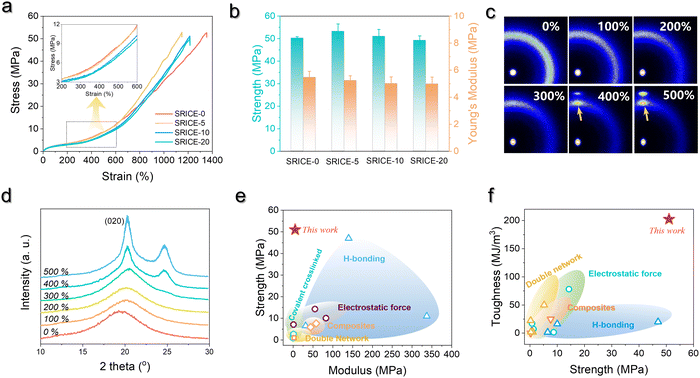 | ||
| Fig. 3 Mechanical properties of SRICEs. (a) Typical engineering stress–strain curves of SRICEs. The inset enlarges the strain range of 200–600%. (b) Strength as well as Young's modulus of SRICEs. (c) and (d) Selected 2D WAXS patterns (c) and the corresponding 1D profiles (d) of SRICEs. The stretching direction is horizon. (e) and (f) Comparison of the tensile strength versus modulus (e) as well as the toughness versus tensile strength (f) of the SRICEs with literature-reported ion-conductive elastomers, and the details can be found in Table S1 (ESI†). | ||
In detail, the stress experienced by SRICE-x (x = 5, 10, and 20) in the mid-deformation region (strain of 200–700%) is initially lower than that of SRICE-0, but it significantly increases and surpasses that of SRICE-0 at the final stage (strain >700%) (Fig. 3a). This phenomenon arises from the requirement for ions to be “excluded” from the lattice during the strain-induced crystallization of the soft segment. The “exclusion” process initially delays strain-induced crystallization, resulting in lower stress during the mid-deformation region. This hypothesis finds support in the crystallinity of PTMEG at a strain of 500%. Specifically, SRICE-10 exhibits lower crystallinity (4.86%) compared to SRICE-0 (6.75%) (Fig. S14, ESI†). Moreover, the size of strain-induced crystals in SRICE-10 (5.9 nm) is smaller than that in SRICE-0 (6.7 nm) according to the Scherrer's equation, indicating a less stable crystal in SRICE-10. Once ions are completely “excluded” from the crystal lattice, the remaining space facilitates conformation regulation, thereby accelerating strain-induced crystallization and resulting in a steeper slope in the stress–strain curves. Most literature-reported supramolecular ion-conductive elastomers exhibit a low modulus to accommodate the curvature of targeted surfaces, but are accompanied by low strength,5a,23 as depicted in Fig. 3e. In this context, SRICEs with high strength but low modulus emerge as suitable candidates for soft yet robust electronics. Moreover, elongation at break of 1348 ± 37.8% (SRICE-0), 1150 ± 26.4% (SRICE-5), 1200 ± 42.3% (SRICE-10), and 1224 ± 29.5% (SRICE-20) and toughness of 198.6 ± 21.6 MJ m−3 (SRICE-5), 202.4 ± 18.9 MJ m−3 (SRICE-10), and 195.3 ± 27.8 MJ m−3 (SRICE-20) are attained. The remarkable values for toughness exceed that of most reported ion-conductive elastomers,5a,17,23a–d,f–j,24 as listed in Fig. 3f. As a demonstration in Fig. S15 (ESI†), when poking SRICE-10 with a sharp pair of tweezers, it resists damage and quickly recovers to its initial state within 5 s, showcasing both excellent toughness and resilience.
The resilience is further quantitatively examined by calculating the recovery efficiency (ηrecovery):25
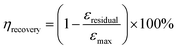 | (1) |
Here, εresidual represents the residual strain when the stress returns to zero, and εmax denotes the maximum strain. Fig. 4a illustrates the cyclic stress–strain curves of SRICE-10, with the curves being adjusted for clarity. Fig. 4b presents the ηrecovery values and hysteresis ratios of SRICE-0 and SRICE-10, respectively. It's evident that SRICE-10 and SRICE-0 exhibit similar trends in ηrecovery and hysteresis ratio. The increase in hysteresis ratio with εmax is attributed to the similar packing of hard phases in both SRICE-0 and SRICE-10. The well-packed hard segments contribute to high ηrecovery values for SRICE-0 (95.1%) and SRICE-10 (92.9%), even when the strain reaches 500%. Notably, such exceptional ηrecovery values also surpass that of most literature-reported resilience, as shown in Fig. 4c.6a,26 To the best knowledge of the authors, the strength of 51.0 MPa and the resilient efficiency of 92.9% set record highs that are achieved simultaneously in one supramolecular ion-conductive elastomer. It is believed that the excellent ηrecovery primarily stems from two factors: (1) the unimpeded hard phase maintaining a complete crosslinking network, and (2) the delayed strain-induced crystals during middle deformation requiring fewer endotherms to melt, thereby reducing the loss of entropy elasticity and promoting shape recovery.
 | ||
| Fig. 4 Resilience of SRICE-10. (a) Cyclic stress–strain curves of SRICE-10. (b) Statistics of the ηrecovery and hysteresis ratio of SRICE-0 and SRICE-10, respectively. (c) ηrecoveryversus εmax of the SRICE-10 and some of the literature-reported ion-conductive elastomers, the details can be found in Table S2 (ESI†). (d) Relationship between cyclic strains and ΔR/R0 of SRICE-10. (e) Digital images of the SRICE-10 loading several dumbbells with weights of 5, 10, 15, and 20 kg, and the resulting change in resistance. The size of the sample is 37 mm × 71 mm × 0.41 mm. | ||
The outstanding resilience is further evidenced by monitoring the resistance variation (ΔR/R0) during cyclic stretching, as depicted in Fig. 4d. As the strain increases, so does the ΔR/R0. And once the strain returns to zero from various maximum strains, the ΔR/R0 rebounds to its initial level. This suggests that the phase-locked ions move collectively, rendering the material suitable for applications in smart artificial muscles. Moreover, SRICE-10 is subjected to loads from several dumbbells of varying weights (5 kg to 20 kg), generating corresponding ΔR/R0 values for recording, as depicted in Fig. 4e and Video S2 (ESI†). The material's high recovery capability in both strain and ΔR/R0 enables repeated loading cycles. Therefore, with its appropriate modulus, excellent strength, toughness, and sensitive strain-resistance response, the colorless and transparent SRICE can be further employed in fabricating flexible electronics, such as grid-free position recognition sensors, as elaborated in the subsequent section.
2.4 Grid-free position recognition sensor
The human–machine interaction interface, a crucial element in information communication, has garnered significant attention,27 driving the recent flourishing development of touch sensing to usher in the era of intelligence.28 Energy-harvesting technologies, exemplified by triboelectric nanogenerators (TENGs) based on contact electrification and electrostatic induction mechanisms, have been harnessed to create various types of touch-sensitive sensors, owing to their notable advantages of self-powering, high sensitivity, and cost-effectiveness properties.29 However, they face challenges in planar site identification unless employing multi-dimensional grid network electrodes. To streamline the design of touch sensors, we present a robust and flexible grid-free 2D position recognition sensor, utilizing SRICE-10 based on triboresistive touch sensing technology.30 The distinction between triboelectric nanogeneration and triboresistance touch sensing lies in the former's requirement of a dielectric layer for contact electrification and an electrode layer for electrostatic induction, while the latter integrates both the dielectric and electrode layers.Hence, the contact electrification and electrostatic induction of SRICE-10 are initially verified before fabricating the grid-free position recognition sensor; the whole results are depicted in Fig. S16 in the ESI.† The power generation mechanism of SRICE-10 is elucidated in a supplementary note (ESI†). The stable incorporation of [EMIM]+[TFSI]− allows the PU matrix to serve not only as a dielectric layer for contact electrification but also as an ion-conducting layer for electrostatic induction. Consequently, the accumulated charges and the output voltage strongly depend on the PU matrix content, slightly decreasing with [EMIM]+[TFSI]−. Similarly, reducing the thickness of SRICE-10 would facilitate the generation of the electric double layer (EDL), resulting in a larger output voltage. Moreover, the low modulus of approximately 5 MPa enables SRICE-10 to deform and expand the contact area when subjected to external force. As a result, an output voltage of up to 90V can be obtained at a pressure of only 12.5 kPa, gradually rising to 110 V as the pressure increases, and then stabilizing steadily once the pressure exceeds 75 kPa. The maximum output power of 60.8 μW, achieved when in contact with PTFE and connected to resistors ranging from 10 kΩ to 10 GΩ in series, is sufficient to illuminate 100 bulbs (Video S3, ESI†). Furthermore, its high strength, toughness, and excellent resilience contribute to its outstanding durability. Even after undergoing contact-separation 9000 times, it maintains a steady output, demonstrating its ability to withstand fatigue impacts (Fig. S17, ESI†).
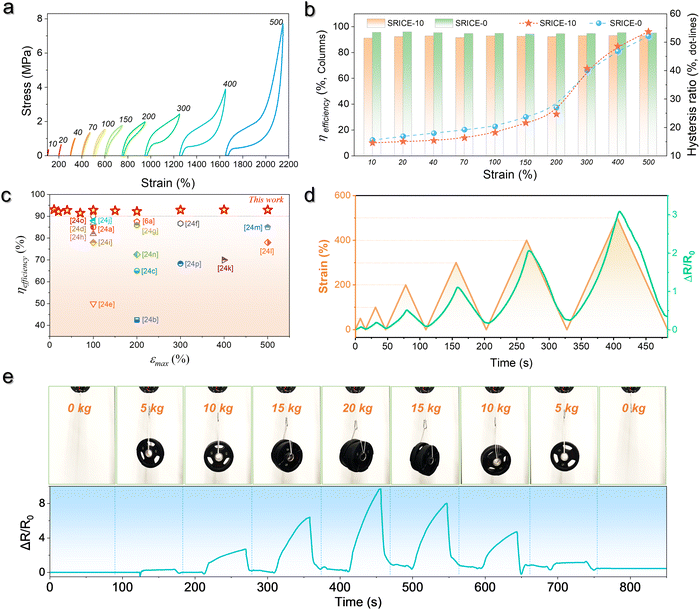
Thus, SRICE-10 is directly employed as a grid-free position recognition sensor. As shown in Fig. 5a, the internal components of SRICE-10 are treated as two resistors from the touch position to each side, where the induced voltages on each side are inversely proportional to the resistance. The induced voltages on each side (V1 and V2) are expressed as follows:
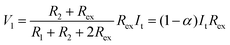 | (2) |
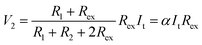 | (3) |
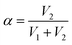 . For demonstration purposes, five positions on the SRICE-10 are touched, each with a gap distance of 1 cm. The induced voltages corresponding to each touch position, inversely proportional to the distance from the touch position according to eqn (2) and (3) respectively, are indicated in Fig. 5b and Video S4 (ESI†). For example, when the 1# position is touched, V1 > V2, and vice versa. Touching the 3# position results in similar V1 and V2, suggesting recognition of the center of the SRICE-10 strip (Fig. 5c). Additionally, besides a single click, the sensor can also detect sliding motion on the strip, as captured in Video S5 (ESI†). Fig. 5d illustrates the variation of V1 and V2 when continuously moving from left to right and vice versa on the strip. V1 gradually decreases as V2 increases, indicating sliding from left to right, and vice versa. Therefore, touching any position can be visualized by expressing the value of α, as depicted in Fig. 5d. Here, the strip-type SRICE-10 is touched every 2.5 mm, demonstrating a spatial resolution of 1.1 × 10−2 mm−1. Considering the width of common touching materials is larger than 1 mm, this sensitivity makes it practically meaningful to distinguish most touches. Moreover, owing to the good stretchability of SRICE-10, it can even recognize positions after being stretched. Strains of 30% and 60% are applied, showing similar sensitivity to the unstretched specimen (Fig. 5e), confirming the independence of the grid-free position recognition sensor based on triboresistive touch sensing technology on deformation.
. For demonstration purposes, five positions on the SRICE-10 are touched, each with a gap distance of 1 cm. The induced voltages corresponding to each touch position, inversely proportional to the distance from the touch position according to eqn (2) and (3) respectively, are indicated in Fig. 5b and Video S4 (ESI†). For example, when the 1# position is touched, V1 > V2, and vice versa. Touching the 3# position results in similar V1 and V2, suggesting recognition of the center of the SRICE-10 strip (Fig. 5c). Additionally, besides a single click, the sensor can also detect sliding motion on the strip, as captured in Video S5 (ESI†). Fig. 5d illustrates the variation of V1 and V2 when continuously moving from left to right and vice versa on the strip. V1 gradually decreases as V2 increases, indicating sliding from left to right, and vice versa. Therefore, touching any position can be visualized by expressing the value of α, as depicted in Fig. 5d. Here, the strip-type SRICE-10 is touched every 2.5 mm, demonstrating a spatial resolution of 1.1 × 10−2 mm−1. Considering the width of common touching materials is larger than 1 mm, this sensitivity makes it practically meaningful to distinguish most touches. Moreover, owing to the good stretchability of SRICE-10, it can even recognize positions after being stretched. Strains of 30% and 60% are applied, showing similar sensitivity to the unstretched specimen (Fig. 5e), confirming the independence of the grid-free position recognition sensor based on triboresistive touch sensing technology on deformation.
Moreover, by simultaneously measuring the voltages at the four corners of a rectangular SRICE-10, touches at any point within the rectangle will be accurately detected. To quantitatively recognize the 2D position, α and β are analogously expressed respectively as follows:30
In this context, assigning α and β as the horizontal and vertical coordinates allows for precise position tracking on the SRICE-10 plane. To illustrate, we use the game of Go as an example, as shown in Fig. 5f. The 5 × 5 grid is merely drawn on the base plate for reference, with no interconnected electrodes on the grid itself. Despite this, it can accurately determine where stones are placed during a complete game of Go, as demonstrated in Video S6 (ESI†). Obviously, the development of these soft, strong, tough, resilient, and responsive ion-conductive elastomers shed light on technical progress in human–machine interaction.
3. Conclusions
In summary, the appropriate interaction between soft segments and ions is established and a straightforward preferential assembly strategy was employed to optimize the microphase-separated structures of PU, effectively trapping the introduced ionic liquids within the soft phase. The self-reinforcement stemming from the strain-induced crystallization of PTMEG segments endows the ion-conductive elastomer with an outstanding strength of approximately 51.0 MPa and an elongation at break of around 1200%. Maintaining an undisturbed physical crosslinking network ensures an excellent instant resilient efficiency of approximately 92.9%. To the best of the authors’ knowledge, these achievements mark record-high values for both ultimate strength and instant resilient efficiency in one ion-conductive elastomer. Moreover, the presence of soft phase-locked ions contributes to lowering rigidity. The appropriate interaction between the ions and soft segments also endows it with remarkable conductive properties, enabling its direct use as a grid-free position recognition sensor based on a triboresistive touch sensing mechanism. Leveraging its suitable modulus, excellent strength, toughness, and sensitive strain-resistance response, the colorless and transparent SRICE can also serve as artificial muscles, holding significant promise for the development of flexible devices.4. Experimental section
The experimental details are placed in the ESI,† including the following files: supplementary videos, figures, note and tables as well as Experimental section.Author contributions
H. Chen conceived the idea, designed the experiments and wrote the manuscript. K. Lu, Z. Sun, J. Liu, and C. Huang carried out the experiments, performed the data, and analyzed the data. H. Chen and D. Mao discussed the results and revised manuscript.Data availability
The data supporting this article have been included as part of the ESI.†Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
The authors gratefully appreciate the financial support provided by the National Natural Science Foundation of China (Grant No. 52103014), the Ningbo Natural Science Foundation (Grant No. 2023J407 and 2023S054), the Foundation of the Director of NIMTE, the Leading Innovative and Entrepreneur Team Introduction Program of Zhejiang (Grant No. 2021R01005), and the Ningbo Yongjiang Talent Introduction Programme (2021A-045-C). H. Chen thanks Mrs Chen for providing helpful suggestions.References
- (a) Y. He, Y. Cheng, C. Yang and C. F. Guo, Nat. Mater., 2024, 23, 1107–1114 CrossRef CAS PubMed; (b) Y. Zhu, Y. Guo, K. Cao, S. Zeng, G. Jiang, Y. Liu, W. Cheng, W. Bai, X. Weng, W. Chen, D. Zhao, H. Yu and G. Yu, Nat. Synth., 2023, 2, 864 CrossRef; (c) H. Tan, L. Sun, H. Huang, L. Zhang, R. E. Neisiany, X. Ma and Z. You, Adv. Mater., 2024, 36, 2310020 CrossRef CAS PubMed; (d) D. Lv, X. Li, X. Huang, C. Cao, L. Ai, X. Wang, S. K. Ravi and X. Yao, Adv. Mater., 2022, 2309821 Search PubMed; (e) S. Lin, W. Yang, X. Zhu, Y. Lan, K. Li, Q. Zhang, Y. Li, C. Hou and H. Wang, Nat. Commun., 2024, 15, 2374 CrossRef CAS PubMed; (f) H. Ye, B. Wu, S. Sun and P. Wu, Nat. Commun., 2024, 15, 885 CrossRef CAS PubMed; (g) J.-S. Benas, F.-C. Liang, M. Venkatesan, Z.-L. Yan, W.-C. Chen, S.-T. Han, Y. Zhou and C.-C. Kuo, Chem. Eng. J., 2023, 466 Search PubMed; (h) J. Chandrasekar, M. Venkatesan, T. W. Sun, Y. C. Hsu, Y. H. Huang, W. W. Chen, M. H. Chen, M. L. Tsai, J. Y. Chen, J. H. Lin, Y. Zhou and C. C. Kuo, Mater. Horiz., 2024, 11, 1395–1413 RSC.
- Y. Shi, B. Wu, S. Sun and P. Wu, Adv. Mater., 2024, 36, 2310576 CrossRef CAS.
- C. Ma, J. Wei, Y. Zhang, X. Chen, C. Liu, S. Diao, Y. Gao, K. Matyjaszewski and H. Liu, Adv. Funct. Mater., 2023, 33, 2211771 CrossRef CAS.
- (a) W. Li, L. Li, S. Zheng, Z. Liu, X. Zou, Z. Sun, J. Guo and F. Yan, Adv. Mater., 2022, 34, 202203049 Search PubMed; (b) L. Li, X. Wang, S. Gao, S. Zheng, X. Zou, J. Xiong, W. Li and F. Yan, Adv. Mater., 2023, 36, 202308547 Search PubMed.
- (a) D. G. Mackanic, X. Yan, Q. Zhang, N. Matsuhisa, Z. Yu, Y. Jiang, T. Manika, J. Lopez, H. Yan, K. Liu, X. Chen, Y. Cui and Z. Bao, Nat. Commun., 2019, 10, 5384 CrossRef PubMed; (b) Y. Tominaga, K. Yamazaki and V. Nanthana, J. Electrochem. Soc., 2015, 162, A3133 CrossRef CAS.
- (a) L. Xu, Z. Huang, Z. Deng, Z. Du, T. L. Sun, Z.-H. Guo and K. Yue, Adv. Mater., 2021, 33, 2105306 CrossRef CAS; (b) K. G. Cho, S. An, D. H. Cho, J. H. Kim, J. Nam, M. Kim and K. H. Lee, Adv. Funct. Mater., 2021, 31, 2102386 CrossRef CAS; (c) H. Dinh Xuan, B. Timothy, H.-Y. Park, T. N. Lam, D. Kim, Y. Go, J. Kim, Y. Lee, S. I. Ahn, S.-H. Jin and J. Yoon, Adv. Mater., 2021, 33, 2008849 CrossRef CAS PubMed; (d) Y. Ding, J. Zhang, L. Chang, X. Zhang, H. Liu and L. Jiang, Adv. Mater., 2017, 29, 1704253 CrossRef.
- (a) E. Kamio, T. Yasui, Y. Iida, J. P. Gong and H. Matsuyama, Adv. Mater., 2017, 29, 1704118 CrossRef PubMed; (b) D. Lv, X. Li, X. Huang, C. Cao, L. Ai, X. Wang, S. K. Ravi and X. Yao, Adv. Mater., 2024, 36, 2309821 CrossRef CAS.
- (a) W. Li, L. Li, S. Zheng, Z. Liu, X. Zou, Z. Sun, J. Guo and F. Yan, Adv. Mater., 2022, 34, 2203049 CrossRef CAS; (b) J. Xiong, X. Wang, L. Li, Q. Li, S. Zheng, Z. Liu, W. Li and F. Yan, Angew. Chem., Int. Ed., 2024, 63, e202316375 CrossRef CAS; (c) W. Li, X. Wang, Z. Liu, X. Zou, Z. Shen, D. Liu, L. Li, Y. Guo and F. Yan, Nat. Mater., 2024, 23, 131 CrossRef CAS.
- K. Cao, Y. Zhu, Z. Zheng, W. Cheng, Y. Zi, S. Zeng, D. Zhao and H. Yu, Adv. Sci., 2023, 10, 2207233 CrossRef CAS.
- Q. Li, W. Li, Z. Liu, S. Zheng, X. Wang, J. Xiong and F. Yan, Adv. Mater., 2024, 36, 2311214 CrossRef CAS.
- (a) C. L. He, F. C. Liang, L. Veeramuthu, C. J. Cho, J. S. Benas, Y. R. Tzeng, Y. L. Tseng, W. C. Chen, A. Rwei and C. C. Kuo, Adv. Sci., 2021, 8, e2102275 CrossRef; (b) F. Ou, T. Xie, X. Li, Z. Zhang, C. Ning, L. Tuo, W. Pan, C. Wang, X. Duan, Q. Liang, W. Gao, Z. Li and S. Zhao, Mater. Horiz., 2024, 11, 2191–2205 RSC.
- W. Li, L. Li, Z. Liu, S. Zheng, Q. Li and F. Yan, Adv. Mater., 2023, 35, 2301383 CrossRef CAS.
- (a) C. Liu, N. Morimoto, L. Jiang, S. Kawahara, T. Noritomi, H. Yokoyama, K. Mayumi and K. Ito, Science, 2021, 372, 1078 CrossRef CAS; (b) K. Hashimoto, T. Enoki, C. Liu, X. Li, T. Sakai and K. Mayumi, Macromolecules, 2024, 57, 1461 CrossRef CAS.
- (a) X. Qi, L. Wang, Y. Zhang, M. Jia, L. Zhang and D. Yue, Macromolecules, 2022, 55, 2758 CrossRef CAS; (b) P. Sotta and P.-A. Albouy, Macromolecules, 2020, 53, 3097 CrossRef CAS.
- C. M. Hartquist, S. Lin, J. H. Zhang, S. Wang, M. Rubinstein and X. Zhao, Sci. Adv., 2023, 9, eadj0411 CrossRef CAS PubMed.
- J. Chen, Y. Gao, L. Shi, W. Yu, Z. Sun, Y. Zhou, S. Liu, H. Mao, D. Zhang, T. Lu, Q. Chen, D. Yu and S. Ding, Nat. Commun., 2022, 13, 4868 CrossRef CAS PubMed.
- (a) M. Venkatesan, J. Chandrasekar, Y. C. Hsu, T. W. Sun, P. Y. Li, X. T. King, M. A. Chung, R. J. Chung, W. Y. Lee, Y. Zhou, J. H. Lin and C. C. Kuo, Adv. Sci., 2024, e2404019, DOI:10.1002/advs.202404019; (b) H. Wu, H. Wang, M. Luo, Z. Yuan, Y. Chen, B. Jin, W. Wu, B. Ye, H. Zhang and J. Wu, Mater. Horiz., 2024, 11, 1548–1559 RSC; (c) H. Wu, H. Wang, M. Luo, Z. Yuan, Y. Chen, B. Jin, W. Wu, B. Ye, H. Zhang and J. Wu, Mater. Horiz., 2024, 11, 1548–1559 RSC.
- S.-M. Kim, H. Jeon, S.-H. Shin, S.-A. Park, J. Jegal, S. Y. Hwang, D. X. Oh and J. Park, Adv. Mater., 2018, 30, 1705145 CrossRef.
- B. Li, F. Xu, T. Guan, Y. Li and J. Sun, Adv. Mater., 2023, 35, 2211456 CrossRef CAS.
- H. Chen, Z. Sun, H. Lin, C. He and D. Mao, Adv. Funct. Mater., 2022, 32, 2204263 CrossRef CAS.
- M. J. Jenkins, Y. Cao and S. N. Kukureka, Polym. Adv. Tech., 2006, 17, 1 CrossRef CAS.
- Y. Eom, S.-M. Kim, M. Lee, H. Jeon, J. Park, E. S. Lee, S. Y. Hwang, J. Park and D. X. Oh, Nat. Commun., 2021, 12, 621 CrossRef CAS.
- (a) K. Cao, Y. Zhu, Z. Zheng, W. Cheng, Y. Zi, S. Zeng, D. Zhao and H. Yu, Adv. Sci., 2023, 10, 2207233 CrossRef CAS; (b) M. T. I. Mredha, H. H. Le, V. T. Tran, P. Trtik, J. Cui and I. Jeon, Mater. Horiz., 2019, 6, 1504 RSC; (c) B. Yiming, Y. Han, Z. Han, X. Zhang, Y. Li, W. Lian, M. Zhang, J. Yin, T. Sun, Z. Wu, T. Li, J. Fu, Z. Jia and S. Qu, Adv. Mater., 2021, 33, 2006111 CrossRef CAS PubMed; (d) B. Yiming, X. Guo, N. Ali, N. Zhang, X. Zhang, Z. Han, Y. Lu, Z. Wu, X. Fan, Z. Jia and S. Qu, Adv. Funct. Mater., 2021, 31, 2102773 CrossRef CAS; (e) Z. Yu and P. Wu, Adv. Funct. Mater., 2021, 31, 2107226 CrossRef CAS; (f) L. Li, W. Li, X. Wang, X. Zou, S. Zheng, Z. Liu, Q. Li, Q. Xia and F. Yan, Angew. Chem., Int. Ed., 2022, 61, e202212512 CrossRef CAS; (g) Q. Xia, W. Li, X. Zou, S. Zheng, Z. Liu, L. Li and F. Yan, Mater. Horiz., 2022, 9, 2881 RSC; (h) C. Shan, M. Che, A. Cholewinski, R. Su and B. Zhao, Cell Rep. Phys. Sci., 2023, 4, 101511 CrossRef CAS; (i) Q. Quan, C. Fan, N. Pan, M. Zhu, T. Zhang, Z. Wang, Y. Dong, Y. Wu, M. Tang, X. Zhou and M. Chen, Adv. Funct. Mater., 2023, 33, 2303381 CrossRef CAS; (j) X. Zhang, Q. Fu, Y. Wang, H. Zhao, S. Hao, C. Ma, F. Xu and J. Yang, Adv. Funct. Mater., 2024, 34, 2307400 CrossRef CAS.
- (a) P. Shi, Y. Wang, K. Wan, C. Zhang and T. Liu, Adv. Funct. Mater., 2022, 32, 2112293 CrossRef CAS; (b) Y. Gong, Z. Li, H. Li, W. Wu, W. Zhou, J. Zhao, C. He and M. Jiang, Adv. Funct. Mater., 2022, 32, 2207452 CrossRef CAS; (c) S. Zhou, K. Guo, D. Bukhvalov, W. Zhu, J. Wang, W. Sun and M. He, J. Mater. Chem. A, 2021, 9, 5533 RSC; (d) M. Fu, Z. Sun, X. Liu, Z. Huang, G. Luan, Y. Chen, J. Peng and K. Yue, Adv. Funct. Mater., 2023, 33, 2306086 CrossRef CAS; (e) C. Xiang, Z. Wang, C. Yang, X. Yao, Y. Wang and Z. Suo, Mater. Today, 2020, 34, 7 CrossRef CAS; (f) X. P. Morelle, W. R. Illeperuma, K. Tian, R. Bai, Z. Suo and J. J. Vlassak, Adv. Mater., 2018, 30, 1801541 CrossRef.
- H. Chen, Z. Sun, K. Lu, J. Liu, C. He and D. Mao, Adv. Mater., 2024, 36, 2311332 CrossRef CAS PubMed.
- (a) Z. Zhang, L. Qian, J. Cheng, C. Ma and G. Zhang, Adv. Funct. Mater., 2024, 34, 2402115 CrossRef CAS; (b) Y. Wang, Z. Wei, T. Ji, R. Bai and H. Zhu, Small, 2023, 2307019 Search PubMed; (c) L. Yang, L. Sun, H. Huang, W. Zhu, Y. Wang, Z. Wu, R. E. Neisiany, S. Gu and Z. You, Adv. Sci., 2023, 10, 2207527 CrossRef CAS; (d) Y. Zhao, D. Gan, L. Wang, S. Wang, W. Wang, Q. Wang, J. Shao and X. Dong, Adv. Mater. Tech., 2023, 8, 2201566 CrossRef; (e) Z. Jin, H. Liu and H. Zhang, Macromol. Rapid Commun., 2024, 45, 2300457 CrossRef CAS PubMed; (f) Y. Wang, S. Sun and P. Wu, Adv. Funct. Mater., 2021, 31, 2101494 CrossRef CAS; (g) T. Li, Y. Wang, S. Li, X. Liu and J. Sun, Adv. Mater., 2020, 32, 2002706 CrossRef PubMed; (h) R. Du, T. Bao, T. Zhu, J. Zhang, X. Huang, Q. Jin, M. Xin, L. Pan, Q. Zhang and X. Jia, Adv. Funct. Mater., 2023, 33, 2212888 CrossRef CAS; (i) L. Jia, J. Xiao, Y. Tan, K. Zhang, Y. Liu and X. Wang, Small, 2023, 20, 2309231 CrossRef PubMed; (j) Y. Sun, J. Huang, Y. Cheng, J. Zhang, Y. Shi and L. Pan, SmartMat, 2024, e1269 CrossRef; (k) J. Tie, Z. Mao, L. Zhang, Y. Zhong and H. Xu, ACS Appl. Polym. Mater., 2023, 5, 9092 CrossRef CAS; (l) H. Peng, F. Yang, X. Wang, E. Feng, K. Sun, L. Hao, X. Zhang and G. Ma, ACS Appl. Mater. Interfaces, 2023, 15, 51763 CrossRef CAS; (m) C. Luo, Y. Chen, Z. Huang, M. Fu, W. Ou, T. Huang and K. Yue, Adv. Funct. Mater., 2023, 33, 2304486 CrossRef CAS; (n) R. Zhou, Y. Jin, W. Zeng, H. Jin, L. Shi, L. Bai and X. Shang, Adv. Funct. Mater., 2023, 33, 2301921 CrossRef CAS; (o) X. Wen, J. Xu, H. Wang, Z. Du, S. Wang and X. Cheng, Polym. Eng. Sci., 2022, 62, 3132 CrossRef CAS; (p) L. Sun, H. Huang, L. Zhang, R. E. Neisiany, X. Ma, H. Tan and Z. You, Adv. Sci., 2024, 11, 2305697 CrossRef CAS PubMed.
- (a) T. Reid and J. Gibert, Science, 2022, 375, 149 CrossRef CAS PubMed; (b) W. Wen and H. Imamizu, Nat. Rev. Psychol., 2022, 1, 211 CrossRef; (c) J. Xue, Y. Zou, Y. Deng and Z. Li, EcoMat, 2022, 4, e12209 CrossRef CAS.
- (a) X. Cao, Y. Xiong, J. Sun, X. Xie, Q. Sun and Z. L. Wang, Nano-Micro Lett., 2022, 15, 14 CrossRef PubMed; (b) F. Wen, C. Wang and C. Lee, Nano. Res., 2023, 16, 11801 CrossRef.
- (a) T. Cheng, J. Shao and Z. L. Wang, Nat. Rev. Methods Primers, 2023, 3, 39 CrossRef CAS; (b) Z. L. Wang, Rep. Prog. Phys., 2021, 84, 096502 CrossRef CAS.
- Y. Lee, S. Lim, W. J. Song, S. Lee, S. J. Yoon, J.-M. Park, M.-G. Lee, Y.-L. Park and J.-Y. Sun, Adv. Mater., 2022, 34, 2108586 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4mh01003e |
| This journal is © The Royal Society of Chemistry 2025 |