Theoretical insights and design of MXene for aqueous batteries and supercapacitors: status, challenges, and perspectives

Abstract

Aqueous batteries and supercapacitors are promising electrochemical energy storage systems (EESSs) due to their low cost, environmental friendliness, and high safety. However, aqueous EESS development faces challenges like narrow electrochemical windows, irreversible dendrite growth, corrosion, and low energy density. Recently, two-dimensional (2D) transition metal carbide and nitride (MXene) have attracted more attention due to their excellent physicochemical properties and potential applications in aqueous EESSs. Understanding the atomic-level working mechanism of MXene in energy storage through theoretical calculations is necessary to advance aqueous EESS development. This review comprehensively summarizes the theoretical insights into MXene in aqueous batteries and supercapacitors. First, the basic properties of MXene, including structural composition, experimental and theoretical synthesis, and advantages in EESSs are introduced. Then, the energy storage mechanism of MXene in aqueous batteries and supercapacitors is summarized from a theoretical calculation perspective. Additionally, the theoretical insights into the side reactions and stability issues of MXene in aqueous EESSs are emphasized. Finally, the prospects of designing MXene for aqueous EESSs through computational methods are given.

---

Jun Zhao

Jun Zhao is currently a doctoral candidate in the Department of Materials Science and Engineering, City University of Hong Kong, supervised by Prof. Jun Fan. He received her M.S. degree from the School of Chemical Engineering, Tianjin University. His current research interests are first-principles calculation of MXene materials in the energy storage field.

Jun Fan

Dr. Jun Fan received her bachelor's and doctoral degrees from Tsinghua University and Princeton University, respectively. She is a tenured associate professor and doctoral supervisor at City University of Hong Kong. Her research interests mainly include (1) two-dimensional material nanopore sequencing of proteins/DNA/RNA, the mechanism of the influence of nanomaterials on cell membranes, and the regulation of protein conformational conversion; (2) research on two-dimensional materials in the field of energy storage and catalysis; (3) the application of machine learning in force field development and material design.

---

1. Introduction

Industrial development and population growth have led to energy shortages and environmental issues, posing significant obstacles to human progress.^1,2 Therefore, developing efficient, reliable, safe, and environmentally friendly energy storage systems is crucial to address these problems.^3–5 Renewable energy sources, such as solar and wind, are intermittent, necessitating effective storage solutions for stable and continuous energy supply.^3,6 Electrochemical energy storage systems (EESSs), including batteries and supercapacitors, play a key role in capturing, storing, and delivering energy.^4,7–9 Among these, aqueous EESSs, especially aqueous batteries and supercapacitors, have garnered significant attention due to their inherent safety, environmental protection, and cost-effectiveness.^7,8,10,11

Compared to traditional non-aqueous EESSs, aqueous EESSs have multiple advantages.^12–14 First, using water as an electrolyte solvent reduces flammability and toxicity, enhancing safety. Second, aqueous EESSs generally have higher ionic conductivity, leading to better device rate performance. Third, the materials and processes for aqueous electrolytes are cheaper, making these systems more economically feasible. However, aqueous EESSs face challenges, such as a narrow electrochemical window, electrode material corrosion, irreversible metal dendrite growth, and low energy density.^15–17

Recently, MXene materials have shown promise in addressing the issues of aqueous EESSs.^10,11,13 Since their first synthesis, MXenes have attracted great interest due to their unique properties, such as high electrical conductivity, excellent mechanical strength, hydrophilicity, and tunability. They have been used in energy storage, biology, sensors, catalysis, optics, electromagnetic shielding, etc.^18–24 These unique properties enable MXene to serve as the intermediates of aqueous EESSs, exhibiting excellent performance.^11,13 Abundant surface sites of MXene provide storage or redox sites for charge carriers, enhancing the energy density of EESSs.^25,26 Besides, their layered structure facilitates rapid ion insertion and de-insertion, contributing to excellent rate performance and inhibiting dendrite formation.^27,28 The inherent high conductivity of MXene ensures efficient electron transport, essential for high power density and fast charging.²⁹ In short, these properties together make MXenes highly effective electrode materials in aqueous batteries and supercapacitors.

Further development of MXene materials for aqueous EESSs requires understanding their properties and energy storage mechanisms at the atomic scale. Compared to experimental methods, theoretical calculations and modeling are indispensable tools with the advantages of low cost, high efficiency, and precision.^30,31 Computational methods such as density functional theory (DFT) and molecular dynamics (MD), multi-physics fields, etc. provide valuable insights into the electronic structure and synthesis, electric field regulation, surface interactions, and charge storage mechanisms of MXene.^{25,30,32–35} However, comprehensive reviews of theoretical calculations for understanding and designing MXene materials for aqueous EESSs are rare. Therefore, we review the current status, challenges, and perspectives in this field to promote the development of more efficient aqueous EESSs.

2. Structural composition, synthesis, and properties of MXene

2.1. Structural composition of MXene

MXene is a class of 2D materials composed of transition metal (TM) carbides and nitrides, attracting widespread attention for their unique layered structure and tunable chemical composition.^36–38 As shown in Fig. 1(a), MXene typically has a multi-layer structure, obtained by selectively etching A elements (e.g., Al, Ga, Sn) in the MAX phases, which can then be further peeled into a single-layer structure.³⁸ MXene shares a similar hexagonal close-packed crystal structure and P63/mmc symmetry with the MAX phases.²⁴ In Fig. 1(b), the general chemical formula of MXene is M_n+1X_nT_x, where M represents the early TM, which can be a single metal or an ordered/disordered mixture of metals; X is carbon and/or nitrogen, and n ranges from 1 to 4 depending on the number of TM layers; T_x indicates the surface functional groups determined by the preparation method.³⁹ This structural and compositional diversity endows MXenes with varied physical, chemical, electronic, and optical properties, giving them significant potential in energy storage applications.^11,13,24,40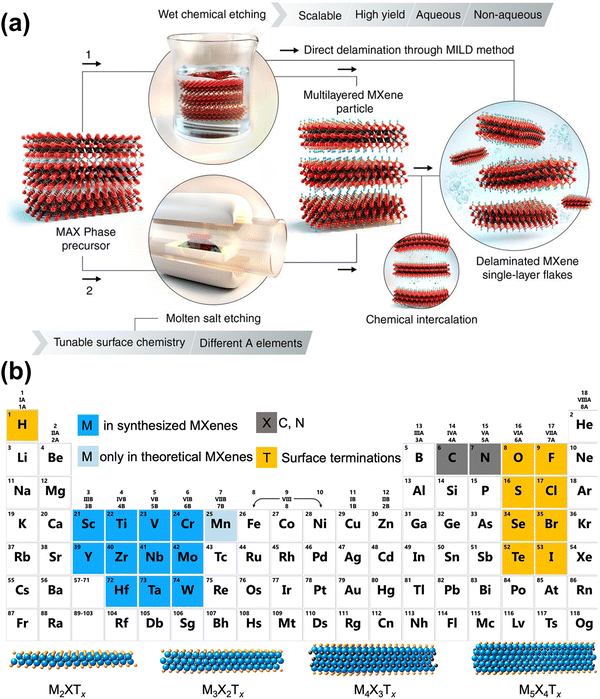

Fig. 1 (a) Schematic illustration of two approaches to produce MXene by removal of A layers from MAX phases and related layered compounds.²⁴ Reproduced with permission ref. 24. Copyright 2021, AAAS. (b) Periodic table showing compositions of MXene. Elements used to build MXene are color-coded. The schematics of four typical structures of MXene are presented at the bottom.³⁹ Reproduced with permission ref. 39. Copyright 2021, American Chemical Society.

The compositional diversity of MXene underpins their unique properties. MXene can be composed of various TMs, such as III B (Sc, Y), IV B (Ti, Zr, and Hf), V B (V, Nb, and Ta), VI B (Cr, Mo, and W), and VII B (Mn, verified only by calculation) elements.^24,39,41,42 These metals can be present as single-layer, double-layer, or multi-layer in the MXene structure.³⁸ Besides a single metal composition, various TM elements can be introduced at the metal site, including bimetallic and high-entropy MXene.^24,30,43,44 The metals in bimetallic MXenes can form ordered and solid solution MXene.^45,46 Ordered bimetallic MXene are divided into in-plane ordered (i-MXene) and out-of-plane ordered (o-MXene) structures. Selective etching of TM elements in i-MXene can produce non-stoichiometric in-plane ordered vacancy-type MXene.⁴⁷ High entropy alloy MXenes contain more than 4 TM elements occupying the M site.³⁰ So far, only a few high-entropy MXenes have been successfully synthesized, but their unique mechanical and electrochemical properties show great potential in batteries and supercapacitors.^44,47,48

The X element in MXene is generally C, N, or a mixture of both. Currently, experimentally synthesized MXenes are mainly carbides, with only a few nitrides.⁴⁹ Although a few nitrides have been synthesized, they exhibit some special properties. For example, compared to Ti₂CT_x, Ti₂NT_x exhibits better structural stability as well as electrocatalytic N₂ reduction reaction (NRR) activity.⁵⁰ Additionally, the choice of X element affects the electronic structure and conductivity of MXenes, with nitrides generally exhibiting higher band gaps than carbides.⁴⁷ For carbonitrides, the occupation of C and N atoms at the X site is generally random, independent of their stoichiometric ratio. Carbonitrides have been proven useful in EESSs.⁵¹

The surface termination group of MXene is very important, which greatly affects the interface properties and thus its performance in electrocatalysis and EESSs.^13,52,53 MXene also has a wide range of surface functional groups, including VA, VIA, and VIIA group elements.^24,38 The type and distribution of these surface functional groups can be adjusted through different synthesis methods. The surface groups can be mixed functional groups such as OH, O, and F atoms, or mixed F, O, and Cl atoms; they can also be single functional groups, such as Ti₂CO₂, Ti₂CCl₂, etc.^38,41 Furthermore, in-plane or out-of-plane ordering at surface sites has not been observed experimentally. However, theoretical calculations show that out-of-plane ordered MXenes based on surface functional group atoms are stable (often called Janus MXene) and have special electronic, magnetic, and optical properties.⁵⁴

2.2. Synthesis of MXene

2.2.1. Experimental synthesis of MXene. MXene synthesis typically employs a top-down strategy, using MAX phase precursors (or MAX phase-like compounds, such as Mo₂Ga₂C) by selective etching of A-layer atoms, as shown in Fig. 1(a). Since the M atoms and A atoms in the MAX phase are strongly bonded, obtaining MXene phases through mechanical peeling is difficult.⁴⁷ M–A bonds are generally weaker than M–X bonds, allowing MXene to be obtained by selectively dissolving A elements through thermodynamically and kinetically favorable chemical reactions, such as chemical or electrochemical etching. Initially, a strong acid (e.g. HF) was used to etch the A layer in the MAX phase to peel off the MXene layer.⁵⁵ After that, Chidiu et al. used a LiF and HCl mixture to selectively etch the A layer atoms, avoiding the direct use of HF.⁴⁰ To develop a simple, low-cost, environmentally friendly, and mass-producible MAX etching method, researchers have developed various methods including NH₄HF₂, NaOH, Lewis acid molten salt, and electrochemical etching methods.^37,56–59 The microstructure and surface properties of MXene are affected by many factors, including the choice of etchant, precursor, synthesis conditions, and intercalation process.^38,57,60,61 These factors ultimately affect the chemical properties of the prepared MXene, determining its applications. It is important to emphasize that we focus on how researchers predict the synthesis of MXene through theoretical calculations, rather than specific experimental synthesis routes, which other excellent reviews have summarized.^{38,41,62–64}

2.2.2. Theoretical prediction of MAX to MXene phase synthesis.
Screening and prediction of MAX phases. As mentioned previously, MXene is synthesized from the precursor MAX phase. Therefore, the composition, structural characteristics, and stability of MAX directly affect the properties of MXene.³⁸ To date, monometallic, bimetallic ordered, bimetallic solid solution and high entropy alloy MAX precursors (shown in Fig. 2(a)) have been synthesized experimentally.^44,65–68 However, as the types of sites (M, A, X sites) and disorder increase, the chemical space of MAX phases expands significantly. Computational screening and prediction can discover new thermodynamically stable MAX phase structures with various compositions, guiding the synthesis of MXene with special properties.

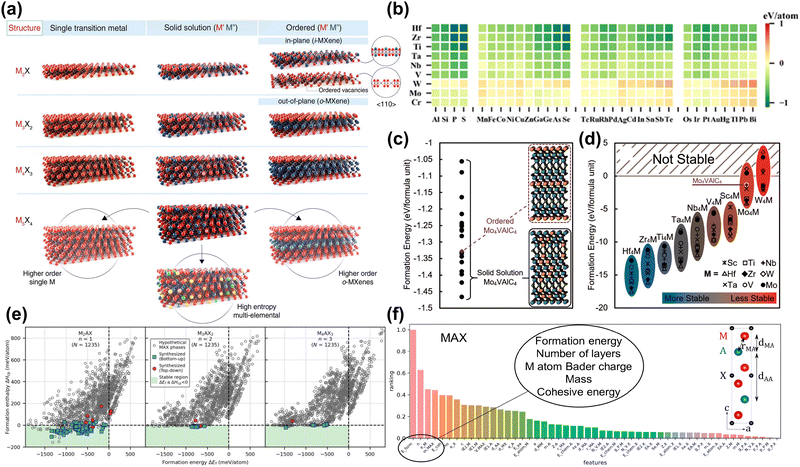Fig. 2 (a) Schematic illustration of the MXene structures.²⁴ Reproduced with permission ref. 24. Copyright 2021, AAAS. (b) ΔE_f for 288 M₂AC phases displayed as a heatmap for 9 metals and 32 different elements at the A site.⁶⁹ Reproduced with permission ref. 69. Copyright 2023, Elsevier. (c) Formation energies for solid-solution Mo₄VAlC₄ configurations (black dots) compared to ordered Mo₄VAlC₄ (purple diamond). (d) DFT calculated formation energies of ordered M′₄M′′AlC₄ MAX phases. Most are predicted to be stable except for some Mo and W compositions.⁷⁰ Reproduced with permission ref. 70. Copyright 2019, American Chemical Society. (e) Calculated formation enthalpy ΔH_cp as a function of formation energy ΔE_f for ternary M_n+1AX_n phases with n = 1, 2, 3. Hypothetical MAX phases are given by grey circles and synthesized MAX phases by blue squares (bottom-up synthesis) and red hexagons (top-down synthesis). The green area marks the region of thermodynamic stability fulfilling ΔH_cp < 0 (and ΔE_f < 0).⁷¹ Reproduced with permission, ref. 71. Copyright 2024, Elsevier. (f) Feature importance ranking for MAX. Layer distances and bond lengths are labeled in the unit cell diagrams.⁷² Reproduced with permission, ref. 72. Copyright 2017, American Chemical Society.

To predict the stability of MAX phases, researchers often use formation energy (ΔE_f) and formation enthalpy (ΔH_cp) as evaluation indicators.^69,73–76 Their calculation equations are as follows:

ΔE_f(M_n+1AX_n) = E(M_n+1AX_n) − (n + 1)μ_M − μ_A − nμ_X (1)

where ΔE_f(M_n+1AX_n) is the formation energy of the MAX phase; E(M_n+1AX_n) is the total energy of the MAX phase, μ_M, μ_A, and μ_X are the chemical potential of element M, A, and X, respectively.

ΔH_cp(MAX) = E(MAX) − E(set of most competing phases) (2)

where ΔH_cp(MAX) is the formation enthalpy of the MAX phase; E(MAX) is the total energy of a MAX phase and E (set of most competing phases) is a combination of the set of most competing phases at the same composition as MAX.

Calculating ΔE_f involves comparing the total energy of the MAX phase with the chemical potential of its constituent elements (generally regarded as the ground state crystal structure energy of the elements). As shown in Fig. 2(b), Wu et al. evaluated the stability of 288 MAX phases based on formation energy through high-throughput computational screening, finding that 222 of these phases have negative formation energy.⁶⁹ In addition, the formation energy is related to the number of valence electrons of the M-site metal, with S₂C and Ti₂C MAX showing the best stability. However, experimental results show that only 50 MAX phases have been synthesized, indicating that this is not a suitable stability criterion. Because only the energy change of MAX decomposing into elemental phases is considered, this method overestimates stability.³⁰ Similarly, various research groups use formation energy to assess the stability of MAX phases.^75,77 Notably, this method is reasonable when evaluating the stability of MAX phases with the same elements. Fig. 2(c) and (d) show stable ordered/disordered multi-metal (M site) MAX phases can be quickly discovered by this method.⁷⁰

To ensure accurate predictions, the energy difference between the MAX phase and all possible competing phases in the M-A-X system must be evaluated. One possible solution is to evaluate the ΔH_cp. This method can accurately evaluate the stability of existing MAX phases and guide the synthesis of new ones. In Fig. 2(e), Dahlqvist et al. evaluated the stability of 3705 MAX phases by calculating the ΔH_cp.⁷¹ The green area is a theoretically stable area based on the criteria of ΔE_f ≤ ΔH_cp < 0. This shows that using ΔH_cp to judge the possibility of MAX phase synthesis is more consistent with the experimental results compared to ΔE_f. In addition, for MAX phases of mixed elements, such as bimetallic ordered/disorder phases and high entropy phases, configurational entropy caused by the element arrangement needs to be considered. Dahlqvist et al. also used a special quasi-random structure method to simulate the distribution of chemically disordered bimetallic sites at M sites.³² When configurational entropy was not considered (at 0 K), the solid solution MAX phase was unstable. However, after introducing configurational entropy (at 1173 K), a stable disordered MAX phase with the lowest energy was found. Through predicting stable MAX phases, bimetallic MAX phases and high entropy phases have been synthesized successfully in experimental work.^48,78–80

Machine learning (ML) is a branch of artificial intelligence that focuses on building models that analyze and predict data. In materials science, ML is used to accelerate the discovery of new materials and predict material properties, thereby changing traditional research methods. For example, experimental testing and computational modeling are often time- and resource-intensive and therefore inefficient for exploring the vast space of possible material configurations. ML leverages large datasets generated by experiments or high-throughput computations to more quickly identify new materials with desirable properties. Researchers could use ML methods to accelerate the discovery of stable MAX phases. Frey et al. adopted a positive and unlabeled ML framework to predict the MAX phase.⁷² Positive and unlabeled machine learning is used to deal with training models using only positive and unlabeled data. This method is beneficial in scenarios where negative examples are scarce or unavailable. By leveraging the available positive instances and treating unlabeled data with sophisticated techniques, this method effectively identifies patterns and makes predictions.⁸¹ Characteristics related to thermodynamic stability, bond strength, and charge distribution were found to be most important in model predictions. In particular, as shown in Fig. 2(f), formation energy, number of layers, Bader charge of the M atoms, mass of MAX, and cohesive energy were key features for predicting the likelihood of MAX phase synthesis. Through prediction, 111 MAX phases were found to be synthesized. However, using ΔE_f as an important descriptor introduces bias in the composition predictions.³⁰

Computationally driven synthesis of MXene. Once a thermodynamically stable MAX phase is identified, the next step is the synthesis of MXenes. This process involves selective stripping of the A element from the MAX phase to obtain a 2D MXene structure.³⁸ Computational studies are crucial for understanding and optimizing the processes of converting MAX phases into MXene. This includes modeling the chemical exfoliation process, assessing the thermodynamic stability of MXene, and predicting the feasibility of synthesizing new MXenes.

Similar to calculating the stability of the MAX phase, the ΔE_f of MXene can be calculated by taking into account the chemical potentials of its constituent elements. Hu et al. used this calculation method to obtain a negative ΔE_f for Sc₂C, suggesting it is stable and can be synthesized.⁸² However, synthesizing this MXene experimentally remains unachievable. As another example, Wyatt et al. predicted 20 bimetallic o-MXenes that could be synthesized through this calculation method, but most MXenes still cannot be synthesized.⁸³ As stated above, this calculation method is flawed and needs to consider competing phases. Afterward, Ashton et al. calculated the formation energies of 54 MXenes considering competing phases, as shown in Fig. 3(a). However, all formation energies are positive (unstable), attributed to the metastable properties of 2D materials. Moreover, there is a lack of correlation between the calculated formation energy trends and experimental results.⁸⁴ In fact, MXene synthesis involves stripping the MAX phase, a process ignored by these two calculation methods.

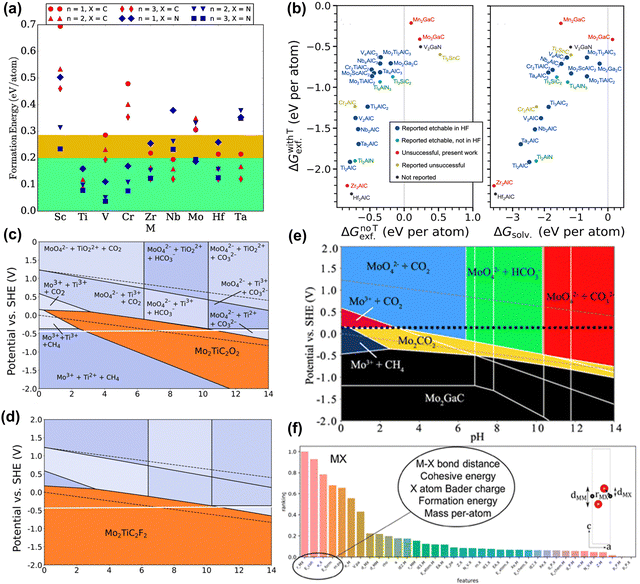Fig. 3 (a) Formation energies for M_n+1X_nO₂, MXene relative to the lowest energy mixture of competing bulk phases. The green region highlights the general 0.2 eV per atom threshold observed for 2D material stability, and the yellow region highlights the 0.285 eV per atom formation energy of the V₂CO₂ MXene, the highest of those that have been synthesized.⁸⁴ Reproduced with permission, ref. 84. Copyright 2016, American Chemical Society. (b) Exfoliation free energies for the chemical exfoliation of MAX phases (left) when including termination groups (ΔG^withT_exf) on the resulting MXene compared to the exfoliation free energy without terminations (ΔG^noT_exf) and (left) the solvation free energies (ΔG_solv).⁸⁵ Reproduced with permission, ref. 85. Copyright 2023, Springer Nature. Etching Pourbaix diagram for Mo₂TiAlC₂, showing regions where (c) Mo₂TiC₂O₂, and (d) Mo₂TiC₂F₂ are stable (orange segments). The dashed black lines indicate the stability range of water. The solid white line shows PZC.⁸⁶ Reproduced with permission, ref. 86. Copyright 2020, American Chemical Society. (e) Etching diagrams of 2D Mo₂CO₂ for Mo₂GaC. The PZC values are shown by the dashed black lines.⁸⁷ Reproduced with permission, ref. 87. Copyright 2019, American Chemical Society. (f) Feature importance ranking for MXene models. Layer distances and bond lengths are labeled in the unit cell diagrams.⁷² Reproduced with permission, ref. 72. Copyright 2019, American Chemical Society.

Therefore, some studies consider the MAX to MXene synthesis process as being achieved by mechanical exfoliation.³⁰ The calculation formula of this process is as follows:

ΔG_exf = ΔE_exf = [E(M_n+1X_n) + E(A) − E(M_n+1AX_n)]/N (3)

where E(M_n+1AX_n), (M_n+1X_n), and E(A) are the total energies of the MAX phase, the MXene, and the A element in its elemental phase, respectively.

This process does not take into account real reactions, such as the formation of functional groups. Therefore, predicting MXene synthesis using this calculation method is difficult. For example, Kahazaei et al. calculated 82 MAX phases and predicted 13 MAX phases that are easily exfoliated, but they could not experimentally synthesize the corresponding MXene phases.⁸⁸

To obtain more accurate predictions, a correct description of the experimental synthesis process is necessary, fully considering the chemical potential of the etched elements A and T_x. Jonas et al. considered how to construct chemical potential in HF, and also considered the stripping energy with or without functional groups.⁸⁵ The results in Fig. 3(b) showed that regardless of functional groups, most MXene phases can be synthesized through exfoliation, differing from the experimental results. This discrepancy arises because MAX may always dissolve to form new species instead of MXene when etched by HF (as shown in Fig. 3(c) and (d)). As another example, Seong et al. considered AlF₃, SiF₄, and H₂ molecules during the HF etching process of the high-entropy MAX phase (A = Si, Al).⁴⁸ The results show that the chemical exfoliation of Al is thermodynamically favorable, while the opposite is true for Si. Despite the successful synthesis of new MXene phases, the etching process still does not consider competing phases (i.e., dissolved products).

The Pourbaix diagram is a calculation method that fully considers competing phases and explores the electrochemical stability of materials. Ashton et al. considered the stability of MXene and MAX phases under the influence of electrode potential (U) and pH (Fig. 3(e)).⁸⁷ The Pourbaix diagram reveals the potential and pH conditions under which Mo₂CO₂ is stable and can be synthesized. Tsounis et al. considered the overall stability of MXene materials. By calculating the Pourbaix diagrams of Mo₂CO₂ and V₂CO₂, MXene has the best thermodynamic stability in the region of high pH and negative potential.⁸⁹ In another work, Caffery et al. used Pourbaix diagrams to predict the possibility of electrochemical etching to improve o-MXene production.⁸⁶ They found that high yields of (Mo, Ti)₂CT_x were possible because they were stable over a wide range of pH and U. Meanwhile, the stability window of F-functionalized MXene is higher than that of an O-functionalized one. Although electrochemical etching is not a universal method for synthesizing MXene, these works can give valuable information on the etching reaction process.

ML is also used in the synthetic discovery of MXene. Instead of constructing the correct synthesis reaction process, ML needs to provide easily accessible descriptors. Frey et al. used ML methods to obtain 20 MAX/MXene combinations that were predicted to be synthesized (Fig. 3(f)).⁷² The most important features include M–X bond length, cohesive energy and formation energy, atomic mass, and Bader charge of M and X atoms. However, this result is considered controversial due to the mechanical peeling energy involved. More precise descriptors such as vacancy formation, chemical stripping energy, etc. need to be developed in the future.³⁰

2.2.3. Properties of MXene. As previously mentioned, MXene is synthesized through the selective etching of the MAX phase. Due to the diverse MAX phase compositions and etching methods, MXene possesses a broad chemical composition space, granting it tunable physicochemical, electronic, optical, and mechanical properties.^11,24,90,91 This review focuses on the properties of MXene that are beneficial for aqueous batteries and supercapacitors. We outline the advantages of MXene in EESS, categorized as follows:
(1) Adjustability. The general chemical formula of MXene is M_n+1X_nT_x, where any variable can be altered, providing a wide chemical composition space. This is the primary distinction from other 2D materials.⁹² Therefore, MXene can serve as the cathode, anode, separator, or electrolyte additive in EESSs.^10,11,13,93
(2) High specific surface area. MXenes have extremely high specific surface areas, providing more active sites per unit of mass or volume. For EESSs, this enhances the contact area between the electrode material and the electrolyte, increasing the rate and efficiency of the chemical reaction, and boosting the theoretical capacity of energy storage.⁹⁴
(3) Excellent mechanical flexibility. The structure of MXene materials remains intact even under strong bending and stretching, crucial for flexible energy storage devices.⁹⁵ When MXene is used as an intercalation electrode, volume changes during ion insertion and extraction are mitigated and their lifetime is enhanced.^96,97 In addition, theoretical calculations show that tensile strain imparts additional physical and chemical properties to MXene, such as improving electrocatalytic water splitting reactions.⁹⁸
(4) Layered structure and fast ion diffusion. The layered structure of MXene provides a convenient diffusion channel for ions, crucial for the rapid insertion and de-intercalation of charge carriers. This improves the rate performance and cycle stability of the battery, extending the battery life. For example, DFT calculations show that MXene can provide a lower ion diffusion barrier (i.e., rate capability) for aqueous Zn-ion batteries.²⁷
(5) Excellent electronic conductivity. Compared to other 2D materials, MXene has superior electronic conductivity.⁹⁹ This property is crucial for energy storage systems, ensuring rapid electron transfer, reducing energy loss, and increasing the charge and discharge rate.¹⁰⁰
(6) Excellent hydrophilicity. The surface of MXene can be occupied by –OH and –O functional groups, giving it excellent hydrophilicity and better wettability between the MXene electrode and the aqueous electrolyte. Additionally, the hydrophilic MXene surface can induce uniform metal nucleation, inhibiting dendrite formation.¹³
(7) Abundant redox sites. TM sites in MXene can provide oxidative activity. Besides, MXene provides additional pseudo-capacitance in acidic electrolyte supercapacitors due to abundant O surface sites.¹¹

In short, due to these excellent characteristics, MXene materials can be used to design high-capacity, long-life, and high-rate aqueous EESSs, providing valuable strategies for other fields.

3. Aqueous metal-ion batteries

Aqueous metal ion battery systems are divided into monovalent metal ion systems (e.g. Li⁺, Na⁺, K⁺) and multivalent metal ion (e.g. Mg²⁺, Zn²⁺, Al³⁺) systems according to the valence state of the charge carrier.^16,17 Among them, although monovalent metal ions have mature battery technology, their relatively low theoretical capacity and higher reactivity with water limit their application in aqueous batteries.^12,13 Multivalent metal ions are gaining attention due to their cost advantages from high abundance and capacity benefits from multi-electron transfer processes, making them suitable for large-scale energy storage devices.^15,16 However, as shown in the Pourbaix diagram of Fig. 4(a)–(c), the narrow electrochemical window of the aqueous electrolyte (∼1.23 V) limits the use of metals (e.g. Al) as anodes.¹⁰¹ Only metallic Zn is an ideal candidate for aqueous batteries due to its high theoretical capacity (5851 mA h cm⁻³), low potential (−0.76 V vs. SHE), high abundance, environmental friendliness, and nontoxicity.^13,15,102 However, aqueous Zn-ion batteries (AZIBs) still face issues such as side reactions (e.g. hydrogen evolution reaction (HER), corrosion), uncontrollable dendrites, host material structural degradation and slow diffusion kinetics.^15,103–107 Recently, MXene was found to alleviate the problems of AZIBs.^108–110 Therefore, we explore the role of MXene in AZIBs from a theoretical calculation perspective.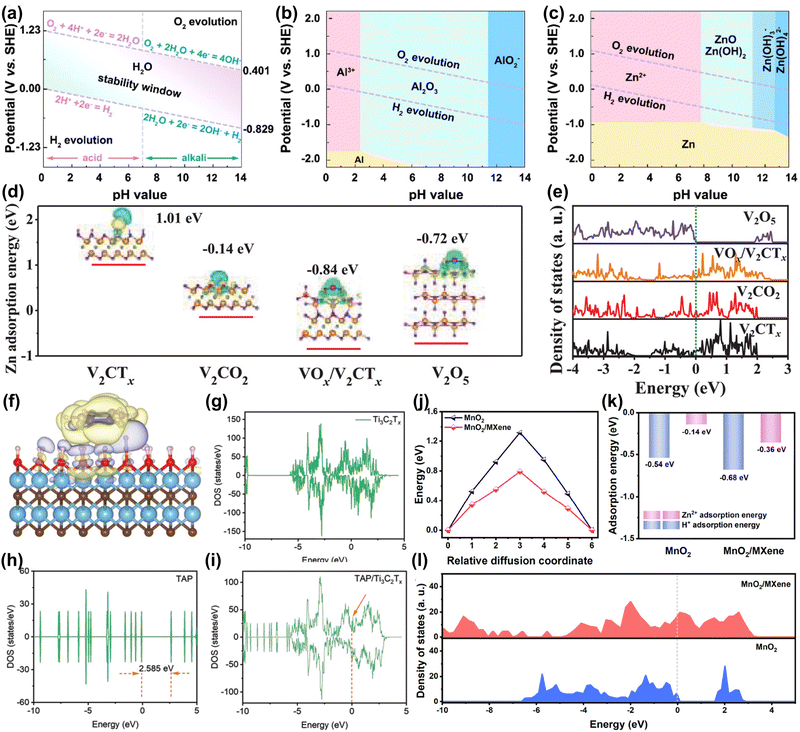

Fig. 4 Pourbaix diagram of (a) aqueous electrolyte, metallic (b) Al and (c) Zn in aqueous electrolyte at 25 °C.¹³ Reproduced with permission, ref. 13. Copyright 2022, Elsevier. Zn²⁺ adsorption energy, charge density difference (d), and DOS (e) of V₂CT_x, V₂CO₂, VO_x/V₂CT_x, and V₂O₅. (V: orange; C: greyish-green; H: red; F: grey; O: purple; Zn: pink).¹¹¹ Reproduced with permission, ref. 111. Copyright 2021, John Wiley and Sons. Charge density difference (f) of TAP/Ti₃C₂T_x. DOS of Ti₃C₂T_x (g), TAP (h), and TAP/Ti₃C₂T_x (i).⁹³ Reproduced with permission, ref. 93. Copyright 2022, John Wiley and Sons. Diffusion energy barriers (j) and absorption energies (k) of H⁺ and Zn²⁺ on the surface of MnO₂ and MnO₂/MXene. (l) DOS for MnO₂ and MnO₂/MXene.¹¹² Reproduced with permission, ref. 112. Copyright 2023, American Chemical Society.

3.1. MXene in cathodes

Commonly used AZIB cathode materials include organic materials, metal oxides, Prussian blue analogs, etc.¹³ However, these materials mainly face problems such as structural phase transition and degradation, poor conductivity, and poor rate performance.^12,113 The main reasons are: (1) highly active materials cause side reactions like water decomposition and metal dissolution.^14,113 (2) The insertion and extraction of high charge density Zn²⁺ cause structural bending and collapse. Additionally, the slow diffusion of Zn²⁺ and subsequent ion accumulation lead to irreversible phase transition.^14,113,114 (3) Materials like organic compounds inherently have low electronic conductivity.¹¹⁵ Therefore, developing new materials is an effective way to alleviate these problems.

3.1.1. MXene compositions for cathode materials. MXene materials have excellent conductivity and open intercalation structures. Combining them with other cathode materials, such as TM oxide, metal–organic frameworks (MOF), and organic cathodes etc., can significantly improve battery performance.

Liu et al. proposed using highly conductive V₂CT_x materials and generating high-valent VO_x by an in situ electrochemistry method to address the low conductivity and the ion diffusion rate issues of V-based cathode materials.¹¹¹ In Fig. 4(d), theoretical calculations showed that original V₂CT_x has difficulty adsorbing Zn²⁺ (adsorption energy +1.01 eV). When a VO_x/V₂CT_x heterostructure forms, the adsorption energy for Zn²⁺ is −0.84 eV, which accelerates the redox kinetics of stored Zn ions. Moreover, in Fig. 4(e), the high electronic state occupancy near the Fermi level indicates that the electrode has high electronic conductivity. The material achieved a specific capacity of 358 mA h g⁻¹ at a high current density of 30 A g⁻¹. Wang et al. designed imine-based tris(aza)pentacene (TAP)/MXene composites to alleviate the problems of poor conductivity and structural degradation of organic electrodes.⁹³ In Fig. 4(f), theoretical calculations reveal that the strong electron transfer interaction between Ti₃C₂T_x and TAP helps maintain the structure of TAP. The density of state (DOS) results in Fig. 4(g–i) show that introducing Ti₃C₂T_x enhances the conductivity of the electrode. Ultimately, the electrode achieves a long cycle life (10 000 times) and a high-capacity retention rate (81.6%). Besides, Wang et al. used MXene to synergistically improve the ion/electron transfer kinetics and structural stability of MnO₂ (Fig. 4(j and k)).¹¹² Calculation results showed that MXene/MnO₂ has a strong adsorption capacity and low diffusion energy barrier for H⁺/Zn²⁺. Besides, the heterostructure increases the electronic state density of electrons at the Fermi level and promotes the transfer of electrons. Wang et al. constructed a MOF/MXene heterostructure material to achieve durable and fast Zn-ion batteries. Although porous 2D MOF is an ideal storage and transport material for Zn ions, its inherent low conductivity leads to low capacity and power density. Theoretical calculations show that MXene can improve the conductivity of MOFs. Therefore, MOF/MXene exhibited a superior electrochemical performance (260.1 mA h g⁻¹ at 0.1 A g⁻¹).¹¹⁶

3.1.2. MXene as the host material of charge carriers. To improve Zn ion affinity and ion diffusion kinetics in F-functionalized MXene, Chen et al. synthesized V₂CT_x MXene with rich –OH functional groups and an interlayer K⁺ pillar.¹¹⁷Fig. 5(a) shows that there is stronger bonding of Li⁺/Zn²⁺ on V₂C(OH)₂ than that on V₂CF₂. The lower electronegativity of –OH weakens the interaction between ions and host materials. Consequently, the calculated migration energy barrier in Fig. 5(b) of Li⁺ and Zn²⁺ in V₂C(OH)₂ is much lower than that in V₂CF₂. As a result, excellent rate performance and outstanding cycle life for V₂C(OH)₂ MXene are achieved.

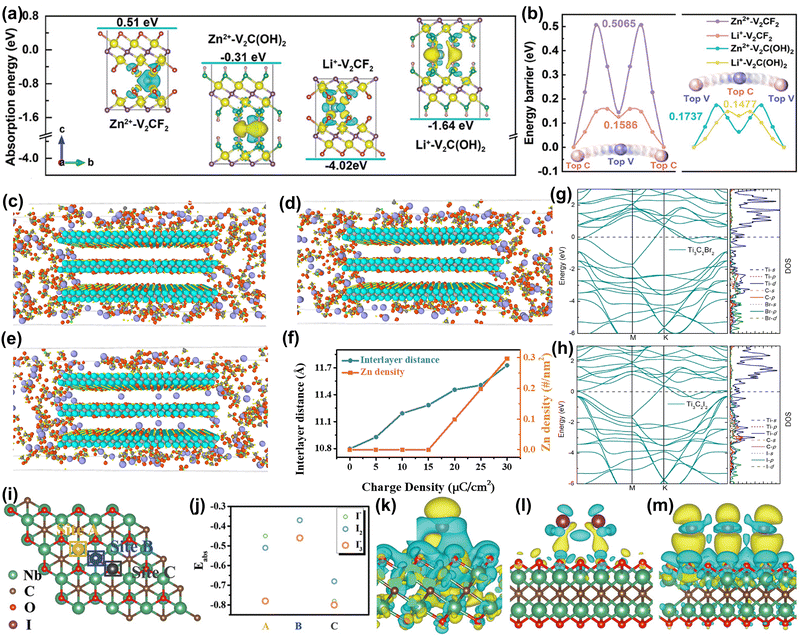Fig. 5 (a) The absorption energies of Li⁺/Zn²⁺ with V₂CF₂ and V₂C(OH)₂ models. Insets provide the corresponding differential charge density diagrams, where the yellow and blue domains represent electron accumulation and depletion, respectively. (b) The migration energy barriers of Li⁺/Zn²⁺ in V₂CF₂ and V₂C(OH)₂ lattices.¹¹⁷ Reproduced with permission ref. 117. Copyright 2024, John Wiley and Sons. Configurations of the Nb₂CT_x cathode were assigned with a charge density of (c) 15 μC cm⁻², (d) 20 μC cm⁻², and (e) 30 μC cm⁻², where the purple, grey, cyan, red, yellow, and green spheres represent Zn, C, Nb, O, F, and S atoms, respectively. (f) Dependence of interlayer distance and inserted Zn density on the charge density of the Nb₂CT_x cathode. Zn²⁺ can only enter the interlayer when the charge density increases to 20 μC cm⁻².¹¹⁸ Reproduced with permission, ref. 118. Copyright 2021, Cell Press. Electronic structure of (g) Ti₃C₂Br₂ and (h) Ti₃C₂I₂.¹¹⁹ Reproduced with permission, ref. 119. Copyright 2021, American Chemical Society. (i) Crystal model of the Nb₂CT_x host with the proposed adsorption sites. (j) Calculated adsorption energy of iodine species (I⁻, I₂, and I₃⁻) on Nb₂CT_x flakes at different sites. Final optimized charge-density-difference patterns of I⁻ (k), I₂ (l), and I₃⁻ (m) on the Nb site. The iso-surface value is set to be 0.001 e Å⁻³.¹²⁰ Reproduced with permission ref. 120. Copyright 2021, John Wiley and Sons.

In addition, MXene electrodes usually exhibit capacitive behavior, leading to a rapid drop in output voltage during discharge, which limits their energy density. Li et al. activated MXene battery behavior by 2.4 V high-voltage scanning, and the Nb₂CT_x cathode gradually showed stable Zn²⁺ storage behavior.¹¹⁸ The battery behavior of MXene results in a 92% higher capacity compared to capacitive behavior. To understand how high-voltage scanning triggers the voltage platform, MD simulation was used. By applying classical mechanics, MD is a computational simulation method used to study the physical movements of atoms and molecules, and provides insights into the structure, dynamics, and thermodynamics of complex molecular systems over time. Simulation results in Fig. 5(c–f) showed that Zn²⁺ ions can only enter the cathode interlayer when the applied charge density increases to 20 μC cm⁻². At lower charge density, the ions cannot overcome the resistance to achieve insertion/extraction and are only adsorbed on the surface or edge area, showing typical pseudocapacitive behavior. In short, high voltage triggers the initial insertion/extraction of Zn²⁺ ions, achieving the high energy density of the MXene positive electrode.

3.1.3. Halogenated and halide-containing MXene as cathode materials. Aqueous Zn-halide batteries have attracted the interest of researchers due to the low cost and safety of halide production at the cathode and the high redox potential (such as I⁰/I⁻ of 0.62 V, I⁰/I⁺ of 0.99 V, Br⁰/Br⁻ of 1.08 V versus SHE).^120–122 However, halides exhibit low electronic conductivity and are prone to shuttle effects, necessitating strong bonding with conductive carriers.^120,121

Li et al. proposed a new method to directly synthesize Ti₃C₂ MXene with single, binary, and ternary halogen end groups (such as –Cl, –Br, –I, –BrI, and –ClBrI). Among these, Ti₃C₂Br₂ and Ti₃C₂I₂ showed clear discharge platforms and high specific capacities.¹¹⁹ The calculated band structure in Fig. 5(g) and (h) shows strong hybridization of Ti d, C p, and Br/I p orbitals in the energy range of −2 to −6 eV, indicating that the outermost Ti atoms form strong coordination bonds with carbon and halogen atoms. In addition, Li et al. used a simple electrodeposition strategy to insert and confine iodine species between MXene layers, effectively suppressing the shuttle effect.¹²⁰ Calculation results in Fig. 5(i) and (j) showed that the adsorption of I species on the MXene surface is spontaneous due to high adsorption stability. Fig. 5(k–m) shows that differential charge density results indicate a strong electronic interaction between I species and the MXene surface, beneficial for achieving fast redox kinetics. Finally, the long cycle life and high-rate capability of Zn–I₂ aqueous batteries were achieved. Similarly, they found that this method can be applied to the Zn–Br₂ aqueous battery system, achieving high energy density and low-temperature cycle stability.¹²² Calculation results showed that this is due to the strong electronic interaction between the MXene surface and the Br species, which benefits the fixation of Br₂ and the rapid transfer of electrons.

3.2. MXene in anodes

Metallic Zn is an ideal anode for AZIBs due to its high abundance, safety, suitable potential, and high capacity. However, there are still some challenges for Zn metal anodes: (1) uneven nucleation of metal Zn can lead to dendrite formation and promote side reactions.^103,123,124 (2) Acidic solutions can exacerbate metal corrosion, HER, and passivation effects.¹² Among them, the uncontrollable dendrite problem of Zn anode is the main obstacle for AZIBs. At present, various strategies, such as regulating the interfacial electric field, Zn deposition process, Zn coordination environment, etc., are used to solve this problem.^125–127 Recently, researchers have applied MXene materials to anodes to enhance Zn metal anode performance, mitigate Zn dendrite growth and side reactions, and elucidate the mechanism of MXene action through computational simulation.^{26–29,35,109,128}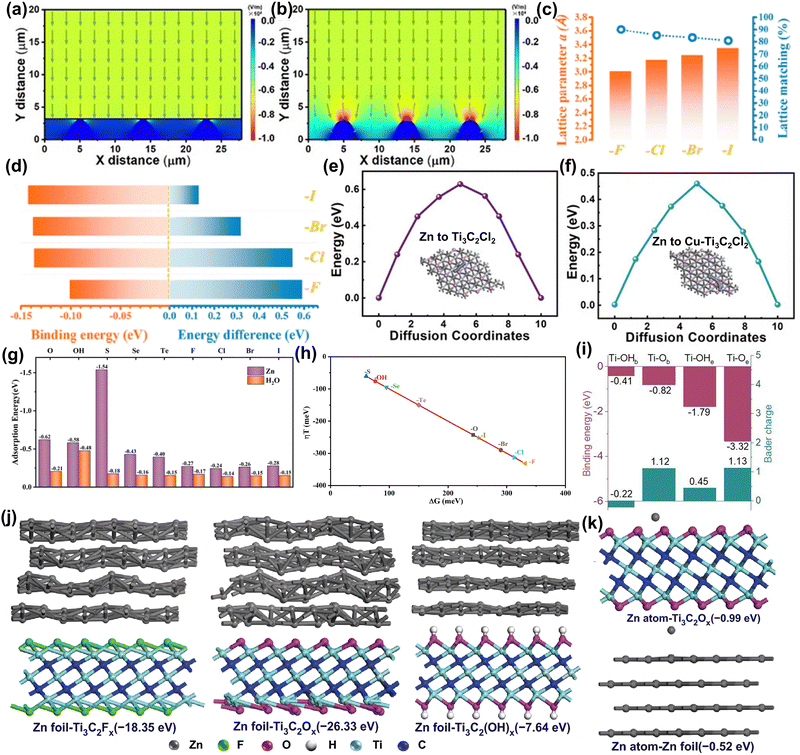

3.2.1. MXene regulates the interfacial electric field. Zhang et al. developed an in situ spontaneous reduction/assembly strategy to directly assemble an ultra-thin and uniform MXene layer on the surface of the Zn anode.¹⁰⁹ To understand how MXene materials modulate electric fields to affect Zn deposition, they used COMSOL simulation methods. It provides a platform for simulating physical phenomena across various domains, such as electromagnetics, structural mechanics, fluid dynamics, and heat transfer, using a multiphysics approach. COMSOL simulation results in Fig. 6(a) show that the favorable charge redistribution effect of MXene achieved a uniform electric field distribution, providing a lower Zn nucleation energy barrier for the Zn anode. In contrast, Fig. 6(b) shows that the pure metal surface exhibited a locally enhanced electric field distribution, promoting more Zn²⁺ deposition nucleation and leading to the tip effect. Ultimately, the local Zn nuclei form larger dendrite flakes, causing battery failure. Yu et al. used the MXene-porous polydopamine (MPP) interface layer to control the electric field distribution to inhibit the generation of Zn dendrites.³⁵ COMSOL simulation results showed that the MPP's moderate electronic conductivity can form a uniform electric field, thereby avoiding the tip effect of Zn deposition. Zhu et al. proposed that the charge redistribution effect and electronic conductivity of MX-TMA (tetramethylammonium) coating helps to homogenize the interfacial electric field on the Zn, achieving uniform Zn ion deposition on its surface.¹²⁸

Fig. 6 Models of the electric field distributions for (a) MXene-coated Zn foil and (b) pure Zn.¹⁰⁹ Reproduced with permission, ref. 109. Copyright 2021, John Wiley and Sons. (c) Lattice parameters vs. calculated lattice matching ratios of halogen-terminated Ti₃C₂(F/Cl/Br/I)₂. (d) Calculated binding energy between two Zn atoms on different MXene surfaces vs. the energy difference for the later Zn atom spread on an MXene surface or stacked on the previous Zn atom.²⁶ Reproduced with permission, ref. 26. Copyright 2021, American Chemical Society. Diffusion energy of Zn on (e) Ti₃C₂Cl₂ and (f) Cu–Ti₃C₂Cl₂ for the original, transition, and final states.²⁷ Reproduced with permission, ref. 27. Copyright 2023, John Wiley and Sons. (g) The adsorption energy of Zn ions and water on MXene surfaces with different functional groups. (h) The volcano plot of the calculated overpotential (η = ±ΔG/e₀) vs. ΔG on Ti₃C₂T_x.²⁸ Reproduced with permission, ref. 28. Copyright 2024, John Wiley and Sons. (i) Binding energies and charge transfer number between the Zn atom and functional groups (Ti–OH_b, Ti–OH_e, Ti–O_b, and Ti–O_e) on Ti₃C₂.¹²⁹ Reproduced with permission, ref. 129. Copyright 2023, American Chemical Society. Calculation models corresponding binding energies of Zn foil (j) adsorbed on Ti₃C₂T_x and Zn atoms (k) absorbed on Zn foil, Ti₃C₂O_x.¹³⁰ Reproduced with permission, ref. 130. Copyright 2021, Springer Nature.

3.2.2. MXene regulates Zn adsorption and diffusion. The adsorption and diffusion capabilities of Zn ions on the substrate material determine the subsequent evolution of Zn metal deposition. Researchers have regulated the adsorption and diffusion of Zn ions by changing the surface functional groups and doping metals of MXene. Li et al. designed Ti₃C₂T₂ (T = F, Cl, Br, I) materials with different surface functional groups for Zn negative electrodes.²⁶ They used DFT calculations to understand the interaction between halogenated MXene and Zn²⁺ ions. This calculation method uses electron density to perform quantum calculations, which can more efficiently study the electronic structure of multi-body systems. DFT calculations can study the structure and physical and chemical properties of materials at the atomic scale.¹³¹Fig. 6(c) shows that all halogenated MXenes exhibit good affinity for Zn ions (adsorption energy less than 0). Meanwhile, there was a high lattice match (90%) between the calculated optimized halogenated MXene and Zn crystals. The regulatory effect of these two helps to form a consistent heterogeneous interface region during the early deposition stage. To prove this, Fig. 6(d) shows that subsequent Zn ions are more likely to adsorb on MXene rather than on existing Zn deposits, meaning Zn tends to form a coherent heterogeneous interface. Experimental results showed that halogenated MXene extended the life of the Zn anode by more than 12 times. Li et al. proposed a Cu-modified Ti₃C₂Cl₂ as a Zn anode with high Zn affinity and hydrophobicity.²⁷ Theoretical calculations in Fig. 6(e and f) showed that Cu-modified MXene has higher adsorption energy for Zn atoms (−1.74 eV) than that of Ti₃C₂Cl₂ (−0.61 eV). This means that the modified MXene provides a large number of Zn nucleation sites for the Zn electrode to achieve uniform deposition. Secondly, the lower migration energy barrier on Cu-MXene means faster Zn²⁺ transport, which accelerates the Zn²⁺ deposition process from 2D diffusion to stable 3D accumulation with minimal dendrite formation. Experimental results confirm that Cu-modified MXene achieves stable and reversible Zn deposition and stripping.

MXene has shown an important role in protecting Zn metal anodes, but the protection mechanism of different functional groups is still unclear. Therefore, Luo et al. used DFT calculations and MD simulations to study the protection mechanism of MXene with nine different surface functional groups (−O, –OH, –S, –Se, –Te, –F, –Cl, –Br, and –I).²⁸ The study found that all tested MXene materials showed good electrical conductivity, structural stability, and stronger adsorption capacity for Zn ions relative to water molecules (Fig. 6g). In particular, MXene containing sulfur (–S) and oxygen (–O) functional groups showed high adsorption energy for Zn²⁺, promoting uniform Zn ion deposition and reduced water contact with the anode, thus enhancing the stability of the anode. In terms of HER side-reaction, as shown in Fig. 6(h), halogen-terminated MXene showed a strong inhibitory effect with a higher absolute value of ΔG. In short, by rationally designing the surface functional groups of MXene, a dendrite-free and side-reaction-free Zn anode can be achieved.

3.3. MXene for separators and electrolytes additives

In addition to being used in cathode and anode electrodes of AZIBs, MXene can also be used as separators and electrolyte additives to improve the performance of AZIBs. To address the inevitable zinc dendrite formation of AZIBs, Bu et al. proposed using a polypropylene separator wrapped with mesoporous Ti₃C₂ MXene with active edge sites to eliminate dendrites.¹²⁹ The edge sites in Ti₃C₂ can convert the formed dead zinc (Zn⁰) dendrites back into electroactive zinc ions (Zn²⁺) through spontaneous redox reactions. DFT calculation results in Fig. 6(i) show that the binding energy between the edge Ti–O sites and Zn atoms is the highest, and the Bader charge results show that Zn transfers more electrons to MXene. This means that they can extract electrons from Zn⁰ dendrites more effectively, promoting the dendrite digestion process. This method enables AZIB to exhibit an ultra-long cycle life of 2200 hours. Sun et al. explored the role of Ti₃C₂T_x as an electrolyte additive in AZIBs.¹³⁰ They found that MXene additives provide abundant Zn-affinity groups (such as –OH, –F, and –O) and good conductivity. DFT calculations in Fig. 6(j) and (k) show that all functionalized MXene have a strong binding ability with Zn, among which O-terminated MXene can provide seed sites for uniform nucleation of Zn ions. The weak binding energy between Zn ions and substrates induces only a small number of nucleation sites. In short, MXene electrolyte additives can control the Zn ion nucleation and growth to inhibit the formation of zinc dendrites.

4. Aqueous supercapacitors

In addition to batteries, supercapacitors are also a key component of electrochemical energy storage systems.^132,133 Due to the fast charge response, supercapacitors show higher power density, although the energy density is low.¹³² For aqueous supercapacitors, although they have advantages in price, safety, and environmental protection, the inherent narrow electrochemical window further limits the improvement of energy density.^133–135 To achieve wider applications, they still need to make breakthroughs in energy density.¹³² In recent years, MXene has greatly improved the performance of aqueous supercapacitors due to its unique advantages (as described in Section 2.2.3).^134,136,137 First, most MXenes are highly conductive metallic materials characterized by a high density of states at the Fermi level.²⁴

Second, the layered two-dimensional structure of MXenes facilitates rapid ion transport and provides redox reaction sites, resulting in high rates and long cycle life.¹¹ Additionally, the transition metal sites and surface functional groups of MXenes are adjustable, allowing for both double-layer capacitance and rapidly reversible redox reactions at or near the surface (i.e., pseudo-capacitor).¹⁰ Finally, the hydrophilic surface of MXenes facilitates efficient charge storage and enables rapid charge and discharge cycles.¹³Table 1 summarizes the capacitance data for various materials in aqueous electrolytes. The results indicate that MXenes exhibit ultra-high capacitance and rate performance. Given the promising potential of MXenes in aqueous supercapacitors, a thorough understanding of their energy storage mechanisms is essential for advancing supercapacitor technology. Therefore, this discussion begins with the charge storage mechanism of supercapacitors, exploring the capacitance mechanism of MXenes in detail through theoretical calculations.

Table 1 Comparison of electrochemical performance of different electrode materials in aqueous supercapacitors

Materials	Electrolyte	Capacitance (scan rate)	Stability (retention/cycles/scan rate)	Energy density (W h kg^−1)	Power density (W h kg^−1)	Ref.
Co9S8	3 M KOH	1775 at 4 A g^−1	91.4% after 2000 cycles at 16 A g^−1	49.9 at 4 A g^−1	900 at 4 A g^−1	138
MoS2	0.5 M Li2SO4	350 F g^−1 at 5 mV s^−1	88.0% after 10 000 cycles at 5 A g^−1	50 at 1 A g^−1	1000 at 1 A g^−1	139
PEDOT	1 M KCl	117 F g^−1 at 100 mV s^−1	86.0% after 1000 cycles at 0.2 A g^−1	11.4 at 0.2 A g^−1	100 at 0.2 A g^−1	140
PPy/Graphene	1 M H2SO4	626 F g^−1 at 0.22 A g^−1	75.4% after 5000 cycles at 4 A g^−1	21.7	110	141
Co-MOF	3 M KOH	534 F g^−1 at 1 A g^−1	99% after 5000 cycles at 5 mV s^−1	9.62 at 4 mA cm^−2	1454 at 4 mA cm^−2	142
ZnCo2O4–MnO2	3 M KOH	2057 F g^−1 at 1 A g^−1	99% after 5000 cycles at 15 A g^−1	—		143
Ti3C2Tx	3 M H2SO4	210 F g^−1 at 10 V s^−1	—			144
Ti3C2Tx	1 M H2SO4	429 F g^−1 at 1 A g^−1	89% after 5000 cycles at 10 A g^−1	29.2 at 1 A g^−1	320 at 1 A g^−1	145

---

4.1. Supercapacitor charge storage mechanism

Battery systems can store higher energy density based on Faraday reactions but are limited by the diffusion capacity of charge carriers, resulting in low charge and discharge rates.¹⁴⁶ In contrast, supercapacitors achieve fast charge and discharge rates due to a fast charge response but have low energy density.¹⁴⁷ Supercapacitors can be classified into electrical double-layer capacitors (EDLCs) and pseudo-capacitors according to the charge storage mechanism of the electrodes.^148,149

The charge storage of EDLCs is not a Faraday process. Charge is stored and released only by physical adsorption and desorption of electrolyte ions on the surface of electrode materials (as shown in Fig. 7(a)). In this energy storage conversion process, the formation of the electrical double-layer (EDL) takes a very short time, and no electron exchange occurs on the EDL, so high power density and fast charging and discharging can be achieved. This surface charge storage process will cause only slight volume changes in the electrode material during long-term operation, thereby achieving excellent cycle stability.¹³²

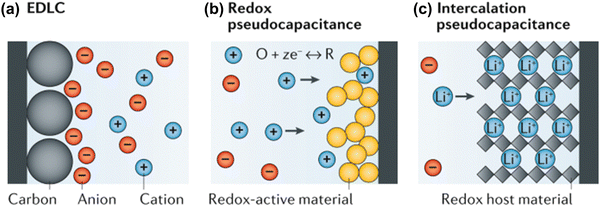Fig. 7 Electrochemical charge-storage mechanisms: (a) ELDC, (b) Redox pseudo-capacitance and (c) intercalation pseudo-capacitance.¹⁴⁹ Reproduced with permission, ref. 149. Copyright 2020, Springer Nature.

Pseudo-capacitors achieve capacitive charge storage through the Faraday process. Because the charge transfer process occurs on or near the surface and is not controlled by semi-infinite diffusion, its charge and discharge rate are comparable to that of EDLCs. Pseudo-capacitors are mainly divided into two types according to their working mechanism: redox pseudo-capacitors and intercalation pseudo-capacitors.¹⁴⁹ Redox capacitors are when ions are adsorbed on the interface of electrode materials and undergo a charge transfer process with nearby electrode materials (i.e., the redox reaction process shown in Fig. 7(b)), thereby achieving energy storage.

Intercalation pseudo-capacitors are capacitors that store energy by inserting electrolyte ions into the interlayer or pores of electrode materials, which involves a charge transfer process (as shown in Fig. 7(c)). The electrode reaction of the battery is also an ion intercalation process similar to that of the intercalation pseudo-capacitor. Unlike the electrode reaction of the battery, the intercalation pseudo-capacitor does not involve a phase change reaction during the Faraday redox reaction and is not diffusion-controlled due to the rapid ion transport process.⁵³

4.2. Computational understanding of MXene for aqueous supercapacitors

4.2.1. Theoretical mechanism of charge storage in different electrolytes. MXene has shown excellent capacitive performance in aqueous supercapacitors.^10,11,53 Understanding the energy storage mechanism in aqueous supercapacitors through theoretical calculations can inspire new designs and optimizations of high-performance aqueous EESSs. Here we review the computational insights into the charge storage mechanism of MXene in different solution electrolytes.
Neutral and alkaline electrolytes. The hydrated metal cations confined in 2D MXene nanosheets are believed to improve capacitance by forming an EDL. First, Sugahara et al. found that water molecules confined in the MXene slits can enhance the EDLC, with the larger-size Li⁺-hydration layer providing the most capacitance (Fig. 8(a)).¹⁵⁰ Besides, they used the three-dimensional reference interaction site model (3D-RISM) to evaluate the hydration structure of various alkali ions in the MXene microslit. 3D-RISM is a computational approach used to study molecular solvation and interactions at the atomic level. It allows for detailed analysis of solvation structures, free energies, and molecular interactions.¹⁵¹ The results show that the highest water density is found in the Li⁺-intercalated MXene in Fig. 8(b and c). Also, in Fig. 8(d and e), they observed that the direction of the electric field of Li intercalation was reversed inside the intercalation hydration layer, meaning a negative dielectric constant of the hydration layer, leading to enhanced capacitance. This phenomenon is caused by the resonance effect between the dipole polarization of water molecules and the external electric field, excessively shielding the external electric field. Ando et al. revealed the charge storage mechanism of MXene electrodes intercalated with hydrated metal cations through DFT calculations.⁹⁴ From an electronic perspective, fully hydrated metal cation intercalation only produces EDL capacitance behavior, attributed to the hydrated shell shielding the orbital coupling between cations and MXene (Fig. 8(f), left). In contrast, partially or completely de-solvated cations are coupled with MXene electronic orbits, resulting in pseudo-capacitance (as shown in the right figure of Fig. 8(g)). Besides, Simon et al. pointed out that due to the small number of intercalated metal cations, the resulting pseudo-capacitance can be ignored compared to EDLC.¹³³

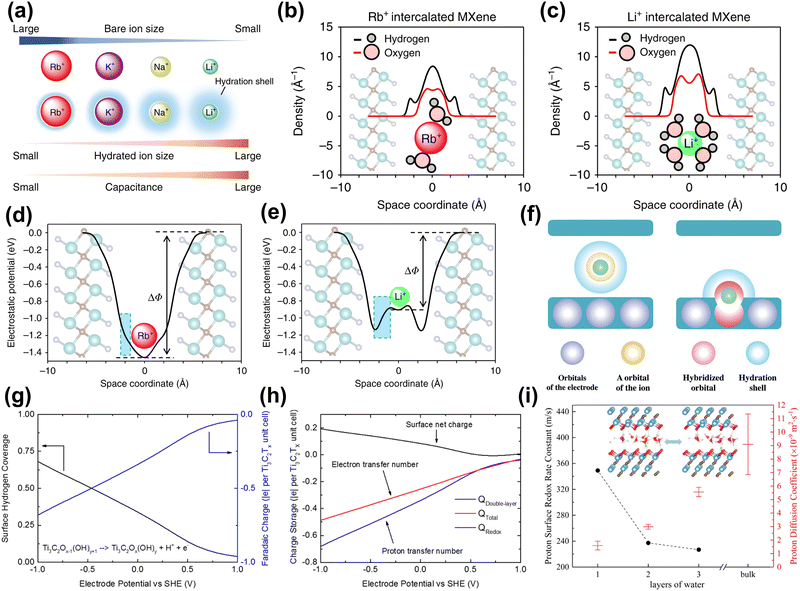Fig. 8 (a) Orders of bare-ion size, hydrated ion size, and observed capacitance. (b) and (c) 3D-RISM calculation results for the hydrated ions confined in the MXene microslit. Hydrogen and oxygen atomic density profiles along the c axis (perpendicular to the MXene layers) in Rb⁺ intercalated and Li⁺ intercalated Ti₂CT_x·nH₂O. The optimized n values are 0.8, and 1.35 for the Rb⁺ intercalated and Li⁺ intercalated MXene, respectively. (d) and (e) Theoretical calculation for the electrostatic potential profile of Rb⁺- and Li⁺-intercalated Ti₂CT_x·nH₂O.¹⁵⁰ Reproduced with permission, ref. 150. Copyright 2019, Springer Nature. (f) Schematic pictures of the capacitive and pseudocapacitive conditions formed inside the MXene electrodes. Green sphere represents a cation. Purple, yellow, red, and blue spheres indicate orbitals of an electrode, orbital of the ion, hybridized orbital of the electrodes and cations, and the hydration shell.⁹⁴ Reproduced with permission, ref. 94. Copyright 2020, John Wiley and Sons. (g) Average H coverage of Ti₃C₂T_x in 1 M H₂SO₄ at different electrode potentials. (h) Faradaic charge (blue, to balance proton transfer), EDL charge (black, due to surface net charge), and total charge (red, net electron transfer number) stored at different electrode potentials.³⁴ Reproduced with permission, ref. 34. Copyright 2018, American Chemical Society. (i) The average number of water molecules hydrogen-bonded to the hydronium ion for different layers of water with protons confined in Ti₃C₂O₂ layers. The inset is a schematic diagram of the structure of the intercalated water-MXene model.²⁵ Reproduced with permission, ref. 25. Copyright 2019, American Chemical Society.

Acidic electrolytes. Compared with alkaline (or neutral) electrolytes, MXene electrodes under acidic electrolytes exhibit higher capacitance due to pseudo-capacitance. This is because the proton undergoes a rapid redox reaction with the MXene surface. Jiang's group revealed the surface redox process of Ti₃C₂T_x (T = O, OH) MXene in 1 M H₂SO₄ electrolyte at constant-electrode potential through DFT calculations and implicit solvation models.³⁴ The calculation results in Fig. 8(h) showed that based on the experimental electrochemical window (0.5 V to −1.0 V vs. SHE), the net surface charge of 0.2|e| per unit MXene was observed, which means that the redox reaction dominates the capacitance. After that, they further investigated the redox process of Ti₃C₂O₂ with protons under the explicit solvent model (acidic electrolyte).²⁵ As shown in Fig. 8(i), the study found that in interlayer-restricted water, protons are rapidly and reversibly exchanged between the MXene surface and interfacial water molecules. In addition, the surface redox rate is related to the number of intercalated water layers, and single-layer water has the highest redox rate.

4.2.2. Approaching real capacitance through the theoretical calculation method. Calculating capacitance through theoretical models is crucial for designing aqueous EESSs. Simulation allows researchers to predict the capacitance behavior of materials without experiments, accelerating the screening and optimization of new materials. Here, we summarize several theoretical models to estimate the theoretical capacitance of MXene.

Ji et al. calculated the work function consistent with a standard hydrogen electrode (SHE) and DOS to obtain the intrinsic capacitance (i.e., quantum capacitance) of Ti₂CT₂.¹⁵² The calculation results show that the predicted pseudo-capacitance of O-functionalized MXene is 56.69 F g⁻¹ in a neutral solution. In addition, they calculated the integrated capacitance of Ti₂CF₂ and Ti₂CO₂ in Na ion capacitors (Fig. 9(a)), reaching 291 F g⁻¹ and 252.2 F g⁻¹, respectively. Combined with the low diffusion barrier of Na ions, MXene is considered to be a good intercalation pseudo-capacitor material. In another work, they used a similar method to explore the effects of terminals (F, O, and OH) and coordinated atoms on capacitance. The results showed that O-functionalized MXene mainly exhibits pseudocapacitive behavior in aqueous electrolytes due to a large number of unoccupied partial DOS (PDOS) of Ti atoms above the Fermi level within the electrolyte window (Fig. 9(b)). In contrast, bare-, F-, and OH-functionalized MXene exhibit EDL characteristics. In addition, the calculation method of quantum capacitance has been used to explore other MXene materials.^153–156

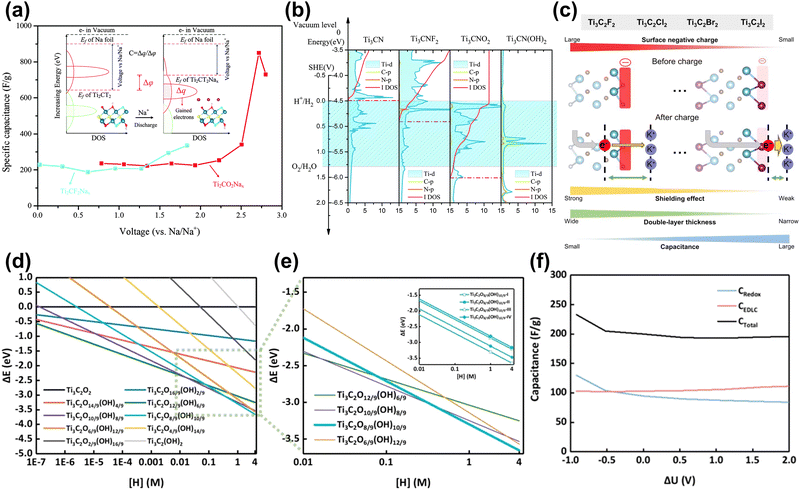Fig. 9 (a) Specific capacitance of Ti₂CO₂ and Ti₂CF₂ nanosheets, and the calculated method is illustrated as the inset.¹⁵² Reproduced with permission, ref. 152. Copyright 2016, Royal Society of Chemistry. (b) Relative PDOS and integral DOS of the d-orbitals of Ti atoms referenced to SHE. The yellow and red lines show the PDOS of C atoms and N atoms, respectively. The red dot lines are the Fermi level positions. The blue region represents the electrolyte window. The Fermi level of Ti₃CN(OH)₂ cannot be marked due to outside of the y-axis range, which lies approximately 1.82 eV relative to the vacuum level.¹⁵⁷ Reproduced with permission, ref. 157. Copyright 2016, Royal Society of Chemistry. (c) Schematics showing the electronic impact of the MXene electrode surface on EDL capacitances depending on the surface functional groups.¹⁵⁸ Reproduced with permission, ref. 158. Copyright 2022, American Chemical Society. (d) Surface Pourbaix diagram of MXene surfaces with various –OH groups as a function of the concentration of hydrogen ions. (e) Dashed-rectangle box-highlighted Pourbaix diagram of MXene surfaces under strongly acidic conditions. The formation energy of each surface is indicated by thin lines, while the most stable surfaces are represented by bold lines. The Pourbaix diagram of the most stable surface with different -OH group distributions Ti₃C₂O_8/9(OH)_10/9-(I, II, III or IV) is the inset. (f) Predicted capacitance performance.¹⁵⁹ Reproduced with permission, ref. 159. Copyright 2024, American Chemical Society.

The real charging and discharging process is more complicated and requires additional constraints. Cheng et al. introduced implicit solvent models and constant electrode potentials into the theoretical calculations of supercapacitors.³⁴ They examined the point of zero charge (PZC) of MXene electrodes at different hydrogen coverage ratios. The results showed that in the redox-dominated region (<0.5 V vs. SHE in Fig. 8(h)), the integrated capacitance of Ti₃C₂T_x was ∼230 F g⁻¹ close to the experimental value. In subsequent work, they used this method and combined it with high-throughput computational screening to find a series of MXene electrodes with high capacitance, among which Ti₂N exhibited the highest specific capacitance of over 450 F g⁻¹.¹⁶⁰ Shimada et al. calculated the EDLC of halogen (F, Cl, Br, I) functionalized MXene by the ESM-RISM method (a hybrid DFT-solvation method).^158,161 The results showed that the capacitance per unit surface area increases with the increase of the halogen atomic number (F < Cl < Br < I). This is because the functional groups with low electronegativity help introduce electrode electrons into the EDL region, thereby increasing the capacitance (Fig. 9(c)). Zheng et al. then used Pourbaix diagrams in Fig. 9(d and e) to study the distribution of functional groups on the surface of MXene in acidic electrolytes and calculated the EDLC and pseudo-capacitance based on the real surface. The results in Fig. 9(f) showed that the theoretical capacitance of MXene was in strong acid ranges from 200 F g⁻¹ to 233 F g⁻¹. In addition, Wang et al. considered the charge storage and release process during capacitor operation.¹⁶² They predicted that the capacitance of the original Ti₃C₂ could be as high as 2131 F g⁻¹.

4.2.3. Transport of charge carriers. Understanding the transport process of charge carriers in aqueous supercapacitors aids in understanding the charge storage mechanism of electrode materials. First, as shown in Fig. 10(a–g), Shao et al. used MD simulation to explore the pseudocapacitive behavior of pristine MXene (P-MXene) and 500 °C annealed MXene (500-MXene) in acidic electrolytes.¹⁶³ The results in Fig. 10(d, f, and g) show that a well-organized monolayer of water molecules was formed within the 500-MXene layer, which facilitated the rapid proton transfer. However, P-MXene had numerous –OH functional groups on the surface, which destroyed this ordered structure and led to low-rate performance, as shown in Fig. 10(c, e, and g). Jiang's group used ab initio molecular dynamics (AIMD) to explore the transport mechanism of protons in different numbers of water layers restricted in the MXene interlayer.²⁵ Unlike classical MD, AIMD combines principles of quantum mechanics with molecular dynamics to simulate the behavior of atoms and molecules. AIMD uses electronic structure calculations to determine forces, providing highly accurate insights into molecular systems. The results in Fig. 8(f) showed that as the number of intercalated water layers increased, the exchange rate of protons with the O-terminals on the MXene surface decreased, but its transfer rate in water increased. When the water layer thickness reaches three layers, the proton transfer rate in the water is close to that of the bulk phase. The group then used the same method to study the graphene-Ti₃C₂O₂ heterogeneous system.¹⁶⁴ The results in Fig. 10(h–j) showed that the proton transfer rate at this heterogeneous interface is higher than that of similar interfaces between Ti₃C₂O₂ layers, which is caused by the interfacial electric field of the heterogeneous structure. The study by Wen et al. revealed different diffusion mechanisms of hydrated protons and K⁺ ions between Ti₃C₂T_x layers.¹⁶⁵ They calculated the migration energy barriers of K⁺ and H⁺ in the presence and absence of water, and the results showed that water molecules can not only stabilize charged ions but also improve the diffusion of ions.

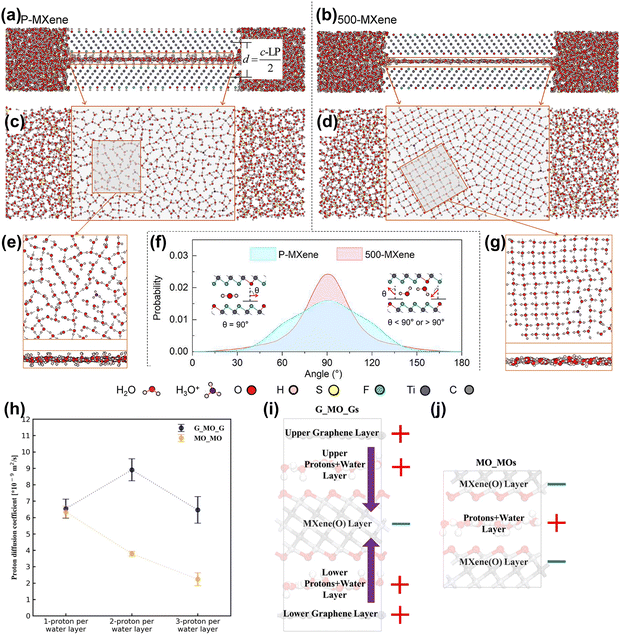Fig. 10 Side view of (a) P-MXene and (b) 500-MXene layers with surrounding electrolytes. Top view of the water molecules between the (c) P-MXene and (d) 500-MXene layers. MXene atoms are not shown here. (e and g) Close-up top view and side view of water molecule distribution between the P-MXene and 500-MXene layers. (f) Comparison of probability profiles of dipole orientation of water molecules inside P-MXene and 500-MXene layers. θ gives the angle between the water molecular dipole moment and the electrode surface normal.¹⁶³ Reproduced with permission, ref. 163. Copyright 2020, American Chemical Society. (h) Proton diffusivity at the Ti₃C₂O₂-graphene (G_MO_G) and Ti₃C₂O₂–Ti₃C₂O₂ (MO_MO) interfaces vs. different amounts of intercalated protons. A schematic of the charge distribution (± signs) and interfacial electric field (purple arrows): (i) water/hydronium confined in the Ti₃C₂O₂-graphene (G_MO_G) interfaces and (j) water/hydronium confined between Ti₃C₂O₂–Ti₃C₂O₂ (MO_MO) layers.¹⁶⁴ Reproduced with permission, ref. 164. Copyright 2021, American Institute of Physics.

5. Challenges

Researchers have demonstrated that using MXene as electrodes can significantly improve the performance of aqueous energy storage systems.^11,13,136 However, some issues remain to be addressed. On the one hand, the highly active surface of MXene further promotes the water-splitting side reaction, resulting in a shortened effective electrochemical window. On the other hand, the structure of MXene is unstable and dynamic under conditions of solution and electric field. In response to these challenges, we reviewed computational studies on MXene in water splitting reactions and stability, which will help to rationally design MXene electrodes for aqueous EESSs.

5.1. Water-splitting reaction of MXene

A major challenge in aqueous energy storage systems is the water-splitting reaction.^16,134,135 As a side reaction, it consumes energy and produces gas during charging and discharging, leading to electrolyte decomposition and corrosion of electrode materials and reducing the electrochemical window and stability.¹¹ Moreover, the good performance of MXene materials in the HER further limits the performance of energy storage devices.^144,166 Therefore, a deep understanding of the behavior of MXene in the HER is crucial for the design and optimization of aqueous batteries and supercapacitors.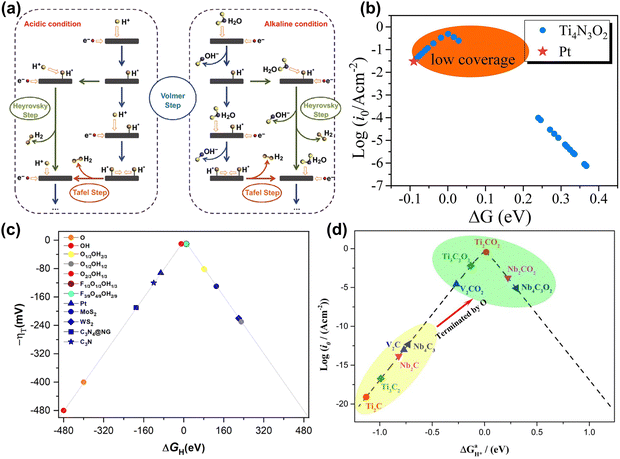

5.1.1. The HER reaction. The HER is a half-reaction in water splitting, primarily following the Volmer–Heyrovsky and Volmer–Tafel mechanisms (Fig. 11(a)).¹⁶⁷ Although there are only two mechanisms in the HER, it shows pH dependence due to changes in the properties of aqueous solutions.¹⁶⁸ Normally, acidic aqueous solutions facilitate the Volmer reaction due to the presence of extra protons, resulting in higher HER activity. In neutral and alkaline solutions, the lack of free protons, which must be generated through additional water dissociation, inhibits the HER process. In aqueous energy storage devices using protons as charge carriers, the HER on MXene electrodes cannot be ignored due to their experimentally proven excellent electrochemical activity.^169–171

Fig. 11 (a) Schematic pathways for the hydrogen evolution reaction under acidic and alkaline conditions.¹⁶⁷ Reproduced with permission, ref. 167. Copyright 2018, Springer Nature. (b) Volcano curve of the exchange current density i₀ of Ti₄N₃O₂ as a function of ΔG. The value of Pt is inserted by a red star for comparison.¹⁷² Reproduced with permission, ref. 172. Copyright 2020, Elsevier. (c) Volcano plot of -η vs. ΔG_H on the different terminated Ti₃C₂ surface models, including fully O- and OH-terminated cases, as well as binary situations represented by the O_1/3OH_2/3, O_1/2OH_1/2, and O_2/3OH_1/3 models, and ternary ones as in the F_1/3O_1/3OH_1/3 and F_3/9O_4/9OH_2/9 models. In addition, reference values for Pt, MoS₂, WS₂, C₃N₄@NG, and C₃N are included for comparison.¹⁷³ Reproduced with permission, ref. 173. Copyright 2023, Royal Society of Chemistry. (d) Volcano curve of the exchange current (i₀) as a function of the average Gibbs free energy of hydrogen adsorption (ΔG_H*).¹⁷⁴ Reproduced with permission ref. 174. Copyright 2017, American Chemical Society.

Generally, researchers evaluate the HER performance by calculating the Gibbs free energy (ΔG) of MXene hydrogen adsorption intermediates, as it is considered the rate-controlling step of the reaction based on the Sabatier principle and Brønsted–Evans–Polanyi relationship.^175–177 The closer ΔG is to 0, the higher the HER catalytic activity.¹⁷² Some research showed that O-terminated MXene tends to exhibit higher HER performance. In Fig. 11(b), Yang et al. found that O-functionalized Ti₄N₃O₂ MXene showed higher HER activity than Pt catalysts at low H coverage.¹⁷² Besides, Abraham et al. compared the HER activity of F, Cl, O, S functionalized MXene and found that the ΔG value of MXene with an O functional group was mainly distributed around 0.¹⁷⁸ Moreover, the surface compositions of MXene under real conditions are often a mixture of multiple elements, such as O, F, and OH, which play an important role in the HER process. Meng et al. used DFT calculations to investigate the surface composition of MXene at specific pH and U. In Fig. 11(c), they found that the surface functional groups are usually mixed, and the higher the oxygen concentration in the mixed functional groups, the better the HER activity.¹⁷³

Adjusting the M site, X site, and layer thickness of MXene will also significantly affect HER activity. In Fig. 11(d), Gao et al. found that when the proton coverage was 1, the HER activity of Nb₂CO₂, Nb₄C₃O₂, and V₂CO₂ was lower than that of Ti₃C₂O₂ and Ti₂CO₂.¹⁷⁴ Bai et al. calculated the HER performance of a series of O-functionalized carbides and nitrides by changing the metal elements. The results indicated that Nb₂NO₂ and Ti₂NO₂ are promising HER electrocatalysts.¹⁷⁹

5.1.2. The OER. The oxygen evolution reaction (OER) is the other half-reaction of the water-splitting process. Electrochemical OER is considered to be a four-electron transfer process involving a variety of adsorption-activated intermediates, such as *O, *OH, and *OOH, making it more complex than the HER process.⁵² So far, neither bare nor functionalized MXene has shown effective OER electrocatalytic activity. Anand et al. explored the different OER mechanisms of M₃X₂O₂-type MXene. The calculation results showed that the original M₃X₂O₂-type MXenes have poor OER activity.¹⁸⁰ Kan et al. also revealed that bare and terminated MXene are not suitable for the OER based on calculation results.¹⁸¹ Although the OER catalytic process can be accelerated by doping or supporting single atoms or diatoms, this is beyond the scope of this review.¹⁸² Here, we focus more on how to screen MXene electrodes that are far away from water-splitting.

5.1.3. Discovery of non-HER-active MXene by HTC and ML. As mentioned above, the chemical space of MXene has expanded due to numerous adjustable components. Screening MXene electrode materials far from HER activity, particularly highly active O-terminal MXene, has become challenging. The diversity of MXene has increased experimental costs. In this case, high-throughput theoretical calculation (HTC) screening and ML methods are crucial as they accelerate the development of MXene electrode materials.^178,183,184 Pandey et al. screened 72 different MXene and found that controlling the thickness of MXene can adjust their catalytic activity.¹⁸⁵ Zeng et al. and Jin et al. searched for materials with the best HER performance by screening oxygen-functionalized double TM MXene, respectively.^184,186 Wang et al. used HTC to screen out 188 catalysts with good mechanical stability and thermal stability from 2520 candidate catalysts, as shown in Fig. 12(a).¹⁸⁷ The predicted 110 experimentally unexplored MXenes surpass the precious metal platinum in both thermal stability and HER activity.

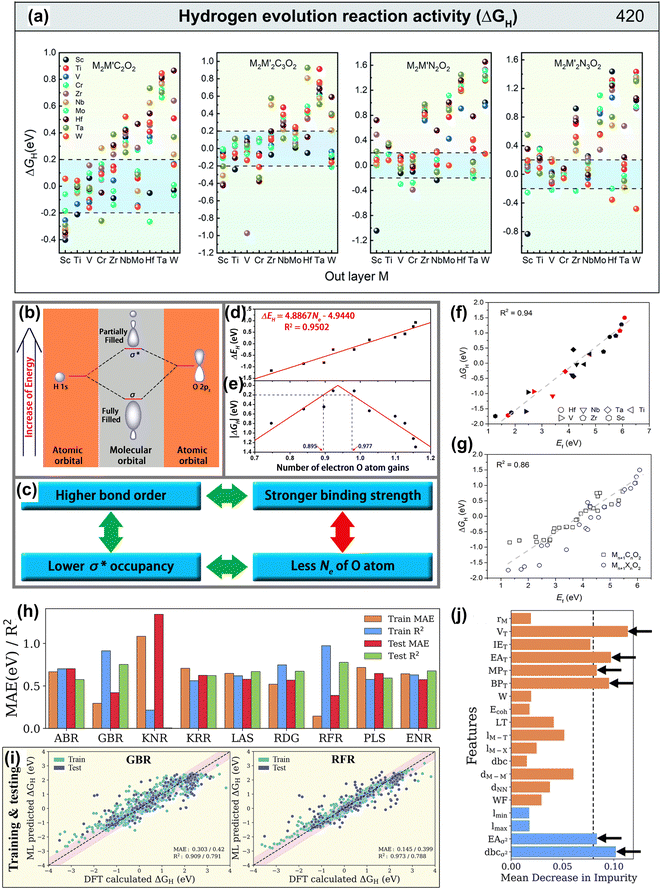Fig. 12 (a) ΔG_H distribution of hydrogen adsorbed by M₂M′X₂ and M₂M′₂X₃O₂, and the black dotted line range represents |ΔG_H| < 0.2 eV of MXene on equilibrium H coverage.¹⁸⁷ Reproduced with permission, ref. 187. Copyright 2020, Royal Society of Chemistry. (b) Schematic of the formation of the H–O bond on the surface of O-terminated MXene, where the linear combination of a H 1s orbital and an O 2p_z orbital forms a fully filled, low-energy bonding orbital (σ) and a partially filled, high-energy antibonding orbital (σ*). (c) The derivation of the correlation between the N_e of the O atom and the H-O binding strength. The calculated (d) ΔE_H and (e) |ΔG_H| as a function of the number of electron O atom gains (N_e), where the R² is 0.95, indicating the high linear correlation between the N_e and ΔE_H.¹⁸⁸ Reproduced with permission, ref. 188. Copyright 2016, American Chemical Society. (f) Linear relationship between the oxygen vacancy formation energy (E_f) and free energy of hydrogen adsorption (ΔG_H) of M_n+1N_nO₂. The black, red, and blue symbols represent M₂XO₂, M₃X₂O₂ and M₄X₃O₂, respectively. (g) The linear relationship between E_f and ΔG_H of both M_n+1C_nO₂ and M_n+1N_nO₂. The gray dashed line represents linear fitting of the data.¹⁸⁹ Reproduced with permission, ref. 189. Copyright 2018, American Chemical Society. (h) Mean absolute error (MAE) and coefficient of determination (R² score) of the ABR, ENR, GBR, KNR, KRR, LAS, PLS, RFR and RDG algorithms using primary (atomistic, structural and electronic indicators) and statistical function-processed features. (i) Parity plots of the best-performing RFR and GBR models using the DFT dataset of hydrogen adsorption Gibbs free energies (ΔG_H). The pink-shaded regions indicate a deviation of up to 0.5 eV. (j) Feature importance from the mean decrease in impurity for the GBR model with RFE-HO-LOO, evaluated via 20-fold cross-validation.¹⁷⁸ Reproduced with permission, ref. 178. Copyright 2023, Royal Society of Chemistry.

In the design of MXene materials, descriptors help understand the relationship between material properties and structure.^190,191 This strategy accelerates materials discovery and provides a deep understanding of the intrinsic properties, guiding optimization and application. For example, Ling et al. screened highly active HER materials based on O-functionalized MXene by establishing a simple descriptor.¹⁸⁸ They found a linear relationship in Fig. 12(b–e) between the number of electrons acquired by surface oxygen atoms (N_e) and the free energy of hydrogen adsorption (ΔG_H). Moreover, in Fig. 12(f), Jiang et al. found a linear relationship between the oxygen vacancy ΔE_f and ΔG_H.¹⁸⁹ Moreover, ΔE_f is also linearly related to the binding strength of Li atoms on MXene, offering a new perspective in the MXene battery materials search.

Furthermore, new materials meeting design requirements can be quickly discovered through ML algorithms and new descriptors. Wang et al. combined five feature descriptors and the Adaboost algorithm to identify the HER activity trend of 2D ordered binary alloy MXene materials.¹⁸⁷ The AdaBoost algorithm is a powerful ensemble learning technique that combines multiple weak classifiers to form a strong classifier, enhancing the model's performance.¹⁹² Zheng et al. used the random forest algorithm by constructing multiple decision trees to efficiently predict the ΔG_H of MXene materials through simple element characteristics and screened out active catalysts with a ΔG_H of close to 0.¹⁹³ Besides, as shown in Fig. 12(g–j), Abraham established a HER performance data set of 4500 MXenes.¹⁷⁸ The gradient boosting regressor algorithm with specific parameters showed the best predictive performance for ΔG_H. This algorithm combines the predictions of multiple weak learners (usually decision trees) to improve prediction accuracy by minimizing the loss function via gradient descent.¹⁹⁴ Among descriptors, the number of valence electrons of terminal atoms is the most important feature descriptor. In short, HTC and ML methods play an indispensable role in the screening and design of MXene electrode materials.

5.2. Stability of MXene in aqueous solution

The stability of MXene in aqueous solutions is crucial as it directly affects performance and lifespan in energy storage devices. However, some studies found MXene has poor stability in aqueous solutions, being corroded by water molecules and oxidatively degraded into TM oxides.^31,195 This structural degradation leads to a loss of electrochemical performance, reducing device lifespan. To overcome this problem, understanding the atomic-level mechanisms of the oxidation process is necessary. In recent years, researchers have used theoretical calculations to reveal atomic details of MXene degradation. These insights help design MXene electrodes with enhanced stability in aqueous solutions.

Early experimental studies found that MXene is easily oxidized and degraded in humid air or aqueous solution environments, hindering its application.¹⁹⁵ Huang et al. found through spectroscopic characterization that water is the key to MXene oxidation.¹⁹⁶ Water “attacks” the metal in MXene, forming oxidized Ti species and leading to degradation. Inspired by this, Wu et al. used first-principles MD to explore how MXene degrades in water.¹⁹⁷ The results in Fig. 13(a) show that water molecules attack MXene through adsorption and pull out Ti atoms. The water molecules are then deprotonated to form Ti–OH, reconstructing the surface. At the same time, the formed Ti–OH substances continue to react with water molecules, causing irreversible degradation.

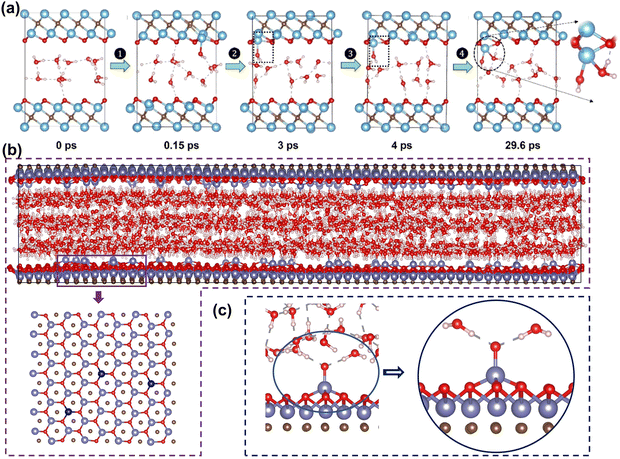Fig. 13 (a) AIMD simulations of two layers of water confined in Ti₃C₂O₂ at 300 K: the figures here are the representative snapshots.¹⁹⁷ Reproduced with permission ref. 197. Copyright 2022, American Chemical Society. (b) The positions of V atoms in vanadium oxides (dark blue atoms). (c) The vanadium oxide with two water molecules.¹⁹⁸ Reproduced with permission, ref. 198. Copyright 2023, John Wiley and Sons.

Hou et al. further studied the oxidation process of MXene in large aqueous solutions on the nanosecond time scale using a neural network potential.¹⁹⁸ Deep neural network potentials provide accurate potential energy surfaces by learning high-fidelity quantum mechanical calculations and capturing complex atomic interactions. These models can achieve quantum mechanics and MD scale accuracy, observing molecular behavior over long time-scales and large atomic scales.¹⁹⁹ As shown in Fig. 13(b and c), the V–O species formed by MXene and water are evenly distributed. The outermost O atom of the V–O species can form hydrogen bonds with two water molecules, preventing the nearby vanadium atoms from being attacked by water molecules. Besides, H generated by water decomposition also prevents MXene oxidation. These protection mechanisms cause the degree of MXene oxidation to decay exponentially over time, consistent with experimental observations. In another study, Song et al. studied the effects of vacancies and F functional groups on the stability of Ti₃C₂O₂ MXene.²⁰⁰ They found that F functional groups can slow down water erosion. In addition, Nesterova et al. used enhanced sampling MD to discover that water attacks on metals in MXene depend on the coordination environment of the metal site and the chemical composition of the MXene surface. Edge and defect sites are believed to enhance water adsorption and subsequent MXene degradation. Zhao et al. calculated that the oxidation process preferentially starts from the edge of the nanosheet.²⁰¹ Marquize et al. found that MXene with vacancies and edge sites exhibits strong water chemical adsorption.²⁰²

The atomic-level mechanism of MXene degradation in aqueous solutions was revealed through theoretical calculations. Improving the stability of MXene has become increasingly important. Researchers have proposed promising strategies from a computational perspective to alleviate MXene degradation. Some reports suggest that MXene hydrolysis products such as protons and oxides can prevent water from continuing to attack the MXene surface and thus slow down the degradation rate.^197,198 Zhao et al. confirmed that the acidic system is more beneficial to the stability of MXene.²⁰¹ Surface modification of MXene has proven to be another effective method. Nesterova et al. proposed that MXene stability can be improved by reducing the MXene work function and avoiding loosely anchored oxygen-coordinated Ti sites.²⁰³ Song et al. found that increasing the coverage of F functional groups on the MXene surface can prevent water oxidation.²⁰⁰

5.3. Electrochemical stability of MXene

In aqueous batteries and supercapacitors, the electrochemical stability of MXene electrode materials is significantly affected by performance at different pH values and potential U.⁸⁹ The distribution and composition of MXene surface functional groups, and the overall structure, change with potential and pH conditions, directly affecting the electrochemical performance of the electrode. However, it is very difficult to experimentally obtain the surface composition under real conditions. Therefore, quickly exploring MXene stability under different conditions through theoretical calculations is crucial for the design and optimization of aqueous batteries and supercapacitors.

Ibragimova et al. studied the distribution and composition of surface functional groups of Ti₂C and Ti₃C₂ MXene, finding that a mixture of O, OH, and F will be formed on the surface.²⁰⁴ The composition of MXene depends on pH, temperature, and work function. Lopez et al. and Meng et al. also concluded that mixed surface functional groups are beneficial.^173,205 Ibragimova further studied other MXene and found that the distribution of mixed functional groups has little to do with the type of metal, carbon, or nitrogen species, and the number of atomic layers of MXene (Fig. 14(a)).²⁰⁶ Wei et al. suggested that the stability of double-TM ordered MXenes is closely related to the type of TM atoms in the outermost layer.²⁰⁷ Gao et al. demonstrated that the surfaces of Ti₂C, V₂C, and Ti₃C₂ are composed of O and OH in the standard state, while Nb₂C is completely functionalized by O atoms.¹⁷⁴ In another study, Fredrickson examined the effects of water intercalation, various functional groups, and applied potential on the stability of Ti₂C and Mo₂C MXenes.²⁰⁸ They found that MXenes are always functionalized with a layer of O functional groups when the external potential is zero, while bare MXenes are unstable at any external potential (Fig. 14(b and c)). Bo et al. found that pH controls surface termination.¹⁵⁹ Acidic pH produces an initial MXene surface with a specific functional group distribution beneficial to capacitive performance.

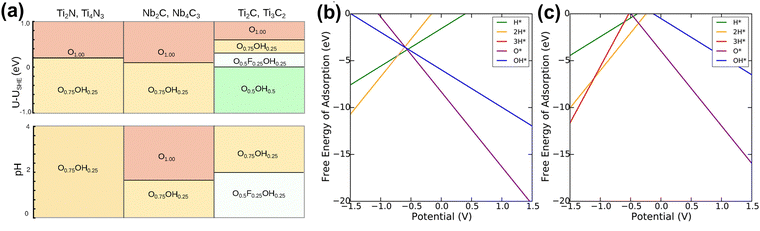Fig. 14 (a) Summary of stable compositions for all systems as a function of the open-circuit potential (at pH 0; top panel) and pH (at U–U_SHE = 0 V; bottom panel).²⁰⁶ Reproduced with permission, ref. 206. Copyright 2021, American Chemical Society. Calculated Pourbaix diagrams for (b) Ti₂C and (c) Mo₂C MXene. Only the lowest free energies at a given potential are labeled by the functionalization.²⁰⁸ Reproduced with permission, ref. 208. Copyright 2016, American Chemical Society.

6. Conclusion and perspectives

With the development of high-performance computing and ML, computational simulations have become crucial for designing and discovering new materials. This is exemplified by the computational insights into MXene materials used in aqueous batteries and supercapacitors. First, theoretical calculations and high-throughput screening of thermodynamically stable MAX precursors guided the experimental synthesis of new MXene phases. Second, multi-scale theoretical simulations elucidated MXene's working mechanisms in aqueous energy storage systems, including Zn deposition inhibition, activation of electrochemical reaction sites, and pseudocapacitive mechanisms. Finally, new MXene materials can be rationally designed to address issues in aqueous energy storage systems, such as the HER. Although computational simulations have achieved significant success in these fields, a substantial gap remains between simulations and actual reactions, necessitating more advanced and comprehensive calculations and modeling. To address this challenge, we propose focusing on the following aspects.

(1) Enhance the complexity of the simulation system. As computing power increases, the dimensional explosion issue caused by system complexity will be mitigated, allowing researchers to consider more realistic systems. For MXene synthesis, current computational systems overly simplify reaction conditions, making it challenging to extend to complex experimental processes. Therefore, additional factors such as etchant type, solution pH, reaction temperature, and kinetics must be considered to establish a comprehensive synthesis theory. For energy storage, simulations must also account for the complexity of MXene surface chemistry and aqueous solutions, including functional group mixing, electrolyte pH, and intercalation thickness.

(2) Employ advanced computational methods. For electrochemical energy storage and catalysis processes, reactions occur under bias conditions, yet most DFT calculations are constant electron simulations. Constant potential simulations, which better mimic electrochemical reactions, allow for clearer insights into the double-layer effect at interfaces, charge transfer processes, and solvent structures.

(3) ML deep potential. ML deep potential provides an accurate and efficient potential energy surface by learning particle motion behavior in AIMD, promising to accelerate MXene research in aqueous energy storage systems. ML potential achieves quantum mechanics and MD scale accuracy, observing molecular behavior over long time-scales and large atomic scales. This understanding aids in comprehending the long-term evolution of MXene electrodes in aqueous devices. Thus, developing robust ML potentials to predict MXene behavior under various electrochemical conditions is crucial. Combining AIMD with advanced sampling methods like metadynamics enhances the exploration of unknown potential energy surfaces, achieving precise descriptions.

(4) Selecting the best descriptors and ML models. Choosing the best descriptors and ML models is vital for accurately predicting MXene's electrochemical properties. Essential descriptors include surface composition, electronic structure, and chemical composition. Dimensional reduction techniques, such as recursive feature elimination and principal component analysis, identify the most relevant descriptors, enhancing model accuracy. Incorporating domain knowledge into descriptors ensures physical relevance to MXene's properties. For ML models, complexity and interpretability must be considered; ensemble methods like random forests or gradient boosting offer strong performance and insights. Future research should develop unique descriptors and interpretable ML models, optimizing hyperparameters to achieve the best prediction performance and promote rational MXene design in aqueous energy storage systems.

(5) High-throughput computational screening and database establishment. High-throughput computational screening systematically explores numerous candidate materials, making it a powerful strategy for discovering and optimizing materials. For MXene, this method can identify compositions, surface terminations, and structural modifications with optimal electrochemical performance. Building high-throughput computational data into accessible MXene databases will significantly advance application research. To enhance usability, researchers should establish standardized data formats and incorporate real-time updates of ongoing research. Integrating these databases with ML tools can predict new MXene compositions for aqueous batteries and supercapacitors.

(6) Multiscale simulation. Multiscale simulation methods are crucial for bridging the gap between atomic-scale phenomena and macroscopic device performance. This review examines how MXene materials impact the electrochemical behavior of aqueous energy storage systems using DFT calculations, classical MD simulations, and COMSOL simulations. Future research should develop integrated multiscale models that combine quantum mechanical calculations with continuum-scale simulations. This integration can provide a comprehensive understanding of performance-limiting factors and degradation mechanisms in MXene-based devices, ultimately leading to the design of MXene materials with enhanced performance and durability.

List of abbreviations

2D	Two-dimensional
3D-RISM	Three-dimensional reference interaction site model
AIMD	Ab initio molecular dynamics
AZIB	Aqueous Zn-ion batteries
DFT	Density functional theory
DOS	Density of state
EDLCs	Electrical double-layer capacitors
EDL	Electrical double-layer
EESS	Electrical energy storage systems
ΔEf	Formation energy
ΔG	Gibbs free energy
ΔGH	Free energy of hydrogen adsorption
HER	Hydrogen evolution reaction
HTC	High-throughput calculation
ΔHcp	Formation enthalpy
i-MXene	In-plane ordered MXene
MOF	Metal–organic frameworks
PEDOT	Poly(3,4-Ethylenedioxythipohene)
PPy	Polypyrrole

Data availability

No primary research results, software or code have been included and no new data were generated or analyzed as part of this review.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the Research Grants Council of Hong Kong (CityU 11305919 and 11308620), CityU project (7005635), and NSFC/RGC Joint Research Scheme N_CityU104/19. Hong Kong Research Grant Council Collaborative Research Fund: C1002-21G and C1017-22G. This research made use of the computing resources of the X-GPU cluster supported by the Hong Kong Research Grant Council Collaborative Research Fund: C6021-19 EF.

References

1. A. M. Omer, Renewable Sustainable Energy Rev., 2008, 12, 2265–2300.
2. N. Armaroli and V. Balzani, Angew. Chem., Int. Ed., 2007, 46, 52–66.
3. J. Mitali, S. Dhinakaran and A. Mohamad, Energy Storage Sav., 2022, 1, 166–216.
4. C. Liu, F. Li, L. P. Ma and H. M. Cheng, Adv. Mater., 2010, 22, E28–E62.
5. M. M. Rana, M. Uddin, M. R. Sarkar, S. T. Meraj, G. Shafiullah, S. Muyeen, M. A. Islam and T. Jamal, J. Energy Storage, 2023, 68, 107811.
6. Y. Liang, C. Z. Zhao, H. Yuan, Y. Chen, W. Zhang, J. Q. Huang, D. Yu, Y. Liu, M. M. Titirici and Y. L. Chueh, InfoMat, 2019, 1, 6–32.
7. G. Liang, F. Mo, X. Ji and C. Zhi, Nat. Rev. Mater., 2021, 6, 109–123.
8. Z. Pan, X. Liu, J. Yang, X. Li, Z. Liu, X. J. Loh and J. Wang, Adv. Energy Mater., 2021, 11, 2100608.
9. Z. Yin, J. Zhao, D. Luo, Y. Y. Chin, C. T. Chen, H. Chen, W. Yin, Y. Tang, T. Yang and J. Ren, Adv. Sci., 2024, 2307397.
10. M. Okubo, A. Sugahara, S. Kajiyama and A. Yamada, Acc. Chem. Res., 2018, 51, 591–599.
11. J. Xu, J. You, L. Wang, Z. Wang and H. Zhang, Sustainable Mater. Technol., 2022, 33, e00490.
12. N. Zhang, X. Chen, M. Yu, Z. Niu, F. Cheng and J. Chen, Chem. Soc. Rev., 2020, 49, 4203–4219.
13. Y. Tian, Y. An, J. Feng and Y. Qian, Mater. Today, 2022, 52, 225–249.
14. F. Wan, X. Zhou, Y. Lu, Z. Niu and J. Chen, ACS Energy Lett., 2020, 5, 3569–3590.
15. M. Li, Z. Li, X. Wang, J. Meng, X. Liu, B. Wu, C. Han and L. Mai, Energy Environ. Sci., 2021, 14, 3796–3839.
16. H. Zhang, X. Liu, H. Li, I. Hasa and S. Passerini, Angew. Chem., Int. Ed., 2021, 60, 598–616.
17. J. Huang, Z. Guo, Y. Ma, D. Bin, Y. Wang and Y. Xia, Small Methods, 2019, 3, 1800272.
18. X. Li, Z. Huang, C. E. Shuck, G. Liang, Y. Gogotsi and C. Zhi, Nat. Rev. Chem., 2022, 6, 389–404.
19. B. Lu, Z. Zhu, B. Ma, W. Wang, R. Zhu and J. Zhang, Small, 2021, 17, 2100946.
20. Y. Pei, X. Zhang, Z. Hui, J. Zhou, X. Huang, G. Sun and W. Huang, ACS Nano, 2021, 15, 3996–4017.
21. A. Morales-Garcia, F. Calle-Vallejo and F. Illas, ACS Catal., 2020, 10, 13487–13503.
22. B. Fu, J. Sun, C. Wang, C. Shang, L. Xu, J. Li and H. Zhang, Small, 2021, 17, 2006054.
23. A. Iqbal, P. Sambyal and C. M. Koo, Adv. Funct. Mater., 2020, 30, 2000883.
24. A. VahidMohammadi, J. Rosen and Y. Gogotsi, Science, 2021, 372, eabf1581.
25. Y. Sun, C. Zhan, P. R. Kent, M. Naguib, Y. Gogotsi and D.-E. Jiang, ACS Appl. Mater. Interfaces, 2019, 12, 763–770.
26. X. Li, M. Li, K. Luo, Y. Hou, P. Li, Q. Yang, Z. Huang, G. Liang, Z. Chen and S. Du, ACS Nano, 2021, 16, 813–822.
27. Y. Li, Q. Zhu, M. Xu, B. Zang, Y. Wang and B. Xu, Adv. Funct. Mater., 2023, 33, 2213416.
28. H. Luo, J. Jiang, M. Li, K. Sun and Y. Zheng, J. Colloid Interface Sci., 2024, 654, 289–299.
29. D. Zhao, Z. Li, D. Xu and Z. Yang, Adv. Funct. Mater., 2024, 2316182.
30. J. Zhou, M. Dahlqvist, J. Björk and J. Rosen, Chem. Rev., 2023, 123, 13291–13322.
31. T. Wu and D.-E. Jiang, MRS Bull., 2023, 48, 253–260.
32. M. Dahlqvist and J. Rosen, Nanoscale, 2020, 12, 785–794.
33. S. Luo, N. Ma, J. Zhao, Y. Wang, Y. Zhang, Y. Xiong and J. Fan, J. Mater. Sci. Technol., 2024, 199, 145–155.
34. C. Zhan, M. Naguib, M. Lukatskaya, P. R. Kent, Y. Gogotsi and D.-E. Jiang, J. Phys. Chem. Lett., 2018, 9, 1223–1228.
35. J. Yu, C. Chen, F. Shi, R. Li, F. Chen, J. Tang, K. C. Chan and Z.-L. Xu, Energy Storage Mater., 2023, 63, 102966.
36. F. Shahzad, M. Alhabeb, C. B. Hatter, B. Anasori, S. Man Hong, C. M. Koo and Y. Gogotsi, Science, 2016, 353, 1137–1140.
37. V. Kamysbayev, A. S. Filatov, H. Hu, X. Rui, F. Lagunas, D. Wang, R. F. Klie and D. V. Talapin, Science, 2020, 369, 979–983.
38. K. R. G. Lim, M. Shekhirev, B. C. Wyatt, B. Anasori, Y. Gogotsi and Z. W. Seh, Nat. Synth., 2022, 1, 601–614.
39. Y. Gogotsi and Q. Huang, ACS Nano, 2021, 15, 5775–5780.
40. M. Ghidiu, M. R. Lukatskaya, M.-Q. Zhao, Y. Gogotsi and M. W. Barsoum, Nature, 2014, 516, 78–81.
41. X. Zhan, C. Si, J. Zhou and Z. Sun, Nanoscale Horiz., 2020, 5, 235–258.
42. D. Gandla, Z. Zhuang, V. V. Jadhav and D. Q. Tan, Energy Storage Mater., 2023, 102977.
43. I. Hussain, M. Ahmad, O. J. Kewate, A. Hanan, F. Bibi, M. S. Javed, I. Shaheen and K. Zhang, ChemSusChem, 2024, e202400283.
44. Z. Du, C. Wu, Y. Chen, Z. Cao, R. Hu, Y. Zhang, J. Gu, Y. Cui, H. Chen and Y. Shi, Adv. Mater., 2021, 33, 2101473.
45. R. Meshkian, Q. Tao, M. Dahlqvist, J. Lu, L. Hultman and J. Rosen, Acta Mater., 2017, 125, 476–480.
46. M. Dahlqvist, J. Lu, R. Meshkian, Q. Tao, L. Hultman and J. Rosen, Sci. Adv., 2017, 3, e1700642.
47. M. Sokol, V. Natu, S. Kota and M. W. Barsoum, Trends Chem., 2019, 1, 210–223.
48. H. W. Seong, M. S. Lee and H. J. Ryu, J. Mater. Chem. A, 2023, 11, 5681–5695.
49. M. Naguib, V. N. Mochalin, M. W. Barsoum and Y. Gogotsi, Adv. Mater., 2014, 26, 992–1005.
50. S.-H. Seok, Y. Sim, J.-H. Han, Y. H. Jin, Y. Chae, J. Park and S.-Y. Kwon, Cell Rep. Phys. Sci., 2023, 4, 101582.
51. C. Fan, P. Zhang, R. Wang, Y. Xu, X. Sun, J. Zhang, J. Cheng and C. Xu, Curr. Nanosci., 2021, 17, 2–13.
52. M. Zubair, M. M. U. Hassan, M. T. Mehran, M. M. Baig, S. Hussain and F. Shahzad, Int. J. Hydrogen Energy, 2022, 47, 2794–2818.
53. P. Bhojane, J. Energy Storage, 2022, 45, 103654.
54. E. M. D. Siriwardane and J. Hu, J. Phys. Chem. C, 2021, 125, 12469–12477.
55. M. Naguib, M. Kurtoglu, V. Presser, J. Lu, J. Niu, M. Heon, L. Hultman, Y. Gogotsi and M. W. Barsoum, MXenes, Jenny Stanford Publishing, 2011, pp. 15–29.
56. T. Li, L. Yao, Q. Liu, J. Gu, R. Luo, J. Li, X. Yan, W. Wang, P. Liu and B. Chen, Angew. Chem., Int. Ed., 2018, 57, 6115–6119.
57. A. Feng, Y. Yu, F. Jiang, Y. Wang, L. Mi, Y. Yu and L. Song, Ceram. Int., 2017, 43, 6322–6328.
58. W. Sun, S. Shah, Y. Chen, Z. Tan, H. Gao, T. Habib, M. Radovic and M. Green, J. Mater. Chem. A, 2017, 5, 21663–21668.
59. X. Xie, Y. Xue, L. Li, S. Chen, Y. Nie, W. Ding and Z. Wei, Nanoscale, 2014, 6, 11035–11040.
60. M. W. Barsoum and T. El-Raghy, J. Am. Ceram. Soc., 1996, 79, 1953–1956.
61. W. Wang, I. Ruiz, S. Guo, Z. Favors, H. H. Bay, M. Ozkan and C. S. Ozkan, Nano Energy, 2014, 3, 113–118.
62. M. Naguib, M. W. Barsoum and Y. Gogotsi, Adv. Mater., 2021, 33, 2103393.
63. O. Salim, K. Mahmoud, K. Pant and R. Joshi, Mater. Today Chem., 2019, 14, 100191.
64. Y. Wei, P. Zhang, R. A. Soomro, Q. Zhu and B. Xu, Adv. Mater., 2021, 33, 2103148.
65. P. P. Michałowski, M. Anayee, T. S. Mathis, S. Kozdra, A. Wójcik, K. Hantanasirisakul, I. Jóźwik, A. Piątkowska, M. Możdżonek and A. Malinowska, Nat. Nanotechnol., 2022, 17, 1192–1197.
66. M. Han, K. Maleski, C. E. Shuck, Y. Yang, J. T. Glazar, A. C. Foucher, K. Hantanasirisakul, A. Sarycheva, N. C. Frey and S. J. May, J. Am. Chem. Soc., 2020, 142, 19110–19118.
67. Z. Liu, E. Wu, J. Wang, Y. Qian, H. Xiang, X. Li, Q. Jin, G. Sun, X. Chen and J. Wang, Acta Mater., 2014, 73, 186–193.
68. N. Kubitza, A. Reitz, A.-M. Zieschang, H. Pazniak, B. Albert, C. Kalha, C. Schlueter, A. Regoutz, U. Wiedwald and C. S. Birkel, Inorg. Chem., 2022, 61, 10634–10641.
69. E. Wu, Y. Zhang, M. Li, Y. Li, K. Liang, S. Du and Q. Huang, Materialia, 2023, 27, 101676.
70. G. Deysher, C. E. Shuck, K. Hantanasirisakul, N. C. Frey, A. C. Foucher, K. Maleski, A. Sarycheva, V. B. Shenoy, E. A. Stach and B. Anasori, ACS Nano, 2019, 14, 204–217.
71. M. Dahlqvist, M. W. Barsoum and J. Rosen, Mater. Today, 2024, 72, 1–24.
72. N. C. Frey, J. Wang, G. I. N. Vega Bellido, B. Anasori, Y. Gogotsi and V. B. Shenoy, ACS Nano, 2019, 13, 3031–3041.
73. M. Dahlqvist, B. Alling, I. A. Abrikosov and J. Rosén, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 024111.
74. M. Dahlqvist, B. Alling and J. Rosén, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 220102.
75. B. Anasori, Y. Xie, M. Beidaghi, J. Lu, B. C. Hosler, L. Hultman, P. R. Kent, Y. Gogotsi and M. W. Barsoum, ACS Nano, 2015, 9, 9507–9516.
76. M. Rougab and A. Gueddouh, J. Phys. Chem. Solids, 2023, 176, 111251.
77. S. Aryal, R. Sakidja, M. W. Barsoum and W. Y. Ching, Phys. Status Solidi B, 2014, 251, 1480–1497.
78. P. Eklund, M. Dahlqvist, O. Tengstrand, L. Hultman, J. Lu, N. Nedfors, U. Jansson and J. Rosén, Phys. Rev. Lett., 2012, 109, 035502.
79. R. Syamsai, J. R. Rodriguez, V. G. Pol, Q. Van Le, K. M. Batoo, S. F. Adil, S. Pandiaraj, M. Muthumareeswaran, E. H. Raslan and A. N. Grace, Sci. Rep., 2021, 11, 688.
80. A. Mockuté, M. Dahlqvist, J. Emmerlich, L. Hultman, J. M. Schneider, P. O. Persson and J. Rosén, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 094113.
81. G. Niu, M. C. Du Plessis, T. Sakai, Y. Ma and M. Sugiyama, Advances in neural information processing systems, 2016, 29, 1–9.
82. Q. Hu, H. Wang, Q. Wu, X. Ye, A. Zhou, D. Sun, L. Wang, B. Liu and J. He, Int. J. Hydrogen Energy, 2014, 39, 10606–10612.
83. B. C. Wyatt, A. Thakur, K. Nykiel, Z. D. Hood, S. P. Adhikari, K. K. Pulley, W. J. Highland, A. Strachan and B. Anasori, Nano Lett., 2023, 23, 931–938.
84. M. Ashton, K. Mathew, R. G. Hennig and S. B. Sinnott, J. Phys. Chem. C, 2016, 120, 3550–3556.
85. J. Björk, J. Halim, J. Zhou and J. Rosen, npj 2D Mater. Appl., 2023, 7, 5.
86. N. M. Caffrey, J. Phys. Chem. C, 2020, 124, 18797–18804.
87. M. Ashton, N. Trometer, K. Mathew, J. Suntivich, C. Freysoldt, S. B. Sinnott and R. G. Hennig, J. Phys. Chem. C, 2019, 123, 3180–3187.
88. M. Khazaei, A. Ranjbar, K. Esfarjani, D. Bogdanovski, R. Dronskowski and S. Yunoki, Phys. Chem. Chem. Phys., 2018, 20, 8579–8592.
89. C. Tsounis, P. V. Kumar, H. Masood, R. P. Kulkarni, G. S. Gautam, C. R. Müller, R. Amal and D. A. Kuznetsov, Angew. Chem., Int. Ed., 2023, 62, e202210828.
90. H. Zhu, Z. Liang, S. Xue, X. Ren, X. Liang, W. Xiong, L. Gao and A. Liu, Ceram. Int., 2022, 48, 27217–27239.
91. Q. Zhu, J. Li, P. Simon and B. Xu, Energy Storage Mater., 2021, 35, 630–660.
92. K. S. Novoselov, A. Mishchenko, A. Carvalho and A. Castro Neto, Science, 2016, 353, aac9439.
93. X. Wang, Y. Liu, Z. Wei, J. Hong, H. Liang, M. Song, Y. Zhou and X. Huang, Adv. Mater., 2022, 34, 2206812.
94. Y. Ando, M. Okubo, A. Yamada and M. Otani, Adv. Funct. Mater., 2020, 30, 2000820.
95. Z. Ling, C. E. Ren, M.-Q. Zhao, J. Yang, J. M. Giammarco, J. Qiu, M. W. Barsoum and Y. Gogotsi, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 16676–16681.
96. M. R. Lukatskaya, O. Mashtalir, C. E. Ren, Y. Dall’Agnese, P. Rozier, P. L. Taberna, M. Naguib, P. Simon, M. W. Barsoum and Y. Gogotsi, Science, 2013, 341, 1502–1505.
97. J. Zhao, N. Ma, T. Wang, N. Li, Y. Wang and J. Fan, J. Mater. Chem. A, 2022, 10, 21611–21621.
98. N. Ma, N. Li, Y. Zhang, T. Wang, J. Zhao and J. Fan, Appl. Surf. Sci., 2022, 590, 153149.
99. J. Zhang, N. Kong, S. Uzun, A. Levitt, S. Seyedin, P. A. Lynch, S. Qin, M. Han, W. Yang and J. Liu, Adv. Mater., 2020, 32, 2001093.
100. Y. T. Liu, P. Zhang, N. Sun, B. Anasori, Q. Z. Zhu, H. Liu, Y. Gogotsi and B. Xu, Adv. Mater., 2018, 30, 1707334.
101. J. Muldoon, C. B. Bucur and T. Gregory, Chem. Rev., 2014, 114, 11683–11720.
102. M. Song, H. Tan, D. Chao and H. J. Fan, Adv. Funct. Mater., 2018, 28, 1802564.
103. Q. Zhang, J. Luan, Y. Tang, X. Ji and H. Wang, Angew. Chem., Int. Ed., 2020, 59, 13180–13191.
104. J. Hao, B. Li, X. Li, X. Zeng, S. Zhang, F. Yang, S. Liu, D. Li, C. Wu and Z. Guo, Adv. Mater., 2020, 32, 2003021.
105. J. Chen, W. Zhao, J. Jiang, X. Zhao, S. Zheng, Z. Pan and X. Yang, Energy Storage Mater., 2023, 59, 102767.
106. K. Guan, L. Tao, R. Yang, H. Zhang, N. Wang, H. Wan, J. Cui, J. Zhang, H. Wang and H. Wang, Adv. Energy Mater., 2022, 12, 2103557.
107. Y. Li, C. B. Musgrave III, M. Y. Yang, M. M. Kim, K. Zhang, M. Tamtaji, Y. Cai, T. W. Tang, J. Wang and B. Yuan, Adv. Energy Mater., 2024, 14, 2303047.
108. X. Li, M. Li, Q. Yang, G. Liang, Z. Huang, L. Ma, D. Wang, F. Mo, B. Dong and Q. Huang, Adv. Energy Mater., 2020, 10, 2001791.
109. N. Zhang, S. Huang, Z. Yuan, J. Zhu, Z. Zhao and Z. Niu, Angew. Chem., Int. Ed., 2021, 60, 2861–2865.
110. X. Li, Q. Li, Y. Hou, Q. Yang, Z. Chen, Z. Huang, G. Liang, Y. Zhao, L. Ma and M. Li, ACS Nano, 2021, 15, 14631–14642.
111. Y. Liu, Y. Jiang, Z. Hu, J. Peng, W. Lai, D. Wu, S. Zuo, J. Zhang, B. Chen and Z. Dai, Adv. Funct. Mater., 2021, 31, 2008033.
112. Y. Wang, L. Liu, Y. Wang, J. Qu, Y. Chen and J. Song, ACS Nano, 2023, 17, 21761–21770.
113. B. Tang, L. Shan, S. Liang and J. Zhou, Energy Environ. Sci., 2019, 12, 3288–3304.
114. H. Zhang, J. Wang, Q. Liu, W. He, Z. Lai, X. Zhang, M. Yu, Y. Tong and X. Lu, Energy Storage Mater., 2019, 21, 154–161.
115. H. Zhang, Y. Fang, F. Yang, X. Liu and X. Lu, Energy Environ. Sci., 2020, 13, 2515–2523.
116. Y. Wang, J. Song and W. Y. Wong, Angew. Chem., Int. Ed., 2023, 135, e202218343.
117. C. Chen, T. Wang, X. Zhao, A. Wu, S. Li, N. Zhang, X. Qu, L. Jiao and Y. Liu, Adv. Funct. Mater., 2024, 34, 2308508.
118. X. Li, X. Ma, Y. Hou, Z. Zhang, Y. Lu, Z. Huang, G. Liang, M. Li, Q. Yang and J. Ma, Joule, 2021, 5, 2993–3005.
119. M. Li, X. Li, G. Qin, K. Luo, J. Lu, Y. Li, G. Liang, Z. Huang, J. Zhou and L. Hultman, ACS Nano, 2021, 15, 1077–1085.
120. X. Li, N. Li, Z. Huang, Z. Chen, G. Liang, Q. Yang, M. Li, Y. Zhao, L. Ma and B. Dong, Adv. Mater., 2021, 33, 2006897.
121. H. Tian, T. Gao, X. Li, X. Wang, C. Luo, X. Fan, C. Yang, L. Suo, Z. Ma and W. Han, Nat. Commun., 2017, 8, 14083.
122. X. Li, N. Li, Z. Huang, Z. Chen, Y. Zhao, G. Liang, Q. Yang, M. Li, Q. Huang and B. Dong, ACS Nano, 2021, 15, 1718–1726.
123. G. Liang, Z. Tang, B. Han, J. Zhu, A. Chen, Q. Li, Z. Chen, Z. Huang, X. Li and Q. Yang, Adv. Mater., 2023, 35, 2210051.
124. C. Li, X. Xie, S. Liang and J. Zhou, Energy Environ. Sci., 2020, 3, 146–159.
125. Z. Cai, Y. Ou, B. Zhang, J. Wang, L. Fu, M. Wan, G. Li, W. Wang, L. Wang and J. Jiang, J. Am. Chem. Soc., 2021, 143, 3143–3152.
126. Y. Zeng, X. Zhang, R. Qin, X. Liu, P. Fang, D. Zheng, Y. Tong and X. Lu, Adv. Mater., 2019, 31, 1903675.
127. L. Cao, D. Li, T. Pollard, T. Deng, B. Zhang, C. Yang, L. Chen, J. Vatamanu, E. Hu and M. J. Hourwitz, Nat. Nanotechnol., 2021, 16, 902–910.
128. X. Zhu, X. Li, M. L. K. Essandoh, J. Tan, Z. Cao, X. Zhang, P. Dong, P. M. Ajayan, M. Ye and J. Shen, Energy Storage Mater., 2022, 50, 243–251.
129. F. Bu, Z. Sun, W. Zhou, Y. Zhang, Y. Chen, B. Ma, X. Liu, P. Liang, C. Zhong and R. Zhao, J. Am. Chem. Soc., 2023, 145, 24284–24293.
130. C. Sun, C. Wu, X. Gu, C. Wang and Q. Wang, Nano-Micro Lett., 2021, 13, 1–13.
131. W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133.
132. Y. Wang, Y. Song and Y. Xia, Chem. Soc. Rev., 2016, 45, 5925–5950.
133. P. Simon and Y. Gogotsi, Nat. Mater., 2020, 19, 1151–1163.
134. T. Guo, D. Zhou, L. Pang, S. Sun, T. Zhou and J. Su, Small, 2022, 18, 2106360.
135. M. Yu, Y. Lu, H. Zheng and X. Lu, Chem. – Eur. J., 2018, 24, 3639–3649.
136. W. Zheng, L. Yang, P. Zhang, V. Natu, Z. Sun, J. Rosen and M. W. Barsoum, Energy Storage Mater., 2023, 103037.
137. Q. Shan, X. Mu, M. Alhabeb, C. E. Shuck, D. Pang, X. Zhao, X.-F. Chu, Y. Wei, F. Du and G. Chen, Electrochem. Commun., 2018, 96, 103–107.
138. J. Pu, Z. Wang, K. Wu, N. Yu and E. Sheng, Phys. Chem. Chem. Phys., 2014, 16, 785–791.
139. X. Geng, Y. Zhang, Y. Han, J. Li, L. Yang, M. Benamara, L. Chen and H. Zhu, Nano Lett., 2017, 17, 1825–1832.
140. R. Ravit, J. Abdullah, I. Ahmad and Y. Sulaiman, Carbohydr. Polym., 2019, 203, 128–138.
141. M. Hou, M. Xu, Y. Hu and B. Li, Electrochim. Acta, 2019, 313, 245–254.
142. S. R. Gurav, G. R. Chodankar, S. A. Sawant, U. V. Shembade, A. V. Moholkar and R. G. Sonkawade, J. Energy Storage, 2023, 73, 109254.
143. V. S. Kumbhar and D.-H. Kim, Electrochim. Acta, 2018, 271, 284–296.
144. M. R. Lukatskaya, S. Kota, Z. Lin, M.-Q. Zhao, N. Shpigel, M. D. Levi, J. Halim, P.-L. Taberna, M. W. Barsoum and P. Simon, Nat. Energy, 2017, 2, 1–6.
145. Z. Zhang, Z. Yao, X. Zhang and Z. Jiang, Electrochim. Acta, 2020, 359, 136960.
146. G. E. Blomgren, J. Electrochem. Soc., 2016, 164, A5019.
147. D. P. Dubal, O. Ayyad, V. Ruiz and P. Gomez-Romero, Chem. Soc. Rev., 2015, 44, 1777–1790.
148. P. Simon, Y. Gogotsi and B. Dunn, Science, 2014, 343, 1210–1211.
149. C. Choi, D. S. Ashby, D. M. Butts, R. H. DeBlock, Q. Wei, J. Lau and B. Dunn, Nat. Rev. Mater., 2020, 5, 5–19.
150. A. Sugahara, Y. Ando, S. Kajiyama, K. Yazawa, K. Gotoh, M. Otani, M. Okubo and A. Yamada, Nat. Commun., 2019, 10, 850.
151. A. Kovalenko and F. Hirata, Chem. Phys. Lett., 1998, 290, 237–244.
152. X. Ji, K. Xu, C. Chen, B. Zhang, Y. Ruan, J. Liu, L. Miao and J. Jiang, Phys. Chem. Chem. Phys., 2016, 18, 4460–4467.
153. R.-Z. Zhang, X.-H. Cui, S.-S. Li, X.-H. Li and H.-L. Cui, J. Mol. Liq., 2022, 345, 118263.
154. Y. Xin and Y.-X. Yu, Mater. Des., 2017, 130, 512–520.
155. H.-T. Yan, X.-H. Li, M.-Z. Liu, X.-H. Cui, S.-S. Li and H.-L. Cui, Vacuum, 2022, 201, 111094.
156. S.-H. Yin, X.-H. Li, R.-Z. Zhang and H.-L. Cui, FlatChem, 2024, 100632.
157. W. Zhang, C. Cheng, P. Fang, B. Tang, J. Zhang, G. Huang, X. Cong, B. Zhang, X. Ji and L. Miao, Phys. Chem. Chem. Phys., 2016, 18, 4376–4384.
158. T. Shimada, N. Takenaka, Y. Ando, M. Otani, M. Okubo and A. Yamada, Chem. Mater., 2022, 34, 2069–2075.
159. Z. Bo, Y. Chen, Q. Yu, J. Yan, K. Cen and Z. Liu, J. Phys. Chem. C, 2024, 128, 2352–2361.
160. C. Zhan, W. Sun, P. R. Kent, M. Naguib, Y. Gogotsi and D.-E. Jiang, J. Phys. Chem. C, 2018, 123, 315–321.
161. S. Nishihara and M. Otani, Phys. Rev. B, 2017, 96, 115429.
162. L. Wang, J. Wang, Z. Zhang, L. Wang, W. Wang, J. Liu, Z. Hong, K. Cho and W. Wang, J. Mater. Chem. A, 2019, 7, 16231–16238.
163. H. Shao, K. Xu, Y.-C. Wu, A. Iadecola, L. Liu, H. Ma, L. Qu, E. Raymundo-Piñero, J. Zhu and Z. Lin, ACS Energy Lett., 2020, 5, 2873–2880.
164. L. Xu and D.-e Jiang, J. Chem. Phys., 2021, 155, 234707.
165. J. Wen, Q. Fu, W. Wu, H. Gao, X. Zhang and B. Wang, ACS Appl. Mater. Interfaces, 2019, 11, 7087–7095.
166. Y. Sui and X. Ji, Chem. Rev., 2021, 121, 6654–6695.
167. J. Wei, M. Zhou, A. Long, Y. Xue, H. Liao, C. Wei and Z. J. Xu, Nano-Micro Lett., 2018, 10, 1–15.
168. X. Tian, P. Zhao and W. Sheng, Adv. Mater., 2019, 31, 1808066.
169. J. Ran, G. Gao, F.-T. Li, T.-Y. Ma, A. Du and S.-Z. Qiao, Nat. Commun., 2017, 8, 13907.
170. A. D. Handoko, K. D. Fredrickson, B. Anasori, K. W. Convey, L. R. Johnson, Y. Gogotsi, A. Vojvodic and Z. W. Seh, ACS Appl. Energy Mater., 2017, 1, 173–180.
171. Y. Jiang, T. Sun, X. Xie, W. Jiang, J. Li, B. Tian and C. Su, ChemSusChem, 2019, 12, 1368–1373.
172. H. Yang, Y. Ma, X. Lv, B. Huang and Y. Dai, J. Catal., 2020, 387, 12–16.
173. L. Meng, L.-K. Yan, F. Viñes and F. Illas, J. Mater. Chem. A, 2023, 11, 6886–6900.
174. G. Gao, A. P. O’Mullane and A. Du, ACS Catal., 2017, 7, 494–500.
175. A. J. Medford, A. Vojvodic, J. S. Hummelshøj, J. Voss, F. Abild-Pedersen, F. Studt, T. Bligaard, A. Nilsson and J. K. Nørskov, J. Catal., 2015, 328, 36–42.
176. J. K. Nørskov, T. Bligaard, A. Logadottir, S. Bahn, L. B. Hansen, M. Bollinger, H. Bengaard, B. Hammer, Z. Sljivancanin and M. Mavrikakis, J. Catal., 2002, 209, 275–278.
177. H. Ooka, J. Huang and K. S. Exner, Front. Energy Res., 2021, 9, 654460.
178. B. M. Abraham, P. Sinha, P. Halder and J. K. Singh, J. Mater. Chem. A, 2023, 11, 8091–8100.
179. X. Bai, C. Ling, L. Shi, Y. Ouyang, Q. Li and J. Wang, Sci. Bull., 2018, 63, 1397–1403.
180. R. Anand, A. S. Nissimagoudar, M. Umer, M. Ha, M. Zafari, S. Umer, G. Lee and K. S. Kim, Adv. Energy Mater., 2021, 11, 2102388.
181. D. Kan, D. Wang, X. Zhang, R. Lian, J. Xu, G. Chen and Y. Wei, J. Mater. Chem. A, 2020, 8, 3097–3108.
182. B. Wei, Z. Fu, D. Legut, T. C. Germann, S. Du, H. Zhang, J. S. Francisco and R. Zhang, Adv. Mater., 2021, 33, 2102595.
183. J. Zheng, X. Sun, C. Qiu, Y. Yan, Z. Yao, S. Deng, X. Zhong, G. Zhuang, Z. Wei and J. Wang, J. Phys. Chem. C, 2020, 124, 13695–13705.
184. D. Jin, L. R. Johnson, A. S. Raman, X. Ming, Y. Gao, F. Du, Y. Wei, G. Chen, A. Vojvodic and Y. Gogotsi, J. Phys. Chem. C, 2020, 124, 10584–10592.
185. M. Pandey and K. S. Thygesen, J. Phys. Chem. C, 2017, 121, 13593–13598.
186. Z. Zeng, X. Chen, K. Weng, Y. Wu, P. Zhang, J. Jiang and N. Li, npj Comput. Mater., 2021, 7, 80.
187. X. Wang, C. Wang, S. Ci, Y. Ma, T. Liu, L. Gao, P. Qian, C. Ji and Y. Su, J. Mater. Chem. A, 2020, 8, 23488–23497.
188. C. Ling, L. Shi, Y. Ouyang and J. Wang, Chem. Mater., 2016, 28, 9026–9032.
189. W. Jiang, X. Zou, H. Du, L. Gan, C. Xu, F. Kang, W. Duan and J. Li, Chem. Mater., 2018, 30, 2687–2693.
190. B. Wang and F. Zhang, Angew. Chem., Int. Ed., 2022, 61, e202111026.
191. N. Dubouis and A. Grimaud, Chem. Sci., 2019, 10, 9165–9181.
192. Y. Freund and R. E. Schapire, J. Comput. Syst. Sci., 1997, 55, 119–139.
193. L. Breiman, Mach. Learn., 2001, 45, 5–32.
194. J. H. Friedman, Ann. Stat., 2001, 1189–1232.
195. R. A. Soomro, P. Zhang, B. Fan, Y. Wei and B. Xu, Nano-Micro Lett., 2023, 15, 108.
196. S. Huang and V. N. Mochalin, ACS Nano, 2020, 14, 10251–10257.
197. T. Wu, P. R. Kent, Y. Gogotsi and D.-E. Jiang, Chem. Mater., 2022, 34, 4975–4982.
198. P. Hou, Y. Tian, Y. Xie, F. Du, G. Chen, A. Vojvodic, J. Wu and X. Meng, Angew. Chem., Int. Ed., 2023, 135, e202304205.
199. L. Zhang, J. Han, H. Wang, R. Car and W. E, Phys. Rev. Lett., 2018, 120, 143001.
200. H. Song and D.-e Jiang, Nanoscale, 2023, 15, 16010–16015.
201. X. Zhao, A. Vashisth, J. W. Blivin, Z. Tan, D. E. Holta, V. Kotasthane, S. A. Shah, T. Habib, S. Liu and J. L. Lutkenhaus, Adv. Mater. Interfaces, 2020, 7, 2000845.
202. E. Marquis, F. Benini, B. Anasori, A. Rosenkranz and M. C. Righi, Nano Convergence, 2023, 10, 16.
203. V. Nesterova, V. Korostelev and K. Klyukin, J. Phys. Chem. Lett., 2024, 15, 3698–3704.
204. R. Ibragimova, M. J. Puska and H.-P. Komsa, ACS Nano, 2019, 13, 9171–9181.
205. M. López, K. S. Exner, F. Viñes and F. Illas, Adv. Theory Simul., 2023, 6, 2200217.
206. R. Ibragimova, P. Erhart, P. Rinke and H.-P. Komsa, J. Phys. Chem. Lett., 2021, 12, 2377–2384.
207. B. Wei, Z. Fu, D. Legut, T. C. Germann, Q. Zhang, S. Du, H. Zhang, J. S. Francisco and R. Zhang, J. Phys. Chem. C, 2021, 125, 4477–4488.
208. K. D. Fredrickson, B. Anasori, Z. W. Seh, Y. Gogotsi and A. Vojvodic, J. Phys. Chem. C, 2016, 120, 28432–28440.

---