High-specificity molecular sensing on an individual whispering-gallery-mode cavity: coupling-enhanced Raman scattering by photoinduced charge transfer and cavity effects†
Xingce
Fan
 a,
Ru
Wang
b,
Mingze
Li
a,
Ru
Wang
b,
Mingze
Li
 a,
Xiao
Tang
a,
Chunxiang
Xu
a,
Xiao
Tang
a,
Chunxiang
Xu
 *b,
Qi
Hao
a and
Teng
Qiu
*b,
Qi
Hao
a and
Teng
Qiu
 *a
*a
aSchool of Physics, Southeast University, Nanjing 211189, China. E-mail: tqiu@seu.edu.cn
bState Key Laboratory of Bioelectronics, School of Biological Science and Medical Engineering, Southeast University, Nanjing 210096, China. E-mail: xcxseu@seu.edu.cn
First published on 22nd November 2022
Abstract
Optical whispering-gallery-mode (WGM) cavities have gained considerable interest because of their unique properties of enhanced light–matter interactions. Conventional WGM sensing is based on the mechanisms of mode shift, mode broadening, or mode splitting, which requires a small mode volume and an ultrahigh Q-factor. Besides, WGM sensing suffers from a lack of specificity in identifying substances, and additional chemical functionalization or incorporation of plasmonic materials is required for achieving good specificity. Herein, we propose a new sensing method based on an individual WGM cavity to achieve ultrasensitive and high-specificity molecular sensing, which combines the features of enhanced light–matter interactions on the WGM cavity and the “fingerprint spectrum” of surface-enhanced Raman scattering (SERS). This method identifies the substance by monitoring the Raman signal enhanced by the WGM cavity rather than monitoring the variation of the WGM itself. Therefore, ultrasensitive and high-specificity molecular sensing can be accomplished even on a low-Q cavity. The working principles of the proposed sensing method were also systematically investigated in terms of photoinduced charge transfer, Purcell effect, and optical resonance coupling. This work provides a new WGM sensing approach as well as a strategy for the design of a high-performance SERS substrate by creating an optical resonance mode.
New conceptsThe proposed WGM sensing method combines the features of enhanced light–matter interactions on the WGM cavity and the “fingerprint spectrum” of surface-enhanced Raman scattering (SERS) to achieve ultrasensitive and high-specificity optical sensing. This method overcomes the drawback of non-specific detection in the conventional WGM sensing method and does not involve any functionalization or introduction of plasmonic structures to realize specific detection. The vertical WGM cavity enables the far-field excitation and collection of cavity-enhanced Raman signals and does not require additional optical components to couple the light in and out of the cavity via an evanescent field. The distinct SERS signals could be even obtained on a low-Q cavity, which does not require high-precise nanofabrication techniques. |
1. Introduction
Optical whispering-gallery-mode (WGM) cavities, confining resonant photons in a microscale volume for long periods of time, could strongly enhance the light–matter interaction through an evanescent field, making them an ideal platform for photonic sensors.1–4 WGM cavities are extremely sensitive to environmental perturbations, and are usually associated with mode shift, mode broadening, and mode splitting mechanisms.5 In 2002, Vollmer et al. achieved the detection of proteins by using microsphere WGM cavities,6 and theoretically predicted that the detection of a single protein molecule could be accomplished with this approach.7 Later on, they successfully realized the detection of a single polystyrene particle and a single flu virus by using the mode shift mechanism.8 In 2010, Yang's group verified the feasibility of the mode splitting sensing mechanism by detecting polystyrene spherical particles and simultaneously verified that the mode splitting mechanism can provide nanoparticle size information.9 Vahala's group further improved the detection sensitivity of the mode splitting mechanism on a high-Q microtoroid cavity to detect an individual nanobead in solution down to a radius of 12.5 nm.10 In 2013, Xiao's group verified the feasibility of the mode broadening mechanism by detecting polystyrene particles and single virus particles.11Although the ultrasensitive detection of particles or biomolecules can be achieved by the aforementioned WGM sensing mechanisms, there are still several challenging issues. (1) WGM cavities suffer from a lack of specificity in identifying the substance. Specific sensing largely depends on the chemical functionalization of the device12,13 or incorporation of plasmonic structures.14,15 (2) It is challenging to couple the light from free space into a WGM cavity due to momentum mismatch. Near-field coupling approaches are generally required to induce light into the cavity, such as prism coupling,16 tapered fiber coupling,17 and waveguide coupling,18 which are complex for optical circuit manipulations and coupling operations. (3) To improve the sensitivity of WGM cavities, a higher Q-factor or a smaller mode volume must be satisfied, requiring high-precision micro- and nanofabrication techniques.
Herein, we propose a new sensing method based on an individual WGM cavity, which combines the features of enhanced light–matter interactions on the WGM cavity and the “fingerprint spectrum” of surface-enhanced Raman scattering (SERS) to achieve ultrasensitive and high-specificity molecular sensing. A microrod WGM cavity composed of nonstoichiometric zinc oxide (ZnO1−x) was selected as an example to show the proof of concept. The proposed method overcomes the drawback of non-specific detection in the conventional WGM sensing method and identifies the substance by monitoring the Raman signal enhanced by the WGM cavity rather than monitoring the variation of the WGM itself. The working principles of the proposed WGM sensing method were systematically investigated in terms of the photoinduced charge transfer, Purcell effect, and optical resonance coupling.
2. Fabrication and characterization of the ZnO1−x cavities
Nonstoichiometric ZnO1−x cavities were grown by high-temperature vapor-transport and subsequent hydrogen-annealing.19Fig. 1a shows the scanning electron microscopy (SEM) image of a ZnO1−x cavity with a hexagonal prism configuration with a side length of ∼ 8 μm. Natural hexagonal cross-section (the inset of Fig. 1a) and smooth facets enable it to be a perfect WGM cavity. As shown in Fig. 1b and c, the elemental mapping images collected from the corresponding area of the SEM image indicate the uniform distribution of Zn and O elements along the profile of the ZnO1−x cavity. High-resolution transmission electron microscopy (HR-TEM) images and the corresponding selected area electron diffraction (SAED) patterns are shown in Fig. 1d and e, in which ZnO1−x is indexed to a wurtzite structure. Fig. 1f presents the X-ray diffraction (XRD) spectrum of the ZnO1−x cavity, whose diffraction peaks are consistent with the indices of the wurtzite phase ZnO (JCPDS: 36-1451) and narrow full-width at half-maximum of diffraction peaks implies its high crystallinity.For demonstrating the nonstoichiometric feature of ZnO1−x cavity, the X-ray photoelectron spectroscopy (XPS) spectrum was recorded and is shown in Fig. 1g, in which the photoelectron emission spectrum of O 1s can be well fitted by three peaks; the peak Oa located at 530.7 eV can be ascribed to the Zn–O bond, the peak Ob located at 531.9 eV is associated with oxygen ions in oxygen-deficient regions within the ZnO matrix, and the peak Oc located at 532.9 eV is attributed to surface-adsorbed H2O or O2 molecules.20 The XPS results indicate that the ZnO1−x cavity possesses a nonstoichiometric feature. Moreover, the electron paramagnetic resonance (EPR) spectrum of the ZnO1−x cavity (Fig. 1h) provides another fingerprint evidence that a distinct signal at g = 2.003 is identified as unpaired electrons trapped on oxygen vacancies.21
3. Ultrasensitive and high-specificity sensing on the ZnO1−x cavity
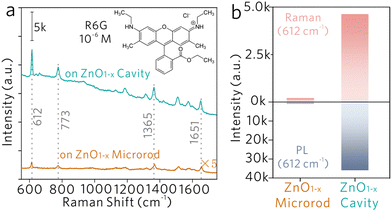
Two samples are selected for comparison, nonstoichiometric ZnO1−x microrods without the WGM (denoted as the ‘ZnO1−x microrod’) and stoichiometric ZnO microrods with WGM (denoted as the ‘ZnO cavity’). The ZnO1−x microrod has the same material compositions as that of the ZnO1−x cavity, but does not support the WGM inside. The ZnO cavity supports the WGM, but without oxygen vacancy defects made by hydrogen annealing. Fig. S1 (ESI†) shows the optical images of the ZnO1−x microrod and the ZnO cavity, in which the former shows dark grey and the latter bright yellow.Rhodamine 6G (R6G) molecules are utilized to demonstrate the proposed WGM sensing mechanisms. As shown in Fig. 2a, four characteristic Raman peaks of R6G molecules are clearly observed on both the ZnO1−x microrod and the ZnO1−x cavity. But on the stoichiometric ZnO cavity, it shows only strong photoluminescence (PL) background, while no Raman peak is observed (Fig. S2, ESI†). The evidence indicates the nonstoichiometric property of ZnO is a prerequisite to producing significant Raman enhancement. By monitoring the Raman peak at 612 cm−1, the SERS intensity on the ZnO1−x cavity shows 22 times stronger than on the ZnO1−x microrod (Fig. 2b). The Raman enhancement factors (EFs) were estimated to be 6.65 × 104 and 1.47 × 106, respectively. The detailed calculations of Raman EFs can be found at the ESI.† The significant Raman enhancement on the nonstoichiometric ZnO1−x cavity is comparable to those on the noble metal substrates (Raman EFs ∼ 104 to 108) and exceeds most of the semiconducting substrates (Raman EFs ∼ 101 to 104).22
The observation of significantly enhanced fingerprint Raman modes on the ZnO1−x cavity verifies the feasibility of ultrasensitive and high-specificity molecular sensing on an individual WGM cavity. The proposed WGM sensing mechanism is totally different from the conventional WGM sensing approaches, which realize sensing by monitoring the mode shift, mode splitting and mode broadening, and severely suffer from the lack of specificity in identifying the substance. While this new WGM sensing method identifies the substance by monitoring the fingerprint Raman mode enhanced by the WGM cavity rather than monitoring the variation of the WGM itself. Besides, the vertical cavity configuration enables the far-field excitation and the collection of enhanced Raman signals and does not require any additional optical components to couple the light in and out of the cavity via an evanescent field. Moreover, further enhanced Raman scattering on the ZnO1−x cavity was observed when compared with the reference sample ZnO1−x microrod (without WGM), suggesting that the SERS activity of semiconducting materials could be further promoted by designing cavity morphologies for better light–matter interactions.
4. WGM cavity sensing mechanisms
Subsequently, the mechanisms of the proposed WGM sensing method on an individual ZnO1−x cavity is systematically investigated through experiments and numerical simulations. As schematically shown in Fig. 3, the charge transfer mechanism and cavity effect both contribute to the overall Raman intensity enhancement.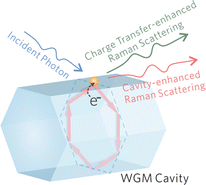 | ||
| Fig. 3 Schematics of the proposed WGM sensing mechanisms. The charge transfer and cavity effect both contribute to the overall Raman intensity enhancement. | ||
4.1 Photoinduced charge transfer
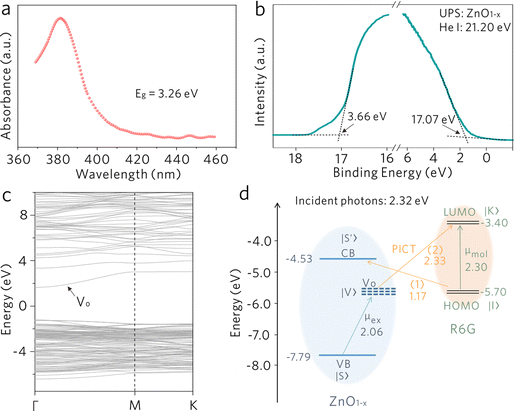
The high-specificity sensing on the WGM cavity is originated from the Raman-enhancing capability of nonstoichiometric ZnO1−x. The oxygen vacancy defect in ZnO1−x is essential to generate significant Raman enhancement. Generally, Raman enhancement on a semiconducting material originates from the vibronic coupling between a semiconducting material and an adsorbate.23–31 As shown in Fig. 4, the electronic band structure of ZnO1−x is investigated by UV-vis and ultraviolet photoelectron spectroscopy (UPS) as well as density functional theory (DFT) calculations. ZnO1−x shows a distinct absorption edge at ∼380 nm (Fig. 4a), which is assigned to the intrinsic bandgap absorption of ZnO.32,33 This evidence confirms the bulk phase of the ZnO1−x cavity and excludes the possible quantum confinement effect induced by the lattice boundaries. Through linear extrapolation of the binding energy axis (Fig. 4b), the values of the work function (ϕ) and the valence band (VB) maximum with respect to the Fermi level are determined to be 4.13 and 3.66 eV, respectively. Hence, the conduction band (CB) minimum and valence band (VB) maximum values are determined as −4.53 and −7.79 eV with respect to the vacuum energy level, respectively. The oxygen vacancy defects in semiconducting metal oxide generally induce defect energy levels within the bandgap.34 DFT calculations were performed to obtain the position of oxygen-vacancy-associated defect energy level (Vo). As shown in Fig. 4c, a distinct defect level appears within the bandgap and is located at approximately 0.30 to 1.60 eV below the CB minimum. Thereby, the electronic band structure of nonstoichiometric ZnO1−x is preliminarily acquired.The energy level diagram of the ZnO1−x/R6G system is shown in Fig. 4d, where the R6G molecule possesses the highest occupied molecule orbital (HOMO) and the lowest unoccupied molecule orbital (LUMO) at −5.70 and −3.40 eV, respectively.35 The molecular energy levels would somehow be modified upon adsorption on the ZnO1−x surface,36,37 but there are no obvious Raman modes shift of R6G in comparison with its bulk phase. We speculate that the molecular energy levels of R6G show a negligible change in the HOMO and the LUMO. Additionally, the modification of organic molecules on the surface of inorganic materials would also create some interfacial states, which may alter the charge transfer process to some extent.38,39 But the molecular concentration is relatively low in this work, we speculate that the induced interfacial states should not be the dominant mechanism to the Raman enhancement. The photoinduced charge transfer (PICT) processes induced by the vibronic coupling between ZnO1−x and R6G molecules are expected to be responsible for the Raman enhancement. The exciton resonance μex induced by the electron transition between the VB state |S〉 and the oxygen-vacancy-associated defect state |V〉 in ZnO1−x, and the molecular resonance μmol induced by electron transition between the HOMO state |I〉 to the LUMO state |K〉 of R6G (2.30 eV) are taken into consideration under 532 nm (2.32 eV) excitation. Generally, in a semiconductor-molecule system, the SERS intensity is proportional to the polarizability tensor of a molecule, which can be expressed as α = A + B + C, where A is relevant to the resonance Raman spectra, B and C originate from molecule-to-substrate and substrate-to-molecule charge transfer transitions, respectively.40 According to the thermodynamically feasible process in this system, the PICT process (1) from the HOMO state |I〉to the CB state |S′〉 (B-term), and the PICT process (2) from the defect state |V〉 to the LUMO state |K〉 (C-term), would be dramatically promoted by borrowing intensity from the nearby exciton resonance μex and molecular resonance μmol. The efficient vibronic coupling between R6G molecules and ZnO1−x modifies both the polarizability tensor and the electron density distribution of the molecules, leading to the observation of significantly enhanced Raman scattering.
4.2 Cavity-enhanced Raman scattering
The Raman signals originating from the vibronic coupling between the molecule and the ZnO1−x cavity will experience additional Raman enhancement due to the optical cavity effects. As pointed out by Purcell, the effectiveness of modification on the spontaneous emission decay rate for a given wavelength depends on the photon density of states at that wavelength.41 As demonstrated in Fig. 2a, b and Fig. S2 (ESI†), the dramatically enhanced PL background is observed on both the ZnO1−x cavity and the ZnO cavity. The PL backgrounds are confirmed from the R6G molecules rather than from the defects in ZnO (as shown in Fig. S3, ESI†). The enhanced PL intensities are attributed to the Purcell effect of the WGM cavity. Notably, this cavity enhancement effect is also applicable in Raman scattering enhancement, which can be understood analogously to PL enhancement in a resonant cavity.42–44 It should be noted that the Raman scattering efficiency would be promoted once a molecule is close to a cavity, regardless of whether there is light propagating along the inner boundaries of the cavity. The spectral density of the Raman scattering light is enhanced by the Purcell factor FP, because of increased vacuum fluctuation and an increased density of states. FP can be expressed by the following formula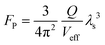 , where Q is the quality factor of the optical cavity and Veff is the effective mode volume. Therefore, a larger Q/Veff can be expected to generate dramatically enhanced Raman signals.
, where Q is the quality factor of the optical cavity and Veff is the effective mode volume. Therefore, a larger Q/Veff can be expected to generate dramatically enhanced Raman signals.
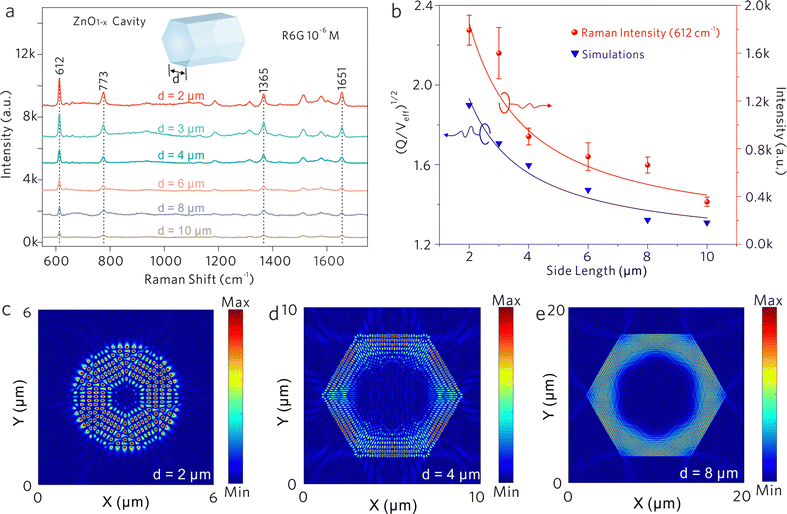
As shown in Fig. 5a, the Raman spectra of the R6G molecule were collected from the ZnO1−x cavities with different side lengths d, in which Raman intensities increase with the decrease of side length. By monitoring the SERS intensities of 612 cm−1, the relationship between the intensity and the side length is shown in Fig. 5b, which is fitted by an inverse proportional function. The variations of Raman intensities are attributed to the difference in WGM cavity parameters. As shown in Fig. 5c–e, the electric fields in ZnO1−x cavities (d = 2, 4, and 8 μm) are simulated by the finite-difference time-domain (FDTD) method. The distinct WGM can be observed, where the ZnO1−x support WGM resonance due to self-interference of light propagating along the hexagonal trajectory defined by the cavity cross section. The Q-factors and effective mode volume Veff were taken into account, which is derived from the measurements and the simulations. The ratios of (Q/Veff)1/2 are calculated as shown in Fig. 5b, which shows an inverse proportional relationship with the side length as well. The Raman intensities of R6G molecules show a positive correlation against the Q/Veff value, suggesting that the SERS signals generated by the vibronic coupling between the R6G molecule and the ZnO1−x cavity undergo another enhancement by the Purcell effect. The largest FP value is estimated to be ∼ 0.29 from the ZnO1−x cavity (d = 2 μm).
Generally, the Raman scattering enhancement on a cavity was always accompanied by the enhanced PL background. In this work, the PL of R6G molecules partially couples into the ZnO1−x cavity via an evanescent field. As shown in Fig. 5c–e, the resonant light is confined by the hexagonal boundaries of the ZnO1−x cavity and the prominent exterior fields (evanescent field) along the cavity boundaries are also observed. As demonstrated in Fig. S4 (ESI†), the portion of the evanescent field increases with the decrease of side length, suggesting that the tunneling effect becomes significant when reducing the dimension of the cavity. Generally, the evanescent field of WGM cavities determines the strength of light–matter interactions.45,46 These distinct evanescent fields outside the cavity walls manifest the feasibility of enhanced light–matter interactions on the ZnO1−x cavities. Therefore, we speculate that the enhanced evanescent field would also strengthen the interactions between the cavity and the adsorbed molecules to some extent.
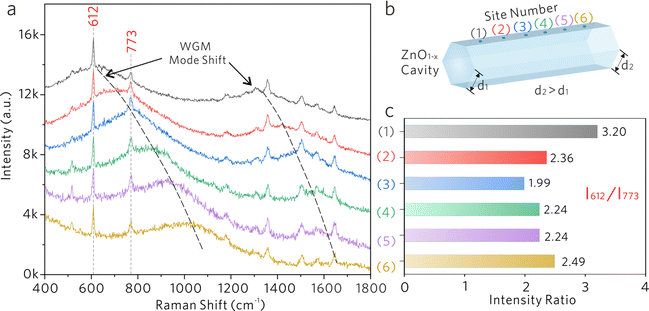
Subsequently, a ZnO1−x cavity with a side length gradient was investigated as depicted in Fig. 6a and b, in which the WGM frequency gradually redshifts with the increase of side length. At different testing sites, the Raman modes at 612 and 773 cm−1 from R6G molecules will experience different spectral overlaps with the WGM. The Raman spectra were normalized by using the Raman peak at 612 cm−1. The intensity ratios of 612 and 773 cm−1 were calculated to depict the selective enhancement of the Raman mode when coupled with the WGM peak. As shown in Fig. 6c sites (1), the Raman signal of 612 cm−1 is selectively enhanced because of the overlap with the WGM peak, demonstrating the largest intensity ratio at this moment. With the redshifts of the WGM, the Raman signal of 773 cm−1 is selectively enhanced at site (3), showing the lowest intensity ratio. The observed selective Raman enhancements suggest that the Raman signal generated on optical cavities will experience further intensity modulation by the optical resonance coupling between the WGM and the Raman mode.
5. Conclusions
In summary, a new WGM sensing method is proposed to achieve ultrasensitive and high-specificity molecular sensing on an individual WGM cavity by taking advantage of WGM cavity effects and the “fingerprint spectrum” of SERS. This method overcomes the drawback of non-specific detection in the conventional WGM sensing method and does not require additional surface functionalization to realize specific detection. The model WGM cavity is composed of nonstoichiometric ZnO1−x and supports WGM simultaneously. The abundant oxygen vacancy defects on the surface of ZnO1−x generate effective vibronic coupling between the cavity and adsorbed molecules, leading to a dramatically enhanced Raman scattering of the latter. Subsequently, the SERS signals will experience additional enhancements induced by the cavity effects. The experiments and simulations evidenced the Purcell effect in promoting the Raman scattering efficiency, and the largest Purcell factor was estimated to be ∼0.29. Moreover, the WGM within the cavity will also alter the Raman intensity via evanescent fields. The results demonstrated that the Raman peak would undergo additional Raman enhancement if coupled with one of the WGMs. The proposed WGM sensing method is promising for both fundamental and application-oriented studies.Author contributions
X. F. and T. Q. conceived and designed experiments. X. F. and R. W. fabricated the samples. R. W. performed the simulations. X. F., M. L., X. T., and Q. H. analyzed the data. The manuscript was written by X. F. and revised by Q. H., C. X., and T. Q. All authors have given approval to the final version of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Natural Science Foundation of China (Grant 11874108). X. F. acknowledges the support funded by the China Postdoctoral Science Foundation funded project (Grant 2021M700773) and Jiangsu Planned Projects for Postdoctoral Research Funds (Grant 2021K509C). We greatly appreciate the fruitful discussion with Prof. John R. Lombardi from The City University of New York, Prof. Gaoshan Huang from Fudan University and Dr Libo Ma from IFW Dresden.References
- M. R. Foreman, J. D. Swaim and F. Vollmer, Adv. Opt. Photon., 2015, 7, 168 CrossRef CAS.
- K. D. Heylman, K. A. Knapper, E. H. Horak, M. T. Rea, S. K. Vanga and R. H. Goldsmith, Adv. Mater., 2017, 29, 1700037 CrossRef.
- E. Kim, M. D. Baaske and F. Vollmer, Lab Chip, 2017, 17, 1190–1205 RSC.
- Y. Chen, Y. Yin, L. Ma and O. G. Schmidt, Adv. Opt. Mater., 2021, 9, 2100143 CrossRef.
- X. Jiang, Abraham J. Qavi, S. H. Huang and L. Yang, Matter, 2020, 3, 371–392 CrossRef PubMed.
- F. Vollmer, D. Braun, A. Libchaber, M. Khoshsima, I. Teraoka and S. Arnold, Appl. Phys. Lett., 2002, 80, 4057–4059 CrossRef.
- S. Arnold, M. Khoshsima, I. Teraoka, S. Holler and F. Vollmer, Opt. Lett., 2003, 28, 272–274 CrossRef CAS.
- F. Vollmer, S. Arnold and D. Keng, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 20701–20704 CrossRef.
- J. Zhu, S. K. Ozdemir, Y. Xiao, L. Li, L. He, D. Chen and L. Yang, Nat. Photonics, 2010, 4, 46–49 CrossRef.
- T. Lu, H. Lee, T. Chen, S. Herchak, J.-H. Kim, S. E. Fraser, R. C. Flagan and K. Vahala, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 5976–5979 CrossRef.
- L. Shao, X. Jiang, X. Yu, B. Li, W. R. Clements, F. Vollmer, W. Wang, Y. Xiao and Q. Gong, Adv. Mater., 2013, 25, 5616–5620 CrossRef.
- U. Bog, F. Brinkmann, H. Kalt, C. Koos, T. Mappes, M. Hirtz, H. Fuchs and S. Köber, Small, 2014, 10, 3863–3868 CrossRef.
- G. C. Righini and S. Soria, Sensors, 2016, 16, 905 CrossRef PubMed.
- J. Lu, C. Xu, H. Nan, Q. Zhu, F. Qin, A. G. Manohari, M. Wei, Z. Zhu, Z. Shi and Z. Ni, Appl. Phys. Lett., 2016, 109, 073701 CrossRef.
- Q. Zhu, C. Xu, D. Wang, B. Liu, F. Qin, Z. Zhu, Y. Liu, X. Zhao and Z. Shi, J. Mater. Chem. C, 2019, 7, 2710–2716 RSC.
- A. Mazzei, S. Götzinger, L. de, S. Menezes, V. Sandoghdar and O. Benson, Opt. Commun., 2005, 250, 428–433 CrossRef.
- S. Böttner, S. Li, M. R. Jorgensen and O. G. Schmidt, Appl. Phys. Lett., 2013, 102, 251119 CrossRef.
- S. Valligatla, J. Wang, A. Madani, E. S. G. Naz, Q. Hao, C. N. Saggau, Y. Yin, L. Ma and O. G. Schmidt, Adv. Opt. Mater., 2020, 8, 2000782 CrossRef.
- J. Lu, C. Xu, F. Li, Z. Yang, Y. Peng, X. Li, M. Que, C. Pan and Z. L. Wang, ACS Nano, 2018, 12, 11899–11906 CrossRef CAS.
- C. Huang, J. Huang, S. Lin, W. Chang, J. He and Y. Chueh, ACS Nano, 2012, 6, 8407–8414 CrossRef CAS PubMed.
- Y. Lv, W. Yao, X. Ma, C. Pan, R. Zong and Y. Zhu, Catal. Sci. Technol., 2013, 3, 3136–3146 RSC.
- S. Cong, X. Liu, Y. Jiang, W. Zhang and Z. Zhao, The Innovation, 2020, 1, 100051 CrossRef PubMed.
- I. Alessandri and J. R. Lombardi, Chem. Rev., 2016, 116, 14921–14981 CrossRef CAS.
- S. Cong, Y. Yuan, Z. Chen, J. Hou, M. Yang, Y. Su, Y. Zhang, L. Li, Q. Li, F. Geng and Z. Zhao, Nat. Commun., 2015, 6, 7800 CrossRef CAS PubMed.
- J. Lin, Y. Shang, X. Li, J. Yu, X. Wang and L. Guo, Adv. Mater., 2017, 29, 1604797 CrossRef PubMed.
- X. X. Han, W. Ji, B. Zhao and Y. Ozaki, Nanoscale, 2017, 9, 4847–4861 RSC.
- X. Fan, P. Wei, G. Li, M. Li, L. Lan, Q. Hao and T. Qiu, ACS Appl. Mater. Interfaces, 2021, 13, 51618–51627 CrossRef CAS.
- X. Hou, X. Fan, P. Wei and T. Qiu, J. Mater. Chem. C, 2019, 7, 11134–11141 RSC.
- L. Lan, Y. Gao, X. Fan, M. Li, Q. Hao and T. Qiu, Front. Phys., 2021, 16, 43300 CrossRef.
- L. Lan, X. Hou, Y. Gao, X. Fan and T. Qiu, Nanotechnology, 2020, 31, 055502 CrossRef PubMed.
- M. Li, X. Fan, Y. Gao and T. Qiu, J. Phys. Chem. Lett., 2019, 10, 4038–4044 CrossRef.
- J. Lu, C. Xu, J. Dai, J. Li, Y. Wang, Y. Lin and P. Li, ACS Photonics, 2015, 2, 73–77 CrossRef.
- W. Ji, L. Li, W. Song, X. Wang, B. Zhao and Y. Ozaki, Angew. Chem., Int. Ed., 2019, 58, 14452–14456 CrossRef PubMed.
- A. Janotti and C. G. Van de Walle, Appl. Phys. Lett., 2005, 87, 122102 CrossRef.
- X. Fan, M. Li, Q. Hao, M. Zhu, X. Hou, H. Huang, L. Ma, O. G. Schmidt and T. Qiu, Adv. Mater. Interfaces, 2019, 6, 1901133 CrossRef.
- J. B. Neaton, M. S. Hybertsen and S. G. Louie1, Phys. Rev. Lett., 2006, 97, 216405 CrossRef.
- C. Lohaus, A. Klein and W. Jaegermann, Nat. Commun., 2018, 9, 4309 CrossRef.
- S. Park, N. Cho and H. J. Yoon, Chem. Mater., 2019, 31, 5973–5980 CrossRef.
- S. Park, S. Kang and H. J. Yoon, ACS Cent. Sci., 2019, 5, 1975–1982 CrossRef.
- J. R. Lombardi and R. L. Birke, J. Phys. Chem. C, 2014, 118, 11120–11130 CrossRef.
- X. Fan, Q. Hao, T. Qiu and P. K. Chu, J. Appl. Phys., 2020, 127, 040901 CrossRef.
- M. Agio and D. M. Cano, Nat. Photonics, 2013, 7, 674–675 CrossRef.
- T. J. Kippenberg, A. L. Tchebotareva, J. Kalkman, A. Polman and K. J. Vahala, Phys. Rev. Lett., 2009, 103, 027406 CrossRef PubMed.
- T. Hümmer, J. Noe, M. S. Hofmann, T. W. Hänsch, A. Högele and D. Hunger, Nat. Commun., 2016, 7, 12155 CrossRef.
- Y. Yin, S. Li, V. Engemaier, S. Giudicatti, E. Saei Ghareh Naz, L. Ma and O. G. Schmidt, Phys. Rev. A, 2016, 94, 013832 CrossRef.
- Y. Yin, S. Li, S. Böttner, F. Yuan, S. Giudicatti, E. Saei Ghareh Naz, L. Ma and O. G. Schmidt, Phys. Rev. Lett., 2016, 116, 253904 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Preparation method and characterization of ZnO1−x cavities; DTF calculations of electronic band structures of ZnO1−x; FDTD simulations of WGM in ZnO1−x cavities; optical images of ZnO1−x microrods and ZnO cavities; Raman spectrum of R6G acquired on ZnO cavities; PL spectra collected from the bare Si substrate, ZnO1−x cavities, the Si substrate with R6G adsorption, and ZnO1−x cavities with R6G adsorption; evanescent fields at the outside of ZnO1−x cavity walls; calculations of Raman EFs. See DOI: https://doi.org/10.1039/d2nh00450j |
| This journal is © The Royal Society of Chemistry 2023 |