Direct thermodynamic characterization of solid-state reactions by isothermal calorimetry†
Marija
Cvetnić‡
 ,
Robert
Šplajt‡
,
Edi
Topić
,
Robert
Šplajt‡
,
Edi
Topić
 ,
Mirta
Rubčić
,
Mirta
Rubčić
 and
Nikola
Bregović
and
Nikola
Bregović
 *
*
University of Zagreb, Faculty of Science, Department of Chemistry, Horvatovac, 102/A, Zagreb 10 000, Croatia. E-mail: nbregovic@chem.pmf.hr; Tel: +385 1 4606 147
First published on 27th October 2023
Abstract
Despite the growing importance of solid-state reactions, their thermodynamic characterization has largely remained unexplored. This is in part due to the lack of methodology for measuring the heat effects related to reactions between solid reactants. We address here this gap and report on the first direct thermodynamic study of chemical reactions between solid reactants by isothermal calorimetry. Three reaction classes, cationic host–guest complex formation, molecular co-crystallization, and Baeyer–Villiger oxidation were investigated, showcasing the versatility of the devised methodology to provide detailed insight into the enthalpy changes related to various reactions. The reliability of the method was confirmed by correlation with the values obtained via solution calorimetry using Hess's law. The thermodynamic characterization of solid-state reactions described here will enable a deeper understanding of the factors governing solid-state processes.
Introduction
During the last few decades research on chemical transformations in the solid state has received tremendous attention.1–13 The related studies have opened up simple synthetic routes to otherwise inaccessible materials or provided greener production processes for numerous valuable chemicals.3,14–21 However, there are still unexplored aspects within this field,22 and we are still far from a complete understanding of the kinetics and thermodynamics governing the outcomes of solid-state reactions. Most recently, advances have been made in elucidating the mechanisms of reactions in the solid state.23,24 This was achieved through in situ monitoring of reaction mixtures using spectroscopic techniques (Raman, NMR and IR spectroscopies) and diffraction methods.23–29On the other hand, thermodynamic studies within the field of mechanochemistry have not yet received appropriate attention. Several reports focusing on solid-state thermodynamics clearly demonstrated that such an approach is fundamental for the systematic advancement of the field. Beleguer et al. reported on the thermodynamic control of the reaction outcome for disulfate exchange reactions relevant for covalent dynamic synthesis.30,31 Monteiro et al. performed measurements of chemical potentials of various solid phases and identified the driving force for the mechanochemical synthesis of strontium titanate.32 Extensive thermodynamic investigations of various metal–organic frameworks have been performed, providing a detailed understanding of the stability and reactivity of these systems.33–36 It should be noted that computational methods have also allowed reasonable assessment of thermodynamic parameters for solid-phase reactions.37,38
Typically, dissolution calorimetry supported by DSC, isothermal adsorption calorimetry, and low temperature heat capacity determination comprise the experimental toolbox for the study of thermodynamics underlying mechanochemically driven processes.39 Hence, the established route towards related reaction enthalpies is a detour involving construction of thermodynamic cycles (TCs), whereas direct determination of the reaction enthalpies by isothermal calorimetry for processes between solids has not yet been unveiled.
Studies which discuss the heat effects during mechanochemical reactions have focused mainly on the mechanistic aspects of the temperature change, rather than its thermodynamic implications.40–43 Research on the thermal effects of mechanochemical reactions performed in a ball-mill reported by Užarević et al. exposed that the temperature in the reactor during milling depended primarily on the frictional properties of the powder material present in the jar.28 Heat resulting from the reaction itself had negligible impact on the measured temperature, and the reaction enthalpy could not have been even roughly assessed by the applied method. In contrast, Kulla et al. did notice a significant effect of the reaction heat on the temperature inside the mill by performing thermographic measurements.44 However, the collected data could not yield reliable reaction enthalpies.
These studies implicate that in order to monitor the thermodynamic parameters of solid-state reactions directly, the focus should be put on performing the experiments in isothermal mode, detecting the heat as it is exchanged with the surrounding, which is the very concept of isothermal calorimetry.45 Indeed, the demand for calorimeters suitable for investigating the processes occurring in the solid state has been identified in the midst of the 20th century.46 High temperature isothermal calorimetry has since been extensively applied in metallurgy,47–49 ceramics and cement-related studies,50–54 while low temperature experiments have mainly been related to in pharmaceutical studies.45,55–57 The research involved calorimetric studies of various solid-state reactions i.e. sintering,58 oxidation of ascorbic acid,59 polymorphic transitions,60 amorphous-to-crystal relaxations61 and other modifications in crystallinity.62,63 In addition, the value of calorimetric methods has been recognized in the process of determining excipient compatibility64 and desolvation characterization.65 It should be stressed out that all of these investigations were performed by placing the reactant in a calorimetric vessel and monitoring the heat slowly evolving as the reaction advanced spontaneously. Arguably, this provided a valuable insight into the kinetic and thermodynamic parameters of important reactions occurring in the solid phase, illustrating the tremendous sensitivity of modern isothermal calorimeters. However, to the best of our knowledge, isothermal calorimetry has not been applied to study reactions between two or more solid reactants taking place upon their mixing, which is of special interest for the field of mechanochemistry.
Although the well-established approach based on Hess's law does provide a path towards solid-state reaction enthalpies, it requires tedious work and involves several long-lasting experiments. More importantly, experimental difficulties related to the construction of thermodynamic cycles such as solubility issues or slow reaction kinetics sometimes hinder the application of the methodology. Thus, applying and optimizing isothermal calorimetry for direct thermodynamic characterization of reactions between two or more solids is vital for further advancement of mechanochemistry.
Herein, we explored the potential of using a robust Calvet-type calorimeter equipped with a cell originally designed for studies of dissolution processes to directly measure the enthalpy of reactions between solid compounds at room temperature. We demonstrated that the commercially available calorimetric system developed by Setaram is suitable for direct enthalpic characterization of a variety of mechanochemically relevant processes.
Experimental
Materials
In this work, the following reactants were used: 4-tert-butylcyclohexanone (4-tBuCH; Sigma Aldrich, 99%), 3-chloroperbenzoic acid (mCPBA; Sigma Aldrich, <77%), KHSO4 (Kemika, ≥99%), 18-crown-6 ether (18C6E; Sigma Aldrich, 99%), benzophenone (BZP; Sigma Aldrich, 99%), and diphenylamine (DPA; Pliva, purissimum). KHSO4 was ground and dried at 155 °C for 3 h before use (grinding was repeated after drying). 18-Crown-6 ether was quickly ground and then placed into a desiccator filled with P2O5 overnight. All other reactants were also finely ground in a mortar prior to their usage for solid-state reactions in the calorimeter.Solvents used were as follows: deionized (MilliQ) water and acetonitrile (MeCN; J. T. Baker, HPLC Gradient Grade).
Database studies
Literature PXRD patterns [refcode] for all reactants and products of solid-state reactions tested in this work were obtained by performing the relevant Cambridge Structural Database (CSD) searches enabled by the Cambridge Crystallographic Data Centre (CDCC): BZP [BPHENO12], DPA [QQQBVP04], BZP–DPA [BZPPAM01], 18C6E [HOXOCD], (18C6EK)HSO4·2H2O [WIGNAC].Preparation of salts, cocrystals and complexes
(18C6EK)HSO4·2H2O was synthesized mechanochemically from 18C6E (120.0 mg; 0.454 mmol) and KHSO4 (61.8 mg; 0.454 mmol) in a 10 mL stainless-steel jar with two stainless-steel balls 7 mm in diameter (Retsch MM200 Shaker Mill operating at a frequency of 25 Hz for up to 90 min). The direct product of ball-milling in this case was a mixture of (18C6EK)HSO4·2H2O and (18C6EK)HSO4. Therefore, the product mixture was transferred into a mortar where it was thoroughly ground with water (16.4 μL; 0.908 mmol) in order to obtain pure (18C6EK)HSO4·2H2O.Metastable liquid BZP–DPA was obtained by thoroughly mixing BZP (147.0 mg; 0.807 mmol) with DPA (136.5 mg; 0.807 mmol) in a small glass beaker with a spatula. BZP–DPA solid molecular complex was obtained by fast crystallization of metastable liquid BZP–DPA induced by cooling (1 h at 4 °C).
Powder X-ray diffraction experiments
PXRD experiments were performed using a Malvern PANalytical Aeris X-ray diffractometer with Cu Kα (1.54056 Å) radiation at 15 mA and 40 kV. The scattered intensities were measured with a line (1D) detector. The angular range was from 5 to 40° (2θ) with a 1/8° used slit and a time of recording of 2.5 min. Data analysis was performed using the program Data Viewer (Omnic Specta Software 9.9.549, Thermo Fisher Scientific, 2018).Calorimetric method for solid-state reactions
Reaction enthalpies of solid-state reactions and dissolution reaction enthalpies were measured using a Calvet calorimeter (SETARAM BT 2.15) at 25.0(1) °C. The temperature of the calorimeter block was controlled by a thermostat (Huber CC 905). Detector calibration tests were done with naphthalene: ΔfusH° = 143.3 J g−1 (vs. theoretical: 147.6 ± 4.3 J g−1; Installation and Commissioning Checklist of SETARAM BT 2.15.). Identical Hastelloy mixing cells (S60/58285) were used as reference and reaction cells. Each cell comprises two compartments (upper volume = 2.9 cm3, lower volume = 2.6 cm3) separated by a PTFE membrane (0.05 mm). Typically, the lower parts of both cells were filled with the same amount of a reactant and in some cases, a minor amount of liquid facilitating the reaction. The second reactant was placed on the membrane of the reaction cell and both reference and reaction cells were mounted inside the calorimeter. When thermal equilibrium was reached and the baseline established, stirrers were pushed down into the cells piercing the membrane. The stirring rate was then set to 120 rpm. Pushing the second reactant (placed on the PTFE disc) into the cell enabled a controlled start and advancement of the reaction. Identical stirring was performed in both cells thus accounting for the heat effects of the stirring. Data acquisition and processing were performed using CALISTO software (Setaram). Processed data were represented using OriginPro 2021.Solid-state reactions were performed with the following amounts of samples in the lower part of the cell (LP) and on the membrane (MEM):
• 200–231 mg of mCPBA (LP) and 15–41 mg of 4-tBuCH (MEM);
• 146–210 mg of 18C6E with 7–10 μL of H2O (LP) and 23–38 mg of KHSO4 (MEM);
• 28 mg of DPA with 0.5 mg of BZP–DPA(s) (LP) and 30 mg of BZP (MEM);
• 50–90 mg of DPA (LP) and 47–86 mg of BZP (MEM);
• 56–111 mg of BZP–DPA(l) (LP) and 0.5–1 mg of BZP–DPA(s) (MEM).
Dissolution enthalpies
Dissolution enthalpies of reactants and products of solid-state reactions were determined by means of Setaram BT 2.15 Calvet calorimeter (at 25.0(1) °C) and TAM IV (TA Instruments) calorimeter (at 25.0000(3) °C) in chosen solvents. When the Setaram Calvet calorimeter was used, dissolutions were performed with 1.5 mL of solvent with the mass of the sample varying from 11 to 40 mg. The solvent volume used for the dissolution experiments in TAM IV was 17 mL. For the TAM IV calorimeter, samples were directly weighed into the cartridges (V = 40 μL), with their mass varying from 6 to 22 mg. The stirring rate in the TAM IV calorimeter was set to 60 rpm, whereas in the Setaram calorimeter, it was set to 120 rpm. In both calorimeters, the samples were expelled into the solution once the equilibrium has been established. The dissolution heats obtained with the TAM IV calorimeter were corrected for the blank experiment (empty cartridge). The heat flow was recorded every 0.5 s (TAM IV) or every 2.7 s (Setaram). Data acquisition and processing were performed using CALISTO software (Setaram). Processed data were represented using OriginPro 7.0.ITC
Microcalorimetric measurements were performed by an isothermal titration calorimeter Microcal VP-ITC at 25.0(1) °C. The enthalpy changes were recorded upon stepwise, automatic addition of titrant solution (2.9 × 10−2 mol dm−3) to the analyte solution (5.4 × 10−4 mol dm−3). A blank experiment was carried out in order to make corrections for the enthalpy changes corresponding to the dilution of the titrant solution in the pure solvent. The dependence of the successive enthalpy change on the titrant volume was processed using the Microcal OriginPro 7.0 program.NMR
NMR spectra were recorded by means of a Bruker Avance III HD 400 MHz/54 mm Ascend spectrometer equipped with a 5 mm PA BBI 1H/D-BB probe head with z-gradient and automated tuning and matching accessory. All proton spectra were acquired at 25.0 °C by using 64 K data points, a spectral width of 20 ppm, a recycle delay of 1.0 s, and 16 scans. CDCl3 was used as a solvent and TMS as an internal standard for proton chemical shifts.Characterization of reactants used for solid-state reactions
Microscopy and XRD experiments were used for aggregate size analysis and crystal domain size analysis of the reactants (see ESI†, Section 1 for details) confirming that the dimensions of the reactant particles are well beyond the nm-scale. Thus, no influence of their size on ΔrH for a solid-state reaction was expected.Results and discussion
Experimental setup for isothermal solid-state calorimetry (ISSC)
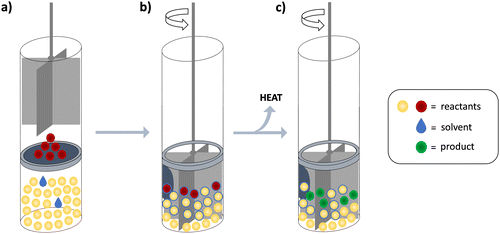
The methodology used in this work was applied in a specific manner, which prompted us to devote this section to the most important aspects of the experimental setup (in addition to the description given in the Experimental section). As already stated, the cell in which we performed the solid–solid reactions has been devised for dissolution experiments (Scheme 1). It is thus equipped with a stirrer that is optimized for mixing liquids. The mechanical force imposed by such a stirrer is mild and introduces rather low and constant heat flow, still ensuring contact between the reactants and thus enabling the reaction progress. Another key advantage of the cell applied in this work was the fact that the two solids could be separated by a membrane, allowing complete thermal equilibration of the cells prior to the mixing of reactants. The reaction is initiated by combining the reactants upon piercing the membrane.The isolated piercing of the membrane and the falling of the solid reactant to the bottom of the cell have negligible heat effects which was demonstrated by numerous experiments (approximately 0.1% of a typical reaction heat signal, Fig. S3, ESI†). The heat introduced by stirring is the same in both cells because the stirrers of the reaction and reference cells are practically identical and are driven by the same motor. Since the generated heat is effectively exchanged with the heat sink, it does not affect the system temperature. However, we did detect a slight shift in the baseline upon turning the mixing on, which could be ascribed to small differences in friction of the two stirring devices (Fig. S4, ESI†). By applying the tangential sigmoidal integration algorithm in the signal processing for solid-state reactions, this effect was almost completely eliminated from the integrated heat. When the analogous integration procedure is performed on blank experiment signals, the resulting heat is <2% from the one obtained for the reactions.
When the reaction does not occur, the signal does not significantly differ from the one obtained by membrane piercing without the reactant present in the cell (Fig. S5, ESI†). Hence, in a case of an unsuccessful experiment (no reaction), a negligible heat signal is expected and such event is easily recognised by the current methodology.
In a typical experiment, the reactant added to the bottom of the cell was in significant excess related to the one placed on the membrane. This ensured that the entire sample of the limiting reactant was in contact with the other reagent and facilitated its complete transformation. Such an experimental design provided a straightforward way to determine the reaction extent as it could be equated to the amount of limiting reagent. Indeed, PXRD analyses of the material produced in the calorimetric experiments confirmed the transformation of the limiting reagents and enabled product identification. Thus, the quantitative characterization of the resulting mixtures was generally not required.
In order to further validate the methodology applied for determination of reaction extent, we determined the limit of detection (LOD) of our experimental setup. Two typical solid-state standards were used and diffractograms of their various mixtures were recorded (ESI†, Section 3). The obtained LOD value was 2–5%, which was within the tolerated experimental error.
The total reaction heat was determined by integrating the measured signal during the experimental procedure, avoiding the requirement for kinetic modelling. A small amount of water was added in the case of potassium complexation by 18-crown[6] ether to aid the grinding process and accelerate the reaction. If possible, the total amount of the material, the molar ratio of the reactants and the volume of the solvent added were varied in repeated experiments to confirm that the measured reaction enthalpy did not depend on these parameters. Typically, the reactions were completed within 0.5–1 hour after combining the reactants and the heat evolved during the experiments could be effectively conducted and measured, providing isothermal conditions (the temperature fluctuation during an experiment was ±0.1 °C or lower). The entire experiment would require from 1.5 to 3 hours (including the pre-reaction thermal equilibration and evolution of the heat signal) depending on the kinetics of the reaction.
The heat generated by mixing was readily accounted for by comparing the heat flow in the reaction cell with that in the reference cell filled with only one of the reactants (the one present in excess) submitted to the same stirring rate as the reaction cell.
The enthalpies for most of the investigated reactions could additionally be elucidated by thermodynamic cycles. The thermodynamic data required for this purpose were determined by measuring dissolution enthalpies of the reactants and products as well as determining the reaction enthalpies in the same solvent. This provided strict cross-evaluation of the methodology by comparing the results measured by the direct solid-state calorimetric procedure with the parameters based on TCs. In all cases, the data obtained by both methods were in satisfactory agreement, demonstrating the applicability of ISSC and the reliability of the corresponding data.
Based on the experience gathered so far using the presented methodology, we can provide a few experimental guidelines in order to obtain the most reliable results:
(1) Using an excess of one reactant is recommended to ensure contact and complete reaction. If stoichiometric amounts of reactants are used, great attention should be put on the quantitative determination of the product mixture. Visual inspection of the calorimetric cell after the experiment is advised to make sure reactants were thoroughly mixed and none of the reactants remained on the cell walls or membranes.
(2) The reactants should be finely ground prior to the experiment to increase the reaction rate. Measurements of the particle size upon sample treatment are recommended.
(3) Addition of a small amount of solvent (LAG conditions) is encouraged to facilitate the reaction. Special care should be taken in such cases to ensure correct identification of the product, considering the possibilities of solvate formation.
(4) The monitored reaction should be relatively fast and heat evolution should be finished within 2 hours after mixing the reactants. This should be taken as a “rule of thumb” and it depends on the total heat exchange during an experiment (with higher enthalpy changes, a longer experiment duration can be used).
Host–guest chemistry – potassium complexation by 18-crown[6] ether
The discovery of crown-ethers has facilitated the development of host–guest chemistry,66 and to date, these macrocycles are the reference point for the supramolecular complexation of various cations.67–69 Numerous hybrid receptors with crown ether functionality as the cation-binding site have been reported and the underlying complexation processes have been investigated in solution by a plethora of methods, including calorimetry.70,71 Most recently, crown-ether derivatives have been exploited in catalysis,72 drug-delivery systems,73 supramolecular polymers,74 ferroelectrics, etc.75 Moreover, these macrocycles have been applied in crystal engineering as modules rendering complex superstructures.76 Braga et al. reported that 15-crown[5] or 18-crown[6] ether (18C6E) form complexes with alkali, transition metal or ammonium cations combined with polyprotic inorganic and organic anions form crystalline molecular salts based on hydrogen bonded anionic networks.76–78 However, to the best of our knowledge, no attempts were made to investigate the heat effects related to the above described reactions.We found that by mixing 18C6E and KHSO4 in the calorimetric cell, the macrocyclic potassium complex (dihydrate) was formed quantitatively (Scheme 2), as confirmed by PXRD of the resulting material (Fig. S7, ESI†). In this experiment, an excess of crown ether relative to KHSO4 was used and a catalytic amount of water was added to 18C6E prior to the measurement. Integration of the exothermic peak which occurred upon mixing of the reactants (Scheme 2b) yielded the reaction enthalpy of the solid-state complexation which amounted to −14.5 kJ mol−1 (Table S3, ESI†).
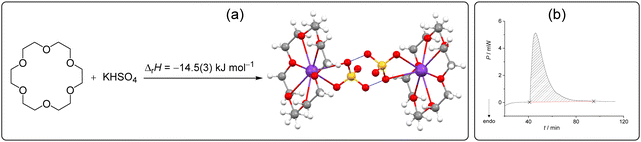 | ||
| Scheme 2 (a) Host–guest complex formation studied in this work and the related reaction enthalpy determined by isothermal solid-state calorimetry at 25 °C. (b) Related thermogram. | ||
The thermodynamic cycle required to calculate the reaction enthalpy in the solid state was constructed by measuring the dissolution enthalpies for 18C6E, KHSO4 and their complex in water (Fig. S8–S10 and Tables S4–S6, Scheme S1, ESI†). In addition, the complexation of potassium ions by 18C6E in water has been investigated earlier, providing the related stability constant and reaction enthalpy (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K = 2.14(2), ΔrH = −23.4(8) kJ mol−1).79 These data were used to account for the complex formation in solution and applied for devising the TC. The enthalpy of the solid-state process calculated from Hess's law (ΔrH = −17.2(7) kJ mol−1) was a bit more negative but still in satisfactory agreement with the value determined directly by ISSC.
K = 2.14(2), ΔrH = −23.4(8) kJ mol−1).79 These data were used to account for the complex formation in solution and applied for devising the TC. The enthalpy of the solid-state process calculated from Hess's law (ΔrH = −17.2(7) kJ mol−1) was a bit more negative but still in satisfactory agreement with the value determined directly by ISSC.
Molecular complexation – reaction between benzophenone and diphenylamine
Co-crystal formation plays a central role in crystal engineering and the benefits of the materials attained by co-crystallization have been utilized in various technologies.21,80–82 The synthesis of co-crystalline materials is strongly dependent on mechanochemical methods, as the reactions performed in the absence of solvent often yield otherwise inaccessible products.83Chadwick et al. found that by placing solid benzophenone and diphenylamine in contact, a molecular complex is formed upon mechanical agitation, accompanied by a yellow coloration of the material at the interphase of the two powders.84,85 The crystal structure of the material revealed that H-bonds between the carbonyl oxygen and the amine NH-group stabilize this co-crystal. It was also found that the binary system containing benzophenone and diphenylamine is characterized by two eutectics.86 The melting points of the mixtures were generally above 30 °C which suggested that melting is not expected at 25 °C. Chadwick et al. thus postulated that the mechanism of co-crystallization involves a metastable liquid state (deep eutectic formed at equimolar ratio) from which the molecular complex is crystallized upon seeding, agitation or cooling. The mechanism of the BZP–DPA complex formation was later studied in detail by Biliškov.87
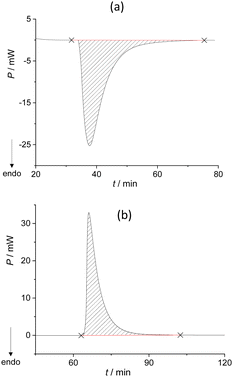
We extended the thermodynamic understanding of the described process by measuring the related enthalpy changes using isothermal calorimetry. When the typical experimental conditions were applied, i.e. when one of the reactants was in excess (n(DPA)/n(BZP) = 4.9), a slurry-like material was obtained, and the expected co-crystal was not detected. In contrast, by mixing the reactants in the equimolar ratio in the calorimetric cell, the metastable liquid was formed, accompanied by an endothermic peak (Fig. 1a).
The system remained in this state for the entire duration of the experiment (>2 h). Although this was not the desired outcome of the experiment, it enabled the calculation of the enthalpy for the formation of the metastable liquid (ΔrH = 30.8 kJ mol−1; Table S7, ESI†). Cooling the metastable liquid containing BZP and DPA yielded yellow crystalline material, i.e. the desired BZP–DPA molecular complex (confirmed by PXRD analysis). This material was subsequently used as a seed in the calorimetric cell. A small amount (0.5 mg) of BZP–DPA was placed with DPA in the calorimetric cell and BZP was set on the PTFE membrane. After thermal equilibration, BZP was combined with DPA containing the seed which resulted in an endothermic signal followed by a prolonged exotherm (Fig. 2 and Table S8, ESI†).
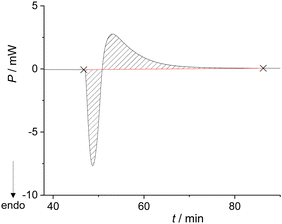 | ||
| Fig. 2 Thermogram for the formation of BZP–DPA cocrystals (n(BZP) = n(DPA) = 0.165 mmol) performed in the Setaram Calvet calorimeter at 25 °C. | ||
The PXRD analysis of the resulting material (Fig. S11, ESI†) suggested that most of the starting material was transformed to the desired BZP–DPA co-crystal with a small amount of the reactants still present in the mixture, probably due to very rapid crystallization. The enthalpy for the reaction (Scheme 3a) was calculated by integration of the entire signal measured during the experiment and assuming complete transformation of the reactants, which provided the value ΔrH = −1.4(3) kJ mol−1.
The reaction enthalpy for the BZP–DPA formation in solid-state was also measured by performing the experiment in a two-step fashion (Scheme 3b). First, a larger amount of metastable liquid BZP–DPA was formed by a thorough mixing of BZP and DPA (n/n = 1) in a beaker. The obtained liquid was weighed into the reaction cell of the calorimeter while the DPA–BZP seed (0.5 mg) was placed on the PTFE membrane. After the equilibration period, the membrane was pierced, allowing contact of the crystal seed with the liquid. This resulted in rapid co-crystal formation accompanied by a significant exothermic signal (Fig. 1b) yielding the reaction enthalpy for crystallization of the molecular complex (Table S9 and Fig. S12, ESI†). As described above, the reaction enthalpy related to the formation of the metastable liquid BZP–DPA has already been determined. The overall enthalpy of the co-crystallization reaction could be calculated as the sum of the two reaction enthalpies providing the value ΔrH = −3.4(7) kJ mol−1. The obtained value was similar to the one determined in the one-step approach, but the two-step method is undoubtedly a more reliable one, as it provides pure product and an unambiguous determination of reaction extent.
It is possible that the discrepancy in the determined values was caused by the fact that a certain amount of reactants remained in the system when the reaction was performed in one step. Both values were more negative but still in acceptable agreement with the one determined by TC (ΔrH = −0.4(7) kJ mol−1; Scheme S2, ESI†). Although the discrepancy in the measured values is somewhat outside the repeatability of the measurements the agreement of data obtained by the two methods is more than acceptable given the complexity of TC construction. It should be noted that in the case of host–guest chemistry, the reaction enthalpy determined by TC was more negative, while the opposite was obtained in the case of the BZP–DPA system. This finding suggests that the two methods applied do not provide systematically different values.
The dissolution experiments were performed in acetonitrile (Fig. S13–S15 and Tables S10–S12, ESI†). Additionally, the dissolution enthalpy of the metastable melt was determined yielding 7.7(8) kJ mol−1 (Fig. S16 and Table S13, ESI†). The complexation between DPA and BZP was not detected in the solution, as shown by ITC (Fig. S17, ESI†). This provided the information required for obtaining the reaction enthalpy related to the formation of the metastable liquid from the TC which was again in good agreement with the value obtained by isothermal calorimetry (Scheme S2, ESI†).
Organic synthesis – Baeyer–Villiger oxidation
The Baeyer–Villiger oxidation is one of the essential transformations in organic synthesis due to its wide applicability and high reaction yields.88 Since it was first reported in 1899,89 this reaction has been applied on an immense number of starting materials.90,91 Most recently, chemists have devoted their attention to performing this reaction with reduced impact on the environment using less harmful oxidants and solvents.92,93 In line with the green approach towards chemical synthesis, it was demonstrated that the Baeyer–Villiger transformation could be readily performed in the absence of solvent.94 It was found that oxidation of 4-tert-butylcyclohexanone (4-tBuCH) by m-chloroperoxybenzoic acid (mCPBA) occurred almost instantly upon grinding the reactants (Scheme 4a), making it an exemplary reaction in organic synthetic mechanochemistry.95 Prompted by its general importance and applicability, we selected this reaction for our solid-state calorimetric investigations based on the available literature data.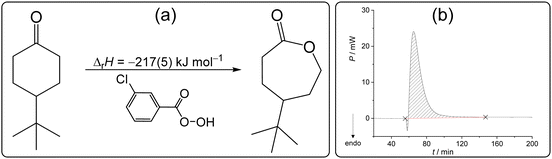 | ||
| Scheme 4 (a) Baeyer–Villiger oxidation studied in this work and the related reaction enthalpy determined by isothermal solid-state calorimetry at 25 °C. (b) Related thermogram. | ||
After mixing the reactants (4-tBuCH placed on the membrane and mCPBA added to the cell in excess), a small endothermic peak was detected in the short initial phase of the reaction, followed by a very pronounced exotherm (Scheme 4b). The minor endothermic process could be ascribed to the formation of eutectic, i.e. melting of the reactants upon mixing, whereas the strong exotherm is the consequence of the oxidation coupled with crystallization of the caprolactone product. The reaction enthalpy could be reliably measured providing the value −217(5) kJ mol−1 (Table S14, ESI†). The mixture obtained after the calorimetric experiment was characterized by 1H NMR and it was evident that the ketone was fully transformed to γ-tert-butyl-ε-caprolactone (Fig. S18, ESI†). On the other hand, in solution (dichloromethane), this reaction took overnight, and the reaction did not proceed quantitatively even with a high excess of the oxidant used. This hindered the determination of the related reaction enthalpy in solution and consequently the construction of the required TC. The fact that the process could not be readily studied by thermodynamic cycle using dissolution calorimetry showcased the advantage of the direct characterization of the reaction by ISSC and emphasized the value of this work.
Conclusion
To the best of our knowledge, this study reports the first isothermal calorimetric investigation of solid-state reactions induced by mechanical agitation and demonstrates a wide applicability of the developed approach to study solid-state reactions of various types featuring reaction enthalpies ranging from only a few kJ mol−1 to more than 200 kJ mol−1. We have directly measured the related reaction enthalpies and cross-evaluated the obtained values with the ones obtained from solution data by Hess's law applying thermodynamic cycles. In all cases, the values obtained by both methodologies were in good agreement. In summary, the described approach may provide the necessary means to fill the gap in the thermodynamic understanding of solid-state and mechanochemical reactions.Author contributions
Conceptualization: N. B.; data curation: M. C., R. Š., E. T., M. R. and N. B.; investigation: M. C., R. Š., E. T., M. R. and N. B.; methodology: M. C., R. Š., E. T. and N. B.; resources: M. R. and N. B.; validation: M. R. and N. B.; visualization: M. C., R. Š. and E. T.; writing – original draft: M. C. and N. B.; writing – review & editing: M. C., E. T., M. R. and N. B.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Croatian Science Foundation, under Project No. IP-2019-04-9560 (MacroSol) and European Regional Development Fund (CIuK, Grant No. KK.01.1.1.02.0016). The authors would like to thank Dr Ivan Halasz for useful discussions.References
- S. L. James and T. Frišcic, Chem. Soc. Rev., 2013, 42, 7494–7496 RSC.
- X. Liu, Y. Li, L. Zeng, X. Li, N. Chen, S. Bai, H. He, Q. Wang and C. Zhang, Adv. Mater., 2022, 2108327, 1–30 Search PubMed.
- T. Friščić, C. Mottillo and H. M. Titi, Angew. Chem., 2020, 132, 1030–1041 CrossRef.
- R. T. O’Neill and R. Boulatov, Nat. Rev. Chem., 2021, 5, 148–167 CrossRef PubMed.
- W. Pickhardt, S. Grätz and L. Borchardt, Chem. – Eur. J., 2020, 26, 12903–12911 CrossRef CAS PubMed.
- E. Boldyreva, Chem. Soc. Rev., 2013, 42, 7719–7738 RSC.
- Y. Chen, G. Mellot, D. Van Luijk, C. Creton and R. P. Sijbesma, Chem. Soc. Rev., 2021, 50, 4100–4140 RSC.
- F. Effaty, X. Ottenwaelder and T. Friščić, Curr. Opin. Green Sustainable Chem., 2021, 32, 100524 CrossRef CAS.
- S. E. Leininger, K. Narayan, C. Deutsch and E. P. O’Brien, Biochemistry, 2019, 58, 4657–4666 CrossRef CAS.
- J. Andersen and J. Mack, Green Chem., 2018, 20, 1435–1443 RSC.
- A. Krusenbaum, S. Grätz, G. T. Tigineh, L. Borchardt and J. G. Kim, Chem. Soc. Rev., 2022, 51, 2873–2905 RSC.
- J. L. Howard, Q. Cao and D. L. Browne, Chem. Sci., 2018, 9, 3080–3094 RSC.
- T. Stolar and K. Užarević, CrystEngComm, 2020, 22, 4511–4525 RSC.
- S. L. James, C. J. Adams, C. Bolm, D. Braga, P. Collier, T. Friščić, F. Grepioni, K. D. M. Harris, G. Hyett, W. Jones, A. Krebs, J. Mack, L. Maini, A. G. Orpen, I. P. Parkin, W. C. Shearouse, J. W. Steed and D. C. Waddell, Chem. Soc. Rev., 2012, 41, 413–447 RSC.
- M. Xuan, C. Schumacher, C. Bolm, R. Göstl and A. Herrmann, Adv. Sci., 2022, 2105497, 1–20 Search PubMed.
- I. N. Egorov, S. Santra, D. S. Kopchuk, I. S. Kovalev, G. V. Zyryanov, A. Majee, B. C. Ranu, V. L. Rusinov and O. N. Chupakhin, Green Chem., 2020, 22, 302–315 RSC.
- Q. Hou, Y. Han, J. Wang, Y. Dong and J. Pan, Sci. Bull., 2017, 62, 965–970 CrossRef CAS PubMed.
- D. Tan and T. Friščić, Eur. J. Org. Chem., 2018, 18–33 CrossRef CAS.
- X. Yang, C. Wu, W. Su and J. Yu, Eur. J. Org. Chem., 2022, 2022(8), e202101440 CrossRef CAS.
- S. Quaresma, V. André, A. Fernandes and M. T. Duarte, Inorg. Chim. Acta, 2017, 455, 309–318 CrossRef CAS.
- V. Nemec, K. Lisac, N. Bedeković, L. Fotović, V. Stilinović and D. Cinčić, CrystEngComm, 2021, 23, 3063–3083 RSC.
- F. Cuccu, L. De Luca, F. Delogu, E. Colacino, N. Solin, R. Mocci and A. Porcheddu, ChemSusChem, 2022, 15(17), e202200362 CrossRef CAS.
- S. Lukin, L. S. Germann, T. Friščić and I. Halasz, Acc. Chem. Res., 2022, 55, 1262–1277 CrossRef CAS.
- A. A. L. Michalchuk and F. Emmerling, Angew. Chem., Int. Ed., 2022, 61, e202117270 CrossRef CAS.
- T. Friščić, I. Halasz, P. J. Beldon, A. M. Belenguer, F. Adams, S. A. J. Kimber, V. Honkimäki and R. E. Dinnebier, Nat. Chem., 2013, 5, 66–73 CrossRef.
- S. Lukin, M. Tireli, T. Stolar, D. Barišić, M. V. Blanco, M. Di Michiel, K. Užarević and I. Halasz, J. Am. Chem. Soc., 2019, 141, 1212–1216 CrossRef CAS.
- H. Kulla, S. Haferkamp, I. Akhmetova, M. Röllig, C. Maierhofer, K. Rademann and F. Emmerling, Angew. Chem., Int. Ed., 2018, 57, 5930–5933 CrossRef CAS.
- K. Užarević, N. Ferdelji, T. Mrla, P. A. Julien, B. Halasz, T. Friščić and I. Halasz, Chem. Sci., 2018, 9, 2525–2532 RSC.
- S. Lukin, T. Stolar, I. Lončarić, I. Milanović, N. Biliškov, M. Di Michiel, T. Friščić and I. Halasz, Inorg. Chem., 2020, 59, 12200–12208 CrossRef PubMed.
- A. M. Belenguer, T. Friščić, G. M. Day and J. K. M. Sanders, Chem. Sci., 2011, 2, 696–700 RSC.
- A. M. Belenguer, G. I. Lampronti and J. K. M. Sanders, Isr. J. Chem., 2021, 61, 764–773 CrossRef CAS.
- J. F. Monteiro, A. A. L. Ferreira, I. Antunes, D. P. Fagg and J. R. Frade, J. Solid State Chem., 2012, 185, 143–149 CrossRef CAS.
- Z. Akimbekov, A. D. Katsenis, G. P. Nagabhushana, G. Ayoub, M. Arhangelskis, A. J. Morris, T. Friščić and A. Navrotsky, J. Am. Chem. Soc., 2017, 139, 7952–7957 CrossRef CAS PubMed.
- D. Wu and A. Navrotsky, J. Solid State Chem., 2015, 223, 53–58 CrossRef CAS.
- H. Sun and D. Wu, Powder Diffr., 2019, 34, 297–301 CrossRef CAS.
- N. Novendra, J. M. Marrett, A. D. Katsenis, H. M. Titi, M. Arhangelskis, T. Friščić and A. Navrotsky, J. Am. Chem. Soc., 2020, 142, 21720–21729 CrossRef CAS PubMed.
- M. Arhangelskis, F. Topić, P. Hindle, R. Tran, A. J. Morris, D. Cinčić and T. Friščić, Chem. Commun., 2020, 56, 8293–8296 RSC.
- L. Kumar, S. G. Dash, K. Leko, D. Trzybiński, N. Bregović, D. Cinčić and M. Arhangelskis, Phys. Chem. Chem. Phys., 2023 10.1039/d3cp04358d.
- V. Stilinović, G. Horvat, T. Hrenar, V. Nemec and D. Cinčić, Chem. – Eur. J., 2017, 23, 5244–5257 CrossRef PubMed.
- L. Takacs and J. S. McHenry, J. Mater. Sci., 2006, 41, 5246–5249 CrossRef CAS.
- K. S. McKissic, J. T. Caruso, R. G. Blair and J. Mack, Green Chem., 2014, 16, 1628–1632 RSC.
- C. Deidda, F. Delogu and G. Cocco, J. Mater. Sci., 2004, 39, 5315–5318 CrossRef CAS.
- G. Manai, F. Delogu, L. Schiffini and G. Cocco, J. Mater. Sci., 2004, 39, 5319–5324 CrossRef CAS.
- H. Kulla, M. Wilke, F. Fischer, M. Röllig, C. Maierhofer and F. Emmerling, Chem. Commun., 2017, 53, 1664–1667 RSC.
- S. Gaisford and G. Buckton, Thermochim. Acta, 2001, 380, 185–198 CrossRef CAS.
- J. D. Boyd, J. Phys. E, 1970, 3, 306 CrossRef.
- B. Predel, I. Arpshofen and M. J. Pool, Thermochim. Acta, 1978, 22, 211–236 CrossRef CAS.
- U. K. Stolz, I. Arpshofen, F. Sommer and B. Predel, J. Phase Equilib., 1993, 14, 473–478 CrossRef CAS.
- R. Ferro, G. Borzone, G. Cacciamani and R. Raggio, Thermochim. Acta, 2000, 347, 103–122 CrossRef CAS.
- R. G. Janssen, J. P. M. Van Duynhoven, W. Verboom, G. J. Van Hummel, S. Harkema and D. N. Reinhoudt, J. Am. Chem. Soc., 1996, 118, 3666–3675 CrossRef CAS.
- F. Matalkah, L. Xu, W. Wu and P. Soroushian, Mater. Struct., 2017, 50, 97 CrossRef.
- J. Bednárek, P. Ptáček, F. Šoukal, J. Havlica, R. Novotný, J. Másilko and P. Šiler, IOP Conf.: Ser. Mater. Sci. Eng., 2018, 379 DOI:10.1088/1757-899X/379/1/012003.
- M. Jerman, V. Tydlitát, M. Keppert, M. Čáchová and R. Černý, Thermochim. Acta, 2016, 633, 108–115 CrossRef CAS.
- V. Tydlitát, J. Zákoutský, P. Volfová and R. Černý, Thermochim. Acta, 2012, 543, 125–129 CrossRef.
- M. A. Phipps and L. A. Mackin, Pharm. Sci. Technol. Today, 2000, 3, 9–17 CrossRef CAS PubMed.
- A. E. Beezer, M. A. A. O’Neill, K. Urakami, J. A. Connor and J. Tetteh, Thermochim. Acta, 2004, 420, 19–22 CrossRef CAS.
- C. V. Skaria, S. Gaisford, M. A. A. O’Neill, G. Buckton and A. E. Beezer, Int. J. Pharm., 2005, 292, 127–135 CrossRef CAS.
- R. M. Morcos and A. Navrotsky, J. Therm. Anal. Calorim., 2009, 96, 353–361 CrossRef CAS.
- R. J. Willson, A. E. Beezer and J. C. Mitchell, Int. J. Pharm., 1996, 132, 45–51 CrossRef CAS.
- K. Urakami and A. E. Beezer, Int. J. Pharm., 2003, 257, 265–271 CrossRef CAS PubMed.
- N. Alem, A. E. Beezer and S. Gaisford, Int. J. Pharm., 2010, 399, 12–18 CrossRef CAS PubMed.
- L. E. Briggner, G. Buckton, K. Bystrom and P. Darcy, Int. J. Pharm., 1994, 105, 125–135 CrossRef CAS.
- L. A. E. Sousa, N. Alem, A. E. Beezer, M. A. A. O’Neill and S. Gaisford, J. Phys. Chem. B, 2010, 114, 13173–13178 CrossRef CAS.
- E. A. Schmitt, K. Peck, Y. Sun and J. M. Geoffroy, Thermochim. Acta, 2001, 380, 175–184 CrossRef CAS.
- J. Baronsky, M. Preu, M. Traeubel and N. A. Urbanetz, Eur. J. Pharm. Sci., 2011, 44, 74–82 CrossRef CAS PubMed.
- J. J. Christensen, D. J. Eatough and R. M. Izatt, Chem. Rev., 1974, 74, 351–384 CrossRef PubMed.
- J. D. Lamb, R. M. Izatt, C. S. Swain and J. J. Christensen, J. Am. Chem. Soc., 1980, 102, 475–479 CrossRef CAS.
- L. X. Dang and P. A. Kollman, J. Phys. Chem., 1995, 99, 55–58 CrossRef CAS.
- J. W. Steed, Coord. Chem. Rev., 2001, 215, 171–221 CrossRef CAS.
- T. Nabeshima, T. Saiki, J. Iwabuchi and S. Akine, J. Am. Chem. Soc., 2005, 127, 5507–5511 CrossRef CAS.
- Z. Liu, H. Zhang and J. Han, Org. Biomol. Chem., 2021, 19, 3287–3302 RSC.
- Z. Zhang, Y. Shao, J. Tang, J. Jiang, L. Wang and S. Li, Green Synth. Catal., 2021, 2, 156–164 CrossRef.
- V. S. Saji, Chem. Rec., 2022, 22, e202200053 CrossRef CAS PubMed.
- Z. Duan, F. Xu, X. Huang, Y. Qian, H. Li and W. Tian, Macromol. Rapid Commun., 2021, 2100775, 1–35 Search PubMed.
- Y. F. Zhang, F. F. Di, P. F. Li and R. G. Xiong, Chem. – Eur. J., 2022, 28, e202102990 CrossRef CAS.
- D. Braga, S. D’Agostino, F. Grepioni, M. Gandolfi and K. Rubini, Dalton Trans., 2011, 40, 4765–4777 RSC.
- D. Braga, L. Maini, S. L. Giaffreda, F. Grepioni, M. R. Chierotti and R. Gobetto, Chem. – Eur. J., 2004, 10, 3261–3269 CrossRef CAS PubMed.
- D. Braga, E. Modena, M. Polito, K. Rubini and F. Grepioni, New J. Chem., 2008, 32, 1718–1724 RSC.
- G. Michaux and J. Reisse, J. Am. Chem. Soc., 1982, 104, 6895–6899 CrossRef CAS.
- P. Vishweshwar, J. A. McMahon, J. A. Bis and M. J. Zaworotko, J. Pharm. Sci., 2006, 95, 499–516 CrossRef CAS PubMed.
- C. B. Aakeröy, M. E. Fasulo and J. Desper, Mol. Pharm., 2007, 4, 317–322 CrossRef.
- M. K. Corpinot and D. K. Bučar, Cryst. Growth Des., 2019, 19, 1426–1453 CrossRef CAS.
- L. S. Germann, M. Arhangelskis, M. Etter, R. E. Dinnebier and T. Friščić, Chem. Sci., 2020, 11, 10092–10100 RSC.
- K. Chadwick, R. Davey and W. Cross, CrystEngComm, 2007, 9, 732–734 RSC.
- K. Chadwick, R. J. Davey, G. Dent, R. G. Pritchard, C. A. Hunter and D. Musumeci, Cryst. Growth Des., 2009, 9, 1990–1999 CrossRef CAS.
- H. H. Lee and J. C. Warner, J. Am. Chem. Soc., 1933, 55, 4474–4477 CrossRef CAS.
- N. Biliškov, Cryst. Growth Des., 2021, 21, 1434–1442 CrossRef.
- J. J. Li, Name Reactions, Springer Berlin Heidelberg, Berlin, Heidelberg, 2006, pp. 14–15 Search PubMed.
- A. Baeyer and V. Villiger, Ber. Dtsch. Chem. Ges., 1899, 32, 3625–3633 CrossRef.
- G.-J. ten Brink, I. W. C. E. Arends and R. A. Sheldon, Chem. Rev., 2004, 104, 4105–4123 CrossRef PubMed.
- M. Ochiai, A. Yoshimura, K. Miyamoto, S. Hayashi and W. Nakanishi, J. Am. Chem. Soc., 2010, 132, 9236–9239 CrossRef CAS.
- Y. Chevalier, Y. Lock Toy Ki, D. le Nouen, J. P. Mahy, J. P. Goddard and F. Avenier, Angew. Chem., Int. Ed., 2018, 57, 16412–16415 CrossRef CAS.
- A. Cavarzan, G. Bianchini, P. Sgarbossa, L. Lefort, S. Gladiali, A. Scarso and G. Strukul, Chem. – Eur. J., 2009, 15, 7930–7939 CrossRef CAS.
- F. Toda, M. Yagi and K. Kiyoshige, J. Chem. Soc., Chem. Commun., 1988, 958–959 RSC.
- J. J. Esteb, J. N. Hohman, D. E. Schlamadinger and A. M. Wilson, J. Chem. Educ., 2005, 82, 1837–1838 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp03933a |
| ‡ Equal contribution of the authors. |
| This journal is © the Owner Societies 2024 |