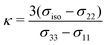Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Machine learning-based correction for spin–orbit coupling effects in NMR chemical shift calculations†
Julius B.
Kleine Büning
 a,
Stefan
Grimme
a,
Stefan
Grimme
 *a and
Markus
Bursch
*a and
Markus
Bursch
 *b
*b
aMulliken Center for Theoretical Chemistry, Clausius Institute for Physical and Theoretical Chemistry, University of Bonn, Beringstr. 4, 53115 Bonn, Germany. E-mail: grimme@thch.uni-bonn.de
bMax-Planck-Institut für Kohlenforschung, Kaiser-Wilhelm-Platz 1, 45470 Mülheim an der Ruhr, Germany. E-mail: bursch@kofo.mpg.de
First published on 9th January 2024
Abstract
As one of the most powerful analytical methods for molecular and solid-state structure elucidation, NMR spectroscopy is an integral part of chemical laboratories associated with a great research interest in its computational simulation. Particularly when heavy atoms are present, a relativistic treatment is essential in the calculations as these influence also the nearby light atoms. In this work, we present a Δ-machine learning method that approximates the contribution to 13C and 1H NMR chemical shifts that stems from spin–orbit (SO) coupling effects. It is built on computed reference data at the spin–orbit zeroth-order regular approximation (ZORA) DFT level for a set of 6388 structures with 38![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 740 13C and 64
740 13C and 64![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 436 1H NMR chemical shifts. The scope of the methods covers the 17 most important heavy p-block elements that exhibit heavy atom on the light atom (HALA) effects to covalently bound carbon or hydrogen atoms. Evaluated on the test data set, the approach is able to recover roughly 85% of the SO contribution for 13C and 70% for 1H from a scalar-relativistic PBE0/ZORA-def2-TZVP calculation at virtually no extra computational costs. Moreover, the method is transferable to other baseline DFT methods even without retraining the model and performs well for realistic organotin and -lead compounds. Finally, we show that using a combination of the new approach with our previous Δ-ML method for correlation contributions to NMR chemical shifts, the mean absolute NMR shift deviations from non-relativistic DFT calculations to experimental values can be halved.
436 1H NMR chemical shifts. The scope of the methods covers the 17 most important heavy p-block elements that exhibit heavy atom on the light atom (HALA) effects to covalently bound carbon or hydrogen atoms. Evaluated on the test data set, the approach is able to recover roughly 85% of the SO contribution for 13C and 70% for 1H from a scalar-relativistic PBE0/ZORA-def2-TZVP calculation at virtually no extra computational costs. Moreover, the method is transferable to other baseline DFT methods even without retraining the model and performs well for realistic organotin and -lead compounds. Finally, we show that using a combination of the new approach with our previous Δ-ML method for correlation contributions to NMR chemical shifts, the mean absolute NMR shift deviations from non-relativistic DFT calculations to experimental values can be halved.
1 Introduction
Nuclear magnetic resonance (NMR) spectroscopy is a highly valuable analytic tool for structure elucidation and has become a standard method that is used on a daily basis throughout various chemical disciplines.1–3 Besides experimental analysis, the computation of NMR parameters can further yield detailed insight into chemical phenomena and complex bonding situations. In particular, density functional theory (DFT) has proven to be a reliable and efficient choice for the calculation of NMR parameters.4–12 Nevertheless, the complex physical relationship between these parameters, the electronic structure, and the chemical environment of the investigated compound remains challenging for quantum chemical methods.13–15There are five main sources of error in quantum chemical NMR prediction as claimed by Lodewyk et al.,13 which are electron correlation, solvation effects, conformational flexibility, rotational-vibrational, and relativistic effects. The latter become specifically relevant when NMR properties of heavy elements (which we refer to as having an atomic number larger than 18 and including Cl) are computed or if such elements are present in close vicinity to the nucleus under consideration. Heavy elements can play major roles in various application areas, including catalysis,16–18 batteries,19,20 and optoelectronics.21,22 Furthermore, there is a great research interest in biology and biochemistry due to the toxicity of some heavy elements (e.g., Ni, Cd, Hg, Pb)23 or their essential role in biochemical processes, as for Zn24–26 and Se.27–29
The most crucial relativistic effects originate from spin–orbit (SO) coupling and can be essential even for qualitative modeling of the heavy atom (HA) itself,11,30,31 but also for the adjacent lighter atoms by the heavy atom on the light atom (HALA) effect.10,32,33 There are several physics-based methods to incorporate relativistic effects into quantum chemical calculations such as the Douglas–Kroll–Hess (DKH)34,35 method, the exact transformation of the four-component Dirac equation to two components (X2C),36–38 and the zeroth-order regular approximation (ZORA).39,40 However, the spin–orbit variants of these methods in combination with NMR shielding tensor calculations typically become computationally unfeasible for larger compounds due to their high computational demand. Further, such methods are not available in many chemical software packages. Accordingly, more efficient and easily accessible methods to include SO-relativistic effects in the calculation of NMR parameters are highly desirable. Such effects are typically neglected in most low-cost approaches, as done in a recently published correction scheme for efficient NMR chemical shielding prediction41 and a study on halogenated natural products.42
One approach to solve this issue and fill this methodological gap can be an empirical model based on machine learning (ML). The field of ML in chemistry has evolved rapidly in the past decade and besides approaches that tackle the complete electronic structure of a quantum chemical system,43–45 several techniques for the calculation of NMR chemical shifts have been developed.46–48 Especially for NMR-aided structure assignment, the popular DP4 method49 was improved with an ML approach called DP4-AI50 and an ML-based technique for structure assignment from two-dimensional NMR spectra has been proposed.51 ML approaches can exploit their full potential for highly accurate predictions if they are combined with DFT and use features from a converged electronic structure as input (Δ-ML). This has been shown to yield highly accurate electronic energies52 and NMR chemical shifts53–56 at costs not significantly higher than for the underlying low-level method.
There is evidence that in order to achieve a good prediction quality for 13C NMR chemical shifts of carbon atoms attached to heavy atoms, it is important to account for both correlation and heavy atom effects.13,57,58 In a test on the o-bromochlorobenzene molecule,59 the pragmatic combination of a non-relativistic second-order Møller–Plesset perturbation theory (MP2) calculation and a SO contribution calculated with DFT yielded the best results compared to experimental data and was the only tested method to achieve a qualitatively correct chemical shift ordering of the six 13C nuclei. We are therefore confident that a combination of separate correlation and spin–orbit corrections will be beneficial for the efficient computation of reasonably accurate NMR chemical shifts. We previously proposed an ML-based correction method that obtains the (beyond DFT) correlation contribution to NMR chemical shifts based on coupled cluster (CCSD(T)) reference data,55 which we now call Δcorr-ML. In this work, we present an efficient and highly transferable approach called ΔSO-ML to compute the spin–orbit relativistic contribution to 13C and 1H NMR chemical shifts. This new approach is validated for a large number of unique chemical shifts computed at the SO-ZORA-DFT level and is exemplarily applied to 13C NMR chemical shifts in experimentally accessible organotin and -lead compounds and in a set of heavy metal–organic compounds with experimental reference data.
2 Methods
2.1 Machine learning data set
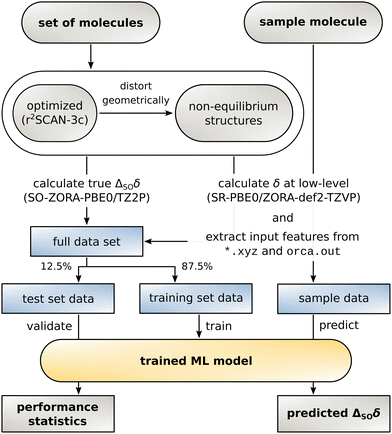
As in our previous work on the correction of 1H and 13C NMR chemical shifts using machine learning,55 quantum chemical ab initio data serve as target for the model presented herein. The use of experimental data would increase the overall complexity thus making the data set less suitable for applying an ML correction procedure. Furthermore, the target was chosen such that it keeps an unadulterated focus on one specific component of the chemical shielding constant calculation, spin–orbit coupling. A clear distinction of SO effects from various other error sources in experimental data would be impossible and such an approach would prevent a targeted elimination of the SO error.The data set is one of the central parts in every ML model and is often particularly challenging to compile for ML applications in chemistry when reference data is sparse. Since it is largely responsible for the performance of the model, we focus on the most common bonding situations in classical (metal-)organic compounds. Further, a focus is set on heavy non-radioactive elements of groups 12 to 17. This includes most p-block elements except for noble gasses and group 12 transition metals as their chemistry is comparably dominated by p-orbitals.33 As NMR parameters tend to be spatially local, the reference molecules can be chosen rather small (3–46 atoms). This allows for the inclusion of many different bonding motifs, covering a wide chemical space with a sufficiently large amount of samples. The data set consists of 1597 unique molecules, in which at least one heavy atom (Z ≥ 17) is covalently bound to a carbon atom. These molecules were created manually, starting with the methyl compounds mentioned in Section 3.3.1, and subsequent substitution of the ligands with larger aliphatic, aromatic, and functional residues that are typically found in compounds of the respective heavy element. Analogous structures are included for all elements within the same group and some more complex compounds were added. The structures were selected such that they are chemically reasonable, yet they do not have to be accessible in an experimental setting. To enrich the data, three geometrically distorted structures, one out of each energy window of 2.5–5.0 kcal mol-1, 10.0–15.0 kcal mol-1, and 30.0–40.0 kcal mol-1 above the optimized structures (at the r2SCAN-3c60 level) were added (for more information on the distortion procedure, see ref. 55 and the ESI†). The overall 6388 structures include data points for 38![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 740 13C and 64
740 13C and 64![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 436 1H NMR chemical shifts, which is illustrated in Fig. 1. The set includes 2264 structures containing Cl, Br, or I; 1440 structures containing Se or Te; 1260 structures containing As, Sb, or Bi; 1680 structures containing Ge, Sn, or Pb; 804 structures containing Ga, In, or Tl; and 868 structures containing Zn, Cd, or Hg.
436 1H NMR chemical shifts, which is illustrated in Fig. 1. The set includes 2264 structures containing Cl, Br, or I; 1440 structures containing Se or Te; 1260 structures containing As, Sb, or Bi; 1680 structures containing Ge, Sn, or Pb; 804 structures containing Ga, In, or Tl; and 868 structures containing Zn, Cd, or Hg.
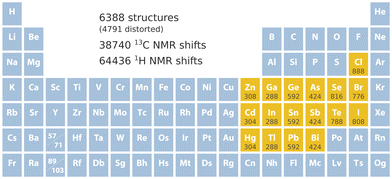 | ||
| Fig. 1 Key specifications of the data set. Included heavy elements are marked in yellow followed by the number of structures that contain them. | ||
2.2 Reference level of theory
The target of the ΔSO-ML approach presented here is the contribution to the chemical shielding constant that originates from the inclusion of spin–orbit relativistic effects with a suitable computational method. Scalar-relativistic approaches that either employ effective core potentials (ECPs) or explicitly use a scalar-relativistic (SR) Hamiltonian are available in many quantum chemical program packages such as ORCA. As all-electron approaches with SR-Hamiltonian can be regarded the more general and reliable choice for the calculation of properties with relevant nucleus effects, we chose an efficient all-electron SR-DFT calculation as origin of the ML input features to predict the additive spin–orbit (SO) correction with our ΔSO-ML model. This contribution ΔSOδ is calculated from chemical shifts δ obtained by including the different levels of relativity:| ΔSOδ = δSO − δSR. | (1) |
In this work, we determine the target ΔSOδ from two-component SR/SO-ZORA (zeroth-order regular approximation) calculations at the PBE061,62 hybrid DFT level of theory with the Slater-type triple-ζ TZ2P63 basis set. Note that the performance of an ML approach is directly influenced and limited by the quality – especially the noisiness – of the reference data.64 PBE0 is a generally robust functional that usually yields good NMR properties and especially the SO-relativistic variant has proven reliable performance in our previous studies on 29Si10 and 119Sn11 NMR chemical shifts. Furthermore, in contrast to full four-component relativistic methods, SO-ZORA-PBE0 is still feasible for the medium-sized (>40 atoms) molecules included in the data set. The transferability of our approach based on the PBE0/TZ2P data to other density functionals and basis sets is further discussed in Section 3.3.1.
To make it easily accessible, the presented method is built onto a scalar-relativistic baseline level of theory calculated using Gaussian-type orbitals with the ORCA program package (although it is in principle not limited to it). The SR-PBE0/ZORA-def2-TZVP level of theory serves as low-level method for most evaluations shown below.
2.3 Neural network architecture and input feature vector
With the data set and the target values ΔSOδ at hand, an ML model can be constructed. For this purpose, the data set is randomly divided into a training set to build the model and a test set that serves as basis for all evaluations made in Section 3. The data is processed in an atom-wise fashion but it is ensured that all atoms from an individual structure are attributed to the same data set (shuffling mode structures, see ESI,† Section 2.2 for details). Data from a sample molecule and its low-level NMR shielding calculation (currently only possible via the ORCA 5 program package) can finally be used to predict ΔSOδ. The complete workflow is illustrated in Fig. 2.The regression artificial neural network used herein is similar to the one used for our previous Δcorr-ML model for correlation contributions of the chemical shift.55 The same multilayer perceptron architecture with two hidden layers was used in TensorFlow 2.12 and the input feature vector was modified to adapt it to the SO contribution problem. After initial testing, the hyperparameters were set to 300/12 nodes for the first/second hidden layer for 13C (384/80 for 1H) with a dropout rate of 0.1 for the first layer for 13C (0.15 on first and 0.1 on second layer for 1H) and the adam optimizer. The activation function on all layers was set to GELU (Gaussian Error Linear Unit) for 13C and the sigmoid function was used for 1H. The distribution of the SO contribution values to the chemical shift in the data set is very heterogeneous. Most of the atoms are not in direct vicinity to a heavy atom, so ΔSOδ is small but few atoms exhibit a very large value. To make the model focus on the important large values while not placing too much weight on unaffected atoms, the root mean squared deviation (RMSD) was chosen as loss function and showed to be superior to the mean absolute deviation (MAD) and the mean squared deviation (MSD). For the same reason, the RMSD is suited better than the MAD for the evaluations below.
The information included as input is of central importance for the quality and performance of the ML model.64 In the case of ΔSO-ML, the input feature vector is constructed such that it contains information about the geometric (solely from the three-dimensional structure), electronic (from the converged density matrix of the DFT single-point calculation), and magnetic (from the DFT NMR shielding constant calculation) surrounding of each atom of interest. The majority of the descriptors of these categories was taken from the Δcorr-ML model and some were omitted. A set of atom-centered symmetry functions65 (ACSF) was further added.
Furthermore, a new range of descriptors was added that contains geometric and electronic information about heavy atoms in the vicinity of the atom of interest. These include:
• The total number of heavy atoms bound to the nucleus of interest via one to five covalent bonds,
• The average atomic mass of all atoms within one to five covalent bonds,
• The atomic number of the heavy atom(s),
• The coordination number (from the D3 model) of the heavy atom(s), and
• The atomic, and s-, p-, and d-orbital Mulliken populations of the heavy atom.
The latter ones are arranged in sets of five descriptors per heavy atom in the first covalent bond shell. The inclusion of the atomic charge and the s- and p-orbital populations was motivated by the findings of Vícha et al. on the spin–orbit heavy-atom (HA) effect on the light atom (LA).33 These suggest that for most heavy elements the chemical shift contribution originating from spin–orbit coupling has a fixed sign. Accordingly, the HA effect on the LA is always shielding or deshielding (this information is covered by the atomic number of the HA). The cause of this trend lies in the electronic configuration, as formally empty valences shells of the HA (e.g., p0, d0) typically lead to a deshielding mechanism whereas partially filled subshells (e.g., p2, p4) result in a shielding effect. In some cases, however, different contributions occur simultaneously with comparable magnitudes so that the sign of ΔSOδ may vary, e.g., depending on the oxidation state of the HA. Therefore, the atomic charge and orbital populations of the HA are included as descriptors. A detailed list of the complete input feature vector is provided in the ESI,† Table S2.
2.4 Computational details
The compounds in the data set were chosen and created manually and a selected structure was pre-optimized at the semiempirical tight-binding GFN2-xTB66 level using the xtb 6.6.067 program package. Subsequent geometry optimizations where performed with the TURBOMOLE 7.7.168–70 program package using the r2SCAN-3c60,71,72 composite DFT method. Throughout the geometry optimizations, the resolution of the identity approach for Coulomb integrals (RIJ)73 was applied and the m4 grid and a radial grid size of 10 were used. For the tests on the experimentally accessible structures in Sections 3.4.2 and 3.4.3, conformer ensembles were generated using the conformer-rotamer ensemble sampling tool (CREST),74,75 version 2.12, using the GFN-FF76 force field and GFN2-xTB with the ALPB77 solvation model (solvent as in the experimental measurement). The ensembles were further refined with the command-line energetic sorting (CENSO)78,79 algorithm, version 1.2.0, at the final level r2SCAN-3c + Gsolv(COSMO-RS)80–82 + GmRRHO(GFN2-xTB)83–85//r2SCAN-3c(DCOSMO-RS).86All NMR shielding constant calculations in this study were performed via the gauge-including atomic orbital (GIAO)87–89 approach using the ORCA 5.0.490–92 program package for calculations with Gaussian-type orbital (GTO) basis sets and the ADF module of the AMS 2022.10393 program package for Slater-type orbital (STO) basis sets. For the low-level shielding calculations (ORCA), the Hamiltonian of the scalar-relativistic (SR) zeroth-order regular approximation (ZORA)39,94 was used in combination with the PBE95 general gradient approximation (GGA) and the PBE061 and r2SCAN096 hybrid density functionals, together with the GTO triple-ζ ZORA-def2-TZVP97,98 basis set for all atoms with Z ≤ 36 and the SARC-ZORA-TZVP99–101 basis set for all atoms with Z > 36. For PBE0, the calculations were also done without ZORA applying the def2-TZVP97 basis set with the def2 effective core potentials (ECP).102,103 For the NMR shielding calculations in Sections 3.4.2 and 3.4.3, the CPCM104 implicit solvation model was used. All calculations applied the RI scheme with the chain-of-spheres approximation for the exchange (RIJCOSX)105,106 in combination with the auxiliary SARC/J basis set. The defgrid3 grid and the tightscf convergence settings were used throughout. For the high-level reference values (ADF), the NMR shielding calculations were performed each with the scalar (SR) and spin–orbit (SO) variant of ZORA40,107,108 and the PBE0 functional using the STO polarized triple-ζ ZORA/TZ2P63 basis set (the “ZORA/” prefix for the basis set is from now assumed for all calculations with ADF and omitted for clarity). The numerical grid quality was set to verygood. For the compounds of the methyl subset, the same calculation settings were applied, but with using the DZ, DZP, TZP, and QZ4P basis sets63 and the PBE, BLYP,109,110 mPW,111 B3LYP,110,112 and mPW1PW111 functionals.
In the ML training, prediction, and evaluation procedures mentioned in the following, statistical fluctuations are to be expected that originate from the randomized weight initialization when the model is build. All statistics presented for the performance of the ΔSO-ML model are therefore obtained as the mean value of ten training runs if not stated otherwise.
3 Results
3.1 Prediction of ΔSOδ for 13C NMR
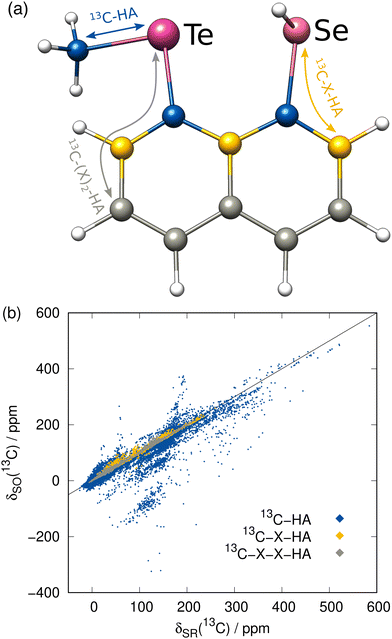
Before focusing on the new ΔSO-ML correction, it is worth investigating the data set itself with the computed low-level SR NMR shifts and the reference ΔSOδ values. As a rather short-range effect, the SO contribution is expected to be small for many C/H atoms, but can be extreme in direct vicinity of a heavy atom. The complete data for the 13C NMR shifts is depicted in Fig. 3(b) including information about the chemical distance (= number of covalent bonds) of each nucleus to the next heavy atom. Thus, 13C nuclei that are directly bound to a HA experience by far the largest spin–orbit coupling effects and these values are most scattered over a wide range of chemical shifts. Still, the SO effect of a HA can propagate which can have significant consequences for the 13C nuclei even three covalent bonds away. Although the nuclei closest to the HA have the potential to lead to the largest errors in a calculation, the proposed ML model should not only be capable of reproducing the rough magnitude of the effect, but should consequently predict a small ΔSOδ value for the weakly affected nuclei.As mentioned earlier, the PBE0/ZORA-def2-TZVP method applying scalar-relativistic SR-ZORA is chosen as low-level method for the following investigations. Several metrics demonstrating the performance of the ΔSO-ML model evaluated for the test data set (12.5% of the data points) for 13C and 1H (discussed in the next section) nuclei are listed in Table 1. The data for one of the runs is exemplarily shown in Fig. 4 in more detail.
| Error metric | 13C | 1H | ||
|---|---|---|---|---|
| Only SR | SR + ML | Only SR | SR + ML | |
| MAX (<0) | −179.07 | −56.34 | −19.569 | −4.772 |
| MAX (>0) | 298.32 | 87.55 | 6.042 | 10.825 |
| MD | 2.84 | −0.05 | −0.185 | −0.005 |
| MAD | 7.26 | 1.07 | 0.281 | 0.090 |
| MSD | 478.82 | 7.60 | 0.645 | 0.056 |
| RMSD | 21.88 | 2.76 | 0.803 | 0.236 |
| SD | 21.67 | 2.75 | 0.782 | 0.236 |
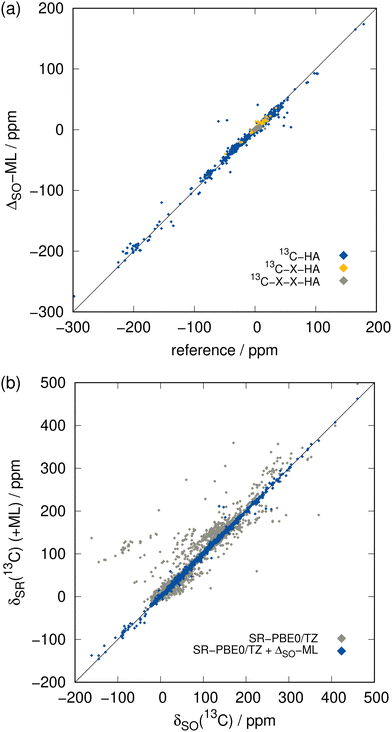 | ||
| Fig. 4 Comparison of the ML-predicted SO contributions to the reference (SR/SO)-ZORA-PBE0/TZ2P ones for the 13C NMR test set. (a) Values of ΔSOδ, color-coded according to their distance to the next heavy atom (see Fig. 3(a)). (b) Total chemical shift δ neglecting SO coupling (gray) and adding the ML-predicted ΔSOδ (blue). | ||
The ΔSO-ML correction clearly succeeds to predict the SO contribution to the 13C NMR chemical shifts with good accuracy. The mean absolute deviation (MAD) from 4843 chemical shifts in the test data set (unknown to the ML model while training) is reduced by 85% from 7.26 to 1.07 ppm and the mean (signed) deviation (MD), which is slightly positive when only SR is applied, essentially reaches zero. More importantly, the root mean square deviation (RMSD), which emphasizes large deviations, is equally reduced (87%, from 21.88 to 2.76 ppm). Thus, it can be concluded that roughly 85% of the SO contribution is recovered by the ML model. Analysis of one of the training runs in Fig. 4(a) shows that accuracy is maintained even for the extreme cases of spin–orbit coupling effects on 13C nuclei directly bound to HAs. The large negative values of ΔSOδ occur especially when several heavy halogen atoms are present, such as in a CI3 moiety.
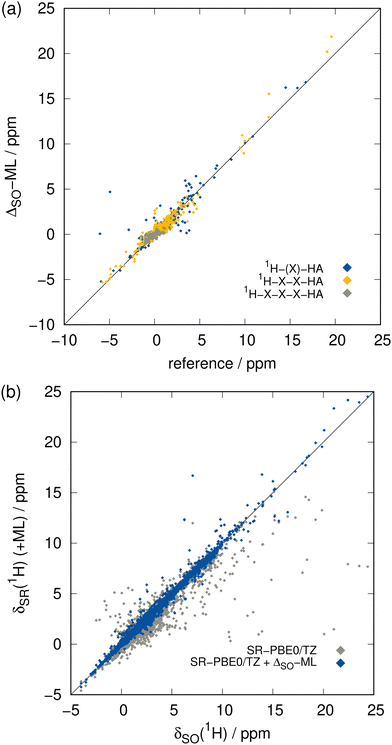
Furthermore, extremely large errors can be avoided with the ΔSO-ML correction as the maximum negative and positive errors are reduced drastically from −179.07/+298.32 to −56.34/+87.55 ppm. This is promising because in this way the ML correction reduces the probability of a complete qualitative failure of a chemical shift prediction. The overall chance for outliers is therefore reduced significantly as underpinned by Fig. 4(b).
It is important to note that an empirical prediction method for spin–orbit effects to NMR chemical shifts is not a straightforward task. It is indeed a rather systematic phenomenon as it strongly depends on the type and the atomic number of the HA as well as the periodic table main group it belongs to. So, when the underlying data only features a certain chemical subgroup of molecules, a simple linear regression approach, which is often used to correct calculated NMR chemical shifts and which we used to compare the performance of the Δcorr-ML model to, can be used to approximate the SO contribution to 13C NMR chemical shifts.113,114 However, this is only possible if all molecules in the data set contain the same number and type of heavy atoms.13 Conversely, in the data set presented here, many different HAs and amounts of HAs are present and therefore, there is not even a slight linear connection between the computed scalar-relativistic chemical shift value and the missing SO contribution (see the ESI,† Fig. S3 to S5). Hence, a linear regression correction approach fails for the SO contribution, as it predicts ΔSOδ ≈ 0 in most cases. However, the additional computational costs of a prediction of ΔSOδ by the a pre-trained ML model is – as for the linear regression approach – negligible (few seconds). This consolidates the significance of the ΔSO-ML model as a general low-cost method to predict the SO contribution of NMR chemical shifts.
3.2 Prediction of ΔSOδ for 1H NMR
The focus of this work lies on the prediction of SO contributions to 13C NMR chemical shifts since in organic compounds, usually the carbon atoms are connected to heavy heteroatoms. However, the 1H nucleus can experience SO contributions from even further HAs as it is more prone to environmental changes and thus can be affected by propagation of the SO contribution via more than three covalent bonds. Compared to heavier elements, the hydrogen atom only comprises a very thin electron shell and the 1H nucleus is thus less shielded from electronic and magnetic fields in its surroundings. This complicates especially the theoretical description of core properties such as NMR parameters. Achieving the same accuracy for 1H NMR as for 13C NMR is therefore difficult, which we already observed for the Δcorr-ML correction and there is no reason to assume that this behavior is different in the case of ΔSO-ML. This is even exacerbated by the fact that the hydrogen atoms are usually further away from the HA than carbon atoms meaning that the ΔSOδ values are smaller and can be less systematic. The data set for 1H NMR SO contributions shows a significant number of large values not only for very close 1H nuclei, but also for those bound to a HA via three covalent bonds (see ESI,† Fig. S2). Hence, the distance criterion is weaker for 1H than it is for 13C, representing a bigger challenge for the ΔSO-ML model.The greater complexity compared to 13C NMR is confirmed by the somewhat weaker performance of the ΔSO-ML approach applied to the low-level method SR-PBE0/ZORA-def2-TZVP for 1H NMR indicated by the metrics in Table 1 and the detailed analysis of a training run in Fig. 5. Compared to the 13C data, the performance of the ML approach for 1H NMR is indeed worse, but the functionality is still retained. The ΔSO-ML method predicts qualitatively correct values within the whole data range even in the extreme regions (Fig. 5(a)) and scattering of the data including the ML-predicted SO contributions is reduced significantly compared to the purely SR values (Fig. 5(b)). It is noticeable that the data of nuclei in close and medium vicinity to a HA is spread over the whole data range, only the 1H nuclei at least four bonds away from the HA are loosely restricted to a region of small ΔSOδ values and small prediction errors. The overall improvement achieved by the correction is also substantiated by the metrics in Table 1. That is, the MAD resulting from the 8055 data points in the test set is reduced by 68% from 0.281 to 0.090 ppm and the overall chance for large errors is reduced, too, as indicated by the 71% decrease of the RMSD from 0.803 to 0.236 ppm. In contrast to the 13C NMR case, the MD for the purely SR 1H NMR chemical shifts is slightly negative, but it is nevertheless basically eliminated. Unfortunately, there is at least one large outlier in the predicted ΔSOδ values leading to an increased positive maximum error of 10.825 ppm. Taking into account the overall reduced error spread and range (reduced from 26.611 to 15.597 ppm) as well as the small RMSD, this can be considered an artifact that occurs only very rarely.
The fundamental non-linear correlation between the scalar-relativistic NMR chemical shift and its missing spin–orbit coupling contribution seems to be general and can at least be transferred form 13C to 1H NMR (see ESI,† Fig. S6 to S8). The linear regression technique is therefore unusable also for the 1H NMR case. To conclude, despite the lower performance of the ΔSO-ML approach for 1H compared to 13C NMR, it still accomplishes a decent improvement, especially if the negligible extra computational expenses and efforts are considered.
3.3 Generalizability of the model
| Functional | Basis set | 13C | 1H | ||
|---|---|---|---|---|---|
| MD | MAD | MD | MAD | ||
| PBE0 | DZ | −1.28 | 1.28 | 0.022 | 0.045 |
| PBE0 | DZP | −0.60 | 0.64 | 0.016 | 0.025 |
| PBE0 | TZP | −0.28 | 0.40 | 0.006 | 0.012 |
| PBE0 | QZ4P | 0.11 | 0.30 | 0.003 | 0.013 |
| PBE | TZ2P | −0.82 | 0.84 | 0.004 | 0.053 |
| BLYP | TZ2P | −1.74 | 1.98 | 0.012 | 0.065 |
| mPW | TZ2P | −0.94 | 0.94 | 0.000 | 0.063 |
| B3LYP | TZ2P | −1.05 | 1.51 | 0.010 | 0.019 |
| mPW1PW | TZ2P | −0.12 | 0.26 | −0.003 | 0.006 |
| PBE0 | TZ2P | 0.00 | 0.00 | 0.000 | 0.000 |
Variation of the basis set size is found to have an almost negligible effect on ΔSOδ when still a triple- or quadruple-ζ size is sustained with maximum mean absolute deviations of 0.40 ppm for 13C (TZP) and 0.013 ppm for 1H (QZ4P). These values lie below the typically expected errors for density functional approximations (DFA) of roughly 3–8 ppm for 13C NMR and 0.1–0.3 ppm for 1H NMR.6 When the basis set size is reduced to double-ζ (DZ, DZP), significantly larger deviations are observed. Therefore, TZ2P is considered a well-balanced and reasonably large basis set for the purpose of this work. The use of different DFAs exhibits a more pronounced effect on the value of ΔSOδ. While for 13C, no dependence on the functional class (GGA/hybrid) is observed, in the 1H case, the deviation from the hybrid PBE0 to the GGAs is larger than for the hybrids DFAs. Nevertheless, even when BLYP is used, which has the largest MAD compared to PBE0 (1.98 ppm for 13C, 0.65 ppm for 1H), the functional differences are still very low. According to these data, the SO prediction method is expected to be generalizable to methods other than PBE0/TZ2P with a small residual method inconsistency error.
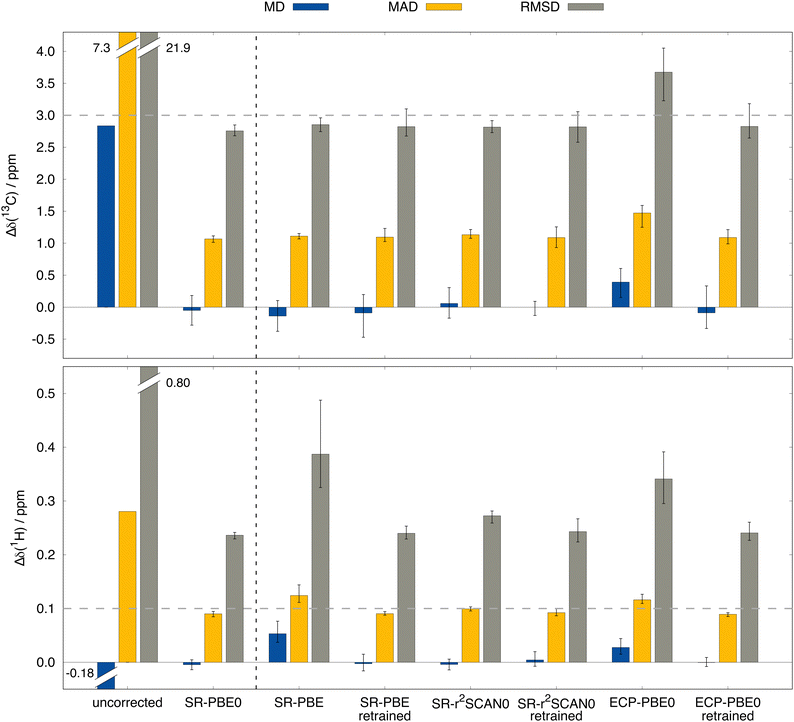
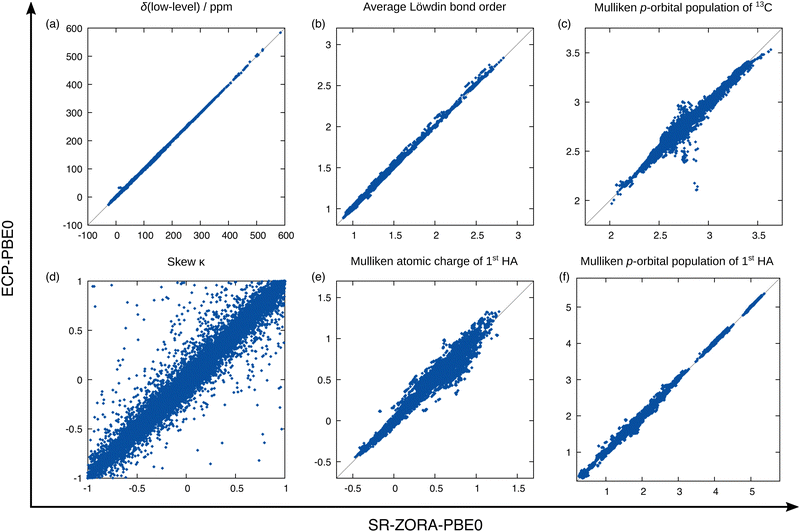
Answers to these questions can be obtained from analyzing the performance differences of the mentioned methods for the test data set depicted in Fig. 6. First, the previously examined performance using the SR-PBE0 method is clearly visible when compared to the uncorrected data (without any SO contribution) and the prediction qualities for all other tested methods are of equal dimension. By taking a closer look, it is surprising to find that in the case of 13C NMR, the performance of the ΔSO-ML method is not reduced noticeably when SR-PBE or SR-r2SCAN0 are used as low-level methods. This means that the electronic and magnetic input features obtained from PBE and r2SCAN0 chemical shielding calculations closely resemble those from a PBE0 calculation (all geometric descriptors are identical). A computationally more affordable level of theory such as PBE can therefore easily be used to reconstruct the SO contribution to the 13C NMR chemical shift at the PBE0 level without changing the ML model. Subsequently, it is not surprising that the ΔSO-ML approaches for PBE and r2SCAN0 retain their performance when the model is trained on data obtained from these respective DFAs. The situation changes slightly, when not the functional, but the relativistic approximation is changed. The use of the simpler ECP variant of PBE0/def2-TZVP and the standard instead of the ZORA Hamiltonian results in a slightly increased RMSD of 3.67 ppm (compared to 2.76 ppm for SR-PBE0/ZORA-def2-TZVP) and a larger error spread. This indicates that the input features differ more severely between the ECP and SR-ZORA approaches than between the different functionals. For some further insights, a selection of six electronic and magnetic 13C descriptors is depicted in Fig. 7 showing their correlation when obtained from the different calculations via the ECP and the SR-ZORA approach. In all cases, a more or less strongly pronounced correlation is found which explains the ability of the ΔSO-ML method to predict reasonable results even without retraining of the model. Since the correlation has an approximately linear character, the ML model is capable of adapting to the different data when it is retrained and thus recovers its initial performance (RMSD of 2.83 ppm). The features from the ECP-PBE0 calculation are therefore not necessarily less suited for use in the ML model.
Analysis of the results for 1H NMR reveals the expected behavior for the more complex circumstances mentioned above. In contrast to 13C, there are significant performance losses if other functionals are used to generate the ML input features. While the initial RMSD of 0.236 ppm for SR-PBE0/ZORA-def2-TZVP is only slightly increased to 0.272 ppm for SR-r2SCAN0, the loss is more drastic for SR-PBE with an RMSD of 0.387 ppm, which is even higher than the RMSD of ECP-PBE0 (0.341 ppm). Apparently, the 1H nucleus is more prone to differences in the input features and the variations between data from different functionals is larger than for 13C NMR. This might, to some extent, originate from the much smaller typical chemical shift range for 1H NMR (about 0–12 ppm) for which deviations of a few tenths of ppm are already substantial. Nonetheless, also for 1H NMR the performance of the original SR-PBE0 method can be recovered when the model is trained on the corresponding data. Thus, RMSDs of 0.240, 0.243, and 0.241 ppm can be achieved for SR-PBE, SR-r2SCAN0, and ECP-PBE0, respectively. Despite the limited number of investigated DFT levels of theory, we feel confident that the presented behaviour of the ΔSO-ML method is of general nature, making it a powerful tool for the low-cost assessment of SO contributions to computed NMR chemical shifts. Even when the base method SR-PBE0 cannot be applied, the ΔSOδ values predicted from lower-level DFT methods are reliable enough for a rough estimation and can serve as diagnostic tool to detect possible severe SO contributions and avoid large computational errors.
3.4 Performance for external test systems
To evaluate the ΔSO-ML method in real-world applications, it was tested on three different sets that are independent from the data set used for training and testing described herein. These are the SnS5111 set containing various organotin compounds and its successor for organolead chemistry115 (Section 3.4.1). In addition, a new set has been compiled for HALA effects on 13C nuclei comprising experimental 13C NMR chemical shifts from structures with all 17 heavy elements included in the training data of the ΔSO-ML method, which we call 17HAC (Section 3.4.2). Finally, the particularly difficult example of a bismabenzene compound is showcased in more detail (Section 3.4.3).The results for 13C NMR are shown in Fig. 8 and segmented into subgroups of atoms with different distances between the heavy and the light atom. It is obvious that in both cases (Sn and Pb), the (virtually costless) ΔSO-ML prediction helps to reduce the relativity-related errors drastically. It stands out that this is especially significant for 13C nuclei directly bound to the HA, which is the clear strength of the method. In the case of organolead compounds, this category undergoes the by far most pronounced HALA effects (RMSD of 29.55 ppm if no SO contribution is included). For 13C nuclei connected to Pb via more than one bond, the initial errors are much smaller due to a notably smaller SO contribution making it more difficult to cover the effect by the correction method. For a distance of three or more bonds, ΔSO-ML does not yield a useful prediction anymore, which, in practice, would not stand out as the average SO contribution of this category (MAD of 2.21 ppm) is below the typical error of DFT in general. The analysis of the organotin compounds suggests a very similar behavior with the main difference that the SO contribution form Sn as HA is generally smaller. Still, the ΔSO-ML method predicts large SO contributions reasonably well and also improved the overall statistics, but the generally smaller ΔSOδ values are lost in the DFT-related noise sooner.
Similar trends are observed for the 1H NMR data, whereas a more pronounced HALA effect on nuclei connected to Sn/Pb via two and three bonds was noticed (see Fig. S9 in the ESI†). However, the overall SO contributions are again significantly smaller so that the ΔSO-ML correction will be less important than the choice of an appropriate density functional in these cases. Nevertheless, it succeeds in predicting large SO contributions in 1H nuclei close to Pb atoms.
| Error metric | SR | +ΔSO-ML | +Δcorr-ML | +Both |
|---|---|---|---|---|
| MAX (<0) | −37.32 | −15.75 | −50.38 | −18.47 |
| MAX (>0) | 112.62 | 73.11 | 104.58 | 61.54 |
| MD | 9.99 | 8.59 | 6.33 | 4.94 |
| MAD | 11.41 | 8.93 | 8.81 | 5.73 |
| RMSD | 20.81 | 12.48 | 18.80 | 9.37 |
The analysis in Table 3 shows that the two Δ-ML corrections tackle different quantities. Upon including the SO effects via ΔSO-ML, the RMSD is reduced drastically, because the focus of the correction lies in detecting large SO-HALA effects which leads to a clear decrease of the large errors in these cases. On the other hand, the Δcorr-ML corrects for a rather systematic correlation-related error which is usually not as large for single cases, but smaller, yet significant, for the majority of the 13C nuclei. Therefore, the RMSD is only slightly reduced, but the MAD is smaller than when only ΔSO-ML is used. Nevertheless, the best results are achieved when both corrections are applied, yielding a roughly halved value for all statistical quantities (MAD reduced by 50%, RMSD by 55%). Hence, a systematic treatment of the typical error sources in the computation of NMR chemical shifts does lead to a systematic decrease of the deviation to experimental data.
| 13C | 1H | ||||
|---|---|---|---|---|---|
| ortho | meta | para | meta | para | |
| Low-level | 241.5 | 147.3 | 121.9 | 8.93 | 7.57 |
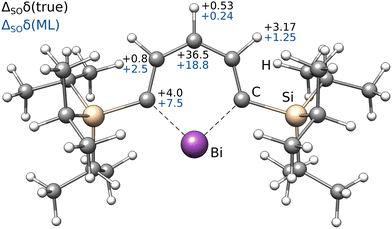
| ΔSOδ (ML) | +7.5 | +2.5 | +18.8 | +1.25 | +0.24 |
| ΔSOδ (true) | +4.0 | +0.8 | +36.5 | +3.17 | +0.53 |
| Δcorrδ (ML) | −13.7 | −2.9 | −4.4 | −0.25 | −0.15 |
| Total (ML/ML) | 235.2 | 147.0 | 136.3 | 9.93 | 7.66 |
| Total (true/ML) | 231.8 | 145.2 | 153.9 | 11.85 | 7.95 |
| Experiment | 222.4 | 136.5 | 153.5 | 11.62 | 7.68 |
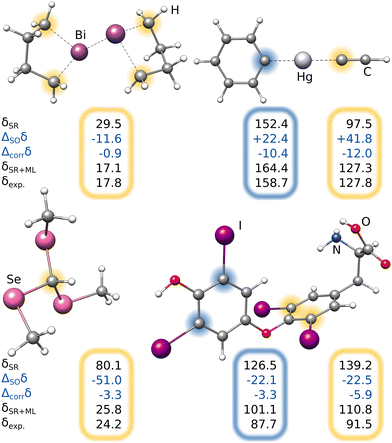
Most importantly, the extreme ΔSOδ value of the para-13C needs to be included in order to achieve a qualitative agreement with the experiment (i.e., δ(13C,meta) < δ(13C,para)). Furthermore, despite being visibly too low for para-13C, the predicted ΔSOδ values are in qualitative agreement with the reference method. Including both ML contributions (SO and corr) does not recover the correct ordering of the chemical shifts, but significantly approaches the experimental results. A similar behavior is observed for 1H NMR with the meta-1H being affected most. Since a satisfying agreeing is not achieved even with including both the true SO contribution and the ML-predicted correlation correction, we attribute the major part of the remaining error to solvation and dynamic effects. Nevertheless, the example of the bismabenzene compound shows that the ΔSO-ML method provides reasonable approximations to the SO contribution to NMR chemical shifts even in potentially unexpected cases.
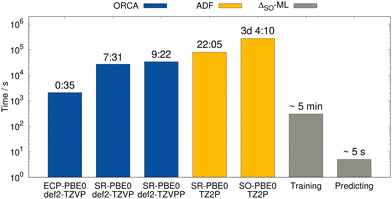
For the lowest-energy conformer of the bismabenzene derivative, timing evaluations were performed at different theory levels (see Fig. 11). While several hours are required using the all-electron SR low-level methods (e.g., PBE0/ZORA-def2-TZVP), the SO reference calculation takes multiple days. In contrast, the training of the ΔSO-ML model lasts a few minutes (for ten training runs for statistical averaging) and the prediction of ΔSOδ is done in seconds on a usual desktop computer. The speed advantage of the presented method is thus evident and it is emphasized that using an ECP-based low-level method has the potential of an even larger speedup with a comparable performance of the ΔSO-ML method.
4 Conclusion
The consideration of relativistic spin–orbit effects for molecules containing heavy atoms is vital for the reliable simulation of their 13C and 1H NMR spectra. This treatment is computationally much more demanding than a non-relativistic calculation and requires non-standard procedures and software, making it less accessible for non-expert users and unsuitable for screening purposes. We presented a machine learning regression-based approach called ΔSO-ML to approximate the SO contribution in 13C and 1H NMR chemical shifts. The underlying data set contains 6388 structures with 17 of the most important heavy elements from group 12 to 17 and NMR calculations at a hybrid DFT level including SO-relativistic treatment via the ZORA technique for 38![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 740 13C and 64
740 13C and 64![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 436 1H NMR chemical shifts. Moreover, the data set can easily be extended by including more diverse structures, e.g., with total charges or further heavy atoms. We showed that the method recovers about 85% of the SO contribution for 13C (70% for 1H) on the test data subset. It is further transferable for use with other density functionals than the base method PBE0 and other approaches for including scalar-relativistic effects, such as ECPs. Since the SO contribution ΔSOδ depends only slightly on the DFA and basis set as shown for heavy atom methyl compounds, the generalizability of the ΔSO-ML method renders it broadly applicable for a wide range of DFT methods with a fairly good accuracy even without retraining the model for other low-level methods. In principle, it is not even limited to DFT, but only needs a method that can provide the required input features. This might be correlated methods such as coupled cluster or semiempirical approaches. Predicting ΔSOδ is done in a few seconds and only requires the converged low-level NMR shielding calculation and the pre-trained ML model, making it superior to other low-cost methods such as linear regression techniques, that are only applicable to special problems.
436 1H NMR chemical shifts. Moreover, the data set can easily be extended by including more diverse structures, e.g., with total charges or further heavy atoms. We showed that the method recovers about 85% of the SO contribution for 13C (70% for 1H) on the test data subset. It is further transferable for use with other density functionals than the base method PBE0 and other approaches for including scalar-relativistic effects, such as ECPs. Since the SO contribution ΔSOδ depends only slightly on the DFA and basis set as shown for heavy atom methyl compounds, the generalizability of the ΔSO-ML method renders it broadly applicable for a wide range of DFT methods with a fairly good accuracy even without retraining the model for other low-level methods. In principle, it is not even limited to DFT, but only needs a method that can provide the required input features. This might be correlated methods such as coupled cluster or semiempirical approaches. Predicting ΔSOδ is done in a few seconds and only requires the converged low-level NMR shielding calculation and the pre-trained ML model, making it superior to other low-cost methods such as linear regression techniques, that are only applicable to special problems.
Off its training and test data set, the method proved powerful for the prediction of SO contributions caused by nearby Sn and Pb atoms in realistic systems. Moreover, a workflow that systematically addresses all main error sources in NMR parameter computation significantly reduces the deviations to experimental data throughout all 17 HAs resulting in an average error reduction by about 50% when both the ΔSO- and Δcorr-ML corrections are applied. If the computational resources allow an explicit treatment of the SO-relativistic effects, the ΔSO-ML method can function as a diagnostic prescreening tool to identify systems with potentially large SO contributions that are subsequently treated on a higher level of theory only if necessary. The potential fields of application of the ΔSO-ML method lie in high-throughput workflows such as structure assignment methods that can be improved when a higher level of theory is used118 and as an additional ingredient in low-cost composite method approaches that rarely include any relativistic treatment.119 To conclude, the new ΔSO-ML method is able to robustly predict SO contributions to NMR chemical shifts for large systems and delivers its full potential when used together with the Δcorr-ML correction in low-cost NMR prediction schemes.
Data availability statement
The implementation of the ΔSO-ML and Δcorr-ML methods as well as the associated data sets can be found at https://github.com/grimme-lab/ml4nmr.Conflicts of interest
There are no conflicts to declare.Acknowledgements
J. B. K. B. is most grateful to the “Fonds der Chemischen Industrie (FCI)” for financial support. S. G. is thankful to the German Research Foundation (DFG) for funding through the SPP 2363: “Utilization and Development of Machine Learning for Molecular Applications – Molecular Machine Learning'”. Further, S. G. and M. B. gratefully acknowledge financial support of the Max Planck Society through the Max Planck fellow program. Open Access funding provided by the Max Planck Society.Notes and references
- A.-H. Emwas, R. Roy, R. T. McKay, L. Tenori, E. Saccenti, G. A. Nagana Gowda, D. Raftery, F. Alahmari, L. Jaremko, M. Jaremko and D. S. Wishart, Metabolites, 2019, 9, 123 CrossRef CAS PubMed.
- D. J. Kubicki, S. D. Stranks, C. P. Grey and L. Emsley, Nat. Rev. Chem., 2021, 5, 624–645 CrossRef CAS PubMed.
- I. Speciale, A. Notaro, P. Garcia-Vello, F. Di Lorenzo, S. Armiento, A. Molinaro, R. Marchetti, A. Silipo and C. De Castro, Carbohydr. Polym., 2022, 277, 118885 CrossRef CAS PubMed.
- C. van Wüllen, in Calculation of NMR and EPR Parameters, ed. M. Kaupp, M. Bühl and V. G. Malkin, Wiley-VCH, Weinheim, 2004, ch. 6, pp. 83–100 Search PubMed.
- A. M. Teale, O. B. Lutnæs, T. Helgaker, D. J. Tozer and J. Gauss, J. Chem. Phys., 2013, 138, 024111 CrossRef PubMed.
- D. Flaig, M. Maurer, M. Hanni, K. Braunger, L. Kick, M. Thubauville and C. Ochsenfeld, J. Chem. Theory Comput., 2014, 10, 572–578 CrossRef CAS PubMed.
- C. van Wüllen, Phys. Chem. Chem. Phys., 2000, 2, 2137–2144 RSC.
- C. J. Schattenberg and M. Kaupp, J. Chem. Theory Comput., 2021, 17, 7602–7621 CrossRef CAS PubMed.
- C. J. Schattenberg, M. Lehmann, M. Bühl and M. Kaupp, J. Chem. Theory Comput., 2022, 18, 273–292 CrossRef CAS PubMed.
- M. Bursch, T. Gasevic, J. B. Stückrath and S. Grimme, Inorg. Chem., 2021, 60, 272–285 CrossRef CAS PubMed.
- J. B. Stückrath, T. Gasevic, M. Bursch and S. Grimme, Inorg. Chem., 2022, 61, 3903–3917 CrossRef PubMed.
- G. L. Stoychev, A. A. Auer and F. Neese, J. Chem. Theory Comput., 2018, 14, 4756–4771 CrossRef CAS PubMed.
- M. W. Lodewyk, M. R. Siebert and D. J. Tantillo, Chem. Rev., 2012, 112, 1839–1862 CrossRef CAS PubMed.
- L. B. Krivdin, Magn. Reson. Chem., 2019, 57, 897–914 CrossRef CAS PubMed.
- L. B. Krivdin, Prog. Nucl. Magn. Reson. Spectrosc., 2019, 112–113, 103–156 CrossRef CAS PubMed.
- Z. Zhang, J. Zhu, S. Chen, W. Sun and D. Wang, Angew. Chem., Int. Ed., 2023, 62, e202215136 CrossRef CAS PubMed.
- K. Chen, Y. Zhang, J. Xiang, X. Zhao, X. Li and K. Chu, ACS Energy Lett., 2023, 8, 1281–1288 CrossRef CAS.
- H. W. Moon and J. Cornella, ACS Catal., 2022, 12, 1382–1393 CrossRef CAS PubMed.
- K. Guan, L. Tao, R. Yang, H. Zhang, N. Wang, H. Wan, J. Cui, J. Zhang, H. Wang and H. Wang, Adv. Energy Mater., 2022, 12, 2103557 CrossRef CAS.
- C. Xiao, W. Song, J. Liang, J. Zhang, Z. Huang, J. Zhang, H. Wang, C. Zhong, J. Ding and W. Hu, J. Mater. Chem. A, 2022, 10, 3667–3677 RSC.
- H. Dong, C. Ran, W. Gao, N. Sun, X. Liu, Y. Xia, Y. Chen and W. Huang, Adv. Energy Mater., 2022, 12, 2102213 CrossRef CAS.
- J. S. Kim, J.-M. Heo, G.-S. Park, S.-J. Woo, C. Cho, H. J. Yun, D.-H. Kim, J. Park, S.-C. Lee, S.-H. Park, E. Yoon, N. C. Greenham and T.-W. Lee, Nature, 2022, 611, 688–694 CrossRef CAS PubMed.
- W. Koch, M. Czop, K. Ilowiecka, A. Nawrocka and D. Wiacek, Nutrients, 2022, 14, 1626 CrossRef CAS PubMed.
- N. Natasha, M. Shahid, I. Bibi, J. Iqbal, S. Khalid, B. Murtaza, H. F. Bakhat, A. B. U. Farooq, M. Amjad, H. M. Hammad, N. K. Niazi and M. Arshad, Sci. Total Environ., 2022, 808, 152024 CrossRef CAS PubMed.
- S. Ruangritchankul, C. Sumananusorn, J. Sirivarasai, W. Monsuwan and P. Sritara, Nutrients, 2023, 15, 322 CrossRef CAS PubMed.
- E. Scarpellini, L. M. Balsiger, V. Maurizi, E. Rinninella, A. Gasbarrini, N. Giostra, P. Santori, L. Abenavoli and C. Rasetti, BioFactors, 2022, 48, 294–306 CrossRef CAS PubMed.
- X. Zheng, B. Ren, X. Li, H. Yan, Q. Xie, H. Liu, J. Zhou, J. Tian and K. Huang, J. Biol. Inorg. Chem., 2020, 25, 1009–1022 CrossRef CAS PubMed.
- M. Schwarz, C. E. Meyer, A. Löser, K. Lossow, J. Hackler, C. Ott, S. Jäger, I. Mohr, E. A. Eklund, A. A. H. Patel, N. Gul, S. Alvarez, I. Altinonder, C. Wiel, M. Maares, H. Haase, A. Härtlova, T. Grune, M. B. Schulze, T. Schwerdtle, U. Merle, H. Zischka, V. I. Sayin, L. Schomburg and A. P. Kipp, Nat. Commun., 2023, 14, 3479 CrossRef CAS PubMed.
- I. A. Gallardo, D. A. Todd, S. T. Lima, J. R. Chekan, N. H. Chiu and E. W. Taylor, Antioxidants, 2023, 12, 559 CrossRef CAS PubMed.
- T. B. Demissie, J. Chem. Phys., 2017, 147, 174301 CrossRef PubMed.
- S. Moncho and J. Autschbach, J. Chem. Theory Comput., 2010, 6, 223–234 CrossRef CAS PubMed.
- Y. Y. Rusakov, I. L. Rusakova and L. B. Krivdin, Int. J. Quantum Chem., 2016, 116, 1404–1412 CrossRef CAS.
- J. Vícha, J. Novotný, S. Komorovsky, M. Straka, M. Kaupp and R. Marek, Chem. Rev., 2020, 120, 7065–7103 CrossRef PubMed.
- B. A. Hess, Phys. Rev. A: At., Mol., Opt. Phys., 1986, 33, 3742–3748 CrossRef CAS PubMed.
- G. Jansen and B. A. Hess, Phys. Rev. A: At., Mol., Opt. Phys., 1989, 39, 6016–6017 CrossRef PubMed.
- W. Kutzelnigg and W. Liu, J. Chem. Phys., 2005, 123, 241102 CrossRef PubMed.
- M. Iliaš and T. Saue, J. Chem. Phys., 2007, 126, 064102 CrossRef PubMed.
- D. Peng, W. Liu, Y. Xiao and L. Cheng, J. Chem. Phys., 2007, 127, 104106 CrossRef PubMed.
- E. van Lenthe, E. J. Baerends and J. G. Snijders, J. Chem. Phys., 1993, 99, 4597–4610 CrossRef CAS.
- E. van Lenthe, J. G. Snijders and E. J. Baerends, J. Chem. Phys., 1996, 105, 6505–6516 CrossRef CAS.
- D. L. Crittenden, Phys. Chem. Chem. Phys., 2022, 24, 27055–27063 RSC.
- A. G. Kutateladze and D. S. Reddy, J. Org. Chem., 2017, 82, 3368–3381 CrossRef CAS PubMed.
- J. S. Smith, O. Isayev and A. E. Roitberg, Chem. Sci., 2017, 8, 3192–3203 RSC.
- T. Zubatiuk, B. Nebgen, N. Lubbers, J. S. Smith, R. Zubatyuk, G. Zhou, C. Koh, K. Barros, O. Isayev and S. Tretiak, J. Chem. Phys., 2021, 154, 244108 CrossRef CAS PubMed.
- D. M. Anstine, R. Zubatyuk and O. Isayev, ChemRxiv, 2023, preprint, DOI:10.26434/chemrxiv-2023-296ch.
- D. Chen, Z. Wang, D. Guo, V. Orekhov and X. Qu, Chem. Eur. J., 2020, 26, 10391–10401 CrossRef CAS PubMed.
- A. Gupta, S. Chakraborty and R. Ramakrishnan, Mach. Learn.: Sci. Technol., 2021, 2, 035010 Search PubMed.
- S. K. Chandy and K. Raghavachari, J. Chem. Theory Comput., 2023, 19, 6632–6642 CrossRef CAS PubMed.
- S. G. Smith and J. M. Goodman, J. Am. Chem. Soc., 2010, 132, 12946–12959 CrossRef CAS PubMed.
- A. Howarth, K. Ermanis and J. M. Goodman, Chem. Sci., 2020, 11, 4351–4359 RSC.
- M. M. Zanardi and A. M. Sarotti, J. Org. Chem., 2015, 80, 9371–9378 CrossRef CAS PubMed.
- M. Ruth, D. Gerbig and P. R. Schreiner, J. Chem. Theory Comput., 2023, 19, 4912–4920 CrossRef CAS PubMed.
- P. Gao, J. Zhang, Q. Peng, J. Zhang and V.-A. Glezakou, J. Chem. Inf. Model., 2020, 60, 3746–3754 CrossRef CAS PubMed.
- P. A. Unzueta, C. S. Greenwell and G. J. O. Beran, J. Chem. Theory Comput., 2021, 17, 826–840 CrossRef CAS PubMed.
- J. B. Kleine Büning and S. Grimme, J. Chem. Theory Comput., 2023, 19, 3601–3615 CrossRef PubMed.
- J. Li, J. Liang, Z. Wang, A. L. Ptaszek, X. Liu, B. Ganoe, M. Head-Gordon and T. Head-Gordon, arXiv, 2023, preprint, arXiv:2306.08269, https://arxiv.org/abs/2306.08269v1 Search PubMed.
- A. Bagno and G. Saielli, Theor. Chem. Acc., 2007, 117, 603–619 Search PubMed.
- T. E. Field-Theodore, M. Olejniczak, M. Jaszunski and D. J. D. Wilson, Phys. Chem. Chem. Phys., 2018, 20, 23025–23033 RSC.
- A. Bagno, F. Rastrelli and G. Saielli, J. Phys. Chem. A, 2003, 107, 9964–9973 CrossRef CAS.
- S. Grimme, A. Hansen, S. Ehlert and J. M. Mewes, J. Chem. Phys., 2021, 154, 064103 CrossRef CAS PubMed.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef CAS.
- C. Adamo and V. Barone, Chem. Phys. Lett., 1998, 298, 113–119 CrossRef CAS.
- E. Van Lenthe and E. J. Baerends, J. Comput. Chem., 2003, 24, 1142–1156 CrossRef CAS PubMed.
- E. Heid, C. J. McGill, F. H. Vermeire and W. H. Green, J. Chem. Inf. Model., 2023, 63, 4012–4029 CrossRef CAS PubMed.
- J. Behler, J. Chem. Phys., 2011, 134, 074106 CrossRef PubMed.
- C. Bannwarth, S. Ehlert and S. Grimme, J. Chem. Theory Comput., 2019, 15, 1652–1671 CrossRef CAS PubMed.
- xTB - Semiempirical Extended Tight-Binding Program Package, Version 6.6.0, Universität Bonn, Mulliken Center for Theoretical Chemistry, Bonn, Germany 2023, https://github.com/grimme-lab/xtb/releases/.
- TURBOMOLE, Version 7.7.1, Universität Karlsruhe & Forschungszentrum Karlsruhe GmbH, Karlsruhe, Germany 2023, https://www.turbomole.org/.
- F. Furche, R. Ahlrichs, C. Hättig, W. Klopper, M. Sierka and F. Weigend, WIREs Comput. Mol. Sci., 2014, 4, 91–100 CrossRef CAS.
- S. G. Balasubramani, G. P. Chen, S. Coriani, M. Diedenhofen, M. S. Frank, Y. J. Franzke, F. Furche, R. Grotjahn, M. E. Harding, C. Hättig, A. Hellweg, B. Helmich-Paris, C. Holzer, U. Huniar, M. Kaupp, A. Marefat Khah, S. Karbalaei Khani, T. Müller, F. Mack, B. D. Nguyen, S. M. Parker, E. Perlt, D. Rappoport, K. Reiter, S. Roy, M. Rückert, G. Schmitz, M. Sierka, E. Tapavicza, D. P. Tew, C. van Wüllen, V. K. Voora, F. Weigend, A. Wodynski and J. M. Yu, J. Chem. Phys., 2020, 152, 184107 CrossRef CAS PubMed.
- J. W. Furness, A. D. Kaplan, J. Ning, J. P. Perdew and J. Sun, J. Phys. Chem. Lett., 2020, 11, 8208–8215 CrossRef CAS PubMed.
- E. Caldeweyher, C. Bannwarth and S. Grimme, J. Chem. Phys., 2017, 147, 034112 CrossRef PubMed.
- K. Eichkorn, O. Treutler, H. Öhm, M. Häser and R. Ahlrichs, Chem. Phys. Lett., 1995, 240, 283–290 CrossRef CAS.
- P. Pracht, F. Bohle and S. Grimme, Phys. Chem. Chem. Phys., 2020, 22, 7169–7192 RSC.
- CREST - Conformer-Rotamer Ensemble Sampling Tool, Version 2.12, Universität Bonn, Mulliken Center for Theoretical Chemistry, Bonn, Germany 2022, https://github.com/crest-lab/crest/releases/.
- S. Spicher and S. Grimme, Angew. Chem., Int. Ed., 2020, 59, 15665–15673 CrossRef CAS PubMed.
- S. Ehlert, M. Stahn, S. Spicher and S. Grimme, J. Chem. Theory Comput., 2021, 17, 4250–4261 CrossRef CAS PubMed.
- S. Grimme, F. Bohle, A. Hansen, P. Pracht, S. Spicher and M. Stahn, J. Phys. Chem. A, 2021, 125, 4039–4054 CrossRef CAS PubMed.
- CENSO - Commandline Energetic Sorting of Conformer-Rotamer Ensembles, Version 1.2.0, Universität Bonn, Mulliken Center for Theoretical Chemistry, Bonn, Germany 2022, https://github.com/grimme-lab/censo/releases/.
- A. Klamt, J. Phys. Chem., 1995, 99, 2224–2235 CrossRef CAS.
- A. Klamt, V. Jonas, T. Bürger and J. C. W. Lohrenz, J. Phys. Chem. A, 1998, 102, 5074–5085 CrossRef CAS.
- F. Eckert and A. Klamt, AIChE J., 2002, 48, 369–385 CrossRef CAS.
- S. Grimme, Chem. – Eur. J., 2012, 18, 9955–9964 CrossRef CAS PubMed.
- S. Spicher and S. Grimme, J. Phys. Chem. Lett., 2020, 11, 6606–6611 CrossRef CAS PubMed.
- S. Spicher and S. Grimme, J. Chem. Theory Comput., 2021, 17, 1701–1714 CrossRef CAS PubMed.
- S. Sinnecker, A. Rajendran, A. Klamt, M. Diedenhofen and F. Neese, J. Phys. Chem. A, 2006, 110, 2235–2245 CrossRef CAS PubMed.
- R. Ditchfield, Mol. Phys., 1974, 27, 789–807 CrossRef CAS.
- K. Wolinski, J. F. Hinton and P. Pulay, J. Am. Chem. Soc., 1990, 112, 8251–8260 CrossRef CAS.
- G. Schreckenbach and T. Ziegler, J. Phys. Chem., 1995, 99, 606–611 CrossRef CAS.
- ORCA - An ab initio, DFT and semiempirical SCF-MO package, Version 5.0.4, Max-Planck-Institut für Kohlenforschung, Mülheim a. d. Ruhr, Germany 2022, https://www.faccts.de/orca/.
- F. Neese, WIREs Comput. Mol. Sci., 2012, 2, 73–78 CrossRef CAS.
- F. Neese, WIREs Comput. Mol. Sci., 2022, 1–15 Search PubMed.
- AMS - Amsterdam Modeling Suite, Version 2022.103, SCM, Vrije Universiteit, Amsterdam, The Netherlands 2022, https://www.scm.com/amsterdam-modeling-suite/.
- S. K. Wolff, T. Ziegler, E. van Lenthe and E. J. Baerends, J. Chem. Phys., 1999, 110, 7689–7698 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- M. Bursch, H. Neugebauer, S. Ehlert and S. Grimme, J. Chem. Phys., 2022, 156, 134105 CrossRef CAS PubMed.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- R. Ahlrichs and K. May, Phys. Chem. Chem. Phys., 2000, 2, 943–945 RSC.
- D. A. Pantazis, X.-Y. Chen, C. R. Landis and F. Neese, J. Chem. Theory Comput., 2008, 4, 908–919 CrossRef CAS PubMed.
- D. A. Pantazis and F. Neese, Theor. Chem. Acc., 2012, 131, 1292 Search PubMed.
- J. D. Rolfes, F. Neese and D. A. Pantazis, J. Comput. Chem., 2020, 41, 1842–1849 CrossRef CAS PubMed.
- D. Andrae, U. Häußermann, M. Dolg, H. Stoll and H. Preuß, Theor. Chim. Acta, 1990, 77, 123–141 CrossRef CAS.
- K. A. Peterson, D. Figgen, E. Goll, H. Stoll and M. Dolg, J. Chem. Phys., 2003, 119, 11113–11123 CrossRef CAS.
- V. Barone and M. Cossi, J. Phys. Chem. A, 1998, 102, 1995–2001 CrossRef CAS.
- F. Neese, F. Wennmohs, A. Hansen and U. Becker, Chem. Phys., 2009, 356, 98–109 CrossRef CAS.
- G. L. Stoychev, A. A. Auer, R. Izsák and F. Neese, J. Chem. Theory Comput., 2018, 14, 619–637 CrossRef CAS PubMed.
- E. van Lenthe, E. J. Baerends and J. G. Snijders, J. Chem. Phys., 1994, 101, 9783–9792 CrossRef CAS.
- M. Krykunov, T. Ziegler and E. van Lenthe, Int. J. Quantum Chem., 2009, 109, 1676–1683 CrossRef CAS.
- A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100 CrossRef CAS PubMed.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS PubMed.
- C. Adamo and V. Barone, J. Chem. Phys., 1998, 108, 664–675 CrossRef CAS.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627 CrossRef CAS.
- D. J. Giesen and N. Zumbulyadis, Phys. Chem. Chem. Phys., 2002, 4, 5498–5507 RSC.
- P. dAntuono, E. Botek, B. Champagne, M. Spassova and P. Denkova, J. Chem. Phys., 2006, 125, 144309 CrossRef PubMed.
- Manuscript in preparation .
- A. A. Auer, J. Gauss and J. F. Stanton, J. Chem. Phys., 2003, 118, 10407–10417 CrossRef CAS.
- T. Ishii, K. Suzuki, T. Nakamura and M. Yamashita, J. Am. Chem. Soc., 2016, 138, 12787–12790 CrossRef CAS PubMed.
- N. Grimblat, M. M. Zanardi and A. M. Sarotti, J. Org. Chem., 2015, 80, 12526–12534 CrossRef CAS PubMed.
- J. Liang, Z. Wang, J. Li, J. Wong, X. Liu, B. Ganoe, T. Head-Gordon and M. Head-Gordon, J. Chem. Theory Comput., 2023, 19, 514–523 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp05556f |
| This journal is © the Owner Societies 2024 |