First principles modeling of composites involving TiO₂ clusters supported on M₂C MXenes

Abstract

First-principles calculations based on density functional theory are performed to investigate the formation of titania/MXene composites taking (TiO₂)₅/M₂C (M = Ti, Zr, Hf, V, Nb, Ta, Cr, Mo, and W) as cases of study. The present systematic analysis confirms a favorable, high exothermic interaction, which promotes important structural reconstructions of the (TiO₂)₅ cluster along with charge transfer from the MXene to titania. MXenes composed of d³ transition metals promote the strongest interaction, deformation energy, and charge transfer, followed by d⁴ and d⁵ M₂C MXenes. We provide evidence that the formation of these (TiO₂)₅/M₂C composites is governed by charge transfer, leading to scaling relationships. By using the electronegativity of the metal composing MXene and the MXene d-band center, we also establish linear correlations that can be used to predict the interaction strength of (TiO₂)₅/M₂C composites just from the knowledge of the MXene composition. It is likely that the present trends hold for other TiO₂/MXene composites.

---

1. Introduction

During recent decades, the relationship between semiconducting transition metal oxides (TMOs) and photocatalysis has been a topic of high interest in the scientific community, especially since the seminal paper published by Fujishima and Honda in 1972.¹ Shortly, a photon of appropriate energy, ideally from sunlight, can be used to activate a catalyst generating electron–hole pairs to drive redox reactions.^2,3 This solar-to-chemical energy transformation induced by semiconducting materials forms the basis of the so-called heterogeneous photocatalysis which plays an important role in a broad range of applications including microorganism inactivation, degradation of pollutants, water splitting, or CO₂ photoreduction among others.^4–7 Different semiconducting materials such as WO₃, ZnO and TiO₂ have been investigated as suitable photocatalysts, with the latter being the most broadly studied candidate.^8–11 However, the full potential of this technology is still limited because of the too wide band gap of these materials—3.0 to 3.2 eV in the case of TiO₂—and fast electron–hole recombination. These drawbacks seriously limit the activation of the semiconductor under sunlight and promote low photoactivity.^12–14

One proven strategy to enhance the photoactivity of a semiconductor is to integrate a new component. This is expected to facilitate charge carriers’ separation by forming an interface with the semiconducting photocatalyst. Also, the new component can participate as an active site for the surface reaction. Experimental and computational studies have proposed both metals (Pt, Pd, Ru, Ag, and Au)^15–19 and nonmetals (C and N)^19–22 as new constituents to anchor over or dope nanostructured TiO₂ materials. The resulting systems show relative photocatalytic activity improvement due to the longer charge carrier lifetimes. In this quest for robust photocatalysts with superior charge carrier separation, low dimensional carbides and/or nitrides (called MXenes)²³ appear as suitable candidates to generate hybrid catalysts together with TMOs to overcome the aforementioned limitations.²⁴

MXenes exhibit a M_n+1X_nT_x general chemical formula where M stands for early transition metals, X corresponds to carbon and/or nitrogen elements, and T_x represents the terminal groups of MXene (i.e., OH, H, O, or F) derived from the top-down synthesis taking MAX phases as a precursor. Finally, n denotes the thickness of the MXene in terms of atomic layers and runs from 1 to 3. MXenes have shown to be versatile materials in a broad landscape of applications, including catalysis.^25–30 In the realm of photocatalysis, a series of photoactive MXene-based compounds have been proposed as promising photocatalysts for efficient CO₂ reduction, and H₂ generation through water splitting.^24,31–33

Concerning TiO₂/MXene composites, several experimental studies have been reported.^34–38 These studies show that the use of MXenes as co-catalysts could improve the photocatalytic activity compared to the use of isolated semiconductors as titania. One important aspect of such improvement resides in the interface contact type between both cocatalysts. A Schottky barrier formed at the interface prevents the back diffusion of the electrons, thus, preventing charge recombination of photogenerated electrons.

Instead of these reports, the interfacial structure and electronic properties of these composites remain largely unknown. Thus, theoretical analyses are necessary to identify and rationalize the structural and electronic aspects that could contribute to the enhancement of catalytic performance,³⁹ and prior further theoretical studies regarding their reactivity in heterogeneous or photocatalytic reactions on these systems can be undertaken. Using extended periodic models, Xu and coauthors investigated the interfacial properties of Ti_n+1C_nT_x/TiO₂ (n = 1, 2) heterostructures including O, OH, and F as T_x termination, and selected the (101) surface to represent the slab model of anatase TiO₂.⁴⁰ This study revealed the strong dependence of the interfacial interaction and properties of the TiO₂/MXene heterostructures on the surface composition of the MXene. One step further was recently carried out by us investigating the TiO₂/MXene composites but considering nanostructured TiO₂ systems, (TiO₂)₅ and (TiO₂)₁₀ clusters, supported on a bare Ti₂C surface.⁴¹ A remarkable exothermic interaction was reported, accompanied by significant deformation of the adsorbed titania clusters and substantial charge transfer from the MXene towards the TiO₂ clusters. Nevertheless, all the heterostructures described so far, both theoretically and experimentally, involved only Ti-based MXenes as the substrate and a comprehensive study comparing the effect of other transition metals composing MXenes on the supported TiO₂ cluster is missing. Thus, we focus here on a systematic computational analysis to gain further knowledge of the effects of MXene composition on the structural and electronic properties of TiO₂/MXene composites. To this end, we select bare M₂C (0001) MXenes (M = Ti, Zr, Hf, V, Nb, Ta, Cr, Mo, and W) as substrates to support a (TiO₂)₅ cluster.

2. Computational details

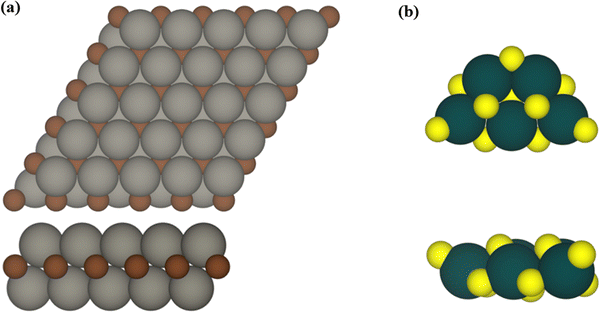
The influence of MXene composition when forming TiO₂/MXene composites was investigated by considering extended M₂C (M = Ti, Zr, Hf, V, Nb, Ta, Cr, Mo, and W) MXene slabs exposing the (0001) surface with ABC stacking as depicted in Fig. 1. From a synthetic point of view, MXenes are generated using a top-down procedure using MAX phases as precursors. This involves chemical etching of the A-element in the MAX phase and further sonication to separate the generated MXenes exposing the basal (0001) surface. The (TiO₂)₅ titania cluster was selected as a representative example to study the interaction with the different MXene surfaces. The (TiO₂)₅ cluster was chosen as it provides a good representative model for experimental composites and a suitable theoretical case to study the chemical bonding in these systems. This selection was based on previous work on the (TiO₂)₅/Ti₂C composite⁴¹ which constitutes an appropriate guide to compare both studies. The atomic structure of the gas phase (TiO₂)₅ cluster used as a reference was obtained using global optimization methods and exhibits the lowest energy in the potential energy surface (PES), see Fig. 1.^42,43 An efficient analysis of the interacting landscape was carried out by generating different conformations by rotating the (TiO₂)₅ nanocluster over the M₂C (0001) MXene surfaces. This screening procedure where a rotational angle α covers a 140° range with a step of 10° and guarantees a thorough assessment of PES attending to the inherent hexagonal symmetry exposed by the MXene slab models. Further details are described in ref. 41.

Fig. 1 Top (top) and side (bottom) views of (a) the p(5 × 5) supercell model of the (0001) M₂C MXene structure with an ABC stacking and (b) planar (TiO₂)₅ cluster. Gray and brown spheres represent transition metal M (M = Ti, Zr, Hf, V, Nb, Ta, Cr, Mo, and W) and C atoms in the M₂C (0001) MXene surface, while yellow and dark green spheres stand for oxygen and titanium atoms of the titania cluster, respectively.

The structural, electronic, and bonding properties of the (TiO₂)₅/M₂C composites were investigated using periodic density functional theory (DFT) based calculations as implemented in the Vienna Ab Initio simulation package (VASP).^44,45 Here, the Kohn–Sham equations are numerically solved using a plane wave basis set to expand the valence electron density with a kinetic energy cut-off of 415 eV. To account for the interaction between the core and valence electron density, the projector augmented wave (PAW) method was used.⁴⁶ The generalized gradient approximation (GGA) Perdew–Burke–Ernzerhof (PBE) exchange correlation density functional was selected to pursue the geometry optimizations.⁴⁷ PBE stands out as a widely recognized and broadly used DFT functional in computational materials science for its ability to accurately depict metallic systems, so it effectively characterizes the structural parameters of MXenes. To properly study the (TiO₂)₅/M₂C composites, a p(5×5) M₂C MXene supercell was selected as it is sufficiently large to minimize the lateral interactions between the periodically repeated titania clusters. A vacuum space of 18 Å along the direction normal to the MXene (0001) surface was included to prevent artificial electrostatic interactions between interleaved composite replicas. Given the rather large size of this supercell, calculations were carried out at the Γ k-point only.⁴⁸ The convergence threshold for the electronic self-consistent field (SCF) calculations was established at 10⁻⁵ eV, and the structural optimization was reached when atomic forces were below 10⁻² eV Å⁻¹.

First, we analyzed the thermodynamic stability of the (TiO₂)₅/M₂C (M = Ti, Zr, Hf, V, Nb, Ta, Cr, Mo, and W) composites based on the adsorption energy, E_ads. This provides a measure of the exothermicity arising from supporting the (TiO₂)₅ cluster over the MXene (0001) surface, and is defined as:

E_ads = E_(TiO2)5/M2C − E_M2C − E_(TiO2)5, (1)

where E_(TiO2)5/M2C, E_M2C, and E_(TiO2)5 correspond to the total energies of the (TiO₂)₅/M₂C composite, the bare (0001) M₂C MXene, and the gas phase (TiO₂)₅ cluster, respectively. Accordingly, (TiO₂)₅/M₂C composite is thermodynamically stable when E_ads < 0. Dispersion corrections were not considered because the interaction is clearly dominated by much stronger chemical interactions, as already discussed⁴¹ and also commented on later.

The composite formation induces a deformation of its (0001) M₂C MXene and (TiO₂)₅ cluster components relative to their isolated configurations, and this energy cost is compensated by the interaction strength, leading to the adsorption process. Therefore, one can define the deformation energy, E_def, of either M₂C or (TiO₂)₅, and adhesion energy, E_adh, all defined as;

E_def(X) = E^sp_X − E_X, (2)

E_adh = E_ads − E_def(TiO2) − E_def(Ti2C), (3)

where E^sp_X stands for the energy of the adsorbed geometry of X = M₂C or (TiO₂)₅ systems, and E_X represents the energy of the isolated components, as defined in eqn (1). The E^sp_X term is obtained from a single-point (sp) calculation at the geometry at the adsorbed conformation removing the other component. On one hand, the E_def(X) describes the energy required to deform any of the involved systems from its optimal structure, while, on the other hand, E_adh quantifies the interaction strength between the deformed fragments, bonded in a lock-key fashion. The more negative E_adh is, the stronger the interaction.

Furthermore, a topological analysis of the electron density was carried out based on the quantum theory of atoms-in-molecules proposed by Bader,⁴⁹ using the VASP-linked code developed by Henkelman et al.⁵⁰ The charge transfer analysis was carried out by quantifying the total number of electrons in each structure in its gas phase and composite conformations. Furthermore, the charge density difference (CDD), and its plane-averaged (PA-CDD) counterpart along the normal direction were also computed as:

Δρ = ρ_(TiO2)5/M2C − ρ_M2C − ρ_(TiO2)5, (4)

where Δρ corresponds to the CDD while, ρ_(TiO2)5/M2C, ρ_M2C, and ρ_(TiO2)5 represent the charge density of (TiO₂)₅/M₂C, M₂C, and (TiO₂)₅, respectively. The analysis of the chemical bond via CCD and PA-CCD provides an eye-catching view of the electron transfer between the components constituting the titania/MXene composites. The command-line VASPKIT program⁵¹ was used to determine the work function, Φ, for bare M₂C MXenes, which involves subtracting the Fermi energy value, E_F, from the electrostatic average potential energy in the vacuum. Finally, additional test caluclations with spin polarization showed that the magnetica moment in Ti₂C, Zr₂C, and Hf₂C composites vanishes which is in line with results the O- or OH-terminated MXenes.

3. Results and discussion

We start this section by discussing in detail the trends of energetic features, i.e., adsorption, adhesion, and deformation energies. Next, we continue with the rationalization of these properties based on the chemical bonding analysis as the charge transfer, the CCD and PA-CDD. Finally, we will propose useful scaling relationships allowing one to establish the structural and bonding properties that govern the formation of titania/MXene composites.

3.1. Energetic stability of (TiO₂)₅/M₂C composites

Exploration of the potential energy surface (PES) of (TiO₂)₅/M₂C systems is carried out by computing the interaction energy, this is, the E_ads, between the (TiO₂)₅ nanocluster over the p(5×5) M₂C (M = Ti, V, Cr, Zr, Nb, Mo, Hf, Ta, and W) MXene supercell (cf.Fig. 1). This interacting process is systematically simulated by rotating the (TiO₂)₅ nanocluster over each M₂C (0001) surface by varying the rotational angle as mentioned above, following a previous scheme recently used in the analysis of (TiO₂)_n/Ti₂C (n = 5 and 10) and titania/titania interfaces.^41,52 Due to the hexagonal symmetry of the MXene, analogous interacting conformations are expected to be found by shifting the titania cluster in the xy plane. See the ESI† for further details.

Table 1 compiles the computed energy values defined by eqn (1)–(3) for the most stable configuration of each (TiO₂)₅/M₂C composite. To avoid misunderstanding, we focus initially on the most stable configurations taking the most exothermic cases (i.e., largest E_ads) for each composite (cf.Table 1). The complete analysis for all plausible conformations in each MXene surface is listed in Tables S1–S9 of the ESI.† First, E_ads indicates an exothermic interaction ranging from −10.12 to −16.99 eV. The composition of the MXene surface promotes different adsorption energies. Indeed, the formation of (TiO₂)₅/M₂C composites is the most exothermic over an MXene surface involving d³ transition metals (M = Ti, Zr, and Hf) with E_ads values of −16.76, −16.78, and −16.99 eV, respectively. On the other hand, we find MXene surfaces composed of d⁵ transition metals (M = Cr, Mo, and W) expose the lowest, yet quite large, exothermicity with E_ads values of −12.59, −10.12, and −10.37 eV, respectively. Finally, the MXenes composed of d⁴ transition metals (M = V, Nb, and Ta) present E_ads values with energies between both extremes with values of −13.47, −13.08, and −14.11 eV, respectively. Attending to the location of the transition metal in the periodic table, one can capture some trends in E_ads. In turn, the adsorption energy becomes less favorable when moving through the period. This indicates that the MXene surface reduces its reactivity with the titania cluster as the number of d electrons increases. This is consistent with the trends reported when M₂C MXenes are used as template generating single-atom catalysts (SACs).⁵³

Table 1 Adsorption (E_ads), adhesion (E_adh), and deformation (E_def) energies (in eV) of (TiO₂)₅/M₂C composites, respectively. Note that the two E_def different sets of data correspond to the M₂C (0001) MXene surface and the (TiO₂)₅ cluster, respectively. Charge transfer of (TiO₂)₅, ΔQ, given in e, and the work function of M₂C, Φ, given in eV, are also included. Only the most stable composite atomic configuration is included, represented by the largest E_ads. Further details are found in the ESI

M2C	E ads	E adh	E def M2C	E def (TiO2)5	ΔQ	Φ
Ti2C	−16.76	−36.95	2.21	17.98	−6.02	4.34
Zr2C	−16.78	−36.03	1.06	18.19	−6.08	4.09
Hf2C	−16.99	−37.06	0.89	19.18	−6.62	4.29
V2C	−13.47	−27.89	0.71	13.71	−4.15	4.40
Nb2C	−13.08	−23.48	0.91	9.49	−3.53	4.26
Ta2C	−14.11	−25.40	1.09	10.19	−3.66	4.59
Cr2C	−12.59	−24.95	1.57	10.79	−3.48	4.71
Mo2C	−10.12	−18.52	1.03	7.37	−2.34	4.99
W2C	−10.37	−17.62	1.76	5.49	−2.04	4.93

---

The E_adh follows a similar trend as E_ads, see Table 1, running from −17.62 to −37.06 eV. Again, the most reactive MXenes are those involving d³ metals with the largest E_adh followed by d⁴ and d⁵ metal ones. In turn, this adhesion energy is directly related to the deformation energy (E_def) of the (TiO₂)₅ cluster and the M₂C (0001) surface that takes place during the formation of titania/MXene composites as listed in Table 1. Here, one can readily see that the formation of (TiO₂)₅/M₂C composites affects in a different way to the structural framework of each constituent. Starting with the M₂C (0001) MXene surface, its E_def is relatively low and ranges in value between 2.21 and 0.71 eV only. On the other hand, one can see that this E_def is significantly larger for the (TiO₂)₅ nanocluster with values encompassing values between 5.49 and 19.18 eV. Clearly, the (TiO₂)₅ cluster always shows the largest deformation when a composite system is formed. Indeed, a quite linear trend emerges (R = 0.78) when plotting E_adsversus E_def (TiO₂)₅ as depicted in Fig. 2. Here, three different regions are delimited: (i) high E_def and E_ads; (ii) intermediate E_def and E_ads; and (iii) low E_def and E_ads, corresponding to titania/MXene composites where the MXene (0001) surface is composed of d³, d⁴, and d⁵ transition metal. In short, the formation of titania/MXene composites induces a large reconstruction of the titania cluster.

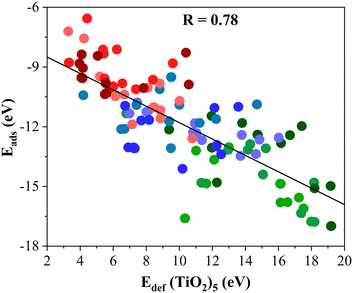Fig. 2 Linear trend between the E_ads of (TiO₂)₅/M₂C composites and E_def (TiO₂)₅. The solid black line is the linear correlation between both quantities where R stands for the regression coefficient between them. The spheres colors are consistent with the colored spheres of the metal atom in the MXene surface, depicted in Fig. 3. Linear fitting analysis is reported in Table S12 of the ESI.†

From a structural point of view, the fully relaxed geometries of the most exothermic configurations of each composite before and after adsorption are presented in Fig. 1 and 3, respectively. Fig. 3 clearly and consistently shows a deformation of titania clusters upon adsorption over M₂C (0001) surfaces, in agreement with the above analyzed deformation energies. In fact, titania clusters are adsorbed in equivalent positions over M₂C composed of d³ and d⁴ metals according to the inherent hexagonal symmetry of M₂C (0001) surfaces and seem to follow the ABC MXene stacking. Despite titania clusters being adsorbed in different positions over M₂C involving d⁵ metals, all titania clusters, regardless of the M₂C metal composition, present O atoms in contact with the M₂C surfaces occupying the high-symmetry adsorption sites (mainly hollow ones) upon adsorption. Indeed, some O atoms change plane in the cluster to maximize the number of contacts between the cluster and the surfaces and occupy the mentioned sites. Further structural analysis concerning atomic distances and angles are reported in Fig. S1 of the ESI.† The initial geometry found in the gas phase configuration of the (TiO₂)₅ cluster is lost when it is anchored on the MXene support.

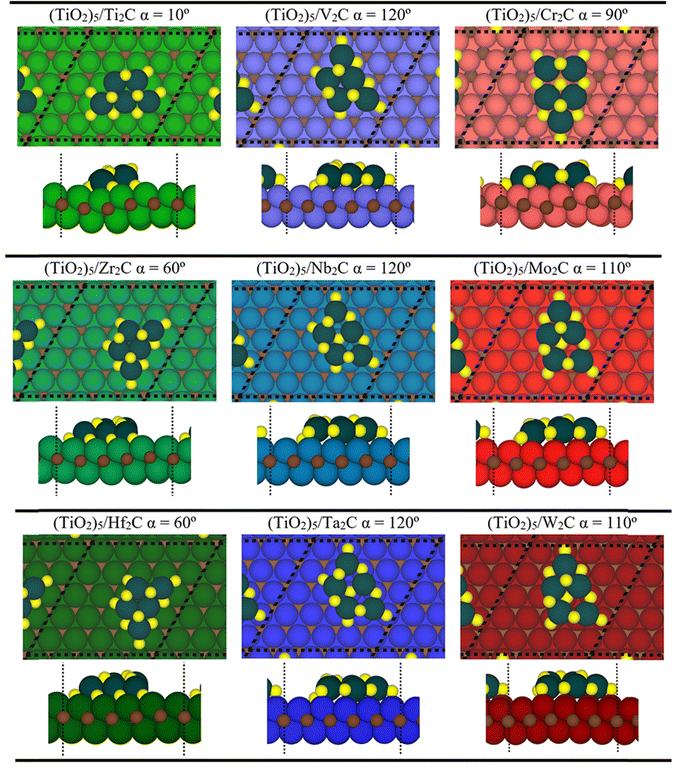Fig. 3 Top (top) and side (bottom) views of the optimized geometries of p(5×5) (dashed black line) (TiO₂)₅/M₂C composite structures. Note that these structures correspond to the most stable configuration for each (TiO₂)₅/M₂C. The color scheme of the C atom and (TiO₂)₅ cluster is the same as in Fig. 1. The green, blue, and red colors denote M atoms of groups IV, V, and VI, respectively, where light, solid, and darker shades imply 3d, 4d, or 5d series, respectively.

3.2. Chemical bonding analysis of (TiO₂)₅/M₂C composites

To gain further insight into the formation of titania/MXene composites depicted in Fig. 3, we conduct a topological analysis of the electron density to obtain Bader charges, and analyze CDD and PA-CDD plots, to investigate electron transfer between the components. Table 1 compiles ΔQ of the supported (TiO₂)₅ cluster resulting from Bader analysis. These data correspond to the most stable configuration for each MXene, while data for other configurations are reported in the ESI.† The ΔQ values in Table 1 represent the difference between the net charge on the titania nanocluster before and after adsorption. Since the isolated titania cluster is neutral, a negative ΔQ means the electron accumulation on the supported titania nanocluster. Thus, ΔQ < 0 implies an electron density excess on the supported cluster resulting from electron transfer from the M₂C (0001) MXene surface towards the (TiO₂)₅ cluster. This electron excess is likely to promote the activation of the supported particle although further work involving study of the reactivity of the supported cluster is required to confirm this hypothesis. The electron density flow towards the titania cluster is systematically observed in all possible configurations regardless of the MXene composition, see Tables S1–S9 in the ESI.† ΔQ runs between −2.04 and −6.62 e and follows a similar trend as observed in E_ads, confirming that a large adsorption energy is coupled with a large charge transfer, as shown in Fig. 4. The electron density accumulation at or near the (TiO₂)₅ cluster is accompanied by electron density depletion at the MXene surface. Usually, the excess electron density of an adsorbate results in structural changes. The case of the CO₂ molecule interacting with MXenes is a clear example as the electron transfer towards CO₂ promotes a considerable bending of the adsorbed molecule.^54,55 To explore this effect in more detail, Fig. 5 plots E_def (TiO₂)₅vs. ΔQ of the supported titania cluster. This plot exhibits a quite clear linear trend (R = 0.91) that the charge transfer is the driving force that promotes the titania cluster deformation.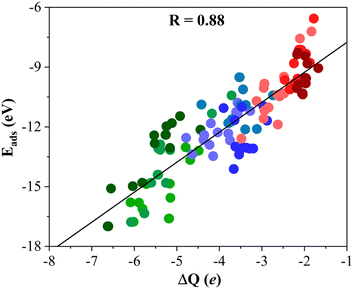

Fig. 4 Linear trend between E_ads and ΔQ of the titania cluster. The solid black line is the linear correlation between both quantities, and R stands for the regression coefficient. Color-coding as in Fig. 3. Linear fitting analysis is reported in Table S12 of the ESI.†

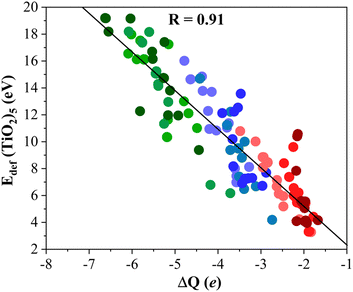Fig. 5 Linear correlation between E_def (TiO₂)₅ and ΔQ. Solid black line is the linear correlation between both quantities, while R stands for the linear correlation regression coefficient. Color coding as in Fig. 3. Linear fitting analysis is reported in Table S12 of the ESI.†

In addition, the CDD and the PA-CDD plots along the surface normal direction are presented in Fig. 6 for the most favorable composites (see Table 1 and Fig. 3). These plots complement the Bader analysis as they provide a visualization of the charge rearrangement induced by the formation of the composites. In all cases, a depletion of charge density is observed at the MXene M atoms and accumulation, at the Ti atoms from the (TiO₂)₅ cluster, consistent with previous work.⁴¹ The inset CDD plots in Fig. 6 show a clear redistribution of the electron density in the interface region. Altogether, both plots demonstrate that the electron density is mainly depleted in the MXene while it mainly accumulates in the (TiO₂)₅ cluster, in agreement with Bader charges. The strong charge transfer from MXene towards the (TiO₂)₅ cluster implies a high contribution of ionic bonding, however, the DOS projected per atomic orbital from Fig. S2 in the ESI† also shows a large mixing of orbitals, in this case, typical of a covalent bond. These two facts allow us to conclude that the chemical bond can be described as a mixture of covalent and ionic bonding. Furthermore, this electron transfer from the M₂C MXene to (TiO₂)₅ clusters could generate a build-in electric field near the interface that can be beneficial in photocatalytic applications acting as a separator of charge carriers.⁵⁶

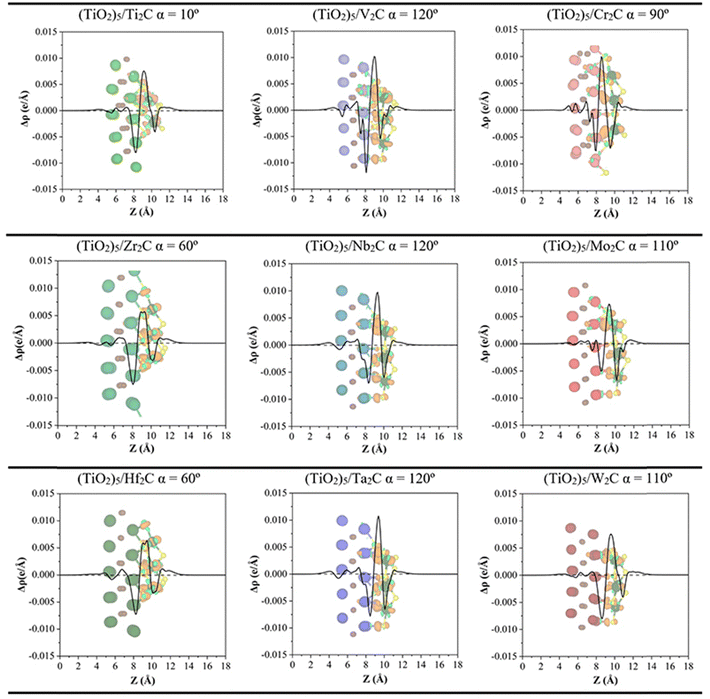Fig. 6 Plane-averaged charge density difference (PA-CDD) Δρ along the direction normal to the MXene surface, Z, for the most stable configurations of M₂C/(TiO₂)₅ as listed in Table 1. Charge density differences, CDD, with an isosurface value of 0.015 e Å⁻³, are depicted inset where pale green and orange isosurfaces correspond to accumulation and depletion charges, respectively. Color coding as in Fig. 3.

Further analysis is performed through the investigation of the work function, Φ, of each M₂C MXene. One would, in general, expect that the lower the Φ, the easier the electron donation to the adsorbed titania cluster. Looking at the results reported in Table 1, the MXenes with the lowest Φ correspond to those composed of d³ transition metals followed by d⁴ and d⁵ ones. Indeed, the emerging trends when plotting E_ads or E_def (TiO₂)₅versus Φ (cf.Fig. 7a and b) are analogous to those in Fig. 4 and 5. This is also consistent with the plot of Φ versus ΔQ in Fig. 7c indicating that, as expected, the electron transfer increased when Φ decreased, indeed with a relatively high regression coefficient, R, of 0.83.

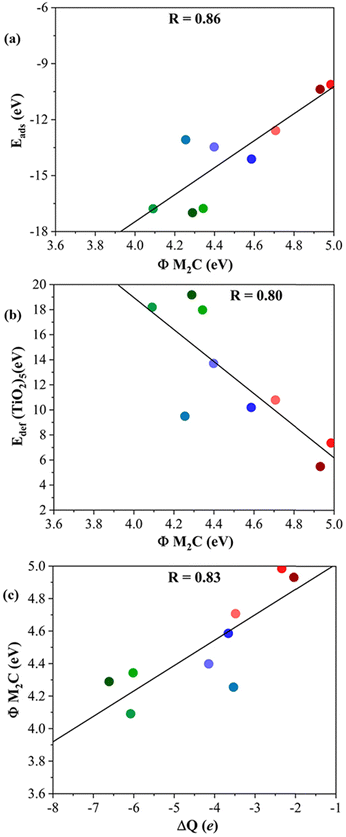Fig. 7 (a) E_adsvs. the work function, Φ, of bare (0001) MXene surfaces; (b) E_def (TiO₂)₅vs. Φ M₂C; and (c) Φ M₂C vs. ΔQ of (TiO₂)₅. The solid black lines correspond to the linear fitting associated with the regression coefficient, R. Color coding as in Fig. 3. Linear fitting analysis is reported in Table S12 of the ESI.†

3.3. Generalized trends of (TiO₂)₅/M₂C composites

The main structural differences of these composites reside in the metal of the MXene. Hence, it is logical to investigate descriptors characteristic of transition metals such as the metal atom electronegativity, χ_M and the d-band center, ε_d, of the metal in the MXene structure.⁵⁷ In particular, we focus on whether these descriptors would help tentatively predict the E_ads and the E_def (TiO₂)₅ of a given M₂C MXene. Fig. 8 shows clear linear correlations associated with the most favorable (TiO₂)₅/M₂C composites listed in Table 1. Starting with the χ_M descriptor (cf.Fig. 8a and b), the adsorption energy increases as χ_M decreases. Thus, MXenes involving a d³ transition metal interact more strongly with the (TiO₂)₅ cluster than those MXene composed of d⁴ or d⁵ metal. This is consistent with the large E_def (TiO₂)₅ observed in MXene composed of d³ metals. In summary, we can conclude that (TiO₂)₅/M₂C composites involving transition metals with a relatively low χ_M will exhibit a large exothermic interaction between the two constituents and a large structural modification on the (TiO₂)₅ nanoclusters.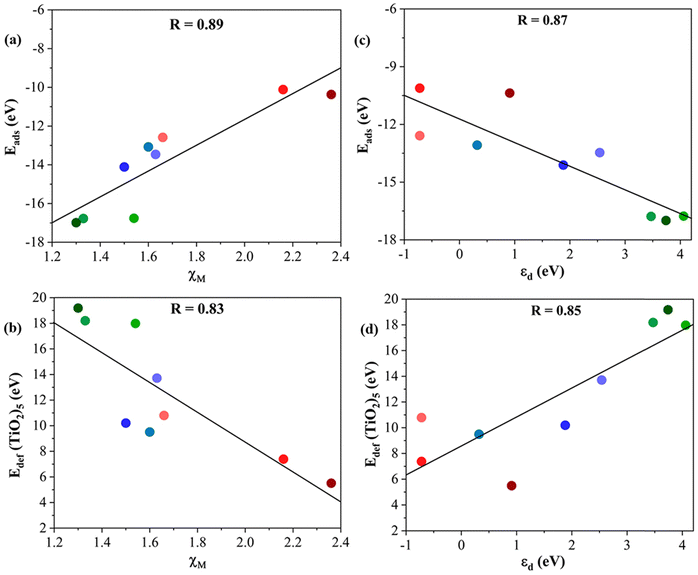

Fig. 8 Tentative linear correlations of (a) E_adsvs. χ_M, (b) E_def (TiO₂)₅vs. χ_M, (c) E_adsvs. ε_d, and (d) E_def (TiO₂)₅vs. ε_d. The linear regression coefficient, R, is given in the inset in each panel. Color coding as in Fig. 3. Linear fitting analysis is reported in Table S12 of the ESI.†

The trends corresponding to the second analyzed descriptor, ε_d, are depicted in Fig. 8c and d which also exhibit a reasonable linear trend. In general, MXenes involving a transition metal with a high ε_d lead to large exothermic adsorption energy and large deformation energy on (TiO₂)₅ nanoclusters. Based on the aforementioned analysis, χ_M and ε_d can be considered feasible descriptors to predict the formation of titania/MXene composites based on the MXene composition.

4. Conclusions

The formation of titania/MXene composites obtained by supporting a (TiO₂)₅ cluster on the basal surface of M₂C MXenes with M = Ti, Zr, Hf, V, Nb, Ta, Cr, Mo, and W has been investigated by means of periodic DFT based calculation on appropriate supercells. The present results systematically show a highly exothermic adsorption energy. The MXenes involving d³ metals (Ti, Zr, and Hf) have the largest interaction followed by d⁴ (V, Nb, Ta) and d⁵ (Cr, Mo, and W) metals. The composite formation involved an important change in the atomic structure of the supported (TiO₂)₅ cluster, relative to the most stable gas phase conformation in such a way that the largest adsorption promotes the largest deformation. The analysis of Bader charge and CDD plots shows a clear electron transfer from the MXene towards the (TiO₂)₅ cluster. The accumulation of electron density in the supported (TiO₂)₅ cluster is at the origin of its deformation.

These systematic trends are rationalized using the MXene work function, the electronegativity of the metal atom, and the d-band center of the metal in the MXene. MXenes with a low work function are those that show high adsorption energy with a concomitant high deformation energy of the (TiO₂)₅ cluster and a large electron transfer. MXenes composed of metals with low electronegativity show high adsorption energies including the high deformation energy of the (TiO₂)₅ nanocluster and high electron transfer. Finally, the higher the d-band center of the metal in the MXene, the higher the adsorption and deformation energies and also the electron transfer. Finally, it has been shown that features of the metal element in the MXene can be used to predict trends in the interaction and in the extent of electron transfer when forming titania/MXene composites, valuable information for experimentalists interested in the synthesis, properties, and possible applications of these composites.

Data availability

The data supporting this article have been included as part of the ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This study has been supported by the Spanish Ministerio de Ciencia e Innovación and Agencia Estatal de Investigación (AEI) MCIN/AEI/10.13039/501100011033 through projects PID2020-115293RJ-I00, PID2021-126076NB-I00, TED2021-129506B-C22, la Unidad de Excelencia María de Maeztu CEX2021-001202-M granted to the IQTCUB and, in part, from COST Action CA18234, and Generalitat de Catalunya 2021SGR00079. N. G.-R. thanks the Generalitat de Catalunya for a predoctoral contract 2022 FISDU 00106. F. V. is thankful for the ICREA Academia Award 2023 Ref. Ac2216561.

References

1. A. Fujishima and K. Honda, Nature, 1972, 238, 37–38.
2. N. Serpone and A. V. Emeline, J. Phys. Chem. Lett., 2012, 3, 673–677.
3. B. Samanta, Á. Morales-García, F. Illas, N. Goga, J. A. Anta, S. Calero, A. Bieberle-Hütter, F. Libisch, A. B. Muñoz-García, M. Pavone and M. C. Toroker, Chem. Soc. Rev., 2022, 51, 3794–3818.
4. P. K. J. Robertson, J. M. C. Robertson and D. W. Bahnemann, J. Hazard. Mater., 2012, 211–212, 161–171.
5. D. Zhu and Q. Zhou, Environ, Nanotechnol. Monit., 2019, 12, 100255.
6. T. Hisatomi and K. Domen, Nat. Catal., 2019, 2, 387–399.
7. X. Jiao, K. Zheng, L. Liang, X. Li, Y. Sun and Y. Xie, Chem. Soc. Rev., 2020, 49, 6592–6604.
8. E. Kozlova, A. Safatov, S. Kiselev, V. Y. Marchenko, A. Sergeev, M. Skarnovich, E. Emelyanova, M. Smetannikova, G. Buryak and A. Vorontsov, Environ. Sci. Technol., 2010, 44, 5121–5126.
9. Y. Li, Y.-K. Peng, L. Hu, J. Zheng, D. Prabhakaran, S. Wu, T. J. Puchtler, M. Li, K.-Y. Wong and R. A. Taylor, Nat. Commun., 2019, 10, 4421.
10. A. Shahzad, K. Rasool, M. Nawaz, W. Miran, J. Jang, M. Moztahida, K. A. Mahmoud and D. S. Lee, Chem. Eng. J., 2018, 349, 748–755.
11. Y. Zhao, N. Liu, S. Zhou and J. Zhao, J. Mater. Chem. A, 2019, 7, 16294–16303.
12. D. O. Scanlon, C. W. Dunnill, J. Buckeridge, S. A. Shevlin, A. J. Logsdail, S. M. Woodley, C. R. A. Catlow, M. J. Powell, R. G. Palgrave and I. P. Parkin, Nat. Mater., 2013, 12, 798–801.
13. M. A. Henderson, Surf. Sci. Rep., 2011, 66, 185–297.
14. Y. Yamada and Y. Kanemitsu, Appl. Phys. Lett., 2012, 101, 133907.
15. R. Reichert, Z. Jusys and R. J. Behm, J. Phys. Chem. C, 2015, 119, 24750–24759.
16. X. Wang, Y. Ruan, S. Feng, S. Chen and K. Su, ACS Sustainable Chem. Eng., 2018, 6, 11424–11432.
17. Y. Chen, Ll Soler, C. Cazorla, J. Oliveras, N. G. Bastús, V. F. Puntes and J. Llorca, Nat. Commun., 2023, 14, 6165.
18. M. Allès, E. R. Remesal, F. Illas and Á. Morales-García, Adv. Theory Simul., 2023, 10, 2200670.
19. C. Di Valentin, E. Finazzi, G. Pacchioni, A. Selloni, S. Livraghi, M. C. Paganini and E. Giamello, Chem. Phys., 2007, 339, 44–56.
20. E. R. Remesal and Á. Morales-García, Phys. Chem. Chem. Phys., 2022, 24, 21381–21387.
21. E. R. Remesal, Á. Morales-García and F. Illas, J. Phys. Chem. C, 2023, 127, 20128–20136.
22. C. Di Valentin, G. Pacchioni, A. Selloni, S. Livraghi and E. Giamello, J. Phys. Chem. B, 2005, 109, 11414–11419.
23. M. Naguib, M. Kurtoglu, V. Presser, J. Lu, J. Niu, M. Heon, L. Hultman, Y. Gogotsi and M. W. Barsoum, Adv. Mater., 2011, 23, 4248–4253.
24. J. Low, L. Zhang, T. Tong, B. Shen and J. Yu, J. Catal., 2018, 361, 255–266.
25. Á. Morales-García, F. Calle-Vallejo and F. Illas, ACS Catal., 2020, 10, 13487–13503.
26. D. Dolz, R. De Armas, P. Lozano-Reis, Á. Morales-García, R. Sayós and F. Illas, ChemCatChem, 2024 DOI:10.1002/cctc.202400122.
27. H. Zhou, Z. Chen, E. Kountoupi, A. Tsoukalou, P. M. Abdala, P. Florian, A. Fedorov and C. R. Müller, Nat. Commun., 2021, 12, 5510.
28. A. Jurado, Á. Morales-García, F. Viñes and F. Illas, ACS Catal., 2022, 12, 15658–15667.
29. S. Kazim, C. Huang, N. H. Hemasiri, A. Kulkarni, S. Mathur and S. Ahmad, Adv. Funct. Mater., 2024, 2315694,  DOI:10.1002/adfm.202315694.
30. A. Dey, S. Varagnolo, N. P. Power, N. Vangapally, Y. Elias, L. Damptey, B. N. Jaato, S. Gopalan, Z. Golrokhi, P. Sonar, V. Selvaraj, D. Aurbach and S. Krishnamurthy, Prog. Mater. Sci., 2023, 139, 101166.
31. G. Gao, A. P. O’Mullane and A. Du, ACS Catal., 2017, 7, 494–500.
32. Z. Guo, J. Zhou, L. Zhu and Z. Sun, J. Mater. Chem. A, 2016, 4, 11446–11452.
33. D. Ontiveros, F. Viñes and C. Sousa, J. Mater. Chem. A, 2023, 11, 13754–13764.
34. J. Chen, H. Zheng, Y. Zhao, M. Que, W. Wang and X. Lei, Ceram. Int., 2020, 46, 20088–20096.
35. S. Debow, T. Zhang, X. Liu, F. Song, Y. Qian, J. Han, K. Maleski, Z. B. Zander, W. R. Creasy and D. L. Kuhn, J. Phys. Chem. C, 2021, 125, 10473–10482.
36. L. Jiao, C. Zhang, C. Geng, S. Wu, H. Li, W. Lv, Y. Tao, Z. Chen, G. Zhou and J. Li, Adv. Energy Mater., 2019, 9, 1900219.
37. R. Li, X. Ma, J. Li, J. Cao, H. Gao, T. Li, X. Zhang, L. Wang, Q. Zhang and G. Wang, Nat. Commun., 2021, 12, 1587.
38. M. M. Nair, A. C. Iacoban, F. Neatu, M. Florea and S. Neatu, J. Mater. Chem. A, 2023, 11, 12559–12592.
39. S. A. Khan, B. Amin, L.-Y. Gan and I. Ahmad, Phys. Chem. Chem. Phys., 2017, 19, 14738–14744.
40. L. Xu, T. Wu, P. R. Kent and D.-E. Jiang, Phys. Rev. Mater., 2021, 5, 054007.
41. N. García-Romeral, M. Keyhanian, Á. Morales-García, F. Viñes and F. Illas, Chem. Eur. J., 2024, 30, e202400255.
42. O. Lamiel-García, A. Cuko, M. Calatayud, F. Illas and S. T. Bromley, Nanoscale, 2017, 9, 1049–1058.
43. Á. Morales-García, R. Valero and F. Illas, J. Chem. Theory Comput., 2017, 13, 3746–3753.
44. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50.
45. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169.
46. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953.
47. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
48. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 5188.
49. R. F. W. Bader, Atoms in Molecules: A Quantum Theory, Clarendon Press, 1994.
50. W. Tang, E. Sanville and G. Henkelman, J. Phys.: Condens. Matter, 2009, 21, 084204.
51. V. Wang, N. Xu, J.-C. Liu, G. Tang and W.-T. Geng, Comput. Phys. Commun., 2021, 267, 108033.
52. G. Di Liberto, Á. Morales-García and S. T. Bromley, Nat. Commun., 2022, 13, 6236.
53. H. Oschinski, Á. Morales-García and F. Illas, J. Phys. Chem. C, 2021, 125, 2477–2484.
54. Á. Morales-García, A. Fernández-Fernández, F. Viñes and F. Illas, J. Mater. Chem. A, 2018, 6, 3381–3385.
55. R. Morales-Salvador, Á. Morales-García, F. Viñes and F. Illas, Phys. Chem. Chem. Phys., 2018, 20, 17117–17124.
56. M.-L. Tsai, S.-H. Su, J.-K. Chang, D.-S. Tsai, C.-H. Chen, C.-I. Wu, L.-J. Li, L.-J. Chen and J.-H. He, ACS Nano, 2014, 8, 8317–8322.
57. B. M. Abraham, O. Piqué, M. A. Khan, F. Viñes, F. Illas and J. K. Singh, ACS Appl. Mater. Interfaces, 2023, 15, 30117–30126.

---

Footnotes

† Electronic supplementary information (ESI) available: Tables S1–S12 and Fig. S1 and S2. See DOI: https://doi.org/10.1039/d4cp01757a

‡ Equally contributed.

---