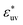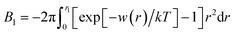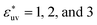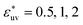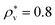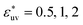Open Access Article
Open Access ArticleHow do water-mediated interactions and osmotic second virial coefficients vary with particle size?
Hidefumi
Naito
 ab,
Tomonari
Sumi
ab,
Tomonari
Sumi
 ab and
Kenichiro
Koga
ab and
Kenichiro
Koga
 *ab
*ab
aDepartment of Chemistry, Faculty of Science, Okayama University, Okayama 700-8530, Japan. E-mail: koga@okayama-u.ac.jp
bResearch Institute for Interdisciplinary Science, Okayama University, Okayama 700-8530, Japan
First published on 25th July 2023
Abstract
We examine quantitatively the solute-size dependences of the effective interactions between nonpolar solutes in water and in a simple liquid. The potential w(r) of mean force and the osmotic second virial coefficients B are calculated with high accuracy from molecular dynamics simulations. As the solute diameter increases from methane's to C60's with the solute–solute and solute–solvent attractive interaction parameters fixed to those for the methane–methane and methane–water interactions, the first minimum of w(r) lowers from −1.1 to −4.7 in units of the thermal energy kT. Correspondingly, the magnitude of B (<0) increases proportional to σα with some power close to 6 or 7, which reinforces the solute-size dependence of B found earlier for a smaller range of σ [H. Naito, R. Okamoto, T. Sumi and K. Koga, J. Chem. Phys., 2022, 156, 221104]. We also demonstrate that the strength of the attractive interactions between solute and solvent molecules can qualitatively change the characteristics of the effective pair interaction between solute particles, both in water and in a simple liquid. If the solute–solvent attractive force is set to be weaker (stronger) than a threshold, the effective interaction becomes increasingly attractive (repulsive) with increasing solute size.
1 Introduction
We report here the results of computer simulation studies on the effective pair interactions between spherical solute particles with varying diameters in water and in a simple liquid.When a hydrophobic molecule is transferred into water from a gas phase or from an oily phase, the change in enthalpy is negative but the change in solvation entropy (the relevant part of the change in entropy) is also negative, and the entropic contribution is greater than the enthalpic one, leading to the positive solvation free energy (change) and the low solubility of the hydrophobe in water. This is the basic mechanism characteristic of the hydrophobic hydration.1–3 When two such hydrophobic solute molecules are in contact with each other in water, the solvation free energy for the pair is less than that for two molecules far apart, resulting in water-mediated attraction between them, the hydrophobic attraction.2,3
The solvent-mediated pair interaction between solute molecules in a solvent is fully described by the potential w(r) of mean force, which is the sum of the direct pair potential ϕ(r) and the solvent-induced part w*(r). The strength of that interaction may be measured by the first minimum of w(r), or equivalently the first peak of the radial distribution function g(r) = e−w(r)/kT, and the osmotic second virial coefficient B. The osmotic B, the second coefficient of the expansion of the osmotic pressure in the solute density ρ at fixed chemical potentials of solvent species and fixed temperature, is given by the correlation-function integral:4
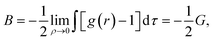 | (1) |
It has been recognized in physical chemistry and biochemistry that the size of solute molecules (inert gases, hydrocarbons, amphiphiles, proteins, and so on) matters to the hydration free energy and the hydrophobic interaction. The subject has been extensively discussed in the literature.19–42 In a wider framework, the solute-size effect on the effective pair potential w(r) in simple liquids has been an important subject in the theory of liquids.43–49
The present paper aims at a quantitative understanding of how the strength of effective pair interaction between solute molecules in water, changes with solute size. Recently it was reported15 that the osmotic second virial coefficient B for Lennard-Jones (LJ) particles in water varies with diameter σ as ∼σα with α ≃ 6 in the range σ ≤ 2σm, where σm is the LJ diameter of methane. The change in B in that range is already enormous because of the large power. Now we extend the upper limit of σ to 3σm ≃ 1.12 nm, which then covers solutes ranging from methane to C60, and examine whether or not the power-law dependence continues to hold. The second issue addressed in the present paper is the effect of the solute–solvent attractive interaction on the solute-size dependences of w(r) and B. At ambient conditions the solvent-mediated interactions between hydrophobic molecules, between amphiphilic molecules, and between hydrophobic groups in proteins in aqueous solution are less attractive than the direct interactions due to the existence of the solute–solvent attractive interactions.7,10,14,50,51 To be specific, take the case of methane in water, as an example: the osmotic B for methane and the gas virial coefficient Bgas are both negative at ambient temperatures, but more importantly B > Bgas, i.e., methane particles are less attractive in water than in vacuum. The difference between B and Bgas becomes greater at lower temperatures.7,10 On the other hand, hard-sphere solutes are more attractive in water than in vacuum as B < 0 and Bgas > 0.9 Thus, the attractive forces between solute and solvent molecules is a key factor that could change the characteristics of the effective interaction between solute molecules.
In the present study we calculate w(r) and B for solute species with different diameters and different strengths of the solute–solvent attraction in order to gain a quantitative understanding of the effect of the solute–solvent attraction on the solute-size dependence of w(r) and B. The next important question to be addressed is what kinds of features in the solute-size dependence of the hydrophobic interaction are universal for liquid mixtures in general and what is unique for water. As a first step, we evaluate the solute size dependences of w(r) and B for LJ mixtures and compare the results with those for water.
2 Computational details
We examine the model systems for aqueous solutions of hydrophobic solutes and, for comparison, those for simple liquid mixtures. Molecular dynamics (MD) simulations are performed for aqueous and non-aqueous solutions to obtain the effective pair potential between solute molecules.The systems for aqueous solutions consist of water molecules interacting with each other via the TIP4P/2005 potential52 and spherical solute particles interacting with each other via the LJ potential:
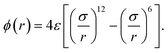 | (2) |
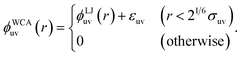 | (3) |
The reference hydrophobic solute is taken to be methane modeled by the TraPPE-UA force field,53 whose LJ parameters are σm = 0.373 nm and εm = 1.23 kJ mol−1. The solute particles with different diameters are those with σ* = σ/σm = 1, 1.5, 2, 2.5, and 3, and ε = εm. Recently the σ dependences of the solute–solute radial distribution function g(r) and the osmotic second virial coefficient B have been reported for the LJ solutes with σ* ≤ 2.15 For the solute–water LJ pair interactions, the size parameter σuv is set to σuv = (σ + σw)/2 with σw of the TIP4P/2005 water. The energy parameter 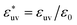 is fixed to either 1, 2, or 3, where ε0 = 0.977 kJ mol−1, the value given by
is fixed to either 1, 2, or 3, where ε0 = 0.977 kJ mol−1, the value given by 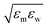 with εw of the TIP4P/2005 model water.
with εw of the TIP4P/2005 model water.
The number Nv of water molecules and the number N of solute particles depend on the model system, as listed in Table 1. For the systems with N = 20, 40, and 80, standard MD simulations were performed to obtain g(r); for those with N = 2, the umbrella sampling method54,55 was applied.
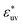 (for WCA solutes this is the parameter in eqn (3)), and numbers Nv and N of solvent and solute molecules, respectively. The solute–solute potential is of the LJ form for all systems.
(for WCA solutes this is the parameter in eqn (3)), and numbers Nv and N of solvent and solute molecules, respectively. The solute–solute potential is of the LJ form for all systems.
We performed isobaric–isothermal MD simulations for the model aqueous solutions under three-dimensional periodic boundary conditions using GROMACS 2018.56 The pressure is set to 1 bar using the Parrinello–Rahman method and the temperature is maintained at 300 K by the Nosé–Hoover method. For the systems with N = 20 and above, the duration time t of the production run is 100 ns, except for the system with the solute particles of diameter σ* = 1.5, in which case t = 200 ns. In the umbrella sampling method, t for each simulation with a given constraint for the distance between two solute particles is 20 ns except for the system with the WCA solute particles of σ* = 1, in which case t = 10 ns. The time step interval of each simulation is 1 fs. The configurations of solute molecules were recorded every 0.05 ps to compute g(r).
In the umbrella sampling simulations, the harmonic potential with the spring constant of 1000 kJ mol−1 nm−2 was applied to constrain the distance between the two solute particles. The constraint distance ranges from 0.6 to 2.9 nm for σ* = 2 and from 0.7 to 2.8 nm for σ* = 2.5, and from 0.8 to 3.1 nm for σ* = 3, in 0.1 nm increments. For the WCA solutes, i.e., those which interact with solvent molecules via the WCA pair potential ϕWCAuv(r), the constraint distance ranges from 0.2 to 2.5 nm for σ* = 1 and from 0.6 to 2.9 nm for σ* = 2, and from 0.8 to 3.1 nm for σ* = 3. The potentials w(r) of mean force were obtained from the weighted histogram analysis method.57,58
All the LJ pair potentials in each model aqueous solution were truncated at a cutoff distance rcut, its value depending on the solute size σ*: rcut = 1.3 nm for σ* = 1 and 1.5, rcut = 2 nm for σ* = 2 and 2.5, and rcut = 2.4 nm for σ* = 3. The Coulomb potentials were treated using the particle mesh Ewald method with the cutoff distances in the real space being the same as rcut of the LJ potentials.
In order to calculate g(r), or equivalently w(r), for hydrophobic solutes at infinite dilution from MD simulations for the model solutions at finite concentration, we employed the following technique when necessary. When performing MD simulations for the systems containing solute particles (N = 40 or 20, Nv = 4000) with σ* = 1 or 1.5 and 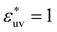 , the LJ potential for the solute–solute interactions was replaced by a repulsive potential ϕrep(r), and then the resulting radial distribution function grep(r) was converted to g(r) by the identity g(r) = limρ→0grep(r)
, the LJ potential for the solute–solute interactions was replaced by a repulsive potential ϕrep(r), and then the resulting radial distribution function grep(r) was converted to g(r) by the identity g(r) = limρ→0grep(r)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[−ϕatt(r)/kT] with ϕatt(r) = ϕLJ(r) − ϕrep(r). Here we assume that grep(r) obtained from the simulation is very close to that at infinite dilution because the solute particles have no tendency of aggregation due to the potential ϕrep(r). For the solute with σ* = 1, ϕrep(r) is the repulsive WCA potential, the solute–solute analog of eqn (3), while for the solute with σ* = 1.5, ϕrep(r) is 4ε(σ/r)12.
exp[−ϕatt(r)/kT] with ϕatt(r) = ϕLJ(r) − ϕrep(r). Here we assume that grep(r) obtained from the simulation is very close to that at infinite dilution because the solute particles have no tendency of aggregation due to the potential ϕrep(r). For the solute with σ* = 1, ϕrep(r) is the repulsive WCA potential, the solute–solute analog of eqn (3), while for the solute with σ* = 1.5, ϕrep(r) is 4ε(σ/r)12.
We also studied models of nonpolar solutions (simple liquid mixtures) to compare the solute-size dependences of w(r) and B with those in the aqueous solutions. The systems consist of two components of LJ particles. All quantities such as the distance, the solvent density, and temperature, are given in reduced units of the LJ parameters σv and εv of solvent particles. We consider solutes with σ*(=σ/σv) = 1, 2, 3 and ε*(=ε/εv) = 1. The solute–solvent LJ potential parameters are set to 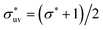 and
and 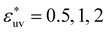 . The solvent number density and the temperature are set to
. The solvent number density and the temperature are set to 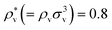 and T*(=kT/εv) = 1.5. This density
and T*(=kT/εv) = 1.5. This density 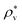 , is close to 0.85, the density of the LJ liquid at the triple point, and the temperature T* is higher than the critical point.59 At this state point, Kimura and Yoshimura calculated g(r) for the solutes with σ* = 0.5, 1, 1.5, ε* = 1, and
, is close to 0.85, the density of the LJ liquid at the triple point, and the temperature T* is higher than the critical point.59 At this state point, Kimura and Yoshimura calculated g(r) for the solutes with σ* = 0.5, 1, 1.5, ε* = 1, and 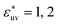 using the integral equation theory.60
using the integral equation theory.60
We performed isochoric–isothermal MD simulations of the LJ mixtures. The numbers of solvent and solute particles are given in Table 1. The duration time t* of the production run and the cutoff distance 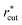 of the LJ potential depend on the system: for the systems with σ* = 1, t* = 84
of the LJ potential depend on the system: for the systems with σ* = 1, t* = 84![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 659 and
659 and 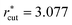 ; for σ* = 2 and 3, t* = 169
; for σ* = 2 and 3, t* = 169![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 318 and
318 and 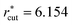 . In the case of σ* = 3, the solute–solute LJ potential was replaced by the repulsive WCA potential and the resulting radial distribution function was converted to g(r) as in the cases of the model aqueous solutions.
. In the case of σ* = 3, the solute–solute LJ potential was replaced by the repulsive WCA potential and the resulting radial distribution function was converted to g(r) as in the cases of the model aqueous solutions.
When one calculates B from eqn (1) using numerical integration, one finds large errors or even diverging behavior of the integral. This is because g(r) obtained for a closed system does not converge to 1, because statistical errors in g(r) at large distances are enhanced by the factor r2, and because there is the finite-size effect in any simulation. To overcome this problem, we employed the method described in our previous paper.7,15 First, we correct the limiting behavior of g(r) so that the average of g(r) over a certain range at long distances becomes 1. Second, we use the method proposed by Krüger et al.61,62 for evaluating the KB integral at the thermodynamic limit from that of the finite systems:
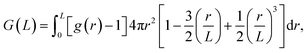 | (4) |
| G(L)L = GL + C. | (5) |
3 Results and discussion
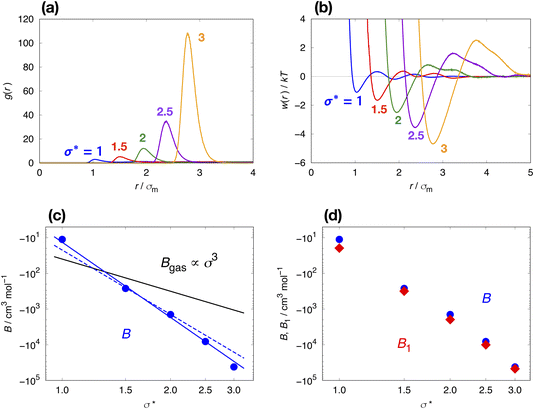
First, we examine how the hydrophobic interaction (the effective pair potential between nonpolar solute particles in water) changes when the solute size increases while nothing else changes. Fig. 1(a) displays the radial distribution functions g(r) for pairs of LJ particles in water, each corresponding to the solute with a different diameter σ but the same energy parameters ε = εm and εuv = ε0. It is clear that the first peak develops rapidly with increasing particle diameter σ. The corresponding potentials w(r) of mean force are shown in Fig. 1(b). The potential well depth becomes deeper as σ increases: w(r)/kT at the first minimum is −1.10, −1.66, − 2.50, −3.56, and −4.69 at σ* = 1, 1.5, 2, 2.5, and 3, respectively.The variation of w(r)/kT at the first minimum with increasing solute size is essentially due to changes in the solvent-induced part of the effective interaction since the solute–solute LJ parameter ε is fixed. In general, solvent-induced attraction at the solute–solute contact distance is largely due to the excluded volume effect. Each particle has an excluded volume from which solvent molecules or co-solvent molecules are excluded. When the two particles are held fixed at some short distance, the two excluded-volume spheres overlap, and the larger the overlapping volume (e.g., the shorter the inter-particle distance) the greater the configurational entropy of solvent (or co-solvent) molecules and thus the lower the solvation free energy of the pair of particles.63,64 When the Asakura–Oosawa (AO) theory65 is applied to a hard-sphere fluid consisting of solvent and solute particles, the effective pair potential at contact distance σ, which is the minimum in the AO potential wAO(r), decreases linearly with σ, the diameter of the solute particles:
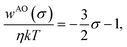 | (6) |
Apart from the size dependence of the first minimum of w(r), Fig. 1(b) also indicates that both the first maximum and the second minimum of w(r) move up with increasing σ, and the second minimum disappears at σ* = 2. This trend may well be characteristic of the hydrophobic interaction. Earlier studies showed that the force curve between hydrophobic planar sheets in water becomes increasingly repulsive as the two sheets approach each other and squeeze bilayer water.66,67 It is possible that the force curve between hydrophobic particles with σ* = 3 already bears a strong resemblance to that between hydrophobic surfaces. However, the correspondence is a matter of conjecture and further analysis is needed.
Fig. 1(c) is the log–log plot of the osmotic second virial coefficients B against σ*. The values of B are negative for all solutes with different σ, i.e., their effective interactions in water are attractive. The magnitude of B becomes larger with increasing σ. The dotted and solid lines indicate linear fits to the data with slopes of 6 and 7, respectively. The log–log plot of B vs. σ* seems to follow a linear relationship, i.e.,
| B ∝ σ*α. | (7) |
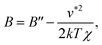 | (8) |
The potential of mean force w(r) between two solute particles or the corresponding pair correlation function g(r) − 1 is not a simple function of r and exhibits damped oscillatory decay, in contrast to the pair potential ϕ(r) in eqn (2) or e−ϕ(r)/kT − 1, which decays monotonically. Thus it is worth examining which range of r contributes primarily to the σ dependence of B. Let B1 be the contribution to B from w(r) in the short range r < r1, where r1 is the distance of the first maximum of w(r): 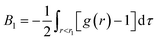 . Comparing the log–log plot of B1 with that of B (Fig. 1(d)), we find that the dominant contribution to the solute-size dependence of B comes from the short range of r.
. Comparing the log–log plot of B1 with that of B (Fig. 1(d)), we find that the dominant contribution to the solute-size dependence of B comes from the short range of r.
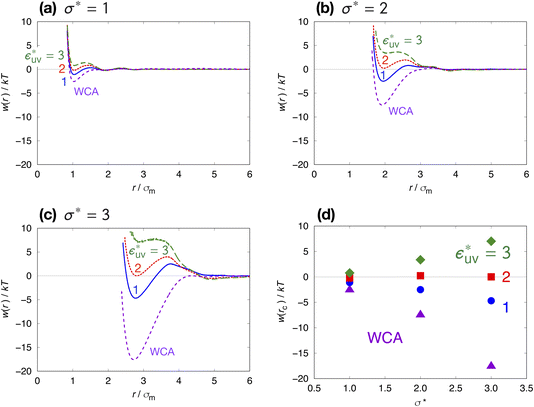
Next, we examine the effect of the solute–solvent attractive interaction on the effective pair potential w(r) between solute particles in water. For solutes with a given σ*, three different solute–solvent LJ potentials are considered: 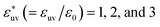 . In addition, the repulsive WCA potential is also assumed for the solute–solvent interaction. For each case of σ* = 1, 2 and 3, as shown in Fig. 2(a)–(c), respectively, the potential curve of w(r) over a short range, including its first minimum and the first maximum, shifts upwards as the solute–solvent attraction is strengthened by increasing
. In addition, the repulsive WCA potential is also assumed for the solute–solvent interaction. For each case of σ* = 1, 2 and 3, as shown in Fig. 2(a)–(c), respectively, the potential curve of w(r) over a short range, including its first minimum and the first maximum, shifts upwards as the solute–solvent attraction is strengthened by increasing 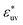 from 1 to 3. When the solute–solvent interaction is purely repulsive, i.e., when it is the repulsive WCA potential, the potential of mean force in the same range is well below that for the reference LJ potential
from 1 to 3. When the solute–solvent interaction is purely repulsive, i.e., when it is the repulsive WCA potential, the potential of mean force in the same range is well below that for the reference LJ potential 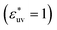 . The results described above are in accord with the observations that the solvent-induced part of w(r) is weakened by the solute–solvent attractive interactions12,29,31,35–37,70–74 and that in some cases the hydrophobic interactions between nonpolar molecules in water are not as attractive as those in other environments.50,51,74
. The results described above are in accord with the observations that the solvent-induced part of w(r) is weakened by the solute–solvent attractive interactions12,29,31,35–37,70–74 and that in some cases the hydrophobic interactions between nonpolar molecules in water are not as attractive as those in other environments.50,51,74
Comparing Fig. 2(a), (b) and (c), it is clear that the effect of the solute–solvent attractive interaction is greater for larger solute particles. To quantify this tendency, we focus on the first minimum in w(r), i.e., w(rc) with rc being the distance of the first minimum, which depends on σ and εuv. Note that rc is close to σ, the solute–solute contact distance, but is slightly smaller. The plots of w(rc)/kT as a function of σ* are shown in Fig. 2(d). Our reference set of solutes is the one with 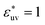 , i.e., εuv = 0.977 kJ mol−1, which corresponds to the dispersion force between methane and water molecules. When the solute–solvent attractive interaction is completely turned off (the repulsive WCA potential), w(rc) for a given σ* becomes more negative than that for the reference set and the rate of change of w(rc) with σ* is much greater than that for the reference set. On the other hand, when εuv is three times greater than that for the methane–water dispersion force, w(rc) is positive for any σ* and increases with increasing σ*. Thus, depending on the strength of solute–solvent attraction being smaller or greater than a certain threshold, the effective pair interaction becomes increasingly attractive or increasingly repulsive with the solute size, respectively. The threshold seems to be around
, i.e., εuv = 0.977 kJ mol−1, which corresponds to the dispersion force between methane and water molecules. When the solute–solvent attractive interaction is completely turned off (the repulsive WCA potential), w(rc) for a given σ* becomes more negative than that for the reference set and the rate of change of w(rc) with σ* is much greater than that for the reference set. On the other hand, when εuv is three times greater than that for the methane–water dispersion force, w(rc) is positive for any σ* and increases with increasing σ*. Thus, depending on the strength of solute–solvent attraction being smaller or greater than a certain threshold, the effective pair interaction becomes increasingly attractive or increasingly repulsive with the solute size, respectively. The threshold seems to be around 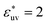 because then w(rc)/kT is close to 0 for any σ* ≤ 3.
because then w(rc)/kT is close to 0 for any σ* ≤ 3.
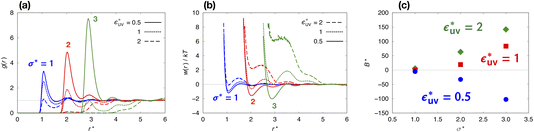
We have seen how the effective pair interactions in water vary with solute size. Now we examine the solute-size dependence in a simple liquid using LJ mixtures. Fig. 3 shows the solute-size dependences of g(r), w(r), and B for three fixed values of the solute–solvent LJ energy parameter: 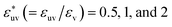 . For
. For 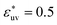 , as σ*(=σ/σv) increases the first peak of g(r) develops, the first minimum of w(r) decreases, and B decreases. These results are analogous to those for LJ solutes with
, as σ*(=σ/σv) increases the first peak of g(r) develops, the first minimum of w(r) decreases, and B decreases. These results are analogous to those for LJ solutes with 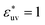 and the WCA solutes in water. We note that as σ* increases the first maximum of w(r) in the LJ solvent does not develop and the second minimum remains. This is a notable difference from what we observed for w(r) in water. When
and the WCA solutes in water. We note that as σ* increases the first maximum of w(r) in the LJ solvent does not develop and the second minimum remains. This is a notable difference from what we observed for w(r) in water. When 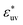 is fixed to 1, the size dependences of g(r), w(r), and B all show the opposite trends to those for
is fixed to 1, the size dependences of g(r), w(r), and B all show the opposite trends to those for 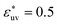 , respectively. And when
, respectively. And when 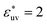 , solute particles of size σ* = 1 in the solvent are barely attractive to each other: w(r) at the first minimum is near zero and B is positive, and as σ* increases, the effective interaction becomes increasingly repulsive. The threshold for
, solute particles of size σ* = 1 in the solvent are barely attractive to each other: w(r) at the first minimum is near zero and B is positive, and as σ* increases, the effective interaction becomes increasingly repulsive. The threshold for 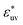 at which the solute-size dependence of w(r) changes its character is between 0.5 and 1.
at which the solute-size dependence of w(r) changes its character is between 0.5 and 1.
4 Conclusions
To understand the hydrophobic interactions between solutes with varying sizes and varying solute–solvent interactions, we calculated and analyzed the effective pair interactions between nonpolar solutes in water, and for comparison, those in a simple liquid. The potentials w(r) of mean force and the osmotic second virial coefficients B, were obtained with high accuracy based on MD simulations, so that their solute-size dependences could be considered quantitatively.For the hydrophobic particles in water – whose solute–solvent LJ energy parameter εuv is fixed to be that of the methane–water pair – as the particle diameter σ increases, the effective pair potential w(rc) at contact distance decreases rapidly compared to the AO potential (eqn (6)), and at the same time the potential barrier following the first minimum becomes higher (Fig. 1(b)). Reflecting on such changes in w(r), B becomes increasingly negative with increasing solute diameter as described by eqn (7). The power-law behavior of B vs. σ has been reported earlier15 and here it is confirmed for a wider range of σ, from methane's to C60's.
The solute–solvent attractive interaction has a great influence on w(r) (Fig. 2). With the solute–water pair, interaction is purely repulsive as given by the repulsive WCA potential, where w(rc) decreases most rapidly with σ. On the other hand, if the solute–water attractive interaction is sufficiently strong (e.g., 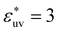 ), w(rc) increases with σ. The threshold value of
), w(rc) increases with σ. The threshold value of 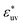 at which the solute-size dependence of w(rc) changes qualitatively is found to be
at which the solute-size dependence of w(rc) changes qualitatively is found to be 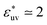 . The effect of
. The effect of 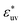 on w(rc) for the solutes in a LJ solvent is qualitatively the same as that in water. It is anticipated that the solute size dependence of the osmotic B also changes qualitatively with the strength of solute–solvent attractive interaction.
on w(rc) for the solutes in a LJ solvent is qualitatively the same as that in water. It is anticipated that the solute size dependence of the osmotic B also changes qualitatively with the strength of solute–solvent attractive interaction.
Qualitatively, the results summarized above could be understood as follows. The main driving force for the effective pair interaction being increasingly attractive with increasing σ is the configurational entropy of solvent molecules (the excluded volume effect). However, the solute–solvent attractive interaction has an opposing effect since the potential energy due to the interactions of a pair of solute particles with surrounding solvent molecules is lower when the two particles are far from each other than when they are in contact. Therefore, when the solute–solvent attractive interaction is sufficiently strong, the effective pair interaction could be increasingly repulsive with increasing σ.
The solute-size dependence of the effective interaction is an important subject in the theory of liquids43–49 and is also relevant to stability and phase separation in real systems such as colloidal solutions75 and aqueous solutions in biological systems.76,77 To understand more rigorously how the potential w(r) of mean force and the osmotic B change with the solute size and how the solute–solvent attractive interaction alters the behaviors of w(r) and B, both simulation-based and theoretical approaches which can examine a wider range of solute sizes are needed.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by KAKENHI (Grant Numbers 18KK0151 and 20H02696) and JST, the establishment of university fellowships towards the creations of science technology innovation (Grant Number JPMJFS2128). Part of the computation was performed at the Research Center for Computational Science, Okazaki, Japan (Project: 21-IMS-C125, 22-IMS-C124, 23-IMS-C112).References
- C. Tanford, The Hydrophobic Effect: Formation of Micelles and Biological Membranes, Wiley, New York, 2nd edn, 1980 Search PubMed.
- A. Ben-Naim, Hydrophobic Interactions, Plenum, Oxford, 1980 Search PubMed.
- B. Widom, P. Bhimalapuram and K. Koga, Phys. Chem. Chem. Phys., 2003, 5, 3085–3093 RSC.
- W. G. McMillan Jr and J. E. Mayer, J. Chem. Phys., 1945, 13, 276–305 CrossRef.
- J. G. Kirkwood and F. P. Buff, J. Chem. Phys., 1951, 19, 774–777 CrossRef CAS.
- L. R. Pratt and D. Chandler, J. Solution Chem., 1980, 9, 1–17 CrossRef CAS.
- K. Koga, J. Phys. Chem. B, 2013, 117, 12619–12624 CrossRef CAS.
- K. Koga and B. Widom, J. Chem. Phys., 2013, 138, 114504 CrossRef CAS.
- M. I. Chaudhari, S. A. Holleran, H. S. Ashbaugh and L. R. Pratt, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 20557–20562 CrossRef CAS.
- H. S. Ashbaugh, K. Weiss, S. M. Williams, B. Meng and L. N. Surampudi, J. Phys. Chem. B, 2015, 119, 6280–6294 CrossRef CAS.
- M. I. Chaudhari, D. Sabo, L. R. Pratt and S. B. Rempe, J. Phys. Chem. B, 2015, 119, 9098–9102 CrossRef CAS.
- M. I. Chaudhari, S. B. Rempe, D. Asthagiri, L. Tan and L. Pratt, J. Phys. Chem. B, 2016, 120, 1864–1870 CrossRef CAS.
- D. Tang, C. Delpo, O. Blackmon and H. S. Ashbaugh, J. Chem. Phys., 2018, 148, 016101 CrossRef PubMed.
- K. Koga and N. Yamamoto, J. Phys. Chem. B, 2018, 122, 3655–3665 CrossRef CAS PubMed.
- H. Naito, R. Okamoto, T. Sumi and K. Koga, J. Chem. Phys., 2022, 156, 221104 CrossRef CAS.
- C. A. Cerdeiriña and B. Widom, J. Phys. Chem. B, 2016, 120, 13144–13151 CrossRef PubMed.
- R. Okamoto and A. Onuki, J. Chem. Phys., 2018, 149, 014501 CrossRef PubMed.
- R. Okamoto and K. Koga, J. Phys. Chem. B, 2021, 125, 12820–12831 CrossRef CAS PubMed.
- G. Hummer, S. Garde, A. E. Garcia, A. Pohorille and L. R. Pratt, Proc. Natl. Acad. Sci. U. S. A., 1996, 93, 8951–8955 CrossRef CAS.
- G. Hummer and S. Garde, Phys. Rev. Lett., 1998, 80, 4193 CrossRef CAS.
- G. Graziano, J. Chem. Soc., Faraday Trans., 1998, 94, 3345–3352 RSC.
- K. Lum, D. Chandler and J. D. Weeks, J. Phys. Chem. B, 1999, 103, 4570–4577 CrossRef CAS.
- D. M. Huang, P. L. Geissler and D. Chandler, J. Phys. Chem. B, 2001, 105, 6704–6709 CrossRef CAS.
- D. M. Huang and D. Chandler, J. Phys. Chem. B, 2002, 106, 2047–2053 CrossRef CAS.
- N. T. Southall, K. A. Dill and A. Haymet, J. Phys. Chem. B, 2002, 106, 521–533 CrossRef CAS.
- D. Chandler, Nature, 2005, 437, 640–647 CrossRef CAS.
- S. Rajamani, T. M. Truskett and S. Garde, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 9475–9480 CrossRef CAS.
- H. S. Ashbaugh and L. R. Pratt, Rev. Mod. Phys., 2006, 78, 159 CrossRef CAS.
- E. Sobolewski, M. Makowski, C. Czaplewski, A. Liwo, S. Ołdziej and H. A. Scheraga, J. Phys. Chem. B, 2007, 111, 10765–10774 CrossRef CAS.
- G. Graziano, J. Phys. Chem. B, 2009, 113, 11232–11239 CrossRef CAS.
- M. Makowski, C. Czaplewski, A. Liwo and H. A. Scheraga, J. Phys. Chem. B, 2010, 114, 993–1003 CrossRef CAS.
- R. Zangi, J. Phys. Chem. B, 2011, 115, 2303–2311 CrossRef CAS PubMed.
- A. S. Thomas and A. H. Elcock, J. Phys. Chem. Lett., 2011, 2, 19–24 CrossRef CAS PubMed.
- B. J. Berne, J. D. Weeks and R. Zhou, Annu. Rev. Phys. Chem., 2009, 60, 85–103 CrossRef CAS PubMed.
- L. R. Pratt, M. I. Chaudhari and S. B. Rempe, J. Phys. Chem. B, 2016, 120, 6455–6460 CrossRef CAS PubMed.
- D. Ben-Amotz, J. Phys. Chem. Lett., 2015, 6, 1696–1701 CrossRef CAS PubMed.
- D. Ben-Amotz, Annu. Rev. Phys. Chem., 2016, 67, 617–638 CrossRef CAS PubMed.
- A. Bartosik, M. Wiśniewska and M. Makowski, J. Phys. Org. Chem., 2015, 28, 10–16 CrossRef CAS.
- M. V. Athawale, S. N. Jamadagni and S. Garde, J. Chem. Phys., 2009, 131, 115102 CrossRef PubMed.
- A. L. Ferguson, P. G. Debenedetti and A. Z. Panagiotopoulos, J. Phys. Chem. B, 2009, 113, 6405–6414 CrossRef CAS PubMed.
- V. Hande and S. Chakrabarty, ACS Omega, 2022, 7, 2671–2678 CrossRef CAS PubMed.
- I. Sinha, S. M. Cramer, H. S. Ashbaugh and S. Garde, J. Phys. Chem. B, 2022, 126, 7604–7614 CrossRef CAS PubMed.
- P. Attard, J. Chem. Phys., 1989, 91, 3083–3089 CrossRef CAS.
- T. Biben, P. Bladon and D. Frenkel, J. Phys.: Condens. Matter, 1996, 8, 10799 CrossRef CAS.
- R. Dickman, P. Attard and V. Simonian, J. Chem. Phys., 1997, 107, 205–213 CrossRef CAS.
- M. Dijkstra, R. van Roij and R. Evans, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1999, 59, 5744 CrossRef CAS PubMed.
- R. Roth, R. Evans and S. Dietrich, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2000, 62, 5360 CrossRef CAS PubMed.
- M. Kinoshita, Chem. Phys. Lett., 2002, 353, 259–269 CrossRef CAS.
- R. Akiyama, Y. Karino, Y. Hagiwara and M. Kinoshita, J. Phys. Soc. Jpn., 2006, 75, 064804 CrossRef.
- T. Sumi and K. Koga, Sci. Rep., 2019, 9, 1–9 CrossRef CAS.
- T. Sumi and H. Imamura, Protein Sci., 2021, 30, 2132–2143 CrossRef CAS.
- J. L. F. Abascal and C. Vega, J. Chem. Phys., 2005, 123, 234505 CrossRef CAS PubMed.
- M. G. Martin and J. I. Siepmann, J. Phys. Chem. B, 1998, 102, 2569–2577 CrossRef CAS.
- G. M. Torrie and J. P. Valleau, Chem. Phys. Lett., 1974, 28, 578–581 CrossRef CAS.
- G. M. Torrie and J. P. Valleau, J. Comput. Phys., 1977, 23, 187–199 CrossRef.
- M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, SoftwareX, 2015, 1–2, 19–25 CrossRef.
- S. Kumar, D. Bouzida, R. H. Swendsen, P. A. Kollman and J. M. Rosenberg, J. Comput. Chem., 1992, 13, 1011–1021 CrossRef CAS.
- M. Souaille and B. Roux, Comput. Phys. Commun., 2001, 135, 40–57 CrossRef CAS.
- J. J. Nicolas, K. E. Gubbins, W. B. Streett and D. J. Tildesley, Mol. Phys., 1979, 37, 1429–1454 CrossRef CAS.
- Y. Kimura and Y. Yoshimura, Mol. Phys., 1991, 72, 279–294 CrossRef CAS.
- P. Krüger, S. K. Schnell, D. Bedeaux, S. Kjelstrup, T. J. Vlugt and J.-M. Simon, J. Phys. Chem. Lett., 2013, 4, 235–238 CrossRef PubMed.
- N. Dawass, P. Krüger, S. K. Schnell, O. A. Moultos, I. G. Economou, T. J. Vlugt and J.-M. Simon, Nanomaterials, 2020, 10, 771 CrossRef CAS.
- G. Graziano, Chem. Phys. Lett., 2010, 499, 79–82 CrossRef CAS.
- G. Graziano, Chem. Phys. Lett., 2017, 685, 54–59 CrossRef CAS.
- S. Asakura and F. Oosawa, J. Chem. Phys., 1954, 22, 1255–1256 CrossRef CAS.
- K. Koga, J. Chem. Phys., 2002, 116, 10882–10889 CrossRef CAS.
- K. Koga and H. Tanaka, J. Chem. Phys., 2005, 122, 104711 CrossRef.
- B. Widom and R. C. Underwood, J. Phys. Chem. B, 2012, 116, 9492–9499 CrossRef CAS.
- K. Koga, V. Holten and B. Widom, J. Phys. Chem. B, 2015, 119, 13391–13397 CrossRef CAS PubMed.
- L. R. Pratt and D. Chandler, J. Chem. Phys., 1980, 73, 3434–3441 CrossRef CAS.
- K. Watanabe and H. C. Andersen, J. Phys. Chem., 1986, 90, 795–802 CrossRef CAS.
- D. Asthagiri, S. Merchant and L. R. Pratt, J. Chem. Phys., 2008, 128, 244512 CrossRef CAS.
- A. Gao, L. Tan, M. I. Chaudhari, D. Asthagiri, L. R. Pratt, S. B. Rempe and J. D. Weeks, J. Phys. Chem. B, 2018, 122, 6272–6276 CrossRef CAS PubMed.
- T. Sumi and H. Sekino, J. Chem. Phys., 2007, 126, 04B614 CrossRef.
- N. W. Lekkerkerker and R. Tuinier, Colloids and the Depletion Interaction, Springer, Heidelberg, 1st edn, 2011 Search PubMed.
- E. Y. Chi, S. Krishnan, T. W. Randolph and J. F. Carpenter, Pharm. Res., 2003, 20, 1325–1336 CrossRef CAS.
- S. Boeynaems, S. Alberti, N. L. Fawzi, T. Mittag, M. Polymenidou, F. Rousseau, J. Schymkowitz, J. Shorter, B. Wolozin, L. V. D. Bosch, P. Tompa and M. Fuxreiter, Trends Cell Biol., 2018, 28, 420–435 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2024 |