Designing molecular and two-dimensional metalloporphyrin catalysts for the electrochemical CO₂ reduction reaction

Abstract

The electrochemical CO₂ reduction reaction (eCO₂R) is an important route toward the sustainable conversion of CO₂ to value-added chemicals. However, developing efficient catalysts with high selectivity and stability remains challenging. Metalloporphyrins (M–PORs) represent an attractive class of molecular catalysts because their structural framework offers a unique combination of tunability of the peripheral ligands, flexibility of the metal centre, and versatility of the oxidation state of the metal. These properties can be exploited to tailor the catalytic properties of M–PORs for the eCO₂R. Here, we present a comprehensive computational study using density functional theory to systematically explore M–POR catalysts with varying metal centers (Ni, Fe, Cu, Co), oxidation states, and anchoring ligands, aimed at enhancing the selective production of the C₁ products (carbon monoxide and formic acid). Thermodynamic and electrochemical stability analyses revealed neutral M–PORs to be significantly more stable than their charged counterparts, providing crucial guidelines for catalyst design. A mechanistic analysis of reaction pathways—proton-coupled electron transfer (PCET) versus sequential proton and electron transfer (PT–ET)—identified PCET as highly favourable, with predominant selectivity towards formic acid. This study identifies Fe–POR as the one showing superior catalytic performance. Importantly, integrating these optimal molecular catalysts into two-dimensional (2D) carbonaceous frameworks led to further enhancement of catalytic performance, identifying 2D Fe–POR as a highly promising material for selective C₁ product formation, thus providing a rational framework for designing effective molecular-to-framework electrocatalysts for the eCO₂R.

---

1. Introduction

Transforming carbon dioxide (CO₂) into valuable chemicals, fuels, and materials holds substantial societal and scientific significance. This process has the potential to mitigate the effects of climate change and advance the use of sustainable energy.^1,2 Electrochemical CO₂ reduction (CO₂R) is considered a promising method thanks to its technical sophistication, maturity, and economic viability, which is why it has gained significant attention from both academic and industrial sectors.^3–5 CO₂R can produce high-energy and high-value one-carbon (C₁) products such as carbon monoxide (CO), methane (CH₄), formic acid (HCOOH), and methanol (CH₃OH), and multi-carbon (C₂₊) products like ethylene (CH₂CH₂), ethanol (CH₃CH₂OH), acetic acid (CH₃COOH), and n-propanol (CH₃CH₂CH₂OH).^6–8 These molecules can then be used as feedstock for the synthesis of long-chain hydrocarbon fuels.^9–11 CO₂R into C₂₊ products stands as the pinnacle achievement in electrochemical synthesis.^12,13 Still, the endeavour to develop efficient catalysts that are capable of high product selectivity remains one of the critical technological hurdles for effective CO₂R.¹⁴

Metalloporphyrin (M–POR) has attracted significant interest.¹⁵ The structure of this molecular catalyst consists of a central metal atom surrounded by a cyclic carbon–nitrogen ring composed of four modified pyrrole subunits. The M–POR structural framework offers a unique combination of tunability of the peripheral ligands, flexibility of the metal centre, and versatility of the oxidation state of the metal, which can be exploited to tailor the catalytic properties of M–PORs for CO₂R¹⁶ and other electrocatalytic reactions such as the oxygen evolution reaction.¹⁷ The synthesis of M–PORs using Earth-abundant elements such as iron^18,19 or nickel²⁰ reduces the synthetic cost of M–PORs compared to rare and precious metals, such as gold²¹ and silver,²² and thus provides a more sustainable alternative to develop a long-term ecologically and economically sustainable process.^23–25

In M–POR complexes, the metal centre can also adopt various oxidation states, specifically neutral [M–POR]⁰, single reduced [M–POR]⁻, or doubly reduced [M–POR]²⁻, which affects the competition between CO₂R and the hydrogen evolution reaction (HER, H⁺ + e⁻ → 1/2H₂), at the cathode.²⁶ A density functional theory (DFT) study by Masood et al. found that lowering the nucleophilicity of the metal centre enhances CO₂ binding relative to proton binding, promoting selectivity for CO₂R.²⁷ Specifically, [Fe–POR]⁻ and [Co–POR]⁻ showed lower electron density at the metal centre, making them less nucleophilic and more selective for CO₂ adsorption and CO formation. In contrast, nucleophilic centres, such as in [RhP]⁰ and [IrP]⁰, favour proton binding, leading to the HER. Fe–POR shows a strong potential in CO₂R applications. In the literature, one of the early studies on the iron tetraphenyl porphyrin complex FeTPP was carried out in the absence of proton donors using NEt₄ClO₄/DMF electrolyte.²⁸ These aprotic conditions showed a moderate yield for CO, which was attributed to the [Fe(TPP)]²⁻ species. The catalyst experienced rapid deactivation during the reaction, primarily due to chemical changes in the ligand, such as carboxylation and hydrogenation. These transformations negatively impacted the catalytic performance, resulting in low FE for CO production. Additionally, the stability of the catalyst was significantly compromised, further limiting its effectiveness in the reaction. In the 1990s, it was discovered that adding mono- (Li⁺, Na⁺) or divalent Lewis acids (Mg²⁺, Ca²⁺, Ba²⁺) to the electrolyte improved the activity and stability of FeTPP catalysts.^29,30 The enhancement followed the order Mg²⁺ ≈ Ca²⁺ > Ba²⁺ > Li⁺ > Na⁺. Long-term electrolysis revealed CO as the major product and formate as a by-product, with the product ratio dependent on the Lewis acid used.

Cyclic voltammetry studies showed that in the presence of CO₂ and a Lewis acid like Mg²⁺, a significant catalytic current appeared at the potential of the [Fe(TPP)]²⁻ species. This indicated that catalysis was initiated during the final electron transfer step. The metal center of [Fe(TPP)]²⁻ underwent nucleophilic attack by CO₂, forming an intermediate Fe(II)–CO₂ adduct. Mg²⁺ facilitated the reaction by forming an ion pair with negatively charged oxygen atoms in the adduct, which pulled an electron pair from Fe(0) to CO₂, weakening C–O bonds and promoting CO release. This demonstrates that Mg²⁺ acts as an efficient Lewis acid, with its ion-pairing ability accelerating the catalytic process. A more significant enhancement of catalytic performance was found with the addition of Brønsted acids (HA). CV performed under CO₂ in the presence of Brønsted acids (HA), yielding an increased catalytic current at the potential of [Fe(TPP)]²⁻ species like that observed when Lewis acid was present.

Additional DFT studies by Cove et al. and Corbin et al. emphasised the importance of oxidation state: reduced forms [M–POR]⁻ and [M–POR]²⁻ showed higher faradaic efficiency (FE) for CO formation compared to neutral [M–POR]⁰, which had weak CO₂-to-formate conversion.^31,32 This highlights that fine-tuning the oxidation state of M–POR catalysts is critical for enhancing CO₂ selectivity and minimising undesired HER activity.^32–35

Following on from our previous computational screening of 110 M–PORs for their ability to activate the CO₂ molecule,³⁶ this study now focuses on the most promising catalysts (Fig. 1) and considers their ability to electrochemically convert the CO₂ molecule to CO and HCOOH. Two-dimensional (2D) models of carbonaceous frameworks made from M–POR were also considered to explore for CO₂R. The objective is to determine what factors could enhance the selectivity towards these C₁ products. This work focuses on C₁ products, such as CO and HCOOH, because atomically dispersed electrocatalysts like M–POR lack the adsorption sites necessary for C–C coupling, which leads to C₂ intermediates.³⁴ Consequently, these catalysts are more likely to facilitate the formation of only C₁ products. Moreover, low-temperature CO₂ electrolysis is very effective in producing high yields of C₁ products, making their production advantageous from a techno-economic evaluation perspective.³² Moreover, C₁ products offer several advantages, including easy storage and transportation, and they serve as valuable chemical intermediates and renewable energy carriers. For example, HCOOH can be used as a fuel in direct formic acid fuel cells,^32,35,37 or CO could be subsequently used as a feedstock for the synthesis of alkanes through the classic Fisher–Tropsch process.³⁸ Moreover, recent advancements in “two-step” tandem electrolysis,^39,40 where CO₂ is initially converted to CO in a CO₂ electrolyser and then CO is further converted to other products in a CO electrolyser, rely on the assumption that the first CO₂ electrolysis cell can convert CO₂ to CO with high selectivity. This necessitates the development of high-performing and sustainable CO₂-to-CO electrocatalysts.

Fig. 1 The metalloporphyrins (M–PORs) with varying metal (M), porphyrin (POR), and oxidation states of the metal (+2, +1, 0). The M–PORs considered are [Ni–POR₁]⁻, [Ni–POR₃]⁻, [Fe–POR₁]⁰, [Fe–POR₁]²⁻, [Fe–POR₂]⁰, [Fe–POR₃]⁰, [Fe–POR₄]⁰, [Fe–POR₄]²⁻, [Fe–POR₅]⁰, [Fe–POR₈]⁰, [Cu–POR₅]²⁻, [Co–POR₂]²⁻, [Co–POR₄]⁻, and [Co–POR₅]⁻.

2. Computational details

2.1 Density functional theory calculations

Depending on the purpose, several DFT codes were used in this study. For the molecular M–PORs, the NWChem software (version 6.6)³⁷ was first used to conduct the full geometry optimisations of the M–PORs in Fig. 1 and the Gaussian16 code⁴¹ was then used to conduct frequency analysis and consider the effect of aqueous environment with the implicit solvation model conductor-like screening model (COSMO).^42,43 The B3LYP functional^44,45 combined with the LANL2DZ basis set⁴⁶ was employed for calculations using both NWChem and Gaussian. This level of theory was selected based on the benchmarking done in our work on CO₂ activation.³⁶ For the 2D M–POR carbonaceous frameworks, the CrystalMaker software⁴⁷ was used to generate 2D models from the optimized structures of the M–PORs. These models were initially subjected to a variable cell optimization at the PBE-D3 level of theory, where the c-axis (perpendicular to the 2D M–POR) was fixed at 20 Å to minimise the interaction between neighbouring cells, and the lengths of the a-axis and b-axis were allowed to relax. Once the unit cell was optimized, the internal coordinates were re-optimized using the hybrid PBE0 exchange correlation functional.⁴⁸ These calculations were conducted using VASP (version 6.4.0).^49,50 VASP was also used to compare the electron localisation function (ELF) of the 1D (molecular) and 2D M–POR systems. The cut-off energy of the plane waves was set to 500 eV, with a 3 × 3 × 3 k-point mesh used for geometry optimisations and a 15 × 15 × 1 k-point mesh used for the static calculation and for the analysis of the electrons and orbitals.⁵¹ Structural relaxations were performed until the maximum residual force on each atom was less than 0.05 eV Å⁻¹. Bader charge analysis was carried out with the core charges included.⁵² The d band centre (e(d)) and projected density of states (PDOS) was calculated using VASPKIT.⁵³

2.2 Thermodynamic and electrochemical stability

The thermodynamic stability of the M–POR and 2D-M–POR catalysts was estimated by computing the binding energy, cohesive energy, and formation energy.^34,54 The binding energy (E_b) was determined using the following equation:

E_b = E_M–POR − E_M − E_POR (1)

where E_M–POR, E_M, and E_POR are the energies of the metalloporphyrin, metal centre, and the porphyrin framework without the metal centre, respectively. The cohesive energy (E_c) was computed using the following equation:where E_M(bulk) is the energy of the bulk unit cell containing N atoms and E_M is the energy of the isolated metal atom in vacuum. The formation energy (E_f) was computed according to:where E_M–POR is the energy of M–POR, E_POR is the energy of the porphyrin framework without the metal centre, E_M(bulk) is the energy of the bulk unit cell containing N atoms and E_M is the energy of the isolated metal atom in vacuum.

The electrochemical stability of the M–POR catalysts was evaluated by computing the dissolution potential (U_diss) of the metal according to the following expression:⁵⁵

where is the standard dissolution potential of the bulk metal and n is the number of electrons involved in the dissolution process. In this work, the values of were taken from Guo et al. and n was set to 2.⁵⁶

2.3 Free energies of reaction

The solution-phase Gibbs free energies (G) of the intermediates involved in the electrochemical CO₂ reduction to CO and HCOOH were calculated according to the expression:

G = E_e + δG_VRT + ΔG_solv (5)

where the first term is the single point electronic energy, the second term is the frequency correction computed within the harmonic potential approximation at standard conditions (T = 298.15 K and p = 1 atm), and the third term is the solvation correction computed using the COSMO model. The calculation of the frequencies was also used to verify the minimum character and, consequently, the stability of the isolated catalysts and intermediates. The free energies of reaction for the concerted proton-coupled electron transfer (PCET) steps involved in the CO₂R were studied based on Nørskov's computational hydrogen electrode (CHE) model.⁵⁷ This model provides an efficient approach to study PCET in electrocatalysis without treating solvated protons explicitly and is widely used in computational electrocatalysis, including the CO₂R on molecular and 2D single metal atomic catalysts.^34,58 In this technique, zero voltage was defined based on the potential energy (μ) of components involved in the reversible hydrogen electrode at all pH, T, and p. Therefore, μ(H⁺) + μ(e⁻) = 1/2μ(H₂) at a potential of 0 V. The limiting potential U_L, an important parameter for evaluating the catalytic activity, was obtained according to the formula:

U_L = −ΔG_max/ne (6)

where ΔG_max is the Gibbs free energy change of the rate-determining step. In the CHE model, the effect of pH and electrode potential U is considered according to:

ΔG = ΔE_e + ΔδG_VRT + ΔΔG_solv + ΔG_pH + ΔG_U (7)

where the fourth term is the free energy correction due to the difference in proton concentration, ΔG_pH = 2.303 × k_B × T × pH, and the last term is the free energy correction due to the difference in electrode potential, ΔG_U = −neU, where n is the number of electrons transferred in the PCET step (n = 1), e is the electronic charge, and U is the applied potential. In this study, both pH and U were set to zero.

3. Results and discussion

3.1 Stability and structural features of M–PORs

As reported in Fig. 2 and Table S1 in the ESI,† the formation energies (E_f) of metal coordination in the M–PORs are all highly negative, indicating the thermodynamic stability of these complexes. However, the formation energies of the M–PORs vary with the metal centre and oxidation state, with the most stable system being [Fe–POR₁]²⁻ (−0.62 eV). Also, the neutral [M–POR]⁰ catalysts are thermodynamically more stable (lower E_b) than the doubly reduced [M–POR]²⁻. According to the values of the dissolution potential of the M–PORs (Table S2 in the ESI†), all of the catalysts have values of U_diss between −0.3 and 0.5 V, which are higher than the experimentally applied potentials for the CO₂R to CO (E⁰ = −0.52 V) and CHCOOH (E⁰ = −0.61 V) and of most products of the CO₂R.⁵⁹ This suggests that these active sites are all generally stable against dissolution in the CO₂R and have good electrochemical stability. Consequently, the reaction energetics of the CO₂R on the M–POR catalysts can be examined.

Fig. 2 Thermodynamic stability of the M–PORs. Values of the cohesive energy (E_c) of the transition metal (M) bulk, binding energy between M and POR (E_b), and formation energy (E_f) of M–POR. Pink, yellow, purple, and blue zones correspond to the Ni–POR, Fe–POR, Cu–POR, and Co–POR catalysts, respectively.

3.2 Mechanisms of reduction reactions on M–PORs

3.2.1 Electrochemical CO₂ reduction to carbon monoxide and formic acid. This section presents calculations of the electrochemical conversion of CO₂ to CO and HCOOH. Two reaction mechanisms are considered: proton-coupled electron transfer (PCET) and separated proton transfer–electron transfer (PT–ET). In the PCET, the transfer of a proton (H⁺) and an electron (e⁻) occurs simultaneously. In contrast, in the PT–ET these steps occur sequentially.
Proton-coupled electron transfer. The mechanism for PCET to generate CO and HCOOH is shown in Scheme 1.⁶⁰ After the adsorption of CO₂ to the catalyst (CO₂ → *CO₂), the first PCET step leads to two possible intermediates, *OCHO or *OCOH, depending on the atom coordinated to the catalyst, O or C, respectively. Depending on the intermediate, the second PCET will then generate HCOOH or CO. The free energy of reactions (ΔG) of the elementary steps leading to the formation of HCOOH and CO were computed using the CHE model. For HCOOH, these steps are the PCET to convert adsorbed to the O-coordinated intermediate (, ΔG_*OCHO) and the next PCET converts adsorbed *OCHO to gas-phase formic acid (*OCHO + H⁺ + e⁻ → HCOOH, ΔG_HCOOH). For CO, the elementary steps are the PCET to convert adsorbed *CO₂ to the C-coordinated intermediate (*CO₂ + H⁺ + e⁻ → *COOH, ΔG_*COOH), and the next PCET converts adsorbed *OCOH to adsorbed carbon monoxide (*COOH + H⁺ + e⁻ → *CO + H₂O, ΔG_*CO), which can then be released from the catalyst surface to form gas-phase CO (ΔG_CO).

Scheme 1 Elementary steps for the two proton/two electron (2H⁺/2e⁻) electrochemical CO₂ conversion to CO and HCOOH according to the PCET mechanism. The (*) is used to show adsorbed species.

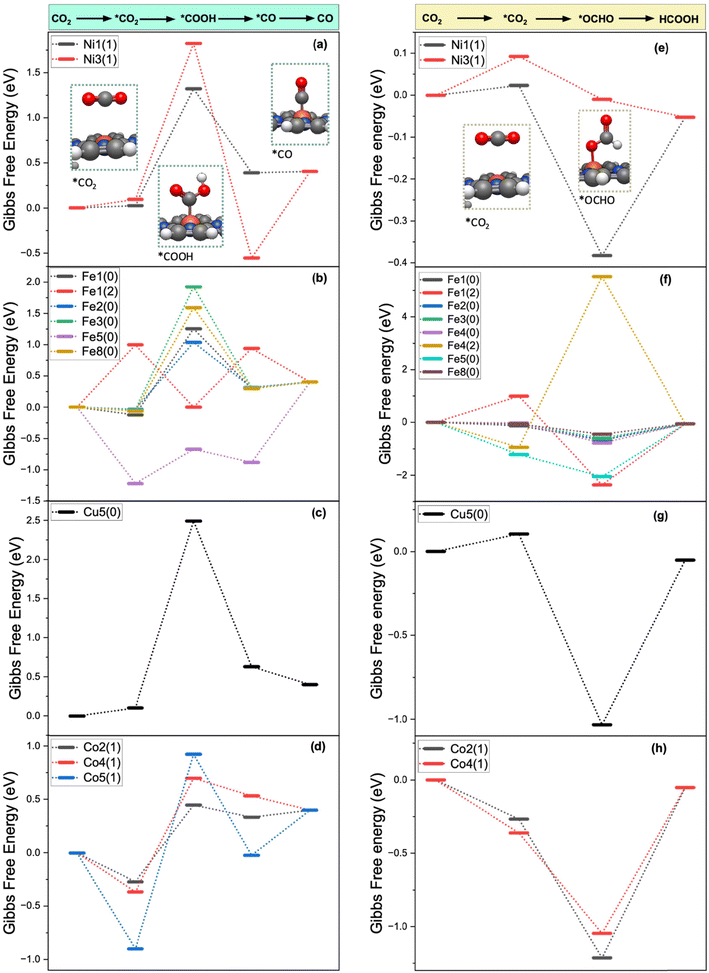
The Gibbs free energy diagrams of the CO₂R for the PCET pathways leading to the formation of CO and HCOOH on Ni–POR ([Ni–POR_1,3]⁻), Fe–POR ([Fe–POR₁]^0,2−, [Fe–POR₂]⁰, [Fe–POR₃]⁰, [Fe–POR₄]^0,2−, [Fe–POR₅]⁰, [Fe–POR₈]⁰), Cu–POR ([Cu–POR₅]²⁻), and Co–POR ([Co–POR_2,4,5]⁻) are reported in Fig. 3. The stability of the intermediates (*OCHO and *CO) controlling the formation of CO is significantly affected by the porphyrin ligands, metal centres, and oxidation state. The potential limiting step (ΔG_PLS), identified as the step with the highest positive ΔG, serves as an indicator of the catalytic performance of an M–POR. Specifically, a high ΔG_PLS signifies poor catalytic performance. The Gibbs free energy diagram for the CO₂R pathways to CO and HCOOH on each M–POR is discussed in detail below.

Fig. 3 Gibbs free energy diagram for the CO₂R to CO according to the PCET mechanism on (a) Ni–POR, (b) Fe–POR, (c) Cu–POR, and (d) Co–POR. Gibbs free energy diagram for the CO₂R to HCOOH according to the PCET mechanism on (e) Ni–POR, (f) Fe–POR, (g) Cu–POR, and (h) Co–POR. Calculations conducted at the B3LYP/LANL2DZ/COSMO level of theory. Values in eV.

Ni–POR. According to Fig. 3(a) and (e), the adsorption of CO₂ is more favourable on [Ni–POR₁]⁻ than on [Ni–POR₃]⁻. This can be justified by the larger orbital splitting on [Ni–POR₁]⁻ (11.1 eV) than on [Ni–POR₃]⁻ (2.32 eV), as a larger orbital splitting leads to a less favourable adsorption (see Fig. S3(a) and (c) in the ESI†), thus making it more difficult to activate CO₂. The formation of *OCHO is most favourable on [Ni–POR₁]⁻ because of the lower free energy of the OCHO* intermediate (ΔG_*OCHO = −0.41 eV), which suggests that the CO₂R is more selective towards HCOOH on this system. Similarly, the formation of OCHO* is most favourable on [Ni–POR₃]⁻¹ (ΔG_*OCHO = −0.10 eV). The formation of *CO is more favourable on [Ni–POR₃]⁻ with ΔG_*CO = −0.55 eV than on [Ni–POR₁]⁻. To summarise, Ni–POR systems favour the formation of HCOOH over the formation of CO.
Fe–POR. For the Fe–POR catalysts in Fig. 3(b) and (f), the most favourable system for the formation of *CO is [Fe–POR₅]⁰ (DG_*CO2 = −1.22 eV), while [Fe–POR₁]²⁻ has the least favourable CO₂ adsorption (DG_*CO2 = 1.0 eV). All Fe–POR systems favour the formation of *OCHO over *COOH except for [Fe–POR₅]⁰, which favours *COOH by 0.04 eV. The overall trend from the most favourable to the least favourable Fe catalyst based on the DG_PLS of the reaction for HCOOH formation is [Fe–POR₄]²⁻ > [Fe–POR₈]⁰ > [Fe–POR₃]⁰ > [Fe–POR₂]⁰ > [Fe–POR₁]⁰ > [Fe–POR₄]⁰ > [Fe–POR₅]⁰. This highlights the significance of the effect of moving from d⁸ to d⁶ electron configuration on the CO₂R: [Fe–POR₁]²⁻ (d⁸) is more reactive than [Fe–POR₁]⁰ (d⁶). These complexes are all high spin. Moreover, ligands with alkyl benzyl ([Fe–POR₄]²⁻ and [Fe–POR₈]⁰ in Fig. 1) are more reactive than those with carboxyl benzyl groups ([Fe–POR₂]⁰). However, the M–POR [Fe–POR₅]⁰ is shown to be the least reactive despite the less steric hindrance, which indicates the importance of the ligands in M–POR catalysts in affecting their catalytic behaviour. Insights into the d-orbital splitting were obtained by computing the PDOS of the d-orbitals of the metal centre (Fig. S3 in the ESI†) to determine the energy difference between the d-orbitals with maximum PDOS (Fig. S4†). The orbitals presented for the PDOS of M–POR-CO and M–POR-HCOOH (Fig. S3†) show strong overlap and, thus, strong bonding. Based on the d-band values, Fe systems exhibit superior catalytic properties compared to other M–POR systems. The d-band centre is calculated in VASP by analysing the PDOS of the metal's d-orbitals in the system. The d-band centre is defined as the energy of the centre of mass of the d-states, often measured relative to the Fermi level.⁶¹ It correlates to catalytic performance because a d-band centre closer to the Fermi level typically enhances adsorption of reaction intermediates, thereby improving catalytic activity. If the d-band centre is too high or low, it may lead to too weak or too strong adsorption, respectively, which can reduce efficiency in catalytic reactions. The [Fe–POR₃-CO]⁰ system has a d-band center value of −0.30 eV, positioned close to the Fermi level (Fig. S4(k)†). According to previous reports,^62,63 the closer the d-band centre is to the Fermi level, the higher the electron occupation of the bonding state is, and the stronger the adsorption strength of the adsorbed molecules on the catalyst surface is because of the increase of orbital overlap and enhancement of electron donation and back-donation between the metal centre and the adsorbed CO₂.⁶⁴ This electronic effect stabilizes the CO₂ adsorption intermediate by forming stronger chemical bonds and lowering the energy of the intermediate state. Consequently, the stabilization provided by the optimal d-band positioning directly contributes to facilitating the CO₂ adsorption step, identified as the rate-determining step in our catalytic mechanism. The [Fe–POR₄]²⁻ system, with a d-band centre value of −0.32 eV (Fig. S4(p)†), demonstrates the best catalytic performance for HCOOH formation. Applying a potential of −1 V makes CO₂R to CO on [Fe–POR₁]⁰ more favourable than at 0 V, as ΔG decreases from −0.39 eV (at 0 V) to −1.39 eV (at −1 V; Fig. S8†). This is consistent with Lu's findings, which show that higher applied potentials increase the FE for CO formation.⁶⁵ The applied potential also favours the HER (−0.39 eV), although it is not as favoured as CO formation.
Cu–POR. [Cu–POR₅]⁰ in Fig. 3 was the only Cu–POR system that activates CO₂ in our previous study.³⁶ This seems feasible as all Cu–PORs are d¹⁰, making them very stable. However, in the neutral state, they are in d⁹ and can donate an electron to CO₂ (Table S2 in the ESI†). In Fig. 3(c), the pathways to both HCOOH and CO formation have very stable intermediates which lead to high DG_PLS. The [Cu–POR₅]²⁻ system shows to be consistent for CO and HCOOH formation with d-band centre values of −2.54 eV and −2.20 eV, respectively (Fig. S4(u) and (v)†), which suggests poor binding of substrates to the Cu centre. In a square planar d⁹ configuration, Cu(II) metal has fewer available low-energy empty orbitals to effectively participate in back-donation to CO₂. In contrast, Fe(II) metals in a d⁶ square planar configuration can engage in stronger π-backbonding, where electron density from the metal is donated into the antibonding π* orbitals of CO₂. This increased electron donation helps activate CO₂ by weakening the C–O bonds and bending its linear structure, facilitating reduction. Because Cu(II) in a d⁹ state lacks a fully effective π-backbonding interaction, it forms weaker bonds with CO₂, making its activation less favorable compared to a d⁶ metal. This could also suggest that the substrates can easily be desorbed from Cu–POR as there is less orbital overlap between the Cu centre and the substrate orbitals, meaning less electrons shared.
Co–POR. In Fig. 3(d) and (h), the CO₂ adsorption is favourable on all Co-MORs, with free energies of adsorption being between DG_*CO2 = −0.90 eV on [Co–POR₅]⁰ and DG_*CO2 = −0.27 eV and the least favourable is on [Co–POR₂]⁰. The [Co–POR₂]⁻ and [Co–POR₄]⁻¹ catalysts favour the formation of the *OCHO intermediate (DG_OCHO* = −0.95 eV and −0.68 eV, respectively) over *COOH (DG_*COOH = 0.45 eV and 0.70 eV, respectively). However, [Co–POR₅]⁻ favours *COOH (DG_COOH* = 0.92 eV) and highly disfavours OCHO* formation. Overall, the most favourable CO₂R pathways to CO and HCOOH occur on [Co–POR₂]⁻¹, where DG = 0.67 eV for CO formation and DG = 0.05 eV for HCOOH formation.
Proton transfer–electron transfer. Gottle and Koper proposed an alternative PT–ET mechanism for the electrochemical CO₂ conversion to CO on M–POR,⁶⁶ which includes the following elementary steps (Scheme 2): (i) CO₂ adsorption onto the metal centre of M–POR; (ii) protonation of the [M–POR(CO₂)] intermediate to form bound formate [M–POR(C(OH)O)]; (iii) protonation of the [M–POR(C(OH)O)] intermediate to form bound CO, [M–POR(CO)]; (iv) electron transfer to the [M–POR(CO)] intermediate to release CO; (v) electron transfer to reduce the metalloporphyrin to its initial oxidation state. In steps 2 and 3, H₃O⁺ was used as the proton source. The reaction free energy diagrams for the PT–ET on Ni–POR ([Ni–POR₁]⁻, [Ni–POR₃]⁻), Fe–POR ([Fe–POR₁]⁰, [Fe–POR₁]²⁻, [Fe–POR₂]⁰, [Fe–POR₃]⁰, [Fe–POR₄]⁰, [Fe–POR₄]²⁻, [Fe–POR₅]⁰, [Fe–POR₈]⁰), Cu–POR ([Cu–POR₅]²⁻), and Co–POR ([Co–POR₂]²⁻, [Co–POR₄]⁻, [Co–POR₅]⁻) are reported in Fig. S3 of the ESI.† The reaction free energies for PT–ET are significantly higher than those of PCET, which makes PCET by far the most favourable pathway for the CO₂R on M–POR.

Scheme 2 Elementary steps in the PT–ET mechanism of CO₂-to-CO conversion with the initial CO₂ adsorption taking place with the metal in the neutral [M–POR]⁰ oxidation state.

3.2.2 Hydrogen evolution reaction. In aqueous solutions, there is a continuous competition between the CO₂R and the HER.⁶⁷ Typically, the FE of the HER outperforms that of CO₂R due to its significantly lower overpotential on most M–POR catalysts.⁶⁸ The free energy of reaction for the HER on 16 M–PORs is reported in Fig. 4. Most systems exhibit a positive free energy of proton H adsorption (ΔG_*H). However, there are exceptions. [Fe–POR₃]⁰ and [Fe–POR₅]⁰ show ΔG_*H values of −0.01 eV and −0.63 eV, respectively, which favours the HER, potentially making them less suitable for CO₂R. This could be because they are both d⁶ systems, and from our previous work on CO₂ activation,³⁶ M–PORs with the metal in the d⁶ configuration were found to not favour both CO₂R and the HER. In contrast, [Ni–POR₃]⁻¹ has the highest ΔG_*H, 2.73 eV, and thus is not active towards the HER.⁵⁶ DFT calculations of the HER on a transition metal embedded in single vacancies of graphene reported ΔG_*H of 1.46 eV for Ni and 0.14 eV for Fe,⁶⁹ supporting the trend that Ni–POR is less favourable to the HER than Fe–POR.

Fig. 4 Gibbs free energy diagram for the HER on (a) Ni–POR, (b) Fe–POR, (c) Cu–POR, and (d) Co–POR. Calculations conducted at the B3LYP/LANL2DZ/COSMO level of theory. Values in eV.

3.2.3 Selectivity. In electrocatalysis, the overpotential (η) represents the extra voltage required beyond the theoretical value necessary to drive an electrochemical reaction. Computationally, the overpotential can be obtained from the difference between the equilibrium (U_eq.) and the limiting (U_eq.) potentials:

η = U_eq. − U_L (8)

Thus, η represents the minimum applied potential required to facilitate the formation of relevant intermediates. This value reflects the thermodynamic barrier the catalyst needs to overcome. Large values of η indicate a poor catalytic performance. Therefore, for efficient CO₂R, the desired catalyst should exhibit lower overpotentials for CO₂R compared to the HER. This ensures that CO₂R is prioritised over the competing HER process. The overpotentials for the CO₂R to CO and HCOOH and for the HER on the M–POR catalysts are summarised in Fig. 5. Almost all systems favour HCOOH formation over H₂ or CO formation. Overall, the systems favourable to HCOOH are ranked in the following order: [Fe–POR₅]⁰ > [Co–POR₅]⁻ > [Co–POR₄]⁻ > [Co–POR₂]⁻ > [Fe–POR₁]⁰ > [Fe–POR₈]⁰ > [Fe–POR₃]⁰ ≃ [Fe–POR₂]⁰ > [Fe–POR₄]⁰ > [Ni–POR₁]⁻ > [Ni–POR₃]⁻. Thus, [Fe–POR₅]⁰ is the most efficient catalyst with the lowest overpotential (−2.06 V). On the other hand, HER is generally favoured over the CO₂-to-CO conversion process, except for [Ni–POR₁]⁻ and [Ni–POR₃]⁻, which exhibit much lower overpotentials (high catalytic activity) for CO formation (η = 1.12 V and 1.82 V, respectively) compared to H₂ (η = 2.41 V and 2.73 V, respectively).

Fig. 5 Overpotential for the electrocatalytic formation of (a) CO, (b) HCOOH, and (c) H₂ on M–POR. Values in V.

3.3 CO₂R and the HER on two-dimensional M–PORs

The versatility of M–PORs, coming from the variety of available metal centres and organic linkers, makes them ideal building blocks for advanced porous frameworks with unique properties for diverse catalytic applications including CO₂ reduction.¹⁶ 2D M–PORs were thus designed using the most promising molecular M–POR catalysts to investigate their activity towards CO₂R. Three Fe–PORs were selected as precursors for the generation of 2D frameworks, as shown in Fig. 6. These systems were chosen based on the efficiency of their 1D counterparts in the CO₂-to-CO or CO₂-to-HCOOH conversion process. Moreover, their potential suitability for forming stable 2D structures was evaluated by computing their cohesive energy, binding energy, formation energy, and dissolution potential (Fig. S6 in the ESI†). The 2D Fe–POR systems display good thermodynamic stability, attributed to the absence of heteroatoms in the peripheral ligands, which often introduces structural or electronic instabilities in similar complexes.^70,71

Fig. 6 1D and 2D Fe–POR systems considered for the carbonaceous framework analysis. Structures obtained at the PBE0 level of theory using VASP.

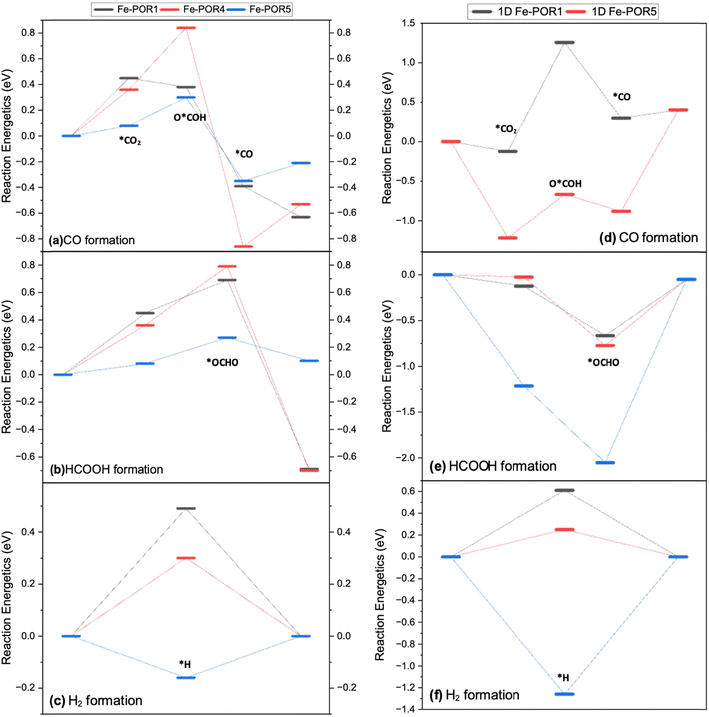
The free energy pathways for the CO₂R to CO and HCOOH and the HER to H₂ on the 2D and 1D Fe–POR catalysts are compared in Fig. 7. The stability of the intermediates *OCHO and *COOH, which control the formation of HCOOH and CO, respectively, is significantly affected by the POR ligands. For CO formation (Fig. 7(a)) the adsorption of CO₂ is more favourable on 2D Fe–POR₅ than on 2D Fe–POR₁ and 2D Fe–POR₄ ( and 0.36, eV respectively). As all systems have the same metal centre, the metal does not influence the stability of the intermediates. The adsorption of *COOH is also most favourable on 2D Fe–POR₅ with DG_*COOH = 0.30 eV, suggesting 2D Fe–POR₅ as the most favourable system for CO formation and this is the G_PLS. The strongest *CO adsorption is found with 2D Fe–POR₄ at −0.86 eV, leading to unfavourable desorption of CO. For HCOOH formation (Fig. 7(b)), 2D Fe–POR₅ shows the most favourable CO₂ adsorption (DG_*CO2 = 0.08 eV) and the most favourable *OCHO intermediate adsorption (DG_*OCHO = 0.27 eV). This suggests that 2D Fe–POR₅ is the most promising candidate for HCOOH formation. 2D Fe–POR₁ and 2D Fe–POR₄ show similar reaction thermodynamics, which suggests poor favourability to HCOOH formation. Therefore, from the free energy profiles, 2D Fe–POR₅ is the most favourable for C₁ product formation. However, when looking at the 1D Fe–POR, the order of reactivity is [Fe–POR₁]⁰ > [Fe–POR₄]⁰ > [Fe–POR₅]⁰, with [Fe–POR₅]⁰ being the least favourable.

Fig. 7 Reaction energetics for the CO₂R to (a) CO and (b) HCOOH formation and (c) the HER to H₂ formation on the 2D Fe–POR_1,4,5 catalysts and reaction energetics for the CO₂R to (d) CO and (e) HCOOH formation and (f) the HER to H₂ formation on the 1D-Fe–POR_1,4,5 catalysts. Calculations conducted at the PBE0 level of theory. Values in eV.

These results suggest that 2D Fe–POR₅ is the most promising candidate for HCOOH formation. In contrast, 2D Fe–POR₁ and 2D Fe–POR₄ exhibit similar reaction thermodynamics, indicating poor favourability for HCOOH production. Interestingly, while Fe–POR₅ is the least reactive in the 1D configuration ([Fe–POR₁]⁰ > [Fe–POR4]⁰ > [Fe–POR₅]⁰), transitioning to the 2D structure significantly enhances its catalytic activity. This trend correlates with the shift in its d-band center, which decreases from −0.64 eV (Fig. S3(q)†) in 1D to −2.14 eV (Fig. S7(e)†) in 2D, suggesting stronger adsorption and activation of CO₂.

A similar trend is observed in the HER. Among the 2D Fe–POR catalysts, Fe–POR₅ exhibits the most favorable adsorption of the H intermediate (DG_*H = −0.16 eV), while 2D Fe–POR₁ and 2D Fe–POR₄ have positive adsorption energies, indicating lower activity. Notably, the reactivity trend for HER in the 2D configuration follows the same order as in the 1D configuration (Fig. 7(d–f)), reinforcing the relationship between electronic structure and catalytic performance.

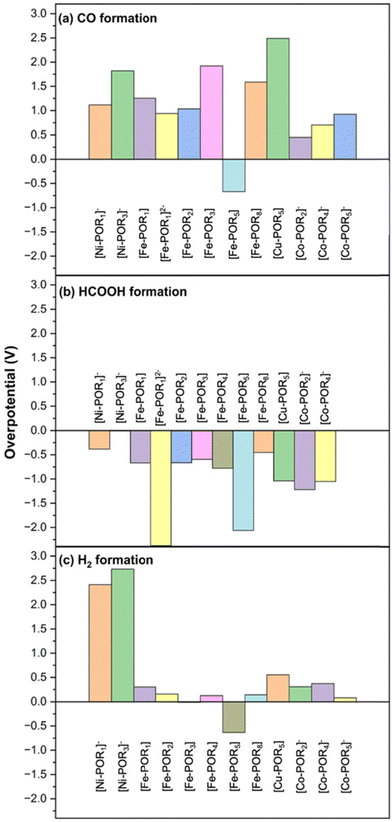
The overpotentials for the eCO₂R and HER on the 2D M–POR are shown in Fig. 8. For Fe–POR₅, negative overpotentials were observed for both HCOOH (−0.09 V) and H₂ (−0.08 V), indicating that both reactions are highly favoured with no significant preference for one over the other. In contrast, Fe–POR₁ exhibited a distinct difference in overpotentials, with HCOOH formation being more favoured (0.12 V) compared to H₂ formation (0.24 V).

Fig. 8 Overpotentials for the H₂, CO, and HCOOH formation on the 2D Fe–POR₅.

To gain deeper insight into the electronic properties influencing CO₂ activation, the electron localisation function (ELF) was computed for 2D Fe–POR_1,4,5 catalysts. The ELF provides a measure of electron density distribution, particularly around the Fe center, helping to visualise the degree of charge accumulation and its influence on adsorption. The ELF maps for CO⁻ and OCOH⁻ adsorbed M–POR systems (Fig. 9) reveal notable differences in electron density distribution. In Fe–POR₁ (Fig. 9(a)), asymmetric electron density accumulation is observed, particularly on one side of the extended porphyrin ring. This localised electron density may guide CO₂ adsorption towards the catalytic Fe center, facilitating activation. In contrast, Fe–POR₄ exhibits a more dispersed and weakly localised electron density, which could contribute to its poorer catalytic performance by reducing effective charge transfer to the adsorbate. Finally, Fe–POR₅ displays strong regions of localized electron density near the Fe center, possibly due to its smaller porphyrin framework restricting charge delocalisation. This localised charge distribution may enhance Fe–CO₂ interactions, leading to improved catalytic activity.

Fig. 9 ELF plots for CO (top) adsorbed on (a) 2D-Fe–POR₁, (b) 2D-Fe–POR₄, and (c) 2D-Fe–POR₅, and for OCOH (bottom) adsorbed on (a) 2D-Fe–POR₁, (b) 2D-Fe–POR₄, and (c) 2D-Fe–POR₅.

Further insights can be drawn from projected density of states (PDOS) analysis (Fig. S7†). Fe–POR₅ exhibits the smallest bandgap (−2.14 eV for CO-adsorbed and −1.91 eV for OCOH-adsorbed configurations), suggesting enhanced electronic conductivity, which may facilitate charge transfer processes during CO₂ reduction. The combination of ELF and PDOS data highlights the importance of electronic structure in governing catalytic performance, with Fe–POR₅ emerging as the most promising candidate among the studied systems.

4. Conclusions

A computational investigation of the electrocatalytic CO₂ reduction reaction on various metalloporphyrin catalysts with different metal centers (Ni, Fe, Cu, and Co), ligands, and oxidation states was conducted using DFT calculations. Thermodynamic and electrochemical stability analyses revealed that neutral systems exhibit higher stability compared to charged systems, with doubly reduced systems being the least stable. Two possible reaction mechanisms—proton-coupled electron transfer and sequential proton transfer–electron transfer—were explored, with PCET identified as the significantly more favourable pathway, predominantly forming HCOOH rather than CO. Among the studied catalysts, Fe–POR demonstrated superior catalytic performance towards these C₁ products. Comparison of overpotentials for CO₂ reduction and the competing hydrogen evolution reaction showed that most systems preferentially produce HCOOH.

Transitioning to two-dimensional (2D) frameworks, particularly with Fe–POR systems, led to enhanced catalytic activity compared to their molecular counterparts, highlighting the potential for these frameworks in practical electrocatalysis applications. The main electronic descriptor impacting catalytic performance and product selectivity in both molecular and 2D M–POR frameworks appears to be the position of the d-band center relative to the Fermi level.

This study provides fundamental insights into the rational design and optimization of effective metalloporphyrin-based electrocatalysts, guiding future development toward efficient and selective CO₂ conversion technologies.

Data availability

The data supporting the findings of this study are openly accessible on ZENODO at https://zenodo.org/records/11361107, reference number 11361107. Additionally, the authors confirm that the data are included in the ESI† and can also be requested from the corresponding author, DDT.

Conflicts of interest

The authors declare no competing financial interest.

Acknowledgements

This work was supported by the UK Royal Society International Exchanges Cost Share (IEC\R3\193106). We thank Prof. Hirotomo Nishihara and his team at Tohoku University for useful discussions. We are grateful to the UK Materials and Molecular Modelling Hub for computational resources, which is partially funded by EPSRC (EP/P020194/1). Further, D. D. T. thanks the Leverhulme Trust (RPG-2023-239) for resources supporting projects advancing materials characterization by computational means. Via our membership of the UK HEC Materials Chemistry Consortium, which is funded by EPSRC (EP/L000202), this work used the ARCHER2 UK National Supercomputing Service (https://www.archer.ac.uk). This research utilised Queen Mary's Apocrita HPC facility, supported by QMUL Research-IT. https://doi.org/10.5281/zenodo.438045.

References

1. P. Friedlingstein, M. W. Jones, M. O'Sullivan, R. M. Andrew, D. C. E. Bakker, J. Hauck, C. Le Quéré, G. P. Peters, W. Peters, J. Pongratz, S. Sitch, J. G. Canadell, P. Ciais, R. B. Jackson, S. R. Alin, P. Anthoni, N. R. Bates, M. Becker, N. Bellouin, L. Bopp, T. T. T. Chau, F. Chevallier, L. P. Chini, M. Cronin, K. I. Currie, B. Decharme, L. M. Djeutchouang, X. Dou, W. Evans, R. A. Feely, L. Feng, T. Gasser, D. Gilfillan, T. Gkritzalis, G. Grassi, L. Gregor, N. Gruber, Ö. Gürses, I. Harris, R. A. Houghton, G. C. Hurtt, Y. Iida, T. Ilyina, I. T. Luijkx, A. Jain, S. D. Jones, E. Kato, D. Kennedy, K. Klein Goldewijk, J. Knauer, J. I. Korsbakken, A. Körtzinger, P. Landschützer, S. K. Lauvset, N. Lefèvre, S. Lienert, J. Liu, G. Marland, P. C. McGuire, J. R. Melton, D. R. Munro, J. E. M. S. Nabel, S.-I. Nakaoka, Y. Niwa, T. Ono, D. Pierrot, B. Poulter, G. Rehder, L. Resplandy, E. Robertson, C. Rödenbeck, T. M. Rosan, J. Schwinger, C. Schwingshackl, R. Séférian, A. J. Sutton, C. Sweeney, T. Tanhua, P. P. Tans, H. Tian, B. Tilbrook, F. Tubiello, G. R. van der Werf, N. Vuichard, C. Wada, R. Wanninkhof, A. J. Watson, D. Willis, A. J. Wiltshire, W. Yuan, C. Yue, X. Yue, S. Zaehle and J. Zeng, Earth Syst. Sci. Data, 2022, 14, 1917–2005.
2. S. Chu and A. Majumdar, Nature, 2012, 488, 294–303.
3. J. B. Greenblatt, D. J. Miller, J. W. Ager, F. A. Houle and I. D. Sharp, Joule, 2018, 2, 381–420.
4. F. A. Rahman, M. M. A. Aziz, R. Saidur, W. A. W. A. Bakar, M. R. Hainin, R. Putrajaya and N. A. Hassan, Renewable Sustainable Energy Rev., 2017, 71, 112–126.
5. L. Chen, C. Tang, K. Davey, Y. Zheng, Y. Jiao and S.-Z. Qiao, Chem. Sci., 2021, 12, 8079–8087.
6. W. Zhang, Y. Hu, L. Ma, G. Zhu, Y. Wang, X. Xue, R. Chen, S. Yang and Z. Jin, Adv. Sci., 2018, 5, 205–239.
7. J. D. Shakun, P. U. Clark, F. He, S. A. Marcott, A. C. Mix, Z. Liu, B. Otto-Bliesner, A. Schmittner and E. Bard, Nature, 2012, 484, 49–54.
8. V. K. Arora, J. F. Scinocca, G. J. Boer, J. R. Christian, K. L. Denman, G. M. Flato, V. V. Kharin, W. G. Lee and W. J. Merryfield, Geophys. Res. Lett., 2011, 38, L05805.
9. W. Lai, Y. Qiao, J. Zhang, Z. Lin and H. Huang, Energy Environ. Sci., 2022, 15, 3603–3629.
10. B. Chang, H. Pang, F. Raziq, S. Wang, K.-W. Huang, J. Ye and H. Zhang, Energy Environ. Sci., 2023, 16, 4714–4758.
11. M. Jouny, W. Luc and F. Jiao, Nat. Catal., 2018, 1, 748–755.
12. C. Chen, X. Yan, S. Liu, Y. Wu, Q. Wan, X. Sun, Q. Zhu, H. Liu, J. Ma, L. Zheng, H. Wu and B. Han, Angew. Chem., 2020, 132, 16601–16606.
13. T. Kim and G. T. R. Palmore, Nat. Commun., 2020, 11, 3622.
14. R. Song, W. Zhu, J. Fu, Y. Chen, L. Liu, J. Zhang, Y. Lin and J. Zhu, Adv. Mater., 2020, 35, 1–25.
15. P. Gotico, Z. Halime and A. Aukauloo, Dalton Trans., 2020, 49, 2381–2396.
16. S. Gu, A. N. Marianov, T. Lu and J. Zhong, Chem. Eng. J., 2023, 470, 144249.
17. H. Lv, X. Zhang, K. Guo, J. Han, H. Guo, H. Lei, X. Li, W. Zhang, U. Apfel and R. Cao, Angew. Chem., Int. Ed., 2023, 62, 1–6.
18. B. Mondal, P. Sen, A. Rana, D. Saha, P. Das and A. Dey, ACS Catal., 2019, 9, 3895–3899.
19. C. Costentin, S. Drouet, M. Robert and J.-M. Savéant, Science, 2012, 338, 90–94.
20. M. Abdinejad, L. F. B. Wilm, F. Dielmann and H. B. Kraatz, ACS Sustainable Chem. Eng., 2021, 9, 521–530.
21. Z. Cao, S. B. Zacate, X. Sun, J. Liu, E. M. Hale, W. P. Carson, S. B. Tyndall, J. Xu, X. Liu, X. Liu, C. Song, J. Luo, M. Cheng, X. Wen and W. Liu, Angew. Chem., 2018, 130, 12857–12861.
22. G. Dutta, A. K. Jana, D. K. Singh, M. Eswaramoorthy and S. Natarajan, Chem. – Asian J., 2018, 13, 2677–2684.
23. X. Zhang, X. Li, D. Zhang, N. Q. Su, W. Yang, H. O. Everitt and J. Liu, Nat. Commun., 2017, 8, 14542.
24. S. Park, D. Bézier and M. Brookhart, J. Am. Chem. Soc., 2012, 134, 11404–11407.
25. A. Klinkova, P. De Luna, C.-T. Dinh, O. Voznyy, E. M. Larin, E. Kumacheva and E. H. Sargent, ACS Catal., 2016, 6, 8115–8120.
26. C. Römelt, S. Ye, E. Bill, T. Weyhermüller, M. van Gastel and F. Neese, Inorg. Chem., 2018, 57, 2141–2148.
27. Z. Masood and Q. Ge, Molecules, 2023, 28, 1–12.
28. M. Hammouche, D. Lexa, J. M. Savéant and M. Momenteau, J. Electroanal. Chem. Interfacial Electrochem., 1988, 249, 347–351.
29. I. Bhugun, D. Lexa and J.-M. Savéant, J. Phys. Chem., 1996, 100, 19981–19985.
30. M. Hammouche, D. Lexa, M. Momenteau and J. M. Saveant, J. Am. Chem. Soc., 1991, 113, 8455–8466.
31. H. Cove, D. Toroz and D. Di Tommaso, Mol. Catal., 2020, 498, 111248.
32. N. Corbin, J. Zeng, K. Williams and K. Manthiram, Nano Res., 2019, 12, 2093–2125.
33. E. Boutin, L. Merakeb, B. Ma, B. Boudy, M. Wang, J. Bonin, E. Anxolabéhère-Mallart and M. Robert, Chem. Soc. Rev., 2020, 49, 5772–5809.
34. D. Di Tommaso, D. Di, T. Q. Zhao, R. Crespo-Otero and B. Y. Xia, J. Energy Chem., 2023, 85, 490–500.
35. H. Shin, K. U. Hansen and F. Jiao, Nat. Sustain., 2021, 4, 911–919.
36. A. T. Uddin, Q. Zhao, D. Toroz, R. Crespo-Otero and D. Di Tommaso, Mol. Catal., 2024, 565, 114386.
37. E. Aprà, E. J. Bylaska, W. A. de Jong, N. Govind, K. Kowalski, T. P. Straatsma, M. Valiev, H. J. J. van Dam, Y. Alexeev, J. Anchell, V. Anisimov, F. W. Aquino, R. Atta-Fynn, J. Autschbach, N. P. Bauman, J. C. Becca, D. E. Bernholdt, K. Bhaskaran-Nair, S. Bogatko, P. Borowski, J. Boschen, J. Brabec, A. Bruner, E. Cauët, Y. Chen, G. N. Chuev, C. J. Cramer, J. Daily, M. J. O. Deegan, T. H. Dunning, M. Dupuis, K. G. Dyall, G. I. Fann, S. A. Fischer, A. Fonari, H. Früchtl, L. Gagliardi, J. Garza, N. Gawande, S. Ghosh, K. Glaesemann, A. W. Götz, J. Hammond, V. Helms, E. D. Hermes, K. Hirao, S. Hirata, M. Jacquelin, L. Jensen, B. G. Johnson, H. Jónsson, R. A. Kendall, M. Klemm, R. Kobayashi, V. Konkov, S. Krishnamoorthy, M. Krishnan, Z. Lin, R. D. Lins, R. J. Littlefield, A. J. Logsdail, K. Lopata, W. Ma, A. v. Marenich, J. Martin del Campo, D. Mejia-Rodriguez, J. E. Moore, J. M. Mullin, T. Nakajima, D. R. Nascimento, J. A. Nichols, P. J. Nichols, J. Nieplocha, A. Otero-de-la-Roza, B. Palmer, A. Panyala, T. Pirojsirikul, B. Peng, R. Peverati, J. Pittner, L. Pollack, R. M. Richard, P. Sadayappan, G. C. Schatz, W. A. Shelton, D. W. Silverstein, D. M. A. Smith, T. A. Soares, D. Song, M. Swart, H. L. Taylor, G. S. Thomas, V. Tipparaju, D. G. Truhlar, K. Tsemekhman, T. van Voorhis, Á. Vázquez-Mayagoitia, P. Verma, O. Villa, A. Vishnu, K. D. Vogiatzis, D. Wang, J. H. Weare, M. J. Williamson, T. L. Windus, K. Woliński, A. T. Wong, Q. Wu, C. Yang, Q. Yu, M. Zacharias, Z. Zhang, Y. Zhao and R. J. Harrison, J. Chem. Phys., 2020, 152, 184102.
38. H. Jahangiri, J. Bennett, P. Mahjoubi, K. Wilson and S. Gu, Catal. Sci. Technol., 2014, 4, 2210–2229.
39. T. Möller, M. Filippi, S. Brückner, W. Ju and P. Strasser, Nat. Commun., 2023, 14, 5680.
40. T. Burdyny and F. M. Mulder, Joule, 2024, 8, 2449–2452.
41. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision C.01, Gaussian, Inc., Wallingford, CT, 2016.
42. A. Klamt and G. Schürmann, J. Chem. Soc., Perkin Trans. 2, 1993, 799–805.
43. A. Klamt, WIREs Comput. Mol. Sci., 2011, 1, 699–709.
44. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
45. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
46. W. R. Wadt and P. J. Hay, J. Chem. Phys., 1985, 82, 284–298.
47. CrystalMaker, CrystalMaker:11, 2024.
48. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
49. R. Jinnouchi, F. Karsai and G. Kresse, Phys. Rev. B, 2019, 100, 014105.
50. R. Jinnouchi, J. Lahnsteiner, F. Karsai, G. Kresse and M. Bokdam, Phys. Rev. Lett., 2019, 122, 225701.
51. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192.
52. M. Yu and D. R. Trinkle, J. Chem. Phys., 2011, 6, 14–134.
53. V. Wang, N. Xu, J.-C. Liu, G. Tang and W.-T. Geng, Comput. Phys. Commun., 2021, 267, 108033.
54. Q. Zhao, K. Lei, B. Y. Xia, R. Crespo-Otero and D. Di Tommaso, J. Energy Chem., 2024, 93, 166–173.
55. J. Greeley and J. K. Nørskov, Electrochim. Acta, 2007, 52, 5829–5836.
56. X. Guo, J. Gu, S. Lin, S. Zhang, Z. Chen and S. Huang, J. Am. Chem. Soc., 2020, 142, 5709–5721.
57. J. K. Nørskov, T. Bligaard, J. Rossmeisl and C. H. Christensen, Nat. Chem., 2009, 1, 37–46.
58. Q. Zhao, K. Lei, B. Y. Xia, R. Crespo-Otero and D. Di Tommaso, J. Energy Chem., 2024, 93, 166–173.
59. D. D. Zhu, J. L. Liu and S. Z. Qiao, Adv. Mater., 2016, 28, 3423–3452.
60. A. J. Göttle and M. T. M. Koper, Chem. Sci., 2016, 8, 458–465.
61. H. Xin, A. Vojvodic, J. Voss, J. K. Nørskov and F. Abild-Pedersen, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 115114.
62. L. Gong, D. Zhang, Y. Shen, X. Wang, J. Zhang, X. Han, L. Zhang and Z. Xia, J. Catal., 2020, 390, 126–134.
63. H. Xu, D. Cheng, D. Cao and X. C. Zeng, Nat. Catal., 2018, 1, 339–348.
64. P. He, H. Feng, S. Wang, H. Ding, Y. Liang, M. Ling and X. Zhang, Mater. Adv., 2022, 3, 4566–4577.
65. X. Lu, H. A. Ahsaine, B. Dereli, A. T. Garcia-Esparza, M. Reinhard, T. Shinagawa, D. Li, K. Adil, M. R. Tchalala, T. Kroll, M. Eddaoudi, D. Sokaras, L. Cavallo and K. Takanabe, ACS Catal., 2021, 11, 6499–6509.
66. A. J. Göttle and M. T. M. Koper, Chem. Sci., 2017, 8, 458–465.
67. J. Rossmeisl, Z.-W. Qu, H. Zhu, G.-J. Kroes and J. K. Nørskov, J. Electroanal. Chem., 2007, 607, 83–89.
68. Y.-J. Zhang, V. Sethuraman, R. Michalsky and A. A. Peterson, ACS Catal., 2014, 4, 3742–3748.
69. M. J. Cheng, Y. Kwon, M. Head-Gordon and A. T. Bell, J. Phys. Chem. C, 2015, 119, 21345–21352.
70. R. Sakamoto, R. Toyoda, G. Jingyan, Y. Nishina, K. Kamiya, H. Nishihara and T. Ogoshi, Coord. Chem. Rev., 2022, 466, 214577.
71. D. Zhao, Z. Zhuang, X. Cao, C. Zhang, Q. Peng, C. Chen and Y. Li, Chem. Soc. Rev., 2020, 49, 2215–2264.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5cy00156k

---