Realising the ambivalent nature of H₂O₂ in oxidation catalysis – its dual role as an oxidant and a substrate

Abstract

H₂O₂ is a desirable terminal oxidant due to its good atom economy with H₂O being the only by-product when used productively. Its relative stability is advantageous in transport and storage, meaning that catalysts can both activate and direct its oxidising power towards selective oxidation of organic substrates. Wasteful disproportionation of H₂O₂ (into H₂O and O₂) is a well-recognised challenge and receives little, if any, attention in catalyst design. Nevertheless, understanding how H₂O₂ reacts during catalysed oxidations is essential to avoid inefficient use of H₂O₂, and, more importantly, hazardous conditions in which large amounts of O₂ are released by disproportionation. Reaction progress monitoring is an essential component in catalyst development, typically focusing on substrate conversion/product yield. In this frontier article, we advocate for multi-spectroscopic reaction progress monitoring in which all reaction components, including the oxidant and O₂, are tracked over the course of catalysed reactions to establish comprehensive time resolved mass balances. This approach provides insight into the reaction pathways that lead to disproportionation and the species responsible for it. We discuss selected cases to highlight the range of pathways possible and how these impact efforts towards reaction optimisation through catalyst design. In particular, the paradigm that the catalyst responsible for substrate oxidation is a distinct species from that responsible for H₂O₂ disproportionation, e.g., catalyst degradation products, is likely often incorrect. Rather, various pathways are possible, e.g., the same catalyst intermediate engages in both H₂O₂ and substrate oxidation. Various reaction pathways with respect to H₂O₂ consumption are discussed in the case studies. Our conclusion is that it is useful to consider that H₂O₂, in addition to being an oxidant, can compete with the intended organic substrate. This aspect is particularly important in efforts to elucidate reaction mechanisms and when redesigning catalysts rationally to improve performance, especially for use on large reaction scales where safety is paramount.

---

Introduction

Despite that H₂O₂ is a potent oxidant, it is remarkably stable from a kinetic perspective and can be transported and stored relatively safely even at high concentrations. Its presence in biological systems is, however, invariably destructive and as a consequence nature has evolved many effective ways to ‘deactivate’ it safely, using oxidases and, when necessary, a wide range of catalases.^1,2 Disproportionation (catalase) neutralises H₂O₂ by converting it to H₂O and O₂, but in doing so chemical potential is wasted, and worse, it can lead to other reactive oxygen species such as hydroxyl radicals, singlet oxygen, and the superoxide radical anion. Hence, the more effective way to deactivate H₂O₂ is to use it as a terminal oxidant releasing water and oxidising an organic substrate. In this way, the generation of reactive oxygen species is minimised.

In synthetic chemistry, this is the route of choice, using H₂O₂ as a reagent and H₂O₂ stands just behind molecular oxygen in terms of atom efficiency, with water as the only by-product in C–H hydroxylation, sulfoxidation and epoxidation, and complete atom economy in alkene dihydroxylation.³ These reactions are important in nearly all branches of the chemical industry, from polymer synthesis to medicinal chemistry.^4–7

Nature inspires synthetic chemists in the design of ligands for transition metal catalysts to use H₂O₂ effectively, and over the last half-century, a small group of ligand families have emerged, primarily for oxidation catalysis based on iron and manganese, but also on other metals such as copper and cobalt.^8–13 In these efforts, the focus is on selectivity, well-defined oxidative transformations, and to a lesser extent on efficiency, primarily in the productive use of H₂O₂. That is, while effectiveness in terms of substrate conversion is readily apparent, and indeed expected, in most studies in the literature, the fate of H₂O₂ in these reactions is unclear, more often than not, in large part due to the challenge in determining H₂O₂ consumed and O₂ released during and after reactions. Moreover, when scaling a catalysed reaction up to an industrial process, with H₂O₂ as a terminal oxidant, efficiency in H₂O₂ use is critically important beyond activity and selectivity, as high concentrations of O₂ can create hazardous conditions.

In this frontier article, we focus on the pathways involved in the competition between the oxidation of organic substrates and the oxidation of H₂O₂. The approaches needed to suppress the latter reaction depend on the mechanisms involved and hence knowledge of the nature of the species responsible is essential.

Reaction progress monitoring, in terms of the oxidation of organic substrates, is well developed, using in-line (Raman, FTIR, and NMR spectroscopy), at-line (GC and HPLC), and off-line (GC, HPLC, and NMR spectroscopy) techniques. In contrast, monitoring the concentration of H₂O₂ and O₂ during a reaction is more challenging and we will discuss first the (spectroscopic) methods currently available.

Analytical tools for reaction monitoring

Spectroscopic tools that are readily available for monitoring the progress of reactions can be divided into those that monitor the liquid (reaction mixture) phase and those that monitor the headspace above the reaction mixture inside a reaction vessel (e.g., a flask, a cuvette, etc.), or pipe in the case of flow chemistry (Fig. 1).

Fig. 1 Analytical tools for reaction monitoring discussed here. (A) Headspace FTIR spectroscopy (CO₂); (B) UV/vis absorption spectroscopy (e.g., catalyst concentration); (C) luminescence spectroscopy (e.g., ¹O₂ luminescence); (D) headspace Raman spectroscopy (gases that evolve from the reaction mixture); and (E) Raman (or resonance Raman) spectroscopy (reaction components in solution).

Monitoring reactions in solution

Optical techniques, e.g., UV/vis absorption spectroscopy, are invaluable in studying reaction mixtures when one or more of the reaction components, typically transition metal catalysts, show significant absorption (Fig. 1B). A 0.01–10 mM concentration window of the absorbing reaction components is typically required, dependent on the molar absorptivity of the compounds present, the optical path length, and the dynamic range of the spectrometer. The concentration of species of interest can be determined readily by the Beer–Lambert relation. Similarly, the liquid phase can also be monitored by (resonance) Raman and luminescence spectroscopy. Raman spectroscopy, although using visible/near-infrared light, provides vibrational spectra of the components at concentrations typically >50 mM or at (sub) mM concentrations where the wavelength of the laser used is resonant with an absorption band of a compound of interest (resonance Raman spectroscopy, Fig. 1E).¹⁴ Since the intensity of Raman scattering is linearly proportional to concentration, it is especially convenient for quantitative studies. Although less obvious in regard to reaction monitoring, luminescence spectroscopy is useful where the substrate, intermediate, product or other component present in the reaction mixture shows photo- or chemiluminescence (Fig. 1C).

As a case in point, the generation of singlet oxygen (¹O₂), e.g., upon the reaction of MoO₄ with H₂O₂, can be followed by the NIR emission of ¹O₂ (1269 nm).^15,16 Quantification of ¹O₂ emission produced through chemiluminescence requires calibration of the spectrometer used to record luminescence intensities to relate it to the transient concentration of ¹O₂. The limit of detection and quantification of ¹O₂ emission for a particular spectrometer can be determined using the reaction of MoO₄ with H₂O₂. ¹O₂ emission intensity is correlated also with the release of ³O₂ into the headspace of a sealed cuvette, e.g., by headspace Raman spectroscopy (vide infra).¹⁷

The reaction intermediates can be monitored by many other analytical techniques, not least online mass spectrometry as discussed in detail elsewhere.¹⁸ In addition to these time-resolved methods, sampling the liquid phase by withdrawing aliquots from the reaction mixture at certain time intervals for off-line analysis by NMR spectroscopy or chromatography methods (e.g., HPLC, GC) is quite standard. However, care should be taken to ensure rapid quenching of the reaction in the sample to maintain time resolution. Furthermore, where reactions are carried out at low temperatures, heating the withdrawn sample before quenching can reduce the reliability of the measurement. It is in these aspects that in-line measurements are particularly beneficial. Finally, often for transition metal based oxidation catalysts, (spectro)electrochemical oxidation/reduction can be useful in identifying potential reaction intermediates,^19,20 as, for example, in the study of [Mn(OTf)₂(^RPDP)] discussed below.²¹

Monitoring the headspace over reaction mixtures

The headspace above the reaction mixture can be monitored for the production or consumption of gases by FT-IR spectroscopy (CO₂) and/or headspace Raman spectroscopy (O₂, N₂, H₂, Fig. 1D). Headspace FT-IR spectroscopy can be performed readily in ordinary glass reaction vessels as the spectral cut-off for glass is ca. 2000 cm⁻¹, at a lower wavenumber than many gases of interest. Indeed, a simple approach is to lower a (sealed) cuvette so that the IR light travels through the headspace of the cuvette rather than the liquid phase (Fig. 1A). In this way the evolution of CO₂ gas can be monitored and quantified using the pathlength and its molar absorptivity.²² Although Raman scattering from gases is much weaker than in the condensed phase, due to both differences in polarisability and more critically the number density in the confocal volume, headspace Raman spectroscopy is effective in monitoring the headspace above reactions for gases such as O₂ (at 1556 cm⁻¹), N₂ (at 2332 cm⁻¹), and H₂ (at 4197 cm⁻¹)²³ (Fig. 1D).²⁴ The gas of interest (usually O₂ in the case of oxidation catalysis) may be quantified by relating the integrated Raman intensity of the ν_O−O,str band to the number of moles of the gas, following the ideal gas law and Henry's law,¹⁷ which accounts for the shift in equilibrium between the gas in the headspace and the gas dissolved in the liquid phase (due to the production/consumption of the gas in the closed volume).

In the next sections, the power of a multi-spectroscopic approach is exemplified by three case studies exhibiting three distinct types of interaction between a Fe- or Mn-catalyst and H₂O₂ with respect to substrate oxidation and H₂O₂ disproportionation.

Case studies in elucidating reaction pathways

In the following examples, we show how understanding which species are responsible for catalysing disproportionation of H₂O₂ enables rational redesign of catalyst systems to minimise waste.

Competition between H₂O₂ and organic compounds as substrates for the activated form of an oxidation catalyst

The [Mn(OTf)₂(^RPDP)] family of complexes (where R = H, OMe and ^RPDP = N,N′-bis(2′′-(4′′-R-pyridylmethyl)-2,2′-bipyrrolidine)) and Mn(II)/pyridine-2-carboxylic acid are two examples of catalysts in which the same reactive species is responsible for both substrate oxidation and H₂O₂ decomposition.

Oxidations with Mn(PDP) catalysts. The [Mn(OTf)₂(^RPDP)] family of complexes (where R = H in ^HPDP–Mn and R = OMe in ^OMePDP–Mn) are remarkably effective in the (enantioselective) oxidation of organic compounds (C–H oxidation and epoxidation/dihydroxylation, Fig. 2).^25–27

Fig. 2 Manganese ((R,R)-[Mn(OTf)₂ (^RPDP)]) catalysed epoxidation of cis-β-methylstyrene with H₂O₂.²⁶

Oxidations with these catalysts are typically carried out with a small (20%) excess of H₂O₂ with respect to the organic substrate.²⁸ Substituents on the pyridine rings show a considerable influence over the efficiency of the reactions, i.e., conversion and product yields (Table 1). Indeed, although the effect of substituents on conversion is considerable, the effect on enantiomeric excess is all the more remarkable considering the lack of proximity of the substituent to the reaction centre. Since the substituents are in the para-position, steric effects are less pronounced than in the other positions, and hence the effect of the substituents on electron density at the metal centre is focused on in regard to rationalisation of trends observed.^26,29

Table 1 Conversion and enantiomeric excess (ee) in the Mn-catalysed epoxidation of cis-β-methylstyrene²⁶

Catalyst	R	Conversion (yield, %)	ee (%)
^HPDP–Mn	–H	61 (38)	43
^OMePDP–Mn	–OMe	80 (59)	69
^MePDP–Mn	–Me	100 (67)	63
^ClPDP–Mn	–Cl	57 (33)	40
^Me2NPDP–Mn	–NMe2	100 (75)	82
^CO2EtPDP–Mn	–CO2Et	44 (22)	43

---

The difference in the performance of the variously substituted catalysts, e.g., between ^HPDP–Mn and ^OMePDP–Mn analogues (Table 1), and in particular the turnover number (TON), has been ascribed tentatively to the resilience of the catalyst toward inactivation/degradation, or to the maximum turn over frequencies (TOF) each catalyst can achieve and hence compete with unproductive reactions (disproportionation of H₂O₂).

A combination of resonance Raman, EPR, and UV/vis absorption spectroscopy under reaction conditions revealed the appearance of multi-nuclear Mn(III) and Mn(IV) complexes, which are reminiscent of dinuclear manganese complexes that show activity in the disproportionation of H₂O₂ (vide infra).^21,30 However, these species were shown, using in-line time resolved spectroscopy, to be mostly resting states. In line reaction monitoring of substrate conversion and evolution of O₂ revealed that the differences in the efficiency of the ^OMePDP–Mn complex and its ^HPDP–Mn analogue were in fact due to the effect substituents on the relative rates of substrate oxidation and H₂O₂ oxidation.²¹

The comparative study focused on the relative efficiency of the two catalysts in the epoxidation of styrene and disproportionation of H₂O₂ over the whole course of the reaction.²¹ Simultaneous headspace/liquid phase in line Raman spectroscopy was used to quantify the loss of H₂O₂/release of O₂, as well as the formation of styrene oxide (Fig. 3). In these experiments, H₂O₂ was added dropwise over 10 min or longer. The spectroscopic data revealed that O₂ was formed concurrent with alkene oxidation and that the relative efficiencies for the two reactions were constant over the entire period of H₂O₂ addition for both catalysts (Fig. 3).

Fig. 3 (A) Manganese catalysed epoxidation of styrene using [Mn(OTf)₂(^RPDP)]. For (B) [Mn^II(OTf)₂(^HPDP)] and (C) [Mn^II(OTf)₂(^OMePDP)] the amount of O₂ released (blue) into the headspace and epoxide formed (red) in the liquid phase, both determined by Raman spectroscopy. Reproduced from Kasper et al. (ACS 2023).²¹

However, the ratio of alkene oxidation to H₂O₂ is different for the two complexes. [Mn(OTf)₂(^OMePDP)] favours alkene oxidation over H₂O₂ oxidation to a greater extent than [Mn(OTf)₂(^HPDP)]. These observations provided a strong indication that H₂O₂ and styrene were competitive substrates for the H₂O₂ activated catalyst, rather than that different species were responsible for alkene oxidation and H₂O₂ disproportionation. Furthermore, the data indicate that the substituents determine the overall efficiency of the catalysts by affecting the selectivity towards oxidation of alkene and H₂O₂.

The influence of substituents on the activity of the catalysts can be estimated from the turnover frequency (TOF) for the formation of epoxide over time after each drop of H₂O₂. The conclusion reached on this basis is that [Mn^II(OTf)₂(^OMePDP)] is a more active catalyst than [Mn^II(OTf)₂(^HPDP)]. However, when the oxidation of H₂O₂ is taken into account, as well, the overall activity of the two catalysts is in fact similar. While it is uncertain whether the same species is responsible for both H₂O₂ and substrate oxidation, the constant relative reactivity over the entire course of the reaction suggests it is.²¹ In conclusion, this example showcases H₂O₂ as a competing substrate for the activated catalyst and how simultaneous in-line monitoring can reveal this.

Oxidations with Mn(II)/pyridine-2-carboxylic acid. That a catalyst shows competition between the desired oxidation of organic substrates and wasteful oxidation of H₂O₂ is not necessarily obvious. In particular, where good to excellent conversions are achieved for many substrates, H₂O₂ oxidation can be overlooked. A case in point is that of the oxidation catalyst prepared in situ from Mn(II)/pyridine-2-carboxylate (PCA) and a ketone (Fig. 4).^31–33

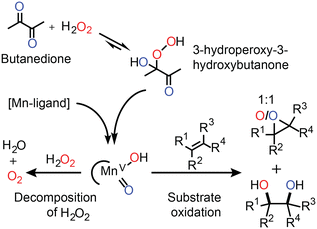Fig. 4 The activation of H₂O₂ by the in situ prepared Mn(II)/PCA catalyst relies on the initial formation of a ketone-hydroperoxide adduct (e.g., with butanedione). Organic substrates compete with H₂O₂ for the reaction with the activated manganese species (tentatively assigned LMn(V)O(OH)).³³ The results of oxygen atom tracking with oxygen in H₂O₂ (red) and oxygen in butanedione (blue) are shown.³¹

Elucidation of the mechanism by which this catalyst operates is challenging since the low concentration of Mn(II) used means that direct observation of catalyst species is impractical. Nevertheless, in line spectroscopy is invaluable in monitoring changes to the major (>50 mM) components of the reaction mixtures and has allowed for a relatively detailed understanding of the role of each reaction component to be established (Fig. 4).^31–33 For example, a ketone such as butanedione acts as a co-catalyst by forming the hydroperoxy-adduct with H₂O₂ from which the oxidising manganese species is formed (Fig. 4). The formation of this species is rate limiting, and unusually the reaction rate shows a zero-order dependence on the substrate concentration. However, the catalyst is still highly selective. For example, while in separate reactions, styrene and 1-phenyl-ethanol are oxidised with the same observed rate, in a mixture styrene is oxidised first with 1-phenyl-ethanol oxidation beginning only after most of the styrene had been consumed.

Although the catalyst is efficient with high to full conversion with many substrates, a small excess of H₂O₂ is still required to reach full conversion of alkene. The inefficiency can be ascribed to the concomitant oxidation of other reaction components (e.g., the ketone used as a co-catalyst). However, headspace reaction monitoring together with ¹⁸O labelling (Fig. 4) confirmed that H₂O₂ oxidation also occurs.

Monitoring the extent of O₂ evolution during the oxidation of styrene indicates that disproportionation is only significant at the end of the reaction and hence contrasts with the observations made with the Mn-PDP catalysts (vide supra). Namely, as the Mn(II)/PCA catalyst shows a zero-order dependence on the substrate, the evolution of O₂ is expected only at the end of the oxidation of styrene. The catalyst shows preference for styrene as the substrate and only when it is consumed does H₂O₂ become a competitive substrate. Indeed in the absence of styrene, O₂ evolves over the entire course of the reaction at the same rate at which styrene had been oxidised (Fig. 5).

Fig. 5 The release of O₂ in the reaction of H₂O₂ catalysed by Mn(II)/PCA was monitored by headspace Raman spectroscopy. In the presence of styrene, O₂ is formed only after almost all styrene has been oxidised to styrene oxide (black dots), while in the absence of styrene O₂ is released quantitatively (red dots) due to oxidation of H₂O₂.³¹

Despite differences in the evolution of O₂ over time between the Mn(II)/PCA and Mn–PDP catalyst systems, the origin of wasteful H₂O₂ disproportionation is in both cases due to competition between the organic substrate and H₂O₂ for the oxidising manganese species. Hence, the overall catalyst efficiency depends on the competition for the activated catalyst.

Identifying competing pathways in organic substrate oxidation and H₂O₂ decomposition through reaction monitoring and kinetic modelling

In contrast to the previous examples, the complex [(N₄Py)Fe(II)(CH₃CN)]²⁺, where N4Py is (1,1-bis(pyridin-2-yl)-N,N′-bis(pyridin-2-ylmethyl)methanamine) (Fig. 6) is an example of an oxidation catalyst in which different species are responsible for substrate oxidation and/or H₂O₂ decomposition.^34–37

Fig. 6 Proposed mechanism for [(N₄Py)Fe^II (CH₃CN)](OTf)₂ with H₂O₂ in methanol.¹⁷

[(N₄Py)Fe(II)(CH₃CN)]²⁺ reacts with H₂O₂ to form an Fe(IV)=O species ([(N₄Py)Fe(IV)=O]²⁺) that can oxidise organic substrates selectively.³⁸ However, the complex reaches the Fe(III) state relatively rapidly both through Fe(II)/Fe(IV) comproportionation and by reduction of the initially formed [(N₄Py)Fe(IV)=O]²⁺ through hydrogen atom transfer with H₂O₂, producing [(N₄Py)Fe(III)(OH)]²⁺ and the superoxide anion radical.^17,39 The Fe(III) complex, e.g., [(N₄Py)Fe(III)(OCH₃)]²⁺, also undergoes ligand exchange with H₂O₂ to form a relatively stable Fe(III)–OOH species. Although this species can be viewed as the precursor to [(N₄Py)Fe(IV)=O]²⁺via homolytic O–O bond cleavage, this reaction is remarkably slow.

Instead, in protic solvents, such as methanol, exceptionally efficient disproportionation of H₂O₂ is observed, due to the direct reaction of [(N₄Py)Fe(III)(OOH)]²⁺ with H₂O₂.^17,39 Hence, in this case, although [(N₄Py)Fe(IV)=O]²⁺ reacts with H₂O₂, it is not actually formed in the reaction and instead it is [(N₄Py)Fe(III)(OOH)]²⁺ that is responsible for the disproportionation of H₂O₂. In this example, the species responsible for substrate oxidation ([(N₄Py)Fe(IV)=O]²⁺) is clearly different to that responsible for H₂O₂ disproportionation ([(N₄Py)Fe(III)(OOH)]²⁺). However, it is an interesting example to show how reaction modelling is important in revealing details of the overall catalytic system.

The reactivity of [(N₄Py)Fe(II)(CH₃CN)]²⁺ with H₂O₂ was elucidated using a range of in situ spectroscopic techniques. Time-resolved (resonance) Raman spectroscopy, headspace Raman spectroscopy, and UV/vis absorption spectroscopy showed that [(N₄Py)Fe(II)(CH₃CN)]²⁺ disproportionates H₂O₂ into H₂O and O₂ in the presence of an excess of H₂O₂.^17,39 Specifically, resonance Raman and UV/vis absorption spectroscopy were used to track the concentration of [(N₄Py)Fe(III)(OOH)]²⁺ in solution, and liquid phase and headspace Raman spectroscopy the concentrations of H₂O₂ and O₂, respectively. The oxygen atom mass balance revealed that all H₂O₂ is disproportionated to H₂O and O₂ under these conditions. Fig. 7 shows the results of the combined, time-resolved liquid phase, headspace Raman and UV/vis absorption spectroscopic approach to follow the concentrations of H₂O₂, O₂, and iron species, respectively.¹⁷

Fig. 7 Reaction progress for the conversion of 400 equiv. of H₂O₂ (0.46 mM [(N₄Py)Fe^II (CH₃CN)](OTf)₂ and 190 mM H₂O₂ in methanol). (A) ³O₂ (red) and H₂O₂ (blue) reaction progress determined by Raman spectroscopy. (B) Concentration of (N₄Py)Fe^III–OOH over time from visible absorption spectroscopy. Experimental data are denoted with dots and the modelled data with dashed lines.¹⁷

The disproportionation of H₂O₂ is wasteful and can generate hazardous conditions in large-scale applications. Under some circumstances, disproportionation of H₂O₂ can involve the generation of the highly reactive species ¹O₂. Singlet oxygen can engage in Diels–Alder type cycloadditions with dienes, for example, but can also trigger radical chain reactions. In the case of disproportionation of H₂O₂ by [(N₄Py)Fe(III)(OOH)]²⁺, the generation of ¹O₂ during the reaction was checked for by concurrently monitoring the O₂ released from the reaction by headspace Raman spectroscopy and by NIR luminescence spectroscopy to determine ¹O₂ concentrations in the liquid phase (vide supra).¹⁷ Quantification of the chemiluminescence and in particular determination of limits of detection are important and the MoO₄⁻ catalyst, which produces ¹O₂ quantitatively, provides a reliable standard. In the case of [(N₄Py)Fe(III)(OOH)]²⁺, only ³O₂ is generated.

The benefit of tacking concentrations of most if not all reaction components over time is that it allows for falsification/validation of proposed mechanisms. In this case, the proposed mechanism for H₂O₂ disproportionation was validated by comparing a microkinetic model constructed on the basis of the proposed mechanism with the experimental data (Fig. 7, dashed lines). In the kinetic model, the known individual rate constants and initial concentrations are used to predict the outcome of the reaction over time, with variation in any unknown rate constants, etc. to achieve a good fit to the experimental data. The outcome of the microkinetic modelling was consistent with the experimentally determined [H₂O₂] and [O₂] over time (Fig. 7A). However, it did not agree with the time dependence of the concentration of [(N₄Py)Fe(III)(OOH)]²⁺ (Fig. 7B). This discrepancy prompted a closer look at the reactivity of [(N₄Py)Fe(III)(OOH)]²⁺ at lower concentrations, which revealed that in addition to the reaction with H₂O₂, the complex also reacts with itself to regenerate two equivalents of [(N₄Py)Fe(III)(OH)]²⁺ and an equivalent of H₂O₂. Furthermore the rate of homolytic O–O bond cleavage in [(N₄Py)Fe(III)(OOH)]²⁺ to form [(N₄Py)Fe(IV)(O)]²⁺ and a hydroxyl radical was much lower than would be expected. Indeed this pathway is essentially irrelevant under normal reaction conditions as the self-decay of [(N₄Py)Fe(III)(OOH)]²⁺ to [(N₄Py)Fe(III)(OH)]²⁺ is faster than the formation of Fe(IV)=O from Fe(III)–OOH (Fig. 8). Inclusion of the additional reaction step (the bimolecular reaction of [(N₄Py)Fe(III)(OOH)]²⁺) in the microkinetic model provided much closer agreement with all of the experimental data (Fig. 7).

Fig. 8 Adapted proposed mechanism for the reaction of [(N₄Py)Fe^II (CH₃CN)](OTf)₂ with H₂O₂ in methanol, including an additional elementary step of the second order decay of (N₄Py)Fe^III–OOH (in red).¹⁷

Switching from H₂O₂ disproportionation to organic oxidations through in situ changes in the catalyst structure

A quite different situation arises where the initial form of a catalyst used is highly active in the disproportionation of H₂O₂ initially, but, following a change in the catalyst structure, the reactivity profile changes to the more desirable oxidation of organic substrates. We highlight this scenario with two manganese based catalysts applied already in the 2000s in the oxidation of organic compounds, namely [Mn₂(μ-O)(μ-OAc)₂TPTN]²⁺ (Fig. 9)^40,41 and [Mn₂(μ-O)₃TMTACN₂]²⁺ (Fig. 11).^42–47

Fig. 9 Decomposition of [Mn₂(μ-O)(μ-OAc)₂TPTN]²⁺ to pyridine-2-carboxylic acid.

Both of these binuclear manganese complexes were inspired by nature's manganese dependent enzymes and the oxygen evolving centre of photosystem II, and each showed early promise in oxidation catalysis. However, both showed substantial inefficiencies due to the disproportionation of H₂O₂ during the oxidation of organic compounds, primarily alcohols and alkenes.

The oxidation of alkenes⁴⁰ and alcohols⁴¹ with H₂O₂ in acetone catalysed by [Mn₂(μ-O)(μ-OAc)₂TPTN]²⁺ proceeds with good to excellent conversion, but required typically an 8-fold excess of H₂O₂ with respect to the substrate, due to excessive disproportionation to H₂O and O₂. It was noted also that a considerable lag period before oxidation of the substrate (e.g., alcohol) begins. It is during the lag period that most of the H₂O₂ is lost due to comproportionation (Fig. 10).

Fig. 10 Reaction progress (conversion of the substrate) following addition of H₂O₂ to [Mn₂(μ-O)(μ-OAc)₂TPTN]²⁺.^40,41

Subsequent studies confirmed that during this lag period, the ligand underwent oxidative decomposition to pyridine-2-carboxylic acid (PCA). It was the PCA, together with manganese ions, that formed the catalyst that was responsible for the oxidation of organic compounds (vide supra), while the vigorous decomposition of H₂O₂ was due to the initial complex [Mn₂(μ-O)(μ-OAc)₂TPTN]²⁺.^48,49

In contrast to [Mn₂(μ-O)(μ-OAc)₂TPTN]²⁺, the catalyst [Mn₂(μ-O)(μ-OAc)₃TMTACN₂]²⁺ shows neither oxidation of organic substrates nor disproportionation of H₂O₂. In CH₃CN containing carboxylic acids, however, a reproducible carboxylic acid dependent lag period is observed prior to a sudden and rapid conversion of [Mn₂(μ-O)₃ TMTACN₂]²⁺ to [Mn₂(μ-O)(μ-RCO₂)₂(TMTACN)₂]²⁺ (Fig. 11, where R is an alkyl or aryl group).⁴⁵ It is notable that with [Mn₂(μ-O)(μ-RCO₂)₂(TMTACN)₂]²⁺ (prepared independently), >95% efficiency in use of H₂O₂ for the epoxidation/syn-dihydroxylation of alkenes is observed (Fig. 12).⁴⁶ However, in the short period where [Mn₂(μ-O)₃ TMTACN₂]²⁺ converts to [Mn₂(μ-O)(μ-RCO₂)₂(TMTACN)₂]²⁺, in line monitoring the concentration of H₂O₂ revealed that disproportionation of H₂O₂ is significant, indicating that an intermediate complex is responsible (Fig. 13).⁴⁷

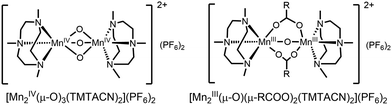Fig. 11 (Left) The Mn(IV) complex [Mn₂(μ-O)₃TMTACN₂]²⁺ and (right) the Mn(III) complex formed after a lag period following addition of H₂O₂ in the presence of a carboxylic acid.

Fig. 12 Reaction progress in the epoxidation of cyclooctene by dropwise addition of H₂O₂ with [Mn₂(μ-O)₃TMTACN₂]²⁺ with 10 eq. of CCl₃CO₂H (1, blue rectangles) or [Mn₂(μ-O)(μ-Cl₃CO₂)₂(TMTACN)₂]²⁺ (2, red circles). Adapted from de Boer et al.⁴⁶ The turn-over-number (TON) for oxidation of substrate is plotted against the number of equivalents of H₂O₂ added (at a constant rate over time). The stepwise addition of H₂O₂ is indicated with a dashed black line. The complexes have different molar absorptivities at 532 nm and hence the conversion from one to the other can be followed over time by the absorbance at 532 nm (dashed line). The change in absorbance with 1 correlates with the switch to fully productive (alkene oxidation) use of H₂O₂.

Fig. 13 Absorbance at 532 nm over time with repeated addition of 50 equiv. of H₂O₂ to [Mn₂(μ-O)(μ-RCO₂)₂(TMTACN)₂]²⁺ (1 mM) with CCl₃CO₂H (10 mM) in acetonitrile (the spikes in absorbance denote the points at which H₂O₂ was added). Inset: overlay of absorbance at 532 nm (blue) and intensity of the Raman band of H₂O₂ (λ_exc 473 nm, red) at [small nu, Greek, tilde] = 869 cm⁻¹.

Hence, this system is similar to the earlier TPTN/PCA based system in that the decomposition of H₂O₂ was primarily due to precursors to the final form of the catalyst that engages in the oxidation of organic compounds. However, in the absence of an oxidisable compound, the complex [Mn₂(μ-O)(μ-RCO₂)₂(TMTACN)₂]²⁺ engages in disproportionation of H₂O₂. This is seen by concomitant monitoring of the concentration of H₂O₂ by Raman spectroscopy and the catalyst by UV/vis absorption spectroscopy. In the absence of an organic substrate, the absorbance decreases as the H₂O₂ is disproportionated and only recovers partly indicating conversion to a Mn(II) state followed by decomposition of the catalyst. This loss is not as pronounced when an alkene substrate is present.

Conclusions

Disproportionation of H₂O₂ to O₂ and H₂O is a challenge in developing industrially applicable catalysts for the selective oxidation of organic substrates. Although it can be seen as a side reaction, typically ascribed to catalyst degradation, the study of several Mn- and Fe-catalysed oxidations that use H₂O₂ as a terminal oxidant has led to the realisation that H₂O₂ oxidation can occur via any of the several pathways. For example, H₂O₂ decomposition may occur via a reaction with the ‘activated catalyst’ (i.e., that is directly responsible for the oxidation of the organic substrate), a resting catalyst state, catalyst degradation products, catalyst precursors, etc. Ultimately, it must be recognised that H₂O₂ is always likely to be a competitive substrate for oxidation.

Quantitative analysis of all reaction components, i.e., catalysts, reagents and reaction products, is the ideal situation, allowing for full mass balance to be established, or at least that gaps in our knowledge of the fate of specific components are well established. Time-resolved spectroscopy techniques are especially useful to relate changes in selectivity to changes in catalyst composition and structure over the entire course of the reaction. This approach has allowed gaining insight into the many reasons why H₂O₂ decomposition can occur and keeping low steady state concentrations of H₂O₂ during catalysis may be of most importance in this regard. In the area of homogeneous oxidation catalysis with H₂O₂ as a terminal oxidant, studies aimed at tuning catalyst reactivity by ligand design, with respect to the organic substrate of interest, can be strengthened by taking into account the role of H₂O₂ disproportionation. In this aspect, there is an opportunity for computational studies to contribute in predicting selectivity.

Author contributions

All authors contributed to the concept and writing of the manuscript.

Conflicts of interest

There are no conflicts to declare.

Data availability

There are no original data associated with this manuscript.

Acknowledgements

This work is funded by the Advanced Research Center for Chemical Building Blocks, ARC CBBC, which is co-founded and co-financed by the Dutch Research Council (NWO) and the Netherlands Ministry of Economic Affairs and Climate Policy.

References

1. J. V. Bannister, W. H. Bannister and G. Rotilio, Crit. Rev. Biochem., 1987, 22, 111–180.
2. P. Chelikani, I. Fita and P. C. Loewen, Cell. Mol. Life Sci., 2004, 61, 192–208.
3. Modern Oxidation Methods, ed. J. Bäckvall, Wiley, 1st edn, 2010.
4. A. Bunescu, S. Lee, Q. Li and J. F. Hartwig, ACS Cent. Sci., 2017, 3, 895–903.
5. M. I. Childers, J. M. Longo, N. J. Van Zee, A. M. LaPointe and G. W. Coates, Chem. Rev., 2014, 114, 8129–8152.
6. A. D. Mohanty and C. Bae, in Advances in Organometallic Chemistry, Elsevier, 2015, vol. 64, pp. 1–39.
7. G. D. Yadav, R. K. Mewada, D. P. Wagh and H. G. Manyar, Catal. Sci. Technol., 2022, 12, 7245–7269.
8. M. Costas, M. P. Mehn, M. P. Jensen and L. Que, Chem. Rev., 2004, 104, 939–986.
9. X. Engelmann, I. Monte-Pérez and K. Ray, Angew. Chem., Int. Ed., 2016, 55, 7632–7649.
10. V. A. Larson, B. Battistella, K. Ray, N. Lehnert and W. Nam, Nat. Rev. Chem., 2020, 4, 404–419.
11. K. Ray, F. F. Pfaff, B. Wang and W. Nam, J. Am. Chem. Soc., 2014, 136, 13942–13958.
12. P. R. Ortiz De Montellano, Chem. Rev., 2010, 110, 932–948.
13. O. Y. Lyakin, K. P. Bryliakov and E. P. Talsi, Coord. Chem. Rev., 2019, 384, 126–139.
14. W. R. Browne, in Practical Approaches to Biological Inorganic Chemistry, Elsevier, 2020, pp. 275–324.
15. V. Nardello, J. Marko, G. Vermeersch and J. M. Aubry, Inorg. Chem., 1995, 34, 4950–4957.
16. V. Nardello, S. Bogaert, P. L. Alsters and J.-M. Aubry, Tetrahedron Lett., 2002, 43, 8731–8734.
17. C. M. de Roo, A. S. Sardjan, R. Postmus, M. Swart, R. Hage and W. R. Browne, ChemCatChem, 2024, 16, e202301594.
18. J. Mehara and J. Roithová, Chem. Sci., 2020, 11, 11960–11972.
19. J. J. A. Lozeman, P. Fuehrer, W. Olthuis and M. Odijk, Analyst, 2020, 145, 2482–2509.
20. A. Salame, M. H. Cheah, J. Bonin, M. Robert and E. Anxolabehere-Mallart, Angew. Chem., Int. Ed., 2024, 63, e202412417.
21. J. B. Kasper, L. Vicens, C. M. de Roo, R. Hage, M. Costas and W. R. Browne, ACS Catal., 2023, 13, 6403–6415.
22. C. Wegeberg, F. R. Lauritsen, C. Frandsen, S. Mørup, W. R. Browne and C. J. McKenzie, Chem. – Eur. J., 2018, 24, 5134–5145.
23. K. Tamura, Determination of Ortho-/Para- Hydrogen Ratio Using Raman Spectroscopy – Application to Fuel Cells, 2025.
24. D. Yang, Q. Nie, M. Cheng, S. Pei, C. Cheng, D. Guo and M. Yang, ACS Sens., 2025, 10, 1113–1122.
25. R. V. Ottenbacher, K. P. Bryliakov and E. P. Talsi, Adv. Synth. Catal., 2011, 353, 885–889.
26. O. Cussó, I. Garcia-Bosch, D. Font, X. Ribas, J. Lloret-Fillol and M. Costas, Org. Lett., 2013, 15, 6158–6161.
27. M. C. White and J. Zhao, J. Am. Chem. Soc., 2018, 140, 13988–14009.
28. C. Claraso, L. Vicens, A. Polo and M. Costas, Org. Lett., 2019, 21, 2430–2435.
29. R. V. Ottenbacher, D. G. Samsonenko, E. P. Talsi and K. P. Bryliakov, ACS Catal., 2014, 1599–1606.
30. G. Yang, E. A. Mikhalyova, A. S. Filatov, S. V. Kryatov and E. V. Rybak-Akimova, Inorg. Chim. Acta, 2023, 546, 121288.
31. J. B. Kasper, P. Saisaha, M. De Roo, M. J. Groen, L. Vicens, M. Borrell, J. W. De Boer, R. Hage, M. Costas and W. R. Browne, ChemCatChem, 2023, 15, e202201072.
32. P. Saisaha, J. J. Dong, T. G. Meinds, J. W. de Boer, R. Hage, F. Mecozzi, J. B. Kasper and W. R. Browne, ACS Catal., 2016, 3486–3495.
33. J. J. Dong, P. Saisaha, T. G. Meinds, P. L. Alsters, E. G. Ijpeij, R. P. van Summeren, B. Mao, B. L. Feringa and W. R. Browne, ACS Catal., 2012, 1087–1096.
34. M. Lubben, A. Meetsma, E. C. Wilkinson, B. Feringa and L. Que, Angew. Chem., Int. Ed. Engl., 1995, 34, 1512–1514.
35. G. Roelfes, M. Lubben, R. Hage, L. Que Jr. and B. L. Feringa, Chem. – Eur. J., 2000, 6, 2152–2159.
36. G. Roelfes, M. Lubben, K. Chen, R. Y. N. Ho, A. Meetsma, S. Genseberger, R. M. Hermant, R. Hage, S. K. Mandal, V. G. Young, Y. Zang, H. Kooijman, A. L. Spek, L. Que and B. L. Feringa, Inorg. Chem., 1999, 38, 1929–1936.
37. J. Kaizer, E. J. Klinker, N. Y. Oh, J.-U. Rohde, W. J. Song, A. Stubna, J. Kim, E. Münck, W. Nam and L. Que, J. Am. Chem. Soc., 2004, 126, 472–473.
38. J. Chen, A. S. Sardjan, C. M. de Roo, M. Di Berto Mancini, A. Draksharapu, D. Angelone, R. Hage, M. Swart and W. R. Browne, Inorg. Chem., 2025, 64, 9408–9417.
39. J. Chen, A. Draksharapu, D. Angelone, D. Unjaroen, S. K. Padamati, R. Hage, M. Swart, C. Duboc and W. R. Browne, ACS Catal., 2018, 8, 9665–9674.
40. J. Brinksma, B. L. Feringa, R. Hage and J. Kerschner, Chem. Commun., 2000, 537–538.
41. J. Brinksma, M. T. Rispens, R. Hage and B. L. Feringa, Inorg. Chim. Acta, 2002, 337, 75–82.
42. D. E. De Vos, B. F. Sels, M. Reynaers, Y. S. Rao and P. A. Jacobs, Tetrahedron Lett., 1998, 39, 3221–3224.
43. D. E. De Vos, S. De Wildeman, B. F. Sels, P. J. Grobet and P. A. Jacobs, Angew. Chem., Int. Ed., 1999, 38, 980–983.
44. A. Berkessel and C. A. Sklorz, Tetrahedron Lett., 1999, 40, 7965–7968.
45. J. W. De Boer, J. Brinksma, W. R. Browne, A. Meetsma, P. L. Alsters, R. Hage and B. L. Feringa, J. Am. Chem. Soc., 2005, 127, 7990–7991.
46. J. W. De Boer, W. R. Browne, J. Brinksma, P. L. Alsters, R. Hage and B. L. Feringa, Inorg. Chem., 2007, 46, 6353–6372.
47. D. Angelone, S. Abdolahzadeh, J. W. De Boer and W. R. Browne, Eur. J. Inorg. Chem., 2015, 2015, 3532–3542.
48. D. Pijper, P. Saisaha, J. W. De Boer, R. Hoen, C. Smit, A. Meetsma, R. Hage, R. P. Van Summeren, P. L. Alsters, B. L. Feringa and W. R. Browne, Dalton Trans., 2010, 39, 10375.
49. It should be noted that the PCA/Mn(II) catalyst mixture formed also disproportionates H₂O₂ (vide supra) but to much less an extent than initially observed with [Mn₂(μ-O)(μ-OAc)₂TPTN]²⁺.

---