 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Dynamics and rupture of doped motility induced phase separation†
Rodrigo
Fernández-Quevedo García
*ab,
Enrique
Chacón
c,
Pedro
Tarazona
d and
Chantal
Valeriani
 *ab
*ab
aDepartamento de Estructura de la Materia, Física Térmica y Electrónica, Universidad Complutense de Madrid, 28040 Madrid, Spain. E-mail: rodfer05@ucm.es; cvaleriani@ucm.es
bGISC – Grupo Interdisciplinar de Sistemas Complejos, 28040 Madrid, Spain
cInstituto de Ciencia de Materiales de Madrid (ICMM), Consejo Superior de Investigaciones Científicas (CSIC), Campus de Cantoblanco, 28049 Madrid, Spain
dDepartamento de Física Teórica de la Materia Condensada, Condensed Matter Physics Center (IFIMAC), Universidad Autónoma de Madrid, 28049 Madrid, Spain
First published on 16th May 2025
Abstract
Adding a small amount of passive (Brownian) particles to a two-dimensional dense suspension of repulsive active Brownian particles does not affect the appearance of a motility-induced phase separation into a dense and a dilute phase, caused by the persistence of the active particles' direction of motion. Unlike a purely active suspension, the dense slab formed in an elongated system of a passive–active mixture may show, over long periods of time, a stable and well-defined propagation of the interfaces, because of the symmetry breaking caused by the depletion of passive particles on one side of the slab. We investigate these dynamical structures via average density profile calculations, revealing an asymmetry between the two interfaces, and enabling a kinetic analysis of the slab movement. The apparent movement of the dense slab is not a pure source/sink effect, nor a rigid displacement of all the particles, but a self-sustained combination of both effects. Furthermore, we analyse the specific fluctuations that produce, cancel and abruptly reverse the slab motion.
1 Introduction
One of the simplest theoretical models proposed to unravel the features of the collective behaviour of active particles is the so-called active Brownian particle (ABP) model, consisting of self-propelling Brownian particles which gradually change their direction of motion.1–4 Numerical simulations of suspensions of repulsive ABPs have demonstrated that ABPs spontaneously aggregate due to the persistence of particles’ direction of motion, undergoing a motility induced phase separation (MIPS)5–9 into a dense and a dilute phase.3,5,9–17 These numerical results have been supported by phase-field calculations18–21 and experimental results on two-dimensional suspensions of active colloids.22–25When MIPS takes place in numerical simulations, dealing with an elongated cylindrical box allows for characterizing its structural features, such as its interfacial properties. As suggested by the authors of ref. 26, considering the swim pressure as a contribution to the total pressure results in a negative interfacial tension. However, different from equilibrium, this leads to a long-time stable MIPS. Patch and coworkers27 have addressed the controversy of a negative surface tension coexisting with a stable interface by discovering a Marangoni-like effect arising from the presence of sustained tangential currents at the interfaces (on both dilute and dense phases). By means of a continuum description, the authors of ref. 28 demonstrated that modelling activity as a spatially varying force allows one to predict consistent pressures and nearly zero surface tension.
Hermann and coworkers29 implemented non-equilibrium generalization of the microscopic treatment of the interface, leading to a positive interfacial tension that directly explained the stability of the interface. The approach in ref. 29 produces the “intrinsic density profile”.30 Thus, one could study capillary wave fluctuations and the wave vector dependence of the interfacial tension. Some of us have recently analysed the features of the dense/dilute interfaces in terms of intrinsic density and force profiles, calculated by means of Capillary Wave Theory.31 In our work, we attributed the MIPS stability to the local rectification of the random active force acting on particles at the dense (inner) side of the MIPS interface. This caused an external potential producing a pressure gradient across the interface and led us to conclude that the MIPS mechanical surface tension could not be described as the surface tension of equilibrium coexisting phases.
The stability of MIPS has been tested against several features. On the one side, hydrodynamics, together with the particles’ shape, has been shown to affect the existence of MIPS. MIPS is suppressed when particles are spherical,32 while it is enhanced when particles are elongated.33 MIPS is also hindered in the case of a suspension of chemotactic active Brownian particles.34 In contrast, MIPS is neither hindered when particles’ equations of motion are characterised by inertia35,36 nor when particles’ motion is on-lattice37,38 rather than off-lattice.
Adding passive particles to an ABP suspension, one could study the physics of a binary mixture. By means of experiments or numerical simulations, mixtures of active and passive particles have been studied by several authors.39–46 When focusing on the behaviour of passive particles, active particles (whether ABP or bacteria) influence not only the structural arrangement of passive particles, but also their dynamic properties, as demonstrated in ref. 41–46. On the other side, adding a small amount of passive particles to a suspension of active particles18,47,48 is not enough to impede MIPS from taking place but can alter its morphology. When MIPS appears, the dense phase is not homogeneous anymore, since active particles are more concentrated at the boundaries and passive ones are mostly concentrated at its inner part. Interestingly, the fluctuations of the MIPS interface are much more pronounced in the binary mixture than in the purely active system.47 In this respect, Wysocki and coworkers18 studied an active/passive binary mixture in a two-dimensional elongated simulation box and identified a collective motion of the dense MIPS phase. This collective motion, completely absent in the purely active ABP suspension,48 consisted of well-defined propagating interfaces caused by a flux imbalance of the active and passive particles in the dilute phase.
In the present work, we investigate the behaviour of a two-dimensional binary mixture of repulsive (WCA) active (A)/passive (P) Brownian particles via simulations by means of the LAMMPS Molecular Dynamics package.49 The active Brownian particles, at temperature T, with Boltzmann constant kB, translational diffusion coefficient Dt, and the stochastic uncorrelated white noise ![[small xi, Greek, vector]](https://www.rsc.org/images/entities/i_char_e1cd.gif) i, have velocities given by
i, have velocities given by
 | (1) |
![[n with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006e_20d1.gif) i = (cos
i = (cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θi,sin
θi,sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θi), with angle θi changing independently for each particle,
θi), with angle θi changing independently for each particle, | (2) |
Using the same equation (eqn (1)), the passive particles are simulated by setting Fa = 0. The interaction potential in the first term of eqn (1), without a distinction between the active or passive character of particles, is chosen as the repulsive WCA potential,50
 | (3) |
In our simulations, we keep the area A applying periodic boundary conditions in a box with lengths Lx > Ly (as in ref. 47). The periodicity along the short edge (Ly) plays the usual role of avoiding finite size effects; however, on the long edge (Lx) its role should be regarded as a system with a real cylindrical geometry. We set the number of active (NA) and passive (NP) particles constant so that the total number of particles is NT = NA + NP. Unless explicitly stated otherwise, we set NT = 8055 with a box size of Lx = 200σ and Ly = 50σ, where σ denotes the particle diameter. The passive particle concentrations vary from ηP = NP/NT = 0.4 down to the purely active system (ηP = 0). Throughout the study, the number density is fixed at ρ = NT/(LxLy) = 0.8055. Almost most of the results correspond to the standard system size (Lx = 200σ, Ly = 50σ, and NT = 8055). However, when explicitly indicated, we will also present results for other system sizes.
The activity is controlled via the Peclet number, defined as Pe = 3ντr/σ, where ν = FaDt/kBT is the self-propulsion velocity and τr = 1/Dr is the reorientation time. We set Dt = 1.5, Dr = 0.6, kBT = 1.5, and Fa = 24, resulting in Pe = 120. This choice of density and Peclet number guarantees phase separation (MIPS) for both the pure system (ηP = 0) and the mixtures studied here, up to ηP = 0.4.47,48
2 Characterization of the dense slab motion
Typical MIPS snapshots, separated by Δt = 100 time intervals (from top to bottom) are reported in Fig. 1 for the pure ηP = 0 system (left) and the ηP = 0.4 mixture (right), (see also Videos Vid_SP_mov_MIX_00.mp4 and Vid_SP_mov_MIX_04.mp4, ESI†).The MIPS in the pure system of ABP (left panels) forms a dense slab (or band) closing itself over the Ly (shorter) period, and filling a fraction Ls/Lx of the (horizontal, in the Figure) X axis. The less dense phase fills the rest ((Lx − Ls) × Ly) of the simulation box. The periodic boundary along X implies that the dense band may appear at any position, even apparently split into two pieces, at the opposite ends of the 0 ≤ x ≤ Lx box. As usual in phase separations, the thickness of each region would readjust to the values of NT and the area A = Lx × Ly, without a change in the coexisting densities.
For the ηP = 0.4 mixture (right column in Fig. 1) the snapshots show also the formation of a dense slab, although thinner than at the left column because in the mixture there is less density difference between the two phases. That could be expected since the active particles are diluted (keeping the same total density) in the mixture with passive particles. The fluctuations at the interfaces are larger in the mixture than in the pure ABP system, but the most important difference comes in the series of snapshots along each column (see also the Videos, ESI†).
In the pure active system, the dense MIPS band has a slow random wandering along the X direction, while in the mixture there is fast translation of the band along the X direction, either to the right (as shown in these snapshots) or to the left (at other times along the simulation). The same sense of motion is kept over long time periods and the band often goes across the periodic boundary x = 0, Lx.
As shown below, this self-sustained movement relies on the inhomogeneity of the whole system along the X direction, including a clear asymmetry between the interfacial structures at the two edges of the moving slab. That contrasts with the homogeneous phases in the MIPS of pure ABP systems, in which the inhomogeneity is restricted to the two symmetric interfacial regions.
The formation of inhomogeneous structures with steady movement is known for systems of Brownian interacting particles kept (by an external force) in steady motion with respect to the bath, so that the balance between the friction, the external force and the interactions creates inhomogeneous “front” and “wake” structures along the direction of motion.51
The use of periodic boundary conditions along the X axis (perpendicular to the interfaces) becomes then a physical choice (like in a real cylindrical or toroidal geometry), rather than a computational trick, since the values of Lx and Ls (that is controlled by NT) affect the whole inhomogeneous structure. Taking Lx as a physical period allows us to explore steady states in which the inhomogeneous density distributions move (over long time periods) without changing their mesoscopic structure.
Our analysis, under these simplified conditions, aims to quantify the (visually observed) difference between pure and mixed systems. The relevance of more complex mesoscopic MIPS structures in mixtures under other geometrical constraints will be discussed later.
First, we need a quantitative mesoscopic description for the motion of these structures, averaging over the rapid changes of the particle positions xi (for i = 1, NT). To that effect, we define (see the ESI† for discussion on alternative definitions) the instantaneous position of the dense band X(t) as‡
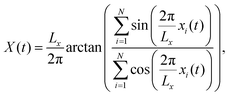 | (4) |
 ; so that X(t) is located at the center of the dense slab, independent of the position of the slab in the 0 ≤ x ≤ Lx interval.
; so that X(t) is located at the center of the dense slab, independent of the position of the slab in the 0 ≤ x ≤ Lx interval.
The results for X(t), reported in Fig. 2, are then used to calculate the velocity of the slab as a mesoscopic structure.
 | (5) |
Then V(t) is averaged as 〈V〉, over 250Δt = 12.5 time intervals, and used to get its autocorrelation (ESI†), 〈(V(to) − 〈V〉)(V(to + t) − 〈V〉)〉 ≈ ΔV2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−t/τp), to characterize rapid fluctuations with persistence time τp ≈ 1.8 ± 0.2, that we find to be similar in pure and mixed systems.
exp(−t/τp), to characterize rapid fluctuations with persistence time τp ≈ 1.8 ± 0.2, that we find to be similar in pure and mixed systems.
For the unbiased random walk (ηP = 0) there is no longer time scale than τp, so that the mean square amplitude of the V(t) fluctuations ΔV2 ≡ 〈(V(t) − 〈V〉)2〉 should produce a random walk of X(t) with diffusion constant D = ΔV2τp ≈ 0.3 ± 0.05; consistent with the observed changes ΔX(t) ∼ ±50 over the full simulation run tmax = 4400. Such a slow drift (that should be size dependent) is typical in any phase separation and it is usually dealt with (small) rigid shifts of all particle positions to keep the dense slab at an approximately fixed position in the periodic cell.
In contrast, mixtures with ηp ≥ 0.2 (Fig. 2, panels b–d) show long steady motion periods (SMPs), marked as red dashed lines, with a nearly constant (either positive or negative) slope X(t) − X(to) ≈ ±V![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) SMP (ηP)(t − to), with (absolute) values of the slope that increase from VSMP (0.2) ≈ 0.30 to VSMP (0.4) ≈ 0.57. The mean square fluctuations ΔV2 = 〈(V(t) − 〈V(t)〉)2〉 ≈ 0.3 (over the same 12.5 time intervals) are just slightly larger than for ηP = 0.
SMP (ηP)(t − to), with (absolute) values of the slope that increase from VSMP (0.2) ≈ 0.30 to VSMP (0.4) ≈ 0.57. The mean square fluctuations ΔV2 = 〈(V(t) − 〈V(t)〉)2〉 ≈ 0.3 (over the same 12.5 time intervals) are just slightly larger than for ηP = 0.
The amplitude  of these fast τp ≈ 1.8 fluctuations are of the same order of magnitude as the mean value VSMP; however, the SMP are clearly identified in X(t) (see Fig. 2) and also in the histograms for V(t), (ESI†) because a much longer time scale emerges, with a typical SMP persistent time τSMP that we can only estimate to be τSMP ∼ 500 for ηP = 0.2, τSMP ∼ 1000 for ηP = 0.3 and larger for ηP = 0.4.
of these fast τp ≈ 1.8 fluctuations are of the same order of magnitude as the mean value VSMP; however, the SMP are clearly identified in X(t) (see Fig. 2) and also in the histograms for V(t), (ESI†) because a much longer time scale emerges, with a typical SMP persistent time τSMP that we can only estimate to be τSMP ∼ 500 for ηP = 0.2, τSMP ∼ 1000 for ηP = 0.3 and larger for ηP = 0.4.
The SMPs are interrupted by large fluctuations in the structure of the MIPS slab, reflected in sharp changes of the nominal position X(t) defined in eqn (4). Then, there may be a rest period, in which X(t) fluctuates without forth-back bias before a new sudden change in X(t) leads to start a new SMP, that may be in the opposite direction (with a U-turn of the slab) or in the same direction as the previous SMP. We may estimate that for ηP = 0.4 there is a typical time τo ∼ 100 (just an order of magnitude) for the rest period between two SMPs. U-turns occur at each ηp during periods of steady motion. As ηp increases, the time required for a U-turn to develop becomes shorter. Thus, at ηp = 0.4, the U-turn is very abrupt. In this respect, given sufficient simulation time, a U-turn d also occurs at ηp = 0.3, although less sharply than at ηp = 0.4, but still more sharply than at ηp = 0.2.
Therefore, for that high concentration of passive particles τp ≪ τo ≪ τSMP gives a good separation of time scales for our analysis of the SMPs. For lower ηP values, τo increases while τSMP decreases, so that for ηP = 0.2 we may estimate τo ∼ τSMP ∼ 500.
Notice that we have only very crude estimations for τSMP(ηP) and τo(ηP) since good statistics would require extremely long simulation runs. As in any mesoscopic characterization there are uncertainties; a red line in Fig. 1 may go through a large fluctuation, and we could take it as a single SMP or as two successive SMPs that keep the same direction of motion, after a very short rest time.
Nevertheless, we find robust indications for the emergence of the time scales τSMP > τo ≫ τp, leading to superdiffusive behaviour of the dense MIPS clusters, as a peculiarity of active–passive mixtures and the subject of our study. In the remaining of our work, we will focus on the ηP = 0.4 case for a detailed analysis, because it provides the best statistics to characterize the structures that produce the SMP.
However, similar behaviour is clearly observed for ηp = 0.3 and 0.2. For ηP = 0.1 we observe sudden changes in X(t), that do not appear in the pure (ηP = 0) MISP slabs, but the time scale separation between SMP and rest periods becomes uncertain.
3 Analysis of the density and current profiles
The instantaneous density profiles , for α = A, P particles, should be averaged over a time interval t ∈ [to,to + Δt] to get smooth mean density profiles ρα(x) = 〈
, for α = A, P particles, should be averaged over a time interval t ∈ [to,to + Δt] to get smooth mean density profiles ρα(x) = 〈![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) α(x,t)〉Δt. However, the fast movement of the band in active–passive mixtures leads to flat ρα(x), unless the time average is chosen to be very narrow, with the consequence of being too noisy ρα(x). This problem can be overcome by evaluating the shifted density profiles5,12
α(x,t)〉Δt. However, the fast movement of the band in active–passive mixtures leads to flat ρα(x), unless the time average is chosen to be very narrow, with the consequence of being too noisy ρα(x). This problem can be overcome by evaluating the shifted density profiles5,12 | (6) |
The emergent time scale separation allows to take τSPM > Δt ≫ τp with a very good average over the rapid fluctuations, but still within a single SMP. Thus, for ηp = 0.4, over a period with 〈V(t)〉 ≈ +0.57 we obtain the strongly asymmetric ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) A(x) and
A(x) and ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) P(x) profiles shown in Fig. 3.
P(x) profiles shown in Fig. 3.
At the back of the moving band, ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) A(x) (dashed red) presents a peak and
A(x) (dashed red) presents a peak and ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) P(x) (dashed orange) drops to a narrow minimum. In contrast, at the front,
P(x) (dashed orange) drops to a narrow minimum. In contrast, at the front, ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) A(x) and
A(x) and ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) P(x) have similar smoother decays. For comparison, the pure ABP system (black line) presents a fairly symmetric profile and a larger MIPS density difference.
P(x) have similar smoother decays. For comparison, the pure ABP system (black line) presents a fairly symmetric profile and a larger MIPS density difference.
The same qualitative features are found at lower concentrations of passive particles, as shown in Fig. 4, for ηP = 0.2.
In panels (b) and (c) eqn (6) is averaged over the SMP with 〈V(t)〉 ≈ ±0.30, respectively (along the periods marked as red-dashed lines in Fig. 2(b)). The asymmetry is (![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) α(x) →
α(x) → ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) α(−x)) in SMP with the opposite velocity. The rest periods (〈V(t)〉 ≈ 0) are now long enough to take good averages, that give the symmetric density profiles in Fig. 4(a). Notice that the steady motion of the band across the system seems to reinforce (rather than to weaken) the MIPS in the mixture, since the density contrast between the maximum density (at x ≈ 0) and the minimum density (at x ≈ ±Lx/2) is higher in the SMP asymmetric profiles, than in the symmetric profiles during the rest periods.
α(−x)) in SMP with the opposite velocity. The rest periods (〈V(t)〉 ≈ 0) are now long enough to take good averages, that give the symmetric density profiles in Fig. 4(a). Notice that the steady motion of the band across the system seems to reinforce (rather than to weaken) the MIPS in the mixture, since the density contrast between the maximum density (at x ≈ 0) and the minimum density (at x ≈ ±Lx/2) is higher in the SMP asymmetric profiles, than in the symmetric profiles during the rest periods.
 | ||
Fig. 4 Full lines: mean total density profiles (eqn (6)) for ηP = 0.2; blue line: total density, red-dashed line: ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) A(x) and orange-dashed line: A(x) and orange-dashed line: ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) P(x). For comparison, the black liners give the density profile in a pure (ηP = 0) ABP system with the same ρT. In panel (a) the average is taken over the rest periods (〈V(t)〉 ≈ 0 in panel (b) of Fig. 2); in panels (b) and (c) the profiles are averaged over the SMP (red-dashed lines in Fig. 2) when the slab moves in the direction of the top blue arrow. P(x). For comparison, the black liners give the density profile in a pure (ηP = 0) ABP system with the same ρT. In panel (a) the average is taken over the rest periods (〈V(t)〉 ≈ 0 in panel (b) of Fig. 2); in panels (b) and (c) the profiles are averaged over the SMP (red-dashed lines in Fig. 2) when the slab moves in the direction of the top blue arrow. | ||
Wysocki et al.18 proposed a source-sink mechanism to explain the band displacement, where the receding interface acts as a source, evaporating particles into the dilute phase, while the advancing front, acting as a sink, captures particles into the dense phase. A representation of this source/sink effect is reported in Fig. 5 for ηP = 0.4, with four snapshots, each with X(t) as a vertical dashed line and the MIPS boundaries as wavy black lines.
 | ||
| Fig. 5 Snapshots showing the slab's movement as a function of time (from top to bottom). Slab boundaries31 underlined by a black line as well as the mass centre position, X(t) (vertical dashed line). Top snapshot: Slab particles on each side are coloured red (source interface) and purple (sink interface). Their colour is maintained in the all snapshots, showing how particles change position with time. | ||
In the top snapshot, particles are coloured in red if close to the source (back) side and in purple if close to the sink (front). From top to bottom, the red particles rapidly escape from the back interface and are added at the front interface. The purple particles remain mostly stationary as the slab moves through them, diffusing slowly within the dense region.
For quantitative analysis, we use Smoluchowski's equation for the instantaneous distributions of density ρ(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ,t) = 〈δ(
,t) = 〈δ(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) −
− ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) i(t))〉n and current
i(t))〉n and current ![[j with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006a_20d1.gif) (
(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ,t) = 〈δ(
,t) = 〈δ(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) −
− ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) i(t)
i(t)![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) i(t))〉n, smoothed by the average 〈…〉n over many realizations of the Brownian noise acting on the particles. Along a SMP the velocity of the MIPS band has rapid (∼τp) fluctuations around a mean value 〈V〉. We assume that the self-averaging of
i(t))〉n, smoothed by the average 〈…〉n over many realizations of the Brownian noise acting on the particles. Along a SMP the velocity of the MIPS band has rapid (∼τp) fluctuations around a mean value 〈V〉. We assume that the self-averaging of ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) (x) gives ρ(
(x) gives ρ(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ,t) = ρ(x,t) ≈
,t) = ρ(x,t) ≈ ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) (
(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ), with
), with ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) = x − 〈V〉t, and the continuity equation for the steady state movement of the band becomes51 ∂tρα(x,t) = −∂xjα(x,t) = −〈V〉∂
= x − 〈V〉t, and the continuity equation for the steady state movement of the band becomes51 ∂tρα(x,t) = −∂xjα(x,t) = −〈V〉∂![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif)
![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) (
(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ), that may be integrated to the current densities
), that may be integrated to the current densities
jα(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ) = 〈V〉 ) = 〈V〉![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) α( α(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ) − Δα ) − Δα | (7) |
![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ) to be lower than the apparent current carried by the moving slab.
) to be lower than the apparent current carried by the moving slab.
In our simulations, we get ΔA and ΔP from 〈V〉 and the mean velocity of the particles, for each species,
 | (8) |
4 Brownian dynamics analysis for the SMP
In the Smoluchowski equation for Brownian particles (with mobility Γ, temperature T and translational diffusion constant Dt = kTΓ) the (noise averaged) currents for each species are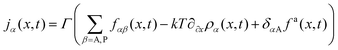 | (9) |
All these force densities may be evaluated in our simulations, and averaged along a SMP in terms of the relative position x = xi(t) − X(t) of each particle from the mesoscopic position of the slab, as done in eqn (6) for the density profile ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) α(x). The results in Fig. 6 correspond to the same SMP, for ηP = 0.4, as the density profiles in Fig. 3.
α(x). The results in Fig. 6 correspond to the same SMP, for ηP = 0.4, as the density profiles in Fig. 3.
The assumption ρ(x,t) ≈ ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) (
(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ), with
), with ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) = x − 〈V〉t, that leads to eqn (7) may now be used for each component of the force densities fα(x,t) ≈
= x − 〈V〉t, that leads to eqn (7) may now be used for each component of the force densities fα(x,t) ≈ ![[f with combining tilde]](https://www.rsc.org/images/entities/i_char_0066_0303.gif) α(
α(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ), to take the time averages along a SMP with mean slab velocity 〈V〉 as (self-averaging) representation of the Brownian noise average in Smoluchowski eqn (9), to get
), to take the time averages along a SMP with mean slab velocity 〈V〉 as (self-averaging) representation of the Brownian noise average in Smoluchowski eqn (9), to get
 | (10) |
Fig. 7 shows a comparison of (again for the same ηP = 0.4 SMP analyzed in Fig. 3) the mean velocities, vα(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ) ≡ jα(
) ≡ jα(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) )/ρα(
)/ρα(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ), obtained viaeqn (7) (i.e. from the density profile, the global mean velocities 〈vα〉 and the slab 〈V〉) and viaeqn (10) with the force densities in Fig. 6.
), obtained viaeqn (7) (i.e. from the density profile, the global mean velocities 〈vα〉 and the slab 〈V〉) and viaeqn (10) with the force densities in Fig. 6.
 | ||
Fig. 7 Particle velocity profiles for ηP = 0.4 calculated viaeqn (7). Using the currents from the forces (noisy solid lines) and the density profiles (dashed lines). Both the profiles of active (red and green lines) and passive (blue and orange lines) particles are included. The horizontal line represents vA(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ) = vP( ) = vP(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ) = 0. ) = 0. | ||
The fairly good agreement between the kinetic and the dynamical results (see also in the ESI† the direct comparison for jα(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) )) gives a strong support to our assumption j(x,t) ≈
)) gives a strong support to our assumption j(x,t) ≈ ![[j with combining tilde]](https://www.rsc.org/images/entities/i_char_006a_0303.gif) (
(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ), i.e. to the self-averaging of the Brownian thermal noise as time averages over the SMP. Therefore we may proceed with the following dynamical interpretation for the structural origin of the SMP based on (10).
), i.e. to the self-averaging of the Brownian thermal noise as time averages over the SMP. Therefore we may proceed with the following dynamical interpretation for the structural origin of the SMP based on (10).
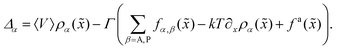 | (11) |
![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) , is a strong link between the results for the density and force profiles when the system is in an SMP. Moreover, taking the average of (11) over the total length 0 ≤
, is a strong link between the results for the density and force profiles when the system is in an SMP. Moreover, taking the average of (11) over the total length 0 ≤ ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ≤ Lx, with periodic boundaries, the contributions from the Brownian diffusion and the active force (both with an independent random direction on each particle) are null.
≤ Lx, with periodic boundaries, the contributions from the Brownian diffusion and the active force (both with an independent random direction on each particle) are null.
The same applies to the repulsion between particles of the same species fAA(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ) and fPP(
) and fPP(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ) that have null integrals. The qualitative difference of a mixture with respect to a pure ABP system is that the integrals of fAP(
) that have null integrals. The qualitative difference of a mixture with respect to a pure ABP system is that the integrals of fAP(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ) and fPA(
) and fPA(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ),
),
 | (12) |
As observed in our simulations, the global movement of the two species has to be in opposite directions, and it is fully determined by their mutual global force FPA = −FAP. The counter currents in eqn (7) may be obtained in terms of the total forces between active and passive particles,
 | (13) |
 | (14) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) T, with ρ
T, with ρ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) T being the total density.
T being the total density.
The velocity profiles in Fig. 7 show that within the dense slab (−25 ≤ ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ≤ 15) the active and passive particles move together, vA(
≤ 15) the active and passive particles move together, vA(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ) ≈ vP(
) ≈ vP(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ) ≈ 〈V(t)〉/3. Therefore, the MIPS kinetics in active–passive mixtures is neither a pure source/sink mechanism (in which the particles of the dense slab would remain at rest), nor a real drift of the particles at the full velocity V(t), as if ΔA = ΔP = 0. Drift and source/sink act in parallel, self-maintained by the asymmetry of ρα(
) ≈ 〈V(t)〉/3. Therefore, the MIPS kinetics in active–passive mixtures is neither a pure source/sink mechanism (in which the particles of the dense slab would remain at rest), nor a real drift of the particles at the full velocity V(t), as if ΔA = ΔP = 0. Drift and source/sink act in parallel, self-maintained by the asymmetry of ρα(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ), which unbalance the local rectifications of the active forces at the front and back edges of the slab. With our ρ(x,t) ≈
), which unbalance the local rectifications of the active forces at the front and back edges of the slab. With our ρ(x,t) ≈ ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) (x − 〈V〉t) hypothesis, if vA(
(x − 〈V〉t) hypothesis, if vA(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ) = vP(
) = vP(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ) at a point
) at a point ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) , their value is
, their value is
 | (15) |
![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ≈ 0), vA(0) ≈ vP(0) ≈ 0.2 ≈ (1 − 2/3)〈V〉, are in good agreement with the total density profile in Fig. 3, being ρT/(ρA(0) + ρP(0)) ≈ 0.8/1.2 = 2/3.
≈ 0), vA(0) ≈ vP(0) ≈ 0.2 ≈ (1 − 2/3)〈V〉, are in good agreement with the total density profile in Fig. 3, being ρT/(ρA(0) + ρP(0)) ≈ 0.8/1.2 = 2/3.
We now demonstrate how the system may develop the asymmetric density profiles, to produce a global force FPA and self-sustain the movement 〈V〉 ≠ 0. In the ABP model the local rectification of the active force31 produces the force density fa(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ) with positive/negative peaks at the back/front edges, compressing (i.e. stabilizing) the dense slab. The null total integral of fa(
) with positive/negative peaks at the back/front edges, compressing (i.e. stabilizing) the dense slab. The null total integral of fa(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ) is forced, on average, by the symmetry of the density profile. However, there are fluctuations such that fa(
) is forced, on average, by the symmetry of the density profile. However, there are fluctuations such that fa(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ) becomes stronger at one edge, in correspondence to a sharper rise in ρA(
) becomes stronger at one edge, in correspondence to a sharper rise in ρA(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ). Such fluctuation pushes the dense band in one direction and the front edge would sweep particles from the low-density phase. In the pure ηP = 0 case, the addition of more particles at the advancing edge would make stronger the rectification of the active force, thus compensating for the initial asymmetry. The short persistence time τp ≈ 1.8 reflects that kind of structural fluctuations, also observed in our binary mixtures.
). Such fluctuation pushes the dense band in one direction and the front edge would sweep particles from the low-density phase. In the pure ηP = 0 case, the addition of more particles at the advancing edge would make stronger the rectification of the active force, thus compensating for the initial asymmetry. The short persistence time τp ≈ 1.8 reflects that kind of structural fluctuations, also observed in our binary mixtures.
In a mixture, the sweeping effect at the advancing edge would be stronger for the (lower mobility) passive particles. That would decrease the local concentration of the (higher mobility) active particles and the (backwards) rectified active force at the advancing edge, enhancing the initial force/density unbalance. Thus, the global motion of the slab may increase, against the friction of the Brownian dynamics.
At a given passive particle concentration ηP, a fluctuation might appear in the system with a typical time τo(ηP): this fluctuation could be strong enough to drive the system into a steady-state motion, with asymmetric density profiles and (action/reaction) opposite global forces on the two species. Eventually, with a typical time τSMP(ηP) ≫ τp, another large fluctuation could break the self-sustained unbalance, leading to the end of the SMP.
5 Size effect analysis
The above analysis underlines the crucial role of passive particles as a reactive bath in which the local rectification of the active forces may produce not only MIPS but also the self-sustained asymmetry and the steady motion of the dense band. Since the unbalanced rectification of fA(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ) at the edges of the slab has to produce the real motion of all particles within, the SMPs are strongly size-dependent.
) at the edges of the slab has to produce the real motion of all particles within, the SMPs are strongly size-dependent.
Fig. 8 presents X(t) values for several simulations characterised by ηP = 0.4 and ρT = 0.8, but different sizes: Lx = 100σ and Ly = 25σ (a, blue); Lx = 400σ and Ly = 50σ (b, purple); Lx = 400σ and Ly = 100σ (c, orange); and Lx = 200σ and Ly = 50σ (d, red), which corresponds to the size used in all previous figures.
 | ||
Fig. 8 Trajectories of MIPS bands (X(t)) with ηP = 0.4 for systems of different sizes at a fixed density ρ = 0.8 are shown. The trajectories correspond to the following system sizes: panel a, blue, Lx = 100σ and Ly = 25σ (NT = 2070); panel b, purple, Lx = 400σ and Ly = 50σ (NT = 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 110); panel c, orange, Lx = 400σ and Ly = 100σ (NT = 32 110); panel c, orange, Lx = 400σ and Ly = 100σ (NT = 32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 220); and panel d, red, Lx = 200σ and Ly = 50σ (NT = 8055), the same simulation as in panel (d) of Fig. 2. 220); and panel d, red, Lx = 200σ and Ly = 50σ (NT = 8055), the same simulation as in panel (d) of Fig. 2. | ||
The smallest system (in blue, panel (a)) has the box lengths (Lx,Ly) and also the slab thickness (Ls), reduced to half of their values in the (original) system in panel (d). The X(t) trajectory in the smallest system shows an SMP as clear as in the original (larger) system, but with a (±) velocity VSMP ≈ 1.04, i.e. much faster than the value VSMP ≈ 0.57 of the original system for the same ηP. That is expected since the total force unbalance has to scale as Ly, since it comes from the interfaces. In contrast, the friction of the Brownian bath has to scale as the total number of particles NT = 0.8LxLy. Notice that, even taking into account that the results of the smallest system are reported over a longer trajectory than those of the larger one, its typical times seem to be shorter (since we observe several U-turns instead of the single U-turn observed in the large system). A quantitative estimate of the size dependence of τSMP and τo would require extremely large simulations, to get a good statistical sampling of these rare events. However, we might expect longer time scales in larger systems, since they need a larger fluctuation to create or destroy a SMP.
The other two panels in Fig. 8 show the results of simulations in systems larger than the original one (reported in panel d). In panels (b) and (c) Lx and the slab thickness Ls are twice as large as in (d). In panel (b) (purple line) we keep the original value of Ly, to get a more elongated aspect ratio for the MIPS band. We observe that after a long equilibration time the slab takes a positive velocity with 〈V(t)〉 ≈ 0.3, i.e. about half the value of the SMP in the original system (d): this is consistent with having similar interfacial forces (∼Ly) against double friction effects (∼NT ∼ LxLy). Thus, the increase of Lx and of the slab thickness Ls leads to V(t) with much larger fluctuations around its mean (SMP) value, alternating fairly long periods characterised by a slab velocity clearly higher or lower than 0.3. Thus, the clean separation of the trajectories in the SMP, with V(t) ≈ ±VSMP, divided by static periods with 〈V(t)〉t ≈ 0, breaks down. This could be caused by the fact that the longer Lx and Ls allow for enough free space for the appearance of frequent fluctuations that break the slab. Thus, our description in terms of the single variable X(t) fails.
Panel (c) (orange line) corresponds to a system with the same Lx and slab thickness Ls as in panel (b), but Ly which is twice as large as in (d) (as a consequence, NT is four times the original value). The trajectory X(t) has (as in panel (b)) a long equilibration period followed by a steady forward motion of the dense slab, with a mean velocity 〈V(t)〉 ≈ 0.34 that is just slightly higher than in panel (c) (the system in panel (c) has twice as much interface than in panel (b), and twice as much NT, i.e. friction from the bath). Even though the larger Ly size reduces the fluctuations of V(t) around that mean value, we still cannot split the trajectory in panel (c) into SMP as cleanly as in the original system. Thus, we may interpret that the larger Lz = 100 makes it less likely than with Ly = 50 that a fluctuation splits the dense slab into two bands so that the description via the variable X(t) (i.e. assuming a single dense band) is more accurate than in panel (b).
The size effects in 〈V〉 are directly transmitted to the mean particle velocities. Thus, compared to the values 〈vA〉 = − 0.03 and 〈vP〉 = 0.05 achieved the original size (panel (d)), in the larger system (orange panel (c)) with (〈V〉 = 0.34), we obtain that the velocities of each species are 〈vA〉 ≈ −0.02 and 〈vP〉 ≈ 0.03. Very similar values are obtained when we duplicate Lx keeping the original value of Ly. Therefore, we conclude that the velocity of the slab is (roughly) inversely proportional to the x-length, such that 〈V〉 ∝ 〈vα〉 ∝ 1/Lx and VSMP ∝ 〈vα〉 ∝ 1/Lx.
6 Analysis of U-turn events
The whole phenomenology described so far has to be interpreted as the appearance of mesoscopic structures, with large spatial and temporal scales that emerge by the presence of passive particles in ABP systems. In general, we may expect complex kinetic behaviours consisting of large and fast moving clusters colliding, merging and splitting. It is only through our choices for Lx and Ly, that we have been able to describe the phenomenology observed using the mesoscopic variable X(t) and the time averages with τp ≪ Δt < τSMP(ηP).The analysis of the events creating and destroying the SMP has to be restricted to shorter time averages and noisier density profiles. Fig. 9-panel (a) represents a zoom-in of the U-turn observed in Fig. 2-panel d at t ≈ 1500 (ηP = 0.4) (see also Video in SM Vid_SP_U-turn_v2.mp4, ESI†).
 | ||
| Fig. 9 (a) Zoom of the slab centre of the mass position (X(t)) of the ηP = 0.4 mixture in Fig. 2-panel (d), undergoing a U-turn. Panels (b)–(e) show the mean density profiles of the different intermediate states in panel a between the change of motion. Active particle density is represented with continuum lines and the passive one with dashed lines. The colour code in panels (b)–(e) refers to the colours along the line in panel (a). | ||
The initial structure, with V(t) = −VSMP, is characterised by the asymmetry reported in Fig. 3. Zooming in, panels (b)–(e) in Fig. 9 present the mean density profiles of active (continuum) and passive (dashed) particles along the U-turn: clearly, the density of the structure is highly disordered, as shown by the appearance of a region with relatively low density of active particles at the middle of the dense slab.
The (nominal) position of the slab X(t), from eqn (4), reflects that a fluctuation period (nearly flat, in blue and in panel b) is followed by a much faster period (in red and in panel c). In fact, the trajectory X(t) itself does not give a reliable representation of the actual kinetics. The Video in the ESI† shows that the dense slab is broken into two pieces (panel c) that move in opposite directions until, due to periodic boundaries, they collide again.
Finally, the system reaches a nearly static structure over a period of Δt ∼ 1000 (in orange and in panel d), in which the density profiles are (nearly) symmetric, with a very high density of passive particles at the centre. Reversing the sequence of events for t < 1500, X(t) has a sudden acceleration (in purple and in panel e) in which the left-right symmetry is broken, to reach a SMP with V(t) = VSMP.
Thus, the large fluctuations that create and destroy the SMP in our simulations overcome our effort, in eqn (4)–(6), to describe the MIPS structure as a single cluster at the position X(t).
7 Discussion and conclusions
In a pure system of active Brownian particles, the motion of particles (induced by the thermal agitation, the active and the interaction forces) is damped by the inert bath, that acts independently on each particle. The addition of repulsive passive particles to ABP systems provides a reactive bath for the active ones. The clustering of active particles in MIPS induces inhomogeneous distributions of the passive particles that would be reflected in the motion of the active ones. Fluctuations that break the (±x) symmetry may create total (opposite) forces that particles of each species induce on those of the other species. Their opposite fluxes on the MIPS less-dense phase may lead to a self-sustained motion of the dense band, by a combination of sink-source effects at the edges and a global shift of the (much rigid) inner dense slab.To characterize and quantify all these effects, we have used simulations of a mixture of active/passive Brownian particles in a simple geometry: dense bands that cover the full period Ly, along the (shorter) Y axis, and move along the (longer) X axis, so that we may define a variable X(t) to localize the position of the dense slab and V(t) for its velocity. In terms of these mesoscopic variables, we observe the emergence of characteristic time scales, much larger than the autocorrelation time τp for V(t) in pure ABP systems. Steady moving structures (either with positive or negative mean velocity, X(t) −X(to) ≈ ±VSMP(ηP)(t − to)) appear with a typical time τo(ηP) and persist for a typical time τSMP(ηP) that may be very long. In our simulations we get fairly accurate estimations for VSMP(ηP) in mixtures with different compositions 0.2 ≤ ηP ≤ 0.4, and for different sizes of the simulation box.
The self-assembly and motion of the MIPS clusters is a mesoscopic phenomenon, depending on the size and geometry of the dense cluster and on the distance between its two edges through the less dense phase (across the periodic boundary conditions). The U-turn events observed in our simulations, when the motion of the dense slab is reversed, correspond to fluctuations that break the slab into two pieces. If the slab is too elongated (large aspect ratio Ls/Ly) these events may become frequent, with small pieces of slab breaking out of the main cluster, at one or the other edge, with the result of a worse defined velocity ±V![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) SMP. On the other hand, larger values of Ly give longer persistence times τ
SMP. On the other hand, larger values of Ly give longer persistence times τ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) SMP, for the steady motion of the slab.
SMP, for the steady motion of the slab.
We compute statistical averages over (long) time intervals in which X(t) keeps the same linear trend (either with V(t) ≈ ±V![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) SMP(ηP)), in terms of particle positions relative to the slab's mesoscopic position X(t). This allows us to obtain density, force and velocity profiles characterizing the kinetics and dynamics of the moving structures. All these variables contribute to the generic terms of the Smoluchoski equation for Brownian particles. The generic mechanism to achieve steady motion is that active particles push (and are pushed by) passive particles, producing stationary density and velocity profiles, in terms of the variable
SMP(ηP)), in terms of particle positions relative to the slab's mesoscopic position X(t). This allows us to obtain density, force and velocity profiles characterizing the kinetics and dynamics of the moving structures. All these variables contribute to the generic terms of the Smoluchoski equation for Brownian particles. The generic mechanism to achieve steady motion is that active particles push (and are pushed by) passive particles, producing stationary density and velocity profiles, in terms of the variable ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) = x − X(t), reflecting (and producing) a global inter-species force FAP = −FPA ≠ 0, either positive or negative.
= x − X(t), reflecting (and producing) a global inter-species force FAP = −FPA ≠ 0, either positive or negative.
Thus, the spontaneous breakage of the (spatial x and temporal t) symmetry cannot appear in a pure (ηP = 0) ABP system. Thus, we might consider the passive particle concentration ηP as the parameter to turn on the most primitive features of hydrodynamics, when collective motions of swimmers are made possible by their global push on a reactive medium. Our detailed statistical analysis for the different kinetic regimes (steady moving structures and the rare events that produce their U-turns) allowed us to interpret their dynamics within the framework of the Smoluchowski equation for interacting Brownian particles, thus providing a clearer physical perspective on MIPS.
The dynamics of the MIPS in active–passive mixtures under different conditions is likely to be much complex, with entangled effects of the different kinetic regimes we have identified and analysed. Nevertheless, we hope that our analysis underlines the essential role of passive particles, allowing for the time-space symmetry breaking, over time scales much larger than the typical fluctuations in ABP, and based on a self-sustained combination of a collective drift of particles in a cluster with local source/sink effects at the edges, leading to the structures’ kinetics apparently faster than the actual particles’ mean motion. As far as we are aware, so far experimental realizations of MIPS have dealt with confined systems. However, in order to observe the experimental equivalent of a travelling band, one might need to be able to implement a cylindrical geometry in an experimental setup.
Data availability
The data that support the findings of this study will be available upon request from Chantal Valeriani, on behalf of all authors.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge the support from the Spanish Secretariat for Research, Development and Innovation (grants no. PID2020-117080RB-C52, PID2022-139776NB-C66, IHRC22/00002 and PID2022-140407NB-C21) and the Maria de Maeztu Programme for Units of Excellence in R&D (CEX2023-001316-M).Notes and references
- M. E. Cates and J. Tailleur, Europhys. Lett., 2013, 101, 20010 CrossRef CAS.
- A. Martin-Gomez, D. Levis, A. Diaz-Guilera and I. Pagonabarraga, Soft Matter, 2018, 14, 2610 RSC.
- P. Digregorio, D. Levis, A. Suma, L. F. Cugliandolo, G. Gonnella and I. Pagonabarraga, Phys. Rev. Lett., 2018, 121, 098003 CrossRef CAS PubMed.
- C. B. Caporusso, P. Digregorio, D. Levis, L. F. Cugliandolo and G. Gonnella, Phys. Rev. Lett., 2020, 125, 178004 CrossRef CAS PubMed.
- J. Stenhammar, D. Marenduzzo, R. Allen and M. Cates, Soft Matter, 2014, 10, 1489 RSC.
- J. J. Bialke, J. T. Siebert, H. Lowen and T. Speck, Phys. Rev. Lett., 2015, 115, 098301 CrossRef PubMed.
- A. K. Omar, Z.-G. Wang and J. F. Brady, Phys. Rev. E, 2020, 101, 012604 CrossRef CAS.
- C. Bechinger, R. D. Leonardo, H. Lowen, C. Reichhardt, G. Volpe and G. Volpe, Rev. Mod. Phys., 2016, 88, 045006 CrossRef.
- G. S. Redner, M. F. Hagan and A. Baskaran, Phys. Rev. Lett., 2013, 110, 055701 CrossRef PubMed.
- M. E. Cates and J. Tailleur, Annu. Rev. Condens. Matter Phys., 2015, 6, 219–244 CrossRef.
- A. Wysocki, R. G. Winkler and G. Gompper, Europhys. Lett., 2014, 105, 48004 CrossRef.
- J. Martin-Roca, R. Martinez, L. Alexander, A. Diez, D. Aarts, F. Alarcon, J. Ramírez and C. Valeriani, J. Chem. Phys., 2021, 154, 164901 CrossRef.
- M. James, E. Clément, J. Robert and B. Maria, Proc. R. Soc. A, 2023, 479, 20230524 CrossRef.
- X. q Shi, G. Fausti, H. Chate, C. Nardini and A. Solon, Phys. Rev. Lett., 2019, 125, 168001 CrossRef.
- D. Levis, J. Codina and I. Pagonabarraga, Soft Matter, 2017, 13, 8113 RSC.
- L. Caprini, E. Hernandez-Garcia, C. Lopez and U. M. B. Marconi, Sci. Rep., 2019, 9, 16687 CrossRef.
- A. P. Solon, J. Stenhammar, M. E. Cates, Y. Kafri and J. Tailleur, New J. Phys., 2018, 20, 075001 CrossRef.
- A. Wysocki, R. G. Winkler and G. Gompper, New J. Phys., 2016, 18, 123030 CrossRef.
- E. Tjhung, C. Nardini and M. E. Cates, Phys. Rev. X, 2018, 8, 031080 Search PubMed.
- S. Hermann, D. de las Heras and M. Schmidt, Mol. Phys., 2021, 119, e1902585 CrossRef.
- G. Gonnella, D. Marenduzzo, A. Suma and A. Tiribocchi, C. R. Phys., 2015, 16, 316 CrossRef.
- I. Buttinoni, J. Bialke, F. Kummel, H. Lowen, C. Bechinger and T. Speck, Phys. Rev. Lett., 2013, 110, 238301 CrossRef PubMed.
- S. Thutupalli, R. Seemann and S. Herminghaus, New J. Phys., 2011, 13, 073021 CrossRef.
- D. D. Nishiguchi and M. Sano, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 92, 052309 CrossRef PubMed.
- G. Briand and O. Dauchot, Phys. Rev. Lett., 2016, 117, 098004 CrossRef PubMed.
- J. Bialké, J. T. Siebert, H. Löwen and T. Speck, Phys. Rev. Lett., 2015, 115, 098301 CrossRef.
- A. Patch, D. M. Sussman, D. Yllanes and M. C. Marchetti, Soft Matter, 2018, 14, 7435–7445 RSC.
- N. Lauersdorf, T. Kolb, M. Moradi, E. Nazockdast and D. Klotsa, Soft Matter, 2021, 17, 6337–6351 RSC.
- S. Hermann, D. de las Heras and M. Schmidt, Phys. Rev. Lett., 2019, 123, 268002 CrossRef.
- E. Chacon and P. Tarazona, J. Phys.: Condens. Matter, 2005, 17, S3493 CrossRef.
- E. Chacon, F. Alarcon, J. Ramírez, P. Tarazona and C. Valeriani, Soft Matter, 2022, 18, 2646 RSC.
- R. Matas-Navarro, R. Golestanian, T. B. Liverpool and S. M. Fielding, Phys. Rev. E, 2014, 90, 032304 CrossRef PubMed.
- M. Theers, E. Westphal, K. Qi, R. G. Winkler and G. Gompper, Soft Matter, 2018, 14, 8590–8603 RSC.
- H. Zhao, A. Košmrlj and S. S. Datta, Phys. Rev. Lett., 2023, 131, 118301 CrossRef PubMed.
- H. Lowen, J. Chem. Phys., 2020, 152, 040901 CrossRef.
- J. Su, H. Jiang and Z. Hou, New J. Phys., 2021, 23, 013005 CrossRef.
- C. M. Barriuso, C. Vanille, F. Alarcon, I. Pagonabarraga, R. Brito and C. Valeriani, Soft Matter, 2021, 17, 10479 RSC.
- F. Dittrich, T. Speck and P. Virnau, Eur. Phys. J. E, 2021, 44, 53 CrossRef PubMed.
- S. Dikshit and S. Mishra, Eur. Phys. J. E: Soft Matter Biol. Phys., 2022, 45, 21 CrossRef.
- B.-Q. Ai, B.-Y. Zhou and X.-M. Zhang, Soft Matter, 2020, 16, 4710–4717 RSC.
- Y. Wang, Z. Shen, Y. Xia, G. Feng and W. Tian, Chin. Phys. B, 2020, 29, 053103 CrossRef.
- F. Hauke, H. Löwen and B. Liebchen, J. Chem. Phys., 2020, 152, 014903 CrossRef CAS.
- C. Valeriani, M. Li, J. Novosel, J. Arlt and D. Marenduzzo, Soft Matter, 2011, 7, 5228–5238 RSC.
- X.-L. Wu and A. Libchaber, Phys. Rev. Lett., 2000, 84, 3017–3020 CrossRef CAS PubMed.
- G. Grégoire, H. Chaté and Y. Tu, Phys. Rev. Lett., 2001, 86, 556 CrossRef PubMed.
- A. E. Patteson, A. Gopinath and P. E. Arratia, Nat. Commun., 2018, 9, 5373 CrossRef CAS.
- D. R. Rodriguez, F. Alarcon, R. Martinez, J. Ramrez and C. Valeriani, Soft Matter, 2020, 16, 1162 RSC.
- J. Stenhammar, R. Wittkowski, D. Marenduzzo and M. E. Cates, Phys. Rev. Lett., 2015, 114, 018301 CrossRef CAS.
- A. P. Thompson, H. M. Aktulga, R. Berger, D. S. Bolintineanu, W. M. Brown, P. S. Crozier, P. J. in’t Veld, A. Kohlmeyer, S. G. Moore, T. D. Nguyen, R. Shan, M. J. Stevens, J. Tranchida, C. Trott and S. J. Plimpton, Comput. Phys. Commun., 2022, 271, 108171 CrossRef CAS.
- J. D. Weeks, D. Chandler and H. C. Andersen, J. Chem. Phys., 1971, 54, 5237–5247 CrossRef CAS.
- F. Penna and P. Tarazona, J. Chem. Phys., 2003, 119, 1766–1776 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5sm00134j |
| ‡ Along the simulation we chose the branch of the arc-tangent in which X(t) is the closest to its previous position X(t − δt), in order to keep the number full Lx rounds. |
| This journal is © The Royal Society of Chemistry 2025 |




