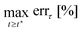Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Modelling the non-linear viscoelastic behaviour of brain tissue in torsion†
Griffen
Small
 *a,
Francesca
Ballatore
*a,
Francesca
Ballatore
 b,
Chiara
Giverso
b,
Chiara
Giverso
 b and
Valentina
Balbi
a
b and
Valentina
Balbi
a
aSchool of Mathematical and Statistical Sciences, University of Galway, College Road, Galway, Ireland. E-mail: g.small1@universityofgalway.ie
bDepartment of Mathematical Sciences “G. L. Lagrange”, Politecnico di Torino, Corso Duca degli Abruzzi 24, Turin, Italy
First published on 23rd May 2025
Abstract
Brain tissue accommodates non-linear deformations and exhibits time-dependent mechanical behaviour. The latter is one of the most pronounced features of brain tissue, manifesting itself primarily through viscoelastic effects such as stress relaxation. To investigate its viscoelastic behaviour, we performed ramp-and-hold relaxation tests in torsion on freshly slaughtered cylindrical ovine brain samples (25 mm diameter and ∼10 mm height). The tests were conducted using a commercial rheometer at varying twist rates of {40, 240, 400} rad m−1 s−1, with the twist remaining fixed at ∼88 rad m−1, which generated two independent datasets for torque and normal force. The complete set of viscoelastic material parameters was estimated via a simultaneous fit to the analytical expressions for the torque and normal force predicted by the modified quasi-linear viscoelastic model. The model's predictions were further validated through finite element simulations in FEniCS. Our results show that the modified quasi-linear viscoelastic model—recently reappraised and largely unexploited—accurately fits the experimental data. Moreover, the estimated material parameters are in line with those obtained in previous studies on brain samples under torsion. These material parameters could enhance our understanding of slow-progressing pathologies such as tumour growth or neurodegeneration and inform the development of improved in silico models for brain surgery planning and training. Our novel testing protocol also offers an efficient, robust and reliable method for determining the viscoelastic properties of brain tissue under much more rapid loading conditions, which are of crucial importance for modelling traumatic brain injury.
1 Introduction
Among all the tissues in the human body, brain tissue is the softest, with a shear modulus of the order of one kilopascal.1 It is also, arguably, the most important, intricate and least understood. As is the case for most biological soft tissues, brain tissue displays highly complex mechanical behaviour: it can accommodate finite deformations and its response to applied forces is markedly non-linear;2,3 it is incompressible and biphasic, consisting of a porous solid matrix saturated with an interstitial fluid;1,4 it is structurally anisotropic1 and it exhibits isotropic, time-dependent mechanical behaviour.5–7 The latter is one of the most pronounced features of brain tissue, manifesting itself primarily through so-called viscoelastic effects. For instance, when brain tissue is deformed rapidly and then held in position, the corresponding stress decreases with time,8 known as stress relaxation. Conversely, when a load is quickly applied and then maintained, the resulting strain increases over time,9 known as creep. This behaviour is commonly observed in many biological tissues and can be attributed to either viscoelastic or plastic effects.10–12 Other time-dependent mechanical effects exhibited by brain tissue include hysteresis and softening resulting from cyclic loading and unloading.8The remarkable growth in computational power and technology since the turn of the millennium has led to increased demand from the clinical and biomedical communities for robust, accurate and efficient in silico mechanical models that can capture the behaviour of brain tissue in complex real-world scenarios, such as predicting disease progression,1 surgical planning and training13 and estimating injury risk for contact14 and equestrian sports.15 The wide range of applications above highlights one of the significant challenges facing the computational mechanics community: realistic predictions of brain tissue's mechanical response require sophisticated constitutive models that capture as much of the underlying physics as possible, yet these models must be simple and tractable enough to enable rapid and reliable estimation of their material parameters through calibration with experimental data.
Viscoelasticity is a major and active area of interest within the field of soft tissue mechanics. For a comprehensive overview of the subject and review of the classical models, the reader is directed to the detailed articles.16,17 The most straightforward constitutive theory that can be used to predict the viscoelastic behaviour of brain tissue is linear viscoelasticity, where the instantaneous stress is determined by convolving the strain history with a time-dependent function that depends on brain tissue's material properties.18,19 In reality, brain tissue's viscoelastic response is markedly non-linear and its stress relaxation curves depend on the strain level. A non-linear viscoelastic constitutive theory is, therefore, essential for accurate predictions. Although the literature is replete with non-linear models,16,17 they are generally difficult to employ in real-world biomechanical scenarios and numerically costly vis-à-vis model fitting and material parameter estimation. To this end, Fung, in his seminal work,20 proposed a compromise approach now known as quasi-linear viscoelasticity (QLV). The QLV model, which falls under the umbrella of the more general Pipkin–Rogers model,16 is the simplest extension of the linear viscoelastic theory to finite deformations. In contrast to the Pipkin–Rogers model, QLV is limited to materials whose viscous relaxation rates are independent of the instantaneous local strain21 and thereby cannot account for the non-linear phenomenon of strain-dependent relaxation commonly observed in biological soft tissues.22–25 Nevertheless, its relative simplicity compared to more general non-linear viscoelastic models has led to its widespread use. The QLV model has been employed to model a myriad of biological soft tissues including the skin,26,27 liver,28 brain,5–7,29–34 lung,35 eye,36 spinal cord,37–39 prostate gland,40 eardrum,41 oesophagal tissue,42 heart muscle tissue,43 ligaments,44–46 tendons,24,47 cartilage,48,49 arteries50 and membranes.51 As noted by De Pascalis et al.,21 QLV has been criticised for not always exhibiting “physically reasonable behaviour.” In that article, the authors thoroughly reappraised the theory and elucidated that its supposed unphysical behaviour stemmed from different interpretations of Fung's original one-dimensional relationship. The main deficiencies in these anterior studies, as summarised by De Pascalis et al.,52 were using an incorrect QLV relation (especially for incompressible materials) and employing a stress measure other than the second Piola–Kirchhoff stress, which guarantees objectivity. Using the reappraised QLV model (subsequently referred to as modified quasi-linear viscoelasticity or MQLV), De Pascalis et al. studied uniaxial tension21 and simple shear,52 while Righi and Balbi53 considered torsion. Balbi et al.54,55 extended the model to transversely isotropic materials. In contrast to Fung's QLV model, the MQLV model has yet to be validated with experimental data. To the authors' knowledge, the only relevant example is the paper by De Pascalis et al.,56 which demonstrated that the MQLV model provided a better fit to the relaxation data from inflation tests on murine bladders compared to Fung's model or linear viscoelasticity. Consequently, MQLV's potential for model fitting and material parameter estimation has yet to be fully exploited.
The development of testing protocols to characterise brain tissue's viscoelastic properties presents numerous challenges.1,23 For instance, brain tissue's fragile, brittle and tacky nature makes it susceptible to damage during sample preparation and testing.1 Furthermore, brain tissue is highly compliant and ultra-soft, which can lead to significant deformation under the action of its own weight, making it difficult to control sample geometry during extraction and testing.1 Additionally, the forces measured during testing often approach the resolution limits of commercially available testing equipment. All these factors and others—for example, age,57 species,57 anatomical region,58 post-mortem storage time59 and temperature60,61—may contribute to the variations in the mechanical properties of brain tissue reported in the literature.
Budday et al.1 and Chatelin et al.23 provide extensive reviews of the viscoelastic properties of brain tissue as measured in various studies, drawing on over 50 years of research in brain mechanics. These studies demonstrate that stress relaxation in brain tissue has been tested under various deformation modes, including uniaxial tension,5 uniaxial compression,7 simple shear6 and torsion.62 Typically, uniaxial tension and compression tests on brain tissue are performed by glueing the ends of a cylindrical sample to the platens,5,7 restricting lateral expansion or contraction at the sample's ends. This restriction leads to inhomogeneous deformations,5,63 which cannot be accurately modelled using the analytical solutions available for such tests;21 instead, the equations of motion must be solved numerically, complicating model fitting. By contrast, compression tests with lubricated platens can achieve homogeneous deformation conditions but only up to a strain of approximately 10%.2,5 Another standard testing protocol for brain tissue that can achieve a stretch of more than 60% is simple shear, which is performed by glueing the opposite faces of a cuboidal sample to the platens and recording the shear and normal forces required to move one platen parallel to the other.3 Additionally, surface tractions must be applied to the slanted faces of the deformed sample to prevent bending.64 In reality, these tractions are never applied; more practically, the effect of deviation from ideal simple shear conditions on the measured shear and normal forces is minimised by using a thin sample whose width is less than four times its height.3,6,64,65 Furthermore, accurately quantifying the normal force is currently neither feasible nor practical, as it requires recently developed, custom-designed testing equipment.64,66 Thus, in practice, simple shear generates a single dataset for the shear force, similar to uniaxial tension or compression tests that produce a single dataset for the tensile or compressive force. Alternatively, torsion is a more robust and reliable testing protocol that can be readily implemented for brain tissue using commercial devices known as rheometers. These devices measure the torque and normal force required to twist a cylindrical sample, generating two independent datasets (the appearance of a normal force as a result of twisting is an example of the so-called Poynting effect67,68). The first study to apply this protocol to brain tissue was carried out by Balbi et al.,2 who showed that the instantaneous elastic response of brain tissue in torsion is well-captured by a hyperelastic Mooney–Rivlin model and estimated the corresponding elastic material parameters (the instantaneous shear modulus and Mooney–Rivlin parameters). Although stress relaxation in torsion has been investigated in animal (porcine and bovine) and human brain tissues,1,23 anterior studies have focused on measuring only the torque, neglecting the normal force. In addition, torsion was modelled as simple shear but only locally is the torsion deformation that of simple shear.2 Consequently, the potential of torsion as a robust and reliable testing protocol for determining the viscoelastic properties of brain tissue has yet to be fully realised. We note that Narayan et al.69 devised a similar protocol for asphalt binders in torsion, measuring both torque and normal force during relaxation. However, to the best of the authors' knowledge, an analogous protocol for soft tissues has yet to be developed.
In this work, we exploit the latent potentials of the torsion protocol and the MQLV model to determine the viscoelastic properties of brain tissue. The remainder of this paper is organised as follows. In Section 2, we describe the procedure for preparing the cylindrical brain samples and testing them with the rotational rheometer, with the results of the torsion tests presented in Section 3. In Section 4, we propose a novel fitting procedure for determining brain tissue's viscoelastic material parameters based on the MQLV model. Following this, we present a finite element implementation of the MQLV model in the open-source software FEniCS, which we use to validate our estimates of the viscoelastic material parameters through numerical simulations of the experiments. We discuss the results and summarise the important features of the paper in Section 5.
2 Materials and methods
In this section, we briefly describe the procedure for preparing the cylindrical brain samples and testing them with the rotational rheometer.2.1 Tissue preparation
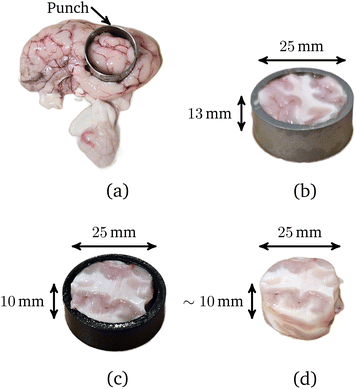
All experiments were performed using brains from 6 to 9-month-old, mixed-sex sheep obtained from a local European Union-approved slaughterhouse (Athenry Quality Meats Ltd, Galway, Ireland, Approval Number EC2875). As the animals were not sacrificed specifically for this study, ethical approval was not required from the University of Galway's Research Ethics Committee.The brains, which were received as separated cerebral hemispheres, were placed in a phosphate buffered saline (PBS) solution within 1 hour post-mortem to avoid tissue dehydration and maintained at 11–15 °C during transportation. All samples were prepared and tested at room temperature (19–23 °C). As shown in Fig. 1(a), mixed grey and white matter cylindrical samples were excised from the sagittal plane using a sharp 25 mm diameter stainless steel punch, with at most two samples extracted from each cerebral hemisphere: one from the frontal portion and the other from the parietal portion. To prepare flat cylindrical samples of radius R0 = 12.5 mm and height H0 = 10 mm for testing, each long sample was first inserted into a cutting guide of height 13 mm. The excess brain matter was then removed from the top of the sample using an 8 inch MacroKnife (CellPath, Wales, United Kingdom), as shown in Fig. 1(b). Finally, the opposite end of the sample was cut flat with the aid of a cutting guide of height 10 mm, as shown in Fig. 1(c); the exact heights of the samples were measured before testing. After this, the prepared sample and cerebral hemisphere were placed in a PBS solution. Instead of preparing all the samples at once, each sample was tested immediately after preparation, and then, if possible, another was extracted from the cerebral hemisphere.6 All samples were tested within 8 hours post-mortem.
2.2 Mechanical testing
An Anton Paar MCR 302e rotational rheometer with parallel plate geometry (Anton Paar, Graz, Austria) was used for the mechanical testing (see Fig. 2). During the tests, the bottom Peltier plate remained fixed, while the motion of the upper plate (which contains the motors and sensors that measure the torque and normal force) was controlled through the software RheoCompass (Version 1.31). A 25 mm diameter upper plate was used, matching the dimension of the samples tested. Masking tape of negligible thickness compared to the sample height was applied to both plates to prevent damage to the rheometer and enable easy removal of the tested samples.2,5,6 The sample was secured to the tape using a thin layer of cyanoacrylate (RS Radionics, Dublin, Ireland).5–7 A small pre-compression of approximately 0.03 N was applied by manually lowering the upper plate to ensure proper sample adhesion to the upper and lower plates. Ninety seconds was sufficient time for the glue to set, after which the position of the upper plate was slowly adjusted until the normal force read 0 N. | ||
| Fig. 2 (a) Anton Paar MCR 302e rotational rheometer with parallel plate geometry used to perform the torsion tests and (b) side view of a twisted sample during testing. | ||
Our torsion testing protocol is summarised in Table 1 and illustrated in Fig. 3. We performed three sets of ramp-and-hold relaxation tests in torsion on the cylindrical samples at varying twist rates of ![[small phi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a3.gif) 0 ∈ {40, 240, 400} rad m−1 s−1 (angular velocity of the upper plate per unit deformed height), while keeping the twist fixed at ϕ0 = 88 rad m−1 (angle of rotation per unit deformed height). Each torsion test consisted of two phases: a ramp phase, in which the twist was increased linearly to ϕ0 = 88 rad m−1 over a time
0 ∈ {40, 240, 400} rad m−1 s−1 (angular velocity of the upper plate per unit deformed height), while keeping the twist fixed at ϕ0 = 88 rad m−1 (angle of rotation per unit deformed height). Each torsion test consisted of two phases: a ramp phase, in which the twist was increased linearly to ϕ0 = 88 rad m−1 over a time  , followed by a hold phase lasting 200 s, during which the final value of the twist reached at the end of the ramp phase was maintained. Both the torque τ and normal force Nz required to twist the sample during the ramp phase and maintain the sample in its deformed state during the hold phase were recorded versus time t. No pre-conditioning was performed on the samples, and each was tested only once before being discarded. A total of 30 samples were tested over several campaigns: 10 at 40 rad m−1 s−1 (samples S1 to S10); 10 at 240 rad m−1 s−1 (samples S11 to S20) and 10 at 400 rad m−1 s−1 (samples S21 to S30).
, followed by a hold phase lasting 200 s, during which the final value of the twist reached at the end of the ramp phase was maintained. Both the torque τ and normal force Nz required to twist the sample during the ramp phase and maintain the sample in its deformed state during the hold phase were recorded versus time t. No pre-conditioning was performed on the samples, and each was tested only once before being discarded. A total of 30 samples were tested over several campaigns: 10 at 40 rad m−1 s−1 (samples S1 to S10); 10 at 240 rad m−1 s−1 (samples S11 to S20) and 10 at 400 rad m−1 s−1 (samples S21 to S30).
3 Experimental results
In this section, we present representative torque and normal force data from the rheometer for each of the twist rates![[small phi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a3.gif) 0 ∈ {40, 240, 400} rad m−1 s−1 and describe the filtering procedure applied to the data to prepare it for model fitting and material parameter estimation.
0 ∈ {40, 240, 400} rad m−1 s−1 and describe the filtering procedure applied to the data to prepare it for model fitting and material parameter estimation.
As an example, the output data for sample S16, recorded during a torsion test performed at a twist rate of ![[small phi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a3.gif) 0 = 240 rad m−1 s−1, are presented in Fig. 4. Fig. 4(a) and (b) show the twist ϕ and twist rate
0 = 240 rad m−1 s−1, are presented in Fig. 4. Fig. 4(a) and (b) show the twist ϕ and twist rate ![[small phi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a3.gif) profiles for the test, while Fig. 4(c) and (d) display the measured torque τ and Fig. 4(e) and (f) the measured normal force Nz. Since the rheometer outputs the normal force exerted by the sample on the upper plate, we changed the sign of the data so that it represents the normal force that must be applied to the sample to maintain the deformation, consistent with the modelling conventions adopted in Section 4 and anterior studies.2,53
profiles for the test, while Fig. 4(c) and (d) display the measured torque τ and Fig. 4(e) and (f) the measured normal force Nz. Since the rheometer outputs the normal force exerted by the sample on the upper plate, we changed the sign of the data so that it represents the normal force that must be applied to the sample to maintain the deformation, consistent with the modelling conventions adopted in Section 4 and anterior studies.2,53
From the data presented in Fig. 4(a) and (b), we can identify four regions: (i) a region (black data) at the start of the ramp phase, where the upper plate accelerates from rest to the target twist rate of ![[small phi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a3.gif) 0 = 240 rad m−1 s−1; (ii) a region (purple data), where this twist rate is maintained until the twist reaches ϕ0 = 85 rad m−1 at the end of the ramp phase at time
0 = 240 rad m−1 s−1; (ii) a region (purple data), where this twist rate is maintained until the twist reaches ϕ0 = 85 rad m−1 at the end of the ramp phase at time 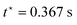 (indicated by a dashed line); (iii) a region (red data) at the start of the hold phase, where the upper plate decelerates to rest and (iv) the remainder (orange data) of the hold phase, where the final value of the twist reached at the end of the ramp phase is maintained. We also note experimental artefacts in the raw torque data in Fig. 4(c) in regions where there is a rapid change in the twist rate—notably at the start of the ramp phase when the upper plate is accelerating (black data) and the start of the hold phase when it is decelerating (red data)—confirmed by conducting control tests without any samples between the plates (see the ESI†). Accordingly, these artefacts—potentially due to the inertia of the motors in the upper plate69—were excluded from the torque data in Fig. 4(d). Following the protocol of Balbi et al.,2 we also excluded the raw normal force data at the start of the ramp phase from the normal force data in Fig. 4(f). However, unlike the torque, the raw normal force data generated at the start of the hold phase does not appear to be adversely affected by the rapid change in twist rate and was therefore included in the normal force data.
(indicated by a dashed line); (iii) a region (red data) at the start of the hold phase, where the upper plate decelerates to rest and (iv) the remainder (orange data) of the hold phase, where the final value of the twist reached at the end of the ramp phase is maintained. We also note experimental artefacts in the raw torque data in Fig. 4(c) in regions where there is a rapid change in the twist rate—notably at the start of the ramp phase when the upper plate is accelerating (black data) and the start of the hold phase when it is decelerating (red data)—confirmed by conducting control tests without any samples between the plates (see the ESI†). Accordingly, these artefacts—potentially due to the inertia of the motors in the upper plate69—were excluded from the torque data in Fig. 4(d). Following the protocol of Balbi et al.,2 we also excluded the raw normal force data at the start of the ramp phase from the normal force data in Fig. 4(f). However, unlike the torque, the raw normal force data generated at the start of the hold phase does not appear to be adversely affected by the rapid change in twist rate and was therefore included in the normal force data.
During the gamut of tests, the achieved twist rates ![[small phi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a3.gif) 0 were measured as 40.26 ± 0.42, 239.95 ± 0.25 and 400.06 ± 0.27 rad m−1 s−1 (mean ± SD). The corresponding ramp times
0 were measured as 40.26 ± 0.42, 239.95 ± 0.25 and 400.06 ± 0.27 rad m−1 s−1 (mean ± SD). The corresponding ramp times  were set to 2.2, 0.367 and 0.22 s to achieve the target twist of ϕ0 = 88 rad m−1 at the end of the ramp phase. However, in practice, the actual twist values reached were slightly lower and decreased with increasing twist rate: 87.48 ± 0.51, 85.25 ± 0.1 and 83.23 ± 0.1 rad m−1. This discrepancy was due to the inertia of the upper plate, which caused the twist to continue increasing slightly at the start of the hold phase while the upper plate decelerated to rest (see Fig. 4(a)). As a result, the target twist was reached during the hold phase rather than at the end of the ramp phase. This deviation between the target and actual twist values at the end of the ramp phase is a practical limitation of our protocol.
were set to 2.2, 0.367 and 0.22 s to achieve the target twist of ϕ0 = 88 rad m−1 at the end of the ramp phase. However, in practice, the actual twist values reached were slightly lower and decreased with increasing twist rate: 87.48 ± 0.51, 85.25 ± 0.1 and 83.23 ± 0.1 rad m−1. This discrepancy was due to the inertia of the upper plate, which caused the twist to continue increasing slightly at the start of the hold phase while the upper plate decelerated to rest (see Fig. 4(a)). As a result, the target twist was reached during the hold phase rather than at the end of the ramp phase. This deviation between the target and actual twist values at the end of the ramp phase is a practical limitation of our protocol.
Following the protocol of Narayan et al.,69 we estimated the rheometer's torque and normal force resolutions to be approximately 0.15 mN m and 0.03 N by performing torsion tests at each of the twist rates {40, 240, 400} rad m−1 s−1 without any samples between the plates. Another source of noise in the experiments was the attached compressor, which was required for the proper operation of the rheometer. During each test, the compressor would activate to supply fresh compressed air to the air bearings of the rheometer's motors, generating vibrations that increased the noise in the torque and normal force measurements (see Fig. 4(d) and (f) at t ≈ 50 s). In preparation for model fitting, we smoothed the data by applying a Savitzky–Golay filter using the MATLAB (Version 23.2.0.2485118 (R2023b)) function sgolayfilt.70 For the 40 rad m−1 s−1 data, we used a polynomial order of 5 and a window length of 61, whereas for the 240 and 400 rad m−1 s−1 data, we used a polynomial order of 5 and a window length of 31 (see the ESI†). Fig. 5 shows representative torque, normal force and filtered data for samples S2, S16 and S24 at each twist rate.
4 Modelling
In this section, we use the MQLV theory to derive analytical expressions for the torque and normal force for a ramp-and-hold test. We then propose a fitting procedure for determining brain tissue's viscoelastic material parameters and apply it to the experimental data. Finally, to validate our fitting results, we perform numerical simulations of the experiments in FEniCS.4.1 Theory
Here, we calculate the torque and normal force required to maintain an isotropic, incompressible, viscoelastic cylinder in a state of torsion, according to the MQLV theory. Although brain tissue is neither strictly isotropic nor incompressible, experiments indicate these are reasonable assumptions.1We consider a cylinder of radius R0 and height H0 subjected to a torsional deformation that takes the point with cylindrical polar coordinates (R,Θ,Z) in the undeformed configuration (at time t = 0) to the point with cylindrical polar coordinates (r,θ,z) in the deformed configuration (at time t > 0), both relative to a fixed origin O. Since the rheometer's normal force sensor has a resolution of approximately 0.03 N, the device cannot detect variations of the normal force within this range. We, therefore, expect the samples to undergo a slight axial contraction before being twisted, even though the upper plate is adjusted until the normal force reads 0 N before each test.2 This combined contraction–torsion can be modelled by the following deformation:2,71
 | (1) |
 | (2) |
 | ||
| Fig. 6 (a) Undeformed and (b) deformed cylinder. Torque and normal force must be applied at the end of the cylinder to maintain the torsion deformation. | ||
Various tensors can be computed from the deformation gradient, such as the left Cauchy–Green deformation tensor B = FFT and right Cauchy–Green deformation tensor C = FTF.
In their experimental study, Balbi et al.2 showed that the instantaneous elastic response of brain tissue in torsion is well-captured by a Mooney–Rivlin strain energy function:21,72,73
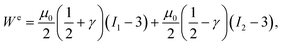 | (3) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) B and I2 = tr
B and I2 = tr![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) B−1. For this model, the Mooney–Rivlin parameters c1 and c2 are connected to μ0 and γ through μ0 = 2(c1 + c2) and γ = 1/2 − 2c2/μ0. The same Mooney–Rivlin behaviour was observed in simple shear3 and at dynamic strain rates in simple shear,6 uniaxial tension5 and uniaxial compression.7 Under our assumptions, the elastic Cauchy stress corresponding to (3) reads:74,75
B−1. For this model, the Mooney–Rivlin parameters c1 and c2 are connected to μ0 and γ through μ0 = 2(c1 + c2) and γ = 1/2 − 2c2/μ0. The same Mooney–Rivlin behaviour was observed in simple shear3 and at dynamic strain rates in simple shear,6 uniaxial tension5 and uniaxial compression.7 Under our assumptions, the elastic Cauchy stress corresponding to (3) reads:74,75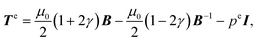 | (4) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) F = 1) and I is the second-order identity tensor.
F = 1) and I is the second-order identity tensor.
According to the MQLV theory, the viscoelastic Cauchy stress can be expressed as follows:21,53,56
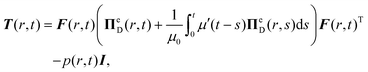 | (5) |
 | (6) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Te/3)I, while the time-dependent behaviour is associated with the scalar relaxation function μ(t), taken to be an n-term Prony series of the form:6,53,76–78
Te/3)I, while the time-dependent behaviour is associated with the scalar relaxation function μ(t), taken to be an n-term Prony series of the form:6,53,76–78 | (7) |
In this work, we assume that the deformation is slow enough that inertial effects can be ignored, although this assumption is not strictly valid during the ramp phase.55,79 In addition, we neglect external body forces. The motion of the cylinder is therefore governed by the momentum balance equation div![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) T = 0, where div is the divergence operator in the deformed configuration.74,75 Upon inspection of the components of the equation of motion, and assuming that the lateral surface of the cylinder is traction-free, we arrive at the following equilibrium problem:53
T = 0, where div is the divergence operator in the deformed configuration.74,75 Upon inspection of the components of the equation of motion, and assuming that the lateral surface of the cylinder is traction-free, we arrive at the following equilibrium problem:53
 | (8) |
Given the expressions for the stress components Tθz and Tzz in the ESI,† the torque  and normal force
and normal force  required to maintain the deformation (1) can be determined by direct integration, with explicit expressions shown in the ESI.† Specialising these equations to a ramp-and-hold test, which corresponds to a twist history of the form (see Fig. 3(a)):
required to maintain the deformation (1) can be determined by direct integration, with explicit expressions shown in the ESI.† Specialising these equations to a ramp-and-hold test, which corresponds to a twist history of the form (see Fig. 3(a)):
 | (9) |
 read respectively:
read respectively: | (10) |
 | (11) |
 are shown in the ESI.† The results of Righi and Balbi53 are recovered by setting λ = 1.
are shown in the ESI.† The results of Righi and Balbi53 are recovered by setting λ = 1.
4.2 Material parameter estimation
Righi and Balbi53 proposed a fitting procedure for estimating brain tissue's viscoelastic properties in torsion based on the MQLV model for the case when there is no pre-stretch (λ = 1). In their method, the material parameters μ∞ and c2 are determined from the long-time (asymptotic) values of the torque and normal force, while μi and τi are obtained by fitting the measured torque for the hold phase to the MQLV analytical prediction. Since this procedure does not incorporate a pre-stretch, an alternative fitting procedure that accounts for the effect of pre-stretch on the torque and normal force is required to fit the experimental data accurately.To this end, we estimated the complete set of viscoelastic material parameters by simultaneously fitting the torque and normal force datasets for each of the twist rates ![[small phi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a3.gif) 0 ∈ {40, 240, 400} rad m−1 s−1 to the MQLV analytical predictions (10) and (11). This was done using the MATLAB function fmincon,80 which implements an algorithm based on the interior-point method for solving constrained non-linear optimisation problems. Due to the increased noise during the ramp phase, we confined the fitting to the final ramp phase point and the entire hold phase, i.e.
0 ∈ {40, 240, 400} rad m−1 s−1 to the MQLV analytical predictions (10) and (11). This was done using the MATLAB function fmincon,80 which implements an algorithm based on the interior-point method for solving constrained non-linear optimisation problems. Due to the increased noise during the ramp phase, we confined the fitting to the final ramp phase point and the entire hold phase, i.e.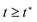 . For the twists ϕ0, we used the measured values at the end of the ramp phase rather than the target value. We minimised the following objective function:
. For the twists ϕ0, we used the measured values at the end of the ramp phase rather than the target value. We minimised the following objective function:
 | (12) |
From each fit, we obtain 10 independent parameters: μ∞, μi, τi and γ. We then calculate a posteriori the instantaneous shear modulus using  and the two Mooney–Rivlin parameters using c2 = μ0(1/2 − γ)/2 and c1 = μ0/2 − c2. The fitting results for each of the twist rates are shown in Tables 2–4, with the a posteriori calculated parameters highlighted in bold. For each sample, we found that c2 ≫ c1, implying that μ0 ≈ 2c2 and consequently γ ≈ −0.5. Therefore, for brevity, the γ values were omitted from the tables. For the parameters μ0, μ∞, μi and c2, we report the mean and standard deviation. For the remaining parameters τi and c1, which have a non-symmetric distribution due to potential outliers, we report the median and interquartile range (IQR). The goodness of fit was assessed based on the relative errors (%) in the torque and normal force, defined by errτ = |(τMQLV − τExp)/τExp| × 100 and errNz = |(NMQLVz − NExpz)/NExpz| × 100. The MQLV model provides good fits to both the torque and normal force datasets simultaneously, exhibiting small to moderate maximal relative errors over the fitting range for all samples, with the exception of S24 (see Tables 2–4). We note that the relative errors observed here for the MQLV model are similar to those reported by Anssari-Benam et al.,81 who simultaneously fit uniaxial tension/compression and simple shear datasets for brain tissue to different hyperelastic models.
and the two Mooney–Rivlin parameters using c2 = μ0(1/2 − γ)/2 and c1 = μ0/2 − c2. The fitting results for each of the twist rates are shown in Tables 2–4, with the a posteriori calculated parameters highlighted in bold. For each sample, we found that c2 ≫ c1, implying that μ0 ≈ 2c2 and consequently γ ≈ −0.5. Therefore, for brevity, the γ values were omitted from the tables. For the parameters μ0, μ∞, μi and c2, we report the mean and standard deviation. For the remaining parameters τi and c1, which have a non-symmetric distribution due to potential outliers, we report the median and interquartile range (IQR). The goodness of fit was assessed based on the relative errors (%) in the torque and normal force, defined by errτ = |(τMQLV − τExp)/τExp| × 100 and errNz = |(NMQLVz − NExpz)/NExpz| × 100. The MQLV model provides good fits to both the torque and normal force datasets simultaneously, exhibiting small to moderate maximal relative errors over the fitting range for all samples, with the exception of S24 (see Tables 2–4). We note that the relative errors observed here for the MQLV model are similar to those reported by Anssari-Benam et al.,81 who simultaneously fit uniaxial tension/compression and simple shear datasets for brain tissue to different hyperelastic models.
| Sample | H 0 [mm] | λ | μ 0 [Pa] | μ ∞ [Pa] | μ 1 [Pa] | μ 2 [Pa] | μ 3 [Pa] | μ 4 [Pa] | τ 1 [s] | τ 2 [s] | τ 3 [s] | τ 4 [s] | c 1 [μPa] | c 2 [Pa] | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| S1 | 9.4065 | 0.99 | 651.16 | 105.67 | 213.34 | 192.34 | 85.831 | 53.892 | 0.8397 | 0.244 | 6.4136 | 55.312 | 0.10225 | 325.58 | 11.609 | 16.054 |
| S2 | 8.8319 | 0.99 | 917.69 | 125.55 | 606.76 | 111.28 | 73.07 | 1.0213 | 0.6811 | 9.5764 | 82.406 | 48.45 | 2.0793 | 458.84 | 13.725 | 18.992 |
| S3 | 8.7603 | 0.99 | 973.9 | 128.37 | 583.34 | 95.025 | 91.207 | 75.954 | 0.443 | 9.4962 | 2.3379 | 75.888 | 0.4711 | 486.95 | 13.415 | 18.628 |
| S4 | 9.2659 | 0.99 | 1048 | 142.97 | 628.57 | 110.42 | 91.321 | 74.705 | 0.4005 | 2.398 | 10.442 | 72.484 | 0.13183 | 523.99 | 14.281 | 19.4 |
| S5 | 8.9006 | 0.99 | 1308.8 | 161.91 | 455.32 | 455.31 | 137.22 | 99.052 | 0.6455 | 0.1715 | 5.9739 | 58.745 | 0.021216 | 654.41 | 18.485 | 25.642 |
| S6 | 9.3734 | 0.99 | 581.02 | 64.313 | 368.49 | 66.885 | 44.183 | 37.148 | 0.3159 | 1.782 | 8.4904 | 65.141 | 1.5548 | 290.51 | 10.915 | 17.506 |
| S7 | 8.3203 | 0.99 | 1195.4 | 116.2 | 816.85 | 137.58 | 70.991 | 53.785 | 0.3639 | 2.5286 | 10.9 | 63.17 | 0.028749 | 597.7 | 14.239 | 19.997 |
| S8 | 8.4103 | 0.99 | 739.23 | 107.05 | 258.68 | 242.45 | 76.34 | 54.709 | 0.194 | 0.7838 | 6.3087 | 43.982 | 0.003838 | 369.61 | 15.575 | 28.523 |
| S9 | 7.9813 | 0.99 | 1216 | 149.53 | 704.25 | 187.15 | 103.02 | 72.031 | 0.3057 | 1.9388 | 10.93 | 78.995 | 0.0094199 | 607.99 | 15.803 | 21.589 |
| S10 | 8.3523 | 0.99 | 754.36 | 71.934 | 437.68 | 151.71 | 55.116 | 37.911 | 0.2027 | 1.1376 | 8.1273 | 58.425 | 4.2268 | 377.18 | 12.582 | 21.687 |
| Mean ± SD/Median (IQR) | — | — | 943 ± 258 | 117 ± 32 | 496 ± 177 | 188 ± 114 | 85 ± 26 | 57 ± 27 | 0.36(0.25–0.59) | 1.52(0.87–2.28) | 8.15(6.33–9.95) | 58.59(55.42–70.65) | 0.3(0.041–1.36) | 471 ± 129 | 14.06 ± 2.2 | 20.8 ± 3.78 |
| Sample | H 0 [mm] | λ | μ 0 [Pa] | μ ∞ [Pa] | μ 1 [Pa] | μ 2 [Pa] | μ 3 [Pa] | μ 4 [Pa] | τ 1 [s] | τ 2 [s] | τ 3 [s] | τ 4 [s] | c 1 [μPa] | c 2 [Pa] | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| S11 | 8.1853 | 0.99 | 1020 | 88.511 | 359.74 | 359.41 | 132.2 | 80.179 | 0.1117 | 0.0941 | 1.2096 | 20.497 | 91.948 | 510.02 | 19.497 | 18.886 |
| S12 | 8.7724 | 0.99 | 861.35 | 105.47 | 334.31 | 315.94 | 61.799 | 43.828 | 0.12 | 0.5626 | 17.937 | 19.834 | 1.39 | 430.68 | 30.806 | 31.609 |
| S13 | 8.8588 | 0.99 | 1253.8 | 177.06 | 740.79 | 194.66 | 141.29 | 3.9931 × 10−4 | 0.209 | 2.9542 | 38.93 | 18.451 | 10.197 | 626.9 | 18.992 | 22.226 |
| S14 | 9.9285 | 0.99 | 714.17 | 107.18 | 181.16 | 154.9 | 153.56 | 117.37 | 0.4112 | 0.4929 | 0.259 | 15.306 | 28.933 | 357.08 | 35.938 | 31.804 |
| S15 | 9.7461 | 0.99 | 809.24 | 110.98 | 267.8 | 240.32 | 108.64 | 81.494 | 0.2705 | 0.1037 | 2.187 | 28.974 | 6.2476 | 335.51 | 23.35 | 30.089 |
| S16 | 9.4673 | 0.99 | 1264.4 | 148.86 | 431.27 | 399.57 | 170.89 | 113.81 | 0.1179 | 0.2148 | 1.7763 | 25.905 | 11.289 | 632.2 | 22.962 | 26.81 |
| S17 | 9.4488 | 0.99 | 941.46 | 142.06 | 605.37 | 130.48 | 63.541 | 0.0062 | 0.2915 | 7.3912 | 89.376 | 105.57 | 1.3055 | 470.73 | 28.384 | 34.375 |
| S18 | 11.341 | 0.99 | 1159.5 | 134.3 | 384.24 | 381.77 | 161.17 | 197.97 | 0.1539 | 0.1917 | 2.0081 | 33.052 | 8.7216 | 579.73 | 25.468 | 31.333 |
| S19 | 8.1197 | 0.99 | 1216 | 149.53 | 704.25 | 187.15 | 103.02 | 72.031 | 0.3057 | 1.9388 | 10.93 | 78.995 | 0.0094199 | 607.99 | 22.622 | 26.891 |
| S20 | 9.0278 | 0.99 | 1238.3 | 168.98 | 389.22 | 377.06 | 171.6 | 131.48 | 0.3024 | 0.1172 | 2.806 | 36.611 | 2.1066 | 619.17 | 21.601 | 25.781 |
| Mean ± SD/Median (IQR) | — | — | 1041 ± 201 | 130 ± 29 | 447 ± 198 | 270 ± 108 | 126 ± 41 | 77 ± 66 | 0.19(0.13–0.27) | 0.35(0.14–1.9) | 2.5(1.83–29.9) | 25.98(20–32.03) | 9.45(3.14–11.02) | 513 ± 111 | 24.96 ± 5.33 | 27.98 ± 4.8 |
| Sample | H 0 [mm] | λ | μ 0 [Pa] | μ ∞ [Pa] | μ 1 [Pa] | μ 2 [Pa] | μ 3 [Pa] | μ 4 [Pa] | τ 1 [s] | τ 2 [s] | τ 3 [s] | τ 4 [s] | c 1 [μPa] | c 2 [Pa] | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| S21 | 11.402 | 0.99 | 989.56 | 116.08 | 359.18 | 344.12 | 170.18 | 2.3359 × 10−4 | 0.114 | 0.2938 | 13.187 | 12.323 | 10.829 | 494.78 | 29.252 | 29.349 |
| S22 | 11.931 | 0.99 | 774.72 | 89.185 | 497.42 | 113.66 | 74.464 | 2.1 × 10−4 | 0.185 | 2.7482 | 33.279 | 8.6742 | 0.92322 | 387.36 | 31.812 | 40.139 |
| S23 | 8.5067 | 0.99 | 388.24 | 58.62 | 133.86 | 123.86 | 71.964 | 4.4007 × 10−5 | 0.6331 | 6.4661 | 40.349 | 60.757 | 0.0059017 | 223.98 | 27.018 | 34.238 |
| S24 | 10.213 | 0.99 | 920.46 | 62.668 | 535.86 | 244.75 | 77.299 | 0.0013 | 0.2815 | 0.0011 | 12.829 | 0.9428 | 42.44 | 460.23 | 69.909 | 32.426 |
| S25 | 10.58 | 0.99 | 1379.5 | 127.36 | 370.45 | 352.02 | 351.55 | 178.14 | 0.0674 | 0.3406 | 0.0671 | 12.155 | 0.10553 | 689.77 | 30.786 | 36.412 |
| S26 | 11.244 | 0.99 | 497.15 | 65.435 | 114.21 | 114.15 | 112.31 | 91.044 | 0.1048 | 0.4212 | 0.397 | 11.621 | 4.0076 | 248.57 | 34.013 | 37.783 |
| S27 | 8.1004 | 0.99 | 1005.8 | 83.491 | 264.95 | 260.9 | 256.02 | 140.45 | 0.1004 | 0.0621 | 0.317 | 11.814 | 6.3762 | 502.91 | 35.692 | 44.153 |
| S28 | 8.6911 | 0.99 | 1178.7 | 157.1 | 304.35 | 274.33 | 267.27 | 175.67 | 0.4461 | 0.0826 | 0.0828 | 14.472 | 9.6969 | 589.36 | 28.884 | 30.932 |
| S29 | 8.8104 | 0.99 | 1495.9 | 137.88 | 512.7 | 507.84 | 216.32 | 121.2 | 0.0826 | 0.1105 | 1.2196 | 24.011 | 3.8003 | 747.97 | 19.828 | 19.538 |
| S30 | 8.8442 | 0.99 | 1161.9 | 125 | 375.42 | 374.91 | 170.68 | 115.85 | 0.114 | 0.1037 | 0.9253 | 19.031 | 7.6129 | 580.93 | 30.257 | 37.282 |
| Mean ± SD/Median (IQR) | — | — | 979 ± 354 | 102 ± 35 | 347 ± 147 | 271 ± 129 | 177 ± 96 | 82 ± 75 | 0.11(0.1–0.26) | 0.2(0.088–0.4) | 1.07(0.34–13.1) | 12.24(11.67–17.89) | 5.19(1.64–9.18) | 493 ± 172 | 33.75 ± 13.41 | 34.23 ± 6.78 |
As an example, Fig. 7 shows the MQLV analytical predictions for the torque and normal force for samples S2, S16 and S24, while Fig. 8 displays the corresponding relative errors. As the insets in Fig. 8 indicate, the relative errors in the torque are initially moderate to large but rapidly decrease towards the end of the ramp phase. By contrast, the relative errors in the force during the ramp phase are small to moderate. Over the fitting range, comprised of the final ramp phase point and the entire hold phase, the relative errors in both the torque and normal force are similarly small to moderate. The exception is sample S24, where the relative error in the torque at the start of the hold phase increases sharply before decreasing at a similar rate. This is likely due to the high twist rate of 400 rad m−1 s−1 and deviations from the ideal cylindrical geometry assumed by the rheometer and MQLV model. Nevertheless, the relative errors for the remainder of the hold phase are in line with those of samples S2 and S16.
4.3 Computational validation
To validate the fitting results from Section 4.2, we conducted brain torsion simulations using the open-source software FEniCS.83,84 FEniCS provides a high-level Python and C++ interface for solving partial differential equations via the finite element method. For the numerical implementation of the problem, the governing equations for the torsion of a solid cylinder were expressed in Cartesian coordinates and formulated using a Lagrangian description of motion, where all quantities of interest are represented in material coordinates.In this framework, the governing equations are written as Div![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P = 0 on the undeformed cylinder, where Div represents the divergence operator with respect to the undeformed configuration and P = JTF−T denotes the first Piola–Kirchhoff stress tensor.74,75 To enforce incompressibility, we included the constraint J = 1 in the model. Before applying torsion, an initial step was introduced to simulate pre-compression, involving an axial pre-stretch of λ = 0.99. For the torsion simulation, a reference point at the centre of the cylinder's top surface was defined and coupled to all other points on the top surface to ensure uniform rotational displacement about the longitudinal axis. Appropriate boundary conditions were applied as follows: the bottom surface of the cylinder was fixed to prevent displacement, while the lateral surface remained traction-free throughout the simulation.
P = 0 on the undeformed cylinder, where Div represents the divergence operator with respect to the undeformed configuration and P = JTF−T denotes the first Piola–Kirchhoff stress tensor.74,75 To enforce incompressibility, we included the constraint J = 1 in the model. Before applying torsion, an initial step was introduced to simulate pre-compression, involving an axial pre-stretch of λ = 0.99. For the torsion simulation, a reference point at the centre of the cylinder's top surface was defined and coupled to all other points on the top surface to ensure uniform rotational displacement about the longitudinal axis. Appropriate boundary conditions were applied as follows: the bottom surface of the cylinder was fixed to prevent displacement, while the lateral surface remained traction-free throughout the simulation.
Numerical simulations were performed for samples S2, S16 and S24 at twist rates of {40, 240, 400} rad m−1 s−1. The twist was ramped linearly to match experimental values at the end of the ramp phase over time periods of {2.2, 0.367, 0.22} s, after which it was held constant (see Fig. 3). The initial cylindrical geometry for each sample was defined with a radius of R0 = 12.5 mm, while the heights H0 were specified in Tables 2–4. Computational meshes were generated in FEniCS, consisting of 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 809, 17
809, 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 391 and 12
391 and 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 547 tetrahedral elements for the respective samples. Although the same mesh density was prescribed for the first two models, the total number of elements differed due to variations in sample height. For the third sample, the mesh density was slightly reduced to manage the increased computational cost caused by a higher twist rate. To enable a solution via the finite element method, the weak formulation of the Lagrangian model was derived and a spatial discretisation of the continuous variational problem was introduced. Specifically, quadratic tetrahedral elements
547 tetrahedral elements for the respective samples. Although the same mesh density was prescribed for the first two models, the total number of elements differed due to variations in sample height. For the third sample, the mesh density was slightly reduced to manage the increased computational cost caused by a higher twist rate. To enable a solution via the finite element method, the weak formulation of the Lagrangian model was derived and a spatial discretisation of the continuous variational problem was introduced. Specifically, quadratic tetrahedral elements ![[Doublestruck P]](https://www.rsc.org/images/entities/char_e173.gif) 2 were employed for the displacement field, while linear tetrahedral elements
2 were employed for the displacement field, while linear tetrahedral elements ![[Doublestruck P]](https://www.rsc.org/images/entities/char_e173.gif) 1 were used for the pressure field. This combination is commonly referred to as Taylor–Hood elements, selected to prevent the locking phenomenon and ensure stability in simulations involving incompressible materials. This strategy was adopted to avoid the use of hexahedral elements, which, although recognised as an effective method for mitigating volumetric locking, require significantly more complex generation procedures, typically involving external meshing tools and manual intervention, and could not be directly implemented within FEniCS. The time step was initially set to a small value (Δt ∈ (0.001, 0.01) s) during the early simulation phases to accurately capture large deformations. As deformation rates decreased, the time step was progressively increased to enhance computational efficiency. The estimated material parameters, determined via the MQLV theory, were assigned as specified in Tables 2–4. The torque and normal force were then computed with ParaView,85 an open-source application for interactive scientific visualisation.
1 were used for the pressure field. This combination is commonly referred to as Taylor–Hood elements, selected to prevent the locking phenomenon and ensure stability in simulations involving incompressible materials. This strategy was adopted to avoid the use of hexahedral elements, which, although recognised as an effective method for mitigating volumetric locking, require significantly more complex generation procedures, typically involving external meshing tools and manual intervention, and could not be directly implemented within FEniCS. The time step was initially set to a small value (Δt ∈ (0.001, 0.01) s) during the early simulation phases to accurately capture large deformations. As deformation rates decreased, the time step was progressively increased to enhance computational efficiency. The estimated material parameters, determined via the MQLV theory, were assigned as specified in Tables 2–4. The torque and normal force were then computed with ParaView,85 an open-source application for interactive scientific visualisation.
As illustrated in Fig. 7, the torque and normal force computed from the numerical solutions closely align with both the MQLV analytical predictions and the experimental data. However, a slight discrepancy is observed between the analytical predictions and the simulations for sample S24, likely due to the high twist rate of 400 rad m−1 s−1. In particular, achieving convergence at high twist rates requires a very small time step, which substantially increases the complexity of the simulations and poses challenges in obtaining accurate results. Finally, in Fig. 9, we present an example of the full 3D simulations, showing the magnitude of the displacement field and the components of the Cauchy stress tensor Tzz and Tθz for sample S24 at t = 5 s.
 | ||
| Fig. 9 Comparison of the displacement field magnitude ‖u‖ and the components of the Cauchy stress tensor Tzz and Tθz for sample S24 at t = 5 s. | ||
5 Discussion and conclusions
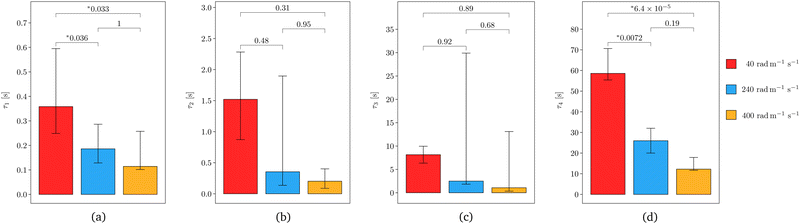
To investigate the differences between the estimated MQLV parameters at the twist rates {40, 240, 400} rad m−1 s−1, we performed Tukey multiple comparisons tests using the R (Version 4.4.2) function TukeyHSD.86 The column plots in Fig. 10 show that there are no statistically significant differences between the shear moduli and second Mooney–Rivlin parameters at the three twist rates, except for the μ3 values at 40 rad m−1 s−1 and 400 rad m−1 s−1. By contrast, there are statistically significant differences between several of the relaxation times at the three twist rates (see Fig. 11). However, the statistically significant differences for these Prony parameters may be attributed to their high variability—in particular, the large standard deviations observed for the shear moduli and the wide interquartile ranges for the relaxation times. In practice, the representation of relaxation data by a Prony series is non-unique, with the Prony parameters being highly sensitive to small changes in the data.20 The apparent strain rate-independence of the material parameters is most likely a consequence of the narrow range of twist rates considered in this study, which fall within the quasi-static to moderate regime. Indeed, the values of μ0 and c2 obtained here for ovine brain tissue using the MQLV model are in line with those obtained by Balbi et al.2 for porcine brain tissue at 300 rad m−1 s−1 using a hyperelastic model. While previous studies have reported a significant increase in brain tissue stiffness with increasing strain rate in uniaxial tension,5 uniaxial compression7 and simple shear6 indicative of a strong strain rate-dependency, the strain rates considered in those studies ({30, 60, 90, 120} s−1) were much higher than those examined here ({0.5, 3, 5} s−1). Nevertheless, the values of μ0 estimated in this study are comparable to those obtained by Rashid et al.6 for porcine brain tissue from simple shear tests conducted at a strain rate of 30 s−1—a rate conducive to conditions associated with traumatic brain injury (TBI), which typically exceed 10 s−1.6,87,88 Moreover, the strains we considered (∼105–110%) are substantially higher than the estimated axonal strain threshold for diffuse axonal injury (∼15% for a 50% risk), which is the most prevalent neurological insult associated with TBI.89 In future work, we will apply our protocol to estimate the material parameters of brain tissue in torsion under conditions more representative of TBI—namely, a minimum strain of 20% applied at a strain rate exceeding 10 s−1.87,88We note in passing that alternative fitting procedures to the one outlined in this study have been proposed in the literature. One common approach that allows for reduced inter-sample variability in the relaxation times involves fixing them a priori at logarithmically spaced intervals over the experimental time range, and then employing an optimisation algorithm to determine the remaining parameters.90,91 See also ref. 92 for a related but more refined procedure.
Our proposed testing protocol presents some challenges and limitations. Due to natural variations in brain size between sheep and brain tissue's highly compliant and ultra-soft nature, it was difficult to consistently and reliably prepare cylindrical samples of similar dimensions, as in Fig. 1. As a result, difficult-to-obtain and otherwise useful brain samples were wasted, leading to a smaller sample size. Furthermore, if the samples are not satisfactorily cylindrical (as the rotational rheometer requires), artefacts could potentially be introduced into the measured torque and normal force.
Currently, there is no consensus on the effects of temperature and post-mortem storage time on the mechanical properties of brain tissue.1 Therefore, it is important to note that the brains in this study were prepared and tested at room temperature (19–23 °C) within 8 hours post-mortem.
Given the limited availability and ethical challenges associated with obtaining fresh human brains in Ireland, ovine brains were used in this work. Despite the widespread use of porcine2,5,30,62 and bovine78,93,94 brain tissues as surrogates for characterising the mechanical properties of human brain tissue, there are relatively few studies that focus on ovine brain tissue.95,96 By contrast, due to the neuroanatomical similarities between the sheep and human brains,97 there is a growing body of literature that utilises the ovine model to investigate brain injuries, including strokes and epilepsy, among others.98 Nevertheless, further comparative research is required to determine whether ovine brain tissue—like porcine and bovine brain tissues—is a suitable mechanical surrogate for characterising human brain tissue.
Additionally, in this study, we treated brain tissue as a single homogeneous material. However, brain tissue is known to be highly heterogeneous, with grey and white matter exhibiting markedly different mechanical behaviour.1,8,9,78 More precise material characterisation could be achieved by applying our testing protocol to grey and white matter samples separately.
Despite the outlined limitations, in this paper, we devised the first experimental protocol to determine the non-linear viscoelastic properties of brain tissue in torsion. This protocol allows us to obtain two independent datasets (torque and normal force) with a single test, providing us with a much more efficient protocol compared to protocols involving multiple loading modes. The latter require a sample to be sequentially tested under different deformation modes to obtain independent datasets. Moreover, they often rely on expensive, custom-made experimental rings or multiple testing devices. Our novel protocol can be easily implemented in any commercially available rheometer and has huge potential to accurately model the non-linear viscoelastic properties of brain tissue.
Here, we applied the protocol to study the non-linear viscoelastic behaviour of the brain in torsion at varying twist rates. This protocol has huge potential not only to study the strain-dependent relaxation of the brain but also its non-linear creep behaviour. From the theoretical viewpoint, we showed that the MQLV model provides a good fit to the experimental data and allows us to estimate the time-dependent shear modulus of an incompressible, viscoelastic, soft material such as the brain. The fitting procedure that we proposed can also be applied to compressible, viscoelastic, soft materials, whose mechanical behaviour is determined by at least two material functions.
In view of the quasi-static to moderate twist rates considered in this study, the estimated viscoelastic material parameters could enhance our understanding of slow-progressing pathologies such as tumour growth or neurodegeneration and inform the development of improved in silico models for brain surgery planning and training. More broadly, our novel testing protocol provides a new experimental method that can be applied to measure the viscoelastic properties of soft tissues other than the brain.
As previously discussed, another major direction in future work will be applying our protocol to investigate the mechanical behaviour of brain tissue at conditions conducive to TBI. When coupled with bespoke finite element models such as the University College Dublin Brain Trauma Model,99 the corresponding viscoelastic material parameters could yield valuable insights into the forces and deformations involved in traumatic brain injury and contribute to the design of improved headgear for sports such as boxing and motorsports.
Author contributions
Griffen Small: investigation, formal analysis, visualization, writing – original draft, writing – reviewing and editing. Francesca Ballatore: investigation, software, visualization, writing – original draft, writing – reviewing and editing. Chiara Giverso: software, visualization, writing – original draft, writing – reviewing and editing. Valentina Balbi: conceptualization, methodology, writing – reviewing and editing.Data availability
The brain torsion data used in this article has been deposited on Mendeley Data at https://doi.org/10.17632/m2jwdfgczs.1. The FEniCS code for the finite element simulations is available on Github at https://github.com/francescaballatore/Brain_QLV_Torsion.Conflicts of interest
There are no conflicts to declare.Appendices
Appendix A
The functions A, B, C, D and E appearing in the torque (10) and normal force (11) are given by | (13) |
 | (14) |
| C(λ) = λ4 + 2λ3 + 2λ − 2, | (15) |
| D(λ) = λ4 − λ3 − λ + 1, | (16) |
| E(λ) = λ4 − λ3 + 2λ − 2. | (17) |
Acknowledgements
This publication has emanated from research jointly funded by Taighde Éireann – Research Ireland under grant number GOIPG/2024/3552 (Griffen Small), and by the College of Science and Engineering at the University of Galway under the Millennium Fund scheme for the project “Modelling Brain Mechanics” (Valentina Balbi). Francesca Ballatore acknowledges support from the PNRR M4C2 through the project “Made in Italy Circolare e Sostenibile (MICS)”, CUP: E13C22001900001. The authors are grateful to the anonymous reviewers for their constructive criticisms, helpful suggestions and insights.References
- S. Budday, T. C. Ovaert, G. A. Holzapfel, P. Steinmann and E. Kuhl, Arch. Comput. Methods Eng., 2020, 27, 1187–1230 Search PubMed.
- V. Balbi, A. Trotta, M. Destrade and A. N. Annaidh, Soft Matter, 2019, 15, 5147–5153 RSC.
- M. Destrade, M. D. Gilchrist, J. G. Murphy, B. Rashid and G. Saccomandi, Int. J. Non Linear Mech., 2015, 75, 54–58 Search PubMed.
- A. Greiner, N. Reiter, F. Paulsen, G. A. Holzapfel, P. Steinmann, E. Comellas and S. Budday, Front. Mech. Eng., 2021, 7, 708350 CrossRef.
- B. Rashid, M. Destrade and M. D. Gilchrist, J. Mech. Behav. Biomed. Mater., 2014, 33, 43–54 CrossRef.
- B. Rashid, M. Destrade and M. D. Gilchrist, J. Mech. Behav. Biomed. Mater., 2013, 28, 71–85 CrossRef PubMed.
- B. Rashid, M. Destrade and M. D. Gilchrist, Comput. Mater. Sci., 2012, 10, 23–38 Search PubMed.
- S. Budday, G. Sommer, J. Haybaeck, P. Steinmann, G. A. Holzapfel and E. Kuhl, Acta Biomater., 2017, 60, 315–329 CrossRef CAS PubMed.
- W. Kang, L. Wang and Y. Fan, J. Biomech., 2024, 162, 111888 CrossRef PubMed.
- C. Giverso and L. Preziosi, Math. Med. Biol., 2010, 29, 181–204 CrossRef.
- D. Ambrosi and L. Preziosi, Biomech. Model. Mechanobiol., 2009, 8, 397–413 CrossRef PubMed.
- C. Giverso and L. Preziosi, Int. J. Non Linear Mech., 2013, 56, 50–55 CrossRef.
- H. Delingette and N. Ayache, Handb. Numer. Anal., 2004, 12, 453–550 Search PubMed.
- S. Ji, M. Ghajari, H. Mao, R. H. Kraft, M. Hajiaghamemar, M. B. Panzer, R. Willinger, M. D. Gilchrist, S. Kleiven and J. D. Stitzel, Ann. Biomed. Eng., 2022, 50, 1389–1408 CrossRef PubMed.
- T. A. Connor, J. M. Clark, J. Jayamohan, M. Stewart, A. McGoldrick, C. Williams, B. M. Seemungal, R. Smith, R. Burek and M. D. Gilchrist, Sports Med., 2019, 5, 1–8 Search PubMed.
- A. Wineman, Math. Mech. Solids, 2009, 14, 300–366 CrossRef.
- C. S. Drapaca, S. Sivaloganathan and G. Tenti, Math. Mech. Solids, 2007, 12, 475–501 CrossRef.
- L. Anand and S. Govindjee, Continuum Mechanics of Solids, Oxford University Press, 2020 Search PubMed.
- R. M. Christensen, Theory of Viscoelasticity: An Introduction, Dover Publications, 2nd edn, 2003 Search PubMed.
- Y. C. Fung, Biomechanics: Mechanical Properties of Living Tissues, Springer Science & Business Media, 2nd edn, 1993 Search PubMed.
- R. De Pascalis, D. I. Abrahams and W. J. Parnell, Proc. R. Soc. A, 2014, 470, 20140058 CrossRef.
- T. Shearer, W. J. Parnell, B. Lynch, H. R. Screen and D. I. Abrahams, J. Biomech. Eng., 2020, 142, 071003 CrossRef PubMed.
- S. Chatelin, A. Constantinesco and R. Willinger, Biorheology, 2010, 47, 255–276 Search PubMed.
- S. E. Duenwald, R. Vanderby and R. S. Lakes, Ann. Biomed. Eng., 2009, 37, 1131–1140 CrossRef PubMed.
- S. Nasseri, L. E. Bilston and N. Phan-Thien, Rheol. Acta, 2002, 41, 180–192 CrossRef CAS.
- A. Karimi, M. Haghighatnama, A. Shojaei, M. Navidbakhsh, A. Motevalli Haghi and S. J. Adnani Sadati, Proc. Inst. Mech. Eng., Part L, 2016, 230, 418–425 Search PubMed.
- C. Flynn, A. J. Taberner, P. M. F. Nielsen and S. Fels, J. Mech. Behav. Biomed. Mater., 2013, 28, 484–494 CrossRef PubMed.
- D. B. MacManus, M. Maillet, S. O'Gorman, B. Pierrat, J. G. Murphy and M. D. Gilchrist, J. Mech. Behav. Biomed. Mater., 2019, 99, 240–246 CrossRef CAS PubMed.
- S. N. Sundaresh, J. D. Finan, B. S. Elkin, A. V. Basilio, G. M. McKhann and B. Morrison III, Ann. Biomed. Eng., 2022, 50, 1452–1460 CrossRef PubMed.
- S. N. Sundaresh, J. D. Finan, B. S. Elkin, C. Lee, J. Xiao and B. Morrison III, Brain Multiphys., 2021, 2, 100041 CrossRef.
- D. B. MacManus, A. Menichetti, B. Depreitere, N. Famaey, J. Vander Sloten and M. Gilchrist, Brain Multiphys., 2020, 1, 100018 Search PubMed.
- M. Hosseini-Farid, A. Rezaei, A. Eslaminejad, M. Ramzanpour, M. Ziejewski and G. Karami, Sci. Iran., 2019, 26, 2047–2056 Search PubMed.
- D. Sahoo, C. Deck and R. Willinger, J. Mech. Behav. Biomed. Mater., 2014, 33, 24–42 Search PubMed.
- S. Chatelin, C. Deck and R. Willinger, J. Biorheol., 2013, 27, 26–37 Search PubMed.
- N. Daphalapurkar, J. Riglin, A. Mohan, J. Harris and J. Bernardin, Int. J. Numer. Methods Biomed. Eng., 2023, 39, e3744 CrossRef.
- Z. H. Zhang, M. X. Pan, J. T. Cai, J. D. Weiland and K. Chen, J. Biomed. Mater. Res., Part A, 2018, 106, 2151–2157 CrossRef CAS.
- A. Rycman, S. McLachlin and D. S. Cronin, Front. Bioeng. Biotechnol., 2021, 9, 693120 CrossRef PubMed.
- J. Yu, N. Manouchehri, S. Yamamoto, B. K. Kwon and T. R. Oxland, J. Mech. Behav. Biomed. Mater., 2020, 112, 104044 CrossRef CAS.
- S. Jannesar, B. Nadler and C. J. Sparrey, J. Biomech. Eng., 2016, 138, 091004 Search PubMed.
- H. Helisaz, E. Belanger, P. Black, M. Bacca and M. Chiao, Acta Biomater., 2024, 173, 184–198 CrossRef PubMed.
- H. Motallebzadeh, M. Charlebois and W. R. J. Funnell, J. Acoust. Soc. Am., 2013, 134, 4427–4434 CrossRef.
- W. Yang, T. C. Fung, K. S. Chian and C. K. Chong, J. Mech. Med. Biol., 2006, 6, 261–272 Search PubMed.
- J. M. Huyghe, D. H. Van Campen, T. Arts and R. M. Heethaar, J. Biomech., 1991, 24, 841–849 CrossRef CAS PubMed.
- G. Criscenti, C. De Maria, E. Sebastiani, M. Tei, G. Placella, A. Speziali, G. Vozzi and G. Cerulli, J. Biomech., 2015, 48, 4297–4302 CrossRef CAS PubMed.
- S. D. Abramowitch and S. L. Woo, J. Biomed. Eng., 2004, 126, 92–97 Search PubMed.
- J. R. Funk, G. W. Hall, J. R. Crandall and W. D. Pilkey, J. Biomech. Eng., 2000, 122, 15–22 CrossRef CAS.
- I. Bah, N. R. J. Fernandes, R. L. Chimenti, J. Ketz, A. S. Flemister and M. R. Buckley, J. Mech. Behav. Biomed. Mater., 2020, 112, 104031 CrossRef CAS PubMed.
- R. Springhetti and N. S. Selyutina, Meccanica, 2018, 53, 519–530 Search PubMed.
- N. S. Selyutina, I. I. Argatov and G. S. Mishuris, Mech. Res. Commun., 2015, 67, 24–30 CrossRef.
- A. Giudici, K. W. F. van der Laan, M. M. van der Bruggen, S. Parikh, E. Berends, S. Foulquier, T. Delhaas, K. D. Reesink and B. Spronck, Biomech. Model. Mechanobiol., 2023, 22, 1607–1623 Search PubMed.
- F. Dadgar-Rad and N. Firouzi, Int. J. Appl. Mech., 2021, 13, 2150036 Search PubMed.
- R. De Pascalis, D. I. Abrahams and W. J. Parnell, Int. J. Eng. Sci., 2015, 88, 64–72 CrossRef.
- M. Righi and V. Balbi, Modeling Biomaterials, Springer, 2021, ch. 3, pp. 71–103 Search PubMed.
- V. Balbi, T. Shearer and W. J. Parnell, Math. Mech. Solids, 2023, 1–25 CAS.
- V. Balbi, T. Shearer and W. J. Parnell, Proc. R. Soc. A, 2018, 474, 20180231 Search PubMed.
- R. De Pascalis, W. J. Parnell, D. I. Abrahams, T. Shearer, D. M. Daly and D. Grundy, Proc. R. Soc. A, 2018, 474, 20180102 CrossRef.
- D. B. MacManus, B. Pierrat, J. G. Murphy and M. D. Gilchrist, Sci. Rep., 2017, 7, 13729 CrossRef PubMed.
- A. Menichetti, D. B. MacManus, M. D. Gilchrist, B. Depreitere, J. Vander Sloten and N. Famaey, Int. J. Eng. Sci., 2020, 155, 103355 CrossRef.
- A. Garo, M. Hrapko, J. A. W. Van Dommelen and G. W. M. Peters, Biorheology, 2007, 44, 51–58 CAS.
- B. Rashid, M. Destrade and M. D. Gilchrist, J. Mech. Behav. Biomed. Mater., 2012, 14, 113–118 CrossRef PubMed.
- B. Rashid, M. Destrade and M. D. Gilchrist, J. Biomech., 2013, 46, 1276–1281 CrossRef PubMed.
- K. B. Arbogast and S. S. Margulies, J. Biomech., 1998, 31, 801–807 Search PubMed.
- B. Rashid, M. Destrade and M. D. Gilchrist, Comput. Mater. Sci., 2012, 64, 295–300 Search PubMed.
- M. Destrade, Y. Du, J. Blackwell, N. Colgan and V. Balbi, Phys. Rev. E, 2023, 107, L053001 CrossRef CAS PubMed.
- British Standards, Physical Testing of Rubber, British Standards Institution Technical Report BS 903-0:2012, 2012.
- S. Yan, D. Jia, Y. Yu, L. Wang, Y. Qiu and Q. Wan, Eur. J. Mech. A/Solids, 2021, 86, 104154 CrossRef.
- R. S. Rivlin, Philos. Trans. R. Soc. London, Ser. A, 1949, 242, 173–195 CrossRef.
- J. H. Poynting, Proc. R. Soc. London, Ser. A, 1909, 82, 546–559 Search PubMed.
- S. P. A. Narayan, J. M. Krishnan, A. P. Deshpande and K. R. Rajagopal, Mech. Res. Commun., 2012, 43, 66–74 Search PubMed.
- The MathWorks Inc., Documentation for sgolayfilt, https://mathworks.com/help/signal/ref/sgolayfilt.html.
- P. Ciarletta and M. Destrade, IMA J. Appl. Math., 2014, 79, 804–819 CrossRef.
- M. Mooney, J. Appl. Phys., 1940, 11, 582–592 Search PubMed.
- R. S. Rivlin, Philos. Trans. R. Soc. London, Ser. A, 1948, 241, 379–397 Search PubMed.
- G. A. Holzapfel, Nonlinear Solid Mechanics: A Continuum Approach for Engineering, John Wiley & Sons Ltd., 2000 Search PubMed.
- R. W. Ogden, Non-Linear Elastic Deformations, Dover Publications, 1997 Search PubMed.
- O. Morrison, M. Destrade and B. B. Tripathi, Acta Biomater., 2023, 169, 66–87 Search PubMed.
- K. M. Labus and C. M. Puttlitz, J. Mech. Phys. Solids, 2016, 96, 591–604 CrossRef.
- S. Budday, R. Nay, R. De Rooij, P. Steinmann, T. Wyrobek, T. C. Ovaert and E. Kuhl, J. Mech. Behav. Biomed. Mater., 2015, 46, 318–330 CrossRef.
- M. D. Gilchrist, B. Rashid, J. G. Murphy and G. Saccomandi, Math. Mech. Solids, 2013, 18, 622–633 Search PubMed.
- The MathWorks Inc., Documentation for fmincon, https://mathworks.com/help/optim/ug/fmincon.html.
- A. Anssari-Benam, M. Destrade and G. Saccomandi, Philos. Trans. R. Soc., A, 2022, 380, 20210325 CrossRef.
- M. Destrade, G. Saccomandi and I. Sgura, Proc. R. Soc. A, 2017, 473, 20160811 Search PubMed.
- M. Alnæs, J. Blechta, J. Hake, A. Johansson, B. Kehlet, A. Logg, C. Richardson, J. Ring, M. E. Rognes and G. N. Wells, Arch. Numer. Software, 2015, 3, 9–23 Search PubMed.
- A. Logg, K. A. Mardal and G. Wells, Automated Solution of Differential Equations by the Finite Element Method, Springer, 2012 Search PubMed.
- U. Ayachit, The ParaView Guide: A Parallel Visualization Application, Kitware Inc., 2015 Search PubMed.
- R Core Team, Documentation for TukeyHSD, https://www.rdocumentation.org/packages/stats/versions/3.6.2/topics/TukeyHSD.
- D. B. MacManus and M. Ghajari, Brain Multiphys., 2022, 3, 100059 CrossRef.
- A. Tamura, S. Hayashi, I. Watanabe, K. Nagayama and T. Matsumoto, J. Biomech. Sci. Eng., 2007, 2, 115–126 CrossRef.
- D. Sahoo, C. Deck and R. Willinger, Accid. Anal. Prev., 2016, 92, 53–70 CrossRef PubMed.
- W. G. Knauss and J. Zhao, Mech. Time-Depend. Mater., 2007, 11, 199–216 CrossRef.
- J. N. Antonakakis, P. Bhargava, K. C. Chuang and A. T. Zehnder, J. Appl. Polym. Sci., 2006, 100, 3255–3263 Search PubMed.
- J. Ciambella, A. Paolone and S. Vidoli, Mech. Mater., 2010, 42, 932–944 Search PubMed.
- E. G. Takhounts, J. R. Crandall and K. Darvish, Stapp Car Crash J., 2003, 47, 107–134 Search PubMed.
- L. E. Bilston, Z. Liu and N. Phan-Thien, Biorheology, 2001, 38, 335–345 Search PubMed.
- R. Lilley, A. Reynaud, P. D. Docherty, N. Smith and N. Kabaliuk, IFAC-Papers Online, 2020, 53, 16275–16280 CrossRef.
- Y. Feng, R. J. Okamoto, R. Namani, G. M. Genin and P. V. Bayly, J. Mech. Behav. Biomed. Mater., 2013, 23, 117–132 Search PubMed.
- A. Banstola and J. N. J. Reynolds, Front. Vet. Sci., 2022, 9, 961413 Search PubMed.
- W. Lee, S. D. Lee, M. Y. Park, L. Foley, E. Purcell-Estabrook, H. Kim and S. S. Yoo, BMC Vet. Res., 2015, 11, 1–8 CrossRef.
- T. J. Horgan and M. D. Gilchrist, Int. J. Crashworthiness, 2003, 8, 353–366 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/D5SM00138B |
| This journal is © The Royal Society of Chemistry 2025 |