Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Flow-dependent separation selectivity for organic molecules on metal–organic frameworks containing adsorbents†
Anton
Peristyy
a,
Pavel N.
Nesterenko
a,
Anita
Das
b,
Deanna M.
D'Alessandro
b,
Emily F.
Hilder
a and
R. Dario
Arrua
*a
aAustralian Centre for Research on Separation Science, University of Tasmania, Private Bag 75, Hobart, TAS 7001, Australia. E-mail: Dario.Arrua@utas.edu.au; Dario.Arrua@unisa.edu.au
bSchool of Chemistry F11, University of Sydney, NSW 2006, Australia
First published on 18th March 2016
Abstract
A new flow-dependent separation selectivity (FDSS) effect was discovered in isocratic HPLC. Significant changes in chromatographic selectivity were achieved by simple variation of the mobile phase flow rate. The FDSS effect was observed for a core–shell stationary phase using silica particles as a core and a Zr-based metal–organic framework (UiO-66) as a shell.
High-performance liquid chromatography (HPLC) is a well established and versatile separation technique which has been developed extensively during the last several decades.1 Key research challenges for the development of HPLC include increasing the separation efficiency, shortening the separation time and, most importantly, achieving new separation selectivity. Chromatographic separation is based on the repetitive distribution of the solute between stationary and mobile phases.2 The distribution coefficient (Kd) in a chromatographic system is a thermodynamic parameter showing the ratio of solute equilibrium concentrations in the mobile and stationary phases; however, for practical purposes the use of the retention factor (k = φ·Kd, where φ is phase ratio, constant for a given column) is more accepted. As free energy is expressed as ΔG = −RT
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k, the separation selectivity (α = k1/k2) of two solutes can be considered a thermodynamic parameter. Correspondingly, new separation selectivities can only be achieved by changing either the chemistry of the stationary phase or the composition of the mobile phase. Thus, it is not possible to expect any change in α for a given column under isocratic elution with a variation of flow rate. In contrast, in such chromatographic systems, the flow rate affects the kinetics of sorption–desorption processes, and, hence, the peak broadening and column efficiency according to the van Deemter equation.2 In this work, for the first time we report a new effect in HPLC, where the separation selectivity can be varied by changing the flow rate of the mobile phase. This effect was discovered using novel UiO-66@SiO2 core–shell particles as the stationary phase.
k, the separation selectivity (α = k1/k2) of two solutes can be considered a thermodynamic parameter. Correspondingly, new separation selectivities can only be achieved by changing either the chemistry of the stationary phase or the composition of the mobile phase. Thus, it is not possible to expect any change in α for a given column under isocratic elution with a variation of flow rate. In contrast, in such chromatographic systems, the flow rate affects the kinetics of sorption–desorption processes, and, hence, the peak broadening and column efficiency according to the van Deemter equation.2 In this work, for the first time we report a new effect in HPLC, where the separation selectivity can be varied by changing the flow rate of the mobile phase. This effect was discovered using novel UiO-66@SiO2 core–shell particles as the stationary phase.
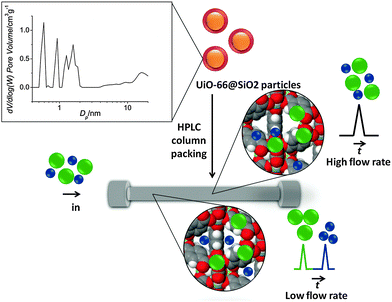
Metal–organic frameworks (MOFs) are well known for having well defined micro/mesoporous structures, very high specific surface areas as well as the possibility of chemical modification. Owing to these properties, MOFs have recently received considerable attention in the field of separation science as stationary phases for GC and HPLC.3,4 In the present work, silica microparticles coated with UiO-66 crystals were used as a packing for HPLC columns (50 × 2.1 mm ID). UiO-66 or [Zr6O4(OH)4(bdc)6] is a MOF based on Zr(IV) ions and the organic linker 1,4-benzene dicarboxylate (bdc).5 The structure of UiO-66 consists of microporous cavities (∼1.1 nm and ∼0.8 nm), which are accessible by ∼0.6 nm windows (see inset Scheme 1).
Recently, the applicability of UiO-66 as a stationary phase in liquid chromatography has been demonstrated.6–10 The first examples of UiO-66 use in HPLC involved the direct packing of solely MOFs within HPLC columns.7,8 Moreira et al. reported a reverse shape selectivity of UiO-66 for the mixture of xylenes using packed crystals, agglomerates or tablets of UiO-66 in columns.7 Meanwhile, Van der Perre et al. exploited the tetrahedral cage geometry of the UiO-66 structure for the selective HPLC separation of isomers of aromatic compounds and cis/trans isomers.8 The disadvantage of column packings composed solely of MOFs arises from the use of fine particles of irregular shapes, resulting in high backpressure and extra peak broadening.11,12
These shortcomings have been addressed in some part by Yan et al., who used a homogeneous mixture of microspherical silica particles and UiO-66 as a mixed bed column packing.9 These composite particles were applied to the separation of polyaromatic hydrocarbons, xylenes and chlorobenzene isomers. More recently, Zhang et al. reported the preparation of UiO-66@SiO2 core–shell microparticles for the separation of various aromatic compounds.10 This approach removed the abovementioned limitations by providing better quality packing with reduced backpressure. Following the rationale of this publication, core–shell microparticles UiO-66@SiO2 were prepared in the present work.
The core–shell particles were synthesized by a two-step procedure. In the first step, the silica particles (dp = 5.0 μm) were modified with glutamic acid as previously described.13 In the second step, the deposition of UiO-66 onto the COOH-modified silica particles was performed by microwave-assisted solvothermal synthesis.14 SEM images (Fig. 1S, ESI†) show the silica particles before and after the loading of UiO-66. The uniform surface coating of modified silica with a 100–300 nm layer of UiO-66 was achieved. Powder X-ray diffraction (PXRD) patterns of UiO-66 nanocrystals, glutamic acid modified silica and the resulting core–shell composite microparticles confirm the presence of UiO-66 on the surface (Fig. 2S, ESI†). As-prepared UiO-66@SiO2 composite particles were packed in a stainless steel HPLC column (50 × 2.1 mm ID) and used in normal-phase mode of HPLC with n-hexane as an eluent.
A common choice for the initial characterisation of a stationary phase is the retention of alkyl benzenes and polyaromatic hydrocarbons (PAH). In this case, the use of inert solutes lacking functional groups allows direct assessment of the retention mechanism and efficiency, as well as providing a comparison with other stationary phases. Taking into account the unique microporous structure of UiO-66, it was necessary to establish the optimum flow rate and to obtain the corresponding van Deemter plot using toluene as a solute. The minimum point of the van Deemter plot corresponds to the optimum value of the flow rate and the maximum column efficiency.2 Surprisingly, during this study some unexpected changes in k values with variation of the flow rate were observed. This precluded the use of a van Deemter plot, since a constant k value is required over the whole range of applied flow rates.15 Nevertheless, the maximum efficiency observed for the UiO-66@SiO2 column was calculated to be 58![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 plates m−1.
100 plates m−1.
To understand the observed k dependence on the flow rate, the retention of five aromatic hydrocarbons at different flow rates was analyzed. Retention factors (k) were calculated via k = (tR− t0)/t0, where tR is the time of the peak maximum for a solute, and t0 is the void time, recorded at the baseline disturbance from an injection. See ESI† for more details on recording retention and void times. The results (Fig. 1) show dramatic changes in the retention for all solutes. This contradicts the aforementioned thermodynamic theory of chromatography. The observed effect is more profound for toluene and ethyl benzene and to a lesser degree for anthracene, cumene and biphenyl. For example, the k value for toluene at 0.03 mL min−1 was 3 times higher than that obtained at 1.5 mL min−1.
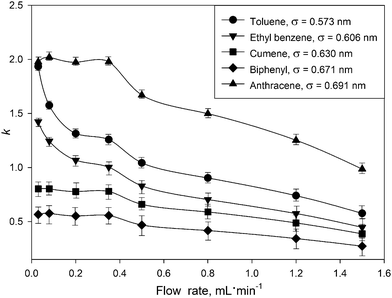 | ||
| Fig. 1 Influence of the mobile phase flow rate on the retention factors for model compounds on the UiO-66@SiO2 column. Mobile phase – n-hexane, 25 °C, sample volume 2 μL of 100 μg mL−1 solutes in n-hexane. Kinetic diameter (σ, nm) for each analyte was calculated as suggested by Jae et al.16 using critical constants from.17 | ||
A further intriguing observation was the inconsistency of the void volume (V0 = t0·F; F is the mobile phase flow rate) with the flow rate. The V0 value increased by almost 60% with the increase in flow rate from 0.03 to 1.5 mL min−1, which is an unusual phenomena in LC, where V0 is defined as the volume of mobile phase contained in the column, and should obviously be a constant quantity.18 For more discussion about the inconsistency in the void volume of the UiO-66@SiO2 column refer to the ESI.† In the situation where void volume is a variable, the comparison of k values may be misleading, and the use of the selectivity (α) should be more appropriate. For this reason, the dependence of the separation selectivity (α) on the flow rate was used for a more representative description of the FDSS phenomenon. Fig. 2 shows the corresponding selectivity plots for toluene, ethyl benzene, cumene and anthracene relative to the least retained biphenyl. It can be seen that α values for toluene and ethyl benzene are flow dependent, especially in the range of lower flow rates of 0.03–0.40 mL min−1. There are few reported flow dependent selectivity effects (FDSS) in various modes of liquid chromatography including hydrodynamic chromatography (HDC), slalom chromatography (SC) and turbulent flow chromatography (TFC). HDC is based on the difference between flow rate values of the mobile phase at the surface of stationary phase particles and in the middle of interparticle space.19 Thus, bulky molecules have a limited possibility of moving in close proximity to the surface of the adsorbent and are likely to migrate to the centres of the spaces between particles at higher flow rates. This results in earlier elution of bulky molecules.19 In contrast, in SC long molecules such as DNA are retained due to their non-linear nature and hence their longer migration pathway via interparticle spaces.20 Retardation is proportional to the length of the molecule, which results in longer elution times for solutes with higher molecular weights. The elevated flow rate results in higher retention of DNA molecules. A different principle is utilised in TFC for isolation of target compounds (drugs or metabolites) from complex samples containing large biomolecules such as proteins or DNA fragments. A size discrimination effect appears at high flow rates of the mobile phase, when the bulky biomolecules with lower diffusion coefficients do not have sufficient time to access the entire porous structure of the stationary phase. This effect is more profound when the size of the target molecule is comparable to the pore size (Dp).21 In this case, bulky molecules are excluded from the column and small molecules are retained. Overall, until now flow rate effects in TFC, HDC and SC have only been used to manipulate the retention of large biomolecules. To the best of our knowledge, no similar effects have been reported for the separation of small molecules such as alkyl benzenes and PAH.
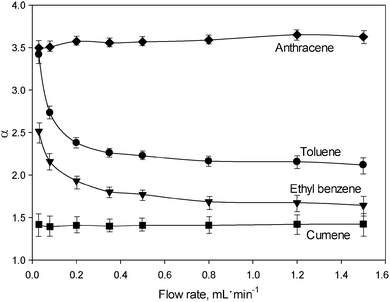 | ||
| Fig. 2 Separation selectivity plots obtained for various solutes relative to biphenyl. The chromatographic conditions are identical to those employed in Fig. 1. | ||
The FDSS effect takes place when the molecular size of the solute is comparable to Dp (0.6–1.1 nm) in UiO-66@SiO2. Presumably, the observed increase in the retention times for toluene (σ = 0.573 nm) and ethyl benzene (σ = 0.606 nm) is associated with their diffusion inside the micropores of UiO-66 through the narrow (∼0.6 nm) windows at low flow rates. Such an assumption is based upon the strong correlation which was established between k values for solutes and their kinetic diameters (σ). As shown in Table 1S and Fig. 3S (ESI†), organic molecules with σ > 0.63 nm are weakly retained, which indicates their exclusion from entry via the windows in the MOF lattice, and their lack of interactions with the internal surface of the UiO-66 framework. This effect resembles size-exclusion chromatography (SEC), where small molecules have access to a larger portion of the total pore volume of the adsorbent in the column, resulting in their stronger retention as compared to bulky molecules. However, in the case of UiO-66@SiO2, the size exclusion effect works in a very narrow mass range of the solutes and, surprisingly, is flow rate dependent.
There are two possible explanations for the extraordinary behaviour of the solutes on UiO-66@SiO2. The first hypothesis is related to the lack of time required for the solute to reach adsorption equilibrium at high flow rates. The equilibrium limiting factor is diffusion through the widows of UiO-66@SiO2, which provides access for the solutes to the entire surface of UiO-66. Molecular diffusion inside the mesopores can be described by the Knudsen model, which states a linear dependence of the diffusion rate on Dp.22 For the pores with Dp < 5 nm, a rapid decrease in diffusion rate is predicted.23,24 Furthermore, for pores with Dp < 1 nm, the diffusion depends strongly on solute size, and for solutes with molecular sizes larger than Dp, diffusion is impossible.25 Thus, the slow diffusion rate through the narrow window openings of UiO-66 should result in stronger retention of small solutes like toluene and ethyl benzene on the UiO-66@SiO2 column.
The second hypothesis is based on the ability of solutes to penetrate the cavities of UiO-66, which in turn depends on the correspondence between the size and geometry of the micropores with the solute molecules. The dependence of the diffusion rate on the solute molecule orientation is well-known for microporous zeolites,26 but so far has not been confirmed for MOF phases. However, similar microporous structure of zeolites and MOFs led us to believe that such hypothesis could be viable for UiO-66@SiO2 particles as well. The crucial factor here is the time during which molecules are present at the windows in the UiO-66 lattice in order to achieve the correct orientation for penetration into the cavities. Obviously, both models take into account the sizes of the solutes and may be used to explain the changes in separation selectivity observed for toluene and ethyl benzene as shown in Fig. 2.
The data clearly indicate the presence of a new FDSS effect, where changes in flow rate can be used to effectively modify both the retention and separation selectivity for small organic molecules, without other changes in experimental conditions. For example, toluene and anthracene cannot be separated at a flow rate of 0.03 mL min−1 (see Fig. 3, top). Gradually increasing the flow rate up to 0.4 mL min−1 does not influence the retention of anthracene, but dramatically reduces the retention factors for toluene. For this reason, at a flow rate of 0.5 mL min−1 the chromatographic peaks of these compounds are resolved. A more impressive change in separation selectivity was achieved for the pair ethyl benzene and cumene (Fig. 3, bottom). Here, a decrease in the flow rate results in stronger retention of ethyl benzene which possesses a smaller molecular size compared to cumene.
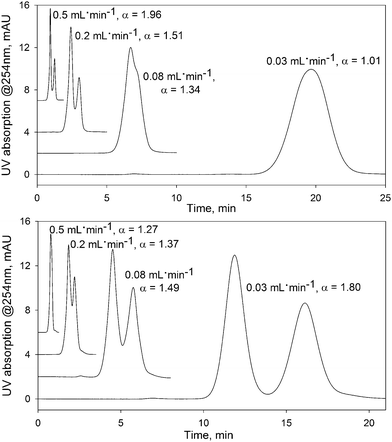 | ||
| Fig. 3 The effect of flow rate on the separation of analytes on the UiO-66@SiO2 column. Upper figure: mixture of toluene (first peak) and anthracene; bottom figure: mixture of cumene (first peak) and ethyl benzene. UV detection at 254 nm. Other conditions as in Fig. 1. | ||
Among the 15 solutes studied in this work (Table 1S, ESI†), the FDSS effect was noted only for toluene and ethyl benzene. For the remainder of the solutes, retention can only arise from interactions with various functional groups located at the outer surface of UiO-66@SiO2 such as residual silanols, epoxy- and glutamic acid groups. π–π interactions, hydrogen bonding and dispersive interactions are also likely to contribute to the retention mechanism.
Thus, it is possible that the retention of the tested solutes obeys a mixed mode mechanism. The retention of alkyl benzenes on UiO-66@SiO2 is generally similar to that observed for silica columns in normal phase HPLC.27 However, for the PAHs the following retention order was obtained: biphenyl < anthracene < naphthalene, which is unusual for this chromatographic mode. Additional experiments are required to understand such selectivity for UiO-66@SiO2, and more detailed investigation about chromatographic performance of UiO-66@SiO2 adsorbent in different chromatographic modes will be presented in a forthcoming paper.
Undoubtedly, the FDSS effect opens new opportunities for HPLC and its use in related applications such as environmental monitoring, pharmaceutical analysis and medical purposes, where sorbents with new selectivity are required. Further research is necessary to elucidate the retention mechanism in flow selective chromatography (FSC) by investigating FDSS for other microporous adsorbents, elution systems, and solutes. If indeed the FDSS effect is based upon the kinetics of diffusion through the micropores, the adsorbents for further research are not to be limited to MOF-based composites, but all microporous materials (including zeolites, clays or nanocarbon composites).
This work was supported by a Research Enhancement Grants Scheme (REGS), University of Tasmania and the Australian Research Council's Discovery funding scheme (DP130101471).
References
- K. K. Unger, R. Ditz, E. Machtejevas and R. Skudas, Angew. Chem., Int. Ed., 2010, 49, 2300 CrossRef CAS PubMed
.
-
V. R. Meyer, Practical High-Performance Liquid Chromatography, Wiley, New York, 2010 Search PubMed
.
- B. Van de Voorde, B. Bueken, J. Denayer and D. De Vos, Chem. Soc. Rev., 2014, 43, 5766 RSC
.
- Y. B. Yu, Y. Q. Ren, W. Shen, H. M. Deng and Z. Q. Gao, TrAC, Trends Anal. Chem., 2013, 50, 33 CrossRef CAS
.
- J. H. Cavka, S. Jakobsen, U. Olsbye, N. Guillou, C. Lamberti, S. Bordiga and K. P. Lillerud, J. Am. Chem. Soc., 2008, 130, 13850 CrossRef PubMed
.
- P. S. Barcia, D. Guimaraes, P. A. P. Mendes, J. A. C. Silva, V. Guillerm, H. Chevreau, C. Serre and A. E. Rodrigues, Microporous Mesoporous Mater., 2011, 139, 67 CrossRef CAS
.
- M. A. Moreira, J. C. Santos, A. F. P. Ferreira, J. M. Loureiro, F. Ragon, P. Horcajada, K. E. Shim, Y. K. Hwang, U. H. Lee, J. S. Chang, C. Serre and A. E. Rodrigues, Langmuir, 2012, 28, 5715 CrossRef CAS PubMed
.
- S. Van der Perre, T. Duerinck, P. Valvekens, D. E. De Vos, G. V. Baron and J. F. M. Denayer, Microporous Mesoporous Mater., 2014, 189, 216 CrossRef CAS
.
- Z. M. Yan, J. N. Zheng, J. F. Chen, P. Tong, M. H. Lu, Z. Lin and L. Zhang, J. Chromatogr. A, 2014, 1366, 45 CrossRef CAS PubMed
.
- X. Q. Zhang, Q. Han and M. Y. Ding, RSC Adv., 2015, 5, 1043 RSC
.
- R. Ameloot, A. Liekens, L. Alaerts, M. Maes, A. Galarneau, B. Coq, G. Desmet, B. F. Sels, J. F. M. Denayer and D. E. De Vos, Eur. J. Inorg. Chem., 2010, 3735 CrossRef
.
- Y. Y. Fu, C. X. Yang and X. P. Yan, Chem. – Eur. J., 2013, 19, 13484 CrossRef CAS PubMed
.
- A. I. Elefterov, M. G. Kolpachnikova, P. N. Nesterenko and O. A. Shpigun, J. Chromatogr. A, 1997, 769, 179 CrossRef CAS
.
- W. B. Liang and D. M. D'Alessandro, Chem. Commun., 2013, 49, 3706 RSC
.
- F. Gritti and G. Guiochon, J. Chromatogr. A, 2013, 1302, 1 CrossRef CAS PubMed
.
- J. Jae, G. A. Tompsett, A. J. Foster, K. D. Hammond, S. M. Auerbach, R. F. Lobo and G. W. Huber, J. Catal., 2011, 279, 257 CrossRef CAS
.
-
D. R. Lide, CRC Handbook of Chemistry and Physics, CRC Press/Taylor and Francis, Boca Raton, FL, 2010 Search PubMed
.
-
G. Guiochon, D. G. Shirazi, A. Felinger and A. M. Katti, Fundamentals of Preparative and Nonlinear Chromatography, Academic Press, Cambridge, MA, 2006 Search PubMed
.
- A. M. Striegel and A. K. Brewer, Annu. Rev. Anal. Chem., 2012, 5, 15 CrossRef CAS PubMed
.
- J. Hirabayashi, N. Ito, K. Noguchi and K. Kasai, Biochemistry, 1990, 29, 9515 CrossRef CAS PubMed
.
- J. L. Herman, T. Edge and R. E. Majors, LCGC North Am., 2012, 30, 200 CAS
.
- K. Malek and M. O. Coppens, J. Chem. Phys., 2003, 119, 2801 CrossRef CAS
.
- R. Takahashi, S. Sato, T. Sodesawa and H. Nishida, Phys. Chem. Chem. Phys., 2002, 4, 3800 RSC
.
- J. Kunetz and L. Hench, J. Am. Ceram. Soc., 1998, 81, 877 CrossRef CAS
.
-
R. M. A. Roque-Malherbe, Adsorption and Diffusion in Nanoporous Materials, CRC Press, Boca Raton, FL, 2007 Search PubMed
.
-
N. Y. Chen, T. F. Degnan and C. M. Smith, Molecular Transport and Reaction in Zeolites: Design and Application of Shape Selective Catalysis, John Wiley & Sons, Hoboken, NJ, 1994 Search PubMed
.
- P. N. Nesterenko and O. N. Fedyanina, J. Chromatogr. A, 2010, 1217, 498 CrossRef CAS PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6cc00111d |
| This journal is © The Royal Society of Chemistry 2016 |