Effect of lattice mismatch and shell thickness on strain in core@shell nanocrystals

Abstract

Bimetallic nanocrystals with a core@shell architecture are versatile, multifunctional particles. The lattice mismatch between core and shell regions induces strain, affecting the electronic properties of the shell metal, which is important for applications in catalysis. Here, we analyze this strain in core@shell nanocubes as a function of lattice mismatch and shell thickness. Coupling geometric phase analysis from atomic resolution scanning transmission electron microscopy images with molecular dynamics simulations reveals lattice relaxation in the shell within only a few monolayers and an overexpansion in the axial direction. Interestingly, many works report core@shell metal nanocatalysts with optimum performance at greater shell thicknesses. Our findings suggest that not strain alone but secondary factors, such as structural defects or structural changes in operando, may account for observed enhancements in some strain-engineered nanocatalysts; e.g., Rh@Pt nanocubes for formic acid electrooxidation.

---

Introduction

Core@shell nanoparticles show great promise for catalytic applications as the core and shell components can be selected to impart distinct functionalities. In the case of metal shells being epitaxially grown on seeds to create bimetallic core@shell nanocrystals, the lattice spacing of the shell will conform to the underlying lattice of the seed, imparting strain into the shell material. The resulting strain modifies the d-band orbital overlap and, thus, the electronic structure of the surface metal.¹ This ability to manipulate the electronic structure at a surface via choice of core and shell components motivates much of the research into metallic core@shell nanocrystals for use as catalysts.² In fact, differences in catalytic performance have been correlated to changes in shell thickness, where the degree of lattice relaxation is anticipated to scale with thickness; however, the relationship between catalytic activity and degree of surface strain is usually only inferred given the difficulty in direct measurement of lattice displacements in nanomaterials.³ An interesting outcome from many studies of core@shell nanocatalysts is that often enhancements are reported for nanoparticles with thick shells (>1 nm shells), where complete lattice relaxation would be anticipated based on surface science studies of epitaxially deposited metals.^2,4–6 Thus, gaining a better understanding of strain in individual core@shell nanocrystals is crucial to the development of strain-engineered nanocatalysts. Here, nanomaterial synthesis, advanced microscopy, and computational tools are combined to provide a systematic analysis of strain in core@shell metal nanocubes.

Strain is the difference in the observed lattice parameter compared to its reference in the relaxed, bulk equilibrium state. Conventional powder X-ray diffraction (XRD) is often used to study strain in materials, revealing changes in lattice parameters as a function of composition (in the case of alloys) or lattice mismatch (in the case of thin films). Advanced methods such as anomalous X-ray diffraction, where diffraction patterns are collected at different X-ray energies near the absorption edge of elements of interest, can correlate lattice parameters with chemical composition, which is particularly useful for understanding the activity of alloyed catalysts.⁷ However, these methods only yield average lattice parameters. In practice there can be substantial differences among nanoparticles in an ensemble as well as within an individual nanoparticle. For example, strain near a face center is expected to be different than strain close to an edge or a vertex. The significance of the latter effect was revealed by Tsung et al. who synthesized extremely monodisperse samples of Pd nanocubes and analyzed them by XRD at the 11-BM beamline of the Advanced Photon Source synchrotron radiation facility.⁸ On account of the exceptional sample monodispersity and high-quality crystallographic data, the authors were able to model the entire XRD pattern with a structure that included cube edge and corner truncation along with a distribution of nanocube sizes and strain effects. This structural characterization was coupled with molecular dynamics simulations of Pd nanocrystal models, which found significant atomic displacement at the corners of the cubes, whereas the edges and faces showed little displacement.⁸ In turn, the electronic structure is also expected to vary as a function of surface position.

Unfortunately, the methods employed by Tsung et al.⁸ cannot be applied to many systems as nanoparticle syntheses rarely achieve the necessary degree of monodispersity.^9,10 Moreover, scattering techniques like coherent X-ray diffraction are currently limited to nanocrystals roughly 60 nm in diameter.¹¹ Thus, to better understand strain in core@shell nanoparticles, techniques that provide greater spatial resolution are required. One such technique is geometric phase analysis (GPA), which uses atomic resolution electron microscopy images to map the lattice deformation observed across individual nanoparticles. GPA is a reciprocal space method through which deviations from the theoretical lattice constants are determined by using Bragg spots in the fast Fourier transform (FFT) of an atomic resolution electron image.¹² One demonstration where GPA was used to understand catalytic results obtained with nanoparticles was presented by Yang et al.¹³ Specifically, they synthesized octahedral and icosahedral Pd@Pt nanoparticles and tested their catalytic activity for the oxygen reduction reaction (ORR). The icosahedral Pd@Pt nanoparticles outperformed octahedral Pd@Pt nanoparticles even though both expressed the favored {111} facets. Strain maps of individual particles obtained by GPA showed that compressive strain dominated the surface of the icosahedron, while the octahedron had regions of surface compression and tension.¹³ Compressed Pt surfaces are known to enhance the rate of the ORR.

Even with the promise of shape-controlled core@shell nanocrystals as catalysts, their strain distributions have not been systematically analyzed.¹⁴ Thus, a series of bimetallic nanocubes with core@shell architectures and variable shell thicknesses (thin versus thick) were synthesized – Pd@Pt, Rh@Pd, and Rh@Pt – and analyzed by GPA to obtain a greater understanding of how lattice mismatch and shell thickness give rise to strained surfaces. These nanostructures were selected to provide a range of lattice mismatches (0.77–3.1%) (Table 1). They are also synthetically accessible and promising electrocatalysts.¹⁵ Conveniently, the nanocubes also orient on TEM grids with their {100} faces perpendicular to the e-beam, minimizing orientation effects from the analysis. The results from GPA are complimented by simulations of atomic displacement in models based on electron microscopy evidence. The simulations show compressively strained surfaces in good agreement with experimental results.

Table 1 Summary of nanocrystal systems studied. The theoretical lattice mismatch is reported based on bulk lattice spacing

Particle	Core lattice constant (nm)	Shell lattice constant (nm)	Theoretical lattice mismatch	Strain type
Pd@Pt	0.389	0.392	0.77%	Compressive
Rh@Pd	0.380	0.389	2.2%	Compressive
Rh@Pt	0.380	0.392	3.1%	Compressive

---

Experimental

Chemicals

Polyvinylpyrrolidone (55 000 MW, PVP), sodium tetrachloropalladate 99.99% (Na₂PdCl₄), and potassium tetrachloropalladate ≥99.99% (K₂PdCl₄) were purchased from Aldrich. L-Ascorbic acid ≥99.0% (L-aa). Potassium chloride (KCl, ≥99.0%) was purchased from Sigma. Rhodium(III) bromide hydrate (RhBr₃·xH₂O), and triethylene glycol (TREG), were acquired from Alfa-Aesar. Potassium bromide (KBr, 99+%) was obtained from Sigma-Aldrich. Nanopure water (18.2 MΩ cm) was used as well as ethylene glycol (anhydrous, 99.8%, EG) purchased from Sigma-Aldrich. Platinum acetylacetonate (Pt(acac)₂) was purchased from Aldrich and unaltered.

Characterization

All nanoparticles were characterized on JEOL JEM 1010 TEM operating at 80 keV and images collected with a ROM CCD camera. TEM samples were drop-casted onto the TEM grid after the entire sample was washed 2–3 times as described below. Additional characterization with STEM-EDX was completed with JEOL JEM 3200FS operating at 300 keV, images taken with Gatan 4k × 4k Ultrascan 4000 camera and the EDX mapping was obtained using an Oxford INCA dispersive X-ray system interfaced with the JEOL JEM 3200FS. High angle annular dark field (HAADF)-STEM images were collected with an aberration corrected Nion UltraSTEM 100 (operating at 100 kV). The TEM samples were prepared as describe above.

Geometric phase analysis

Geometric phase analysis (GPA) was developed by Hÿtch et al.¹² Further details concerning the theory behind GPA method can be found in the original report.¹² In this work, GPA was performed in Digital Micrograph version 3.21 using a FRWR plugin from Humboldt-Universität Berlin (https://www.physics.hu-berlin.de/en/sem/software/software_frwrtools).¹⁶

Atomistic simulations

Models of core@shell nanocatalysts were built by selecting from an infinite fcc lattice sites that are within the nanocrystal shapes. The selected sites were filled with atoms of an element type assigned according to the experimental chemical composition of the core and shell regions. As-built configurations were equilibrated at room temperature (300 K) with molecular dynamics simulations using the LAMMPS software package.¹⁷ Atom pair interactions were computed with long-range Finnis–Sinclair potentials^18,19 based on the quantum Sutton-Chen many-body force field.²⁰ No constraints to the mobility of atoms were applied to impose the expected elemental composition across the nanocrystals. After energy minimization, the system was equilibrated for 1 ns in subsequent NVE and NVT ensemble runs using a Nosè–Hoover thermostat with a 1 fs time step. Langevin dynamic was employed in the initial stage to smoothen the evolution of the system. After equilibration, NVE ensemble simulations recorded trajectories of 500 independent configurations sampled at 2 ps interval time. Time-average (TA) microstructures were obtained by averaging trajectory configurations to cancel the thermal atom vibrations out of the crystalline lattice.²¹

Synthesis

Pd nanocubes. The Pd nanocube synthesis was followed as given in Xia et al.²² In a 8 dram vial 105 mg of PVP (55 000 MW), 64 mg L-aa, 180 mg KCl, 5 mg of KBr, and 8.0 mL of nanopure water was placed in a 80 °C oil bath for approximately 10 minutes. Once all reagents were dissolved, 56 mg of Na₂PdCl₄ in 3.0 mL of nanopure water was added to the solution. This solution was allowed to heat and stir for 3 hours. The particles were precipitated with acetone and collected by centrifugation and redispersed in 5 mL of ethanol. Using K₂PdCl₄ gives the same result.

Rh nanocubes. Synthesis of Rh nanocubes was adapted from a report by Schaak et al.²³ 102 mg RhBr₃·xH₂O was placed in a vial with enough ethanol to completely dissolve the rhodium salt. The solution was then placed in a 50 mL three-necked round bottom flask with 230 mg PVP (55 000 MW) and 10.0 mL of TREG. Argon gas was continuously purged through the solution, and the reaction vessel was equipped with stir bar and a condenser. The solution temperature was heated to 110 °C in an oil bath for 15 minutes to initiate nucleation. The temperature was then raised to 145 °C for 90 minutes. The solution was allowed to cool to room temperature. The product was then washed with acetone and collected by centrifugation as previously described and redispersed in 10 mL ethanol (for Rh@Pt) or water (for Rh@Pd).

Pd@Pt nanocubes. 1 mL of the as-prepared Pd nanocubes was added to 10 mL of EG containing 100 mg of PVP (55 K) in a round bottom flask (RBF). This was heated to 110 °C with stirring. Then Pt(acac)₂ (5 mg for thin shells or 20 mg for thicker shells) in 1 mL of acetone was injected dropwise into the solution. The temperature what then raised to 160 °C and was allowed to stir for two hours. The solution was cooled and washed as previously described.

Rh@Pd nanocubes. 1.0 mL of the Rh nanocubes were added to a 10 mL solution of 119 mg KBr and 17.6 mg L-aa in a vial. The vial was heated to 80 °C in an oil bath and stirred for 10 minutes until dissolved. Then 1 mL of 5 mM Na₂PdCl₄ was injected into the solution and further incubated for 3 hours. The products were collected through centrifugation and washed as previously described. For the thicker shelled sample 1 mL of 10 mM Na₂PdCl₄ was injected.

Rh@Pt nanocubes. Rh@Pt nanocubes were synthesized as reported by Skrabalak et al.² 1.0 mL of Rh cubic seeds and 10.0 mL of ethylene glycol was placed in a 50 mL three-necked round bottom flask with stir bar. The solution was purged with argon gas as it was rapidly heated to 160 °C over the course of 6–8 minutes. Meanwhile, the desired amount of Pt(acac)₂ (5 mg for thinner shell or 12 mg for thicker shell) was placed in a vial and acetone was added until the salt had completely dissolved (roughly 2 mL). Once the Rh cube/ethylene glycol solution had reached 160 °C, the Pt(acac)₂ solution was rapidly hot-injected into the flask, and the reaction was heated for two hours. The solution was allowed to cool to room temperature. The product was then washed with acetone, collected by centrifugation, and redispersed in 10 mL of ethanol.

Results and discussion

Synthesis and characterization of core@shell nanoscrystals

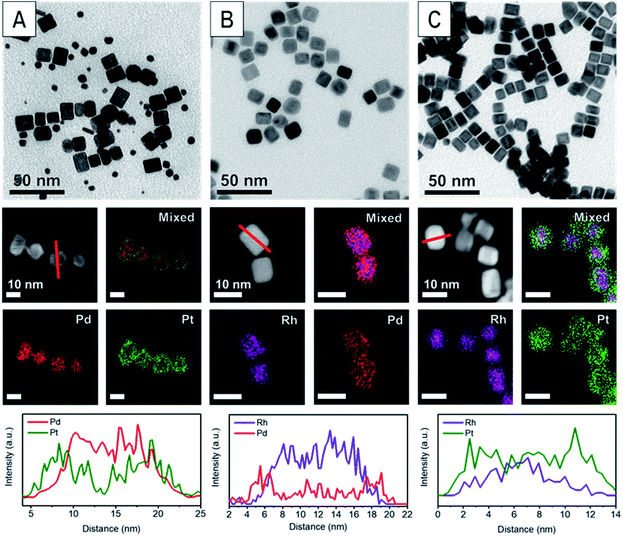
The various core@shell nanoparticles were synthesized with similar sizes and shell thicknesses by seeded growth methods.²⁴ Specifically, Pd and Rh nanocubes were synthesized by previously reported methods (Fig. S1†).^2,25 These nanocubes were then used as seeds to produce Pd@Pt, Rh@Pd and Rh@Pt core@shell nanoparticles. These nanoparticles were characterized by transmission electron microscopy (TEM) and scanning transmission electron microscopy-energy dispersive X-ray spectroscopy (STEM-EDX) (Fig. 1). The core@shell architectures are supported by elemental analysis and line scans. Samples with different shell thicknesses could be accessed simply by increasing the concentration of the shell metal precursor in the overgrowth step, with sample characterization shown in Fig. 2 and 3. Thin shelled samples have 2–4 monolayers (MLs) of shell material deposited, and thick shelled samples have 5–7 MLs deposited.

Fig. 1 Characterization of (A) Pd@Pt, (B) Rh@Pd, and (C) Rh@Pt. The first row contains TEM images of each sample. The second and third row are STEM images and corresponding STEM-EDX elemental maps of the core@shell nanocrystals where green represents Pt, red Pd, and purple Rh. The last row is the line profiles indicated by the red line in the STEM image in the second row for each nanocrystal sample.

Fig. 2 HAADF-STEM images and corresponding GPA for the thin (2–4 ML) shelled samples (A–C) Pd@Pt, (D–F) Rh@Pd, and (G–I) Rh@Pt nanocubes. The first column consists of the HAADF-STEM images of the nanocrystal examined by GPA. The second column contains the corresponding GPA colors maps which correspond to the in-plane strain (ε_xx) field (which is the strain in the plane of the crystal face) where the intensity scale shows relative deformation. The third column contains line profiles of the lattice difference determined by GPA with the line profile locations indicated by arrow in the GPA color maps where the start of the line profile begins at the dot and ends at the arrow head.

Fig. 3 HAADF-STEM images and corresponding GPA for the thick (5–7 ML) shelled samples (A–C) Pd@Pt, (D–F) Rh@Pd, and (G–I) Rh@Pt nanocubes. The first column consist of the HAADF-STEM images of the nanocrystal examined by GPA. The second column contains the corresponding GPA color maps which correspond to the in-plane strain (ε_xx) field (which is the strain in the plane of the crystal face) where the intensity scale shows relative deformation. The third column contains line profiles of the lattice difference determined by GPA with the line profile locations indicated by arrow in the GPA color maps where the start of the line profile begins at the dot and ends at the arrow head.

Geometric phase analysis of core@shell nanocrystals

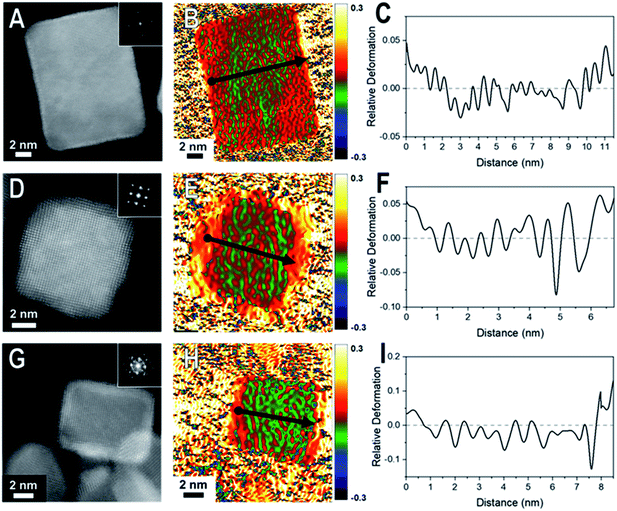
Core@shell particles with varying degrees of lattice mismatch and different core and shell compositions should show shells with varying degrees of atomic displacement by GPA. In Fig. 2 are HAADF-STEM images and the corresponding GPA for the thinner shelled Pd@Pt, Rh@Pd, and Rh@Pt nanocubes.

Due to the difference in Z-contrast, the Pt shell can be seen as the brighter region on the exterior of the Pd@Pt and Rh@Pt nanoparticles (Fig. 2A and G). The Z-contrast between Rh and Pd is not as evident as their atomic numbers are similar but this contrast difference can be seen near the corner of the nanoparticle. GPA was performed on the whole nanocrystal (Fig. 2). The false-colored images represent the in-plane (ε_xx) strain fields determined by GPA showing lattice deformation relative to a reference, in this case a selected core region was used as the reference (Fig. 2B, E, and H). No shear strain was observed by GPA. The red coloring (or warm coloration) on the particle represents an expansive lattice deformation relative to the reference and the green coloring (cool coloration) represents a contraction relative to the reference. The oscillation in coloring is characteristic of GPA and may originate from imperfect defocus in the atomic level image and/or from the masks applied to select diffraction spots in the FFT pattern and the oscillation periodicity is related to the mask size used during the GPA.²⁶ If the shell material conforms to the core's interplanar distance via epitaxy, then there should be no obvious regions of red or green on the exterior of the particle, indicating minimal lattice deformation relative to the core. However, if the shell's lattice relaxes, then there should be uniform regions of red or green (depending on the shell material) on the exterior of the particle in the GPA strain fields from the deformation of the lattice relative to the reference.²⁷ The lattice deformation is also described by a line profile of the selected region shown by the black arrow on each strain field map, where the y-axis is the relative lattice deformation compared to the core reference (Fig. 2C, F and I). The line profiles extend across the particle in the x direction from face-to-face, where the black dot marks the start of the line profile (0 nm).

The ε_xx strain field for a representative Pd@Pt nanocube is shown in Fig. 2B and reveals minimal red coloration on the exterior of the particle, indicating that there is minimal deformation of the shell material relative to the reference. The lack of deformation indicates that there is little change in the interplanar distances between the core and shell, implying a strained shell. At these thin shells, 1–3 ML determined by HAADF-STEM, the Pt lattice is matching the Pd core's interplanar distance, straining the Pt surface. The GPA strain fields for Rh@Pd and Rh@Pt show similar trends; however, there seems to be some deformation occurring (Fig. 2E and H) which may be resulting from the additional atomic layers on the Rh cores when compared to the Pd core sample. The increased expansive deformation caused by lattice relaxation is evident by the concentration of red near the exterior of the particle in the ε_xx strain fields; however, the thickness of the red coloration appears to be narrower than the deposited shell material indicating that this lattice relaxation only occurs at the outmost layers.

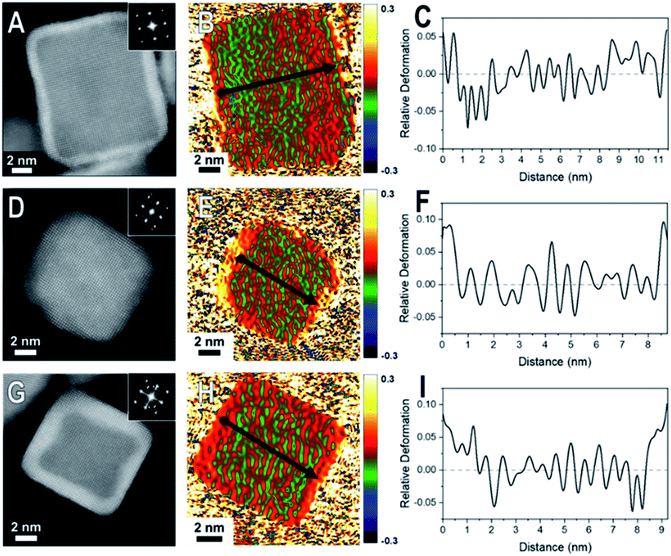
When comparing these results to samples with thicker shells (5–7 MLs), the strain field maps show significantly more red coloration near the surfaces of the nanoparticles (Fig. 3). Uniform red coloration in the strain field maps indicates expansive deformation for the shell regions relative to the core regions. This finding is consistent with relaxation of the shell's lattice as the three nanocrystal systems have shells of metals with larger bulk lattice spacings compared to their core metals (Table 1). For example, there is a larger area of red on the exterior of the thicker shelled Rh@Pt compared to the thinner shelled sample (Fig. 3H). Because the bulk lattice spacing of Pt is larger than Rh, these observations suggest that at a Pt shell thickness of ∼5 MLs is undergoing significant expansive deformation due to lattice relaxation often observed when transitioning from the core–shell interface to the free surface. This lattice relaxation would decrease the occurrence of surface strains (from lattice mismatch) observed with thicker shelled particles.

The observed shell relaxation is expected because strain effects decrease with distance from the interface.³ When comparing the line profiles of the thin shelled samples to the thicker shelled samples, the relative deformation near the edge of a nanocrystal is larger for the thicker shelled samples, indicating that more relaxation is occurring (e.g., Fig. 2F to Fig. 3F). Another interesting observation gathered from the line profiles is the overexpansive deformation near the edge of the particles when compared to the bulk lattice differences. Due to the limited resolution of GPA, the exact deformation values cannot be considered definitive; however, the origin of this overexpansion can also be explored through simulations. It is interesting to note that there is relatively uniform deformation across the surface of the core@shell particles, a phenomenon supported by our simulations (Fig. S2†).

Collectively, GPA provided semi-quantitative visualization of lattice relaxations that occurs in core@shell nanoparticles, where an increase in shell thickness results in more lattice relaxation. GPA, however, cannot give information about the strain relaxation mechanisms or possible anisotropy in the lattice deformations as resolution is limited.^26–31 These factors can contribute towards catalytic enhancements found with core@shell catalysts. Given the limitations of GPA and synthetic versatility, simulations of atomic displacements in core@shell nanocrystals were undertaken and allow for the systematic manipulation of all nanocrystal design parameters (e.g. core size, shell thickness, and composition).

Simulations of atomic displacement in core@shell nanocrystals

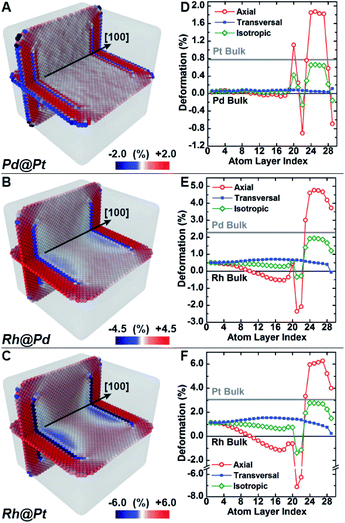
Molecular dynamics simulations were used to complement the experimental observations and develop a more complete understanding of lattice distortion in core@shell nanocubes.³² Specifically, atomistic models based on the synthesized core@shell nanostructures were constructed with known size, shape, and shell thickness. To clean the atomistic model from noise such as thermal atom displacements, a time average configuration was computed after achieving thermodynamic equilibrium.³³ The variation of the axial lattice parameter normal to the exposed facets of the cubic nanocrystals μ_⊥, was evaluated as a proxy of the lattice deformation parameter measured by GPA (Fig. 4A–C). This allows for validating simulations against experimental data. The relative variation of μ_⊥ over a central cross-section of the time-averaged atomistic models compares well with the strain maps obtained by GPA. The lattice parameters in the Pd@Pt, Rh@Pd, and Rh@Pt nanocrystals increases from the core to the shell as revealed by GPA. Simulations show an overexpansion of the axial parameter in the shell consistent with the GPA results (Fig. 4D–F). Simulations also predict deformation of the core, which is not accounted for in the GPA. These observations are explained with more rigor below considering the full three-dimensional deformation.

Fig. 4 Effect of different composition on compressive lattice mismatch with molecular dynamics simulation. (A–C) The lattice deformation field as measured by the axial lattice parameter normal to the nanocrystal surface facets in Pd@Pt (upper row), Rh@Pd (middle row) and Rh@Pt (bottom row) core@shell nanocrystals nanocubes was investigated with classical molecular dynamics simulations. The color maps show the deformation field of the axial lattice parameter normal to the nanocrystal surface facets for cube (A–C), core@shell nanocrystals. (D–F) Variation of the axial (red open circle), transversal (blue full square) and isotropic (green open diamond) deformation of the lattice parameter along a central line section normal to the nanocrystal surface as a function of the distance from the center.

In addition to the surface relaxation phenomena that affects the two outermost atomic monolayers,^34,35 a wide fluctuation of the lattice parameter is revealed originating at the core–shell interface (Fig. 4D–F). There is also deformation in the core region as a response to the change in local environment when a shell is epitaxially grown. For example, the lattice parameter for the Rh core systems (Fig. 4E and F) shrinks towards the interface because of the shell's mechanical tension, causing expansive deformation to propagate into the core. The Pd@Pt system does not show this phenomenon due to the minimal lattice mismatch between Pt and Pd (Table 1), where the confining tension is cancelled by surface relaxation (Fig. 4D).

The average per atom first-neighbor pair-distance was computed to fully capture the local structure deformation. As expected, on average the structure expands in the core region and contracts in the shell in agreement with the lattice mismatch defined by the composition and structure. Contrary to what is observed for larger crystals, this balancing effect emerges because both core and shell crystalline domains have comparably low mechanical rigidity due to the small sizes, allowing the core region to deform in response to the deposition of the shell. Lattice deformation at the free surface is uniform on the exposed {100} planes and it is predominantly controlled by the lattice mismatch. When comparing the surfaces of core@shell nanocrystals to monometallic nanocrystals, the surface deformation of monometallic nanocrystals has more variation and results in non-homogenous strain fields.⁸ The core@shell architecture gives rise to uniformly strained surfaces on the projection of the core region to the exposed facets, which allows for tuning of surface-adsorbate binding strength to optimize catalysis.

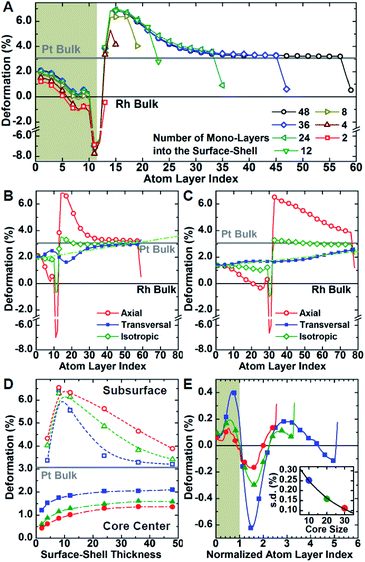
Atomistic simulations offer a facile way to probe a wide scenario of design parameters and examine their individual contribution to the resulting lattice distortion. Here, a systematic investigation was undertaken to correlate lattice deformation with core size and shell thickness using the Rh@Pt structure as a model system (Fig. 5). The expansion of the axial lattice parameter achieves a maximum within a range of 4 to 8 atomic layers apart from the core@shell interface. Notably, in this initial range, the deformation path does not change with the variation of core size and/or shell thickness (Fig. 5A–D). The two outermost atomic layers contract by the same deformation ratio as for a monometallic particle.⁸ Because of the overlap of the two opposing behaviors (shell expansion and surface relaxation), thin shells (thinner than eight atomic layers) do not show complete expansion to the bulk equilibrium lattice parameter. The overexpansion of the axial lattice parameter relaxes across the thicker shells approaching the ideal bulk reference. As an example, the lattice parameter fully relaxes at a thickness of about 40 atomic layers for the Rh@Pt nanocrystals, more than half the size of the core region (e.g., cores with 10, 20, or 30 unit cells require 50, 60, and 70 atomic layers for complete relaxation, respectively). The deformation at the core@shell interface and center of the core scales with core size (Fig. 5D). For example, when the core size is larger, there is less deformation in the core as the mechanical rigidity is increased. Also for particles with the same shell thickness but different core sizes, the shell deformation relative to the core is less for the larger core sample, again due the increase of mechanical rigidity (Fig. 5D).

Fig. 5 Deformation of the lattice structure. Systematic investigation of the lattice distortion as a function of core-size and shell-thickness for Rh@Pt core@shell nanocrystals with molecular dynamics simulation. (A) Variation of the axial deformation of the lattice parameter along a central line section normal to the surface as a function of the distance from the center for a set of nanocrystals with increasing surface-shell thickness from 0.5 to 9 nm. Variation of the axial (red, open circle), transversal (blue, full square) and average (green, open diamond) lattice parameters for small- and large-core nanocrystals (B and C, respectively) with thick (9 nm) surface-shell. Linear trend of the transversal component across the nanocrystals are shown in green. (D) Deformation of the axial lattice parameter at the center (full dot) and sub-surface (open dot), or rather two atom layers far from the nanocrystal surface, of 4, 8 and 12 nm core-size nanocrystals (blue, green and red, respectively) as a function of the thickness of the surface-shell. (E) Deviation of the transversal lattice parameter from the linear trend for thick-shell nanocrystals with increasing core size as a function of the distance from the nanocrystal center normalized by the core size. The profiles are rescaled such that the core–shell interface is set at a normalized distance of 1.0. The inset shows the standard deviations.

Although the shell region shows large axial deformations, the core region directly affects the transversal deformation at the core@shell interface. The transversal lattice parameter parallel to the exposed facets of the cubic nanocrystals u_∥, was calculated (Fig. S3†). A deformation that preserves the orthogonal angles of the cubic cell was assumed, consistent with GPA observations. The transversal lattice parameter was calculated from the average neighbor distance and axial lattice parameter. Comparison of the neighbor distances and lattice parameter information indicates that the transverse deformation compensates for the axial structural changes normal to the nanocrystal surface (Fig. 5B and C). Compared to the axial deformation, the transverse component shows more continuous variation throughout the nanocrystals from the core to the shell ideal reference parameters. The transversal deformation outlines a smooth sinusoidal deviation path centered at the core@shell interface. Such deviation can be directly related to the anisotropic rigidity of the cubic structure. The deviation is larger for nanocrystals with smaller core sizes and larger lattice mismatch, which strengthen the non-homogeneous deformation of the core (Fig. 5E). Although the structure deformation at the exposed surface is directly controlled by the shell thickness, the same deformation is achieved for a larger shell thickness grown on a larger core. In addition, nanocrystals with larger cores show smaller variations in shell deformation with respect to changes in shell thickness. This understanding allows for both easier and more reliable nanostructure design, where nanocatalysts can be synthesized with high accuracy of surface distortions.

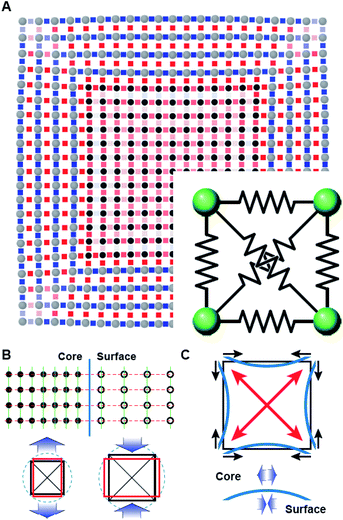
The deformation of the crystal structure at a local scale follows the linear elastic theory of classical solid mechanics.³⁶ Nonetheless, the small size of nanocrystals affect the propagation of the deformation field (Fig. 6A). Simplified models that ignore the shape boundary effect will fail to predict the strain.³ In agreement with high resolution TEM evidence, atoms align in straight lines throughout the nanocrystal and across the core–shell interface (Fig. 6B). The atom spacing in the core region sets the pattern for the transverse epitaxial growth of the shell. Therefore, the transversal unit cell parameter stretches in the shell to match the core's atomic structure.

Fig. 6 (A) Elastic deformation of a core@shell 2D square lattice nodes connected with elastic springs as in the inset. Stiffer elastic constants were used for springs connecting nodes in the shell than in the core. Lattice bonds are coloured according to the stretch of the bond distance compared to the equilibrium spring length (blue to red for shorter to longer, respectively). (B and C) Schemes of the deformation mechanism at the core–shell interface. (B) The shared structure pattern leads to opposite stress fields in the bonded regions where the deformation of the cubic lattice is governed by the Poisson ratio. (C) The core–shell interface bends because of the anisotropic rigidity of the cubic structure (i.e., larger deformability along with the 100 directions) resulting in an additional tangential stress component.

The transverse strain imposed by the epitaxial growth imposes an axial deformation as a function of the material Poisson's ratio, 0.39 for Pt and Pd, and 0.26 for Rh.³⁷ Because of the over-imposed stress from the free surface and core@shell interface, a validation of the Poisson's ratio value is not feasible. The deformation is smaller towards the corners than the facets of the cubic shape because of the mechanical anisotropy of the fcc crystal structure.³⁸ As a consequence, the core@shell interface bends inwards, inducing an additional transversal tension (Fig. 6C). The sinusoidal variation of the transversal deformation can be directly related to the curvature of the interface. Certainly, the curvature locally imposes a distortion to preserve the orthogonal relationship between the interface and the column of atoms spanning through. This condition opens the lattice towards the core, resulting in the expansive deviation of the transversal lattice parameter observed in the core.

Conclusions

GPA and simulations of Pd@Pt, Rh@Pd, and Rh@Pt nanocubes reveal that thin metal shells largely conform to the underlying lattice. Through the use of GPA, expansive deformation was observed near the edge of the particles, seemingly larger than the bulk lattice differences. Also observed through GPA, the uniformly strained surface that arises from the core@shell architecture that is not present in monometallic crystals, allowing for precise tuning of surface strains to meet the surface catalysis needs. The exploration of these core@shell systems via atomistic simulations revealed that the core size contributed to the shell relaxation mechanisms. Lastly, the small sizes of the cores (<10 nm) typically used in fuel cell applications can have deformation due to the deposition of the shell that is rarely accounted for when calculation surface strains. We can imagine using the model system developed in this work to help describe more complex nanoparticles (e.g., alloy nanocatalysts with monometallic skins).

The implications of such compressed Pt and Pd surfaces are significant to many catalytic processes. For example, in the case of Pt nanoparticles catalyzing the ORR, compression of Pt–Pt bonds has been correlated with a d-band down-shift that weakens the bonding between Pt and oxygenated species and increases catalytic activity.^39,40 A similar effect has been observed in Pd-based systems for the ORR as well as for other reactions.^40,41 Moreover, weaker CO binding is observed on compressed Pt surfaces, which is important to a number of reactions where CO is a common poison.⁴² Thus, the catalytic enhancements observed in many systems from compressed Pd or Pt surfaces are unsurprising. For example, Xia and co-workers studied Pd@Pt nanocubes as catalysts for the ORR and found that nanoparticles with 2–3 atomic layers provide the highest specific activity, which they attributed in part to compressive lateral strain.⁴³

A systematic analysis of shell thickness in the Pd@Pt nanocube system by Xia and co-workers found that the specific activity actually followed a volcano trend, with thinnest (∼1 ML) and thickest (4–6 MLs) samples having decreased specific activities.⁴³ This dependence on shell thickness is consistent with the Pt surfaces having different degrees of strain depending on the shell thickness. Interestingly, our analysis indicates that relaxation should occur by ∼5–6 MLs and Xia and co-workers reported that Pd@Pt nanocubes with shells of that thickness have performance similar to an unstrained Pt reference. Still, enhancements have been reported with thicker shelled samples, where our GPA suggests that surfaces should be relaxed. For example, our group studied the Rh@Pt nanocubes discussed in this manuscript for formic acid electrooxidation and previously reported a volcano trend, with a decrease in CO poisoning maximized for samples with Pt shells of ∼6 MLs.² While the volcano trend is expected, weakened CO absorption at this thickness is not based on our studies reported here. Further examination of the microscopy images of Rh@Pt nanocubes reveal that the Pt shell is thinner at corners than at faces. Taken together, the enhanced performance at thicker shelled samples may arise from non-conformal shell metal deposition and enhanced activity at corner sites, although in operando structural changes cannot be ruled out.⁴⁴ Interestingly, in contrast to Rh@Pt nanocubes, the Pt shell is thicker at corners than at faces for Pd@Pt nanocubes, which may be a result of differences in surface diffusion and adatom deposition rates during synthesis.

The GPA and simulations of atomic displacement show that metal–metal bonds can be compressed in core@shell metal nanostructures across a series of systems where the lattice parameter of the core metal is less than that of the depositing metal. They show a deformation overexpansion near the edge of the particle when compared to the reference lattice mismatch. Revealed by simulations, uniformly strained surfaces are achieved in core@shell nanoparticles. Larger cores show smoother variations in deformation throughout the shell. The controlled tuning of surface strains is a promising strategy to optimize catalytic activity on nanoparticle surfaces. Not surprisingly, the greatest degree of compression is observed for thin shells, where the deposited metal largely conforms to the underlying lattice. This compression is released within ∼5–6 MLs in systems of both small (0.77%) and moderate (3.1%) lattice mismatch (0.77–3.1%).

As the degree of surface strain correlates with the position of the shell metal's d-band center (and adsorbate binding strength), shell thickness affords a facile way to tune the strength of surface-adsorbate interactions. However, rarely is deposition conformal in colloidal nanoparticle systems and the nature of the non-uniformity may depend on the metal system (e.g., Pd@Pt versus Rh@Pt).^2,25,45,46 The small size of nanocrystals affect the propagation of the deformation field. Simplified models that ignore the shape boundary effect will fail to predict the strain. Surface relaxation can also be affected by surface ligands, but such effects are assumed to be negligible in this work on account of the sample washing procedures and electron beam flooding technique required to obtain atomic resolution images, which would remove such capping ligands. Significantly, these variations within individual particles may account for macroscopic catalytic trends and should be considered in any analysis.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

S. E. S, J. T. L. G.; K. M. K. acknowledge financial support from Indiana University and U.S. DOE BES Award DE-SC0018961. We also want to thank the IU Electron Microscopy Center and Nanoscale Characterization Facility for access to the necessary instrumentation. A. L. and M. E. acknowledge funding from Deutsche Forschungsgemeinschaft through the Cluster of Excellence Engineering of Advanced Materials (EXC 315/2). Supercomputer time for this research was supported in part by the Lilly Endowment, Inc., through its support for the Indiana University Pervasive Technology Institute, and in part by the Indiana META Cyt Initiative. The Indiana META Cyt Initiative at IU was also supported in part by the Lilly Endowment, Inc. A portion of the electron microscopy characterization was conducted as part of a user proposal at Oak Ridge National Laboratory's Center for Nanophase Materials Sciences, a U.S. Department of Energy Office of Science User Facility.

References

1. Z. Chen, X. Zhang and G. Lu, J. Phys. Chem. C, 2017, 121, 1964–1973.
2. E. W. Harak, K. M. Koczkur, D. W. Harak, P. Patton and S. E. Skrabalak, ChemNanoMat, 2017, 3, 815–821.
3. B. T. Sneed, A. P. Young and C.-K. Tsung, Nanoscale, 2015, 7, 12248–12265.
4. J. Park, L. Zhang, S.-I. Choi, L. T. Roling, N. Lu, J. A. Herron, S. Xie, J. Wang, M. J. Kim, M. Mavrikakis and Y. Xia, ACS Nano, 2015, 9, 2635–2647.
5. M. Laskar and S. E. Skrabalak, J. Mater. Chem. A, 2016, 4, 6911–6918.
6. J. T. L. Gamler, H. M. Ashberry, X. Sang, R. R. Unocic and S. E. Skrabalak, ACS Appl. Nano Mater., 2019, 2, 4538–4546.
7. P. Strasser, S. Koh, T. Anniyev, J. Greeley, K. More, C. Yu, Z. Liu, S. Kaya, D. Nordlund, H. Ogasawara, M. F. Toney and A. Nilsson, Nat. Chem., 2010, 2, 454–460.
8. P. Scardi, A. Leonardi, L. Gelisio, M. R. Suchomel, B. T. Sneed, M. K. Sheehan and C.-K. Tsung, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 155414.
9. J. Solla-Gullon, E. Garnier, J. M. Feliu, M. Leoni, A. Leonardi and P. Scardi, J. Appl. Crystallogr., 2015, 48, 1534–1542.
10. A. Leonardi and D. L. Bish, Acta Mater., 2017, 133, 380–392.
11. I. Robinson, J. Phys. Soc. Jpn., 2012, 82, 021012.
12. M. J. Hÿtch, E. Snoeck and R. Kilaas, Ultramicroscopy, 1998, 74, 131–146.
13. Y. Xiong, H. Shan, Z. Zhou, Y. Yan, W. Chen, Y. Yang, Y. Liu, H. Tian, J. Wu, H. Zhang and D. Yang, Small, 2016, 13, 1603423.
14. Y. Luo and R. Qin, Surf. Sci., 2014, 624, 103–111.
15. F. J. Vidal-Iglesias, R. M. Aran-Ais, J. Solla-Gullon, E. Garnier, E. Herrero, A. Aldaz and J. M. Feliu, Phys. Chem. Chem. Phys., 2012, 14, 10258–10265.
16. Useful Plugins and Scripts for DigitalMicrograph — Strukturforschung/Elektronenmikroskopie, https://www.physics.hu-berlin.de/en/sem/software/software_frwrtools, accessed December 13, 2019.
17. S. Plimpton, J. Comput. Phys., 1995, 117, 1–19.
18. H. Rafil-Tabar and A. P. Sulton, Pattern Recogn. Lett., 1991, 63, 217–224.
19. A. P. Sutton and J. Chen, Philos. Mag. Lett., 1990, 61, 139–146.
20. Y. Kimura, Y. Qi, T. Cagin and W. A. Goddard III, The Quantum-Sutton-Chen Many-Body Potential for Properties of fcc Metals, CalTech ASCI Technical Report 003, California Institute of Technology, Pasadena, 1998.
21. A. Leonardi, K. Beyerlein, T. Xu, M. Leoni and P. Scardi, Z. Krist. Proc., 2011, 1, 37–42.
22. M. Jin, H. Liu, H. Zhang, Z. Xie, J. Liu and Y. Xia, Nano Res., 2011, 4, 83–91.
23. A. J. Biacchi and R. E. Schaak, ACS Nano, 2011, 5, 8089–8099.
24. Y. Xia, K. D. Gilroy, H.-C. Peng and X. Xia, Angew. Chem., Int. Ed., 2017, 56, 60–95.
25. S. E. Habas, H. Lee, V. Radmilovic, G. A. Somorjai and P. Yang, Nat. Mater., 2007, 6, 692–697.
26. J. Chung and L. Rabenberg, Ultramicroscopy, 2008, 108, 1595–1602.
27. M. J. Hÿtch, J.-L. Putaux and J. Thibault, Philos. Mag., 2006, 86, 4641–4656.
28. M. J. Hÿtch and T. Plamann, Ultramicroscopy, 2001, 87, 199–212.
29. E. Guerrero, P. Galindo, A. Yáñez, T. Ben and S. I. Molina, Microsc. Microanal., 2007, 13, 320–328.
30. J. L. Taraci, M. J. Hÿtch, T. Clement, P. Peralta, M. R. McCartney, J. Drucker and S. T. Picraux, Nanotechnology, 2005, 16, 2365–2371.
31. Y. Zhu, C. Ophus, J. Ciston and H. Wang, Acta Mater., 2013, 61, 5646–5663.
32. A. Leonardi, M. Leoni, M. Li and P. Scardi, J. Nanosci. Nanotechnol., 2012, 12, 8546–8553.
33. P. M. Derlet, S. Van Petegem and H. van swygenhoven, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 024114.
34. D. Wolf, Surf. Sci., 1990, 226, 389–406.
35. J. Wan, Y. L. Fan, D. W. Gong, S. G. Shen and X. Q. Fan, Modell. Simul. Mater. Sci. Eng., 1999, 7, 189–206.
36. M. Tchonkova and S. Sture, Arco, 2001, 8, 41–74.
37. Materials Handbook: A Concise Desktop Reference, ed. F. Cardarelli, Springer London, London, 2008, pp. 1–57.
38. N. C. Popa, J. Appl. Crystallogr., 1998, 31, 176–180.
39. J. T. L. Gamler, H. M. Ashberry, S. E. Skrabalak and K. M. Koczkur, Adv. Mater., 2018, 30, 1801563.
40. S. Mukerjee, S. Srinivasan, M. P. Soriaga and J. McBreen, J. Electrochem. Soc., 1995, 142, 1409–1422.
41. L. Zhang and G. Henkelman, J. Phys. Chem. C, 2012, 116, 20860–20865.
42. K. Jiang, H.-X. Zhang, S. Zou and W.-B. Cai, Phys. Chem. Chem. Phys., 2014, 16, 20360–20376.
43. S. Xie, S.-I. Choi, N. Lu, L. T. Roling, J. A. Herron, L. Zhang, J. Park, J. Wang, M. J. Kim, Z. Xie, M. Mavrikakis and Y. Xia, Nano Lett., 2014, 14, 3570–3576.
44. G. A. Somorjai and Y. Li, Introduction to Surface Chemistry and Catalysis, John Wiley & Sons, 2010.
45. N. Lu, J. Wang, S. Xie, J. Brink, K. McIlwrath, Y. Xia and M. J. Kim, J. Phys. Chem. C, 2014, 118, 28876–28882.
46. J. S. Santana, J. T. L. Gamler and S. E. Skrabalak, Part. Part. Syst. Charact., 2019, 36, 1900142.

---

Footnote

† Electronic supplementary information (ESI) available: Additional characterization by STEM and atomistic simulations. See DOI: 10.1039/d0na00061b

---