A broadly applicable quantitative relative reactivity model for nucleophilic aromatic substitution (S_NAr) using simple descriptors

Abstract

We report a multivariate linear regression model able to make accurate predictions for the relative rate and regioselectivity of nucleophilic aromatic substitution (S_NAr) reactions based on the electrophile structure. This model uses a diverse training/test set from experimentally-determined relative S_NAr rates between benzyl alcohol and 74 unique electrophiles, including heterocycles with multiple substitution patterns. There is a robust linear relationship between the experimental S_NAr free energies of activation and three molecular descriptors that can be obtained computationally: the electron affinity (EA) of the electrophile; the average molecular electrostatic potential (ESP) at the carbon undergoing substitution; and the sum of average ESP values for the ortho and para atoms relative to the reactive center. Despite using only simple descriptors calculated from ground state wavefunctions, this model demonstrates excellent correlation with previously measured S_NAr reaction rates, and is able to accurately predict site selectivity for multihalogenated substrates: 91% prediction accuracy across 82 individual examples. The excellent agreement between predicted and experimental outcomes makes this easy-to-implement reactivity model a potentially powerful tool for synthetic planning.

---

Introduction

Making reliable predictions about the reactivity of organic molecules under specific conditions is the cornerstone of organic synthesis.¹ Every organic chemist learns to qualitatively predict and/or rationalize reactivity based on the properties of functional groups and substituents, and to use these predictions in designing effective syntheses.^2,3 Quantitative predictions of reactivity and selectivity are generally more challenging to achieve, and rely on sufficient experimental data to build structure-reactivity correlations, extensive theoretical calculations, or a combination of the two.^4–9 Recent advances in this area combine techniques such as high-throughput experimentation, descriptor generation, multivariate statistical analysis, and machine learning to generate robust quantitative structure-reactivity relationships (QSRR) and/or quantitative structure-selectivity relationships (QSSR) for specific reactions.^10–22 However, many significant challenges remain, including reliable data collection for a large enough set of chemical space, broad applicability of the resulting models beyond the specific training/test sets examined, and deployment in complex molecule synthesis planning and design.^23–25

One class of organic reactions for which accurate predictive models would be invaluable is nucleophilic aromatic substitution (S_NAr). S_NAr is one of the most important and well-studied transformations in organic synthesis.^26–29 It is extensively used in total synthesis of natural products,^30–37 medicinal chemistry and agrochemistry,^38–43 and manufacturing of active pharmaceutical and agrochemical ingredients.^44–48 For example, S_NAr reactions are particularly powerful for the synthesis and functionalization of N-heterocycles, which are among the most ubiquitous structural components in active pharmaceutical ingredients.^49–51

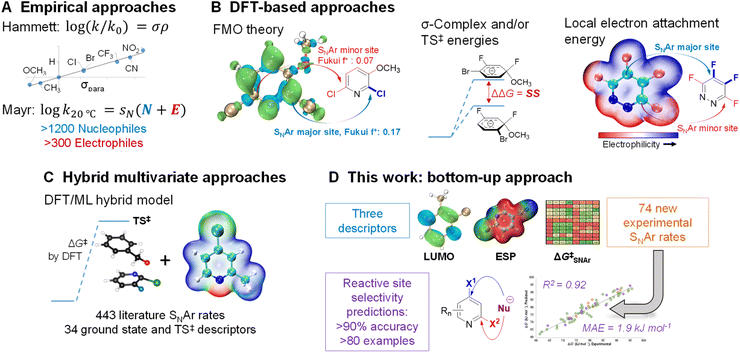
Because of its importance in synthesis, designing efficient and highly selective S_NAr reactions involving complex molecules is crucial. Substantial research over the past 100 years has been devoted to understanding the operative reaction mechanisms, whether stepwise or concerted,^26,52–54 and in collecting experimental reactivity and selectivity data for myriad substrate combinations. For example, Hammett⁵⁵ and/or Mayr parameters⁴ are often used as mechanistic probes and to correlate/predict S_NAr reactivity (Fig. 1A).^56–62

Fig. 1 Approaches to developing quantitative structure-reactivity relationships (QSRR) for S_NAr reactions. (A) Empirical parameters derived from experimental data. (B) Calculated descriptors from DFT analysis (FMO = frontier molecular orbital theory; TS = transition state). (C) Recent hybrid DFT/ML approach. D) Bottom-up approach combining new experimental data with simple calculated descriptors.

Theoretical and computational methods have been used to develop predictive models for specific subsets of S_NAr chemistry (Fig. 1B). Early work focused on stability of the σ-complex intermediates using I_π-repulsion theory,^63,64 or frontier molecular orbital considerations⁶⁵ to explain and predict regioselectivity.⁶⁶ Baker and Muir^67,68 as well as Brinck, Svensson, and co-workers^69–71 have published several works on predicting regioselectivity for S_NAr reactions using DFT-calculated transition state energies and/or stability of the σ-complex intermediates (SS).⁷¹

Quantum chemical transition state calculations are undeniably a powerful tool to explore reaction mechanisms and provide theoretical evidence to support experimental findings; however, the computational cost of performing transition state analyses remains high, and the complexity and nuance of these calculations make them beyond the expertise of many synthetic research groups. More desirable from an end-user perspective are models built from easily obtained molecular descriptors. In addition to established electronic and steric descriptors,^55,72,73 in 2016 Brinck and co-workers introduced the local electron attachment energy (analogous to the local electron affinity) as a molecular descriptor for electrophilicity,⁷⁴ and have applied it toward reactivity/selectivity predictions for S_NAr reactions.⁷⁵ While this descriptor correlates well with sets of experimental rates, and is able to provide qualitative selectivity predictions in multihalogenated systems, there is a need for new and more varied data and descriptor sets as foundations to build broadly applicable models for synthetic planning.

Recently, Jorner, Brinck, Norrby, and Buttar reported the use of a hybrid DFT/machine learning (ML) approach to predicting experimental activation energies (Fig. 1C).²¹ This important study collates more than 440 S_NAr reaction rates from the existing literature, and uses 34 ground state and transition state descriptors as the training/test set. Notably, DFT-calculated transition state energies are a crucial descriptor in the best-performing model. This hybrid approach is demonstrably powerful, able to generate a broadly applicable and accurate model; however, the existing experimental rate data contains key gaps, such as an overemphasis on nitroarenes, and relatively few heterocyclic electrophiles. The hybrid DFT/ML approach also requires transition state calculations for maximum accuracy, especially if relatively few data points are available.

In this work, we consider the following three aspects of a predictive model to have equal importance: (1) the prediction accuracy the model provides, especially for new (external) predictions; (2) the breadth of applicability the model affords across chemical space; and (3) the ease and simplicity of applying the model to new systems. In the previously described examples, reaction rate/selectivity data used to train and validate the QSRR/QSSR models are taken from literature values, skewing the chemical space coverage toward well-studied systems. To complement the existing S_NAr rate data from the literature, we measured relative reaction rates for 74 individual electrophiles – including many nitrogen heterocycles relevant to pharmaceutical synthesis – using a competition experiment approach, which is commonly used to generate univariate Hammett plots.^76–81 Having control over the composition of our training set gives us the flexibility to have a varied and balanced distribution of structural features, which is necessary to ensure both accuracy and applicability in making new predictions. To make the model easy to implement, and to reduce the computational cost required, we combined simple and easy-to-obtain ground state molecular descriptors with our own experimentally determined S_NAr rates. From this combination of factors, we have constructed a QSRR model for S_NAr reactions with excellent performance in predicting reactivity trends and site selectivity for many different electrophiles, including for multiple external test sets with significantly different molecular structures (Fig. 1D).

Results and discussion

Creating the training/test set

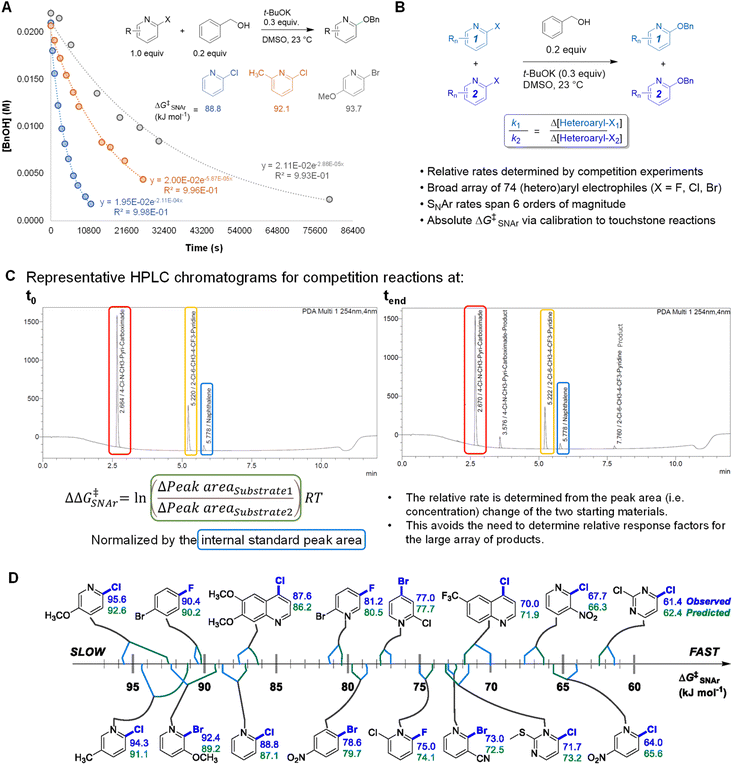
An efficient approach to collect a large and diverse data set of reaction rates is critical to our bottom-up approach. To determine a large number of reaction rates in a timely manner, we followed a workflow of high-throughput competition experimentation shown in Fig. 2. This experimental approach can be summarized in three steps: first, we monitored the reaction progress of three touchstone reactions under pseudo first order conditions. We determined absolute rate constants and free energies of activation (ΔG^‡_SNAr) for S_NAr between benzyl alkoxide and 2-chloropyridine, 2-chloro-6-methylpyridine, or 2-chloro-5-methoxypyridine as the electrophile (Fig. 2A). Next, we determined relative rate constants for the electrophile substrate library by a series of 94 individual competition experiments under analogous conditions (Fig. 2B and Table S2†). Competition reactions were conducted under pseudo first-order conditions by having two electrophiles in excess but equal amount to compete with one nucleophile. The reaction solutions were quantitatively analyzed using UPLC. For each competition experiment, chromatograms were recorded for the reaction solutions at two time points: the start of the reaction (t₀) and completion of the reaction (t_end). The ratio between the two S_NAr rates is obtained from the relative concentrations of the two remaining substrates at t_end. This method of quantification avoids the need to obtain relative response factors between all 74 new S_NAr products and the internal standards. All experimental details of competition experiment set-up, LC method parameters, and experimentally determined relative rates for the entire array of 74 electrophiles are detailed in the ESI.

Fig. 2 Experimental approach to collecting free energies of activation for 74 S_NAr reactions; Bn = benzyl. (A) Touchstone reaction progress analysis under pseudo first order conditions. (B) Competition experiments to establish relative rates across electrophile library. (C) Representative primary data for determining ΔΔG^‡_SNAr from competition experiments. (D) Quantitative reactivity scale for representative electrophiles.

Finally, we calibrated these relative rate constants using the touchstone reactions, giving absolute rate constants and the corresponding ΔG^‡_SNAr values for the entire array of S_NAr reactions (Table S3†). We used the absolute ΔG^‡_SNAr value for the 2-chloropyridine touchstone reaction (88.8 kJ mol⁻¹) as the calibration point, with the other two touchstone reactions (2-chloro-6-methylpyridine, and 2-chloro-5-methoxypyridine) used to confirm the validity of the competition determined ΔG^‡_SNAr values. We obtain a percent difference between the competition values and touchstone values of <2% (Fig. S3†). In addition, we determined independent ΔG^‡_SNAr values for 17 substrates using multiple competition experiments, giving an estimate of the error for the relative ΔG^‡_SNAr values; the difference between the average ΔG^‡_SNAr value and the individual measurements is between 0.2 – 1.7 kJ mol⁻¹ (Table S5†).

Using this competition approach, we were able to rapidly build a reliable and self-consistent data set from a library of 74 (hetero)aryl halides. This includes 6-membered aromatic electrophiles with many different substitution patterns – electron donating/withdrawing groups in all possible positions, multiple substituents, and several heterocycle classes – and thus a variety of electronic effects. The reactivity of these substrates crosses a broad range, with the reaction rates spanning 6 orders of magnitude; a quantitative reactivity scale for several representative electrophiles is shown in Fig. 2D. As an initial check on the validity of our data set, we assessed the general reactivity trends against the known features of S_NAr reactivity. As expected, electron-deficient arenes react much faster than electron-rich ones; furthermore, the reactivity of the halides leaving groups follows the established trend, with rates decreasing as Ar–F >> Ar–Cl ∼ Ar–Br.⁸² We also constructed Hammett plots for four sets of 2-X-pyridine substrates (X = Cl, Br), giving linear correlations with rho values of ∼4–5 (Fig. S4–S7†). Finally, we have prepared and isolated 5 representative S_NAr products (compounds S1-S5), and confirmed their structures using NMR spectroscopy and high-resolution mass spectrometry (Fig. S8–S17†).

Model generation and performance

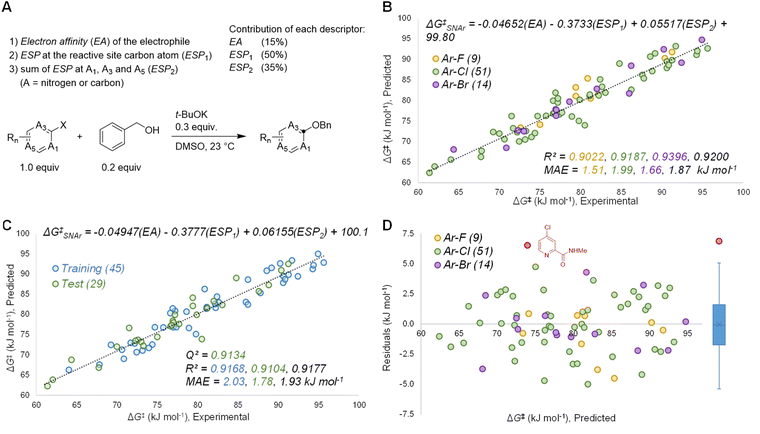
Based on the known aspects of S_NAr reaction mechanisms, and our prior work⁸³ in applying ground state molecular descriptors⁸⁴ to reactivity predictions, we built a quantitative structure-reactivity model for S_NAr electrophiles using only three descriptors. These include a global descriptor in the electron affinity (EA) of the electrophile, and two local descriptors based on average molecular electrostatic potentials (ESP).^85–88 In addition to the ESP at the carbon undergoing substitution (ESP₁), we also discovered that the sum of ESP values for the ortho and para ring atoms is required for accurate predictions (ESP₂) (Fig. 3A).

Fig. 3 Quantitative model generation and performance. (A) Molecular descriptors used in multivariate regression analysis, with percent contribution determined by min/max normalization. (B) All data linear regression analysis for experimental versus predicted ΔG^‡_SNAr with accompanying statistics (MAE = mean absolute error); linear correlation uses non-normalized descriptors. (C) One of five 60/40 training/test validations, with accompanying statistics. (D) Predicted versus residuals plot for the 74 data points, with accompanying box plot (right); one outlier is identified (|R| > 5 kJ mol⁻¹, red point with accompanying structure).

By building a multivariate linear correlation between these three ground state descriptors and our experimentally obtained ΔG^‡_SNAr values, we have established a unified structure-reactivity model able to accurately predict S_NAr rates for electrophiles with various structural features and leaving groups under our reaction conditions. There is an excellent linear correlation between the predicted and actual ΔG^‡_SNAr values (R² = 0.92) and a mean absolute error (MAE) of only 1.8 kJ mol⁻¹ (0.43 kcal mol⁻¹) (Fig. 3B). Performing a min/max normalization of the descriptors reveals their percentage contribution to the model, with ESP₁ being most important (50%), followed by ESP₂ (35%), and finally only a modest contribution from the EA (15%). We note that including steric-based descriptors was not necessary to obtain good correlations for our data set; adding substituent A-values as an additional factor in our multivariate regression led to no change in the model, and a very small coefficient for the A-value term (Table S7†). Further work to explore steric effects in a wider range of S_NAr reactions is ongoing.

We have assessed the robustness of the model using cross-validation with five different random 60/40 training/test set data splits (Fig. 3C and S20–24†) and one structured split (Fig. S25†). All of these regression analyses give essentially identical results, with excellent correlation statistics as indicated by the range of Q² values⁸⁹ from 0.86 to 0.93, and MAE values from 1.6 to 2.3 kJ mol⁻¹ for the test sets. We also evaluated the 95% prediction intervals for the 29 members of the test set in Fig. 3C, giving a range of ±5.1 kJ mol⁻¹ to ±5.5 kJ mol⁻¹ (Fig. S20†). Finally, we also assessed the model performance by analysing the distribution of residuals across the data set, and identifying any possible outliers. As shown in Fig. 3D, the residuals are randomly distributed, almost exclusively in the range −5 to +5 kJ mol⁻¹ (i.e. within an order of magnitude of the experimental rate). A box plot reveals only one significant outlier (|residual| > 5 kJ mol⁻¹): 2-(N-methylcarboxamide)-4-chloropyridine.

The selection of these specific molecular descriptors was guided by the mechanistic features of nucleophilic aromatic substitution, as well as our previous work on a multivariate model for oxidative addition with (hetero)aryl halides.⁸³ We also carried out an iterative refinement of the included descriptors based on our experimental observations and model performance (Table S5†). The following discussion provides more detail on creation and refinement of the model and its mechanistic basis.

A classic approach to describing nucleophile/electrophile reactivity involves frontier molecular orbital (FMO) theory.^90,91 At a basic level, a lower LUMO energy for the electrophile leads to smaller HOMO–LUMO gap between nucleophile and electrophile. This results in a lower energy transition state, and therefore a faster reaction. On the other hand, this simple connection between electrophilicity and LUMO energy is not necessarily valid for every system: in one recent example, Zipse, Ofial, and Mayr have demonstrated poor correlation between LUMO energy and electrophilicity for a series of Michael acceptors.⁹² This is attributed to substituent effects that increase π-conjugation (lowering LUMO energy), but decrease electrophilicity. Nevertheless, we considered including LUMO energies as a potential molecular descriptor for S_NAr reactivity.

As a substitute for LUMO energies, we initially used calculated electron affinity (EA) values for each electrophile, since EA is a physical observable that can be experimentally measured. Conceptually, EA and LUMO energy are related according to the Koopmans's theorem approximation (that the LUMO energy is the negative of the EA),^93,94 enabling an intuitive analogy to be made to FMO treatments. To confirm this analogy for the substrate set under study, we compared our calculated EA values to LUMO energies obtained via DFT (B3LYP/def2-TVZPD, Fig. S26†), revealing a strong linear correlation (R² = 0.94). We also investigated an operationally simpler approach to calculating LUMO energies using Entos Envision,⁹⁵ an open online interactive platform for molecular simulation and visualization that performs rapid semi-empirical calculations using GFN1-xTB.⁹⁶ Comparing these semi-empirical LUMO energies to our EA calculations also reveals a strong linear correlation (R² = 0.88, Fig. S28†). In addition, using either set of LUMO energies in lieu of EA values gives nearly identical linear regression models to that in Fig. 3B (Figs. S27 and S29†). While we retained the EA values for our subsequent validation and external predictions, LUMO energies from DFT or semi-empirical calculations could certainly be a rapid and easy to calculate alternative for synthesis-focused research groups.

To account for substituent effects beyond those on FMO energies, we used average molecular ESP at individual aromatic ring atoms as a local descriptor.^85–88 The extent of electron deficiency at the reactive carbon is a key factor in determining S_NAr rates, and the corresponding ESP is a quantitative descriptor of this molecular feature. Previously, we observed excellent correlation between ESP-based descriptors and rates of Ar–X oxidative addition to Pd(0),⁸³ which shares mechanistic aspects with S_NAr reactivity.⁹⁷ All ESP calculations were performed using the freely available Multiwfn application (version 3.7).^98,99

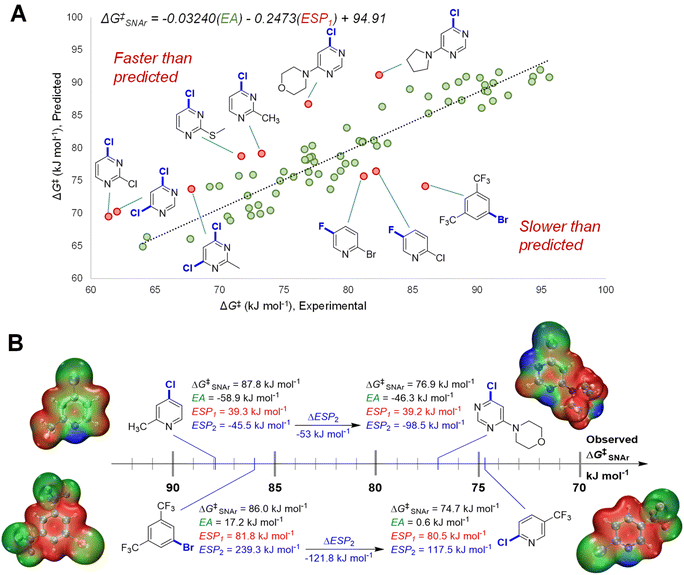
We initially constructed a bivariate linear model using just two descriptors: EA and ESP₁ (at the carbon undergoing substitution) (Fig. 4A). This model gives good predictions for halogenated pyridines and quinolines; however, it significantly underestimates the reactivity of halogenated pyrimidines, and overestimates the reactivity of several non-heterocyclic haloarenes. The nature of these outliers led us to consider the electronic structure of the Meisenheimer intermediate and S_NAr transition state more generally. During substitution, the excess negative charge in the intermediate/TS^‡ is distributed via resonance to the ortho and para positions relative to the reactive site; the degree to which these atoms can stabilize this negative charge should therefore affect the reaction rate. Thus, we included the ESP₂ descriptor to account for these additional electronic effects, giving the superior model shown previously in Fig. 3B (vide supra).

Fig. 4 Importance of ESP₂ descriptor in predicting ΔG^‡_SNAr for multiple substrate classes. (A) Bivariate model incorporating only EA and ESP₁ descriptors, with two sets of outliers highlighted. (B) Comparison of substrate pairs with very similar EA and ESP₁ values but significantly different ΔG^‡_SNAr values, revealing the importance of ESP₂ in differentiating reactivity. ESP maps for each substrate structure are shown, with colour gradient indicating local ESP (red = maximum positive; green = 0; blue = maximum negative).

To highlight the importance of ESP₂ in making accurate predictions for multiple electrophile classes, we examined the two largest outliers from the bivariate model on either side of the distribution. We paired these two outliers with halopyridines that have very similar ESP₁ values, but significantly different observed ΔG^‡_SNAr (Fig. 4B). In the first case, the faster than predicted outlier 4-chloro-6-morpholinopyridine has very similar EA and nearly identical ESP₁ values to 4-chloro-2-methylpyridine; however, these two electrophiles have a ΔΔG^‡_SNAr = 10.9 kJ mol⁻¹ (∼100 fold rate difference at 298 K). These substrates have strikingly different ESP₂ characteristics, with the pyrimidine exhibiting a substantially larger negative value due to the additional nitrogen in the ring. The same situation is observed for the slower than predicted outlier 1-bromo-3,5-bis(trifluoromethyl)benzene and 2-chloro-5-(trifluoromethyl)-pyridine (ΔΔG^‡_SNAr = 11.3 kJ mol⁻¹): both substrates have nearly identical EA and ESP₁ descriptor values, but a more than 120 kJ mol⁻¹ difference in ESP₂.

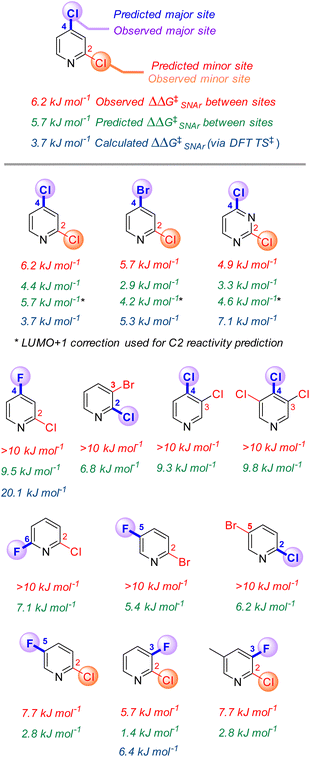
Site selectivity in multihalogenated heterocycles

One of the most powerful applications of quantitative models in synthesis is to predict selectivity for one product over another. Many prior efforts in S_NAr reactivity prediction focused on exactly this problem, developing qualitative and quantitative models for site selectivity involving multihalogenated electrophiles.^{21,63–71,74,75,100} Within our 74-member substrate training library are several electrophiles with multiple reactive positions. The reactivity of these substrates provides an opportunity to test the model's applicability for quantitative selectivity predictions, despite not being explicitly trained for this purpose. Importantly, the major contributors to the model (ESP₁ and ESP₂) are local descriptors, which is key to enabling differential predictions for each reactive site.¹⁰¹

For the 13 multihalogenated substrates in our library, we determined the experimental site selectivity and compared the resulting ΔΔG^‡_SNAr to that predicted by our descriptor-based model. We also calculated ΔΔG^‡_SNAr values for 5 of the substrates from DFT analysis of the corresponding transition states (Fig. 5). In every case, using the three-descriptor model from Fig. 3B to independently predict ΔG^‡_SNAr for each site correctly identifies the most reactive position, with reasonable quantitative accuracy that is comparable to that obtained via transition state analysis; however, the model-predicted ΔΔG^‡_SNAr between sites does appear to be systematically low (i.e. selectivity is consistently underestimated).

Fig. 5 Site selectivity in multihalogenated heterocycles that are part of the training set. LUMO+1 energies are approximated by subtracting the LUMO/LUMO+1 energy gap from the EA value for the substrate.

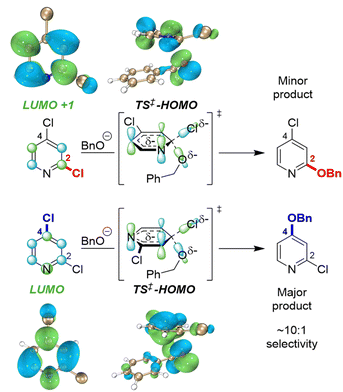
To identify possible reasons for this systematic underestimation, we considered that our global EA descriptor may not be optimal in these cases, and chose the first three substrates from Fig. 5 for further investigation. To assess the FMOs involved in these specific regioselective S_NAr reactions, we examined the symmetries of the LUMO and LUMO + 1 orbitals of the substrates, and calculated the structures and energies of the S_NAr transition states (Fig. 6 and S30–S39†). In each case, we could not locate a Meisenheimer-type intermediate along the reaction coordinate, but did locate transition states consistent with concerted S_NAr reactions.^29,53,54,102 As shown for 2,4-dichloropyridine in Fig. 6, the relevant electrophile FMO for attack at C4 is the LUMO, whereas for attack at C2 it is the LUMO+1; this is evident from the LUMO/LUMO+1 symmetries of the substrate, and the HOMO symmetries of two transition states. Subtracting the calculated LUMO/LUMO+1 gap from the EA as a correction when applying the model from Fig. 3B for C4 versus C2 predictions of the first three substrates does give increased accuracy, with errors of 0.3–1.5 kJ mol⁻¹ for ΔΔG^‡_SNAr.

Fig. 6 FMO analysis of S_NAr selectivity with 2,4-dichloropyridine, revealing orbital symmetry effects in the substrate (LUMO versus LUMO+1) and transition states (HOMO contributions from ortho and para sites).

External case study #1: S_NAr rate correlations

With our three descriptor model performance validated against internal data, we sought to assess its performance and generality when applied to new predictions beyond the training set. To challenge the scope of applicability to S_NAr reactions with different solvents and/or nucleophile classes, we first examined several correlations between predicted ΔG^‡_SNAr values from the model and three sets of experimental ΔG^‡_SNAr values from the literature (Fig. 7).^56,103–105 In these experimental data sets, a variety of (hetero)aromatic halides (F, Cl, and Br as leaving groups) are reacted with either alkoxide (Fig. 7A) or amine (Fig. 7B and C) nucleophiles. While the absolute ΔG^‡_SNAr values from the prediction model are specific to the reaction conditions of the training set, we do obtain good to excellent correlation between the predicted ΔG^‡_SNAr and experimental ΔG^‡ values (R² = 0.72–0.99). This is remarkable considering only two of the 34 electrophiles from these data sets are included in our training data (compounds 3B and 4B in Fig. 7B), and these reactions are conducted with different nucleophiles, solvents, and temperatures. We do note the diminished performance for set 7B, which may be because our model is predominantly trained using substrates with Cl or Br leaving groups, whereas the 7B set contains several substrates with F leaving groups.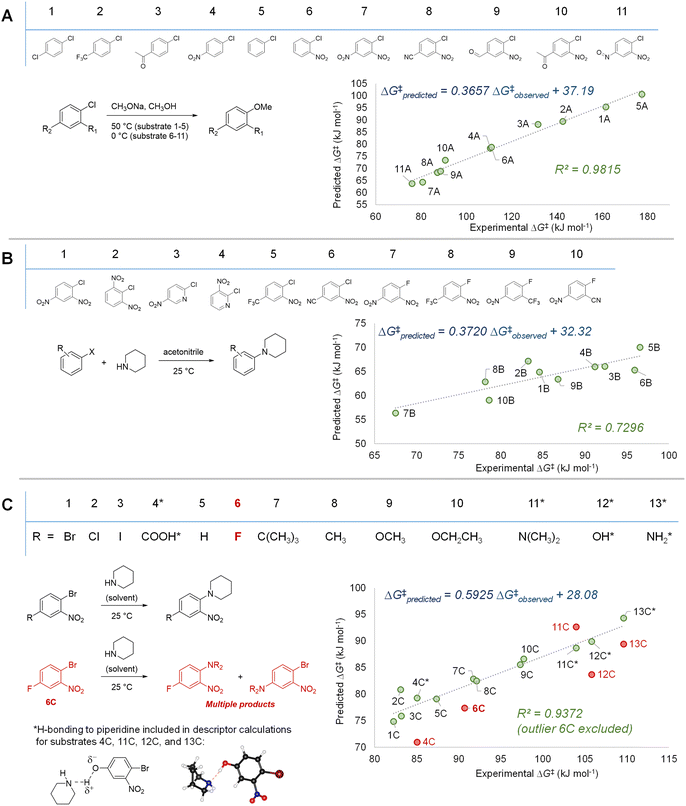

Fig. 7 Model validation through assessing correlations between experimental ΔG^‡ values and predicted ΔG^‡_SNAr for three external data sets. (A) S_NAr between chlorobenzene derivatives and methoxide; experimental data from ref. 56 and 103 (B) S_NAr between (hetero)aryl chlorides/fluorides and piperidine; experimental data from ref. 105 (C) S_NAr between substituted 1-bromo-2-nitrobenzenes and piperidine; experimental data from ref. 104.

Notably, we are able to account for solvation effects on electrophile reactivity during descriptor generation. In data set C (Fig. 7C), there are several substrates containing acidic or basic functional groups where the initial correlation between experimental and predicted reactivity is poor (Fig. 7C, substrates 4C, 11–13C, red points). Given that these functional groups will hydrogen-bond with the piperidine solvent, significantly altering the electronics of the substrate, we included one explicit solvent molecule and recalculated the ESP descriptors for these four electrophiles.⁷⁵ Using these revised ESP values, we obtain excellent linear correlation across the entire substrate set.

In addition to the success in applying the ESP/EA model beyond the training set, and in identifying solvation effects on reactivity, we can also identify potential experimental outliers. For example, the data set in Fig. 7C contains one significant outlier (6C). In this case, 6C has two potentially reactive positions (Ar–Br and Ar–F). We have experimentally confirmed that reacting 6C with piperidine leads to a mixture of the two S_NAr products, in a 1.5 : 1 ratio, slightly favouring Ar–Br substitution (Fig. S40†).

External case study #2: site selectivity predictions

To further examine the potential applicability of our ESP/EA model beyond the training set, we assessed 63 external examples of site selectivity in S_NAr reactions under a variety of conditions. We first applied predictions to three data sets previously used as a testing ground for site selectivity predictions using other approaches (Fig. 8–10).^69–71,75 These data sets also contain experimentally-determined rates, providing an additional opportunity to test the model's performance.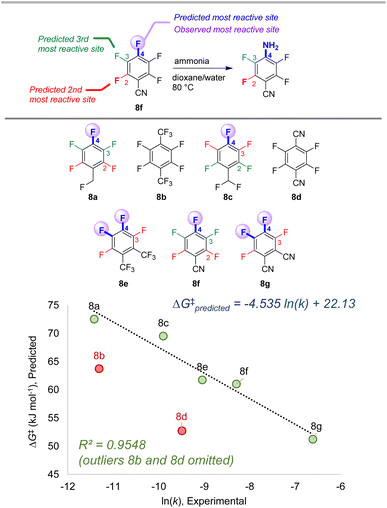

Fig. 8 Site selectivity predictions and rate correlation for S_NAr between fluorinated arenes and ammonia. Experimental data from ref. 99

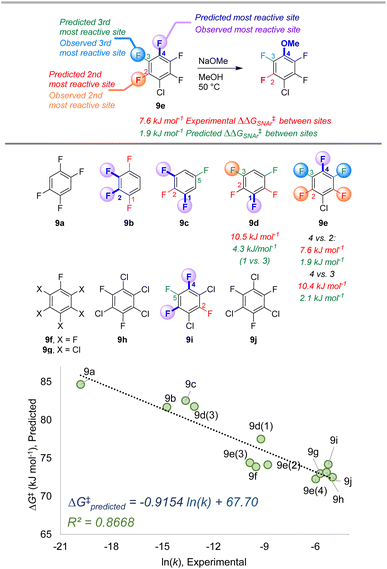Fig. 9 Site selectivity predictions and rate correlation for S_NAr between fluorinated arenes and methoxide. Experimental data from ref. 100

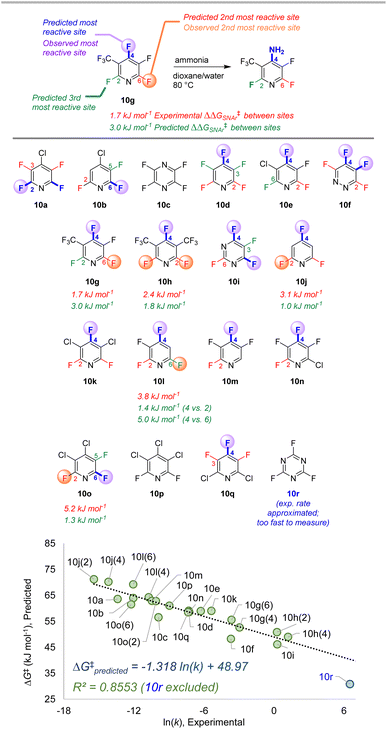Fig. 10 Site selectivity predictions and rate correlation for S_NAr between fluorinated heterocycles and ammonia. Experimental data from ref. 99, 101, and 102.

The first data set involves 7 multiply fluorinated arenes undergoing substitution with ammonia, where 5 substrates have potential for regioisomer formation (Fig. 8).¹⁰⁶ In each case, the predicted major site based on the ESP/EA model matches the experimental site. Furthermore, the predicted ΔG^‡_SNAr values correlate well with the experimental ln (k) values for these 5 substrates (R² = 0.95). Notably, ln (k) for substrates 8b and 8d do not correlate; this exact situation was noted by Stenlid and Brinck, who also observed these two substrates as significant outliers when correlating ln (k) with the local electron attachment energy.⁷⁵ While these authors attributed this discrepancy between prediction and experiment to steric effects, there may be a different underlying reason considering the small size of both the nucleophile (ammonia) and the cyano group in 8d.

The second data set also involves multiply fluorinated arenes, this time undergoing S_NAr with the methoxide anion as the nucleophile in methanol solvent (Fig. 9).¹⁰⁷ Across these 10 substrates, 5 have the potential to form regioisomers. In each of these cases, the ESP/EA model correctly predicts the major site of reaction. For substrate 9d, the predicted second most reactive site is incorrect (C2) based on experimental observation (C3); however, for 9e the predicted reactivity order from first to third site is correct. While we again observe an underestimation of selectivity based on predicted ΔG^‡_SNAr values, we do observe excellent linear correlation with experimental ln (k) across the entire substrate set. This is notable in the context of Stenlid and Brinck's prior work with local electron attachment energy, where the experimental ln (k) for 9g-j does not correlate with that descriptor. Here, the ESP/EA model correctly predicts that these four substrates should have similar S_NAr rates (within a factor of 10 of each other).

The third data set contains 18 multiply fluorinated nitrogen heterocycles undergoing S_NAr with ammonia, with 15 examples where regioisomers can be formed (Fig. 10).^106,108,109 In every case ESP/EA model correctly predicts the major site of reaction, and in all but one case (10l) it also predicts the second site of reaction. The quantitative selectivity predictions are also much closer to the experimental values within this data set. We again observe excellent linear correlation between experimental ln (k) and predicted ΔG^‡_SNAr. Note that substrate 10r, which has a rate “too fast … to measure”,¹⁰⁹ is estimated to have an ∼10⁵-fold larger rate constant than 10d; this estimated data point is not included in the linear correlation.

Finally, to challenge the qualitative accuracy of the model, we applied it toward a series of more complex S_NAr examples with a wider variety of nucleophiles (Fig. 11). Sets A–D were previously collated and categorized by Brinck, Svensson, and co-workers and categorized depending on the nature of the nucleophile/electrophile pairing.^70,109–127 Using only the structure of the electrophile, our ESP/EA model is able to correctly predict the major site of reaction in 26 of the 32 cases. Within sets A and C – (hetero)aryl halides reacting with anionic nucleophiles – the two incorrect predictions are for relatively non-polar fluorinated arenes. For sets B and D, which employ neutral nucleophiles, the incorrect examples all involve secondary amine nucleophiles. In these cases, steric effects appear to play a significant role in overriding the electronic nature of the electrophile; for example, pentachloropyridine reacts preferentially at C4 (as predicted) with alkoxide or ammonia nucleophiles, but switches to C2 selectivity with diethylamine. We also applied predictions to 6 mixed halide electrophiles reacting with a variety of nucleophiles in set E, drawn from examples in medicinal/agrochemical discovery.^128–133 The model is able to correctly identify the major site of reactivity for each example, except for a case where the predicted site is at an Ar–F, and the observed reactivity is at a 2-Cl-pyridine site.

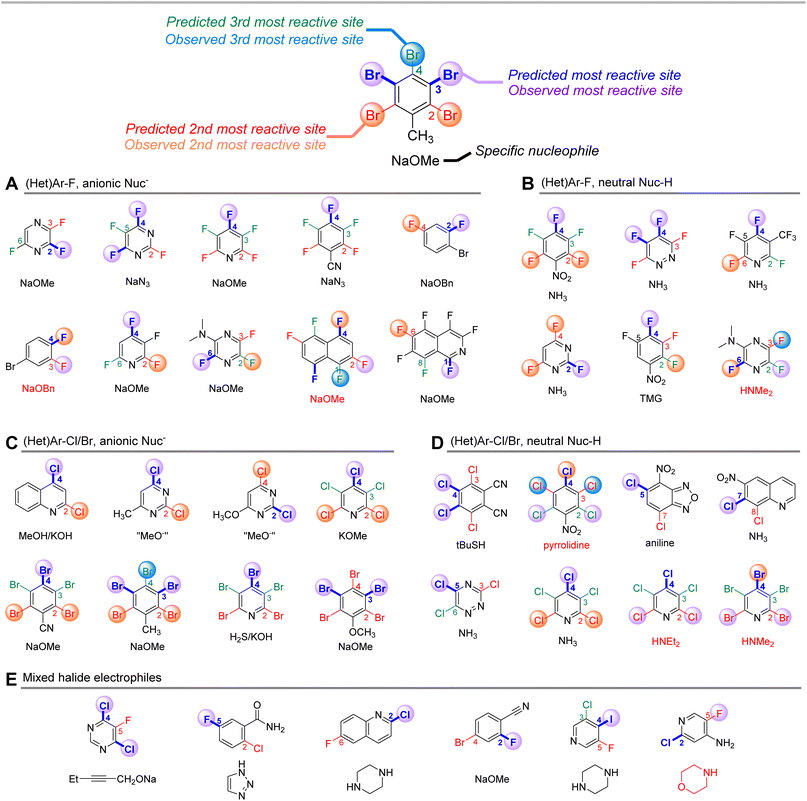Fig. 11 Qualitative site selectivity predictions for combinations of (hetero)aryl halides with anionic (A and C) and neutral (B and D) nucleophiles, and for mixed halide aromatics (E).

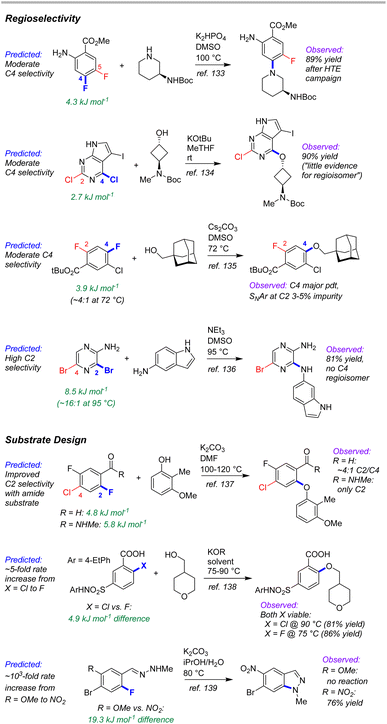
External case study #3: complex molecule synthetic planning

As a test of the ESP/EA model's potential utility in real-world synthetic planning, we sought to validate its predictions against S_NAr reactions used to prepare clinical candidate active pharmaceutical ingredients (APIs). These include recent reports on branebrutinib,¹³⁴ an EGFR T790 M inhibitor,¹³⁵ a Nav1.7 inhibitor,¹³⁶ a tyrosine kinase inhibitor,¹³⁷ an SRI/5-HT_2A antagonist,¹³⁸ an RoRγ inverse agonist,¹³⁹ and merestinib¹⁴⁰ (Fig. 12).

Fig. 12 Example applications of S_NAr predictions to route development for investigational API synthesis, including regioselectivity for specific substrates, and comparison of potential substrate regioselectivity/reactivity.

The first four examples concern site selective S_NAr to generate a variety of targets from structurally complex substrates. In each of these cases, the ESP/EA model is able to predict the correct reactive site. Thus, applying these predictions during synthetic design would help pharmaceutical process chemists to proceed with confidence that selective substitution is feasible. In fact, the chemists at Pfizer used an internal prediction tool (based on Fukui indices) to help guide their synthetic planning toward the EGFR T790 M inhibitor (2nd example in Fig. 12).¹³⁵

A particularly powerful aspect of in silico reactivity predictions is the ability to evaluate multiple options in substrate design before committing experimental resource. We have examined three examples where the substitution pattern of the S_NAr electrophile affects the site selectivity or reactivity. In the first case, synthesis of the target SRI/5-HT_2A antagonist requires a site selective S_NAr to install an aryl ether ortho to a carbonyl functionality.¹³⁸ This was initially performed using an aldehyde moiety; however, the relatively poor site selectivity meant column chromatography was required to purify the intermediate. Further process developments identified an N-methylamide as a more selective alternative that retained key functionality for progressing to the target API. This improved selectivity is predicted by the ESP/EA model. A second case involves choice of either an Ar–F or Ar–Cl electrophile for S_NAr with an alkoxide nucleophile.¹³⁹ Experimental evaluation of each revealed that both substrates are viable, with the Ar–Cl version requiring slightly higher reaction temperature than the Ar–F analogue. The ESP/EA model predicts that the F for Cl switch would result in a relatively modest reactivity decrease, indicating both should be suitable substrates.

The final example concerns an intramolecular S_NAr to generate an indazole en route to merestinib.¹⁴⁰ The final API contains a methoxy group para to the indazole nitrogen; however, attempts to perform the intramolecular S_NAr with this strong electron donating group para to the substitution site were not successful. Instead, the researchers installed a nitro group to enable the S_NAr to proceed, but which would require multiple functional group interconversions. The substantial difference in reactivity between –OMe and –NO₂ derivatives is conceptually obvious (and borne out by the ESP/EA model); however, the orders-of-magnitude difference in predicted rate between the two means that the more desirable –OMe substrate could be ruled out earlier on in synthetic development. Furthermore, additional hypothetical substrates that retain the required oxygen (such as a sulfonate) could be evaluated using the prediction model (the –OMs derivative has a predicted ΔG^‡_SNAr halfway between the –NO₂ and –OMe derivatives).

Conclusions

We have demonstrated an effective bottom-up approach to developing a quantitative structure-reactivity model for nucleophilic aromatic substitution reactions. By curating a diverse library of (hetero)aromatic electrophiles, and determining their corresponding relative S_NAr reaction rates through a series of competition experiments, we rapidly assembled a reliable and diverse data set as an experimental foundation. Pairing this set of reactivity data with simple ground state molecular descriptors – electron affinity and molecular electrostatic potentials – results in a robust multivariate linear correlation between relative rate and the molecular structure of the electrophile.

Importantly, even though the model was trained using only one set of reaction conditions with a single nucleophile, it is suitable for making correlations and predictions about S_NAr reactivity for a wide variety of nucleophiles, solvents, and temperatures. These include a >90% success rate in predicting the major reaction site for multihalogenated arenes (>80 cases), and examples where substrate design for active pharmaceutical ingredient synthesis can be informed by predicted reactivity. Thus, this simple and easy-to-apply model can generate rapid and accurate predictions for complex molecule targets. There are still specific limitations to be addressed, including the inability of the model to properly predict selectivity outcomes for non-halogenated leaving groups (e.g. –NO₂ or –OMe) and for bulky nucleophiles (as shown in Fig. 11). Further work to build additional targeted models for these effects in S_NAr chemistry, as well as for additional commonly-used organic reaction classes is currently underway in our laboratories.

Data availability

Additional data files are available as part of the ESI,† including machine readable tables of descriptors (xlsx format) and coordinate files for calculated structures (xyz format).

Author contributions

J. Lu: conceptualization, methodology, investigation, validation, formal analysis, writing. I. Paci: conceptualization, methodology, formal analysis, supervision, writing. D. C. Leitch: conceptualization, methodology, formal analysis, supervision, writing.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We acknowledge and respect the Lekwungen peoples on whose traditional territory the University of Victoria (UVic) stands, and the Songhees, Esquimalt and WSÁNEĆ peoples whose historical relationships with the land continue to this day. We also acknowledge funding from the New Frontiers in Research Fund – Exploration (DCL) and NSERC Discovery Grant program (IP and DCL). Supercomputing resources at Westgrid and Compute Canada were integral to this work.

Notes and references

1. R. C. Larock, Comprehensive Organic Transformations: A Guide to Functional Group Preparations; Wiley, 2018.
2. E. J. Corey and X.-M. Cheng, The Logic of Chemical Synthesis, John Wiley & Sons, Nashville, TN, 1995.
3. The Art of Writing Reasonable Organic Reaction Mechanisms, ed., R. B. Grossman, Springer: New York, NY, 2003.
4. H. Mayr and M. Patz, Angew. Chem., Int. Ed. Engl., 1994, 33, 938–957.
5. H. Mayr, B. Kempf and A. R. Ofial, Acc. Chem. Res., 2003, 36, 66–77.
6. H. Mayr and A. R. Ofial, Pure Appl. Chem., 2005, 77, 1807–1821.
7. H. Mayr and A. R. Ofial, J. Phys. Org. Chem., 2008, 21, 584–595.
8. H. Mayr and A. R. Ofial, Acc. Chem. Res., 2016, 49, 952–965.
9. H. Mayr and A. R. Ofial, Pure Appl. Chem., 2017, 89, 729–744.
10. M. S. Sigman, K. C. Harper, E. N. Bess and A. Milo, Acc. Chem. Res., 2016, 49, 1292–1301.
11. Z. L. Niemeyer, A. Milo, D. P. Hickey and M. S. Sigman, Nat. Chem., 2016, 8, 610–617.
12. K. Wu and A. G. Doyle, Nat. Chem., 2017, 9, 779–784.
13. D. T. Ahneman, J. G. Estrada, S. Lin, S. D. Dreher and A. G. Doyle, Science, 2018, 360, 186–190.
14. B. Maryasin, P. Marquetand and N. Maulide, Angew. Chem., Int. Ed., 2018, 57, 6978–6980.
15. O. Engkvist, P.-O. Norrby, N. Selmi, Y. Lam, Z. Peng, E. C. Sherer, W. Amberg, T. Erhard and L. A. Smyth, Drug Discov. Today, 2018, 23, 1203–1218.
16. A. F. Zahrt, J. J. Henle, B. T. Rose, Y. Wang, W. T. Darrow and S. E. Denmark, Science, 2019, 363, eaau5631.
17. T. Toyao, Z. Maeno, S. Takakusagi, T. Kamachi, I. Takigawa and K. Shimizu, ACS Catal., 2020, 10, 2260–2297.
18. E. N. Muratov, J. Bajorath, R. P. Sheridan, I. V. Tetko, D. Filimonov, V. Poroikov, T. I. Oprea, I. I. Baskin, A. Varnek, A. Roitberg, O. Isayev, S. Curtalolo, D. Fourches, Y. Cohen, A. Aspuru-Guzik, D. A. Winkler, D. Agrafiotis, A. Cherkasov and A. Tropsha, Chem. Soc. Rev., 2020, 49, 3525–3564.
19. B. Mahjour, Y. Shen and T. Cernak, Acc. Chem. Res., 2021, 54, 2337–2346.
20. L. C. Gallegos, G. Luchini, P. C. St. John, S. Kim and R. S. Paton, Acc. Chem. Res., 2021, 54, 827–836.
21. K. Jorner, T. Brinck, P.-O. Norrby and D. Buttar, Chem. Sci., 2021, 12, 1163–1175.
22. M. Orlandi, M. Escudero-Casao and G. Licini, J. Org. Chem., 2021, 86, 3555–3564.
23. Y. Shen, J. E. Borowski, M. A. Hardy, R. Sarpong, A. G. Doyle and T. Cernak, Nat. Rev. Methods Primers, 2021, 1, 23.
24. I. O. Betinol and J. P. Reid, Org. Biomol. Chem., 2022, 20, 6012–6018.
25. W. Beker, R. Roszak, A. Wołos, N. H. Angello, V. Rathore, M. D. Burke and B. A. Grzybowski, J. Am. Chem. Soc., 2022, 144, 4819–4827.
26. J. Meisenheimer, Justus Liebigs Ann. Chem., 1902, 323, 205–246.
27. J. F. Bunnett and R. E. Zahler, Chem. Rev., 1951, 49, 273–412.
28. The S_NAr Reactions: Mechanistic Aspects. in Modern Nucleophilic Aromatic Substitution; Wiley-VCH Verlag: Weinheim, Germany, 2013; pp pp 1–94.
29. S. Rohrbach, A. J. Smith, J. H. Pang, D. L. Poole, T. Tuttle, S. Chiba and J. A. Murphy, Angew. Chem., Int. Ed., 2019, 58, 16368–16388.
30. D. A. Evans, M. R. Wood, B. W. Trotter, T. I. Richardson, J. C. Barrow and J. L. Katz, Angew. Chem., Int. Ed., 1998, 37, 2700–2704.
31. D. A. Evans, C. J. Dinsmore, P. S. Watson, M. R. Wood, T. I. Richardson, B. W. Trotter and J. L. Katz, Angew. Chem., Int. Ed., 1998, 37, 2704–2708.
32. K. C. Nicolaou, S. Natarajan, H. Li, N. F. Jain, R. Hughes, M. E. Solomon, J. M. Ramanjulu, C. N. C. Boddy and M. Takayanagi, Angew. Chem., Int. Ed., 1998, 37, 2708–2714.
33. K. C. Nicolaou, N. F. Jain, S. Natarajan, R. Hughes, M. E. Solomon, H. Li, J. M. Ramanjulu, M. Takayanagi, A. E. Koumbis and T. Bando, Angew. Chem., Int. Ed., 1998, 37, 2714–2716.
34. K. C. Nicolaou, M. Takayanagi, N. F. Jain, S. Natarajan, A. E. Koumbis, T. Bando and J. M. Ramanjulu, Angew. Chem., Int. Ed., 1998, 37, 2717–2719.
35. A. J. Zhang and K. Burgess, Angew. Chem., Int. Ed., 1999, 38, 634–636.
36. L.-J. Cheng, J.-H. Xie, Y. Chen, L.-X. Wang and Q.-L. Zhou, Org. Lett., 2013, 15, 764–767.
37. K. Yamashita, Y. Kume, S. Ashibe, C. A. D. Puspita, K. Tanigawa, N. Michihata, S. Wakamori, K. Ikeuchi and H. Yamada, Chem.– Eur. J., 2020, 26, 16408–16421.
38. J. T. Bork, J. W. Lee and Y.-T. Chang, QSAR Comb. Sci., 2004, 23, 245–260.
39. D. G. Brown and J. Boström, J. Med. Chem., 2016, 59, 4443–4458.
40. S. Preshlock, M. Tredwell and V. Gouverneur, Chem. Rev., 2016, 116, 719–766.
41. C. N. Neumann and T. Ritter, Acc. Chem. Res., 2017, 50, 2822–2833.
42. J. Boström, D. G. Brown, R. J. Young and G. M. Keserü, Nat. Rev. Drug Discovery, 2018, 17, 709–727.
43. Y. Y. See, M. T. Morales-Colón, D. C. Bland and M. S. Sanford, Acc. Chem. Res., 2020, 53, 2372–2383.
44. M. Baumann and I. R. Baxendale, Beilstein J. Org. Chem., 2013, 9, 2265–2319.
45. A. C. Flick, C. A. Leverett, H. X. Ding, E. McInturff, S. J. Fink, C. J. Helal, J. C. DeForest, P. D. Morse, S. Mahapatra and C. J. O'Donnell, J. Med. Chem., 2020, 63, 10652–10704.
46. A. C. Flick, C. A. Leverett, H. X. Ding, E. McInturff, S. J. Fink, S. Mahapatra, D. W. Carney, E. A. Lindsey, J. C. DeForest, S. P. France, S. Berritt, S. V. Bigi-Botterill, T. S. Gibson, Y. Liu and C. J. O'Donnell, J. Med. Chem., 2021, 64, 3604–3657.
47. S. Jeanmart, A. J. F. Edmunds, C. Lamberth and M. Pouliot, Bioorg. Med. Chem., 2016, 24, 317–341.
48. S. Jeanmart, A. J. F. Edmunds, C. Lamberth, M. Pouliot and J. A. Morris, Bioorg. Med. Chem., 2021, 39, 116162.
49. E. Vitaku, D. T. Smith and J. T. Njardarson, J. Med. Chem., 2014, 57, 10257–10274.
50. M. D. Delost, D. T. Smith, B. J. Anderson and J. T. Njardarson, J. Med. Chem., 2018, 61, 10996–11020.
51. P. Das, M. D. Delost, M. H. Qureshi, D. T. Smith and J. T. Njardarson, J. Med. Chem., 2019, 62, 4265–4311.
52. F. Terrier, Chem. Rev., 1982, 82, 77–152.
53. C. N. Neumann, J. M. Hooker and T. Ritter, Nature, 2016, 534, 369–373.
54. E. E. Kwan, Y. Zeng, H. A. Besser and E. N. Jacobsen, Nat. Chem., 2018, 10, 917–923.
55. C. Hansch, A. Leo and R. W. Taft, Chem. Rev., 1991, 91, 165–195.
56. J. Miller and W. Kai-Yan, J. Chem. Soc., 1963, 3492–3495.
57. S. E. Fry and N. J. Pienta, J. Am. Chem. Soc., 1985, 107, 6399–6400.
58. A. H. M. Renfrew, J. A. Taylor, J. M. J. Whitmore and A. Williams, J. Chem. Soc., Perkin trans. 2, 1993, 1703–1704.
59. A. Hunter, M. Renfrew, D. Rettura, J. A. Taylor, J. M. J. Whitmore and A. Williams, J. Am. Chem. Soc., 1995, 117, 5484–5491.
60. I.-H. Um, L.-R. Im, J.-S. Kang, S. S. Bursey and J. M. Dust, J. Org. Chem., 2012, 77, 9738–9746.
61. N. ElGuesmi, G. Berionni and B. H. Asghar, J. Fluorine Chem., 2014, 160, 41–47.
62. F. Mahdhaoui, R. Zaier, N. Dhahri, S. Ayachi and T. Boubaker, Int. J. Chem. Kinet., 2019, 51, 249–257.
63. J. Burdon, Tetrahedron, 1965, 21, 3373–3380.
64. J. Burdon and I. W. Parsons, J. Am. Chem. Soc., 1977, 99, 7445–7447.
65. N. D. Epiotis and W. Cherry, J. Am. Chem. Soc., 1976, 98, 5432–5435.
66. S. Scales, S. Johnson, Q. Hu, Q.-Q. Do, P. Richardson, F. Wang, J. Braganza, S. Ren, Y. Wan, B. Zheng, D. Faizi and I. McAlpine, Org. Lett., 2013, 15, 2156–2159.
67. M. Muir and J. Baker, J. Fluorine Chem., 2005, 126, 727–738.
68. J. Baker and M. Muir, Can. J. Chem., 2010, 88, 588–597.
69. M. Liljenberg, T. Brinck, B. Herschend, T. Rein, G. Rockwell and M. Svensson, Tetrahedron Lett., 2011, 52, 3150–3153.
70. M. Liljenberg, T. Brinck, B. Herschend, T. Rein, S. Tomasi and M. Svensson, J. Org. Chem., 2012, 77, 3262–3269.
71. M. Liljenberg, T. Brinck, T. Rein and M. Svensson, Beilstein J. Org. Chem., 2013, 9, 791–799.
72. J. A. Hirsch, Table of Conformational Energies—1967. in Topics in Stereochemistry, John Wiley & Sons: Nashville, TN, 1967, Vol. 1, pp 199–222.
73. H. Clavier and S. P. Nolan, Chem. Commun., 2010, 46, 841–861.
74. T. Brinck, P. Carlqvist and J. H. Stenlid, J. Phys. Chem. A, 2016, 120, 10023–10032.
75. J. H. Stenlid and T. Brinck, J. Org. Chem., 2017, 82, 3072–3083.
76. R. J. Mullins, A. Vedernikov and R. Viswanathan, J. Chem. Educ., 2004, 81, 1357.
77. K. W. Fiori and J. Du Bois, J. Am. Chem. Soc., 2007, 129, 562–568.
78. J. B. C. Mack, T. A. Bedell, R. J. DeLuca, G. A. B. Hone, J. L. Roizen, C. T. Cox, E. J. Sorensen and J. Du Bois, J. Chem. Educ., 2018, 95, 2243–2248.
79. H. M. Yau, A. K. Croft and J. B. Harper, Chem. Commun., 2012, 48, 8937–8939.
80. H. M. Yau, R. S. Haines and J. B. Harper, J. Chem. Educ., 2015, 92, 538–542.
81. N. W. Fenwick, R. Telford, A. Saidykhan, W. H. C. Martin and R. D. Bowen, Molecules, 2021, 26, 5077.
82. G. Bartoli and P. E. Todesco, Acc. Chem. Res., 1977, 10, 125–132.
83. J. Lu, S. Donnecke, I. Paci and D. C. Leitch, Chem. Sci., 2022, 13, 3477–3488.
84. P. Geerlings, F. De Proft and W. Langenaeker, Chem. Rev., 2003, 103, 1793–1874.
85. C. H. Suresh, P. Alexander, K. P. Vijayalakshmi, P. K. Sajith and S. R. Gadre, Phys. Chem. Chem. Phys., 2008, 10, 6492–6499.
86. F. B. Sayyed and C. H. Suresh, New J. Chem., 2009, 33, 2465–2471.
87. G. S. Remya and C. H. Suresh, Phys. Chem. Chem. Phys., 2016, 18, 20615–20626.
88. S. R. Gadre, C. H. Suresh and N. Mohan, Molecules, 2021, 26, 3289.
89. V. Consonni, D. Ballabio and R. Todeschini, J. Chem. Inf. Model., 2009, 49, 1669–1678.
90. K. Fukui, T. Yonezawa, C. Nagata and H. Shingu, J. Chem. Phys., 1954, 22, 1433–1442.
91. K. N. Houk, Acc. Chem. Res., 1975, 8, 361–369.
92. D. S. Allgäuer, H. Jangra, H. Asahara, Z. Li, Q. Chen, H. Zipse, A. R. Ofial and H. Mayr, J. Am. Chem. Soc., 2017, 139, 13318–13329.
93. T. Koopmans, Physica, 1934, 1, 104–113.
94. J. P. Perdew, R. G. Parr, M. Levy and J. L. Balduz, Phys. Rev. Lett., 1982, 49, 1691–1694.
95. Entos Envision, https://www.entos.ai/envision (accessed 2022-07-07).
96. S. Grimme, C. Bannwarth and P. Shushkov, J. Chem. Theory Comput., 2017, 13, 1989–2009.
97. B. U. W. Maes, S. Verbeeck, T. Verhelst, A. Ekomié, N. von Wolff, G. Lefèvre, E. A. Mitchell and A. Jutand, Chem.– Eur. J., 2015, 21, 7858–7865.
98. T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592.
99. T. Lu and F. Chen, J. Mol. Graph. Model., 2012, 38, 314–323.
100. B. Wang, C. Rong, P. K. Chattaraj and S. Liu, Theor. Chem. Acc., 2019, 138, 124.
101. R. K. Roy and S. Saha, Annu. Rep. Sect. C Phys. Chem., 2010, 106, 118–162.
102. S. Rohrbach, J. A. Murphy and T. Tuttle, J. Am. Chem. Soc., 2020, 142, 14871–14876.
103. J. Miller and A. J. Parker, Aust. J. Chem., 1958, 11, 302–308.
104. E. Berliner and L. C. Monack, J. Am. Chem. Soc., 1952, 74, 1574–1579.
105. M. R. Crampton, T. A. Emokpae and C. Isanbor, Eur. J. Org. Chem., 2007, 2007, 1378–1383.
106. R. D. Chambers, P. A. Martin, G. Sandford and D. L. H. Williams, J. Fluorine Chem., 2008, 129, 998–1002.
107. R. Bolton and J. P. B. Sandall, J. Chem. Soc., Perkin trans. 2, 1976, 1541–1545.
108. R. D. Chambers, D. Close, W. K. R. Musgrave, J. S. Waterhouse and D. L. H. Williams, J. Chem. Soc., Perkin trans. 2, 1977, 1774–1778.
109. R. D. Chambers, P. A. Martin, J. S. Waterhouse, D. L. H. Williams and B. Anderson, J. Fluorine Chem., 1982, 20, 507–514.
110. R. D. Chambers, W. K. R. Musgrave and P. G. Urben, J. Chem. Soc., Perkin trans. 1, 1974, 2580–2584.
111. R. E. Banks, A. Prakash and N. D. Venayak, J. Fluorine Chem., 1980, 16, 325–338.
112. R. D. Chambers, M. J. Seabury, D. L. H. Williams and N. Hughes, J. Chem. Soc., Perkin trans. 1, 1988, 251–254.
113. R. D. Chambers, M. J. Seabury, D. L. H. Williams and N. Hughes, J. Chem. Soc., Perkin trans. 1, 1988, 255–257.
114. J. F. W. Keana and S. X. Cai, J. Org. Chem., 1990, 55, 3640–3647.
115. R. Dirr, C. Anthaume and L. Désaubry, Tetrahedron Lett., 2008, 49, 4588–4590.
116. G. M. Brooke, R. D. Chambers, C. J. Drury and M. J. Bower, J. Chem. Soc., Perkin trans. 1, 1993, 2201–2209.
117. K. Tanaka, M. Deguchi and S. Iwata, J. Chem. Res. Synop., 1999, 528–529.
118. G. Schroeder, K. Eitner, B. Gierczyk, B. Rózalski and B. Brzezinski, J. Mol. Struct., 1999, 478, 243–253.
119. T. J. Delia, D. P. Anderson and J. M. Schomaker, J. Heterocycl. Chem., 2004, 41, 991–993.
120. M. L. Belli, G. Illuminati and G. Marino, Tetrahedron, 1963, 19, 345–355.
121. M. Yukawa, T. Niiya, Y. Goto, T. Sakamoto, H. Yoshizawa, A. Watanabe and H. Yamanaka, Chem. Pharm. Bull., 1989, 37, 2892–2896.
122. W. T. Flowers, R. N. Haszeldine and S. A. Majid, Tetrahedron Lett., 1967, 8, 2503–2505.
123. I. Collins and H. Suschitzky, J. Chem. Soc. C, 1969, 2337–2341.
124. K. A. Volkov, G. V. Avramenko, V. M. Negrimovskii and E. A. Luk’yanets, Russ. J. Gen. Chem., 2007, 77, 1108–1116.
125. Z. Xinzhuo and T. Ibata, Chin. J. Org. Chem., 2002, 22, 778.
126. A. Carta, M. Palomba and P. Corona, Heterocycles, 2006, 68, 1715.
127. I. Collins and H. Suschitzky, J. Chem. Soc. C, 1970, 1523–1530.
128. H. Mizuno and A. Manabe, Pyrimidine Compounds and Pests Controlling Composition Containing the Same. WO2004099160A1, 2004.
129. J. M. Allen, R. J. Butlin, C. Green, W. Mccoull, G. R. Robb and J. M. Wood, Benzothiazoles as Ghrelin Receptor Modulators. WO2009047558A1, 2009.
130. D. Zhou, G. P. Stack, J. Lo, A. A. Failli, D. A. Evrard, B. L. Harrison, N. T. Hatzenbuhler, M. Tran, S. Croce, S. Yi, J. Golembieski, G. A. Hornby, M. Lai, Q. Lin, L. E. Schechter, D. L. Smith, A. D. Shilling, C. Huselton, P. Mitchell, C. E. Beyer and T. H. Andree, J. Med. Chem., 2009, 52, 4955–4959.
131. O. Weber, V. Voehringer, H.-G. Lerchen, F.-T. Hafner, J. Keldenich, K.-H. Schlemmer, U. Krenz and B. Riedl, Benzofuran and Benzothiophene Derivatives Useful in the Treatment of Cancers of the Central Nervous System. WO2008025509A1, 2008.
132. N. Ahmad, D. Boyall, J.-D. Charrier, C. Davis, R. Davis, S. Durrant, G. E. I. Jardi, D. Fraysse, J.-M. Jimenez, D. Kay, R. Knegtel, D. Middleton, M. O'Donnell, M. Panesar, F. Pierard, J. Pinder, D. Shaw, P.-H. Storck, J. Studley and H. Twin, Compounds Useful as Inhibitors of Atr Kinase. WO2014089379A1, 2014.
133. R. Al-Awar, M. Isaac, A. M. Chau, A. Mamai, I. Watson, G. Poda, P. Subramanian, B. Wilson, D. Uehling, M. Prakesch, B. Joseph and J.-A. Morin, Inhibitors of the Bcl6 Btb Domain Protein-Protein Interaction and Uses Thereof. WO2019153080A1, 2019.
134. J. M. Stevens, E. M. Simmons, Y. Tan, A. Borovika, J. Fan, R. V. Forest, P. Geng, C. A. Guerrero, S. Lou, D. Skliar, S. E. Steinhardt and N. A. Strotman, Org. Process Res. Dev., 2022, 26, 1174–1183.
135. Y. Tao, N. F. Keene, K. E. Wiglesworth, B. Sitter and J. C. McWilliams, Org. Process Res. Dev., 2019, 23, 382–388.
136. A. Stumpf, Z. K. Cheng, D. Beaudry, R. Angelaud and F. Gosselin, Org. Process Res. Dev., 2019, 23, 1829–1840.
137. U. Bremberg, J. Eriksson-Bajtner, F. Lehmann, V. Oltner, E. Sölver and J. Wennerberg, Org. Process Res. Dev., 2018, 22, 1360–1364.
138. Y. Tao, D. W. Widlicka, P. D. Hill, M. Couturier and G. R. Young, Org. Process Res. Dev., 2012, 16, 1805–1810.
139. G. A. Barcan, J. J. Conde, M. K. Mokhallalati, M. G. Nilson, S. Xie, C. L. Allen, Y. W. Andemichael, N. A. Calandra, D. C. Leitch, L. Li and M. J. Morris, Org. Process Res. Dev., 2019, 23, 1396–1406.
140. Y. Lu, K. P. Cole, J. W. Fennell, T. D. Maloney, D. Mitchell, R. Subbiah and B. Ramadas, Org. Process Res. Dev., 2018, 22, 409–419.

---

Footnote

† Electronic supplementary information (ESI) available: detailed experimental and computational procedures, statistical modeling information, supplementary figures, tables of molecular descriptors, and coordinate files for calculated structures. See DOI: https://doi.org/10.1039/d2sc04041g

---