Two-body dissociation of isoxazole following double photoionization – an experimental PEPIPICO and theoretical DFT and MP2 study

Abstract

The dissociative double photoionization of isoxazole molecules has been investigated experimentally and theoretically. The experiment has been carried out in the 27.5–36 eV photon energy range using vacuum ultraviolet (VUV) synchrotron radiation excitation combined with ion time-of-flight (TOF) spectrometry and photoelectron–photoion–photoion coincidence (PEPIPICO) technique. Five well-resolved two-body dissociation channels have been identified in the isoxazole's coincidence maps, and their appearance energies have been determined. The coincidence yield curves of these dissociation channels have been obtained in the photon energy ranges from their appearance energies up to 36 eV. The double photoionization of isoxazole produces a C₃H₃NO²⁺ transient dication, which decomposes into fragments differing from previously reported photofragmentation products of isoxazole. We have found no evidence of pathways leading to the C₃H₂NO⁺, HCN⁺, C₂H₂O⁺, C₃HN⁺, or C₂H₂⁺ fragments or their neutral counterparts that have been observed in previous neutral photodissociation and single photoionization studies. Instead, the dissociation of isoxazole after the ejection of two electrons is bond-selective and is governed by two reactions, HCO⁺ + H₂CCN⁺ and H₂CO⁺ + HCCN⁺, whose appearance energies are 28.6 (±0.3) and 29.4 (±0.3) eV, respectively. A third dissociation channel turns out to be a variant of the most intense channel (HCO⁺ + H₂CCN⁺), where one of the fragment ions contains a heavy isotope. Two minor dissociation channels occurring at higher energies, CO⁺ + CH₃CN⁺ and CN⁺ + H₃CCO⁺, are also identified. The density functional and ab initio quantum chemical calculations have been performed to elucidate the dissociative charge-separating mechanisms and determine the energies of the observed photoproducts. The present work unravels hitherto unexplored photodissociation mechanisms of isoxazole and thus provides deeper insight into the photophysics of five-membered heterocyclic molecules containing two heteroatoms.

---

1. Introduction

Probing the interaction of light with matter is of immense importance for understanding physical and chemical phenomena occurring in nature. Photoisomerization of 11-cis-retinal is, for example, a primary process of vision,¹ while photoabsorption, ionization, and isomerization are fundamental processes of photosynthesis.² Photon-induced bond-breaking, new bond-forming, and structural rearrangement processes also promise far-reaching applications in chemistry, biology, medicine, and various engineering and technology fields. However, these applications require controllable photoresponsive molecular units to be incorporated into molecular motors, switches, electronics, or drugs (see, e.g., ref. 3–8).

Heterocyclic molecules form more than half of all known chemical compounds.⁹ They are embedded in all nucleic acids, most drugs, biomasses, amino acids, natural resins, alkaloids, enzymes, vitamins, and many natural and synthetic dyes. Many experiments probing heterocyclic molecules' absorption, excitation, ionization, and isomerization have thus been reported in the literature. Some have been performed using strong-field ionization,^10,11 excitation and dissociation by laser light,^12,13 and synchrotron radiation,^14,15 or impact with charged particles: electrons^16,17 or ions.^18–23 Specifically, in photochemical reactions, heterocyclic molecules have shown potential to withstand or transform light efficiently^8,24,25 and can therefore be readily utilized as photoactive molecular entities. Isoxazole (C₃H₃NO, see Fig. 1) is a prototype bioactive compound with a distinctive ring structure that can be regarded as a light-sensitive moiety. Indeed, its ring contains three regular sp² carbon atoms, which are attached to adjacent oxygen and nitrogen atoms and linked by a fragile bond, and has a fully conjugated p-electron set functioning in a pseudo-aromatic manner. Such a specific electronic structure influences its reactivity causing, for example, a nonconventional response to light leading to unexpected photodissociation pathways.²⁶ Hence, isoxazole's interactions with UV and soft X-ray photons have recently been the subject of several experimental and theoretical surveys.^26–35

Fig. 1 The courses of plausible dissociation channels that are accessible in the double photoionization of isoxazole. The numbers of the dissociation channels refer to those observed in the experiment (Section 3). Dissociation channel no. 3 is not shown here because it represents a heavy-isotope variant of dissociation channels 1 and 2 (see Discussion in the text).

However, a limited number of works have been performed on photofragmentation processes of the isoxazole ring. The photon-induced decomposition of isoxazole was studied below the first ionization threshold,^29,30,35 in the valence range,^28,33 and K-edges.³⁴ Specifically, Nunes et al.²⁹ and Dias et al.³⁰ conducted experimental studies of isoxazole's photofragmentation in the energy range below the first ionization potential. These studies demonstrated²⁹ that isoxazole's breakup into ketene (H₂C=C=O) and hydrogen cyanide (HCN) starts upon low-energy narrow-band tunable UV laser light irradiation at 5.21 eV (λ = 238 nm). At 5.61 eV (λ = 221 nm), the primary fragmentation mechanism was additionally accompanied by the formation of the five isomeric forms of isoxazole, which are 2-formyl-2H-azirine, 3-formylketenimine, 3-hydroxypropenenitrile, imidoylketene, and 3-oxopropanenitrile. Later, Dias et al.³⁰ increased the photon energy to 6.42 eV (193 nm) and observed HCN and CH₃CO as the major dissociation products with branching ratios of 53.8% and 23.4%, respectively, as well as a few fragments with branching fractions below 10%, namely HCO, CH₂CN, CH₂CO, HCCCN, HCN, and HNC. The theoretical calculations by Nunes et al.²⁹ and Cao³⁵ complemented these measurements. These calculations indicated^29,35 that the N–O bond is the most fragile to scission, and its cleavage occurs ultrafast along the two lowest-lying excited states S₁(¹ππ*) and S₂(¹n_Nπ*) and creates an intermediate vinylnitrene that gives rise to the formation of 2-formyl-2H-azirine and 3-formylketenimine, which further dissociate into HCN + CHCHO and HCO + CHCHN diradicals, respectively. Based on these simulations, Dias et al.³⁰ suggested the possible contributions of direct or indirect ultrafast photodissociation processes that elucidate the relative branching ratios of the experimental photoproducts.

Above the first ionization threshold, the photofragmentation of isoxazole was investigated using synchrotron radiation excitation combined with ion time-of-flight spectrometry³³ and photon-induced fluorescence spectroscopy.^26,28 The former study probed the formation of twenty-one well-resolved cations in the photon energy range of 9–32 eV.³³ Apart from the intense parent ion (C₃H₃NO⁺), the mass-resolved cation spectra showed five other major cations: C₃H₂NO⁺ (formed by loss of an H atom), C₂H₂N⁺ (resulting from loss of a CHO molecule), C₂H₃N⁺ (resulting from loss of a CO molecule), HCO⁺ (obtained from the loss of a C₂H₂N) and N⁺/CH₂⁺ formed via multifragmentation of isoxazole. Other cations occurred with relative intensities below nine percent. This study showed additionally that photon-induced dissociation of isoxazole starts from the ring-opening and its rearrangements, and further, it proceeds strictly via ionic states of isoxazole.³³ The studies of ref. 26 and 28 focused on identifying the neutral dissociation products of isoxazole by detecting their emission. Emission from the excited hydrogen atoms H(n), as well as from vibrationally and rotationally excited diatomic CH(A²Δ), CH(B²Σ), CN(B²Σ), C₂(d³Π_g), and NH(A³Π) fragments was observed in the fluorescence spectra. It was found that neutral photofragmentation of isoxazole in the valence region occurs through its excitation to superexcited states that are embedded in the ionization continuum and further decay into two-, three-, or even four-fragment channels.^26,28 In addition, the theoretical calculations established the critical role of the ring-opening via the N–O bond breakage and hydrogen migration mechanism via superexcited states in the photofragmentation process.²⁶ Note that Linert et al.³⁶ earlier suggested that electron-induced dissociative excitation can also generate superexcited states of isoxazole, which subsequently undergo decomposition following energetically and dynamically the most convenient pathways on the hyperdimensional potential energy surface.

The most recent study investigated the near-edge X-ray absorption fine structure (NEXAFS) structures at the C, N, and O K-edges experimentally and theoretically.³⁴ Apart from the NEXAFS spectra of the gas-phase isoxazole, the yields of neutral fragments in high-Rydberg (HR) states were measured indirectly by ionizing such fragments in a static electric field and by recording resulting positive ions without mass resolution as a function of the photon energy.³⁴

However, dissociation following double photoionization has not been investigated for the gas-phase isoxazole molecule to our knowledge. In the present work, we have focused on measuring two-body dissociation pathways of isoxazole using vacuum ultraviolet (VUV) synchrotron radiation excitation combined with ion time-of-flight (TOF) spectrometry and photoelectron–photoion–photoion coincidence (PEPIPICO) technique. To aid in interpreting the PEPIPICO spectra, we have used quantum chemical calculations at density functional theory (DFT) and Møller–Plesset (MP2) levels. Concerning the possibility of using isoxazole in designing novel light-sensitive moieties of pharmaceutical or technological importance, the present work gives further insight into the photon-induced dissociation of its ring.

2. Methods

2.1. Experimental

The experiment was conducted at the Circular Polarization (CiPo) beamline³⁷ of the Elettra synchrotron radiation facility in Trieste, Italy. The beamline delivers synchrotron radiation from an electromagnetic elliptical undulator/wiggler. It contains a Normal Incidence Monochromator for low photon energies. We used an undulator mode that produced linearly polarized light, dispersed in the energy range 27.5–36 eV by a gold holographic spherical grating with 2400 grooves mm⁻¹ (Au-NIM). It has been estimated that the contribution of the second-order light in the exciting radiation of the CiPo beamline in the photon energy range above 15 eV is less than 1%,³⁷ so our data above 27 eV photon energy were collected without the use of filters. The valence excitations in noble gases were used to calibrate the photon energy scale.³³

The measurements were performed using the ion time-of-flight (TOF) spectrometer developed by Kivimäki and co-workers.³⁸ It consists of a modified Wiley–McLaren TOF spectrometer used initially to detect photoelectron–photoion coincidences and neutral-particle-photoion coincidences.³⁹ We have also exploited this apparatus to measure the yields and TOF spectra of neutral high-Rydberg fragments at the K edges of the CO₂,⁴⁰ H₂O,⁴¹ and isoxazole³⁴ molecules. In a rearranged configuration, this device can also record PEPIPICO spectra. The experimental chamber consisted of an interaction cell and the TOF spectrometer, with a 203 mm long drift tube, which was mounted parallel to the electric vector of the linearly polarized synchrotron radiation. In the interaction region, the incident photon beam from the undulator crossed the effusive beam of isoxazole gas emanating from a hypodermic needle.⁴⁰ During the measurements, the ambient pressure in the collision chamber was kept at 4.8–5.5 × 10⁻⁷ mbar. However, it was estimated to be 10–30 times higher in the interaction region. The base pressure without the sample was 7.0 × 10⁻⁸ mbar.

When synchrotron light interacts with studied molecules, some are singly ionized. When the energy rises, some molecules can be double-ionized. This mechanism produces the doubly charged parent ion after the emission of two correlated electrons. This dication is usually unstable and dissociates into ionic and neutral fragments. In our experiment, electrons and ions produced in the interaction region were accelerated towards opposite directions using a constant extraction field. Electrons were detected with a microchannel plate (MCP) detector placed close to the interaction region and they provided START signals for the flight time measurements of positive ions, which were detected using another MCP detector. The detection of positive ions provided STOP signals. Possible double ionization events were sorted out from the stored data under the condition that two ions were detected close to each other or, in other words, in coincidence with an electron. (These events also included false coincidences.) The PEPIPICO method yields coincidence maps plotted as the arrival time of the second ion vs. that of the first ion, both referenced to the detection event of one of the photoelectrons. The start and stop signals were fed into a time-to-digital converter system (ATMD-GPX from Acam Messelectronic GmBH), whose time resolution was 80 ps. The collection window remained open for 5000 ns after each start signal. Each coincidence map was collected at a fixed energy point, typically 100–140 min. Due to time constraints typical for synchrotron measurements, the incident photon energy was scanned in relatively large steps of 0.25 eV from 27.5 up to 33 eV, but there was a 1 eV gap between 30–31 eV. The incident photon flux was simultaneously measured using an Au mesh installed before the experimental chamber.³³

Liquid isoxazole with a stated purity of 99% was purchased from Sigma-Aldrich. We performed several freeze–pump–thaw cycles of the sample to eliminate all traces of residual gases. Isoxazole evaporates rapidly because its vapor pressure is 51.7 ± 0.2 mmHg at 25 °C.⁴² Therefore, the sample did not require additional heating.

2.2. Computational

Mass spectrometry provides information about the masses of the detected (charged) particles – chemical products. To a certain extent, it is sufficient to decipher the molecular formulae. However, it does not provide any information about the structure of molecules, and it also fails wherever there is more than one way of assigning the chemical formula (i.e., isotopes or questions like “CH₂ or N?”).

Hence, we decided to conduct quantum chemical simulations on these dissociation pathways of doubly photoionized isoxazole, which can lead to experimentally observed products. In the first step, we have built all the possible molecular fragments from the available atoms constituting isoxazole: 3C, N, O, and 3H. Then, we performed a conformational search of the neutral potential energy surface (PES) using the Merc MMFF94 force field⁴³ implemented in the Conflex 8 Rev B software.⁴⁴ All the conformers with a population above 1% have been further re-optimized at the DFT and MP2 levels. Parallel to the systematical PES search, we have stochastically generated “by hand” the set of starting molecules based on chemical insights. This approach proved to be more effective in the case of charged particles. It appears that the PES for neutral molecules (provided by force field computations) is quite different from the PES of the dication. At the DFT and MP2 levels, all the molecules were fully optimized without any constraints, and the second derivatives were computed analytically to ensure that there were no imaginary frequencies (confirming the minima, not maxima, on the PES). For both the methods, the same basis set 6-31+G(d′,p′) designed by Petersson and co-workers as part of the Complete Basis Set approach⁴⁵ with an additional set of diffuse functions was utilized. The very popular hybrid Becke, three-parameter, Lee–Yang–Parr (B3LYP) functional was used for the DFT simulation.^46–48 We have performed additional computations for the systems with rarer isotopes wherever it was relevant. All the open-shell systems were calculated as doublets, whereas charged compounds with two unpaired electrons were treated in two ways – as triplets and as singlets (with multiplicity of 3 and 1, respectively).

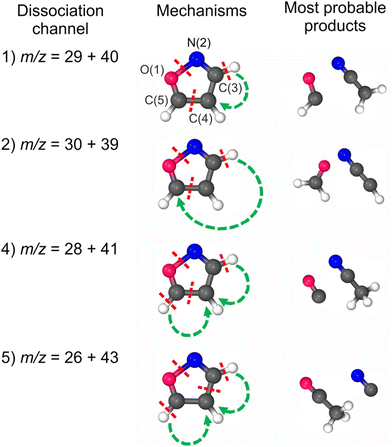
Even though we have considered here only two-body dissociation channels, each pathway leading to a stable product required substantial molecule reorganization and the breakage of at least three bonds (see Fig. 1). As there is more than one reaction coordinate, it is virtually impossible to detect one transition state (TS) or to describe it correctly using a one-electron wave function. On the other hand, as it is unlikely that all the products were adiabatically stable under experimental conditions, it was essential to find a way of estimating the kinetic energy barriers. We have approached it as follows: (1) we considered only bond cleavages between heavy atoms (C–H bonds were not stretched); (2) we stretched simultaneously two bonds to about 2 Å with an increment of 0.2 Å; (3) at each distance, these two bonds were frozen and the other parameters were optimized; (4) the set of molecules with energies higher than products and geometries slightly resembling those of the products was then fully optimized as TS; (5) in such a pool of molecules, we were inspecting these molecules with not one, but two imaginary frequencies with their vectors being responsible for the bond-stretching of the two bonds undergoing the breakage. It needs to be underlined that none of these structures is a saddle point in the strict sense, as each of them was characterized by more than one negative eigenvalue of the Hessian matrix. We are aware that these are just crude estimates, but we believe they are the best ones possible.

Tables S1 and S2 of the electronic ESI† present a detailed list of the obtained parameters that were calculated using both methods. Specifically, these tables contain the electron energies (E), electron energies with zero vibration corrections (E + ZPVE), enthalpies (dH), and Gibbs-free energies, including entropic factors (dG). Although the state-of-the-art MP2 method is more advanced than the DFT one, both gave remarkably consistent results that support the observations. However, to simplify the discussion, we only refer to the results obtained by the DFT method.

All quantum chemical calculations were performed using the Gaussian 16 RevC.01 software suite⁴⁹ available at Wrocław Centre for Networking and Supercomputing.⁵⁰ The molecules were visualized using Chemcraft software.⁵¹

3. Results and discussion

3.1. PEPIPICO maps

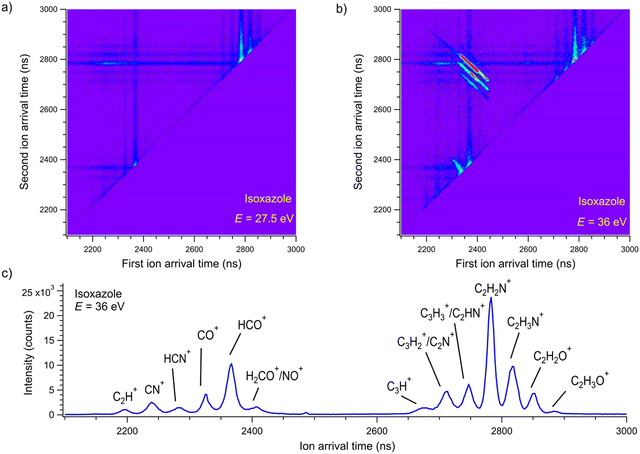
Dissociative double photoionization of isoxazole has not been studied experimentally or theoretically to the best of our knowledge. Therefore, the PEPIPICO coincidences have been measured in this work. The examples of PEPIPICO maps recorded at 27.5 and 36 eV are shown in Fig. 2(a) and (b), respectively. The pairs of correlated ions show up on the coincidence maps as tilted areas of higher point density (so-called “islands”) and represent dissociation channels initiated by double ionization. In Fig. 2(a) and (b), vertical and horizontal stripes represent points where uncorrelated ions appeared. Fig. 2(a) does not show tilted islands but only vertical and horizontal stripes, which indicates that no correlated coincidences are distinguished at an energy of 27.5 eV. In contrast, Fig. 2(b) displays evident islands representing pairs of correlated ions. The mass spectrum was also measured to identify which cations pairs arrived at the detector. The time-of-flight mass spectrum of the cations detected at the 36 eV photon energy is presented in Fig. 2(c). The mass peak assignments were made according to the data presented in ref. 33.

Fig. 2 The coincidence maps of isoxazole measured at (a) 27.5 eV and (b) 36 eV. The vertical and horizontal stripes represent points where uncorrelated ions appeared. (c) The time-of-flight mass spectrum of the cations detected at the 36 eV photon energy.

A thorough examination of Fig. 2(b) allows the identification of five two-body dissociation channels accessible in the double photoionization of isoxazole. The most probable assignments of the cations forming these two-body channels are given in Table 1. We do not observe an island corresponding to a perhaps expected C₃H₂NO⁺ + H⁺ dissociation channel at any energy considered. The dissociation energy limit for this reaction is estimated to be 24.79 eV. This value is obtained from the well-known ionization energy of hydrogen (13.6 eV) and the appearance energy of the C₃H₂NO⁺ cation (11.19 eV) obtained in the single photoionization of isoxazole.³³ However, the opening of this pathway may require more energy than that or even more than was available in the present measurements. It is also possible that its ion–ion coincidence signal is very low and obscured by a much stronger signal of false coincidences.

Table 1 The most probable assignments of the two-body dissociation channels observed following double photoionization of isoxazole at the photon energy of 36 eV. Slopes, determined appearance energies E_th (in eV), calculated energy barriers E^TS (in eV), and relative abundances RA (%) of the dissociation channels at 36 eV are also listed

No.	Masses of dissociation ion products (u)	Assignment of dissociation ion products	Slope	E th (eV)	E ^TS (eV)	RA (%)
1	29 + 40	HCO^+ + C2H2N^+	−0.99 (0.02)	28.6 (0.3)	28.2–28.8	48.0
2	30 + 39	H2CO^+ + C2HN^+	−1.09 (0.06)	29.4 (0.3)	29.2–29.8	14.6
3	29 + 41 and 30 + 40	HCO^++ C2H2N^+	−0.89 (0.02)	29.8 (0.6)	28.2–29.8	2.3
		H2CO^+ + C2HN^+ (heavy isotopes)
4	28 + 41	CO^+ + C2H3N^+	−1.16 (0.18)	34.0 (1.1)	28.2–28.8	1.3
5	26 + 43	CN^+ + C2H3O^+	−1.04 (0.03)	34.0 (1.1)		0.6

---

In addition to two-body pathways, Fig. 2(b) shows few many-body dissociation channels (for example, CO⁺ + CH₃N⁺ + C, HCO⁺ + C₂HN⁺ + H, HCO⁺ + C₂N⁺ + 2H/H₂). Their detailed analysis would require more elaborate calculations than presented here and is outside of the scope of this article.

If the parent dication breaks into two singly charged fragments, the slope of the island should be equal to minus one according to the ratio of the charges of these cations.⁵² Thus, we have determined the slopes of the islands representing two-body dissociation channels to check this theoretical consideration. These experimental slopes are given in Table 1. Apart from channel number three, all slopes agree with the theoretical value within the limits of the uncertainties. The discrepancy observed in channel no. 3 could be related to the altered momentum of the fragments with masses of 40/41 u due to the appearance of heavier isotopes in the natural composition of individual elements in these cations or to the opening of other competitive fragmentation channels (see Discussion below).

3.2. Coincidence yields

In the next step, the coincidence yield curves of these two-body dissociation channels were determined by recording the coincidence maps as a function of the incident photon energy. The measurements were carried out in the photon energy range from the respective threshold values up to 36 eV. One can determine the coincidence yield by counting the coincidences within each island and normalizing them to the incident photon flux, recording time, and pressure. A contribution from false coincidences to the islands can be removed by subtracting the background from the horizontal and vertical lines forming the island in question. Fig. 3 shows the coincidence yields of the two-body dissociation channels accessible in the double photoionization of isoxazole in the photon energy range of 27.5–36 eV. These coincidence yields provide the relative cross-sections for the two body fragmentation channels open in the double photoionization of isoxazole. Fig. 3 shows that all the yields rise gradually above their respective thresholds, thus suggesting a cross-section increase for the dissociative double photoionization of isoxazole.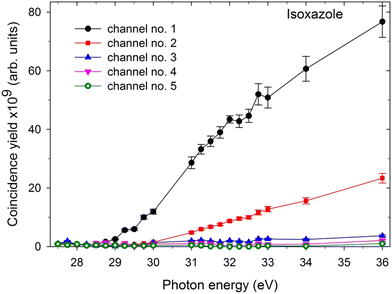

Fig. 3 The coincidence yields of two-body dissociation channels following double photoionization of isoxazole in the 27.5–36 eV photon energy range (the assignments of the channels are given in Table 1).

3.3. Appearance energies

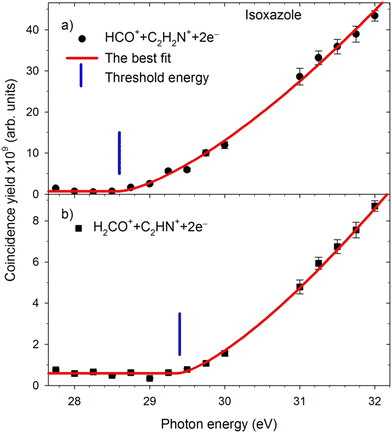
The appearance energies (E_th) of these two-body decay channels were obtained from their coincidence yield curves measured in narrow energy regions around the expected positions of the E_th thresholds. The example patterns of such curves are shown in Fig. 4.

Fig. 4 The yield curves of major dissociation channels measured in narrow energy regions near the expected AE thresholds. The solid red lines represent the best fits to the experimental data. The vertical blue bars show the energy positions of the thresholds.

The respective appearance energies were determined by fitting a modified Wannier function⁵³ describing the energy dependence of the dissociation cross-section in the near-threshold regions using the “ThreSpect” software⁵⁴ freely available in the Most Wiedzy Open Research Data Catalog (i.e., the Gdansk University of Technology Bridge of Knowledge repository).⁵⁵ This program has recently been successfully applied to determine thirty-two thresholds measured in the electron-induced dissociative ionization of pyridine.⁵⁶ The results of curve fitting to the experimental points are shown with solid red lines in Fig. 4. The extracted E_th of the two-body decay channels and their uncertainties (consisting of the uncertainty in the photon energy scale calibration and the uncertainty from the fittings) are listed in Table 1. The HCO⁺ + C₂H₂N⁺ and H₂CO⁺ + C₂HN⁺ channels (and their isotopic counterparts) have the lowest appearance energies. Opening the other two-body decay channels requires 4 eV more energy than pathways 1–3.

3.4. Branching fractions

The last column of Table 1 gives the relative abundances (RA) of individual two-body dissociation channels extracted as the fractional yields of these channels with respect to the total coincidence yield of all identified ion–ion pairs at 36 eV. In the studied energy range, two-body dissociation channels govern the double photoionization of isoxazole, and their total abundance reaches 66.9% of all decay channels at 36 eV. In particular, the dissociation channel HCO⁺ + C₂H₂N⁺ is dominant (48.0%) in our PEPIPICO experiment. The second channel, H₂CO⁺ + C₂HN⁺, is three times less abundant than channel no. 1. Other two-body dissociation channels are of minor importance. As mentioned earlier, many-body dissociation channels are outside the scope of the present work, although they account for the remaining 33.1% of the total abundance at 36 eV.

3.5. Fragmentation channels

Because of the lack of double photoionization studies of isoxazole, no direct comparison could be made to the literature data. Therefore, we performed in-depth calculations to describe the target molecule and the fragmentation products. We first computed the energy for the neutral ring geometry and the ionization potentials of the canonical isoxazole cation and dication (see Table S1, ESI†). This calculation predicted the first adiabatic ionization energy at 9.94 eV, in excellent agreement with the result of 9.96 (±0.02) eV reported in the newest spectroscopic photoionization study³³ and with the ionization energy of 9.976 eV reported from the threshold photoelectron spectrum of isoxazole.⁵⁷

Our theoretical work shows that the lowest energy level of the (C₃H₃NO)²⁺ dication is a singlet state, although the triplet state is located just above, separated by only 0.29 eV. The calculated energies for the double photoionization of isoxazole are 27.47 eV (for singlet states) and 27.76 eV (for triplet states). Experimentally, we do not observe double photoionization of isoxazole at 27.5 eV (Fig. 2(a)), but the appearance thresholds of the lowest energy dissociation channels were found at slightly higher energies, as given in Table 1. Possible reasons for the difference between experiment and theory are: (i) the calculation could slightly underestimate the double ionization energy (as it seemed to do for the first ionization energy); (ii) dissociation after double ionization does not start at the thermochemical threshold (due to potential barriers as is shown below); (iii) the experimental method does not allow us to distinguish ion–ion coincidences at very low intensity levels.

If single and double ionization energies are known, one can estimate the plausible Coulomb repulsion contribution to the double ionization energies.⁵⁸ The Coulomb energies depend on the inter-charge distances r₁₂ corresponding to the approximate dimensions of the molecules. By applying an empirical formula given by Eland and co-workers in ref. 58 as eqn (3) to the obtained ionization energies, we have calculated the distance r₁₂ between two charges to be 205 (195) pm in the singlet (triplet) state of the (C₃H₃NO)²⁺ dication. The r₁₂ values agree with distances obtained for isoxazole analogs furan (196 pm) and pyrrole (195 pm).⁵⁸ These results can be rationalized concerning isoxazole dication geometries (shown in Table 2) and the partial charge distributions (Table S3, ESI†) calculated by DFT and MP2 methods. Calculations of the isoxazole dication's geometries indicate that the most suitable sites for electron ejections are the N(2) and C(4) vicinities about 200 pm apart. Indeed, the highest densities of unpaired electrons are just on nitrogen (1.5) and on carbon C(4) (1.0). The partial charge densities are also high on N(2) and C(4), although the effect is masked due to the influence of the strongly electronegative oxygen on the adjacent C(3) carbon atom.

Table 2 The calculated bond lengths (in Å) of different isoxazole geometries. The subscripts S and T indicate singlet and triplet states, respectively

Bond	C3H3NO	C3H3NO^+	C3H3NO^2+S	C3H3NO^2+T
O(1)–N(2)	1.40	1.50	1.69	1.37
N(2)=C(3)	1.31	1.28	1.30	1.29
C(3)–C(4)	1.43	1.42	1.43	1.47
C(4)=C(5)	1.36	1.44	1.56	1.47
C(5)–O(1)	1.35	1.28	1.23	1.31

---

Next, we estimated the energies of the transition states and calculated the energies of the products for each reaction pathway as the energy differences between both decay products and the energy of the canonical structure of isoxazole. The calculations were performed for the fully relaxed systems in the case of PES minima and with some constraints in the case of transition states (see Section 2.2. Computational).

It is worth noting that these systems have probably not yet reached equilibrium under the measurement conditions (as the energies of the fully optimized products are systematically lower, particularly for the singlet states). Hence, we can assign the measured appearance energies to the barrier heights.

Due to spin conservation, one can assume that these reactions likely originate from the (C₃H₃NO)²⁺ dication in the singlet state. Indeed, the quantum chemical computations of Nunes et al.²⁹ and Cao³⁵ independently established that forming products in the open-shell singlet states could play a fundamental role in the neutral photodissociation of isoxazole. Note that based on the calculations at CCSD(T)/aug-cc-pVTZ level, Alagia et al. drew similar conclusions for the dissociative double photoionization of benzene.⁵⁹ In addition, the (C₃H₃NO)²⁺ dication in a singlet state has the most stretched O(1)–N(2) bond (see Table 2). Since the O(1)–N(2) bond has been identified as the most fragile in the isoxazole backbone,^26,29,35 elongation of this bond increases the probability of its breakage.

m/z = 29 + 40 dissociation channel. Table 1 shows that this reaction pathway opens first and governs the dissociation of doubly ionized isoxazole in the 27.5–36 eV energy range. Our calculations show that the cation with mass m/z = 29 is HCO⁺ and that with the mass m/z = 40 is C₂H₂N⁺. These fragments were observed as the second and fifth most abundant ones in single photoionization of isoxazole.³³ Moreover, C₂H₂N⁺ and HCO⁺ appeared at almost the same energy in the mass spectra of isoxazole and had similar cation yield curves.³³ Thus, these fragments were possibly formed after similar single photoionization processes.

Fig. 5 presents the simplified potential energy profiles of this two-body fragmentation channel, drawn using data from Table S1, ESI.† The calculations suggest that the transition state for this reaction occurs at 28.2–28.8 eV, which is in excellent agreement with the experimental appearance energy (E_th), and that the C₂H₂N⁺ and HCO⁺ cations are most likely produced by a transition state of doubly ionized isoxazole in which almost simultaneous rupture of the O(1)–N(2) and C(4)=C(5) bonds occurs. Indeed, Dias et al.³⁰ suggested that the neutral dissociation of isoxazole into the neutral C₂H₂N + HCO fragments can be viewed as a nonstatistical, ultrafast, direct process immediately following internal conversion to the ground state. Moreover, there are no traces of the doubly ionized (C₃H₃NO)²⁺ parent molecule at m/z = 34.5 in the mass spectrum shown in Fig. 2(c). No evidence of the formation of a stable (C₃H₃NO)²⁺ molecular dication was found in any of our recorded spectra. If such a dication were metastable, characteristic bent tails would be revealed on the recorded coincidence maps. No such features appear in the coincidence plots at any investigated photon energies. These observations indicate that the dication of isoxazole is a short-living transient molecule that rapidly undergoes decomposition into the fragments observed in the present work.

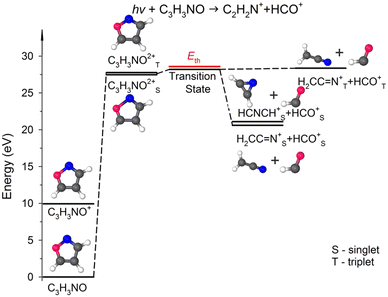Fig. 5 Relevant points in the potential energy surface of the isoxazole dication elucidating the HCO⁺ + C₂H₂N⁺ dissociation channel. The scheme is based on the data presented in Table S1, ESI.†

In our calculations, both these cationic fragments can be formed in the singlet or triplet state, or one fragment can be formed in the singlet and the other in the triplet state. As seen in Fig. 5, the transition state can rearrange into two minima of the PES in singlet states, i.e., stable cyanomethyl–formyl and 1H-azirin-1-yl-formyl radical cations that differ in energy by 0.48 eV. The calculations indicate, however, that the formation of the cyanomethyl-formyl cations is more probable than that of the 1H-azirin-1-yl-formyl cations. This observation agrees with the results obtained by Bouchoux and Hoppilliard,⁶⁰ who investigated the electron-induced dissociative ionization of isoxazole. Their analysis of the kinetic energy release and comparison with the decomposition of acetonitrile suggested that C₂H₂N⁺ was most likely generated in the form of the cyanomethyl cation.⁶⁰ Cyanomethyl-formyl radicals can additionally form stable structures in triplet states. However, the reaction leading to the products in triplet states is highly endothermic and thus less likely. The channels that produce singlet–triplet products are not shown in Fig. 5 because they also lead to relatively high-energy fragments (occurring ∼5 eV above the products in the singlet states; see Table S1, ESI† data).

m/z = 30 + 39 dissociation channel. The 30 and 39 u fragments are assigned to the H₂CO⁺ and C₂HN⁺ cations, respectively. The dissociation channel H₂CO⁺ + C₂HN⁺ is the second most intense one following double photoionization of isoxazole. This observation is somewhat surprising since all former photodissociation studies, notably³⁰ and,³³ showed that the branching ratios of both fragments were relatively low. This is because the ring opening and isomerization precede the formation of these products. Isomerization is often associated with the intramolecular migration of hydrogen atoms from one molecular site to another. Isoxazole is particularly prone to such a rearrangement. Indeed, in a recent study,²⁶ we provided direct evidence for isomerization connected with H atom movements in neutral isoxazole. Hydrogen migration usually occurs on a femtosecond timescale^61,62 and is swifter than bond breaking in dissociation. Here, the isoxazole dication is in a transient singlet state, and apart from the O(1)–N(2) and C(4)=C(5) bond breakage, the creation of the m/z = 30 and 39 fragments also requires simultaneous ultrafast hydrogen shift from C(3) to C(5) (see Fig. 1). As a result, the cation with m/z = 30 is in the form of formaldehyde (H₂CO⁺), while the cation with m/z = 39 is in the form of cyanomethylene (HCCN⁺), as seen in Fig. 6. Moreover, the computations show that the energy barrier for this reaction lies between 29.2 and 29.8 eV. The experimental E_th equals 29.4 eV, again in agreement with the calculations (Fig. 6).

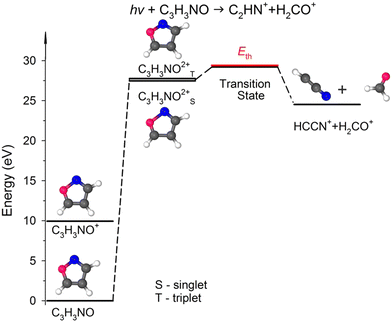Fig. 6 The simplified potential energy profile for the dissociation of the isoxazole dication into H₂CO⁺+ HCCN⁺. The scheme is based on the data presented in Table S1, ESI.†

For completeness, we also calculated an alternative dissociation pathway leading to the m/z = 30, 39 fragments (see DC no. 2B in Table S2, ESI†). In this scenario, isoxazole ring disintegration requires O(1)–C(5) single bond cleavage and, before other competing processes occur, breakage of the double bond between N(2)=C(3). This reaction leads to the formation of stable NO⁺ and C₃H₃⁺ cations. However, this reaction is a higher energy pathway (TS was estimated at 31.2 eV) and thus is less probable than the two-body decomposition leading to H₂CO⁺ + C₂HN⁺. Moreover, the previous calculations^26,29,35,60 indicate that dissociation of isoxazole starts from the O(1)–N(2) single bond rupture because it is the weakest bond in the skeleton of isoxazole. The N(2)=C(3) bond length is shorter than the C(4)=C(5) one (see Table 2), further strengthening the N(2)=C(3) side of the isoxazole structures. As a result, NO and C₃H₃ fragments were not identified in isoxazole's photodissociation,^{26,28–30,33} collision-induced fragmentation^36,60,63 or under pyrolytic conditions.^64–66

m/z = 29 + 41 and 30 + 40 dissociation channels. In our experiment, the islands representing both these reactions are weak and overlap each other. It is very difficult to separate them, as they form one island. In these dissociation channels, the sum of the fragments equals 70 u and is higher than that of normal isoxazole (69 u). This observation can only be explained if we assume that one of the fragments contains a heavy isotope. This signal likely combines m/z = 29 + 41 and 30 + 40 channels, making it a heavy-isotope variant of dissociation channel no. 1 and, to a lesser extent, of dissociation channel no. 2. An m/z = 40 fragment may then consist of ¹³CCHN⁺/C₂²HN⁺/C₂H¹⁵N⁺ isotopes, while the fragment with mass 41 u may be built as ¹³CCH₂N⁺/C₂²HHN⁺/C₂H₂¹⁵N⁺. Taking into account the natural abundance of the heavier isotopes ²H (0.015%), ¹³C (1.1%), ¹⁵N (0.4%), and ¹⁷O (0.038%), the heavy-isotope channels m/z = 30 + 40 (²HCO⁺/H¹³CO⁺/HC¹⁷O⁺ + C₂H₂N⁺) and 31 + 39 (²HHCO⁺/H₂¹³CO⁺/H₂C¹⁷O⁺ + C₂HN⁺) cannot be ruled out, with both signals likely to interfere with the counts of the m/z = 29 + 41 and 30 + 40 channels. The altered slope value of the experimental island of this reaction could be due to such interference (see Table 1). Note that the ion mass spectrum of isoxazole showed weak peaks with masses 70 and 71 u, which were the heavy-isotope variants of the parent ion.³³ Thus, the existence of this dissociation channel is natural, and it appeared in the PEPIPICO spectrum because the experiment was very sensitive.

The appearance energy of dissociation channel no. 3 was determined to be higher than that of the first dissociation channel (Table 1), even though they should be the same if pathway 3 is a heavy-isotope variant of dissociation channel no. 1. This observation let us conclude that the determination of the appearance energies depends on the intensities of the dissociation channels and that the experimental method used may not be capable of resolving ion–ion coincidences at the lowest intensity levels, due to overlapping false coincidences (which leads to a signal-to-noise ratio problem). Consequently, the real experimental appearance energy of dissociation channel no. 1 (or any dissociation channel) could be at a lower energy than determined here. The experimental appearance energies given in Table 1 should therefore be considered as upper estimates.

We also performed calculations of the alternative dissociation pathway leading to NO⁺ and ¹³CC₂H₃⁺/C₃²HH₂⁺ cations (see DC no. 3B in Table S2, ESI†). We only obtained the stable products in DFT predictions. Besides, the energy barrier was estimated to be 31.2 eV, which is higher than the experimental E_th value. Thus, given the reasons outlined for the m/z = 30 + 39 reactions, the NO⁺ + ¹³CC₂H₃⁺/C₃²HH₂⁺ formation is unlikely to happen.

m/z = 28 + 41 dissociation channel. The fourth dissociation pathway opens at a relatively high energy of 34 eV (see Table 1), and its relative abundance at 36 eV is only 1.3 percent. In contrast, fragments with masses of 28 and 41 u were detected as the major products in collision-induced fragmentation⁶⁰ and pyrolysis.^64–66 Also, these fragments were relatively abundant in our previous experiment on the dissociative photoionization of isoxazole.³³ Other photodissociation studies^26,28–30 did not, however, recognize their presence.

Our calculations predict that in the fourth reaction, isoxazole decomposes into carbon monoxide (CO⁺) and acetonitrile (CH₃CN⁺) cations according to the scheme shown in Fig. 1. Moreover, the lowest transition state energy was estimated for the pair of CO⁺ and CH₃CN⁺. These calculations agree with Bouchoux and Hoppilliard's investigations.⁶⁰ They considered two cationic conformations of C₂H₃N⁺, namely acetonitrile CH₃CN⁺ and ketenimine H₂C=C=NH⁺. Their analysis of the reacting configuration of C₂H₃N⁺ indicated its similarity to acetonitrile.⁶⁰ Acetonitrile and carbon monoxide were also detected as the major products of the thermal decomposition of neutral isoxazole.^64,65 Moreover, an analogous process was observed in the fragmentation of the isoelectronic molecule furan, which decomposed into methylacetylene (isoelectronic with acetonitrile) and carbon monoxide.⁶⁷ Only high-pressure pulse pyrolysis of isoxazole produced ketenimine instead of acetonitrile.⁶⁶

In comparative studies of dissociative electron attachment to isoxazole and its methylated derivatives, Li et al.⁶⁸ observed an anion with 41 u mass and assigned it to acetyl enolate (HC₂O⁻). Therefore, we additionally calculated the energies for the pair of cations consisting of ethynyloxy radical (C₂HO⁺) and amidogen methylene-(CH₂N⁺). The details are given in Table S2, ESI.† However, this pathway is more endothermic and leads to fragments that have not been observed yet. Thus, this dissociation channel can be ruled out.

m/z = 26 + 43 dissociation channel. The fifth two-body fragmentation channel is the weakest one. Its relative abundance only accounts for 0.6 percent. Here, the loss of a cyano radical cation (CN⁺) from the isoxazole dication followed by migration of two hydrogens leads to the formation of the methylcarbonyl cation H₃C₂O⁺ (see Fig. 1 and Table S1, ESI†), which requires at least 34 eV of energy. Both cations were observed in photoionization studies³³ as minor products. Moreover, the CN(B²Σ⁺) radical was previously identified as one of the most prominent emitters in the fluorescence spectra in the investigations of neutral fragmentation of isoxazole.^28,36 Since this fragment was observed in neutral dissociation and dissociative ionization of isoxazole, it can be assumed that the pathway leading to the production of CN⁺ is plausible, even if there may not be a straightforward correspondence between CN and CN⁺ formation.

The energies of the fragments arising in alternative dissociation channels (C₂H₂⁺ + HCNO⁺, C₂H₂⁺ + HCON⁺) were calculated to complete the picture. These data are listed in Table S2, ESI† (DC no. 5B). As in the m/z = 30 + 39 and 30 + 40 dissociation channels, O(1)–N(2) bond preservation and N(2)=C(3) bond breaking are unlikely. Thus, these fragmentation pathways can be excluded.

4. Conclusions

We have investigated the dissociative double photoionization of isoxazole through PEPIPICO experiments and quantum chemical calculations. We have not observed any stable or metastable (C₃H₃NO)²⁺ dication of isoxazole in our experiments; hence, the parent molecule dissociates swiftly after double photoionization. Five well-resolved two-body dissociation channels have been identified in the ion–ion coincidence maps of isoxazole, and their appearance energies and coincidence yield curves have been determined. The computational DFT and MP2 predictions have been employed to shed light on the most likely dissociative charge-separating mechanisms. The calculations indicate that removal of two electrons leads to isoxazole ring deformations, resulting in bond-selective fragmentation. Specifically, the (C₃H₃NO)²⁺ dication in the singlet state is most likely the starting point for fragmentation after double photoionization of isoxazole. The O(1)–N(2) and C(4)=C(5) bonds are then the most stretched, which makes them vulnerable to cleavage. On the other hand, the N(2)=C(3) and C(5)–O(1) bonds are shorter than in a canonical form of neutral isoxazole which reduces the probability of fragmentation by breaking these chemical bonds. As a result, the O(1)–N(2) bond breaks in each dissociation channel, and the C(4)=C(5) bond does so in the four most intensive dissociation channels. Therefore, double photoionization of isoxazole promotes different dissociation channels than single photoionization or neutral photofragmentation (which generated fragments such as C₃H₂NO⁺, HCN⁺, C₂H₂O⁺, C₃HN⁺, or C₂H₂⁺ or their neutral counterparts). Indeed, the primary channel of two-body dissociation occurs via the HCO⁺ + H₂CCN⁺ formation and is a simple isoxazole separation reaction arising from the simultaneous breaking of the O(1)–N(2) and C(4)=C(5) bonds. The remaining fragmentation reactions, H₂CO⁺ + HCCN⁺, CO⁺ + CH₃CN⁺, and CN⁺ + H₃CCO⁺, are examples of dissociation processes associated with isomerization of the isoxazole backbone.

The bond-selectivity of isoxazole photodissociation could be utilized to light-control bond-breaking and new bond-forming processes, and isoxazole thus holds promise for its far-reaching application as a photoactive molecular entity. However, photodissociation of isoxazole has not yet been fully unraveled.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

We are grateful to the Elettra-Sincrotrone Trieste for providing beamtime no. 20165364. The staying of T. J. W. in Elettra was financially supported by COST Action CM1204 XLIC (COST-STSM-CM1204-36527). T. J. W. also acknowledges financial support from the Gdansk University of Technology. The authors thank Daniele Catone and Sandro Rinaldi (the Circular Polarization beamline) for their help during the experiments. The assistance of the staff of the Sincrotrone Trieste is also gratefully acknowledged.

References

1. P. S. Bernstein, W. C. Law and R. R. Rando, Isomerization of all-trans-retinoids to 11-cis-retinoids in vitro, Proc. Natl. Acad. Sci. U. S. A., 1987, 84, 1849–1853,  DOI:10.1073/pnas.84.7.1849.
2. D. O. Hall and K. Rao, Photosynthesis, Cambridge University Press, 6th edn, 1999.
3. I. Conti, W. J. Buma, M. Garavelli and S. Amirjalayer, Photoinduced Forward and Backward Pedalo-Type Motion of a Molecular Switch, J. Phys. Chem. Lett., 2020, 11, 4741–4746,  DOI:10.1021/acs.jpclett.0c01094.
4. T. R. Nelson, A. J. White, J. A. Bjorgaard, A. E. Sifain, Y. Zhang, B. Nebgen, S. Fernandez-Alberti, D. Mozyrsky, A. E. Roitberg and S. Tretiak, Non-adiabatic Excited-State Molecular Dynamics: Theory and Applications for Modeling Photophysics in Extended Molecular Materials, Chem. Rev., 2020, 120, 2215–2287,  DOI:10.1021/acs.chemrev.9b00447.
5. M. Filatov, M. Paolino, S. K. Min and C. H. Choi, Design and photoisomerization dynamics of a new family of synthetic 2-stroke light driven molecular rotary motors, Chem. Commun., 2019, 55, 5247,  10.1039/c9cc01955c.
6. X. Guo, S. Xiao, M. Myers, Q. Miao, M. L. Steigerwald and C. Nuckolls, Photoresponsive nanoscale columnar transistors, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 691–696,  DOI:10.1073/pnas.0807596106.
7. E. R. Ruskowitz and C. A. DeForest, Photoresponsive biomaterials for targeted drug delivery and 4D cell culture, Nat. Rev. Mater., 2018, 3, 17087,  DOI:10.1038/natrevmats.2017.87.
8. I. M. Welleman, M. W. H. Hoorens, B. L. Feringa, H. H. Boersma and W. Szymański, Photoresponsive Molecular Tools for Emerging Applications of Light in Medicine, Chem. Sci., 2020, 11, 11672–11691,  10.1039/D0SC04187D.
9. C. W. Rees, Polysulfur-Nitrogen Heterocyclic Chemistry, J. Heterocyclic Chem., 1992, 29, 639–651,  DOI:10.1002/jhet.5570290306.
10. Y. Yihui, J. Long and Y. Liu, Study on photodynamics of furan via strong field multiphoton ionization by velocity map imaging technique, Chem. Phys., 2020, 530, 110611,  DOI:10.1016/j.chemphys.2019.110611.
11. M. Spanner, S. Patchkovskii, C. Zhou, S. Matsika, M. Kotur and Th. C. Weinacht, Dyson norms in XUV and strong-field ionization of polyatomics: Cytosine and uracil, Phys. Rev. A, 2012, 86, 053406,  DOI:10.1103/PhysRevA.86.053406.
12. A. Röder, A. B. Skov, A. E. Boguslavskiy, R. Lausten and A. Stolow, VUV excited-state dynamics of cyclic ethers as a function of ring size, Phys. Chem. Chem. Phys., 2020, 22, 26241–26254,  10.1039/D0CP04292G.
13. S. SenGupta, H. P. Upadhyaya, A. Kumar, P. D. Naik and P. Bajaj, Detection of OH Radical in Laser Induced Photodissociation of Tetrahydrofuran at 193 nm, J. Chem. Phys., 2005, 122, 124309,  DOI:10.1063/1.1867354.
14. T. J. Wasowicz, I. Dabkowska, A. Kivimäki, M. Coreno and M. Zubek, Elimination and migration of hydrogen in the vacuum-ultraviolet photodissociation of pyridine molecules, J. Phys. B Atom. Mol. Opt. Phys., 2017, 50, 015101,  DOI:10.1088/1361-6455/50/1/015101.
15. G. Vall-llosera, M. Coreno, P. Erman, M. A. Huels, K. Jakubowska, A. Kivimäki, E. Rachlew and M. Stankiewicz, VUV photoionisation of free azabenzenes: Pyridine, pyrazine, pyrimidine, pyridazine and s-triazine, Int. J. Mass Spectrom., 2008, 275, 55–63,  DOI:10.1016/j.ijms.2008.05.019.
16. T. J. Wasowicz, I. Linert, I. Lachowicz and M. Zubek, Electron impact fragmentation of pyrrole molecules studied by fluorescence emission spectroscopy, Photonics Lett. Pol., 2011, 3, 110–112,  DOI:10.4302/plp.2011.3.07.
17. J. A. Trocchi, J. Dech, W. Kedzierski and J. W. McConkey, Production of excited H–atoms in electron collisions with adenine, J. Phys. B At. Mol. Opt. Phys., 2019, 52, 055204,  DOI:10.1088/1361-6455/ab0222.
18. Z. Deng, I. Bald, E. Illenberger and M. A. Huels, Beyond the Bragg Peak: Hyperthermal Heavy Ion Damage to DNA Components, Phys. Rev. Lett., 2005, 95, 153201,  DOI:10.1103/PhysRevLett.95.153201.
19. F. Alvarado, S. Bari, R. Hoekstra and T. Schlathöter, Quantification of Ion-Induced Molecular Fragmentation of Isolated 2-Deoxy-D-ribose Molecules, Phys. Chem. Chem. Phys., 2006, 8, 1922–1928,  10.1039/B517109A.
20. T. J. Wasowicz and B. Pranszke, Observation of the Hydrogen Migration in the Cation-Induced Fragmentation of the Pyridine Molecules, J. Phys. Chem. A, 2016, 120, 964–971,  DOI:10.1021/acs.jpca.5b11298.
21. C. Mejía, G. S. Vignoli Muniz, M. Bender, D. Severin, C. Trautmann, B. Augé, A. N. Agnihotri, P. Boduch, A. Domaracka and H. Rothard, Swift heavy ion irradiation of thymine at cryogenic temperature, Nucl. Instrum. Methods Phys. Res. B, 2023, 534, 11–15,  DOI:10.1016/j.nimb.2022.10.024.
22. T. J. Wasowicz and B. Pranszke, Interactions of protons with furan molecules studied by collision-induced emission spectroscopy at the incident energy range of 50–1000 eV, Eur. Phys. J. D, 2016, 70, 175,  DOI:10.1140/epjd/e2016-70308-1.
23. T. J. Wasowicz, M. Łabuda and B. Pranszke, Charge Transfer, Complexes Formation and Furan Fragmentation Induced by Collisions with Low-Energy Helium Cations, Int. J. Mol. Sci., 2019, 20, 6022,  DOI:10.3390/ijms20236022.
24. N. Hoffmann, Photochemical Reactions as Key Steps in Organic Synthesis, Chem. Rev., 2008, 108, 1052–1103,  DOI:10.1021/cr0680336.
25. L. Čechová, J. Kind, M. Dračínský, J. Filo, Z. Janeba, C. M. Thiele, M. Cigáň and E. Procházková, Photoswitching Behavior of 5-Phenylazopyrimidines: in situ Irradiation NMR and Optical Spectroscopy Combined with Theoretical Methods, J. Org. Chem., 2018, 83, 5986–5998,  DOI:10.1021/acs.joc.8b00569.
26. M. Zubek, T. J. Wasowicz, I. Dąbkowska, A. Kivimäki and M. Coreno, Hydrogen Migration in Formation of NH(A³Π) Radicals Via Superexcited States in Photodissociation of Isoxazole Molecules, J. Chem. Phys., 2014, 141, 064301,  DOI:10.1063/1.4891808.
27. I. C. Walker, M. H. Palmer, J. Delwiche, S. V. Hoffmann, P. L. Vieora, N. J. Mason, M. F. Guest, M.-J. Hubin-Franskin, J. Heinesch and A. Giuliani, The Electronic States of Isoxazole Studied by V.U.V. Absorption, Electron Energy-loss Spectroscopies and Ab Initio Multi-reference Configuration Interaction Calculations, Chem. Phys., 2004, 297, 289–306,  DOI:10.1016/j.chemphys.2003.10.012.
28. T. J. Wasowicz, A. Kivimäki, M. Coreno and M. Zubek, Superexcited States in the Vacuum-Ultraviolet Photofragmentation of Isoxazole Molecules, J. Phys. B: At. Mol. Opt. Phys., 2012, 45, 205103,  DOI:10.1088/0953-4075/45/20/205103.
29. C. M. Nunes, I. Reva, T. M. V. D. Pinho e Melo and R. Fausto, UV-laser photochemistry of isoxazole isolated in a low-temperature matrix, J. Org. Chem., 2012, 77, 8723–8732,  DOI:10.1021/jo301699z.
30. N. Dias, B. Joalland, N. M. Ariyasingha, A. G. Suits and B. M. Broderick, Direct versus indirect photodissociation of isoxazole from product branching: a chirped-pulse Fourier transform mm-wave spectroscopy/pulsed uniform flow investigation, J. Phys. Chem. A, 2018, 122, 7523–7531,  DOI:10.1021/acs.jpca.8b04713.
31. A. A. Wallace, Y. Dauletyarov and A. Sanov, Deprotonation of Isoxazole: A Photoelectron Imaging Study, J. Phys. Chem. A, 2020, 124, 7768–7775,  DOI:10.1021/acs.jpca.0c06838.
32. T. Geng, J. Ehrmaier, O. Schalk, G. W. Richings, T. Hansson, G. Worth and R. D. Thomas, Time-Resolved Photoelectron Spectroscopy Studies of Isoxazole and Oxazole, J. Phys. Chem. A, 2020, 124, 3984–3992,  DOI:10.1021/acs.jpca.9b11788.
33. T. J. Wasowicz, A. Kivimäki, D. Catone and R. Richter, Vacuum Ultraviolet Photo-ionization and Ionic Fragmentation of the Isoxazole Molecules, Int. J. Mass Spectrom., 2020, 449, 116276,  DOI:10.1016/j.ijms.2019.116276.
34. T. J. Wasowicz, I. Ljubić, A. Kivimäki and R. Richter, Core-shell excitation of isoxazole at the C, N, and O K-edges – an experimental NEXAFS and theoretical TD-DFT study, Phys. Chem. Chem. Phys., 2022, 24, 19302–19313,  10.1039/D2CP02366K.
35. J. Cao, Photoinduced Reactions of Both 2-Formyl-2h-Azirine and Isoxazole: A Theoretical Study Based on Electronic Structure Calculations and Nonadiabatic Dynamics Simulations, J. Chem. Phys., 2015, 142, 244302,  DOI:10.1063/1.4922742.
36. I. Linert, I. Lachowicz, T. J. Wasowicz and M. Zubek, Fragmentation of isoxazole molecules by electron impact in the energy range 10-85 eV, Chem. Phys. Lett., 2010, 498, 27,  DOI:10.1016/j.cplett.2010.08.034.
37. A. Derossi, F. Lama, M. Piacentini, T. Prosperi and N. Zema, High flux and high resolution beamline for elliptically polarized radiation in the vacuum ultraviolet and soft x-ray regions, Rev. Sci. Instrum., 1995, 66, 1718,  DOI:10.1063/1.1145828.
38. A. Kivimäki, A. Sankari, J. A. Kettunen, C. Stråhlman, J. Alvarez Ruiz and R. Richter, Field ionization of high-Rydberg fragments produced after inner-shell photoexcitation and photo-ionization of the methane molecule, J. Chem. Phys., 2015, 143, 114305,  DOI:10.1063/1.4931105.
39. A. Kivimäki, J. Alvarez-Ruiz, R. Sergo and R. Richter, Production of excited H atoms at the C 1s edge of the methane molecule studied by VUV-photon-photoion and metastable-fragment-photoion coincidence experiments, Phys. Rev. A, 2013, 88, 043412,  DOI:10.1103/PhysRevA.88.043412.
40. A. Kivimäki, C. Stråhlman, T. J. Wasowicz, J. A. Kettunen and R. Richter, Yields and time-of-flight spectra of neutral high-Rydberg fragments at the K edges of the CO₂ molecule, J. Phys. Chem. A, 2016, 120, 4360–4367,  DOI:10.1021/acs.jpca.6b04495.
41. A. Kivimäki, T. J. Wasowicz and R. Richter, Soft X-ray induced production of neutral fragments in high-Rydberg states at the O 1s ionization threshold of the water molecule, J. Phys. Chem. A, 2021, 125, 713–720,  DOI:10.1021/acs.jpca.0c06940.
42. CSID:8897, https://www.chemspider.com/Chemical-Structure.8897.html, accessed 17:33, February 14, 2023.
43. T. A. Halgren, Merck molecular force field. V. Extension of MMFF94 using experimental data, additional computational data, and empirical rules, J. Comput. Chem., 1996, 17, 616,  DOI:10.1002/(SICI)1096-987X(199604)17:5/6<616::AID-JCC5>3.0.CO;2-X.
44. https://www.conflex.net, accessed November 21, 2021.
45. G. A. Petersson and M. A. Al-Laham, A complete basis set model chemistry. II. Open-shell systems and the total energies of the first-row atoms, J. Chem. Phys., 1991, 94, 6081,  DOI:10.1063/1.460447.
46. A. D. Becke, Density-functional thermochemistry. III. The role of exact exchange, J. Chem. Phys., 1993, 98, 5648,  DOI:10.1063/1.464913.
47. P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, Ab Initio Calculation of Vibrational Absorption and Circular Dichroism Spectra Using Density Functional Force Fields, J. Phys. Chem., 1994, 98, 11623,  DOI:10.1021/j100096a001.
48. B. Jeziorski and H. Monkhorst, Coupled-cluster method for multideterminantal reference states, Phys. Rev. A, 1981, 24, 1668,  DOI:10.1103/PhysRevA.24.1668.
49. M. J. Frisch, et al., Gaussian 16, Revision C.01, Gaussian, Inc., Wallingford CT, 2016.
50. Wroclaw Centre for Networking and Supercomputing: https://www.wcss.pl/.
51. Chemcraft – graphical software for visualization of quantum chemistry computations. https://www.chemcraftprog.com.
52. J. H. D. Eland, Dynamics of Fragmentation Reactions From Peak Shapes in Multiparticle Coincidence Experiments, Laser Chem., 1991, 11, 259–263,  DOI:10.1155/LC.11.259.
53. G. H. Wannier, The threshold law for single ionization of atoms or ions by electrons, Phys. Rev., 1953, 90, 817,  DOI:10.1103/PhysRev.90.817.
54. M. K. Jurkowski, D. Glowienka and T. J. Wasowicz, ThreSpect − a Program for the Determination of the Appearance Energies of Neutral and Ionized Species, Rom. J. Phys., 2023, 68, 203.
55. M. Jurkowski, D. Glowienka and T. Wasowicz, ThreSpect a program for the determination of the Appearance Energies [Data set], Gdansk University of Technology, 2023,  DOI:10.34808/hwc6-be20.
56. M. K. Jurkowski and T. J. Wasowicz, Dehydrogenation in electron-induced dissociative ionization of pyridine molecule, Rom. J. Phys., 2023, 68, 205,  DOI:10.59277/RomJPhys.2023.68.205.
57. M. Dampc, B. Mielewska, M. R. F. Siggel-King, G. C. King, B. Sivaraman, S. Ptasinska, N. Mason and M. Zubek, Threshold photoelectron studies of isoxazole over the energy range 9.9–30 eV, Chem. Phys., 2010, 367, 75–79,  DOI:10.1016/j.chemphys.2009.10.024.
58. R. D. Molloy, A. Danielsson, L. Karlsson and J. H. D. Eland, Double photoionisation spectra of small molecules and a new empirical rule for double ionisation energies, Chem. Phys., 2007, 335, 49,  DOI:10.1016/j.chemphys.2007.03.016.
59. M. Alagia, P. Candori, S. Falcinelli, F. Pirani, M. S. Pedrosa Mundim, R. Richter, M. Rosi, S. Stranges and F. Vecchiocattivi, Dissociative double photo-ionization of benzene molecules in the 26–33 eV energy range, Phys. Chem. Chem. Phys., 2011, 13, 8245–8250,  10.1039/c0cp02678f.
60. G. Bouchoux and Y. Hoppilliard, Fragmentation mechanisms of isoxazole, Org. Mass Spectrom., 1981, 16, 459,  DOI:10.1002/oms.1210161009.
61. Y. H. Jiang, A. Rudenko, O. Herrwerth, L. Foucar, M. Kurka, K. U. Kühnel, M. Lezius, M. F. Kling, J. van Tilborg, A. Belkacem, K. Ueda, S. Düsterer, R. Treusch, C. D. Schröter, R. Moshammer and J. Ullrich, Ultrafast Extreme Ultraviolet Induced Isomerization of Acetylene Cations, Phys. Rev. Lett., 2010, 105, 263002,  DOI:10.1103/PhysRevLett.105.263002.
62. M. Zhang, T. Ando, A. Iwasaki, L. Wang, S. Koh and K. Yamanouchi, Ionization and ultrafast hydrogen migration of methylamine in few-cycle intense near-infrared laser fields, Chem. Phys. Lett., 2022, 806, 140061,  DOI:10.1016/j.cplett.2022.140061.
63. H. Priya and M. Paranjothy, Collision Induced Dissociation of Deprotonated Isoxazole and 3-Methyl Isoxazole via Direct Chemical Dynamics Simulations, J. Am. Soc. Mass Spectrom., 2023, 34, 710–719,  DOI:10.1021/jasms.2c00366.
64. A. Lifshitz and D. Wohlfeiler, Thermal-decomposition of isoxazole -experimental and modeling study, J. Phys. Chem., 1992, 96, 4505–4515,  DOI:10.1021/j100190a070.
65. G. I. Yranzo and E. L. Moyano, Flash vacuum pyrolysis of isoxazoles, pyrazoles and related compounds, Curr. Org. Chem., 2004, 8, 1071,  DOI:10.2174/1385272043370113.
66. C. M. Nunes, I. Reva, T. M. V. D. Pinho e Melo, R. Fausto, T. Solomek and T. Bally, The pyrolysis of isoxazole revisited: a new primary product and the pivotal role of the vinylnitrene, A low-temperature matrix isolation and computational study, J. Am. Chem. Soc., 2011, 133, 18911,  DOI:10.1021/ja207717k.
67. E. E. Rennie, L. Cooper, C. A. F. Johnson, J. E. Parker, R. A. Mackie, L. G. Shpinkova, D. M. P. Holland, D. A. Shaw and M. A. Hayes, A study of the unimolecular decomposition of internal-energy-selected furan molecular ions by threshold-photoelectron-photoion coincidence spectroscopy, Chem. Phys., 2001, 263, 149,  DOI:10.1016/S0301-0104(00)00346-3.
68. Z. Li, I. Carmichael and S. Ptasinska, Dissociative electron attachment induced ring-opening in five-membered heterocyclic compounds, Phys. Chem. Chem. Phys., 2018, 20, 18271–18278,  10.1039/C8CP02718H.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp03760f

---