 Open Access Article
Open Access ArticleHow machine learning can accelerate electrocatalysis discovery and optimization
Stephan N.
Steinmann
 *a,
Qing
Wang
*a,
Qing
Wang
 a and
Zhi Wei
Seh
a and
Zhi Wei
Seh
 *b
*b
aUniv Lyon, ENS de Lyon, CNRS, Laboratoire de Chimie UMR 5182, Lyon, France. E-mail: stephan.steinmann@ens-lyon.fr
bInstitute of Materials Research and Engineering, Agency for Science, Technology and Research (A*STAR), 2 Fusionopolis Way, Innovis, 138634, Singapore. E-mail: sehzw@imre.a-star.edu.sg
First published on 9th December 2022
Abstract
Advances in machine learning (ML) provide the means to bypass bottlenecks in the discovery of new electrocatalysts using traditional approaches. In this review, we highlight the currently achieved work in ML-accelerated discovery and optimization of electrocatalysts via a tight collaboration between computational models and experiments. First, the applicability of available methods for constructing machine-learned potentials (MLPs), which provide accurate energies and forces for atomistic simulations, are discussed. Meanwhile, the current challenges for MLPs in the context of electrocatalysis are highlighted. Then, we review the recent progress in predicting catalytic activities using surrogate models, including microkinetic simulations and more global proxies thereof. Several typical applications of using ML to rationalize thermodynamic proxies and predict the adsorption and activation energies are also discussed. Next, recent developments of ML-assisted experiments for catalyst characterization, synthesis optimization and reaction condition optimization are illustrated. In particular, the applications in ML-enhanced spectra analysis and the use of ML to interpret experimental kinetic data are highlighted. Additionally, we also show how robotics are applied to high-throughput synthesis, characterization and testing of electrocatalysts to accelerate the materials exploration process and how this equipment can be assembled into self-driven laboratories.
Introduction
In recent years, machine learning (ML) has become a buzz word, covering distinct realities,1 sometimes simply rebranding established methods such as (multi-)linear regressions, while in other cases ML enables operations through novel mathematical tools. At the same time, electrocatalysis has also been touted as a promising approach to sustainably produce important fuels and chemicals (e.g., hydrogen, hydrocarbons, and ammonia).2 The traditional trial-and-error approach of developing new electrocatalysts is time-consuming and only samples a small chemical space. ML, being data-driven in nature, can learn continuously from experience to accelerate the discovery and to optimize processes.1 This has the potential to significantly shorten the time it takes to bring new electrocatalysts from the lab bench to a commercial application.In this review, we focus on the impact of ML on the understanding and development of heterogeneous electrocatalysts, with examples preferentially taken from the very recent literature. Our aim is to provide a primer in the currently feasible acceleration of the discovery and optimization of electrocatalysts via a tight collaboration between computational models and experiments. We do not provide an actual introduction into ML, which can be found elsewhere,2 but we draw the reader's attention to the danger of overfitting when using ML with small datasets, where “small” is relative to the number of (hyper-) parameters of the ML model.3 Instead, we aim to give an overview of the different roles ML can play in the activities of all kinds of researchers in heterogeneous electrocatalysis, from theoreticians to experimentalists. As such, we do not focus on a particular method, material, or a single reaction (e.g., ML for theoretical chemists,4 for MXenes5 or for hydrogen evolution6). The focus of this review on electrocatalysis is motivated by the comparatively underdeveloped understanding of the atomistic origins of the observed catalytic activities compared to heterogeneous catalysis in the gas phase. This lack of rational understanding is related to the complexity of the reaction environment and the challenges to achieve detailed characterizations of the functional (operando) interface. Despite this focus on electrocatalysis, most of the discussed approaches are also applicable to thermal catalysis.
Our interest is two-fold: First, how can ML help to gain a reliable, detailed understanding of the nature and working principles of a given electrocatalyst? And second, how can ML accelerate the discovery of stable, more active electrocatalysts? While the two questions can be related in some instances, the examples discussed below demonstrate that there is not necessarily a direct link: understanding why Pt is such a good hydrogen evolution reaction (HER) catalyst in acidic solutions does not magically lead to propositions of excellent HER catalysts in alkaline solutions. Similarly, having discovered that Cu possesses a unique CO2 reduction reaction selectivity does not bring us closer to understanding the underlying reasons. In fact, there is no reason to expect ML to make a solid link between understanding, prediction, synthesis and operation-condition optimization. In other words, ML is not a panacea that will completely revolutionize chemistry. Nevertheless, it is clearly a powerful tool and our aim is to point out the areas connected to electrocatalysis where we currently see major impacts of ML and expect this trend to continue, as summarized in Fig. 1.
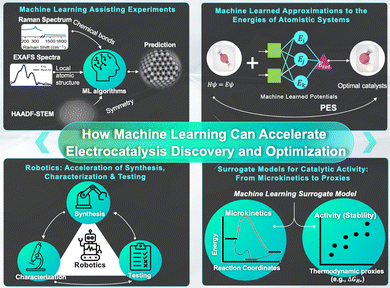 | ||
| Fig. 1 Schematic and summary of the impact of ML on electrocatalyst development and optimization as discussed in this review. | ||
We start our review with the impact of ML on simulations at the atomic scale. This scale is critical for a deep understanding of the working principles (reaction mechanism and structure–property relationships) of electrocatalysts. In this context, ML essentially represents an approximate solution to the Schrödinger equation and could be seen as an alternative to density functional theory (DFT) computations. As we discuss in detail below, ML is actually not a replacement for DFT, but is a promising and popular approach to mimic DFT computations to accumulate thermodynamically relevant statistics of well-defined systems for which the ML model has been trained based on the indispensable DFT computations. In this sense, ML is closer to empirical force fields than DFT. Note that we do not cover ML techniques that aim at speeding up the (static) DFT computations themselves, as they have been discussed earlier by us.7
Next, we move one step closer to the specificities of electrocatalysis: instead of investigating the atomistic mechanism, one can identify surrogate models that link simple-to-obtain “descriptors” or proxies to electrocatalytic activity. This activity can take the form of microkinetic simulations or more approximate variants thereof. This topic is very popular among computational chemists, as it allows performing in silico screening of hypothetical materials. Here, the main caveat stems from the (necessary) simplifications: disregarding feasibility and stability (especially under the electrocatalytic reaction conditions) leads more often than not to unrealistic propositions.
The third aspect which will be scrutinized is the intimate interplay between ML and experiments. This covers several application domains of ML: on the one hand, ML in the sense of data analysis can be exploited to extract the maximum information from experimental characterization methods, be it kinetic signatures of the catalysts to gain insight into the mechanism, or spectroscopic and microscopic data to reconstruct an atomic representation of the (active) material. On the other hand, ML also lends itself perfectly to a modern incarnation of design of experiments in order to optimize synthesis and operation conditions.
Finally, we discuss automated and computer-controlled (robotic) laboratory equipment, which can be coupled to the ML-driven design of experiments. Indeed, such a hardware infrastructure is system specific to some extent, but over the last couple of years, general pieces of equipment have been developed that can be integrated into the human-time efficient ML-assisted development of heterogeneous (electro-)catalysts. It is our strong belief that such “autonomous” laboratories will give rise to a new subdiscipline in chemistry: liberated from the necessity to master the practicalities of experimental chemistry and from the constraints of owning state-of-the-art lab equipment, certain chemists will be able to get specialized in coming up with creative ways to explore chemical space and reaction conditions for numerous applications in electrocatalysis and beyond. Of course, this vision relies on heavy investments by states, universities and companies into the development and installation of the required infrastructure in analogy with high-performance computing facilities. As a matter of example, such a platform that will be accessible for various research groups, is currently being developed under the SwissCat+ initiative.8
Machine-learned approximations to the energies of atomistic systems
DFT is the well-established workhorse for the atomistic understanding of electrocatalytic systems,9 but comes with a rather high computational cost. This motivates the development and usage of more efficient methods, especially in view of the size of the electrocatalytic interface (thousands of atoms), its dynamics (at least nanoseconds) and even the sheer number of catalysts one would like to computationally assess. In this context, ML is currently best seen as a way of constructing system-specific “force fields”, i.e., mathematical functions that output the system energy as a function of the positions and nature of the atoms. These functions are commonly called machine-learned potentials (MLP) and are many orders of magnitude faster than DFT. Of course, other levels of theory can be used instead of DFT if accumulating sufficient training data is feasible. As an example, we mention ANI-1ccx,10 which achieves near-coupled-clusters singles, doubles and perturbative triples accuracy for organic molecules via a neural network, and for the condensed-phase the random-phase approximation has been exploited to go beyond DFT accuracy with an MLP.11 There are several approaches to constructing MLPs, but kernel ridge or Gaussian process regression12 and neural networks are most popular.13 While the former is easier to train, the latter is mathematically even more flexible, not imposing any physical constraints on the structure–energy relationship. It is worth noting that for a given accuracy of the MLP, the computational cost to use it can vary by two orders of magnitude depending on its mathematical form.14 Similarly, the increase in the computational cost (related to the number of parameters) when adding more and more chemical elements depends on the architecture of the MLP, but more than about four elements is currently at the limit of feasibility for MLPs that cover large reaction phase-spaces. The common MLPs are “short-sighted”, i.e., the energy of the system is the sum of energies of each atom, with each atomic energy depending only on the local (≲4 Å) environment. Concurrently, these MLPs are “brute force”, i.e., do not contain any physical knowledge in their functional forms. However, there is a current trend towards “physics-based” MLPs. These more advanced functional forms have the advantage that the short-range and long-range interactions are separately accounted for, instead of neglecting the latter altogether.13,15Independent of the architecture of the MLP, it is the training of the MLP that is most time-intensive as a user: since MLPs are system specific, for each application a dedicated training set needs to be constructed. The size of the training set is on the order of 103–4 DFT energy evaluations and the quality of the MLP is at least as dependent on the representative diversity of the training set as it is on the architecture of the MLP: Geometries that deviate too much from the training set will have completely wrong energies and forces. Since the flexibility and absence of physical constraints make MLPs unreliable for extrapolation, they tend to only work well for the systems and reactions they have been trained for. To give a hypothetical example: If one trains an MLP on liquid water, the corresponding MLP certainly cannot describe the combustion of O2 and H2 to yield H2O nor the decomposition of H2O2. It is also unlikely to properly describe excess or defects of protons, or the self-ionization of water. Nevertheless, the MLP will, of course, provide an energy for such systems: after all, it is trained for systems containing any numbers of H and O atoms. However, this energy will be meaningless. To adequately describe these additional stoichiometries and configurations, the MLP has to be improved by including the corresponding geometries in the training set. Indeed, recent studies have demonstrated that proton dynamics in liquid water can be well captured if the training set contains sufficient data points corresponding to proton transfers.16
In practice, the currently most popular software for parametrizing and utilizing MLPs in electrocatalysis are LASP17 and DeepMD.18,19 The power of the former is the availability of a large set of predefined MLPs, while the latter has very powerful active-learning capabilities, enabling an efficient parametrization of system-specific MLPs. Once the MLP is trained, the usual arsenal of atomistic simulation techniques can be applied. Nanosecond simulations of systems with >100 atoms would be computationally prohibitively expensive at the DFT level of theory, but are necessary to reach converged results due to the slow diffusion at the solid/liquid interface.20,21 These simulations are easily reachable with MLPs.
For example, the free energy profiles of proton transfers on the prototypical photo-electrocatalyst anatase TiO2/water interface have been studied via an MLP driven by the DPMD package.22 Trajectories of more than 2 ns could be achieved with the MLP, which compares to 40 ps at the DFT level of theory (see Fig. 2). This extensive phase-space sampling was necessary, as the half-life time of OH groups at the interface was estimated to be 300 ps. Furthermore, relying on umbrella sampling, the dissociation barrier of chemisorbed water molecules was estimated to be 30 kJ mol−1, leading to a stabilization of the interface of about 8 kJ mol−1. Note, that this thermodynamic driving force is not very strong, which imposes not only the use of accurate energy expressions, but also extensive phase-space sampling. The same conclusions have also been reached at other interfaces, e.g., ethanol adsorption on alumina, relevant for biomass processing.23
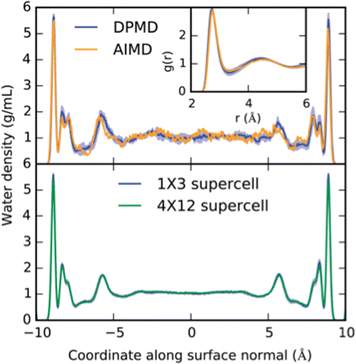 | ||
| Fig. 2 Example of interfacial structure and the effect of long sampling times at the MLP level compared to short sampling at the DFT level. Top: The density profile of water confined between two TiO2 surfaces and the oxygen radial distribution functions as obtained from DFT and from an MLP are compared. Statistics were accumulated over 40 ps. Bottom: Equivalent density profile, but this time obtained from an equilibrated 2.5 ns molecular dynamics run. Note the differences for the “second” layer, which depends strongly on the phase-space sampling and only minimally on the chosen unit-cell size. Reproduced from ref. 22. | ||
In order to simulate the hydrogen evolution reaction in acidic medium over Pt, a MLP for Pt/H2O/HCl has been developed in LASP. Then, at a given chemical composition (and thus in absence of “potential control”), the free energy profiles for H2 generation have been assessed via umbrella sampling. These simulations demonstrated the co-existence of the Volmer–Tafel mechanism for high-coverage areas with the Volmer–Heyrovsky mechanism occurring at low to intermediate hydrogen coverages.24
Another application of MLPs is the identification of realistic surface structures for catalysts that are not fully crystalline. For instance, reduced copper oxide surfaces, which are promising for CO2 electroreduction, expose metallic copper sites that are not completely smooth. This has been evidenced via MLP simulations driven by LASP of several nanoseconds that aimed at reproducing the experimental protocol, where the system undergoes stepwise reduction reactions.25 These defect-rich surfaces (see Fig. 3) were shown to feature various active sites with contrasting selectivities for CO2 electroreduction products. They suggest that the square-step active sites are responsible for alcohol products, while planar and convex-square active sites are more favorable for ethylene production.
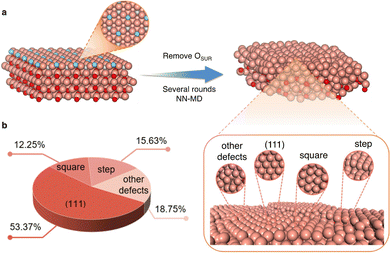 | ||
| Fig. 3 Example of construction of disordered surfaces (here oxide derived Cu) and the statistics of the obtained local active sites. Color code: brown: Cu, blue: surface O, red: subsurface and bulk O. Reproduced from ref. 25. | ||
The effect of an aqueous environment (as in electrocatalysis) compared to gas-phase reactivity has been determined for the prototypical oxidation of CO via a combination of MLP and umbrella sampling, accumulating around 2 ns molecular dynamics.26 These explicit solvent simulations show that water stabilizes one of the reactants (OH*) and thus increases the barrier. Furthermore, the activation entropy was found to change sign between the gas phase and the solution phase, as the solvent forms stronger H-bonds with the initial state (CO, OH*) compared to the transition state (TS), so that the “configurational” entropy (translation and rotation) is more restricted in the initial state than in the TS.
We conclude this part by pointing out a particular challenge for the MLPs in the context of electrocatalysis: In principle, one would wish to simulate the electrochemical potential, as is done in grand-canonical DFT.27 Indeed, the electrochemical potential has a direct impact on the activation energies of the electrocatalytic reactions and is, therefore, necessary to gain the most detailed atomistic insight.28 However, all popular MLPs are agnostic to the electronic structure, thus the electrochemical potential is simply not defined. Hence, further developments are required, e.g., to combine MLPs with simplified physical models that mimic the behavior of electrified interfaces but are, currently, “non-reactive”, i.e., an electron transfer to-/from the electrode to reactants cannot be described.29
Surrogate models for catalytic activity: from microkinetics to proxies
Atomic scale computations give relatively easy access to thermodynamic quantities, but obtaining kinetic information is generally more involved: transition states need to be identified and competing reaction pathways assessed and compared via micro-kinetic simulations, i.e., solving differential equations to obtain the various reaction rates as a function of time. Hence, thermodynamic quantities are rarely enough to fully understand electrocatalysts and even less to discover new ones. The most famous thermodynamic proxy for an electrocatalytic reaction is the hydrogen adsorption energy to construct a so-called volcano plot for the hydrogen evolution reaction.30,31 These thermodynamic proxies can be rationalized by so-called scaling-relations, which establish a close link between the reaction rates as obtained from micro-kinetic simulations and the thermodynamics of key intermediates,32 which usually also holds in electrocatalysis.33 Indeed, scaling relations and the related volcano plots have been very popular about ten years ago34–37 and are still in use due to their favorable complexity–accuracy tradeoff and the thus comparably limited number of datapoints necessary to reliably train them.38,39 However, scaling relations do not provide an actual understanding of the working principles and reaction mechanisms of electrocatalysts.In this context, ML can be exploited for various tasks: first, it can be used to directly learn microkinetics, i.e., identify the most relevant reaction pathways40 and surface states.41 This still requires many expensive DFT computations, but leads to the highest confidence in the obtained results. However, this application of ML is still very much in development and is, so far, not applied to electrocatalysis. This absence of purely theoretical ML-enhanced microkinetic algorithms is probably best explained by the difficulty to identify transition states in electrocatalysis in general.28 Hence, performing these computations in a semi-automatic and semi-systematic manner seems currently too challenging and the community prefers to make more drastic approximations. Nevertheless, the knowledge of the surface reconstruction and dynamics of ternary alloys in the absence of the electrochemical environment can be accelerated via ML41 and is already very valuable for detailed atomistic studies of electrocatalysis. The use of ML to interpret experimental kinetic data will be discussed in the next section.
Second, ML can be used to rationalize thermodynamic proxies, i.e., adsorption energies of H*, OH*, CO*, etc., as a function of material properties. These “surrogate models”, which link atomic or elemental properties (size, number of d-electrons, electronegativity and d-band energies are most popular) to catalytic activity, most often generate insight into the key factors for discriminating activities across materials but are not directly exploitable for catalyst optimization. Still, given the abundance of studies along these lines in the literature, we discuss typical examples. Note that, as reviewed recently,42,43 the rationalization of trends in adsorption energies critically relies on the use of physically relevant descriptors and interpretable ML frameworks.
To start, Liu et al. have reported DFT results of 16 in silico designed transition metal single-atom catalysts stabilized on doped and defective AlP monolayers for oxygen evolution and reduction reaction (OER/ORR). These results have then been rationalized by gradient-boosted regression.44 This study is very typical for the application of ML that rationalizes the DFT data (see ref. 45 for the analogous study of single-atom catalysts stabilized on C2N, which identifies the corresponding transition metal oxide formation energy as an easy descriptor for the 27 tested catalysts). However, this study does not, by construction, lead to the identification of more promising catalysts, as all the possibilities have already been explored via DFT. Similarly, analyzing the DFT data for more than 400 transition metal atoms adsorbed on (reduced) metal oxide, the coordination number of adsorbed species attached to the single-atom catalysts has been identified as a key descriptor for their stability. In this series, oxygen-vacancy stabilized Os on zirconia was found to be most promising for CO2 to CO electroreduction, including in the presence of reaction intermediates.46 However, other physical parameters of the catalysts, such as the electrical conductivity of these oxide supports, have been completely neglected. When investigating and rationalizing the nitrogen-reduction reaction activity of single-atom-alloys, the authors critically assessed the feasibility and the dissolution potentials of the investigated catalysts. This has allowed them to narrow down the number of promising catalysts to only Mo, W, Ru, and Ta/Au (111).47 This study illustrates that stability arguments are very important and at least partially amenable for atomistic simulations.
Going one step further towards catalyst discovery, surrogate models can also be used for in silico screening as exemplified by dual-metal phthalocyanine catalysts for CO2 reduction, see Fig. 4. In this study, a machine-learning model based on 40 systems studied by DFT was used to screen the remaining 250 systems considered.48 Then, the formation energy was computed only for the most relevant ones and their dynamical stability was assessed via short molecular dynamics simulations (5 ps). Finally, Ag-MoPc was suggested to be the most promising CO2 reduction catalyst, which should produce CO at only −0.3 V vs. RHE. However, in contrast to the previous study, the stability of this catalyst under realistic conditions (electrochemical potential, solvent, etc.) has not been considered, i.e., the propensity to react with water or to form hydrides has not been assessed.
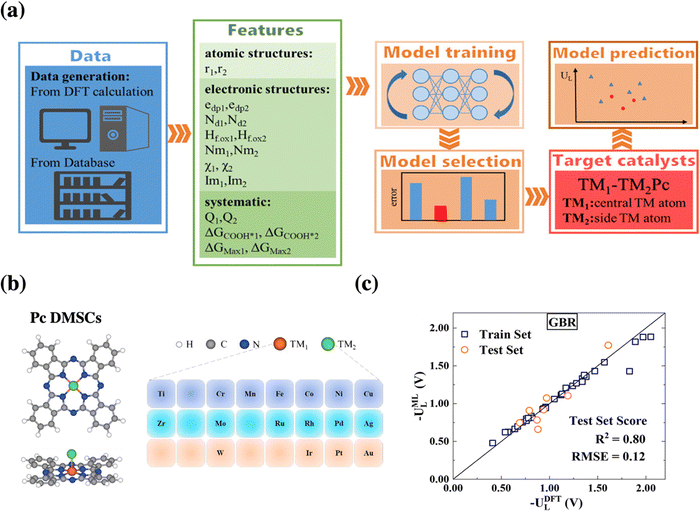 | ||
| Fig. 4 (a) Schematic procedure of the machine-learning-accelerated prediction of catalytic activity of dual metal phthalocyanines, whose structure is illustrated in (b). (c) Presents the parity plot and linear regression between the DFT reference data and the best performing gradient boosting regression (GBR) model for the limiting potential UL for CO2 electroreduction. Reprinted (adapted) with permission from ref. 48. Copyright 2021 American Chemical Society. | ||
In the case of the identification of possible HER catalysts in the MA2Z4 family (where M is a transition metal, A is C, Si, Ge or Sn and Z is N, P or As), DFT computations have been performed on prototype surfaces, i.e., the arrangement was kept fixed across the series to reduce the workload.49 DFT computations of 150 out of 276 considered structures were performed to train an ML-model. Combinations that lead to strong deformations were treated as outliers and removed. The resulting surrogate model estimating the hydrogen adsorption energy was used to predict the HER activity of the remaining 126 catalysts. Subsequently, DFT computations have been performed for the twenty most promising candidates, followed by estimates of their stability. This typical workflow (see ref. 50 for a similar study in the MXene material family for HER catalysts) leads to moderate savings in terms of computational power (only about 30% of the systems have not been computed via DFT). This illustrates a general observation: on the one hand, the larger the combinatorial space, the larger the training set needs to be. On the other hand, in absolute terms, the computational savings do, of course, also increase with increasing search space.
Instead of such “global” ML models, which learn based on “system-wide” descriptors (such as stoichiometry), ML models that only rely on the local description are more powerful for catalysts with a diversity of active sites, such as high-entropy alloys, ensembles of nanoparticles or irregular objects such as dealloyed nanostructures, oxide-derived metal surfaces, etc. Intriguingly, advanced local active-site models do not even rely on geometry optimizations, taking the relaxation energy implicitly into account via graph-convolutional neural networks.51
A prototyping approach, i.e., assuming the same atomic arrangements across the entire family, has been applied to screen 870 M3M′ binary alloys as potential nitrogen reduction catalysts.52 This study was driven by crystal (for assessing the formation energy) and surface (for adsorption energies) graph convolutional neural networks, which were trained on 3040 DFT computations. Screening the 870 potential catalysts with this surrogate model and discarding alloys with positive formation energies, only 10 catalysts have been identified to be sufficiently promising to warrant further DFT computations. Finally, the most promising materials were V3Ir, Tc3Hf, V3Ni and Tc3Ta. Given that the synthetic and radioactive element Tc is not a credible ingredient for practical electrocatalysts, this study also highlights that significant reductions in computational efforts can be achieved by applying reasonable chemical boundaries beforehand.
High-entropy alloys (HEA) are typical examples of a large composition space combined with a very large number of local adsorption sites of different chemical compositions. In order to predict the most promising HEA for CO2 electroreduction, Rossmeisl and co-workers have developed a local description of the active sites via a Gaussian process regression. This model has been exploited to determine the adsorption energy of H and CO and, thus to predict the most promising compositions in terms of selectivity and activity compared to Cu.53 One of the most promising HEA (AuAgPtPdCu) has independently, but concurrently, been tested experimentally and found to be, indeed, highly active.54
As an example of irregular objects, we highlight the study of highly disordered dealloyed Au electrocatalysts for CO2 reduction. Based on a systematic approach, an ML model was built for the properties of active sites. The ML model was trained on about 1000 active sites computed at the DFT level and then applied to the total of more than 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 active sites.55 Later, this approach has been extended to include more realistic activities based on advanced solvation treatments of about 1000 active site motives.56 While the solvation contribution is not negligible, the overall conclusion, i.e., that the rough surfaces are much more active than flat surfaces, remains unchanged, which is reassuring given that it is in agreement with experiment. What this study demonstrates, however, is that even sophisticated solvation energies can be conveniently incorporated in the activity of local active site models.
000 active sites.55 Later, this approach has been extended to include more realistic activities based on advanced solvation treatments of about 1000 active site motives.56 While the solvation contribution is not negligible, the overall conclusion, i.e., that the rough surfaces are much more active than flat surfaces, remains unchanged, which is reassuring given that it is in agreement with experiment. What this study demonstrates, however, is that even sophisticated solvation energies can be conveniently incorporated in the activity of local active site models.
If enough computational power is available and combined with well-crafted workflows and powerful surrogate models, one can perform a catalyst screening in a very diverse compositional space. For instance, Ulissi and co-workers have started with all bulk materials available in the Materials Project, filtering the resulting chemical space according to well defined criteria, with the aim to find a selective partial oxygen reduction catalyst, which would produce H2O2 and not H2O.57 The main results are summarized in Fig. 5. The successive filtering of materials started with bulk materials containing the 48 selected elements available in the Materials Project database (more than ten thousand). From this database, only combinations of one oxophilic metal (e.g., Pd or Al) with an “inactive” element (e.g., Au, S) were kept, leading to more than 900 entries. The next level was removing materials which were estimated to be unstable under reaction conditions relevant for the oxygen reduction reaction according to the corresponding Pourbaix diagrams. This left only about 70 materials to be investigated in more detail. Generating low Miller-index surfaces would give rise to about 70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 active sites for oxygen adsorption. In order to significantly reduce the number of required DFT computations, these active sites have been further categorized according to their likelihood to interact with oxygen. In the end, only about one thousand DFT computations have been performed to identify the most promising candidates that might reduce O2 selectively to H2O2 (see Fig. 5). Note, however, that no oxides have been considered, a family that is likely to be very promising.
000 active sites for oxygen adsorption. In order to significantly reduce the number of required DFT computations, these active sites have been further categorized according to their likelihood to interact with oxygen. In the end, only about one thousand DFT computations have been performed to identify the most promising candidates that might reduce O2 selectively to H2O2 (see Fig. 5). Note, however, that no oxides have been considered, a family that is likely to be very promising.
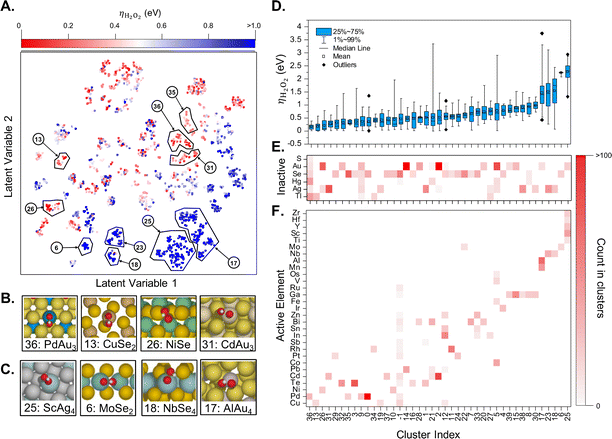 | ||
| Fig. 5 (A) Two-dimensional latent space of surfaces with competitive thermodynamic overpotentials for the production of H2O2, ηH2O2. Examples of catalytically (B) active and (C) inactive surfaces. (D) Box plot of ηH2O2 distribution in each cluster and occurrence heatmaps of (E) inactive and (F) active elements in each cluster. Reprinted (adapted) with permission from ref. 57. Copyright 2021 American Chemical Society. | ||
A second example along the same lines that we would like to highlight is the screening of CO2 electrocatalysts aiming at higher efficiencies for C2 products.58 The computational screening started with the observation that copper seems an essential building block. Therefore, only copper containing intermetallic compounds have been investigated, which still amounts to more than 200 candidates of the Materials Project database. Generating likely surfaces and enumerating the potential active sites for CO adsorption as a proxy led to more than 200![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 active site motives. To explore this huge space, an active-learning algorithm has been applied to limit the DFT computation only to the most important region. Still, some 4000 DFT computations have been performed. From the analysis of the most promising active sites, it became clear that Al–Cu intermetallics seemed very promising. Therefore, corresponding experiments have been performed, demonstrating a significant increase (from 35% to 60%) in ethylene faradaic efficiency compared to bare copper, validating the screening strategy.
000 active site motives. To explore this huge space, an active-learning algorithm has been applied to limit the DFT computation only to the most important region. Still, some 4000 DFT computations have been performed. From the analysis of the most promising active sites, it became clear that Al–Cu intermetallics seemed very promising. Therefore, corresponding experiments have been performed, demonstrating a significant increase (from 35% to 60%) in ethylene faradaic efficiency compared to bare copper, validating the screening strategy.
A fascinating idea to reduce the size of the training sets while spanning the whole periodic table is the use of interpolations across the periodic table.59 In this case, instead of element-specific parameters, period and column-related descriptors are exploited to describe the properties of the various atoms. This is especially valuable for screening bi- and multi-metallic alloys, which are typical electrocatalysts.60 Finally, if sufficient data is available, special ML techniques might be able to perform the so-called inverse design: Instead of “blindly” screening materials to identify the most promising ones, the ML model can predict a material that would correspond most closely to the desired target via generative models. This has recently been exemplified for photoanode properties of Mg–Mn–O ternary materials. The generative model has predicted 23 previously unknown crystal structures with reasonable calculated stability and band gaps.61 If in silico screening could be properly combined with stability and synthesizability models, the road for a fully in silico design of electrocatalysts would be open. For now, the reliable prediction of material stability is restricted to a given class (e.g., perovskites),62 and the best synthesizability models rely on the natural language processed literature,63 which means that they are mostly applicable to well-studied systems.
Despite some successes, inverse design is still in its infancy in heterogeneous (electro-)catalysis and it remains doubtful that the complexity of general inorganic materials (including polymorphism and phase-separation) is amenable to this type of ML. This contrasts with the chemical64 and conformational complexity65 of organic molecules and their adsorption modes on (electro-)catalysts,66 which is at least partially amenable to ML-augmented workflows and generative models.7 Indeed, the reactivity of flexible, polyfunctional molecules such as polyols has been a long-standing issue, addressed via scaling-relations36 and group-additivity,67 before the advent of the more advanced ML-based exploration algorithms.66,68 As an alternative to generative models, materials with potentially suitable properties can be directly retrieved from the literature via natural language processing as exemplified for electron-conducting polymers.69 In general, a word of caution is in place: ML models can be made excellent for interpolations, but tend to fail for extrapolations. This somewhat disappointing feature of ML is intimately linked to its strength: the flexibility of ML models allows them to fit arbitrary functions. However, this comes at the cost of the loss of physical bounds. From this point of view, only introducing physically motivated mathematical descriptions of the problem is likely to lead to better extrapolation capabilities. Therefore, it is likely that (near) optimal materials are already identified during the construction of the training set for the ML model, questioning the added value of the resulting ML model itself.
Assisting experiments: enhanced characterization and synthesis or operation condition optimization
Since ML is closely related to data analysis, it can help in interpreting experimental data, typically obtained during catalyst characterizations, and even much older deconvolution techniques as applied to mass-spectrometry70 or NMR spectra71 of complex mixtures are part of ML. Modern data analysis methods have already been applied to decompose Raman spectra of mixtures,72e.g., of carbon nanotubes, a typical support in electrocatalysis. A recent development that we would like to highlight is the ML-enhanced extended X-Ray absorption fine structure (EXAFS) analysis. For example, an artificial intelligence augmented tool, relying on a genetic algorithm, has been shown to be very powerful across domains, from molecular complexes, to metallic copper and operando studies of the role and location of Sn in Li-ion batteries.73 A competitor of this tool has been developed based on neural networks.74 This NN-EXAFS method specifically targets the elucidation of the structure of mono- and bi-metallic nanoparticles (NPs) and in particular allows to gain insights into thermal disorder effects. Additionally, if the size of the NPs is well defined, this method allows one to reconstruct likely morphologies, which is very valuable for structure–property relationships, including in electrocatalysis. With applications in molten salts,75 the transferability of the NN-EXAFS approach to very challenging media, has already been demonstrated.Analogously, combining an atomistic DFT-based reference library with machine-learning for assignments of the experimental spectra, X-ray absorption near edge structure (XANES) spectra of mixtures can now be easily and consistently analyzed, as demonstrated for iron adsorbed in silica.76 Similarly, the acceleration of the analysis of small-angle X-ray scattering (SAXS) experiments by machine-learning has been proposed.77 This hybrid genetic-algorithm, neural-network approach allows obtaining insights into mixtures of NPs more easily. Likewise, image-processing ML-techniques have been found to be highly beneficial for the high-throughput analysis of transmission electron microscopy (TEM) images.78 Complementarily, a more atomistic approach based on Bayesian deep learning has been developed to reconstruct an atomistic view of (noisy) TEM images.79 This approach, called ARISE, allows the identification of known polymorphs in complex mixtures and has been successfully applied to atomic electron tomography data of metallic FePt nanoparticles, highlighting its relevance for electrocatalytic operando studies. In summary, in these cases ML serves either of two purposes: reducing human-time consuming data analysis (image analysis) and extracting a maximum amount of data based on the recorded spectra via a comparison with a library of (hypothetical and/or previously recorded) materials of the same family. Clearly, these tools will also be very valuable for applications in electrocatalysis.
While the characterization of catalysts is very important for establishing structure–property relationships and understanding trends, it is not directly connected with the catalytic activity itself. For further integration between machine-learning and experiments, we highlight the use of ML to interpret kinetic data. For example, ML was exploited to identify “optimally complex” reaction mechanisms for the hydrogen peroxide reduction and oxidation reaction over carbon nanotubes. Here, ML identified which mechanistic details can, and which cannot, be supported by the available experimental data. Indeed, the data analysis and uncertainty estimations demonstrated that even the simplest “common” three-step model cannot be parametrized satisfactorily, i.e., with enough independent parameters.80 A similar approach, where the experimental kinetic data for proton reduction in acidic medium over platinum was reproduced by a ML-fitted microkinetic model, has been used to determine the adsorption energy of hydrogen on Pt, which was found to be slightly positive.81 This finding suggests that optimal HER activity is related to optimal H adsorption near the relevant (hence slightly larger than the equilibrium) overpotential, in agreement with suggestions from Exner's purely theoretical work on potential dependent volcano curves.82 Analogous analysis of kinetic data of oxygen reduction in acidic medium over platinum single-crystal surfaces demonstrated that the determination of potential-independent kinetic parameters is a drastic approximation.83 Moreover, the obtained results challenged the common idea of a single rate determining step. Instead, again in line with the concept of potential-dependent volcano curves,82 the dominant mechanism changes as a function of the potential, with intermediate regimes where two competing mechanisms coexist. These three studies clearly demonstrate that the interpretation of kinetic data of electrocatalytic reactions can strongly benefit from ML to maximize the compromise between gained insights and data over-interpretation.
As mentioned at the end of the previous subsection, we have substantial doubts that a fully in silico design of electrocatalysts is a goal worth pursuing. However, the literature on ML-accelerated design of experiments, i.e., the ML-driven experimental exploration of a given chemical space seems very promising. This includes catalyst synthesis and operation condition optimizations, both of which can be quite time and resource intensive if done in a “blind” manner. The overall procedure is as follows: The factors that can be varied experimentally (typically reactant concentrations, reaction time, temperature, etc.) are used as input parameters for a ML model that is trained to predict the experimentally measured catalytic activity. The most common ML model for this is a Bayesian Gaussian regression, which includes uncertainties and tends to deliver smooth inter- and extrapolation results, so that new experiments can be proposed reliably in regions where the uncertainty is high (extrapolation), but are predicted to lead to more active materials/conditions. Of course, this supposes that there is a so far undetected optimum in the explored parameter space, which is not always the case. For example, the impact of the ratio between Fe and Ni in an oxide catalyst on the OER activity in alkaline medium has been described via symbolic regression. The model was well able to reproduce the training set, but it turned out that the training set already included the optimal ratio, as subsequently confirmed by additional experiments in its vicinity.84
One way to exploit machine-learning for synthesis optimization is to extract a database of literature results. Then, analyzing the differences in synthesis protocols can allow the identification of the critical parameters. This has been achieved for the specific case of acidic ORR catalysts that are derived from the pyrolysis of zeolite imidazole frameworks (ZIF) impregnated with non-precious metal salts. The database analysis consisting of about 100 entries suggested that in addition to the more obvious factors such as the nature of the transition-metal and the pyrolysis temperature, the pyrolysis time also has a significant influence, likely linked to the formation of pyridinic N–Fe entities which has to be balanced against the evaporation of nitrogen-containing transition metal species. This data-derived hypothesis was then confirmed via dedicated experiments.85
For practitioners, we would also like to highlight that already small training sets can benefit from ML: for the noble-metal free ZIF-derived catalysts for ORR, only 36 datapoints synthesized on a three-dimensional grid (iron precursor, iron/zinc ratio and pyrolysis temperature) were enough to train an ML model that could predict an improved combination. Once synthesized, this formulation was indeed found to lead to a higher activity compared to the training set.86
When more data are available, the loop between experiment for training the ML model and supplementary experiments becomes more impressive. For example, the OER activity of 18 perovskites has been evaluated in alkaline solution under various current densities, leading to a set of 1080 data points, where each experiment had been replicated three times to account for reproducibility and variability of the measurements. Based on this dataset, symbolic regression was able to identify a simple linear relationship between the octahedral and tolerance factors of the perovskites and their OER activity (see Fig. 6). Subsequently, 3000 hypothetical structures have been screened in silico. The synthesis of thirteen of the most promising perovskites was attempted. Five of them have been successfully and purely been obtained and four found to be more active than the previously known perovskites, without dramatic degradation over time.87 This demonstrates both the data intensiveness and also the practical usefulness of such tight experiment/theory feedback-loops.
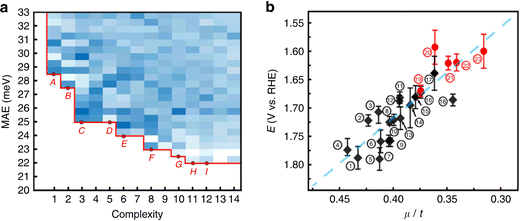 | ||
| Fig. 6 (a) Density plot and Pareto front of the mean absolute error as a function of the complexity of 8640 mathematical formulas. (b) Onset potentials for the OER reaction as a function of the ratio between the octahedral and tolerance factors (μ/t) (black: previously known perovskites; red dots: discovered perovskites). Reproduced from ref. 87. | ||
To close this section and bridge it to the next one mostly dealing with automation, we mention a typical high-dimensional optimization of experimental reaction conditions: To explore the relation between photocatalytic HER activity of an organic polymeric catalyst, the ionic strength, scavengers, presence of organic dyes and the pH, a 10 dimensional search space was explored using a mobile robot.88 With only 688 experiments over eight days driven by a Bayesian search algorithm, the HER activity could be optimized, leading to a six-fold increase in H2 yield compared to the baseline (catalyst plus scavenger). This example perfectly illustrates the combination of robotics and ML-driven design of experiment that strongly facilitates and accelerates catalytic system-optimizations under the constraint that the hardware needs to be available and adapted to the specific reaction at hand.
Acceleration of synthesis, characterization and testing via robotics
High-throughput experiments involving electrocatalyst synthesis, characterization and testing are crucial to provide sufficient high-quality, consistent training data for the ML models.89 Such robotic setups can be effectively combined with ML to create a closed-loop approach for accelerated catalyst development.90First, combinatorial high-throughput synthesis of electrocatalysts can be performed using robotics, which has the ability to automatically tune key parameters such as reaction sequence, temperature, mixing speed, etc.91 These high-throughput techniques enable rapid synthesis of a large variety of catalyst materials with diverse constituents and phases.92 For example, thin film sputtering and pulsed laser deposition have been combined with robotic arms and shadow masks to synthesize a large family of catalysts with variable compositions and thicknesses.93 Jet dispensing was explored as a high-throughput approach to screen and synthesize materials, while controlling important variables such as stoichiometry, solid content and solvent grade.94 Sol–gel synthesis of catalysts can also be performed using multi-channel pipetting robots to dispense precursor solutions into reaction vials automatically.95 Similarly, the synthesis conditions of a metal–organic framework (MOF) in a nine dimensional space has been explored via a robotic platform coupled to a microwave heating system. This has allowed generating and recording sufficient experimental data to reconstruct “chemical intuition”, which relies not only on optimized synthesis conditions, but also on the knowledge of failed attempts. As the authors pointed out, the literature on failed experiments is rather sparse, which limits the application of machine-learning to experimental data.96
Second, high-throughput characterization is important to ensure that the electrocatalyst materials have been synthesized using the correct chemical composition, phase, structure, etc.97 For example, Raman spectroscopy can be combined with automatic translation and rotation stages with a laser autofocus technology to allow rapid characterization of catalyst compositions, surface states and reaction intermediates.98–100 In addition, X-ray-based techniques such as X-ray diffraction and absorption spectroscopy can be equipped with automatic sample changers to characterize a large number of catalysts with minimum human intervention. A new system called RoboRiff with a robotic sample changer and goniometer has been used in cryogenic crystallography for beamline experiments.101 A robotic sample changer has also been developed for high-throughput small-angle X-ray scattering at beamlines, able to characterize hundreds of samples per day.102
Third, high-throughput electrocatalyst testing is key in elucidating structure–property relations.103 Microfluidic reactors can be designed with miniature working, counter and reference electrodes to test catalytic activity in a parallel manner.104 For example, a 100-channel microreactor array is able to measure the catalytic activity of metal alloys with a spatial resolution of 1 mm2.105 High-throughput electrocatalyst screening can also be done using automated scanning droplet cells, which is a scanning probe electrochemistry technique where the droplet probe acts as the electrochemical cell to measure the properties of the sample. This has been used for high-throughput screening of HEA for ORR, identifying the model system Ag–Ir–Pd–Pt–Ru with maximum activity.106 In addition, continuous flow cells with gas diffusion layers may help to automate the quantification of products in CO2 electroreduction.58 In these flow systems, gas chromatography and NMR spectroscopy can be used to detect gaseous and liquid reaction products rapidly in real-time using automatic sample handling and injection systems.107
Outlook and conclusions
Despite the progress and successes achieved in recent years for the acceleration of discovery and optimization of electrocatalysts via machine learning, there are still some challenges and room for the development and improvement of ML methods.MLPs become advantageous when dynamic simulations of nanoseconds for large size electrocatalytic interfaces are necessary. Their training remains challenging, but has become accessible in the last couple of years. Recent successful applications of MLPs are the identification of realistic surface structures of rough catalyst surfaces and the HER mechanism over Pt in acidic medium. However, the construction of MLPs is time consuming since they are system specific. Another limitation is that MLPs cannot describe the electrochemical potential, which is problematic for electrocatalytic reactions. It would thus be desirable to develop MLPs that can mimic the behavior of electrified interfaces.108
As for the discovery of catalysts using surrogate models, the typical approach is using DFT to compute a number of data points to train a ML model, then using the resulting surrogate model to predict the activity of the remaining catalysts. Such an approach can effectively reduce computational efforts. We have also highlighted a recent successful prediction of promising perovskite photocatalysts by performing a technique called “inverse design”. However, this technique is not yet broadly applicable in electrocatalysis due to the complexity of general inorganic materials. Indeed it is challenging to create unique and invertible ML representations for complex materials with specific symmetries, amorphous phases, defects, etc., requiring further research efforts in this direction.109
In terms of ML assisting experiments, two tools for ML-enhanced EXAFS analysis have been reported to be powerful for molecular complexes, bulk crystals and bi-metallic NPs and can capture the thermal disorder effects of materials. In addition, many other ML techniques, i.e., image-processing (high-throughput TEM) and SAXS analysis were also highlighted in this review. These techniques allow human intervention to be significantly reduced, thus accelerating the data generation process, which will be useful in electrocatalytic studies. These applications of ML in experimental data analysis are also strongly connected with ongoing research in explainable artificial intelligence, which seeks to improve interpretability of results and to build trust in human users.110
Finally, in the area of robotics, it is noteworthy that the majority of high-throughput electrocatalysis experiments are still being performed on a laboratory scale. The automated processes need to be scaled up substantially for future commercial applications. Moreover, many experiments are only partially automated, with the need for handling samples manually between steps. This can be potentially addressed by using conveyor belts to transport samples between workstations and hence minimize human intervention. It is also promising to integrate automation into a broader range of characterization techniques, such as using reel-to-reel tape translation systems in high-throughput TEM to enable continuous imaging of samples.111 The use of autonomous laboratories is a promising way to generate high-throughput experimental data for screening within a well-defined family of catalysts or for the optimization of catalytic systems without much human intervention. The automation generally reduces human errors and improves the productivity and reproducibility of experiments but requires large capital investments from research facilities and higher levels of maintenance compared to manually operated machines.
The different approaches covered in this review are perfectly complementary: MLPs target mechanistic understanding, surrogate models (e.g., scaling relations) are aimed at screening, and ML-augmented experiments are most useful for the optimization of catalysts. The ultimate goal is to combine ML and robotics into a truly automated and continuous workflow for closed-loop discovery of materials. Such a self-driving laboratory can accelerate electrocatalyst development, bringing us closer towards a sustainable energy future.112
Author contributions
All authors contributed to researching data and writing the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Z. W. S. acknowledges the Agency for Science, Technology and Research (Central Research Fund Award). S. N. S. and Q. W. benefitted from the support by the LABEX iMUST of the University of Lyon (ANR-10-LABX-0064), created within the “Plan France 2030” set up by the French government and managed by the French National Research Agency (ANR).References
- F. Dinic, K. Singh, T. Dong, M. Rezazadeh, Z. Wang, A. Khosrozadeh, T. Yuan and O. Voznyy, Adv. Funct. Mater., 2021, 31, 2104195 CrossRef CAS.
- H. Mai, T. C. Le, D. Chen, D. A. Winkler and R. A. Caruso, Chem. Rev., 2022, 122, 13478–13515 CrossRef CAS PubMed.
- G. C. Cawley and N. L. C. Talbot, J. Mach. Learn. Res., 2010, 11, 2079–2107 Search PubMed.
- N. Zhang, B. Yang, K. Liu, H. Li, G. Chen, X. Qiu, W. Li, J. Hu, J. Fu, Y. Jiang, M. Liu and J. Ye, Small Methods, 2021, 5, 2100987 CrossRef CAS PubMed.
- A. D. Handoko, S. N. Steinmann and Z. W. Seh, Nanoscale Horiz., 2019, 4, 809–827 RSC.
- M. Wang and H. Zhu, ACS Catal., 2021, 11, 3930–3937 CrossRef CAS.
- S. N. Steinmann, A. Hermawan, M. Bin Jassar and Z. W. Seh, Chem. Catal., 2022, 2, 940–956 CrossRef.
- SwissCAT+, https://swisscatplus.ch, (accessed October 12, 2022).
- Z. W. Seh, J. Kibsgaard, C. F. Dickens, I. Chorkendorff, J. K. Nørskov and T. F. Jaramillo, Science, 2017, 355, eaad4998 CrossRef PubMed.
- J. S. Smith, B. T. Nebgen, R. Zubatyuk, N. Lubbers, C. Devereux, K. Barros, S. Tretiak, O. Isayev and A. E. Roitberg, Nat. Commun., 2019, 10, 2903 CrossRef PubMed.
- P. Liu, C. Verdi, F. Karsai and G. Kresse, Phys. Rev. B, 2022, 105, L060102 CrossRef CAS.
- V. L. Deringer, A. P. Bartók, N. Bernstein, D. M. Wilkins, M. Ceriotti and G. Csányi, Chem. Rev., 2021, 121, 10073–10141 CrossRef CAS.
- J. Behler, Chem. Rev., 2021, 121, 10037–10072 CrossRef CAS.
- Y. Zuo, C. Chen, X. Li, Z. Deng, Y. Chen, J. Behler, G. Csányi, A. V. Shapeev, A. P. Thompson, M. A. Wood and S. P. Ong, J. Phys. Chem. A, 2020, 124, 731–745 CrossRef CAS.
- A. Gao and R. C. Remsing, Nat. Commun., 2022, 13, 1572 CrossRef CAS.
- A. Gomez, Z. A. Piskulich, W. H. Thompson and D. Laage, J. Phys. Chem. Lett., 2022, 13, 4660–4666 CrossRef CAS PubMed.
- S.-D. Huang, C. Shang, P.-L. Kang, X.-J. Zhang and Z.-P. Liu, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2019, 9, e1415 CAS.
- L. Zhang, D.-Y. Lin, H. Wang, R. Car and E. Weinan, Phys. Rev. Mater., 2019, 3, 023804 CrossRef CAS.
- H. Wang, L. Zhang, J. Han and E. Weinan, Comput. Phys. Commun., 2018, 228, 178–184 CrossRef CAS.
- D. T. Limmer, A. P. Willard, P. Madden and D. Chandler, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 4200 CrossRef CAS.
- S. N. Steinmann, R. Ferreira De Morais, A. W. Götz, P. Fleurat-Lessard, M. Iannuzzi, P. Sautet and C. Michel, J. Chem. Theory Comput., 2018, 14, 3238–3251 CrossRef CAS PubMed.
- M. F. C. Andrade, H.-Y. Ko, L. Zhang, R. Car and A. Selloni, Chem. Sci., 2020, 11, 2335–2341 RSC.
- J. Rey, P. Clabaut, R. Réocreux, S. N. Steinmann and C. Michel, J. Phys. Chem. C, 2022, 126, 7446–7455 CrossRef CAS.
- P. S. Rice, Z.-P. Liu and P. Hu, J. Phys. Chem. Lett., 2021, 12, 10637–10645 CrossRef CAS PubMed.
- D. Cheng, Z.-J. Zhao, G. Zhang, P. Yang, L. Li, H. Gao, S. Liu, X. Chang, S. Chen, T. Wang, G. A. Ozin, Z. Liu and J. Gong, Nat. Commun., 2021, 12, 395 CrossRef CAS.
- L.-H. Luo, S.-D. Huang, C. Shang and Z.-P. Liu, ACS Catal., 2022, 12, 6265–6275 CrossRef CAS.
- N. Abidi, K. R. G. Lim, Z. W. Seh and S. N. Steinmann, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2021, 11, e1499 CAS.
- N. Abidi and S. N. Steinmann, Curr. Opin. Electrochem., 2022, 33, 100940 CrossRef CAS.
- A. Coretti, C. Bacon, R. Berthin, A. Serva, L. Scalfi, I. Chubak, K. Goloviznina, M. Haefele, A. Marin-Laflèche, B. Rotenberg, S. Bonella and M. Salanne, J. Chem. Phys., 2022, 157, 18480 Search PubMed.
- R. Parsons, Trans. Faraday Soc., 1958, 54, 1053–1063 RSC.
- S. Trasatti, J. Electroanal. Chem. Interfacial Electrochem., 1972, 39, 163–184 CrossRef CAS.
- T. Bligaard, J. K. Norskov, S. Dahl, J. Matthiesen, C. H. Christensen and J. Sehested, J. Catal., 2004, 224, 206–217 CrossRef CAS.
- J. K. Norskov, J. Rossmeisl, A. Logadottir, L. Lindqvist, J. R. Kitchin, T. Bligaard and H. Jonsson, J. Phys. Chem. B, 2004, 108, 17886–17892 CrossRef CAS.
- P. Ferrin, A. U. Nilekar, J. Greeley, M. Mavrikakis and J. Rossmeisl, Surf. Sci., 2008, 602, 3424–3431 CrossRef CAS.
- I. C. Man, H.-Y. Su, F. Calle-Vallejo, H. A. Hansen, J. I. Martinez, N. G. Inoglu, J. Kitchin, T. F. Jaramillo, J. K. Norskov and J. Rossmeisl, ChemCatChem, 2011, 3, 1159–1165 CrossRef CAS.
- J. Zaffran, C. Michel, F. Auneau, F. Delbecq and P. Sautet, ACS Catal., 2014, 4, 464–468 CrossRef CAS.
- F. Calle-Vallejo, D. Loffreda, M. T. M. Koper and P. Sautet, Nat. Chem., 2015, 7, 403–410 CrossRef CAS.
- E. A. Monyoncho, S. N. Steinmann, P. Sautet, E. A. Baranova and C. Michel, Electrochim. Acta, 2018, 274, 274–278 CrossRef CAS.
- K. Yang, J. Zaffran and B. Yang, Phys. Chem. Chem. Phys., 2020, 22, 890–895 RSC.
- T. Lan and Q. An, J. Am. Chem. Soc., 2021, 143, 16804–16812 CrossRef CAS PubMed.
- J. Yoon, Z. Cao, R. K. Raju, Y. Wang, R. Burnley, A. J. Gellman, A. B. Farimani and Z. W. Ulissi, Mach. Learn. Sci. Technol., 2021, 2, 045018 CrossRef.
- M. Andersen and K. Reuter, Acc. Chem. Res., 2021, 54, 2741–2749 CrossRef CAS.
- B. Wang and F. Zhang, Angew. Chem., Int. Ed., 2022, 61, e202111026 CAS.
- X. Liu, Y. Zhang, W. Wang, Y. Chen, W. Xiao, T. Liu, Z. Zhong, Z. Luo, Z. Ding and Z. Zhang, ACS Appl. Mater. Interfaces, 2022, 14, 1249–1259 CrossRef CAS.
- Y. Ying, K. Fan, X. Luo, J. Qiao and H. Huang, J. Mater. Chem. A, 2021, 9, 16860–16867 RSC.
- R. Qi, B. Zhu, Z. Han and Y. Gao, ACS Catal., 2022, 12, 8269–8278 CrossRef CAS.
- G. Zheng, Y. Li, X. Qian, G. Yao, Z. Tian, X. Zhang and L. Chen, ACS Appl. Mater. Interfaces, 2021, 13, 16336–16344 CrossRef CAS.
- X. Wan, Z. Zhang, H. Niu, Y. Yin, C. Kuai, J. Wang, C. Shao and Y. Guo, J. Phys. Chem. Lett., 2021, 12, 6111–6118 CrossRef CAS.
- J. Zheng, X. Sun, J. Hu, S. Wang, Z. Yao, S. Deng, X. Pan, Z. Pan and J. Wang, ACS Appl. Mater. Interfaces, 2021, 13, 50878–50891 CrossRef CAS.
- X. Wang, C. Wang, S. Ci, Y. Ma, T. Liu, L. Gao, P. Qian, C. Ji and Y. Su, J. Mater. Chem. A, 2020, 8, 23488–23497 RSC.
- G. H. Gu, J. Noh, S. Kim, S. Back, Z. Ulissi and Y. Jung, J. Phys. Chem. Lett., 2020, 11, 3185–3191 CrossRef CAS.
- M. Kim, B. C. Yeo, Y. Park, H. M. Lee, S. S. Han and D. Kim, Chem. Mater., 2020, 32, 709–720 CrossRef CAS.
- J. K. Pedersen, T. A. A. Batchelor, A. Bagger and J. Rossmeisl, ACS Catal., 2020, 10, 2169–2176 CrossRef CAS.
- S. Nellaiappan, N. K. Katiyar, R. Kumar, A. Parui, K. D. Malviya, K. G. Pradeep, A. K. Singh, S. Sharma, C. S. Tiwary and K. Biswas, ACS Catal., 2020, 10, 3658–3663 CrossRef CAS.
- Y. Chen, Y. Huang, T. Cheng and W. A. Goddard, J. Am. Chem. Soc., 2019, 141, 11651–11657 CrossRef CAS PubMed.
- S. Naserifar, Y. Chen, S. Kwon, H. Xiao and W. A. Goddard, Matter, 2021, 4, 195–216 CrossRef CAS.
- S. Back, J. Na and Z. W. Ulissi, ACS Catal., 2021, 11, 2483–2491 CrossRef CAS.
- M. Zhong, K. Tran, Y. Min, C. Wang, Z. Wang, C.-T. Dinh, P. De Luna, Z. Yu, A. S. Rasouli, P. Brodersen, S. Sun, O. Voznyy, C.-S. Tan, M. Askerka, F. Che, M. Liu, A. Seifitokaldani, Y. Pang, S.-C. Lo, A. Ip, Z. Ulissi and E. H. Sargent, Nature, 2020, 581, 178–183 CrossRef CAS PubMed.
- M. J. Willatt, F. Musil and M. Ceriotti, Phys. Chem. Chem. Phys., 2018, 20, 29661–29668 RSC.
- X. Li, R. Chiong and A. J. Page, J. Phys. Chem. Lett., 2021, 12, 5156–5162 CrossRef CAS.
- S. Kim, J. Noh, G. H. Gu, A. Aspuru-Guzik and Y. Jung, ACS Cent. Sci., 2020, 6, 1412–1420 CrossRef CAS.
- G. H. Gu, J. Jang, J. Noh, A. Walsh and Y. Jung, npj Comput. Mater., 2022, 8, 1–8 CrossRef.
- H. Huo, Z. Rong, O. Kononova, W. Sun, T. Botari, T. He, V. Tshitoyan and G. Ceder, npj Comput. Mater., 2019, 5, 1–7 CrossRef.
- M. Krenn, F. Häse, A. Nigam, P. Friederich and A. Aspuru-Guzik, Mach. Learn. Sci. Technol., 2020, 1, 045024 CrossRef.
- X. Guo, L. Fang, Y. Xu, W. Duan, P. Rinke, M. Todorović and X. Chen, J. Chem. Theory Comput., 2022, 18, 4574–4585 CrossRef CAS PubMed.
- G. H. Gu, M. Lee, Y. Jung and D. G. Vlachos, Nat. Commun., 2022, 13, 2087 CrossRef CAS PubMed.
- G. H. Gu, B. Schweitzer, C. Michel, S. N. Steinmann, P. Sautet and D. G. Vlachos, J. Phys. Chem. C, 2017, 121, 21510–21519 CrossRef CAS.
- J. Järvi, B. Alldritt, O. Krejčí, M. Todorović, P. Liljeroth and P. Rinke, Adv. Funct. Mater., 2021, 31, 2010853 CrossRef.
- P. Shetty and R. Ramprasad, iScience, 2021, 24, 101922 CrossRef CAS PubMed.
- J. Meija, Anal. Bioanal. Chem., 2006, 385, 486–499 CrossRef CAS PubMed.
- R. R. Forseth and F. C. Schroeder, Curr. Opin. Chem. Biol., 2011, 15, 38–47 CrossRef CAS PubMed.
- E. Flores, J. Ouyang, F. Lapointe and P. Finnie, Sci. Rep., 2022, 12, 11666 CrossRef CAS.
- J. Terry, M. L. Lau, J. Sun, C. Xu, B. Hendricks, J. Kise, M. Lnu, S. Bagade, S. Shah, P. Makhijani, A. Karantha, T. Boltz, M. Oellien, M. Adas, S. Argamon, M. Long and D. P. Guillen, Appl. Surf. Sci., 2021, 547, 149059 CrossRef CAS.
- J. Timoshenko, C. J. Wrasman, M. Luneau, T. Shirman, M. Cargnello, S. R. Bare, J. Aizenberg, C. M. Friend and A. I. Frenkel, Nano Lett., 2019, 19, 520–529 CrossRef CAS.
- S. Roy, Y. Liu, M. Topsakal, E. Dias, R. Gakhar, W. C. Phillips, J. F. Wishart, D. Leshchev, P. Halstenberg, S. Dai, S. K. Gill, A. I. Frenkel and V. S. Bryantsev, J. Am. Chem. Soc., 2021, 143, 15298–15308 CrossRef CAS.
- A. A. Guda, S. A. Guda, A. Martini, A. N. Kravtsova, A. Algasov, A. Bugaev, S. P. Kubrin, L. V. Guda, P. Šot, J. A. van Bokhoven, C. Copéret and A. V. Soldatov, npj Comput. Mater., 2021, 7, 1–13 CrossRef.
- C. M. Heil, A. Patil, A. Dhinojwala and A. Jayaraman, ACS Cent. Sci., 2022, 8, 996–1007 CrossRef CAS PubMed.
- L. Yao, Z. Ou, B. Luo, C. Xu and Q. Chen, ACS Cent. Sci., 2020, 6, 1421–1430 CrossRef CAS.
- A. Leitherer, A. Ziletti and L. M. Ghiringhelli, Nat. Commun., 2021, 12, 6234 CrossRef CAS PubMed.
- A. A. Kurilovich, C. T. Alexander, E. M. Pazhetnov and K. J. Stevenson, Phys. Chem. Chem. Phys., 2020, 22, 4581–4591 RSC.
- H. Ooka, M. E. Wintzer and R. Nakamura, ACS Catal., 2021, 11, 6298–6303 CrossRef CAS.
- K. S. Exner, ACS Catal., 2020, 12607–12617 CrossRef CAS.
- K. Sakaushi, A. Watanabe, T. Kumeda and Y. Shibuta, ACS Appl. Mater. Interfaces, 2022, 14, 22889–22902 CrossRef CAS.
- J. Park, S. Kang and J. Lee, J. Mater. Chem. A, 2022, 10, 15975–15980 RSC.
- R. Ding, Y. Chen, P. Chen, R. Wang, J. Wang, Y. Ding, W. Yin, Y. Liu, J. Li and J. Liu, ACS Catal., 2021, 11, 9798–9808 CrossRef CAS.
- M. R. Karim, M. Ferrandon, S. Medina, E. Sture, N. Kariuki, D. J. Myers, E. F. Holby, P. Zelenay and T. Ahmed, ACS Appl. Energy Mater., 2020, 3, 9083–9088 CrossRef.
- B. Weng, Z. Song, R. Zhu, Q. Yan, Q. Sun, C. G. Grice, Y. Yan and W.-J. Yin, Nat. Commun., 2020, 11, 3513 CrossRef CAS.
- B. Burger, P. M. Maffettone, V. V. Gusev, C. M. Aitchison, Y. Bai, X. Wang, X. Li, B. M. Alston, B. Li, R. Clowes, N. Rankin, B. Harris, R. S. Sprick and A. I. Cooper, Nature, 2020, 583, 237–241 CrossRef CAS PubMed.
- H. W. Turner, A. F. Volpe and W. H. Weinberg, Surf. Sci., 2009, 603, 1763–1769 CrossRef CAS.
- D. P. Tabor, L. M. Roch, S. K. Saikin, C. Kreisbeck, D. Sheberla, J. H. Montoya, S. Dwaraknath, M. Aykol, C. Ortiz, H. Tribukait, C. Amador-Bedolla, C. J. Brabec, B. Maruyama, K. A. Persson and A. Aspuru-Guzik, Nat. Rev. Mater., 2018, 3, 5–20 CrossRef CAS.
- N. M. Nursam, X. Wang and R. A. Caruso, ACS Comb. Sci., 2015, 17, 548–569 CrossRef CAS.
- K. Potgieter, A. Aimon, E. Smit, F. von Delft and R. Meijboom, Chem.: Methods, 2021, 1, 192–200 CAS.
- Y. Shi, B. Yang, P. D. Rack, S. Guo, P. K. Liaw and Y. Zhao, Mater. Des., 2020, 195, 109018 CrossRef CAS.
- N. Scoutaris, A. Nion, A. Hurt and D. Douroumis, CrystEngComm, 2016, 18, 5079–5082 RSC.
- P. Cong, R. D. Doolen, Q. Fan, D. M. Giaquinta, S. Guan, E. W. McFarland, D. M. Poojary, K. Self, H. W. Turner and W. H. Weinberg, Angew. Chem., Int. Ed., 1999, 38, 483–488 CrossRef PubMed.
- S. M. Moosavi, A. Chidambaram, L. Talirz, M. Haranczyk, K. C. Stylianou and B. Smit, Nat. Commun., 2019, 10, 539 CrossRef CAS PubMed.
- A. Ludwig, npj Comput. Mater., 2019, 5, 1–7 CrossRef.
- C. Westley, Y. Xu, A. J. Carnell, N. J. Turner and R. Goodacre, Anal. Chem., 2016, 88, 5898–5903 CrossRef CAS PubMed.
- A. S. Mondol, M. D. Patel, J. Rüger, C. Stiebing, A. Kleiber, T. Henkel, J. Popp and I. W. Schie, Sensors, 2019, 19, 4428 CrossRef CAS.
- S. Goldrick, A. Umprecht, A. Tang, R. Zakrzewski, M. Cheeks, R. Turner, A. Charles, K. Les, M. Hulley, C. Spencer and S. S. Farid, Processes, 2020, 8, 1179 CrossRef CAS.
- D. Nurizzo, M. W. Bowler, H. Caserotto, F. Dobias, T. Giraud, J. Surr, N. Guichard, G. Papp, M. Guijarro, C. Mueller-Dieckmann, D. Flot, S. McSweeney, F. Cipriani, P. Theveneau and G. A. Leonard, Acta Crystallogr., Sect. D: Struct. Biol., 2016, 72, 966–975 CrossRef CAS PubMed.
- A. Round, F. Felisaz, L. Fodinger, A. Gobbo, J. Huet, C. Villard, C. E. Blanchet, P. Pernot, S. McSweeney, M. Roessle, D. I. Svergun and F. Cipriani, Acta Crystallogr., Sect. D: Biol. Crystallogr., 2015, 71, 67–75 CrossRef CAS PubMed.
- C. Ortega, D. Otyuskaya, E.-J. Ras, L. D. Virla, G. S. Patience and H. Dathe, Can. J. Chem. Eng., 2021, 99, 1288–1306 CrossRef CAS.
- E. J. Roberts, S. E. Habas, L. Wang, D. A. Ruddy, E. A. White, F. G. Baddour, M. B. Griffin, J. A. Schaidle, N. Malmstadt and R. L. Brutchey, ACS Sustainable Chem. Eng., 2017, 5, 632–639 CrossRef CAS.
- P. Kondratyuk, G. Gumuslu, S. Shukla, J. B. Miller, B. D. Morreale and A. J. Gellman, J. Catal., 2013, 300, 55–62 CrossRef CAS.
- T. A. A. Batchelor, T. Löffler, B. Xiao, O. A. Krysiak, V. Strotkötter, J. K. Pedersen, C. M. Clausen, A. Savan, Y. Li, W. Schuhmann, J. Rossmeisl and A. Ludwig, Angew. Chem., Int. Ed., 2021, 60, 6932–6937 CrossRef CAS PubMed.
- S. W. Krska, D. A. DiRocco, S. D. Dreher and M. Shevlin, Acc. Chem. Res., 2017, 50, 2976–2985 CrossRef CAS.
- S. N. Steinmann and Z. W. Seh, Nat. Rev. Mater., 2021, 6, 289–291 CrossRef CAS.
- B. Sanchez-Lengeling and A. Aspuru-Guzik, Science, 2018, 361, 360–365 CrossRef CAS.
- A. Barredo Arrieta, N. Díaz-Rodríguez, J. Del Ser, A. Bennetot, S. Tabik, A. Barbado, S. Garcia, S. Gil-Lopez, D. Molina, R. Benjamins, R. Chatila and F. Herrera, Inf. Fusion, 2020, 58, 82–115 CrossRef.
- W. Yin, D. Brittain, J. Borseth, M. E. Scott, D. Williams, J. Perkins, C. S. Own, M. Murfitt, R. M. Torres, D. Kapner, G. Mahalingam, A. Bleckert, D. Castelli, D. Reid, W.-C. A. Lee, B. J. Graham, M. Takeno, D. J. Bumbarger, C. Farrell, R. C. Reid and N. M. da Costa, Nat. Commun., 2020, 11, 4949 CrossRef CAS PubMed.
- Z. Yao, Y. Lum, A. Johnston, L. M. Mejia-Mendoza, X. Zhou, Y. Wen, A. Aspuru-Guzik, E. H. Sargent and Z. W. Seh, Nat. Rev. Mater., 2022 DOI:10.1038/s41578-022-00490-5.
| This journal is © The Royal Society of Chemistry 2023 |



