Ab initio treatment of molecular Coster–Kronig decay using complex-scaled equation-of-motion coupled-cluster theory

Abstract

Vacancies in the L₁ shell of atoms and molecules can decay non-radiatively via Coster–Kronig decay whereby the vacancy is filled by an electron from the L_2,3 shell while a second electron is emitted into the ionization continuum. This process is akin to Auger decay, but in contrast to Auger electrons, Coster–Kronig electrons have rather low kinetic energies of less than 50 eV. In the present work, we extend recently introduced methods for the construction of molecular Auger spectra that are based on complex-scaled equation-of-motion coupled-cluster theory to Coster–Kronig decay. We compute ionization energies as well as total and partial decay widths for the 2s⁻¹ states of argon and hydrogen sulfide and construct the L₁L_2,3M Coster–Kronig and L₁MM Auger spectra of these species. Whereas our final spectra are in good agreement with the available experimental and theoretical data, substantial disagreements are found for various branching ratios suggesting that spin–orbit coupling makes a major impact on Coster–Kronig decay already in the third period of the periodic table.

---

1 Introduction

Core-vacant states of atoms and molecules can relax by means of Auger decay, where the core vacancy is filled, while a second electron is emitted carrying away the excess energy.^1,2 By measuring the kinetic energy of these Auger electrons, information on the electronic structure of molecules,^3–5 materials,⁶ surfaces,⁷ and nanostructures^8,9 can be obtained. While Auger electrons originating from states with K-shell vacancies typically have energies of hundreds or even thousands of electron volts, electrons originating from states with vacancies in higher shells can be substantially slower with energies in the range of 25–50 eV, i.e., more similar to intermolecular Coulombic decay^10,11 than to K-shell Auger decay.

These low-energy electrons stem from Coster–Kronig transitions¹² in which the core hole is filled by an electron from the same shell, while a second electron from a higher shell is emitted. Electronic states of atoms in the third period of the periodic table with empty 2s orbitals, i.e., L₁-shell vacancies in X-ray notation, are perhaps the simplest electronic structures where Coster–Kronig decay is energetically possible. These states can be specifically prepared by X-rays but they are also the result of Auger decay of K-shell vacancies. Because of the relatively low energy of Coster–Kronig electrons, they can interact more strongly with matter than Auger electrons, which implies that they are relevant for radiation damage of biological systems similar to other secondary electrons.

In Coster–Kronig decay of L₁-shell vacancies, an electron from a 2p orbital, i.e., the L_2,3 shell in X-ray notation, fills the empty 2s orbital and an electron from the M shell, which is formed by the 3s, 3p, and potentially 3d orbitals, is emitted. It is well established that this process is more efficient than K-shell Auger decay,^2,13–18 resulting in large decay widths of the order of several eV, which corresponds to extraordinarily short lifetimes of less than one femtosecond.

Coster–Kronig decay of L₁-shell vacancies is always accompanied by decay channels in which both electrons stem from higher-lying shells, i.e., in the case of the third period of the periodic table L₁MM decay. These latter decay channels have, however, much smaller widths than the Coster–Kronig channels. Notably, a decay process where all three involved orbitals belong to the same shell is energetically forbidden in the third period of the periodic table. These so-called super-Coster–Kronig transitions have, however, been described for 3d transition metals and heavier elements.^19–21

Ample experimental data have been reported about Coster–Kronig decay in atoms, especially in noble gases^22–29 but also, for example, in magnesium³⁰ and potassium.³¹ For argon, in particular, the Coster–Kronig spectrum and the branching ratios between different peaks are known with considerable precision.²⁵ Thanks to theoretical modeling using approximate Hartree–Fock theory,³² Dirac–Hartree–Slater theory,^17,18 Dirac–Hartree–Fock theory,^33–36 multiconfigurational Dirac–Hartree–Fock (MCDHF) theory,^{27,28,37–41} and many-body Green's function theory^42,43 most aspects of these spectra are now well understood and signals have been unequivocally assigned to decay channels.

For molecules, on the other hand, much less data are available. Noteworthy are experimental studies of hydrogen chloride,⁴⁴ silicon dioxide,⁴⁵ hydrogen sulfide,^46,47 thiouracil,⁴⁸ and solvated sodium, magnesium and aluminium cations.⁴⁹Ab initio modeling of molecular Coster–Kronig decay based on many-electron wave functions has not been reported, which illustrates that it is difficult to extend theoretical methods designed for atoms to molecules.

Some of us recently developed a method to compute Auger decay rates from complex-scaled wave functions of core-ionized states.^50,51 In complex scaling (CS),^52–55 the Hamiltonian has complex eigenenergies whose imaginary parts describe the decay width. There is no need to model the wave function of the emitted electron explicitly. Whereas the direct application of CS to the Hamiltonian only works for atoms but not for molecules, the approach has been extended to molecules by means of complex-scaled basis functions (CBFs).^56,57 The CBF method has been used to model KLL Auger spectra in the second period of the periodic table,^58,59 interatomic and intermolecular Coulombic decay,⁶⁰ autoionization of Rydberg states,⁶¹ and most recently K-edge Auger decay of the zinc atom and the hexaaquazinc(II) complex.⁶²

In the present work, we extend this approach to Coster–Kronig decay of L₁-shell vacancies, taking argon and hydrogen sulfide as examples. In addition, we also study the L₁MM Auger spectra of these two species. The investigation of argon serves to establish the accuracy of our approach as there are two well-resolved experimental Coster–Kronig spectra available,^23,25 and in addition a theoretical spectrum based on MCDHF wave functions²⁵ as well as partial decay widths computed with MCDHF.⁴¹ Additional validation is provided by the comparison between CS and CBF results, which is only possible for atoms. With the investigation of hydrogen sulfide, for which only experimental spectra with much lower resolution are available,^46,47 we show that our approach can be easily applied to molecular Coster–Kronig decay as well.

The remainder of the manuscript is structured as follows: in Section 2, the details of our computations are given, whereas Section 3 presents our results for ionization energies and total decay widths as well as the L₁L_2,3M Coster–Kronig spectra and L₁MM Auger spectra of argon and hydrogen sulfide. Section 4 provides our general conclusions.

2 Computational details

To simulate an Auger or Coster–Kronig spectrum, two quantities are needed for each decay channel: the kinetic energy of the emitted electrons and the decay rate. To compute these quantities, we use an approach that is based on complex-scaled equation-of-motion coupled-cluster (EOM-CC) theory.^50,63–66

We treat the decay as a two-step process in which the second step, the filling of the core hole and the ejection of the electron is independent of the creation of the core hole.^67,68 Because of energy conservation, the energy of the emitted electron equals the energy difference between the initial core-ionized state and the final doubly ionized states. To compute the energies of these states, we use the ionization potential and the double ionization potential variants of EOM-CC with singles and doubles excitations (EOM-IP-CCSD and EOM-DIP-CCSD).^69–73

The decay widths are obtained from EOMIP-CCSD calculations on the initial core-ionized states in which either the Hamiltonian is complex scaled (CS-EOMIP-CCSD) or functions with a complex-scaled exponent are included in the basis set (CBF-EOM-IP-CCSD). The total width Γ is obtained from

Γ = 2·(Im(E_coreIP) − Im(E₀)) (1)

where E_coreIP and E₀ are the energies of the core-ionized state and the neutral reference state. The optimal complex scaling angles θ_opt are determined by minimizing |d(E_coreIP − E₀)/dθ|⁷⁴ and reported in the ESI.†

The partial widths for the decay channels are determined at θ_opt by means of the Auger Channel Projector that excludes certain amplitudes from the EOM-CC excitation manifold.⁵¹ This can be viewed as a generalized core–valence separation (CVS).⁷⁵ Specifically, to compute the width γ_ij of a decay channel that involves the valence orbitals i and j, a complex-variable EOM-IP-CCSD calculation is performed in which the corresponding doubles amplitudes r^a_ij are set to zero for all a. The difference between Γ obtained in this calculation and Γ from a complex-variable EOM-IP-CCSD calculation with the full excitation manifold defines γ_ij.

The Auger Channel Projector calculations yield the partial widths in terms of orbital pairs of the initial state and hence do not account for relaxation in the final states. To incorporate these relaxation effects into the description, the partial widths are assigned to the EOM-DIP-CCSD energies using the squared EOM-DIP-CCSD amplitudes as weighting factors.^58,59 In all calculations reported here, these weighting factors are close to one, indicating relatively little relaxation of the wave function upon filling a 2s⁻¹ core hole in comparison to what we observed in earlier work on 1s⁻¹ core holes.

Notably, we were not able to describe the 2s⁻¹ states of argon and hydrogen sulfide in terms of CCSD wave functions based on core-vacant Hartree–Fock determinants. The CCSD equations for these states suffer from convergence problems because the unoccupied 2s orbital is close in energy to other occupied orbitals. As a consequence, the evaluation of partial widths from a decomposition of the CCSD energy that we previously used for 1s⁻¹ states^50,62 is not possible for the 2s⁻¹ states that are of interest here.

For comparison purposes, we also performed Fano-EOM-CCSD calculations in which the partial widths are obtained as transition amplitudes between an initial state represented by a CVS-EOM-IP-CCSD⁷⁶ wave function and a final state represented by a product of an EOM-DIP-CCSD wave function and a plane wave.⁷⁷ We note that the core orbitals are frozen in the CCSD reference state on which the Fano-EOM-CCSD calculations are based, whereas no orbitals are frozen in all other calculations. Additionally, we constructed spectra in which the density of EOM-DIP-CCSD states replaces the partial decay widths, which is equivalent to assuming that every channel has the same decay width.

CS-EOM-IP-CCSD and EOM-DIP-CCSD calculations on argon were carried out using the aug-cc-pCV5Z basis that was further augmented by up to eight complex-scaled s, p, and d-shells for the corresponding CBF-EOM-IP-CCSD calculations. EOM-DIP-CCSD calculations on hydrogen sulfide were done in a basis set denoted as aug-cc-pCVTZ(5sp), which uses s and p-shells from the aug-cc-pCV5Z basis, whereas the shells with higher angular momentum are taken from aug-cc-pCVTZ. For the corresponding CBF-EOM-IP-CCSD calculations, four to eight complex-scaled s, p, and d-shells were added to the basis sets of sulfur and hydrogen. The exponents of all complex-scaled shells were determined using the procedure described in ref. 50 and are reported in the ESI.† They roughly span the range from 10 to 0.01 and include thus functions that are significantly more diffuse than those that we used in previous studies of K-shell Auger decay.

The SH bond length and the HSH bond angle of hydrogen sulfide are 1.3338 Å and 92.2°, respectively, in all calculations. All spectra are normalized such that the most intense peak has the same height with every computational approach. To construct the final spectra, we used a Lorentzian broadening function with a full width at half maximum (FWHM) of 2 eV, except for the L₁MM spectrum of argon, where the FWHM is 3 eV. All electronic-structure calculations were carried out using the Q-Chem program package, version 6.0.⁷⁸ Note that all irreducible representations are reported according to Q-Chem's convention, which differs from Mulliken's convention.

3 Results

3.1 Ionization energies

Table 1 shows the ionization energies for the 2s⁻¹ states of argon and hydrogen sulfide computed with different flavors of EOM-IP-CCSD. The corresponding double ionization energies are reported in the ESI.† The CBF-EOM-IP-CCSD results in Table 1 agree with the experimentally determined ionization energies for argon³⁶ and H₂S⁴⁷ within 0.3 eV and less than 0.1 eV, respectively, although we note that a rigorous comparison would require the consideration of triple excitations as well as relativistic corrections, and for H₂S also the treatment of vibrational effects.

Table 1 Ionization energies of the 2s⁻¹ states of argon and hydrogen sulfide in eV computed with different methods. The aug-cc-pCV5Z basis set is used for Ar, the aug-cc-pCVTZ(5sp) basis set for H₂S. In CBF calculations, the basis sets are further augmented by 8 complex-scaled s, p, and d-shells

	Ar	H2S
EOM-IP-CCSD	326.58	—
CVS-EOM-IP-CCSD	324.87	234.50
CS-EOM-IP-CCSD	325.90	—
CBF-EOM-IP-CCSD	325.96	234.99
Experiment^36,47	326.25 ± 0.05	235.0 ± 0.1

---

Our results for argon illustrate that complex scaling decreases the ionization energy by about 0.7 eV even though a very large basis set is used. The difference between complex scaling of the Hamiltonian and of the basis set is, however, negligible. Notably, CVS decreases the energy by 1.7 eV with respect to regular EOM-IP-CCSD and by 1.0 eV with respect to CBF-EOM-IP-CCSD, leading to a significantly less good agreement with the experiment. This is similar to the 1.3 eV difference between CBF-EOM-IP-CCSD and CVS-EOM-IP-CCSD that we observed in recent work on 1s⁻¹ states of benzene.⁵⁸ In the case of H₂S, the difference between CBF-EOM-IP-CCSD and CVS-EOM-IP-CCSD amounts to only 0.5 eV. Here, we were, however, not able to converge the EOM-IP-CCSD equations without CVS or employing CBFs.

3.2 Decay width of the 2s⁻¹ state of argon

The upper part of Table 2 shows total decay widths for the 2s⁻¹ state of argon computed with CS-EOM-IP-CCSD and CBF-EOM-IP-CCSD using different basis sets. This state has a decay width of more than 2 eV, which corresponds to a very short lifetime of less than one third of a femtosecond. The width is 4–5 times as large as that of the 1s⁻¹ state of argon (0.46 eV)⁷⁹ and almost 10 times as large as that of the 1s⁻¹ state of neon (0.26 eV).⁸⁰

Table 2 Total decay widths and sum of partial decay widths of the 2s⁻¹ states of argon and hydrogen sulfide in meV computed with different methods. For CBF calculations, the complex-scaled shells are denoted in italics. Experimental values are given as well

Method	Basis set	Total width from eqn (1)	Sum of all partial widths	Sum of partial widths of
				L2,3M channels	MM channels
Argon
CS-EOM-CCSD	aug-cc-pCVQZ	2531.8	2347.3	2273.2	74.1
CS-EOM-CCSD	aug-cc-pCV5Z	2632.3	2450.2	2373.3	77.0
CBF-EOM-CCSD	aug-cc-pCV5Z+4(spd)	1053.8	872.2	820.0	52.4
CBF-EOM-CCSD	aug-cc-pCV5Z+6(spd)	2100.9	2294.6	2216.4	78.2
CBF-EOM-CCSD	aug-cc-pCV5Z+8(spd)	2668.6	2334.2	2259.0	75.3
Semi-empirical theory^15		1630
Dirac–Hartree–Slater^17		2716		2595	121
Dirac–Hartree–Fock^36		1850
MCDHF^23				2330
MCDHF^41		2092		2037	55
Experiment^36		2250 ± 50
Experiment^22		1840 ± 200
Hydrogen sulfide
CBF-EOM-CCSD	aug-cc-pCVTZ(5sp)+4(spd)	1119.1	1020.0	963.4	56.9
CBF-EOM-CCSD	aug-cc-pCVTZ(5sp)+6(spd)	1603.2	1407.4	1362.4	44.9
CBF-EOM-CCSD	aug-cc-pCVTZ(5sp)+8(spd)	1672.2	1440.5	1396.5	44.1
Semi-empirical theory^15	(S atom)	1490
Approximate HF theory^32	(S atom)	2590
Experiment^47		1800

---

If double Auger decay and other processes involving more than two electrons are neglected, the 2s⁻¹ state of argon has 14 decay channels that are in principle open, meaning that the final electronic state has a lower energy so that the decay process is energetically allowed. The partial widths for these 14 channels are reported in the ESI.† Eight of them involve the 2p shell and form the L₁L_2,3M Coster–Kronig spectrum. These channels account for more than 96% of the total decay width, whereas the remaining six channels, which form the L₁MM Auger spectrum, account for less than 4%. A conspicuous difference to K-shell Auger decay is the 25% contribution that the triplet decay channels deliver to the total width. By contrast, triplet states contribute only 6% to the decay width of the 1s⁻¹ state of neon.^80,81 Notably, MCDHF calculations, which take account of spin–orbit coupling, yielded a 55% contribution of triplet channels to the width of the 2s⁻¹ state of argon.⁴¹

The comparison of our results to the experimental value for the total width (2.25 eV)³⁶ suggests that the sum of partial widths is a better estimate of the total width than the value obtained from eqn (1). Using the former approach, CBF-EOM-IP-CCSD overestimates the experimental value by less than 4%. Interestingly, Dirac–Hartree–Fock theory combined with the Green's function method yielded a value for the total width that is 20% lower, while MCDHF theory yielded a value that is only 10% lower.⁴¹ This suggests that electron correlation increases the decay width, which is in line with previous results for other electronic resonances.⁵⁵ We also note a second MCDHF value²³ for the sum of the width of the L_2,3M Coster–Kronig channels that differs from our result by no more than 3%.

The significant difference of 7–20% between the sum of all partial widths and the total width evaluated according to eqn (1) is similar to what has been observed in previous treatments of Auger decay with CBF- and CS-EOM-CCSD. It can be traced back to EOM-IP-CCSD doubles amplitudes r^a_ij where i or j is a core orbital. The resulting configurations in the EOM-IP-CCSD wave function where the 2s⁻¹ orbital is unoccupied do not correspond to open decay channels as they are too high in energy, but they deliver a non-zero contribution to the total width. This effect is, in principle, present in every CS or CBF calculation, but it is in the present case apparently more pronounced in the CBF calculations. Table 2 shows deviations of 330 meV (14%) between Γ from eqn (1) and the sum of partial widths for CBF-EOM-IP-CCSD in the largest basis set, whereas this value amounts to 180 meV (7%) for CS-EOM-IP-CCSD. Between each other, CS and CBF calculations differ by no more than 5%.

Table 2 also illustrates a need for large basis sets, which is typical for complex-scaled calculations. However, there are some aspects that are different from calculations on 1s⁻¹ states: firstly, the aug-cc-pCVQZ basis already recovers 96% of the total decay width in the present case, whereas this value amounted to only 64% in previous CS-EOM-IP-CCSD calculations on the 1s⁻¹ state of neon.⁵⁰ Secondly, more diffuse complex-scaled shells are required for the description of Coster–Kronig decay than for the description of K-shell Auger decay. Whereas two to four complex-scaled s, p, and d shells are sufficient for K-shell Auger decay, Table 2 demonstrates that the use of four complex-scaled s, p, and d-shells produces a width for the 2s⁻¹ state of argon that is too small by a factor of ca. 2.7. Upon including six complex-scaled shells the sum of partial widths is recovered almost in full, but the branching ratios between the channels still change substantially if two further shells are added as is apparent from the values reported in the ESI.† This need for more diffuse shells may be related to the substantially lower energy of the emitted electron in Coster–Kronig decay as compared to K-shell Auger decay.⁵⁰

Notably, the basis-set dependence of the decay channels is very different. The six MM decay channels as well as some of the eight L_2,3M Coster–Kronig channels are already well described with six or even four complex-scaled s, p, and d shells, whereas the width of other channels changes by more than a factor of three when going from six to eight complex-scaled shells. Also, we note that the agreement between CBF- and CS-EOM-IP-CCSD is somewhat better for the MM decay channels than for the L_2,3M channels.

3.3 Decay width of the 2a₁⁻¹ state of hydrogen sulfide

The lower part of Table 2 shows total decay widths for the 2a₁⁻¹ state of H₂S. Because of the lower point group, the 14 decay channels of the 2s⁻¹ state of argon correspond to 40 channels in the case of H₂S. Partial widths for all of them are reported in the ESI.† There are 24 L_2,3M channels, which form the Coster–Kronig spectrum and account for 97% of the total decay width, while the remaining 16 MM channels account for only 3% of the width. Similar to argon, triplet channels contribute ca. 25% to the decay width, both for the L_2,3M and the MM channels. Interestingly, Fano-EOM-CCSD yields a triplet contribution of 82%, which neither agrees with CBF-EOM-IP-CCSD nor MCDHF results for argon. Notably, it has been argued that the representation of the emitted electron by a plane wave in Fano-EOM-CCSD calculations may lead to an overestimation of the triplet contribution.⁸²

Whereas CBF-EOM-IP-CCSD yields very similar branching ratios for argon and H₂S, a big difference is found for the total widths themselves as that of the 2a₁⁻¹ state of H₂S is only 62% of that of the 2s⁻¹ state of argon. Very similar ratios are observed for the widths of the L_2,3M and MM channels separately. Although this is qualitatively in line with previous results that found a stronger dependence on nuclear charge for Coster–Kronig widths than for K-shell Auger widths,¹⁶ the comparison of the experimentally determined widths of argon (2.25 eV)³⁶ and hydrogen sulfide (1.80 eV)⁴⁷ delivers a value of 80% for this ratio.

Similar to argon, we observe a significant difference of ca. 15% between the sum of all partial widths and the total width from eqn (1). Different from argon, however, the value from eqn (1) is in better agreement with the experiment. A rigorous statement about the exact value of the total width is difficult to make because only one experimental value and no other theoretical values have been reported for H₂S. Also, there is a big disagreement of more than 1 eV between values computed for the total width of the sulfur atom with lower-level theories.^15,32 In any case, the 2a₁⁻¹ state of H₂S is much broader than the 1a₁⁻¹ states of H₂S (0.59 eV)¹⁵ and H₂O (0.16 eV),⁸³ illustrating again the efficiency of Coster–Kronig decay.

We note that the basis-set dependence of the width is somewhat less pronounced for H₂S than for argon. With 6 complex-scaled s, p, and d shells, more than 95% of the total width are captured and almost all partial widths are converged as well. This may be related to the lower point group of H₂S as similar trends were observed for K-shell Auger decay before.⁵⁹ Interestingly, there are three decay channels of H₂S that have negative widths of 5 to 15 meV even in the largest basis set. This unphysical result has not been encountered for K-shell Auger decay and may indicate incompleteness of the basis set.

3.4 L₁L_2,3M Coster–Kronig spectrum of argon

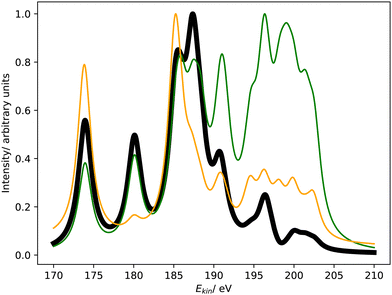
Fig. 1 compares the Coster–Kronig spectra of argon computed with CS- and CBF-EOM-IP-CCSD to two experimental spectra.^23,25 In addition, we compare in Fig. 2 our CS-EOM-IP-CCSD spectrum to results from MCDHF calculations and experimental data that were obtained from Auger multi-electron coincidence spectroscopy.²⁵ Because the resolution of the experimental data is higher, we applied a broadening function with a FWHM of only 0.5 eV to the theoretical spectra in this figure. In addition, the convergence of the CBF-EOMIP-CCSD spectrum with respect to the number of complex-scaled shells in the basis set is illustrated in the ESI.†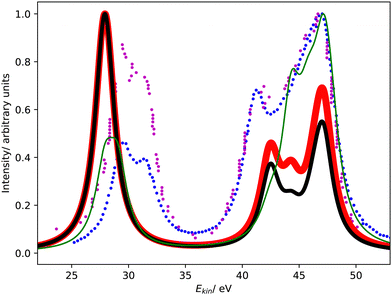

Fig. 1 L₁L_2,3M Coster–Kronig spectrum of argon. Partial decay widths were computed with CS-EOM-CCSD (red solid line) and CBF-EOM-CCSD (black solid line), and assuming the same width for every channel (green solid line). The experimental Coster–Kronig spectra reported in ref. 23 and 25 are shown as blue and purple dotted lines, respectively. The theoretical spectra are shifted to higher kinetic energy by 3.4 eV.

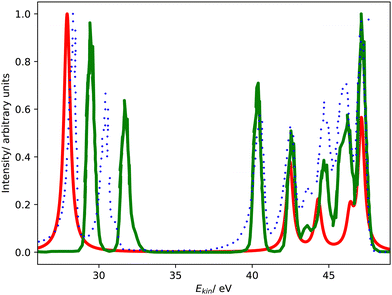Fig. 2 L₁L_2,3M Coster–Kronig spectrum of argon. Comparison of CS-EOM-CCSD results (red solid line, this work) with MCDHF results (green solid line, ref. 25) and the experimental spectrum (blue dotted line, ref. 25) The theoretical spectra are shifted to higher kinetic energy by 3.4 eV and 1.3 eV, respectively.

It is seen from Fig. 1 that the Coster–Kronig spectrum of argon consists of two features at 27–33 eV and 38–48 eV, which correspond to the L_2,3M₁ and L_2,3M_2,3 channels, respectively. While the intensity is evenly split between these two features in our computations, the experiments found an intensity distribution of 23 : 77²³ and 27 : 73,²⁵ respectively, in favor of the L_2,3M_2,3 channels, and MCDHF calculations delivered a ratio of 33 : 67.⁴¹ Interestingly, assuming that every channel has the same width delivers a ratio of 25 : 75, in good agreement with the experiment.

Furthermore, Fig. 1 and 2 show that the experimental spectra and the theoretical MCDHF spectrum have two peaks in the L_2,3M₁ region below 33 eV, whereas our spectra have just one peak. This mismatch is related to the ³P (2p⁻¹3s⁻¹) state having zero intensity in our computations but accounting for 250 meV in the MCDHF computations.⁴¹ Also in the experiment, the ¹P and ³P states are both clearly visible. Similar disagreements are also present in the L_2,3M_2,3 region in Fig. 2: our calculations yield four peaks each corresponding to one decay channel, whereas MCDHF yields six peaks some of which are composed of more than one channel.

All of these shortcomings suggest that spin–orbit coupling, which is missing in our theoretical model, changes the intensity distribution in the Coster–Kronig spectrum of argon significantly. Notably, the importance of spin–orbit interaction for the branching ratio between the ¹P (2p⁻¹3s⁻¹) and ³P (2p⁻¹3s⁻¹) states was established already 40 years ago.^37,39,40 However, it should also be noted that the overall shape of the experimental spectrum is well reproduced by our computations despite the neglect of spin–orbit coupling.

3.5 L₁L_2,3M Coster–Kronig spectrum of hydrogen sulfide

Fig. 3 shows the Coster–Kronig spectrum of hydrogen sulfide computed with CBF-EOM-IP-CCSD and Fano-EOM-CCSD as well as the available experimental results, which are of lower quality than in the case of argon. The convergence of the CBF-EOM-IP-CCSD spectrum with respect to the number of complex-scaled shells in the basis set is illustrated in the ESI.†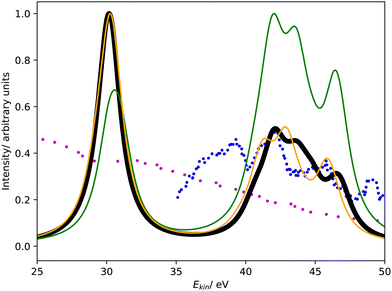

Fig. 3 L₁L_2,3M Coster–Kronig spectrum of hydrogen sulfide. Partial decay widths were computed with CBF-EOM-CCSD (black solid line), Fano-EOM-CCSD (orange solid line), and assuming the same width for every channel (green solid line). The experimental data reported in ref. 47 and 46 are shown as blue and purple dotted lines. The theoretical spectra are shifted to higher kinetic energy by 7.5 eV.

As expected, this spectrum has the same general structure as that of argon shown in Fig. 1. It consists of two features corresponding to the L_2,3M₁ and L_2,3M_2,3 decay channels. Similar to argon, CBF-EOM-IP-CCSD delivers a roughly even distribution of the intensity between the two features. The feature at lower energy is composed of three singlet decay channels involving the 4a₁ orbital, which forms the M₁ shell, and the 3a₁, 1b₁, and 1b₂ orbitals, which form the L_2,3 shell. Notably, the three corresponding triplet channels have a slightly negative decay width in the CBF-EOM-IP-CCSD calculations, indicating basis-set incompleteness. The feature at higher energy is composed of 18 L_2,3M_2,3 decay channels, where M_2,3 = 2b₁, 5a₁, 2b₂.

In the Fano-EOM-CCSD treatment, the intensity is also roughly evenly distributed between the L_2,3M₁ and L_2,3M_2,3 features. Interestingly, the L_2,3M₁ triplet channels that have slightly negative intensity in the CBF-EOM-IP-CCSD calculations are very pronounced with Fano-EOM-CCSD. The final spectra computed with the two methods are, however, in fairly good agreement.

Given the disagreements we observed for argon between CBF-EOM-IP-CCSD on the one hand and MCDHF and the experimental data on the other hand, the correctness of the H₂S spectra in Fig. 3 and the branching ratios can be questioned. Unfortunately, the experimental H₂S spectrum⁴⁷ only covers the energy range between 35 and 50 eV, i.e., it does not cover the L_2,3M₁ feature so that a definitive statement is difficult. We note, however, that theory and experiment agree about the L_2,3M_2,3 feature of the spectrum having a different shape for H₂S than for argon.

Regarding the energies of the emitted electrons, our calculations suggest that the two features of the Coster–Kronig spectrum lie somewhat closer to each other in the case of H₂S as compared to argon. Whereas the L_2,3M₁ feature is only 1 eV lower in energy for hydrogen sulfide than for argon, the L_2,3M_2,3 feature moves by 4–5 eV. Note that the trends in the absolute energies are not immediately apparent from Fig. 1 and 3 as different shifts were applied to the theoretical spectra. Also, because the experimental spectrum for H₂S is incomplete, it cannot be confirmed if the trend is correct.

3.6 L₁MM Auger spectrum of argon

Fig. 4 compares the L₁MM Auger spectrum of argon computed with CS-EOM-IP-CCSD and CBF-EOM-IP-CCSD to the experimental spectrum.²⁵ The theoretical spectra consist of two features: the feature at an Auger electron energy of around 250 eV corresponds to the M₁M₁ (3s⁻²) channel, whereas the broader feature with two peaks between 262 eV and 272 eV corresponds to the M₁M_2,3 (3s⁻¹3p⁻¹) channels. Notably, the M_2,3M_2,3 (3p⁻²) channels have very low intensity in our calculations and are barely visible in Fig. 4.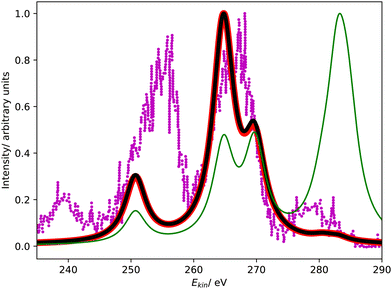

Fig. 4 L₁MM Auger spectrum of argon. Partial decay widths were computed with CS-EOM-CCSD (red solid line), CBF-EOM-CCSD (black solid line), and assuming the same width for every channel (green solid line). The experimental spectrum reported in ref. 25 is shown as purple dotted line. The theoretical spectra are shifted to higher kinetic energy by 2.0 eV.

Despite the fairly low resolution of the experimental spectrum, which is a consequence of the low intensity of the MM channels, a mismatch with the theoretical spectrum about the distribution of intensity between the M₁M₁ and M₁M_2,3 channels is apparent: in the theoretical spectra, the M₁M_2,3 channels account for 80% of intensity, whereas a roughly even distribution is found in the experiment. The low intensity of the M_2,3M_2,3 channels is, however, found in the experiment as well.

3.7 L₁MM Auger spectrum of hydrogen sulfide

Fig. 5 shows the L₁MM Auger spectrum of hydrogen sulfide computed with CBF-EOM-IP-CCSD and Fano-EOM-CCSD. Although there is no experimental spectrum available, several differences between this spectrum and the corresponding spectrum of argon in Fig. 4 are interesting. First, the spectrum covers a different energy range extending roughly from 170 to 205 eV, whereas the L₁MM spectrum of argon extends from 245 to 280 eV. This is a direct consequence of the MM double ionization energies differing by no more 5 eV between argon and H₂S, while the core ionization energies (see Table 1) differ by 90 eV. Notably, the Coster–Kronig spectra shown in Fig. 1 and 3 cover a very similar energy range because the energies of initial and final states are subject to almost the same shift when going from argon to H₂S.

Fig. 5 L₁MM Auger spectrum of hydrogen sulfide. Partial decay widths were computed with CBF-EOM-CCSD (black solid line), Fano-EOM-CCSD (orange solid line), and assuming the same width for every channel (green solid line).

Second, the L₁MM Auger spectrum of H₂S computed with CBF-EOM-IP-CCSD has a different structure than that of argon comprising seven peaks as compared to three. This is again different to the Coster–Kronig spectrum, where the differences between argon and hydrogen sulfide are more subtle. The first peak from the left in Fig. 5 at around 173 eV corresponds to the M₁M₁ (4a₁⁻²) channel, whereas the second peak at 180 eV and the feature between 183 and 191 eV stem from the M₁M_2,3 channels. The 2 remaining peaks at 196 eV and 200 eV correspond to the M_2,3M_2,3 channels, which account for a contribution of 10% to the total L₁MM width in H₂S as opposed to a negligible contribution in argon. Interestingly, the branching ratio between the M₁M₁ and the M₁M_2,3 channels only changes from 80 : 20 to 72 : 17 when going from argon to hydrogen sulfide.

4 Conclusions

We have investigated the nonradiative decay of the 2s⁻¹ states of argon and hydrogen sulfide using the EOM-IP-CCSD method combined with complex scaling of the Hamiltonian or, alternatively, the basis set. These 2s⁻¹ states have lifetimes of less than 1 femtosecond and are thus much shorter lived than 1s⁻¹ states of light elements, which reflects the efficiency of L₁L_2,3M Coster–Kronig decay whereby an L₁-core hole is filled by an electron from the L_2,3-shell.

In agreement with previous investigations, we find that Coster–Kronig decay channels account for more than 95% of the total decay width of 2s⁻¹ states. This branching ratio is very similar for argon and H₂S, but the total width of 2s⁻¹ states depends more strongly on the nuclear charge than that of 1s⁻¹ states. Theory and experiment agree about these trends qualitatively, but there remain several discrepancies about other trends. Firstly, according to our CBF-EOM-IP-CCSD results, the 2s⁻¹ state of H₂S has 62% of the width of the corresponding state of argon, while experiment suggests a ratio of 80%. Secondly, CBF-EOM-IP-CCSD suggests for argon and hydrogen sulfide a contribution of 25% by triplet decay channels, whereas Fano-EOM-CCSD yields a contribution of more than 80% for H₂S and previous MCDHF calculations yielded a value of 55% for argon. All in all, however, there can be no doubt that triplet decay channels are more important for L₁L_2,3M Coster–Kronig decay than for KLL Auger decay. A third discrepancy occurs for the L₁L_2,3M₁:L₁L_2,3M_2,3 branching ratio where CBF-EOM-IP-CCSD suggests equal contributions, whereas the L₁L_2,3M_2,3 channels account for ca. 75% of intensity in experiments on argon and MCDHF calculations suggest a contribution of 67%.

Despite these substantial discrepancies, the final L₁L_2,3M Coster–Kronig spectra and L₁MM Auger spectra obtained with different theoretical methods are in fairly good agreement with each other and also with the available experimental data. Notably, Coster–Kronig electrons emitted by argon and H₂S have approximately the same energy, whereas electrons stemming from L₁MM Auger decay are about 80 eV faster for argon. Also, the L₁L_2,3M Coster–Kronig spectra differ much less between the two species than the L₁MM Auger spectra.

Besides these results on 2s⁻¹ states, our work offers insights into the workings of the method of complex basis functions: because of the simultaneous presence of L₁L_2,3M decay channels that produce electrons with kinetic energies of only 25 to 50 eV and L₁MM decay channels that produce electrons with kinetic energies of more than 100 eV, steep and diffuse complex-scaled basis functions are required at the same time. As a result, larger basis sets are needed for the description of 2s⁻¹ states with the CBF method than for the description of 1s⁻¹ states.

Our results, in particular the discrepancies between different theoretical approaches, also demonstrate the need for further experimental and theoretical work in the area of Coster–Kronig decay, especially about molecules. We believe that the CBF method offers some critical advantages for such investigations: foremost, atoms and molecules can be treated on an equal footing at the same level of accuracy. Also, the total width can be accessed more easily than with approaches that rely on a channel-by-channel treatment. At the same time, our work illustrates the need for further development: in particular, the consideration of spin–orbit coupling in CBF-EOM-CC and Fano-EOM-CC calculations is likely to change several branching ratios significantly.

Data availability

The data supporting this article have been included as part of the ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

T.-C. J. gratefully acknowledges funding from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation program (Grant Agreement No. 851766) and the KU Leuven internal funds (Grant No. C14/22/083).

Notes and references

1. P. Auger, CR Acad. Sci. (F), 1923, 177, 169.
2. B. K. Agarwal, X-ray spectroscopy: An introduction, Springer, 2013.
3. K. Ramasesha, S. R. Leone and D. M. Neumark, Annu. Rev. Phys. Chem., 2016, 67, 41–63.
4. P. Norman and A. Dreuw, Chem. Rev., 2018, 118, 7208–7248.
5. P. M. Kraus, M. Zürch, S. K. Cushing, D. M. Neumark and S. R. Leone, Nat. Rev. Chem., 2018, 2, 82–94.
6. S. Hofmann, Auger- and X-ray photoelectron spectroscopy in materials science: A user-oriented guide, Springer Science & Business Media, 2012, vol. 49.
7. P. Weightman, Rep. Prog. Phys., 1982, 45, 753–814.
8. S. N. Raman, D. F. Paul, J. S. Hammond and K. D. Bomben, Microsc. Today, 2011, 19, 12–15.
9. W. E. S. Unger, T. Wirth and V.-D. Hodoroaba, Auger electron spectroscopy, Characterization of nanoparticles, Elsevier, 2020, ch. 4.3.2, pp. 373–395.
10. L. S. Cederbaum, J. Zobeley and F. Tarantelli, Phys. Rev. Lett., 1997, 79, 4778–4781.
11. T. Jahnke, U. Hergenhahn, B. Winter, R. Dörner, U. Frühling, P. V. Demekhin, K. Gokhberg, L. S. Cederbaum, A. Ehresmann, A. Knie and A. Dreuw, Chem. Rev., 2020, 120, 11295–11364.
12. D. Coster and R. de Laer Kronig, Physica, 1935, 2, 13–24.
13. E. J. McGuire, Phys. Rev. A: At., Mol., Opt. Phys., 1971, 3, 587–594.
14. W. Bambynek, B. Crasemann, R. W. Fink, H.-U. Freund, H. Mark, C. D. Swift, R. E. Price and P. V. Rao, Rev. Mod. Phys., 1972, 44, 716–813.
15. M. O. Krause and J. H. Oliver, J. Phys. Chem. Ref. Data, 1979, 8, 329–338.
16. M. O. Krause, J. Phys. Chem. Ref. Data, 1979, 8, 307–327.
17. M. H. Chen, B. Crasemann and H. Mark, Phys. Rev. A: At., Mol., Opt. Phys., 1981, 24, 177–182.
18. S. Puri, D. Mehta, B. Chand, N. Singh and P. N. Trehan, X-Ray Spectrom., 1993, 22, 358–361.
19. C. Guillot, Y. Ballu, J. Paigné, J. Lecante, K. P. Jain, P. Thiry, R. Pinchaux, Y. Pétroff and L. M. Falicov, Phys. Rev. Lett., 1977, 39, 1632–1635.
20. R. Bruhn, B. Sonntag and H. W. Wolff, Phys. Lett., 1978, 69A, 9–11.
21. L. C. Davis and L. A. Feldkamp, Phys. Rev. B: Condens. Matter Mater. Phys., 1981, 23, 6239–6253.
22. W. Mehlhorn, Z. Phys., 1968, 208, 1–27.
23. T. Kylli, J. Karvonen, H. Aksela, A. Kivimäki, S. Aksela, R. Camilloni, L. Avaldi, M. Coreno, M. De Simone, R. Richter, K. C. Prince and S. Stranges, Phys. Rev. A: At., Mol., Opt. Phys., 1999, 59, 4071–4074.
24. P. Lablanquie, F. Penent, R. I. Hall, H. Kjeldsen, J. H. D. Eland, A. Muehleisen, P. Pelicon, V. Šmit, M. Žitnik and F. Koike, Phys. Rev. Lett., 2000, 84, 47–50.
25. P. Lablanquie, S.-M. Huttula, M. Huttula, L. Andric, J. Palaudoux, J. H. D. Eland, Y. Hikosaka, E. Shigemasa, K. Ito and F. Penent, Phys. Chem. Chem. Phys., 2011, 13, 18355–18364.
26. L. Avaldi, J. J. Jureta and B. P. Marinkovič, J. Electron Spectrosc., 2019, 237, 146898.
27. N. Boudjemia, K. Jänkälä, T. Gejo, Y. Kohmura, M. Huttula, M. N. Piancastelli, M. Simon, M. Oura and R. Püttner, Phys. Rev. A, 2021, 104, 012804.
28. Y. Hikosaka and S. Fritzsche, Phys. Chem. Chem. Phys., 2022, 24, 17535–17541.
29. J. J. Jureta, B. P. Marinkovič and L. Avaldi, Adv. Space Res., 2023, 71, 1338–1351.
30. A. G. Kochur, D. Petrini and E. P. da Silva, Astron. Astrophys., 2001, 365, 248–251.
31. J. Soronen, S.-M. Aho, K. Jänkälä, M. Huttula, J.-M. Bizau, D. Cubaynes, L. Andric, J. Feng, I. Ismail, P. Lablanquie, F. Penant and J. Palaudoux, Phys. Rev. A, 2024, 109, 013108.
32. T. S. Axelrod, Phys. Rev. A: At., Mol., Opt. Phys., 1976, 13, 376–382.
33. M. H. Chen, B. Crasemann, K.-N. Huang, M. Aoyagi and H. Mark, At. Data Nucl. Data Tables, 1977, 19, 97–151.
34. F. P. Larkins, J. Phys. C: Solid State Phys., 1978, 11, 1965–1971.
35. M. Ohno, J. Phys. B: At. Mol. Phys., 1984, 17, 195–208.
36. P. Glans, R. E. LaVilla, M. Ohno, S. Svensson, G. Bray, N. Wassdahl and J. Nordgren, Phys. Rev. A: At., Mol., Opt. Phys., 1993, 47, 1539–1542.
37. J. Bruneau, J. Phys. B: At. Mol. Phys., 1983, 16, 4135–4151.
38. K. R. Karim, M. H. Chen and B. Crasemann, Phys. Rev. A: At., Mol., Opt. Phys., 1984, 29, 2605–2610.
39. K. R. Karim and B. Crasemann, Phys. Rev. A: At., Mol., Opt. Phys., 1984, 30, 1107–1108.
40. K. R. Karim and B. Crasemann, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 31, 709–713.
41. Z. Liu, Q. Liu, Y. Ma, F. Zhou and Y. Qu, Phys. Rev. A, 2021, 103, 063102.
42. M. Ohno, J. Electron Spectrosc., 2003, 131–132, 3–28.
43. M. Ohno and G. A. van Riessen, J. Electron Spectrosc., 2003, 128, 1–31.
44. T. Kaneyasu, T. Aoto, Y. Hikosaka, E. Shigemasa and K. Ito, J. Electron Spectrosc., 2006, 153, 88–91.
45. D. E. Ramaker, J. S. Murday, N. H. Turner, G. Moore, M. G. Lagally and J. Houston, Phys. Rev. B: Condens. Matter Mater. Phys., 1979, 19, 5375–5387.
46. A. Cesar, H. Ågren, A. N. de Brito, S. Svensson, L. Karlsson, M. P. Keane, B. Wannberg, P. Baltzer, P. G. Fournier and J. Fournier, J. Chem. Phys., 1990, 93, 918–931.
47. Y. Hikosaka, P. Lablanquie, F. Penent, J. G. Lambourne, R. I. Hall, T. Aoto and K. Ito, J. Electron Spectrosc., 2004, 137, 287–291.
48. F. Lever, D. Mayer, J. Metje, S. Alisauskas, F. Calegari, S. Düsterer, R. Feifel, M. Niebuhr, B. Manschwetus, M. Kuhlmann, T. Mazza, M. S. Robinson, R. J. Squibb, A. Trabattoni, M. Wallner, T. J. A. Wolf and M. Gühr, Molecules, 2021, 26, 6469–6479.
49. G. Öhrwall, N. Ottosson, W. Pokapanich, S. Legendre, S. Svensson and O. Björneholm, J. Phys. Chem. B, 2010, 114, 17057–17061.
50. F. Matz and T.-C. Jagau, J. Chem. Phys., 2022, 156, 114117.
51. F. Matz and T.-C. Jagau, Mol. Phys., 2023, 121, e2105270.
52. J. Aguilar and J.-M. Combes, Commun. Math. Phys., 1971, 22, 269–279.
53. E. Balslev and J.-M. Combes, Commun. Math. Phys., 1971, 22, 280–294.
54. N. Moiseyev, Non-Hermitian quantum mechanics, Cambridge University Press, 2011.
55. T.-C. Jagau, Chem. Commun., 2022, 58, 5205–5224.
56. C. W. McCurdy Jr and T. N. Rescigno, Phys. Rev. Lett., 1978, 41, 1364–1368.
57. A. F. White, M. Head-Gordon and C. W. McCurdy, J. Chem. Phys., 2015, 142, 054103.
58. N. K. Jayadev, A. Ferino-Pérez, F. Matz, A. I. Krylov and T.-C. Jagau, J. Chem. Phys., 2023, 158, 064109.
59. F. Matz, J. Nijssen and T.-C. Jagau, J. Phys. Chem. A, 2023, 127, 6147–6158.
60. V. Parravicini and T.-C. Jagau, J. Chem. Phys., 2023, 159, 094112.
61. J. Creutzberg, W. Skomorowski and T.-C. Jagau, J. Phys. Chem. Lett., 2023, 14, 10943–10950.
62. A. Ferino-Pérez and T.-C. Jagau, J. Phys. Chem. A, 2024, 128(20), 3957–3967.
63. K. B. Bravaya, D. Zuev, E. Epifanovsky and A. I. Krylov, J. Chem. Phys., 2013, 138, 124106.
64. D. Zuev, T.-C. Jagau, K. B. Bravaya, E. Epifanovsky, Y. Shao, E. Sundstrom, M. Head-Gordon and A. I. Krylov, J. Chem. Phys., 2014, 141, 024102.
65. A. F. White, C. W. McCurdy and M. Head-Gordon, J. Chem. Phys., 2015, 143, 074103.
66. A. F. White, E. Epifanovsky, C. W. McCurdy and M. Head-Gordon, J. Chem. Phys., 2017, 146, 234107.
67. G. Wentzel, Z. Phys., 1927, 43, 524–530.
68. H. Ågren, A. Cesar and C.-M. Liegener, Adv. Quantum Chem., 1992, 23, 1–82.
69. J. F. Stanton and R. J. Bartlett, J. Chem. Phys., 1993, 98, 7029–7039.
70. J. F. Stanton and J. Gauss, J. Chem. Phys., 1994, 101, 8938–8944.
71. K. W. Sattelmeyer, H. F. Schaefer and J. F. Stanton, Chem. Phys. Lett., 2003, 378, 42–46.
72. R. J. Bartlett and I. Shavitt, Many-Body Methods in Chemistry and Physics: MBPT and Coupled-Cluster Theory, Cambridge University Press, 2009.
73. K. Sneskov and O. Christiansen, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 566–584.
74. N. Moiseyev, P. R. Certain and F. Weinhold, Mol. Phys., 1978, 36, 1613–1630.
75. L. S. Cederbaum, W. Domcke and J. Schirmer, Phys. Rev. A: At., Mol., Opt. Phys., 1980, 22, 206–222.
76. M. L. Vidal, X. Feng, E. Epifanovski, A. I. Krylov and S. Coriani, J. Chem. Theory Comput., 2019, 15, 3117–3133.
77. W. Skomorowski and A. I. Krylov, J. Chem. Phys., 2021, 154, 084124.
78. E. Epifanovsky, A. T. B. Gilbert, X. Feng, J. Lee, Y. Mao, N. Mardirossian, P. Pokhilko, A. F. White, M. P. Coons, A. L. Dempwolff, Z. Gan, D. Hait, P. R. Horn, L. D. Jacobson, I. Kaliman, J. Kussmann, A. W. Lange, K. U. Lao, D. S. Levine, J. Liu, S. C. McKenzie, A. F. Morrison, K. D. Nanda, F. Plasser, D. R. Rehn, M. L. Vidal, Z.-Q. You, Y. Zhu, B. Alam, B. J. Albrecht, A. Aldossary, E. Alguire, J. H. Andersen, V. Athavale, D. Barton, K. Begam, A. Behn, N. Bellonzi, Y. A. Bernard, E. J. Berquist, H. G. A. Burton, A. Carreras, K. Carter-Fenk, R. Chakraborty, A. D. Chien, K. D. Closser, V. Cofer-Shabica, S. Dasgupta, M. de Wergifosse, J. Deng, M. Diedenhofen, H. Do, S. Ehlert, P.-T. Fang, S. Fatehi, Q. Feng, T. Friedhoff, J. Gayvert, Q. Ge, G. Gidofalvi, M. Goldey, J. Gomes, C. E. González-Espinoza, S. Gulania, A. O. Gunina, M. W. D. Hanson-Heine, P. H. P. Harbach, A. Hauser, M. F. Herbst, M. H. Vera, M. Hodecker, Z. C. Holden, S. Houck, X. Huang, K. Hui, B. C. Huynh, M. Ivanov, A. Jász, H. Ji, H. Jiang, B. Kaduk, S. Kähler, K. Khistyaev, J. Kim, G. Kis, P. Klunzinger, Z. Koczor-Benda, J. H. Koh, D. Kosenkov, L. Koulias, T. Kowalczyk, C. M. Krauter, K. Kue, A. Kunitsa, T. Kus, I. Ladjánszki, A. Landau, K. V. Lawler, D. Lefrancois, S. Lehtola, R. R. Li, Y.-P. Li, J. Liang, M. Liebenthal, H.-H. Lin, Y.-S. Lin, F. Liu, K.-Y. Liu, M. Loipersberger, A. Luenser, A. Manjanath, P. Manohar, E. Mansoor, S. F. Manzer, S.-P. Mao, A. V. Marenich, T. Markovich, S. Mason, S. A. Maurer, P. F. McLaughlin, M. F. S. J. Menger, J.-M. Mewes, S. A. Mewes, P. Morgante, J. W. Mullinax, K. J. Oosterbaan, G. Paran, A. C. Paul, S. K. Paul, F. Pavošević, Z. Pei, S. Prager, E. I. Proynov, A. Rák, E. Ramos-Cordoba, B. Rana, A. E. Rask, A. Rettig, R. M. Richard, F. Rob, E. Rossomme, T. Scheele, M. Scheurer, M. Schneider, N. Sergueev, S. M. Sharada, W. Skomorowski, D. W. Small, C. J. Stein, Y.-C. Su, E. J. Sundstrom, Z. Tao, J. Thirman, G. J. Tornai, T. Tsuchimochi, N. M. Tubman, S. P. Veccham, O. Vydrov, J. Wenzel, J. Witte, A. Yamada, K. Yao, S. Yeganeh, S. R. Yost, A. Zech, I. Y. Zhang, X. Zhang, Y. Zhang, D. Zuev, A. Aspuru-Guzik, A. T. Bell, N. A. Besley, K. B. Bravaya, B. R. Brooks, D. Casanova, J.-D. Chai, S. Coriani, C. J. Cramer, G. Cserey, A. E. DePrince, R. A. DiStasio, A. Dreuw, B. D. Dunietz, T. R. Furlani, W. A. Goddard, S. Hammes-Schiffer, T. Head-Gordon, W. J. Hehre, C.-P. Hsu, T.-C. Jagau, Y. Jung, A. Klamt, J. Kong, D. S. Lambrecht, W. Liang, N. J. Mayhall, C. W. McCurdy, J. B. Neaton, C. Ochsenfeld, J. A. Parkhill, R. Peverati, V. A. Rassolov, Y. Shao, L. V. Slipchenko, T. Stauch, R. P. Steele, J. E. Subotnik, A. J. W. Thom, A. Tkatchenko, D. G. Truhlar, T. V. Voorhis, T. A. Wesolowski, K. B. Whaley, H. L. Woodcock, P. M. Zimmerman, S. Faraji, P. M. W. Gill, M. Head-Gordon, J. M. Herbert and A. I. Krylov, J. Chem. Phys., 2021, 155, 084801.
79. J. Vayrynen, R. N. Sodhi and R. G. Cavell, J. Chem. Phys., 1983, 79, 5329–5336.
80. A. Müller, D. Bernhardt, A. Borovik, T. Buhr, J. Hellhund, K. Holste, A. L. D. Kilcoyne, S. Klumpp, M. Martins, S. Ricz, J. Seltmann, J. Viefhaus and S. Schippers, Astrophys. J., 2017, 836, 166.
81. A. Albiez, M. Thoma, W. Weber and W. Mehlhorn, Z. Phys. D: At., Mol. Clusters, 1990, 16, 97–106.
82. W. Skomorowski and A. I. Krylov, J. Chem. Phys., 2021, 154, 084125.
83. R. Sankari, M. Ehara, H. Nakatsuji, Y. Senba, K. Hosokawa, H. Yoshida, A. D. Fanis, Y. Tamenori, S. Aksela and K. Ueda, Chem. Phys. Lett., 2003, 380, 647–653.

---

Footnote

† Electronic supplementary information (ESI) available: Exponents of complex basis functions, optimal complex scaling angles, partial decay widths and double ionization energies for all L_2,3M and MM decay channels of argon and hydrogen sulfide, comparison of spectra computed with different basis sets. See DOI: https://doi.org/10.1039/d4cp02085e

---