Open Access Article
Open Access ArticleUnderstanding magnetic hyperthermia performance within the “Brezovich criterion”: beyond the uniaxial anisotropy description
Daniel
Faílde
ab,
Victor
Ocampo-Zalvide
a,
David
Serantes
 *ac and
Òscar
Iglesias
*ac and
Òscar
Iglesias
 *d
*d
aApplied Physics Department, Universidade de Santiago de Compostela, 15782 Santiago de Compostela, Spain
bGalicia Supercomputing Center (CESGA), Santiago de Compostela, Spain
cInstituto de Materiais (iMATUS), Universidade de Santiago de Compostela, 15782 Santiago de Compostela, Spain. E-mail: david.serantes@usc.gal
dDepartament de Física de la Matèria Condensada and Institut de Nanociència i Nanotecnologia Universitat de Barcelona (IN2UB), Martí i Franquès 1, 08028 Barcelona, Spain. E-mail: oscariglesias@ub.edu
First published on 4th July 2024
Abstract
Careful determination of the heating performance of magnetic nanoparticles under AC fields is critical for magnetic hyperthermia applications. However, most interpretations of experimental data are based on the uniaxial anisotropy approximation, which in the first instance can be correlated with the particle aspect ratio. This is to say, the intrinsic magnetocrystalline anisotropy is discarded, under the assumption that the shape contribution dominates. We show in this work that such a premise, generally valid for large field amplitudes, does not hold for describing hyperthermia experiments carried out under small field values. Specifically, given its relevance for in vivo applications, we focus our analysis on the so-called “Brezovich criterion”, H·f = 4.85 × 108 A m−1 s−1. By means of a computational model, we show that the intrinsic magnetocrystalline anisotropy plays a critical role in defining the heat output, determining also the role of the shape and aspect ratio of the particles on the SLP. Our results indicate that even small deviations from spherical shape have an important impact on optimizing the heating performance. The influence of interparticle interactions on the dissipated heat is also evaluated. Our results call, therefore, for an improvement in the theoretical models used to interpret magnetic hyperthermia performance.
1 Introduction
Magnetic hyperthermia cancer treatment with magnetic nanoparticles (NPs) has received intense research attention in the last decades based on its huge potential for cancer treatment, especially for aggressive tumour types such as brain glioblastoma or pancreas, which have poor prognosis with the usual techniques.1 However, despite the early success in the treatment of patients with recurrent glioblastoma multiforme,2 even reaching regulatory approval in the EU,3 the fact is that magnetic hyperthermia did not meet the generated expectations as a promising tool for cancer treatment.4,5 Various reasons lie behind such poor success, ranging from biocompatibility and toxicity concerns of the particles within the biological media6 to the common problem for nanomedicine approaches of achieving significant doses within the desired target.7 Clearly, several factors need to be improved in order to improve the success of magnetic hyperthermia.8 The aim of this work is to study a generally overlooked aspect of magnetic hyperthermia studies: the applicability of the usually effective uniaxial anisotropy approximation to describe the heating performance of magnetic NPs under field conditions suitable for in vivo applications.The magnetic anisotropy is the key parameter determining the heat released by the NPs under the AC field,9 as it stands for the coupling of the magnetic moment to the lattice. In fact, it defines both the achievable heat and the performance under a given field amplitude; see details of this double role in Section 2. Thus, the anisotropy defines the conversion of the absorbed electromagnetic energy – usually described in terms of the specific loss power, SLP – into heat.10,11 For a magnetic field of amplitude Hmax and frequency f, SLP = HL·f, where HL stands for the hysteresis losses, which can be evaluated as the area of the M(H) loop. Please note that while the related specific absorption rate (SAR) parameter is widely used in materials science focused hyperthermia studies, the SAR has a different meaning in the medical field and thus the SLP parameter should be preferably used.12
The problem is that defining the magnetic anisotropy of the NP is not a simple task, as different sources may strongly define the orientation of the particle magnetisation. In addition to the intrinsic (material-defined) magnetocrystalline term, the particle shape11,13 and surface14,15 may also strongly influence the behaviour of the particle magnetisation. Furthermore, combination of material properties also leads to very different particle behaviours, for example, by creating core/shell morphologies,16,17 or by fine-tune doping.18,19 Given the complexity of the problem, and the difficulties in theoretically interpreting data with competing anisotropies, in the magnetic hyperthermia literature, experimental data are often interpreted in terms of an effective uniaxial anisotropy.20–22 Such a simplification is based on the assumption that for iron oxides (the most common system for hyperthermia applications23), the particle shape makes the key contribution to the anisotropy, dominating over the intrinsic magnetocrystalline one.24,25
Recent theoretical works have suggested, however, that the contribution of this intrinsic magnetocrystalline term is not only non-negligible, but also may play a critical role.26,27 Thus, when considering the intrinsic magnetocrystalline contribution in addition to a shape uniaxial one (i.e. a more realistic approach), it has been shown that in the small-field range, the effective uniaxial-only approximation deviates significantly from the more realistic case.27 Given the importance of the small-field range for in vivo applications, such results suggest that further investigation of the applicability of the effective uniaxial approximation is highly necessary. We will show in this work that while the uniaxial-only approximation can reasonably describe large fields and frequencies, it may be completely off for in vivo field conditions. Given the complexity of the problem, we have used a computational technique that allows us to accurately control the different parameters governing the heating performance.
The work is organised as follows. In Section 2, the details of the physical model are described, together with the implications regarding heating and the Brezovich criterion. In Section 3, the details of the computational model are provided. The results are described in Section 4, including general field-dependence considerations, specific details regarding the SLP under the Brezovich criterion, and the role of interparticle interactions. The conclusions of the work are summarised in Section 5.
2 Physical model
The physical model corresponds to the macrospin approximation, i.e. the NPs are small enough that their magnetisation is dominated by the exchange energy, leading to coherent rotation of the atomic magnetic moments. Thus, each i particle can be characterised by its magnetic supermoment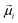 of magnitude μi = MsV, where Ms is the saturation magnetization and V is the particle volume. In the current work, we will consider magnetite nanoparticles, thus Ms = 4.8 × 105 A m−1.
of magnitude μi = MsV, where Ms is the saturation magnetization and V is the particle volume. In the current work, we will consider magnetite nanoparticles, thus Ms = 4.8 × 105 A m−1.
For ideal non-interacting conditions, the hysteresis behaviour (i.e. heating capability) of each magnetic moment under the AC field is, in the first instance, defined by the particle anisotropy energy, as the main cause responsible for creating the local energy barriers that cause irreversible behaviour.4 Furthermore, from the point of view of heating efficiency, it can be said that the anisotropy plays a double role:10 on the one hand, it defines the maximum energy that can be dissipated; on the other hand, it defines the performance under a given field amplitude. Thus, considering magnetic NPs with uniaxial anisotropy constant K and volume V, the theoretical maximum energy losses HLmax would be 8 kV for easy axes parallel to the field,9 and ∼2 kV for a randomly distributed system.28 However, significant heat can only be achieved if a minimum field threshold is overcome; namely, Hmax ≳ 0.5HK is required for significant heating29 (for random easy axis distributions). The HK value is the so-called anisotropy field, defined as HK = 2K/μ0Ms, where μ0 is the vacuum permeability. Given its critical role, intense research attention has been devoted to studying the role of the anisotropy on the heating efficiency.11,30–35
The previous uniaxial-anisotropy description implicitly assumes that the particle has an elongated shape that brings into play a shape anisotropy energy density, Ksh, that dominates the intrinsic magnetocrystalline energy density,24,31 which for magnetite is cubic and negative, Kc = −1.1 × 104 J m−3. This is to say, the above description considers only the magnetization and ignores magnetocrystalline anisotropy. This is a crucial aspect since, as described above, the anisotropy defines the energy barriers responsible for the irreversible path that results in the released energy. For the KC < 0 case of the magnetite, the energy barrier EB is reduced by a factor of 12 as compared to the case of uniaxial anisotropy,36 thus allowing much less energy to be dissipated, but also lowering the required minimum field amplitude to achieve significant heating. The key point of the present work is to study what is the role of this intrinsic magnetocrystalline anisotropy in the behaviour of the heating performance of the particles, under suitable field conditions for in vivo applications. A schematic illustration of the difference between the common uniaxial-only model and the “realistic” one used in this work is depicted in Fig. 1.
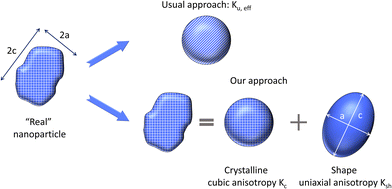 | ||
| Fig. 1 Scheme illustrating the difference between the usual uniaxial-only approximation and the more realistic approach considered in this work. | ||
In Fig. 1, the difference between the usual approximation and ours is illustrated: while the usual approach describes a “real” nanoparticle (which is never perfectly spherical) solely in terms of an effective uniaxial anisotropy constant, Ku,eff, our approach maintains the intrinsic magnetocrystalline contribution KC (which is always present), and considers the sphericity through an additional uniaxial shape anisotropy term, Ksh, approximated through the aspect ratio of an ellipsoid; see details in Section 3.
At this point, it is very important to highlight that safe in vivo applications impose limitations on the field properties. It was first discussed by Brezovich and collaborators37,38 that to avoid discomfort in patients, the product of field frequency (f) and amplitude (Hmax) should meet the condition Hmax·f = 4.85 × 108 A m−1 s−1 (the so-called “Brezovich criterion”). From a pure materials science perspective, however, such a limitation is usually overlooked, the hyperthermia characterisation often being carried out under much higher Hmax·f values. While the possibility of surpassing this limit without causing damage to the patient has been suggested,39–41 given its historical relevance, we have focused our analysis on field conditions matching the Brezovich criterion.
3 Simulation details
In order to model the NP ensembles, we consider magnetite particles with sizes below the single domain limit and, as discussed in Section 2, represent them by macrospins having a magnetic supermoment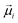 . The NPs have randomly distributed easy axes with a cubic anisotropy constant Kc = −1.1 × 104 J m−3; if an additional uniaxial term (see below) is included, the corresponding easy axes are also distributed at random, and uncorrelated from the cubic ones. Typically, we simulated a system of 1000 macrospins, unless otherwise stated.
. The NPs have randomly distributed easy axes with a cubic anisotropy constant Kc = −1.1 × 104 J m−3; if an additional uniaxial term (see below) is included, the corresponding easy axes are also distributed at random, and uncorrelated from the cubic ones. Typically, we simulated a system of 1000 macrospins, unless otherwise stated.
The simulations were performed as in previous works27,42 using the OOMMF software43 to track the temporal evolution of the system of macrospins under the influence of a sinusoidal alternating field of maximum amplitude H and frequency f. The dynamic evolution of each macrospin is described by the Landau–Lifschitz–Gilbert equation, with a random field to account for a finite temperature T = 300 K.44 From the simulated hysteresis loops, we obtained the HL value by averaging over different simulation runs and the SLP in W g−1 as SLP = HL·f/ρ, where ρ = 5170 kg m−3 is the mass density of magnetite.
To incorporate the deviation of particle shape from an ideal sphere of diameter D, we consider an additional shape anisotropy corresponding to the demagnetizing energy. For a prolate ellipsoid of the long axis c and short axes b = a, this energy can be written as uniaxial,45 with the energy density constant Ksh given by
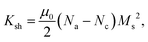 | (1) |
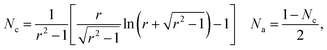 | (2) |
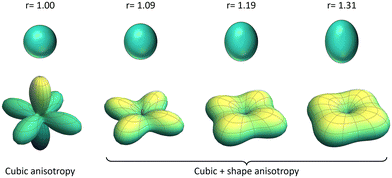 | ||
| Fig. 2 Schematic figure showing our approach to incorporate real particle shape effects. Upper panels show the particle shape with the associated aspect ratio r. Lower panels show the anisotropy energy surfaces in spherical coordinates obtained by adding a uniaxial contribution given by eqn (1) to the crystal cubic anisotropy of KC = −11 kJ m−3. | ||
In general, we have focused our study on non-interacting particles, the logical first step to understand the complex system under study. In that case, in the simulations we can identify each particle as the basic cubic cell discretization, setting the volume L3 equal to the NP volume V. Therefore, given a cell size L, the diameter of the sphere having the same volume is D = 1.24L. However, given its importance for the application (particles tend to agglomerate when internalized within the cells48), we have also considered the role of interparticle interactions. In this second case, to vary the sample volume concentration, c, we generated assemblies of randomly distributed NPs by adapting the simulation atlas size (Latlas) so that c = NV/Latlas3, where N is the number of NPs. In OOMMF, this is done by setting the saturation magnetization of the cells not assigned to a particle to Ms = 0. In all cases, the minimum amount of particles considered in the simulations was N = 1000. The dipolar interactions between macrospins were taken into account through the demagnetizing energies between simulation cells by switching on the class module Ox_Demag. In general, the size of the plotted point data for the non-interacting results is bigger than the error bars. However, this is not the case for the interacting conditions, and in those cases, the results are averaged over 4 different runs.
4 Results and discussion
Before analysing in detail the specific aspect of heating performance defined by the different anisotropy contributions, we will first revise the general picture. Thus, in section 4.1, we analyze the heating performance (in terms of the SLP) as a function of the field amplitude, Hmax, for the usual anisotropy-only approach, and the combined cubic plus uniaxial one. This is a very convenient procedure from the theoretical viewpoint, as the double role of the anisotropy is emphasized through the characteristic sigmoidal shape49–51 corresponding to the minor-to-major loop transition,52 where the maximum heat at large fields is proportional to the anisotropy.10 Then, in section 4.2, we focus specifically on field/frequency combinations corresponding to the Brezovich criterion. For simplicity, this analysis is at first carried out for non-interacting conditions, so that the role of the different anisotropy contributions is not counteracted by interparticle interactions.21 Nevertheless, as previously mentioned, interacting conditions are very relevant for the application. Therefore, in section 4.3, we study the effect of interparticle interactions on the SLP.4.1 Field dependence of the SLP
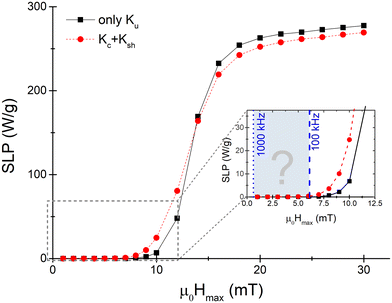
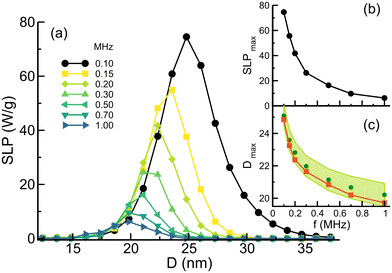
Let us first consider a non-interacting assembly of spherical particles and assume they have only uniaxial anisotropy (the “only Ku” case), as in many models and experimental studies. As a representative size, we started by choosing D ≈ 25 nm (discretization cell size L = 20 nm), as this size is interesting from the application point of view and, furthermore, we have previously obtained rich behaviour if the magnetocrystalline term is also considered.27 For the uniaxial anisotropy constant, we chose the usual magnetite-like value, Ku = 1.1 × 104 J m−3. In order to study the range of magnetic fields necessary to induce appreciable heating, we simulated hysteresis loops with increasing values of the maximum ac field Hmax to obtain a complete SLP vs. Hmax curve. For the sake of generality, we did this systematically for two values of the frequency f = 100 kHz, and f = 1000 kHz, so that we covered the usual frequency range in magnetic hyperthermia. The results for the f = 100 kHz case are shown in Fig. 3.In Fig. 3, the SLP shows a sigmoidal field dependence (black squares), increasing abruptly for fields higher than 10 mT, and showing a tendency towards saturation for fields higher than the anisotropy field Hk. This corresponds to a transition from minor to major loop conditions. However, if the spherical particles are assumed to have only cubic anisotropy with Kc = −1.1 × 104 J m−3 instead of uniaxial, the obtained SLP is negligible for all Hmax values and the range of frequencies considered. Therefore, these data have not been included in the figure.
If now a shape anisotropy contribution with the same value as the cubic one (Ksh = 1.1 × 104 J m−3) is added to include a change of the shape from spherical to ellipsoidal (i.e. the particles have now combined Kc + Ksh), the general qualitative of SLP does not change (red circles in Fig. 3). Only a slight increase (decrease) of the SLP with respect to the uniaxial case is obtained at low (high) fields. Note that the increase at low fields can be explained by the appearance of small energy barriers due to the magnetocrystalline term (which can be overcome by smaller fields). Similarly, the decrease at high fields can be interpreted as a result of the appearance of easier reversal paths (smaller energy barriers) again due to the presence of the magnetocrystalline anisotropy.
Since the SLP is proportional to f, an increase in frequency up to 1000 kHz just increases the SLP by an order of magnitude with values approaching the SW limit, without changing the qualitative behavior (to make the figure clearer, these results have not been included). This is the usual sigmoidal variation of SLP with Hmax reported in most models of NP assemblies when studying magnetization dynamics in the macrospin approximation, also with the same effect of such changes with frequency.51
However, note that the Hmax values that give appreciable SLP are beyond the physiological limits imposed by the Brezovich criterion even for the lowest frequency. Considering that in most experimental set-ups f can be varied within the range 100–1000 kHz, if physiological limits are to be respected, the maximum allowed fields will range from 6.1 mT to 0.61 mT as indicated by vertical dashed blue lines in the zoomed in region of Fig. 3. These fields are too low to induce any heating, at least for the particle size considered here, which is typical of particles studied experimentally. Therefore, an important conclusion of this observation is that the approximation of considering uniaxial anisotropy is invalid to explain why heating occurs under the Brezovich criterion conditions. But then, what is the reason why appreciable heating is observed experimentally? In what follows, we will try to shed some light on this issue.
4.2 SLP under Brezovich criterion conditions
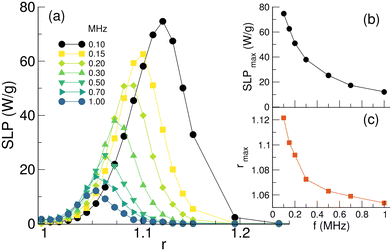
First, we will show how small departures from perfect spherical shape affect the SLP. Fig. 4 displays the SLP dependence on the elongation ratio r obtained by adding the corresponding shape uniaxial effective anisotropy to the cubic magnetocrystalline anisotropy for particles with the same size as before. All the hysteresis loops were simulated at field amplitudes Hmax that maximize the Brezovich criterion at the corresponding frequency.As can be seen in Fig. 4, even small changes in the particle shape (aspect ratio, r) have an important impact on the heating performance. Notice that the SLP increases first with increasing r, reaching a maximum at a value that depends on the frequency, while for higher aspect ratios, it progressively decreases towards zero. This behavior can be understood noting that an increase in r means an increase in the uniaxial shape anisotropy (see eqn (1)) added to the cubic crystalline one. Therefore, the effective anisotropy of a spherical particle with crystalline cubic anisotropy will eventually be dominated by the uniaxial shape contribution for sufficiently large aspect ratios, i.e. sufficiently large Ksh values.
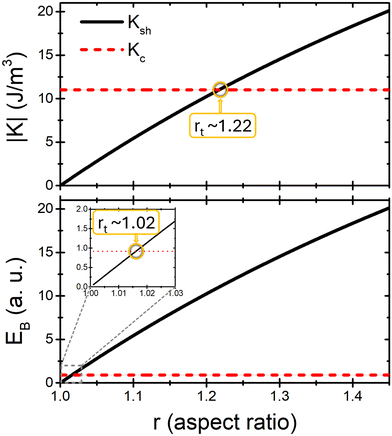
At this point, it may be worth emphasising that while heating is defined by the anisotropy, it is not only the anisotropy constant that is important, but also its symmetry. Thus, what matters regarding the hysteresis loop area is the relaxation time, which depends exponentially on the energy barriers separating energy minima and saddle points in the energy landscape induced by the anisotropy. In the case of uniaxial anisotropy, the energy barriers at zero field are simply proportional to the volume EB,u = KuV, but, for cubic anisotropy, the energy barrier separating the minima along the [111] directions from the saddle points along the [110] planes is lower by a factor of 12: EB,c = |Kc|V/12. Therefore, in this case, while the anisotropy constant of the shape contribution becomes bigger than the magnetocrystalline one when the aspect ratio becomes bigger than rt = 1.22 [see Fig. 5(a)], which corresponds to Ksh = 1.1 × 104 J m−3, the shape contribution to the energy barrier dominates over the cubic crystalline at aspect ratios as small as rt = 1.02 [see Fig. 5(b)].
The schemes displayed in Fig. 5 explain why, even if a spherical particle with the considered size would not dissipate significant heat, a slight distortion from its spherical shape will allow it to dissipate in the considered frequency range. The critical importance of this fact is the reason why we decided to explicitly show these otherwise simple schemes. The maximum SLP (SLPmax) is reached for the lowest considered frequency f = 100 kHz and the aspect ratio rmax that maximizes the SLP varies with the frequency of the AC field. The value of SLPmax rapidly decreases with increasing frequency [see Fig. 4(b)], which can be understood by the fact that the maximum field at high f is so small that the hysteresis loops are almost closed. The same tendency is obtained for the aspect ratio at which the SLP is maximized [see Fig. 4(c)]. These results have important implications for hyperthermia design, as it is suggested that for this particle size, the maximum heating will be obtained by the smaller frequency, at a moderate aspect ratio of r ≃ 1.12.
From these observations, we conclude that the best choice for the optimization of SLP under physiological limits corresponds to lower frequencies and slightly elongated NP shapes. Increasing the frequency would help if the condition of major loops (fields higher than the anisotropy field) was accomplished, which is clearly not the case if the Brezovich criterion has to be respected.
One may wonder if the SLP could also be tuned by varying the particle size for a given value of the aspect ratio r. For this, we have simulated hysteresis loops at different frequencies again respecting the Brezovich criterion, varying the simulation cell size between L = 10–30 nm and keeping r = 1.12 (Ksh ≃ 6.5 kJ m−3), which corresponds to particle diameters in the range of D = 12.4–37.2 nm. The corresponding SLP values deduced from the areas of the loops are shown in Fig. 6.
 | ||
| Fig. 6 (a) Dependence of the SLP on nanoparticle diameter D and aspect ratio r = 1.12 (Ksh ≃ 6.5 kJ m−3) for the frequencies indicated in the legend, and AC fields respecting the Brezovich criterion. A cubic anisotropy constant equal to that of magnetite has been considered. (b) and (c) display the frequency dependence of the maximum value of SLP and the diameter at which Dmax is obtained. In (c), the green circles indicate the Dmax values obtained from eqn (3), using a value of f0 = 109 Hz and the green shaded region indicates the range obtained when varying f0 between 0.5 and 1.5 × 109 Hz. | ||
As expected, particles with sizes below ∼15 nm do not heat at any frequency, since they are superparamagnetic at the considered temperature and frequency range. Particles above a certain size do not heat because the associated energy barriers are too high to be overcome by the considered combinations of H and f. At each frequency, there is a particle size Dmax that optimizes the SLP and it increases as the frequency decreases, whereas the maximum SLP shows the contrary tendency [see insets (b) and (c) of Fig. 6], in a way similar to the previously studied dependence of the SLP on r in Fig. 6.
We have found that the sizes that maximize the SLP are in very good agreement with the critical size deduced from the Arrhenius–Neél relaxation law for uniaxial anisotropy and randomly oriented axes53
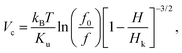 | (3) |
It is very interesting to observe that varying the size has a very similar frequency-dependence to varying the aspect ratio. This is to say, just as the highest SLP for a given size is obtained for a smaller f, the SLP is also maximised for smaller f also for a given aspect ratio (i.e. anisotropy). This is a very important aspect to keep in mind, as a common consideration in the literature has been whether a large field or large frequency would be preferred.54
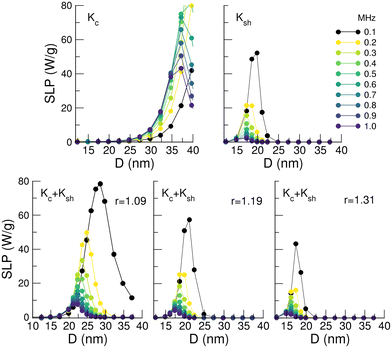
In order to complete the previous description about the influence of the size and shape on the SLP, we will now compare the size dependence of SLP of particles having only cubic anisotropy (corresponding to spherical shape), only uniaxial shape anisotropy (usual approach in the literature for spherical particles) and ellipsoidal particles with different aspect ratios. The results of the simulations obtained again for a wide range of frequencies and fields matching the Brezovich criterion for the physiological conditions are presented in Fig. 7, for the only cubic and only uniaxial cases (top panels, left and right, respectively), and for cubic plus uniaxial cases, for the aspect ratios r = 1.09, 1.19, 1.31 corresponding to shape anisotropies Ksh = 5, 10, 15 kJ m−3, respectively (bottom panels Fig. 7, from left to right).
The variation of the heating properties as displayed in Fig. 7 is complex but presents some systematic characteristics. First, notice that the SLP is always maximized for a certain particle size for all the frequencies and aspect ratios. The SLP attains maximum values always at the lowest studied frequency f = 100 kHz, which corresponds to Hmax = 6.1 mT, independently of the model used for the anisotropy and decreases rapidly with increasing frequency for all r. This is accompanied by a reduction of the optimum NP diameter Dmax, as can be seen in Fig. 8(b).
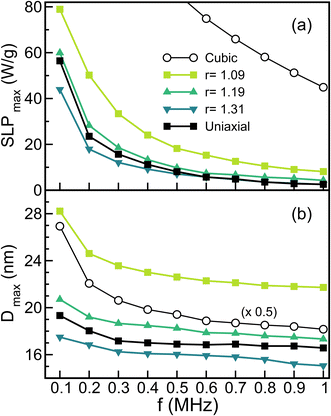 | ||
| Fig. 8 Frequency dependence of the (a) maximum SLP and (b) the corresponding particle size extracted from the curves in Fig. 7 for different nanoparticle elongation ratios r = 1.09, 1.19, and 1.31 (colored symbols) and also for the cases of only uniaxial (black squares) or only cubic contribution (empty circles) with Ku,c = 1.1 × 104 J m−3. Notice that Dmax for the last case has been rescaled by 0.5. | ||
Secondly, the values of SLPmax are considerably lowered even for moderate increases of the aspect ratio, while the optimal sizes Dmax are more moderately reduced by r. This can be understood as follows: an increase of the aspect ratio increases the uniaxial shape anisotropy which, for NPs with relatively high values of Ms, dominates the crystalline cubic contribution for aspect ratios as low as r = 1.02 (see Fig. 5). Therefore, in order to have appreciable magnetization reversal probability, the particle volume has to be reduced so as to have sizeable energy losses. We also observe that the window of NP sizes around Dmax that give sizable SLP values is reduced when increasing the r value, which is related again to the increase of the effective shape anisotropy that translates into more pronounced changes of the energy barriers with volume.
Next, we compare these results for elongated NPs to the case of spherical ones with crystalline cubic anisotropy only, to show the critical role played by the magnetocrystalline contribution. The results are shown in the upper left panel of Fig. 7. Notice that, although for the lowest frequencies the peaks are not visible in the represented scale, they range from Dmax = 54 to Dmax = 36 nm, as shown in Fig. 8(a) (empty circles). We observe that the maximum SLP of NPs with cubic anisotropy increases by a factor that varies between ∼2 at f = 0.1 MHz (133 W g−1) and ∼8 at f = 1.0 MHz (45 W g−1) when compared to the SLPmax of NPs with only Ku. Moreover, the sizes for optimal heating performance are also more than doubled as compared to those of the only uniaxial anisotropy case [see the black squares in Fig. 8(b); notice the reduction factor used for the cubic case]. The reason for this has to be traced back to the abovementioned reduction in the anisotropy energy barriers by a factor of 12 as compared to uniaxial anisotropy. According to eqn (3), this decrease is translated into an increase of the critical volume and in a higher SLPmax when the real cubic anisotropy of the NP is included. Nevertheless, it is important to remember that this ideal case is only shown for theoretical purposes, as experimentally it is not possible to synthesize particles with such a small sphericity; for the sake of comparison, experimental data reporting “spherical particles” are usually considered for aspect ratios between 1.05 and 1.10.
4.3 Interaction effects
So far, we have not taken into account dipolar interparticle interactions; this is a reasonable first approach for theoretical considerations, but is only a valid assumption for highly dispersed NP ensembles. Different degrees of dilution and interparticle distances can be somehow regulated ex vivo when NPs are still dissolved in water by employing different coatings that adhere to the NP surface and thus avoiding close proximity between them. However, when administered to biological media, NPs tend to aggregate, forming clusters or agglomerates whose size and spacial distribution cannot be deliberately controlled.48 Moreover, in order to achieve significant local heating, high enough NP doses have to be administered to the tumor and, when they are internalized by cells, their aggregation may be forced by the reduced volume of the vesicles in which they may be contained.55 It is thus crucial to understand how interactions may affect heating production in physiological conditions.Neither experimental nor theoretical published works on the subject have reached a consensus regarding the effect of dipolar interactions on the SLP. The disparity of the results stems from the fact that depending on the spatial NP arrangement and orientation of their easy-axes, dipolar interactions can increase or decrease the energy barriers responsible for magnetization reversal, thus affecting their hysteretic properties. In spite of the variety of results, a model based on the simulations of NPs with different intrinsic magnetic features, magnetic field conditions and concentrations showed that the variety of conflicting heat dissipation results can actually be described by a single picture.21 Moreover, several works have demonstrated that a considerable increase of heating power can be achieved in spite of interactions by NP chain formation favoured by cubic shaped NPs,11 promoted by the applied AC field20 along the applied field direction, or naturally present in magnetosomes.56–58 In contrast, the variety of results in assemblies with no particular spatial order arises from the fact that, while in some cases samples may contain diluted suspensions of individual aggregates or small NP clusters uniformly distributed in space, others are formed by larger multicore NP aggregates.59
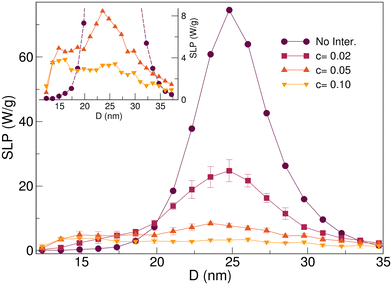
In what follows, we present simulations of hysteresis loops based on the ensembles of NPs randomly distributed in space with different volume concentrations, prepared following the strategy presented in Section 3. We will focus on ellipsoidal NPs with r = 1.12 under an f = 100 kHz AC field, since they gave the highest SLP in the non-interacting case. The results of the SLP extracted from the simulated hysteresis loops after averaging over 4 independent runs are presented in Fig. 9 for volume concentrations c = 2%, 5%, and 10%. Notice that due to the intrinsic limitations of the OOMMF code, more diluted samples were not considered since simulation times become too long due to the large atlas sizes that have to be considered (OOMMF deals with all simulation cells in the atlas, even those not assigned to a NP). Compared to the hysteresis loops of the non-interacting case, those of interacting NPs become more tilted with a considerable decrease of the remanent magnetization and a decrease of the magnetization at the maximum field. Although the coercive field does not present such an appreciable reduction, the overall result on the HL is a pronounced decrease of the SLPmax, which is reduced from 75 W g−1 to 25 W g−1 for a concentration c = 2% and to values below 10 W g−1 for higher c values. A similar reduction of the SLP has also been reported in a work by Gubanova et al.60 under different AC field conditions. Although the NP size for optimizing heating seems not to be much affected by the interaction, being around Dmax = 25 nm, the window of dissipating sizes becomes broader, extending to smaller sizes as c is increased. Looking at the zoomed-in inset of Fig. 9, it is worth highlighting that the interparticle interactions seem to activate the heat release of small sized NPs that did not heat in the absence of interactions, while leaving unaffected the big ones that did not dissipate in the non-interacting case. This is an indication that dipolar interactions act to increase the effective energy barriers of otherwise superparamagnetic NPs at room temperature. This has important consequences when aiming at precisely controlling the SLP in real samples, which will always have some degree of polydispersion.
We speculate that the drastic reduction of SLP values even for moderate concentrations, although it may seem surprising at first sight, could be due to local non-homogeneities of the NP positions. Although, as explained in Section 2, the NPs were distributed at random inside a cube, we have detected the presence of NPs in close contact for all the studied concentrations, being more numerous for increasing c. In particular, the percentage of touching NPs is 6.6% for c = 2% and, for c = 10% the number increases up to 26.2%. We have ascertained by visual inspection of the NP spatial distributions that most of the cases correspond to dimers, although we cannot exclude the existence of a smaller fraction of trimers in the most concentrated case. Since the interactions are most important for these clusters, even the presence of a small fraction of them could significantly influence the global heating behavior of the assembly, as reported elsewhere.61 The results of a study about the heating properties of small NP clusters by Ortega-Julia et al.62 also indicate this fact.
Hysteresis loops at f = 1000 kHz (not shown) were also simulated and become very narrow and elongated, giving much lower values of SLP that do not show any discernible trend with D due to noisiness. The interactions completely suppress any heating at c = 10%.
5 Discussion and conclusions
A key general conclusion of our work is related to the choice of the field amplitude/frequency combination to be used in hyperthermia treatments: the results suggest that, independently of the anisotropy model used to describe the particles, the best strategy is to use the highest Hmax value possible (equivalently, the smallest f). This is a rather general result that we think deserves further experimental testing.In relation to one of the main objectives of the work, which was to study the applicability of the usual uniaxial-only anisotropy to describe hyperthermia performance under the Brezovich criterion conditions, we have shown that the magnetocrystalline contribution definitively plays a key role. This is to say, the usual uniaxial-only magnetic anisotropy approximation seems quite limited for guiding/understanding in vivo biological conditions for hyperthermia applications. This is also very relevant from the application viewpoint, as it is directly related to the role of the NP shape: even very small deviations in shape can have an important impact on the heating performance. This is also an important factor to take into account for the standardization of magnetic hyperthermia as a clinical protocol.8
Regarding the role of dipolar interactions on the SLP, we have shown that in ensembles of NPs randomly distributed in space, even concentrations as small as 2% hinder the approach to saturation causing a prominent decrease in the hysteresis loops area and heating performance, even at the optimum NP size and field conditions obeying the Brezovich criterion. This degradation of the heating properties can be partially mitigated in practice by covering the NPs with surfactants to avoid close contact between them and the formation of clusters.
Finally, it is also important to stress the fact that all results presented here correspond to the ideal “frozen ferrofluid” assumption, i.e. that the particles do not move under the action of the external AC field. While this has been a common theoretical assumption for AC fields with frequencies ≥ 100 kHz as considered in this work,24 it has also been theoretically pointed out that a strong reorientation effect could take place at very small frequencies.63 More work is necessary to clarify this matter, from both the theoretical64 and experimental65 points of view, as it is known that magnetic NPs in living systems may adopt several spatial configurations in biological environments, in general intermediate between the ideal frozen ferrofluid and the fully movable situation. For example, particles may be internalized within endosomes or lysosomes, resulting in agglomerated arrangements;48,66 may have an extracellular location, for example, located within the extracellular matrix with different aggregation degrees,67 or may even exhibit either quite diluted distributions or chain-like ones depending on the particle compositions (even for very similar samples68). Furthermore, it would also be important to consider the possible reorientation of the interacting NPs with respect to the AC field,69 with the role of the dynamic colloidal evolution per se, as it has been shown that particles may form elongated structures under the application of the AC field.70,71 And it is well known that chaining may strongly change the heating performance.11,20,56,72,73 The possibility that chain-like NP formation could push the SLPmax to values similar to those for the non-interacting case under Brezovich conditions is an interesting alternative that we are planning to study in forthcoming studies.
Data availability
All the simulation results presented in this article have been obtained using the micromagnetic simulator OOMMF, available from the NIST website, https://math.nist.gov/oommf/software.html.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge the financial support by Spanish Ministerio de Ciencia, Innovación y Universidades through projects PID2019-109514RJ-I00 and PID2021-127397NB-I00, “ERDF A way of making Europe”, by the “European Union” and Catalan DURSI (2021SGR0032). Xunta de Galicia is acknowledged for projects ED431F 2022/005 and ED431B 2023/055. AEI is also acknowledged for the Ramón y Cajal grant RYC2020-029822-I that supports the work of D. S. We also acknowledge the Centro de Supercomputacion de Galicia (CESGA) for computational resources.Notes and references
- W. Tian, P. Wang, Z. Wang, H. Qi, J. Dong and H. Wang, Front. Oncol., 2021, 11, 790676 CrossRef CAS.
- K. Maier-Hauff, F. Ulrich, D. Nestler, H. Niehoff, P. Wust, B. Thiesen, H. Orawa, V. Budach and A. Jordan, J. Neurooncol., 2011, 103, 317–324 CrossRef PubMed.
- K. Mahmoudi, A. Bouras, D. Bozec, R. Ivkov and C. Hadjipanayis, Int. J. Hyperthermia, 2018, 34, 1316–1328 CrossRef.
- S. Dutz and R. Hergt, Nanotechnology, 2014, 25, 452001 CrossRef PubMed.
- I. Rubia-Rodríguez, A. Santana-Otero, S. Spassov, E. Tombácz, C. Johansson, P. De La Presa, F. J. Teran, M. Morales, S. Veintemillas-Verdaguer and N. Thanh, et al. , Materials, 2021, 14, 1–37 CrossRef.
- Y. Portilla, Y. Fernández-Afonso, S. Pérez-Yagüe, V. Mulens-Arias, M. P. Morales, L. Gutiérrez and D. F. Barber, J. Nanobiotechnol., 2022, 20, 543 CrossRef CAS PubMed.
- S. Wilhelm, A. J. Tavares, Q. Dai, S. Ohta, J. Audet, H. F. Dvorak and W. C. Chan, Nat. Rev. Mater., 2016, 1, 1–12 Search PubMed.
- L. Beola, L. Gutiérrez, V. Grazú and L. Asín, Nanomaterials for magnetic and optical hyperthermia applications, Elsevier, 2019, pp. 317–337 Search PubMed.
- C. L. Dennis and R. Ivkov, Int. J. Hyperthermia, 2013, 29, 715–729 CrossRef.
- C. Munoz-Menendez, D. Serantes, J. M. Ruso and D. Baldomir, Phys. Chem. Chem. Phys., 2017, 19, 14527–14532 RSC.
- C. Martinez-Boubeta, K. Simeonidis, A. Makridis, M. Angelakeris, O. Iglesias, P. Guardia, A. Cabot, L. Yedra, S. Estrade, F. Peiro, Z. Saghi, P. A. Midgley, I. Conde-Leboran, D. Serantes and D. Baldomir, Sci. Rep., 2013, 3, 1652 CrossRef.
- F. Soetaert, S. K. Kandala, A. Bakuzis and R. Ivkov, Sci. Rep., 2017, 7, 6661 CrossRef PubMed.
- R. Moreno, S. Poyser, D. Meilak, A. Meo, S. Jenkins, V. K. Lazarov, G. Vallejo-Fernandez, S. Majetich and R. F. Evans, Sci. Rep., 2020, 10, 2722 CrossRef CAS.
- D. Garanin and H. Kachkachi, Phys. Rev. Lett., 2003, 90, 065504 CrossRef CAS PubMed.
- O. Iglesias and A. Labarta, Physica B, 2004, 343, 286–292 CrossRef CAS.
- O. Iglesias, A. Labarta and X. Batlle, J. Nanosci. Nanotechnol., 2008, 8, 2761–2780 CrossRef CAS.
- H. Khurshid, J. Alonso, Z. Nemati, M. Phan, P. Mukherjee, M. Fdez-Gubieda, J. Barandiarán and H. Srikanth, J. Appl. Phys., 2015, 117, 17A337 CrossRef.
- S. Del Sol-Fernández, Y. Portilla-Tundidor, L. Gutiérrez, O. F. Odio, E. Reguera, D. F. Barber and M. Morales, ACS Appl. Mater. Interfaces, 2019, 11, 26648–26663 CrossRef.
- A. Sathya, P. Guardia, R. Brescia, N. Silvestri, G. Pugliese, S. Nitti, L. Manna and T. Pellegrino, Chem. Mater., 2016, 28, 1769–1780 CrossRef CAS.
- D. Serantes, K. Simeonidis, M. Angelakeris, O. Chubykalo-Fesenko, M. Marciello, M. D. P. Morales, D. Baldomir and C. Martinez-Boubeta, J. Phys. Chem. C, 2014, 118, 5927–5934 CrossRef CAS.
- I. Conde-Leboran, D. Baldomir, C. Martinez-Boubeta, O. Chubykalo-Fesenko, M. del Puerto Morales, G. Salas, D. Cabrera, J. Camarero, F. J. Teran and D. Serantes, J. Phys. Chem. C, 2015, 119, 15698–15706 CrossRef CAS.
- K. Simeonidis, M. P. Morales, M. Marciello, M. Angelakeris, P. de la Presa, A. Lazaro-Carrillo, A. Tabero, A. Villanueva, O. Chubykalo-Fesenko and D. Serantes, Sci. Rep., 2016, 6, 38382 CrossRef CAS PubMed.
- F. Soetaert, P. Korangath, D. Serantes, S. Fiering and R. Ivkov, Adv. Drug Delivery Rev., 2020, 163, 65–83 CrossRef PubMed.
- N. Usov, J. Appl. Phys., 2010, 107, 123909 CrossRef.
- G. Vallejo-Fernandez and K. O'Grady, Appl. Phys. Lett., 2013, 103, 142417 CrossRef.
- N. A. Usov, M. S. Nesmeyanov, E. M. Gubanova and N. B. Epshtein, Beilstein J. Nanotechnol., 2019, 10, 305–314 CrossRef CAS PubMed.
- H. Gavilán, K. Simeonidis, E. Myrovali, E. Mazario, O. Chubykalo-Fesenko, R. Chantrell, L. Balcells, M. Angelakeris, M. P. Morales and D. Serantes, Nanoscale, 2021, 13, 15631–15646 RSC.
- C. Munoz-Menendez, I. Conde-Leboran, D. Baldomir, O. Chubykalo-Fesenko and D. Serantes, Phys. Chem. Chem. Phys., 2015, 17, 27812–27820 RSC.
- R. Hergt, S. Dutz, R. Müller and M. Zeisberger, J. Phys.: Condens. Matter, 2006, 18, S2919 CrossRef CAS.
- H. Sohn and R. Victora, J. Appl. Phys., 2010, 107, 09B312 CrossRef.
- G. Vallejo-Fernandez and K. O'Grady, Appl. Phys. Lett., 2013, 103, 142417 CrossRef.
- Z. Nemati, J. Alonso, L. Martinez, H. Khurshid, E. Garaio, J. Garcia, M. Phan and H. Srikanth, J. Phys. Chem. C, 2016, 120, 8370–8379 CrossRef CAS.
- A. McGhie, C. Marquina, K. O'Grady and G. Vallejo-Fernandez, J. Phys. D: Appl. Phys., 2017, 50, 455003 CrossRef.
- H. Mamiya, H. Fukumoto, J. L. Cuya Huaman, K. Suzuki, H. Miyamura and J. Balachandran, ACS Nano, 2020, 14, 8421–8432 CrossRef CAS.
- D. P. Valdés, E. Lima, R. D. Zysler, G. F. Goya and E. De Biasi, et al. , Phys. Rev. Appl., 2021, 15, 044005 CrossRef.
- R. Yanes, O. Chubykalo-Fesenko, H. Kachkachi, D. Garanin, R. Evans and R. Chantrell, Phys. Rev. B, 2007, 76, 064416 CrossRef.
- W. J. Atkinson, I. A. Brezovich and D. P. Chakraborty, IEEE Trans. Biomed. Eng., 1984, 31, 70–75 CAS.
- I. A. Brezovich, Med. Phys. Monogr., 1988, 16, 82–111 Search PubMed.
- B. Herrero de la Parte, I. Rodrigo, J. Gutiérrez-Basoa, S. Iturrizaga Correcher, C. Mar Medina, J. J. Echevarría-Uraga, J. A. Garcia, F. Plazaola and I. García-Alonso, Cancers, 2022, 14, 3084 CrossRef CAS.
- M. K. Kwok, C. C. Maley, A. Dworkin, S. Hattersley, P. Southern and Q. A. Pankhurst, Appl. Phys. Lett., 2023, 122, 240502 CrossRef CAS.
- I. Rodrigo, I. Castellanos-Rubio, E. Garaio, O. K. Arriortua, M. Insausti, I. Orue, J. Á. García and F. Plazaola, Int. J. Hyperthermia, 2020, 37, 976–991 CrossRef CAS.
- D. Serantes and D. Baldomir, Nanomaterials, 2021, 11, 2786 CrossRef CAS PubMed.
- M. J. Donahue and D. G. Porter, National Institute of Standards and Technology, Gaithersburg, MD, 1999, vol. 1, p. 157.
- O. Lemcke, Thetaevolve module for OOMMF, 2002.
- G. Bertotti, Hysteresis in magnetism: for physicists, materials scientists, and engineers, Gulf Professional Publishing, 1998 Search PubMed.
- J. A. Osborn, Phys. Rev., 1945, 67, 351–357 CrossRef.
- E. C. Stoner, Philos. Mag., 1945, 36, 803–821 Search PubMed.
- L. Beola, L. Asín, C. Roma-Rodrigues, Y. Fernández-Afonso, R. M. Fratila, D. Serantes, S. Ruta, R. W. Chantrell, A. R. Fernandes, P. V. Baptista, J. M. de la Fuente, V. Grazú and L. Gutiérrez, ACS Appl. Mater. Interfaces, 2020, 43474–43487 CrossRef CAS.
- C. Iacovita, A. Florea, L. Scorus, E. Pall, R. Dudric, A. I. Moldovan, R. Stiufiuc, R. Tetean and C. M. Lucaciu, Nanomaterials, 2019, 9, 1489 CrossRef CAS PubMed.
- I. Castellanos-Rubio, O. Arriortua, D. Iglesias-Rojas, A. Barón, I. Rodrigo, L. Marcano, J. S. Garitaonandia, I. Orue, M. L. Fdez-Gubieda and M. Insausti, Chem. Mater., 2021, 33, 8693–8704 CrossRef CAS PubMed.
- J. G. Ovejero, I. Armenia, D. Serantes, S. Veintemillas-Verdaguer, N. Zeballos, F. López-Gallego, C. Grüttner, J. M. de la Fuente, M. del Puerto Morales and V. Grazu, Nano Lett., 2021, 21, 7213–7220 CrossRef CAS.
- E. L. Verde, G. T. Landi, M. Carrião, A. L. Drummond, J. Gomes, E. Vieira, M. Sousa and A. F. Bakuzis, AIP Adv., 2012, 2, 032120 CrossRef.
- R. H. Victora, Phys. Rev. Lett., 1989, 63, 457–460 CrossRef.
- N. Liu, A. Pyatakov, A. Saletsky, M. Zharkov, N. Pyataev, G. Sukhorukov, Y. Gun'ko and A. Tishin, J. Magn. Magn. Mater., 2022, 555, 169379 CrossRef CAS.
- B. Sanz, M. P. Calatayud, E. De Biasi, E. Lima, M. V. Mansilla, R. D. Zysler, M. R. Ibarra and G. F. Goya, Sci. Rep., 2016, 6, 1–10 CrossRef.
- D. Gandia, L. Gandarias, I. Rodrigo, J. Robles-García, R. Das, E. Garaio, J. Á. García, M.-H. Phan, H. Srikanth, I. Orue, J. Alonso, A. Muela and M. L. Fdez-Gubieda, Small, 2019, 15, 1902626 CrossRef CAS.
- M. L. Fdez-Gubieda, J. Alonso, A. García-Prieto, A. García-Arribas, L. Fernández Barquín and A. Muela, J. Appl. Phys., 2020, 128, 070902 CrossRef CAS.
- L. Marcano, I. Orue, A. García-Prieto, R. Abrudan, J. Alonso, L. Fernández Barquín, S. Valencia, A. Muela and M. L. Fdez-Gubieda, J. Phys. Chem. C, 2020, 124, 22827–22838 CrossRef CAS.
- H. Gavilán, S. K. Avugadda, T. Fernández-Cabada, N. Soni, M. Cassani, B. T. Mai, R. Chantrell and T. Pellegrino, Chem. Soc. Rev., 2021, 50, 11614–11667 RSC.
- E. M. Gubanova, N. A. Usov and V. A. Oleinikov, Beilstein J. Nanotechnol., 2021, 12, 1404–1412 CrossRef CAS PubMed.
- D. Niculaes, A. Lak, G. C. Anyfantis, S. Marras, O. Laslett, S. K. Avugadda, M. Cassani, D. Serantes, O. Hovorka, R. Chantrell and T. Pellegrino, ACS Nano, 2017, 11, 12121–12133 CrossRef CAS.
- J. Ortega-Julia, D. Ortega and J. Leliaert, Nanoscale, 2023, 15, 10342–10350 RSC.
- H. Mamiya and B. Jeyadevan, Sci. Rep., 2011, 1, 1–7 CrossRef PubMed.
- N. A. Usov and J. M. Barandiarán, J. Appl. Phys., 2012, 112, 053915 CrossRef.
- X. Wang, D. Cabrera, Y. Yang and N. Telling, Front. Nanotechnol., 2023, 5, 1214313 CrossRef.
- J. M. Rojas, H. Gavilán, V. del Dedo, E. Lorente-Sorolla, L. Sanz-Ortega, G. B. da Silva, R. Costo, S. Perez-Yagüe, M. Talelli, M. Marciello, M. P. Morales, D. F. Barber and L. Gutiérrez, Acta Biomater., 2017, 58, 181–195 CrossRef CAS PubMed.
- L. Beola, V. Grazú, Y. Fernández-Afonso, R. M. Fratila, M. de las Heras, J. M. de la Fuente, L. Gutiérrez and L. Asín, ACS Appl. Mater. Interfaces, 2021, 12982–12996 CrossRef CAS.
- P. B. Balakrishnan, N. Silvestri, T. Fernandez-Cabada, F. Marinaro, S. Fernandes, S. Fiorito, M. Miscuglio, D. Serantes, S. Ruta, K. Livesey, O. Hovorka, R. Chantrell, T. Pellegrino, N. Silvestri, T. Fernandez-Cabada, F. Marinaro, S. Fernandes, S. Fiorito, M. Miscuglio, D. Serantes, S. Ruta, K. Livesey, O. Hovorka, R. Chantrell and T. Pellegrino, Adv. Mater., 2020, 32, 2003712 CrossRef CAS.
- E. M. Gubanova, N. A. Usov and V. A. Oleinikov, Beilstein J. Nanotechnol., 2021, 12, 1404–1412 CrossRef CAS PubMed.
- S. L. Saville, B. Qi, J. Baker, R. Stone, R. E. Camley, K. L. Livesey, L. Ye, T. M. Crawford and O. T. Mefford, J. Colloid Interface Sci., 2014, 424, 141–151 CrossRef CAS.
- I. Morales, R. Costo, N. Mille, J. Carrey, A. Hernando and P. de la Presa, Nanoscale Adv., 2021, 3, 5801–5812 RSC.
- I. Orue, L. Marcano, P. Bender, A. García-Prieto, S. Valencia, M. A. Mawass, D. Gil-Cartón, D. A. Venero, D. Honecker, A. García-Arribas, L. F. Barquín, A. Muela and M. L. Fdez-Gubieda, Nanoscale, 2018, 10, 7407–7419 RSC.
- L. Marcano, I. Orue, D. Gandia, L. Gandarias, M. Weigand, R. M. Abrudan, A. García-Prieto, A. García-Arribas, A. Muela, M. L. Fdez-Gubieda and S. Valencia, ACS Nano, 2022, 16, 7398–7408 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2024 |