Hidden symmetry lowering, nanoscale order–disorder transition and ionic conductivity in Na_1/2−xLa_1/2−xBa_2xZrO₃

Abstract

This work concerns the local/nano-scale effects of Ba²⁺ substitution on the structure and ionic conductivity of Na_1/2−xLa_1/2−xBa_2xZrO₃, 2/32 ≤ x ≤ 8/32. Samples were investigated in detail by neutron total scattering analysis in combination with synchrotron X-ray and neutron powder crystallography, X-ray absorption spectroscopy, and solid-state nuclear magnetic resonance spectroscopy. Substitution of Ba²⁺ onto the perovskite A-site causes all members of the series to adopt a crystallographic average I4/mcm symmetry analogous to the high temperature phase of Na_1/3La_1/3Sr_1/3ZrO₃, but a deviation from Vegard's law at x = 6/32 indicates the presence of more complex nanoscale structural features. Above this deviation, analysis of neutron total scattering and extended X-ray absorption fine structure data show that the structure can only be modelled accurately by lowering the symmetry from tetragonal I4/mcm to orthorhombic P4₂/nmc space group to capture the local features. Further refinements conducted using reverse Monte Carlo methods allowed for the quantification of cation ordering, octahedral tilting angles, and element-specific thermal motion. Based on this model, we used a combination of bond valence sum energy mapping and molecular dynamics simulations to develop a detailed model of the effects of Ba²⁺ substitution on Na⁺ conductivity in Na_1/2−xLa_1/2−xBa_2xZrO₃.

---

Introduction

Research into higher-performance and safer energy storage devices is driven by the need for sustainable and efficient methods of renewable energy storage and distribution.¹ Solid-state batteries offer a potential solution to some of the challenges associated with current commercial batteries based on liquid electrolytes, such as high flammability and the complexity of the solid–electrolyte interface.^2–6

Perovskite-type structures have been widely investigated for potential solid-state electrolytes due to their high chemical, thermal, and electrochemical stability, as well as their crystal-chemically tuneable structures and therefore ionic conductivity.^7–16 This study concerns the relationship between A-site substitution and ionic conductivity in Na_3xLa_1.33−xTiO₃, an ordered double perovskite with orthorhombic Ibmm symmetry. The unsubstituted parent phase has a maximum conductivity of only 10⁻⁷ S cm⁻¹ at 400 °C for x = 0.16.¹⁷ This low conductivity was attributed to the narrow bottleneck formed by TiO₆ octahedra, which creates a higher activation energy for the movement of large Na⁺ ions (effective ionic radius 1.39 Å).¹⁸ By replacing Ti⁴⁺ (0.605 Å) with Zr⁴⁺ (0.72 Å), Toyomura et al. synthesised Na_3xLa_2/3−xZrO₃ with the orthorhombic Pnma perovskite structure.¹⁹ This increased the conductivity by a factor of ∼10 to 7.2 × 10⁻⁵ S cm⁻¹ at 350 °C, ascribed to widening of the octahedral bottleneck.¹⁹ To further increase the size of the bottleneck and reduce the activation energy associated with sodium conduction, Zhao et al. substituted the A-site Na⁺ (1.39 Å) and La³⁺ (1.36 Å) with larger Sr²⁺ ion (1.44 Å), synthesising a series of materials Na_1/2−xLa_1/2−xSr_2xZrO₃ (x = 1/16, 1/8, 1/6, 1/4).^7,18 These materials, reported in cubic P2₁3 symmetry, were shown to have a maximum conductivity of 1.025 × 10⁻⁵ S cm⁻¹ at 25 °C,⁷ further supporting the hypothesis that the size of the bottleneck dictates conductivity in sodium perovskites.

The limits to this structure–property relationship appear to have been found by Lin et al., who showed that Ba²⁺-substituted Na_xLa_1/3−1/3xBa_1/2ZrO₃ has lower ionic conductivity than its unsubstituted counterpart Na_xLa_2/3−1/3xZrO₃, despite the inclusion of large Ba²⁺ ions (1.61 Å) which should widen the bottleneck further.²⁰ This is in direct contrast to the mechanism proposed by Ruiz et al. Lin et al. concluded that this was likely due to a combination of lower Na⁺ concentration and the larger Ba²⁺ ions causing a structural deviation away from the optimal conduction pathway. Additionally, they showed that in this system the inclusion of A-site vacancies decreased conductivity.²⁰ However, a complete structural study of these materials was never undertaken.

To better understand the structure–property relationship in this material, more detailed characterisations of the material structures and changes to interatomic distances at the nanometre scale are required. In the present work we pursue this using neutron total-scattering experiments together with computational dynamics modelling, supported by other methods of local structure analysis including solid-state nuclear magnetic resonance spectroscopy and X-ray absorption spectroscopy.

Experimental methods

Ten members of the Na_1/2−xLa_1/2−xBa_2xZrO₃ series (x = 2/32–8/32, and x = 12/32) were synthesised via solid-state rection. Na₂CO₃ (>99.9%, Merck) and BaCO₃ (>99%, Sigma-Aldrich) were dried at 200 °C overnight to remove surface water while ZrO₂ (99%, Sigma-Aldrich) and La₂O₃ (99.999%, Aithaca) were dried at 1000 °C for 15 h to remove trace moisture and carbon dioxide. Stoichiometric amounts of each reagent were ground using a planetary ball mill with agate jars and 1 : 1 ratio of sample : acetone for 2 h at 400 rpm, 10 wt% excess Na₂CO₃ was added to compensate for sodium loss during synthesis. The ground powders were then pressed into 5 cm rods at 30 MPa using a hydrostatic press before being buried in mother powder and heated at 1300 °C for 10 h, heating at 3.5 °C min⁻¹, cooling at 7 °C min⁻¹.

Initial characterisation to determine purity was conducted using X-ray powder diffraction (XRPD) on a PANalytical X'pert PRO with a Cu radiation source (λ = 1.5406 Å) in the Sydney Analytical Core Research Facility at the University of Sydney. Data were collected over the range 10 < 2θ < 90° in Bragg–Brentano geometry.

Further analyses of the long-range average crystal structures were carried out using neutron powder diffraction (NPD) and synchrotron X-ray powder diffraction (SXRPD) at the Australian Centre for Neutron Scattering (ACNS) and the Australian Synchrotron, respectively. SXRPD was carried out using the powder diffraction beamline rapid access mail-in program.²¹ Samples were loaded into glass capillaries (0.2 mm diameter) and data were collected using both 16 keV [λ = 0.82646(1) Å], and 2 1 keV [λ = 0.59057(1) Å] X-rays over an angular range of 2 < 2θ < 81° at room temperature. NPD was carried out using the high-resolution powder diffractometer Echidna.²² All samples were sealed in 6 mm vanadium cans, and data were collected with an incident neutron wavelength of 1.62373(1) Å from 5 < 2θ < 160° with a step size of 0.05° at room temperature. Wavelengths for both the NPD and SXRPD experiments were calibrated and refined using a La¹¹B₆ (NIST SRM 660b) standard reference material.

Refinements of the long-range average structure were conducted using the Rietveld method implemented in the TOPAS Academic (v6) software package against combined SXRPD and NPD datasets.²³ The peak shapes were modelled using a Thompson-Cox-Hastings pseudo-Voigt function²⁴ and the background was modelled using a twelfth and sixth order Chebyshev polynomial for SXRPD and NPD respectively. Scale factors, lattice parameters, fractional atomic coordinates, and atomic displacement parameters (ADPs) were refined along with the peak shape parameters. ADPs were taken to be anisotropic and equal for each Wyckoff position.

Extended X-ray absorption fine structure (EXAFS) data were collected on the XAS beamline at the Australian Synchrotron. Room-temperature fluorescence measurements were conducted at the Zr K-edge (17 998 eV) using pellets of Na_1/2−xLa_1/2−xBa_2xZrO₃, x = 6/32–8/32, containing 1000 ppm of Zr diluted in cellulose. Four scans were conducted to ensure sample homogeneity and allow for better statistics. Data were processed using the Demeter software package.²⁵ Absorption edges were calibrated to a Zr foil, S₀ and Δe₀ values were fitted and fixed using a perovskite BaZrO₃ standard. The sample data were fitted in real space from 1.0 to 4.5 Å using data transformed from k-space from 3.0 to 15.0 Å⁻¹ with a sine window function. Calculations using FEFF9 were conducted using the tetragonal I4/mcm average structure models to allow for a comparison of the local and average structures.²⁷ Multiple scattering paths with weightings of <10 were excluded from the refinements.

Neutron total scattering data were collected for Na_1/2−xLa_1/2−xBa_2xZrO₃, x = 6/32–8/32, on the D4 beamline at the Institut Laue-Langevin (ILL), Grenoble, France.^26,27 Samples were sealed in 6 mm vanadium cans and measured from 0.7 > Q > 23.5 A⁻¹ [λ = 0.49680(1) Å] at room temperature. Data were also collected for an empty vanadium can, a vanadium standard, and the empty sample environment to allow for the processing of diffraction data into pair distribution functions (PDFs). The wavelength was calibrated and refined using an fcc Ni standard reference material.

Local-scale structural models were initially refined using a rietveld-like method for fitting PDF data as implemented in TOPAS. Further analyses of the PDF data were conducted using the reverse Monte Carlo (RMC) program RMCprofile.^28,29 For all compositions, starting configurations were generated from both the best fit of the P4₂/nmc model to the PDF data from 1.0 to 8.0 Å and the best fit of the I4/mcm model to the average structure data. Boxes were 5 × 5 × 5 unit cells, containing 2500 atomic sites with dimensions of ∼30 × 30 × 41 ų for the I4/mcm configuration and 5000 atomic sites with dimensions ∼41 × 41 × 41 ų for the P4₂/nmc configuration. Fits were conducted against the PDF from 1.90 to 20.0 Å using the notation from eqn (10) in Keen,³⁰ as the local structure has a greater influence over the RMC fitting algorithm in this notation. This format of the PDF was calculated using the StoG routine distributed as part of the RMCProfile package.^30,31 The Bragg data were omitted from the RMC fitting to emphasise any differences between the long- and short-range structures. The weight optimisation algorithm in RMCProfile was implemented with the PDF data being weighted the highest. The bond valence sum (BVS) was implemented as a soft chemical restraint to reduce unphysical bonding configurations.³¹ The ‘distance-window’ constraint was implemented to set hard minimum and maximum nearest neighbour pair distances and prevent unphysical pair distances. Swapping between different cations occupying the sites in the ABO₃ structure was allowed. Hence, Na, La, and Ba atoms were allowed to swap. RMC refinements were repeated 10 times to assess variations between the results and to improve statistics. For interpretation of how the local structure deviates from the average, atomic displacements were compared to those of the initial I4/mcm structure. ADPs and cation ordering were also analysed in the P4₂/nmc “big-box” using the thermal ellipsoid tool in RMCProfile. All structure representations were drawn with VESTA.³²

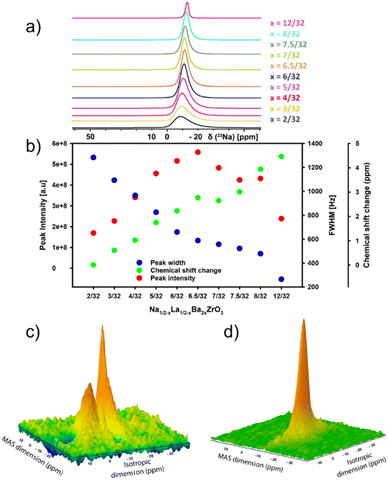
²³Na 1D MAS Hahn-echo and 2D MQMAS spectra of the 10 Na_1/2−xLa_1/2−xBa_2xZrO₃, x = 2/32–12/32, samples were collected on a Bruker AVANCE III 400WB spectrometer (²³Na transmitter frequency of 105.8 MHz) with a Bruker CPMAS probe at a sample spinning frequency of 14 kHz. All spectra were collected at room temperature using a 4 mm rotor. The MQMAS (mp3qzqf) experiment (x = 2/32) was acquired with a relaxation delay of 1 s and 60 increments in the indirect F1 dimension with 4096 transients per t1 increment. The MQMAS experiment (x = 8/32) was acquired with a relaxation delay of 1 s and 52 increments in the indirect F1 dimension with 1024 transients per t1 increment. 1D ²³Na MAS Hahn-echo experiments were performed with 49 152 transients, a spectral width of 860 ppm (²³Na carrier frequency of 0 ppm) and a relaxation delay of 0.5 s. Magic angle was calibrated by detecting ⁷⁹Br signal in a KBr sample before ²³Na NMR data acquisition. The data were processed and analysed using Topspin 4.4 or Dmfit software.³³ An exponential line broadening of 50 Hz was applied to the 1D ²³Na time domain data before the Fourier transformation. The spectra were processed using identical processing parameters. Spectrometer performance, including chemical shift referencing, was assessed using a sodium carbonate (Na₂CO₃) sample.³⁴

Bond valence sum energy (BVSE) mapping was conducted on both the I4/mcm long-range average and RMCprofile-produced P4₂/nmc structural models for x = 6/32–8/32 using the SoftBVgui (v1.3.1) program.³⁵ Models were modified to have 100% Na⁺ occupancy on the A-site to allow for a complete analysis of all potential Na⁺ pathways in each structure. This energy map was then used to calculate saddle-point activation energies for Na⁺ conductivity in each compositional structure. A Na⁺ test atom was used, and total energy surfaces were calculated with a resolution of 0.1 Å. Screening factors were auto calculated.³⁶

Molecular dynamics (MD) simulations were conducted on the supercells produced through RMCprofile refinements of the total scattering data using GULP with bond-valence-based forcefield as part of the SoftBVgui suite. Starting from the supercell produced by RMC profile lattice parameters were relaxed by brief NPT simulations at 300 K to yield a pressure in the range ±0.1 GPa, followed by NVT production runs over 2000 ps in steps of 1 fs. All atomic positions were fixed except those occupied by Na⁺, allowing for the calculation of Na⁺ mobility and conductivity across the latter half of the compositional series.

Results

All synthesised samples were single-phase with insignificant impurities and can be refined using the tetragonal I4/mcm space group with a a⁰a⁰c⁻ tilting pattern in Glazer notation.³⁷ Increased Ba²⁺ substitution causes two anticipated changes to the crystal structure: firstly, an increase in the unit cell size, shown by the decrease in all reflection angles; and secondly, a reduction in intensity of the R-point (211) reflection at ∼2.5 Å⁻¹, indicating a straighten of the c⁻ tilt (Fig. 1a). Fitting the tetragonal I4/mcm structure to the members of this series yield adequate fits with low residuals. However, the unit cell parameters do not change as expected. There are significant deviations from a smooth trend in both Zr–O–Zr bond angle and unit cell volume (Fig. 1c and d). Unit cell volume is linear at low x but diverges from the linear trend predicted by Vegard's law at x = 6/32. Coinciding with these divergences is a broadening of the SXRPD peak width, most noticeable in x = 7/32 and x = 7.5/32. Both the O1 oxygen (Wyckoff position 4a) and O2 oxygen (Wyckoff position 8h) refine to have zero displacements parallel to the Zr–O–Zr bond axis and large displacements in the perpendicular directions, i.e., non-positive definite ellipsoids (Fig. 2 and Table S1†). While these results yield reasonable structural models in terms of atomic positions, they indicate the presence of nanoscale structural features that cannot be adequately modelled by conventional crystallography.

Fig. 1 (a) Stacked SXRPD data for the Na_1/2−xLa_1/2−xBa_2xZrO₃ series in Q-space. The inset highlights the change in peak position and peak width. Peaks shift to lower Q and broaden with increasing Ba²⁺ substitution. (b) Combined SXRPD (upper) and NPD (lower) Rietveld refinement for Na_1/2−xLa_1/2−xBa_2xZrO₃, x = 5/32 of the tetragonal I4/mcm model in Q-space (R_wp = 3.02). (c) Vegard's law plot for the Na_1/2−xLa_1/2−xBa_2xZrO₃ series with unit cell volumes obtained from combined SXRPD and NPD Rietveld refinements. Note the deviation from a linear trend at higher Ba²⁺ substitution. (d) Zr–O–Zr bond angle with increasing Ba²⁺ substitution showing deviation from a smooth trend. The red line in plots (c) and (d) are linear fits drawn between the minimum and maximum compositions. Refinements for remaining compositions and complete data tables are in Fig. S1–S9 and Table S1.†

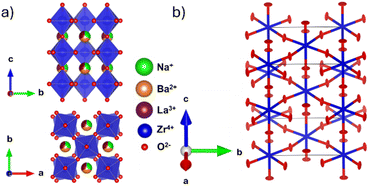Fig. 2 (a) I4/mcm structural model obtained from the combined SXRPD and NPD refinement showing out-of-phase tilting down the c-axis. (b) Oxygen ADP ellipsoids obtained from an NPD Rietveld refinement of Na_1/2−xLa_1/2−xBa_2xZrO₃, x = 6/32. The refinement yields a model with highly anisotropic ellipses with eccentricity perpendicular to the Zr–O–Zr bond axis in the U₃₃ direction for O1 and in the U₁₁ and U₁₂ direction for O2. Refined values are contained in Table S1.†

EXAFS refinements were conducted via FEFF9 calculations of the I4/mcm structural models obtained from the combined SXRPD and NPD refinements and the resulting single scatter distances are presented in Table 1. Fig. 3 contains the EXAFS radial distance plots for samples x = 6/32–8/32. The overlaid data show that Ba²⁺ substitution causes no significant changes to the first shell Zr–O distances at 1.6 Å. Furthermore, the intensities of the peaks at both 3.3 Å and 3.8 Å increase with higher Ba content, likely due to increased signal intensity caused by higher average Z number on the A-site, as expected.³⁸

Table 1 Single scatter path lengths between a Zr absorber atom and a single scatter partner atom. The lengths r (Å) are the atom-atom distances calculated in the EXAFS refinement, Δr (Å) is the change in distance compared to the tetragonal I4/mcm structural model, and σ² is the Debye–Waller factor. Complete refinement tables for all compositions are in Tables S2–S6

	x = 6/32			x = 6.5/32			x = 7/32
Single scatter partner	r (Å)	Δr (Å)	σ ^2	r (Å)	Δr (Å)	σ ^2	r (Å)	Δr (Å)	σ ^2
O1	2.0924	0.0089	0.005	2.0941	0.0094	0.005	2.0950	0.0101	0.004
Zr1	4.1540	0.0245	0.014	4.1617	0.0260	0.013	4.1420	0.0036	0.014
Zr2	4.1216	−0.0139	0.010	4.1317	−0.0095	0.008	4.1391	−0.0053	0.007

---

	x = 7.5/32			x = 8/32
Single scatter partner	r (Å)	Δr (Å)	σ ^2	r (Å)	Δr (Å)	σ ^2
O1	2.0949	0.0091	0.004	2.0955	0.0095	0.005
Zr1	4.1646	0.0221	0.013	4.1647	0.0200	0.012
Zr2	4.1483	−0.0022	0.006	4.1484	−0.0023	0.006

---

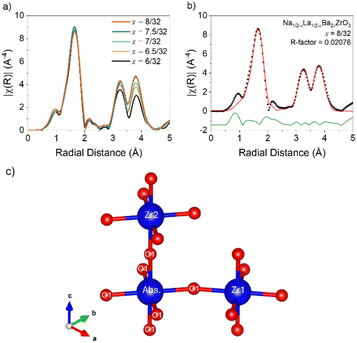Fig. 3 (a) EXAFS radial distance plots as a function of composition in the Na_1/2−xLa_1/2−xBa_2xZrO₃ series from x = 6/32 to 8/32. (b) Radial distance plot of the Na_1/2−xLa_1/2−xBa_2xZrO₃, x = 8/32 EXAFS refinement between 1.0 and 4.5 Å. Refinements for remaining compositions are in Fig. S10–S15†. (c) ZrO₆ octahedral schematic with the labelling scheme of oxygen positions used in EXAFS refinements.

Table 1 contains the EXAFS refinement data for the single scatter distances Abs-O1, Abs-Zr1, and Abs-Zr2, shown schematically in Fig. 3c. The first shell fits required only one Zr–O distance to be modelled correctly, demonstrating that the octahedra are rigid and symmetrical in all measured samples. However, Δr for the Abs-O1 distances indicate an enlargement of the ZrO₆ octahedra compared to the I4/mcm model. The Abs-Zr1 distances also increase in all samples. However, these increases are only partially accounted for by the increase in Abs-O1 distances, implying a straightening of the Zr–O–Zr bond angle towards 180° compared to the I4/mcm model. It is worth noting that for x = 7/32, the Abs-Zr1 distance does not change despite the increase in Abs-O1 distance. Along the c axis, the Abs-Zr2 distances in all samples are shorter than in the I4/mcm model, despite the increase in Abs-O1 distance. This indicates a decrease in the Zr–O–Zr bond angle from 180° along the c-axis and the presence of additional octahedral tilting in the local structure. In all refinements the large Debye–Waller factors for Abs-Zr1 distances imply disordered octahedral tilting. However, EXAFS data are insufficient for a full structural model in this instance.

²³Na magic-angle-spinning (MAS) solid-state NMR (ssNMR) spectroscopy is a powerful technique for studying the non-crystalline structure of inorganic materials.³⁹ To gain insights into local structure in Na_1/2−xLa_1/2−xBa_2xZrO₃ samples, ²³Na 1D MAS and 2D multiple-quantum magic angle spinning (MQMAS) were conducted. Results from 1D ²³Na ssNMR show that increasing Ba²⁺ substitution leads to a decrease in signal FWHM across the series (Fig. 4a and b). This is associated with an increase in peak intensity to a maximum at x = 6.5/32 before decreasing, suggesting a decrease in the average quadrupolar coupling constant. The peak broadening at low Ba²⁺ content suggests rapid quadrupolar relaxation due to the large quadrupolar interaction.⁴⁰ The decreasing trend of peak intensity after x = 6.5/32 is most likely due to a decrease in Na⁺ content. Though the impact of the short relaxation delay on the intensity analysis cannot be ruled out, as the magnetization may not have fully recovered to the Boltzmann equilibrium between scans. There is also a change in chemical shift with environments becoming more negative relative to the signal at x = 2/32, indicating an increase in electron density around the nuclear site and an increased shielding effect. This suggests slightly longer average Na–O bond lengths with increasing Ba²⁺ concentration.^41–43 Overlapping central transition signals in Na_1/2−xLa_1/2−xBa_2xZrO₃, x = 2/32 and x = 8/32, were resolved through 2D ²³Na MQMAS spectroscopy. The resulting spectra provide two non-equivalent crystallographic sites with different quadrupolar coupling constants (C_Q of site 1 and site 2 of 1550 kHz and 64 kHz, respectively) in the indirect isotropic dimension at low Ba²⁺ substitution (x = 2/32) and one site for (x = 8/32) with a C_Q of 55 kHz (Fig. 4c, d, S18 and S19†). The reduction in C_Q is likely driven by the straightening of the Zr–O–Zr bonds with higher Ba²⁺ content, which leads to a greater symmetry in the AO₁₂ polyhedral site, thereby causing a reduction in C_Q. For compositions x = 2/32–6/32, the central transition of the 1D ²³Na spectra are all comprised of a similarly featureless asymmetric line shape, confirming that these samples present in a locally disordered phase. Comparison of 1D ²³Na experimental spectra of Na_1/2−xLa_1/2−xBa_2xZrO₃ (x = 2/32 and x = 8/32) against simulated spectra are presented in Fig. S20 and S21.†

Fig. 4 Experimental ²³Na 1D MAS and 2D MQMAS NMR data of Na_1/2−xLa_1/2−xBa_2xZrO₃. (a) Superimposed 1D²³Na MAS spectra of Na_1/2−xLa_1/2−xBa_2xZrO₃ (x = 2/32–12/32). Only the center bands of the central transition are shown. Extremely broad and asymmetric central transitions are observed for lower Ba²⁺ composition, whereas it is symmetric at higher Ba²⁺ composition. (b) The full width half maximum (FWHM), peak intensity and chemical shift change of each peak relative to peak at x = 2/32 plotted against different Ba²⁺ compositions. (c) 2D MQMAS ²³Na NMR spectra of Na_1/2−xLa_1/2−xBa_2xZrO₃ (x = 2/32). The resulting spectrum clearly shows two overlapping peaks, one with a narrower peak and the other with a broader peak in the isotropic dimension. (d) 2D MQMAS ²³Na NMR spectra of Na_1/2−xLa_1/2−xBa_2xZrO₃ (x = 8/32) shows only one peak.

Neutron total scattering data were collected for the latter half of the series x = 6/32–8/32. Neutron data have better relative sensitivity than X-rays to light oxygen (in particular) atoms in the presence of heavy elements, allowing for more accurate quantification of both the local anion and cation lattices. The processed PDF fits are shown overlayed in Fig. 5a. The peaks in these data represent most of the characteristic peaks for the nearest neighbour distances in an I4/mcm perovskite. These peaks include Zr–O at ∼2.1 Å, A–O at 2.3–3.6 Å, O–O at 2.8–3.1 Å, A–Zr at 3.4–3.6 Å, and A–A/Zr–Zr at ∼4.1 Å. With increasing Ba²⁺ substitution, there is a decrease in the intensity of the shoulder peak at 2.5 Å as well as a splitting and broadening of the peak system at 4.7 Å. Small-box fits conducted from 1.0 to 8.0 Å using the I4/mcm models obtained from the long-range average structure indicate that the local cation lattice in this system can be modelled by the average structure. However, these fits do not accurately model the features in the regions located at 3.0 Å and 4.5 Å, associated with the A–O and O–O distances. Finally, there is a peak at 2.5 Å that is unaccounted for by the I4/mcm structure model (Fig. 5b). These poorly fit nearest neighbour distances are in the same region as other nearest-neighbour cation-oxygen distances, indicating that additional octahedral tilting is present in the local structure, in agreement with the EXAFS results.

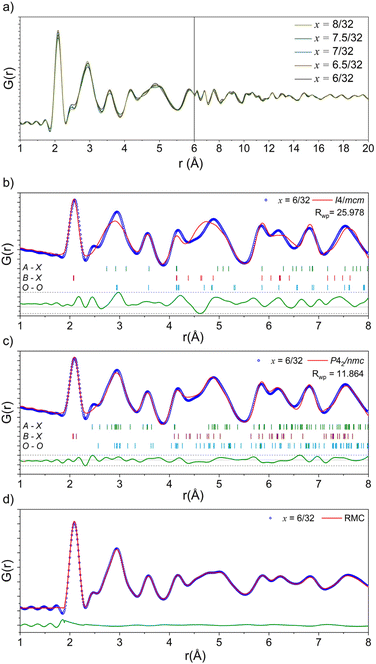Fig. 5 (a) Neutron PDF data as a function of composition in the Na_1/2−xLa_1/2−xBa_2xZrO₃ series from 1.0–20.0 Å. (b) Small box modelling with the tetragonal I4/mcm structure against the neutron PDF data of Na_1/2−xLa_1/2−xBa_2xZrO₃, x = 6/32. (c) Small box modelling with the orthorhombic P4₂/nmc structure against the neutron PDF data of Na_1/2−xLa_1/2−xBa_2xZrO₃, x = 6/32. (d) RMC fit to the neutron PDF data of Na_1/2−xLa_1/2−xBa_2xZrO₃, x = 6/32 over 1.8–8.0 Å. Neutron PDF refinements for remaining compositions are in Fig. S24–S27.†

Following the work of Howard and Stokes,⁴⁴ three models were made to model additional octahedral tilting: P4₂/nmc (a⁺a⁺c⁻),⁴⁵Cmcm (a⁰b⁺c⁻),⁴⁶ and C2/c (a⁻b⁻b⁻).⁴⁷ These models were built using the structures of well-known perovskites modified to have the correct composition and refined to have suitable unit cell parameters using the SXRPD data discussed above. After trialling the potential models, the a⁺a⁺c⁻ tilting scheme present in the P4₂/nmc model most accurately reflected the local-scale structure of the latter members of this series (Fig. 5d, S22 and S23†). In addition to the out-of-phase tilting along the c-axis, this space group also allows for in-phase tilting modes along both the a- and b-axes. This additional tilting creates the distances necessary to properly fit the peaks at ∼2.4, 3.0, and 4.5 Å.

The small-box fits are sufficient to prove that the local-scale nanostructure in these systems deviates from the long-range crystallographic average structure. However, there are still features in the data that the small-box fit does not account for. An RMC “big-box” model incorporates more degrees of freedom through the inclusion of cation swapping and the removal of symmetry constraints, allowing it to capture local, nanoscale features more effectively (Fig. 5d). In these fits, ADPs are modelled using the statistics of static disorder across the supercell and allow for the interpretation of displacement parameters. The shoulder A–O peak at ∼2.4 Å was accounted for in the RMC model through the displacement of Na⁺ off the centre of the AO₁₂ polyhedral site (Fig. 6).

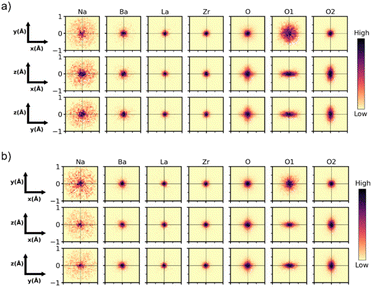Fig. 6 Cumulative 2D probability distributions viewed down each orthogonal axis for the A, B and O sites in the RMC model of Na_1/2−xLa_1/2−xBa_2xZrO₃ for (a) x = 6/32, and (b) 8/32. The displacement of each atom is calculated relative to the initial input configuration. The A-site has been split into the constituent elements. The O site has been split into the O1 and O2 sites from the I4/mcm model. The intensity of the color scale in each plot is normalized to itself, which means the maximum intensity between each plot is not comparable. Heat maps for remaining compositions are in Fig. S28–S32.†

The heat maps associated with atomic displacement in the supercell show that Na⁺ experiences a large degree of displacement, while the remaining A-site cations have limited displacement around the crystallographic site (Fig. 6). This is true for all members of the compositional series. With respect to the oxygen lattice, the combined elemental heat map of all oxygens ‘O’ shows that compared to an initial I4/mcm lattice, the oxygens in the supercell are distributed in a cross pattern when observed down the a- and b-axes. Along the c-axis, the RMC model of O2 site (Wyckoff 8h) produces a narrow Gaussian distribution centred on the I4/mcm site in the ab-plane. This indicates that the c⁻ tilting pattern present in the average structure model is preserved on the local scale. Conversely, the O1 site (Wyckoff 4a) has a broader distribution correlating with increased site disorder. The deconvolution of the O1 and O2 oxygens shows the presence of displacement perpendicular to both the a- and b-axes. The Gaussian nature of these distributions suggests that the additional octahedral tilting modes present are variable but average to the Wyckoff positions expected by the I4/mcm lattice. These distributions can be inspected further by plotting the O1 and O2 atomic distribution FWHMs along each unit cell axis (Fig. 7a and b). With increasing Ba²⁺ substitution, the O1 oxygen moves closer to the 4a site along the a- and b-axes, leading to a straightening of the Zr–O–Zr bond along the c-axis. The O2 oxygen does not follow this trend, instead plateauing at x = 7/32. Furthermore, the FWHM of the O2 oxygen reaches a maximum at x = 7/32 before reducing again. These results indicate that there is an unexpected non-linear change in the displacement of the O2 oxygen around the x = 7/32 composition. Overall, an increase in Ba²⁺ substitution coincides with an increase in the average Zr–O–Zr bond angle and a corresponding decrease in the overall average magnitude of octahedral tilting (Fig. 7c).

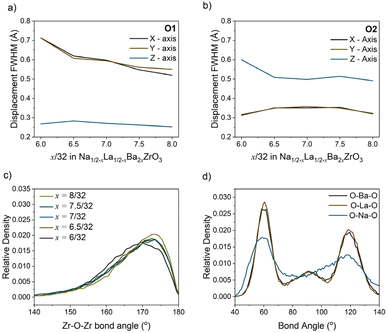Fig. 7 (a) O1 and (b) O2 displacement full width at half maximum (FWHM) along the x-, y- and z-axis with composition, calculated from the probability distributions shown in Fig. 6. (c) Histograms of the Zr–O–Zr bond angles with composition which pertain to the distribution of octahedral tilt magnitudes. (d) Histograms of the AO₁₂ polyhedral cation–oxygen bond angles in the RMC model of Na_1/2−xLa_1/2−xBa_2xZrO₃, x = 6/32.

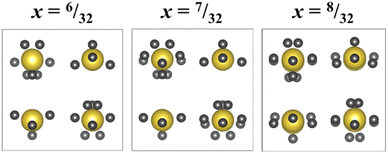
Fig. 8a shows a supercell collapsed into a P4₂/nmc unit cell. One of the key results from these RMC models is that there is clear cation ordering present in the system which is reduced with increasing Ba²⁺ substitution. While all A-sites in the unit cell can be occupied by Na⁺, Ba²⁺, or La³⁺, site 1 (highlighted in yellow in Fig. 8b) is Na⁺-dominant with >50% occupancy at x = 6/32, while site 2 (green) has sub-stoichiometric Na⁺ occupancy until x = 8/32. Fig. 8c shows the trend of Na⁺ occupancy on these two site types with increasing Ba²⁺ substitution. At x = 8/32 all A-sites contain 25% Na⁺ as expected from the stoichiometry and the site is fully compositionally disordered. Fig. 7d shows the average O–A–O bond angles in x = 6/32. Na⁺ has broadened features compared to La³⁺ and Ba²⁺, indicating that the displacement of Na⁺ around the A-site is uniform.

Fig. 8 (a) P4₂/nmc unit cell of Na_1/2−xLa_1/2−xBa_2xZrO₃, x = 6/32 created from a supercell using the displacement ellipsoid tool in RMCprofile. (b) The Na⁺ occupancy of site 1 and site 2 as a function of composition compared to expected stoichiometric occupancy. The A-site displacement ellipsoids of Na_1/2−xLa_1/2−xBa_2xZrO₃ are shown in (c) and (d) for x = 6/32 and x = 8/32, respectively. For x = 6/32, site 1 is highlighted in yellow, site 2 in green. However, all sites are equivalent in x = 8/32.

Fig. 9b shows the 3D percolation saddle points associated with the P4₂/nmc structural models produced by RMCprofile. These saddle points, represented in black, are necessary for a 3D conductivity network between A-sites, which allows for conductivity when the charge-carrying cation does not have 100% site occupancy. The activation energies of these saddle points were calculated for x = 6/32–8/32 and the results shown in Fig. 9a. The activation energy of the P4₂/nmc saddle points reduces sharply from 0.753 eV at x = 6/32 to 0.527 eV at x = 7/32 before plateauing, indicating a change in the Na⁺ conduction pathway.

Fig. 9 (a) Calculated activation energies for the 3D percolation network saddle point in the P4₂/nmc unit cells of Na_1/2−xLa_1/2−xBa_2xZrO₃, x = 6/32–8/32. (b) BVSE map of the Na⁺ conductivity network in Na_1/2−xLa_1/2−xBa_2xZrO₃, x = 6/32, with 3D percolation network saddle point highlighted in black. (c) Bulk Na⁺ conductivity, and (d) Na⁺ mobility, of Na_1/2−xLa_1/2−xBa_2xZrO₃, x = 6/32–8/32 as calculated by GULP MD.

The MD simulations conducted allow for a calculation of both Na⁺ conductivity and mobility in this series (Fig. 9c and d). These simulations show that a maximum conductivity is expected at a composition of x = 7/32 with a maximum bulk conductivity of 9.65 × 10⁻³ S cm⁻¹ at 300 K, coinciding with the maximum in Na⁺ mobility. These conductivity numbers are likely highly idealised due to the fixed site assumption made for the remaining elements, particularly oxygen, and do not account for grain boundary effects. Fig. 10 depicts the interstitials in the Na⁺ conduction pathway, determined from BVSE mapping. With increasing Ba²⁺ substitution the interstitials move outwards, away from the centre of the A-site polyhedra and towards the ‘window’ formed by the surrounding BO₆ octahedra. Furthermore, at a composition of x = 7/32 additional interstitial points appear along the Na⁺ conduction pathway. This movement, and increasing number of these interstitials provide plausibly explain the reduction in activation energy and increase in both mobility and conductivity at x = 7/32.

Fig. 10 Depictions of the calculated Na⁺ conduction pathway interstitial sites (black) viewed along the a-axis in the P4₂/nmc unit cells of Na_1/2−xLa_1/2−xBa_2xZrO₃, x = 6/32, 7/32, and 8/32, with the A site highlighted in yellow.

Discussion

A combination of Goldschmidt tolerance factors and the group theory approach of Howard and Stokes indicate that this system should undergo a transition from I4/mcm (a⁰b⁰c⁻) to Pm3̄m (a⁰a⁰a⁰).^44,48 Our SXRPD and NPD data agree with this transformation, both showing a reduction in the intensity of the R-point reflection indicative of an increase in the c⁻ Zr–O–Zr bond angle to 180°. However, there are multiple indicators that suggest the model obtained from these data is not accurate, starting with a significant deviation from Vegard's law at higher x values. While deviations from Vegard's law are well known,⁴⁹ in this case it is accompanied by a deviation in the Zr–O–Zr bond angle obtained from NPD Rietveld refinements. These factors, along with broadened peaks in diffraction studies, can be caused by low crystallinity. However, the shape of the oxygen ADPs at both the Wyckoff 4a and 8h positions are highly elliptical and irregular, suggesting the presence of additional octahedral tilting that is not accounted for in the I4/mcm model.^50,51

EXAFS refinements indicate that the first shell Zr–O peak is unchanged by increasing Ba²⁺ substitution and can be fit by one Zr–O distance of 2.09 Å, 0.1 Å longer than when modelled with the powder diffraction combined refinement. This implies the ZrO₆ octahedra in this system are uniform, rigid, and undistorted by Ba²⁺ substitution. However, distortions are required to make the I4/mcm model fit the EXAFS data. As mentioned above, the Abs-Zr2 distance is shorter for all samples than in the I4/mcm model despite the lengthening of the first shell Abs-O1 bond. This can only be true if the Zr–O–Zr bond angle along the c-axis is less than 180°. The discrepancy can be explained via the addition of a single octahedral tilt perpendicular to the O–Zr–O axis: any tilt away from this perpendicular would lead to a shortening of the Abs-Zr1 distance, which is not seen in the EXAFS refinements. As this tilt would occur at an angle to both the a- and b-axes, it would change the I4/mcm a⁰b⁰c⁻ tilting scheme to an a⁺a⁺c⁻ tilting scheme, as in the P4₂/nmc space group (Fig. 11). This further supports the rejection of the potential Cmcm and C2/c models used for PDF small box analysis.

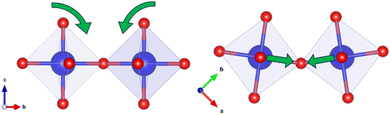Fig. 11 Schematic depicting the rotation of adjacent ZrO₆ octahedra required to modify the I4/mcm structural average to obtain the P4₂/nmc local structure.

²³Na MAS ssNMR and MQMAS reveal two distinct Na⁺ sites at low Ba²⁺ substitution, each with a unique structural and electronic environment. This is not possible in the I4/mcm model where AO₁₂ polyhedra are equivalent, but it is possible in P4₂/nmc where they are split. These experimental results solidify the choice of a P4₂/nmc symmetry for the immediate local structure of these materials and agree with both the small- and big-box PDF modelling approaches.

Atomic displacements can be analysed via the big-box RMC refinements. As stated previously, the O1 and O2 heat maps in Fig. 6 represent the oxygen Wyckoff 4a and 8h sites respectively in the I4/mcm structure. These heat maps allow for a comparison of the oxygen positions as determined by the I4/mcm model (at 0,0 in each plot) and the distribution obtained from the big-box model. The elliptical displacement maps from the central I4/mcm positions are further evidence for the presence of the cooperative in-phase octahedral tilts suggested by both the EXAFS data and the ADPs from NPD refinements. Although these tilts are cooperative, they have a short correlation length so that no M- or X-point reflections are visible in the powder diffraction data. The large, uniform, circular displacement of the O1 oxygen in the ab-plane suggests that the Zr–O–Zr bond angle along the c-axis is highly disordered even over length scales of ∼20 Å. It is this disorder of the O1 oxygen that allows for the averaging of the P4₂/nmc a⁺ tilts to a⁰, and the long-range structure to appear as I4/mcm.

The “big-box” model also produces cation ordering in the P4₂/nmc setting, as depicted in Fig. 8b. The displacement ellipsoids of these sites show that the model, based upon total scattering data, possesses two non-equivalent Na⁺ sites which become equivalent with increasing Ba²⁺ substitution: one with large average displacements from the central Wyckoff position; and one with significantly smaller displacements. This is verified experimentally by the ²³Na MQMAS SSNMR data where two unique Na⁺ environments are apparent at low Ba²⁺ substitution (x = 2/32) and only one is present at high substitution (x = 8/32). As noted in the Results section above, the environment with a large FWHM at x = 2/32 must experience a large quadrupolar interaction. Therefore, it can be assigned as the Na⁺ site with the larger displacement ellipsoid, as a large quadrupolar interaction implies displacement from the centre of the AO₁₂ polyhedra and a reduction of coordination symmetry. Conversely, the site with a narrow FWHM and a small quadrupolar interaction must be more centralised. At x = 8/32 the one Na⁺ site present also has a small quadrupolar interaction, indicating increased centralisation of Na⁺ in the AO₁₂ polyhedra. This is further reflected in both the trend of isotropic chemical shift, which indicates longer average Na–O bonds with increasing Ba²⁺, and the reduced Na⁺ displacement refined from total scattering shown in Fig. 6b.

The structural models produced by RMC fitting indicate that there may be a preference for Na⁺ to occupy the displaced site rather than its symmetrical counterpart as the displaced site has a higher than stochiometric Na⁺ concentration (Fig. 8b). A potential explanation is that favourable tilting on this site allows for a more stable Na⁺ bond valence sum arrangement. The reduction of tilting with increased Ba²⁺ substitution makes Na⁺ occupancy less favourable and thereby also reduces the potential for Na⁺ displacement. It is likely this pseudo-phase transition between cation order and disorder produces the increased peak broadening in SXRPD data at x = 7/32 and x = 7.5/32.

In the previously studied Sr²⁺ substituted system it was established that Sr²⁺ reduces the activation energy via an increase in unit cell volume and the size of the ‘conductivity window’ between adjacent A-sites, but causes minimal changes to the overall nature of the Na⁺ conduction pathway. The justification for this is that Sr²⁺ (1.44 Å), Na⁺ (1.39 Å), and La³⁺ (1.36 Å) have a small discrepancy in their ionic radii,¹⁸ allowing for minimal octahedral disorder to occur locally.⁵¹ In contrast, it is clear from the results of the present study that Ba²⁺ substitution significantly alters the local octahedral tilting of the structure due to the strain created by the much larger Ba²⁺ (1.61 Å) occupying the same crystallographic site as Na⁺ and La³⁺.¹⁸ This creates a more complicated relationship between composition and conductivity. In this system the calculated conductivity reaches a maximum at x = 7/32 rather than at x = 1/6 as expected from the results of the Sr substituted system. As shown with BVSE mapping and the changing interstitials in Fig. 10, subtle changes in octahedral tilting driven by Ba²⁺ substitution lead to significant modifications of the Na⁺ conduction pathway. More specifically, the combination of octahedral tilt angles and increased average displacement of the O2 oxygen in the ab-plane leads to the creation of additional interstitial sites along the Na⁺ conduction pathway and the movement of existing interstitials to locations that further reduce activation energy. These modifications to the conduction pathway correlate with the decrease in the activation energy of Na⁺ conductivity, as calculated by BVS mapping, and a peak in both Na⁺ diffusivity and mobility. The reduction in ionic conductivity past this point is likely driven by a combination of decreasing O2 displacement, further changes to octahedral tilting angles, and the complete disorder of the A-site composition.

Conclusions

We have thoroughly characterised the local structure of Na_1/2−xLa_1/2−xBa_2xZrO₃, 2/32 ≤ x ≤ 8/32 using a combination of neutron total scattering, EXAFS, and ssNMR, allowing us to analyse the effects of Ba²⁺ substitution on ionic conductivity using BVSE mapping and MD simulations. While conventional crystallographic refinements against powder diffraction data yield I4/mcm symmetry analogous to the high-temperature phase of Na_1/3La_1/3Sr_1/3ZrO₃, small-box refinements against PDF data unequivocally show that the local nanostructure has P4₂/nmc symmetry. This “hidden” symmetry lowering is a result of additional octahedral tilting that we confirmed using Zr K-edge EXAFS spectroscopy. We used structural models produced via RMC methods to further quantify this tilting, providing a complete model of local octahedral order/disorder in these systems. The RMC models contain two distinct A-sites with different Na⁺ displacements. We identified these two sites and characterised them by ssNMR, which showed evidence for significant local displacements of Na⁺ from the centre of AO₁₂ polyhedra, particularly at low Ba²⁺ concentrations. It is also evident that there is an A-site cation order-disorder transition in the latter half of the compositional series. BVSE mapping and MD calculations indicate that this subtle transition has a significant impact on Na⁺ conduction pathway and hence the conductivity of the system, giving rise to a maximum mobility and conductivity at x = 7/32. Our local/nano-scale structure analysis thereby provides a clearer understanding of the complex composition-structure–property relationships in perovskite-type solid-state ionic conductors and highlights the need for thorough structural analysis when investigating the structure–property relationships of these systems.

Data availability

Additional data supporting this article are included in the ESI.† Raw data collected at the Australian Synchrotron and Australian Centre for Neutron Scattering are available as outlined in the ANSTO data policy https://www.ansto.gov.au/facilities/user-access/updates/proposed-facility-access-terms-and-conditions with experiment reference numbers P16684 (NPD), PDR21530 and PDR18668 (SXRPD) and M20120 (XAS).

Author contributions

M. J. B. performed all the synthesis, led all the experiments and analysis, and led the writing. C. D. L. and S. S. supervised the project and were involved in all aspects. Other authors made significant contributions to: synthetic methodology (F. Z. T. Y.); neutron total scattering (G. J. C. and F. P. M.); nuclear magnetic resonance (B. M. and N. D.); X-ray spectroscopy (B. J.); neutron diffraction (M. A.); and structure–conductivity relations (O. J. W.).

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

Data for this research were collected on the XAS and PD Beamlines at the Australian Synchrotron, and the Echidna beamline at the Australian Centre for Neutron Scattering, both part of ANSTO; and at Sydney Analytical, a Core Research Facility at the University of Sydney. BJ acknowledges a Professorial Fellowship at the University of Wollongong. CDL and MA acknowledge support from the Australian Research Council (DP230100558). MJB was supported by an AINSE Ltd. Postgraduate Research Award (PGRA). OJW acknowledges Durham University for a Durham Doctoral Scholarship.

References

1. J. Ma, et al., The 2021 battery technology roadmap, J. Phys. D: Appl. Phys., 2021, 54, 183001.
2. M. D. Slater, D. Kim, E. Lee and C. S. Johnson, Sodium-ion batteries, Adv. Funct. Mater., 2013, 23, 947–958.
3. Z. P. Li, P. Liu, K. J. Zhu, Z. Y. Zhang, Y. C. Si, Y. J. Wang and L. F. Jiao, Solid-state electrolytes for sodium metal batteries, Energy Fuels, 2021, 35, 9063–9079.
4. N. Yabuuchi, K. Kubota, M. Dahbi and S. Komaba, Research development on sodium-ion batteries, Chem. Rev., 2014, 114, 11636–11682.
5. J.-Y. Hwang, S.-T. Myung and Y.-K. Sun, Sodium-ion batteries: present and future, Chem. Soc. Rev., 2017, 46, 3529–3614.
6. H. S. Hirsh, Y. Li, D. H. S. Tan, M. Zhang, E. Zhao and Y. S. Meng, Sodium-ion batteries paving the way for grid energy storage, Adv. Energy Mater., 2020, 10, 2001274.
7. Y. Z. Zhao, Z. Y. Liu, J. X. Xu, T. F. Zhang, F. Zhang and X. G. Zhang, Synthesis and characterization of a new perovskite-type solid-state electrolyte of Na_1/3La_1/3Sr_1/3ZrO₃ for all-solid-state sodium-ion batteries, J. Alloys Compd., 2019, 783, 219–225.
8. S. Zhang, H. Zhao, J. Guo, Z. Du, J. Wang and K. Świerczek, Characterization of Sr-doped lithium lanthanum titanate with improved transport properties, Solid State Ionics, 2019, 336, 39–46.
9. Z. R. Yurong, Y. Chen and F. Al, Doped new perovskite lithium fast ion conductor Li_3xLa_2/3−xTi_1−yAl_y O_3−yF_y (x = 0.11), Ionics, 2006, 12, 63–67.
10. R. Yu, Q.-X. Du, B.-K. Zou, Z.-Y. Wen and C.-H. Chen, Synthesis and characterization of perovskite-type (Li,Sr)(Zr,Nb)O₃ quaternary solid electrolyte for all-solid-state batteries, J. Power Sources, 2016, 306, 623–629.
11. F. Z. T. Yang, V. K. Peterson and S. Schmid, Composition and temperature dependent structural investigation of the perovskite-type sodium-ion solid electrolyte series Na_1/2−xLa_1/2−xSr_2xZrO₃, J. Alloys Compd., 2021, 863, 158500.
12. S. Yan, C. H. Yim, V. Pankov, M. Bauer, E. Baranova, A. Weck, A. Merati and Y. Abu-Lebdeh, Perovskite solid-state electrolytes for lithium metal batteries, Batteries (Basel), 2021, 7, 75.
13. L. L. Sun, Y. F. Li, G. Li, L. G. Wang and Y. Y. Tong, Perovskite-type compounds in anion-substituted LiSr_1−0.5xTiTaO_6−xF_x electrolyte for improving lithium-ion conduction, Ceram. Int., 2019, 45, 2381–2384.
14. M. E. Sotomayor, A. Várez, W. Bucheli, R. Jimenez and J. Sanz, Structural characterisation and Li conductivity of Li_1/2−xSr_2xLa_1/2−xTiO₃ (0 < x < 0.5) perovskites, Ceram. Int., 2013, 39, 9619–9626.
15. Y. Y. Lin, W. J. Gustafson, S. E. Murray, D. P. Shoemaker, E. Ertekin, J. A. Krogstad and N. H. Perry, Perovskite Na-Ion conductors developed from analogous Li_3xLa_2/3−xTiO₃ (LLTO): chemo-mechanical and defect engineering, J. Mater. Chem. A, 2021, 9, 21241–21258.
16. Y. Inaguma, T. Katsumata and M. Itoh, Lithium ion conductivity in A site deficient perovskites Sr_0.5La_0.05Li_0.35Ti_0.5Ta_0.5O₃ and Sr_0.35La_0.15Li_0.35Ti_0.5Ta_0.5O₃, Electrochemistry, 2000, 68, 534–536.
17. A. I. Ruiz, M. A. L. López, C. Pico and M. A. L. Veiga, New La_2/3TiO₃ derivatives: structure and impedance spectroscopy, J. Solid State Chem., 2002, 163, 472–478.
18. R. Shannon, Revised effective ionic radii and systematic studies of interatomic distances in halides and chalcogenides, Acta Crystallogr., A, 1976, 32, 751–767.
19. N. Toyomura, G. Hasegawa, K. Nishimi, M. Inada, N. Enomoto and K. Hayashi, Sodium ion conduction in sodium lanthanum zirconate ceramics prepared by spark plasma sintering, Scr. Mater., 2021, 200, 113887.
20. Y.-Y. Lin, W. J. Gustafson, S. E. Murray, D. P. Shoemaker, E. Ertekin, J. A. Krogstad and N. H. Perry, Perovskite Na-Ion conductors developed from analogous Li_3xLa_2/3−xTiO₃ (LLTO): chemo-mechanical and defect engineering, J. Mater. Chem. A, 2021, 9, 21241–21258.
21. K. S. Wallwork, B. J. Kennedy and D. Wang, The high resolution powder diffraction beamline for the australian synchrotron, AIP Conf. Proc., 2007, 879, 879–882.
22. M. Avdeev and J. R. Hester, Echidna: a decade of high-resolution neutron powder diffraction at OPAL, J. Appl. Crystallogr., 2018, 51, 1597–1604.
23. A. Coelho, Topas and Topas-Academic: an optimization program integrating computer algebra and crystallographic objects written in C++, J. Appl. Crystallogr., 2018, 51, 210–218.
24. P. Thompson, D. E. Cox and J. B. Hastings, Rietveld refinement of debye-scherrer synchrotron X-Ray data from Al₂O₃, J. Appl. Crystallogr., 1987, 20, 79–83.
25. B. Ravel, M. Newville and A. Athena, Hephaestus: data analysis for X-ray absorption spectroscopy using ifeffit, J. Synchrotron Radiat., 2005, 12, 537–541.
26. H. E. Fischer, G. J. Cuello, P. Palleau, D. Feltin, A. C. Barnes, Y. S. Badyal and J. M. Simonson, D4c: a very high precision diffractometer for disordered materials, Appl. Phys. A, 2002, 74, s160–s162.
27. M. J. Brennan, G. J. Cuello, N. Dupré, P. Morreau, Ionic Conductivity and Disorder in Na_1/2−xLa_1/2−xBa_2xZrO₃ Perovskite Solid-State Electrolytes, Institut Laue-Langevin (ILL), 2023,  DOI:10.5291/ILL-DATA.5-26-220.
28. Y. Zhang, M. Eremenko, V. Krayzman, M. G. Tucker and I. Levin, New capabilities for enhancement of RMCprofile: instrumental profiles with arbitrary peak shapes for structural refinements using the reverse monte carlo method, J. Appl. Crystallogr., 2020, 53, 1509–1518.
29. M. G. Tucker, D. A. Keen, M. T. Dove, A. L. Goodwin and Q. Hui, RMCprofile: reverse monte carlo for polycrystalline materials, J. Phys.: Condens. Matter, 2007, 19, 335218.
30. D. Keen, A comparison of various commonly used correlation functions for describing total scattering, J. Appl. Crystallogr., 2001, 34, 172–177.
31. S. T. Norberg, M. G. Tucker and S. Hull, Bond valence sum: a new soft chemical constraint for RMCprofile, J. Appl. Crystallogr., 2009, 42, 179–184.
32. K. Momma and F. Izumi, Vesta 3 for three-dimensional visualization of crystal, volumetric and morphology data, J. Appl. Crystallogr., 2011, 44, 1272–1276.
33. D. Massiot, F. Fayon, M. Capron, I. King, S. Le Calvé, B. Alonso, J.-O. Durand, B. Bujoli, Z. Gan and G. Hoatson, Modelling one- and two-dimensional solid-state NMR spectra, Magn. Reson. Chem., 2002, 40, 70–76.
34. Z. E. M. Reeve, C. J. Franko, K. J. Harris, H. Yadegari, X. Sun and G. R. Goward, Detection of electrochemical reaction products from the sodium–oxygen cell with solid-state ²³Na NMR spectroscopy, J. Am. Chem. Soc., 2017, 139, 595–598.37.
35. H. Chen, L. L. Wong and S. Adams, Softbv – a software tool for screening the materials genome of inorganic fast ion conductors, Acta Crystallogr., B, 2019, 75, 18–33.
36. L. L. Wong, K. C. Phuah, R. Dai, H. Chen, W. S. Chew and S. Adams, Bond valence pathway analyzer—an automatic rapid screening tool for fast ion conductors within softbv, Chem. Mater., 2021, 33, 625–641.
37. A. Glazer, The classification of tilted octahedra in perovskites, Acta Crystallogr., B, 1972, 28(11), 3384–3392.
38. P. A. Lee, Theory of extended X-Ray absorption fine structure, in Exafs Spectroscopy: Techniques and Applications, ed. B. K. Teo and D. C. Joy, Springer US, Boston, MA, 1981, pp. 5–11.
39. K. Gotoh, ²³Na solid-state NMR analyses for na-ion batteries and materials, Batteries Supercaps, 2021, 4, 1267–1278.
40. I. P. Gerothanassis and C. G. Tsanaktsidis, Nuclear electric quadrupole relaxation, Concepts Magn. Reson., 1996, 8, 63–74.
41. N. Barrow, M. Packard, S. Vaishnav, M. C. Wilding, P. A. Bingham, A. C. Hannon, M. Appler and S. Feller, MAS-NMR studies of carbonate retention in a very wide range of Na₂O-SiO₂ glasses, J. Non-Cryst. Solids, 2020, 534, 119958.
42. J. Steinadler, O. E. O. Zeman and T. Bräuniger, Correlation of the isotropic NMR chemical shift with oxygen coordination distances in periodic solids, Oxygen, 2022, 2, 327–336.
43. S. E. Ashbrook, L. Le Pollès, R. Gautier, C. J. Pickard and R. I. Walton, ²³Na multiple-quantum MAS NMR of the perovskites NaNbO₃ and NaTaO₃, Phys. Chem. Chem. Phys., 2006, 8, 3423–3431.
44. C. J. Howard and H. T. Stokes, Structures and phase transitions in perovskites – a group-theoretical approach, Acta Crystallogr., A, 2005, 61, 93–111.
45. K. Leinenweber and J. Parise, High-pressure synthesis and crystal structure of CaFeTi₂O₆, a new perovskite structure type, J. Solid State Chem., 1995, 114, 277–281.
46. P. Sciau, A. Kania, B. Dkhil, E. Suard and A. Ratuszna, Structural investigation of AgNbO₃ phases using X-ray and neutron diffraction, J. Phys.: Condens. Matter, 2004, 16, 2795.
47. A. Komeno, Y. Aoyama, K. Toda, M. Sato and K. Uematsu, Structure analysis of A site defect perovskite-type crystal, Key Eng. Mater., 2004, 269, 11–14.
48. V. M. Goldschmidt, Die gesetze der krystallochemie, Naturwissenschaften, 1926, 14, 477–485.
49. L. Zhang and S. C. Li, Empirical atom model of Vegard's law, Phys. B, 2014, 434, 38–43.
50. B. G. Mullens, F. P. Marlton, M. Saura-Múzquiz, M. K. Nicholas, A. J. Permana, B. C. Cowie, V. Mitchell, C. Li, Z. Zhang and B. J. Kennedy, Emerging anion disorder in CaTi_1−xFe_xO_3−x/2 perovskites by X-ray spectroscopy and neutron total scattering, Chem. Mater., 2024, 36, 8811–8824.
51. F. P. Marlton, F. Z. T. Yang, S. M. Everett, J. Neuefeind and S. Schmid, Understanding the influence of local structure distortions on Na-Ion migration in perovskite solid electrolytes, J. Power Sources, 2024, 617, 235154.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ta07291j

---