Dynamic DNA nanotechnology: toward functional nanoscale devices
Marcello
DeLuca
a,
Ze
Shi
b,
Carlos E.
Castro
cd and
Gaurav
Arya
 *a
*a
aDepartment of Mechanical Engineering and Materials Science, Duke University, Durham, North Carolina 27708, USA. E-mail: gaurav.arya@duke.edu
bDepartment of NanoEngineering, University of California San Diego, La Jolla, California 92093, USA
cDepartment of Mechanical and Aerospace Engineering, The Ohio State University, Columbus, Ohio 43210, USA
dBiophysics Graduate Program, The Ohio State University, Columbus, Ohio 43210, USA
First published on 15th October 2019
Abstract
Dynamic DNA nanotechnology involves the creation of nanoscale devices made of DNA whose primary function arises from their ability to undergo controlled motion or reconfiguration. In the past two decades, dynamic DNA nanotechnology has evolved to the point where it is now being employed in devices intended for applications in sensing, drug delivery, computation, nanorobotics, and more. In this review article, we discuss the design of dynamic DNA nanodevices and the characterization and prediction of device behavior. We also identify a number of continuing challenges in dynamic DNA nanotechnology and discuss potential solutions to those challenges.
1 Introduction
DNA nanotechnology is a rapidly growing field that uses DNA as a material for creating nanoscale structures and devices. DNA is an attractive candidate for this application for several reasons. Firstly, DNA is truly nanoscopic. Its smallest structural unit, the nucleotide, occupies approximately the space of a 0.34 nm wide and 1 nm long cylinder. One should thus be able to design structures at a similar resolution, which makes DNA one of the finest nanoscopic building blocks currently available. Secondly, DNA is highly programmable. Sequences of DNA bind specifically to each other via strict base-pairing rules.1 This means that the lengths, positions, and orientations of the hybridized, double-helical elements of the structure can be readily and rationally programmed into the DNA sequence. Lastly, DNA can be readily synthesized at reasonable cost and its properties are also generally well understood.In biology, one major role of DNA is encoding the structure of proteins, many of which are quite complex, but as far as DNA's own structural form is concerned, it is mostly limited to that of a linear double helix. This raises the natural question as to whether DNA can encode its own structure in a manner that produces geometry more complex than the double helix.2 Ned Seeman addressed this question in the early 1980s when he proposed the design of an immobile four-way junction with sticky ends made from four different DNA sequences.3 This concept represented the first major step towards synthetic DNA structures spanning two or even three dimensions, marking the birth of structural DNA nanotechnology. However, structures created using junctions alone were not stiff enough to find practical use except for simple shapes of small length scales. This problem was solved in 1993 with the invention of the double-crossover motif,4 which allowed for 2D structures of large span to be created while maintaining stiffness. Ten years later, the introduction of DNA origami5 democratized the design process and enabled the creation of larger and more complex structures. Further breakthroughs in the design of 3D shapes6 and curved structures,7 along with technologies focused on creating larger structures8,9 have enabled the design of even more complex DNA geometries of sizes ranging from 10 nm up to microns.8,10
Fairly early on in the development of the field, there was interest in mechanizing DNA nanostructures.11,12 These so-called “dynamic” structures are defined as structures whose functions rely upon changing of their conformations. Despite early interest in the topic of dynamic mechanisms, a vast majority of progress in DNA nanotechnology focused on enhancing the size and geometric complexity of static objects, namely, structural DNA nanotechnology. The past decade, however, has witnessed a tremendous surge of interest toward dynamic DNA nanotechnology and DNA-based nanoscale devices,13 resulting in diverse applications including but not limited to sensors,14–20 molecular algorithms,18,21–23 biological assays,24–26 cargo sorting27 and delivery28–31 devices, tunable plasmonic devices,32–36 and nanoscale robotic arms.37,38 A pictorial timeline of the progression of dynamic DNA nanotechnology toward increasingly complex and useful devices is presented in Fig. 1.
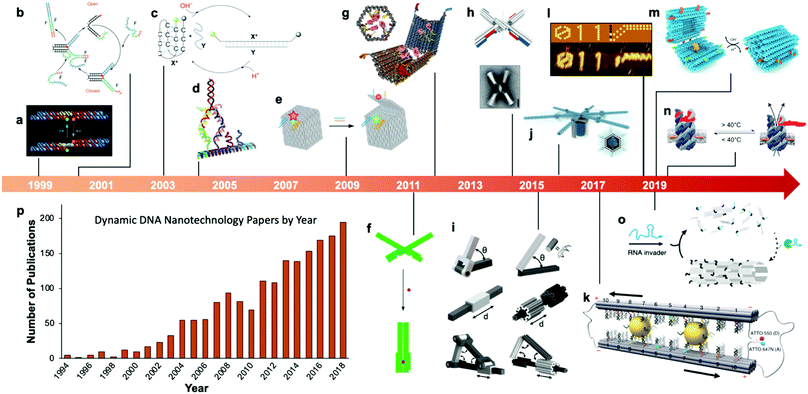 | ||
| Fig. 1 Timeline of the increasing complexity of dynamic DNA nanostructures over the past two decades. (a) Paired double crossover structure actuated by the B–Z transition. (b) Toehold-mediated strand displacement (TMSD) based DNA tweezers. (c) pH-Based DNA device. (d) DNA walker. (e) DNA box actuated by TMSD. (f) DNA beacon which detects biomolecules by changing its conformation. (g) Logic-gated DNA box which detects biomolecules and displays molecular cargo. (h) DNA structure connected with shape complementarity. (i) DNA-based hinges, sliders, and hybrid mechanisms. (j) Rotary device made from multiple tightly-fitted components. (k) Gold nanocrystal-mediated slider. (l) Molecular algorithm that executes logic and outputs literal arabic numerals. (m) DNA box actuated by changing pH. (n) Thermally-actuated nanovalve. (o) Self-regulating DNA nanotubes. (p) Publication trend in dynamic DNA nanotechnology. (a) Reproduced with permission from ref. 11. Copyright 1999 Springer Nature. (b) Reproduced with permission from ref. 12. Copyright 2000 Springer Nature. (c) Reproduced with permission from ref. 92. Copyright 2003 Angewandte Chemie. (d) Reproduced with permission from ref. 173. Copyright 2004 American Chemical Society. (e) Reproduced with permission from ref. 63. Copyright 2009 Springer Nature. (f) Adapted from ref. 79 under terms of the CC-NC license. Published by Springer Nature Publishing AG, 2011. (g) Reproduced with permission from ref. 29. Copyright 2012 AAAS. (h) Reproduced with permission from ref. 46. Copyright 2015 AAAS. (i) Reproduced with permission from ref. 45. Reproduction rights managed by National Academy of Sciences. (j) Reproduced from ref. 49 under terms of the CC BY 4.0 license. Published by AAAS, 2016. (k) Reproduced from ref. 174 under terms of the CC BY 4.0 license. Published by Springer Nature Publishing AG, 2018. (l) Adapted with permission from ref. 22 Copyright 2019 Springer Nature. (m) Reproduced with permission from ref. 42. Copyright 2019 American Chemical Society. (n) Reproduced with permission from ref. 30. Copyright 2019 American Chemical Society. (o) Reproduced with permission from ref. 162. Copyright 2019 Springer Nature. (p) Data obtained from ref. 175 using search terms “Dynamic”, “DNA”, and (“Nanotechnology”, “Nanodevice”, or “Device”). | ||
At the macroscale, devices as simple as a pair of tweezers or as complicated as a gasoline-powered automobile engine qualify as dynamic. A large span of complexity also exists in DNA devices, from the first dynamic mechanism which induced a simple twist in a connected pair of double-crossover molecules11 to a recent device which performs calculations given an input and then produces output by conforming DNA into literal arabic numerals that can be read by atomic force microscopy.22 Whether simple or complex, the incorporation of dynamic mechanisms into DNA systems can dramatically broaden their potential applications. For example, where a static DNA device might have a unique plasmonic signature,39 a dynamic one might be able to modify that signature between multiple states for applications in sensing35,36,40 or optics;40,41 and while a static DNA box might be designed to hold molecular cargo, a dynamic one can be designed to open and release that cargo once the device enters a specific microenvironment or detects a particular molecule, enabling important functions like targeted drug delivery.28,29,42
In general, artificial molecular machines and devices can be designed using two different approaches. One approach treats these devices as macroscopic machines, which are designed according to the principles of mechanical engineering, and, consequently, input to a device will produce a single deterministic response. Devices can also be designed to mimic biomolecular machines like enzymes and molecular motors which are inherently flexible and incorporate some degree of stochasticity into their function. DNA nanodevices exist at the interface of macroscopic and biomolecular machines; specifically, these devices can exhibit many macroscopic device behaviours, but flexibility and thermal motion are critical to the function of most DNA devices and cannot be ignored.
Many of the dynamic DNA devices developed so far have been inspired by macroscopic machines. In general, machines are made up of a collection of structural elements connected by kinematic mechanisms such as hinges, sliders, and gears to produce precise and complex motions. Machines also typically employ actuation mechanisms to convert an energy source into useful mechanical work, e.g., the internal combustion chamber in automobiles that converts the chemical energy stored in gasoline into translational motion and force of the pistons. Furthermore, many modern machines carry sophisticated control elements including sensors and computer chips to sense their surroundings and regulate their function. Considerable effort has been devoted to translating these three fundamental characteristics of modern machines—kinematic control, actuation, and computation—to DNA nanodevices. Classic examples of such features implemented in DNA nanotechnology include a DNA origami crank-slider mechanism that couples linear and rotary motions (Fig. 1i); a DNA box with a lid that can be actuated using strand displacement (Fig. 1e); and DNA tiles that implement complex logical operations like addition and subtraction (Fig. 1l), respectively.
Whereas the design, modelling, and characterization of macroscopic machines follows established approaches based on the principles of kinematics and continuum mechanics, corresponding approaches for DNA devices are still in their infancy. The nanoscopic length scale of the devices, the significance of thermal fluctuations and associated stochasticity at this scale, and the flexibility of structural elements and joints made out of DNA all make the task of modelling, characterizing, and controlling the structural dynamics of DNA nanodevices highly challenging. Only in the past few years have molecular-scale modelling approaches and advanced microscopy techniques begun to capture the dynamics of DNA nanostructures at high spatial and temporal resolution.
This review article discusses the latest developments in dynamic DNA nanotechnology, focusing on the rapidly growing set of mechanisms being developed to actuate DNA devices and to kinematically control their motion. We also discuss new approaches being used to experimentally characterize and model the dynamics of the resulting DNA devices. We end the review by identifying major challenges in the field that, once solved, should allow dynamic DNA nanotechnology to gather more widespread adoption in science and potentially in commercial applications. Given the large independent body of work on DNA computing and its limited implementation so far towards mechanical devices, the topic of DNA computing will not be discussed here.
2 Kinematic mechanisms
The most basic requirement for a dynamic nanodevice is the incorporation of movable components that enable the device to change its conformation. For dynamic DNA devices this is typically achieved by combining the well-defined structure afforded by programmed DNA base-pairing with strategically incorporated local flexibility, usually involving single-stranded DNA (ssDNA). The structural components consist of helices of double-stranded DNA (dsDNA) or bundles of dsDNA helices. Since the persistence length of dsDNA is around 50 nm,43 these components, especially bundles of dsDNA, are rather stiff on the length scale of typical devices (∼10–100 nm). Single-stranded DNA, on the other hand, has a persistence length of about 1 nm44 and hence provides an excellent means to incorporate local rotational or translational flexibility.These stiff and flexible domains of DNA devices are analogous to the folded and disordered domains of protein-based molecular machines. The ability to make structural components of well-defined shape also enables the arrangement of flexible domains to make joints that exhibit constrained motion much like joints in macroscopic machines. For example, a single ssDNA connection can enable relative motion of two components. If the ssDNA is short, up to a few nucleotides, there will be little relative translation, but this connection can provide three rotational degrees of freedom, similar to a macroscopic spherical joint. Placing two such connections between stiff components along an edge can further constrain the motion to primarily a single rotational degree of freedom.45,46
While using short ssDNA connections allows for primarily rotational motions, it is challenging to achieve well-defined translational motions since extending the length of ssDNA connections leads to random thermal fluctuations. However, this challenge can be overcome, much like in macroscopic translational joints, by using complementary geometries, such as a cylinder inside a tube,45,47,48 where one component can only move along certain degrees of freedom to avoid interference with other components. This approach of complementary geometries has also been used as an alternative strategy to achieve rotational motion with a cylinder in a hollow tube with translation constraint49 or a lever that is pinned to a platform.37,38 More broadly, these kinematic design approaches allow for design of multi-component devices that exhibit complex motion. Examples include linkages that combine several rotational joints to generate straight-line motion,50 convert rotational motion to linear translation,45,51 or exhibit collapsed to expanded conformation changes with programmed 3D motion.45,51,52
While these design strategies provide an effective means to constrain motion primarily along specific degrees of freedom, the flexible ssDNA and even the stiff dsDNA components are still subject to thermal fluctuations that can lead to some motion in unintended degrees of freedom and deviation from designed motion paths.50,53 One approach to well-defined structures with reduced thermal fluctuations that can still undergo conformational changes is to follow a compliant mechanism design approach.53–55 In compliant mechanisms, motion is achieved by deformation of compliant components, usually bending, rather than motion being concentrated at flexible joints. The advantage of this approach is the mitigation of thermal fluctuations; however, these structures would likely require higher energy input to achieve reconfiguration. This challenge can be overcome by careful design of device energy landscapes; for example, designing multiple stable conformations separated by an energy barrier that is on the scale of thermal energy.56
Overall, these strategies enable design of dynamic devices that can exhibit programmed structural states, conformational changes, motion paths, and energy landscapes (conformational distributions).
3 Actuation mechanisms
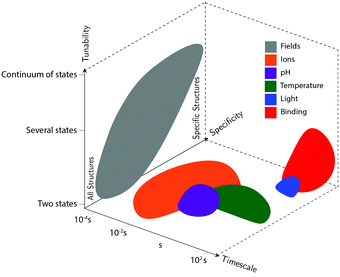
Actuation mechanisms harness energy to produce motion. Actuation is critical to every dynamic device because moving a device or device component from one position to another in a deterministic and controllable manner cannot be achieved passively. Forcing DNA to switch between one state and another is also nontrivial. DNA nanodevices are typically actuated very differently from macroscopic machines: transitions are typically based on a change in the configurational energy landscape of the device that produces a new globally stable state. There is usually an energy barrier to this transition that must be overcome by thermal fluctuations. This stands in contrast to the purely field-driven transitions of macroscopic mechanical devices where thermal fluctuations are insignificant and the energy landscape is monotonically downhill. With this in mind, the use of sufficiently strong fields to actuate DNA devices, which will be discussed further below, shift the configurational energy landscape globally to realize transitions without the assistance of thermal fluctuations, making devices designed using these techniques more akin to conventional macroscopic machines.DNA device actuation was first demonstrated using a connected pair of double-crossover molecules that rotated 180° relative to each other upon exposure to environmental conditions that induce a B–Z transition in the DNA.11 While this approach is not ideal for actuating DNA devices, as it could disturb the entire structure, this work nevertheless provided inspiration for future mechanical devices made of DNA. A variety of actuation strategies have since been developed, which may be broadly grouped into three classes: molecular binding-based actuation, environmental cues-based actuation, and field-induced actuation. While most devices incorporate a single actuation mechanism, some devices make use of multiple actuation mechanisms to react to multiple classes of input and cooperatively enhance response kinetics in the presence of multiple triggering conditions.31,57 A comparison of the various kinds of actuation mechanisms in terms of response times, specificity, and tunability is provided in Fig. 2.
3.1 Molecular binding
This class of mechanisms actuates devices based on the binding of an external molecule. The most popular method is the toehold-mediated strand displacement (TMSD) method,12,58,59 which uses DNA strands for actuation. As illustrated in Fig. 3a and b, an “incumbent” DNA strand X hybridized to a single-stranded region Y of the DNA device is displaced by an “invading” strand Z which can bind more strongly to Y. This displacement process is initiated at a short unhybridized region or “toehold” on Y. In a variant of TMSD known as toehold exchange, strand Z does not bind to the entire length of Y, but leaves a small region still bound to X. Subsequent thermal dissociation of X then completes the displacement reaction, affording more control over the overall kinetics of strand displacement.60 The dissociation of X also leaves a new toehold in place of the original one, allowing for further displacement reactions to be carried out. The energy needed for actuation through TMSD is provided by the difference in the free energies of hybridization of the incumbent and invader strands.61 The kinetics of TMSD60,62 can be controlled by the length of the toehold, up to a length of about 5 to 7 nucleotides (nt) beyond which the rate constant becomes independent of toehold length.60 For a 15 nt-long sequence Y comprising of a 7 nt toehold domain and a 8 nt hybridization domain, for example, the rate constant is on the order of 106 M−1 s−1; below the critical toehold length specified above, a 1–2 orders of magnitude reduction in rate constant is observed for each nucleotide that is removed from the toehold domain.60 Practically speaking, using TMSD to control devices leads to typical response times of minutes to tens of minutes.27,63,64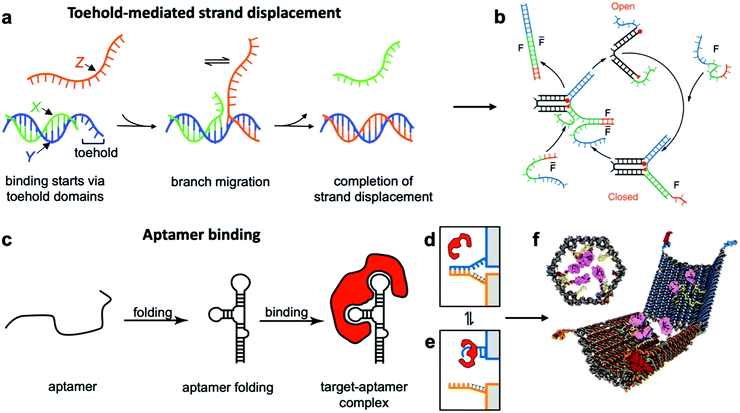 | ||
| Fig. 3 Molecular binding-based DNA device actuation. (a) TMSD mechanism. (b) First application of TMSD to make a pair of “tweezers” which close and open with the addition of fuel (F) or antifuel (F-bar) strands, respectively. (c) Description of aptamer function. (d–f) This device is held together by DNA base pairing (d). Upon the introduction of a protein matching the aptamer formed by the blue strand, the blue strand tends to dissociate from the orange strand and bind the target (e). When this happens on both sides of the DNA device, it is no longer held shut and spring energy drives the device open (f). (a) Adapted with permission from ref. 176. Copyright 2018 American Chemical Society. (b) Reproduced with permission from ref. 12. Copyright 2000 Springer Nature. (c) Adapted from ref. 177 under terms of the CC BY 4.0 license. Published by the Society for Neuroscience, 2017. (d–f) Adapted with permission from ref. 29. Copyright 2012 AAAS. | ||
The high specificity of DNA-based actuating molecules (invader strands) combined with the ease with which a DNA-based binding domain (toehold and hybridization domains) can be incorporated into DNA structures have made TMSD a highly popular approach for actuating DNA devices.29 It should thus come as no surprise that devices utilizing this approach are plentiful.12,18,21,63 Device applications of TMSD include precisely-controlled DNA walkers,27,65,66 biologically-inspired linear actuators,67 drug-containing boxes which release drugs upon exposure to DNA sequences that are known markers of diseases,63,68 and detection of single-nucleotide polymorphisms by using the expected sequence at the site of the polymorphism as the key for a toehold mechanism.14,64 TMSD is also the most popular technique for computational devices as it can be used to instigate a cascading signal. User-inserted DNA “keys” each displace a strand or multiple strands from one device; those displaced strands can be used to actuate another device or devices whose displaced strands will actuate another device, etc., analogous to an electrical circuit. A complete basis set of logical elements can be created21 with the order of actuation simply designed into the displaced and key strands, allowing logical operations to be executed with DNA “circuits” in solution. Indeed, some pioneering work in DNA computing, much of which can be leveraged in nanoscale machines to program the order in which events occur, was achieved long before we could assemble complex multi-component machines out of DNA.27,69,70 Another implementation of this concept of controllable and ordered signal transduction involves the design of a unique interconnected structure that effectively passes signals hundreds of nanometres mechanically from a single input location to globally reconfigure itself.71 Recent work has also leveraged the sequence specificity of DNA to actuate dynamic devices with multiple degrees of freedom where the order of actuation was also critical to achieve the desired conformation changes.72
Aptamer binding provides another approach for actuation, with the primary advantage being that aptamers can interface with proteins and small molecules. Aptamers are oligonucleotides which bind specifically to proteins and a range of other targets.73 An illustration of their function can be found in Fig. 3c–e. The versatility of aptamers comes from the availability of a vast sequence space, which can provide tertiary structure and charge distribution compatible with the binding pocket of a protein or a small molecule. The challenge in designing aptamers lies in efficiently sorting through the multitude of possible sequences and finding the one with the best binding affinity. Fortunately, powerful techniques like systematic evolution of ligands by exponential enrichment (SELEX)74 exist, and many aptamers for common proteins and small molecules have already been discovered and documented.75 This provides an opportunity to interface DNA devices with a wide variety of other molecules and also to design devices that detect the presence of biomolecules other than nucleic acids, which provides exciting potential in sensing and diagnostics applications.15,29,35,41,76
Since most aptamers are made of DNA or RNA, their integration into DNA devices is usually quite straightforward. The aptamer's sequence can be designed as an overhang, a single-stranded section that protrudes from the body of the device.77 Several aptamer-activated DNA devices that actuate upon contact with protein targets have been developed.15,29,78,79 The first such device was a beacon designed for the detection of proteins;15 another application used an aptamer to hold two arms of a spring-loaded hinge in closed position. Upon introduction of the binding target, the aptamer dissociated from one of the arms and bound instead to the target, causing the hinge to open (Fig. 3f).29 Such a mechanism could be very useful in biomedical settings, and has also found use in DNA computing.23
A major disadvantage of aptamer-based actuation is that it is usually not reversible. However, one can add reversibility via a hybrid TMSD–aptamer approach.80
3.2 Environmental factors
So far, we have discussed actuation of DNA devices based on DNA strands or proteins. While versatile and easy to implement, actuating devices using large molecules is very slow, often requiring minutes to hours to complete. Environmental cues such as pH,31,42,81–85 ionic concentration,11,46,86 light,87 temperature,30,46 and hydrophobicity88 can also be used to actuate DNA devices, often on a faster timescale and with fewer waste products than molecule-based methods. Furthermore, such approaches may also be useful for sensing changes in the local environment.Hoogsteen base pairing31,33,89,90 and i-motifs81–85,91–95 can be leveraged to actuate devices in response to changes in pH (Fig. 4d–g).85 Hoogsteen base pairing occurs when the dihedral angle of bases changes from the anti to the syn conformation, which is promoted under low-pH conditions. This allows base pairing to occur between three bases at once, causing the formation of a DNA triplex. This means that a single-stranded DNA end can be designed to float freely in high-pH conditions and then Hoogsteen-pair to a duplex under low-pH conditions. This has formed the basis for DNA cargo transport devices which open and close reversibly in response to pH change.31,42 i-motifs are single-stranded motifs primarily consisting of cytosines. At neutral or high pH, the cytosines do not interact with each other. However, under low-pH conditions, some cytosines become protonated and C–C+ binding becomes highly favourable at a base pairing energy of about 170 kJ mol−1,96 much stronger than canonical base pairing (C–G and A–T pair at energies of 97 kJ mol−1 and 68 kJ mol−1). This binding ties the motif into an intercalated structure, causing the length of the DNA to be reduced substantially, which can be used to drive actuation. A dynamic device utilizing i-motifs to shorten and lengthen a DNA nanostructure in response to pH change can be found in Fig. 4.
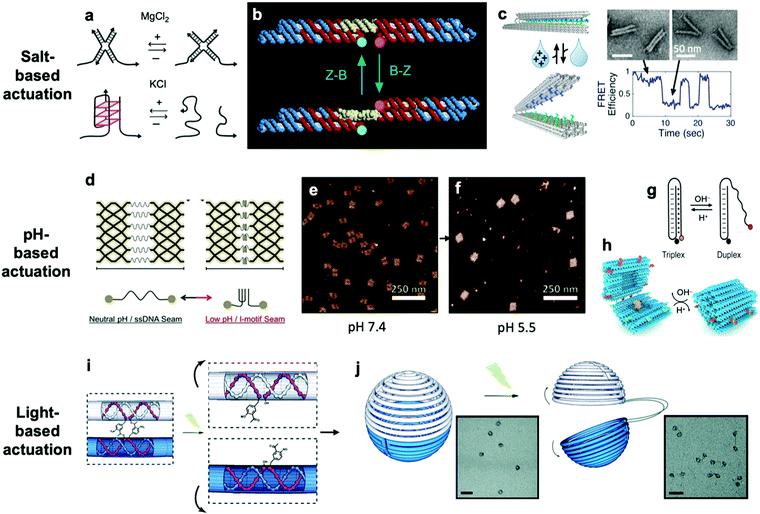 | ||
| Fig. 4 (a) Salt-based actuation mechanisms based on MgCl2 and KCl, respectively. (b) First salt-actuated nanomechanical device made of DNA. (c) Salt-actuated device exhibiting reversible actuation with response time on the order of hundreds of milliseconds. (d–f) i-motif based device which compresses into an intercalated structure in low-pH conditions and associated AFM images of device operation. (g and h) Hoogsteen base pairing-based box whose overhangs form a triplex and close in low-pH conditions. (i and j) ortho-Nitrobenzyl functionalized DNA capsule which opens upon exposure to light. (a) Reproduced with permission from ref. 99. Copyright 2018 IUPAB and Springer-Verlag GmbH. (b) Reproduced with permission from ref. 11. Copyright 1999 Springer Nature. (c) Reproduced with permission from ref. 86. Copyright 2018 American Chemical Society. (d–f) Reproduced with permission from ref. 81. Copyright 2017 American Chemical Society. (g) Reproduced with permission from ref. 178. Copyright 2014 American Chemical Society. (h) Reproduced with permission from ref. 42. Copyright 2019 American Chemical Society. (i and j) Reproduced with permission from ref. 87. Copyright 2015 Royal Society of Chemistry. | ||
The first actuatable DNA device11 was based on ionic concentration, specifically that of Co(NH3)6Cl3, which causes a B–Z transition in the paired double-crossover structure discussed earlier around a critical concentration of 0.25 mM. Several other ion-based actuation mechanisms have since been proposed. One mechanism86 involves placing several mutually complementary loose single strands of DNA (overhangs) on the two freely rotatable arms of a DNA hinge. In high-salt conditions, hybridization of the overhangs becomes favourable, the arms come together, and the device becomes “closed”; in low-salt conditions, the strands are driven apart by unshielded backbone repulsion and the device maintains the “open” configuration (Fig. 4c). Two other actuation mechanisms involving ionic concentration97–99 are summarized in Fig. 4a. So far, ion-mediated actuation in most devices, except one,46 involves two states: one which is closed, and another that is open and moves freely. This simple two-state behaviour is already quite useful for many applications, especially those in the biomedical sciences where this mechanism could be used to deliver drugs inside cells as a result of changing ionic conditions when DNA devices are uptaken.
Light can also be used to actuate DNA devices. One approach involves incorporation of an ortho-nitrobenzyl moiety into the DNA origami;87 light at a wavelength of 302 nm induces a conformational change in the moiety and detaches it from DNA at one end, thereby allowing any DNA connected by this moiety to separate. Such an approach was used to open a DNA nanocontainer (Fig. 4i and j)87 and to probe the interactions of nanomotors.24 Another approach involves attachment of azobenzene to the DNA backbone100–104via a chemistry that is now well-established.105 Azobenzene undergoes isomerization from the trans to cis conformation upon exposure to UV light and returns to the trans conformation when exposed to visible light. Since azobenzene-fused DNA duplexes exhibit different melting temperatures depending on the isomeric form of azobenzene, this difference has been exploited to stabilize or melt DNA duplexes based on exposure to UV or visible light. One disadvantage of light-based actuation is that it is relatively slow; devices using ortho-nitrobenzyl and azobenzene actuation have been observed to switch between states on timescales on the order of minutes,87,101 although a different approach utilizing photocaged trigger strands can operate on much shorter timescales.106 Nevertheless, actuating devices using light is relatively non-invasive and has great potential for use in cancer therapy.
Thermally-actuated devices have also been developed.46 One such device is a nanovalve30 that opens or closes a membrane-embedded DNA origami pore at temperatures above or below a threshold (Fig. 5a). This was achieved via a short, hybridized region of DNA that keeps the pore blocked at low temperature but dissociates above its melting temperature to open the pore. Another thermally-actuated device relies on poly(N-isopropylacrylamide), or pNIPAM,107,108 which undergoes an extended-to-collapsed coil transition at a tunable temperature depending upon the length of the polymer. It is worth mentioning here that latched devices that move via Brownian motion (thermal fluctuations) have also been created.49,109 These devices could be engineered in the future to undergo more directed motion with the input of energy from an external source. Furthermore, the temperature-dependence of DNA base stacking interactions can be used to actuate structures. Base stacking combined with the idea of shape complementarity inspired from biomolecular complexes has allowed for the development of multi-part devices46 and even large assemblies10 which connect with stacking bonds rather than direct base pairing.110 Increasing the temperature of devices with these connections provides the ability to reversibly create and break stacking bonds,46 thus allowing for temperature-sensitive adjustability. These base stacking interactions can also be controlled using ionic concentration due to the shielding of electrostatic repulsion between the interacting components.46
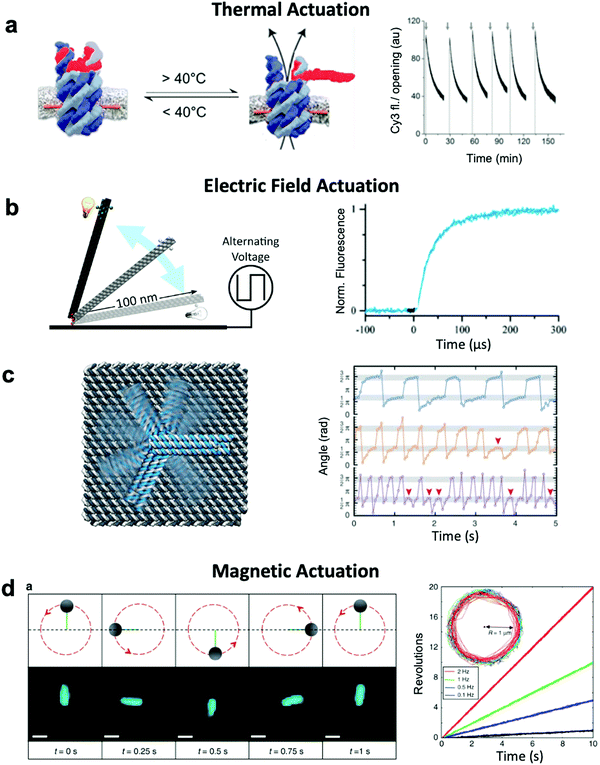 | ||
| Fig. 5 Thermal and field-based actuation. (a) Reversible thermally-actuated DNA nanovalve with bulk response time on order tens of minutes. (b) Switching DNA origami device actuated by electric fields with response on order hundreds of microseconds. (c) Electric field-actuated robotic arm which is controllable on order hundreds of milliseconds. (d) A magnetically-actuated DNA device whose rotational speed can be adjusted by changing the frequency of the magnetic signal and has a response time on the order of hundreds of milliseconds. (a) Reproduced with permission from ref. 30. Copyright 2019 American Chemical Society. (b) Reproduced with permission from ref. 111, Copyright 2017 American Chemical Society. (c) Reproduced with permission from ref. 37, Copyright 2018 AAAS. (d) Reproduced from ref. 38 under terms of the CC BY 4.0 license. Published by Springer Nature Publishing AG, 2018. | ||
3.3 Externally applied fields
Both molecular-based and environment-based mechanisms inherently rely on thermal fluctuation-dependent molecular processes such as diffusion and binding for actuation. Hence, the actuation response times for these mechanisms are limited by the timescales of these processes, which can range from hundreds of milliseconds86 to minutes.87 Actuation via electric and magnetic fields offers a faster alternative given the instantaneous manner in which the field permeates a structure and exerts force on its electrically- or magnetically-responsive elements to directly produce motion. Indeed, the use of fields has enabled response times as short as ∼100 μs to be achieved.111 Furthermore, while environmentally actuated systems are typically designed to exist in two states,12,28,29,63,86,92 and for molecular binding-based actuation, a distinct chemical key must be designed for each state and careful design of the transitions between states must be performed,18 field-based methods offer the opportunity to induce alignment of components in DNA devices with the field enabling a continuum of states to be achieved.An electric field can be used to actuate devices through electrostatic forces acting on the negatively-charged backbone of DNA.37,111 Such an approach has been used to actuate an origami nanolever, which is tethered via one of its ends to a surface, between horizontal and vertical orientations by applying positive or negative voltage to the surface (Fig. 5b).37,111 In another study, an intricate cross-shaped electrophoretic setup was used to switch the electric field sequentially between four mutually orthogonal directions and actuate semi-continuous rotation of an end-tethered origami arm (Fig. 5c).37,111 However, actuating one DNA-based component with an electric field will affect all DNA-based elements in that system, which could present a challenge in more complex implementations where separate components might need to respond to separate stimuli.
Magnetic actuation offers a promising alternative. Systems leveraging magnetic beads can be designed such that only a subset of components are actuated upon the application of a magnetic field. The use of magnetic fields to actuate DNA devices is still relatively new, with the first published work regarding this technique released in 2018.38 In this implementation, a DNA origami rod was functionalized with a magnetic bead and locked onto a platform with flexible linkers. By applying a rotating magnetic field, the rod could be rotated in a continuous manner at frequencies on the order of 1 Hz (Fig. 5d). The obvious disadvantage to this technique is that it requires the functionalization of DNA with magnetic beads, a process that adds complexity and bulk. Nevertheless, functionalization with magnetic beads enables field-based actuation with more specificity than electric field-based methods.
4 Characterizing device dynamics
The effective development of dynamic devices requires validation of their structure, motion, dynamics, and mechanical properties. The structure and motion of the devices are evaluated using typical characterization methods for visualization, namely atomic force microscopy (AFM) and transmission electron microscopy (TEM) (Fig. 6e). These methods allow characterization of the basic structure and the range of conformations.45,46,112 In addition, quantification of the conformational distribution (i.e., probability as a function of key coordinates such as angle or length), also allows for determination of the underlying free-energy landscape of the device, and hence its stiffness along that coordinate. This has been used to quantify the torsional properties of rotational devices25,26,38,45 and extensional properties of translational devices.45,113 Imaging methods also allow characterization of the actuated conformations of DNA devices.32,45,46,79 However, these imaging methods are largely limited to capturing 2D, or planar, snapshots of structures. While cryo-electron microscopy (cryoEM) has been used to determine the 3D structure of DNA devices,114 this requires averaging over many structures and hence is more suitable for static DNA structures. To address this challenge, individual particle electron tomography (IPET), where 3D conformations are determined for individual particles,115,116 has been used to study the 3D conformations of a dynamic DNA device (Fig. 6f).52 This approach enables determination of structure at low resolution (∼5–10 nm). Although this resolution is not sufficient to reveal molecular details, it is an excellent approach for determining the overall conformation of dynamic DNA devices, especially DNA origami devices with thick bundle components.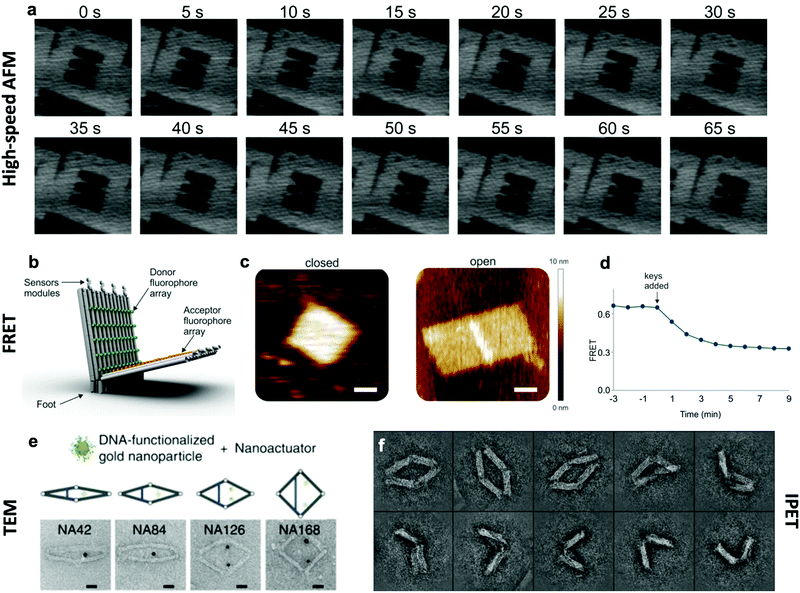 | ||
| Fig. 6 Characterization methods for obtaining information about the dynamics of DNA devices. (a) High-speed AFM scans of a device undergoing a dynamic transition between two states. (b) DNA based device using several arrays of FRET donor and acceptor fluorophores to create a large response upon opening. (c) AFM images of the device in the closed and open states. (d) FRET curve of the devices allows for the characterization of kinetics. (e) TEM images of the various conformations of a DNA device. (f) IPET images of a device's conformations. (a) Reproduced with permission from ref. 98. Copyright 2010 American Chemical Society. (b–d) Reproduced with permission from ref. 16. Copyright 2018 American Chemical Society. (e) Reproduced from ref. 112 under terms of the CC BY 4.0 license. Published by Springer Nature Publishing AG, 2016. (f) Reproduced from ref. 52 under terms of the CC BY 4.0 license. Published by Springer Nature Publishing AG, 2018. | ||
In addition to characterizing structure and motion via static imaging methods, validating and studying the dynamic properties requires methods that quantify conformations in real time. While there have been significant efforts towards enabling TEM imaging in liquids,117 this has primarily been used to study electron-dense systems like nanoparticles that give very high contrast. In contrast, AFM imaging in liquids, especially high-speed AFM,118,119 has provided a useful tool to study dynamic DNA devices (Fig. 6a). In particular, this approach has been used to quantify local98 and global conformation changes of DNA devices, motion of DNA walkers,120 binding of biomolecules to DNA structures,79 and higher order assembly of DNA nanostructures.121 However, the time resolution is still limited to seconds or longer and the AFM approach requires adsorption to a surface, which could influence motion and dynamic behaviour.
To enable direct measurement of conformational changes in solution, researchers have widely turned to fluorescence methods, especially fluorescence quenching122 or Förster resonance energy transfer (FRET)123 methods (Fig. 6b–d). In these approaches, the relative separation between two molecules (fluorophore and quencher or donor and acceptor fluorophores) is quantified by measuring the intensity of one fluorophore (fluorescence quenching) or the relative intensities of two fluorophores (FRET). While these approaches are limited to providing a single separation distance between two points on the structure, they can still provide a readout of the overall conformation (e.g., open versus closed, or latched versus freely fluctuating). While the time resolution of fluorescence methods is insufficient to measure inherent dynamics (i.e., thermal fluctuations), bulk fluorescence methods have been widely used to measure the actuation and response times of actuating DNA devices.45,46,63,112 Since the time resolution of bulk methods is typically on the order of seconds, single-molecule fluorescence methods have been employed to quantify dynamics of individual DNA devices at faster timescales. In particular, single-molecule FRET has revealed that actuation can occur at millisecond timescales,37,86 and this is likely still limited by the time resolution of detection methods. In addition, single-molecule fluorescence has been used to probe the conformational dynamics of DNA devices that transiently transition between discrete states due to thermal fluctuations.46,124 In addition to fluorescence methods, the incorporation of gold nanoparticles, especially gold nanorods, allows for probing DNA device conformations by circular dichroism, which has been used to quantify the actuation of DNA devices.32,33,56,104
Another recently applied technique used to capture information about conformational changes is small-angle X-ray scattering (SAXS). This technique allows for distinction between multiple conformational states through the interpretation of devices’ X-ray scattering profiles in each state.125 Time-resolved SAXS provides rich information about the timescales of these transitions on the order of milliseconds and can be used to obtain reaction rate constants for large conformational changes without introducing large dye molecules which can affect device conformation and thus bias the rate constant.126 Additional applications of SAXS for DNA origami characterization have included global twist measurement127 and measurement of the position accuracy of attached particles used to functionalize DNA origami.128 The major disadvantage of this technique is that it cannot be used to characterize local conformational changes like FRET. This technique instead provides more globally relevant information such as the radius of gyration, which is useful but can potentially be misinterpreted if non-predicted conformational behaviour arises and might not be as useful when measuring relatively small conformational changes in a large structure.
5 Modelling dynamic DNA devices
Over the past two centuries, success achieved in the design of macroscopic devices and machines has largely been attributable to our ability to quantitatively predict macroscale mechanical behaviour. For example, understanding the dynamics of automotive suspension has allowed us to design vehicles which ride smoothly yet do not feel wayward. It would be wonderful to have a similar level of understanding of the dynamics of DNA nanodevices, but there is still much progress to be made. Many challenges inhibit our understanding of these devices, first and foremost that DNA nanodevices are much more susceptible to deformation by thermal fluctuations than, for example, a steel beam. We are thus forced to evaluate these structures in statistical terms. Even predicting equilibrium (minimum energy) conformations of DNA nanostructures has proven challenging. The reality of DNA's mechanical behaviour is much more complicated than that of a linearly elastic rod. Furthermore, while the environment around macroscopic machines plays a relatively small role in their overall function (with the exception of extreme conditions such as those in space), interactions as simple as those of DNA with magnesium ions, while very common, have a severe effect on device conformation and function and are still poorly understood. Most of this lack of understanding comes from the complex, quantum-mechanical nature of molecular interactions, which we are still struggling to pragmatically incorporate into device models. Nevertheless, substantial progress has been made in modelling these devices by applying similar ideas to those employed in the relatively more mature fields of protein folding, colloidal physics, and polymers. As a result, dynamic DNA nanodevices can now be studied at many length and time scales, from the coarsest models which apply continuum mechanics and equilibrium statistical mechanics to the finest techniques which model every single atom in a system (Fig. 7a).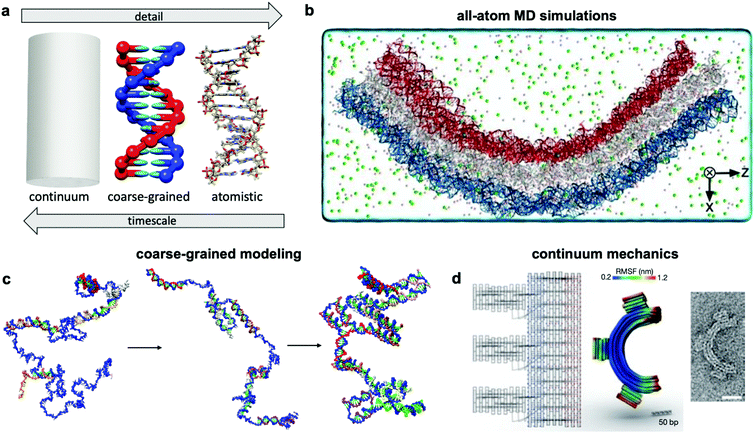 | ||
| Fig. 7 Three current approaches for modelling dynamic devices. (a) 12 base pairs of DNA visualized at the three different levels of simulation detail. (b) Image of an all-atom simulation trajectory output. (c) Direct simulation of DNA origami assembly in a small system using OxDNA coarse-grained molecular dynamics. (d) Left: caDNAno schematic of a gear-shaped device. Middle: Equilibrium conformation of the device produced from the schematic as determined by CanDo. Right: TEM image of the executed design. (a) Coarse-grained model image reproduced with permission from ref. 135. All-atom representation prepared with UCSF Chimera.179 Reproduction rights managed by Journal of Chemical Physics. (b) Reproduced with permission from ref. 132. Reproduction rights managed by National Academy of Sciences. (c) Adapted with permission from ref. 141. Copyright 2016 American Chemical Society. (d) Reproduced with permission from ref. 148. Copyright 2011 Springer Nature. | ||
5.1 Molecular simulations
An ideal approach to modelling dynamic DNA nanostructures is all-atom molecular dynamics (MD) simulations.129 In this approach, each and every atom of the device and surrounding solvent and ions is modelled (Fig. 7b), interaction forces between all atoms are calculated explicitly, and their dynamics are propagated using Newton's equations of motion over femtosecond time steps. All-atom simulations provide the most detailed and arguably the most predictive description of device motion and may be necessary to gain a mechanistic understanding of device behaviour.130,131 Unfortunately, this approach is heavily size- and timescale-limited, and all-atom MD is practically applicable only to the scale of hundreds of thousands of atoms and microseconds of device motion.132 All-atom simulations of DNA structures have therefore typically been restricted to studying local structural features of devices rather than entire devices and their atomic-scale dynamics at equilibrium configurations rather than global motions and transitions.132–134The most common approach for addressing this limitation and thus enabling modelling of slow processes such as strand displacement, self-assembly, and structural transitions that underlie dynamic DNA nanotechnology is coarse-graining.135–140 This approach involves redefining the molecular structure of DNA in terms of a smaller number of representative particles (beads) in place of atoms. In most cases, three representative beads are used to define a nucleotide in place of the >30 atoms that define a nucleotide in an all-atom model. Undoubtedly, the most popular implementation of coarse-graining in DNA nanotechnology has been oxDNA.135–137 This model coarsens DNA to three rigidly-connected beads per nucleotide, and the dielectric and electrostatic screening effects of solvent molecules and ions are treated using continuum electrostatic models, although this can also be done in all-atom simulations to reduce computational burden. With these two simplifications, the number of particles to be simulated is cut down by multiple orders of magnitude, leading to similarly drastic improvements in the timescales accessible by simulation, from microseconds132 to milliseconds, or even seconds in case of small systems.141 With access to such timescales, researchers have begun to computationally study origami assembly,141 strand-displacement based actuation,142 and other moderate-timescale phenomena138 directly on small DNA nanostructures (Fig. 7c).
However, to study the structural dynamics of DNA devices at even longer timescales, additional coarse graining of the structures might be required. Alternatively, approaches based on polymer and colloid physics, statistical mechanics, and continuum mechanics can provide access to phenomena at long timescales.
5.2 Continuum mechanics
Solid mechanics, which treats DNA as a continuum elastic body rather than a discrete collection of connected or interacting atoms or particles (Fig. 7d), can be very effective for modelling the equilibrium conformation and small-deformation mechanical behaviour of DNA devices at large length scales. A finite elements-based approach and its accompanying software, CanDo, which use effective moduli reflecting the mechanical properties of DNA,103,143–147 have been developed to predict equilibrium conformations of DNA structures.148 Predictions from this approach have found generally good agreement with experiments carried out in conditions of structure assembly. The wormlike chain model149 is another example of continuum approximation, albeit one based on statistical mechanics, that has found use in modelling force-extension behaviour of ssDNA elements in DNA devices.150 Unfortunately, each of these continuum approaches are still static, and one must rely on more complex methods for prediction of nonequilibrium behaviour. Furthermore, these models do not capture changes in DNA form (e.g., B–Z transition), salt- and pH-dependent effects, sequence specificity, and other molecular effects that are better captured in all-atom simulations.5.3 Secondary structure prediction algorithms
Even before the inception of DNA nanotechnology, there was interest in predicting the secondary structure of nucleic acids. The earliest methods performed brute-force calculations of the free energies of all possible base-pairing combinations of an RNA sequence and chose the binding arrangement with the lowest free energy as the stable structure.151 The main issue with this strategy is that the total number of base-pairing combinations increases exponentially with sequence length, making structure determination computationally expensive for long sequences. Furthermore, base stacking free energies and the effects of bulges were not considered, and ensemble effects were not properly addressed. Subsequent improvements have sought to more methodically search the configurational space,152,153 account for bulges, and incorporate nearest-neighbour interactions to account for base stacking.61,153,154 Eventually, server-based solutions were created which allowed for rapid determination of the secondary structure of oligonucleotides thousands of units in length.155–157 Such algorithms can be useful for determining the free energy change of toehold-mediated strand displacement used to drive dynamic mechanisms in DNA nanotechnology.62 However, because these algorithms do not account for the 3D geometry of nucleic-acid structural elements and the steric and energetic interactions between such elements, they are not suitable for predicting the 3D conformation of DNA origami devices. Thus, structural and dynamical modelling of such devices is best left for approaches like MD simulations that inherently account for geometry and intermolecular interactions.53,132,134,1415.4 Statistical mechanics
The theory of statistical mechanics158 stipulates that physical systems display an ensemble of configurations whose statistics at equilibrium follow specific probability distribution functions governed by the thermodynamic state of the system (e.g., systems held at constant temperature follow the Boltzmann distribution). The experimentally measured properties of the system are then simply given by the average values, which are appropriately weighted based on the distribution function of those properties over the ensemble. While statistical mechanics has been used extensively in physics for modelling a wide variety of phenomena ranging from phase transitions to polymer dynamics and also forms the basis of all molecular simulations, it has only recently found application in DNA nanotechnology. In particular, statistical mechanics was used for modelling the salt-induced actuation of DNA origami hinges between open and closed states.86 This involved deriving the partition functions of the hinge in the two states, taking advantage of predictions of DNA hybridization free energies readily available from secondary structure prediction algorithms. The relative magnitudes of these partition functions determine the proportion of time spent in each state, and the dependence of their relative magnitudes on salt concentration then enables prediction of the critical salt concentration value that will induce an open–closed transition. This approach offers a computationally inexpensive way of modelling thermodynamic transitions that underlie most of the actuation mechanisms in dynamic DNA devices.5.5 Kinetic models
This is a common approach used for modelling the behaviour of a system of reacting chemical species, or interacting components transitioning between distinct physical states;159 the behaviour usually sought is the variation in species concentrations or state probabilities with time. In this approach, individual reaction or transition rates are described in terms of simple rate laws and rate constants, and the time evolution in concentrations or probabilities are written down in terms of ordinary differential equations (ODEs). A system containing several interdependent reactions is fully described by the set of ODEs; solving the system of ODEs then provides the overall time-resolved behaviour of the system, which can be obtained at equilibrium or in response to perturbations. In the context of DNA nanotechnology, kinetic models have been used to predict and design the dynamical behaviour of systems composed of multiple interacting DNA strands encountered in DNA walkers160 and self-regulating systems.161–163 One caveat is the requirement for additional experimentation to determine and measure the rate laws and rate constants for each and every reaction in the system. However, once the kinetics of individual reactions are established, kinetic models can be very powerful tools for predicting the dynamic properties of DNA systems undergoing several different interdependent reactions.162,163 While predicting rate constants from scratch has proven difficult, a recent study has produced a substantial dataset describing the kinetics of DNA origami assembly,164 which should aid computational efforts to efficiently model these kinetics by providing a reference against which new models can be tested.6 Grand challenges
Significant challenges still inhibit the development of functional dynamic DNA devices. Many of these challenges arise because DNA presents an entirely new type of a building block for constructing devices—one that exposes a new horizon in nanoscale functions, but also one that we have limited experience with in using as a material. In contrast, macroscopic machines have been modelled, characterized, and refined for hundreds of years, and proteins, which represent nature's most efficient nanoscale machines, have undergone their own brand of refinement through evolution for billions of years. With DNA nanotechnology, scientists were faced with the challenge of starting from scratch. Forty years down the line, we have achieved an enormous amount of progress, but there is far to go. Some of the most pressing issues deal with precision and control of DNA devices that are prone to stochasticity due to thermal fluctuations. Other challenges have to do with the speed and size limitations of these devices, and their integrability with other materials and platforms, key to making these structures practically useful.6.1 Achieving fast actuation
Real-time actuation of DNA devices is critical to many of their proposed applications, especially in sensing, computation, and robotics. While TMSD remains by far the most popular method for actuation because of its ease of implementation, robustness, and specificity, the kinetics of TMSD are prohibitively slow. Hence, one fruitful direction of research is to improve its kinetics. The use of polar solvents, where up to a 28-fold improvement in the TMSD rate constant was achieved,165 provides one such promising strategy. If found to not interfere significantly with device function, this strategy could cut reaction time from hours to minutes in almost all TMSD-based devices, improving their usefulness in various applications. Efforts to develop entirely new actuation methods should also continue. Amongst these, field-based methods37,38 provide some of the most responsive mechanisms for actuation, though these methods require significant external instrumentation and have not yet been widely implemented. With continued development, field-based methods could enable applications such as: drug delivery, where they could non-invasively induce drug release via an already-existing device like a magnetic resonance imaging machine, or improvements to DNA computation, where inputs could take the form of electrical or magnetic pulses instead of DNA strands. Cooperativity between mechanisms provides another way to improve device speed. This can take the form of multiple actuation mechanisms that speed up kinetics when multiple triggering environmental conditions are present at the same time,31 or a set of adjacent mechanisms on a single device that synergistically improve actuation speed, e.g. through a “zippering” action.86 Further advances in cooperative-mechanism design may provide additional speed-up when other techniques fail.6.2 Hybrid actuation mechanisms
The luxury of having a variety of actuation mechanisms to choose from not only gives us the ability to design dynamic devices for a wide range of solution conditions and tasks, but also carry out functions not possible by a single mechanism alone. For example, one might want a substantial amount of a chemical to be released upon contact with a biological target that is only present in small quantities. An aptamer-based actuation would be an obvious choice here, but the small quantity of target may only be able to produce a tiny signal. One potential solution to this problem, commonly used in other fields,166 is signal amplification. In particular, a set of DNA devices could be actuated by the target to release many DNA keys that help amplify the target's signal, while another set of devices could be actuated by the keys from the first device and release the chemical. This would produce a much larger response than similarly sized devices actuated only by the target. The ability to integrate multiple mechanisms thus offers enormous opportunities for carrying out sophisticated functions.Another issue with existing DNA device designs is that they often do not offer satisfactory control over the exact condition for triggering actuation. For example, salt-actuated devices can usually only be designed to actuate via large changes in salt concentration, and the critical ionic concentration that triggers the response is not very tunable. We can leverage hybrid bio-electrical control devices to solve this problem. For example, an electrically actuated DNA nanovalve coupled to a salinity sensor via a microcontroller would provide finely adjustable actuation at a wide range of salinity values. This would provide the speed, modularity, and tunability of electronics with the flexibility and ease of nanoscale design of DNA devices. Many other fields have solved the problems that we are currently addressing here – with a relatively clear path to hybrid device implementation through the use of field-based actuation, there are clear opportunities to translate these solutions to DNA-based devices.
Furthermore, the ability of DNA devices to harness chemical energy remains limited, especially compared to evolved protein machines that often use energy from ATP hydrolysis. Incorporating such mechanisms that generate processive motion or rotation with the structural precision of DNA origami could be a highly promising direction for future dynamic hybrid biomolecular systems. A shorter-term goal could also leverage the chemical or catalytic function of some RNA constructs, which may be easier to integrate with DNA-based devices.
6.3 Developing larger structures
The largest assembled DNA origami structure contains around 2 million nucleotides and spans about a micron in size—truly impressive but tiny compared to the human genome of ∼3 billion nucleotides and to the size of most mammalian cells.167 If we are to design dynamic DNA devices that interface with the human body or other microscale-to-macroscale objects, much larger structures are desirable. Consider for instance the newly developed DNA nanotubes that exhibit controllable assembly-disassembly dynamics akin to cytoskeletal fibres.162 Further advancements in the scale of such devices (and in their control, complexity, and bio-integration) could one day make autonomous regulation of cell structures a reality. Large assemblies of devices will likely also be required to achieve high signal-to-noise ratio in sensing applications or high throughput in applications such as nanomanufacturing. Enormous strides are currently being made in expanding the size scale of static DNA structures. Translating some of those ideas to dynamic devices would be the most fruitful approach to creating microscopic and perhaps even macroscopic assemblies with dynamic properties. However, this will likely come with new challenges, namely in ensuring that individual devices retain their dynamic functionality within assemblies, having control over the behaviour of individual devices, and leveraging possibilities for cooperative dynamic function of many devices.6.4 Interfacing multiple devices
In mechanical engineering, one might employ a nut and bolt to rigidly connect two components; no such universal interface exists within DNA nanotechnology, although shape-complementarity46,110 may begin to fill this role in the near future. Furthermore, the interaction between dynamic DNA devices is poorly controlled because most of these devices float in solution. While this works for DNA computing, devices which interface mechanically need to be positioned relative to each other in order to cooperate. It also might be desired to assemble the machines in a way that allows their absolute position to be known. Progress has been made in interfacing DNA origami with lithographically-defined substrates in order to achieve precision placement,168 but only one species of device can currently be used to populate a substrate. Placing many devices at high density where the devices can possibly interact in a pre-programmed way remains a challenge. Being able to make DNA nanomachines containing several different components or collections of nanomachines which lock onto a substrate would enable the development of miniature manufacturing floors or nanoscale gear trains. Similarly, while recent work has demonstrated the ability to connect multiple rigid elements and joints into larger assemblies to achieve complex motions,45 creating even larger assemblies of these components remains a challenge. Incorporating independent sensing and control elements within each such mechanism as a route to creating robust, self-regulating machines also presents a worthwhile but challenging endeavour.6.5 Mesoscopic modelling of DNA devices
All-atom and coarse-grained MD simulations are now relatively established approaches for modelling the dynamics of DNA nanostructures (though force-field refinement efforts will and should continue). However, these methods cannot access mesoscopic length and time scales (>100 nm and >1 ms) relevant to many of the DNA structures being currently developed. There is a clear need to develop mesoscopic models of DNA nanostructures, as no such approaches currently exist. One strategy would be to borrow ideas from mesoscopic models developed in biophysics for studying macromolecular complexes. For instance, the dynamics of chromatin fibres could be efficiently described by using flexible bead-chain models to treat components like DNA linkers that play a dominant role in the large-scale motion of the fibres and rigid-body models to treat less flexible components like nucleosomes.169–172 The fibre dynamics could then be simulated using Brownian dynamics approaches that afford significantly larger time steps. A similar philosophy could be used for modelling DNA devices where connected bundles of DNA may be treated as rigid bodies while the more flexible ssDNA and dsDNA portions may be treated using flexible bead-chains of appropriate resolutions. Analytical models or more computationally tractable models based on statistical mechanics, colloid and polymer physics, and fluid mechanics may also be leveraged to predict transition rates, diffusive behaviour, and hydrodynamic effects on these larger DNA structures. These theoretical approaches are prevalent in biophysics, but they have not yet been applied in DNA nanotechnology. Lastly, multi-scale or hybrid approaches that integrate particle- and continuum-based models may enable predictions for large structures governed by fast and local phenomena.6.6 Work output of DNA devices
While there have been significant efforts to study and speed up the actuation response time of dynamic DNA devices, still little is known about the capacity for these devices to perform work. Performing mechanical work requires the generation of a force, the characterization of which remains largely unexplored for DNA devices. While TMSD may not directly be suitable for generating force, it is certainly possible that DNA devices can be locked into energetically unfavourable states that effectively store mechanical energy. Hence, actuating the DNA device could then release that stored energy in the form of work. This or other mechanisms that exploit distinct energy sources could serve as a basis for DNA motors that drive the function of mechanical DNA devices or even couple to drive other nano- or micro-scale devices or material systems.7 Conclusion
In this review, we have outlined recent progress in the field of dynamic DNA nanotechnology, focusing on the diverse dynamic mechanisms that have been created to actuate structures and control their motion. Approaches to experimentally characterize and computationally model the motions and conformations of these complex dynamic structures have also been discussed. We conclude by identifying several key challenges that must be overcome in order to realize the enormous potential of dynamic DNA nanotechnology in applications ranging from medicine to robotics.Conflicts of interest
There are no conflicts to declare.Acknowledgements
MD was funded by a graduate fellowship from Duke. This work was supported in part by the National Science Foundation (CMMI 1921955 and EFMA 1933344).References
- J. D. Watson and F. H. C. Crick, Molecular Structure of Nucleic Acids: A Structure for Deoxyribose Nucleic Acid, Nature, 1953, 171, 737–738 CrossRef CAS
.
- N. C. Seeman, DNA in a material world, Nature, 2003, 421, 427–431 CrossRef
.
- N. C. Seeman, Nucleic acid junctions and lattices, J. Theor. Biol., 1982, 99, 237–247 CrossRef CAS
.
- X. Li, X. Yang, J. Qi and N. C. Seeman, Antiparallel DNA double crossover molecules as components for nanoconstruction, J. Am. Chem. Soc., 1996, 118, 6131–6140 CrossRef CAS
.
- P. W. K. Rothemund, Folding DNA to create nanoscale shapes and patterns, Nature, 2006, 440, 297–302 CrossRef CAS
.
- S. M. Douglas, H. Dietz, T. Liedl, B. Högberg, F. Graf and W. M. Shih, Self-assembly of DNA into nanoscale three-dimensional shapes, Nature, 2009, 459, 414–418 CrossRef CAS
.
- H. Dietz, S. M. Douglas and W. M. Shih, Folding DNA into twisted and curved nanoscale shapes, Science, 2009, 325, 725–730 CrossRef CAS
.
- L. L. Ong, N. Hanikel, O. K. Yaghi, C. Grun, M. T. Strauss, P. Bron, J. Lai-Kee-Him, F. Schueder, B. Wang, P. Wang, J. Y. Kishi, C. Myhrvold, A. Zhu, R. Jungmann, G. Bellot, Y. Ke and P. Yin, Programmable self-assembly of three-dimensional nanostructures from 10,000 unique components, Nature, 2017, 552, 72–77 CrossRef CAS
.
- G. Tikhomirov, P. Petersen and L. Qian, Fractal assembly of micrometre-scale DNA origami arrays with arbitrary patterns, Nature, 2017, 552, 67–71 CrossRef CAS
.
- K. F. Wagenbauer, C. Sigl and H. Dietz, Gigadalton-scale shape-programmable DNA assemblies, Nature, 2017, 552, 78–83 CrossRef CAS PubMed
.
- C. Mao, W. Sun, Z. Shen and N. C. Seeman, A nanomechanical device based on the B-Z transition of DNA, Nature, 1999, 397, 144–146 CrossRef CAS
.
- A. P. Mills, F. C. Simmel, A. J. Turberfield, J. L. Neumann and B. Yurke, A DNA-fuelled molecular machine made of DNA, Nature, 2002, 406, 605–608 Search PubMed
.
- Y. Krishnan and F. C. Simmel, Nucleic Acid Based Molecular Devices, Angew. Chem., Int. Ed., 2011, 50, 3124–3156 CrossRef CAS PubMed
.
- D. Wang, W. Tang, X. Wu, X. Wang, G. Chen, Q. Chen, N. Li and F. Liu, Highly selective detection of single-nucleotide polymorphisms using a quartz crystal microbalance biosensor based on the toehold-mediated strand displacement reaction, Anal. Chem., 2012, 84, 7008–7014 CrossRef CAS PubMed
.
- N. Hamaguchi, A. Ellington and M. Stanton, Aptamer beacons for the direct detection of proteins, Anal. Biochem., 2001, 294, 126–131 CrossRef CAS
.
- D. Selnihhin, S. M. Sparvath, S. Preus, V. Birkedal and E. S. Andersen, Multifluorophore DNA Origami Beacon as a Biosensing Platform, ACS Nano, 2018, 12, 5699–5708 CrossRef CAS
.
- D. Koirala, P. Shrestha, T. Emura, K. Hidaka, S. Mandal, M. Endo, H. Sugiyama and H. Mao, Single-molecule mechanochemical sensing using DNA origami nanostructures, Angew. Chem., Int. Ed., 2014, 53, 8137–8141 CrossRef CAS
.
- M. N. Stojanovic and D. Stefanovic, A deoxyribozyme-based molecular automaton, Nat. Biotechnol., 2003, 21, 1069–1074 CrossRef CAS
.
- F. Pu, C. Wang, D. Hu, Z. Huang, J. Ren, S. Wang and X. Qu, Logic gates and pH sensing devices based on a supramolecular telomere DNA/conjugated
polymer system, Mol. BioSyst., 2010, 6, 1928–1932 RSC
.
- C. Zhou, X. Duan and N. Liu, A plasmonic nanorod that walks on DNA origami, Nat. Commun., 2015, 6, 8102 CrossRef CAS
.
- B. Ding and N. C. Seeman, Operation of a DNA robot arm inserted into a 2D DNA crystalline substrate, Science, 2006, 314, 1583–1585 CrossRef CAS
.
- D. Woods, D. Doty, C. Myhrvold, J. Hui, F. Zhou, P. Yin and E. Winfree, Diverse and robust molecular algorithms using reprogrammable DNA self-assembly, Nature, 2019, 567, 366–372 CrossRef CAS
.
- Y. Amir, E. Ben-Ishay, D. Levner, S. Ittah, A. Abu-Horowitz and I. Bachelet, Universal computing by DNA origami robots in a living animal, Nat. Nanotechnol., 2014, 9, 353–357 CrossRef CAS PubMed
.
- N. D. Derr, B. S. Goodman, R. Jungmann, A. E. Leschziner, W. M. Shih and S. L. Reck-Peterson, Tug-of-War in Motor Protein Ensembles Revealed with a Programmable DNA Origami Scaffold, Science, 2012, 338, 662–665 CrossRef CAS PubMed
.
- J. J. Funke, P. Ketterer, C. Lieleg, S. Schunter, P. Korber and H. Dietz, Uncovering the forces between nucleosomes using DNA origami, Sci. Adv., 2016, 2, e1600974 CrossRef
.
- J. V. Le, Y. Luo, M. A. Darcy, C. R. Lucas, M. F. Goodwin, M. G. Poirier and C. E. Castro, Probing Nucleosome Stability with a DNA Origami Nanocaliper, ACS Nano, 2016, 10, 7073–7084 CrossRef CAS
.
- A. J. Thubagere, W. Li, R. F. Johnson, Z. Chen, S. Doroudi, Y. L. Lee, G. Izatt, S. Wittman, N. Srinivas, D. Woods, E. Winfree and L. Qian, A cargo-sorting DNA robot, Science, 2017, 357, eaan6558 CrossRef
.
- R. M. Zadegan, M. D. E. Jepsen, K. E. Thomsen, A. H. Okholm, D. H. Schaffert, E. S. Andersen, V. Birkedal and J. Kjems, Construction of a 4 Zeptoliters Switchable 3D DNA Box Origami, ACS Nano, 2012, 6, 10050–10053 CrossRef CAS
.
- S. M. Douglas, I. Bachelet and G. M. Church, A logic-gated nanorobot for targeted transport of molecular payloads, Science, 2012, 335, 831–834 CrossRef CAS
.
- P. M. Arnott and S. Howorka, A Temperature-Gated Nanovalve Self-Assembled from DNA to Control Molecular Transport across Membranes, ACS Nano, 2019, 13, 3334–3340 CrossRef CAS
.
- D. Mariottini, A. Idili, A. Vallée-Bélisle, K. W. Plaxco and F. Ricci, A DNA Nanodevice That Loads and Releases a Cargo with Hemoglobin-Like Allosteric Control and Cooperativity, Nano Lett., 2017, 17, 3225–3230 CrossRef CAS
.
- A. Kuzyk, R. Schreiber, H. Zhang, A. O. Govorov, T. Liedl and N. Liu, Reconfigurable 3D plasmonic metamolecules, Nat. Mater., 2014, 13, 862–866 CrossRef CAS
.
- A. Kuzyk, M. J. Urban, A. Idili, F. Ricci and N. Liu, Selective control of reconfigurable chiral plasmonic metamolecules, Sci. Adv., 2017, 3, e1602803 CrossRef
.
- Q. Liu, A. Kuzyk, M. Endo and I. I. Smalyukh, Colloidal plasmonic DNA-origami with photo-switchable chirality in liquid crystals, Opt. Lett., 2019, 44, 2831 CrossRef CAS
.
- T. Funck, F. Nicoli, A. Kuzyk and T. Liedl, Sensing Picomolar Concentrations of RNA Using Switchable Plasmonic Chirality, Angew. Chem., Int. Ed., 2018, 57, 13495–13498 CrossRef CAS
.
- Y. Huang, M.-K. Nguyen, A. K. Natarajan, V. H. Nguyen and A. Kuzyk, A DNA Origami-Based Chiral Plasmonic Sensing Device, ACS Appl. Mater. Interfaces, 2018, 10, 44221–44225 CrossRef CAS
.
- E. Kopperger, J. List, S. Madhira, F. Rothfischer, D. C. Lamb and F. C. Simmel, A self-assembled nanoscale robotic arm controlled by electric fields, Science, 2018, 359, 296–301 CrossRef CAS
.
- S. Lauback, K. R. Mattioli, A. E. Marras, M. Armstrong, T. P. Rudibaugh, R. Sooryakumar and C. E. Castro, Real-time magnetic actuation of DNA nanodevices via modular integration with stiff micro-levers, Nat. Commun., 2018, 9, 1446 CrossRef
.
- C. Zhu, M. Wang, J. Dong, C. Zhou and Q. Wang, Modular Assembly of Plasmonic Nanoparticles Assisted by DNA Origami, Langmuir, 2018, 34, 14963–14968 CrossRef CAS PubMed
.
- A. Kuzyk, R. Jungmann, G. P. Acuna and N. Liu, DNA Origami Route for Nanophotonics, ACS Photonics, 2018, 5, 1151–1163 CrossRef CAS PubMed
.
- R. Schreiber, N. Luong, Z. Fan, A. Kuzyk, P. C. Nickels, T. Zhang, D. M. Smith, B. Yurke, W. Kuang, A. O. Govorov and T. Liedl, Chiral plasmonic DNA nanostructures with switchable circular dichroism, Nat. Commun., 2013, 4, 2948 CrossRef PubMed
.
- H. Ijäs, I. Hakaste, B. Shen, M. A. Kostiainen and V. Linko, Reconfigurable DNA Origami Nanocapsule for pH-Controlled Encapsulation and Display of Cargo, ACS Nano, 2019, 13, 5959–5967 CrossRef
.
- N. Borochov, H. Eisenberg and Z. Kam, Dependence of DNA conformation on the concentration of salt, Biopolymers, 1981, 20, 231–235 CrossRef CAS
.
- Q. Chi, G. Wang and J. Jiang, The persistence length and length per base of single-stranded DNA obtained from fluorescence correlation spectroscopy measurements using mean field theory, Phys. A, 2013, 392, 1072–1079 CrossRef CAS
.
- A. E. Marras, L. Zhou, H.-J. Su and C. E. Castro, Programmable motion of DNA origami mechanisms, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 713–718 CrossRef CAS
.
- T. Gerling, K. F. Wagenbauer, A. M. Neuner and H. Dietz, Dynamic DNA devices and assemblies formed by shape-complementary, non-base pairing 3D components, Science, 2015, 347, 1446–1452 CrossRef CAS
.
- J. List, E. Falgenhauer, E. Kopperger, G. Pardatscher and F. C. Simmel, Long-range movement of large mechanically interlocked DNA nanostructures, Nat. Commun., 2016, 7, 12414 CrossRef CAS
.
- J. T. Powell, B. O. Akhuetie-Oni, Z. Zhang and C. Lin, DNA Origami Rotaxanes: Tailored Synthesis and Controlled Structure Switching, Angew. Chem., Int. Ed., 2016, 55, 11412–11416 CrossRef CAS
.
- P. Ketterer, E. M. Willner and H. Dietz, Nanoscale rotary apparatus formed from tight-fitting 3D DNA components, Sci. Adv., 2016, 2, e1501209 CrossRef
.
- C. M. Huang, A. Kucinic, J. V. Le, C. E. Castro and H. J. Su, Uncertainty quantification of a DNA origami mechanism using a coarse-grained model and kinematic variance analysis, Nanoscale, 2019, 11, 1647–1660 RSC
.
- R. Sharma, J. S. Schreck, F. Romano, A. A. Louis and J. P. K. Doye, Characterizing the Motion of Jointed DNA Nanostructures Using a Coarse-Grained Model, ACS Nano, 2017, 11, 12426–12435 CrossRef CAS
.
- D. Lei, A. E. Marras, J. Liu, C. M. Huang, L. Zhou, C. E. Castro, H. J. Su and G. Ren, Three-dimensional structural dynamics of DNA origami Bennett linkages using individual-particle electron tomography, Nat. Commun., 2018, 9, 592 CrossRef
.
- Z. Shi, C. E. Castro and G. Arya, Conformational Dynamics of Mechanically Compliant DNA Nanostructures
from Coarse-Grained Molecular Dynamics Simulations, ACS Nano, 2017, 11, 4617–4630 CrossRef CAS
.
- L. Zhou, A. E. Marras, H.-J. Su and C. E. Castro, DNA Origami Compliant Nanostructures with Tunable Mechanical Properties, ACS Nano, 2014, 8, 27–34 CrossRef CAS
.
- L. Zhou, A. E. Marras, C. E. Castro and H.-J. Su, Pseudorigid-Body Models of Compliant DNA Origami Mechanisms, J. Mech. Robot., 2016, 8, 051013 CrossRef
.
- L. Zhou, A. E. Marras, H.-J. Su and C. E. Castro, Direct Design of an Energy Landscape with Bistable DNA Origami Mechanisms, Nano Lett., 2015, 15, 1815–1821 CrossRef CAS
.
- C. Zhou, L. Xin, X. Duan, M. J. Urban and N. Liu, Dynamic Plasmonic System That Responds to Thermal and Aptamer-Target Regulations, Nano Lett., 2018, 18, 7395–7399 CrossRef CAS
.
- D. Y. Zhang and G. Seelig, Dynamic DNA nanotechnology using strand-displacement reactions, Nat. Chem., 2011, 3, 103–113 CrossRef CAS PubMed
.
- F. C. Simmel, B. Yurke and H. R. Singh, Principles and Applications of Nucleic Acid Strand Displacement Reactions, Chem. Rev., 2019, 119, 6326–6369 CAS
.
- D. Y. Zhang and E. Winfree, Control of DNA strand displacement kinetics using toehold exchange, J. Am. Chem. Soc., 2009, 131, 17303–17314 CrossRef CAS
.
- J. SantaLucia and D. Hicks, The Thermodynamics of DNA Structural Motifs, Annu. Rev. Biophys. Biomol. Struct., 2004, 33, 415–440 CrossRef CAS PubMed
.
- N. Srinivas, T. E. Ouldridge, P. Šulc, J. M. Schaeffer, B. Yurke, A. A. Louis, J. P. K. Doye and E. Winfree, On the biophysics and kinetics of toehold-mediated DNA strand displacement, Nucleic Acids Res., 2013, 41, 10641–10658 CrossRef CAS PubMed
.
- E. S. Andersen, M. Dong, M. M. Nielsen, K. Jahn, R. Subramani, W. Mamdouh, M. M. Golas, B. Sander, H. Stark, C. L. P. Oliveira, J. S. Pedersen, V. Birkedal, F. Besenbacher, K. V. Gothelf and J. Kjems, Self-assembly of a nanoscale DNA box with a controllable lid, Nature, 2009, 459, 73–76 CrossRef CAS
.
- M. T. Hwang, P. B. Landon, J. Lee, D. Choi, A. H. Mo, G. Glinsky and R. Lal, Highly specific SNP detection using 2D graphene electronics and DNA strand displacement, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 7088–7093 CrossRef CAS
.
- W. B. Sherman and N. C. Seeman, A precisely controlled DNA biped walking device, Nano Lett., 2004, 4, 1203–1207 CrossRef CAS
.
- J. Pan, F. Li, T. G. Cha, H. Chen and J. H. Choi, Recent progress on DNA based walkers, Curr. Opin. Biotechnol., 2015, 34, 56–64 CrossRef CAS
.
- P. Zhan, S. Both, T. Weiss and N. Liu, DNA-Assembled Multilayer Sliding Nanosystems, Nano Lett., 2019, 19, 6385–6390 CrossRef CAS
.
- S. Li, Q. Jiang, S. Liu, Y. Zhang, Y. Tian, C. Song, J. Wang, Y. Zou, G. J. Anderson, J. Y. Han, Y. Chang, Y. Liu, C. Zhang, L. Chen, G. Zhou, G. Nie, H. Yan, B. Ding and Y. Zhao, A DNA nanorobot functions as a cancer therapeutic in response to a molecular trigger in vivo, Nat. Biotechnol., 2018, 36, 258–264 CrossRef CAS PubMed
.
- Z. Chen, Y. Liu, C. Xin, J. Zhao and S. Liu, A cascade autocatalytic strand displacement amplification and hybridization chain reaction event for label-free and ultrasensitive electrochemical nucleic acid biosensing, Biosens. Bioelectron., 2018, 113, 1–8 CrossRef CAS PubMed
.
- L. Qian and E. Winfree, Scaling up digital circuit computation with DNA strand displacement cascades, Science, 2011, 332, 1196–1201 CrossRef CAS
.
- J. Song, Z. Li, P. Wang, T. Meyer, C. Mao and Y. Ke, Reconfiguration of DNA molecular arrays driven by information relay, Science, 2017, 357(6349), eaan3377 CrossRef PubMed
.
- L. Zhou, A. E. Marras, C. M. Huang, C. E. Castro and H. J. Su, Paper Origami-Inspired Design and Actuation of DNA Nanomachines with Complex Motions, Small, 2018, 14, 1802580 CrossRef PubMed
.
- J. Zhou and J. Rossi, Aptamers as targeted therapeutics: Current potential and challenges, Nat. Rev. Drug Discovery, 2017, 16, 181–202 CrossRef CAS PubMed
.
- A. D. Ellington and J. W. Szostak, In vitro selection of RNA molecules that bind specific ligands, Nature, 1990, 346, 818–822 CrossRef CAS PubMed
.
- J. Cruz-Toledo, M. McKeague, X. Zhang, A. Giamberardino, E. McConnell, T. Francis, M. C. DeRosa and M. Dumontier, Aptamer base: a collaborative knowledge base to describe aptamers and SELEX experiments, Database, 2012, 2012, bas006 CrossRef PubMed
.
- H.-K. Walter, J. Bauer, J. Steinmeyer, A. Kuzuya, C. M. Niemeyer and H.-A. Wagenknecht, “DNA Origami Traffic Lights” with a Split Aptamer Sensor for a Bicolor Fluorescence Readout, Nano Lett., 2017, 17, 2467–2472 CrossRef CAS PubMed
.
- Y. Sakai, M. S. Islam, M. Adamiak, S. C. C. Shiu, J. A. Tanner and J. G. Heddle, DNA aptamers for the functionalisation of DNA origami nanostructures, Genes, 2018, 9, 571 CrossRef PubMed
.
- S. Beyer, W. U. Dittmer and F. C. Simmel, Design Variations for an Aptamer-Based DNA Nanodevice, J. Biomed. Nanotechnol., 2005, 1, 96–101 CrossRef CAS
.
- A. Kuzuya, Y. Sakai, T. Yamazaki, Y. Xu and M. Komiyama, Nanomechanical DNA origami ‘single-molecule beacons’ directly imaged by atomic force microscopy, Nat. Commun., 2011, 2, 448–449 CrossRef
.
- P. Peng, L. Shi, H. Wang and T. Li, A DNA nanoswitch-controlled reversible nanosensor, Nucleic Acids Res., 2017, 45, 541–546 CrossRef CAS PubMed
.
- J. M. Majikes, L. C. C. Ferraz and T. H. LaBean, PH-Driven Actuation of DNA Origami via Parallel I-Motif Sequences in Solution and on Surfaces, Bioconjugate Chem., 2017, 28, 1821–1825 CrossRef CAS PubMed
.
- W. Wang, Y. Yang, E. Cheng, M. Zhao, H. Meng, D. Liu and D. Zhou, A pH-driven, reconfigurable DNA nanotriangle, Chem. Commun., 2009, 824–826 RSC
.
- D. Liu, A. Bruckbauer, C. Abell, S. Balasubramanian, D. J. Kang, D. Klenerman and D. Zhou, A reversible pH-driven DNA nanoswitch array, J. Am. Chem. Soc., 2006, 128, 2067–2071 CrossRef CAS PubMed
.
- T. Li and M. Famulok, I-motif-programmed functionalization of DNA nanocircles, J. Am. Chem. Soc., 2013, 135, 1593–1599 CrossRef CAS PubMed
.
- S. Modi, M. G. Swetha, D. Goswami, G. D. Gupta, S. Mayor and Y. Krishnan, A DNA nanomachine that maps spatial and temporal pH changes inside living cells, Nat. Nanotechnol., 2009, 4, 325–330 CrossRef CAS PubMed
.
- A. E. Marras, Z. Shi, M. G. Lindell, R. A. Patton, C. M. Huang, L. Zhou, H. J. Su, G. Arya and C. E. Castro, Cation-Activated Avidity for Rapid Reconfiguration of DNA Nanodevices, ACS Nano, 2018, 12, 9484–9494 CrossRef CAS PubMed
.
- R. E. Kohman and X. Han, Light sensitization of DNA nanostructures via incorporation of photo-cleavable spacers, Chem. Commun., 2015, 51, 5747 RSC
.
- J. List, M. Weber and F. C. Simmel, Hydrophobic actuation of a DNA origami bilayer structure, Angew. Chem., Int. Ed., 2014, 53, 4236–4239 CrossRef CAS PubMed
.
- Y. Chen, S. H. Lee and C. Mao, A DNA nanomachine based on a duplex-triplex transition, Angew. Chem., Int. Ed., 2004, 43, 5335–5338 CrossRef CAS PubMed
.
- X. Han, Z. Zhou, F. Yang and Z. Deng, Catch and release: DNA tweezers that can capture, hold, and release an object under control, J. Am. Chem. Soc., 2008, 130, 14414–14415 CrossRef CAS PubMed
.
- L. Shi, P. Peng, Y. Du and T. Li, Programmable i-motif DNA folding topology for a pH-switched reversible molecular sensing device, Nucleic Acids Res., 2017, 45, 4306–4314 CrossRef CAS
.
- D. Liu and S. Balasubramanian, A Proton-Fuelled DNA Nanomachine, Angew. Chem., Int. Ed., 2003, 42, 5734–5736 CrossRef CAS PubMed
.
- H. Liu, Y. Xu, F. Li, Y. Yang, W. Wang, Y. Song and D. Liu, Light-driven conformational switch of i-motif DNA, Angew. Chem., Int. Ed., 2007, 46, 2515–2517 CrossRef CAS PubMed
.
- Q. Jiang, Q. Liu, Y. Shi, Z. G. Wang, P. Zhan, J. Liu, C. Liu, H. Wang, X. Shi, L. Zhang, J. Sun, B. Ding and M. Liu, Stimulus-Responsive Plasmonic Chiral Signals of Gold Nanorods Organized on DNA Origami, Nano Lett., 2017, 17, 7125–7130 CrossRef CAS PubMed
.
- S. Shimron, N. Magen, J. Elbaz and I. Willner, PH-programmable DNAzyme nanostructures, Chem. Commun., 2011, 47, 8787–8789 RSC
.
- S. Benabou, A. Aviñó, R. Eritja, C. González and R. Gargallo, Fundamental aspects of the nucleic acid i-motif structures, RSC Adv., 2014, 4, 26956–26980 RSC
.
- D. M. Lilley, Structures of helical junctions in nucleic acids, Q. Rev. Biophys., 2000, 33, 109–159 CrossRef CAS PubMed
.
- Y. Sannohe, M. Endo, Y. Katsuda, K. Hidaka and H. Sugiyama, Visualization of dynamic conformational switching of the G-quadruplex in a DNA nanostructure, J. Am. Chem. Soc., 2010, 132, 16311–16313 CrossRef CAS PubMed
.
- J. K. Daljit Singh, M. T. Luu, A. Abbas and S. F. J. Wickham, Switchable DNA-origami nanostructures that respond to their environment and their applications, Biophys. Rev., 2018, 10, 1283–1293 CrossRef CAS PubMed
.
- H. Asanuma, X. Liang, T. Yoshida and M. Komiyama, Photocontrol of DNA Duplex Formation by Using Azobenzene-Bearing Oligonucleotides, ChemBioChem, 2001, 2, 39–44 CrossRef CAS PubMed
.
- Y. Yang, M. Endo, K. Hidaka and H. Sugiyama, Photo-controllable DNA origami nanostructures assembling into predesigned multiorientational patterns, J. Am. Chem. Soc., 2012, 134, 20645–20653 CrossRef CAS PubMed
.
- X. Liang, T. Mochizuki and H. Asanuma, A supra-photoswitch involving sandwiched DNA base Pairs and azobenzenes for light-driven nanostructures and nanodevices, Small, 2009, 5, 1761–1768 CrossRef CAS PubMed
.
- M. D. Wang, H. Yin, R. Landick, J. Gelles and S. M. Block, Stretching DNA with optical tweezers, Biophys. J., 1997, 72, 1335–1346 CrossRef CAS
.
- A. Kuzyk, Y. Yang, X. Duan, S. Stoll, A. O. Govorov, H. Sugiyama, M. Endo and N. Liu, A light-driven three-dimensional plasmonic nanosystem that translates molecular motion into reversible chiroptical function, Nat. Commun., 2016, 7, 10591 CrossRef CAS PubMed
.
- H. Asanuma, X. Liang, H. Nishioka, D. Matsunaga, M. Liu and M. Komiyama, Synthesis
of azobenzene-tethered DNA for reversible photo-regulation of DNA functions: hybridization and transcription, Nat. Protoc., 2007, 2, 203–212 CrossRef CAS
.
- M. Liu, S. Jiang, O. Loza, N. E. Fahmi, P. Šulc and N. Stephanopoulos, Rapid Photoactuation of a DNA Nanostructure using an Internal Photocaged Trigger Strand, Angew. Chem., Int. Ed., 2018, 57, 9341–9345 CrossRef CAS PubMed
.
- V. A. Turek, R. Chikkaraddy, S. Cormier, B. Stockham, T. Ding, U. F. Keyser and J. J. Baumberg, Thermo-Responsive Actuation of a DNA Origami Flexor, Adv. Funct. Mater., 2018, 28, 1–7 CrossRef
.
- T. R. Wilks, J. Bath, J. W. De Vries, J. E. Raymond, A. Herrmann, A. J. Turberfield and R. K. O’Reilly, ‘giant surfactants’ created by the fast and efficient functionalization of a DNA tetrahedron with a temperature-responsive polymer, ACS Nano, 2013, 7, 8561–8572 CrossRef CAS PubMed
.
- J. H. Reif, The design of autonomous DNA nano-mechanical devices: Walking and rolling DNA, Nat. Comput., 2003, 2, 439–461 CrossRef CAS
.
- S. Woo and P. W. K. Rothemund, Programmable molecular recognition based on the geometry of DNA nanostructures, Nat. Chem., 2011, 3, 620–627 CrossRef CAS PubMed
.
- F. Kroener, A. Heerwig, W. Kaiser, M. Mertig and U. Rant, Electrical Actuation of a DNA Origami Nanolever on an Electrode, J. Am. Chem. Soc., 2017, 139, 16510–16513 CrossRef CAS PubMed
.
- Y. Ke, T. Meyer, W. M. Shih and G. Bellot, Regulation at a distance of biomolecular interactions using a DNA origami nanoactuator, Nat. Commun., 2016, 7, 10935 CrossRef CAS PubMed
.
- A. E. Marras, L. Zhou, V. Kolliopoulos, H. J. Su and C. E. Castro, Directing folding pathways for multi-component DNA origami nanostructures with complex topology, New J. Phys., 2016, 18, 055005 CrossRef
.
- X.-C. Bai, T. G. Martin, S. H. W. Scheres and H. Dietz, Cryo-EM structure of a 3D DNA-origami object, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 20012–20017 CrossRef CAS PubMed
.
- X. Zhang, L. Zhang, H. Tong, B. Peng, M. J. Rames, S. Zhang and G. Ren, 3D Structural Fluctuation of IgG1 Antibody Revealed by Individual Particle Electron Tomography, Sci. Rep., 2015, 5, 9803 CrossRef PubMed
.
- L. Zhang, D. Lei, J. M. Smith, M. Zhang, H. Tong, X. Zhang, Z. Lu, J. Liu, A. P. Alivisatos and G. Ren, Three-dimensional structural dynamics and fluctuations of DNA-nanogold conjugates by individual-particle electron tomography, Nat. Commun., 2016, 7, 11083 CrossRef CAS PubMed
.
- H.-G. Liao and H. Zheng, Liquid Cell Transmission Electron Microscopy, Annu. Rev. Phys. Chem., 2016, 67, 719–747 CrossRef CAS PubMed
.
- T. Ito, N. Kodera and T. Ando, A high-speed atomic force microscope for studying biological macromolecules, Seibutsu Butsuri, 2017, 41, S92 CrossRef
.
-
M. Endo and H. Sugiyama, Methods in Molecular Biology, 2018, vol. 1814, pp. 213–224 Search PubMed
.
- Y. Yang, M. A. Goetzfried, K. Hidaka, M. You, W. Tan, H. Sugiyama and M. Endo, Direct Visualization of Walking Motions of Photocontrolled Nanomachine on the DNA Nanostructure, Nano Lett., 2015, 15, 6672–6676 CrossRef CAS PubMed
.
- C. Kielar, S. Ramakrishnan, S. Fricke, G. Grundmeier and A. Keller, Dynamics of DNA Origami Lattice Formation at Solid-Liquid Interfaces, ACS Appl. Mater. Interfaces, 2018, 10, 44844–44853 CrossRef CAS PubMed
.
- G. K. Rollefson and H. Boaz, Quenching of Fluorescence in Solution, J. Phys. Colloid Chem., 2005, 52, 518–527 CrossRef PubMed
.
-
Th. Foerster, Delocalized Excitation and Excitation Transfer, Bulletin No. 18, United States, N. p., 1964, DOI:10.2172/4626886
.
- M. W. Hudoba, Y. Luo, A. Zacharias, M. G. Poirier and C. E. Castro, Dynamic DNA Origami Device for Measuring Compressive Depletion Forces, ACS Nano, 2017, 11, 6566–6573 CrossRef CAS PubMed
.
- L. K. Bruetzel, T. Gerling, S. M. Sedlak, P. U. Walker, W. Zheng, H. Dietz and J. Lipfert, Conformational Changes and Flexibility of DNA Devices Observed by Small-Angle X-ray Scattering, Nano Lett., 2016, 16, 4871–4879 CrossRef CAS PubMed
.
- L. K. Bruetzel, P. U. Walker, T. Gerling, H. Dietz and J. Lipfert, Time-Resolved Small-Angle X-ray Scattering Reveals Millisecond Transitions of a DNA Origami Switch, Nano Lett., 2018, 18, 2672–2676 CrossRef CAS PubMed
.
- M. A. B. Baker, A. J. Tuckwell, J. F. Berengut, J. Bath, F. Benn, A. P. Duff, A. E. Whitten, K. E. Dunn, R. M. Hynson, A. J. Turberfield and L. K. Lee, Dimensions and Global Twist of Single-Layer DNA Origami Measured by Small-Angle X-ray Scattering, ACS Nano, 2018, 12, 5791–5799 CrossRef CAS PubMed
.
- C. Hartl, K. Frank, H. Amenitsch, S. Fischer, T. Liedl and B. Nickel, Position Accuracy of Gold Nanoparticles on DNA Origami Structures Studied with Small-Angle X-ray Scattering, Nano Lett., 2018, 18, 2609–2615 CrossRef CAS
.
-
M. P. Allen and D. J. Tildesley, Computer Simulation of Liquids, Oxford University Press, Oxford, 2nd edn, 2017 Search PubMed
.
- C. Y. Li, E. A. Hemmig, J. Kong, J. Yoo, S. Hernández-Ainsa, U. F. Keyser and A. Aksimentiev, Ionic conductivity, structural deformation, and programmable anisotropy of DNA origami in electric field, ACS Nano, 2015, 9, 1420–1433 CrossRef CAS PubMed
.
- N. Wu, D. M. Czajkowsky, J. Zhang, J. Qu, M. Ye, D. Zeng, X. Zhou, J. Hu, Z. Shao, B. Li and C. Fan, Molecular threading and tunable molecular recognition on DNA origami nanostructures, J. Am. Chem. Soc., 2013, 135, 12172–12175 CrossRef CAS PubMed
.
- J. Yoo and A. Aksimentiev, In situ structure and dynamics of DNA origami determined through molecular dynamics simulations, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 20099–20104 CrossRef CAS PubMed
.
- S. M. Slone, C. Y. Li, J. Yoo and A. Aksimentiev, Molecular mechanics of DNA bricks: In situ structure, mechanical properties and ionic conductivity, New J. Phys., 2016, 18, 055012 CrossRef
.
- C. Maffeo, J. Yoo and A. Aksimentiev, De novo reconstruction of DNA origami structures through atomistic molecular dynamics simulation, Nucleic Acids Res., 2016, 44, 3013–3019 CrossRef CAS PubMed
.
- T. E. Ouldridge, A. A. Louis and J. P. K. Doye, Structural, mechanical, and thermodynamic properties of a coarse-grained DNA model, J. Chem. Phys., 2011, 134, 085101 CrossRef PubMed
.
- P. Šulc, F. Romano, T. E. Ouldridge, L. Rovigatti, J. P. K. Doye and A. A. Louis, Sequence-dependent thermodynamics of a coarse-grained DNA model, J. Chem. Phys., 2012, 137, 135101 CrossRef PubMed
.
- B. E. K. Snodin, F. Randisi, M. Mosayebi, P. Šulc, J. S. Schreck, F. Romano, T. E. Ouldridge, R. Tsukanov, E. Nir, A. A. Louis and J. P. K. Doye, Introducing improved structural properties and salt dependence into a coarse-grained model of DNA, J. Chem. Phys., 2015, 142, 234901 CrossRef
.
- B. E. K. Snodin, J. S. Schreck, F. Romano, A. A. Louis and J. P. K. Doye, Coarse-grained modelling of the structural properties of DNA origami, Nucleic Acids Res., 2019, 47, 1585–1597 CrossRef CAS
.
- R. V. Reshetnikov, A. V. Stolyarova, A. O. Zalevsky, D. Y. Panteleev, G. V. Pavlova, D. V. Klinov, A. V. Golovin and A. D. Protopopova, A coarse-grained model for DNA origami, Nucleic Acids Res., 2018, 46, 1102–1112 CrossRef CAS
.
- J. J. Uusitalo, H. I. Ingólfsson, S. J. Marrink and I. Faustino, Martini Coarse-Grained Force Field: Extension to RNA, Biophys. J., 2017, 113, 246–256 CrossRef CAS
.
- B. E. K. Snodin, F. Romano, L. Rovigatti, T. E. Ouldridge, A. A. Louis and J. P. K. Doye, Direct Simulation of the Self-Assembly of a Small DNA Origami, ACS Nano, 2016, 10, 1724–1737 CrossRef CAS PubMed
.
- P. Šulc, T. E. Ouldridge, F. Romano, J. P. K. Doye and A. A. Louis, Modelling toehold-mediated RNA strand displacement, Biophys. J., 2015, 108, 1238–1247 CrossRef PubMed
.
- Z. Bryant, J. Gore, C. Bustamante, M. D. Stone, S. B. Smith and N. R. Cozzarelli, Structural transitions and elasticity from torque measurements on DNA, Nature, 2003, 424, 338–341 CrossRef CAS PubMed
.
- C. Bustamante, S. B. Smith, J. Liphardt and D. Smith, Curr. Opin. Struct. Biol., 2000, 10, 279–285 CrossRef CAS
.
- C. Bustamante, Z. Bryant and S. B. Smith, Ten years of tension: single-molecule DNA mechanics, Nature, 2003, 421, 423–427 CrossRef
.
- S. B. Smith, L. Finzi and C. Bustamante, Direct_Mechanical_Measurements_of_the_El.pdf, Science, 1992, 258, 1122–1126 CrossRef CAS PubMed
.
- S. Sb, Y. Cui and C. Bustamante, Overstretching B-DNA: the elastic response of individual double-stranded and single-stranded DNA molecules, Science, 1996, 271, 795–798 CrossRef PubMed
.
- C. E. Castro, F. Kilchherr, D. N. Kim, E. L. Shiao, T. Wauer, P. Wortmann, M. Bathe and H. Dietz, A primer to scaffolded DNA origami, Nat. Methods, 2011, 8, 221–229 CrossRef CAS PubMed
.
- O. Kratky and G. Porod, Röntgenuntersuchung gelöster Fadenmoleküle, Recl. Trav. Chim. Pays-Bas, 1949, 68, 1106–1122 CrossRef CAS
.
- J. F. Marko and E. D. Siggia, Stretching DNA, Macromolecules, 1995, 28, 8759–8770 CrossRef CAS
.
- I. Tinoco, O. C. Uhlenbeck and M. D. Levine, Estimation of secondary structure in ribonucleic acids, Nature, 1971, 230, 362–367 CrossRef CAS PubMed
.
- M. S. Waterman, Secondary Structure of Single-Stranded Nucleic Acids, Stud. Found. Comb. Adv. Math Supp. Stud., 1978, 1, 167–212 Search PubMed
.
- M. S. Waterman and T. F. Smith, RNA secondary structure: a complete mathematical analysis, Math. Biosci., 1978, 42, 257–266 CrossRef CAS
.
- R. A. Dimitrov and M. Zuker, Prediction of hybridization and melting for double-stranded nucleic acids, Biophys. J., 2004, 87, 215–226 CrossRef CAS PubMed
.
- M. Zuker, Mfold web server for nucleic acid folding and hybridization prediction, Nucleic Acids Res., 2003, 31, 3406–3415 CrossRef CAS PubMed
.
- J. S. Reuter and D. H. Mathews, RNAstructure: Software for RNA secondary structure prediction and analysis, BMC Bioinf., 2010, 11, 129 CrossRef PubMed
.
- M. Afzal, RDNAnalyzer: A tool for DNA secondary structure prediction and sequence analysis, Bioinformation, 2012, 8, 687–690 CrossRef
.
-
R. W. Zwanzig, Statistical Mechanics, Harper and Row, New York, 1st edn, 1962, vol. 84 Search PubMed
.
-
K. Lindenberg, R. Metzler and G. Oshanin, Chemical Kinetics, McGraw-Hill, New York, 1st edn, 2019 Search PubMed
.
- T. G. Cha, J. Pan, H. Chen, H. N. Robinson, X. Li, C. Mao and J. H. Choi, Design Principles of DNA Enzyme-Based Walkers: Translocation
Kinetics and Photoregulation, J. Am. Chem. Soc., 2015, 137, 9429–9437 CrossRef CAS PubMed
.
- D. Soloveichik, G. Seelig and E. Winfree, DNA as a universal substrate for chemical kinetics, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 5393–5398 CrossRef CAS PubMed
.
- L. N. Green, H. K. K. Subramanian, V. Mardanlou, J. Kim, R. F. Hariadi and E. Franco, Autonomous dynamic control of DNA nanostructure self-assembly, Nat. Chem., 2019, 11, 510–520 CrossRef CAS
.
- H. Chen, T. W. Weng, M. M. Riccitelli, Y. Cui, J. Irudayaraj and J. H. Choi, Understanding the mechanical properties of DNA origami tiles and controlling the kinetics of their folding and unfolding reconfiguration, J. Am. Chem. Soc., 2014, 136, 6995–7005 CrossRef CAS
.
- F. Schneider, N. Möritz and H. Dietz, The sequence of events during folding of a DNA origami, Sci. Adv., 2019, 5, eaaw1412 CrossRef PubMed
.
- D. Kang, R. Duan, Y. Tan, F. Hong, B. Wang, Z. Chen, S. Xu, X. Lou, W. Wei, B. Yurke and F. Xia, Speeding up the self-assembly of a DNA nanodevice using a variety of polar solvents, Nanoscale, 2014, 6, 14153–14157 RSC
.
- M. Ye, Y. Han, J. Tang, Y. Piao, X. Liu, Z. Zhou, J. Gao, J. Rao and Y. Shen, A Tumor-Specific Cascade Amplification Drug Release Nanoparticle for Overcoming Multidrug Resistance in Cancers, Adv. Mater., 2017, 29, 1702342 CrossRef
.
- S. R. Patel, J. H. Hartwig and J. E. Italiano, The biogenesis of platelets from megakaryocyte proplatelets, J. Clin. Invest., 2005, 115, 3348–3354 CrossRef CAS PubMed
.
- A. Gopinath, C. Thachuk, A. Mitskovets, H. A. Atwater, D. Kirkpatrick and P. W. K. Rothemund, Absolute and arbitrary orientation of single molecule shapes, 2018, ArXiv.
- G. Arya and T. Schlick, Role of histone tails in chromatin folding revealed by a mesoscopic oligonucleosome model, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 16236–16241 CrossRef CAS PubMed
.
- G. Arya, Q. Zhang and T. Schlick, Flexible histone tails in a new mesoscopic oligonucleosome model, Biophys. J., 2006, 91, 133–150 CrossRef CAS PubMed
.
- S. A. Grigoryev, G. Arya, S. Correll, C. L. Woodcock and T. Schlick, Evidence for heteromorphic chromatin fibers from analysis of nucleosome interactions, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 13317–13322 CrossRef CAS
.
- G. Arya and T. Schlick, A tale of tails: how histone tails mediate chromatin compaction in different salt and linker histone environments, J. Phys. Chem. A, 2009, 113, 4045–4059 CrossRef CAS
.
- J. S. Shin and N. A. Pierce, A synthetic DNA walker for molecular transport, J. Am. Chem. Soc., 2004, 126, 10834–10835 CrossRef CAS
.
- M. J. Urban, S. Both, C. Zhou, A. Kuzyk, K. Lindfors, T. Weiss and N. Liu, Gold nanocrystal-mediated sliding of doublet DNA origami filaments, Nat. Commun., 2018, 9, 1454 CrossRef
.
- Dynamic DNA Nanotechnology Publication Trend, https://wcs.webofknowledge.com/RA/analyze.do?product=WOS&SID=8ANgJWwumoKsYaVYJKE&field=PY_PublicationYear_PublicationYear_en&yearSort=true, (accessed 4 August 2019).
- N. Liu and T. Liedl, DNA-Assembled Advanced Plasmonic Architectures, Chem. Rev., 2018, 118, 3032–3053 CrossRef CAS PubMed
.
- O. Wolter and G. Mayer, Aptamers as Valuable Molecular Tools in Neurosciences, J. Neurosci., 2017, 37, 2517–2523 CrossRef CAS PubMed
.
- A. Idili, A. Vallée-Bélisle and F. Ricci, Programmable pH-triggered DNA nanoswitches, J. Am. Chem. Soc., 2014, 136, 5836–5839 CrossRef CAS
.
- E. F. Pettersen, T. D. Goddard, C. C. Huang, G. S. Couch, D. M. Greenblatt, E. C. Meng and T. E. Ferrin, UCSF Chimera – A visualization system for exploratory research and analysis, J. Comput. Chem., 2004, 25, 1605–1612 CrossRef CAS PubMed
.
| This journal is © The Royal Society of Chemistry 2020 |