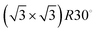Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Alkali metal adsorption on metal surfaces: new insights from new tools†
Arjun
Raghavan‡
 a,
Louie
Slocombe
b,
Alexander
Spreinat
c,
David J.
Ward
a,
Louie
Slocombe
b,
Alexander
Spreinat
c,
David J.
Ward
 a,
William
Allison
a,
John
Ellis
a,
Andrew P.
Jardine
a,
Marco
Sacchi
a,
William
Allison
a,
John
Ellis
a,
Andrew P.
Jardine
a,
Marco
Sacchi
 b and
Nadav
Avidor
b and
Nadav
Avidor
 *a
*a
aCavendish Laboratory, University of Cambridge, Cambridge CB30HE, UK. E-mail: na364@cam.ac.uk
bDepartment of Chemistry, University of Surrey, Guildford, GU2 7XH, UK
cInstitute of Physical Chemistry, Göttingen University, Göttingen, Germany
First published on 5th November 2020
Abstract
The adsorption of sodium on Ru(0001) is studied using 3He spin-echo spectroscopy (HeSE), molecular dynamics simulations (MD) and density functional theory (DFT). In the multi-layer regime, an analysis of helium reflectivity, gives an electron–phonon coupling constant of λ = 0.64 ± 0.06. At sub-monolayer coverage, DFT calculations show that the preferred adsorption site changes from hollow site to top site as the supercell increases and the effective coverage, θ, is reduced from 0.25 to 0.0625 adsorbates per substrate atom. Energy barriers and adsorption geometries taken from DFT are used in molecular dynamics calculations to generate simulated data sets for comparison with measurements. We introduce a new Bayesian method of analysis that compares measurement and model directly, without assuming analytic lineshapes. The value of adsorbate–substrate energy exchange rate (friction) in the MD simulation is the sole variable parameter. Experimental data at a coverage θ = 0.028 compares well with the low-coverage DFT result, giving an effective activation barrier Eeff = 46 ± 4 meV with a friction γ = 0.3 ps−1. Better fits to the data can be achieved by including additional variable parameters, but in all cases, the mechanism of diffusion is predominantly on a Bravais lattice, suggesting a single adsorption site in the unit cell, despite the close packed geometry.
1 Introduction
Understanding the interactions between adsorbates and their adsorbing surface is key to predicting surface dependent processes such as chemical reactions and growth of layered materials. An important property in characterising this interaction is the determination of the lowest energy adsorption site. The lowest energy site itself is one part of the broader energy landscape on which the adsorbate diffuses. Therefore, studying adsorbate diffusion provides an excellent method to experimentally evaluate adsorbate–substrate energy landscapes, as well as the frictional coupling between them.The interactions between alkali metals (AM) and transition metals (TM) has generated significant recent interest from the scientific community, with AM finding use in many current and future technological solutions.1,2 The AM–TM interaction is reported to vary with coverage. While the intuitive expectation is for TM to adsorb on hollow sites, some AM–TM systems are reported to show adsorption on top sites, for hexagonal surfaces. Diehl and McGrath1 first posed the question of why some AM adsorb on top sites on hexagonal surfaces of TM. Interestingly, however, the ab initio computations and experiments which were considered in posing the question all referred to ordered adsorbate systems, at coverages of 0.25 monolayers or higher.
Diffusion measurements of Na on TM have been conducted in the past using quasi-elastic helium scattering experiments (QHAS), on copper and nickel surfaces.3–6 In these studies, as well as in many other QHAS studies, the diffusion was usually simulated using Langevin molecular dynamics (LMD), and the potential energy surface (PES) was deduced by comparison with the experiment assuming analytical models of the expected experimental line-shape. An early qualitative comparison between a Langevin model and experiment suggests that assumptions about line-shape might be avoided.7 In the present work we develop such a non-parametric approach and make it quantitative by comparing the measurement and the model directly without assumptions about line-shape.
The sodium–ruthenium adsorbate/substrate system studied in this work is of significant practical interest as a platform for catalytic reactions.1,8,9 In addition, sodium intercalants play an essential role in graphene/Ru(0001) anodes for lithium-ion batteries.10–14 More recently, the development of Na-ion batteries in response to possible depletion of Li resources could give the present work even greater relevance in the context of energy storage devices.2
Na/Ru(0001) was among the first examples of an alkali metal overlayer as a model 2D system, and has thus been studied extensively in the past.1 However, these studies have been limited to structural low-energy electron diffraction (LEED) and work function measurements, and to date, adsorbate dynamics and electron–phonon coupling in the system have not been addressed.15–17 LEED indicates that sodium primarily adsorbs onto HCP and FCC hollow sites at 2 × 2 coverage and above, for measurements in the 80–600 K temperature range.15–17 Work function measurements suggest a maximum at monolayer coverage of approximately 3 eV.
Here, Na/Ru(0001) is investigated using 3He spin-echo spectroscopy (HeSE) in conjunction with DFT calculations. DFT suggests that the adsorption changes from hollow site to top site at coverages somewhere below 0.25 adsorbates per substrate atom. HeSE is a quasielastic scattering method with sufficient sensitivity to access this low-coverage regime. It combines a sub-nanosecond temporal window and sensitivity to Angstrom-scale surface dynamics.18–20 The technique has been used to study adsorbate motion in a wide range of systems and materials, including alkali metals, organic molecules, and water, and for understanding inelastic scattering processes from surface phonons.4,5,7,20–25
A direct comparison between candidate energy landscapes from DFT and the experiment provides strong support for a diffusion mechanism involving hops on a Bravais lattice. It follows that degenerate sites within the unit cell, such as degenerate HCP and FCC sites, can be excluded.
2 Experimental methods
Experiments in this study were performed on the 3He spin-echo spectrometer (HeSE) at the Cambridge Atom Scattering Facility (CASF).19,26,27 The spectrometer measures the Intermediate Scattering Function (ISF), a measure of time correlations on the surface, in reciprocal space. This technique is explained in detail elsewhere.19,20 Magnetic manipulation of the nuclear spin of 3He atoms prior to and after the scattering event allows for selective detection of scattered atoms based on the change in their spin polarization. Correlations on the surface are then investigated over a range of correlation times, tSE, which extend from 0 ps to 680 ps for an 8 meV beam in the Cambridge spectrometer.The spectrometer was used with a supersonic 8.1 meV 3He beam for surface dynamics measurements, which can be carried out in a temperature range from 100–1300 K using liquid nitrogen cooling and a combination of radiation and electron bombardment heating. A 10 mm diameter Ru(0001) single crystal from Surface Preparation Laboratory is used, with crystal cleaning by Ar+ sputtering, annealing up to 1250 K, and O2 dosing to remove carbon contaminants. Measurements are performed only after obtaining a 3He specular reflectivity of ≈25% or higher, indicating a clean and flat surface; the crystal is aligned using oxygen diffraction peaks.22 Sodium is dosed with a retractable arm attached to the Cambridge spectrometer, with a commercial Na dispenser source from SAES Getters, and a dispenser current of 5.5–6.5 A. The scattered signal is detected with a mass-spectrometer detector, consisting of a solenoidal ionizer and ion optics, followed by a channel electron multiplier.27–29
3 Results and discussion
3.1 Na/Ru(0001) growth uptake and electron–phonon coupling
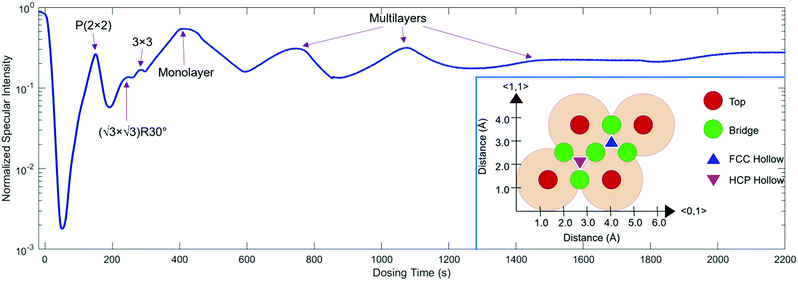
For growth uptake measurements in this work, 3He specular scattering intensity is monitored as a function of time while Na is dosed onto the Ru(0001) surface at a steady rate. Fig. 1 shows a Na uptake curve taken at a temperature of 300 K. The inset of Fig. 1 shows the hexagonal Ru(0001) unit cell with a lattice constant of 2.71 Å, along with the high symmetry top, bridge, FCC Hollow, and HCP hollow adsorption sites. In addition, the 〈0,1〉 and 〈1,1〉 azimuth directions, also known as 〈01![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0〉 and 〈11
0〉 and 〈11![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 0〉, respectively, are shown; data presented in this work are taken along 〈1,1〉.
0〉, respectively, are shown; data presented in this work are taken along 〈1,1〉.
Low energy electron diffraction (LEED) studies by Hertel et al. (1994) identify three ordered phases prior to the monolayer in growth uptake measurements, which are, in order, P(2 × 2), 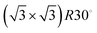 , and (3 × 3).15 These phases have coverages θ of 1/4, 1/3, and 4/9, respectively, and from work function measurements, the monolayer coverage is 0.56; θ gives the number of Na atoms per Ru surface atom.15 The peaks in the growth uptake curve presented in Fig. 1 are assigned in order according to the LEED measurements. Differences between expected and measured dosing times at which peaks occur for the three ordered structures are small, with an average less than 12%, hence supporting the conclusions from LEED, and confirming that similar Na structures are being formed.
, and (3 × 3).15 These phases have coverages θ of 1/4, 1/3, and 4/9, respectively, and from work function measurements, the monolayer coverage is 0.56; θ gives the number of Na atoms per Ru surface atom.15 The peaks in the growth uptake curve presented in Fig. 1 are assigned in order according to the LEED measurements. Differences between expected and measured dosing times at which peaks occur for the three ordered structures are small, with an average less than 12%, hence supporting the conclusions from LEED, and confirming that similar Na structures are being formed.
Uptake curve analysis is especially useful as it can allow for the electron–phonon coupling strength in metallic overlayer systems to be deduced. This coupling strength is an essential parameter in understanding such systems and can affect processes, including chemisorption, physisorption, and surface superconductivity. Specifically, it has been shown by Benedek and co-authors that from He specular scattering uptake measurements, the electron–phonon coupling can be found using the relative intensities of monolayer and multilayer peaks.30–32 Scattering occurs from the outermost electron density of states approximately 3 Å above the surface layer in low-energy helium scattering, so the probe is highly sensitive to the coupling of electrons to phonon modes, and can be applied for measuring this coupling strength. From a single uptake curve, the electron–phonon coupling constant is given by
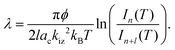 | (1) |
In eqn (1), ϕ is the work function, obtained here from measurements given in Hertel, et al. (1994),15 l is the number of layers, ac is the area of the Ru(0001) unit cell, kiz is the incident momentum perpendicular to the surface, T is temperature, and I are the intensities of given layers.30
By applying eqn (1) to the monolayer and three subsequent multilayer peaks shown in Fig. 1, an electron–phonon coupling value of λ = 0.64 ± 0.06 for the Na/Ru(0001) system is obtained; further details on this process are given in the ESI.† This value is the first measured electron–phonon coupling parameter for sodium on Ru(0001), and is higher than values for all alkali metal/transition metal systems reported by Benedek, et al. (2018), which have a maximum value of λ = 0.47 ± 0.11 for Li/W(110).30 However, λ = 0.64 ± 0.06 for Na/Ru(0001) is lower than λ = 1.18 for Pb/Cu(111), the only system without an alkali metal reported by Benedek, et al. (2018).30 The relationship between the electron–phonon coupling and relative intensities of overlayer peaks in helium scattering uptake measurements assumes an approximately linear dependence of the Debye–Waller factor 2 W on temperature. For the present analysis, this assumption is valid given the measurement temperature of 300 K, which is above the surface Debye temperature of 288 K, and significantly outside the low-temperature nonlinear regime.30,31,33
3.2 HeSE adsorbate dynamics – preliminary analysis
Our analysis of the HeSE data is presented in two stages. First, we perform a preliminary analysis using analytic lineshapes to illustrate the general features of the data. Secondly, we perform a comprehensive, but less intuitive, analysis using DFT calculations combined with MD simulations and a Bayesian analysis to examine possible potential energy surfaces (PESs).The preliminary analysis proceeds conventionally by least-square fitting individual ISF's with an approximate lineshape for random diffusion, given by P(t) = Ae−αt + C. The decaying exponential describes diffusion through the dephasing rate, α, while the constant term, C, accounts for scattering from quasi-static features that do not contribute to the dynamics in the time-range of the measurement, as well as for any type of confined diffusion. The fit to the data is unconstrained, and error bars bellow correspond to 66% confidence intervals of each single exponential fit. Fig. 2 shows the results of the preliminary analysis. Panel (a) shows a typical ISF plotted on a logarithmic time scale. Data for times t < 5 ps are not shown as they contain contributions from inelastic phonon scattering, and we exclude them from the analysis. The dephasing rates obtained in this way vary with temperature at a given momentum transfer, and vary with momentum transfer at a given surface temperature.
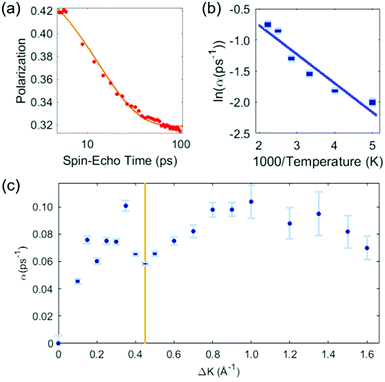 | ||
| Fig. 2 Preliminary analysis of the HeSE measurements. (a) Time dependence of the polarization, as measured at temperature of T = 200 K, along the 〈1,1〉 azimuth (see Fig. 1), at a momentum transfer of ΔK = 0.45 Å−1 (red data points). The solid line shows a single exponential to describe the dephasing rate plus a constant fitted to the data. Times below 5 ps are not included in the fit (see text). (b) Temperature dependence of the exponential dephasing rate, α, from data such as panel (a), plotted as an Arrhenius plot. The solid line is a straight-line fit and yields an effective activation energy of 44 ± 6 meV. (c) The dephasing rate, α, determined as in panel (a), on momentum transfer, ΔK. The shape is complex but typical of systems exhibiting strong repulsive forces. In particular, the distinct dip commonly known as de Gennes narrowing, marked by the vertical line at ΔK = 0.45 Å−1, leads to a coverage estimate of θ = 0.028 ± 0.007 (see text). | ||
Fig. 2(b) presents the temperature dependence of the data in panel (a) between 200 K and 450 K shown as an Arrhenius plot. A simple activated process with effective activation energy, Eeff, will give a dephasing rate varying with temperature, T, as
| α = α0e−Eeff/kBT. | (2) |
The solid line in Fig. 2(b) is a fit to the data and gives an activation energy Eeff = 44 ± 6 meV.
Fig. 2(c) shows the dephasing rate plotted as a function of momentum transfer. The scatter of the fitted dephasing rate for low ΔK is unexpectedly large compared to the error bars. We can conclude this scatter is not due to experimental effects. However, within the scope of this work, we can not disentangle the effect a He-sodium form-factor can result, from the result of fitting a decaying exponent to the data. Nevertheless, the observation illustrates the weakness of using approximations to the line-shape. We will return to the data in panel (c) when we discuss the results of our comprehensive analysis (below). Here we note the effect of strong repulsive interactions between adsorbates, which lead to a prominent peak and dip seen between approximately ΔK = 0.2 Å−1 and ΔK = 0.6 Å−1. The dip, commonly known as de Gennes narrowing, corresponds to the formation of quasi-hexagonal structures due to mutually repulsive interactions between adsorbates.19 It follows that the dip in the dephasing rate at a momentum transfer value of ΔKDip = 0.45 Å−1 (vertical bar in Fig. 2(c)), depends on the nearest neighbour distance ahex in the quasi-hexagonal arrangement as
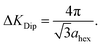 | (3) |
Since the Ru atom nearest neighbour distance on the hexagonal Ru(0001) surface is given by the lattice constant aRu(0001) = 2.71 Å, the coverage can be estimated by a ratio of areas as
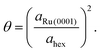 | (4) |
From this analysis, the coverage at which the present measurements are performed is found to be θ = 0.028 ± 0.007. This value agrees very closely with that obtained by growth uptake curve analysis; details of this comparison are given in the ESI.†
Moreover, given a value for the coverage, and using work function measurements from Hertel et al. (1994), the strength of repulsive interadsorbate forces can be found using the Topping model for surface depolarization.5,15 By comparing with analysis of other alkali metal systems measured by HeSE, pairwise, dipole–dipole repulsive interactions can be assumed.5,28 At low coverages, the alkali metal–substrate bond is primarily ionic and using the Topping model, we obtain an interadsorbate force strength of 1.34 × 105/rij4 meV Å−1, with rij as the distance between two adsorbates.15,28,34
3.3 Diffusion energy landscape using density functional theory
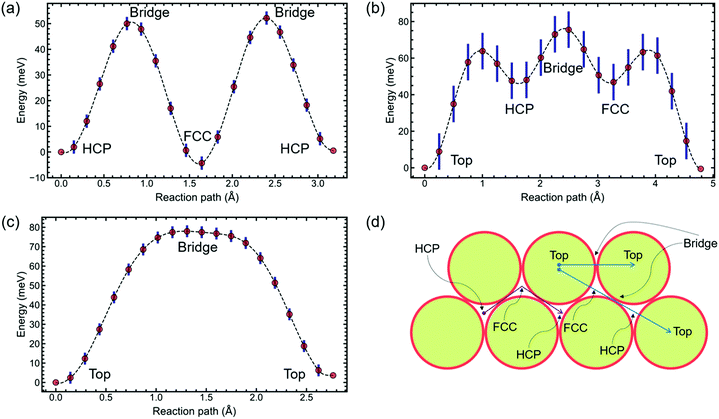
With the interadsorbate force strength, coverage, and approximate activation energy barrier extracted from the preliminary analysis based on exponential fitting, the potential energy surface remains to be studied. Hence, we pursue density functional theory modelling to suggest possible PES configurations. DFT is used to calculate PESs for 2 × 2 and 4 × 4 structures. Results presented here were conducted using CASTEP 19.1;35–39 further details are given in the ESI.†The calculations on a (2 × 2) unit cell, Fig. 3(a), reveal that Na adsorbs preferentially on hollow sites. DFT suggests that FCC and HCP are, within the calculation accuracy, identically favourable as global minima for this coverage. We perform Transition State searches using the Machine Learning Nudged Elastic Band (ML-NEB) algorithm of ref. 40 and 41. The ML-NEB algorithm incorporates a Gaussian regression model to produce a surrogate description of the true Molecular Electrostatic Potential (MEP). Thus the statistical uncertainty in the surrogate model associated with the ML-NEB calculations is computed and displayed (Fig. 3). The ML-NEB calculations confirm that the transition state for this process is located just above the bridge site, with a barrier of approximately 54 meV. The lowest energy pathway for jump diffusion between equivalent HCP sites proceeds via a neighbouring FCC site with two sets of jumps over the same barrier. Other paths between identical hollow sites are energetically unfavourable compared to direct jumps FCC ↔ HCP and HCP ↔ FCC. This DFT-based PES for the (2 × 2) coverage agrees with the conclusions from previous LEED studies discussed above.15–17
The PES obtained with the DFT calculations on a (4 × 4) unit cell, Fig. 3(b) and (c), interestingly predicts a change in global minimum from hollow sites to top sites. A change in the position of the global minimum when reducing coverage is most probably caused by the presence of long-range repulsive interactions between the Na atoms due to surface dipole interactions. Adsorbate-induced stress in the substrate can also cause a change in the PES corrugation, but further work is needed to separate the contribution of these and other factors on the PES of this system. For a straight path between nearest neighbours, the highest barrier, over a bridge site, is 78 meV. Between a top site and a second-nearest neighbour top site, there are a series of local minima located on hollow sites (Fig. 3(b)). The highest barrier is still at a bridge site, with hollow sites at an energy of 50 meV.
3.4 Molecular dynamics simulations and Bayesian data analysis
Here we explore the extent to which the two potential energy surfaces illustrated in Fig. 3 are compatible with the measurements. The process complements and extends the preliminary analysis described above. Instead of treating individual ISF measurements separately and analysing each with an approximate lineshape as we did earlier, we consider the experimental dataset as a single entity, within a Bayesian description of the experiment. In addition, we make comparisons with dynamical models without recourse to assumptions about the lineshape. The comparison with experiment is effected through calculated ISFs from extensive molecular dynamics (MD) calculations using Langevin dynamics. The process extends earlier work by Lechner et al.42 and is a more general approach as it does not rely on the lineshape assumptions of that work.The simulations are carried out on the Cambridge High Performance Computing cluster using the PIGLE MD Simulator.43 PIGLE MD simulations used in this work follow the Langevin equation, in which a static Potential Energy Surface (PES), a drag term proportional to particle velocity, Gaussian distributed stochastic forces satisfying the fluctuation dissipation theorem, and pairwise, radial interadsorbate interactions, are applied. Since the decay of the ISFs tends to zero as ΔK approaches zero, we have concluded that perpendicular motion is insignificant in the measured ISFs, and hence carried out 2D simulations. The Langevin equation is given by
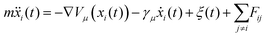 | (5) |
Using PIGLE, ISFs for each type of PES and across a wide range of friction values are calculated from the simulated adsorbate dynamics. As in the analysis method carried out in Lechner, et al. (2014),42 the probability that a given data point di is described by a corresponding simulation point si at the same ΔK value and spin-echo time tSE is modelled using a Gaussian probability distribution. It follows that the probability, P, is given by
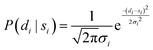 | (6) |
We run MD simulations with both the 2 × 2 and 4 × 4 PESs. For each simulation, the PES was generated using Fourier interpolation between the DFT values for the principal adsorption sites (top, bridge and hollow), and assuming the potential at half way between the top and hollow sites, is an average of the two.43 In both cases the coverage is θ = 0.028 ML, as determined above, and the repulsive forces are calculated from the dipole interactions and the known changes in the work-function. The simulations are performed for a range of friction values from 0 to 4 ps−1. Thus, the friction is the sole variable parameter used the comparison between experiment and DFT calculations. The ISFs calculated from the MD simulation are treated in the same way as those from experiment and, in order to compare like with like, we discard values at short spin-echo times, below 5 ps.
The best fit friction values are determined from the peaks of the respective Bayesian probability distributions. The best fits for the two PESs result in very different values for the friction. For the 2 × 2 PES the optimum friction is 0.05 ps−1, while for 4 × 4 PES the best fit results in 0.3 ps−1. The fit is done for measured data and MD simulations at T = 200 K.
To illustrate the quality of the fits obtained, we then subject the calculated ISFs to the same preliminary analysis as the experiment in Section 3.2. The procedure allows for a direct comparison of the momentum dependence of the dephasing rates between the candidate PES models and the experiment. Fig. 4 shows the three data sets (experiment, 2 × 2, and 4 × 4 PES). It is immediately clear that the 2 × 2 PES misfits the data throughout the range of ΔK. Firstly, the overall scale of the dephasing rates is too high. Moreover, the de Gennes feature is much larger than seen in the data, a misfit similar to that found in a previous modelling of an alkali/transition metal system by a degenerate preferred hollow site PES.5
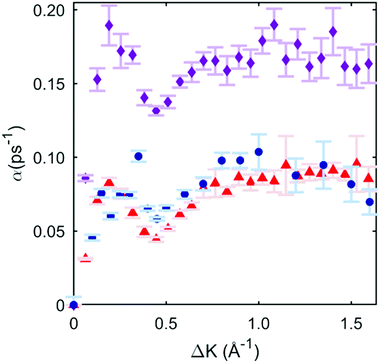 | ||
| Fig. 4 Blue circles are exponential dephasing rates plotted as a function of momentum transfer, the same points as those in Fig. 2(c). Red triangles are the exponential decay dephasing rate plotted as a function of momentum transfer with the 4 × 4 DFT-based PES, and the corresponding best-fit friction of 0.3 ps−1. Magenta diamonds are from the 2 × 2 case, with a corresponding best-fit friction of 0.05 ps−1. | ||
In contrast, the 4 × 4 PES, with a corresponding best-fit friction of 0.3 ps−1, fits the data very well. Bayesian-derived relative probabilities for different friction values are shown in the ESI.† The dephasing rate matches the data through all regions of ΔK, and the de Gennes feature follows the measured points closely. For further confirmation, a simulated Arrhenius measurement with the 4 × 4 PES and 0.3 ps−1 friction is carried out, yielding a simulated activation energy of 46 ± 4 meV. This value is in strong agreement with the experimental value of 44 ± 6 meV, and provides additional support for the 4 × 4 PES model. Comparisons for sample ISFs between the 4 × 4 PES MD simulation best-fit and single exponential fitting are shown in the ESI;† it is evident that that the combined MD simulations and Bayesian method models the data better than using only a single exponential fit.
The comparison of our DFT results with the data, directly, without using intermediate fitting to analytical expressions, is novel in quasi-elastic scattering analysis, and specifically in HeSE spectroscopy. Based on our analysis, we can rule out the possibility that Na follows the adsorption model suggested by the 2 × 2 DFT PES. The 4 × 4 PES fits well and suggests adsorption on top sites, effectively jump diffusion on a Bravais lattice with one dominant adsorption site. We have further explored the interpretation of the data by free fitting to the MD PES parameters, beyond the DFT values, and the interadsorbate force constant, beyond the Topping model. From this, we find additional PES configurations for diffusion with one dominant adsorption site which satisfactorily compare to the data, such as adsorption on highly nondegenerate hollow sites, and diffusion on top sites with a second adsorption well at the bridge site. In each of these cases, though, the primary feature remains as effective diffusion on a single dominating site in the unit cell. However, due to our need to omit data at spin-echo times below 5 ps, and limited computational resources, we were unable to explore in greater detail the complete 6-dimensional space of parameters, consisting of top, FCC hollow, HCP hollow, bridge, friction, and interadsorbate force constant. Thus, at present, without additional experimental and extensive computational work, we cannot definitively confirm the adsorption site of Na experimentally, but we can conclusively show that the trend observed in the DFT calculations, of a shift from two degenerate Hollow sites to a single dominating adsorption site, is strongly corroborated by our measurements. As mentioned above, P(2 × 2) AM–TM systems are reported to have a variability in adsorption sites,1 where some systems show adsorption on top sites, others on hollow sites, and one on bridge sites. In light of our results, we suspect that AM–TM are characterized by adsorption on top sites at the isolated adsorbate coverage regime, and depending on the balance between interadsorbate and adsorbate–substrate interactions, the preferred adsorption site shifts with coverage: some before a (2 × 2) adsorbate structure is formed, and some at higher coverage.
4 Conclusions
This work elucidates fundamental properties relating to the electron–phonon coupling and atomistic adsorbate dynamics in the prototypical catalytic system Na/Ru(0001). We conclude that the electron–phonon coupling in this system is stronger than other alkali/transition metal systems, with a coupling parameter of λ = 0.64 ± 0.06. A significant contribution to λ comes from the density of low-frequency phonons.30,44 In the adsorbed structures, the lowest phonon modes correspond to in-plane vibrations of adsorbed atoms, which facilitate their diffusion along the surface. Thus, the strong electron–phonon coupling we observe may have an impact on the adsorbate diffusion observed in the experiments at low coverage. Our measurements of diffusion are performed at low coverage and the analysis is performed without assumptions about the quasielastic lineshape. The results indicate motion on a Bravais lattice with a Langevin friction of 0.3 ps−1.DFT calculations suggests that the preferred adsorption sites shift from the higher coverage configuration of preferred degenerate Hollow sites, a non-Bravais lattice, to a lower coverage configuration with a preferred top site, a Bravais lattice. Analysis of the experiment confirms that jump diffusion occurs between a single dominant adsorption site in each Bravais lattice unit cell. Given that previously AM–TM systems were not considered at low coverage, we pose the question of whether the trend in adsorption site is common and can explain the top site/Hollow site variation at higher coverage. The present work thus contributes an atomic-scale picture of adsorbate properties and dynamics in the technologically important Na/Ru(0001) system, and more generally, suggests intriguing trends relating to the coverage dependence of alkali metal adsorption properties on transition metal surfaces.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank Prof. J. R. Manson of Clemson University for helpful discussions regarding the electron–phonon coupling data presented. The work was conducted in the Cambridge Atom Scattering Facility (CASF), which is supported by the Engineering and Physical Sciences Research Council (EPSRC) via grant EP/T00634X/1. The CASF management committee acknowledges both the EPSRC and the Herchel Smith Fund. N. A. gratefully acknowledges financial support from the Blavatnik Foundation. MS acknowledges the Royal Society for funding his University Research Fellowship and the UK Materials Chemistry Consortium for supporting the computational work on the ARCHER HPC cluster via the EPSRC grant EP/R029431. This work has been performed using resources provided by the Cambridge Tier-2 system operated by the University of Cambridge Research Computing Service (www.hpc.cam.ac.uk) funded by EPSRC Tier-2 capital grant EP/P020259/1.References
- R. D. Diehl and R. McGrath, Surf. Sci. Rep., 1996, 23, 43–171 CrossRef CAS
.
- F. Wang, Z. Liu, P. Zhang, H. Li, W. Sheng, T. Zhang, R. Jordan, Y. Wu, X. Zhuang and X. Feng, Small, 2017, 13, 1702449 CrossRef
.
-
S. Paterson, PhD thesis, University of Cambridge, 2012
.
- G. Alexandrowicz, A. Jardine, H. Hedgeland, W. Allison and J. Ellis, Phys. Rev. Lett., 2006, 97, 156103 CrossRef CAS
.
- S. P. Rittmeyer, D. J. Ward, P. Gütlein, J. Ellis, W. Allison and K. Reuter, Phys. Rev. Lett., 2016, 117, 196001 CrossRef
.
- J. Ellis, A. Graham, F. Hofmann and J. Toennies, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 195408 CrossRef
.
- A. Jardine, G. Alexandrowicz, H. Hedgeland, R. Diehl, W. Allison and J. Ellis, J. Phys.: Condens. Matter, 2007, 19, 305010 CrossRef
.
- J. J. Mortensen, B. Hammer and J. K. Nørskov, Phys. Rev. Lett., 1998, 80, 4333 CrossRef CAS
.
- J. J. Mortensen, B. Hammer and J. Nørskovi, Surf. Sci., 1998, 414, 315–329 CrossRef CAS
.
- D. Martoccia, P. Willmott, T. Brugger, M. Björck, S. Günther, C. Schlepütz, A. Cervellino, S. Pauli, B. Patterson and S. Marchini,
et al.
, Phys. Rev. Lett., 2008, 101, 126102 CrossRef CAS
.
- S. Marchini, S. Günther and J. Wintterlin, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 075429 CrossRef
.
- M. Kühne, F. Paolucci, J. Popovic, P. M. Ostrovsky, J. Maier and J. H. Smet, Nat. Nanotechnol., 2017, 12, 895 CrossRef
.
- L. Mandeltort and J. T. Yates Jr, J. Phys. Chem. C, 2012, 116, 24962–24967 CrossRef CAS
.
- C. Virojanadara, S. Watcharinyanon, A. Zakharov and L. I. Johansson, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 205402 CrossRef
.
- T. Hertel, H. Over, H. Bludau, M. Gierer and G. Ertl, Surf. Sci., 1994, 301, 1–10 CrossRef CAS
.
- R. Duszak and R. Prince, Surf. Sci., 1989, 216, 14–22 CrossRef CAS
.
- D. Doering and S. Semancik, Surf. Sci., 1983, 129, 177–191 CrossRef CAS
.
- A. Jardine, J. Ellis and W. Allison, J. Phys.: Condens. Matter, 2002, 14, 6173 CrossRef CAS
.
- A. Jardine, G. Alexandrowicz, H. Hedgeland, W. Allison and J. Ellis, Phys. Chem. Chem. Phys., 2009, 11, 3355–3374 RSC
.
- A. Jardine, H. Hedgeland, G. Alexandrowicz, W. Allison and J. Ellis, Prog. Surf. Sci., 2009, 84, 323–379 CrossRef CAS
.
- P. Rotter, B. A. Lechner, A. Morherr, D. M. Chisnall, D. J. Ward, A. P. Jardine, J. Ellis, W. Allison, B. Eckhardt and G. Witte, Nat. Mater., 2016, 15, 397–400 CrossRef CAS
.
- N. Avidor, H. Hedgeland, G. Held, A. Jardine, W. Allison, J. Ellis, T. Kravchuk and G. Alexandrowicz, J. Phys. Chem. A, 2011, 115, 7205–7209 CrossRef CAS
.
- P. Kole, A. Jardine, H. Hedgeland and G. Alexandrowicz, J. Phys.: Condens. Matter, 2010, 22, 304018 CrossRef CAS
.
- A. P. Jardine, S. Dworski, P. Fouquet, G. Alexandrowicz, D. J. Riley, G. Y. Lee, J. Ellis and W. Allison, Science, 2004, 304, 1790–1793 CrossRef CAS
.
- A. Tamtögl, M. Sacchi, N. Avidor, I. Calvo-Almazán, P. S. Townsend, M. Bremholm, P. Hofmann, J. Ellis and W. Allison, Nat. Commun., 2020, 11, 1–9 Search PubMed
.
- Cambridge Atom Scattering Facility, https://atomscattering.phy.cam.ac.uk/.
- P. Fouquet, A. Jardine, S. Dworski, G. Alexandrowicz, W. Allison and J. Ellis, Rev. Sci. Instrum., 2005, 76, 053109 CrossRef
.
-
A. Raghavan, MSc thesis, University of Cambridge, 2018
.
-
D. M. Chisnall, PhD thesis, University of Cambridge, 2012
.
- G. Benedek, S. Miret-Artes, J. Toennies and J. Manson, The, J. Phys. Chem. Lett., 2018, 9, 76–83 CrossRef CAS
.
- A. Tamtögl, P. Kraus, N. Avidor, M. Bremholm, E. M. Hedegaard, B. B. Iversen, M. Bianchi, P. Hofmann, J. Ellis and W. Allison,
et al.
, Phys. Rev. B, 2017, 95, 195401 CrossRef
.
- J. Manson, Private Communication, 2018.
- G. Anemone, A. A. Taleb, W. Hayes, J. Manson and D. Faras, J. Phys. Chem. C, 2017, 121, 22815–22825 CrossRef CAS
.
- G. Alexandrowicz, P. R. Kole, E. Y. Lee, H. Hedgeland, R. Ferrando, A. P. Jardine, W. Allison and J. Ellis, J. Am. Chem. Soc., 2008, 130, 6789–6794 CrossRef CAS
.
- P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864–B871 CrossRef
.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133–A1138 CrossRef
.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192 CrossRef
.
- M. C. Payne, M. P. Teter, D. C. Allan, T. Arias and J. D. Joannopoulos, Rev. Mod. Phys., 1992, 64, 1045–1097 CrossRef CAS
.
- S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. J. Probert, K. Refson and M. Payne, Z. Kristall., 2005, 220, 567–570 CAS
.
- M. H. Hansen, J. A. G. Torres, P. C. Jennings, Z. Wang, J. R. Boes, O. G. Mamun and T. Bligaard, arXiv preprint arXiv:1904.00904, 2019.
- J. A. G. Torres, P. C. Jennings, M. H. Hansen, J. R. Boes and T. Bligaard, Phys. Rev. Lett., 2019, 122, 156001 CrossRef
.
- B. Lechner, P. Kole, H. Hedgeland, A. Jardine, W. Allison, B. Hinch and J. Ellis, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 121405 CrossRef
.
- N. Avidor, P. Townsend, D. Ward, A. Jardine, J. Ellis and W. Allison, Comput. Phys. Commun., 2019, 242, 145–152 CrossRef CAS
.
- J. Vega, R. Guantes, S. Miret-Artés and D. Micha, J. Chem. Phys., 2004, 121, 8580–8588 CrossRef CAS
.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0cp05365a |
| ‡ Present address: Department of Physics, University of Illinois at Urbana-Champaign, 1110 West Green Street, Urbana, IL 61801, USA. |
| This journal is © the Owner Societies 2021 |