Open Access Article
Open Access ArticlePredicting glass transition temperature and melting point of organic compounds via machine learning and molecular embeddings†
Tommaso
Galeazzo
 * and
Manabu
Shiraiwa
* and
Manabu
Shiraiwa
 *
*
Department of Chemistry, University of California, Irvine, CA92697, USA. E-mail: tommaso.galeazzo@gmail.com; m.shiraiwa@uci.edu
First published on 5th April 2022
Abstract
Gas-particle partitioning of secondary organic aerosols is impacted by particle phase state and viscosity, which can be inferred from the glass transition temperature (Tg) of the constituting organic compounds. Several parametrizations were developed to predict Tg of organic compounds based on molecular properties and elemental composition, but they are subject to relatively large uncertainties as they do not account for molecular structure and functionality. Here we develop a new Tg prediction method powered by machine learning and “molecular embeddings”, which are unique numerical representations of chemical compounds that retain information on their structure, inter atomic connectivity and functionality. We have trained multiple state-of-the-art machine learning models on databases of experimental Tg of organic compounds and their corresponding molecular embeddings. The best prediction model is the tgBoost model built with an Extreme Gradient Boosting (XGBoost) regressor trained via a nested cross-validation method, reproducing experimental data very well with a mean absolute error of 18.3 K. It can also quantify the influence of number and location of functional groups on the Tg of organic molecules, while accounting for atom connectivity and predicting different Tg for compositional isomers. The tgBoost model suggests the following trend for sensitivity of Tg to functional group addition: –COOH (carboxylic acid) > –C(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)OR (ester) ≈ –OH (alcohol) > –C(
O)OR (ester) ≈ –OH (alcohol) > –C(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)R (ketone) ≈ –COR (ether) ≈ –C(
O)R (ketone) ≈ –COR (ether) ≈ –C(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)H (aldehyde). We also developed a model to predict the melting point (Tm) of organic compounds by training a deep neural network on a large dataset of experimental Tm. The model performs reasonably well against the available dataset with a mean absolute error of 31.0 K. These new machine learning powered models can be applied to field and laboratory measurements as well as atmospheric aerosol models to predict the Tg and Tm of SOA compounds for evaluation of the phase state and viscosity of SOA.
O)H (aldehyde). We also developed a model to predict the melting point (Tm) of organic compounds by training a deep neural network on a large dataset of experimental Tm. The model performs reasonably well against the available dataset with a mean absolute error of 31.0 K. These new machine learning powered models can be applied to field and laboratory measurements as well as atmospheric aerosol models to predict the Tg and Tm of SOA compounds for evaluation of the phase state and viscosity of SOA.
Environmental significanceSecondary organic aerosols (SOA) represent a major component of atmospheric particulate matter and their accurate representation in aerosol models is a demanding problem in atmospheric chemistry. SOA partitioning is impacted by the particle phase state, viscosity and glass transition temperature (Tg) of organic compounds. Here, we develop a machine learning model to predict glass transition temperature of organic compounds. The new model considers molecular structure, functionality and atomic interconnectivity, discerning compositional isomers. It reproduces experimental measurements very well, outperforming previous compositional parametrizations. This powerful tool offers state-of-the-art performances and its implementation in aerosol models would contribute to a better evaluation of SOA effects on climate and air quality. |
1. Introduction
Secondary organic aerosols (SOA) are major components of particulate matter in the atmosphere, influencing climate, air quality, and public health.1,2 SOA formation and evolution are complex processes, which have been the subjects of extensive investigations with field observations, laboratory experiments, and modeling.3,4 Aerosol models are useful computational tools which can simulate the formation and evolution of SOA chemical composition and properties. The development of SOA models represents one of the most demanding and challenging problems in atmospheric chemistry.5 These models rely on accurate representation of physical properties including particle viscosity and bulk diffusivity that influence gas-particle partitioning of semi-volatile and low volatility organic compounds.6SOA viscosity can be estimated using the glass transition temperature (Tg) of the constituting organic compounds.7–9 While there is a fair amount of measured Tg of organic compounds,7 there are only limited number of Tg measurements for SOA compounds.10–12 To fill such measurement gaps, various Tg parametrizations have been developed based on molecular properties including molar mass and atomic oxygen to carbon ratio,13 saturation mass concentration,12,14,15 and elemental composition (e.g., number of C, H, N, O, S atoms).8,15 Moreover, Rothfuss and Petters16 have introduced an empirical group contribution estimation based on functional groups presence within a molecule. Their results suggest functionalization is a crucial predictive parameter for molecular Tg. These parameterizations are simple, practical, and versatile prediction methods, which have been applied to estimate SOA viscosity for high-resolution mass spectrometry8,17–19 and also implemented into thermodynamic,20,21 gas-phase chemistry models9 and chemical transport models.5,22,23 These parameterizations, however, have relatively larger uncertainties (∼25 K) and they do not account for molecular structure and functional groups presence. Notably, Rothfuss and Petters16 found that viscosity of weakly functionalized organic compounds is highly sensitive to functional groups addition and location within a molecule. Thus, there is a strong need to discern between compositional isomers and to account explicitly for functionality and molecular structure.
In cheminformatics molecular descriptors are mathematical objects representing chemical species at different levels of complexity, covering from 0-D atomic information to 3-D molecular structures.24 They are commonly used in medicinal chemistry to develop models predicting chemical activities (Quantitative Structure–Activity Relationship, QSAR) or physical properties (Quantitative Structure–Property Relationship, QSPR) of pure compounds in absorption, distribution, metabolism, excretion and toxicity (ADMET) studies.25 Over the years there have been studies focusing on the prediction of the melting point (Tm) of an organic compound via QSPR models: it is a task of particular interest because of the correlation of the Tm with the vapor pressure, boiling point, glass transition temperature, and water solubility.26–28 In environmental sciences, the MPBPWIN module from the EPI Suite software by the Environmental Protection Agency (EPA) is the standard reference for the estimation of the Tm of environmentally-relevant organic compounds.29 This QSPR model is built on a simple group-contribution-method where a vectorized list of functional groups acts as the molecular descriptor of a species. The EPI Suite performs well for predicting the Tm of small molecules with a few functional groups, but it overestimates Tm of more structurally complex and aromatic compounds.29 Therefore, the need for a powerful estimation model that could be more accurate in its prediction and in capturing molecular complexity. However, developing an accurate Tm model is challenging due to the quality of the available datasets and the variability of the used molecular descriptors which induce large errors and uncertainty in model generalizability (i.e., accurate error estimation when analyzing new molecules).
Over the last years, developments in artificial intelligence and machine learning (ML) have overspilled to cheminformatics. Notably, text analysis techniques borrowed from Natural Language Processing (NLP) have been used to learn chemically contextualized molecular descriptors from canonical molecular representations including SMILES (Simplified Molecular Input Line Entry System: molecular strings notations to describe unique chemical structures). Jastrzębski et al.30 showed that SMILES can be used to learn contextualized chemical descriptors of molecules via convolutional neural networks (CNN). Recently, Gómez-Bombarelli et al.31 developed a chemical Variational Auto Encoder (VAE): a generative model based on a Recurrent Neural Network (RNN) that learns compressed numerical representations from SMILES (encoding step) and generates molecules with target properties from the chemical space (generative step). Segler et al.32 showed that SMILES can be used to generate bioactive molecular candidates from small datasets using RNNs and by transferring the learned molecular descriptors and knowledge to large datasets. Jaeger et al.33 developed mol2vec, an algorithm that learns molecular descriptors as high dimensional embeddings of molecular substructures (i.e. “molecular embeddings”) from SMILES notations by combining the word2vec and Morgan algorithms.
Recently, a few studies have explored the performances of different combinations of ML models and molecular descriptors in predicting the Tm of organic compounds.34–36 The resulting models largely outperform the EPI Suite in predicting Tm, suggesting an increasing ability of ML models and complex molecular descriptors in predicting Tm of pure compounds and potentially their Tg. These studies have focused on the development of molecular descriptors from molecular graphs via convolutional embedding methods.60,61 The developed embeddings (i.e., convolutional embeddings) reach extremely high prediction accuracies, but they can result in significant drawbacks with regards to model deployment and portability. In these approaches both the embedding and the property prediction steps are engrained in the Convolutional Neural Network (CNN). The major caveat of using the former approach is that the dataset and CNN architecture cannot be decoupled, and the embeddings are generated in situ from the very specific dataset. Therefore, the resulting convolutional embeddings are dataset specific and cannot be loaded and used for other tasks. Moreover, in such approaches the development of the target QSAR model requires the optimization and training of the CNN, which are very computationally demanding tasks. As a consequence, these models lack portability, transferability and scalability due to the in situ generation of molecular descriptors dependent on the dataset of origin, and the absence of a finalized trained model which could be transferred to other datasets. On the other hand, mol2vec reaches state-of-the-art performances to statistically infer various molecular properties in supervised learning tasks by generating unique high-dimensional vectors from a pretrained embedding model. As a result, it can be easily transferred and included in the analysis of complex chemical systems with large numbers of diverse compounds.
Here we introduce the first ML-driven Tg prediction method based on molecular embeddings. We use different machine learning algorithms to predict Tg by explicitly considering molecular structure, functionality and atomic interconnectivity, outperforming previous Tg parameterizations. The new model can reproduce experimental Tg data and the influence of number and location of functional groups within the molecule on Tg. We extend the investigation to the prediction of Tm using a large experimental dataset with ∼200![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 compounds. We develop a new model for Tm prediction, reaching close to state-of-the-art performances. These new ML powered Tg and Tm models can be exploited to predict viscosity in aerosol models involving organic molecules, with future applications that go beyond aerosol chemistry and extend to modeling of organic mixtures.
000 compounds. We develop a new model for Tm prediction, reaching close to state-of-the-art performances. These new ML powered Tg and Tm models can be exploited to predict viscosity in aerosol models involving organic molecules, with future applications that go beyond aerosol chemistry and extend to modeling of organic mixtures.
2. Methods
2.1 Datasets and preprocessing
We have compiled available datasets of Tg and Tm for organic compounds with SMILES strings. The datasets are cleaned using RDKit, a publicly available python library for cheminformatics tasks.37 Data cleaning is composed by three different steps: filtering of molecules that cannot be recognized by RDKit, conversion of SMILES strings to their canonical form, and averaging over the target property for compounds that have multiple entries with different Tg or Tm values. We have performed initial screening to delete most of the heavier compounds from the datasets (MW > 600) and to include only compounds with H, C, O, N, S, F, Cl, and Br atoms.The largest measurement dataset reporting Tg of organic compounds (Tg-Measured) contains 394 measurements.7 The original dataset has been enriched with recently measured Tg for 7 atmospheric compounds12 and with theoretically-derived Tg for 9 linear alkanes from molecular dynamics simulations.38 The Tg-Measured dataset is composed of 415 entries and after the cleaning step it comprises 298 unique entries. Due to the scarcity of available experimental Tg data, we train separate Tm models using larger datasets of experimental Tm. Tg can be estimated from Tm using the structure–activity relationship known as the Boyer-Kauzmann rule: Tg = g × Tm with g as a constant to be 0.7 based on analysis by Koop et al.7 The first experimental Tm dataset is formed by values extracted from patents by Tetko et al.39 (Tm-Tetko), while the second dataset is the “Bradley good Tm dataset” (Tm-Bradley),40 a highly curated experimental Tm dataset of drug-like small molecules. The Tm-Tetko dataset is the largest publicly available Tm dataset: it contains 228![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 174 entries and it accounts for 220
174 entries and it accounts for 220![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 348 species after cleaning.
348 species after cleaning.
The final step of dataset preprocessing is the conversion of canonical SMILES into molecular embeddings. We have used the mol2vec library to generate unique 300-dimensional embeddings (i.e., “molecular embedding”) for each chemical species in the different datasets (Table 1).
2.2 Model selection and training
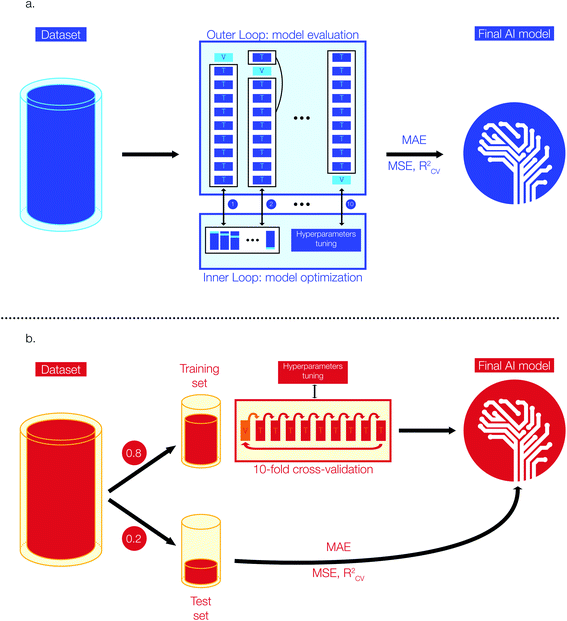
Model selection and optimization are conducted via a nested cross-validation (also known as “double cross-validation”). This model development technique allows to estimate an almost unbiased and low variance true error when data are scarce.42–44 A previous study has shown that a nested cross-validation is particularly suitable for QSAR/QSPR model development and when datasets are small (i.e. <1000 entries).43Fig. 1a shows a simplified representation of the 10-fold nested cross-validation implemented for the training of Tg models with the Tg-Measured dataset. The model development task is structured as a double loop composed by an outer loop for model evaluation (i.e., outer K-loop) and an inner loop for model selection and optimization (i.e., inner J-loop).44 Initially, the entire dataset is divided into K folds (K = 10 in this study): K-1 folds are used to train the model on the best set of hyperparameters and one fold is kept aside to evaluate the error of the trained model on unseen data for model evaluation. At each i iteration of the outer loop (1 < i < K), the ith fold used for model training (i.e., Ki) is passed to the inner J-loop for model optimization via hyperparameters selection. To carry the optimization of the model, Ki is further divided into J sub-folds with J = 10 in this study.
During this step, J-1 sub-folds are used to select the best hyperparameters (i.e., hyperparameters tuning based on the specific model architecture) and the remaining J sub-fold is a validation set used to evaluate the performance of the model developed with this specific parameter combination. The process is repeated for J times on the different J-folds combinations obtained from further split of Ki. The model optimization step is repeated for each K-fold of the outer loop, resulting in K different models developed from the K data combinations. As a result, for each model architecture (e.g., RF, XGBoost) we have conducted n × 10 × 10 fits and error estimations, where n is the total number of single values that can be assumed by individual model architecture parameters. Once we have identified the best model parameters, we have trained the model on the whole dataset and used the estimated errors from the outer cross-validation as the final true value of MAE. This approach enables to reach the best trade-off between bias and variance by selecting the best model parameters, while obtaining a true error estimation by accounting for a vast number of possible data combinations and cross-validation. The RF regressor model is implemented in Python using scikit-learn, a library for scientific computing and machine learning.45 The XGBoost regressor model is implemented via xgboost, a Python library for optimized distributed gradient boosting model development.41 The hyperparameters of our regressor models were selected through a grid search approach: we selected a range of plausible values for each hyperparameter (e.g., estimators, maximum depth of trees, learning rate, etc.) and we have trained as many models as the possible combinations of available hyperparameters. Finally, we selected the best Tg regression model whose combination of hyperparameters provided the lowest error in the nested cross-validation step. The best Tg regression model (tgBoost) developed via a XGBoost regressor and through the nested cross-validation is composed by: 100 estimators, a maximum depth of 9 trees, a learning rate of 0.1, and a γ equal to 30.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000) we built the Tm regression models using Deep Neural Network (DNN) and XGBoost architectures.33–35 The performance metrics employed to evaluate these regression models are MAE, MSE, and RCV2 similarly to the development of the Tg model. All the Tm datasets are composed by enough entries to allow model validation via a simple 10-fold cross-validation approach.46Fig. 1b shows a simplified representation of the stages implemented to develop the Tm models. Initially, the preprocessed data have been divided into a training and test set respectively composed by 80 and 20% of the input data. The test set is kept aside during model development and used to evaluate the performances of the models on unseen data. The training sets have been further divided into 10 folds and model parameters have been selected (i.e., hyperparameters tuning) using iteratively 9 folds for training and one fold for validation. Similar to the process used to select the best regressor model for Tg, we have used a grid search approach to select the best hyperparameters for developing the Tm regression. We selected a range of plausible values for each hyperparameter (e.g., number of nodes in the activation layer, number of hidden layers, optimizer, number of nodes in hidden layers, activation functions, dropout, learning rate, etc.) and we have trained as many models as the possible combinations of available hyperparameters. The parameters for the best Tm model are the ones reporting the lowest average error on the 10-fold cross-validation step. The DNN models have been implemented using Keras, a Python machine learning library for deep learning and based on Theano.47 The best DNN model was obtained using the Tm-Tetko dataset, and its detailed architecture is: 1 input layer with 300 nodes, 3 hidden layers with 32 nodes each, ReLU activation functions for the hidden layers followed by a linear activation function on the single node of the output layer, an Adam optimizer added to the loss function, mini-batches of 32 datapoints during training, a learning rate of 0.001, 100 epochs of training and no dropout.
000) we built the Tm regression models using Deep Neural Network (DNN) and XGBoost architectures.33–35 The performance metrics employed to evaluate these regression models are MAE, MSE, and RCV2 similarly to the development of the Tg model. All the Tm datasets are composed by enough entries to allow model validation via a simple 10-fold cross-validation approach.46Fig. 1b shows a simplified representation of the stages implemented to develop the Tm models. Initially, the preprocessed data have been divided into a training and test set respectively composed by 80 and 20% of the input data. The test set is kept aside during model development and used to evaluate the performances of the models on unseen data. The training sets have been further divided into 10 folds and model parameters have been selected (i.e., hyperparameters tuning) using iteratively 9 folds for training and one fold for validation. Similar to the process used to select the best regressor model for Tg, we have used a grid search approach to select the best hyperparameters for developing the Tm regression. We selected a range of plausible values for each hyperparameter (e.g., number of nodes in the activation layer, number of hidden layers, optimizer, number of nodes in hidden layers, activation functions, dropout, learning rate, etc.) and we have trained as many models as the possible combinations of available hyperparameters. The parameters for the best Tm model are the ones reporting the lowest average error on the 10-fold cross-validation step. The DNN models have been implemented using Keras, a Python machine learning library for deep learning and based on Theano.47 The best DNN model was obtained using the Tm-Tetko dataset, and its detailed architecture is: 1 input layer with 300 nodes, 3 hidden layers with 32 nodes each, ReLU activation functions for the hidden layers followed by a linear activation function on the single node of the output layer, an Adam optimizer added to the loss function, mini-batches of 32 datapoints during training, a learning rate of 0.001, 100 epochs of training and no dropout.
3. Results
3.1 T g regression model performance
Table 2 shows the performances of our Tg models trained on the Tg-Measured dataset by using molecular embeddings from mol2vec as molecular descriptors. The results are compared to our previous compositional parametrizations based on elemental composition where the input variables are the number of C, O, H, N and S atoms of species: the equations on which the compositional parametrizations are implemented are logarithmic ordinary least squared (OLS) regressions.8,15 All the models developed in this study using ensemble method algorithms (RF, XGBoost) perform better than the compositional parametrizations. The RF regression model has an estimated MAE of 22.2 K. The best results are achieved by the XGBoost algorithm, which performs remarkably well in predicting the Tg of compounds from the Tg-Measured dataset, as shown in the correlation plot in Fig. 2, with R = 0.99 and RCV2 = 0.99 with no significant outliers. The MAE of the single best tgBoost model developed on the whole Tg-Measured dataset is 3 K, which represents a dramatic improvement compared to the compositional parametrizations with MAE of 27.2 K. Note, however, that the true cross-validation MAE of the tgBoost model on unseen data is 18.3 K as measured on the validation sets of the outer loop 10-fold cross-validation. This is the true error which is statistically inferred by the outer validation loop of the nested cross-validation, and which should be considered for model predictions on molecules outside of the Tg-Measured dataset.| Dataset | Algorithma | MAE (K) | RMSE | R CV 2 | R | Study |
|---|---|---|---|---|---|---|
| a RF = random forest, XGBoost = extreme gradient boosting method, OLS = ordinary least squares (i.e., compositional parametrizations8,15), DNN = deep neural network, CNN = convolutional neural network, GCNN = graph convolutional neural network, ASNN = adversarial neural network, GPR = Gaussian process regression. b The datasets used in these studies are all different variations of the “Bradley Good Melting Points Dataset” from Bradley et al.40 | ||||||
| T g-Measured | RF | 22.2 | 26.9 | 0.86 | 0.94 | This work |
| XGBoost | 18.3 | 15.3 | 0.99 | 0.99 | This work | |
| OLS | 27.2 | 0.83 | 0.91 | 8 and 15 | ||
| T m-Tetko | DNN | 31.0 | 40.1 | 0.6 | 0.77 | This work |
| T m-Bradley | CNN | 26.2 | 35.5 | 35 | ||
| Baseline | 43.3 | 57.7 | 35 | |||
| ASNN | 32.0 | 34 | ||||
| GCNN | 28.85 | 0.78 | 36 | |||
| RF | 34.62 | 0.66 | 36 | |||
| GPR | 29.41 | 0.75 | 36 | |||
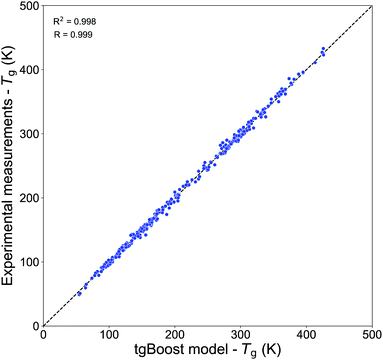 | ||
| Fig. 2 Correlation plot between the predicted Tg values by the tgBoost model and the experimental Tg values from the Tg-Measured dataset. | ||
3.2 T g model evaluation
To evaluate if the tgBoost model has learnt to recognize the relationship between molecular properties/structure and Tg, we assess the performance of the tgBoost model by simulating Tg in relation to the molecular structure and the presence of functional groups within a molecule, along with comparison with reported values and the Tg compositional parameterization. Fig. 3 shows the predicted Tg for the linear n-alkane series (n = 2–20) modeled via the tgBoost model and the Tg compositional parametrization.8 The results are compared to the simulated values for n-alkanes (n = 2–10) by molecular dynamics (MD) simulations,38 which were validated against measurements and included in the training dataset. The tgBoost model shows an excellent agreement with MD values, reproducing a smooth increase of Tg. Compared to the tgBoost model, the compositional parametrization underestimates Tg for n < 8, while overestimating for n > 13, as the Tg predicted by the parametrization follow a logarithmic growth (i.e., ingrained in the original equation) proportional to the number of C atoms added to the alkane chain.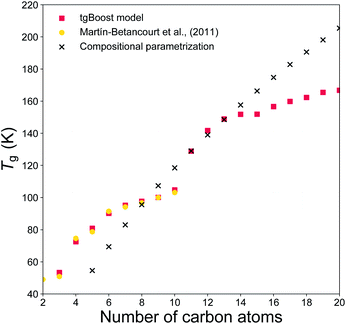 | ||
| Fig. 3 T g values predicted for the n-alkanes (n = 2–20) by the developed tgBoost model (red dots), molecular dynamics simulations (yellow squares),38 the Tg compositional parametrizations (black crosses).8 | ||
Remarkably, the tgBoost model repeats a smooth increase of Tg for n > 11 after a dip between n = 10–11. MD simulations suggest that the slower Tg increase is a non-linear phenomenon resulting from the combination of structural inner- and inter-molecular effects occurring in the bulk phase of pure n-alkanes.38 It is possible to assume that the higher degree of available conformational rearrangements of longer n-alkanes would lead to a lower Tg with each addition of a C atom to the alkyl chain. However, MD simulations suggest that longer n-alkanes can be easily trapped in pipe cages within the bulk phase of the glassy material and be prevented from rearranging in stable conformations that would lead to crystallization. With each addition of a C atom to the alkyl chain the interplay between these contrasting effects would need to be taken into account for Tg evaluation. As the MD values were included in the training dataset for the tgBoost model, it is possible that the tgBoost model might have extrapolated the trend observed for the lower mass molecules (i.e., n < 10) and expanded it to n > 11 based on the similarity between molecular embeddings of n-alkanes. To validate and resolve this issue, Tg measurements or MD simulations for higher n-alkanes are necessary. This result confirms the high performance of ML driven molecular descriptors (i.e., information rich embeddings) in capturing subtle variations in experimental/simulated data in relation to changes in the molecular structures and non-linear combinatorial physical effects.
Fig. 4 compares the experimental Tg measurements of n-alkyl alcohols (n = 1–16) with the respective Tg values predicted by the tgBoost model and the compositional parametrization.8 Primary, secondary and tertiary alcohols are all isomers with same elemental composition and consequently the compositional parametrization predicts the same values for all species, representing its major limitation. Overall, the compositional parametrization tends to overestimate the Tg of primary alcohols and to underestimate for secondary alcohols. In contrast, the tgBoost model predicts Tg in consistence with measurements, showing lower Tg for primary alcohols and higher Tg for secondary and tertiary alcohols when n < 7. This behavior is consistent with the results by Rothfuss and Petters,16 who highlighted that smaller Tg values are typically observed for primary alcohols whereas longer chain alcohols with branching and midchain –OH group have larger Tg values. The values modeled by tgBoost for secondary and tertiary alcohols overlap at this stage. It is hard to refine the tgBoost model performance for this task due to the lack of sufficient experimental measurements for tertiary alcohols. However, our results indicate that molecular embeddings would be able to capture oscillations in Tg due to small variations in molecular structures (such as the displacement of the –OH group along the alkyl chain) if more data were included during model training.
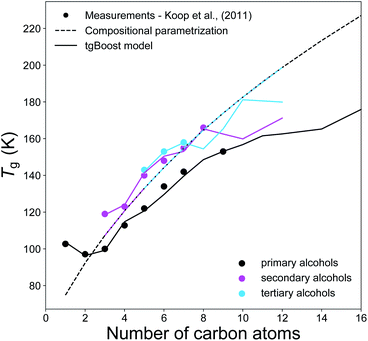 | ||
| Fig. 4 T g values of primary alcohols (black), secondary alcohols (magenta), and tertiary alcohols (light blue) as a function of the number of carbons of the n-alkyl chain. The markers represent the available experimental measurements,7 the solid lines represent the predicted values by the tgBoost model, and the dashed lines represent the Tg predictions by the compositional parametrization.8 Note that primary alcohols have a terminal –OH group, and secondary and tertiary alcohols have one –OH group placed on the second and third carbon atoms of the alkyl chain, respectively. | ||
Fig. 5 shows the experimental and modeled Tg of n-alkanes, monoalcohols, diols and triols. Note that, monoalcohols have the –OH group attached at the end of their alkyl chain, diols have the two –OH groups attached at the two opposite ends of their alkyl chain, and triols have the same structure of diols with an additional –OH group attached to the second carbon of their alkyl chain counted from one of its ends. The measurements are compared to the corresponding predictions by the tgBoost model and the compositional parametrization.8 Both models reproduce an increase in Tg observed with the addition of one to three –OH groups to the alkyl chain. Remarkably, both models reproduce the increase of 30–50 K observed with the addition of each –OH group. These results are in good agreement with a previous study, which reported an almost linear increase in Tg value for the addition of –OH groups to the skeleton of raw alkyl chains.16 The compositional parametrization exhibits a logarithmic growth upon an increase of n, overestimating in general Tg values of alcohols. These results emphasize the predictive power of molecular embeddings and ML models in aerosol modeling over simple compositional parametrizations, given that atmospheric SOA contain many alcohols.48–50
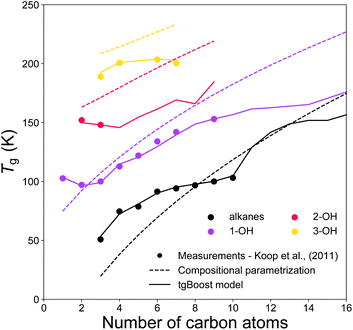 | ||
| Fig. 5 T g values of n-alkanes (black), monoalcohols (magenta), diols (red), and triols (yellow) as a function of the number of carbons of the n-alkyl chain. The markers represent experimental measurements,7 the solid lines represent the predicted values by the tgBoost model, and the dashed lines represent the Tg predictions by the compositional parametrization.8 Note that mono-alcohols have one terminal –OH group, diols have two –OH groups placed at the extremities of the carbon chain, and triols have a similar structure to diols but with an additional –OH group placed on the second carbon atom of the chain counted from one of the extremities. | ||
These results should motivate future studies to adopt molecular embeddings and machine learning algorithms to develop predictive models of organic molecules. Note that there are limitations to be accounted when using models like tgBoost. As reported in Fig. 4 and 5 the model can discern among compositional isomers of simple mono-alcohols (i.e. primary, secondary and tertiary alcohols) and it can simulate the increase in Tg by each –OH addition similarly to the compositional parametrization and the few available experimental data points of diols and triols. However, tgBoost should be used with precautions when working with these compound classes: as there are limited amount of observational data for tertiary alcohols, diols and triols, tgBoost might neglect possible trends in Tg for those molecular classes. Therefore, when possible, it would be good to compare tgBoost predictions with other Tg QSPR models developed on different datasets and physical properties. These limitations underline the importance of collecting more experimental data on Tg of atmospherically-relevant organic molecules.
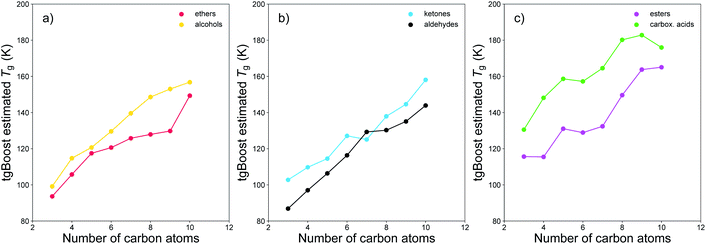
We have conducted further proof-of-concept investigations on the performance of tgBoost in distinguishing other compositional isomers and on the effects on Tg due to the addition of carboxylic groups to an alkyl chain. Fig. 6 shows the Tg of different compositional isomers as predicted by tgBoost. It illustrates the Tg predictions as a function of the number of carbon atoms of the species in compositional isomers grouped as (a) ethers and alcohols, (b) ketones and aldehydes, and (c) esters and carboxylic acids, with the respective functional groups positioned at the end of the alkyl chain. Our results suggest the following trend for sensitivity of Tg to functional group addition: –COOH (carboxylic acid) > –C(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)OR (ester) ≈ –OH (alcohol) > –C(
O)OR (ester) ≈ –OH (alcohol) > –C(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) (carbonyl) ≈ –COR (ether) where the carbonyl group category comprises –C(
O) (carbonyl) ≈ –COR (ether) where the carbonyl group category comprises –C(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)R (ketone) and –C(
O)R (ketone) and –C(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)H (aldehyde). Overall, the results are in good agreement with previous viscosity measurements, which suggested the following trend in viscosity sensitivity to functional group addition –COOH (carboxylic acid) ≈ –OH (alcohol) > –ONO2 (nitrate) > –C(
O)H (aldehyde). Overall, the results are in good agreement with previous viscosity measurements, which suggested the following trend in viscosity sensitivity to functional group addition –COOH (carboxylic acid) ≈ –OH (alcohol) > –ONO2 (nitrate) > –C(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) (carbonyl) ≈ –C(
O) (carbonyl) ≈ –C(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)OR (ester) > –CH2 (methylene).16 Our results suggest that for weakly functionalized compounds the addition of an ester functional group to the alkyl chain can strongly increase the Tg of a molecule, particularly for smaller compounds with n < 6 (see Fig. S4† in ESI). This effect may be due to conformational effects resulting from the addition of an alkoxycarbonyl group, which would induce lower flexibility in the aliphatic component and a lower degree of transformation between trans- and cis-stereoisomers in the carbon chain. It is expected that ketones and aldehydes have a relatively lower Tg compared to alcohols and carboxylic acids as there are no functional groups that may be involved directly in hydrogen bonds in the bulk phase of pure materials. However, their potential role in increasing the overall Tg of SOA mixtures should be noted since the carbonyl group may still participate in hydrogen bonds in presence of hydrogen donors. Further investigations are needed to assess how the interplay of multiple functional groups can affect Tg of multicomponent complex mixtures.
O)OR (ester) > –CH2 (methylene).16 Our results suggest that for weakly functionalized compounds the addition of an ester functional group to the alkyl chain can strongly increase the Tg of a molecule, particularly for smaller compounds with n < 6 (see Fig. S4† in ESI). This effect may be due to conformational effects resulting from the addition of an alkoxycarbonyl group, which would induce lower flexibility in the aliphatic component and a lower degree of transformation between trans- and cis-stereoisomers in the carbon chain. It is expected that ketones and aldehydes have a relatively lower Tg compared to alcohols and carboxylic acids as there are no functional groups that may be involved directly in hydrogen bonds in the bulk phase of pure materials. However, their potential role in increasing the overall Tg of SOA mixtures should be noted since the carbonyl group may still participate in hydrogen bonds in presence of hydrogen donors. Further investigations are needed to assess how the interplay of multiple functional groups can affect Tg of multicomponent complex mixtures.
Carboxylic acids represent a major fraction of SOA50 and a better representation of carboxylic acids data is particularly relevant for aerosol models. Fig. 7 illustrates the predicted Tg by the tgBoost model and the compositional parametrization8 for the addition of one to three carboxylic groups to the alkyl chain. Both methods predict increasing Tg values for each addition of a carboxylic group to the molecule. At equal number of C atoms in the molecule, the mean increase in Tg between mono carboxylic and dicarboxylic acids is 63 and 53 K for the tgBoost model and compositional parametrizations, respectively. The tgBoost model shows a steady increase in Tg for mono-carboxylic acids and interestingly it predicts a decline in Tg for dicarboxylic acids with n > 5 and no increase in Tg value for tricarboxylic acids. It should be noted that the acidity of dicarboxylic acids lowers with the addition of C atoms to their alkyl chain due to the electron donating nature of the alkyl group. This decrease is proportional to the addition of new C atoms to the aliphatic chain with the highest reductions observed for the first four carbon additions.51 The acidity of dicarboxylic acids depends also on the conformation of the species, with trans-structural isomers being considerably more acidic than the equivalent cis-structural isomers. A lower acidity implies a reluctancy for the molecule to release protons, therefore a more stable structure and a lower strength in hydrogen bonding.52,53 It has been shown that Tg is strongly influenced by the presence of hydrogen bonds, notably because hydrogen bonds promote the crystallization process that leads to the transition into a solid state.54Tg is also strongly affected by stereoisomerism because rotamers and conformers slow down the crystallization process.55 Similar acidity and the presence of more stereoisomers in di- and tri-carboxylic acids with longer alkyl chains would combine and result in comparable strengths of hydrogen bonds with addition of C atoms to the molecular structure. It is possible that this effect may justify the decreasing or constant predicted Tg of dicarboxylic and tricarboxylic acids upon increasing carbon number.
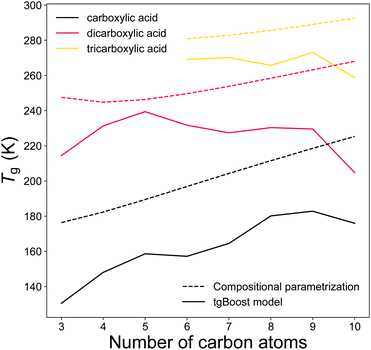 | ||
| Fig. 7 T g of linear monocarboxylic, dicarboxylic and tricarboxylic acids as a function of the number of carbon atoms in the alkyl chain as predicted by the tgBoost model (solid lines) and the Tg compositional parametrization (dashed lines).8 | ||
3.3 Domain of application and model comparison
It is fundamental to verify the correct domain of applicability of developed QSAR/QSPR models because potentially any of these models could be used to predict the physical properties of any chemically acceptable molecule. Since our domain pertains to atmospheric chemistry, we test how well the tgBoost model predictions compare to the values from atmospherically-relevant compounds. There are unfortunately no large available datasets reporting experimental Tg values of atmospheric species and the data can only be estimated from the best available Tm models through the Boyer-Kauzman rule where Tg = g × Tm, with g = 0.70085 (±0.00375).7 Similarly to the approach used to develop the Tg compositional parametrizations,8,15 we have used a list of SOA compounds compiled by Shiraiwa et al.56 and we have estimated the Tg of these compounds from the computed Tm values by EPI Suite. The estimated Tg are compared to the Tg predictions from the tgBoost model to assess its application to atmospheric chemistry modeling.
Fig. 8a shows the results of such comparison. Overall, the values predicted using the tgBoost are similar to the ones estimated using the Tm from EPI Suite with MAE = 27.6 K, R = 0.794, and RCV2 = 0.455. Many datapoints are positioned below the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 correlation line, indicating that the tgBoost model tends to underpredict the Tg of SOA compounds compared to EPI Suite. This behavior is consistent with the EPI Suite guideline that reports a tendency for the MPBPWIN module to overestimate the Tm of large and multi-functionalized molecules, such as aromatics and complex carbonyl bearing compounds.29 The shaded pink square in Fig. 8a highlights a cluster of 20 molecules whose values are overpredicted by a factor of 100–150 K by EPI Suite, and which are all complex multi-functional branched carbonyl compounds with ether and alcohol segments within their molecular structure (see Fig. S2†).
1 correlation line, indicating that the tgBoost model tends to underpredict the Tg of SOA compounds compared to EPI Suite. This behavior is consistent with the EPI Suite guideline that reports a tendency for the MPBPWIN module to overestimate the Tm of large and multi-functionalized molecules, such as aromatics and complex carbonyl bearing compounds.29 The shaded pink square in Fig. 8a highlights a cluster of 20 molecules whose values are overpredicted by a factor of 100–150 K by EPI Suite, and which are all complex multi-functional branched carbonyl compounds with ether and alcohol segments within their molecular structure (see Fig. S2†).
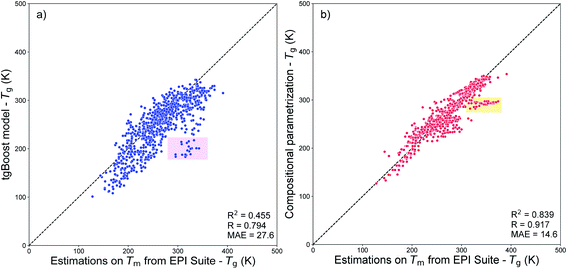 | ||
| Fig. 8 (a) Correlation plot between the Tg values predicted by the tgBoost model and by the MPBPWIN module of EPI Suite for SOA compounds from Shiraiwa et al.56 The pink squared area highlights the cluster of 20 molecules with the highest deviation between predictions. (b) Correlation plot between the Tg values predicted by the compositional parametrizations8,15 and by the MPBPWIN module of EPI Suite for SOA compounds from Shiraiwa et al.56 The orange squared area highlights the cluster of 30 molecules with the highest deviation between predictions. | ||
Fig. 8b shows the correlation between the Tg values predicted from the compositional parametrization8 and those estimated from EPI Suite Tm. In this case the Tg values predicted by the two models are very similar with a very low MAE of 14.6 K, a high positive correlation of R = 0.917, and a relatively low variance of RCV2 = 0.839. This result suggests that the models have similar prediction capability and the molecular descriptors used to develop the models have similar limitations. Notably, due to the limitations of EPI Suite, the compositional parametrizations may also tend to overestimate Tg of organic species as pointed by the high correlation between the two methods. The shaded orange square highlights a cluster of 30 molecules whose values are overpredicted by a factor of 55–75 K by EPI Suite. The largest divergences are observed for nitrogen bearing large compounds with carbonyl, alkane ring and alcohol segments within their molecular structures (see Fig. S3†).
These results imply that the tgBoost model is applicable to SOA compounds, providing more realistic Tg of organic molecules with complex structure and multiple functional groups compared to the EPI Suite. Remarkably, we observe that molecular embeddings can overcome the limitations affecting the performances of the EPI Suite and the compositional parametrizations. The tgBoost model performs well in predicting Tg of SOA compounds and it has good potential for applications to the modelling of aerosol chemistry.
3.4 T m regression model performance
We have also trained multiple ML models on publicly available datasets of Tm with the aim to build a Tm regression model based on large amounts of experimental data to be used for the estimation of Tg using the Boyer-Kauzmann rule. Table 2 shows the performances of our Tm models trained using molecular embeddings from mol2vec as molecular descriptors. The best results were achieved with the Tm-Tetko dataset using a deep neural network (DNN) with MAE = 31.0 K, R = 0.6 and RCV2 = 0.77. This result is already a good improvement compared to the EPI Suite with MAE = 48.6 K29 and it is comparable to other state-of-the-art Tm regression models. As shown in Table 2, the best results have been achieved by Tetko et al.30 using an Associative Neural Network (ASNN) and a combination of 14 classic molecular descriptors on 2078 points from the “Bradley Good Melting Point Dataset”.33 Coley et al.35 built a Tm prediction model with MAE of 26.2 K, with very similar performances to Tetko et al. (2014) using a Convolutional Neural Network and the Attributed Molecular Graphs of 3019 chemical species from the “Bradley Good Melting Point Dataset”.31 Good results with MAE of 28.85 K were also achieved by Sivaraman et al.,36 who developed a machine learning framework (MOLAN) for QSPR model development based on dataset specific derived embeddings and a Gaussian Process.32 It is worth noting that the models developed in all these studies use slight variations of the “Bradley good melting point dataset” (Tm-Bradley, 3092 data points), a highly curated but very small dataset of molecules Tm (i.e., Tm-Tetko > 200![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 data points). The developed DNN model performs slightly worse than our initial expectations, even though the performance of machine learning models tend to refine with the increase in the amount of data used during training. A reasonable source of error might lay in the lower quality of data within the Tm-Tetko data points, which may be associated with larger experimental uncertainties compared to the Tm-Bradley dataset. Another source of error could reside in limitations of molecular embeddings and into their application to complex and large datasets. We suggest further analysis to investigate if different molecular descriptors would perform better on the Tm-Tetko dataset, but this task is beyond the scope of this study. Nevertheless, our model still performs very well in predicting Tm from their molecular structure. Remarkably, it has a lower MAE compared to Tm estimations by EPI Suite.
000 data points). The developed DNN model performs slightly worse than our initial expectations, even though the performance of machine learning models tend to refine with the increase in the amount of data used during training. A reasonable source of error might lay in the lower quality of data within the Tm-Tetko data points, which may be associated with larger experimental uncertainties compared to the Tm-Bradley dataset. Another source of error could reside in limitations of molecular embeddings and into their application to complex and large datasets. We suggest further analysis to investigate if different molecular descriptors would perform better on the Tm-Tetko dataset, but this task is beyond the scope of this study. Nevertheless, our model still performs very well in predicting Tm from their molecular structure. Remarkably, it has a lower MAE compared to Tm estimations by EPI Suite.
Molecular embeddings have already shown to be able to capture slight variations in molecular structures and physical trends for predicting Tg as discussed above. Therefore, we expect similar behavior for Tm and here we have focused our analysis on the assessment of the domain of applicability of the DNN model developed from the Tm-Tetko dataset. Fig. 9 exhibits the correlation plot between the Tm predictions from the DNN model and EPI Suite for SOA compounds from Shiraiwa et al.56 It shows a positive correlation with R = 0.582, a high variance of RCV2 = 0.261 and a substantial divergence with MAE = 48.7 K. A deep investigation shows that the Tm of complex multi-functional species is overpredicted by EPI Suite, while the DNN model tends to overestimate the Tm of very simple compounds. The highest divergences are observed for complex multi-functional nitrate groups (EPI Suite predictions are on average 170–150 K higher than DNN ones) and for simple hydroxy acids (DNN predictions are on average 100–150 K higher than EPI Suite ones). These results suggest that our Tm model has limitations that need to be accounted if to be used to predict the Tm of atmospheric species composing SOA. The prime cause of the discrepancy between the predictions of the two models is likely linked to the different nature of the chemical species of the datasets. Notably, the Tm-Tetko dataset has an abundance of drug-like complex compounds such as alkaloids, aromatic cyclic nitrogen bearing compounds, steroids, and polycyclic molecules as well as more molecules with Br and Cl in their structures. This chemical dissimilarity could be responsible for the low performance of the model when it tries to predict the Tm of small low functionalized organic compounds. Despite the general good performance of the DNN model on complex molecules, its application to SOA chemistry may be limited. Further investigations are needed to develop a better Tm prediction model for applications to atmospheric chemistry. Notably, future work should focus on the retrieval of a more representative dataset of experimental Tm for atmospheric species to be used for model development.
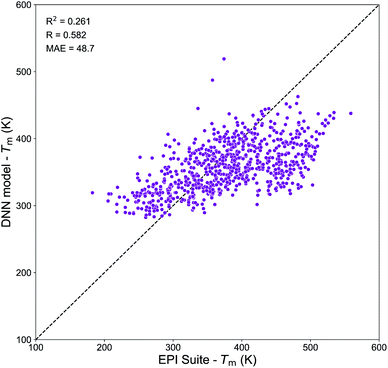 | ||
| Fig. 9 Correlation plot between the Tm values predicted by the DNN model and by the MPBPWIN module of EPI Suite for SOA compounds from Shiraiwa et al.56 | ||
4. Conclusions
We used state-of-the-art molecular descriptors and machine learning algorithms to develop QSPR models to be used for the prediction of Tg and Tm of atmospheric organic molecules. A range of different model architectures and datasets were tested and explored for their ability to reach the best trade-off between error minimization and target prediction performance. The predictions from the developed models have been compared with available experimental data and the previously-developed Tg compositional parameterizations. Finally, the models have been tested for their applicability to SOA compounds.The developed tgBoost model for Tg estimation is a very powerful tool: it has a low MAE of 18.3 K and its predictions are in very good agreement with experimental measurements, even capturing very subtle trends in data. The tgBoost model can reproduce non-linear trends observed in Tg for n-alkanes due to inter- and intra-molecular interactions in the bulk phase. The model can also distinguish structural isomers and discern how the positioning of a functional group within the molecular structure can influence its Tg. For this task, the tgBoost model was tested on primary, secondary and tertiary alcohols, showing how the displacement of an –OH group along the alkyl chain can influence Tg. The advantage of the tgBoost model lies in its ability to discern structural isomers; it can distinguish between aldehydes and ketones, alcohols and ethers, and esters and carboxylic acids, predicting different Tg for all pairs of isomeric chemical classes. The tgBoost model predicts the following trend in Tg sensitivity to functional group addition: –COOH (carboxylic acid) > –C(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)OR (ester) ≈ –OH (alcohol) > –C(
O)OR (ester) ≈ –OH (alcohol) > –C(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) (carbonyl) ≈ –COR (ether). This result is in good agreement with the trend in sensitivity to viscosity to functional group addition observed by Rothfuss and Petters.16 The tgBoost model has also been tested on mono-, di- and tri-carboxylic acids in order to assess if it can capture how the interplay between multiple functional groups can affect Tg. The results are in relatively good agreement with experimental measurements, but further investigations and data are needed to refine the model for this task. Finally, the model has been tested for its applicability to SOA compounds by comparing the tgBoost model with the compositional parametrizations and EPI Suite. The tgBoost model predicts Tg in reasonable agreement with or somewhat lower compared to EPI Suite and the compositional parametrizations. This is reasonable because a major limitation of EPI Suite is known to be the overprediction of Tm of structurally complex and multi-functionalized chemical species.29
O) (carbonyl) ≈ –COR (ether). This result is in good agreement with the trend in sensitivity to viscosity to functional group addition observed by Rothfuss and Petters.16 The tgBoost model has also been tested on mono-, di- and tri-carboxylic acids in order to assess if it can capture how the interplay between multiple functional groups can affect Tg. The results are in relatively good agreement with experimental measurements, but further investigations and data are needed to refine the model for this task. Finally, the model has been tested for its applicability to SOA compounds by comparing the tgBoost model with the compositional parametrizations and EPI Suite. The tgBoost model predicts Tg in reasonable agreement with or somewhat lower compared to EPI Suite and the compositional parametrizations. This is reasonable because a major limitation of EPI Suite is known to be the overprediction of Tm of structurally complex and multi-functionalized chemical species.29
The DNN model developed for the prediction of the Tm of organic molecules performs well against the available dataset with MAE of 31.0 K. The model has been tested for its applicability to SOA compounds in comparison with the EPI Suite. The model performance was limited for SOA compounds, which may be due to the nature of the training dataset that is rich in drug-like complex molecules with heavy atoms within their structures. Nevertheless, the model has great potential of improvement and further studies should concentrate on the retrieval of better experimental datasets with higher fraction of atmospheric organic compounds for model training.
Considerable progress has been made with regards of the development of a Tg prediction model that includes the effects of functionality and molecular structure on Tg explicitly. This aspect is crucial for aerosol models treating gas-particle partitioning of semi-volatile compounds as strongly affected by Tg and viscosity. A difference in Tg of a few K between compositional isomers could affect the viscosity of a particle. As a result, aerosol models of complex SOA systems such as GECKO-A,57 AIOMFAC-VISC20 and the Master Chemical Mechanism (MCM)58,59 would highly benefit from a more complex treatment of Tg to estimate particle viscosity. For instance, GECKO-A can generate complex chemical mechanisms formed by the reactions and partitioning between gas and particle phases. These SOA chemical systems are rich in alcohols, carboxylic acids and multi-functionalized compounds. A detailed treatment of Tg based on functionality would enhance the accuracy of model simulations and provide better insight on complex aerosol systems. The developed tgBoost model offers state-of-the-art performances in predicting the Tg of organic molecules involved in SOA chemistry. It is a very useful and powerful tool for estimations of SOA phase state and hence it can contribute to a better evaluation of SOA effects on climate and air quality.
Code availability
https://github.com/U0M0Z/tgpipe.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was funded by the Department of Energy (DE-SC0022139) and the National Science Foundation (AGS-1654104). We thank Dr Ying Li for sharing the Tg dataset and stimulating discussions.References
- J. L. Jimenez, M. R. Canagaratna, N. M. Donahue, A. S. H. Prevot, Q. Zhang and J. H. Kroll,
et al. Evolution of organic aerosols in the atmosphere, Science, 2009, 326(5959), 1525–1529 CrossRef CAS
.
- U. Pöschl and M. Shiraiwa, Multiphase Chemistry at the Atmosphere-Biosphere Interface Influencing Climate and Public Health in the Anthropocene, Chem. Rev., 2015, 115(10), 4440–4475 CrossRef PubMed
.
- K. Tsigaridis, N. Daskalakis, M. Kanakidou, P. J. Adams, P. Artaxo and R. Bahadur,
et al. The AeroCom evaluation and intercomparison of organic aerosol in global models, Atmos. Chem. Phys., 2014, 14(19), 10845–10895 CrossRef
.
- G. Ciarelli, A. Colette, S. Schucht, M. Beekmann, C. Andersson and A. Manders-Groot,
et al. Long-term health impact assessment of total PM2.5 in Europe during the 1990–2015 period, Atmos. Environ. X, 2019, 3(998), 100032, DOI:10.1016/j.aeaoa.2019.100032
.
- M. Shrivastava, C. D. Cappa, J. Fan, A. H. Goldstein, A. B. Guenther and J. L. Jimenez,
et al. Recent advances in understanding secondary organic aerosol: Implications for global climate forcing, Rev. Geophys., 2017, 55(2), 509–559 CrossRef
.
- Y. Li and M. Shiraiwa, Timescales of secondary organic aerosols to reach equilibrium at various temperatures and relative humidities, Atmos. Chem. Phys., 2019 May 7, 19(9), 5959–5971 Search PubMed
.
- T. Koop, J. Bookhold, M. Shiraiwa and U. Pöschl, Glass transition and phase state of organic compounds: Dependency on molecular properties and implications for secondary organic aerosols in the atmosphere, Phys. Chem. Chem. Phys., 2011, 13(43), 19238–19255 RSC
.
- W. S. W. DeRieux, Y. Li, P. Lin, J. Laskin, A. Laskin and A. K. Bertram,
et al. Predicting the glass transition temperature and viscosity of secondary organic material using molecular composition, Atmos. Chem. Phys., 2018, 18(9), 6331–6351 CrossRef
.
- T. Galeazzo, R. Valorso, Y. Li, M. Camredon, B. Aumont and M. Shiraiwa, Estimation of Secondary Organic Aerosol Viscosity from Explicit Modeling of Gas-Phase Oxidation of Isoprene and α-pinene, Atmos. Chem. Phys., 2021, 1–23 Search PubMed
.
- H. P. Dette, M. Qi, D. C. Schröder, A. Godt and T. Koop, Glass-forming properties of 3-methylbutane-1,2,3-tricarboxylic acid and its mixtures with water and pinonic acid, J. Phys. Chem. A, 2014, 118(34), 7024–7033 CrossRef CAS
.
- S. S. Petters, S. M. Kreidenweis, A. P. Grieshop, P. J. Ziemann and M. D. Petters, Temperature- and Humidity-Dependent Phase States of Secondary Organic Aerosols, Geophys Res. Lett., 2019, 46(2), 1005–1013 CrossRef
.
- Y. Zhang, L. Nichman, P. Spencer, J. I. Jung, A. Lee and B. K. Heffernan,
et al. The Cooling Rate- And Volatility-Dependent Glass-Forming Properties of Organic Aerosols Measured by Broadband Dielectric Spectroscopy, Environ. Sci. Technol., 2019, 53(21), 12366–12378 CrossRef CAS
.
- M. Shiraiwa, Y. Li, A. P. Tsimpidi, V. A. Karydis, T. Berkemeier and S. N. Pandis,
et al. Global distribution of particle phase state in atmospheric secondary organic aerosols, Nat. Commun., 2017, 8(1), 15002 CrossRef PubMed
.
- N. E. Rothfuss and M. D. Petters, Influence of Functional Groups on the Viscosity of Organic Aerosol, Environ. Sci. Technol., 2017, 51(1), 271–279 CrossRef CAS
.
- Y. Li, D. A. Day, H. Stark, J. L. Jimenez and M. Shiraiwa, Predictions of the glass transition temperature and viscosity of organic aerosols from volatility distributions, Atmos. Chem. Phys., 2020, 20(13), 8103–8122 CrossRef CAS
.
- N. E. Rothfuss and M. D. Petters, Influence of Functional Groups on the Viscosity of Organic Aerosol, Environ. Sci. Technol., 2017, 51(1), 271–279 CrossRef CAS PubMed
.
- S. K. Schum, B. Zhang, K. Dzepina, P. Fialho, C. Mazzoleni and L. R. Mazzoleni, Molecular and physical characteristics of aerosol at a remote free troposphere site: Implications for atmospheric aging, Atmos. Chem. Phys., 2018, 18(19), 14017–14036 CrossRef CAS
.
- J. C. Ditto, T. Joo, P. Khare, R. Sheu, M. Takeuchi and Y. Chen,
et al. Effects of Molecular-Level Compositional Variability in Organic Aerosol on Phase State and Thermodynamic Mixing Behavior, Environ. Sci. Technol., 2019, 53(22), 13009–13018 CrossRef CAS PubMed
. Available from: https://pubs.acs.org/doi/abs/10.1021/acs.est.9b02664.
- M. Song, A. M. MacLean, Y. Huang, N. R. Smith, S. L. Blair and J. Laskin,
et al. Liquid-liquid phase separation and viscosity within secondary organic aerosol generated from diesel fuel vapors, Atmos. Chem. Phys., 2019, 19(19), 12515–12529 CrossRef CAS
.
- N. R. Gervasi, D. O. Topping and A. Zuend, A predictive group-contribution model for the viscosity of aqueous organic aerosol, Atmos. Chem. Phys., 2020, 20(5), 2987–3008 CrossRef CAS
.
- M. Octaviani, M. Shrivastava, R. A. Zaveri, A. Zelenyuk, Y. Zhang and Q. Z. Rasool,
et al. Modeling the Size Distribution and Chemical Composition of Secondary Organic Aerosols during the Reactive Uptake of Isoprene-Derived Epoxydiols under Low-Humidity Condition, ACS Earth Sp Chem, 2021, 5(11), 3247–3257 CrossRef CAS
.
- R. Schmedding, M. Ma, Y. Zhang, S. Farrell, H. O. T. Pye and Y. Chen,
et al. A-Pinene-Derived organic coatings on acidic sulfate aerosol impacts secondary organic aerosol formation from isoprene in a box model, Atmos. Environ., 2019, 213(June), 456–462, DOI:10.1016/j.atmosenv.2019.06.005
.
- R. Schmedding, Q. Z. Rasool, Y. Zhang, H. O. T. Pye, H. Zhang and Y. Chen,
et al. Predicting secondary organic aerosol phase state and viscosity and its effect on multiphase chemistry in a regional-scale air quality model, Atmos. Chem. Phys., 2020, 20(13), 8201–8225 CrossRef CAS PubMed
.
-
R. Todeschini and V. Consonni. Molecular Descriptors for Chemoinformatics Volume I: Alphabetical Listing/Volume II: Append. 2nd edn, Weinheim, Wiley-VCH, 2009 Search PubMed
.
- H. van de Waterbeemd and E. Gifford, ADMET in silico modelling: towards prediction paradise?, Nat.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Rev.
Rev.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Drug
Drug![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Discovery, 2003, 2(3), 192–204 CrossRef CAS PubMed
Discovery, 2003, 2(3), 192–204 CrossRef CAS PubMed . Available from: http://www.nature.com/articles/nrd1032.
- Y. Ran, N. Jain and S. H. Yalkowsky, Prediction of Aqueous Solubility of Organic Compounds by the General Solubility Equation (GSE), J. Chem. Inf. Comput. Sci., 2001, 41(5), 1208–1217 CrossRef CAS PubMed
. Available from: https://pubs.acs.org/doi/10.1021/ci010287z.
- J. Nikmo, J. Kukkonen and K. Riikonen, A model for evaluating physico-chemical substance properties required by consequence analysis models, J. Hazard. Mater., 2002, 91(1–3), 43–61 CrossRef CAS PubMed
. Available from: https://linkinghub.elsevier.com/retrieve/pii/S030438940100379X.
- U. P. Preiss, W. Beichel, A. M. T. Erle, Y. U. Paulechka and I. Krossing, Is Universal, Simple Melting Point Prediction Possible?, ChemPhysChem, 2011, 12(16), 2959–2972 CrossRef CAS PubMed
. Available from: https://onlinelibrary.wiley.com/doi/10.1002/cphc.201100522.
-
EPA U. Estimation Programs Interface SuiteTM for Microsoft Windows v4.1.1. Washington, DC, USA: United States Environmental Protection Agency; 2017 Search PubMed
.
-
S. Jastrzębski, D. Leśniak, W. M. Czarnecki. Learning to SMILE(S). 2016;1–5. Available from: http://arxiv.org/abs/1602.06289 Search PubMed
.
- R. Gómez-Bombarelli, J. N. Wei, D. Duvenaud, J. M. Hernández-Lobato, B. Sánchez-Lengeling and D. Sheberla,
et al. Automatic Chemical Design Using a Data-Driven Continuous Representation of Molecules, ACS Cent. Sci., 2018, 4(2), 268–276 CrossRef PubMed
.
- M. H. S. Segler, T. Kogej, C. Tyrchan and M.
P. Waller, Generating focused molecule libraries for drug discovery with recurrent neural networks, ACS Cent. Sci., 2018, 4(1), 120–131 CrossRef CAS PubMed
.
- S. Jaeger, S. Fulle and S. Turk, Mol2vec: Unsupervised Machine Learning Approach with Chemical Intuition, J. Chem. Inf. Model, 2018, 58(1), 27–35 CrossRef CAS PubMed
.
- I. V. Tetko, Y. Sushko, S. Novotarskyi, L. Patiny, I. Kondratov and A. E. Petrenko,
et al. How accurately can we predict the melting points of drug-like compounds?, J. Chem. Inf. Model, 2014, 54(12), 3320–3329 CrossRef CAS PubMed
.
- C. W. Coley, R. Barzilay, W. H. Green, T. S. Jaakkola and K. F. Jensen, Convolutional Embedding of Attributed Molecular Graphs for Physical Property Prediction, J. Chem. Inf. Model, 2017, 57(8), 1757–1772 CrossRef CAS PubMed
.
- G. Sivaraman, N. E. Jackson, B. Sanchez-Lengeling, Vázquez-Mayagoitia Á, A. Aspuru-Guzik and V. Vishwanath,
et al. A machine learning workflow for molecular analysis: application to melting points, Mach Learn Sci Technol, 2020, 1(2), 025015 CrossRef
.
-
RDKit.03.1, 2021, Open-source cheminformatics Search PubMed
.
- M. Martín-Betancourt, J. M. Romero-Enrique and L. F. Rull, Molecular simulation study of the glass transition for a flexible model of linear alkanes, Mol. Simul., 2009, 35(12–13), 1043–1050 CrossRef
.
- I. V. Tetko, M. Lowe D and A. J. Williams, The development of models to predict melting and pyrolysis point data associated with several hundred thousand compounds mined from PATENTS, J. Cheminform., 2016, 8(1), 1–18 CrossRef PubMed
.
-
J.-C. Bradley, A. Lang and A. J. Williams, Jean-Claude Bradley Double Plus Good (Highly Curated and Validated) Melting Point Dataset, 2014 Search PubMed
.
-
T. Chen, C. Guestrin. XGBoost: A Scalable Tree Boosting System, in 22nd SIGKDD Conference on Knowledge Discovery and Data Mining. 2016 Search PubMed
.
- G. Varoquaux, P. R. Raamana, D. A. Engemann, A. Hoyos-Idrobo, Y. Schwartz and B. Thirion, Assessing and tuning brain decoders: Cross-validation, caveats, and guidelines, Neuroimage, 2017, 145, 166–179 CrossRef PubMed
.
- D. Krstajic, L. J. Buturovic, D. E. Leahy and S. Thomas, Cross-validation pitfalls when selecting and assessing regression and classification models, J. Cheminform., 2014 Dec 29, 6(1), 10 Search PubMed
. Available from: https://jcheminf.biomedcentral.com/articles/10.1186/1758-2946-6-10.
- G. C. Cawley and N. L. C. Talbot, On over-fitting in model selection and subsequent selection bias in performance evaluation, J. Mach. Learn. Res., 2010, 11, 2079–2107 Search PubMed
.
- F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion and O. Grisel,
et al. Scikit-learn: Machine Learning in Python, J. Mach. Learn. Res., 2011, 12, 2825–2830 Search PubMed
. Available from: https://jmlr.org/papers/volume12/pedregosa11a/pedregosa11a.pdf.
-
T. Hastie, R. Tibshirani and J. H. Friedman. The Elements of Statistical Learning: Data Mining, Inference, and Prediction. 2nd edn New York, NY, USA, Springer, 2009, p. 745 Search PubMed
.
-
F. Chollet, Keras Github, 2015, https://github.com/fchollet/keras Search PubMed
.
- J. D. Surratt, A. W. H. Chan, N. C. Eddingsaas, M. N. Chan, C. L. Loza and A. J. Kwan,
et al. Reactive intermediates revealed in secondary organic aerosol formation from isoprene, Proc.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Natl.
Natl.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Acad.
Acad.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Sci.
Sci.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) U.
U.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S.
S.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A., 2010, 107(15), 6640–6645 CrossRef CAS PubMed
A., 2010, 107(15), 6640–6645 CrossRef CAS PubMed .
- H. Zhang, J. D. Surratt, Y. H. Lin, J. Bapat and R. M. Kamens, Effect of relative humidity on SOA formation from isoprene/NO photooxidation: Enhancement of 2-methylglyceric acid and its corresponding oligoesters under dry conditions, Atmos. Chem. Phys., 2011, 11(13), 6411–6424 CrossRef CAS
.
- P. J. Ziemann and R. Atkinson, Kinetics, products, and mechanisms of secondary organic aerosol formation, Chem.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Soc.
Soc.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Rev., 2012, 41(19), 6582–6605 RSC
Rev., 2012, 41(19), 6582–6605 RSC .
- M. C. Etter, Encoding and Decoding Hydrogen-Bond Patterns of Organic Compounds, Acc.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Chem.
Chem.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Res., 1990, 23(4), 120–126 CrossRef CAS
Res., 1990, 23(4), 120–126 CrossRef CAS .
- T. L. McConnell, C. A. Wheaton, K. C. Hunter and S. D. Wetmore, Effects of Hydrogen Bonding on the Acidity of Adenine, Guanine, and Their 8-Oxo Derivatives, J. Phys. Chem. A, 2005 Jul 1, 109(28), 6351–6362 Search PubMed
. Available from: https://pubs.acs.org/doi/10.1021/jp0509919.
- J. Graton, F. Besseau, A. M. Brossard, E. Charpentier, A. Deroche and J. Y. Le Questel, Hydrogen-bond acidity of OH groups in various molecular environments (phenols, alcohols, steroid derivatives, and amino acids structures): Experimental measurements and density functional theory calculations, J. Phys. Chem. A, 2013, 117(49), 13184–13193 CrossRef CAS PubMed
.
- A. Laventure, A. Gujral, O. Lebel, C. Pellerin and M. D. Ediger, Influence of Hydrogen Bonding on the Kinetic Stability of Vapor-Deposited Glasses of Triazine Derivatives, J.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Phys.
Phys.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Chem.
Chem.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) B, 2017, 121(10), 2350–2358 CrossRef CAS PubMed
B, 2017, 121(10), 2350–2358 CrossRef CAS PubMed .
- A. Laventure, G. De Grandpré, A. Soldera, O. Lebel and C. Pellerin, Unraveling the interplay between hydrogen bonding and rotational energy barrier to fine-tune the properties of triazine molecular glasses, Phys. Chem. Chem. Phys., 2016, 18(3), 1681–1692 RSC
.
- M. Shiraiwa, T. Berkemeier, K. A. Schilling-Fahnestock, J. H. Seinfeld and U. Pöschl, Molecular corridors and kinetic regimes in the multiphase chemical evolution of secondary organic aerosol, Atmos. Chem. Phys., 2014, 14(16), 8323–8341 CrossRef
.
- B. Aumont, S. Szopa and S. Madronich, Modelling the evolution of organic carbon during its gas-phase tropospheric oxidation: development of an explicit model based on a self generating approach, Atmos. Chem. Phys., 2005, 5(1), 703–754 Search PubMed
.
- M. E. Jenkin, S. M. Saunders, V. Wagner and M. J. Pilling, Protocol for the development of the Master Chemical Mechanism, MCM v3 (Part B): Tropospheric degradation of aromatic volatile organic compounds, Atmos. Chem. Phys., 2003, 3(1), 181–193 CrossRef CAS
.
- M. E. Jenkin, J. C. Young and A. R. Rickard, The MCM v3.3.1 degradation scheme for isoprene, Atmos. Chem. Phys., 2015, 15(20), 11433–11459 CrossRef CAS
.
- D. K. Duvenaud, D. Maclaurin, J. Aguilera-Iparraguirre, R. Gomez-Bombarelli, T. Hirzel, A. Aspuru-Guzik and R. P. Adams, Convolutional Networks on Graphs for Learning Molecular Fingerprints, Adv. Neural Inf. Process. Syst., 2015, 2215–2223 Search PubMed
, https://doi.org/10.48550/arXiv.1509.09292.
- S. Kearnes, K. McCloskey, M. Berndl, V. Pande and P. Riley, Molecular Graph Convolutions: Moving Beyond Fingerprints, J. Comput.-Aided Mol. Des., 2016, 30, 595–608 CrossRef CAS PubMed
, https://doi.org/10.1007/s10822-016-9938-8.
Footnote |
| † Electronic supplementary information (ESI) available. See https://doi.org/10.1039/d1ea00090j |
| This journal is © The Royal Society of Chemistry 2022 |