Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Crossed-beam and theoretical studies of multichannel nonadiabatic reactions: branching fractions and role of intersystem crossing for O(3P) + 1,3-butadiene†
C.
Cavallotti
 *a,
A.
Della Libera
a,
C.-W.
Zhou
*a,
A.
Della Libera
a,
C.-W.
Zhou
 bc,
P.
Recio
bc,
P.
Recio
 d,
A.
Caracciolo
d,
A.
Caracciolo
 d,
N.
Balucani
d,
N.
Balucani
 *d and
P.
Casavecchia
*d and
P.
Casavecchia
 *d
*d
aDipartimento di Chimica, Materiali e Ingegneria Chimica “Giulio Natta”, Politecnico di Milano, 20131 Milano, Italy. E-mail: carlo.cavallotti@polimi.it
bSchool of Energy and Power Engineering, Beihang University, Beijing, 100191, PR China
cCombustion Chemistry Centre, School of Chemistry, Ryan Institute, National University of Ireland, Galway, H91 TK33, Ireland
dDipartimento di Chimica, Biologia e Biotecnologie, Università degli Studi di Perugia, 06123 Perugia, Italy. E-mail: piergiorgio.casavecchia@unipg.it; nadia.balucani@unipg.it
First published on 30th March 2022
Abstract
Atomic oxygen reactions can contribute significantly to the oxidation of unsaturated aliphatic and aromatic hydrocarbons. The reaction mechanism is started by electrophilic O atom addition to the unsaturated bond(s) to form “chemically activated” triplet oxy-intermediate(s), which can evolve adiabatically on the triplet potential energy surface (PES) and nonadiabatically via intersystem crossing on the singlet PES, forming intermediates that undergo unimolecular decomposition to a variety of bimolecular product channels. Here, we apply a combined crossed molecular beam (CMB)–theoretical approach to the study of the O(3P) + 1,3-butadiene reaction. Although the kinetics of this reaction have been extensively investigated, little is known about the primary products and their branching fractions (BFs). In the present work, a total of eight product channels were observed and characterized in a CMB experiment at a collision energy of 32.6 kJ mol−1. Synergic ab initio transition-state theory-based master equation simulations coupled with nonadiabatic transition-state theory on coupled triplet/singlet PESs were employed to compute the product BFs and assist the interpretation of the CMB experimental results. The good agreement found between the theoretical predictions and CMB experiments supported the use of the adopted methodology for the prediction of channel-specific rate constants as a function of temperature and pressure suitable to be used for the kinetic modeling of 1,3-butadiene oxidation and of systems where 1,3-butadiene is an important intermediate.
1. Introduction
The reactions between ground state atomic oxygen, O(3P), and unsaturated hydrocarbons (UHs) have an impact on a large variety of gaseous chemical and physical systems, going from combustion flames1–8 to plasma discharges,9 and to the Earth’s atmosphere.10 In addition, they also play an important role in the reactivity of oxygen-rich interstellar and circumstellar environments,11–13 as well as in the upper atmosphere of Titan.14,15During the oxidation of UHs and AHs (aromatic hydrocarbons) by O(3P), the “chemically activated” triplet oxy-intermediate(s) formed following electrophilic O atom addition to the unsaturated bond(s), can evolve adiabatically on the triplet potential energy surface (PES) and/or nonadiabatically (via intersystem crossing, ISC) on the singlet PES, undergoing unimolecular decomposition to a variety of bimolecular product channels. In recent years, this picture has been documented in several multichannel nonadiabatic reactions of O(3P) with 2C, 3C, and 4C UHs, such as ethylene,16–19 propene,20 propyne,21,22 allene,23,24 1-butene,25 1,2-butadiene,26 and AHs, such as benzene,27,28 by combining, in a synergistic fashion, crossed-molecular-beam (CMB) experiments with theoretical calculations of the underlying triplet/singlet PESs and statistical calculations of product branching fractions (BFs), taking into account ISC. The theoretical and experimental predictions20,28 were found to be in good agreement also with several kinetic studies on various O(3P) reactions with UHs using product detection by ionization with tunable vacuum ultraviolet synchrotron radiation.29,30 The capability of the developed model to reconcile CMB and kinetic thermal experiments, which differ significantly for operative conditions, supported the theoretical foundations of the model and allowed us to obtain a qualitative interpretation of the reactive dynamics of these systems that we used to develop rate rules for the whole O(3P) + alkene reaction class.31 According to this model, the reactivity is started on the triplet PES by oxygen addition to form an adduct, which can then decompose (but not isomerize) or perform ISC to the singlet PES, and then dissociate, isomerize, or undergo collisional stabilization. Recently, Ramasesha et al.32 found that this reaction mechanism is not adequate to predict the reactivity of cyclopentene with O(3P), as they found evidence that ISC does not take place from the entrance well, but from an isomer formed after ring opening and H-transfer on the triplet PES. The authors suggested that this peculiar reactivity could be due to the cyclic nature of the reactant. We believe that this is a reasonable explanation, as ring opening should have a rate constant similar to that of other bond breaking reactions that take place on the triplet PES for other O(3P) + alkene systems we have studied, such as for example in propene + O(3P), the pathway leading to the formation of H2CO + CH3CH.33 Following ring opening, it is then possible that other isomerization reactions on the triplet PES become competitive with ISC.
In the present work, we apply the synergistic experiment–theory approach we developed for this class of reactions to the study of the O(3P) + 1,3-butadiene reaction, a system of interest for atmospheric and combustion kinetics both from a fundamental and an applied perspective. From a fundamental standpoint, 1,3-butadiene is the simplest alkene with two conjugated double bonds. It can thus serve as a prototype to study the kinetics of O(3P) + alkene with conjugated dienes. In this respect, it will be interesting to check whether the simple reaction scheme we proposed for the O(3P) + alkene reaction class can be extended to this system. From an application perspective, an accurate knowledge of 1,3-butadiene reaction chemistry is necessary to further develop models of PAHs and soot formation. It is in fact known that 1,3-butadiene is a significant intermediate towards the formation of large hydrocarbons during the combustion of olefins in flames.5,34–38 Furthermore, it is also among the possible precursors to benzene formation through several addition reactions of C2 to C4 hydrocarbons.39–42 1,3-butadiene is also an air pollutant due to its toxic nature.43,44 Although the primary use of 1,3-butadiene is the production of synthetic rubber, it is nevertheless found in ambient air in urban and suburban areas as a consequence of its emission from motor vehicles, both from its presence in fuels and as a combustion product.6,8,45
Because of its relevance, the O(3P) + 1,3-butadiene global reaction kinetics have been extensively studied at room and higher temperatures (k{298K} ≈ 2 × 10−11 cm3 per molecule per s).46–51 However, little is known about the nature of its primary products and BFs. In 2000, Laskin et al.52 did a kinetic modeling experiment on the oxidation of 1,3-butadiene and suggested that the main channels of this reaction are the elimination of atomic and molecular hydrogen, as well as the formation of CO and H2CO (formaldehyde). However, combustion models of 1,3-butadiene flames were still not satisfactory because of the lack of detailed knowledge about the nature of the possible primary products and their BFs as a function of temperature. In 2018, Zhou et al.7 performed a detailed chemical kinetic mechanism (AramcoMech 3.0) and experimental study of 1,3-butadiene combustion over a wide range of temperature, pressure, and equivalence ratios. They found that O(3P) addition to 1,3-butadiene greatly influences the fuel reactivity from intermediate to high temperatures (>800 K). However, in the mechanism, the O(3P) + 1,3-butadiene reaction kinetics were derived by analogy with those of O(3P) + propene.20 Thus, three possible product channels were considered: H + C3H5O, H2CO + C3H4, and C2H3 (vinyl) + CH2CHO (vinoxy), with H elimination being the minor channel and the vinoxy radical formation the main one. A sensitivity analysis showed that this reaction, and in particular the reaction channel leading to H2CO + C3H4, is the most important in inhibiting ignition delay times at temperatures higher than 950 K. The reason is that this pathway acts as a chain termination reaction, while the other two are branching steps, as they lead to the formation of two radicals. The proper determination of the partition of the reactive flux between termination and branching pathways therefore plays a central role in determining the reaction kinetics of this system.7,52 In this framework, the aim of this paper is to investigate the O(3P) + 1,3-butadiene reaction with the intent of understanding its chemical dynamics and determining BFs and rate constants that can be used for future kinetic simulations of systems in which this reaction plays an important role.
The paper is organized as follows. In section 2, we describe the experimental and theoretical methods adopted to investigate the title reaction. In section 3, we first report the PES that we used to interpret the reactivity of this system, followed by the experimental results, and the results of the ME simulations in CMB conditions and as a function of temperature. A general discussion of the results is given in the Master equation section, before the conclusions.
2. Methods
2.1 Experimental technique
The experiments were carried out using a CMB apparatus featuring two supersonic beam sources of the reactants crossing at 90°, a rotatable quadrupole mass spectrometer detector with both hard (70 eV) and soft (17 eV) electron ionization, and a real-time TOF (time-of-flight) system for reactants and products. The apparatus has been described in some detail elsewhere.21,53–57 For the present study, the atomic oxygen beam was generated using a supersonic beam source53,58,59 in which a 5% O2/He gas mixture, at a pressure of 8.5 kPa (85 mbar), was discharged through a 0.48 mm diameter water-cooled quartz nozzle at 300 W of RF power, followed by a 1.0 mm diameter boron nitride skimmer and a further collimating aperture. The atomic oxygen beam mainly contains O(3P) and a small amount of O(1D) (≤10%).59 Under the present experimental conditions, the reactive scattering is expected to be dominated by O(3P) (see the ESI†). The molecular beam of 1,3-butadiene was obtained by expanding 57.3 kPa (573 mbar) of the neat gas (99.3% gas purity) through a 0.1 mm diameter stainless-steel nozzle, followed by a 0.8 mm skimmer, and a further defining aperture. In these conditions, the reactant velocities were 2180 and 715 m s−1, with speed ratios of 4.7 and 5.9 for the oxygen and 1,3-butadiene beams, respectively. The resulting collision energy was 32.6 kJ mol−1. Product laboratory angular distributions at selected mass-to-charge (m/z) ratios were acquired by modulating the 1,3-butadiene beam at 160 Hz for background subtraction. Product TOF distributions were measured by the pseudo-random chopping method at 6 μs per channel.Quantitative information on the reaction dynamics was derived from the raw data by moving from the laboratory (LAB) to the center-of-mass (CM) coordinate systems and by analyzing the product angular, T(θ), and translational energy, 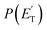 , distributions into which the CM product flux can be factorized.55,57 The best-fit CM functions were derived from the forward convolution fit of the total product LAB angular, N(θ), and TOF distributions, N(θ, t), at a specific mass-to-charge (m/z) ratio value, according to the relation:
, distributions into which the CM product flux can be factorized.55,57 The best-fit CM functions were derived from the forward convolution fit of the total product LAB angular, N(θ), and TOF distributions, N(θ, t), at a specific mass-to-charge (m/z) ratio value, according to the relation: 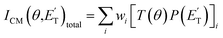 . As described elsewhere,57 the best-fit values of wi allow the derivation of the relative yields of the different channels. It should be noted that with this technique, in which the number density of the scattered products is detected, heavy and thus slow products in the CM system, which are left by a light co-product (such as a H atom), are strongly amplified in the LAB system because of the favorable Jacobian transformation which relates the LAB number density N(θ,v) to the CM flux I(θ,u) through the relation N(θ,v) = ICM(θ,u)v/u2, where v and u and the LAB and CM product velocity, respectively. During the data analysis, the quantity ICM(θ,u)total is usually expressed in terms of the product translational energy,
. As described elsewhere,57 the best-fit values of wi allow the derivation of the relative yields of the different channels. It should be noted that with this technique, in which the number density of the scattered products is detected, heavy and thus slow products in the CM system, which are left by a light co-product (such as a H atom), are strongly amplified in the LAB system because of the favorable Jacobian transformation which relates the LAB number density N(θ,v) to the CM flux I(θ,u) through the relation N(θ,v) = ICM(θ,u)v/u2, where v and u and the LAB and CM product velocity, respectively. During the data analysis, the quantity ICM(θ,u)total is usually expressed in terms of the product translational energy, 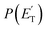 , as
, as 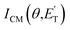 .
.
2.2 Theoretical methods
The system reactivity was investigated using the ab initio transition state theory-based master equation methodology60 we have used in recent years to study several reactions of addition of O(3P) to unsaturated hydrocarbons20–22,25,26,33 and benzene.27,28 This computational procedure is composed of three steps: investigation of the PES through electronic structure calculations, determination of the rate constants of elementary steps using the form of transition state theory (TST) that is most suitable for the specific reaction channel (variational or conventional), and determination of rate constants, solving the master equation. Details are reported below for each step.The C4H6O PES was investigated by determining the structures of the stationary points (wells and saddle points) at two levels of theory. At the lowest level of theory (Level 0), a preliminary scan of all relevant wells and reaction channels was performed using the ωB97X-D functional61 and the 6-311+G(d,p) basis set. Structures were then refined at the ωB97X-D/aug-cc-pVTZ level (Level 1), which is also used to compute Hessians. When necessary, such as, for example, for O(3P) addition to the terminal carbon atom of 1,3 butadiene, structures and energies along the minimum energy paths (MEPs) were determined at Level 1 of theory. This was, however, not the case for barrierless reactions, for which MEP structures were determined at the CASPT2 level. Energies were computed at two levels of theory. For stationary points with single reference character (generally with T1 diagnostic values smaller than 0.03), high level energies (HL) were determined on Level 1 structures at the CCSD(T) level corrected with a density fitted (DF) MP2 extrapolation to the complete basis set (CBS) and with corrections for core electron excitations as:
| E(HL) = E(CCSD(T)/aug-cc-pVTZ) + [E(CCSD(T,core)/cc-pVTZ) − E(CCSD(T)/cc-pVTZ)] + [E(DF-MP2/CBS) − E(DF-MP2/aug-cc-pVTZ)] | (1) |
| E(DF-MP2/CBS) = E(DF-MP2/aug-cc-pVTZ)] + 0.58[E(DF-MP2/aug-cc-pVQZ) − E(DF-MP2/aug-cc-pVTZ)]. | (2) |
The E(MP2/CBS) extrapolation was performed using Martin’s two parameter scheme.62 For systems with high multireference character, energies were computed at the CASPT2/aug-cc-pVTZ level on Level 1 structures using active spaces (AS) selected to include all orbitals and electrons directly involved in the reactive process. More specific details on the adopted active spaces are reported in the Results section. The minimum energy crossing point (MECP) between triplet and singlet PESs was determined at Level 1 of theory using the methodology recently implemented in EStokTP.28,63 All Level 0 and Level 1 electronic structure calculations were performed with Gaussian 09,64 while DF-MP2, CCSD(T), and CASPT2 calculations were performed with Molpro.65
Rate constants for reactions passing from a distinct transition state (TS) were evaluated using conventional TST, with partition functions determined in the rigid rotor harmonic oscillator (RRHO) approximation. Internal torsional motions were described using the 1D hindered rotor (HR) approximation, computing the associated partition functions from the 1D-HR eigenvalues. Vibrational frequencies were then computed after projecting the torsional motion from the Hessian. Rate constants for seven barrierless reactions on the singlet PES were determined using variable reaction coordinate TST (VRC-TST).66 A dedicated publication on the reactivity of the singlet PES and the implementation of VRC-TST in EStokTP is in preparation, which will report specific details on the study of these barrierless reactions. Here, we only mention that the VRC-TST stochastic scan of the 6 dimensional space defined by the transitional coordinates was performed at the CASPT2(2e,2o)/cc-pVDZ level using correction potentials for geometry relaxation and energy determined along the MEP on structures optimized at the CASPT2 level with large ASs (inclusive of all π bonding and antibonding orbitals and of the σ and σ* orbitals of the breaking bond) and with energies determined with the same AS and the aug-cc-pVTZ basis set. A standard 0.9 correction factor for recrossing was used to scale the VRC-TST rate constants. The rate constant for ISC from the triplet to the singlet PES was determined from the MECP using non adiabatic TST (NA-TST)67 as implemented in EStokTP63 using Level 1 singlet and triplet Hessians. ISC probabilities were computed using Landau–Zener theory.68 Spin–orbit couplings (SOC) between singlet and triplet PESs were determined using a Breit-Pauli Hamiltonian with Molpro.65 The three components of the coupling matrix computed with symmetry adapted wave functions were then square root averaged to compute a single SOC, which was then adopted for the determination of the ISC probabilities.
Master equation (ME) simulations were performed using our stochastic MC-RRKM code,69,70 which implements NA-TST and is therefore able to account explicitly for the coupling between the singlet and triplet PESs. Two distinct ME simulations were performed, depending on whether the triplet PES is accessed from addition to the terminal or central C atoms. The branching fraction for addition at the terminal and central carbon atoms for CMB simulations was determined at 300 K, thus implicitly assuming that the energy of the beam does not contribute to the density of states (DOS) at the TS. A total of 104 stochastic simulations was performed for each examined condition. Thermal simulations were performed in the 300–2200 K and 0.1–10 bar temperature and pressure ranges, respectively, in an Ar thermal bath. The intermolecular collisional energy transfer was calculated with Lennard-Jones collisional rates using σ = 4.21 Å and ε = 331 K average Lennard-Jones parameters and a single exponential down model with an average downward energy computed as ΔEdown = 395(T/300)0.49 cm−1, determined following the procedures suggested by Jasper.71
3. Results and discussion
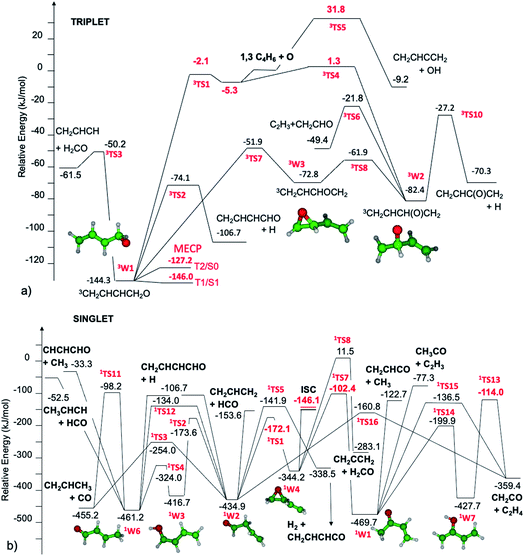
3.1 Potential energy surface
The triplet and singlet potential energy surfaces determined theoretically and then used to investigate the reactivity that follows the addition of O(3P) to 1,3-butadiene are shown in Fig. 1a and b, respectively.The initial step of the O(3P) + 1,3-C4H6 reaction is O(3P) addition on the triplet PES to the terminal or central carbon atom. Depending on the entrance well, the reactive system evolves along two different pathways. Oxygen addition to the 1,3-C4H6 terminal carbon atom leads to the formation of 3W1. The energy barrier, −2.1 kJ mol−1, is slightly submerged with respect to the reactants. It should be noted that, differently from what was found for the reactions between O(3P) and alkenes, there is no barrier if calculations are performed at the ωB97X-D/aug-cc-pVTZ level, both if energies are computed at the ωB97X-D and CCSD(T) levels. However, this is not the case when energies are computed on ωB97X-D structures at the CASPT2 level using a (8e,7o) active space formed by the oxygen (4e,3o) p electrons and orbitals and the (4e,4o) π and π* bonding and antibonding orbitals of 1,3-butadiene in Fig. 1. The significant impact of the theoretical level used for the calculations on the estimated energy barriers (or lack thereof) for the entrance channels is a consequence of the multireference nature of O(3P) addition to alkenes, as described by Sabbah et al. in a seminal paper.72 The CASPT2 barrier height is about 3 kJ mol−1 from the entrance van der Waals well, which is common to both addition channels and lies about 5.3 kJ mol−1 below the reactants. Four reaction channels are possible for 3W1: decomposition to H2CO and the 3CH2CHCH diradical, H β-scission to form the CH2CHCHCHO radical, isomerization to the 3W3 oxirane well, and ISC to the singlet PES. There are interesting similarities and differences with respect to the reaction mechanisms of O(3P) with alkenes. The bond breaking reactions leading to H2CO and H formation are quite similar to those we observed for propene.20 The energy barrier for H2CO formation from 3W1 (94 kJ mol−1) is slightly higher than that found for propene (81 kJ mol−1), while those for H β-scission are similar (69.9 vs. 61.9 kJ mol−1). The most notable difference is the isomerization reaction pathway by which 3W1 can be converted to the oxirane diradical well 3W3, which can then further isomerize to 3W2. The existence of a relatively fast isomerization pathway between the two entrance wells 3W1 and 3W2 is related to the presence of the conjugated π bonds, which allow the formation of the relatively stable intermediate well 3W3. As will be discussed in section 3.3, this pathway is of particular relevance for what concerns O(3P) addition to the central carbon atom. Similarly to what was found for alkenes, the structure of the MECP between the triplet and singlet PESs is near that of the entrance well. Differently from what was found for alkenes, the T2/S0 and T1/S1 energies differ substantially by about 20 kJ mol−1, while the SOCs are similar: 31.2 and 36.8 cm−1, respectively. This means that ISC will take place much faster from the T1 electronic state than from the T2 state. Following ISC, it is reasonable to expect rapid S1/S0 internal conversion.
Oxygen addition to the 1,3-C4H6 central carbon atom leads to the formation of 3W2. The small energy barrier for addition, 1.3 kJ mol−1 with respect to the reactants, means that addition to the terminal carbon is favored at low temperatures. It is interesting to notice that the HL energy barrier, 9.5 kJ mol−1, is much higher than the CASPT2 energy. This means that BFs for addition at the terminal and central carbon atoms differ substantially if computed using a single or multiple reference approach. The entrance well, 3W2, can evolve along three different reaction paths: H β-scission, decomposition to C2H3 + CH2CHO, and isomerization to 3W1 through 3W3. ISC to the singlet PES may also be possible, but according to our previous studies of alkene20 reactivity, this pathway is not competitive with the fast decomposition channels that can be accessed following addition to the central carbon atom. In particular, for this system, isomerization to 3W3 requires overcoming a small energy barrier, 20.5 kJ mol−1, thus indicating that this is a fast reaction pathway.
The singlet PES is accessed through ISC from 3W1. As shown in the PES diagram presented in Fig. 1b, we assume that the whole reaction flux going through ISC proceeds to the formation of the oxirane well 1W4. This is a simplification of what is likely to be the reactivity of this system following ISC. Detailed studies of ISC for O(3P) + C2H4 (ref. 17, 18 and 73) and O(3P) + C3H6 (ref. 20 and 30) have in fact shown that the diradical singlet formed upon ISC can follow three reaction pathways: isomerization to the oxirane well (1W4), to the aldehyde well (1W2) through H transfer, or formation of an unsaturated ketene upon H2 loss. The determination of the proper partition of the fluxes requires some complicated analysis of the reactivity of the intermediate species formed following ISC, which has strong multireference character and is, for the reasons explained above, in the S1 excited state. However, some specificities of this system indicate that it is reasonable to describe its reactivity assuming that the whole reaction flux goes to the 1W4 well. In fact, differently from what was found for propene20 and 1-butene,25 the two main pathways for the isomerization of 1W4, leading to 1W2 and 1W1, have very different energy barriers. The reason is that isomerization to 3-butenal (1W2) is favored over isomerization to methyl vinyl ketone (1W1) by the resonant stabilization of the TS. The two isomerization TSs for 1W4, 1TS1 and 1TS7, have strong diradical multireference character, with one radical centered on the oxygen atom and one on the carbon atom whose bond with oxygen is broken in the reactive process. It is this second radical, which is centered on the central carbon atom, that in 1TS1 can take advantage of resonance stabilization with the π bond of the spectator vinyl group, while this is not possible for 1TS7, where the radical is located on the terminal carbon atom. As a consequence, the energy barriers for 1TS1 and 1TS7 from 1W4, computed at the CASPT2/aug-cc-pVTZ level to properly describe their multireference character, are 172 and 242 kJ mol−1, respectively, thus indicating that the most favored reaction channel for 1W4 leads to the formation of 3-butenal (1W2). This reaction mechanism is well described by assuming that the whole ISC reactive flux leads to 1W4, as this well will eventually evolve to 1W2 and there is thus no need to account for the possible direct formation of 1W2 after ISC. The 3-butenal well 1W2 has two barrierless decomposition pathways to CH2CHCH2 + HCO and CH2CHCHCHO + H, which can eliminate CO to give C3H6, or isomerize to the 2-butenal 1W6 well through two pathways: directly through 1TS12 or via keto–enol tautomerization via1TS2 and 1TS4. The 2-butenal well 1W6 has three barrierless decomposition pathways to CH3CHCH + HCO, CH2CHCHCHO + H, and CH3 + CHCHCHO, and one elimination reaction leading to CO and C3H6. An alternative pathway suggested in the literature74 to lead to CO + C3H6, in which 2-butenal isomerizes to a ketene intermediate that then eliminates CO, has been investigated as well and was found to not be competitive with the pathways reported in Fig. 1b. The vinyl methyl ketone well 1W1, which is the minimum energy well among those considered in the present investigation, can be accessed from 1W4 and then further reacts though two barrierless decomposition channels, leading to C2H3 + COCH3 and C2H3CO + CH3, or decomposes to C2H4 + CH2CO through two pathways.
Additional details on the reactivity on the singlet PES, concerning in particular the AS used for CASPT2 calculations and details of VRC-TST calculations will be published in a companion paper on the study of the reactivity of 2-butenal, 3-butenal, and methyl vinyl ketone.
3.2 Experimental results
The energetically allowed primary product channels of the title reaction that have been experimentally observed in this work are listed below. The reaction enthalpies are those derived from the present electronic structure calculations (accuracy ±4 kJ mol−1) (see Fig. 1).| O(3P) + 1,3-C4H6 → CH2CHCHCHO + H, ΔH00 = −106.7 kJ mol−1 | (3) |
| → CH2CHCOCH2 + H, ΔH00 = −70.3 kJ mol−1 | (4) |
| → CH2CHCHCO + H2, ΔH00 = −338.5 kJ mol−1 | (5) |
| → C3H6 + CO, ΔH00 = −455.2 kJ mol−1 | (6) |
| → CH2CO + C2H4, ΔH00 = −359.4 kJ mol−1 | (7) |
| → C3H5 (allyl) + HCO, ΔH00 = −153.6 kJ mol−1 | (8) |
| → CH2CHO + C2H3, ΔH00 = −49.4 kJ mol−1 | (9) |
| → CH3CO + C2H3, ΔH00 = −77.4 kJ mol−1 | (10) |
| → H2CO + C3H4 (allene), ΔH00 = −283.3 kJ mol−1 | (11) |
| → H2CO + CH2CHCH, ΔH00 = −61.5 kJ mol−1 | (12) |
The CH3 elimination channels, leading to CH3 + CH2CHCO and CH3 + CHCHCHO, are also exothermic (ΔH00 = −122.6 and −33.5 kJ mol−1, respectively) (see Fig. 1); however, CH3 was found below detectable limits which, within our sensitivity, puts it at a BF ≤ 1–2%. The direct H abstraction forming OH is slightly exothermic (ΔH00 = −9.2 kJ mol−1), but has a barrier of 31.8 kJ mol−1 (Fig. 1a), which makes it negligible under our experimental conditions (see, for instance, Fig. 4a in section 3.3).
The velocity vector (so called “Newton”) diagram, describing the kinematics of the reactive system, is depicted in Fig. 2a. We detected reactive signal at mass-to-charge (m/z) ratios m/z = 69 (C4H5O+), 68 (C4H4O+), 43 (C2H3O+), 42 (C3H6+, CH2CO+), 41 (C3H5+), 30 (CH2O+), and 29 (HCO+). The measured relative intensities at the CM angle (θ = 48°) for these m/z values (at 17 eV) are 0.04, 0.21, 0.02, 0.14, 1.00, 0.12, and 0.13, respectively. The product LAB angular distributions, N(θ), were acquired only at m/z = 69, 68, 43, 42, 41 and 29; those at m/z = 68, 42, 41, and 29 are displayed in Fig. 2b, while the complete data set is reported in Fig. S1b† of the ESI. Exemplary TOF distributions at some selected LAB angles for m/z = 68, 42, 41, 30, and 29 are displayed in Fig. 2c (again, the complete TOF data set is reported in Fig. S2 and S3† of the ESI).
 | ||
| Fig. 2 (a) Velocity vector diagram for the O(3P) + 1,3-butadiene reaction (Ec = 32.6 kJ mol−1). The color-coded circles, concentric to the CM, delimit the maximum velocity that the indicated primary products can attain in the CM frame by assuming that all the available energy (given by Ec − ΔH00) is channeled into product translational energy. Eight product channels were identified: C4H5O + H (red), C4H4O + H2 (orange), C3H6 + CO (green), C3H5 + HCO (purple), CH2CO + C2H4 (green-olive), CH2CHO + C2H3 (pink), CH3CO + CH2CH (garnet), and H2CO + C3H4 (blue). (b) LAB product angular distributions N(θ) measured at m/z = 68, 42, 41, and 29. Experimental error bars indicate ±1σ. (c) Product TOF distributions measured for m/z = 68 (70 eV), 42 (17 eV), 41 (17 eV), 30 (70 eV), and 29 (17 eV) at the indicated LAB angles θ. The partial contributions of different products at the five masses are indicated. Note that the integrated signal at θCM = 48° (at 17 eV) for m/z = 41 is seven times larger than that for m/z = 42, and five times larger than that for m/z = 68, as reflected in the S/N of the spectra. In (b) and (c), the black line superimposed on the experimental data corresponds to the global best-fit calculated using the CM functions shown in Fig. 3. The distinct contributions to the calculated global N(θ) (b) and N(θ,t) (c) are colored coded as in (a), and indicated with the formula of the corresponding product. | ||
Most measurements were carried out by exploiting soft ionization at 17 eV electron energy, which was sufficient to suppress most of the interferences from the dissociative ionization processes of reactants and background gases; however, data at some masses were collected at both 70 eV and 17 eV for normalization purposes. The black continuous curves in Fig. 2b and c represent the global best-fit for the indicated m/z data, while the labeled color coded curves are the partial contributions from the various indicated products when using the best-fit CM product angular, T(θ), and translational energy,  , distributions reported in Fig. 3 for the eight characterized product channels. We describe below, separately, how the information on the dynamics of the eight detected channels was derived.
, distributions reported in Fig. 3 for the eight characterized product channels. We describe below, separately, how the information on the dynamics of the eight detected channels was derived.
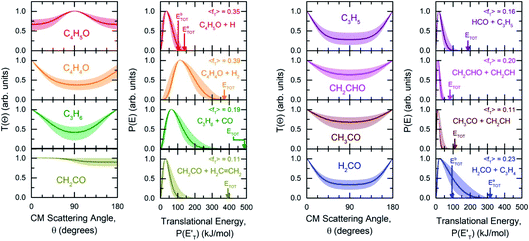 | ||
| Fig. 3 First and third panel (from left): best-fit CM angular distributions of C4H5O, C4H4O, propene (C3H6), and ketene (CH2CO), and of allyl (C3H5), vinoxy (CH2CHO), acetyl (CH3CO), and formaldehyde (H2CO), respectively. Second and fourth panel: best-fit CM translational energy distributions for each corresponding channel. Color coding is as in Fig. 2. The arrows indicate the total energy (ETOT) and <fT> the average translational energy fraction (referred to the most exothermic isomeric channel) determined for each reaction channel. The shaded areas represent the error bars determined for the best-fit CM functions. | ||
The facts that the co-product of C4H4O has a mass twice that of the co-product of C4H5O, and that the H2 channel (5) is much more exothermic and exhibits a much higher exit barrier than the H displacement channel(s) (3) and (4), are the characteristics which determine the broader angular distribution of C4H4O with respect to C4H5O in the LAB frame (see Fig. 2b) and its faster TOF distributions at the various LAB angles (see Fig. 2c). The large width of the C4H4O LAB angular distribution and the fast contribution to the TOF spectra determine the 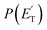 peaking much further away from zero and extending to much higher energies than the
peaking much further away from zero and extending to much higher energies than the 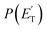 for the H forming channel, as can be clearly appreciated in Fig. 3. Notably, both channels exhibit a backward–forward symmetric T(θ) because both proceed via a long-lived complex mechanism,75–77 but with different dynamics, which are reflected in the shapes of the corresponding T(θ): that of C4H5O is in fact sideways distributed (see below), while that of C4H4O is polarized (see Fig. 3). It should be noted that the experimental data do not permit the quantification of the relative contribution of the two C4H5O isomer products (channels (3) and (4)), but theory can disentangle them because they involve different pathways along the triplet PES (see the Discussion section). It should be noted that the heavy co-products of the H and H2 channels are also observed at lower m/z ratios as daughter ions (see Fig. 2b and c, and the next section).
for the H forming channel, as can be clearly appreciated in Fig. 3. Notably, both channels exhibit a backward–forward symmetric T(θ) because both proceed via a long-lived complex mechanism,75–77 but with different dynamics, which are reflected in the shapes of the corresponding T(θ): that of C4H5O is in fact sideways distributed (see below), while that of C4H4O is polarized (see Fig. 3). It should be noted that the experimental data do not permit the quantification of the relative contribution of the two C4H5O isomer products (channels (3) and (4)), but theory can disentangle them because they involve different pathways along the triplet PES (see the Discussion section). It should be noted that the heavy co-products of the H and H2 channels are also observed at lower m/z ratios as daughter ions (see Fig. 2b and c, and the next section).
Concerning the N(θ) at m/z = 43 (see Fig. S1b†), the only possible product contributing to this mass, apart from the co-products of the H and H2 channels, is C2H3O+, which can be the only acetyl radical parent ion (CH3CO+), since it is known that vinoxy does not produce a stable parent ion (CH2CHO+) for electron energies >12 eV.55 Notably, acetyl was also observed in the isomeric reaction O(3P) + 1,2-butadiene.26 LAB angular distributions at m/z = 42 and 41 show a shape similar to that at m/z = 43 due to the large contribution of the H elimination channel (which is amplified in the LAB frame by a favorable CM → LAB Jacobian transformation54,57). However, in the m/z = 42 and 41 data, new reaction channels can also be identified, as demonstrated by the TOF distributions; in fact, these are very different from those recorded at m/z = 68, because, in addition to the slow peak due to the H and H2 co-products, they also exhibit fast, broad components that reflect more than one C–C bond breaking channel. In fact, the fast peak at m/z = 42 (Fig. 2c and S2†) is unambiguously attributed, by energy and momentum conservation, to the propene product from channel (6), detected at its parent ion. Furthermore, the reactive signal between this fast peak and the C4H5O peak is attributed in a larger part to the vinoxy radical from channel (9), detected at its main (daughter) ion mass, and in a smaller part to ketene, detected at its parent ion mass, from channel (7). The occurrence of the propene channel (6) was also assessed through its (−1) daughter ion at m/z = 41 as a fast shoulder superimposed on a rather broad, slower peak centered at around 180 μs (see Fig. 2c). This peak cannot originate from the dissociative ionization of vinoxy and ketene, because the signal intensity at m/z = 41 is about seven times larger than that at m/z = 42, and ketene and vinoxy fragment little to the (−1) daughter ion at 17 eV (less than 30% at 70 eV). This important feature is rather attributed to the parent ion of the allyl radical (C3H5) from reaction channel (8) (C3H5 + HCO). Allyl is known to fragment little at 17 eV.55,78
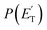 , distributions for the eight detected channels are depicted in Fig. 3. As can be seen, the majority of the T(θ)s of the detected primary products are backward–forward symmetric in the 0–180° CM angular range, with varying degrees of polarization (depending on the product), and this indicates that the corresponding reactive channels proceed via a long-lived complex mechanism, or rather, the corresponding intermediate lifetime is longer than 5–6 rotational periods of the decomposing complex.75–77 Interestingly, the H elimination channel clearly presents a sideways distribution, indicating that this product is not formed on the same plane as the reactants (i.e., the reaction is not co-planar), but rather the atomic hydrogen is emitted perpendicularly to the plane of the heavy atoms,75–77 and this is corroborated by the theoretical calculations of the TS geometries (see Fig. S5† in the ESI and the Discussion). In Fig. 3, the average translational energy fractions <fT> and the total available energy (ETOT), given by Ec − ΔH00, are also indicated for each channel. The high <fT> of 0.35 and 0.39 for the reaction channels (3, 4) and (5) (C4H5O + H and C4H4O + H2) reflect the presence of high exit energy barriers in the relevant triplet/singlet PESs (see Fig. 1) and are corroborated by theory (see the Discussion). The size of <fT> (<0.2) for the other channels indicates that the molecular/radical products are internally highly excited.
, distributions for the eight detected channels are depicted in Fig. 3. As can be seen, the majority of the T(θ)s of the detected primary products are backward–forward symmetric in the 0–180° CM angular range, with varying degrees of polarization (depending on the product), and this indicates that the corresponding reactive channels proceed via a long-lived complex mechanism, or rather, the corresponding intermediate lifetime is longer than 5–6 rotational periods of the decomposing complex.75–77 Interestingly, the H elimination channel clearly presents a sideways distribution, indicating that this product is not formed on the same plane as the reactants (i.e., the reaction is not co-planar), but rather the atomic hydrogen is emitted perpendicularly to the plane of the heavy atoms,75–77 and this is corroborated by the theoretical calculations of the TS geometries (see Fig. S5† in the ESI and the Discussion). In Fig. 3, the average translational energy fractions <fT> and the total available energy (ETOT), given by Ec − ΔH00, are also indicated for each channel. The high <fT> of 0.35 and 0.39 for the reaction channels (3, 4) and (5) (C4H5O + H and C4H4O + H2) reflect the presence of high exit energy barriers in the relevant triplet/singlet PESs (see Fig. 1) and are corroborated by theory (see the Discussion). The size of <fT> (<0.2) for the other channels indicates that the molecular/radical products are internally highly excited.
| Product channel | CMB expt. Ec = 32.6 kJ mol−1 | RRKM/ME Ec = 32.6 kJ mol−1 | RRKM/ME 300 K, 1 bar | RRKM/ME 1000 K, 1 bar |
|---|---|---|---|---|
| BF (%) | BF (%) | BF (%) | BF (%) | |
| CH2CHCHCHO + H | 6.2 ± 2.2 | 13.7 (T) | 5.5 (T) | 18.0 (T) |
| CH2CHCOCH2 + H | 2.2 (T) | 2.3 (T) | 8.6 (T) | |
| C4H4O + H2 | 1.8 ± 0.6 | — | — | — |
| C3H6 + CO | 20.2 ± 7.0 | 22.8 (S) | 19.4 (S) | 6.7 (S) |
| CH2CO + C2H4 | 6.9 ± 3.4 | — | — | — |
| C3H5 + HCO | 36.2 ± 12.0 | 44.4 (S) | 20.3 (S) | 19.0 (S) |
| CH2CHO + C2H3 | 9.5 ± 3.3 | 6.3 (T) | 6.3 (T) | 27.4 (T) |
| CH3CO + C2H3 | 0.4 ± 0.2 | 0.5 (S) | — | 0.4 (S) |
| H2CO + C3H4 | 18.6 ± 9.3 | 9.2 (T) | 1.9 (T) | 20.1 (T) |
As can be seen, the O(3P) + 1,3-butadiene reaction mainly leads to the formation of HCO + C3H5 (formyl + allyl, BF = 36.2 ± 12.0%) and CO + C3H6 (CO + propene, BF = 20.2 ± 7.0%). Other important products formed are formaldehyde + 3CH2CHCH (H2CO + C3H4, BF = 18.6 ± 9.3%), vinoxy + vinyl radicals (CH2CHO + C2H3, BF = 9.5 ± 3.3%), ketene + ethylene (CH2CO + C2H4, BF = 6.9 ± 3.4%), and the atomic hydrogen displacement channel (C4H5O + H, BF = 6.2 ± 2.2%). Minor channels are the formation of molecular hydrogen (C4H4O + H2, BF = 1.8 ± 0.6%), as well as the formation of acetyl + vinyl radicals (CH3CO + C2H3, BF = 0.4 ± 0.2%). In Table 1, the experimental BFs are compared with the theoretical BFs calculated for the conditions of the CMB experiment: they will be discussed in the next section.
3.3 Master equation simulations and discussion
The BFs determined through ME simulations in CMB conditions are compared with experimental results in Table 1. On the whole, it can be noted that the agreement is quite good, with most of the calculated BFs falling within the uncertainty bounds of the experimental determinations. It is useful here to compare and discuss experimental measurements and theoretical predictions channel by channel and with respect to our previous investigations of the O(3P) + alkene reactions.20,25 The main reaction channels in CMB conditions are active on the singlet PES and lead to the formation of HCO + C3H5 and C3H6 + CO in a nearly 2 to 1 ratio (experimentally 1.8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.0, theoretically 1.9
1.0, theoretically 1.9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.0). These two reaction channels account for about 60% of the reactive flux and are both accessed after ISC from the 3-butenal well. It is important to note that a significant portion of this reaction flux comes from isomerization from 3W2 to 3W1 through 3W3 and successive ISC to the singlet PES. About 60% of the flux accessing the triplet PES from addition to the central carbon atom follows this reaction pathway. The agreement between experiments and theory is quite good. For the CO + C3H6 channel, the
1.0). These two reaction channels account for about 60% of the reactive flux and are both accessed after ISC from the 3-butenal well. It is important to note that a significant portion of this reaction flux comes from isomerization from 3W2 to 3W1 through 3W3 and successive ISC to the singlet PES. About 60% of the flux accessing the triplet PES from addition to the central carbon atom follows this reaction pathway. The agreement between experiments and theory is quite good. For the CO + C3H6 channel, the 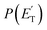 exhibits a late onset and peaks at 63 kJ mol−1, which indicates the presence of a significant exit barrier. This is corroborated by theory, which indeed finds a very significant exit energy barrier (1TS3) of ∼200 kJ mol−1 with respect to the products (Fig. 1b). The symmetric T(θ) is indicative of a long-lived complex mechanism, consistent with the large stability of 1W2. In contrast, the dominant radical channel C3H5 + HCO, which has a similarly polarized, symmetric T(θ), exhibits a
exhibits a late onset and peaks at 63 kJ mol−1, which indicates the presence of a significant exit barrier. This is corroborated by theory, which indeed finds a very significant exit energy barrier (1TS3) of ∼200 kJ mol−1 with respect to the products (Fig. 1b). The symmetric T(θ) is indicative of a long-lived complex mechanism, consistent with the large stability of 1W2. In contrast, the dominant radical channel C3H5 + HCO, which has a similarly polarized, symmetric T(θ), exhibits a 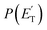 which rises very quickly and peaks at a very low energy (∼17 kJ mol−1) and dies off at less than one half of the total available energy, with only 16% of the available energy released in product translation, a feature expected for the barrierless decomposition of the intermediate 1W2.
which rises very quickly and peaks at a very low energy (∼17 kJ mol−1) and dies off at less than one half of the total available energy, with only 16% of the available energy released in product translation, a feature expected for the barrierless decomposition of the intermediate 1W2.
The reactions leading to H loss take place on the triplet PES and are expected, according to theoretical calculations, to account for about 16% of the reactive flux. This is higher than the BF found experimentally for this channel (6.2 ± 2.2%). This difference in BFs for the H channels was also found in our investigations of the O(3P) + 1-butene and O(3P) + propene reactions.20,25 In both these studies, it was attributed to a non-RRKM behavior of this reaction channel, determined probably by a slow rate of thermalization of the C–H stretching modes of the methylene group following terminal O addition. Apart from the difference in the BFs, there is good agreement between the calculated structures and energy barriers of the TSs and experimental evidence. The best-fit T(θ) for the C4H5O product exhibits a pronounced sideways peaking, which indicates that the H atom is emitted orthogonally to the plane of the molecular intermediate at 3TS2 (also at 3TS10), and the best-fit 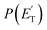 peaks away from zero, at about 34 kJ mol−1, which is consistent with the high exit barriers from both 3W1 and 3W2, and extends up to about 135 ± 10 kJ mol−1. This is well matched by the total available energy for channel (3) (135.1 kJ mol−1), given by the sum of the reaction ΔH00 (102.5 kJ mol−1) and the collision energy (32.6 kJ mol−1). The high average fraction of total available energy released in translation (<fT>= 0.34, referring to channel (3)) reflects, in fact, a high exit potential barrier that the theory finds of 32.5 kJ mol−1 for channel (3) and 43.1 kJ mol−1 for channel (4), with respect to products (Fig. 1a). The sideways dynamics for H emission from transition state 3TS2 (and also 3TS10) are corroborated by the calculated structure of 3TS2 and 3TS10, which show that the direction of the departing H atom is about orthogonal to the molecular plane (see Fig. S5† in the ESI).
peaks away from zero, at about 34 kJ mol−1, which is consistent with the high exit barriers from both 3W1 and 3W2, and extends up to about 135 ± 10 kJ mol−1. This is well matched by the total available energy for channel (3) (135.1 kJ mol−1), given by the sum of the reaction ΔH00 (102.5 kJ mol−1) and the collision energy (32.6 kJ mol−1). The high average fraction of total available energy released in translation (<fT>= 0.34, referring to channel (3)) reflects, in fact, a high exit potential barrier that the theory finds of 32.5 kJ mol−1 for channel (3) and 43.1 kJ mol−1 for channel (4), with respect to products (Fig. 1a). The sideways dynamics for H emission from transition state 3TS2 (and also 3TS10) are corroborated by the calculated structure of 3TS2 and 3TS10, which show that the direction of the departing H atom is about orthogonal to the molecular plane (see Fig. S5† in the ESI).
The fourth channel in the order of relevance predicted by the ME simulations is that leading to formaldehyde + vinylmethylene (channel (12)). The agreement between simulations and experimental BFs is reasonable, with the theoretical results (9.2%) underestimating the experimental determination (18.6 ± 9.3%), but within the lower limit of its uncertainty. This difference is similar to what was found in our study of O(3P) + propene,20 while experiments and theory were in good agreement for the O(3P) + 1-butene system.25 We note that the derived 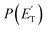 peaks at about 20 kJ mol−1 (Fig. 3), which reflects a relatively small exit barrier, consistent with the formation of H2CO + 3CH2CHCH on the triplet PES from 3W1 (Fig. 1a). However, the
peaks at about 20 kJ mol−1 (Fig. 3), which reflects a relatively small exit barrier, consistent with the formation of H2CO + 3CH2CHCH on the triplet PES from 3W1 (Fig. 1a). However, the 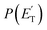 extends up to about 250 ± 70 kJ mol−1, which is beyond the total available energy of channel (12), whose ETOT is ∼95 kJ mol−1. The experiments appear then to suggest that not all of the H2CO channel originates from the triplet PES, but a fraction of it could originate from a more exoergic pathway, as that on the singlet PES, after ISC, leading to H2CO + CH2CCH2 (allene) (channel (11)) (see Fig. 1b). Notably, comparable fractions of H2CO produced on the triplet PES were also observed in the reactions of O(3P) with ethylene,19 allene,23 propene,20 1-butene,25 and 1,2-butadiene.26
extends up to about 250 ± 70 kJ mol−1, which is beyond the total available energy of channel (12), whose ETOT is ∼95 kJ mol−1. The experiments appear then to suggest that not all of the H2CO channel originates from the triplet PES, but a fraction of it could originate from a more exoergic pathway, as that on the singlet PES, after ISC, leading to H2CO + CH2CCH2 (allene) (channel (11)) (see Fig. 1b). Notably, comparable fractions of H2CO produced on the triplet PES were also observed in the reactions of O(3P) with ethylene,19 allene,23 propene,20 1-butene,25 and 1,2-butadiene.26
The main channel on the triplet PES arising from addition to the terminal carbon atom is that leading to vinoxy + vinyl, for which both experiments and theory are in good agreement (see Table 1). The corresponding 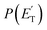 peaks at ∼13 kJ mol−1, which is consistent with the calculated exit barrier, and reflects an average fraction of energy in product translation of ∼20%. With the T(θ) being symmetric, this channel also proceeds via a long-lived complex mechanism.
peaks at ∼13 kJ mol−1, which is consistent with the calculated exit barrier, and reflects an average fraction of energy in product translation of ∼20%. With the T(θ) being symmetric, this channel also proceeds via a long-lived complex mechanism.
The most significant difference between experiment and theory concerns the CH2CO + C2H4 molecular channel, for which the experimental BFs (6.9 ± 3.4%) are much larger than those computed theoretically for this reaction. This suggests that it is possible that a reaction path that we could not find despite an extensive PES investigation is missing from those reported in Fig. 1.
Experimental evidence was also found for two other minor channels, leading to H2 + C4H4O (vinylketene) and CH3CO + C2H3 formation. While the latter’s experimental BFs are well predicted by theory, this is not the case for the H2 channel (see Table 1). This may be due to the simplified form of the PES used in the ME simulations, in which we did not investigate in detail the reaction dynamics that follow ISC. In our previous study of O(3P) + propene,20 we had in fact found that some molecular hydrogen can be produced through elimination from the diradical complex formed upon ISC.
Finally, the extent of ISC in O(3P) + 1,3-butadiene, estimated experimentally and theoretically in CMB conditions, amounts to about 66 ± 20% and 67%, respectively. This is not surprising considering that the extent of ISC in other O(3P) reactions, at comparable Ecs with unsaturated 4C hydrocarbons, such as 1-butene25 and 1,2-butadiene,26 is about 50% and 70%, respectively. Notably, ISC is about 50% in O + ethylene19 and about 90% in O + allene.23
The product distribution is different from what was observed in any of the four-carbon atom systems so far investigated, namely O + 1-butene25 and O + 1,2-butadiene,26 at comparable Ecs. In O + 1-butene, the CO channel was not observed, while HCO formation, although not the minor channel, was detected in a smaller amount (BF = 17%). On the other hand, in O + 1,2-butadiene,26 the CO channel was detected as the main channel (BF = 49%) while HCO formation was the minor channel and was almost negligible (BF = 1%). Even if the three hydrocarbons (1-butene, 1,2-butadiene, and 1,3-butadiene) present different structures, some similarities would be expected in their product BFs. However, the results for 1,3-butadiene seem closer to those observed for the reaction of 1-butene25 than 1,2-butadiene.26 This is reasonable, since with two non-consecutive double bonds, the reactivity of 1,3-butadiene will be more similar to that of a molecule with only one terminal unsaturated bond.
Master equation simulations were finally performed in thermal equilibrium conditions in order to determine the temperature and pressure dependent rate constants to be used for the kinetic modeling of this system. Simulations were performed in the 300–2200 K temperature range at 0.1, 1, and 10 bar. The calculated total rate constants are reported in Fig. 4a, together with the contributions for terminal and central addition and for H abstraction. The rate constants calculated as a function of temperature at 1 bar for the most relevant channels are reported in Fig. 4b, while those calculated at 0.1 and 10 bar are reported in the ESI.† It is found that the extent of ISC decreases with the increase of the temperature from 84% at room temperature to 26% at 1000 K and 1 bar. At 1000 K, the main termination channels lead to H2CO + CH2CHCH and CO + C3H6 formation and account for about 27% of the reactive flux, while the H + C4H5O and HCO + C3H5 channels contribute about 20% each and the main reaction channel becomes C2H3 + CH2CHO. Collisional stabilization is important only at low temperatures and accounts for 44% of the reaction flux at 300 K and 1 bar, which decreases to 10% already at 500 K (see ESI†). At 10 bar and 500 K, collisional stabilization is still important, accounting for about 57% of the total reaction flux, which decreases to 24% at 750 K (see ESI†). It can thus be inferred that collisional stabilization can become relevant in combustion conditions at relatively low temperatures and only at pressures higher than 10 bar. The reason is that, since collisional stabilization is a termination reaction alternative to the HCO + C3H5 branching channel, it is possible that it may influence the system reactivity, such as, for example, high pressures delay ignition times, to some extent.
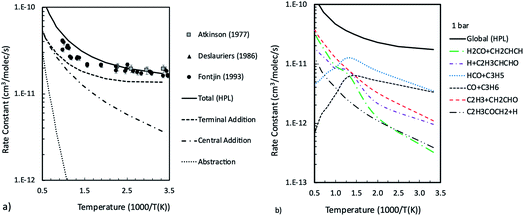 | ||
| Fig. 4 Total rate constants for the O(3P) + 1,3-butadiene reaction compared with experimental data48,50,51 and contributions of addition to central and terminal carbon atoms and abstraction (a), and channel specific rate constants computed as a function of temperature at 1 bar (b). | ||
4. Conclusion
The dynamics of the O(3P) + 1,3-butadiene reaction were investigated through a synergic experimental and theoretical approach, finding a good agreement between CMB results and statistical calculations of the product BFs. It was found that the reaction kinetics for this system are rich, with many active channels with relevant BFs both on the singlet and the triplet PESs. The main reaction channels lead to the formation of HCO + C3H5 and CO + C3H6, which account for about 60% of the total reactive flux both experimentally and theoretically, followed by H + C4H5O, H2CO + CH2CHCH, and C2H3 + CH2CHO. The ME simulations show that, differently from what was found for the O(3P) + alkene reaction class, isomerization reactions are active on the triplet PES when it is accessed through addition to the central carbon atom. The reason why this happens is that, because of the presence of two conjugated unsaturated bonds, it is possible for the adduct formed by oxygen and 1,3 butadiene upon addition to isomerize to form an oxirane triplet well, whose formation requires only a bond forming reaction, thus without any H transfer step involved. It seems thus that the reaction mechanism we proposed to interpret the reactivity of alkenes with atomic oxygen,31 according to which the reactivity on triplet PESs is governed by bond breaking reactions and ISC, should be extended to conjugated dienes to account for the scrambling of atomic oxygen between the possible addition sites. This mechanism thus favors the formation of the lowest energy triplet isomer. However, as simulations performed in thermal equilibrium show, when the temperature increases, the relevance of decomposition to C2H3 + CH2CHO increases correspondingly, as it becomes the dominant channel for oxygen addition to the central carbon atom. With respect to existing kinetic models of the O(3P) + 1,3-butadiene reaction, we find that in thermal conditions, in addition to the channels already included in existing models, the formation of HCO + C3H5 can also play a relevant role. The thermal simulations show that the system behavior as a function of temperature is characterized by low and high temperature regimes, with the first being dominated by ISC to the singlet PES and the second by the reactivity on the triplet PES. Interestingly, the transition between the two regimes takes place at about 1000 K, thus at a temperature that is of key relevance for combustion modeling. As rate constants in this transition regime assume a significant non-Arrhenius behavior, it will be interesting to test if and how this affects the oxidation kinetics of this system once the calculated channel-specific rate constants are introduced in kinetic models.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Financial support from Italian "Ministry of University and Research" (MUR) (PRIN 2017, MAGIC DUST, Prot. 2017PJ5XXX) is gratefully acknowledged. P. R., A. C., N. B., and P. C. acknowledge support also from the Italian MUR and the University of Perugia within the program “Department of Excellence-2018-2022-Project AMIS”.References
-
H. Schobert, Chemistry of Fossil Fuels and Biofuels, Cambridge University Press, Cambridge, UK., 2013 Search PubMed
.
- M. Frenklach, D. W. Clary, W. C. Gardiner and S. E. Stein, Symp. (Int.) Combust., [Proc.], 1988, 21, 1067–1076 CrossRef
.
-
W. C. Gardiner, Gas-Phase Combustion Chemistry, Springer, New York, 2000 Search PubMed
.
- K. Kohse-Höinghaus, P. Oßwald, T. A. Cool, T. Kasper, N. Hansen, F. Qi, C. K. Westbrook and P. R. Westmoreland, Angew. Chem., Int. Ed., 2010, 49, 3572–3597 CrossRef PubMed
.
- J. M. Simmie, Prog. Energy Combust. Sci., 2003, 29, 599–634 CrossRef CAS
.
- P. Zhao, W. Yuan, H. Sun, Y. Li, A. P. Kelley, X. Zheng and C. K. Law, Proc. Combust. Inst., 2015, 35, 309–316 CrossRef CAS
.
- C. W. Zhou, Y. Li, U. Burke, C. Banyon, K. P. Somers, S. Ding, S. Khan, J. W. Hargis, T. Sikes, O. Methieu, E. L. Petersen, M. AlAbbad, A. Farooq, Y. Pan, Y. Zhang, Z. Huang, J. Lopez, Z. Loparo, S. S. Vasu and H. J. Curran, Combust. Flame, 2018, 197, 423–438 CrossRef CAS
.
- W. K. Metcalfe, S. Dooley and F. L. Dryer, Energy Fuels, 2011, 25, 4915–4936 CrossRef CAS
.
- J. Yiguang and S. Wenting, Prog. Energy Combust. Sci., 2015, 48, 21–83 CrossRef
.
-
R. P. Wayne, Chemistry of Atmospheres: an Introduction to the Chemistry of the Atmospheres of Earth, the Planets, and their Satellites, Oxford University Press, Oxford, UK., 3rd edn, 2000 Search PubMed
.
-
A. M. Shaw, Astrochemistry: from Astronomy to Astrobiology, Wiley, 2007 Search PubMed
.
- A. G. G. M. Tielens, Rev. Mod. Phys., 2013, 85, 1021–1081 CrossRef CAS
.
- A. Occhiogrosso, S. Viti and N. Balucani, Mon. Not. R. Astron. Soc., 2013, 432, 3423–3430 CrossRef CAS
.
- M. Dobrijevic, E. Hebrard, J. C. Loison and K. M. Hickson, Icarus, 2014, 228, 324–346 CrossRef CAS
.
- L. M. Lara, E. Lellouch, M. Gonzales, R. Moreno and M. A. Rengel, Astron. Astrophys., 2014, 566, A143 CrossRef
.
- P. Casavecchia, G. Capozza, E. Segoloni, F. Leonori, N. Balucani and G. G. Volpi, J. Phys. Chem. A, 2005, 109, 3527–3530 CrossRef CAS PubMed
.
- B. Fu, Y.-C. Han, J. M. Bowman, L. Angelucci, N. Balucani, F. Leonori and P. Casavecchia, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 9733–9738 CrossRef CAS PubMed
.
- B. Fu, Y.-C. Han, J. M. Bowman, F. Leonori, N. Balucani, L. Angelucci, A. Occhiogrosso, R. Petrucci and P. Casavecchia, J. Chem. Phys., 2012, 137, 22A532 CrossRef PubMed
.
- N. Balucani, F. Leonori, P. Casavecchia, B. Fu and J. M. Bowman, J. Phys. Chem. A, 2015, 119, 12498–12511 CrossRef CAS PubMed
.
- F. Leonori, N. Balucani, V. Nevrly, A. Bergeat, S. Falcinelli, G. Vanuzzo, P. Casavecchia and C. Cavalloti, J. Phys. Chem. C, 2015, 119, 14632–14653 CrossRef CAS
.
- G. Vanuzzo, N. Balucani, F. Leonori, D. Stranges, V. Nevrly, S. Falcinelli, A. Bergeat, P. Casavecchia and C. Cavallotti, J. Phys. Chem. A, 2016, 120, 4603–4618 CrossRef CAS PubMed
.
- I. Gimondi, C. Cavallotti, G. Vanuzzo, N. Balucani and P. Casavecchia, J. Phys. Chem. A, 2016, 120, 4619–4633 CrossRef CAS PubMed
.
- F. Leonori, A. Occhiogrosso, N. Balucani, A. Bucci, R. Petrucci and P. Casavecchia, J. Phys. Chem. Lett., 2012, 3, 75–80 CrossRef CAS
.
- G. Vanuzzo, N. Balucani, F. Leonori, D. Stranges, S. Falcinelli, A. Bergeat, P. Casavecchia, I. Gimondi and C. Cavallotti, J. Phys. Chem. Lett., 2016, 7, 1010–1015 CrossRef CAS PubMed
.
- A. Caracciolo, G. Vanuzzo, N. Balucani, D. Stranges, P. Casavecchia, L. Pratali Maffei and C. Cavallotti, J. Phys. Chem. A, 2019, 123, 9934–9956 CrossRef CAS PubMed
.
- A. Caracciolo, G. Vanuzzo, N. Balucani, D. Stranges, S. Tanteri, C. Cavallotti and P. Casavecchia, Chin. J. Chem. Phys., 2019, 32, 113–122 CrossRef CAS
.
- C. Cavallotti, C. De Falco, L. P. Maffei, A. Caracciolo, G. Vanuzzo, N. Balucani and P. Casavecchia, J. Phys. Chem. Lett., 2020, 11, 9621–9628 CrossRef CAS PubMed
.
- G. Vanuzzo, A. Caracciolo, T. K. Minton, N. Balucani, P. Casavecchia, C. de Falco, A. Baggioli and C. Cavallotti, J. Phys. Chem. A, 2021, 125, 8434–8453 CrossRef CAS PubMed
.
- J. D. Savee, O. Welz, C. A. Taatjes and D. L. Osborn, Phys. Chem. Chem. Phys., 2012, 14, 10410–10423 RSC
.
- C. A. Taatjes, D. L. Osborn, T. Selby, G. Meloni, A. J. Trevitt, E. Epifanovsky, A. I. Krylov, B. Sirjean, E. Danes and H. Wang, J. Phys. Chem. A, 2010, 114, 3355–3370 CrossRef CAS PubMed
.
- L. Pratali Maffei, C. Cavallotti, A. Caracciolo, N. Balucani and P. Casavecchia, Fuel, 2020, 263, 116536 CrossRef CAS
.
- K. Ramasesha, J. D. Savee, J. Zádor and D. L. Osborn, J. Phys. Chem. A, 2021, 125, 9785–9801 CrossRef CAS PubMed
.
- C. Cavallotti, F. Leonori, N. Balucani, V. Nevrly, A. Bergeat, S. Falcinelli, G. Vanuzzo and P. Casavecchia, J. Phys. Chem. Lett., 2014, 5, 4213–4218 CrossRef CAS PubMed
.
- Y. Zhang, J. Cai, L. Zhao, J. Yang, H. Jin, Z. Cheng, Y. Li, L. Zhang and F. Qi, Combust. Flame, 2012, 159, 905–917 CrossRef CAS
.
- Y. Fenard, G. Dayma, F. Halter, F. Foucher, Z. Serinyel and P. Dagaut, Energy Fuels, 2015, 29, 1107–1118 CrossRef CAS
.
- M. Schenk, L. Leon, K. Moshammer, P. Osswald, T. Zeuch, L. Seidel, F. Mauss and K. Kohse-Hoinghaus, Combust. Flame, 2013, 160, 487–503 CrossRef CAS
.
- L. Ruwe, K. Moshammer, N. Hansen and K. Kohse-Hoinghaus, Combust. Flame, 2017, 175, 34–46 CrossRef CAS
.
- C.-W. Zhou, Y. Li, E. O’Connor, K. P. Somers, S. Thion, C. Keesee, O. Mathieu, E. I. Petersen, T. A. DeVerter, M. A. Oehlschlaeger, G. Kukkadapu, C.-J. Sung, M. Alrefae, K. Khaled, A. Farooq, P. Dirrenberger, P.-A. Glaude, F. Battin-Leclerc, J. Santner, Y. Ju, T. Held, F. M. Haas, F. L. Dryer and H. J. Curran, Combust. Flame, 2016, 167, 353–379 CrossRef CAS
.
- Z. J. Buras, E. E. Dames, S. S. Merchant, G. Liu, R. M. Elsamra and W. H. Green, J. Phys. Chem. A, 2015, 119, 7325–7338 CrossRef CAS PubMed
.
- Y. Li, C.-W. Zhou, K. P. Somer, K. Zhang and H. J. Curran, Proc. Combust. Inst., 2017, 36, 403–411 CrossRef CAS
.
- Y. Li, C.-W. Zhou and H. J. Curran, Combust. Flame, 2017, 181, 198–213 CrossRef CAS
.
- C. Huang, B. Yang and F. Zhang, Combust. Flame, 2017, 184, 167–175 CrossRef CAS
.
- R. L. Melnick and J. Huff, Rev. Environ. Contam. Toxicol., 1992, 124, 111–144 CAS
.
- US Environmental Protection Agency (EPA), Health Effects Notebook for Hazardous Air Pollutants: 1,3-butadiene, retrieved April 2020, https://www.epa.gov/haps/health-effects-notebook-hazardous-air-pollutants Search PubMed.
-
I. Kirshenbaum, Encyclopedia of Chemical Technology, John Wiley & Sons, New York, 3nd edn, 1978, vol. 4 Search PubMed
.
- J. J. Havel and K. H. Chan, J. Org. Chem., 1974, 39, 2439–2441 CrossRef CAS
.
- X. S. Nip, D. L. Singleton and R. J. Cvetanovic, Can. J. Chem., 1979, 57, 949–952 CrossRef
.
- R. Atkinson and J. N. Pitts Jr, J. Chem. Phys., 1977, 67, 2492–2495 CrossRef CAS
.
- K. Sugawara, Y. Ishikawa and S. Sato, Bull. Chem. Soc. Jpn., 1980, 53, 1344–1351 CrossRef CAS
.
- H. Deslauriers and G. J. Collin, Can. J. Chem., 1986, 64, 1925–1929 CrossRef CAS
.
- G. Y. Adusei and A. Fontijn, J. Phys. Chem., 1993, 97, 1406–1408 CrossRef CAS
.
- A. Laskin, H. Wang and C. K. Law, Int. J. Chem. Kinet., 2000, 32, 589–614 CrossRef CAS
.
- M. Alagia, N. Balucani, P. Casavecchia, D. Stranges and G. G. Volpi, J. Chem. Soc., Faraday Trans., 1995, 91, 575–596 RSC
.
- P. Casavecchia, Rep. Prog. Phys., 2000, 63, 355–414 CrossRef CAS
.
- P. Casavecchia, F. Leonori, N. Balucani, R. Petrucci, G. Capozza and E. Segoloni, Phys. Chem. Chem. Phys., 2009, 11, 46–65 RSC
.
- N. Balucani, G. Capozza, F. Leonori, E. Segoloni and P. Casavecchia, Int. Rev. Phys. Chem., 2006, 25, 109–163 Search PubMed
.
- P. Casavecchia, F. Leonori and N. Balucani, Int. Rev. Phys. Chem., 2015, 34, 161–204 Search PubMed
.
- S. J. Sibener, R. J. Buss, C. Y. Ng and Y. T. Lee, Rev. Sci. Instrum., 1980, 51, 167–182 CrossRef CAS
.
- M. Alagia, V. Aquilanti, D. Ascenzi, N. Balucani, D. Cappelletti, L. Cartechini, P. Casavecchia, F. Pirani, G. Sanchini and G. G. Volpi, Isr. J. Chem., 1997, 37, 329–342 CrossRef CAS
.
- S. J. Klippenstein and C. Cavallotti, Comput.-Aided Chem. Eng., 2019, 45, 115–167 CAS
.
- J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620 RSC
.
- J. M. L. Martin, Chem. Phys. Lett., 1996, 259, 669–678 CrossRef CAS
.
- C. Cavallotti, M. Pelucchi, Y. Georgievskii and S. J. Klippenstein, J. Chem. Theory Comput., 2019, 15, 1122–1145 CrossRef CAS PubMed
.
-
M. Frisch, et al., Gaussian 16, Revision C.01, 2016 Search PubMed
.
-
H.-J. Werner, et al., MOLPRO, version 2020.2, a package of ab initio programs, see E-mail: https://www.molpro.net, 2010 Search PubMed
.
- Y. Georgievskii and S. J. Klippenstein, J. Phys. Chem. A, 2003, 107, 9776–9781 CrossRef CAS
.
- J. N. Harvey, Phys. Chem. Chem. Phys., 2007, 9, 331–343 RSC
.
- C. Zener, Proc. R. Soc. London, Ser. A, 1932, 137, 696–702 Search PubMed
.
- A. Barbato, C. Seghi and C. Cavallotti, J. Chem. Phys., 2009, 130, 074108 CrossRef PubMed
.
- D. Polino and C. Cavallotti, J. Phys. Chem. A, 2011, 115, 10281–10289 CrossRef CAS PubMed
.
- A. W. Jasper, Int. J. Chem. Kinet., 2020, 52, 387–402 CrossRef CAS
.
- H. Sabbah, L. Biennier, I. R. Sims, Y. Georgievskii, S. J. Klippenstein and I. W. M. Smith, Science, 2007, 317, 102–105 CrossRef CAS PubMed
.
- X. Li, A. W. Jasper, J. Zádor, J. A. Miller and S. J. Klippenstein, Proc. Combust. Inst., 2017, 36, 219–227 CrossRef CAS
.
- J. Shu, D. S. Peterka, S. R. Leone and M. Ahmed, J. Phys. Chem. A, 2004, 108, 7895–7902 CrossRef CAS
.
-
R. D. Levine, Molecular Reaction Dynamics, Cambridge University Press, 2005 Search PubMed
.
- W. B. Miller, S. A. Safron and D. R. Herschbach, Discuss. Faraday Soc., 1967, 44, 108–123 RSC
.
- G. A. Fisk, J. D. McDonald and D. R. Herschbach, General discussion, Discuss. Faraday Soc., 1967, 44, 228–230 Search PubMed
.
- F. Leonori, N. Balucani, G. Capozza, E. Segoloni, D. Stranges and P. Casavecchia, Phys. Chem. Chem. Phys., 2007, 9, 1307–1311 RSC
.
- A. M. Schmoltner, P. M. Chu and Y. T. Lee, J. Chem. Phys., 1989, 91, 5365–5373 CrossRef CAS
.
- H. Pan, K. Liu, A. Caracciolo and P. Casavecchia, Chem. Soc. Rev., 2017, 46, 7517–7547 RSC
.
Footnote |
| † Electronic supplementary information (ESI) available: Crossed-beam experimental results for O(3P) + 1,3-butadiene, thermal rate constants (0.1, 1, 10 atm and 300–2200 K), master equation inputs. See DOI: 10.1039/d2fd00037g |
| This journal is © The Royal Society of Chemistry 2022 |