Open Access Article
Open Access ArticleCritical stresses in mechanochemical reactions†
Resham
Rana
a,
Nicholas
Hopper
a,
François
Sidoroff
b and
Wilfred T.
Tysoe
 *a
*a
aDepartment of Chemistry and Biochemistry, University of Wisconsin-Milwaukee, Milwaukee, WI 53211, USA. E-mail: wtt@uwm.edu
bLaboratoire de Tribologie et Dynamique des Systèmes, CNRS UMR5513, Ecole Centrale de Lyon, F-69134 Ecully Cedex, France
First published on 26th October 2022
Abstract
The rates of mechanochemical reactions are generally found to increase exponentially with applied stress. However, a buckling theory analysis of the effect of a normal stress on an adsorbate that is oriented perpendicularly to the surface that reacts by tilting suggests that a critical value of the stress should be required to initiate a mechanochemical reaction. This concept is verified by using density functional theory calculations to simulate the effect of compressing a homologous series of alkyl thiolate species on copper by a hydrogen-terminated copper counter-face. This predicts that a critical stress is indeed needed to initiate methyl thiolate decomposition, which has a perpendicular C–CH3 bond. In contrast, no critical stress is found for ethyl thiolate with an almost horizontal C–CH3 bond, while a critical stress is required to isomerize propyl thiolate from a trans to a cis configuration. These predictions are tested by measuring the mechanochemical reaction rates of these alkyl thiolates on a Cu(100) substrate by sliding an atomic force microscope tip over the surface and finding a critical stress of ∼0.43 GPa for methyl thiolate, ∼0.33 GPa for propyl thiolate, but no evidence of a critical stress for ethyl thiolate, in accord with the predictions. These results provide insights not only into mechanochemical reaction mechanisms on surfaces, but also on the origin of critical phenomena in stress-induced processes in general. It also suggests novel approaches to designing robust surface films that can resist wear and damage.
Introduction
Mechanochemical reactions have been known for many millennia; such a reaction was described by Theophrastus in his treatise “On Stones” ( ).1 Historically, the first theories of mechanically induced processes were developed to describe the energy dissipated during solid–solid sliding (friction),2–5 and liquid shear (viscosity).6,7 The physical principles that underpin these theories of mechanical energy dissipation also apply to mechanochemistry.5 Evans and Polanyi presented an early analyses of mechanochemical reaction rates8 by using transition-state theory to show that the pressure-dependent rate constant of a chemical reaction, k(P) could be written as
).1 Historically, the first theories of mechanically induced processes were developed to describe the energy dissipated during solid–solid sliding (friction),2–5 and liquid shear (viscosity).6,7 The physical principles that underpin these theories of mechanical energy dissipation also apply to mechanochemistry.5 Evans and Polanyi presented an early analyses of mechanochemical reaction rates8 by using transition-state theory to show that the pressure-dependent rate constant of a chemical reaction, k(P) could be written as 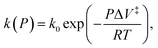 where k0 is the rate at zero pressure, P is the pressure and ΔV‡ is an activation volume and is broadly interpreted as the difference in volume between the reactant and transition states. If the reaction activation energy in the absence of an imposed stress is Eact0, and assuming that the pre-exponential factor is constant, the above equation is equivalent to writing Eact(F) = Eact0 + PΔV‡. This is commonly known as the Bell equation,9 and predicts that the stress-induced activation energy, and therefore the reaction rate, tends continuously to the zero-pressure value as the pressure decreases to zero. The following paper demonstrates that this is not always the cases and that situations exist in which there is a critical stress below which a mechanochemical reaction does not occur.
where k0 is the rate at zero pressure, P is the pressure and ΔV‡ is an activation volume and is broadly interpreted as the difference in volume between the reactant and transition states. If the reaction activation energy in the absence of an imposed stress is Eact0, and assuming that the pre-exponential factor is constant, the above equation is equivalent to writing Eact(F) = Eact0 + PΔV‡. This is commonly known as the Bell equation,9 and predicts that the stress-induced activation energy, and therefore the reaction rate, tends continuously to the zero-pressure value as the pressure decreases to zero. The following paper demonstrates that this is not always the cases and that situations exist in which there is a critical stress below which a mechanochemical reaction does not occur.
Fundamental mechanochemical experiments have been carried out by attaching a reactant (known as a mechanophore) to an atomic force microscopy (AFM) tip and measuring the force need to extend and finally cleave one or more bonds at some well-defined force reminiscent of the critical forces found here for sliding on an adsorbed monolayer, but with a different physical origin.10–17 Because of the ability to accurately measure the force acting directly on the mechanophore, this can lead to extremely precise measurements of force-induced bond scission rates, but which are often difficult to interpret because of the uncertainty in the way in which the force is exerted by the tip. More recently, mechanochemical reactions have been induced by sliding over adsorbate-covered surfaces16,18–26 where it is found that the decomposition of surface-anchored hydrocarbon species occurs by the adsorbate initially tilting towards the surface to weaken the bond and ultimately induce its cleavage to result in a mechanochemical reaction. The energetics of reaction pathways can be calculated using quantum mechanical methods27 so that, for example, it is found that methyl thiolate (CH3–S(ads)) overlayers adsorbed on copper react by the C–S bond tilting towards the surface to react to form adsorbed sulfur and to evolve small hydrocarbons.24,26–28 Similar reaction pathways occur for acetate species. Here, the mechanochemical reaction products depend on the direction of the applied stress relative to the carboxylate plane.20 Because of the molecular tilt, intuitively one might expect that either normal or lateral forces, or both, should, in principle, increase the reaction rate. It has been shown that normal stresses alone can induce methyl thiolate decomposition,29 and this work considers the combined effects of normal and lateral forces.
If we consider the simple phenomenological buckling of a vertical molecular adsorbate for which a chemical reaction is induced by a molecular tilt,30 an applied normal force F can cause an adsorbed molecule with chain length l to tilt. If the initially vertical adsorbate is tilted by some angle θ, the tilting stiffness constant kt creates a restoring torque Mr = −ktθ. The corresponding torque that opposes this tilting motion is given by Fl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ, so that the equilibrium tilt angle is given by the balance:
θ, so that the equilibrium tilt angle is given by the balance: 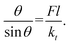 However, because
However, because 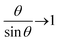 as θ → 0, it is then an increasing function of θ. The only solution is θ = 0 below a critical force
as θ → 0, it is then an increasing function of θ. The only solution is θ = 0 below a critical force 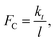 and there should be no tilting below this normal force, so that, under these conditions, the adsorbate should be mechanochemically stable. This implies that, if the critical stress is high, it should be possible to synthesize very mechanically resistant overlayers. Note that an imposed lateral stress caused by sliding will perturb the system but should not change the corresponding critical stress.
and there should be no tilting below this normal force, so that, under these conditions, the adsorbate should be mechanochemically stable. This implies that, if the critical stress is high, it should be possible to synthesize very mechanically resistant overlayers. Note that an imposed lateral stress caused by sliding will perturb the system but should not change the corresponding critical stress.
We investigate this idea first by rubbing a saturated overlayer of methyl thiolate species on copper as a function of normal stress by measuring the depth of the groove formed in the film as a function of the number of rubbing cycles. In this case, the C–S bond of the reactant, methyl thiolate, is close to perpendicular to the surface; there should be a critical stress for the mechanochemical reaction. These results are compared with the mechanochemical reactivity of ethyl thiolate species on Cu(100) for which sp3 hybridization of carbon will cause the C–C bond of the terminal CH3–C group to be oriented relatively close to parallel to the surface and should therefore not have a critical force; the reaction rate should follow the Bell law.9 Finally, in the case of propyl thiolate species adsorbed on Cu(100), where the terminal CH3–C group is again oriented relatively close to perpendicular to the surface, critical effects should be observed. These systems are studied experimentally by inducing mechanochemical reactions by sliding an AFM tip over the surface20–22 and are supplemented by density functional theory (DFT) calculations to investigate how the structures deform under the influence of normal stresses.
Experimental methods
Experiments were carried out using an RHK Variable-Temperature Ultrahigh Vacuum (UHV) 750 AFM operating at a base pressure of ∼2 × 10−10 torr following bakeout, as described previously.29 The apparatus also contained an analysis chamber for sample cleaning and was equipped with a Scienta Omicron SPECTALEED combined low-energy electron diffraction (LEED)/Auger system for assessing sample cleanliness, crystalline order and the orientation of the Cu(100) single crystal relative to the AFM sliding direction. Sliding was carried out along the [110] directions of the Cu(100) crystal by determining its orientation using LEED and relating this to the sliding direction of the AFM tip using a clean Au(111) single crystal, where the scanning orientation relative to the substrate lattice could be measured from the clearly visible “herringbone” reconstruction seen by scanning tunneling microscopy (STM).31Reaction rates were measured by reciprocating sliding of a silicon μ-masch (HQ:NSC19/NO AL) AFM tip with a nominal 8 nm radius using a sliding speed of 120 nm s−1 for a length of 60 nm at various applied normal loads, which were corrected for adhesion forces.21 Lateral forces are also necessarily exerted during sliding, but their values were not specifically measured. The rates were obtained from the depths of the wear tracks, which were measured using AFM at a low, non-perturbative load, as a function of time.29
The chamber was also equipped with a Dycor quadrupole mass analyzer for leak checking and background gas analysis. The Cu(100) single crystal was cleaned by argon ion bombardment (∼1 kV, ∼2 μA cm−2) and then by annealing to ∼850 K to remove any surface damage induced by the cleaning procedure. Saturated overlayers of alkyl thiolate species were prepared by dosing a clean Cu(100) sample held at ∼298 K in UHV by background exposure at a pressure of 1 × 10−8 torr of dimethyl disulphide (DMDS, Aldrich, 99.0% purity), ethanethiol (Aldrich, 97.0% purity), diethyl disulphide (DEDS, Aldrich, 99.0% purity), or 1-propanethiol (Aldrich, 99.0% purity) for 500 s, where the pressures were measured using a nude ionization gauge included in the UHV chamber. The pressures were not corrected for ionization gauge sensitivity.32 The compounds were transferred to glass bottles and attached to the gas-handling system of the vacuum chamber and cleaned by several freeze-pump-the cycles. The purity was monitored using mass spectroscopy.
The cantilever force constant was obtained from the geometry of the cantilever measured by scanning electron microscopy as described in ref. 33 and by the Sader method.34 Scanning electron microscopy (SEM) was also used to verify the integrity of the AFM tips and to measure the tip radius (see Fig. S1†). The measured cantilever tilt angle in the RHK AFM is ∼22.5°, so that a tilt correction was applied as suggested by Hutter35 using the values of the length of the cantilever and the length of the tip, obtained from a scanning electron microscope image of the cantilever. These values were used to calculate the normal stress at the center of the contact, which is where the reaction rate was measured. Force–distance curves measured periodically between experiments verified that the tip shape had not changed. The tips were found to remain stable over multiple sliding experiments, but the maximum pressure exerted was limited to decrease the chance of tip failure. The normal stresses were obtained by using the width of the wear track to estimate the contact area and combined with previous results using just normal loads.29 The contact radii at each load were determined both from the images of the indents29 and the width of the wear tracks after sliding (Fig. S2†).
Theoretical methods
Density functional theory (DFT) calculations were performed with the projector augmented wave method36,37 as implemented in the Vienna ab initio simulation package, VASP.38–40 The exchange–correlation potential was described using the generalized gradient approximation of Perdew, Burke and Ernzerhof.41 A cutoff of 400 eV was used for the planewave basis set, and the wavefunctions and electron density were converged to within 1 × 10−6 eV. The first Brillouin zone was sampled with a 4 × 4 × 1 Monkhorst–Pack grid.42 Geometric relaxations were considered to be converged when the force was less than 0.01 eV Å−1 on all unrestricted atoms. van der Waals' interactions were implemented using the DFT-D3 method as described by Grimme et al.43The lattice constant used for Cu(100) was 3.575 Å. The system consisted of two (2 × 2) Cu(100) slabs to mimic the experimental saturated coverages of alkyl thiolates on Cu(100).44 The alkyl thiolate molecule was adsorbed onto a 6-layer slab in a hollow site. The bottom three layers of that slab were frozen while the top three layers were allowed to relax. The second slab was 3-layers thick and passivated with hydrogen to render the interacting surface inert. All atoms in this slab were kept frozen to simulate an infinitely hard surface. Compression of the methyl thiolate molecule was simulated by bringing the small, infinitely hard slab down in 0.1 Å steps, and decompression was simulated by raising the slab up in 0.1 Å steps.
Results and discussion
To investigate critical phenomena in the methyl thiolate mechanochemical decomposition, the most stable structure was compressed by a slab consisting of stiff, passivated Cu(100) counterface. The separation between the slabs was decreased from an initial value of 0.85 nm and decreased in 0.01 nm steps. The structure was relaxed at each interval and a movie of the process is shown in Fig. S3.† This shows that the methyl thiolate first compresses elastically while maintaining its vertical geometry, but then suddenly tilts to an angle of ∼68° to drastically decrease the energy of the system. The slab is then retracted to allow the methyl thiolate molecule to move back to its original vertical configuration. The resulting plot of energy versus slab separation is shown in Fig. 1( ), which also schematically illustrates the critical buckling process described above. A long-range interaction is seen as the slabs approach, and is due to the different charges that are present on the methyl-thiolate and hydrogen-covered surfaces due to their different work-functions.45 This is consistent with the snap into contact seen in force–distance curves measured by an AFM.29 This results in an energy minimum at a slab separation of ∼0.66 nm and then a rapid parabolic increase as the slabs come closer together. As the slabs reach a critical separation of ∼0.5 nm, the methyl thiolate undergoes a sudden tilt to reduce the energy from ∼150 kJ mol−1 to ∼52 kJ mol−1. The compressed state was then relaxed by incrementally moving the slabs apart and the resulting energies are also plotted in Fig. 1(■). Now the tilt angle decreases as the slab separation increases to ∼0.66 nm when the C–S bond of the methyl thiolate becomes vertical once again. At larger slab separations, the energy follows the variation as found during the approach.
), which also schematically illustrates the critical buckling process described above. A long-range interaction is seen as the slabs approach, and is due to the different charges that are present on the methyl-thiolate and hydrogen-covered surfaces due to their different work-functions.45 This is consistent with the snap into contact seen in force–distance curves measured by an AFM.29 This results in an energy minimum at a slab separation of ∼0.66 nm and then a rapid parabolic increase as the slabs come closer together. As the slabs reach a critical separation of ∼0.5 nm, the methyl thiolate undergoes a sudden tilt to reduce the energy from ∼150 kJ mol−1 to ∼52 kJ mol−1. The compressed state was then relaxed by incrementally moving the slabs apart and the resulting energies are also plotted in Fig. 1(■). Now the tilt angle decreases as the slab separation increases to ∼0.66 nm when the C–S bond of the methyl thiolate becomes vertical once again. At larger slab separations, the energy follows the variation as found during the approach.
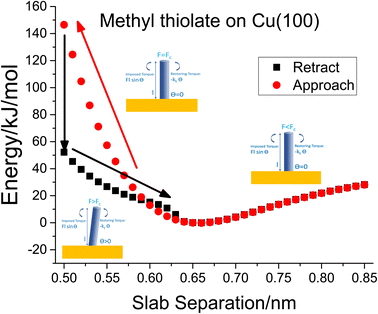 | ||
Fig. 1 Plot of the energy versus slab separation for the compression of a vertical methyl thiolate species on Cu(100) as a function of the distance from a hydrogen-atom-covered Cu(100) surface for the approach of the two slabs ( ) until the initially vertical methyl thiolate species tilts. The structural changes associated with the approach and retraction of the slabs is shown in movie S3.† Shown also are cartoons that illustrate the onset of critical buckling. ) until the initially vertical methyl thiolate species tilts. The structural changes associated with the approach and retraction of the slabs is shown in movie S3.† Shown also are cartoons that illustrate the onset of critical buckling. | ||
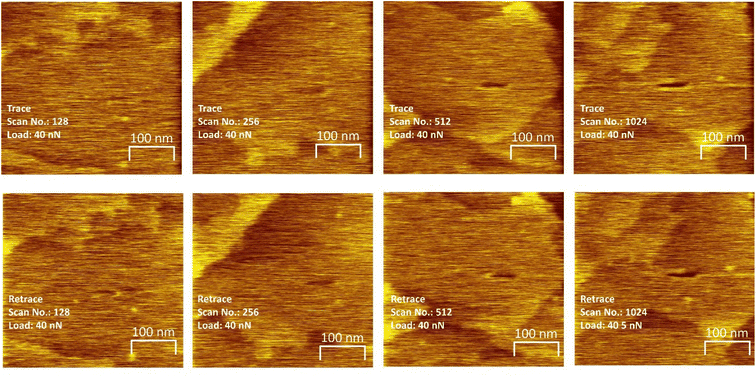
To investigate whether critical stresses can be found, experiments were carried out by sliding an AFM tip over a saturated methyl thiolate overlayer at various normal loads and by imaging the sample at a low, non-perturbative load to observe the grooves formed on the surface due to the shear-induced removal of the methyl thiolate species from the surface. As shown in Fig. 2, linear features are formed on the surfaces in flat regions that are away from surface steps that become deeper as sliding proceeds. The depth of the groove is taken to be proportional to the extent of the reaction. Note that sliding was along the direction that gave the maximum rate46 and rastering experiments showed that the methyl thiolate decomposes via C–S bond scission to adsorb sulfur on the surface in a similar reaction as found for a ball-on-flat rubbing.24–26,28 In addition, the width of the wear track for each experiment is taken to correspond to the outer diameter of the contact and enables the normal contact stresses to be measured with reasonable accuracy.29 Both the width of the wear tracks and the values of indentation diameters measured during compression obtained in previous experiments29 are plotted versus normal load in the Fig. S2.† Note that the shape of the indentation profile could be modeled by assuming a Hertzian stress distribution with a Bell-like dependence of mechanochemical reaction rate with contact pressure.9,29 The variation of contact area with normal load is modeled using both the Derjaguin–Muller–Toporov (DMT)47 and Johnson–Kendall–Roberts (JKR)48 contact theories using the measured tip radius, where the JKR model gives reasonable agreement with the experimental values which were used to calculate the contact stresses (Fig. S2†). The influence of the presence of a thin film of methyl thiolate on the copper substrate was also gauged49 and the thin films present on the copper surface made a negligible difference to the calculated results.
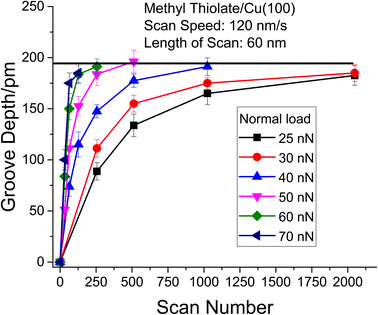
The resulting groove depths are plotted as a function of the number of passes over the surface for several values of the normal load of the AFM tip in Fig. 3 for loads for which a groove could be detected. The groove depth increases exponentially with the number of passes to an asymptotic value that is in accord with the height of a methyl thiolate species above the surface indicating a first-order reaction rate where the total reaction time equals the number of passes multiplied by the time that a point on the surface is in contact with the tip, tC. The results are analyzed to yield a rate constant, kp per the number of passes. The lowest loads showed no detectable wear, and the maximum reaction rates for these loads (normal stresses) were calculated by assuming that the wear depth was equal to or less than the noise in the AFM image. Note that these experiments were interspersed with those at higher loads where a wear track was observed to ensure that there were no changes to the tip that might have prevented reaction. In addition, pull-off forces were measured periodically between experiments, and showed no significant variation.
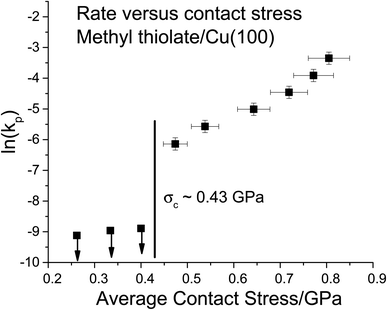
The results are plotted in Fig. 4 as ln(kp) versus the average contact stress,16,19 and reveal a clear threshold normal stress of ∼0.43 GPa below which no mechanochemical reaction could be detected. The points below this threshold represent the maximum possible reaction rate assuming that the groove depth is of the order of the noise in the image of the surface, and the arrows emphasize this. The variation in rate with stress above this threshold can be described using the Bell model9 in which the mechanochemical rate constant under the influence of some stress, k(σ), is given by 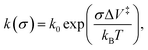 where kB is the Boltzmann constant, and k0 is the rate constant in the absence of an applied stress so that
where kB is the Boltzmann constant, and k0 is the rate constant in the absence of an applied stress so that 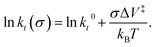 This analysis is for reaction kinetics measured as a function of time, kt, while the experiment yielded rates as a function of the number of passes, but they are related by kt ≅ kp/tC. tC depends on the sliding speed and contact width. Since the sliding speed was constant for all experiments, and the contact width varies only slowly with the force exerted on the tip, the activation volume measured from plots of either ln(kt) or ln(kp) versus stress will be approximately the same. It should, however, be noted that this analysis does not take into account the stress distribution across the contact. Nevertheless, the relative values of activation volumes for different adsorbates collected under identical conditions should be correct. A linear fit to the data above the critical stress of ∼0.43 GPa yields an activation volume of 32 ± 3 Å3 per molecule (Table 1).
This analysis is for reaction kinetics measured as a function of time, kt, while the experiment yielded rates as a function of the number of passes, but they are related by kt ≅ kp/tC. tC depends on the sliding speed and contact width. Since the sliding speed was constant for all experiments, and the contact width varies only slowly with the force exerted on the tip, the activation volume measured from plots of either ln(kt) or ln(kp) versus stress will be approximately the same. It should, however, be noted that this analysis does not take into account the stress distribution across the contact. Nevertheless, the relative values of activation volumes for different adsorbates collected under identical conditions should be correct. A linear fit to the data above the critical stress of ∼0.43 GPa yields an activation volume of 32 ± 3 Å3 per molecule (Table 1).
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kp(0) and critical stresses for the mechanochemical reactions of methyl, ethyl and propyl thiolate on copper measured from the slopes and intercepts of plots of ln
kp(0) and critical stresses for the mechanochemical reactions of methyl, ethyl and propyl thiolate on copper measured from the slopes and intercepts of plots of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kpversus normal stress
kpversus normal stress
| Activation volume/Å3 | ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kp(0) kp(0) |
Critical stress/GPa | |
|---|---|---|---|
| Methyl thiolate | 31.6 ± 2.5 | −9.9 ± 0.5 | 0.43 |
| Ethyl thiolate | 42.6 ± 1.1 | −11.3 ± 0.2 | None |
| Propyl thiolate | 39.4 ± 3.0 | −9.9 ± 0.4 | 0.33 |
To further investigate critical phenomena, calculations and experiments were carried out for ethyl and propyl thiolate species on Cu(100). The terminus of adsorbed ethyl thiolate species is expected to be relatively close to parallel to the surface as illustrated by the most stable structure determined by DFT (Fig. 5A and S3†). The compression of an ethyl thiolate slab is illustrated in Fig. S3,† which shows that the molecule tilts under compression and returns to its original structure when the slab is retracted. This is emphasized by the data in Fig. 5A, which plots the S–C1 angle (indicated as an inset to Fig. 5A) as a function of slab separation. This remains reasonably constant as the slab approaches at an angle of ∼10° as the slab separation decreases to ∼7.4 Å so that the van der Waals' interaction of the terminal ethyl group with the surface causes the adsorbate to tilt slightly compared to methyl thiolate on Cu(100). As the slab separation decreases further, the molecule starts to tilt to reach a maximum angle of ∼50° at a slab separation of ∼5 Å; normal stresses can significantly distort the molecule. The tilt angle follows exactly the same reverse pathway when the slabs are separated; there is no evidence of hysteresis. The corresponding plot of energy versus distance for ethyl thiolate (analogous to that shown in Fig. 1) is displayed in Fig. S4.† This predicts that there should be no critical stresses for the sliding-induced mechanochemical decomposition of ethyl thiolate species on Cu(100) and this is borne out by the results shown in Fig. 5B, which plots ln(kp) versus contact stress. The rate constants are obtained from the groove depths as a function of the number of passes over the surface as shown in Fig. S5.† Here, the ethyl thiolate was grafted onto the surface from both diethyl disulfide25,50 and ethanethiol. They should form identical ethyl thiolate species, and this is verified by finding that they have identical mechanochemical reactions rates. The results show that the rate constant per pass again varies linearly with the applied normal stress over a wide range of values from ∼0.2 to ∼1.1 GPa, so obeys the Bell model over the whole range; there is no evidence of the existence of a critical stress for ethyl thiolates adsorbed on Cu(100). Note that the lowest applied stress here corresponds to an almost zero applied normal force (where the actual forces and normal stresses are calculated by including the adhesion between the tip and the substrate). The slope yields a value of activation volume of 43 ± 1 Å3 per molecule (Table 1).
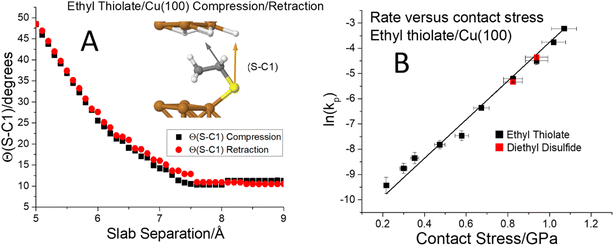 | ||
Fig. 5 (A) Plot of the C–S bond angle with respect to the surface normal for an ethyl thiolate species on Cu(100) for the approach of the two slabs (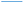 ) and the after the retraction to the original separation ( ) and the after the retraction to the original separation ( ) showing that the structural change is completely reversible. The structural changes associated with the approach and retraction of the slabs is shown in movie S3.† (B) Plot of ln(kp) versus the normal stress in GPa (■) for the rate of mechanochemical decomposition of ethyl thiolate species on Cu(100), where kp is the rate constant calculated per pass over the surface. ) showing that the structural change is completely reversible. The structural changes associated with the approach and retraction of the slabs is shown in movie S3.† (B) Plot of ln(kp) versus the normal stress in GPa (■) for the rate of mechanochemical decomposition of ethyl thiolate species on Cu(100), where kp is the rate constant calculated per pass over the surface. | ||
The terminal C–C group of propyl thiolate on Cu(100) is close to perpendicular to the surface, but now with a bend in the chain (see inset to Fig. 6A). Similar compression calculations were carried out and the results are displayed in Fig. S3† where a normal stress induces a significant geometrical change. This is illustrated in Fig. 6A, which plots the angle of the CH3–S plane with respect to the surface as a function of the slab separation. The plane is close to perpendicular to the surface during approach, but then undergoes a drastic change to an isomeric state as the slab separation reaches ∼5.2 Å, where the plane moves to an angle of ∼8° with respect to the surface, but with only a slightly higher energy than the initial configuration. As the slab retracts, the CH3–S plane angle increases slightly to ∼20° at a slab separation of 7.9 Å, but the angle remains constant indicating that the propyl thiolate reaches a new stable configuration to forms a metastable isomer. The approach/retract curve has a significant hysteresis suggesting that there should be a critical stress for the initiation of mechanochemical reactivity. This effect is emphasized by the plot of energy versus distance in Fig. S6.†
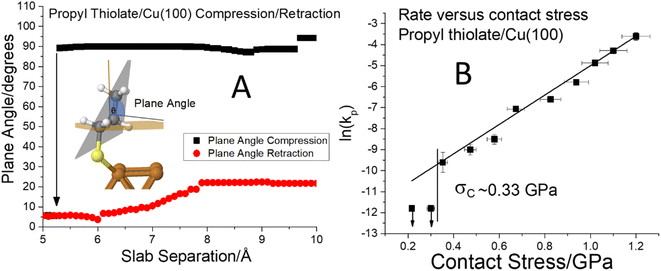 | ||
Fig. 6 (A) Plot of the C–S bond angle with respect to the surface normal for a propyl thiolate species on Cu(100) for the approach of the two slabs ( ) and the after the retraction to the original separation ( ) and the after the retraction to the original separation ( ) showing that there is a considerable hysteresis in the approach/retract curve. The structural changes associated with the approach and retraction of the slabs is shown in movie S3.† (B) Plot of ln(kp) versus the normal stress in GPa (■) for the rate of mechanochemical decomposition of propyl thiolate species on Cu(100), where kp is the rate constant calculated per pass over the surface. Note that the rates for low values of normal stress were estimated by assuming that the depth of any wear track was less than the noise in the image of the scanned surface. Here the arrows indicate that the points represent the maximum rates. The vertical line shows the value of the critical stress, σC ∼ 0.33 GPa. ) showing that there is a considerable hysteresis in the approach/retract curve. The structural changes associated with the approach and retraction of the slabs is shown in movie S3.† (B) Plot of ln(kp) versus the normal stress in GPa (■) for the rate of mechanochemical decomposition of propyl thiolate species on Cu(100), where kp is the rate constant calculated per pass over the surface. Note that the rates for low values of normal stress were estimated by assuming that the depth of any wear track was less than the noise in the image of the scanned surface. Here the arrows indicate that the points represent the maximum rates. The vertical line shows the value of the critical stress, σC ∼ 0.33 GPa. | ||
To explore whether this hysteresis also results in a critical stress for propyl thiolate, a graph of ln(kp) versus normal stress is shown in Fig. 6B. The reaction rates are again obtained from plots of groove depth versus the number of scans for various loads (Fig. S7†). The plot is linear over a wide range of stresses from ∼0.35 to ∼1.3 GPa, indicating that the Bell equation is obeyed, but for stresses below ∼0.33 GPa, there is no detectable reaction. Again, the maximum rates below the critical stress were estimated from the image noise and are also plotted in Fig. 6B along with vertical arrows to indicate that these represent maximum values. These points are clearly lower than the rate that would be expected from an extrapolation of the Bell equation, indicating that the critical stress for this system is ∼0.33 GPa. This appears to be associated with a conformational change rather than a tilt as found for methyl thiolate species. In this case, the slope of the linear portion of the plot yields an activation volume of 39 ± 3 Å3 per molecule (Table 1).
These results clearly show how adsorbate geometries can result in mechanochemical reaction rates that do not decrease smoothly to the thermal rate as the stress decreases to zero but can exhibit critical stresses below which the adsorbate is completely mechanically stable. The mechanistic origin of the critical stress depends on the molecular architecture, where a critical stress due to buckling is specific to methyl thiolate, completely absent for ethyl-thiolate, and is present also for propyl thiolate but with a different mechanism that involves a trans–cis isomerization. Thus, buckling, whenever it occurs, depends strongly on the molecular geometry and on the bifurcation mechanism involved. Roughly speaking there seems to be a general tendency that a shorter molecular length and higher tilting stiffness constants will result in a higher critical force, but this trend will depend in detail on the structure and should be determined for each specific case.
However, this general concept offers the possibility of being able to design tailored adsorbates that are very mechanochemically resistant and could find applications as lubricant additives, as so-called friction modifiers.51–53 As an example, carbon nanotube have been proposed to deform by buckling54,55 so that assemblies of short, monodispersed, vertical carbon nanotubes can be expected to be very resistant to mechanical damage.
It should also be noted that similar critical effects have been noted for a classical surface tribochemical reaction, that of the antiwear lubricant additive, ZDDP,56 and other examples of effects that occur only when a critical stress is applied are given in ref. 54.
The values of the activation volumes, calculated from the linear portion of the plots of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kpversus normal stress, are summarized in Table 1. The value for ethyl thiolate decomposition, in which there is no critical stress, is larger than for the other two alkyl thiolates, when there are critical stresses. Furthermore, the values of
kpversus normal stress, are summarized in Table 1. The value for ethyl thiolate decomposition, in which there is no critical stress, is larger than for the other two alkyl thiolates, when there are critical stresses. Furthermore, the values of 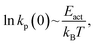 which depend on the reaction activation energy, are different when there is a critical stress (methyl and propyl thiolate, ln
which depend on the reaction activation energy, are different when there is a critical stress (methyl and propyl thiolate, ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kp(0) ∼ −9.9) compared to when there is not (ethyl thiolate, nkp(0) ∼ −11.3). However, because the thermal reactions have similar activation barriers,57 according to the Bell model, they should have essentially identical asymptotic values of ln
kp(0) ∼ −9.9) compared to when there is not (ethyl thiolate, nkp(0) ∼ −11.3). However, because the thermal reactions have similar activation barriers,57 according to the Bell model, they should have essentially identical asymptotic values of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kp(0). The observation that they do not could have two sources. The first is that the simple linear Bell model is not sufficient to describe the experimental results and requires the inclusion of quadratic terms in the stress as in the extended-Bell model.58 In this case, the reactions could have identical ln
kp(0). The observation that they do not could have two sources. The first is that the simple linear Bell model is not sufficient to describe the experimental results and requires the inclusion of quadratic terms in the stress as in the extended-Bell model.58 In this case, the reactions could have identical ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kp(0) values, but have different coefficients of the F2 term. Alternatively, the structural change that occurs when the normal stress exceeds the critical stress leads to an initial structure with a lower energy than that of the original reactant that could manifest as an overall lower reaction energy barrier. If this is the case, the activation volume for the conversion of this new initial-state structure to the activated complex would be lower than the activation volume from the lowest-energy initial state to the activated complex. Being able to test whether these ideas are correct will require predictive models for mechanochemical reactions rates.
kp(0) values, but have different coefficients of the F2 term. Alternatively, the structural change that occurs when the normal stress exceeds the critical stress leads to an initial structure with a lower energy than that of the original reactant that could manifest as an overall lower reaction energy barrier. If this is the case, the activation volume for the conversion of this new initial-state structure to the activated complex would be lower than the activation volume from the lowest-energy initial state to the activated complex. Being able to test whether these ideas are correct will require predictive models for mechanochemical reactions rates.
Conclusions
These results illustrate how adsorbed mechanophores consisting of alkyl thiolate species on copper that react by tilting towards the surface to weaken the C–S bond can exhibit critical stresses in cases in which there is hysteresis in the approach/retract curve. In the case of a vertical methyl thiolate species, the critical stress induces molecular tilt predicted by beam stability theory where a critical normal force is needed to induce molecular tilt. This is confirmed by DFT calculations of the compression of a methyl thiolate species adsorbed on a Cu(100).These ideas are further tested using longer-chain alkyl thiolates and are confirmed by finding that an ethyl thiolate, which has a terminus of the alkyl group that is close to parallel to the surface has no hysteresis in the approach/retract curve and the mechanochemical activity shows no critical stress. Critical behavior is found for propyl thiolate where the critical process involves a conformational change due to a normal-stress induced rotation about a C–C bond, implying that critical phenomena can occur either by structural or conformational changes.
The existence of such critical mechanochemical stresses implies that these overlayers are extremely durable under stresses below the critical value and will not be removed. A more fundamental understanding of such effects may result in the design of super mechanically stable surface films.
Data availability
The experimental data can be found in the ESI† and manuscript and is referred to throughout the manuscript.Author contributions
W. T. T. designed the experiment and wrote the paper and analyzed the data with F. S. R. R. collected the experimental data and N. H. performed the calculations.Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
We gratefully acknowledge the Civil, Mechanical and Manufacturing Innovation (CMMI) Division of the National Science Foundation under grant number 2020525 for support of this work. We also thank Drs Juliette Cayer-Barrioz and, Denis Mazuyer and for very useful discussions.References
- H. J. Theophrastus, Theophrastus's History of Stones: With an English Version, and Critical and Philosophical Notes, Including the Modern History of the Gems, & c., Described by that Author, and of Many Other of the Native Fossils, London, 1774 Search PubMed.
- L. Prandtl, Z. Angew. Math. Mech., 1928, 8, 85 CrossRef.
- O. J. Furlong, S. J. Manzi, V. D. Pereyra, V. Bustos and W. T. Tysoe, Tribol. Lett., 2010, 39, 177–180 CrossRef CAS.
- M. Müser, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 125419 CrossRef.
- H. Spikes and W. Tysoe, Tribol. Lett., 2015, 59, 1–14 CrossRef CAS.
- H. Eyring, J. Chem. Phys., 1936, 4, 283–291 CrossRef CAS.
- W. Kauzmann and H. Eyring, J. Am. Chem. Soc., 1940, 62, 3113–3125 CrossRef CAS.
- M. G. Evans and M. Polanyi, Trans. Faraday Soc., 1935, 31, 875–894 RSC.
- G. Bell, Science, 1978, 200, 618–627 CrossRef CAS PubMed.
- J. J. Gilman, Science, 1996, 274, 65 CrossRef CAS.
- F. K. Urakaev and V. V. Boldyrev, Powder Technol., 2000, 107, 93–107 CrossRef CAS.
- F. K. Urakaev and V. V. Boldyrev, Powder Technol., 2000, 107, 197–206 CrossRef CAS.
- M. K. Beyer and H. Clausen-Schaumann, Chem. Rev., 2005, 105, 2921–2948 CrossRef CAS PubMed.
- D. A. Davis, A. Hamilton, J. Yang, L. D. Cremar, D. Van Gough, S. L. Potisek, M. T. Ong, P. V. Braun, T. J. Martínez, S. R. White, J. S. Moore and N. R. Sottos, Nature, 2009, 459, 68–72 CrossRef CAS PubMed.
- H. M. Klukovich, T. B. Kouznetsova, Z. S. Kean, J. M. Lenhardt and S. L. Craig, Nat. Chem., 2013, 5, 110–114 CrossRef CAS PubMed.
- J. R. Felts, A. J. Oyer, S. C. Hernández, K. E. Whitener Jr, J. T. Robinson, S. G. Walton and P. E. Sheehan, Nat. Commun., 2015, 6, 6467 CrossRef CAS PubMed.
- P. Seema, J. Behler and D. Marx, Phys. Chem. Chem. Phys., 2013, 15, 16001–16011 RSC.
- T. D. B. Jacobs and R. W. Carpick, Nat. Nanotechnol., 2013, 8, 108–112 CrossRef CAS PubMed.
- N. N. Gosvami, J. A. Bares, F. Mangolini, A. R. Konicek, D. G. Yablon and R. W. Carpick, Science, 2015, 348, 102–106 CrossRef CAS PubMed.
- R. Rana, R. Bavisotto, N. Hopper and W. T. Tysoe, Tribol. Lett., 2021, 69, 32 CrossRef CAS.
- R. Rana, R. Bavisotto, K. Hou and W. T. Tysoe, Phys. Chem. Chem. Phys., 2021, 23, 17803–17812 RSC.
- R. Rana, R. Bavisotto, K. Hou, N. Hopper and W. T. Tysoe, Tribol. Lett., 2021, 70, 5 CrossRef.
- B. Miller, P. Kotvis, O. Furlong and W. Tysoe, Tribol. Lett., 2013, 49, 21–29 CrossRef CAS.
- B. Miller, O. Furlong and W. Tysoe, Tribol. Lett., 2013, 49, 39–46 CrossRef CAS.
- H. Adams, B. P. Miller, P. V. Kotvis, O. J. Furlong, A. Martini and W. T. Tysoe, Tribol. Lett., 2016, 62, 1–9 CrossRef CAS.
- H. Adams, B. P. Miller, O. J. Furlong, M. Fantauzzi, G. Navarra, A. Rossi, Y. Xu, P. V. Kotvis and W. T. Tysoe, ACS Appl. Mater. Interfaces, 2017, 9, 26531–26538 CrossRef CAS PubMed.
- H. L. Adams, M. T. Garvey, U. S. Ramasamy, Z. Ye, A. Martini and W. T. Tysoe, J. Phys. Chem. C, 2015, 119, 7115–7123 CrossRef CAS.
- O. J. Furlong, B. P. Miller, P. Kotvis and W. T. Tysoe, ACS Appl. Mater. Interfaces, 2011, 3, 795–800 CrossRef CAS PubMed.
- A. Boscoboinik, D. Olson, H. Adams, N. Hopper and W. T. Tysoe, Chem. Commun., 2020, 56, 7730–7733 RSC.
- S. Jerath, Structural Stability Theory and Practice Buckling of Columns, Beams, Plates, and Shells, 2021 Search PubMed.
- J. V. Barth, H. Brune, G. Ertl and R. J. Behm, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 42, 9307–9318 CrossRef CAS PubMed.
- O. J. Furlong, B. P. Miller, Z. Li, J. Walker, L. Burkholder and W. T. Tysoe, Langmuir, 2010, 26, 16375–16380 CrossRef CAS PubMed.
- E. Meyer, H. J. Hug and R. Bennewitz, Scanning Probe Microscopy: The Lab on a Tip, Springer, Berlin; London, 2011 Search PubMed.
- S. M. Cook, K. M. Lang, K. M. Chynoweth, M. Wigton, R. W. Simmonds and T. E. Schäffer, Nanotechnology, 2006, 17, 2135–2145 CrossRef CAS.
- J. L. Hutter, Langmuir, 2005, 21, 2630–2632 CrossRef CAS PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192 CrossRef.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- M. Wühn, J. Weckesser and C. Wöll, Langmuir, 2001, 17, 7605–7612 CrossRef.
- A. Clark, The Theory of Adsorption and Catalysis, Academic Press, New York, 1970 Search PubMed.
- R. Rana, G. Djuidje Kenmoe, F. Sidoroff, R. Bavisotto, N. Hopper and W. T. Tysoe, J. Phys. Chem. C, 2022, 126(28), 11585–11593 CrossRef CAS.
- B. V. Derjaguin, V. M. Muller and Y. P. Toporov, J. Colloid Interface Sci., 1975, 53, 314–326 CrossRef CAS.
- K. L. Johnson, K. Kendall, A. D. Roberts and D. Tabor, Proc. R. Soc. London, Ser. A, 1971, 324, 301–313 CAS.
- E. D. Reedy, J. Mater. Res., 2006, 21, 2660–2668 CrossRef CAS.
- O. Furlong, B. Miller, Z. Li and W. T. Tysoe, Surf. Sci., 2011, 605, 606–611 CrossRef CAS.
- S. Campen, J. H. Green, G. D. Lamb and H. A. Spikes, Tribol. Lett., 2015, 57, 18 CrossRef.
- H. Spikes, Tribol. Lett., 2015, 60, 5 CrossRef.
- M. I. De Barros Bouchet, J. M. Martin, C. Forest, T. le Mogne, M. Mazarin, J. Avila, M. C. Asensio and G. L. Fisher, RSC Adv., 2017, 7, 33120–33131 RSC.
- C. Q. Ru, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, 10405–10408 CrossRef CAS.
- W. Wong Eric, E. Sheehan Paul and M. Lieber Charles, Science, 1997, 277, 1971–1975 CrossRef.
- S. V. Sukhomlinov and M. H. Müser, Tribol. Lett., 2021, 69, 89 CrossRef CAS.
- S. Vollmer, G. Witte and C. Wöll, Langmuir, 2001, 17, 7560–7565 CrossRef CAS.
- S. S. M. Konda, J. N. Brantley, C. W. Bielawski and D. E. Makarov, J. Chem. Phys., 2011, 135, 164103–164108 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2sc04000j |
| This journal is © The Royal Society of Chemistry 2022 |