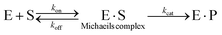Open Access Article
Open Access ArticlePicking the lock of coordination cage catalysis
Tomasz K.
Piskorz
 a,
Vicente
Martí-Centelles
a,
Vicente
Martí-Centelles
 b,
Rebecca L.
Spicer
b,
Rebecca L.
Spicer
 c,
Fernanda
Duarte
c,
Fernanda
Duarte
 *a and
Paul J.
Lusby
*a and
Paul J.
Lusby
 *d
*d
aChemistry Research Laboratory, University of Oxford, Oxford, OX1 3TA, UK. E-mail: fernanda.duartegonzalez@chem.ox.ac.uk
bInstituto Interuniversitario de Investigación de Reconocimiento Molecular y Desarrollo Tecnológico (IDM), Universitat Politècnica de València, Universitat de València, Camino de Vera, s/n 46022, Valencia, Spain
cDepartment of Chemistry, Lancaster University, Lancaster, LA14YB, UK
dEaStCHEM School of Chemistry, University of Edinburgh, Edinburgh, Scotland EH9 3FJ, UK. E-mail: Paul.Lusby@ed.ac.uk
First published on 8th September 2023
Abstract
The design principles of metallo-organic assembly reactions have facilitated access to hundreds of coordination cages of varying size and shape. Many of these assemblies possess a well-defined cavity capable of hosting a guest, pictorially mimicking the action of a substrate binding to the active site of an enzyme. While there are now a growing collection of coordination cages that show highly proficient catalysis, exhibiting both excellent activity and efficient turnover, this number is still small compared to the vast library of metal–organic structures that are known. In this review, we will attempt to unpick and discuss the key features that make an effective coordination cage catalyst, linking structure to activity (and selectivity) using lessons learnt from both experimental and computational analysis of the most notable exemplars. We will also provide an outlook for this area, reasoning why coordination cages have the potential to become the gold-standard in (synthetic) non-covalent catalysis.
1 Introduction, motivation and context
The area of supramolecular chemistry has been dominated by making and studying systems that use weak reversible interactions.1 These interactions can be exploited for many purposes such as the preparation of complex structures and topologies, from metallo-organic cages2–4 or H-bonded capsules,5–7 through to infinite networks8–10 and interlocked and topologically non-trivial molecules.11–14 All of these complex, multi-component architectures stem from the simplest expression of self-assembly; the molecular recognition of a single guest by a single host. Investigating host–guest systems can provide a fundamental understanding of the different factors that govern association, from the nature of individual weak interactions through to electrostatic pre-organisation. In turn, this facilitates the design of new hosts that exhibit both stronger and more selective binding. Studying non-covalent complexes also has much wider implications beyond supramolecular chemistry, as synthetic host–guest assemblies provide a minimalist design that can aid in understanding much more complex biological systems.15In many areas of science, fundamental discoveries and their understanding quickly evolve into applications.16 The ability to use one molecular entity to bind another can be exploited in a number of different settings. Primary applications include separation,17–19 transport and delivery,20–22 wherein the key feature is the selective recognition and/or retention of a single species within a complex mixture. In these cases, there is no requirement to significantly change the fundamental property of the recognised species; function is merely achieved through the process of binding itself. In more complex applications, such as supramolecular catalysis, the host must not only recognise the substrate, it must also change its reactivity, for example by modulating its electronic structure, conformation, co-localisation or how it interacts with the solvent.
For over 60 years, the structures of synthetic hosts have changed enormously. They have evolved from acyclic then macrocyclic topologies, to fully three-dimensional structures that can completely envelop guest species. This increase in structural complexity has led to ever more effective molecular recognition but at a cost: macromolecular hosts are invariably more complex to prepare. This is especially true for the fully-covalent receptors (e.g., hemicarcerands) that came to the fore during the late 1980s.23 Self-assembly, and in particular coordination (or metallosupramolecular) assembly, has transformed the field of molecular containers, where now 3D synthetic hosts are readily attainable from simple ligands and metal-ion precursors. Many of the host–guest principles that were established using covalent molecular containers apply to coordination cages and other metallosupramolecular hosts. Moreover, the catalytic strategies (e.g., dual or constrictive substrate binding) that were utilised with the early supramolecular catalysts (e.g., cyclodextrins) have been similarly exploited with coordination cages.
1.1 The link to biological catalysis. An inspiration or a blueprint?
It is difficult to discuss cage catalysis without invoking parallels to nature. Biomimetic catalysis is not a new concept; Cramer made reference to the conceptual similarities between catalysis with synthetic inclusion compounds and enzymology more than 70 years ago.24 In the intervening period, many research groups have explored catalysis with a variety of molecular hosts (Fig. 1),15,25–32 all of which function by binding substrates in a hollow interior that is reminiscent of an enzyme active site. This comparison is still as strong today, with many current articles citing attempts to match the efficacy of biocatalysts as a primary driver.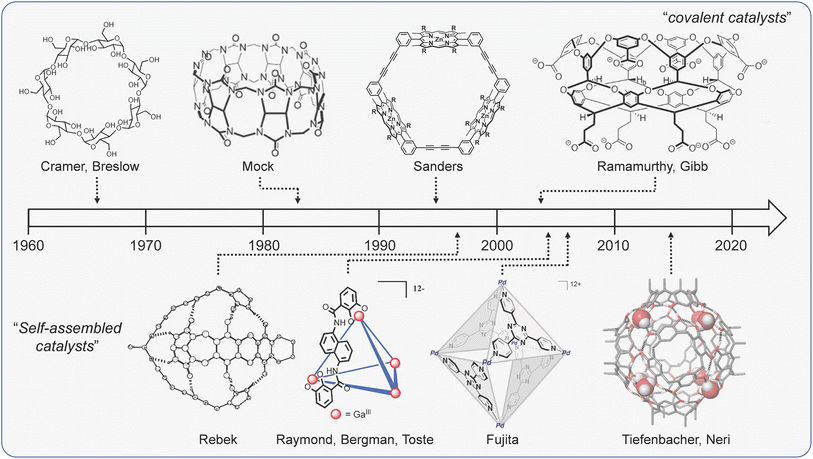 | ||
| Fig. 1 A brief (and select) history of bio-inspired supramolecular catalysts. Structures adapted with permission from ref. 32, Copyright 2018 Wiley-VCH; ref. 81, 122, 133 and 168, Copyright 2010, 1998, 2022, 2021 American Chemical Society. | ||
But what are the similarities between supramolecular and enzyme catalysis, and where do they end? It is easy to see why these analogies arise; molecular containers superficially look like an enzyme, possessing an internal 3D microenvironment where catalysis takes place. There are other similarities as well: (1) most supramolecular catalysts involve some sort of pre-association (Michaelis) complex; (2) enzymes and supramolecular catalysts often accelerate chemical reactions without changing the fundamental uncatalysed mechanism (cf., organometallic complexes); (3) activity is often derived from entropic factors, making it distinct from most synthetic catalysts, and more akin to enzyme reactivity (although how much of a role entropy reduction plays within enzymes remains a debated topic, see below); (4) many examples of cage catalysis also occur in water. However, it is clear that enzymes are much more complex, asymmetric structures, which provide highly directional and precise interactions tailored to select specific substrates and facilitate electronic re-organisation during catalysis, leading to remarkable acceleration and selectivity. In contrast, synthetic supramolecular catalysts often interact with bound species in a poorly defined manner, relying heavily on non-directional interactions (e.g., coulombic and van der Waals forces), and are often selective on the basis of minimising steric clash as opposed to the formation favourable interactions.33 This likely explains why the catalytic proficiency of supramolecular catalysts are many, many orders of magnitude less than most enzymes.
It also has to be remembered that enzymes have evolved to catalyse reactions in order to sustain life. As a result, they have to work in water, and be able to select substrate(s) that are often present in low concentration(s) as part of a library of structurally similar compounds. This is partly why enzymes utilise mechanisms that involve the strong pre-association of reactants, which then necessitates even more effective transition state (TS) recognition. Chemists who are designing catalysts for synthetic applications do not have to meet these same challenges; most laboratory reactions utilise a single substrate and take place at several orders of magnitude greater concentration compared to a cellular environment.
2 Scope of review
This review provides a perspective on the intrinsic catalytic properties of coordination cages. We take intrinsic catalysis to mean where the cage acts independently and sub-stoichiometrically to accelerate the conversion of bound reactants into products. With a few exceptions, we will limit examples where encapsulation-based reactivity is not accompanied by turnover,34 nor will we cover catalysis that involves bound transition metal (TM) complexes.35–37 For catalysis with covalent cages38–41 and macrocycles,42,43 hydrogen-bonded capsules,44,45 metal–organic frameworks (MOFs),46,47 and covalent organic frameworks (COFs),48,49 we point the reader to relevant review articles. The review is also non-comprehensive; we do not aim to cover every example of cages catalysis; instead, we have selected specific articles that we feel best support the different subjects discussed.3 Coordination cages: from self-assembled systems to molecular hosts and catalysts
3.1 What are coordination cages?
Over the past three decades, the self-assembly of simple building blocks into species of greater complexity through reversible “non-covalent” interactions has become a prominent area of interest. It has allowed access to a range of structures that would be virtually unattainable using “conventional” synthetic methods. At the heart of self-assembly protocols sits metallosupramolecular chemistry, which uses the reversible interactions of TMs and multitopic ligands to facilitate access to macromolecular species. The conceptual simplicity of this method is exemplified by Fujita's 1990 landmark paper, which described the quantitative formation of a molecular square by mixing 4,4′-bipyridine and an ethylenediamine palladium complex.50 Over the intervening period, many coordination assemblies of increasing complexity have been reported, which have been summarised in many excellent reviews.2–4Several features of metallo-organic assembly have made this the go-to method for preparing cages of varying shapes and sizes. Firstly, TM ions often possess well-defined coordination geometries, which has facilitated access to predictable structures via different design approaches (Fig. 2).2,51–54 Many of these structures utilise rigid ligands that are relatively simple and easy to prepare such that the overall assembly can be prepared in just a few steps. Secondly, the dynamics of (certain) metal–ligand (M–L) interactions are optimal as they balance lability and strength. This allows access to higher-order species through error checking while giving relatively stable ensembles aided by cooperative effects.55
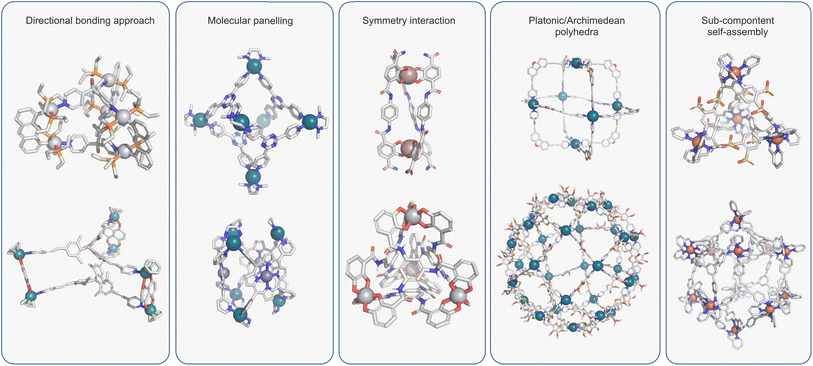 | ||
| Fig. 2 Design approaches for coordination cages include: directed bonding and the related molecular panelling;2,51 symmetry interaction strategy;52 platonic or archimedean polyhedral;60 sub-component self-assembly.54 | ||
Despite its many positives, coordination self-assembly is not a complete panacea. For instance, self-assembled architectures will almost always lack the robustness of species prepared using covalent chemistry. From the perspective of catalysis, this can limit the types of reactions promoted, e.g., it is difficult to mediate reactions that involve a large excess of a substrate that can coordinate to the metal. It is also challenging to generate low-symmetry assemblies (cf., enzymes), although significant progress has been made in this area in the past ten years.56 Nonetheless, self-assembly can be viewed as an enabling method because (i) it has widened the field to those who do not have expertise in conventional synthetic methods, and (ii) it promotes easy access to cage-like host systems that previously were considered synthetically challenging.
3.2 Coordination cages as molecular hosts
Many 3D coordination assemblies have one key aspect: they possess a central cavity. This is the main feature that leads to a variety of functions, from the encapsulation of cytotoxic drugs57 through to the protection of air-sensitive species,58 and obviously catalysis. It is easy to assume that all hollow molecular structures will intrinsically act as hosts; simply mixing the two species will lead to encapsulation (assuming the size/shape is matched). However, different factors can influence guest binding, including properties specific to the system and external factors such as solvent. For closed-shell organic hosts, Rebek introduced the “55% rule” to predict host–guest binding, which states that the guest should fill 55% ± 9% volume of the host cavity.59This guide has also been used with coordination cages,61–64 however, because most possess a porous structure with multiple large portals, the concept of internal volume can sometimes be meaningless. For example, it could lead to a significant underestimation in the size of the guest that will be bound.
Coordination cages are different to many other host systems in that they invariably possess permanent charge (i.e., pH independent). This can have profound and varying implications. In many cases, counterions act as strong binding guests. For example, small M4L6 tetrahedral cages are often shape and/or size complementary for common weakly coordinating anions (e.g., BF4−, PF6−) that are used in self-assembly reactions.65 Counterions can also alter the solubility of metallo-organic cages, which then dramatically influence host–guest chemistry. This is particularly evident for cages with small, charge-dense, counterions; Fujita pioneered the use of NO3− to make cationic assemblies that are soluble in water, while Raymond's use of K+ to charge-balance his anionic cages has a similar effect. These counterions almost certainly impart their solubilising properties via strong external hydration, which means the cage is left “empty” (i.e., except for solvent) to bind less polar guests, often with the exclusion of the internal solvent as a major driving force (i.e., the hydrophobic effect). This approach has been particularly successful for cages that possess flat aromatic, panel-like ligands, as they provide relatively large, hydrophobic surfaces. To date, water-soluble cages have dominated the area of cage catalysis because this mode of binding can be applied to many different neutral organic substrates.
Creating a cage that binds organic substrates can also be accomplished using counterions that are too large to become encapsulated. The Lusby group have used this approach, exploiting tetrakis[3,5-bis(trifluoromethyl)phenyl]borate (BArF4−) anions.66 This strategy also has an opposite solubilising effect compared to the use of small, charge-dense counterions; it allows charged cages to dissolve in apolar solvents such as dichloromethane. This has the knock-on effect that the internal cavity is polar with respect to the solvent phase, thereby promoting encapsulation via the formation of polar host–guest interactions. From a catalysis perspective, using polar interactions as a means to drive substrate encapsulation also facilitates reactivity based on electrostatic mechanisms (see below).
3.3 What are the structural features that make coordination cages potentially good catalysts?
The last fifty years have seen major advances in catalyst design and development with several Nobel prizes in chemistry recognising progress in asymmetric catalysis in 2001 (Knowles, Noyori and Sharpless), metathesis in 2005 (Chauvin, Grubbs and Schrock), cross couplings in 2010 (Heck, Negishi and Suzuki), biocatalysis in 2018 (Arnold, Smith and Winter) and organocatalysis in 2021 (List and MacMillan). The first three of these awards have in common that they recognise research based on reactive organometallic species. This approach has proven to be extremely successful due to its many benefits (e.g., excellent substrate scope), and lends itself to the evolution of catalyst design, leading to ever more efficient systems. Despite the clear success of these methods, there are challenges. For example, organometallic complexes and/or their catalytic intermediates can require manipulation under an inert atmosphere. Chemo- and regioselectivity can also be difficult to achieve when the catalyst needs to target a single site in a substrate that possesses many (similar) functional groups.An alternative to this catalytic paradigm is the use of weak, non-covalent interactions, as demonstrated in biocatalysis and organocatalysis. The challenges with these approaches are the complete opposite; these catalysts are inherently benign and easy to handle but designing systems with high activity towards a range of reactions is difficult. This is unsurprising as the stabilisation of intermediates and TS using only weak, non-covalent bonds is very challenging, necessitating multiple interactions with the catalyst.
Enzymes show us that highly efficient catalysis can be achieved using only non-covalent interactions.67 This activity is built upon engineered collections of non-covalent bonding and is part of the reason enzymes have evolved with interior active sites; the peptidic structure envelops the substrate(s), providing an array of stabilising interactions. It is this similar propensity to encapsulate whole substrates and provide many interactions that makes coordination cages stand out as potentially excellent catalysts.
Compared to other synthetic host–guest systems, coordination cages possess a number of specific features that make them appealing from a catalysis perspective. Firstly, it is relatively straightforward to create cages of varying shapes and sizes using metallosupramolecular chemistry meaning that it is (relatively) easy to tailor the cavity towards different reactions and substrates. Secondly, many coordination cages are often porous, possessing relatively large portals (cf., H-bonded organic capsules). This allows the flow of substrates and products in and out of the cavity, facilitating turnover – even if the thermodynamics of the system dictates that a diminishing quantity of substrate-cage complex will eventually halt catalysis. For the few cages that appear closed-shell, it has been shown that the structure can readily deform to promote reversible guest exchange without breakage of the M–L bonds.68 Thirdly, certain cages are intrinsically chiral e.g., those built on tris(bidentate) octahedral metal coordination units,69 facilitating possibilities in asymmetric catalysis. Finally, the presence of a metal ion embedded in the structure can impart additional functionality. The most common functionality is simply charge, which can stabilise reactive intermediates through electrostatic interactions. In addition, metal ions can also provide the assembly with photochemical properties,63,70 or if they possess a vacant coordination site, Lewis acidic reactivity.71
4 How do we probe coordination cage catalysis?
4.1 Experimental analysis of cage-catalysed reactions
In all catalyst development, a key to producing ever more effective systems is to obtain a detailed mechanistic understanding. In cage catalysis, experimental interrogation has often focused on answering questions in three broad areas:(a) Is the observed catalytic behaviour directly attributable to interactions between the cage and the substrate?
(b) How effective is the catalyst? What acceleration does the catalyst provide compared to the reference reaction? Does it operate under sub-stoichiometric conditions? How selective is the catalyst?
(c) How does the cage leverage activity? What are the factors that lead to a higher rate constant inside the cage compared to the equivalent bulk-phase reaction?
In the following sections, we will briefly discuss the types of experiments commonly undertaken to answer these fundamental points.
4.2 Linking catalysis to encapsulation
As with any catalytic reaction, it must be established whether the observed activity comes from the presumed compound and not, for example, from either impurities or break-down species. For cage systems, impurities and break-down species are both likely to be the self-assembly constituents i.e., the free metal and ligand. Undertaking control experiments with these species can be useful but only up to a point. For example, many “naked” metal ions are often reactive (e.g., Lewis acidic), so the observation of catalysis with only the metal ion does not prove that the cage is not also a catalyst. A further difficulty often stems from practical issues such as solubility (e.g., control reactions using organic ligands in water).Assuming that catalysis does stem from the cage, showing that reactivity is due to encapsulation is key. As in any mechanistic investigation, evidence to support such a hypothesis can be obtained through a combination of different analyses.
Host–guest studies are, of course, not only limited to the substrate. Assessing the strength of product binding is important for understanding any inhibition, and probing the interactions with a TS mimic can provide clues as to the origins of catalysis.
While the use of inhibitors demonstrate that catalysis stems from encapsulation, what they do not always show is which encapsulated species is responsible for the activity. The most common assumption would be that an inhibitor blocks substrate binding. However, cage catalysis does not need to result from substrate binding, rather encapsulation of a co-factor can trigger bulk-phase reactivity in which the substrates are never bound.72,73 It is also feasible that a cage can activate an impurity e.g., a cationic cage could activate trace weak acid through stabilisation of the conjugate anion, leading to “hidden” Brønsted acid catalysis.
With cages that use building blocks with catalytically-capable groups (see below), the use of model compounds are essential to understand whether catalysis truly represents an enhancement of some intrinsic property.
4.3 Assessing catalytic performance
Undoubtedly the quickest and most facile way to show catalytic capability is to compare the yield of the product in the presence and absence of a cage. While it seems intuitive that a comparison to the reference reaction should be made, this is often uncommon with other types of catalysis as there is often no background process (e.g. transition metal-catalysed cross coupling). For many cage-catalysed reactions, this is not the case (e.g., hydrolysis, Diels–Alder (DA) and other pericyclic reactions) hence the comparison is necessary. Solubility also plays a key role in these comparisons i.e., does the cage show “catalysis” because it simply solubilises the reactants? This is particularly relevant to aqueous cage catalysis, where the solubility of the reactants can be minimal. This can be difficult to ascertain, but showing that structurally similar cages, which both bind the same reactants but show very different catalytic properties, can be very convincing. In addition, the practical aspects of monitoring the change in temporal concentrations of a heterogenous mixtures can be problematic.Kinetic analysis is a more thorough tool for analysing cage-catalysed reactions because it can be used to determine mechanistic information, such as de-convoluting pre-association and subsequent catalytic rate-limiting steps, and provide other vital information, such as product inhibition. By obtaining various kinetic parameters, it is possible to quantify catalytic properties and make meaningful comparisons. These kinetic parameters (unlike yields) ultimately give access to catalytic activation energies, which facilitates the involvement of computational tools to shed light on the origins of catalytic activity.
The most common method of determining kinetic constants for cage-catalysed reactions is through saturation methods. This uses the model derived by Michaelis and Menten (and Briggs and Haldane) in the early 20th Century to probe enzyme kinetics,75 which involves the rapid and reversible pre-association of a substrate, S, to an enzyme, E, to form the Michaelis complex, E·S, followed by a rate-limiting, product forming step (kcat):
Using the assumptions that (a) the steady-state concentration of [E·S] remains constant and (b) the rate of reaction is measured under conditions where [S] ≈ [S]total, because commonly [S]total ⋙ [E]total, they arrived at eqn (1). This equation has most commonly been applied in its linear forms, such as Lineweaver–Burke (eqn (2)) and Eddie–Hoffstee (eqn (3)) plots:
| v = Vmax[S]/Km + [S] | (1) |
| 1/v = Km/Vmax(1/[S]) + 1/Vmax | (2) |
| v = −Km(v/[S]) + Vmax | (3) |
Experimentally, the initial reaction velocity (v) is determined over a range of substrate concentrations ([S]). The rate when the enzyme is saturated, Vmax, can be obtained directly from the relevant plot, and corresponds to the maximal rate that will occur at a given enzyme concentration. Under this regime, the reaction cannot go any faster as the enzyme-substrate complex is fully formed (i.e., [E·S] is maximised). From Vmax, the rate constant (turnover number) for the product forming step, kcat, can be easily calculated according to eqn (4):
| kcat = Vmax/[E]total | (4) |
The Michaelis constant, Km, is the composite of the in, out and catalytic rate constants, according to eqn (5).
| Km = (koff + kcat)/kon | (5) |
Depending on the relative rates of kcat and koff, Km can have different meanings. For relatively inefficient enzymes, where substrate dissociation is quicker than product formation (kcat ≪ koff), then Km tends towards the dissociation constant for the E·S complex. For many supramolecular catalysts that provide relatively small acceleration, using Km as a proxy for the dissociation constant offers a reasonable interpretation. For many highly effective enzymes, where kcat ≫ koff, the value of Km approaches kcat/kon, which is simply the ratio of the second order to first order rate constants in the sequence of reaction steps (E + S → E·S → E·P).
Recently, numerical methods have been used to calculate key parameters, such as kcat, which has been facilitated by access to relevant software.76,77 There are advantages of this approach, such as (a) several parameters can be extracted from a single experiment; (b) it removes several of the assumptions made in deriving the Michaelis–Menten equation (e.g., it is not the case that [S] ⋙ [E]); (c) it can be used when multiple reactions contribute to the overall rate (e.g., catalysed + uncatalysed process).
Clearly, many cage-catalysed reactions follow a similar general mechanism to enzymes i.e., the reversible pre-association of a substrate followed by an irreversible product forming step, hence the relevance of calculating enzyme-like parameters. But what do these parameters actually mean? Probably the most commonly reported measure of catalytic performance is the ratio of kcat/kuncat; this is quite frequently unitless because the uncatalysed reaction and conversion of the cage-substrate complex are unimolecular (there are exceptions to this, for example in dual-binding catalysis that has units of concentration). This reflects how effective the catalyst is at converting the bound substrate into the bound product in comparison to non-bound reactants being transformed into non-bound product. It is directly related to the relative energy barriers of the catalysed versus the uncatalysed reaction, and provides an understanding of how well the catalyst stabilises the TS relative to the substrate. The value of kcat/Km is the second-order rate constant that corresponds to the efficiency with which a substrate is converted into product following a collision with the enzyme.78 There are examples of enzymes that show diffusion-limited reactions rates (i.e., every collision results in a chemical reaction).79 This is frequently seen as the key parameter in enzyme kinetics because it is relevant to sub-saturation conditions (i.e., where [S] is lower than Km). This can be viewed as less significant in cage catalysis because there is no limit in the concentration of substrate that can be used. This second-order proportionality constant is also referred to as the specificity factor – it shows how efficiently different substrates can compete for the active site. Finally, the term catalytic proficiency, (kcat/kuncat)(1/Km), has also been used to estimate how effective a catalyst is at recognising, and thus stabilising the TS. This has units of reciprocal concentration and can be viewed as a TS association constant. Remarkably, enzymes can exhibit catalytic proficiencies of more than 1020 M−1.80
Table 1 provides a summary of these catalytic performance measures for some of the most efficient cage-catalysts and a comparison to their biological counterparts. While there have been great strides made in the field of cage catalysis, it is clear there is some way to go to reach the overall efficiencies that enzymes achieve!
While having access to these kinetic parameters provides a measure of how effective a given catalyst is, it offers little clue as to the origin of the activity. Although further experimental methods are available for probing how the catalyst might affect both the entropy and enthalpy of activation (e.g., Eyring analysis), it is ultimately the use of in silico methods that will help shed light on structure-function relationships (see below). In this regard, kinetic analysis is key to help benchmark the computational tools that are being developed.
5 Computational analysis – opportunities and challenges
Over the past two decades, computational chemistry has played a crucial role in shaping our understanding of homogeneous and enzymatic catalytic reactions.85,86 This research field has not only provided atomic-level insights into the fundamental aspects driving catalysis and selectivity but also facilitated the prediction of possible outcomes and the design of new catalysts.86–88In the realm of supramolecular chemistry, one of the most promising applications of computation has been the prediction of synthetically viable structures via in silico screening. In such cases, even qualitative analyses related to cavity structure and volumes have shown to be suitable for identifying and screening multiple cage designs before attempting their synthesis in the laboratory.89–92 However, the application of similar strategies to explore cage catalysis and even binding strength has largely been absent, with the few computational studies limited to specific host–guest cages and reactions. Recent advances in computational methods and automation, as well as a closer interaction between experimental and computational chemists, hold the potential to change this situation. However, to achieve this, a deep understanding of the chemical processes at play and the associated computational limitations is necessary. Below we briefly discuss each of these aspects and refer the readers to specialised reviews for more detail.93
5.1 Practical considerations
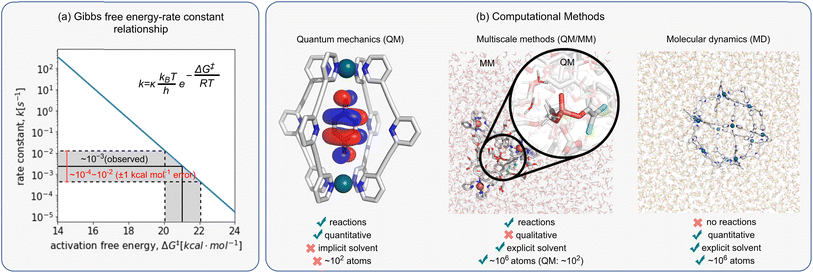
When comparing computed results against experiments, it is helpful to appreciate the inherent accuracy of the chosen computational methodology. This can be done by analysing the Eyring equation (eqn (6)), which relates the macroscopic rate constant, k, with the Gibbs free energy of activation, ΔG‡:| k = κ(kBT/h)exp(−ΔG‡/RT) | (6) |
The exponential nature of eqn (6) also means that even small errors in computing ΔG‡ can lead to several orders of magnitude differences in rate, making the comparison to experimental data impossible. Therefore, errors lower than the so-called “chemical accuracy” (<1.0 kcal mol−1) are required when computing ΔG‡, even though there is no guarantee this can be achieved with current approaches (Fig. 3a).
5.2 Technical considerations
Today, a number of computational approaches are available to model catalytic processes. They include quantum mechanical (QM) methods, such as ab initio and density functional theory (DFT) approaches and combined quantum mechanics/molecular mechanics (QM/MM) methods, where the reaction is modelled at the QM level and the environment described using force field (FFs)-based approaches, including classical molecular dynamics (MD) and Monte Carlo simulations.In recent years, the emergence of efficient DFT94,95 and ab initio approaches96 has enabled us to model systems of increasing size and complexity using QM only. However, these approaches alone cannot guarantee quantitative accuracy because they often fail to account for solvent, entropy, and dynamical effects, which may introduce errors of as much as 10 kcal mol−1 when computing ΔG‡.97–100 This translates into differences in rate constants of many orders of magnitude. In many cases, solvent effects are included via a computationally cheap implicit solvent model calculation (e.g., PCM, CPCM, SMD), either as a correction on the energy of the system or during the geometry optimisation calculation. However, their use may be insufficient when specific interactions between substrate with the solvent and/or cage are important, e.g., due to enthalpic H-bonding interactions or entropic effects. For large and flexible systems, such is the case for many host–guest complexes, identifying the conformations accessible under the experimental conditions also becomes an important issue. However, recent advances in the automated sampling of both reactant and TS geometries promise to overcome such limitations.101 Luckily, even when these limitations are present, some systems benefit from error cancellation due to the structurally similar competing pathways, enabling one to obtain reasonable agreement with experiments using only electronic energy differences. This is the case, for example, when exploring enantioselectivity, where relative rather than absolute rates (energy differences) are required.102
To account for solvent and entropy effects, computational chemists have often relied on MD approaches. While much cheaper than QM methods, they do not allow for the study of bond formation and breakage/cleavage, making them unsuitable for cage catalysis. Combined QM/MM, pioneered by Warshel and Levitt in 1976 to study enzyme catalysis,103 provides a practical alternative to include solvent effects in catalysis. However, while classical MM methods have been used to study metallo-cage self-assembly104,105 and guest binding,97–100 applying QM/MM strategies to supramolecular catalysis has not been extensively explored. This is partly due to the lack of accurate and efficient protocols to model these systems. For example, while extensively validated and ready-to-use FFs exist for standard protein amino acids, their generation for metallo-cages, particularly metal centres, remains a lengthy endeavour. Ab initio MD, wherein MD trajectories are propagated using forces computed “on the fly” from electronic structure calculations, has been used recently to study cage catalysis.106,107 Nonetheless, they remain computationally expensive, and have limited application to large systems or studying long-time processes.
One of the most extensively computationally studied cage catalysts is the tetrahedron [Ga4L6]12− cage experimentally investigated by Bergman, Raymond, and Toste.108 This is likely due to the large amount of experimental information available for this cage, including rate constants for a range of different reactions. This has enabled computational chemists to quantitatively compare their modelling results to experiments. Indeed, several groups have modelled these reactions, including the hydrolysis of orthoformates, the aza-Cope rearrangement, reductive elimination and the Nazarov cyclization (see Sections 5.6 and 5.7). The catalysed hydrolysis of orthoformates and acetals was the first cage-catalysed reaction studied computationally by Warshel and co-workers using the Empirical Valence Bond (EVB) approach.
Later Nakajima and co-workers studied the aza-Cope rearrangement using QM/MM methods.109 In recent years, Head-Gordon and co-workers have employed DFT and ab initio MD methods to investigate the C–C reductive elimination reaction of high-valent Au(III) metal alkyl complexes and the role of water in the reaction.110 The same reaction has also been studied by Ujaque and co-workers, using MD simulations with methanol explicit solvent and DFT.111 They explored the role of solvent on the activation barrier as well as the effect of increasing the substrate size. We have also employed MD simulations and DFT to study the contrasting catalytic ability of two Pd2L4 cages to catalyse Diels–Alder reactions of quinone dienophiles.112 As more examples of (combined) experimental and computational studies emerge, it will be important to model different cages and reactions – including negative data and repeated measurements – to ensure that computational results are “right for the right reason” and not just coincidental for a single type of reaction or cage. The ultimate test will be the ability of computations to predict novel catalytic cages.
6 How does cage catalysis work?
6.1 Is there a universal set of features that makes a good coordination cage catalyst?
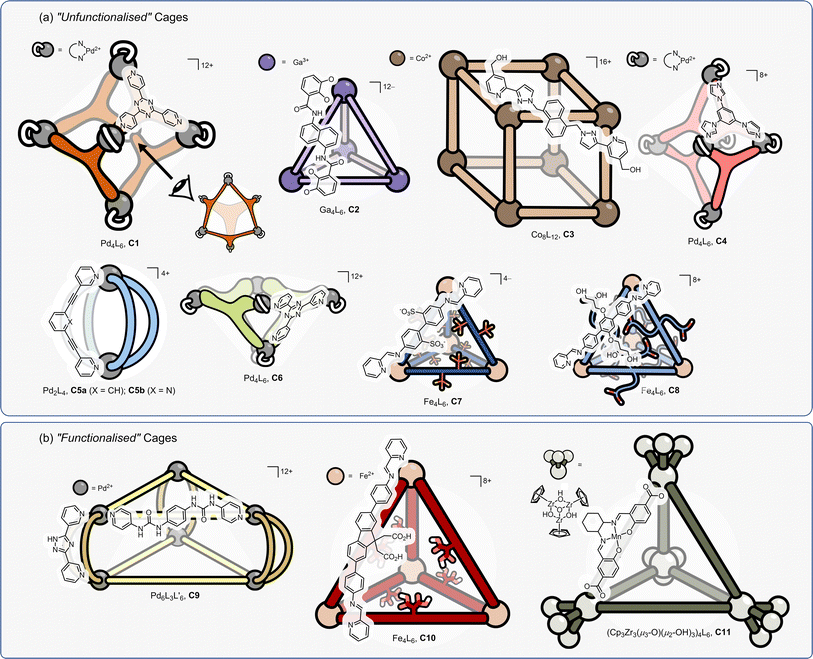
Despite the hundreds of coordination cages reported in the past 20 years, only a handful have been shown to be proficient catalysts. This begs a couple of questions: are these privileged structures? And if so, are there specific features of the systems that make them effective catalysts?Coordination cage catalysts can be classified into two types; those whose catalytic behaviour stems from extrinsic or intrinsic factors (Fig. 4).
Those that fit into the extrinsic category (Fig. 4a, C1–C8) can be thought of as “unfunctionalised” cages; the metal centres are coordinatively saturated and the ligands do not possess any obvious functional group that on their own may display some latent activity. For example, in cage C5a, neither a representative metal vertex complex (e.g., Pd(pyridine)4·2BArF) or the uncoordinated bridging ligand, would show any catalytic properties. With these cages, catalysis can be thought of as an emergent property – similar to enzymes, wherein most amino acid residues show no catalytic potential, yet highly effective catalysis emerges from folding. While cages C1–C8 are not structurally similar, there are some similar features that stand out, such as they utilise relatively small cavities that can control and precisely position substrate(s), intermediates or TS.
Cages whose behaviour can be classed as stemming from intrinsic factors (Fig. 4b, C9–C11) are composed of components that already possess functionalities that could be expected to display some catalytic properties independently.113–116 In these examples, the cage's catalysis can be seen as an enhanced property, wherein the presence of multiple catalytic groups leads to cooperative effects. The cages in this category can possess relatively open and large cavities; it is less imperative that the substrate is internalised because enhanced function may arise from the localisation of groups that are already weakly active, and this can easily occur at a portal.
6.2 Is a good host automatically a good catalyst (or is a good guest a good substrate)?
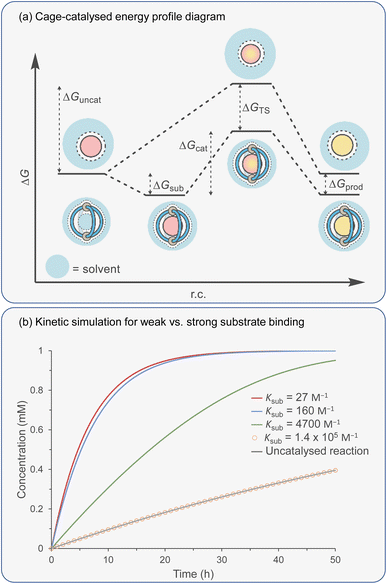
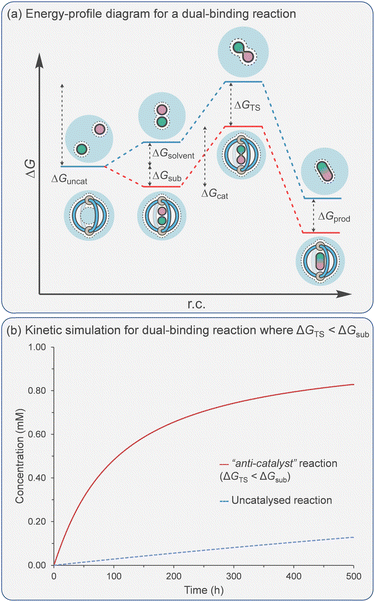
Catalytic studies with cages have invariably followed on from host–guest studies. This appears to be a logical strategy: first, identify a good guest and then find a reaction in which it can act as a substrate. This approach has some clear benefits; it will ensure that the substrate-cage complex will be present in high concentration throughout the reaction, which is beneficial as the observed rate is proportional to [substrate⊂cage]. However, strong substrate binding can lead to an opposing detrimental factor that can be easily visualised in an energy profile diagram (Fig. 5a). According to the energy span model,117 the activation energy is determined from the lowest energy state to the highest. Consequently, tighter binding of the substrate can lead to over stabilisation of this state (ΔGS) with respect to the TS binding energy (ΔGTS), producing a greater overall catalytic energy barrier (ΔGcat) (assuming no product inhibition). This scenario can occur in any situation where substrate binding is favourable i.e., Ksub > 1 M−1, ΔGsub is negative. When binding becomes unfavourable (i.e., Ksub < 1 M−1, ΔGsub is positive), then the catalytic activation barrier ΔGcat is solely determined by the magnitude of TS stabilisation. Of course, the energetic differences between substrate and TS binding are not the sole arbiter of catalytic effectiveness; it is also dependent on concentration and relative catalyst loading, which in combination with binding affinities determine catalyst speciation (i.e., how much substrate is bound). These factors can be simulated using software that solves the relevant differential equations. What becomes obvious from this simulation is that under realistic laboratory conditions (e.g., 0.1 mmol concentration of catalyst and 1 mmol of substrate), with effective transition state stabilisation (ΔGTS = −7 kcal mol−1), then the best acceleration is observed with surprisingly weak substrate binding (Fig. 5b).The challenge of course comes in designing a catalyst that can differentially stabilise the TS compared to the substrate. Often, the same interactions that cause binding of the substrate are present in the TS. For example, some small molecule H-bond donor organocatalysts will interact with only a single functional group e.g., a urea hydrogen bonding to the heteroatom of a substrate (Fig. 6a).118 In this case, the changes in electronic structure over the course of the reaction can mean that non-covalent bonding of the TS is inherently stronger than the substrate, which provides some acceleration. However, this effect in isolation is relatively modest and the difference between catalysed and uncatalysed reaction can be masked in polar solvents. Additional selectivity for the TS over the substrate can arise due to a greater number of interactions and/or due to recognising a specific 3D orientation of reactive functionality (Fig. 6b).119 Occasionally, hosts can be much better binders for the substrate than the TS such that “anti-catalytic” properties are observed. This can be due to either an increased steric bulk of the TS, which is inhibited by a confined environment (Fig. 6c),58 or by binding the substrate in a conformationally unreactive state, causing an energetically disfavoured rearrangement in order to reach the TS (Fig. 6d).120
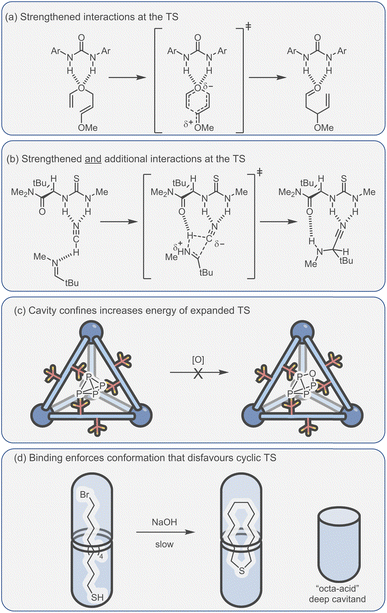 | ||
| Fig. 6 Catalytic activity due to enhanced TS binding can arise from (a) the strengthened interactions between the catalyst and TS;118 (b) additional interactions that are specific to the TS;119 (c and d) conversely, confinement effects can also lead to a higher TS energy, allowing the protection of reactive species.58,120 | ||
6.3 Product inhibition: the tail wagging the dog
In the same way that it is difficult to discuss cage catalysis without mentioning bio-inspiration, it is equally difficult to ignore product inhibition. This adverse effect has become synonymous with all types of bio-inspired catalysts, from macrocycles25,121 to self-assembled capsules15 and coordination cages (see below).30 As a consequence, and because in many cases product inhibition is often extreme (i.e., there is no turnover), it has had a profound effect on shaping the field of supramolecular catalysis.Product inhibition is almost invariably observed in catalysis that involves the co-binding and fusion of two substrates. In these examples, co-binding is both a friend and a foe; dual-encapsulation leads to acceleration, however, turnover necessitates the entropically uphill process of displacing a single product by two substrates. This paradigm is universal, independent of how the substrates/products interact with the host, having been observed in systems that utilise the hydrophobic effect,25,30 metal–ligand (M–L) interactions121 or dispersion interactions.15 Occasionally, autoexclusion, which necessitates weakened product binding, has been observed.30,41,122 This most commonly occurs when the product size or shape is mismatched to the catalyst. Engineering this scenario is non-trivial and is also quite specific to processes that generate conformationally locked products e.g., fused ring adducts resulting from pericyclic transformations.
As a consequence of product inhibition, supramolecular catalysts have often been applied to specific types of processes. In his excellent 1998 review,123 Sanders classified reaction types as “transformations”, “transfer”, “fission” and “fusion” (Fig. 7). The key difference in these reactions is whether the turnover step is entropically neutral (“transformations” and “transfer”), entropically downhill (“fission”) or entropically disfavoured (“fusion”). This is likely why certain transformations, such as hydrolysis and rearrangements, are popular choices for exemplifying the catalytic properties of supramolecular systems. Considering the synthetic utility of the different reaction types, being unable to catalyse the fusion of molecular fragments can be seen as a major limitation.
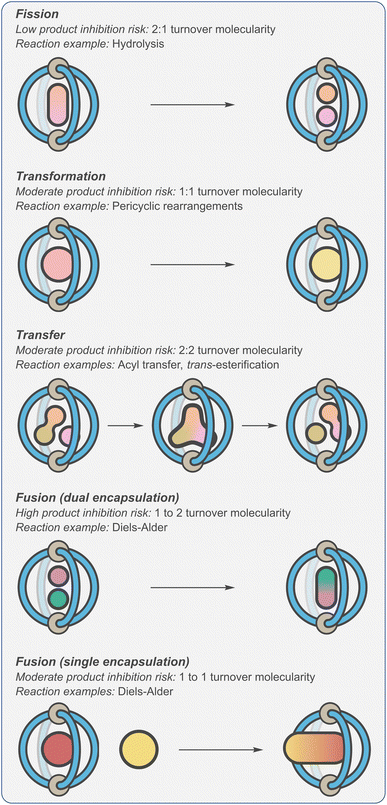 | ||
| Fig. 7 Classification of cage-catalysed reactions defined by propensity to display product inhibition.123 | ||
Alternatively, it has been shown that controlling the relative number of reactants and products that are bound, rather than the overall reaction molecularity, can be an effective and more reliable method (cf., autoexclusion) of avoiding turnover problems.83,124,125 For example, it becomes possible to negate thermodynamic sinks if only one of the two substrates to be fused is encapsulated (Fig. 7, “fusion (single encapsulation)”). In this scenario, the rate-limiting step is bimolecular, with any subsequent three-component Michaelis complex being transient. Crucially, turnover in this type of mechanism is entropically neutral i.e., one product is displaced by one substrate. This approach has been enabled by a shift towards modes of acceleration that involve electrostatic modulation of substrates and TS.
Product inhibition can also be influenced by kinetic factors. The most obvious extreme of this would be a ship-in-a-bottle scenario, wherein the substrates are small enough to enter the cavity but because the fused product is much larger it cannot escape. However, because most coordination cages possess relatively large portals (or portals that can readily deform) this is very rarely a problem.126 A more subtle form of kinetic product inhibition would be if the strength of binding means that the off rates are particularly slow. In reality, even with high affinity complexes, the dissociation rate is often significantly faster than the rate limiting breaking or making of covalent bonds.
6.4 Understanding the origins of catalysis: Where does rate acceleration stem from?
Unpicking the factors that determine how an effective (or ineffective) cage catalyst operates is both a fundamental academic question and also key to developing better systems. The most fundamental feature of a catalyst is its ability to speed up the reaction without being consumed in the process. In the following sections, we discuss the most common mechanisms by which a cage can influence the rate of a given chemical reaction. We group these mechanisms according to whether the lowering in the free energy of activation principally comes from a reduced ΔH or ΔS component (which is supported, in limited examples, by Eyring analysis). It should be noted that these mechanisms are not mutually exclusive and might operate in tandem to produce the observed acceleration.6.5 Cage catalysis mechanisms that rely on reducing the entropy of activation. Part 1: dual-binding catalysis
Reactivity that is based on binding two substrates has defined supramolecular catalysis more than any other approach. Various molecular hosts have been exploited to probe this strategy; examples include Breslow's use of cyclodextrins in the 1970s,25 acyclic H-bond receptors,127 the porphyrin macrocycles of Sanders' in the early 1990s,27,121 Rebek's hydrogen-bond capsules later that decade,15 and, more recently, several metallo-organic cage systems. Many of the themes to emerge from these investigations (e.g., product inhibition) appear universal, irrespective of the system or even the types of association. Often, acceleration stems solely from reducing the entropic penalties associated with progressing from a bimolecular reactant state to a unimolecular TS rather than from catalytic activation of the individual components. This is probably part of the reason why the catalysis of cycloaddition reactions has been a popular choice, as the uncatalysed processes possess a large entropy of activation.Considering an energy profile for a dual-binding mechanism (Fig. 8a), the reduction in ΔGcat, compared to the reference reaction ΔGuncat most obviously stems from the energy difference of the Michaelis complex (ΔGsub) compared to the dual reactants within a solvent shell (ΔGsolvent). This difference in energy can be thought of as the sum of two separate parts; the energetic penalty of bringing two reactants together into a solvent shell (ΔGsolvent) and the energetic gain of forming the ternary Michaelis complex with reactants A and B (ΔGsub). While the magnitude of both ΔGsolvent and ΔGsub will depend on the identity of the ternary complex/solvent, the summation of these values will serve as a baseline for catalysis. If further degrees of freedom other than translational are frozen in the Michaelis complex (e.g., rotational or torsional), then a bigger decrease in the activation barrier will be observed for the catalysed reaction (i.e., ΔGTS > ΔGsolvent + ΔGsub).
If the bound substrates need to undergo some distortion in order to react, raising ΔH‡ compared to the uncatalysed reaction within the solvent shell, then a smaller decrease (i.e., ΔGTS < ΔGsolvent + ΔGsub) will occur.
As previously discussed, binding the reactants is beneficial due to the higher concentration of the Michaelis complex (since rate = kcat[A·B⊂Cage] for the catalysed reaction vs. rate = kuncat[A][B] for the uncatalysed reaction). It also has a detrimental effect as it can increase the catalytic activation barrier when ΔGsub < 0 (reactant stabilisation). However, unlike the catalysis of unimolecular reactions, acceleration can still be observed even when ΔGcat > ΔGuncat. Such an apparent “anti-catalyst” scenario is simulated in Fig. 8b.
In many examples of dual binding catalysis, the effectiveness of the catalyst is assessed using the ratio of the rate of product formation in the catalysed vs. the uncatalysed reaction. However, this measure is highly dependent on the set of experimental conditions. For example, this ratio is often very high when catalysis is carried out at low concentration versus high concentration. A more reliable measure is kcat/kuncat, which can also be expressed as Effective Molarity (EM), as outlined in the excellent review by Mandolini.128 This represents the hypothetical concentration of one of the reactants needed for the uncatalysed bimolecular reaction to occur at the rate equal to that of the catalysed reaction under pseudo-first-order conditions.
It has been estimated that the theoretical limit for kcat/kuncat or EM, based solely on entropic arguments (“passive binding”129), can lead to an acceleration as much as 106 to 108 M.130–132 With the exception of a few stand-out examples, notably cucurbituril-mediated cycloadditions,26,133 many examples of supramolecular catalysis show EM many orders of magnitude less than the theoretical limit, often below 1 M. As described above, the reasons for this may be that there are still degrees of freedom that are not frozen by the catalyst (i.e., torsional or rotational), or that the substrates are not optimally aligned such that there is an enthalpic penalty on progression towards the transition state.
Considering the leading role that Fujita has played in the area of metal–organic assembly, it is not surprising that some of the first coordination cage catalysis came from his laboratory. Many of the examples derive their acceleration from co-encapsulation, often exploiting the hydrophobic binding of apolar diene and dienophile reactants in water to increase the rate of cycloaddition (Fig. 9a).30,134–138 The spatial demands of the cavity frequently impart unusual reactivity; anthracenyl dienes can react to give the highly unusual 1,4-position regioisomer (Fig. 9b(i)). Tight packing also affects reactivity; naphthyl dienes only undergo cycloaddition when they are structurally tuned to sufficiently fill the cavity (Fig. 9b(ii)). Eyring analysis indicates that this is predominantly an entropic effect; the ΔS‡ term is less for larger naphthalenes, consistent with tighter binding leading to fewer degrees of freedom being lost at the TS. Reactivity can also be enhanced by subtly changing the cage size (Fig. 9b(iii)), wherein swapping a smaller Pd-capping ligand for a larger one causes “pinching” of the cavity.
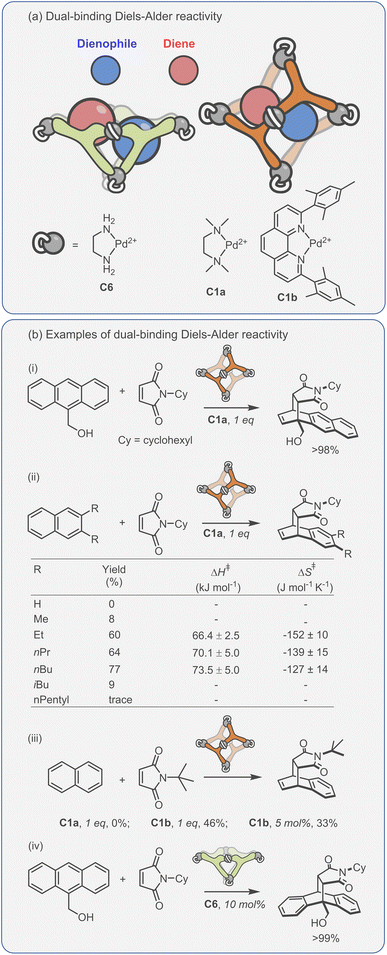 | ||
| Fig. 9 Enhanced metallo-organic cage reactivity derived from dual-substrate encapsulation.30,134–138 | ||
As could be expected, many of the Pd-cage mediated Diels–Alder reactions suffer from severe product inhibition, yet this is not always the case. For example, Pd-bowl, C6, can turnover, giving 100% yield with just 10 mol% cage (Fig. 9b(iv)). It is suggested that the “bent” product auto-excludes because it weakly interacts with the flat aromatic walls of the cage in comparison to the planar anthracene substrate. Equally, both substrate and product are more likely to be weakly bound by the “open” bowl C6 in comparison to the more closed C1, allowing a flux between reactants and cyclised adduct. Mukherjee has also observed turnover of similar Diels–Alder reactions when employing a more cylindrical Pd6L4 cage C4.139 It is much less obvious why the “pinched” octahedral cage structure, C1b, has been observed to turnover reactions of naphthalene substrates.
Another form of dual-binding catalysis has recently been described by Ward and co-workers. However, this method does not involve co-encapsulation, rather it exploits both the cavity and the charged periphery to orthogonally bind different species. This concept was first exemplified using the Kemp elimination of benzisoxazole to give 2-cyano-phenolate, which is triggered via deprotonation (Fig. 10a).140 Here, the heterocycle is bound within the hydrophobic interior of the water-soluble [Co8L12]16+ cubic cage C3, while the exterior cationic surface can attract hydroxide ions via ion-pairing. As in many cases of aqueous cage catalysis, acceleration is pH dependent; the rates of the uncatalysed and catalysed reactions are similar at high pH, however, as the solution becomes more acidic the rate of the uncatalysed reaction diminishes while the cage-mediated process remains unchanged. This is because the bound benzisoxazole continues to experience a locally higher pH as the low concentration of hydroxide ions are attracted to the cage's cationic surface. At pH 8.5, the rate enhancement is 2 × 105, while the ratio of the second-order rate constant for the cage (kcat·Ka) versus the bulk process mediated by free hydroxide (kOD−, in D2O) is 440. The ion-pairing mechanism is supported by separate inhibition experiments; the addition of either a strongly binding “internal” guest (cycloundecanone, Ka = 106 M−1), or chloride, which displaces the surface-bound hydroxide anions, halts acceleration.
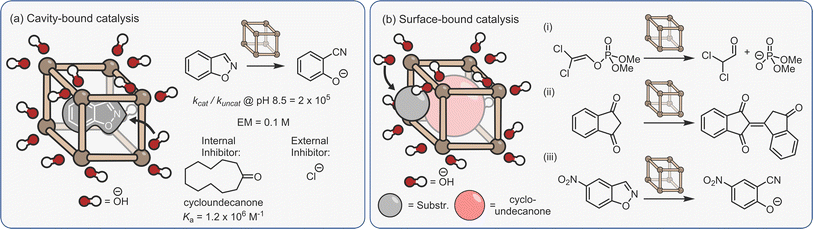 | ||
| Fig. 10 Ion-pair dual-binding catalysis based on both (a) encapsulated;140 (b) surface bound reactivity.141–143 | ||
It appears intuitive that coulombic stabilisation of the negatively charged TS through encapsulation within the 16+ cage would also contribute to catalysis. It is suggested that this is unlikely because the apolar cavity is much poorer at stabilising the anionic TS compared to bulk phase water; previous studies have shown that the hydrogen bond accepting functional groups are actually destabilised relative to solvation by water.61 By extension, the desolvation costs for an anionic species would be even greater. This argument does not take into account the energy involved in solvent re-organisation, which would almost certainly be different for the cage and bulk-phase reactions. Nonetheless, this astute suggestion that the stabilisation of a charged intermediate by a complementary cage is less than the energy gained by hydration has significant mechanistic implications for other examples of water-based cage catalysis.
Ion-pairing catalysis has been shown to be applicable to other reactions, including the hydrolysis of organophosphorous insecticides (Fig. 10b(i))141 and the homo-aldol condensation of indane-1,3-dione (Fig. 10b(ii)).142 However, these studies revealed an unexpected “twist”; addition of the internal inhibitor did not affect the rate of catalysis. It was therefore concluded that in these reactions, catalysis takes place entirely on the cage surface, wherein the amphiphilicity allows co-binding of neutral and charged species. Even more surprisingly, the Kemp elimination of 5-nitrobenzisoxazole is a surfaced catalysed process (Fig. 10b(iii)).143 In this instance, the reason for the different mechanism relates to the orientation of the encapsulated substrate; molecular modelling shows that unsubstituted benzisoxazole is bound with the reactive H-atom of the oxazole ring pointed towards the portal, allowing attack by hydroxide, whereas this position is not accessible with 5-nitrobenzisoxazole. However, it is also notable that the catalysis on the inside of the cage is two orders of magnitude faster than surface reactivity based on the ratio of the second-order rate constants. These studies emphasise a key point; it should not be assumed that catalysis takes place inside the cage just because the substrate is a guest. Only the correct controls (i.e., inhibitor and/or size selectivity experiments) can provide support for an encapsulated mechanism.
None of the examples of cage catalysis by the Ward group suffer from noticeable product inhibition. In the case of the Kemp elimination, the product is much more hydrophilic than the substrate, such that there is a strong energetic driving force for product extrusion. For the reactions that take place on the surface, it could be anticipated that much weaker binding of species to the cage periphery will facilitate the constant exchange of reactants and products.
6.6 Cage catalysis mechanisms that rely on reducing the entropy of activation. Part 2: unimolecular constrictive binding catalysis
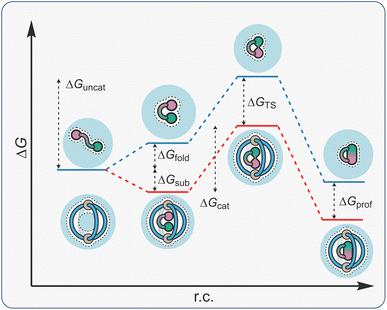
The term constrictive binding was initially coined by Cram in 1991 to explain the steric inhibition that was observed for the decomplexation of hemicarcerand host–guest complexes.144–146 This form of constrictive binding can be observed in any host–guest complex where the activation barrier for decomplexation is higher than the free energy of binding (making the assumption that complexation occurs without an energy barrier).147 With hemicarcerands, the constrictive binding energies were significant as the host portals are small compared even to the lowest molecular weight guests. For self-assembled host systems, constrictive binding energy can also be associated with the rupture of the non-covalent interactions that drive assembly.In the context of supramolecular catalysis, constrictive binding describes the effect of binding an acyclic reactant in a way that forces reactive functional groups into close proximity, thereby enhancing the rate of reactions that proceed via a cyclic TS (Fig. 11). The reduced energy barrier in these reactions is associated with a lowering in the torsional entropy costs because the substrate is conformationally restricted in a folded, higher energy state (ΔGfold). This description suggests catalysis is due to substrate destabilisation, a mechanism that has been invoked in enzyme catalysis.148 It should be noted that the free energy of the catalyst-folded-substrate complex will be lower than the unbound, conformationally unrestricted state; the energetic folding penalty is masked by the binding energy (ΔGsub). The result is that the ΔGfold component is absent from ΔGcat, so that this energy barrier is less than ΔGuncat. Acceleration in these types of reactions can also be discussed in terms of TS stabilisation; cyclic compounds are more strongly bound than acyclic species because the former are less well solvated/have fewer degrees of freedom to lose (cf., macrocyclic effect). This would mean that ΔGTS is greater than ΔGsub so that ΔGcat is smaller than ΔGuncat.
One of the benefits of constrictive binding catalysis is that product inhibition is rare. This is because the energetics of turnover are often neutral in terms of translational entropy (C·P + S → C·S + P). Constrictive binding catalysis can also be subdivided into cyclisation and rearrangements. While both suffer from low inhibition, reactions that give cyclic products are more prone because these generally have higher affinity than acyclic reactants.
Constrictive-binding catalysis using a coordination cage was first reported by Raymond and Bergman in 2004,29 exploiting the tetranuclear Ga4L6 tetrahedron C2 that was described six years earlier. This system, more than any other, has gone on to define metallo-organic cage catalysis.149 Several of its features are similar to those described so far; it is water-soluble and possesses a relatively apolar cavity. Distinctly, it carries a highly negative 12− charge due to the six chelating catecholate ligands. Consequently, it shows a high affinity for “greasy” cations. Additionally, the arrangement of the naphthyl spacers produce a closed-shell system, making it reminiscent of an organic capsule. This causes bound acyclic substrates to fold rather than protrude through a portal.
Constrictive binding catalysis was first exemplified using the aza-Cope rearrangement of diene enammonium substrates (Fig. 12a).29 Catalytic turnover is aided by the bulk-phase hydrolysis of the iminium intermediate to give the weaker binding neutral aldehyde. Activity is highly dependent on substrate size and shape, mirroring what is seen with co-encapsulation. With substrates that are too small, the loss in conformational flexibility is minimal, leading to poor acceleration. Isomeric reactants can even possess kcat/kuncat ratios more than an order of magnitude apart, presumably due to subtle differences in the way the substrate folds. The measured activation parameters show that acceleration is primarily an entropic effect, with substrate-dependent reductions in TΔS‡ ranging from 1.5–3.0 kcal mol−1 (at 298 K).150 The reduction in entropic cost is even greater for the aza-Cope rearrangement of propargylic enamines; as much as 6 kcal mol−1 (at 298 K).151 A small reduction in the enthalpy of activation for certain substrates is also observed, which is thought to arise from the release of strain that is present in the reactant state. It is important to note that the charge of the cage does not affect the activation barrier; the structurally homologous Si(IV) cage, which only bares an 8− charge, possesses a kcat/kuncat similar to that of C2.152 This lack of coulombic activation is easily explained considering that both the substrate and TS are cationic.
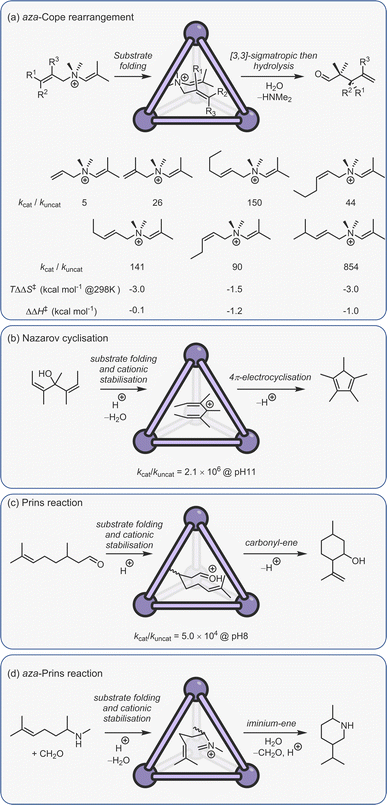 | ||
| Fig. 12 Examples of constrictive binding catalysis.29,81,150,153,154 | ||
In addition to the aza-Cope rearrangement, several other reactions that involve constrictive-binding mechanisms have been described, including the Nazarov81 and Prins153/aza-Prins reactions (Fig. 11b–d).154 In these instances, however, there is additional coulombic component to the observed rate enhancement because each reaction proceeds from a neutral reactant state via charged higher energy species. This supposition was confirmed by similar studies with the Si(IV) analogue of C2, wherein the Nazarov cyclisation showed an almost 103 lower difference in rate.152 The overall 106 rate enhancement for the C2 catalysed Nazarov reaction remains the highest acceleration seen for a cage-catalysed transformation. It is also a rare example of a unimolecular reaction that suffers from product inhibition. However, this could be conveniently side-stepped by performing catalysis in the presence of maleimide, which captures the strongly binding Cp* product to generate the cycloadduct that is too large to fit in the cavity.
The Nazarov cyclisation has been computationally studied independently by Bergman, Raymond, Toste, Tantillo and co-workers,155 and Ujaque and co-workers.156 Both groups used MD, DFT and QM/MM methods. However, while Ujaque and co-workers investigated the parent gallium tetrahedron C2, the former employed the analogous [Al4L6]12− cage. Both groups concluded that constructive binding plays a minor part compared to stabilising protonation. It has also been found that the aromatic walls of the cage, as well as the charge, play a role in cationic stabilisation.
6.7 Cage catalysis mechanisms that rely on reducing the enthalpy of activation
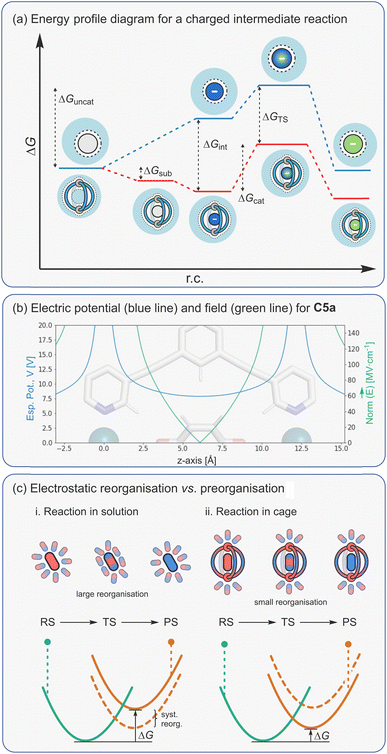
It has been convincingly argued that the selective stabilisation of intermediates and transition states using pre-organised electrostatic forces is the basis for highly efficient enzyme catalysis.157 This proposal is supported by the very large rate enhancements that certain enzymes show. For example, orotidines-monophosphate decarboxylase exhibits a 1017 rate acceleration,80,158,159 which is far beyond the theoretical limit that is possible through entropic mechanisms alone.128,130,131 Part of the reason why enzymes are such effective non-covalent catalysts is because their active sites provide a 3D-array of many stabilising interactions, which separately would show little or no activity. While the cavity of a metallo-organic cage is clearly very different to the structure of an enzyme active site, the similarities are clear; they also provide a 3D microenvironment from which multiple interactions can act cooperatively to bring about catalytic function.Electrostatic interactions can affect the stability of many different species in a catalytic reaction. For an effective catalyst, these interactions should selectively attenuate what would be higher energy species in the uncatalysed reaction. In the simplest scenario that involves a single charged intermediate (Fig. 13a), the overall difference in activation barriers between the catalysed and uncatalysed reaction can derive from selective stabilisation of the intermediate (ΔGint) and/or the TS (ΔGTS). The overall rate enhancement (where rate = k[int]) therefore comes from a higher [int⊂catalyst] compared to [int], in the case of intermediate stabilisation, and/or a faster kcat compared to kuncat due to a lowering of the TS energy. In many scenarios, intermediate and TS stabilisation will likely be interlinked (Bell–Evans–Polanyi principle) and difficult to distinguish. The only cases where acceleration can solely be attributed to selective TS stabilisation are with reactions that do not involve any formal intermediates (e.g. pericyclic reactions).
| ΔU = ΔqV | (7) |
Since the electrostatic potential is nondirectional and long-ranged (depends on ∼1/r), a cage that possesses a symmetrical distribution of several peripheral metal ions can create a strong potential at the centre of the cavity, as shown for a representative Pd2L4 cage, C5a (Fig. 13b). This propensity to selectively stabilise charged species has been studied by the Raymond group using their anionic Ga4L6 cage, C2. Specifically, it was shown that the cage stabilises the conjugate acid of weakly basic guests, leading to a decrease in acidity by as much as four pKa units.82 This ability to basify bound substrates has been exploited several times by the same group to promote acid-catalysed reactions at high pH (see below). More recently, we have ascertained that the Pd2L4 cage C5a shifts the reduction potential of bound quinones by as much as 1 eV.72 In energetic terms, this corresponds to a remarkable 23 kcal mol−1 stabilisation of the quinone radical anion. If this capacity to stabilise reactive species could be fully translated into lowering the activation energy of a catalysed reaction, then true enzyme-like performance with rate enhancements greater than 1015 could be attained. While this is clearly an extremely ambitious goal, it nonetheless provides a rough guide as to what may be possible by developing cage catalysis methods that rely on electrostatic mechanisms.
To understand how electrostatics may lower an activation barrier, it is worth considering a hypothetical reaction that follows the same mechanism in solution and within the catalyst (Fig. 13c(i)). In the uncatalyzed reaction, solvent molecules arrange first to stabilize the ground state (be it a reactant or intermediate). As the reaction progresses, the positions of atoms and the distribution of electrons change as the reaction moves towards the TS. In the uncatalyzed reaction, the surrounding solvent molecules reorganize to stabilize the new state. As a result, the local environment stabilises both reactant and transition states. In contrast, the structure of an effective catalyst (e.g., an enzyme active site and some cages) arranges the electrostatic interactions to specifically stabilize the transition state rather than the ground state (Fig. 13c(ii)). This effect, coined by Warshel as electrostatic preorganisation, is believed to be a dominant contribution to lowering the activation barrier of enzymatic reactions.157 This type of solvent reorganisation is also key to electron-transfer reactions, as described by Marcus Theory.161,162
Recently, there has been significant interest in the use of electric fields in chemical reaction control and catalysis.120,163–169 The different distributions and relative positions of charges in the reactant/intermediate state and TS can be approximately described by dipole moments. Thus, the classical contribution to the activation energy could be estimated (eqn (8)):
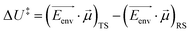 | (8) |
![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) is a dipole moment of the state and
is a dipole moment of the state and 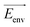 is an electric field of the environment. When the change in dipole along the reaction axis is aligned in the correct direction with respect to the electric field, it is possible that the activation barrier can be reduced by tens of kcal mol−1, leading to significant acceleration. It is also possible, depending on the orientation of the electric field, to control stereochemistry. Clearly, the key to success is not only the strength of the external field but also the orientation relative to the substrates.
is an electric field of the environment. When the change in dipole along the reaction axis is aligned in the correct direction with respect to the electric field, it is possible that the activation barrier can be reduced by tens of kcal mol−1, leading to significant acceleration. It is also possible, depending on the orientation of the electric field, to control stereochemistry. Clearly, the key to success is not only the strength of the external field but also the orientation relative to the substrates.
Electric fields can originate both externally, for example from a capacitor or surface of an electrode, or from the inside of supramolecular cavities through so called local electric fields (LEF). At the molecular level, electric fields emanate most strongly from charged functional groups placed in close proximity to the reaction axis. The most effective catalysts position the substrate such that the change in dipole moment that occurs in the rate limiting step is aligned in an optimal orientation with respect to the LEF. Recently, Boxer and co-workers measured the electric field in the active site of ketosteroid isomerase using vibrational Stark effect spectroscopy.170 They attributed the enzyme's high activity to the high electric field that the local environment exerts (144 MV cm−1 compared to 80 MV cm−1 of water) on the carbonyl bond as it becomes enolised.
It is worth noting that the electric field depends on ∼1/r2 so in a coordination cage this would be more localised at the metal ions than the ESP. The symmetric distribution of the charges at the periphery of the cage also makes the electric field in the centre of the cavity minimal, as illustrated for representative Pd2L4 cage C5a (Fig. 13b). A cage will therefore most effectively stabilize a TS when the redistribution of electrons (i.e., bond forming/breaking) occurs close to the source of the field effect. For optimal catalysis, the substrate should be bound in an orientation that places the reacting functional groups close to the metal ion, with the direction of the dipole change of the reaction axis aligned in a complementary direction to the electric field. This may mean that the “active site” of a coordination cage may not be at the centre of the cavity but rather skewed towards a single vertex. Alternatively, encapsulated solvent can break the symmetry of the cage, leading to a large directional electric field, as shown computationally by Head-Gordon.106 However, encapsulated solvent can also have a negative effect on catalysis, particularly when reactant binding is enhanced by internalised solvation, as has been shown by Ujaque.111,171
There are now several examples of cage catalysis where the origin of rate enhancement is likely due to enthalpic factors (Fig. 14). However, in many instances a full range of controls and/or detailed kinetic analysis is absent, making is difficult to conclude with certainty that the reduction in energy barrier is due to electrostatic stabilising effects. It is also worth weighting the following discussion against the observation that there could be significant stabilisation of charged intermediates by hydration in the reference reaction, which could offset any favourable interactions with a complementary cage.61 For the following discussion, we have classified catalytic reactions based on the apparent charge complementarity i.e., anionic or cationic cages that promote transformations that feature either cationic, anionic or neutral intermediates (Fig. 14).
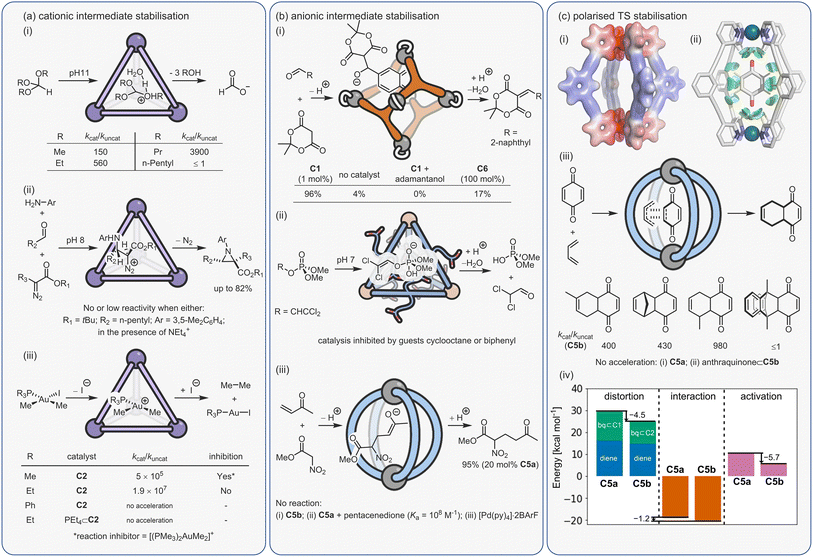 | ||
| Fig. 14 Electrostatic cage catalysis involving stabilisation of (a) cationic intermediates;82,173,175 (b) anionic intermediates;74,124,179 (c) polarised TS.83,112 | ||
One of the first examples of cage catalysis that derives from the complementary stabilisation of charged intermediates came from Raymond, Bergman and co-workers, who showed that their Ga4L6 tetrahedron C2 can catalyse the hydrolysis of normally base stable orthoformates and acetals at high pH (Fig. 14a(i)).82,172 The key to this catalysis is the cage's high negative charge, which enhances protonation of the bound substrate. Unsurprisingly, this effect is most obvious at high pH. As with several other studies using C2, the strongly binding inhibitor tetraethylammonium halts acceleration, showing that reactivity is a cavity rather than a surface-based effect. This is re-emphasised by substrate-size studies, wherein “all-or-nothing” catalysis is observed i.e., substrates up to a certain shape and size fully hydrolyse but beyond that there is no reactivity (Fig. 14a(i)). These hydrolysis reactions are also notable because of the low cage loading—just 1 mol%—due to the auto-exclusion mechanism caused by the favourable solvation of the smaller, more hydrophilic products. It has also been shown that there are nuanced differences in the mechanisms of cage-catalysed acetal and orthoformate hydrolysis, wherein the rate-limiting step can switch from protonation of the encapsulated substrate (orthoformate) to attack of the reactant by bound water (acetal). The orthoformate hydrolysis by C2 was also the first reaction investigated computationally.108 Using the EVB approach, Warshel and co-workers showed that the cage provides a cavity with “low pH”, stabilising the formation of hydronium ion, H3O+. TS stabilisation was identified as having a secondary effect on catalytic efficiency.
It has also been shown that C2 can function through the stabilisation of nitrogen and carbon-based cations. This feature has recently been exploited to promote a 3-component aza-Darzens reaction (Fig. 14a(ii)) – the first time C2 has been used to catalyse a “fusion” transformation.173 The three reactants reveal size-dependent reactivity, showing that all species must enter the cage at some point during the catalytic cycle. Saturation kinetic studies reveal some surprising features. Firstly, the resting state for catalysis appears not to be the iminium ion inside the cage but rather the encapsulated neutral diazocompound. Secondly, the first-order rate dependence on the aldehyde indicates that the Michaelis-complex with both the diazocompound and the iminium ion is only transient on the way to the final aziridine product. Recently, it has been shown that a 3d–4f heterometallic cage can also catalyse the 3-component aza-Darzens reaction.174 In this example, catalysis appears to be driven by a more conventional Lewis acid type mechanism via interactions with the 4f metal ion.
Toste, Raymond and Bergman have also shown that C2 can catalyse the C–C reductive elimination of Pt and Au organometallic complexes such as [(X3P)Au(I)(CH3)2] (Fig. 14a(iii)).175 The reaction follows Michaelis–Menten kinetics, where a pre-equilibrium halide dissociation is followed by the encapsulation of the transient cationic Au(III) complex, which then undergoes irreversible elimination inside the cavity. Again, reactivity is highly dependent on size; changing X3P from Et3P, Me3P, and Ph3P gives kcat/kuncat values of 1.9 × 107, 5.0 × 105 and zero, respectively. The lack of acceleration with Ph3P almost certainly stems from its size preventing encapsulation. An increase in reaction rate was also observed with a higher water content in the methanol solvent.
The origin of the reductive elimination catalysis has been computationally investigated separately by different researchers.107,110,111,171,176 Head-Gordon and co-workers employed DFT methods to establish that electrostatic stabilisation of the positively charged intermediate and TS by the anionic cage was key to lowering the activation energy. This was computationally confirmed by switching the neutral substrate to a charged intermediate, and by reducing the overall charge of the cage. In both cases, the activation energy increased. In a subsequent study, they investigated the same reaction in the presence of explicit water solvent using ab initio MD simulations.106 They found that stabilisation of the TS is due to interactions with both the cage (∼5 kcal mol−1) and a single encapsulated water molecule (∼4 kcal mol−1). Moreover, they observed that the lack of solvent preorganisation at the cage interface destabilises the TS by ∼10 kcal mol−1. Their calculations suggest that changing the metal centre from gallium to indium (which possesses the same charge but larger metallicity than gallium), could reduce the cost of solvent reorganisation and provide an acceleration rate of ∼150.107 Ujaque and co-workers also investigated the role of the co-encapsulated solvent, and catalysis with different substrates. Using energy decomposition analysis, they showed that solvent molecules co-encapsulated in the cage are central to catalysis, with fewer producing a larger catalytic effect. As a result, increased reactivity was observed for the bulkier Et3P, which limits the number of solvent molecules inside the cavity, compared to Me3P.171 They extended this analysis to the reductive elimination of a Pt(IV) complex, where catalytic activity was found to arise from interaction with the cage (6.5 kcal mol−1) rather than microsolvatation (0.5 kcal mol−1) as observed in the Au(III) complex.176
Reactions that involve anionic cages have not been limited to C2. Recently, Symes and co-workers have exploited the anionic [Fe4L6]4− cage, C7, originally described by Nitschke,177 to facilitate reduction of aldehydes using cyanoborohydride at pH 7.178 Presumably, this catalysis also relies on the cage stabilising the protonated substrate by providing a locally acidic environment. Convincing evidence for a cavity-based reaction was provided by size-selective experiments.
The research from Raymond, Bergman and Toste has shown the effectiveness of using a charged cage to catalyse reactions that involve intermediates (and TS) of complementary charge. Translating this concept from anionic to cationic cages has proved to be harder than maybe could be expected – not least considering the much greater availability of metallo-organic systems that carry a positive charge. There may be several reasons for this anomaly: (a) anions are generally harder to desolvate than cations, which will reduce the effectiveness of cationic cage catalysis in water; (b) many cages are composed of flat aromatic ligands, and cation-π interactions are generally more stable than the equivalent anion-π; (c) anions can be strongly coordinating, leading to problems of incompatibility with the coordination structure as a whole.
One of the first examples of anion-stabilising catalysis using a cationic coordination cage was reported by Fujita, who showed that C1 mediates the Knoevenagel reaction between Meldrum's acid and various naphthaldehydes (Fig. 14b(i)).180 Unlike the C1-promoted DA reactions described above, this catalysis occurs with low catalyst loading. Facile turnover is likely linked to the mechanism of the catalytic cycle, which involved binding of only the aldehyde substrate, with C–C bond formation occurring by external (bimolecular) attack of the enolate. This scenario means that the product displacement step is entropically neutral. This mechanistic hypothesis is supported by host–guest studies and inhibitor control reactions: (i) the smaller benzaldehyde, which is a weak guest, only elicits a small acceleration; (ii) C1 does not encapsulate Meldrum's acid; (iii) the reaction is inhibited when adamantanol, a high-affinity guest for C1, is added to the reaction. The poor solubility/structural mismatch of product for the cage also ensures that the adduct is readily excluded.
There appear several possibilities that could explain the origin of catalysis. First, the cage lowers the acidity of the nucleophile – mirroring the ability of C2 to increase the basicity of substrates. This appears unlikely because Meldrum's acid is (a) already significantly acidic to undergo reaction at neutral pH (pKa ≈ 7) and (b) not a guest. Secondly, acceleration could be the consequence of a high local concentration of electrophile and deprotonated nuclepheophilic anion, due to a dual encapsulation-ion pairing mechanism described by Ward and co-workers. Thirdly, the encapsulated oxoanion intermediate is stabilised by the cationic cage. Interestingly, Fujita and co-workers showed that Knoevenagel catalysis is very specific to C1; bowl C6, which possesses the same number of Pd ions, ligands and overall charge, and is a host for the same substrate, shows minimal reactivity. This contrasting reactivity was rationalised considering that in C1 the enolate can attack the aldehyde in one of the cage windows, whereas C6 do not have these portals. The resultant oxyanion adduct is then stabilised by three adjacent Pd2+ centres, where it is likely that the ESP will be highest. This illustrates the point that the “active site” of a cage catalyst need not be at the centre of the cavity. The groups of Mukherjee139,181,182 and Sun183 have reported the catalysis of Knoevenagal reactions between similar nucleophiles (e.g., Meldrum's acid and dimethylbarbituric acid) and extended aromatic aldehydes. The cages used in these studies possess cavities of different sizes and shapes, and are surrounded by varying numbers and distributions of metal ions, however, all possess the portals identified by Fujita as being key to stabilising the oxyanion intermediates.
Another reaction likely involving an anionic intermediate and a cationic cage is the [Fe4L6]8+C8 catalysed hydrolysis of dichlorvos, as described by Nitschke (Fig. 14b(ii)).179 Unlike the example of Ward, this takes place within the cavity, since experiments with strongly encapsulating guests inhibit catalysis. Still, the rate enhancement in this example could stem from either stabilisation of the oxyphosphate anion intermediate (either by coulombic interactions or H-bonding to the multiple hydroxyl groups) or high effective concentration of hydroxide and the substrate.
The examples of coordination cage catalysis discussed so far all involve water-soluble cages that utilise the hydrophobic effect. We have been developing an alternative approach where we engineer the cage to act as a polar reaction vessel surrounded by an apolar bulk-phase.66 This can be viewed as a counterpoint to the hydrophobic cavity concept. As such, guest binding is not driven by the displacement of “high-energy” solvent, rather by the formation of polar interactions between the cage and the substrate. This means that binding is invariably “active”, i.e., the interactions that cause encapsulation also electrostatically modulate the reactivity of bound species.
The cages we have used in our studies, C5a/b, are part of the larger family of Pd2L4 systems described by Steel,184 Shionoya,185 Clever,186 Hooley,187 Crowley,57 Yoshizawa,188 and Lewis,189 to name a few. Unlike cages such as C1 and C2, the cavities of C5a/b systems are often not surrounded by π-surfaces because the ligands sit perpendicular with respect to the cavity. Consequently, these Pd2L4 cages possess large portals meaning they are not well suited to hydrophobic-type binding. However, because of this edge-on alignment, ligand substituents can point into the cavity and thus potentially form directional interactions. In the case of C5a, there are no substituents, however, the ESP energy surface (Fig. 14c(i)) shows that the ortho-pyridyl CH bonds adjacent to the Pd ions are highly polarised by the proximal 2+ charge, and thus become moderate H-bond donors. With 1,4-quinones being ideally sized to simultaneously form interactions with all eight orthopyridyl (Fig. 14c(ii)), it was envisaged that this electrostatic binding would enhance the dieonophilicity of the bound substrate, thus making it more reactive without the need to co-bind a diene. However, C5a is inactive towards the many combinations of substrates that were tried. Instead, the homologous C5b is a very effective catalyst (Fig. 14c(iii)), with this cage showing an approximate 4 kcal mol−1 reduction in activation barrier,83 which is comparable to the most effective catalytic antibody.190 Diels–Alder catalysis with C5b also exhibits little product inhibition, as turnover is facilitated by the molecularity of the turnover step, which is entropically neutral because the product is displaced by only the dienophile.
The difference in reactivity between homologous cages C5a and C5b was highly unexpected, with no obvious reason why the strength of the LUMO lowering hydrogen-bond interactions would be different. Indeed, computational studies have shown that the two cages are comparable at electronically “activating” the substrate.112 However, distortion–interaction analysis (Fig. 14c(iv)) showed that the inactive cage has to undergo significant distortion such that the favourable interaction energy is completely masked. In contrast, C5b provides a similar interaction energy but because the distortion is only slightly greater than the uncatalysed reaction, significant acceleration is observed. MD simulations indicate that the smaller distortion component could be because C5b is more flexible; there is significantly less bias towards the D4h conformation with helical twisting being accommodated with little energy change.
Cage catalysis of reactions under non-aqueous conditions also reduces the strong desolvation penalties that can occur with charged intermediates in water. Accordingly, we have found that the Pd2L4 system is very effective at promoting Michael addition in dichloromethane (Fig. 14b(iii)).74 In this example, the cage reactivity is reversed, wherein C5a is an excellent catalyst while C5b is inactive. One possible reason is that the central nitrogen atoms of C5b significantly attenuate the ESP of the cavity. This would hinder the ability to acidify the bound pro-nucleophile and stabilise any subsequent negatively charged intermediates. In contrast, C5a is an excellent catalyst, so much so that catalysis occurs under “base-free” conditions with residual water eliciting pro-nucleophile deprotonation. This indicates that the cage shifts the acidity equilibrium of the pro-nucleophile by many orders of magnitude. It also appears that catalysis is dependent on the formation, if only transiently, of a three-component Michaelis complex since the cage does not accelerate reactions involving either complementary nucleophiles (e.g. Meldrum's acid) or electrophiles (e.g. benzoquinones). Instead, catalysis only occurs when two weakly interacting substrates are used. This re-emphasises the point that good guests do not always make the best substrates.
Electrostatically stabilising polar, high-energy species is one way that a cage can influence the enthalpy of activation. Recently, it has been shown that binding a substrate in a more reactive enthalpic state can also lead to rate acceleration. Using the platinum cage C1c, Fujita has demonstrated that electron-rich aromatic amides can bind in the less stable cis-conformation, facilitated by interactions with the electron-poor triazine ligands (Fig. 15).191 This binding also twists the amide group away from planarity, thereby reducing the conjugation of the nitrogen lone pair with the carbonyl π* orbital, and attenuating the chemical inertness of this group. Consequently, it was found that the rate of hydrolysis of the encapsulated, twisted amides (i.e., where the dihedral angle for C–N–C(O)–C deviates from 0°) showed measurable acceleration compared to the background reaction. Additionally, amides bound in a less reactive trans-conformation, with dihedral angles close to 180°, either showed much smaller acceleration or none at all. This would suggest that the origin of rate acceleration is due to substrate destabilisation rather than electrostatic stabilisation and/or increasing the effective concentration of hydroxide ions.
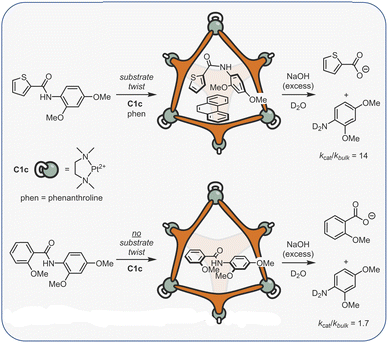 | ||
| Fig. 15 Enhanced amide hydrolysis by encapsulated-induced twisting of the substrate.191 | ||
A computational view of this reaction has been provided by Pavan and co-workers.192 Using MD simulations, they showed that the energy required to form the cis-conformer is lower inside the cage than in solution due to the crowding effect (Ktrans/cis = 105 in solution vs. Ktrans/cis = 102 in the cage), resulting in the acceleration of the reaction.
7 Utilisation of cages for selective catalysis
The spatial demand of confined reactivity naturally lends itself to creating catalysts that can show both enhanced or unusual forms of selectivity that are not easily attainable using traditional catalysts. With small molecule catalysts, rate acceleration is often due to a single point interaction (e.g., Fig. 6a, or a carbonyl group interacting with a Lewis acid) whereas cage catalysis involves contact with the whole substrate. This can lead to a specific reactant(s) orientation or conformation that favours pathways normally disfavoured in the bulk phase. Conceptually, specific orientations or conformations can be favoured by the energetic gain of forming non-covalent interactions. Conversely, the minimisation of unfavourable interactions (i.e., steric “clash”) can also lead to a specific binding mode. Considering the shapes of many cage structures, which lack inward facing functional groups, it is likely that the latter scenario is responsible for many examples of interesting selectivity. In the following section, we will highlight examples of selectivity that have defined this area to date.7.1 Stereoselective catalysis
One of the first examples of stereoselective catalysis came from Raymond and Bergman, who showed that C2 can influence the enantioselectivity of the aza-Cope rearrangement of pro-chiral allyl enammonium salts (Fig. 16a).193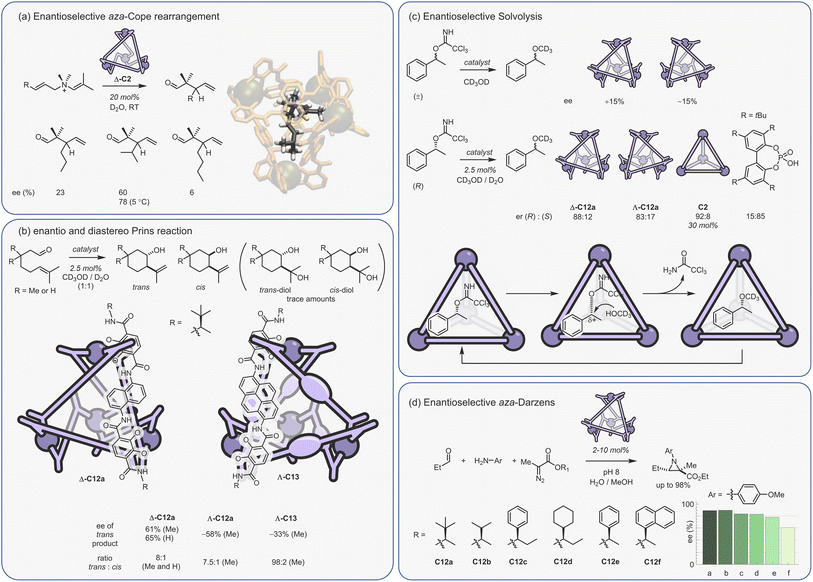 | ||
| Fig. 16 Examples of Ga4L6 catalysed enantio- and diastereoselective transformations.193,195–198 Figure (a) and (d) adapted with permission from ref. 193 and 198 , Copyright 2009, 2022 American Chemical Society. | ||
Like many M4L6 tetrahedra, C2 is intrinsically chiral because the four tris(chelate)-metal stereogenic units are mechanically coupled so the assembly exists as either the ΔΔΔΔ or ΛΛΛΛ enantiomers. Racemic C2 can be resolved as the (S)-nicotinium diastereomeric cage salt. This is then converted into the enantiopure form by exchange of (S)-nicotinium with either K+ or NMe4+.194 However, the NMe4+ salt, which exists as the inclusion complex (NMe4)11[NMe4⊂C2], is significantly more stable towards racemisation (>90% optical activity after 30 days at room temperature) compared to the “empty” K+ salt (i.e., (K+)12[solvent⊂C2]), which shows no CD signal after a few hours. Applying the enantiomerically stable NMe4+ cage towards the aza-Cope rearrangement, showed that the magnitude of chiral induction was highly dependent on small modifications to the substrate. For example, changing the substituent on the pro-chiral centre from propyl to iso-propyl, and then to n-butyl, results in enantiomeric excesses (ee) of 23%, 60% and 6%, respectively (Fig. 16a). This suggests that chiral induction is highly dependent on efficient packing – similar to the sensitivity of the substrate size-activity relationship (see Section 5.4). Sampling torsional angles of the bound iso-propyl substrate using MM indicated that the pro-chiral carbon is directed towards one of the metallic stereocentres (Fig. 16a). Close contact with the chiral element has been suggested to explain enantioselectivity. An alternative enantioselectivity origin was provided by Nakajima and co-workers, who performed a computational QM/MM study. They suggested that enantioselectivity stems from different stability of pro-chiral structures due to steric hindrance of the bulky substituents inside the cage.109 Confinement-based stereoinduction utilising efficient substrate packing within a chiral host offers an alternative to the more conventional approach of binding a substrate through a functional group (e.g. a carbonyl group interacting with a chiral Lewis acid), and extends asymmetric catalysis to reactants without obvious chemical “handles” that are difficult to control.
The challenge with using the resolved NMe4+ salt of C2 in asymmetric catalysis arises when the substrate is neutral, as this needs to displace the bound cationic guest. Consequently, Raymond, Toste and Bergman developed a second generation Ga4L6 chiral cage systems, C12 (Fig. 16b).195 These cages utilise pendant chiral amide groups to quantitatively bias the metal-vertex stereochemistry,199 removing the need for any resolution (and the subsequent loss of material). Crucially, the “empty” K+ salt of these cages are stable towards racemisation. The catalytic properties of C12 were initially tested using the Prins-cyclisation of citronellal (Fig. 16b), wherein it was found that Δ-C12a and Λ-C12a, gave the trans-product with ee of up to 65%.195 While the extent of stereoinduction is similar to the aza-Cope rearrangement, the Prins reaction appears to be less sensitive to substrate size, as the dimethyl and methylene analogues, give very similar ee. Similarly, increasing the size of the cavity significantly using the larger pyrene-spacer enantiopure cage, C13,196 still resulted in significant stereoinduction. The change in diastereoselectivity between C12 and C13 is also interesting, and perhaps counterintuitive; the larger cage is more selective, giving a trans![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cis ratio of 50
cis ratio of 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, compared to 8
1, compared to 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 for the smaller cage. It is suggested that the higher trans selectivity is due to a concerted mechanism, which is favoured by the larger apolar pyrene surfaces. Further support for a concerted mechanism stems from only trace amounts of hydration adducts being formed, which are the main products when the reaction is carried out in the absence of the cage.153
1 for the smaller cage. It is suggested that the higher trans selectivity is due to a concerted mechanism, which is favoured by the larger apolar pyrene surfaces. Further support for a concerted mechanism stems from only trace amounts of hydration adducts being formed, which are the main products when the reaction is carried out in the absence of the cage.153
It has been shown that Ga4L6 cages can also be used to catalytically control stereochemistry in reactions that do not involve constrictive binding. The solvolysis of a racemic benzyl-trichloroacetimidate substrate mediated by enantiopure cage C12 shows modest (≈15% ee) and opposite stereoinduction based on the handedness of the cage (Fig. 16c).197 These results infer an SN1-type mechanism, with the chiral cavity modestly influencing which face of the encapsulated carbocation is attacked by solvent. However, this interpretation was contradicted by further experiments, wherein enantiopure substrates give products with high stereoretention (up to 90% er), both when enantiopure C12 and racemic C2 are used. Control experiments using an achiral phosphoric acid showed that bulk-phase acid hydrolysis of the same substrate led to the expected stereochemical inversion. It was suggested that these results could be explained by the cage promoting a hybrid substitution mechanism involving some partial rupture of the group bond, as full dissociation would be disfavoured due to the mismatch between the tetrahedral cavity and the trigonal planar carbocationic intermediate. The partial benzylic carbocation would then interact with the naphthyl walls of the cage, favouring attack from just one face. This example highlights how confinement effects can alter apparently inherent mechanisms, leading to selectivity that is otherwise difficult to achieve.
Very recently, Toste, Raymond, Bergman and co-workers have described the enantioselective catalysis of the aza-Darzens reaction.198 This investigation revealed that ee greater than 90% could be obtained – among the highest reported for a cage-catalysed enantioselective transformation (Fig. 16d). The effect that changing the chiral-directing group at the periphery of the cage has on enantioinduction was also studied. Despite the remoteness of the directing group with respect to the cavity, ee ranging from 60–90% were obtained using cages C12a–f. The authors show that cages that possess smaller host–guest exchange energy barriers (increased flexibility) deliver greater enantioinduction. A comparison between an analogous Ga(III) and In(III) cage showed the same relationship.
Unlike M4L6 tetrahedra such as C2, the many Pd-based assemblies are almost always inherently achiral.200 Nonetheless, these type of constructs can have a significant influence on diastereoselectivity. As an example, the [2 + 2] photodimerisation of acenaphthalene within C1a yields exclusively the syn-stereoisomer (Fig. 17a), whereas in the absence of cage, a low yield of a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture of the stereoisomers is obtained.201 Presumably, the steric confinement of the cage prevents the offset arrangement of substrates that would be required to generate the anti-isomer. When methyl-substituted acenaphthalene is used, the cage promotes the exclusive formation of the head-to-tail syn-isomer over the other three possible products (Fig. 17a), thereby simultaneously controlling both stereo- and regiochemistry.
1 mixture of the stereoisomers is obtained.201 Presumably, the steric confinement of the cage prevents the offset arrangement of substrates that would be required to generate the anti-isomer. When methyl-substituted acenaphthalene is used, the cage promotes the exclusive formation of the head-to-tail syn-isomer over the other three possible products (Fig. 17a), thereby simultaneously controlling both stereo- and regiochemistry.
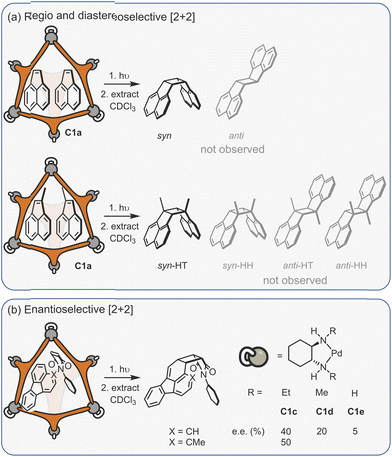 | ||
| Fig. 17 Examples of Pd6L4 photomediated [2 + 2] cycloadditions.201,202 | ||
Chiral analogues of C1a have been prepared using 1,2-diaminocyclohexyl cis-protecting groups (Fig. 17b).202 While it might be anticipated that the remote positioning of these units with respect to the bound substrates would be ineffective, the extent of stereoselectivity is surprisingly high. For example, the [2 + 2] cross photo-dimerisation of fluoranthene and N-cyclohexyl maleimide within the chiral cage can give up to 40% ee, while using the methyl-substituted fluoranthene substrate gives an even higher ee of 50% (Fig. 17b). This again suggests that packing effects play a large part in stereoinduction. Also, when the size of the groups on the chiral 1,2-diaminocyclohexyl ligand are decreased from ethyl to methyl and hydrogen, the ee drops to 20% and 5%, respectively. Molecular mechanics calculations suggest that the extent of enantioinduction is controlled by the allosteric effects between the cis-protecting group and the tritopic triazine “walls” of the cage. With the achiral ethylene diamine-capped parent cage C1, the tritopic ligand is planar. However, as the steric bulk increases, the planarity is broken causing a helical tilt, which increases with the size of the steric bulk on the capping ligand.
The group of Su have also investigated the photodimerisation of 1-substituted acenaphthalene (and other photolytic reactions) utilising a heterometallic [Pd6Ru8L24]24+ cage, C14 (Fig. 18).203 This structure combines several aspects of transition metal chemistry, with the Ru “metalloligand” being utilised to create both a chiral and a photoactive cage. Unlike Raymond's C2 cage, the octahedral metal stereocentres in C14 are not formed during the cage assembly process. Instead, the pre-formed, enantiopure Ru metalloligand, Δ-RuL3, is prepared from the resolved Δ-Ru(phen)3 complex, and then assembled with Pd2+ ions (Fig. 18a). In contrast to the [2 + 2] reactions mediated by the Pd4L6 assemblies from the Fujita group, irradiation of bromoacenaphthalene in the presence of C14 gives the anti-head-to-head isomer with 99% selectivity (Fig. 18b). This difference in selectivity appears not to be related to the different light source (e.g., UV mercury lamp vs. blue LED); 454 nm irradiation of the substrate in the presence of just RuL3 produces low levels of selectivity, with anti-HH compound marginally preferred (39%). Moreover, enantiopure C14 cage generated the anti-HH product in close to 90% ee, with the different handed cages giving the opposite enantiomer adducts (Fig. 18b).
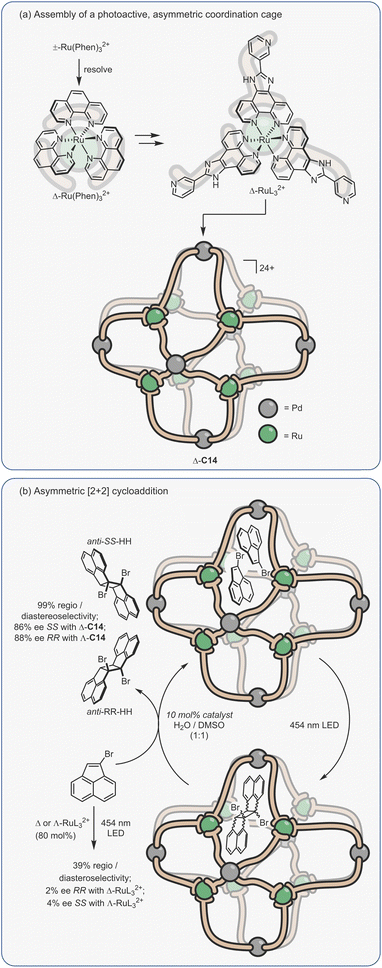 | ||
| Fig. 18 Regio-, diastereo- and enantioselective [2 + 2] dimerisation in a photoactive Pd6Ru8 cage.203 | ||
Considering the size of the central cavity compared to the substrates, it is perhaps unexpected that cage C14 shows such excellent selectivity. However, calculations suggest that the reactants bind in the much smaller, rhombic box-like portals formed between adjacent ligands. It is likely that these microenvironments would lead to (a) much stronger, well-defined binding, (b) more efficient photo-induced energy transfer and (c) much better expression of the Ru stereochemistry due to the close proximity of the stereogenic metal centre. This is another excellent example which highlights that the “active-site” of a metallo-organic cage catalyst need not necessarily be the central cavity but rather in the constricted environment that separate the outer and inner phases. The presence of multiple “active sites” may also be one reason that this photolytic reaction is truly catalytic (however, multiple additions of substrate, which exceed the saturation of the catalyst, suggest some auto-exclusion of the product).
7.2 Regio and chemoselective catalysis
Utilising confinement effects to achieve high levels of chemo- and regioselectivity is another clear area of opportunity in cage catalysis. It is a powerful approach that can be used to divert reactions along a pathway that is normally unavailable, or down a single route where multiple others exist to avoid complex product mixtures. It has the potential to transform synthetic strategies by (a) facilitating one-pot multi-step/multi-substrate reactions; (b) removing the need for protecting groups; (c) facilitating late-stage, selective functionalisation.Promoting chemo- and/or regio(site)selectivity using cage catalysts can conceptually occur in two obvious ways:
(i) substrate(s) that contains multiple reactive groups pack so that only a specific site(s) can react;
(ii) “Molecular filtering” leads to the selective activation of smaller, usually less reactive substrates (aka size-selective catalysis).
Fujita and co-workers have shown that the octahedral cage C1a can bias the bromination of a representative diterpenoid, wherein encapsulation promotes selective reaction at the terminal, tri-substituted alkene (Fig. 19).204 In the absence of C1a, bromination occurs both at the terminal and internal alkene sites (and also leaves unreacted starting material). Evidence for packing effects being the origin of selectivity comes from the 1H NMR of the host-guest complex. This shows that the two internal olefins are shifted notably more upfield (by up to 2.8 ppm), suggesting that the inner double bonds are more strongly interacting with the panels (i.e., triazine ligands) whereas the end groups are exposed within the portals. Consequently, the reaction with the nonbinding N-bromosuccinamide (NBS) leads exclusively to bromination at the terminal trisubstituted alkene. It is also interesting to note that the product of the cage reaction is the unusual nitratobrominated compound, as opposed to bromohydrin, indicating that the bromonium intermediate is intercepted by the nitrate counteranions of the cage. It is interesting that the control reaction with (tmeda)Pd(ONO2)2 does not produce this nitrato species, which suggests that the cage reaction involves an attack of the surface-bound nitrate on the bound intermediate. This is reminiscent of Ward's research (see above) and further emphasises the commonality of certain cage catalysis mechanisms.
 | ||
| Fig. 19 Regioselective bromination within a Pd6L4 cage.204 | ||
Raymond and Toste have also demonstrated selective hydrogenation reactions of polyene substrates using an encapsulated rhodium catalyst (Fig. 20).205 In this example, selectivity towards the terminal groups is thought to arise from only partial ingress of the more hydrophobic end of the substrate, with the long linear substrate protruding through the portals exposing the end alcohol group. Interestingly, only the larger pyrene-based C13 cage is able to mediate this reaction, with the smaller parent cage C2 switching off reactivity, presumably because there is insufficient space to co-bind both the rhodium catalyst and the substrate. Unsurprisingly, “bulk-phase” hydrogenation of the same substrate leads to a complex mixture.
 | ||
| Fig. 20 Ga4L6 catalysed regioselective hydrogenation.205 | ||
One of the key attributes of enzyme catalysis is that they can differentiate from a pool of structurally similar substrates. Using two dienes and two quinone dienophiles, it was shown that C5b can bias the reactions towards a specific pathway that is normally disfavoured (Fig. 21).83 Using a conventional Lewis acid catalyst, this multi-substrate competition reaction favours the product that forms from the cycloaddition of the two most reactive partners, while the remaining less reactive starting material then undergo [4 + 2] cyclisation. In the presence of C5b, this reactivity pattern is altered because (a) the tert-butyl-substituted quinone dienophile is not a guest for the cage and (b) the bulky anthracene diene is sufficiently bulky that it cannot access the frontier molecular orbitals of activated benzoquinone. Consequently, the cage selectively enhances the reaction of the most reactive dienophile and the least reactive diene. It should be noted that without a catalyst, the anthracene diene is sufficiently reactive to readily undergo cycloaddition at room temperature. Therefore, as only 20 mol% of C5b is used in this reaction, it is not simply acting as a “whole-molecule protecting group”206 for the bound quinone. Instead, C5b is accelerating the less-favourable reaction so that it occurs at a greater rate than the bulk-phase more reactive pathway.
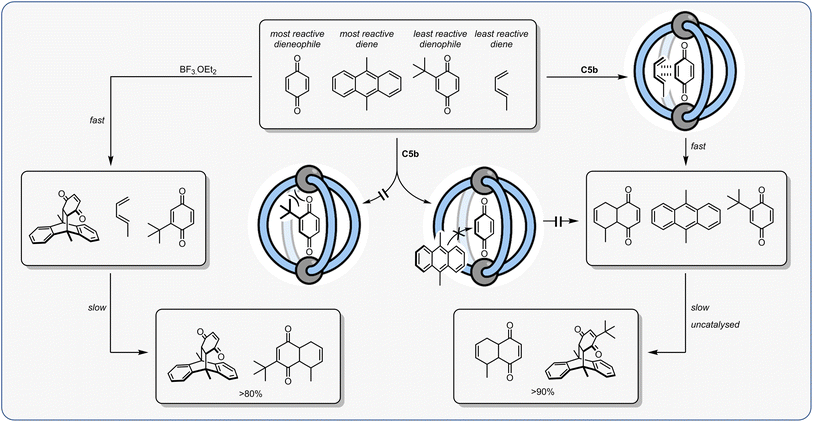 | ||
| Fig. 21 Multi-substrate, chemoselective cage catalysis using a Pd2L4 cage and comparsion to a conventional Lewis acid catalyst.83 | ||
8 Holistic view of where cage catalysis currently stands and future opportunities
The pioneering work of Lehn, Fujita, Stang and others has paved the way to making metallo-organic assembly the go-to method for preparing large, three-dimensional hollow structures. While this area still faces significant synthetic challenges, there is now as much focus on utilising the cavity that these species possess for various applications. Unlike many other porous materials, the internal space of a coordination cage is monodisperse and uniform (cf., micelles, vesicles, polymer nanoparticles). Moreover, the shape and, in particular, size of the cavity can be precisely controlled with almost angstrom-size precision, even at the sub-nm scale. This can lead to well-defined and often tightly-packed binding, such that the cage microenvironment is well expressed and distinct from the outer phase (cf., MOFs and zeolites). Coordination cages also introduce other features lacking in many other porous compounds, most obviously permanent charge (cf., H-bond capsules and fully organic cages), which can amplify the physiochemical differences between the outside and inside of the structure. All of these features combine to make coordination cages excellent catalysts—as has been shown. Indeed, measured rate enhancements in excess of 106 show that coordination cages can exhibit performance that exceeds almost all other bio-inspired catalyst systems. Other (non-catalytic) experimental data suggests even this is far from the ultimate potential of coordination cage catalysts, raising the real possibility that these fully synthetic systems may one day rival the activity of naturally occurring or bio-engineered enzymes.Despite the progress made in the past twenty years, it is difficult to argue that coordination cage catalysis is not an underdeveloped area. The vast majority of research in this area stems from a very small set of cage systems. Moreover, the variety of reactions that are known to be promoted by cages remains limited. For a long time, this stemmed from product inhibition—meaning researchers have avoided certain reaction types, often those that are most synthetically important (e.g., fusion reactions). Different approaches to circumvent this problem have now been described, which include engineering autoexclusion or controlling the molecularity of the catalysed process. A less discussed problem with cage catalysis, which has almost certainly contributed to the lack of reaction diversity, is compatibility of the reactants (or products) with the self-assembled structure. For example, strongly coordinating nucleophiles or leaving groups can both disassemble the structure and/or block the cavity. This may be another reason why pericyclic reactions, which feature non-coordinating π-“functional groups” have been extensively studied. While the use of more robust cage complexes, which utilise less dynamic metal-ion interactions, could be a way to solve this problem, an alternative and unexplored strategy would involve the use of masked reactants.
The discovery of new catalytic reactions goes hand-in-hand with the identification of new cage catalysts. At present, this appears very much a process that is led by chemical intuition, yet is still based on a time-consuming trial-and-error approach. Moreover, catalysis often appears not to be the principal driver; novel cage structures are often published first, followed by host–guest studies and then finally catalysis. A successful host–guest study invariably involves identifying high-affinity guests; subsequently using these guests as substrates in a catalytic reaction may not be the best approach as overstabilisation of the reactant state can lead to poor activity (see Section 5.2). This general workflow almost certainly arises because it has been developed by supramolecular chemists; the involvement of researchers who are not primarily trained in this area would almost certainly aid scientific discovery (as has been the case with the highly successful collaboration of Toste and Bergman, with Raymond).
The use of computational analysis and prediction will almost certainly play a large role in the future growth of this area. At present, computational studies are very much targeted at understanding known examples of catalysis. This is a necessity as these investigations will form the foundation of predictive tools. It is clear that computational benchmarking relies on quantitative catalytic data, and in particular the extraction of energetics from detailed kinetic studies. The combined use of detailed physical-organic analysis and computation can shed light on the true origins of catalysis, which in turn will provide a natural feedback loop for evolving cage designs. The modularity of certain cage topologies (e.g., Pd2L4) would appear well suited to realising better catalysts using small, iterative changes. The ultimate long-term goal in this area has to be a predictive bottom-up approach for de novo catalyst design.
Coordination cage catalysis goes beyond simply making very active catalysts. For example, precisely controlling regioselectivity for late-stage functionalisation of complex biological targets remains a significant and unsolved challenge in contemporary catalysis. Confined reactivity has the potential to make a real contribution to this area, providing control that would otherwise be difficult or impossible to achieve with a small molecule catalyst. Multi-step catalytic reactions is another area where cage systems have the potential to lead; compartmentalisation of reactions that would be otherwise incompatible,207,208 or passing one product to another through the process of molecular recognition are just two ways that cages could promote one-pot, multi-processes transformations. And of course, virtually all cage catalysis – as is the same with all methods that rely solely on weak interactions – is inherently benign and provides a sustainable alternative to using reactive, difficult to handle organometallic species. It is clear that the next decades will be an exciting period in the area of cage catalysis, with the potential to significantly impact contemporary synthetic methods.
Author contributions
P. J. L., T. K. P. and F. D. prepared the perspective with input from V. M.-C. and R. L. S.Conflicts of interest
There are no conflicts to declare.Acknowledgements
T. K. P., P. J. L., and F. D. acknowledge the financial support from EPSRC (EP/W010666/1 and EP/W009803/1). V. M.-C. acknowledges the financial support from Generalitat Valenciana (CIDEGENT/2020/031).Notes and references
- J. W. Steed and J. L. Atwood, Supramolecular chemistry, John Wiley & Sons, 2022 Search PubMed.
- R. Chakrabarty, P. S. Mukherjee and P. J. Stang, Chem. Rev., 2011, 111, 6810–6918 CrossRef CAS PubMed.
- T. R. Cook, Y.-R. Zheng and P. J. Stang, Chem. Rev., 2013, 113, 734–777 CrossRef CAS PubMed.
- T. R. Cook and P. J. Stang, Chem. Rev., 2015, 115, 7001–7045 CrossRef CAS.
- L. R. MacGillivray and J. L. Atwood, Nature, 1997, 389, 469–472 CrossRef CAS.
- R. S. Meissner, J. Rebek and J. de Mendoza, Science, 1995, 270, 1485–1488 CrossRef CAS PubMed.
- Y. Liu, C. Hu, A. Comotti and M. D. Ward, Science, 2011, 333, 436–440 CrossRef CAS PubMed.
- B. F. Hoskins and R. Robson, J. Am. Chem. Soc., 1989, 111, 5962–5964 CrossRef CAS.
- H. Furukawa, K. E. Cordova, M. O'Keeffe and O. M. Yaghi, Science, 2013, 341, 1230444 CrossRef.
- Y. Inokuma, S. Yoshioka, J. Ariyoshi, T. Arai, Y. Hitora, K. Takada, S. Matsunaga, K. Rissanen and M. Fujita, Nature, 2013, 495, 461–466 CrossRef CAS PubMed.
- R. S. Forgan, J.-P. Sauvage and J. F. Stoddart, Chem. Rev., 2011, 111, 5434–5464 CrossRef CAS PubMed.
- D. B. Amabilino and J. F. Stoddart, Chem. Rev., 1995, 95, 2725–2828 CrossRef CAS.
- J. E. Beves, B. A. Blight, C. J. Campbell, D. A. Leigh and R. T. McBurney, Angew. Chem., Int. Ed., 2011, 50, 9260–9327 CrossRef CAS PubMed.
- B. Hasenknopf, J.-M. Lehn, B. O. Kneisel, G. Baum and D. Fenske, Angew Chem. Int. Ed. Engl., 1996, 35, 1838–1840 CrossRef CAS.
- J. Kang and J. Rebek, Nature, 1997, 385, 50–52 CrossRef CAS PubMed.
- E. G. Percástegui, T. K. Ronson and J. R. Nitschke, Chem. Rev., 2020, 120, 13480–13544 CrossRef.
- G. D. Y. Sogah and D. J. Cram, J. Am. Chem. Soc., 1979, 101, 3035–3042 CrossRef CAS.
- T. Mitra, K. E. Jelfs, M. Schmidtmann, A. Ahmed, S. Y. Chong, D. J. Adams and A. I. Cooper, Nat. Chem., 2013, 5, 276–281 CrossRef CAS PubMed.
- S. J. Dalgarno, P. K. Thallapally, L. J. Barbour and J. L. Atwood, Chem. Soc. Rev., 2007, 36, 236–245 RSC.
- B. Therrien, G. Süss-Fink, P. Govindaswamy, A. K. Renfrew and P. J. Dyson, Angew. Chem., Int. Ed., 2008, 47, 3773–3776 CrossRef CAS PubMed.
- B. P. Burke, W. Grantham, M. J. Burke, G. S. Nichol, D. Roberts, I. Renard, R. Hargreaves, C. Cawthorne, S. J. Archibald and P. J. Lusby, J. Am. Chem. Soc., 2018, 140, 16877–16881 CrossRef CAS PubMed.
- B.-N. T. Nguyen, J. D. Thoburn, A. B. Grommet, D. J. Howe, T. K. Ronson, H. P. Ryan, J. L. Bolliger and J. R. Nitschke, J. Am. Chem. Soc., 2021, 143, 12175–12180 CrossRef CAS.
- D. J. Cram, S. Karbach, Y. H. Kim, L. Baczynskyj and G. W. Kallemeyn, J. Am. Chem. Soc., 1985, 107, 2575–2576 CrossRef CAS.
- F. Cramer and W. Kampe, J. Am. Chem. Soc., 1965, 87, 1115–1120 CrossRef CAS.
- D. C. Rideout and R. Breslow, J. Am. Chem. Soc., 1980, 102, 7816–7817 CrossRef CAS.
- W. L. Mock, T. A. Irra, J. P. Wepsiec and T. L. Manimaran, J. Org. Chem., 1983, 48, 3619–3620 CrossRef CAS.
- L. G. Mackay, R. S. Wylie and J. K. M. Sanders, J. Am. Chem. Soc., 1994, 116, 3141–3142 CrossRef CAS.
- L. S. Kaanumalle, C. L. D. Gibb, B. C. Gibb and V. Ramamurthy, J. Am. Chem. Soc., 2004, 126, 14366–14367 CrossRef CAS PubMed.
- D. Fiedler, R. G. Bergman and K. N. Raymond, Angew. Chem., Int. Ed., 2004, 43, 6748–6751 CrossRef CAS PubMed.
- M. Yoshizawa, M. Tamura and M. Fujita, Science, 2006, 312, 251–254 CrossRef CAS PubMed.
- Q. Zhang and K. Tiefenbacher, Nat. Chem., 2015, 7, 197–202 CrossRef CAS PubMed.
- P. La Manna, C. Talotta, G. Floresta, M. De Rosa, A. Soriente, A. Rescifina, C. Gaeta and P. Neri, Angew. Chem., Int. Ed., 2018, 57, 5423–5428 CrossRef CAS PubMed.
- R. R. Knowles and E. N. Jacobsen, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 20678–20685 CrossRef CAS.
- M. Yoshizawa, J. K. Klosterman and M. Fujita, Angew. Chem., Int. Ed., 2009, 48, 3418–3438 CrossRef CAS PubMed.
- D. H. Leung, R. G. Bergman and K. N. Raymond, J. Am. Chem. Soc., 2007, 129, 2746–2747 CrossRef CAS PubMed.
- Q.-Q. Wang, S. Gonell, S. H. A. M. Leenders, M. Dürr, I. Ivanović-Burmazović and J. N. H. Reek, Nat. Chem., 2016, 8, 225–230 CrossRef CAS.
- M. Otte, P. F. Kuijpers, O. Troeppner, I. Ivanović-Burmazović, J. N. H. Reek and B. de Bruin, Chem.–Eur. J., 2014, 20, 4880–4884 CrossRef CAS PubMed.
- X. Feng, P. Liao, J. Jiang, J. Shi, Z. Ke and J. Zhang, ChemPhotoChem, 2019, 3, 1014–1019 CrossRef CAS.
- G. Montà-González, F. Sancenón, R. Martínez-Máñez and V. Martí-Centelles, Chem. Rev., 2022, 122, 13636–13708 CrossRef.
- M. Sharafi, K. T. McKay, M. Ivancic, D. R. McCarthy, N. Dudkina, K. E. Murphy, S. C. Rajappan, J. P. Campbell, Y. Shen, A. R. Badireddy, J. Li and S. T. Schneebeli, Chem, 2020, 6, 1469–1494 CAS.
- A. Dhamija, A. Gunnam, X. Yu, H. Lee, I.-C. Hwang, Y. Ho Ko and K. Kim, Angew. Chem., Int. Ed., 2022, 61, e202209326 CrossRef CAS PubMed.
- K. I. Assaf and W. M. Nau, Chem. Soc. Rev., 2015, 44, 394–418 RSC.
- R. Breslow and S. D. Dong, Chem. Rev., 1998, 98, 1997–2012 CrossRef CAS PubMed.
- A. Pappalardo, R. Puglisi and G. Trusso Sfrazzetto, Catalysts, 2019, 9, 630 CrossRef CAS.
- Y. Zhu, J. Rebek Jr and Y. Yu, Chem. Commun., 2019, 55, 3573–3577 RSC.
- J. Lee, O. K. Farha, J. Roberts, K. A. Scheidt, S. T. Nguyen and J. T. Hupp, Chem. Soc. Rev., 2009, 38, 1450–1459 RSC.
- V. Pascanu, G. González Miera, A. K. Inge and B. Martín-Matute, J. Am. Chem. Soc., 2019, 141, 7223–7234 CrossRef CAS PubMed.
- S.-Y. Ding and W. Wang, Chem. Soc. Rev., 2013, 42, 548–568 RSC.
- J. Guo and D. Jiang, ACS Cent. Sci., 2020, 6, 869–879 CrossRef CAS PubMed.
- M. Fujita, J. Yazaki and K. Ogura, J. Am. Chem. Soc., 1990, 112, 5645–5647 CrossRef CAS.
- M. Fujita, K. Umemoto, M. Yoshizawa, N. Fujita, T. Kusukawa and K. Biradha, Chem. Commun., 2001, 509–518 RSC.
- D. L. Caulder and K. N. Raymond, Acc. Chem. Res., 1999, 32, 975–982 CrossRef CAS.
- D. Fujita, Y. Ueda, S. Sato, N. Mizuno, T. Kumasaka and M. Fujita, Nature, 2016, 540, 563–566 CrossRef CAS.
- D. Zhang, T. K. Ronson and J. R. Nitschke, Acc. Chem. Res., 2018, 51, 2423–2436 CrossRef CAS.
- S. Sato, Y. Ishido and M. Fujita, J. Am. Chem. Soc., 2009, 131, 6064–6065 CrossRef CAS.
- S. Pullen, J. Tessarolo and G. H. Clever, Chem. Sci., 2021, 12, 7269–7293 RSC.
- J. E. M. Lewis, E. L. Gavey, S. A. Cameron and J. D. Crowley, Chem. Sci., 2012, 3, 778–784 RSC.
- P. Mal, B. Breiner, K. Rissanen and J. R. Nitschke, Science, 2009, 324, 1697–1699 CrossRef CAS PubMed.
- S. Mecozzi and J. Rebek, Chem.–Eur. J., 1998, 4, 1016–1022 CrossRef CAS.
- K. Harris, D. Fujita and M. Fujita, Chem. Commun., 2013, 49, 6703–6712 RSC.
- S. Turega, W. Cullen, M. Whitehead, C. A. Hunter and M. D. Ward, J. Am. Chem. Soc., 2014, 136, 8475–8483 CrossRef CAS PubMed.
- Y. R. Hristova, M. M. J. Smulders, J. K. Clegg, B. Breiner and J. R. Nitschke, Chem. Sci., 2011, 2, 638–641 RSC.
- O. Chepelin, J. Ujma, X. Wu, A. M. Z. Slawin, M. B. Pitak, S. J. Coles, J. Michel, A. C. Jones, P. E. Barran and P. J. Lusby, J. Am. Chem. Soc., 2012, 134, 19334–19337 CrossRef CAS.
- P. R. Symmers, M. J. Burke, D. P. August, P. I. T. Thomson, G. S. Nichol, M. R. Warren, C. J. Campbell and P. J. Lusby, Chem. Sci., 2015, 6, 756–760 RSC.
- J. S. Fleming, K. L. V. Mann, C.-A. Carraz, E. Psillakis, J. C. Jeffery, J. A. McCleverty and M. D. Ward, Angew. Chem., Int. Ed., 1998, 37, 1279–1281 CrossRef CAS.
- D. P. August, G. S. Nichol and P. J. Lusby, Angew. Chem., Int. Ed., 2016, 55, 15022–15026 CrossRef CAS.
- Proteinase and Peptidase Inhibition: Recent Potential Targets for Drug Development, ed. H. J. Smith and C. Simons, CRC Press, 1st edn, 2002 Search PubMed.
- A. V. Davis and K. N. Raymond, J. Am. Chem. Soc., 2005, 127, 7912–7919 CrossRef CAS PubMed.
- A. M. Castilla, W. J. Ramsay and J. R. Nitschke, Acc. Chem. Res., 2014, 47, 2063–2073 CrossRef CAS PubMed.
- K. Li, L.-Y. Zhang, C. Yan, S.-C. Wei, M. Pan, L. Zhang and C.-Y. Su, J. Am. Chem. Soc., 2014, 136, 4456–4459 CrossRef CAS PubMed.
- L.-H. Liu, L. Liu, H.-R. Chi, C.-N. Li and Z.-B. Han, Chem. Commun., 2022, 58, 6417–6420 RSC.
- R. L. Spicer, A. D. Stergiou, T. A. Young, F. Duarte, M. D. Symes and P. J. Lusby, J. Am. Chem. Soc., 2020, 142, 2134–2139 CrossRef CAS.
- Z. Lu, R. Lavendomme, O. Burghaus and J. R. Nitschke, Angew. Chem., Int. Ed., 2019, 58, 9073–9077 CrossRef CAS PubMed.
- J. Wang, T. A. Young, F. Duarte and P. J. Lusby, J. Am. Chem. Soc., 2020, 142, 17743–17750 CrossRef CAS.
- K. A. Johnson and R. S. Goody, Biochemistry, 2011, 50, 8264–8269 CrossRef CAS.
- R Core Team, R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, 2015, https://www.R-project.org/ Search PubMed.
- v. R. Studio Team. RStudio: Integrated Development for R, Inc., Boston, MA, 2015, https://www.rstudio.com/ Search PubMed.
- C. Park, J. Chem. Educ., 2022, 99, 2556–2562 CrossRef CAS.
- D. W. Christianson and C. A. Fierke, Acc. Chem. Res., 1996, 29, 331–339 CrossRef CAS.
- A. Radzicka and R. Wolfenden, Science, 1995, 267, 90–93 CrossRef CAS.
- C. J. Hastings, M. D. Pluth, R. G. Bergman and K. N. Raymond, J. Am. Chem. Soc., 2010, 132, 6938–6940 CrossRef CAS PubMed.
- M. D. Pluth, R. G. Bergman and K. N. Raymond, Science, 2007, 316, 85–88 CrossRef CAS.
- V. Martí-Centelles, A. L. Lawrence and P. J. Lusby, J. Am. Chem. Soc., 2018, 140, 2862–2868 CrossRef.
- D. M. Quinn, Chem. Rev., 1987, 87, 955–979 CrossRef CAS.
- R. P. Magalhães, H. S. Fernandes and S. F. Sousa, Isr. J. Chem., 2020, 60, 655–666 CrossRef.
- A. J. Sterling, S. Zavitsanou, J. Ford and F. Duarte, WIREs Comp. Mol. Sci., 2021, 11, e1518 CrossRef CAS.
- M. H. S. Segler, M. Preuss and M. P. Waller, Nature, 2018, 555, 604–610 CrossRef CAS PubMed.
- S. Ahn, M. Hong, M. Sundararajan, D. H. Ess and M.-H. Baik, Chem. Rev., 2019, 119, 6509–6560 CrossRef CAS PubMed.
- L. Turcani, E. Berardo and K. E. Jelfs, J. Comput. Chem., 2018, 39, 1931–1942 CrossRef CAS PubMed.
- T. A. Young, R. Gheorghe and F. Duarte, J. Chem. Inf. Model., 2020, 60, 3546–3557 CrossRef CAS PubMed.
- C. E. Wilmer, M. Leaf, C. Y. Lee, O. K. Farha, B. G. Hauser, J. T. Hupp and R. Q. Snurr, Nat. Chem., 2012, 4, 83–89 CrossRef CAS PubMed.
- R. Custelcean, J. Bosano, P. V. Bonnesen, V. Kertesz and B. P. Hay, Angew. Chem., Int. Ed., 2009, 48, 4025–4029 CrossRef CAS PubMed.
- S. Grimme and P. R. Schreiner, Angew. Chem., Int. Ed., 2018, 57, 4170–4176 CrossRef CAS PubMed.
- M. Elstner, D. Porezag, G. Jungnickel, J. Elsner, M. Haugk, T. Frauenheim, S. Suhai and G. Seifert, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 7260–7268 CrossRef CAS.
- M. Gaus, Q. Cui and M. Elstner, J. Chem. Theory Comput., 2011, 7, 931–948 CrossRef CAS PubMed.
- P. R. Nagy and M. Kállay, J. Chem. Theory Comput., 2019, 15, 5275–5298 CrossRef CAS PubMed.
- G. Norjmaa, P. Vidossich, J.-D. Maréchal and G. Ujaque, J. Chem. Inf. Model., 2021, 61, 4370–4381 CrossRef CAS PubMed.
- C. Fuertes-Espinosa, C. García-Simón, M. Pujals, M. Garcia-Borràs, L. Gómez, T. Parella, J. Juanhuix, I. Imaz, D. Maspoch, M. Costas and X. Ribas, Chem, 2020, 6, 169–186 CAS.
- C. García-Simón, C. Colomban, Y. A. Çetin, A. Gimeno, M. Pujals, E. Ubasart, C. Fuertes-Espinosa, K. Asad, N. Chronakis, M. Costas, J. Jiménez-Barbero, F. Feixas and X. Ribas, J. Am. Chem. Soc., 2020, 142, 16051–16063 CrossRef PubMed.
- S. Juber, S. Wingbermühle, P. Nuernberger, G. H. Clever and L. V. Schäfer, Phys. Chem. Chem. Phys., 2021, 23, 7321–7332 RSC.
- T. A. Young, J. J. Silcock, A. J. Sterling and F. Duarte, Angew. Chem., Int. Ed., 2021, 69, 4266–4274 CrossRef.
- Q. Peng, F. Duarte and R. S. Paton, Chem. Soc. Rev., 2016, 45, 6093–6107 RSC.
- A. Warshel and M. Levitt, J. Mol. Biol., 1976, 103, 227–249 CrossRef CAS PubMed.
- M. Yoneya, T. Yamaguchi, S. Sato and M. Fujita, J. Am. Chem. Soc., 2012, 134, 14401–14407 CrossRef CAS PubMed.
- M. Yoneya, S. Tsuzuki, T. Yamaguchi, S. Sato and M. Fujita, ACS Nano, 2014, 8, 1290–1296 CrossRef CAS.
- V. V. Welborn, W.-L. Li and T. Head-Gordon, Nat. Commun., 2020, 11, 415 CrossRef CAS PubMed.
- W.-L. Li, H. Hao and T. Head-Gordon, ACS Catal., 2022, 12, 3782–3788 CrossRef CAS.
- M. P. Frushicheva, S. Mukherjee and A. Warshel, J. Phys. Chem. B, 2012, 116, 13353–13360 CrossRef CAS PubMed.
- Y. Ootani, Y. Akinaga and T. Nakajima, J. Comput. Chem., 2015, 36, 459–466 CrossRef CAS.
- V. Vaissier Welborn and T. Head-Gordon, J. Phys. Chem. Lett., 2018, 9, 3814–3818 CrossRef CAS PubMed.
- G. Norjmaa, J.-D. Maréchal and G. Ujaque, J. Am. Chem. Soc., 2019, 141, 13114–13123 CrossRef CAS PubMed.
- T. A. Young, V. Martí-Centelles, J. Wang, P. J. Lusby and F. Duarte, J. Am. Chem. Soc., 2020, 142, 1300–1310 CrossRef PubMed.
- P. Howlader, P. Das, E. Zangrando and P. S. Mukherjee, J. Am. Chem. Soc., 2016, 138, 1668–1676 CrossRef CAS PubMed.
- L. Li, L. Yang, X. Li, J. Wang, X. Liu and C. He, Inorg. Chem., 2021, 60, 8802–8810 CrossRef CAS.
- L. R. Holloway, P. M. Bogie, Y. Lyon, C. Ngai, T. F. Miller, R. R. Julian and R. J. Hooley, J. Am. Chem. Soc., 2018, 140, 8078–8081 CrossRef CAS PubMed.
- J. Jiao, C. Tan, Z. Li, Y. Liu, X. Han and Y. Cui, J. Am. Chem. Soc., 2018, 140, 2251–2259 CrossRef CAS PubMed.
- S. Kozuch and S. Shaik, Acc. Chem. Res., 2011, 44, 101–110 CrossRef CAS PubMed.
- D. P. Curran and L. H. Kuo, Tetrahedron Lett., 1995, 36, 6647–6650 CAS.
- C. Uyeda and E. N. Jacobsen, J. Am. Chem. Soc., 2008, 130, 9228–9229 CrossRef CAS PubMed.
- K. Wang, X. Cai, W. Yao, D. Tang, R. Kataria, H. S. Ashbaugh, L. D. Byers and B. C. Gibb, J. Am. Chem. Soc., 2019, 141, 6740–6747 CrossRef CAS PubMed.
- C. J. Walter, H. L. Anderson and J. K. M. Sanders, J. Chem. Soc., Chem. Commun., 1993, 458–460 RSC.
- J. Kang, J. Santamaría, G. Hilmersson and J. Rebek, J. Am. Chem. Soc., 1998, 120, 7389–7390 CrossRef CAS.
- J. K. M. Sanders, Chem.–Eur. J., 1998, 4, 1378–1383 CrossRef CAS.
- T. Murase, Y. Nishijima and M. Fujita, J. Am. Chem. Soc., 2012, 134, 162–164 CrossRef CAS PubMed.
- R. J. Hooley and J. Rebek Jr, Org. Biomol. Chem., 2007, 5, 3631–3636 RSC.
- M. Yoshizawa, T. Kusukawa, M. Fujita and K. Yamaguchi, J. Am. Chem. Soc., 2000, 122, 6311–6312 CrossRef CAS.
- T. R. Kelly, G. J. Bridger and C. Zhao, J. Am. Chem. Soc., 1990, 112, 8024–8034 CrossRef CAS.
- R. Cacciapaglia, S. Di Stefano and L. Mandolini, Acc. Chem. Res., 2004, 37, 113–122 CrossRef CAS PubMed.
- A. J. Kirby, Angew Chem. Int. Ed. Engl., 1996, 35, 706–724 CrossRef.
- M. I. Page and W. P. Jencks, Proc. Natl. Acad. Sci. U. S. A., 1971, 68, 1678–1683 CrossRef CAS PubMed.
- A. J. Kirby, in Advances in Physical Organic Chemistry, ed. V. Gold and D. Bethell, Academic Press, 1980, vol. 17, pp. 183–278 Search PubMed.
- L. Mandolini, in Advances in Physical Organic Chemistry, ed. V. Gold and D. Bethell, Academic Press, 1986, vol. 22, pp. 1–111 Search PubMed.
- F. N. Tehrani, K. I. Assaf, R. Hein, C. M. E. Jensen, T. C. Nugent and W. M. Nau, ACS Catal., 2022, 12, 2261–2269 CrossRef CAS.
- K. Takahiro, N. Tatsuya, O. Takashi and F. Makoto, Chem. Lett., 2003, 32, 284–285 CrossRef.
- T. Murase, S. Horiuchi and M. Fujita, J. Am. Chem. Soc., 2010, 132, 2866–2867 CrossRef CAS PubMed.
- Y. Nishioka, T. Yamaguchi, M. Yoshizawa and M. Fujita, J. Am. Chem. Soc., 2007, 129, 7000–7001 CrossRef CAS PubMed.
- S. Horiuchi, T. Murase and M. Fujita, Chem.–Asian J., 2011, 6, 1839–1847 CrossRef CAS PubMed.
- Y. Fang, T. Murase and M. Fujita, Chem. Lett., 2015, 44, 1095–1097 CrossRef CAS.
- D. Samanta, S. Mukherjee, Y. P. Patil and P. S. Mukherjee, Chem.–Eur. J., 2012, 18, 12322–12329 CrossRef CAS PubMed.
- W. Cullen, M. C. Misuraca, C. A. Hunter, N. H. Williams and M. D. Ward, Nat. Chem., 2016, 8, 231–236 CrossRef CAS PubMed.
- C. G. P. Taylor, A. J. Metherell, S. P. Argent, F. M. Ashour, N. H. Williams and M. D. Ward, Chemistry, 2020, 26, 3065–3073 CrossRef CAS PubMed.
- C. Mozaceanu, C. G. P. Taylor, J. R. Piper, S. P. Argent and M. D. Ward, Chemistry, 2020, 2, 22–32 CrossRef CAS.
- M. D. Ludden, C. G. P. Taylor, M. B. Tipping, J. S. Train, N. H. Williams, J. C. Dorrat, K. L. Tuck and M. D. Ward, Chem. Sci., 2021, 12, 14781–14791 RSC.
- M. L. C. Quan, C. B. Knobler and D. J. Cram, J. Chem. Soc., Chem. Commun., 1991, 660–662 RSC.
- M. L. C. Quan and D. J. Cram, J. Am. Chem. Soc., 1991, 113, 2754–2755 CrossRef CAS.
- J. K. Judice and D. J. Cram, J. Am. Chem. Soc., 1991, 113, 2790–2791 CrossRef CAS.
- F. Liu, R. C. Helgeson and K. N. Houk, Acc. Chem. Res., 2014, 47, 2168–2176 CrossRef CAS PubMed.
- M. Biler, R. M. Crean, A. K. Schweiger, R. Kourist and S. C. L. Kamerlin, J. Am. Chem. Soc., 2020, 142, 20216–20231 CrossRef CAS PubMed.
- D. L. Caulder, R. E. Powers, T. N. Parac and K. N. Raymond, Angew. Chem., Int. Ed., 1998, 37, 1840–1843 CrossRef CAS.
- D. Fiedler, H. van Halbeek, R. G. Bergman and K. N. Raymond, J. Am. Chem. Soc., 2006, 128, 10240–10252 CrossRef CAS PubMed.
- C. J. Hastings, D. Fiedler, R. G. Bergman and K. N. Raymond, J. Am. Chem. Soc., 2008, 130, 10977–10983 CrossRef CAS PubMed.
- C. M. Hong, M. Morimoto, E. A. Kapustin, N. Alzakhem, R. G. Bergman, K. N. Raymond and F. D. Toste, J. Am. Chem. Soc., 2018, 140, 6591–6595 CrossRef CAS PubMed.
- W. M. Hart-Cooper, K. N. Clary, F. D. Toste, R. G. Bergman and K. N. Raymond, J. Am. Chem. Soc., 2012, 134, 17873–17876 CrossRef CAS PubMed.
- D. M. Kaphan, F. D. Toste, R. G. Bergman and K. N. Raymond, J. Am. Chem. Soc., 2015, 137, 9202–9205 CrossRef CAS PubMed.
- Q. N. N. Nguyen, K. T. Xia, Y. Zhang, N. Chen, M. Morimoto, X. Pei, Y. Ha, J. Guo, W. Yang, L.-P. Wang, R. G. Bergman, K. N. Raymond, F. D. Toste and D. J. Tantillo, J. Am. Chem. Soc., 2022, 144, 11413–11424 CrossRef CAS PubMed.
- G. Norjmaa, F. Himo, J.-D. Maréchal and G. Ujaque, Chem.–Eur. J., 2022, 28, e202201792 CrossRef CAS PubMed.
- A. Warshel, P. K. Sharma, M. Kato, Y. Xiang, H. Liu and M. H. M. Olsson, Chem. Rev., 2006, 106, 3210–3235 CrossRef CAS PubMed.
- J. K. Lee and K. N. Houk, Science, 1997, 276, 942–945 CrossRef CAS PubMed.
- A. Warshel, M. Štrajbl, J. Villà and J. Florián, Biochemistry, 2000, 39, 14728–14738 CrossRef CAS PubMed.
- R. R. David Halliday and J. Walker, Fundamentals of Physics, John Wiley & Sons, 1997 Search PubMed.
- R. A. Marcus, J. Chem. Phys., 1956, 24, 966–978 CrossRef CAS.
- J. R. Miller, L. T. Calcaterra and G. L. Closs, J. Am. Chem. Soc., 1984, 106, 3047–3049 CrossRef CAS.
- R. Meir, H. Chen, W. Lai and S. Shaik, ChemPhysChem, 2010, 11, 301–310 CrossRef CAS PubMed.
- A. C. Aragonès, N. L. Haworth, N. Darwish, S. Ciampi, N. J. Bloomfield, G. G. Wallace, I. Diez-Perez and M. L. Coote, Nature, 2016, 531, 88–91 CrossRef PubMed.
- H. M. Aitken and M. L. Coote, Phys. Chem. Chem. Phys., 2018, 20, 10671–10676 RSC.
- V. V. Welborn, L. Ruiz Pestana and T. Head-Gordon, Nat. Catal., 2018, 1, 649–655 CrossRef.
- T. Stuyver, R. Ramanan, D. Mallick and S. Shaik, Angew. Chem., Int. Ed., 2020, 59, 7915–7920 CrossRef CAS PubMed.
- W. Yao, K. Wang, Y. A. Ismaiel, R. Wang, X. Cai, M. Teeler and B. C. Gibb, J. Phys. Chem. B, 2021, 125, 9333–9340 CrossRef CAS PubMed.
- S. Shaik, D. Danovich, J. Joy, Z. Wang and T. Stuyver, J. Am. Chem. Soc., 2020, 142, 12551–12562 CrossRef CAS PubMed.
- D. Chen and T. Savidge, Science, 2015, 349, 936 CrossRef CAS PubMed.
- G. Norjmaa, J.-D. Maréchal and G. Ujaque, Chem.–Eur. J., 2020, 26, 6988–6992 CrossRef CAS PubMed.
- M. D. Pluth, R. G. Bergman and K. N. Raymond, Angew. Chem., Int. Ed., 2007, 46, 8587–8589 CrossRef CAS PubMed.
- S. M. Bierschenk, R. G. Bergman, K. N. Raymond and F. D. Toste, J. Am. Chem. Soc., 2020, 142, 733–737 CrossRef CAS PubMed.
- S. Zhou, Z. Zhang, D. Bai, J. Li, X. Cui, Z. J. Xu, Y. Tang, X. Tang and W. Liu, Inorg. Chem., 2022, 61, 4009–4017 CrossRef CAS PubMed.
- D. M. Kaphan, M. D. Levin, R. G. Bergman, K. N. Raymond and F. D. Toste, Science, 2015, 350, 1235–1238 CrossRef CAS PubMed.
- G. Norjmaa, J.-D. Maréchal and G. Ujaque, Chem.–Eur. J., 2021, 27, 15973–15980 CrossRef CAS PubMed.
- P. Mal, D. Schultz, K. Beyeh, K. Rissanen and J. R. Nitschke, Angew. Chem., Int. Ed., 2008, 47, 8297–8301 CrossRef CAS PubMed.
- A. Paul, M. A. Shipman, D. Y. Onabule, S. Sproules and M. D. Symes, Chem. Sci., 2021, 12, 5082–5090 RSC.
- J. L. Bolliger, A. M. Belenguer and J. R. Nitschke, Angew. Chem., Int. Ed., 2013, 52, 7958–7962 CrossRef CAS PubMed.
- T. Murase, Y. Nishijima and M. Fujita, J. Am. Chem. Soc., 2012, 134, 162–164 CrossRef CAS PubMed.
- D. Samanta and P. S. Mukherjee, Chem. Commun., 2013, 49, 4307–4309 RSC.
- P. Das, A. Kumar, P. Howlader and P. S. Mukherjee, Chem.–Eur. J., 2017, 23, 12565–12574 CrossRef CAS PubMed.
- S.-C. Li, L.-X. Cai, M. Hong, Q. Chen and Q.-F. Sun, Angew. Chem., Int. Ed., 2022, 61, e202204732 CrossRef CAS PubMed.
- D. A. McMorran and P. J. Steel, Angew Chem. Int. Ed. Engl., 1998, 37, 3295–3297 CrossRef CAS PubMed.
- G. H. Clever, S. Tashiro and M. Shionoya, Angew. Chem., Int. Ed., 2009, 48, 7010–7012 CrossRef CAS PubMed.
- W. M. Bloch, J. J. Holstein, W. Hiller and G. H. Clever, Angew. Chem., Int. Ed., 2017, 56, 8285–8289 CrossRef CAS PubMed.
- P. Liao, B. W. Langloss, A. M. Johnson, E. R. Knudsen, F. S. Tham, R. R. Julian and R. J. Hooley, Chem. Commun., 2010, 46, 4932–4934 RSC.
- N. Kishi, Z. Li, K. Yoza, M. Akita and M. Yoshizawa, J. Am. Chem. Soc., 2011, 133, 11438–11441 CrossRef CAS PubMed.
- J. E. M. Lewis, A. Tarzia, A. J. P. White and K. E. Jelfs, Chem. Sci., 2020, 11, 677–683 RSC.
- S. P. Kim, A. G. Leach and K. N. Houk, J. Org. Chem., 2002, 67, 4250–4260 CrossRef CAS PubMed.
- H. Takezawa, K. Shitozawa and M. Fujita, Nat. Chem., 2020, 12, 574–578 CrossRef CAS PubMed.
- M. Delle Piane, L. Pesce, M. Cioni and G. M. Pavan, Chem. Sci., 2022, 13, 11232–11245 RSC.
- C. J. Brown, R. G. Bergman and K. N. Raymond, J. Am. Chem. Soc., 2009, 131, 17530–17531 CrossRef CAS PubMed.
- A. V. Davis, D. Fiedler, M. Ziegler, A. Terpin and K. N. Raymond, J. Am. Chem. Soc., 2007, 129, 15354–15363 CrossRef CAS PubMed.
- C. Zhao, Q.-F. Sun, W. M. Hart-Cooper, A. G. DiPasquale, F. D. Toste, R. G. Bergman and K. N. Raymond, J. Am. Chem. Soc., 2013, 135, 18802–18805 CrossRef CAS PubMed.
- W. M. Hart-Cooper, C. Zhao, R. M. Triano, P. Yaghoubi, H. L. Ozores, K. N. Burford, F. D. Toste, R. G. Bergman and K. N. Raymond, Chem. Sci., 2015, 6, 1383–1393 RSC.
- C. Zhao, F. D. Toste, K. N. Raymond and R. G. Bergman, J. Am. Chem. Soc., 2014, 136, 14409–14412 CrossRef CAS PubMed.
- S. M. Bierschenk, J. Y. Pan, N. S. Settineri, U. Warzok, R. G. Bergman, K. N. Raymond and F. D. Toste, J. Am. Chem. Soc., 2022, 144, 11425–11433 CrossRef CAS PubMed.
- N. Ousaka, J. K. Clegg and J. R. Nitschke, Angew. Chem., Int. Ed., 2012, 51, 1464–1468 CrossRef CAS PubMed.
- P. J. Stang, B. Olenyuk, D. C. Muddiman and R. D. Smith, Organometallics, 1997, 16, 3094–3096 CrossRef CAS.
- M. Yoshizawa, Y. Takeyama, T. Kusukawa and M. Fujita, Angew. Chem., Int. Ed., 2002, 41, 1347–1349 CrossRef CAS PubMed.
- Y. Nishioka, T. Yamaguchi, M. Kawano and M. Fujita, J. Am. Chem. Soc., 2008, 130, 8160–8161 CrossRef CAS PubMed.
- J. Guo, Y. Z. Fan, Y. L. Lu, S. P. Zheng and C. Y. Su, Angew. Chem., Int. Ed., 2020, 59, 8661–8669 CrossRef CAS PubMed.
- H. Takezawa, T. Kanda, H. Nanjo and M. Fujita, J. Am. Chem. Soc., 2019, 141, 5112–5115 CrossRef CAS PubMed.
- T. A. Bender, R. G. Bergman, K. N. Raymond and F. D. Toste, J. Am. Chem. Soc., 2019, 141, 11806–11810 CrossRef CAS PubMed.
- M. M. J. Smulders and J. R. Nitschke, Chem. Sci., 2012, 3, 785–788 RSC.
- Y. Ueda, H. Ito, D. Fujita and M. Fujita, J. Am. Chem. Soc., 2017, 139, 6090–6093 CrossRef CAS PubMed.
- Z. J. Wang, K. N. Clary, R. G. Bergman, K. N. Raymond and F. D. Toste, Nat. Chem., 2013, 5, 100–103 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2023 |