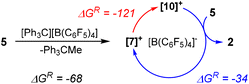Selective synthesis of germasila-adamantanes through germanium–silicon shift processes

Abstract

The regioselective synthesis of germasila-adamantanes with the germanium atoms in the bridgehead positions is described starting from cyclic precursors by a cationic sila-Wagner–Meerwein (SWM) rearrangement reaction. The SWM rearrangement allows also a deliberate shift of germanium atoms from the periphery and within the cage structures into the bridgehead positions. This opens the possibility for a synthesis of germasila-adamantanes of defined germanium content and controlled regiochemistry. In the same way that sila-adamantane can be regarded as a molecular building block of elemental silicon, the germasila-adamantane molecules represent cutouts of silicon/germanium alloys.

---

Introduction

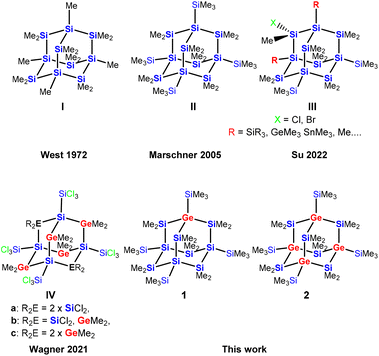
The chemistry of polysilanes has now been studied for more than 100 years.^1–5 While their structural chemistry resembles that of alkanes, their property of electron conjugation suggests some similarity to unsaturated hydrocarbons. Structurally, cyclic and polycyclic polysilanes are the higher congeners of cyclo- and polycycloalkanes.^6,7

Adamantane cage structures of polysilanes are of particular interest as they represent the building blocks of elemental silicon. The synthesis of sila-adamantane cages nicely reflects the development of preparative approaches towards this type of compounds (Fig. 1). The first synthetic attempt, which was reported by West and Indriksons as early as in 1972, employed a Wurtz type condensation of Me₂SiCl₂ and MeSiCl₃ with sodium/potassium alloy.⁸ As the Wurtz-type approach is not very selective, the formation of the expected permethylsilaadamantane cage I could not unambiguously be proven. Salt elimination reactions between oligosilanides and silyl halides represented a major advancement.⁹ This method allowed access to a cyclohexasilanyl substituted bicylo[2.2.1]heptasilane, which served as the structural isomer required for sila-Wagner–Meerwein (SWM) rearrangement to the first structurally verified example of a sila-adamantane molecule II.¹⁰ Recently, Su and co-workers demonstrated site selective functionalization of both the bridging and the bridgehead positions as in adamantane III.¹¹ Wagner and co-workers presented a surprising simple but high yielding synthesis of germasila-adamantanes. Reactions of Si₂Cl₆ with Me₂GeCl₂ in the presence of (ⁿBu₄N)Cl form adamantane cages with silicon atoms in the bridgehead and either SiCl₂- or GeMe₂-units in the bridging positions (compounds IVa–IVc, Fig. 1).¹²

Fig. 1 Progress of the synthesis of oligosilane-adamantane type cage structures.

Our present contribution deals with the selective synthesis of germasila-adamantanes from cyclic germa-oligosilanes, the deliberate formal exchange of a sila-adamantane's bridgehead silicon for an attached germanium atom, and the shift of four germanium atoms from bridging into bridgehead positions, both without affecting the integrity of the adamantane cage. These transformations showcase the high synthetic capacity of SWM reactions for the tailored construction of complex germasila-adamantane structures, which might serve as molecular models for nano-sized silicon/germanium materials. Silicon/germanium nanostructures, Si_xGe_1−x, are extensively used in applications such as advanced transistors, quantum devices and photodetectors, electro-optical modulators, photovoltaics, microelectromechanical systems and thermoelectric generators.^13–19 All silicon and germanium atoms of the here investigated Si/Ge cluster molecules are tetracoordinated⁶ and therefore clearly distinguished from substituent-free silicon and germanium atoms in mixed Si/Ge Zintl ions^20–22 and germa-siliconoids.^23–26

Oligosilanyl cations are capable of undergoing Wagner–Meerwein rearrangement chemistry in a similar way as alkanes.²⁷ This was discovered by Kumada and Ishikawa, who reported AlCl₃-mediated rearrangement of permethylated linear oligosilanes to branched structures and related chemistry of cyclosilanes.^28–30 The strictly thermodynamic driving force of this reaction bears some synthetic potential.^10,31,32 In addition to structural rearrangements of oligosilanes, the Wagner–Meerwein chemistry of germa-oligosilanes allows also a selective intramolecular shift of germanium atoms into more silylated positions.³³ For instance, under the influence of a strong Lewis acid tris(trimethylsilyl)trimethylgermylsilane is quantitatively converted to tetrakis(trimethylsilyl)germane.^34,35

Results and discussion

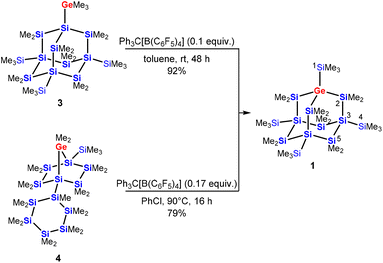
Utilizing this chemistry on a more complex substrate, we treated the trimethylgermylated sila-adamantane 3 ¹¹ with a catalytic amount of Ph₃C[B(C₆F₅)₄] in toluene and observed clean conversion to compound 1 with a germa-nonasila-adamantane cage structure in 92% isolated yield (Scheme 1). Adamantane 1 was also obtained from polycyclic starting materials via the established route to all-sila-adamantanes: the tricyclic adamantane precursor 4 with a dimethylgermylene unit rearranges quantitatively and selectively to the germasila-adamantane 1 (79% isolated yield). In this case, slightly enforced reaction conditions had to be applied (Scheme 1).

Scheme 1 Cationic rearrangements of the trimethylgermyl-substituted sila-adamantane 3 and of the polycyclic precursor 4 to adamantane 1 with the germanium atom shifted into a bridgehead position of the adamantane cage. The descriptive numbers at compound 1 refer to NMR spectroscopic assignments.

The NMR spectrum of 1 exhibits the expected pattern. Five signals in the ¹H NMR spectrum at δ = 0.65 (18H), 0.62 (9H), 0.61 (9H), 0.38 (9H), and 0.35 (27H) ppm correspond to the methyl groups at Si², Si⁵ (2 × for Me_ax and Me_eq), Si¹, and Si⁴ (Si numbering in accordance with the structural formula of 1 in Scheme 1), respectively. The same number of five signals was found for the methyl groups in the ¹³C NMR spectrum at 5.5 (Si¹), 5.0 (Si⁴), 4.8 (Si²), 4.2, and 4.1 (Si⁵) ppm. Also the ²⁹Si NMR spectrum features five signals at 0.8 (Si¹), −5.6 (Si⁴), −20.9 (Si²), −26.3 (Si⁵), and −118.5 (Si³) ppm (assignment of Si² and Si⁵ by ¹H–²⁹Si HMBC). Comparison to the ¹H NMR spectrum of the all-sila-adamantane II (¹H: δ = 0.60) (s, 36H, SiMe₂), 0.35 (s, 36H, SiMe₃)¹⁰ shows the chemical shifts of 1 to be very similar, with all SiMe₂ signals around 0.60 ppm and the SiMe₃ signals around 0.35 ppm. The ²⁹Si NMR chemical shifts of the cyclohexasilanyl unit of the bottom part of compound 1 (i.e. Si³, Si⁴, and Si⁵) are very close to those of the all-sila adamantane II (²⁹Si: δ = −4.8, −26.0, and −118.6), indicating no major influence of the germanium atom.

The recently published synthesis of germanium-containing sila-adamantane IVa describes the use of the Si₂Cl₆/Me₂GeCl₂/(ⁿBu₄N)Cl system to obtain a germasila-adamantane with two SiCl₂ and four GeMe₂ units in the bridging positions as well as four SiCl₃-substituted silicon atoms as the bridgeheads.¹² Exhaustive methylation of this product led to germasila-adamantane 5 (Scheme 2).³⁶

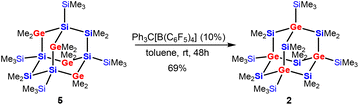Scheme 2 Cationic rearrangement of the tetragermasila-adamantane 5 to the isomeric product 2 with the four germanium atoms of the adamantane cage moving from bridging into bridgehead positions.

Subjecting compound 5 to the rearrangement conditions (Ph₃C[B(C₆F₅)₄]/toluene) led to the clean formation of the adamantane cage product 2 with all germanium atoms shifted to the bridgehead positions in 69% isolated yield (Scheme 2).

Due to the higher symmetry of 2 compared to 1, NMR spectroscopic analysis of 2 exhibited a simpler pattern. The two signals in the ¹H NMR spectrum at δ = 0.69 (36H) and 0.38 (36H) ppm correspond to the SiMe₂ and SiMe₃ groups, respectively. The two signals for the methyl groups in the ¹³C NMR spectrum were observed at 5.6 and 5.4 ppm. Compared to the all-sila-adamantane II (δ = −4.8, −26.0, and −118.6 ppm), the ²⁹Si NMR spectrum of 2 features only the two signals at −0.5 (SiMe₃) and −15.7 (SiMe₂), with the downfield-shift behavior typical for neighboring germanium atoms.^37,38

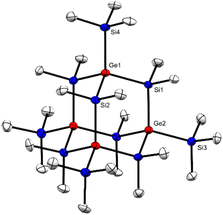
Single crystal XRD analysis of 2 (ref. 39) (Fig. 2) provided a structure isotypic to the all-sila-adamantane II.¹⁰ Both compounds crystallize in the space group R3̄ and the reduced cell parameters of 2 (14.171 Å and 77.13 deg.) give rise to a cell volume of 2659 ų compared to the 2636 ų observed for the all-sila-adamantane II.¹⁰ The Si–Ge bond length in adamantane 2 is 238.7 pm, which is close to the median of the Si–Ge bond lengths in molecular compounds (239.7 pm) and close to the sum of the single bond covalent radii of both elements (237 pm).^40,41 Interestingly, it is only 1.7 pm larger than the Si–Si bonds in all-sila-adamantane. The bond angles around the germanium atoms are close to the tetrahedral ideal of 109.5° (108.5–110.1°). Judged from these molecular parameters, the germasila-adamantane 2 appears to be completely unstrained. The UV(vis) spectrum of adamantane 2 in n-hexane shows a strong absorption at λ_max = 224 nm (molar absorption ε = 2 × 10⁴ L mol⁻¹ cm⁻¹), also very similar to the UV data reported for all-sila-adamantane II (λ_max = 222 nm, ε = 1.2 × 10⁵ L mol⁻¹ cm⁻¹).¹⁰

Fig. 2 Molecular structure of 2 (thermal ellipsoid plot drawn at the 30% probability level). All hydrogen atoms are omitted for clarity (bond lengths in [pm], angles in [deg]): Ge(1)–Si(1) 238.59(12), Ge(1)–Si(2) 238.62(11), Ge(1)–Si(4) 239.22(12), Ge(2)–Si(1) 238.72(11), Ge(2)–Si(3) 239.3(2); Si(2)–Ge(1)–Si(1) 108.53(4), Si(4)–Ge(1)–Si(1) 109.76(4), Si(4)–Ge(1)–Si(2) 110.05(4), Si(4)–Ge(1)–Si(2)#1 109.82(4), Si(1) Ge(2)–Si(1)#2 109.33(3), Si(1)#1–Ge(2)–Si 032 109.33(3), Si(1)#1–Ge(2)–Si(1) 109.33(3), Si(3)–Ge(2)–Si(1)#2 109.61(3), Si(3)–Ge(2)–Si(1) 109.61(3), Ge(2)#1–Si(1)–Ge(1) 109.97(4).

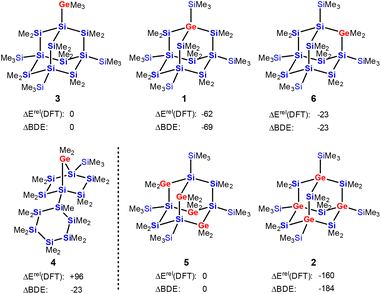
The results of density functional calculations⁴² at the M06-2X/6-311+G(d,p) level show that the formation of the sila-adamantane cluster is thermodynamically strongly favored, i.e. the isomerization of polycyclic germasilane 4 into germasilaadamantane 1 is exothermic by 158 kJ mol⁻¹ (Fig. 3 and ESI†). Adamantane 1 with the germanium atom in a bridgehead position is also the most stable of the three positional isomers 1, 3, and 6. It is energetically favored by 39 kJ mol⁻¹ over the adamantane isomer 6 with the germanium atom in the bridging position and by 62 kJ mol⁻¹ over germylsila-adamantane 3 with an exocyclic germyl substituent. Similarly, the tetragermasila-adamantane 5 with four bridging GeMe₂ units is less stable than its isomer 2 with four germanium atoms in the bridgehead positions by 160 kJ mol⁻¹. The thermodynamic preference of adamantane isomers with germanium in the bridgehead positions is a consequence of the relative strength of the Si–C bond (373 kJ mol⁻¹) versus the Ge–C bond (326 kJ mol⁻¹), which outcompetes the formation of Si–Ge bonds (294 kJ mol⁻¹) on the cost of Si–Si linkages (318 kJ mol⁻¹, see Table S3† for calculated BDEs). For example, the transformation of germasila-adamantane 6 into its isomer 1 needs an exchange of two Ge–C bonds for two stronger Si–C bonds (−94 kJ mol⁻¹) and of two Si–Si bonds for two weaker Ge–Si bonds (+48 kJ mol⁻¹). The estimation of the energy difference 6vs.1 based on these increments results in −46 kJ mol⁻¹ in preference of the germasila-adamantane 1, which is close to the DFT-computed energy difference of −39 kJ mol⁻¹ (Fig. 3). While the transformation of the germasila-adamantane cages 1, 3, 6, and 2, 5 can be understood on this basis, their formation from polycyclic precursors such as 4 is less straightforward. In addition, other effects such as release of ring strain and attractive London dispersion forces between silyl groups add to the thermodynamic preference of the adamantane cluster.^43,44 For example, the ring strain of the bicycloheptane part of the tricyclic germasilane 4 is according to an isodesmic reaction 47 kJ mol⁻¹ and the consideration of dispersion energy favors the adamantane 1 over 4 by 37 kJ mol⁻¹ (for details, see ESI, Fig. S33 and S34†).

Fig. 3 Relative energies ΔE^rel(DFT), in kJ mol⁻¹, of selected Si₁₃Ge₁Me₂₄ and Si₁₀Ge₄Me₂₄ isomers. Both calculated at M06-2X/6-311+G(d,p) and estimated on the basis of bond dissociation energies ΔBDE.

We investigated the intriguing skeletal rearrangement of the germasila-adamantane cage during the transformation 5 → 2 in detail. Previous experimental and computational studies on related systems demonstrated that the initial step in this type of rearrangement is the formation of silyl- or germyl cations by transfer of a methyl group from the germa-oligosilane to the trityl cation.³³ After rearrangement to the more stable silyl or germyl cation, the reaction terminates with a final methyl group transfer. Methyl-anion abstraction from tetragermasila-adamantane 5 allows the formation of three different cations [7]⁺–[9]⁺. The secondary germylium cation [7]⁺ is the most stable one, followed by the secondary silylium cation [8]⁺ and the primary silylium cation [9]⁺ with an exo-cage dimethylsilylium substituent is the least stable cation in this series (Fig. 4) (Note: In the context of this manuscript the terms primary or secondary cation are used for cations with either one silyl/germyl substituent or with two such substituents). These cations are significantly higher in energy than the two silyl cations ([10]⁺ and [11]⁺) that are possible immediate precursors for tetragermasila-adamantane 2. The reason for the higher stability of the cations [10]⁺ and [11]⁺ is the bridgehead position of all four germanium atoms. Therefore, the isomerization of the germylium cation [7]⁺ to the secondary silyl cation [10]⁺ is exothermic by 120 kJ mol⁻¹ (Fig. 4). Association of the cations [7]⁺–[11]⁺ to the solvent benzene is not of importance as the energy differences between the benzene complexes [7(C₆H₆)]⁺–[11(C₆H₆)]⁺ are similar to those of the isolated cations and inclusion of entropy effects shows that these complexes do not exist under ambient conditions (free association enthalpy ΔG^A,298 > 0 kJ mol⁻¹ ([7]⁺, [8]⁺, [10]⁺)) or are only weakly bonded (ΔG^A,298 > −15 kJ mol⁻¹ ([9]⁺, [11]⁺), see Table S4†).⁴⁵

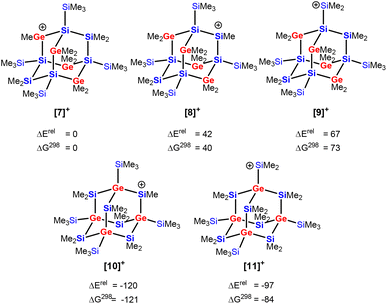Fig. 4 Relative energies ΔE^rel and free enthalpies ΔG²⁹⁸ of Si₁₀Ge₄Me₂₃ cations derived from heteroadamantanes 3 ([7]⁺–[9]⁺) and 4 from ([10]⁺, [11]⁺, in kJ mol⁻¹, at M06-2X/6-311+G(d,p)).

Based on these relative cation stabilities, we suggest the following mechanistic scenario for the trityl-induced rearrangement 5 → 2. The initial step, the exergonic methyl-anion transfer from a germylene unit of adamantane 5 to the trityl cation and formation of the germylium cation [7]⁺ (ΔG^R = −68 kJ mol⁻¹), is followed by its transformation to the more stable adamantyl cation [10]⁺ (ΔG^R = −121 kJ mol⁻¹). Also the terminating methyl-anion transfer from adamantane 5 to silyl cation [10]⁺ is thermodynamically favored (ΔG^R = −34 kJ mol⁻¹) and closes the catalytic cycle (Scheme 3). The endergonic methyl-anion transfer from Ph₃CMe to cation [10]⁺ (ΔG^R = +35 kJ mol⁻¹) suggests that the trityl borate is only the initiating reagent and not the actual catalyst.

Scheme 3 Catalytic cycle for the transformation of germa-adamantane 5 into its isomer 2 initiated by trityl tetrakis-pentafluorophenylborate. Free reaction enthalpies ΔG^R are given in kJ mol⁻¹ in italics (calculated at M06-2X/6-311+G(d,p)).

The isomerization of secondary germylium cation [7]⁺ with four germanium atoms in the bridging position of the adamantane cage into the silylium cation [10]⁺ with all four germanium atoms in the bridgehead position is a multistep process involving several cationic intermediates. To understand this process we investigated the migration of one germanium center of cation [7]⁺ into a neighboring bridgehead position, i.e. the transformation of cation [7]⁺ into the germylium cation [12]⁺ (Scheme 4). This isomerization is thermodynamically favored (by 39 kJ mol⁻¹) and involves three cationic intermediates and the rate determining step (rtds) is a [1,2] methyl-group shift, 159 kJ mol⁻¹ above the initially formed cation [7]⁺ (see Fig. S32 and Table S2† for details). Finally, three similar consecutive processes transform the germylium cation [12]⁺ into the more stable cation [10]⁺.

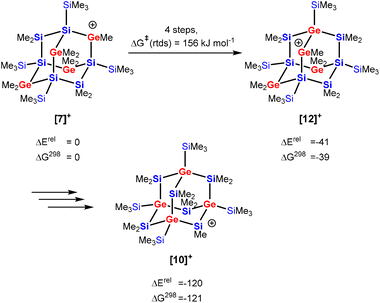Scheme 4 Recapitulation of the isomerization reaction of tetragerma-adamantyl cations [7]⁺ into [10]⁺via [12]⁺ (energies and free enthalpies are given in kJ mol⁻¹ at M06-2X/6-311+G(d,p), for details see Fig. S32†).

Conclusions

Our results indicate that sila-Wagner–Meerwein rearrangement reactions initiated by trityl cation paired with a weakly coordinating anion can be used to prepare a germasila-adamantane from a germa-oligosilane in high yields. The rearrangement reaction is highly selective, only the thermodynamic most stable isomer with the germanium atom in the bridgehead position of the adamantanes is formed. Additionally, we have shown that germanium atoms, installed at the periphery (as in 3) or in the bridging positions of an all-sila-adamantane cage (as in 5), can be shuttled into the bridgehead positions of the cage. The major driving force for these rearrangements is the formation of a maximum of strong Si–C bonds. These results suggest that a stepwise doping of sila-adamantanes with germanium is possible and that adamantanes obtained by different synthetic routes with variable numbers of germanium atoms can be transformed into the most stable isomers without interfering with the cage structure. Therefore, this method allows a rational design of molecular models for mixed silicon germanium alloys. The extension of this method to Sn/Si hetero-adamantanes³⁶ and related main group element hetero-adamantanes is currently investigated in our laboratories and will further broaden the scope of this method.⁴⁶

Data availability

All data we wish to disclose are in the ESI.†

Author contributions

Investigation and validation: S. K., C. T., L. A., B. K., T. M. Conceptualisation, methodology, supervision: M. W., C. M., T. M. Writing – original draft: C. M, T. M. Writing – review and editing: M. W., C. M. T. M.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors thank Dr Judith Baumgartner for crystallographic advice. Computations were done at the HPC Cluster, CARL, University of Oldenburg, funded by the DFG (INST 184/108-1 FUGG) and the Ministry of Science and Culture (MWK) of the Lower Saxony State.

References

1. R. D. Miller and J. Michl, Chem. Rev., 1989, 89, 1359–1410.
2. J. Koe and M. Fujiki, in Organosilicon Compounds, ed. V. Y. Lee, Academic Press, 2017, pp. 219–300.
3. J. Beckmann, in Comprehensive Organometallic Chemistry III, ed. D. M. P. Mingos and R. H. Crabtree, Elsevier, Oxford, 2007, pp. 409–512.
4. C. Marschner, in Functional Molecular Silicon Compounds I: Regular Oxidation States, ed. D. Scheschkewitz, Springer International Publishing, Cham, 2014, pp. 163–228.
5. J. Baumgartner and C. Grogger, in Comprehensive Inorganic Chemistry II, ed. J. Reedijk and K. Poeppelmeier, Elsevier, Amsterdam, Second Edition, 2013, pp. 51–82.
6. Y. Heider and D. Scheschkewitz, Chem. Rev., 2021, 121, 9674–9718.
7. E. Hengge and R. Janoschek, Chem. Rev., 1995, 95, 1495–1526.
8. R. West and A. Indriksons, J. Am. Chem. Soc., 1972, 94, 6110–6115.
9. C. Marschner, Organometallics, 2006, 25, 2110–2125.
10. J. Fischer, J. Baumgartner and C. Marschner, Science, 2005, 310, 825.
11. T. C. Siu, M. Imex Aguirre Cardenas, J. Seo, K. Boctor, M. G. Shimono, I. T. Tran, V. Carta and T. A. Su, Angew. Chem., Int. Ed., 2022, 61, e202206877.
12. B. Köstler, M. Bolte, H.-W. Lerner and M. Wagner, Chem.–Eur. J., 2021, 27, 14401–14404.
13. J. Aberl, M. Brehm, T. Fromherz, J. Schuster, J. Frigerio and P. Rauter, Opt. Express, 2019, 27, 32009–32018.
14. G. L. Wang, M. Moeen, A. Abedin, M. Kolahdouz, J. Luo, C. L. Qin, H. L. Zhu, J. Yan, H. Z. Yin, J. F. Li, C. Zhao and H. H. Radamson, J. Appl. Phys., 2013, 114, 123511.
15. D. Marris-Morini, V. Vakarin, J. M. Ramirez, Q. Liu, A. Ballabio, J. Frigerio, M. Montesinos, C. Alonso-Ramos, X. Le Roux, S. Serna, D. Benedikovic, D. Chrastina, L. Vivien and G. Isella, Nano, 2018, 7, 1781–1793.
16. V. Vakarin, W. N. Ye, J. M. Ramírez, Q. Liu, J. Frigerio, A. Ballabio, G. Isella, L. Vivien, C. Alonso-Ramos, P. Cheben and D. Marris-Morini, Opt. Express, 2019, 27, 9838–9847.
17. B. Mheen, Y.-J. Song, J.-Y. Kang and S. Hong, ETRI J., 2005, 27, 439–445.
18. S. Sedky, A. Witvrouw and K. Baert, Sens. Actuators, A, 2002, 97–98, 503–511.
19. G. Scappucci, C. Kloeffel, F. A. Zwanenburg, D. Loss, M. Myronov, J.-J. Zhang, S. De Franceschi, G. Katsaros and M. Veldhorst, Nat. Rev. Mater., 2021, 6, 926–943.
20. T. Henneberger, W. Klein and T. F. Fässler, Z. Anorg. Allg. Chem., 2018, 644, 1018–1027.
21. M. Waibel, G. Raudaschl-Sieber and T. F. Fässler, Chem.–Eur. J., 2011, 17, 13391–13394.
22. M. Waibel and T. F. Fässler, Inorg. Chem., 2013, 52, 5861–5866.
23. A. Jana, V. Huch, M. Repisky, R. J. F. Berger and D. Scheschkewitz, Angew. Chem., Int. Ed., 2014, 53, 3514–3518.
24. L. Klemmer, V. Huch, A. Jana and D. Scheschkewitz, Chem. Commun., 2019, 55, 10100–10103.
25. N. E. Poitiers, V. Huch, B. Morgenstern, M. Zimmer and D. Scheschkewitz, Angew. Chem., Int. Ed., 2022, 61, e202205399.
26. J. Helmer, J. Droste, M. R. Hansen, A. Hepp and F. Lips, Dalton Trans., 2022, 51, 10535–10542.
27. H. F. T. Klare, L. Albers, L. Süsse, S. Keess, T. Müller and M. Oestreich, Chem. Rev., 2021, 121, 5889–5985.
28. M. Ishikawa and M. Kumada, Chem. Commun., 1969, 567b–568b.
29. M. Kumada, Chem. Commun., 1970, 157a.
30. M. Ishikawa, M. Watanabe, J. Iyoda, H. Ikeda and M. Kumada, Organometallics, 1982, 1, 317–322.
31. H. Wagner, A. Wallner, J. Fischer, M. Flock, J. Baumgartner and C. Marschner, Organometallics, 2007, 26, 6704–6717.
32. H. Wagner, J. Baumgartner, C. Marschner and P. Poelt, Organometallics, 2011, 30, 3939–3954.
33. T. Müller, in Organogermanium compounds: theory, experiment and applications, ed. Lee V. Y., Wiley, Hoboken N.J., 2023, pp. 299–338.
34. H. Wagner, J. Baumgartner, T. Müller and C. Marschner, J. Am. Chem. Soc., 2009, 131, 5022–5023.
35. L. Albers, M. Aghazadeh Meshgi, J. Baumgartner, C. Marschner and T. Müller, Organometallics, 2015, 34, 3756–3763.
36. B. Köstler, J. Gilmer, M. Bolte, A. Virovets, H.-W. Lerner, P. Albert, F. Fantuzzi and M. Wagner, Chem. Commun., 2023, 59, 2295–2298.
37. J. Hlina, J. Baumgartner and C. Marschner, Organometallics, 2010, 29, 5289–5295.
38. J. Fischer, J. Baumgartner and C. Marschner, Organometallics, 2005, 24, 1263–1268.
39. Deposition number CCDC 2257841 for 2, contains the supplementary crystallographic data for this paper. These data are provided free of charge by the joint Cambridge Crystallographic Data Centre and Fachinformationszentrum Karlsruhe Access Structures service.
40. P. Pyykkö and M. Atsumi, Chem.–Eur. J., 2009, 15, 12770–12779.
41. C. Hemmert and H. Gornitzka, in Organogermanium compounds: theory, experiment and applications, ed. V. Ya. Lee, Wiley, Hoboken, N.J., 2023, pp. 667–743.
42. The Gaussian-16 program was used. For details, see ESI† material.
43. L. Albers, J. Baumgartner, C. Marschner and T. Müller, Chem.–Eur. J., 2016, 22, 7970–7977.
44. L. Albers, S. Rathjen, J. Baumgartner, C. Marschner and T. Müller, J. Am. Chem. Soc., 2016, 138, 6886–6892.
45. For an arene complex of a silaadamantyl cation, see: R. J. Wehmschulte, K. K. Laali, G. L. Borosky and D. R. Powell, Organometallics, 2014, 33, 2146–2149.
46. During the refereeing process of this manuscript, we became aware of strongly related work by Timothy Su and coworkers. M. I. Aguirre Cardenas, T. C. Siu, M. G. Shimono, S. Thai, V. Carta and T. Su, ChemRxiv, 2023, preprint,  DOI:10.26434/chemrxiv-2023-dk558.

---

Footnote

† Electronic supplementary information (ESI) available: Experimental procedures analytical data, NMR spectra, computational details, crystallographic information. CCDC 2257841. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d3sc03301e

---