Open Access Article
Open Access ArticlePrediction of total organic carbon and E. coli in rivers within the Milwaukee River basin using machine learning methods
Nabila
Nafsin
 and
Jin
Li
*
and
Jin
Li
*
Department of Civil and Environmental Engineering, University of Wisconsin-Milwaukee, WI 53211, USA. E-mail: nnafsin@uwm.edu; li@uwm.edu
First published on 12th December 2022
Abstract
Urban water undergoes physical and chemical changes due to various contaminants from point sources and non-point sources, including organic matter pollution and fecal bacterial contamination. Machine learning (ML) algorithms can be used as potential tools in surface water quality monitoring due to their capacity of finding underlying patterns and non-linear relationships among water quality parameters, unattainable by traditional or process-based water quality analysis. In this study, several standalone ML models such as artificial neural network (ANN), support vector machine (SVM), gradient boosting machine (GBM), random forest (RF) and ensemble-hybrid models such as RF-SVM, ANN-SVM, GBM-SVM, RF-ANN, GBM-ANN, and RF-GBM were developed for predicting total organic carbon (TOC) and E. coli in the Milwaukee River system. The significance of the study is the application of the ensemble-hybrid models for TOC and bacterial contamination prediction for the first time, which provides a reliable and direct approach to complement existing monitoring techniques in the Milwaukee River system with satisfactory prediction accuracies. The ensemble-hybrid models for TOC prediction resulted in R2 values within a range of 0.95–0.97. However, for E. coli prediction it was difficult to explain the greater amount of unexplained variation in bacterial data based on the physicochemical water quality parameters, resulting in R2 values within a range of 0.29–0.42. The hybrid model ANN-GBM outperformed others for both TOC and E. coli with prediction accuracies of 97% and 42%, respectively. An attempt was made to explain the variability in living microorganism behavior based on specific physicochemical parameters by developing prediction models for E. coli.
Environmental significanceThere is a need to improve the water quality monitoring program with an accurate, reliable, and cost-effective method for measuring water quality parameters. Traditional approaches used for measuring water quality parameters are time-consuming and inaccurate due to the inconsistencies between the actual field condition during sampling and the lab environment. Advanced machine learning (ML) techniques have been developed for a more accurate and reliable prediction of water quality. The novelty of this study is the successful application of ensemble-hybrid ML models that were not previously used for TOC and E. coli prediction. These ML models can provide timely prediction on significant changes of TOC and E. coli levels in a river, allowing decisionmakers a quicker response in water management. |
1 Introduction
Surface water is one of the most important natural resources used for numerous purposes including drinking water, public use, irrigation, and the aquatic environment. Various contaminants such as microbial pollutants, inorganic matter, synthetic and volatile organic compounds, and radioactive materials enter the source water through point source and nonpoint source pollution. Microbial pollution caused by the presence of bacteria and viruses in sewage treatment plants, septic systems, wildlife, and agricultural livestock operations transmits water-borne infectious diseases. Oxygen-demanding organic substances causes dissolved oxygen (DO) depletion in surface water, which can severely affects fish and aquatic life. TOC is one of the convenient ways of directly measuring organic contamination in surface water. A high level of organic content stimulates bacterial growth, and the decomposition of organic matter contributes to the depletion of oxygen supply in surface water. The concentration of fecal indicator bacteria (FIB) is measured to assess surface water quality for drinking and recreational purposes. Fecal coliform and Escherichia coli (E. coli) are commonly used as surrogates to indicate the presence of fecal matter in surface water. The presence of high concentrations of FIB indicates a high probability of pathogenic microbial contamination in water.1This research focuses on the analysis of water quality in terms of TOC and fecal bacterial contamination (E. coli) in natural streams. The study area is located within the Milwaukee River basin which includes three major rivers: Milwaukee River, Menomonee River, and Kinnickinnic River flowing into the harbor of Milwaukee, Wisconsin. The Milwaukee River starts from the north of Wisconsin and flows towards the south in downtown Milwaukee and discharges into Lake Michigan. Menomonee River and Kinnickinnic River are two main tributaries of the Milwaukee River. Urban and agricultural runoff, municipal and industrial point sources, construction site erosion, stream bank erosion, stream and wetland modification, contaminated sediments, and changes in land use are the major contributors to the degradation of water quality of the river system.2,3 The urbanized Milwaukee River basin is greatly affected by urban runoff and stormwater is considered one of the most significant sources of pathogenic microorganisms.3,4
To detect surface water contamination more rapidly and accurately, early warning systems (EWS) and ML techniques have been developed. Nafsin and Li (2021)5 and Nafsin et al., (2022)6 applied statistical event detection software CANARY for the analysis of surface water quality. The application of ML techniques is useful in predicting water quality as the models can provide data-driven decisions by extracting predictive information from a large dataset. Several studies7–10 developed ML models for event detection in water distribution systems. Other studies11–16 investigated the performances of different ML models for predicting water quality parameters of natural source water. ML models have also been developed to predict the water quality index and water quality class.17–23
Several studies explored different ML techniques in predicting TOC to characterize the hydrocarbon potential of source rocks, soil, organic shale, and mudstone.24–28 However, to the best of the authors' knowledge limited studies have been made for developing TOC prediction models in natural streams. Yeon et al. (2008),29 Goz et al. (2019),30 and Kim et al. (2021)31 explored the application of ANN, kernel extreme machine learning, and extreme machine learning models with different activation functions to estimate TOC of rivers. In addition, several studies4,32–37 investigated regression-based techniques for microbial analysis of surface water and groundwater using physicochemical and hydrometeorological parameters. However, development of such predictive models for fecal indicator bacteria analysis based on physicochemical and hydrometeorological parameters is site and bacteria group specific. The survival of FIB can be affected by complex interactions among physicochemical and hydrometeorological parameters, and land use patterns of the study area.38
In this study, we applied several standalone and ensemble-hybrid ML algorithms that can potentially be very effective tools in predicting TOC and E. coli in natural streams of the Milwaukee River basin. The developed ensemble-hybrid methods were not previously used for TOC and E. coli prediction and proved to provide a reliable and direct approach to complement existing monitoring techniques in the Milwaukee River system with satisfactory prediction accuracies. Limited studies have been conducted so far for developing TOC prediction models using ML in natural streams. Living microorganism behavior is harder to predict than physical and chemical processes. We developed prediction models for E. coli and efforts were made to explain the variability in living microorganism behavior based on the specific physicochemical parameters and to identify the most influential water quality parameters in predicting E. coli. These algorithms analyzed real-time data of source water, found the underlying pattern in a large volume of data using a mapping function, and identified complex relationships among the outputs and inputs, which are unattainable by traditional or process-based methods for water quality analysis.
This study predicted TOC and E. coli concentration in three major rivers: the Milwaukee River, Menomonee River, and Kinnickinnic River within the Milwaukee River basin during a sampling period of 2000–2020 using ML methods. We developed and evaluated the efficiencies of different regression ML models including ANN, SVM, GBM, RF, and ensemble-hybrid models such as RF-SVM, ANN-SVM, GBM-SVM, RF-ANN, GBM-ANN, and RF-GBM in predicting TOC and E. coli using the specific water quality parameters. Also, identifying the most influential physicochemical parameters in predicting both TOC and E. coli is one of the objectives of the study. More importantly, we conducted a comprehensive assessment of the employed ML techniques and evaluated the differences in model performances for predicting two different outputs (TOC and E. coli) using a specific dataset.
2 Materials and methods
2.1 Study area and data collection
Water quality monitoring data of the Milwaukee River, Menomonee River, and Kinnickinnic River in Wisconsin were provided by the Milwaukee Metropolitan Sewerage District (MMSD). There were a total of 32 active monitoring sites scattered throughout Milwaukee, Waukesha, Ozaukee, and Washington counties in Wisconsin (Fig. 1). After data cleaning and processing, the complete dataset used for the analysis composed of 5976 sample observations with 18 water quality parameters: total solids (TS), total suspended solids (TSS), volatile suspended solids (VSS), chlorophyll a, turbidity, pH, electrical conductivity (EC), temperature, dissolved oxygen (DO), sampling depth, nitrate, alkalinity, total phosphorous (Total P), chloride, biochemical oxygen demand (BOD5), TOC, dissolved organic carbon (DOC), and E. coli. The data collection period was during different months of 2000–2020 so that generalized ML models could be developed and trained with water quality data with local and seasonal variations.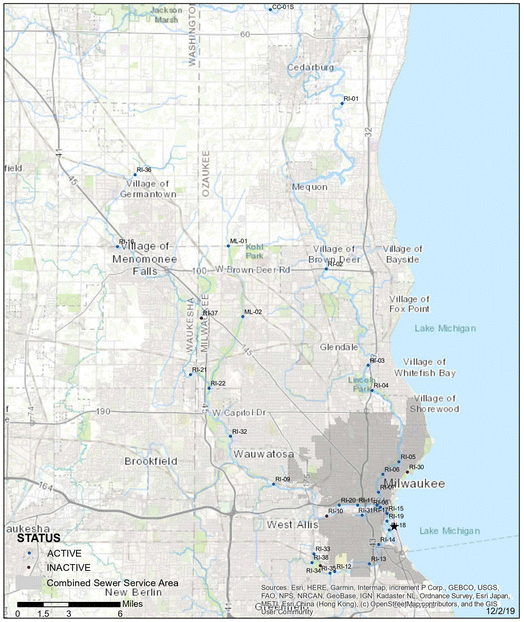 | ||
| Fig. 1 Water quality monitoring sites of the Milwaukee River, Menomonee River, and Kinnickinnic River in Wisconsin. | ||
2.2 Data preprocessing for ML models
For model development, data splitting was performed on a training set for model training and validation, and a test set for model performance evaluation. The training and testing size was selected based on the default train-test-split (75/25) in the scikit_learn machine learning toolkit of the python library. In this analysis, 75% of the dataset (4482 samples) was considered as the training set and 25% (1494 samples) as the test set. Again, 75% of the training set was considered for training (3362 samples) and 25% for validation (1120 samples). Data normalization was performed to transform the data into a standard range so that all the predictors are on the same scale. We used the ‘RobustScaler’ in the scikit learn python library that used median and quartiles (25th and 75th quartile) to standardize the predictors.2.3 Machine learning tools
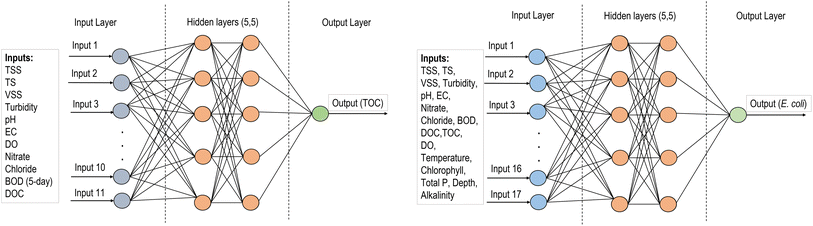
Supervised ML algorithms including ANN, SVM, RF, and GBM were used to develop regression models for predicting TOC and E. coli of the natural streams in Wisconsin. The reason for using different ML algorithms is to evaluate and compare the prediction performances of models with different working mechanisms. For example, the decision-tree based RF algorithm performs efficiently on a large dataset with a reduced chance of overfitting and robustness to outliers, while the boosting mechanism of GBM improves the prediction performance by building one decision tree at a time and learning from the mistakes from previous decision trees. ANN and SVM can identify complex non-linear relationships between the inputs and outputs. Ensemble-hybrid models were developed by integrating standalone ML models to improve prediction performances by incorporating the strength of standalone models and overcoming their weaknesses. Moreover, consistency in prediction performances was identified when using different ML models with a specific dataset. A python program was used for data analysis that has a built-in machine learning toolkit scikit-learn (version 0.21).ANN is a good approach for regression problems with complex datasets. The model consists of one input layer, one or several hidden layers, and one output layer. The hidden layers include many interconnected units (neurons) arranged with the input vectors to convert them into output using an activation function. In a feed-forward network such as multilayer perceptron (MLP), each unit feeds its output to all the units on the next layer. In this analysis, we used MLP (Fig. 2) with two hidden layers and five units in each layer which resulted in the best model performances for predicting both TOC and E. coli.
SVM is used as a SVR in regression problems which finds a decision boundary or hyperplane to classify data points appropriately. SVM uses a kernel method (e.g., RBF, sigmoid kernel, linear kernel, and polynomial kernel) that converts the original input 2-dimensional data space into a higher dimensional feature space. We used the RBF kernel function and optimized the two key parameters: regularization parameter (C) and kernel width (gamma).
RF is an ensemble ML model that combines multiple decision trees to build an effective prediction model. The model makes different random choices to develop several independent trees. The trees are randomized by selecting the data points to build trees and the maximum features in each split test. Each tree in the forest predicts the output, and the final output is determined by averaging the outputs from all the decision trees.
GBM works by building multiple models or decision trees sequentially and reducing the errors from the previous model. Each decision tree takes a portion of the input data and makes predictions. The new models are built over the errors or residuals of the previous predictions. Several decision trees are added iteratively to improve the prediction performance. The degree to which each model is allowed to correct the errors from the previous tree is controlled by the key parameters: number of decision trees and learning rate.
In addition, several ensemble-hybrid models such as RF-SVM, ANN-SVM, GBM-SVM, RF-ANN, GBM-ANN, and RF-GBM were developed by integrating the standalone traditional ML algorithms. An ensemble meta estimator ‘voting regressor’ was used to fit the dataset on each contributing standalone model in this hybridization process. The final prediction of the hybrid model was determined by averaging the individual prediction of each standalone model. The contributing models were optimized to achieve the best performance of the ensemble-hybrid model. The generalization performances of ML models were improved by the model's parameter tuning. We used the grid search and five-fold cross-validation method and examined possible combinations of the hyperparameters that control the learning process.
2.4 Performance evaluation metrics
In this analysis, we used statistical metrics such as coefficient of determination (R2), mean absolute error (MAE), mean squared error (MSE), and root mean squared error (RMSE) to evaluate the performances of different models. The R2 or ‘goodness-of-fit’ describes the variability in the dependent variables that can be explained by using the independent variables. The range of values is from 0.0 to 1.0, which means 0% to 100% variation in the dependent variable can be explained by using independent variables. An R2-value of 0 indicates that the model is unable to explain the variability in the data resulting in high errors while an R2-value of 1 indicates that the model is a perfect fit to explain the variability accurately. Based on the R2, the regression models were evaluated to see whether they resulted in very satisfactory (R2 ≥ 0.90), fairly satisfactory (0.5 < R2 < 0.90), or unsatisfactory model execution (R2 ≤ 0.50). The MAE represents the average of the absolute difference between the actual and predicted value. It measures the average of the residuals in the dataset. The standard deviation of the residuals is indicated by the RMSE. The RMSE score measures the distance between the regression fit line and the actual data. The amount of error in regression models is also determined by using the MSE which measures the average squared difference between the actual and predicted value. A high value of R2 and low values of errors indicate satisfactory model performance that can predict the output accurately.3 Results and discussion
3.1 Statistical analysis of water quality data
We performed statistical analysis to visualize water quality data of the Milwaukee River, Menomonee River, and Kinnickinnic River during the sampling periods in 2000–2020. The basic statistical parameters such as the minimum, maximum, mean, standard deviation, and coefficient of variation (CV) of the water quality data are presented in Table 1. The CVs of all the parameters ranged from 4.73% to 451.82%. During the sampling period, the water quality of the Milwaukee River system varied significantly for E. coli, BOD5, and TSS with high values of CV. The higher value of CV indicates relatively high variability in the dataset. Among the parameters, the E. coli dataset had the highest variability during the twenty years sampling period with a CV of 452.82%. The E. coli level varied within a range of 0.00–250000 MPN/100 mL with a mean value of 3643 MPN/100 mL. The level of TOC in the river system was found to be within a range of 0.67–190 mg L−1 with a mean value of 8.25 mg L−1 and CV of 88.13%. BOD5 and TSS had high variabilities with % CVs greater than or about 300%. Other parameters such as turbidity, VSS, chlorophyll a, and chloride resulted in greater than 100% CV.| Parameter | Unit | Minimum | Maximum | Mean | Standard deviation | Coefficient of variation % |
|---|---|---|---|---|---|---|
| TS | mg L−1 | 100.00 | 8400.00 | 633.57 | 412.17 | 65.05 |
| TSS | mg L−1 | 0.80 | 2700.00 | 20.18 | 60.37 | 299.20 |
| VSS | mg L−1 | 0.30 | 260.00 | 5.07 | 8.49 | 169.71 |
| Chlorophyll a | mg m−3 | 0.08 | 280.00 | 9.83 | 15.68 | 159.45 |
| Turbidity | NTU | 0.60 | 378.00 | 14.19 | 23.49 | 165.52 |
| pH | — | 5.50 | 9.93 | 8.05 | 0.38 | 4.73 |
| EC | μS cm−1 | 101.00 | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 600 |
1045.18 | 765.44 | 73.23 |
| Temperature | °C | −0.50 | 33.44 | 14.12 | 7.92 | 56.12 |
| DO | mg L−1 | 0.00 | 25.70 | 9.88 | 3.36 | 33.97 |
| Nitrate | mg L−1 | 0.00 | 4.30 | 0.81 | 0.56 | 69.68 |
| Alkalinity | mg L−1 | 4.50 | 440.00 | 223.38 | 71.04 | 31.80 |
| Total P | mg L−1 | 0.00 | 2.60 | 0.12 | 0.11 | 88.38 |
| Chloride | mg L−1 | 5.00 | 3100.00 | 174.84 | 210.51 | 120.40 |
| BOD5 | mg L−1 | 0.00 | 310.00 | 3.98 | 12.00 | 301.03 |
| TOC | mg L−1 | 0.67 | 190.00 | 8.25 | 7.27 | 88.13 |
| DOC | mg L−1 | 0.52 | 190.00 | 7.89 | 7.04 | 89.27 |
| E. coli | MPN/100 mL | 0.00 | 250![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
3643.51 | 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 461.95 461.95 |
451.82 |
We performed Pearson's correlation analysis at a 0.05 level of significance to identify the input parameters that could impact the output variables such as TOC and E. coli. The results in Table 2 indicated significant correlations (p-value < 0.05) between TOC and input variables. Among the parameters, DOC was strongly positively correlated with TOC (R-value = 0.975, p < 0.05). BOD5 had a moderately strong linear correlation with TOC (R-value = 0.725, p < 0.05). TS, chloride, and EC had weak linear correlations with R-values of 0.423, 0.408, and 0.405, respectively. Temperature and pH were negatively correlated with TOC. Other parameters had very weak or non linear correlation with TOC. Similarly, Table 3 shows the Pearson's correlation coefficient between E. coli and other input variables. The results indicated that the physicochemical parameters had weak (R-value < 0.3) or non linear correlations with E. coli.
| Parameter | Correlation coefficient | P-Value | Parameter | Correlation coefficient | P-Value |
|---|---|---|---|---|---|
| TS | 0.423 | 0.000 | Temperature | −0.147 | 0.000 |
| TSS | 0.036 | 0.005 | DO | −0.018 | 0.003 |
| VSS | 0.091 | 0.000 | Nitrate | 0.055 | 0.000 |
| Chlorophyll | −0.010 | 0.032 | Alkalinity | 0.048 | 0.000 |
| Turbidity | 0.013 | 0.039 | Chloride | 0.408 | 0.000 |
| pH | −0.105 | 0.000 | BOD5 | 0.725 | 0.000 |
| EC | 0.405 | 0.000 | DOC | 0.975 | 0.000 |
| Depth | −0.054 | 0.000 | E. coli | 0.058 | 0.000 |
| Total P | 0.089 | 0.000 |
| Parameter | Correlation coefficient | P-Value | Parameter | Correlation coefficient | P-Value |
|---|---|---|---|---|---|
| a TS: total solids; TSS: total suspended solids; VSS: volatile suspended solids; EC: electrical conductivity; Total P: total phosphorus; DO: dissolved oxygen; BOD5: 5 day biochemical oxygen demand; DOC: dissolved organic carbon; TOC: total organic carbon. | |||||
| TS | −0.056 | 0.000 | Temperature | 0.108 | 0.000 |
| TSS | 0.110 | 0.000 | DO | −0.136 | 0.000 |
| VSS | 0.178 | 0.000 | Nitrate | −0.049 | 0.000 |
| Chlorophyll | −0.001 | 0.027 | Alkalinity | −0.247 | 0.000 |
| Turbidity | 0.151 | 0.000 | Chloride | −0.034 | 0.009 |
| pH | −0.131 | 0.000 | BOD5 | 0.079 | 0.000 |
| EC | −0.076 | 0.000 | DOC | 0.047 | 0.000 |
| Depth | 0.001 | 0.048 | TOC | 0.058 | 0.000 |
| Total P | 0.258 | 0.000 | |||
3.2 Feature importance
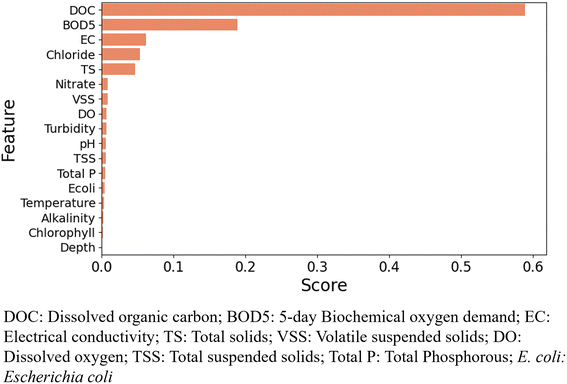
Although Pearson's correlation analysis indicated the statistical relationship between the independent and dependent variables, it can only explain linear relationships without considering the non-linearity of a complex dataset. In this analysis, we used the decision-tree based RF algorithm to identify the relative importance of each feature in predicting the output. The feature importance assigns a score typically numbered between 0 and 1 to individual features which is normalized to add to 1. The higher the score, the more relevant the feature is for predicting the output. Fig. 3 and 4 show the feature importance chart for the prediction of TOC and E. coli, respectively. For the particular test-train split of the dataset, DOC had the largest feature importance score of 0.58 in the prediction of TOC. BOD5 was the second most important feature, with a feature score of 0.18. EC, chloride, and TS had feature scores of 0.07, 0.06, and 0.05, respectively. TOC, DOC, and BOD5 indicate organic matter pollution in water and wastewater. TOC is a measure of organic carbon that can be present in water as dissolved organic carbon (DOC) and non-dissolved organic carbon (NDOC). DOC is considered as the particulate TOC that can pass through a 0.45 μm filter, while the larger size of TOC is known as NDOC. Because of the direct association of TOC with DOC, the feature importance analysis showed a significant correlation between the parameters. Also, TOC and BOD5 are correlated as they both indicate the presence of organic matter in water. TOC provides a direct measure of organic carbon while BOD5 measures the amount of oxygen consumed by microorganisms to oxidize soluble organic matter. High content of organic carbon increases the growth of microorganisms and as a result, consumption of DO increases which eventually increases BOD5.To improve the model performance efficiency, we extracted the important predictors from the feature importance chart, eliminated the predictors with lower scores, and developed models with only feature importance. The results indicated that the model performance was significantly improved with higher accuracy (accuracy 90%) and lower values of error with the input variable combination of BOD5, DOC, EC, chloride, TS, nitrate, VSS, DO, turbidity, pH, and TSS. Based on the analysis, we selected the input combination of 11 water quality parameters out of the 18 parameters that had comparatively higher feature importance scores to develop TOC prediction models. For selecting the best combination of input variables for TOC prediction models, we evaluated the models based on RMSE scores with seven different combinations (category 1–category 7) of input variables as shown in Table 4. The models were trained using each of the categories of input variables and evaluated on the test set to identify the best combination of input variables that resulted in the lowest RMSE scores. For each category of input variables, the models were optimized to find the hyperparameters that resulted in the lowest RMSE scores. In category 1, all of the input variables were considered for predicting the output, while categories 2 to 7 include the variables that had relatively higher feature importance scores. The results indicate that for both RF and GBM models, the lowest RMSE scores were found for category 2 (BOD5, DOC, EC, chloride, TS, nitrate, VSS, DO, turbidity, pH, and TSS). For ANN, category 3 (BOD5, DOC, EC, chloride, TS, nitrate, VSS) had the lowest RMSE score of 1.601, which is close to the RMSE score for category 2 (1.669). Based on the analysis, category 2 was considered the optimal combination of input variables that had the lowest RMSE scores for most of the ML models. Due to the different structures of the ML models contributing to the variations in their learning process and prediction capability, the best combination of input variables was not consistent for them.
| Category | Input variable combinations | RMSE score | |||
|---|---|---|---|---|---|
| ANN | SVM | RF | GBM | ||
| 1 | DOC, BOD5, EC, chloride, TS, nitrate, VSS, DO, turbidity, pH, TSS, Total P, E. coli, temperature, alkalinity, chlorophyll, and depth | 2.917 | 2.469 | 3.135 | 2.485 |
| 2 | BOD5, DOC, EC, chloride, TS, nitrate, VSS, DO, turbidity, pH, and TSS | 1.669 | 2.297 | 2.596 | 2.077 |
| 3 | BOD5, DOC, EC, chloride, TS, nitrate, and VSS | 1.601 | 2.675 | 3.114 | 2.450 |
| 4 | BOD5, DOC, EC, chloride, TS, and nitrate | 2.191 | 2.636 | 2.944 | 2.110 |
| 5 | BOD5, DOC, EC, chloride, and TS | 1.715 | 2.216 | 2.963 | 2.577 |
| 6 | BOD5, DOC, EC, and chloride | 2.415 | 2.662 | 2.696 | 2.670 |
| 7 | BOD5, DOC, and EC | 2.732 | 2.461 | 2.831 | 2.110 |
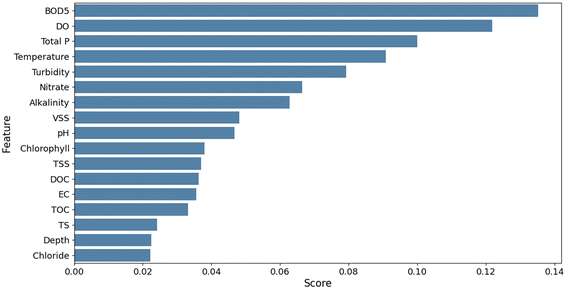
For the prediction of E. coli, although Pearson’s analysis indicated a poor correlation between E. coli and other parameters, the feature importance analysis computed from the RF algorithm was able to capture non-linear relationships between the input and output. The result indicated that BOD5 was the most important variable for predicting bacteria with a feature importance score of 0.13 (Fig. 4). Other influential variables were DO, Total P, temperature, turbidity, and nitrate with feature scores of 0.12, 0.10, 0.09, 0.08, and 0.07, respectively. The feature importance scores were comparatively lower for E. coli prediction than for TOC. For developing prediction models of E. coli, only the predictors (BOD5, DO, total phosphorous, temperature, turbidity, nitrate, and alkalinity) that had relatively higher feature importance scores were selected. For selecting the input variables for E. coli prediction, the models were evaluated based on the RMSE scores and the best combination of input variables was selected as category 3 (BOD5, DO, Total P, temperature, turbidity, nitrate, and alkalinity) that resulted in the lowest RMSE for all the models as shown in Table 5.
| Category | Input variable combinations | RMSE score | |||
|---|---|---|---|---|---|
| ANN | SVM | RF | GBM | ||
| 1 | DOC, BOD5, EC, chloride, TS, nitrate, VSS, DO, turbidity, pH, TSS, Total P, TOC, temperature, alkalinity, chlorophyll, and depth | 5873.52 | 6313.48 | 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 257.70 257.70 |
12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 598.07 598.07 |
| 2 | BOD5, DO, Total P, temperature, turbidity, nitrate, alkalinity, VSS, and pH | 6612.67 | 6364.12 | 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 599.84 599.84 |
13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 030.61 030.61 |
| 3 | BOD5, DO, Total P, temperature, turbidity, nitrate, and alkalinity | 5820.09 | 6184.76 |
12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) 040.45 040.45
|
12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) 221.30 221.30
|
| 4 | BOD5, DO, Total P, temperature, and turbidity | 6315.40 | 6477.71 | 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 038.27 038.27 |
12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 801.73 801.73 |
| 5 | BOD5, DO, Total P, and temperature | 6796.09 | 6730.16 | 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 970.40 970.40 |
13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 015.61 015.61 |
| 6 | BOD5, DO, and Total P | 6583.24 | 6829.70 | 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 788.59 788.59 |
13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500.69 500.69 |
The result indicated that the E. coli concentration was associated with BOD5 and DO in surface water. With the increasing growth of microorganisms, the rate of decomposition of organic matter also increases, which results in dissolved oxygen level depletion and an increased BOD level in water.39 The growth of bacteria depends on the availability of nutrients (e.g., nitrogen and phosphorus) and the appropriate temperature. Turbidity can also affect microbial growth in water. Bacteria have the potential to attach to the surface of a particulate turbidity causing material influencing the inactivation of microorganisms.40 Alkalinity also contributes to some extent to the prediction of bacteria levels. A previous study41 shows that an appropriate alkaline environment can effectively inhibit the growth of microorganisms through the inactivation of ATP synthesis. Although the influence of the physical and chemical parameters on the prediction of E. coli was poor, the decision tree-based ML algorithm was able to extract data-driven information about the non-linear relationships that could exist between the inputs and output.
3.3 Optimization of model parameters
The grid search method found the best parameters for the models, and with the parameters, fit the models on the whole training set that yielded the best cross-validation performance. We evaluated the models using the test set to identify how well the best-found parameters were generalized. The optimized key parameters used for the models are summarized in Tables 6 and 7.| Model's key parameters | Optimal values | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| ANN | SVM | RF | GBM | RF-SVM | GBM-SVM | RF-GBM | RF-ANN | GBM-ANN | ANN-SVM | |
| Hidden layer | (5,5) | (4,4) | (4,4) | (5,5) | ||||||
| Activation | ‘relu’ | ‘relu’ | ‘relu’ | ‘relu’ | ||||||
| Alpha | 0.1 | 0.005 | 0.01 | 0.22 | ||||||
| Solver | ‘lbfgs’ | ‘lbfgs’ | ‘lbfgs’ | ‘lbfgs’ | ||||||
| Kernel | Rbf | ‘rbf’ | ‘rbf’ | ‘rbf’ | ||||||
| C | 500 | 500 | 700 | 650 | ||||||
| Gamma | 0.001 | 0.001 | 0.0001 | 0.0001 | ||||||
| n-Estimators | 150 | 100 | 150 | 500 | 100 | 50 | 250 | |||
| Max-features | 8 | 8 | 5 | 8 | ||||||
| Max-depth | 3 | 2 | 6 | 3 | 6 | 5 | 3 | |||
| Learning rate | 0.08 | 0.085 | 0.08 | 0.085 | ||||||
| Model's key parameters | Optimal values | |||||||
|---|---|---|---|---|---|---|---|---|
| ANN | SVM | RF | GBM | RF-GBM | RF-ANN | GBM-ANN | ANN-SVM | |
| Hidden layer | (5,5) | (4,4) | (4,4) | (5,5) | ||||
| Activation | ‘relu’ | ‘relu’ | ‘relu’ | ‘relu’ | ||||
| Alpha | 0.025 | 0.02 | 1.1 | 0.6 | ||||
| Solver | ‘lbfgs’ | ‘lbfgs’ | ‘lbfgs’ | ‘lbfgs’ | ||||
| Kernel | Rbf | ‘rbf’ | ||||||
| C | 500 | 500 | ||||||
| Gamma | 0.05 | 0.06 | ||||||
| n-Estimators | 200 | 200 | 10 | 12 | 100 | |||
| Max-features | 8 | 4 | 4 | |||||
| Max-depth | 9 | 2 | 9 | 11 | 5 | |||
| Learning rate | 0.08 | 0.06 | 0.08 | |||||
3.4 Model performance evaluation for TOC
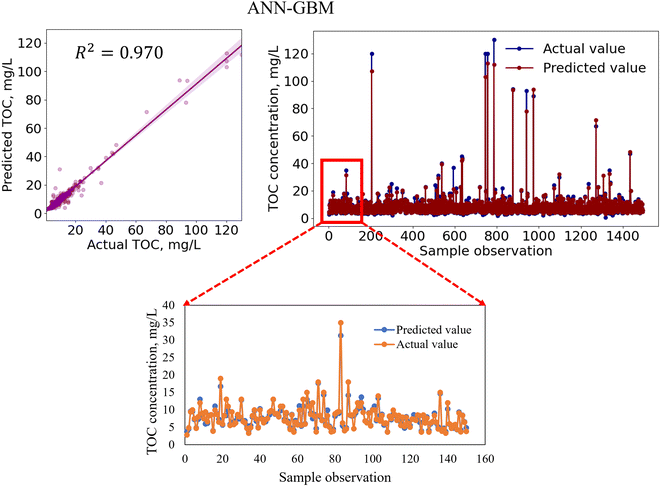
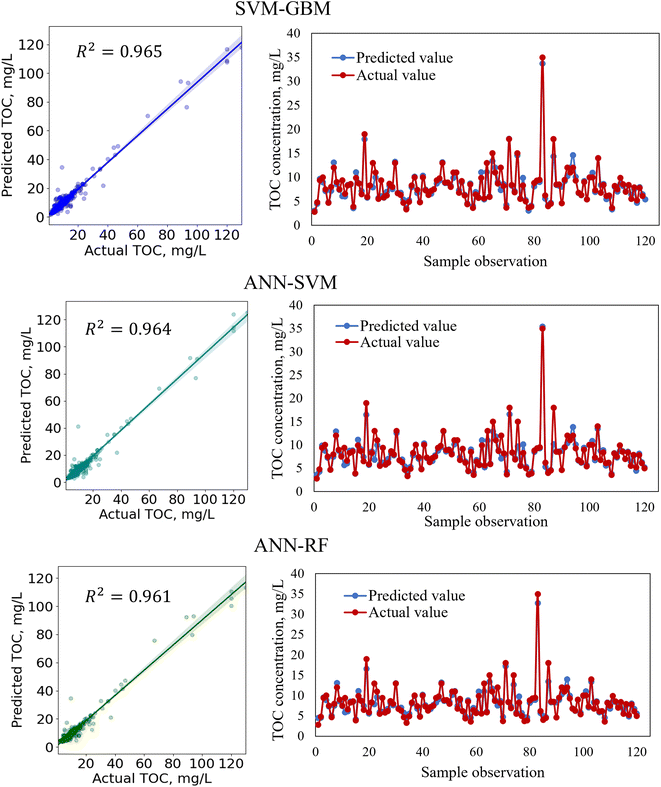
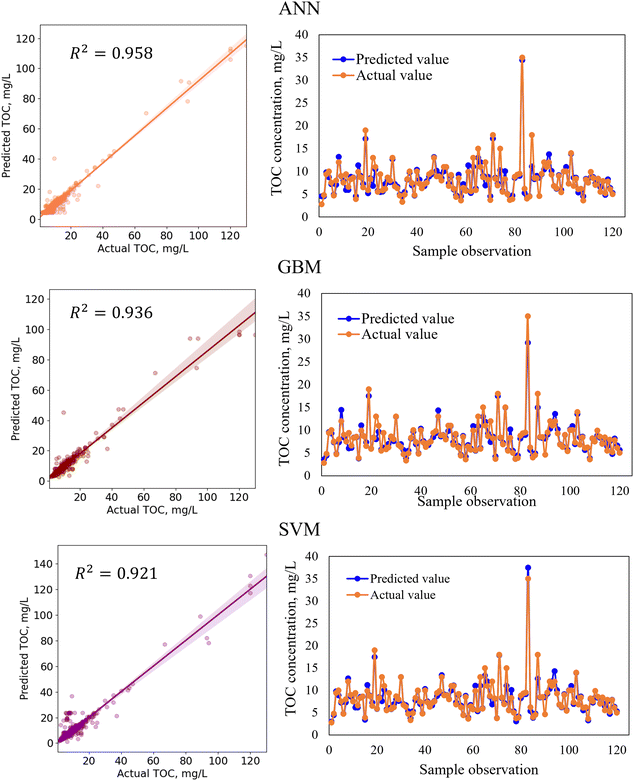
In regression analysis, the most important statistical measure is the R2 which represents the proportion of variance in the output that the model can explain based on the predictors. For the nonlinear ML models, besides the R2 value, other statistical measures such as the MAE, MSE, and RMSE were determined to evaluate the models' performance efficiencies.Table 8 shows the performances of the developed four standalone and six hybrid ML models for TOC prediction based on the R2-value, RMSE, MSE, and MAE. The results indicated that the standalone ML models had prediction accuracies within a range of 89.9–95.8% indicating that the models performed satisfactorily in predicting TOC and that the models are considered as a good fit for the dataset. We also developed ensemble-hybrid models that further improved the prediction performances of the models, ranging from 94.8–97.0% accuracy. Based on the R2-value and errors, the developed models were ranked from the best performing to the worst performing model as shown in Table 8. Among the developed TOC prediction models, the best four performing models were the ensemble-hybrid models ANN-GBM, SVM-GBM, ANN-SVM, and ANN-RF with prediction accuracies greater than 96%. The hybrid model ANN-GBM outperformed others with an R2 value of 0.97, MAE of 0.664, MSE of 2.334, and RMSE of 1.528 when using the selected input features computed from the feature importance analysis. The performance metrics indicated that the employed regression models can efficiently predict TOC based on the combination of input features: BOD5, DOC, EC, chloride, TS, nitrate, VSS, DO, turbidity, pH, and TSS. The correlation between the actual and predicted TOC for the employed ML models is presented in Fig. 5 and 7. From the scatter plots we observed that most of the data points best fit with the regression line that explained the percent of variance of the output through the input variables. The time variation graphs in Fig. 5–7 indicate that the prediction models exhibited a small deviation between the predicted and actual value for each sample observation of the test set, verifying a good generalization capacity of the models with satisfactory R2 values.
| Algorithms | MAEa | MSEa | RMSEa | R 2 | Rank |
|---|---|---|---|---|---|
| a The units for MAE, MSE, and RMSE are in ‘mg L−1’. | |||||
| ANN | 0.750 | 2.788 | 1.669 | 0.958 | 5 |
| GBM | 0.718 | 4.315 | 2.077 | 0.936 | 8 |
| SVM | 0.807 | 5.276 | 2.297 | 0.921 | 9 |
| RF | 1.177 | 6.739 | 2.596 | 0.899 | 10 |
| ANN-GBM | 0.664 | 2.334 | 1.528 | 0.970 | 1 |
| SVM-GBM | 0.652 | 2.366 | 1.538 | 0.965 | 2 |
| ANN-SVM | 0.672 | 2.394 | 1.547 | 0.964 | 3 |
| ANN-RF | 0.703 | 2.626 | 1.620 | 0.961 | 4 |
| SVM-RF | 0.722 | 2.888 | 1.699 | 0.957 | 6 |
| RF-GBM | 0.738 | 3.514 | 1.875 | 0.948 | 7 |
In the hybridization process of model development, two base algorithms were integrated to develop a model with greater flexibility and higher prediction accuracy than the standalone models. For example, the standalone model ANN and GBM had TOC prediction accuracies of 95.8% and 93.6%, respectively. Although both standalone models performed satisfactorily, the performances of the models were further improved by hybridizing ANN with the GBM algorithm with a TOC prediction accuracy of 97.0%. When developing the ANN-GBM model, the hyperparameters for both algorithms (hidden layer size, number of nodes, activation function, solver, alpha, learning rate, n_estimators, and max_depth) were defined and optimized to achieve the best performance of the hybrid model. The ensemble meta-estimator ‘VotingRegressor’ was applied to fit the standalone algorithms on each dataset and the final prediction was determined by averaging the individual predictions of the contributing models. The ensemble-hybrid model ANN-GBM outperformed others because of the significant advantages of ANN over other regression models, i.e. ANN's ability to learn and model complex non-linear relationships between the dependent and independent variables and establish all possible interactions between the dependent variables without requiring the need for making assumptions about data properties, data distribution, and specific hypothesis for testing. The ANN model benefitted from the mathematical functions of hidden layers consisting of neurons that assigned weights to the inputs, directed them to an activation function, and performed specific non-linear transformations of the input data. The activation function allowed complex functional mapping of the network's input and output with the dataset of non-linearity. In addition, the boosting mechanism of GBM with properly optimized hyperparameters allowed the building individual decision trees at a time and learn from the mistakes of previous trees to improve the overall performance sequentially with each iteration. GBM overcame the errors of decision trees by using gradients in the loss function and optimizing the model's coefficients to fit the underlying data. The incorporation of a boosting mechanism along with the non-linear transformation of the input data using an activation function allowed the extraction of specific patterns from the data and minimized the difference between the actual and the predicted output, resulting in a more powerful ensemble-hybrid model ANN-GBM.
Learning curves were developed to indicate whether the models were a good fit, underfit, or overfit, based on the performance of the training and validation sets. The plots of learning curves in Fig. 8 indicate the learning and generalization performance of the standalone models: RF, GBM, and ANN over experience. A good fit model is represented by a training and validation score that approaches a point of stability with a minimal gap between these two scores. The score should be lower on the training set than the validation set, creating a generalization gap between the two curves. The MSE score was used to evaluate the performances of the models for the specific training size. For RF and GBM, the training score and validation score moved toward a stable point with a small gap between the curves which decreased with the increase in training size. When the training size increased to 3000, the training MSE remained constant, while the validation MSE started decreasing significantly. Similarly, the learning curves for the ANN model indicated that the model generalized well with the specific training size, and the training score and cross validation score converged at the point of stability with a minimum training size of 4000. The results indicated that the models generalized well on the validation set with a training size of 4482 sample observations and were considered as good fit models with lower MSE scores.
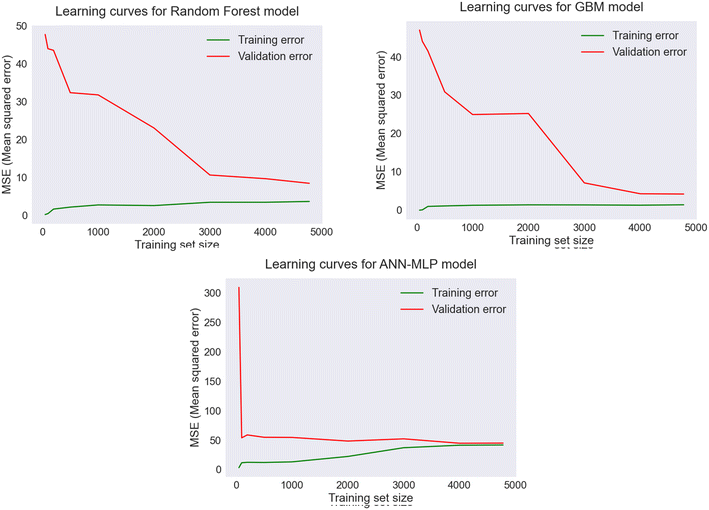 | ||
| Fig. 8 Learning curves indicating performances of RF, GBM, and ANN (MLP) models for TOC prediction based on the MSE score with varying training size. | ||
3.5 Model performance evaluation for E. coli
We developed ML prediction models for E. coli using a specific dataset to analyze the microbial data, find specific patterns in the data, and establish complex non-linear relationships that might exist between physiochemical and microbiological parameters during the sampling period. An attempt was made to predict living microorganism behavior that had a greater degree of unexplainable variation in the data. In general, data on living objects such as a microbial community are harder to predict than physical and chemical processes. Our goal was to develop models using ML algorithms that can predict bacteria concentrations and explain the variability in the dependent variable through the independent physicochemical water quality parameters. Based on the established relationship between the microbial population and surface water environment, the models could provide favorable support to understand disease outbreaks and risks to human health associated with exposure to contaminated water.Prediction models for E. coli were developed using four standalone and four hybrid ML algorithms. Initially, the models were developed using all input features. To reduce the number of redundant features and improve performance efficiency, the important variables with relatively higher feature importance scores were considered. The prediction performances of the developed ML models with all input features and the feature importance (BOD5, DO, total phosphorous, temperature, turbidity, nitrate, and alkalinity) are shown in Table 9. The results indicated that the R2 values ranged from 0.26–0.40 when using all input variables while with the feature importance the prediction performances of the models were found to be within a range of 0.29–0.42. Among the developed ML models, the hybrid model ANN-GBM exhibited the highest prediction accuracy of 42%.
From the statistical analysis of microbial data, we observed that E. coli concentrations varied significantly during the twenty years sampling period. The ML models performed poorly because of the high variation in bacterial data, and it was difficult to explain such variability based on the input variables of physicochemical water quality parameters. Also, no significant strong linear correlation was found between E. coli and input variables. The ML algorithms were able to explain some percentage of variability in the data by extracting useful data-driven information about the existing hidden non-linear relationships between the output and input variables. However, as ML models were used as black boxes in predicting the output, there was little understanding of how the models explained such variability and arrived at a prediction with prediction accuracies within a range of 29–42%. In addition, we observed higher values of MAE for the prediction models. The MAE measures the difference between the actual and predicted value. As the measuring values were found to be within a high range with a maximum value of 250![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 MPN per mL, the difference between the actual and predicted value was also found to be higher. The models' performances might be improved if, besides the physicochemical parameters, other hydrometeorological variables such as air temperature, air humidity, atmospheric pressure, precipitation level, and stormwater runoff flow would be available during the sampling period to consider as inputs to the models. Because of the unavailability of the hydrometeorological data for the corresponding E. coli concentrations, we only used the available physicochemical parameters measured by MMSD for the river system.
000 MPN per mL, the difference between the actual and predicted value was also found to be higher. The models' performances might be improved if, besides the physicochemical parameters, other hydrometeorological variables such as air temperature, air humidity, atmospheric pressure, precipitation level, and stormwater runoff flow would be available during the sampling period to consider as inputs to the models. Because of the unavailability of the hydrometeorological data for the corresponding E. coli concentrations, we only used the available physicochemical parameters measured by MMSD for the river system.
A previous study29 applied neural network models (LMNN and MDNN), and an adaptive neuro-fuzzy inference system (ANFIS) which is a combination of a neural network and fuzzy system for forecasting TOC in a river in South Korea. The study used continuous water quality monitoring data of DO, water temperature, discharge, and TOC from a specific monitoring station. The results indicated that the R-values ranged from 0.489 to 0.783 for the prediction models. Also, the result showed that the ANN model was better with an R-value of 0.743 than the conventional model used in that study. Kim et al. (2021)31 developed standalone (MARS and M5Tree) and hybrid models (CEEMDAN-MARS, CEEMDAN-M5Tree, MARS-CSA, and CEEMDAN-MARS-CSA) for predicting TOC in a river using water quality data of pH, electrical conductivity, temperature, DO, COD, and suspended solids (SS) that were collected from two monitoring stations of that river. The R-values ranged from 0.458–0.728 for the standalone models, while for the hybrid models the range was found to be 0.539–0.762. The CEEMDAN-MARS-CSA (completely enhanced EMD with adaptive noise) model was found to be the most accurate in predicting TOC with a correlation coefficient of 0.762. To the best of the authors' knowledge, no studies have been conducted so far that employed the specific ensemble-hybrid models for TOC prediction that we developed in this study. The novel ensemble-hybrid models in our study exhibited a high prediction accuracy of greater than 96% (R2 > 0.96). Previous studies29–31 applied different ML models for predicting TOC. However, they did not apply any tree-based RF and GBM algorithms that proved to be effective in our study, especially when ensembled with other algorithms. Most of the previous studies were conducted within a specific location and from one or two monitoring stations. In this study, we used several water quality parameters and data with large spatial and temporal variations from 32 monitoring stations of three different rivers during a twenty years sampling period. Also, we performed an analysis of feature importance using a tree-based algorithm that identified the most important parameters for predicting the output, while other studies29–31 considered several water quality parameters that were available (Kim et al. (2021):31 pH, electrical conductivity, temperature, DO, COD, and SS; Goz et al. (2019):30 pH, temperature, conductivity, and turbidity; Yeon et al. (2008):29 DO, temperature, and discharge as inputs for TOC prediction models without analysis of feature importance.
For the prediction of E. coli, several studies32–35 investigated regression-based techniques for microbial analysis of surface water and groundwater using both physicochemical and hydrometeorological parameters. He et al. (2008)34 applied ANN for the prediction of total coliform, fecal coliform, and Enterococci using pH, conductivity, water temperature, rainfall, wave height, tide height, and flow rate as inputs to the models, and the models resulted in R2 values within a range of 0.620–0.883. However, in this study, we considered only the physicochemical water quality parameters to explain the variability in living microorganism behavior through the independent water quality parameters. Our goal was to investigate how accurately we can predict the microbial concentration (using ML algorithms) only from the water quality parameters without considering physical characteristics such as flow, velocity, river width, etc. The results of our study indicated that for E. coli prediction, because of the high variability of bacterial data, it was difficult to explain such a large amount of unexplained variation in the dataset based on the available physicochemical parameters, resulting in relatively lower R2 values within a range of 0.37–0.42 for the ensemble-hybrid models.
In this study, we developed and evaluated the efficiency of several standalone and hybrid ML models for the prediction of TOC and E. coli in the major rivers of the Milwaukee River basin. Also, we identified the most influential parameters in predicting TOC and E. coli by interpreting a large water quality dataset. For TOC prediction, the most influential variables were identified as BOD5, DOC, EC, chloride, TS, nitrate, VSS, DO, turbidity, pH, and TSS, while for E. coli prediction the decision-tree-based algorithm indicated BOD5, DO, total phosphorous, temperature, turbidity, nitrate, and alkalinity as the relatively important features. The feature importance scores of the input variables for E. coli prediction were less than those for TOC prediction. However, the ML algorithm was able to extract useful data-driven information about the hidden complex non-linear relationships between the bacteria concentration and other physicochemical parameters and indicated BOD5, DO, and total phosphorous to be the most influential parameters for predicting E. coli. With a specific dataset, the ML models performed satisfactorily for TOC prediction with high prediction accuracies of greater than 96%. However, for E. coli prediction, as living microorganism behavior is harder to predict than physicochemical parameters, and because of the presence of a greater amount of unexplained variation in the dataset that could be explained based on the available physicochemical parameters, the models resulted in relatively lower R2 values. The results indicated that for both TOC and E. coli prediction with a specific dataset, ANN-GBM outperformed others with prediction accuracies of 97% (Table 8) and 42% (Table 9), respectively. The reason is that the hybrid model benefitted from the advantages of the specific activation function of ANN in performing non-linear transformations of the input data and allowing complex functional mapping of the network's input and output. In addition, the errors in the prediction of individual trees developed by the GBM algorithm were overcome by boosting mechanisms and optimizing the coefficients to fit the underlying data. The incorporation of a boosting mechanism along with the non-linear transformation of the input data using an activation function allowed the extraction of specific patterns from the data and minimized the difference between the actual and the predicted output, resulting in a more powerful ensemble-hybrid model ANN-GBM. The results indicate that the ANN algorithm fits the data well with R2-values of 0.958 and 0.38, respectively for TOC and E. coli. However, when ensembled with other algorithms, for example, the tree-based algorithm GBM and RF, performance accuracies were further improved for ANN-GBM (TOC: 0.970, E. coli: 0.42) and ANN-RF (TOC: 0.961, E. coli: 0.41). In addition, similar performances were noticed for most of the employed ensemble-hybrid models.
4 Conclusion
We developed several regression ML models to predict TOC and E. coli in the major rivers: Milwaukee River, Menomonee River, and Kinnickinnic River within the Milwaukee River basin. The standalone ML models accurately and directly measured TOC with prediction accuracies ranging from 89.9–95.8%. The prediction performances were further improved (R2 > 0.96) by developing ensemble-hybrid models such as ANN-GBM, SVM-GBM, ANN-SVM, and ANN-RF using the selected input features with relatively higher feature importance scores. The ensemble-hybrid model ANN-GBM achieved the highest prediction accuracy of 97% and lowest error values (MAE = 0.664, MSE = 2.334, and RMSE = 1.528) in predicting TOC of the river system. The ensemble-hybrid models for TOC prediction were able to successfully explain the variability in the dataset based on the combination of input variables: DOC, BOD5, EC, chloride, TS, nitrate, VSS, DO, turbidity, pH, and TSS. The developed ensemble-hybrid methods were not previously used for TOC and E. coli prediction that can provide a reliable and direct approach to complement existing monitoring techniques in the Milwaukee River system with satisfactory prediction accuracies. However, for E. coli prediction it was difficult to explain the greater amount of unexplained variations in bacteria data based on the physicochemical water quality parameters, resulting in R2 values within a range of 0.29–0.42; the hybrid model ANN-GBM outperformed others with a prediction accuracy of 42%. Although the statistical analysis identified no significant linear correlation between bacteria concentrations and physicochemical parameters, the ML models provided data-driven decisions by extracting predictive information from the dataset and established hidden non-linear relationships between the output and input variables that explained some percentages of variability in the data. The model performances might be improved if other hydrometeorological variables such as air temperature, air humidity, atmospheric pressure, and precipitation level would be available for the corresponding E. coli data to consider as inputs to the models. The developed ensemble-hybrid models can be potentially useful in forecasting river water quality in future time steps, eliminating the longer computational time in traditional methods for measuring TOC and E. coli. This will alert the river water operators about the water quality associated with possible future organic matter pollution and microbial contamination. In future work, ML regression models can be developed for the prediction of E. coli considering both the hydrometeorological variables and physicochemical parameters measured in a controlled laboratory environment that would explain the variability in microbial data successfully.Data availability
Data will be made available on reasonable request.Author contributions
The original concept and supervision of the research by Jin Li; figures, data analysis, writing and editing of the article by Nabila Nafsin.Conflicts of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.Acknowledgements
The authors acknowledge help from MMSD for providing necessary data.References
- R. L. Whitman and M. B. Nevers, Foreshore sand as a source of Escherichia coli in nearshore water of a Lake Michigan beach, Appl. Environ. Microbiol., 2003, 69(9), 5555–5562 CrossRef CAS PubMed.
- Milwaukee Riverkeeper, Milwaukee River Basin Report Card, Milwaukee Riverkeeper, 2018, https://milwaukeeriverkeeper.org/wp-content/uploads/2019/11/2018MKERiverBasinReportCard.pdf Search PubMed.
- M. Burzynski, The State of the Milwaukee River Basin. A Report by the Wisconsin Department of Natural Resources, 2001 August, PUBL WT 704 2001, https://dnr.wi.gov/water/basin/milw/milwaukee_801.pdf Search PubMed.
- M. A. Paule-Mercado, J. S. Ventura, S. A. Memon, D. Jahng, J. H. Kang and C. H. Lee, Monitoring and predicting the fecal indicator bacteria concentrations from agricultural, mixed land use and urban stormwater runoff, Sci. Total Environ., 2016, 550, 1171–1181 CrossRef CAS PubMed.
- N. Nafsin and J. Li, Using CANARY event detection software for water quality analysis in the Milwaukee River, J. Hydro-Environ. Res., 2021, 38, 117–128 CrossRef.
- N. Nafsin, B. Bevers, R. Schruender, Q. Liao and J. Li, Escherichia coli and enterococci bacteria in Lake Michigan Beach sand, Environ. Eng. Sci., 2022, 39(1), 3–14 CrossRef CAS.
- F. Muharemi, D. Logofătu and F. Leon, Machine learning approaches for anomaly detection of water quality on a real-world data set, J. Inf. Telecommun. Technol., 2019, 3(3), 294–307 Search PubMed.
- L. Perelman, J. Arad, M. Housh and A. Ostfeld, Event detection in water distribution systems from multivariate water quality time series, Environ. Sci. Technol., 2012, 46(15), 8212–8219 CrossRef CAS PubMed.
- S. Tinelli and I. Juran, Artificial intelligence-based monitoring system of water quality parameters for early detection of non-specific bio-contamination in water distribution systems, Water Supply, 2019, 19(6), 1785–1792 CrossRef.
- X. Y. Zou, Y. L. Lin, B. Xu, Z. B. Guo, S. J. Xia, T. Y. Zhang, A. Q. Wang and N. Y. Gao, A novel event detection model for water distribution systems based on data-driven estimation and support vector machine classification, Water Resour. Manage., 2019, 33(13), 4569–4581 CrossRef.
- A. N. Ahmed, F. B. Othman, H. A. Afan, R. K. Ibrahim, C. M. Fai, M. S. Hossain, M. Ehteram and A. Elshafie, Machine learning methods for better water quality prediction, J. Hydrol., 2019, 578, 124084 CrossRef.
- S. Emamgholizadeh, H. Kashi, I. Marofpoor and E. Zalaghi, Prediction of water quality parameters of Karoon River (Iran) by artificial intelligence-based models, Int. J. Environ. Sci. Technol., 2014, 11(3), 645–656 CrossRef CAS.
- A. H. Haghiabi, A. H. Nasrolahi and A. Parsaie, Water quality prediction using machine learning methods, Water Qual. Res. J., 2018, 53(1), 3–13 CrossRef CAS.
- G. Hayder, I. Kurniawan and H. M. Mustafa, Implementation of machine learning methods for monitoring and predicting water quality parameters, Biointerface Res. Appl. Chem., 2020, 11, 9285–9295 Search PubMed.
- N. Nafsin and J. Li, Prediction of 5-day biochemical oxygen demand in the Buriganga River of Bangladesh using novel hybrid machine learning algorithms, Water Environ. Res., 2022, 94(5), e10718 CrossRef CAS PubMed.
- A. Najah, A. El-Shafie, O. A. Karim and A. H. El-Shafie, Application of artificial neural networks for water quality prediction, Neural. Comput. Appl., 2013, 22(1), 187–201 CrossRef.
- U. Ahmed, R. Mumtaz, H. Anwar, A. A. Shah, R. Irfan and J. García-Nieto, Efficient water quality prediction using supervised machine learning, Water, 2019, 11(11), 2210 CrossRef CAS.
- R. Babbar and S. Babbar, Predicting river water quality index using data mining techniques, Environ. Earth Sci., 2017, 76(14), 1–5 Search PubMed.
- D. T. Bui, K. Khosravi, J. Tiefenbacher, H. Nguyen and N. Kazakis, Improving prediction of water quality indices using novel hybrid machine-learning algorithms, Sci. Total Environ., 2020, 721, 137612 CrossRef CAS PubMed.
- K. Chen, H. Chen, C. Zhou, Y. Huang, X. Qi, R. Shen, F. Liu, M. Zuo, X. Zou, J. Wang and Y. Zhang, Comparative analysis of surface water quality prediction performance and identification of key water parameters using different machine learning models based on big data, Water Res., 2020, 171, 115454 CrossRef CAS PubMed.
- M. Hameed, S. S. Sharqi, Z. M. Yaseen, H. A. Afan, A. Hussain and A. Elshafie, Application of artificial intelligence (AI) techniques in water quality index prediction: a case study in tropical region, Malaysia, Neural. Comput. Appl., 2017, 28(1), 893–905 CrossRef.
- M. Sakizadeh, Artificial intelligence for the prediction of water quality index in groundwater systems, Model. Earth Syst. Environ., 2016, 2(1), 1–9 CrossRef.
- X. Wang, F. Zhang and J. Ding, Evaluation of water quality based on a machine learning algorithm and water quality index for the Ebinur Lake Watershed, China, Sci. Rep., 2017, 7(1), 1–8 CrossRef PubMed.
- L. O. Lawal, M. Mahmoud, O. S. Alade and A. Abdulraheem, Total organic carbon characterization using neural-network analysis of XRF data, Petrophysics-The SPWLA Journal of Formation Evaluation and Reservoir Description, 2019, 60(04), 480–493 CrossRef.
- P. P. Mandal, R. Rezaee and I. Emelyanova, Ensemble Learning for Predicting TOC from Well-Logs of the Unconventional Goldwyer Shale, Energies, 2021, 15(1), 216 CrossRef.
- S. A. Ouadfeul and L. Aliouane, Total organic carbon prediction in shale gas reservoirs from well logs data using the multilayer perceptron neural network with Levenberg Marquardt training algorithm: Application to Barnett Shale, Arabian J. Sci. Eng., 2015, 40(11), 3345–3349 CrossRef CAS.
- J. Rong, Z. Zheng, X. Luo, C. Li, Y. Li, X. Wei, Q. Wei, G. Yu, L. Zhang and Y. Lei, Machine Learning Method for TOC Prediction: Taking Wufeng and Longmaxi Shales in the Sichuan Basin, Southwest China as an Example, Geofluids, 2021 DOI:10.1155/2021/6794213.
- X. Wang, R. Xie, T. Wang, R. Liu and L. Shao, Total organic carbon content prediction of source rocks with conventional well log data based on regression committee machine, Arabian J. Geosci., 2021, 14(15), 1 CAS.
- I. S. Yeon, J. H. Kim and K. W. Jun, Application of artificial intelligence models in water quality forecasting, Environ. Technol., 2008, 29(6), 625–631 CrossRef CAS PubMed.
- E. Goz, M. Yuceer and E. Karadurmus, Total organic carbon prediction with artificial intelligence techniques, in Computer Aided Chemical Engineering, Elsevier, 2019, vol. 46, pp. 889–894 Search PubMed.
- S. Kim, N. Maleki, M. Rezaie-Balf, V. P. Singh, M. Alizamir, N. W. Kim, J. T. Lee and O. Kisi, Assessment of the total organic carbon employing the different nature-inspired approaches in the Nakdong River, South Korea, Environ. Monit. Assess., 2021, 193(7), 1–22 CrossRef PubMed.
- M. Bourel, A. M. Segura, C. Crisci, G. López, L. Sampognaro, V. Vidal, C. Kruk, C. Piccini and G. Perera, Machine learning methods for imbalanced data set for prediction of faecal contamination in beach waters, Water Res., 2021, 202, 117450 CrossRef CAS PubMed.
- M. M. David and B. E. Haggard, Development of regression-based models to predict fecal bacteria numbers at select sites within the Illinois River Watershed, Arkansas and Oklahoma, USA, Water, Air, Soil Pollut., 2011, 215(1), 525–547 CrossRef CAS.
- L. M. He and Z. L. He, Water quality prediction of marine recreational beaches receiving watershed baseflow and stormwater runoff in southern California, Water Res., 2008, 42(10–11), 2563–2573 CrossRef CAS PubMed.
- I. M. Herrig, S. I. Böer, N. Brennholt and W. Manz, Development of multiple linear regression models as predictive tools for fecal indicator concentrations in a stretch of the lower Lahn River, Germany, Water Res., 2015, 85, 148–157 CrossRef CAS PubMed.
- F. M. Khan, R. Gupta and S. Sekhri, Superposition learning-based model for prediction of E. coli in groundwater using physico-chemical water quality parameters, Groundw. Sustain. Dev., 2021, 13, 100580 CrossRef.
- H. Mohammed, A. Longva and R. Seidu, Predictive analysis of microbial water quality using machine-learning algorithms, Environ. Res. Eng. Manag., 2018, 74(1), 7–20 Search PubMed.
- J. M. Hathaway, W. F. Hunt and O. D. Simmons III, Statistical evaluation of factors affecting indicator bacteria in urban storm-water runoff, J. Environ. Eng., 2010, 136(12), 1360–1368 CrossRef CAS.
- C. Averill and B. Waring, Nitrogen limitation of decomposition and decay: How can it occur?, Global Change Biol., 2018, 24(4), 1417–1427 CrossRef PubMed.
- C. Farrell, F. Hassard, B. Jefferson, T. Leziart, A. Nocker and P. Jarvis, Turbidity composition and the relationship with microbial attachment and UV inactivation efficacy, Sci. Total Environ., 2018, 624, 638–647 CrossRef CAS PubMed.
- J. Tan, D. Wang, H. Cao, Y. Qiao, H. Zhu and X. Liu, Effect of local alkaline microenvironment on the behaviors of bacteria and osteogenic cells, ACS Appl. Mater. Interfaces, 2018, 10(49), 42018–42029 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2023 |