Open Access Article
Open Access ArticleOn the physical processes of mechanochemically induced transformations in molecular solids
Adam A. L.
Michalchuk
 ab
ab
aSchool of Chemistry, University of Birmingham, Edgbaston, UK. E-mail: a.a.l.michalchuk@bham.ac.uk
bFederal Institute for Materials Research and Testing (BAM), Richard Wilstaetter Str 11, 12489 Berlin, Germany
First published on 25th November 2024
Abstract
Initiating or sustaining physical and chemical transformations with mechanical force – mechanochemistry – provides an opportunity for more sustainable chemical processes, and access to new chemical reactivity. These transformations, however, do not always adhere to ‘conventional’ chemical wisdom, making them difficult to design and rationalise. This challenge is exacerbated by the fact that not all mechanochemical transformations are equal, with mechanical force playing a different role in different types of processes. In this review we discuss some of the different roles mechanical force can play in mechanochemical transformations, set primarily against the author's own research. We classify mechanochemical reactions broadly as those (1) where mechanical energy is for mixing, (2) where mechanical energy alters the stability of the reagent, and (3) where mechanical energy directly excites the solid. Finally, we demonstrate how – while useful – these classifications have fuzzy boundaries and concepts from across them are needed to understand many mechanochemical reactions.
The subdisciplines of chemistry have been traditionally defined by the type of energy used to activate the transformation, thermo-, photo- and electro-chemistry being well-known examples. Following scientific developments of the late 19th century,1,2 W. Ostwald added a new branch of chemistry to the repertoire, coining the term mechanochemistry in his seminal textbook ‘Lehrbuch Der Allgemeinen Chemie’. The subsequent developments of mechanochemistry have been reviewed extensively elsewhere,3–7 but suffice it to say that while the field has grown enormously over the last century, we are still only scratching the surface of understanding and realising its true potential.
The implications of mechanochemistry are broad. Without the need for solvent, and typically exhibiting higher yields in shorter reaction times,8,9 mechanochemical transformations are emerging as a cornerstone of green and sustainable chemistry.10 Moreover, the ability to initiate and sustain physical and chemical transformations in and between solids using mechanical force leads to very unique reactivity,11,12 and provides an opportunity to access unusual molecules and materials that are difficult – or even impossible – to prepare by other methods.13,14 The continued development of the field therefore promises to impact across the breadth of the physical and chemical sciences.
Despite the broad applications of mechanochemical processes, and the many decades of detailed research, we know remarkably little about how these transformations occur.5 In many respects this is because understanding mechanochemical transformations requires understanding and correlating phenomena across lengths of scale and time that transcend the traditional disciplinary boundaries of physics, chemistry, and engineering. Moreover, it is emerging that there may even be different types of mechanochemical transformation.15
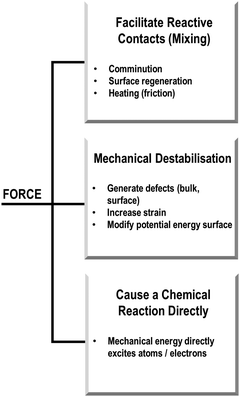
In our own studies of mechanically induced physical and chemical transformations in molecular solids, we have tried to rationalise the types of possible mechanisms associated with various systems. Based on our experience, we have found it useful to think about mechanochemical transformations in terms of the role of mechanical energy. With a focus on solid state phenomena (and noting that covalent synthetic mechanochemistry is beyond our scope), we have broadly envisioned three types of transformation, Scheme 1: (Type 1) those where mechanical energy acts to mix the powder (at the scale of bulk powder and individual molecules) to generate new interfaces for reagents to interact, often facilitated by bulk or local heating (e.g. through friction); (Type 2) those where the mechanical energy modifies the stability of the material to induce or alter its reactivity; and (Type 3) cases where the mechanical energy is directly absorbed, and leads directly to a physico-chemical transformation. These classifications are suggested with the caveat that this demarcation is largely fictitious, with any real mechanochemical transformation likely adopting some features from across these classifications. However, this separation has proved to be helpful when beginning to study mechanochemical transformations and make sense of how and why they occur.
In this Feature Article we will discuss recent progress towards understanding mechanochemical transformations, framed within the context of these three Types of mechanochemical processes, drawing largely from our own developments in the field. In doing so it is our aim to demonstrate how viewing mechanochemical transformations from such a perspective allows us to hone in on the types of physical processes that must be considered in any given system, and which can be (largely) ignored. Moreover, throughout the discussion we hope to show how – regardless of the mechanochemical mechanism – the properties and behaviours of the solid state plays a central role. It is our hope to entice the growing mechanochemical community not to overlook the unique aspects of the solid state.
1. Mixing-induced mechanochemical transformations in powders (type 1)
Unlike in fluids, it is impossible to have a truly homogeneous powder mixture. Reactions within powder samples are therefore inhomogeneous, Fig. 1a. Moreover, bulk thermal diffusion of powders is not possible, and reactions are restricted to interparticle interfaces. To sustain a reaction in a powder sample, we therefore need to agitate the powder to generate new particle–particle interfaces and remove product from particle surfaces to expose more unreacted reagent. These two processes are at the core of many mechanochemical transformations and are likely the dominant roles for the mechanical treatment in systems where thermal energy alone can cause the reaction to occur. This is especially relevant to low melting point, or volatile molecular solids,16 such as in the mechanosynthesis of phthalylsulphathiazole, where the mechanical treatment acts only to refresh reagent surfaces.17 Importantly – in the present context – the process of mixing includes the physical mixing of macroscopic particles and the comminution of particles. Both processes enhance the overall homogeneity of the material.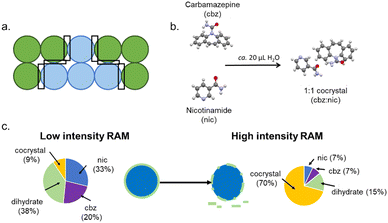 | ||
| Fig. 1 Mixing-induced mechanochemical transformations. (a) The composition of a bulk powder showing the significant inhomogeneity and the localisation of reaction zones at heterogeneous particle contacts. (b) The reaction scheme for the co-crystallisation of carbamazepine (cbz) and nicotinamide (nic) to form the stoichiometric cocrystal under liquid assisted grinding conditions. (c) The product composition achieved for the co-crystallisation under low intensity RAM conditions and the hypothesised hydrate layer on unreacted nicotinamide, and the change in hydrate surface layer with high intensity RAM mixing and the effect on the final reaction composition. Example taken from ref. 18. | ||
An excellent example of the crucial role of mixing for many mechanochemical processes in solids is found in Resonant Acoustic Mixing (RAM). Within the RAM, a low frequency (ca. 60 Hz) acoustic wave causes mixing inside a bulk powder sample, which can be used to drive chemical synthesis.19 RAM mixing has been used as a medium free (i.e. without any milling bodies) method to conduct a range of chemistries, from multi-component crystal formation20,21 to the synthesis of metal nanoparticles,22 metal–organic frameworks23 and pharmaceutical molecules.24 Notably, no RAM transformations have yet been shown to occur without some degree of heating or the addition of liquid to facilitate molecular-level mixing. The mechanical forces experienced by powders within the RAM are so low that even highly explosive materials can be processed without their mechanical initiation.25,26 In fact, we performed scanning electron microscopy (SEM) imaging on organic powders processed by high-intensity RAM mixing and found minimal damage to particle surfaces.26 These findings indicate strongly that RAM mixing is just that – mixing – providing an excellent opportunity to study the role of mixing in mechanochemical transformations.
To this end, we studied the co-crystallisation of nicotinamide + carbamazepine, driven by RAM.18 Under completely dry conditions, we did not observe any reaction between the starting powders. In contrast, the cocrystal formed readily when RAM mixing was performed with a drop (ca. 20 μL) of water, Fig. 1. Using time-resolved in situ (TRIS) X-ray diffraction monitoring we followed the RAM co-crystallisation under both low- and high-intensity RAM mixing. At low intensity mixing conditions, the reaction proceeded quickly, though only small amounts of the co-crystal were found to form. In contrast, the particles of carbamazepine reacted with the water to form a carbamazepine hydrate phase, which inhibited the continuation of the reaction. In contrast, when the co-crystallisation was performed under high intensity mixing conditions, the hydrate phase behaved as an intermediate, and the reaction progressed towards the co-crystal product. Following from our previous findings in a related RAM-induced cocrystallisation,26 it seems that under low-intensity mixing the hydrate intermediate formed a coating on the unreacted carbamazepine particles and inhibited the reaction from proceeding. However, with sufficient mixing intensity this coating layer could be removed, and the reaction progressed.
The effective mixing of reagents is key for controlling reaction kinetics in mechanochemical reactions within powders.27 We observed this, for example, when studying the ball milling induced polymorphic transformation of caffeine.28 In the early stage of the transformation, the kinetics was determined by the milling frequency alone (i.e., the number of collisions per unit time). However, as the transformation progressed and the mono-phase powder became a binary mixture (two polymorphs), the reaction kinetics were instead determined by the number of collisions striking untransformed powder – dependent on the efficiency of powder mixing within the bulk. As the milling ball size was increased to strike a larger portion of the powder (hence minimizing the need for mixing), the kinetics were again found to depend only on the milling frequency.
Though mixing is of course important for making contacts between reagent particles, we still need a mechanism to drive mixing at the molecular/atomic level. An obvious origin of molecular level mixing is surface melting, for example initiated by frictional heating that occurs during the mixing processes. Early experimental evidence for surface temperatures at tribological interfaces do suggest that transient temperatures in excess of 400 K are achievable,29 with more recent molecular dynamics simulations suggesting similar orders of magnitude.30 Recent photographic evidence of dynamically impacted powders31 suggest that these transient, local temperatures are undoubtedly important in many mechanochemical reactions. Heating at inter-particle surfaces is especially important for molecular crystal systems that comprise low-melting eutectic mixtures, as has been shown by Rothenberg et al.32 who demonstrate contact melting as a key mechanism in ‘solid state reactions’ of molecular crystals. This concept was recently extended to mechanochemistry by Mazzeo and colleagues recently used time-resolved in situ powder X-ray diffraction to follow the mechanochemical cocrystallisation of hexamethylenetetramine and thymol.33 In their work they demonstrated that the frictional heating caused by mixing powders was sufficient to induce eutectic melting at particle interfaces, through which the cocrystal nucleated. Given the low melting temperature of many organic crystals, the authors have suggested this to be a more general mechanism for mechanochemical cocrystallisation and have since prepared an approach to predict this phenomenon and help design mechanochemical protocol.34
Other readily accessible mechanisms are also available to facilitate molecular-level mixing in powders. For the mechanochemical formation of the stoichiometric co-crystal of glycine + malonic acid,35 we found that the ball milling reaction only progressed when performed under ambient atmospheric conditions. In contrast, when milling was done in a nitrogen atmosphere, no transformation occurred. A closer look at the materials revealed that one reagent – malonic acid – is highly hygroscopic. Malonic acid therefore ‘pulls’ water from the atmosphere into the powder mixture causing dissolution of the reagents in a process dubbed inadvertent liquid assisted grinding. Similar dependencies of ‘solid state’ synthesis on the inadvertent introduction of liquids have been reported.36–38
Despite their diversity, the mechanochemical transformations in the preceding discussion have one thing in common: the primary role of the mechanical treatment is to facilitate mixing. In contrast, the molecular-level processes are instead dominated by conventional thermal phenomena, including diffusion through either a melt (potentially achieved by frictional heating) or dissolution in sorbed or explicitly added liquid. Given the low melting temperature, solubility, hygroscopicity, and high volatility of many organic solids, it is likely that these types of mixing induced processes are very common across organic solid state mechanochemistry.
It is important to recognise these transformations, as it is only in doing so that we gain an understanding for how to start to control them. For example, we have discussed how for such cases the bulk mixing dominates the kinetics of these transformations. Numerical kinetic models of mechanochemical reactions in molecular crystal systems are also supporting this concept, and indicate that it is the amount of material involved in a collision, and the formation of interparticle contacts that determine the transformation kinetics.39,40 In contrast to Type 3 transformations (see Section 3) these simulations also suggest for Type 1 transformations we can increase reaction rates through increased mechanical energy, not because we have overcome an energy threshold, but rather because we enhance comminution and mixing. If we therefore aim to understand why mechanochemical parameters have the effect they do on any given reaction, we need to understand its role for a given reaction type.
2. Mechanically modified crystal stability (type 2)
When mechanical mixing (at both bulk and molecular levels, Section 1) is insufficient to incite a physico-chemical transformation, alternative mechanisms can take over. Where mechanical force is applied slowly to a system – i.e. on time scales slower those needed for nuclear rearrangements to occur41 – at least two different ‘mechanisms’ for mechanochemical transformations can occur. In the former, the nuclear positions of the chemical system adjust to minimise the internal strain introduced by the external mechanical force. The physical and chemical properties can of course be very different under this mechanically strained state42 and both physical and chemical transformations can occur. An excellent example of chemical transformations initiated by slowly applied mechanical strain is the dark dimerization of crystalline benzene by Hoffmann and colleagues,43 where mechanical strain forces the overlap of the aromatic π systems of adjacent benzene molecules causing them to react. A similar process was observed in crystalline anthracene.44 Another elegant demonstration for the onset of chemical reactivity under mechanical strain is in the case of copper(I) m-carborane-9-thiolate, wherein electron transfer across the Cu–S interaction was controllable under applied hydrostatic loading.45In a related mechanism, the bulk solid system can seek to accommodate the strain by introducing imperfections (defects) in the bulk crystal, a process called mechanical activation.46 While these defects may (or may not) directly influence the nuclear geometries at the individual molecule scale, they affect the overall stability of the extended crystallite, can affect diffusion rates through the lattice,47 and can therefore affect the overall transformation. In fact, such mechanically induced defects can even entirely change the reactivity of the material, as was shown in silver oxalate.48
2.1 Mechanical destabilisation of extended structures
There are a number of excellent examples in the literature of mechanical destabilisation of individual molecules, and readers are referred elsewhere for this discussion.42,49,50 In our own work we have instead focused on the physico-chemical behaviour of extended crystal structures under mechanical loading. In this section we focus on the role of mechanical destabilisation for the physical transformation of bulk structures, and will extend this discussion to its effect on molecular level reactivity in Section 3.As a representative example we have studied the mechanical (high pressure) response of a 1-dimensional coordination polymer, [Zn(μ-Cl)2(3,5-dichloropyridine)2]n.51 Experimental results showed a crystallographic phase transition at ca. 5 GPa, associated with distortion of the 3,5-dichloropyridine packing geometries. By probing the pressure behaviour in greater detail through density functional theory (DFT) calculations we observed a systematic softening (decrease) of a low frequency vibrational mode. This vibrational mode continued to soften before becoming dynamically unstable at the phase transition pressure. Through these DFT calculations we were able to follow how mechanical force changed the underlying potential energy surface, destabilising the nuclear arrangement, and eventually driving the system to new energetic minimum that corresponded to the high-pressure crystal structure, Fig. 2.
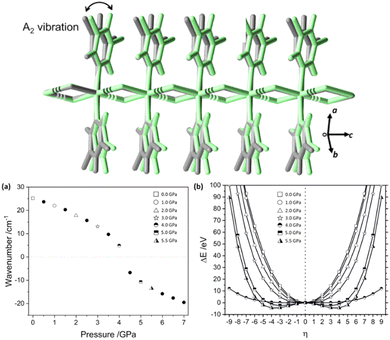 | ||
| Fig. 2 Force-induced crystal instability driving the high pressure structural phase transition in [Zn(μ-Cl)2(3,5-dichloropyridine)2]n. (Top) The structural diagram showing the phase transition associated with an A2 vibrational mode, indicating the structure before (grey) and after (green) the transition. (a) The simulated frequency of the A2 vibration with increasing pressure. (b) Force modified potential energy surface of the A2 vibration, showing the appearance of a new minimum at ca. 4.5 GPa. Figure adapted from ref. 51 with permission from Springer Nature. | ||
The mechanical modification of stabilities is an incredibly common phenomenon, including in the crystalline graphene,52 for metal halide clusters,53 and for innumerable other cases. Despite this prevalence, this common phenomenon is seldom considered when seeking to rationalise the outcomes of modern mechanochemistry. However, we can observe this phenomenon in various places in the literature. For example, when chlorpropamide is ball milled under ambient conditions, effectively no transformation is observed.54 In contrast, when chlorpropamide is cooled (and adopts a new crystal structure), the application of mechanical force by ball milling causes it to transform into yet a new crystal structure. Similarly, there is indication that crystal forms otherwise only obtainable by applying pressure can also be generated by high energy ball milling.55 These transformations of course have nothing to do with particle mixing (i.e. are not Type 1), but instead on the ability of mechanical strain to induce instability in the nascent solid form. Thus, understanding the structural response of materials to mechanical loading is essential to elucidate this type of mechanically induced transformation.
While mechanically induced instabilities can lead to both chemical and physical transformations, they can also affect the nascent reactivity of the material: i.e. mechanical activation. This is particularly important for understanding mechanochemical processes as mechanical activation can cause melting temperatures to reduce,56 change diffusion barriers (and hence transformation kinetics),47,57,58 and even change the pathways for chemical reactions. Thus, Type 2 processes can both facilitate new reactivity whilst also enhancing mechanochemical transformations dominated by mixing (Type 1) described in Section 1.
As an example, we have investigated through a combination of μ-focus X-ray diffraction and DFT simulations how the uniaxial strains associated with mechanical bending affect the crystal structure of 2,4-dichloro-6-[(6-methylpyridin-2-ylimino)methyl]phenol, DMP.59 DMP crystallises from solution as long needle-like crystals with herringbone layers running perpendicular to the long crystal axis. When bent over the long crystal axis, the orthogonal uniaxial compression at the concave face of the bend caused the herringbone structure to flatten, Fig. 3. In contrast, the uniaxial tension experienced at the convex surface caused these layers to bend further. Importantly, as the layers flattened within the concave surface, DFT simulations revealed that intermolecular spacings increased, reducing the energy barriers needed for plastic deformation to occur. These results therefore showed that uniaxial mechanical force can destabilise a crystal, and facilitate subsequent mechanical activation.
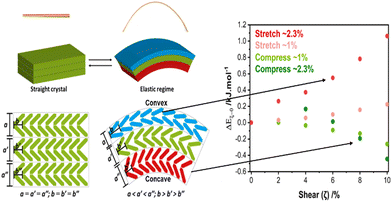 | ||
| Fig. 3 Mechanical bending causes FMPES through uniaxial strain. Bending causes uniaxial tension (stretching) on the convex surface, and uniaxial compression on the concave surface. The latter reduces energy barriers needed for subsequent plastic deformation and the onset of mechanical activation. Figure adapted from ref. 59 with permission from the Royal Society of Chemistry. | ||
We have observed similar effects in other uniaxially strained crystals,60 including in coordination polymer crystals,61 and similar processes have since been observed by other research groups,62 demonstrating the breadth of applicability of this coupling between mechanical stress, force-modified nuclear geometries and material activation.
2.2 Mechanical activation and the onset of mechanochemistry
Where relaxation to the mechanical stress occurs at the level of bulk crystallites, defects are instead introduced into the structure. Growing evidence suggests that this process of activation is incredibly important for mechanochemical transformations in molecular crystals, and likely provides a physical basis for the unique kinetic behaviour exhibited by these reactions.63With the development of time-resolved in situ (TRIS) methods to study mechanochemical transformations,64 and particularly TRIS PXRD,65,66 the community has obtained a much clearer picture of reaction kinetics under mechanochemical conditions. Typically, mechanochemical reactions in bulk powders comprise three kinetic zones: (1) an induction period, (2) a reaction phase, and (3) a steady-state reaction plateau. The first zone – the induction period – is particularly notable, as it can extend from seconds to hours. From conventional chemical intuition, it was initially thought that these induction periods were simply a result of the system needing to heat (e.g. from friction) until the activation temperature was reached. However, TRIS thermal analysis of ball milling has shown time and again that induction periods extend far beyond any heating processes that are associated with the early stages of a mechanochemical reaction.67 Moreover, any heating that is achieved is often well below the temperatures that are needed to initiate the physical or chemical transformation.68,69 This suggests that induction periods do not arise from ‘conventional’ chemical processes, but instead are a unique manifestation of solid state mechanochemical phenomena.
In our TRIS PXRD studies on the cocrystallisation of theophylline (tp) and benzamide (ba), Fig. 4Ia and b, we observed the typical reaction profile with a ca. 10 min induction period followed by rapid onset of the transformation. With our methodological developments we were for the first time able to extract more than just phase composition during ball milling; we extracted crystal size and strain. This new analysis showed that the induction period – though chemically benign – corresponded to significant physical changes in the powder, with the crystal sizes decreasing to some ‘critical size’ before the transformation ensued, Fig. 4Ic and d. This was reminiscent of Boldyrev's previously hypothesised link between comminution limits and particle activation.70
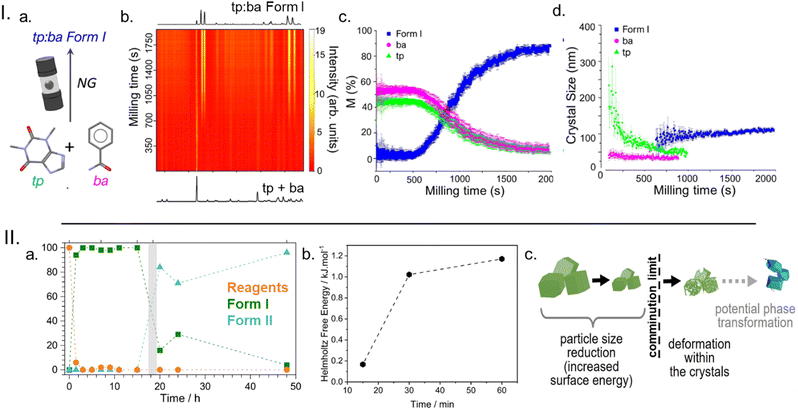 | ||
| Fig. 4 The role of mechanical activation in the onset of mechanochemical transformations in molecular solids. I. Time-resolved in situ (TRIS) powder X-ray diffraction monitoring of the cocrystallisation of theophylline (tp) and benzamide (ba) with the (a) reaction scheme, (b) TRIS PXRD data, (c) quantitative phase analysis, and (d) crystal size. Figure adapted from ref. 45 with permission from Springer Nature. II. The ex situ analysis of the mechanochemical polymorphic transformation of a carbamazepine – nicotinamide cocrystal, showing (a) the phase composition with time, (b) the Free energy of Form I with increased milling time, and (c) a schematic for the comminution and activation that precedes polymorphism. Figure adapted from ref. 50 with permission from Wiley-VCH. | ||
Inspired by these findings we conducted a series of ex situ studied on the polymorphic transformation of the stoichiometric carbamazepine (cbz) and isonicotinamide (ina) cocrystal, cbz-ina, Fig. 4II.71 This system was selected because the induction period could be extended from 1 h at high milling energy to over 7 h at low milling energies, and thus provided a strong correlation between energy input and a physico-chemical transformation. Our DFT simulations showed that Form I of cbz-ina, which formed first during ball milling the starting reagents, is the stable polymorph by ca. 2–3 kJ mol−1. However, when Form I was ball milled for extended periods of time, it transformed to Form II, even though the milling jar temperature did not change significantly. By thermal analysis of milled Form I we instead found that ball milling systematically increased the free energy of the material, Fig. 4IIb. This suggests that Form I is systematically destabilised (activated) until a critical energy barrier is overcome and the material is driven to undergo the polymorphic transformation.
From recent progress in understanding mechanochemical kinetics it is emerging that mechanical activation is a key component to understanding the unique reaction profiles observed under mechanochemical conditions. When coupled to seminal theory,70,72 these findings suggest that some degree of comminution is the first process to occur during milling, Fig. 4IIc. However, once a comminution limit is reached, continued milling introduces defects (potentially facilitated through mechanically modified nuclear geometries) that modify the stability of the solid reagents. This may lead to changes in melting or fluidisation behaviour and facilitate the onset of mixing-induced mechanisms or may modify the reactivity in other ways – e.g. by lowering diffusion barriers.48 Regardless, it is becoming clear that understanding the role of mechanical activation in molecular solids is crucial for learning to design and control mechanochemical processes more generally.
2.3 Combined role of mixing and mechanical destabilisation
We have discussed briefly how various forms of mechanical destabilisation can be synergistic, and activation can reduce barriers to melting. However, recent research into thermo-mechanochemical processes is showing that there are additional routes to the coupling between heating (Type 1) and mechanical destabilisation (Type 2) processes.Our DFT calculations have shown that the polymorphic transformation from Form I to Form II of the stoichiometric cocrystal of glutaric acid (glu) and isonicotinamide (ina) is enantiotropic – i.e. that the relative polymorphic stability crosses over before the onset of melting.68 Thermal analysis and variable temperature powder X-ray diffraction showed that the transition from Form II to Form I occurs at 363 K. Remarkably, however, we found that the same transition could be driven at temperatures 20 K below this thermodynamic transition point when performed under heated ball milling conditions.
In a second example we studied the polymorphic transformation of a cocrystal of nicotinamide (nic) and pimelic acid (pa).69 Once again our DFT showed an enantiotropic relationship between these polymorphs, with thermal analysis and variable temperature powder X-ray diffraction showing the transition to occur at 363 K. As for glu-ina, when the nic-pa cocrystal was ball milled at elevated temperatures, the polymorphic transformation was instead observed <340 K.
We have not yet identified the physical origin for this remarkable ability to couple thermal and mechanical energy to accelerate structural phase transitions in molecular crystals. However, it is very clear that there is a synergistic effect between mechanical stress and thermally driven transformations. Such studies provide exciting examples of the sheer complexity of mechanochemical transformations. Though it is helpful for discussion purposes to separate mechanochemical reactions into various subclasses, the true mechanisms result from an interplay between many processes, whose connectivity will surely provide a dynamic and fruitful direction of research for years to come.
3. Direct mechanochemical excitation (type 3)
We have discussed briefly how mechanical force can modify or induce physico-chemical transformations in extended solids through processes of mechanically induced destabilisation. In this final section we will turn our attention to emerging mechanisms of directly excited mechanochemical reactions, which result from the direct injection of energy into a system from mechanical excitation. Energetic materials (explosives, propellants, pyrotechnics; EMs) are a particularly useful family of compounds for such studies, as they provide a clear ability to convert a single mechanical insult into a very visible chemical response. Many EMs cannot be initiated thermally, demonstrating a clear demarcation with Type 1 reactions. Moreover, EMs provide a subset of mechanochemical reactions that have a true energy threshold for the initiation of their chemistry. This is to say that – contrary to Type 1 reactions (mixing induced) where the intensity of mechanical treatment affects the kinetics only via mixing efficiency – Type 3 reactions must have a minimum intensity of mechanical treatment to even get the chemistry to go. There are limited clear examples of Type 3 transformations beyond EMs (their decoupling from Type 2 processes requires dedicated studies into their slow compression behaviour), but based on literature, which indicates minimum energy thresholds for their reactivity, one might suspect e.g. the single crystal reactions in cocrystals73 or Diels–Alder reactions74 could proceed by related mechanisms.To understand how mechanical energy can initiate a chemical transformation within an extended solid, we first need to determine what mechanism is available to carry the energy into the molecule itself. Unlike photo-chemical transformations where our energy source excites directly the electronic degrees of freedom, mechanical strain instead distorts the bulk crystal. We can therefore think of a mechanical insult as injecting an acoustic (compressive) wave into a crystal. These low-frequency acoustic waves can only travel through the crystal by coupling to low frequency vibrations. Experimental spectroscopic and thermometric evidence for such processes have been reported.75,76 We have seen already in Section 2.1 how the mechanical manipulation of these low frequency vibrations can drive structural instabilities. But, can the manipulation of vibrations similarly cause chemistry to happen?
3.1 Phonons as a conduit of mechanical energy
To first convince ourselves that vibrational modes could induce chemical (electronic) processes, we studied how the vibrational modes of a simple azido anion, N3−, affect its electronic structure, with the aim to induce rupture of an N–N covalent bond. In the gas phase, a conical intersection was reached through the bending mode,77 with additional calculations showing that the N–N bond dissociates readily on the low-lying excited state potential energy surfaces.77 This same effect was also observed for the bending mode in the crystal structure of NaN3,78 a phenomenon denoted as dynamic metallization, Fig. 5a. The ability to close the band gap of a crystal (akin to the HOMO–LUMO gap for isolated molecules) and initiate chemistry by bending molecules is reminiscent of the early theories for shear-induced mechanochemical reactivity in solids proposed by Gilman.79,80 Though only a simple model system, these results do show how, by exciting a specific vibration with enough energy, we can activate a chemical (electronic) process. This finding supports the idea that phonons can act as carriers from an external source to an internal degree of freedom.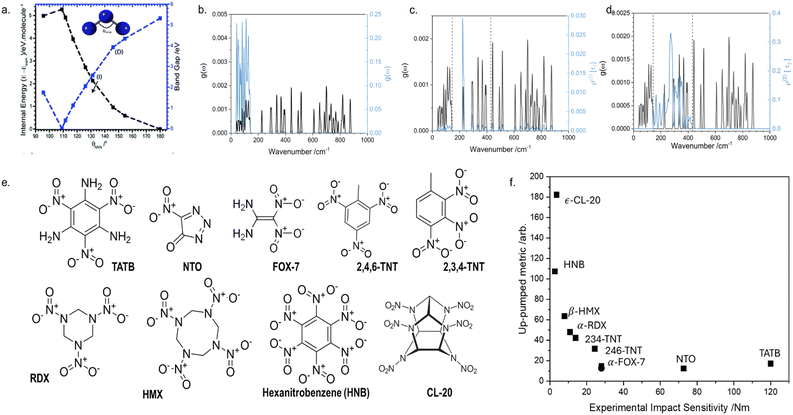 | ||
| Fig. 5 Initiation of mechanochemical reaction through vibrational excitation. (a) Transient, dynamic metallisation achieved in crystalline NaN3 through excitation of the azido anion bending mode. (b)–(d) Initial mechanical excitation of low frequency vibrations and subsequent energy transfer to higher frequency molecular vibrations. In each case, the fundamental frequencies are shown in black, and the associated vibrational populations are shown in blue. (b) Initial excitation following mechanical insult, (c) and (d) step-wise transfer of vibrational energy into higher frequency vibrations. (e) Molecular diagrams for the EMs whose mechanochemical reactivity was studied by phonon up-pumping. (f) Semi-quantitative prediction of EM mechanochemical reactivity, with experimental values shown on the x axis and predicted ordering plotted on the y axis. Data are taken from ref. 58. | ||
Experimental work has shown that on short time-scales, energy injected into low frequency vibrations in a crystal can lead to excitations in higher frequency vibrations.75,76 The mechanism that underpins this energy transfer originates from the anharmonic behaviour of crystal and molecular vibrations. Immediately following mechanical impact, there is an excess (i.e. above that expected thermally) amount of energy in the lowest frequency modes. By interacting with other ‘hot’ low frequency vibrations this energy can move into ‘colder’ vibrations at higher frequencies – i.e. the energy is up-pumped. One can think of this process as being analogous to overtone or combination bands in spectroscopy. This up-pumping process continues, and eventually molecular vibrations become excited to high quantum states, Fig. 5b–d. As we have seen in Fig. 5a, molecular vibrations can cause significant perturbation of the underlying electronic structure and can lead to the onset of chemistry (in this case, the rupture of covalent bonds).
Armed with an understanding that excited vibrational states can cause chemistry, and that mechanical insult can lead to vibrational excitations through phonon up-pumping mechanisms, we aimed to identify if mechanochemical reactivity in EMs could be predicted.81,82 Inspired by early work of Dlott and Fayer,83,84 we approximate the magnitude of the initial mechanical excitation using a simplified adiabatic compression scheme (anisotropic equivalents have been also explored85), which links material compressibility, V/V0, and its frequency response to compression via the Gruneisen parameter γ, to the temperature-equivalent excitation, T/T0,
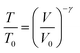 | (1) |
Our model was tested against a broad range of EMs, including a breadth of chemistries and crystallographies, Fig. 5e. Remarkably, for EMs known to have very low mechanochemical reactivity, our model predicted the capture of effectively no vibrational energy, Fig. 5f. In contrast, significant amounts of vibrational energy were captured by highly mechanochemically reactive EMs. Though based on significant physical approximations, this in silico model provides a compelling mechanism for predicting – and ultimately understanding – how mechanical energy can directly initiate a chemical reaction at an elementary scale. Note that this model only applies to systems exposed to high velocity mechanical loading conditions (under low velocity loading, Type 2 mechanisms will dominate; see ref. 86 for a more detailed discussion on this).
Having benchmarked the model (both by ourselves and by various independent researchers87,88) and demonstrated its predictive capabilities, we sought to explore its use for understanding the timescales associated with elementary mechanochemical reactions. Using as a model system crystalline LiN3 (which is a notably unreactive EM), we performed a semi-quantitative up-pumping calculation at different degrees of mechanical insult, Fig. 6.85 Numerical simulation demonstrated that the up-pumping process was complete within ca. 100 ps, reaching increasingly high quasi-temperatures with more significant mechanical loads. By coupling these numerical simulations to ab initio molecular dynamics we were subsequently able to investigate how this degree of mechanical excitation affected both the structural and electronic behaviour of LiN3, Fig. 6b. Importantly, we found for a mechanical perturbation of ca. 5 GPa that the electronic band gaps reduce by ca. 25% over a period of ca. 250 fs, with marked changes in molecular geometry.
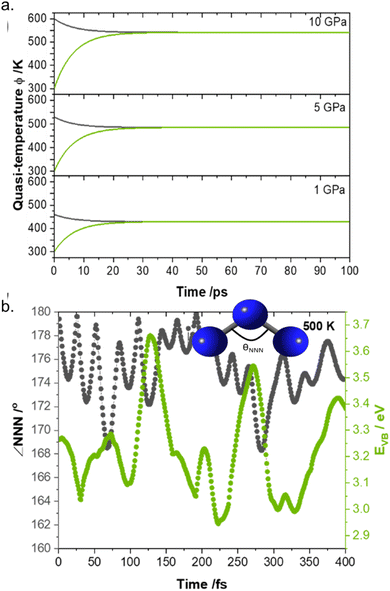 | ||
| Fig. 6 Semi-quantitative phonon up-pumping model for LiN3. (a) Time dependent vibrational quasi-temperatures for the (black) external and (green) molecular vibrations as a function of the initial mechanical insult pressure. (b) Ab initio molecular dynamics simulation of a 5 GPa excitation of LiN3, plotting the evolution of the electronic band gap and NNN bend angle following ‘equilibration’ the 500 K. Figure adapted from ref. 85 with permission from the Royal Society of Chemistry. | ||
Though such simulations need to be extended to mechanochemically reactive materials, they do show that – at an elementary level – some mechanochemical reactions likely occur under highly non-equilibrium conditions. To this end, emerging results do suggest that if we wish to truly understand mechanochemical processes at an elementary level we need to understand the highly non-equilibrium and high distorted states and structures associated with them.
3.2 Polymorph dependence of mechanochemical reactivity
Our model for the elementary mechanism of EM mechanochemistry is based on understanding how vibrational energy is transmitted through a crystal. It stands to reason that we should therefore also be able to predict the effect of polymorphism (crystal packing) on EM mechanochemistry, with hopes to understand why different crystal forms can sometimes exhibit varied mechanochemical reactivity.89As an intriguing case study, we first targeted the ‘unwritten’ rule in EM mechanochemistry that layered materials are less reactive than non-layered materials. Rationales for this have been proposed based on slip plane energies90 though an elementary mechanism is still missing, providing an excellent target for the up-pumping mechanism. To eliminate any influence of molecular structure on EM reactivity, we selected FOX-7 (1,1-diamino-2,2-dinitroethene; DADNE; see Fig. 5 for structure) as model system.91 FOX-7 exists in three crystal forms92 – α, β, and γ – which become progressively more layered. Thus one should expect the herringboned α form to be more mechanochemically reactive than the layered γ form.93 Unfortunately, all attempts to verify this experimentally were unsuccessful as mechanical impact of the γ form caused the powder to convert back to the α form.91 However, our up-pumping calculations did show a measurable difference in the reactivity of the two forms, with the reactivity of α > γ, Fig. 7a. Further inspection of the up-pumping mechanism revealed this trend to result from the softening of the external lattice vibrations in layered γ-FOX-7, reducing the material's ability to effectively up-pump vibrational energy into the individual molecules. This provided the first elementary rationale for why layered materials may be less mechanochemically reactive than their non-layered counterparts. It follows from these results that the up-pumping process – and hence mechanochemical reactivity – should be a designable property. One should be able to harness crystal engineering to design crystal packings that have soft external vibrations (e.g. layered materials) and are therefore ineffective at transmitting vibrational energy. As the field of crystal engineering in EMs continues to grow,94 we suspect this to become a useful design target.95
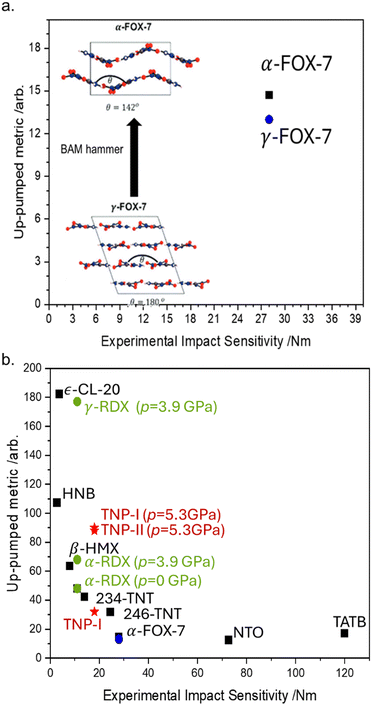 | ||
| Fig. 7 Predicting effects of crystal structure on the mechanochemical sensitivity of EMs. (a) Effect of polymorphic interconversion on the predicted sensitivity of FOX-7 polymorphs, and the conversion of γ-FOX-7 to α-FOX-7 on mechanical impact. (b) The effect of pressure on the sensitization of polymorphs of RDX and TNP, demonstrating the influence of a force-modified potential energy surface on the elementary mechanochemical reactivity of EMs. Data combined from ref. 91, 96 and 97. | ||
3.3 Relation of mechanically induced destabilisation and elementary reactivity
Equation 1 provides a hint that one should expect a clear link between the force-modified mechanisms (Type 2) discussed in Section 2 and the elementary mechanisms (Type 3) outlined here in Section 3. This again shows how intertwined and multi-faceted we must think to understand mechanochemical reactivity.To demonstrate this interconnection, we have explored the effect pressure on the mechanochemical sensitivity of EMs. In a routine high pressure study of 3,4,5-trinitro-1H-pyrazole (TNP),96 the sample initiated unexpectedly upon compression at around 5 GPa. During a second, slower compression, no initiation was observed, though neutron powder X-ray diffraction did reveal the onset of a polymorphic transformation (from Form I to Form II). Notably, this was a subtle phase transition associated with minimal change in crystallographic or molecular geometry. With this minimal difference, it was surprising to find that the phonon up-pumping calculations on the two polymorphs of TNP suggested a significant difference in the sensitivity between the two polymorphs, Fig. 7b. However, when the up-pumping calculations were repeated for Form I, compressed in silico to the same pressure as Form II, up-pumping showed effectively no difference in the reactivity of the phases. Thus, we found that the hardening (increase) of vibrational frequencies that result from the force modified structure enhance their ability to transmit vibrational energy, leading to a force-enhanced phonon up-pumping and mechanical sensitization.
In a similar study we sought to understand the mechanochemical reactivity of RDX. This is a particularly challenging material to model, as spectroscopic studies have found that the material undergoes a transient polymorphic transformation in response to mechanical insult.98 Our initial phonon up-pumping calculations on α-RDX (the ambient pressure phase) showed it to be significantly less sensitive than the high pressure phase (γ-RDX) that is obtained during mechanical insult.97 Importantly, to contrast the case of TNP, the difference in mechanochemical reactivity between the two polymorphs was not simply the result of force-modified vibrational frequencies, Fig. 7b. Although pressure did lead to sensitization of α-RDX, its high-pressure reactivity was still significantly less than that of γ-RDX. Instead, computational analysis showed that the sensitisation of γ-RDX resulted from the conformational changes of the RDX molecule across the phase transition.
When contextualised with the sheer number of examples of mechanically induced structural transformations (see Section 2), our findings therefore show that high pressure studies of EMs (and more broadly of any mechanochemically reacting system) are essential for understanding their reactivity behaviour. Where no structural phase transitions are found, or transitions accompanied by minimal molecular-level change, one can expect a predictable increase in sensitization with pressure. In contrast, unpredictable sensitization results from pressure-induced phase transitions, which can lead to entirely unexpected material behaviour, with the potential for catastrophic consequences.
4. Summary
Mechanochemistry is a rapidly emerging area of chemistry. By initiating or sustaining chemical and physical transformations with mechanical force, chemical processes are becoming more sustainable, whilst providing researchers access to entirely new chemical and material reactivity. However, the mechanisms underpinning mechanochemical transformations are poorly understood, hindering full realisation of its potential.Elucidating the mechanisms of mechanochemical transformations is a great challenge, as we must unravel interconnected processes that span enormous lengths of scale and time. Through this Feature Article we have suggested that solid state mechanochemical transformations can – to a good extent – be classified based on the primary role of mechanical energy in the reaction. Broadly, based on our own work we have discussed three such classifications: (Type 1) where mixing is the dominant role, including the generation of frictional heating; (Type 2) where mechanical energy is key to modifying the stability of the reagents; and (Type 3) where mechanical energy directly excites the system and causes the reaction to occur. Importantly, in devising these classifications we have not considered covalent synthetic mechanochemistry, for which additional considerations will be likely required.
By viewing mechanochemical reactions in this way, we hope to demonstrate that there is no ‘one size fits all’ process to describe all mechanochemical transformations. Instead, viewing mechanochemistry in this way allows us to discuss specific processes that are associated with a given transformation, whilst providing a route to distinguish between transformations wherein some processes may be entirely irrelevant. This said, we emphasise that classifying mechanochemical reactions with such clear boundaries is entirely fictitious. It is highly unlikely that any real mechanochemical transformation will fit squarely within one class or another. As we have demonstrated throughout the text, many mechanochemical reactions in fact occur through a combination of mechanisms associated with different classes of reaction.
As we continue to probe mechanochemical mechanisms from its various angles our view on the mechanisms – and suitable classifications – will certainly evolve. It is our only our aim to begin this discussion. For example, with the rapid progress of time-resolved in situ (TRIS) analytics64,99 new mechanistic details at the scale of bulk powders are being rapidly uncovered, with promise that these methods will soon provide access to more subtle chemical and crystal structural information. Similarly, the computational tools being used to probe mechanochemical reactions at their elementary level have developed enormously in recent years100–102 and are providing increasingly accurate detail for increasingly realistic system sizes. With progress in machine learning and computing infrastructure, it is only a matter of time before atomistic models of ‘real’ bulk mechanochemical reactions become possible.
With the rapidly growing community of mechanochemists, tackling an increasingly diverse number of chemical and materials problems, the importance of understanding how and why these reactions occur is more important than ever before. There is no doubt that research into the complex and diverse processes that underpin them will provide a dynamic and thought-provoking research field far into the future.
Data availability
No primary research results, software or code have been included and no new data were generated or analysed as part of this review.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The author is grateful to Profs CA Morrison, CR Pulham, EV Boldyreva, and F Emmerling for years of stimulating discussion and collaboration across many areas of mechanochemical research, which have led to the results discussed in this work.Notes and references
- M. Carey-Lea, Philos. Mag., 1892, 34, 46 Search PubMed.
- M. Carey-Lea, Philos. Mag., 1894, 37, 470 Search PubMed.
- L. Takacs, J. Mater. Sci., 2018, 53, 13324–13330 CrossRef CAS.
- V. V. Boldyrev, Herald Russ. Acad. Sci., 2018, 88, 142–150 CrossRef.
- A. A. L. Michalchuk, E. V. Boldyreva, A. M. Belenguer, F. Emmerling and V. V. Boldyrev, Front. Chem., 2021, 9, 29 Search PubMed.
- L. Takacs, Bull. Hist. Chem., 2003, 28, 9 Search PubMed.
- L. Takacs, Chem. Soc. Rev., 2013, 42, 7649 RSC.
- B. D. Egleston, M. C. Brand, F. Greenwell, M. E. Briggs, S. L. James, A. I. Cooper, D. E. Crawford and R. L. Greenaway, Chem. Sci., 2020, 11, 6582–6589 RSC.
- O. Maurin, P. Verdié, G. Subra, F. Lamaty, J. Martinez and T.-X. Métro, Beilstein J. Org. Chem., 2017, 13, 2087–2093 CrossRef CAS PubMed.
- O. Galant, G. Cerfeda, A. S. McCalmont, S. L. James, A. Porcheddu, F. Delogu, D. E. Crawford, E. Colacino and S. Spatari, ACS Sustainable Chem. Eng., 2022, 10, 1430–1439 CrossRef CAS.
- K. Suwada, A. W. Ieong, H. L. H. Lo and G. De Bo, J. Am. Chem. Soc., 2023, 145, 20782–20785 CrossRef CAS PubMed.
- F. H. Bhuiyan, Y.-S. Li, S. H. Kim and A. Martini, Sci. Rep., 2024, 14, 2992 CrossRef CAS PubMed.
- M. Senna, Trans. Indian Inst. Met., 2023 DOI:10.1007/s12666-023-03075-0.
- Y. Teoh, G. Ayoub, I. Huskić, H. M. Titi, C. W. Nickels, B. Herrmann and T. Friščić, Angew. Chem., Int. Ed., 2022, 61, e202206293 CrossRef CAS PubMed.
- A. A. L. Michalchuk, Mechanochemistry and Emerging Technologies for Sustainable Chemical Manufacturing, CRC Press, Boca Raton, 1st edn, 2023, pp. 59–92 Search PubMed.
- E. Boldyreva, Chem. Soc. Rev., 2013, 42, 7719 RSC.
- M. A. Mikhailenko, T. P. Shakhtshneider and V. V. Boldyrev, J. Mater. Sci., 2004, 39, 5435–5439 CrossRef CAS.
- A. A. L. Michalchuk, K. S. Hope, S. R. Kennedy, M. V. Blanco, E. V. Boldyreva and C. R. Pulham, Chem. Commun., 2018, 54, 4033–4036 RSC.
- C. B. Lennox, T. H. Borchers, L. Gonnet, C. J. Barrett, S. G. Koenig, K. Nagapudi and T. Friščić, Chem. Sci., 2023, 14, 7475–7481 RSC.
- S. Nagapudi and K. Nagapudi, Phys. Chem. Chem. Phys., 2024, 26, 12545–12551 RSC.
- D. J. am Ende, S. R. Anderson and J. S. Salan, Org. Process Res. Dev., 2014, 18, 331–341 CrossRef CAS.
- A. Guilherme Buzanich, C. T. Cakir, M. Radtke, M. B. Haider, F. Emmerling, P. F. M. de Oliveira and A. A. L. Michalchuk, J. Chem. Phys., 2022, 5, 0130673 Search PubMed.
- H. M. Titi, J.-L. Do, A. J. Howarth, K. Nagapudi and T. Friščić, Chem. Sci., 2020, 11, 7578–7584 RSC.
- L. Gonnet, C. B. Lennox, J. Do, I. Malvestiti, S. G. Koenig, K. Nagapudi and T. Friščić, Angew. Chem., Int. Ed., 2022, 61(13), e202115030 CrossRef CAS PubMed.
- S. R. Anderson, D. J. am Ende, J. S. Salan and P. Samuels, Propellants, Explos., Pyrotech., 2014, 39, 637–640 CrossRef CAS.
- K. S. Hope, H. J. Lloyd, D. Ward, A. A. L. Michalchuk and C. R. Pulham, New Trends in Research of Energetic Materials, University of Pardubice, Pardubice, Czech Republic, 2015 Search PubMed.
- O. V. Lapshin, V. V. Boldyrev and E. V. Boldyreva, Russ. J. Phys. Chem., 2019, 93, 1592–1597 CrossRef CAS.
- A. A. L. Michalchuk, I. A. Tumanov and E. V. Boldyreva, J. Mater. Sci., 2018, 53, 13380–13389 CrossRef CAS PubMed.
- F. P. Bowden, M. A. Stone and G. K. Tudor, Proc. R. Soc. London, Ser. A, 1947, 188, 329–349 CAS.
- F. Delogu, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 205415 CrossRef.
- M. Carta, L. Vugrin, G. Miletić, M. J. Kulcsár, P. C. Ricci, I. Halasz and F. Delogu, Angew. Chem., Int. Ed., 2023, 62, e202308046 CrossRef CAS PubMed.
- G. Rothenberg, A. P. Downie, C. L. Raston and J. L. Scott, J. Am. Chem. Soc., 2001, 123, 8701–8708 CrossRef CAS PubMed.
- P. P. Mazzeo, M. Prencipe, T. Feiler, F. Emmerling and A. Bacchi, Cryst. Growth Des., 2022, 22(7), 4260–4267 CrossRef CAS PubMed.
- M. Prencipe, P. P. Mazzeo and A. Bacchi, RSC Mechanochem., 2024 10.1039/D4MR00080C.
- I. A. Tumanov, A. A. L. Michalchuk, A. A. Politov, E. V. Boldyreva and V. V. Boldyrev, CrystEngComm, 2017, 19, 2830–2835 RSC.
- D. E. Crawford, C. K. G. Miskimmin, A. B. Albadarin, G. Walker and S. L. James, Green Chem., 2017, 19, 1507–1518 RSC.
- R. F. Lonergan, G. A. Conway, P. W. Doheny and H. J. Shepherd, Chem. – Eur. J., 2022, 28, e202201823 CrossRef CAS PubMed.
- D. Zheltikova, E. Losev and E. Boldyreva, CrystEngComm, 2023, 25, 4879–4888 RSC.
- L. Casali, M. Carta, A. A. L. Michalchuk, F. Delogu and F. Emmerling, Phys. Chem. Chem. Phys., 2024, 26, 22041–22048 RSC.
- M. Carta, S. Lukin, F. Delogu and I. Halasz, Phys. Chem. Chem. Phys., 2024, 26, 16438–16443 RSC.
- E. V. Boldyreva, H. Sowa, Yu. V. Seryotkin, T. N. Drebushchak, H. Ahsbahs, V. Chernyshev and V. Dmitriev, Chem. Phys. Lett., 2006, 429, 474–478 CrossRef CAS.
- J. Ribas-Arino and D. Marx, Chem. Rev., 2012, 112, 5412–5487 CrossRef CAS PubMed.
- X.-D. Wen, R. Hoffmann and N. W. Ashcroft, J. Am. Chem. Soc., 2011, 133, 9023–9035 CrossRef CAS PubMed.
- A. A. Politov, A. P. Chupakhin, V. M. Tapilin, N. N. Bulgakov and A. G. Druganov, J. Str. Chem., 2010, 51, 1064–1069 CrossRef CAS.
- H. Yan, F. Yang, D. Pan, Y. Lin, J. N. Hohman, D. Solis-Ibarra, F. H. Li, J. E. P. Dahl, R. M. K. Carlson, B. A. Tkachenko, A. A. Fokin, P. R. Schreiner, G. Galli, W. L. Mao, Z.-X. Shen and N. A. Melosh, Nature, 2018, 554, 505–510 CrossRef CAS PubMed.
- V. V. Boldyrev, Russ. Chem. Rev., 2006, 75, 177–189 CrossRef CAS.
- A. Yu Dolgoborodov, A. N. Streletskii, A. A. Shevchenko, G. A. Vorobieva and G. E. Val’yano, Thermochim. Acta, 2018, 669, 60–65 CrossRef CAS.
- M. Rossberg, E. F. Khairetdinov, E. Linke and V. V. Boldyrev, J. Solid State Chem., 1982, 41, 266–271 CrossRef CAS.
- M. Horst, J. Meisner, J. Yang, T. B. Kouznetsova, S. L. Craig, T. J. Martínez and Y. Xia, J. Am. Chem. Soc., 2024, 146(1), 884–891 CrossRef CAS PubMed.
- Y. Liu, S. Holm, J. Meisner, Y. Jia, Q. Wu, T. J. Woods, T. J. Martinez and J. S. Moore, Science, 2021, 373, 208–212 CrossRef CAS PubMed.
- X. Liu, A. A. L. Michalchuk, B. Bhattacharya, F. Emmerling and C. R. Pulham, Nat. Commun., 2021, 12, 3871 CrossRef CAS PubMed.
- X.-D. Wen, L. Hand, V. Labet, T. Yang, R. Hoffmann, N. W. Ashcroft, A. R. Oganov and A. O. Lyakhov, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 6833–6837 CrossRef CAS.
- V. Labet, R. Hoffmann and N. W. Ashcroft, New J. Chem., 2011, 35, 2349 RSC.
- T. N. Drebushchak, A. A. Ogienko and E. V. Boldyreva, CrystEngComm, 2011, 13, 4405 RSC.
- L. L. Driscoll, E. H. Driscoll, B. Dong, F. N. Sayed, J. N. Wilson, C. A. O’Keefe, D. J. Gardner, C. P. Grey, P. K. Allan, A. A. L. Michalchuk and P. R. Slater, Energy Environ. Sci., 2023, 16, 5196–5209 RSC.
- E. Ahmed, D. P. Karothu, L. Pejov, P. Commins, Q. Hu and P. Naumov, J. Am. Chem. Soc., 2020, 142, 11219–11231 CrossRef CAS PubMed.
- R. Hüttenrauch, S. Fricke and P. Zielke, Pharm. Res., 1985, 02, 302–306 CrossRef PubMed.
- R. Singla, T. C. Alex and R. Kumar, Powder Technol., 2020, 360, 337–351 CrossRef CAS.
- B. Bhattacharya, A. A. L. Michalchuk, D. Silbernagl, N. Yasuda, T. Feiler, H. Sturm and F. Emmerling, Chem. Sci., 2023, 14, 3441–3450 RSC.
- T. Feiler, N. Yasuda, A. A. L. Michalchuk, F. Emmerling and B. Bhattacharya, Cryst. Growth Des., 2023, 23, 6244–6249 CrossRef CAS.
- B. Bhattacharya, A. A. L. Michalchuk, D. Silbernagl, M. Rautenberg, T. Schmid, T. Feiler, K. Reimann, A. Ghalgaoui, H. Sturm, B. Paulus and F. Emmerling, Angew. Chem., Int. Ed., 2020, 59, 5557–5561 CrossRef CAS PubMed.
- R. Samanta, S. Das, S. Mondal, T. Alkhidir, S. Mohamed, S. P. Senanayak and C. M. Reddy, Chem. Sci., 2023, 14, 1363–1371 RSC.
- A. M. Belenguer, A. A. L. Michalchuk, G. I. Lampronti and J. K. M. Sanders, Beilstein J. Org. Chem., 2019, 15, 1226–1235 CrossRef CAS PubMed.
- A. A. L. Michalchuk and F. Emmerling, Angew. Chem., Int. Ed., 2022, 61(21), e202117270 CrossRef CAS PubMed.
- T. Friščić, I. Halasz, P. J. Beldon, A. M. Belenguer, F. Adams, S. A. J. Kimber, V. Honkimäki and R. E. Dinnebier, Nat. Chem., 2013, 5, 66–73 CrossRef PubMed.
- G. I. Lampronti, A. A. L. Michalchuk, P. P. Mazzeo, A. M. Belenguer, J. K. M. Sanders, A. Bacchi and F. Emmerling, Nat. Commun., 2021, 12, 6134 CrossRef CAS PubMed.
- K. Linberg, F. Emmerling and A. A. L. Michalchuk, Cryst. Growth Des., 2023, 23, 19–23 CrossRef CAS.
- K. Linberg, B. Röder, D. Al-Sabbagh, F. Emmerling and A. A. L. Michalchuk, Faraday Discuss., 2023, 241, 178–193 RSC.
- K. Linberg, P. C. Sander, F. Emmerling and A. A. L. Michalchuk, RSC Mechanochem., 2024, 1, 43–49 RSC.
- V. V. Boldyrev, S. V. Pavlov and E. L. Goldberg, Int. J. Miner. Process., 1996, 44, 181–185 CrossRef.
- K. Linberg, P. Szymoniak, A. Schönhals, F. Emmerling and A. A. L. Michalchuk, Chem. – Eur. J., 2023, e202302150 CrossRef CAS PubMed.
- K. Tkáčová, H. Heegn and N. Števulová, Int. J. Miner. Process., 1993, 40, 17–31 CrossRef.
- S. Lukin, M. Tireli, I. Lončarić, D. Barišić, P. Šket, D. Vrsaljko, M. di Michiel, J. Plavec, K. Užarević and I. Halasz, Chem. Commun., 2018, 54, 13216–13219 RSC.
- J. M. Andersen and J. Mack, Chem. Sci., 2017, 8, 5447–5453 RSC.
- B. P. Johnson, X. Zhou, H. Ihara and D. D. Dlott, J. Phys. Chem. A, 2020, 124, 4646–4653 CrossRef CAS PubMed.
- S. Chen, W. A. Tolbert and D. D. Dlott, J. Phys. Chem., 1994, 98, 7759–7766 CrossRef CAS.
- A. A. L. Michalchuk, P. T. Fincham, P. Portius, C. R. Pulham and C. A. Morrison, J. Phys. Chem. C, 2018, 122, 19395–19408 CrossRef CAS.
- A. A. L. Michalchuk, S. Rudić, C. R. Pulham and C. A. Morrison, Phys. Chem. Chem. Phys., 2018, 20, 29061–29069 RSC.
- J. J. Gilman, Science, 1996, 274, 65 CrossRef CAS.
- J. J. Gilman, Philos. Mag. B, 1993, 67, 207–214 CAS.
- A. A. L. Michalchuk, M. Trestman, S. Rudić, P. Portius, P. T. Fincham, C. R. Pulham and C. A. Morrison, J. Mater. Chem. A, 2019, 7, 19539–19553 RSC.
- A. A. L. Michalchuk, J. Hemingway and C. A. Morrison, J. Chem. Phys., 2021, 154, 064105 CrossRef CAS PubMed.
- D. D. Dlott and M. D. Fayer, J. Chem. Phys., 1990, 92, 3798–3812 CrossRef CAS.
- J. R. Hill, E. L. Chronister, T. Chang, H. Kim, J. C. Postlewaite and D. D. Dlott, J. Chem. Phys., 1988, 88, 949–967 CrossRef CAS.
- A. A. L. Michalchuk, Faraday Discuss., 2023, 241, 230–249 RSC.
- B. W. Hamilton, M. N. Sakano, C. Li and A. Strachan, Annu. Rev. Mater. Res., 2021, 51, 101–130 CrossRef CAS.
- X. Bidault and S. Chaudhuri, RSC Adv., 2022, 12, 31282–31292 RSC.
- J. Bernstein, J. Chem. Phys., 2018, 148, 084502 CrossRef PubMed.
- B. Asay, B. Henson, L. Smilowitz and P. M. Dickson, J. Energ. Mater., 2003, 21, 223–235 CrossRef CAS.
- C. Zhang, F. Jiao and H. Li, Cryst. Growth Des., 2018, 18, 5713–5726 CrossRef CAS.
- A. A. L. Michalchuk, S. Rudić, C. R. Pulham and C. A. Morrison, Chem. Commun., 2021, 57, 11213–11216 RSC.
- J. Evers, T. M. Klapötke, P. Mayer, G. Oehlinger and J. Welch, Inorg. Chem., 2006, 45, 4996–5007 CrossRef CAS PubMed.
- M.-J. Crawford, J. Evers, M. Göbel, T. M. Klapötke, P. Mayer, G. Oehlinger and J. M. Welch, Propellants, Explos., Pyrotech., 2007, 32, 478–495 CrossRef CAS.
- S. R. Kennedy and C. R. Pulham, in Monographs in Supramolecular Chemistry, ed. C. B. Aakeröy and A. S. Sinha, Royal Society of Chemistry, Cambridge, 2018, pp. 231–266 Search PubMed.
- I. L. Christopher, X. Liu, H. J. Lloyd, C. L. Bull, N. P. Funnell, P. Portius, A. A. L. Michalchuk, S. R. Kennedy, C. R. Pulham and C. A. Morrison, Phys. Chem. Chem. Phys., 2024, 26, 16859–16870 RSC.
- N. Atceken, J. Hemingway, C. L. Bull, X. Liu, A. A. L. Michalchuk, S. Konar, C. A. Morrison and C. R. Pulham, Phys. Chem. Chem. Phys., 2023, 25, 31646–31654 RSC.
- I. L. Christopher, C. R. Pulham, A. A. L. Michalchuk and C. A. Morrison, J. Chem. Phys., 2023, 158, 124115 CrossRef CAS PubMed.
- J. E. Patterson, Z. A. Dreger and Y. M. Gupta, J. Phys. Chem. B, 2007, 111, 10897–10904 CrossRef CAS PubMed.
- S. Lukin, L. S. Germann, T. Friščić and I. Halasz, Acc. Chem. Res., 2022, 55, 1262–1277 CrossRef CAS PubMed.
- N. Hopper, F. Sidoroff, J. Cayer-Barrioz, D. Mazuyer, B. Chen and W. T. Tysoe, RSC Mechanochem., 2024, 1, 402–412 RSC.
- Y. S. Zholdassov, L. Yuan, S. R. Garcia, R. W. Kwok, A. Boscoboinik, D. J. Valles, M. Marianski, A. Martini, R. W. Carpick and A. B. Braunschweig, Science, 2023, 380, 1053–1058 CrossRef CAS PubMed.
- H. Adams, B. P. Miller, O. J. Furlong, M. Fantauzzi, G. Navarra, A. Rossi, Y. Xu, P. V. Kotvis and W. T. Tysoe, ACS Appl. Mater. Interfaces, 2017, 9, 26531–26538 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2024 |