DOI:
10.1039/D3CP04794F
(Communication)
Phys. Chem. Chem. Phys., 2024,
26, 3795-3799
Classically forbidden nonadiabatic transitions in multidimensional chemical dynamics
Received
3rd October 2023
, Accepted 6th January 2024
First published on 10th January 2024
Abstract
An accurate method is proposed to deal with such nonadiabatic transitions as those energetically inaccessible, namely, classically forbidden transitions. This is formulated by using the corresponding Zhu–Nakamura formulas and finding the optimal paths in the classically forbidden tunneling regions that maximize the overall transition probabilities. This can be done for both the nonadiabatic tunneling type (so-called normal case in electron transfer) in which two diabatic potentials have opposite signs of slopes and the Landau–Zener type (inverted case) in which two diabatic potentials have the same sign of slopes. The method is numerically demonstrated to be useful for clarifying chemical and biological dynamics.
I. Introduction
Nonadiabatic transition presents a very basic mechanism of state and phase change in various branches of science.1,2 As is well known, in the case of chemical and biological dynamics, for instance, this transition is ubiquitous and occurs through the conical intersection of adiabatic potential energy surfaces.1–3 In the one-dimensional picture, there are two types of transitions; nonadiabatic tunneling (NT) type and Landau–Zener (LZ) type, which correspond to the normal and inverted cases in the electron transfer problems as Marcus named.4
For these two types of transitions, the analytical Zhu–Nakamura formulas are available for the whole energy region and the whole electronic coupling strength.1,2,5 Although the Zhu–Nakamura theory has been formulated for one-dimensional problems, the formulas are actually applicable to multidimensional dynamics, since the nonadiabatic transition occurs predominantly along the direction of nonadiabatic coupling vector. Multidimensional potential energy surfaces are cut along this direction and the formulas are employed along these one-dimensional potential curves. Practical applications have been made successfully to real chemical and biological systems, not only to triatomic reaction systems but also to reactions in the environment.1,2,6–8 The electron transfer processes can also be treated for the whole range of electronic coupling strengths.9–12 In such a way, a semiclassical molecular dynamics simulation method can be developed with quantum mechanical effects taken into account.13 The quantum mechanical effects meant here are nonadiabatic transition, quantum mechanical tunneling, and phases associated with these transitions.
The above mentioned reduction to the one-dimensional system is a good approximation in the case that the corresponding nonadiabatic transition, i.e., conical intersection position, is located in the energetically accessible, namely, classically allowed region. It naturally becomes less accurate in the case of classically forbidden transitions, since the quantum mechanical tunneling in the multidimensional space occurs simultaneously. What is the best way to use the Zhu–Nakamura formulas in this case? This is the main theme of this paper. Our basic strategy is as follows: (1) run a classical trajectory. (2) When a caustic is detected, draw a straight line tunneling path (blue line in Fig. 1) from the caustic and calculate the nonadiabatic transition probability. (3) Optimize the tunneling path (the purple line) to achieve the maximum transition probability. (4) Run the classical trajectory to find the next caustic. Owing to the localizability of nonadiabatic transitions in the adiabatic state representation, the dynamics along a tunneling path can be decomposed into localized nonadiabatic transition and adiabatic tunneling processes, the former of which can be treated nicely with Zhu–Nakamura formulas, and the latter is treated by calculating the tunneling action. The methods of finding caustics and calculating tunneling action were proposed by us in ref. 13 for multi-dimensional pure tunneling. In this paper, we combine the two theories of nonadiabatic transition and multi-dimensional tunneling to develop a new theory for multi-dimensional classically forbidden nonadiabatic transitions.
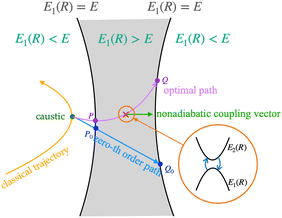 |
| | Fig. 1 Schematic view of the zero-th order and the optimal nonadiabatic tunneling path. | |
This paper is organized as follows: Section II presents the main formulation of this paper, namely, it describes how to treat the classically forbidden transitions in multidimensional space. In Section III, the method presented in Section II is numerically demonstrated to work well by using a two-dimensional model system. Our conclusions and future perspectives are given in Section IV.
II. Method
A. Basic idea
Let us consider a general system composed of n atoms with masses mk(k = 1 ∼ n). First, the mass-scaled relative internal coordinates and momenta {qj,pj}(j = 1 ∼ 3n − 3) are introduced. Then the Hamiltonian is given by| | 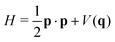 | (1) |
In the Zhu–Nakamura trajectory surface hopping (ZN-TSH) method the following two approximations are employed:1,2 (i) the minimum energy separation between two relevant adiabatic potential energy surfaces Ej(q)(j = 1,2) is detected along each classical trajectory, which is used as the transition point, and (ii) the nonadiabatic coupling vector is evaluated there, along which direction the potential energy surfaces are cut to define two potential energy curves that are used to calculate the transition probability. This method has been proven to work well.1,2,7,8 In the case of classically forbidden transitions, however, this method becomes naturally less accurate, since the quantum mechanical tunneling in a multidimensional space is involved and the straight line path does not necessarily provide the optimal path. First, we have to detect caustics along each classical trajectory, since the caustics define the boundary between classically allowed and forbidden regions. It is also easily conjectured that the optimal tunneling path in the classically forbidden region is not just a straight line.
In Zhu–Nakamura theory, there are two basic parameters, σZN and δZN, which represent the effects of nonadiabatic transition and the tunneling, respectively, can be evaluated separately.1,2 This scheme of separate evaluation of σZN and δZN is guaranteed by the fact that the nonadiabatic transition is localized in the vicinity of the avoided crossing point. The parameter σZN can be estimated locally at the minimum energy separation position and the parameter δZN can be given by the action integral along the tunneling path. This theory has been demonstrated to work well in the various one-dimensional potential systems.1,2 Thus what we have to do is to determine the optimal tunneling path in multi-dimensional space that maximizes the overall transition probability. This can be done by using a method similar to the one that we have proposed before to treat multidimensional tunneling (see ref. 13–16). Besides, the Zhu–Nakamura theory provides the explicit analytical expressions of the overall transition probabilities PZN for both NT and LZ types. The main objective of this paper is to propose an accurate method usable in multi-dimensional nonadiabatic chemical dynamics.
The detection of caustics is made by propagating the matrix
| | 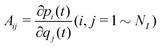 | (2) |
along the classical trajectory, where
pi(
qj) is the
i-th (
j-th) component of the momentum vector
p(
q) in the
NI-dimensional space. At the caustics the maximum absolute value of the eigenvalues of this matrix diverges,
| | | Maxj|Diag(A)jj| = ∞ or Minj|Diag(B)jj| = 0, | (3) |
where Diag(
X) means the diagonalized matrix of
X and
B =
A−1.
Depending on the types of the nonadiabatic transition, we have different ways of representing the tunneling path, basically because the trajectory runs on the same adiabatic potential surface in the NT type, while the LZ type induces a jump from one potential surface to another. This indicates that it is necessary to have a priori knowledge about the potential topography, i.e., NT type or LZ type, before starting the dynamics calculation. Hereafter, our treatments for the two types are explained, respectively.
B. In the case of NT-type
Starting from the caustic, the tunneling path runs through the potential barrier of the adiabatic potential E1(q). It is noted that the overall tunneling is affected by the nonadiabatic coupling as explained below. In order to determine the optimal tunneling path, we can employ basically the same method used in ref. 13. The optimal path is determined variationally by maximizing the probability PZN given by the Zhu–Nakamura theory (see, for instance, eqn (8.119) of ref. 2). As the zero-th order approximation to start with, two straight lines, one in the steepest ascent direction and the other in the direction of the nonadiabatic coupling vector at the caustic (C) are employed. Then the one providing the larger probability is selected to start with. This enables the computation time for optimization to be reduced, but it is possible to start with any linear path in principle.
The tunnel action in the m-th order approximation is expressed as
where
P(
Q) is the crossing point of the path with the equipotential surface at the entrance to (exit from) the tunneling region (see
ref. 13). The tunneling path {
q(m)j} is expressed geometrically as a function of parameter
z ∈ (0,1) as
| | 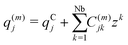 | (5) |
where
qCj represents the coordinate at the caustic C,
Nb is a certain number to guarantee the convergence, the parameter
z runs from
z = 0 at C to
z = 1 at
Q, and
C(m)jk are the expansion coefficients to be determined.
The procedure to determine the optimal path is summarized as follows:
(1) When the trajectory enters the reaction zone, the first caustic is detected and the straight line is drawn from there. This straight line is extended and the crossing point P0 with the equipotential surface, i.e. the entrance to the tunneling region, should be detected. The zero-th order action integral along this line is denoted as
| | 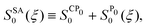 | (6) |
where
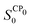
is the action from
C(
ξ = 0) to
P0(
ξ =
P0). The action
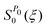
from the point
P0 is evaluated step by step up to
ξ. When the total action
SSA0 becomes bigger than a certain criterion,
then the tunneling there is not carried out and the trajectory is further propagated. If the straight line reaches the equipotential surface in the exit channel at
ξ =
ξQ0 and the total action is smaller than the above criterion, then the determination of the optimal tunneling path is carried out.
On this straight line, the minimum adiabatic energy difference position R0(z = z0) is detected and the normalized nonadiabatic coupling vector enad is evaluated there. Along the direction of this vector two adiabatic potentials are calculated and the basic parameter σZN is evaluated. The negative kinetic energy Ktr in this direction is given by
| | | K(m=0)tr = Eeff − E1(q) | (8) |
with
| |  | (9) |
where
E is the total energy,
ej is the
j-th component of the coupling vector
enad, and
Eeff represents the effective total energy along the transition direction. This is employed to evaluate the parameter
b2. The overall Zhu–Nakamura transition probability
P(0)ZN is calculated, where
δZN =
S(0) ≡
SSA0(
ξQ0). The parameter
σZN originally defined by the complex phase integral up to the complex crossing point from the real axis is given by the simple analytical expression by using the linear potential model (see
ref. 1 and 2). If this probability is smaller than a certain critical value, say
ε,
then the search of the optimal path is stopped and the classical trajectory is further propagated to detect the next caustic. If
P(0)ZN is larger than
ε, then we proceed to find the optimal path.
(2) The tunneling path {q(m)j} in the m-th order approximation is obtained by slightly modifying the coefficients C(m−1)jk in the (m − 1)th order approximation in the direction of increasing P(m−1)ZN. The pure imaginary actions SCPm and SPQm are calculated separately: SCPm is the action along the steepest ascent direction and SPQm is the action along the tunneling path from P to Q. Then δZN is given by Sm(=SCPm + SPQm). The minimum energy separation position R0(z = z0) is detected along the path and the parameter σZN is evaluated as mentioned above, where the negative kinetic energy K(m)tr at R0 is calculated by eqn (8).
(3) The above procedure to find the optimal path is repeated until the required convergence of the probability P(m)ZN is attained. Then the overall nonadiabatic tunneling probability is determined in the same way as that in ref. 13 by
| |  | (11) |
where
i designates the
i-th caustic in the reaction zone (see eqn (122) of
ref. 13).
(4) After a sufficient number of trajectories is run, the final reaction probability preact is calculated by taking the average of the probabilities over the total number of trajectories satisfying a given quantum mechanical initial condition.
C. In the case of LZ type
The situation in this case is a bit more complicated than in the case of NT type, since the tunneling path jumps from E1(q) to E2(q) at R0, giving rise to the non-smoothness of the tunneling path at the crossing point. In the semiclassical Zhu–Nakamura theory, the transition is assumed to occur locally at the avoided crossing point and thus the tunneling processes before and after the transition can be treated separately. This means that the second portion of the whole tunneling path, namely the path from R0 to Q, can be determined separately from the first one in each iteration process. Such a separated treatment for before and after the crossing point makes it possible to represent the non-smooth path, which climbs (descends) the potential E1(q) (E2(q)) before (after) passing the crossing point. This treatment for the LZ type relies on the localizability of nonadiabatic transition the same as the NT type. Owing to the usefullness of the Zhu–Nakamura formulas both for the NT and the LZ types, we expect that our method for the LZ type should work as well as the NT type.
In the zero-th order approximation, the straight line from the caustic C(z1 = 0) on E1(q) is extended to R0(z1 = 1) and the second one is a straight line in the steepest descent direction from R0(z2 = 0) on E2(q) to the exit Q0(z2 = 1). In the higher order approximations, the second path from R0 to the exit Q is determined so that the total transition probability PZN is maximized. The first path from C to R0 gives the action,
| |  | (12) |
and the second path from
R0 to
Q provides the action,
| | 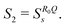 | (13) |
The basic parameters
σZN and
δZN are given by (see
ref. 1 and 2)
| | | σZN = σZN0 and δZN = −S1 + S2 + δZN0, | (14) |
where
| |  | (15) |
where
R* is the complex crossing point and
| |  | (16) |
The overall transition probability
PZN is given in the analytical form in terms of
σZN and
δZN (see, for instance, eqn (8.90) of
ref. 2).
III. Numerical demonstration
As mentioned above, the nonadiabatic transition and the multi-dimensional tunneling can be treated separately once the tunneling path is given. The nonadiabatic transitions are well localized in the vicinity of avoided crossing points and the Zhu–Nakamura theory has been demonstrated to work well even for the energetically inaccessible transitions in one-dimensional systems.1,2,5 The method to determine the optimal tunneling path in the multi-dimensional space, on the other hand, has been well tested to work well.13–16 Thus, the method proposed here is supposed to be accurate. In this section it is numerically demonstrated that the Zhu–Nakamura formulas of PZN in the linear approximation can be very much improved by using the present method with the use of the same analytical expressions of PZN. In the linear approximation, the tunneling path is assumed to be linear along the direction of the nonadiabatic coupling vector at the caustic.
Here, the NT-type two-dimensional model reaction system A + BC → AB + C proposed in ref. 17 is used.‡ The adiabatic potentials E1(r,R) and E2(r,R) are given as follows:
| |  | (17) |
| | 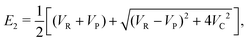 | (18) |
with
| |  | (19) |
| | 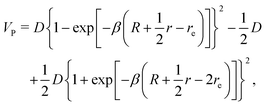 | (20) |
| | VC = A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp{−γ[(r − rC)2+ (R − RC)2]} exp{−γ[(r − rC)2+ (R − RC)2]} | (21) |
where
r and
R are the distance between B and C and the distance of A from the center of mass of BC, respectively. The various parameters are
D = 4.9 eV,
β = 1.877 Å,
re = 0.7417 Å,
rC = 1.5707
re,
RC = 1.5
rC,
A = 0.3 eV, and
γ = 1.0 Å
−2, which are the same as
ref. 17 except
A. The coupling strength
A is taken to be smaller than the original one in order to emphasize the difference between the pure and nonadiabatic tunneling. The smaller the parameter
A, the larger the difference, naturally.
Fig. 2 shows the numerical result of tunneling probability against total energy. It is clearly seen that the present optimized nonadiabatic tunneling probability improves the one in the linear approximation. The difference is emphasized naturally in the low energy region.
 |
| | Fig. 2 Nonadiabatic tunneling probability against energy. PT: optimized pure tunneling through E1(r,R), NT: optimized nonadiabatic tunneling, NTSL: nonadiabatic tunneling along a straight line. The saddle point energy of the lower adiabatic potential is Esp = 2.275 eV. | |
IV. Concluding remarks
A method has been proposed to treat energetically inaccessible, namely, classically forbidden, nonadiabatic transitions in multi-dimensional space for both NT and LZ types of transitions. Since the nonadiabatic transition itself is localized, it can be treated by the Zhu–Nakamura formulas along the direction of the nonadiabatic coupling vector at the minimum energy separation position in the tunneling region.1,2 The multi-dimensionality effect, on the other hand, comes from the tunneling, namely, the optimal tunneling path is not a straight line in general. Determination of the optimal tunneling path can be achieved by the method proposed by the authors.13 The caustics are detected along a classical trajectory and the optimal path up to and from the nonadiabatic transition position can be determined geometrically. The simple linear approximation in which the tunneling path is assumed to be linear from the caustic can be very much improved by using the present method. The method proposed in this paper properly takes into account the effect of multi-dimensionality and is expected to be usefully utilized to clarify the classically forbidden nonadiabatic chemical dynamics. For instance, the spin crossover of thiophosgene is a good example.18,19 The detailed description of the method together with applications to real reaction systems will be reported in a full paper.
Conflicts of interest
The authors declare no competing financial interest.
Acknowledgements
I-Y. H. and Y. T. would like to express their sincere thanks for the support by the National Yang Ming Chiao Tung University. This work is partially supported by the National Science and Technology Council in Taiwan, Grant No. 109-2113-M-009-020.
References
-
H. Nakamura, Nonadiabatic Transition: Concepts, Basic Theories And Applications, World Scientific, 2nd edn, 2012, and references therein Search PubMed.
-
H. Nakamura, Introduction To Nonadiabatic Dynamics, World Scientific, 2019, and references therein Search PubMed.
-
Conical intersections: theory, computation and experiment, ed. W. Domcke, D. R. Yarkony and H. Koppel, World Scientific, 2011 Search PubMed.
- see for instance, R. A. Marcus and N. Sutin, Electron transfers in chemistry and biology, Biochim. Biophys. Acta, Rev. Bioenerg., 1985, 811(3), 265–322 CrossRef CAS; A. V. Barzykin,
et al., Solvent Effects in Nonadiabatic Electron-Transfer Reactions: Theoretical Aspects, Adv. Chem. Phys., 2002, 123, 511–616 CrossRef; J. Jortner, From Energetic Control to Thermally Induced Hopping, Chem. Phys., 1999, 106, 35 Search PubMed.
- C. Zhu, Y. Teranishi and H. Nakamura, Nonadiabatic transitions due to curve crossings: Complete Solutions of the LandauZener-Stueckelberg problems and their applications, Adv. Chem. Phys., 2001, 127–233 CrossRef CAS.
- H. Nakamura, Nonadiabatic Chemical Dynamics: Comprehension and control of dynamics, and manifestation of molecular functions, Adv. Chem. Phys., 2008, 95–212 CrossRef CAS.
- S. Nanbu, T. Ishida and H. Nakamura, Future perspectives of Nonadiabatic Chemical Dynamics, Chem. Sci., 2010, 1(6), 663 RSC.
- T. Ishida, S. Nanbu and H. Nakamura, Clarification of nonadiabatic chemical dynamics by the Zhu-Nakamura Theory of nonadiabatic transition: From tri-atomic systems to reactions in solutions, Int. Rev. Phys. Chem., 2017, 36(2), 229–285 Search PubMed.
- Y. Zhao, W. Z. Liang and H. Nakamura, Semiclassical treatment of thermally activated electron transfer in the intermediate to strong electronic coupling regime under the fast dielectric relaxation, J. Phys. Chem. A, 2006, 110(26), 8204–8212 CrossRef CAS PubMed.
- Y. Zhao, M. Han, W. Liang and H. Nakamura, Semiclassical treatment of thermally activated electron transfer in the inverted region under the fast dielectric relaxation, J. Phys. Chem. A, 2007, 111(11), 2047–2053 CrossRef CAS PubMed.
- Y. Zhao and H. Nakamura, Electron transfer rate uniformly valid from nonadiabatic to adiabatic regime based on the zhu–nakamura theory, J. Theor. Comput. Chem., 2006, 05(spec01), 299–306 CrossRef CAS.
- Y. Zhao, X. Li, Z. Zheng and W. Liang, Semiclassical calculation of nonadiabatic thermal rate constants: Application to condensed phase reactions, J. Chem. Phys., 2006, 124(11), 114508 CrossRef.
- H. Nakamura, S. Nanbu, Y. Teranishi and A. Ohta, Development of semiclassical molecular dynamics simulation method, Phys. Chem. Chem. Phys., 2016, 18(17), 11972–11985 RSC.
- P. Oloyede, G. Mil’nikov and H. Nakamura, On the determination of Caustics, J. Theor. Comput. Chem., 2004, 03(01), 91–102 CrossRef CAS.
-
H. Nakamura and G. Mil’nikov, Quantum Mechanical Tunneling in Chemical Physics, CRC Press, 2013 Search PubMed.
- G. V. Mil’nikov and H. Nakamura, Practical implementation of the instanton theory. II. decay of metastable state through tunneling, J. Chem. Phys., 2002, 117(22), 10081–10087 CrossRef; G. Mil’nikov and H. Nakamura, Tunneling splitting and decay of metastable states in polyatomic molecules: Invariant instanton theory, Phys. Chem. Chem. Phys., 2008, 10(10), 1374 RSC.
- C. Shin and S. Shin, Reactive scattering on multiple electronic surfaces: Collinear A + BC → AB + C reaction, J. Chem. Phys., 2000, 113(16), 6528–6535 CrossRef CAS.
- A. O. Lykhin and S. A. Varganov, Intersystem crossing in tunneling regime: T1 → S0 relaxation in thiophosgene, Phys. Chem. Chem. Phys., 2020, 22(10), 5500–5508 RSC.
- E. R. Heller and J. O. Richardson, Spin crossover of thiophosgene via multidimensional heavy-atom quantum tunneling, J. Am. Chem. Soc., 2021, 143(49), 20952–20961 CrossRef CAS PubMed.
Footnotes |
| † Present address: Nakamura Institute of Chemical Dynamics, 3-10-20 Tatsumi Higashi, Okazaki, Japan. |
| ‡ The potential functions given in ref. 17 do not agree with the potential contours depicted there. Instead, the contours seem to be consistent with the potentials used here. However, the tunneling probabilities given in ref. 17 cannot be reproduced by these potentials. |
|
| This journal is © the Owner Societies 2024 |
Click here to see how this site uses Cookies. View our privacy policy here.  a,
Yoshiaki
Teranishi
*a and
Hiroki
Nakamura†
b
a,
Yoshiaki
Teranishi
*a and
Hiroki
Nakamura†
b
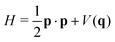
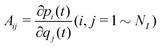
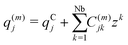
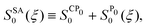
 is the action from C(ξ = 0) to P0(ξ = P0). The action
is the action from C(ξ = 0) to P0(ξ = P0). The action  from the point P0 is evaluated step by step up to ξ. When the total action SSA0 becomes bigger than a certain criterion,
from the point P0 is evaluated step by step up to ξ. When the total action SSA0 becomes bigger than a certain criterion,


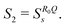



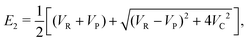

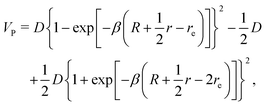
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp{−γ[(r − rC)2+ (R − RC)2]}
exp{−γ[(r − rC)2+ (R − RC)2]}

