Accurate state energetics in spin-crossover systems using pure density functional theory

Abstract

The energy difference between different spin states of systems with transition metals is an outstanding challenge for electronic structure calculation methods. The small energy difference between high- and low-spin states in spin-crossover systems makes most post-Hartree–Fock or density functional theory-based methods provide inaccurate values. A test case of twenty systems showing spin transitions has been used to evaluate the accuracy of a new family of training meta-GGA (Generalized Gradient Approximation) functionals. One of the functionals of this new family provides comparable or even better values than the best functional reported so far for this type of system, the TPSSh hybrid meta-GGA functional, but without having to use the exact exchange term. It also improves the results obtained with the r²SCAN meta-GGA functional, which was the best alternative to the TPSSh hybrid functional. This makes it possible to calculate the spin energetics of any kind of compound, especially large systems or periodic structures where the exact exchange requires large computational resources.

---

1. Introduction

One of the challenges that still exist in computational chemistry at the level of energy calculations is a correct description of the relative energies of the different spin states of metal complexes.^1,2 Within this field, systems with spin transitions are particularly difficult to obtain accurate results for.^3–7 The fundamental spin state at low temperature in spin-crossover compounds is low spin, and with increasing temperature, the spin transition occurs, due to entropic contributions favouring it. These enthalpic contributions can only compensate for an energy approximately below 10 kcal mol⁻¹.^2,5 It means that the energy difference between the low- and high-spin states must be under this relatively small value. This makes spin-crossover systems probably the most demanding test for assessing the accuracy of spin energetics calculations.

From the outset, one would expect that standard ab initio methods such as complete active space self-consistent field (CASSCF) methods with the addition of dynamical correlation (CASPT2 or NEVPT2) or coupled cluster should provide good results in calculating the energy difference between the low and high spin states.^8,9 However, these post-Hartree–Fock methods have one problem, which is the strong overestimation of the stability of the high-spin state provided by the Hartree–Fock method. Only the inclusion of additional terms (3s3p metal correlation effects)^8,9 provides reasonable results for some Fe^II model complexes, similar to those obtained with the (multiconfiguration pair-density functional theory) MCpDFT approach.^10,11 Hence, conventional post-Hartree–Fock methods, for instance CASSCF approaches, produce considerable overestimation of the high-spin state stability, typically finding high-spin energies on the order of 10–30 kcal mol⁻¹ more stable than the low-spin state. In addition to the problem of estimating the energy difference of the states,¹² it is worth mentioning that spin-crossover systems exhibit this spin transition when measured in the solid state.¹³ Thus, it would be preferable to use methods with periodic boundary conditions (PBCs) for extended system calculations.^14–16 In addition, an important challenge is to calculate the temperature at which the spin transition occurs. At that temperature, the free energies of the low- and high-spin states are equal by compensation with the entropic contribution. Therefore, it will be necessary to calculate the energies associated with the vibrations. Obviously, in this case, the ideal situation would be to combine the calculations of periodic systems and the phonons associated with the low- and high-spin states of such compounds.¹⁵ This makes methods based on density functional theory (DFT) probably the best alternative for a complete study of these complex periodic systems. Calculations of periodic systems and vibrations (phonons) are in most cases not implemented in post Hartree–Fock methods. In the case of the few available implementations, typically at the coupled cluster level, or the GW¹⁷ and Random-Phase Approximations (RPA)^18,19 methods with PBC, these approaches are limited to computing relatively simple systems.^20,21

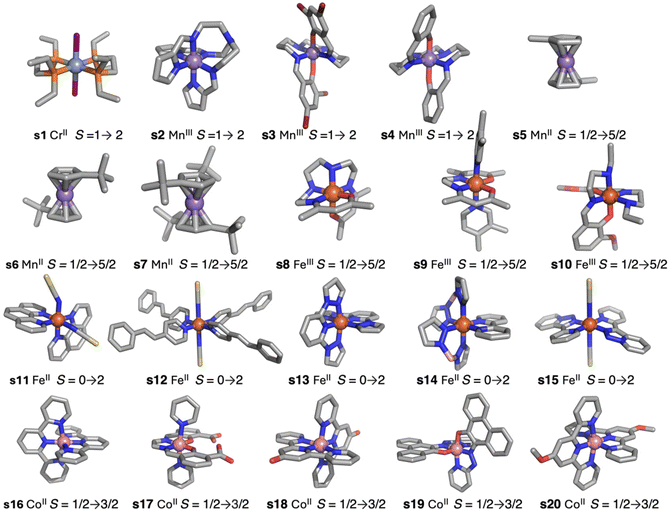
The simplest DFT functionals such as local approximations or generalized gradient approximation (GGA) provide results with an overestimation of the stability of low-spin states.⁵ Logically, taking into account the opposite situation provided by the Hartree–Fock method, as mentioned above, hybrid functionals can compensate for both errors. To check the accuracy of DFT methods, a test case of twenty systems (Fig. 1) was employed.^5,15 Such systems were selected because they cover different families of ligands with diverse transition metal cations and they show abrupt spin transitions. Hybrid functionals like TPSSh (Tao–Perdew–Staroverov–Scuseria), with 10% exact exchange,^5,15,22 give the best results. They reproduce well which one is the fundamental state. A modification of the popular B3LYP (Becke's 3-parameter exchange + Lee–Yang–Parr),²³ including only 15% exact exchange,²⁴ especially designed for spin-crossover systems results in less accurate values. However, the energy differences, even with the TPSSh functional, are usually still a bit larger in many systems, slightly over-stabilizing the low spin states. These hybrid functionals also carry the problem of their use in periodic system calculations due to the enormous computational cost, both CPU time and memory, to compute the exact exchange term.²⁵

Fig. 1 Representation of the spin-crossover systems employed as a benchmark set, indicating the label, the metal cation and the spin of the low- and high-spin states. s1 [Cr^II(L_s1)₂I₂] L_s1 = 1,2-bis(diethylphosphino)ethane-P,P′, s2 [Mn^III(L_s2)] L_s2 = tris(2-((pyrrol-2-yl)methyleneamino) ethyl)amine, s3 [Mn^III(L_s3)]⁺¹ L_s3 = 2,2′-(2,6,9,13-tetraazatetradeca-1,13-diene-1,14-diyl)bis(4,6-dibromophenolato), s4 [Mn^III(L_s4)]⁺¹ L_s4 = 2,2′-(2,6,9,13-tetra-azatetradeca-1,13-diene-1,14-diyl)bis(phenolato), s5 [Mn^II(L_s5)₂] L_s5 = η⁵-methylcyclopentadiene, s6 [Mn^II(L_s6)₂] L_s6 = η⁵-tert-butylcyclopentadienyl, s7 [Mn^II(L_s7)₂] L_s7 = η⁵-1,3-tert-butylcyclopentadienyl, s8 [Fe^III(L_s8)]⁺¹ L_s8 = N¹,N⁴-bis(acetylacetonato)triethylenetetramine, s9 [Fe^III(L_s9a)(L_s9b)₂]⁺¹ L_s9a = ethylenebis(acetylacetoneiminato), L_s9b = 3,4-dimethylpyridyl, s10 [Fe^III(L_s10)₂]⁺¹L_s10 = 2-(((2-(ethylamino)ethyl)imino)methyl)-6-methoxyphenolato-N,N′,O, s11 [Fe^II(L_s11)₂(NCS)₂] L_s11 = bis(1,10-phenanthroline-N,N′), s12 [Fe(L_s12)₄(NCS)₂] L_s12 = 4-styrylpyridine, s13 [Fe^II(L_s13)₂]⁺² L_s13 = ((2,6-dipyrazol-1-yl)pyridine), s14 [Fe^II(L_s14a)₂(L_s14b)] L_s14a = dihydrogen bis(pyrazol-1-yl)borate, L_s14b = 2,2′-bipyridyl, s15 [Fe^II(L_s15)₂(NCS)₂] L_s15 = 3-(2-pyridyl)(1,2,3)triazolo(1,5-a)pyridine, s16 [Co^II(L_s16)₂]⁺² L_s16 = 2,2′:6′,2′′-terpyridine, s17 [Co^II(L_s17)(py)₂] L_s17 = 3-formylsalicylic acid-ethylendiamine, s18 [Co^II(L_s18)₂]⁺² L_s18 = (2,2′:6′,2′′-terpyridin-4′-ol), s19 [Co^II(L_s19)₂] L_s19 = 10-((pyridin-2-yl)diazenyl)phenanthren-9-olato, s20 [Co^II(L_s20)₂]⁺² L_s20 = 4′-methoxy-2,2′:6′,2′′-terpyridine.

Meta-GGA functionals are an alternative that include, in addition to the density gradient as the GGA functionals, a dependence on the density Laplacian or through the orbital kinetic energy density.^15,26 Within these functionals, there is also the TPSS functional,^27,28 without including the exact exchange as in TPSSh, but the SCAN (Strongly Constrained and Appropriately Normed) family of functionals are currently the ones that provide the best results at the meta-GGA level.²⁹ Although the original SCAN functional²⁹ already provides quite accurate values of the energy difference, it is the revised version r²SCAN functional,³⁰ the one that stands out above other functionals of this family,^31–34 including r⁴SCAN or rSCAN.^35,36 The r²SCAN functional provides values almost comparable to those of the hybrid functional TPSSh for spin-state energy differences of spin-crossover systems but with the obvious advantage of not having to include the exact exchange.³²

In this paper, new results are provided using an extensive recently developed family of functionals for solids with the aim of weighting errors in the lattice structure, cohesive energy and gap values in the functional expression.³⁷ These results using meta-GGA functionals without exact exchange provide more accurate values for spin-crossover systems than those previously reported. Also, the way these functionals have been developed shows that the calculation of the energy difference between spin states is directly related to the weights of the band gap energy and cohesive energy in the functional expression. This provides important information for further improving the accuracy of the DFT functionals to reproduce the values of the spin state energies in systems with transition metals which are crucial in many research fields, from molecular magnetism, transition metal catalysis and bioinorganic chemistry among others.

2. Results and discussion

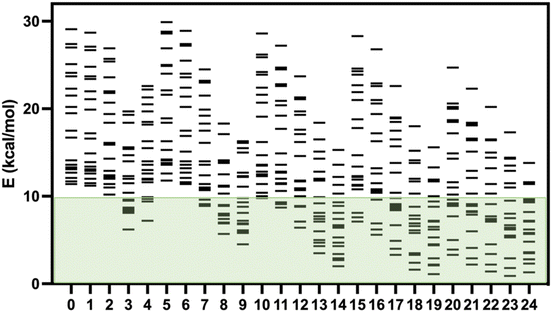
Recently, Kovács et al. have developed a new series of meta-GGA-type training functionals specially dedicated to reproduce cell parameters, cohesive energies and band gaps.³⁷ In this case, three coefficients in the expression of the functionals are used to control the weight of the average errors in these magnitudes. In this way, these coefficients can be used to weight which of these three quantities will be best reproduced by the functional. These authors have proposed 25 combinations of these three coefficients generating 25 expressions for the exchange part of the functional (KTBM0-KTBM24, Kovács–Tran–Blaha–Madsen), while correlation contribution is included with that of the SCAN functional (see Table S2†).²⁹

As mentioned above, some of us had proposed a set of 20 spin-crossover systems to evaluate the accuracy of theoretical approaches performing calculations with the isolated molecules, and this set of cases has been lately employed by different authors.^5,15,16,32 The results for the 25 KTBM functionals are collected in Fig. 2 and Table S1.† All functionals reproduce well the fundamental low-spin state at 0 K of systems with spin transition. However, in many cases, the high- and low-spin energy difference is too high, above 10 kcal mol⁻¹, for most molecular models. The results of the functionals KTBM14, KTBM19 and especially KTBM24 are remarkable. For the functional with the best results, the criterion to choose the parameters is based on the reduction of the cell parameter and band gap estimation errors. However, the element that all three functionals have in common is that they do not consider the error in the cohesive energy (see Table S2†).

Fig. 2 High- and low-spin energy differences (in kcal mol⁻¹) using s1–s20 molecular models (positive values indicate a low-spin ground state) using the twenty-five KTBM0-KTBM24 exchange functionals + SCAN correlation using PBE + MB optimized geometry. The green region corresponds to the usual energy differences of spin crossover systems.

To compare the results obtained with the KTBM24 functional and the best functionals reported so far, TPSSh and r²SCAN for spin-crossover systems, the values of high- and low-spin states energy differences with these functionals are shown in Table 1. In the case of r²SCAN, the results are presented with the same program, basis set, and grid to allow a direct comparison of the functionals.

Table 1 High- and low-spin state energy differences (in kcal mol⁻¹) using discrete molecular models (positive values indicate a low-spin ground state). If two functionals are indicated, the first one was employed for the energy values and the second one to optimize the geometry. MB indicates the inclusion of many-body dispersion in the geometry optimization. See ligand formulas in the caption of Fig. 1. Calculations were performed with the FHI-aims code⁴² by using the Libxc 6.2 library of the exchange–correlation functionals⁴³ using by default the tight basis set. The last column corresponds to an estimation of the high- and low-spin states energy difference by using the experimental transition temperature (see text and Table S3† for details)^44–63

Molecular system	Ref.	TPSSh^a	r^2SCAN	r^2SCAN//PBE + MB	KTBM24	KTBM24//PBE + MB	From Exp. T1/2
a Ref. 15.
s1 [Cr^II(Ls1)2I2]	44	6.5	8.6	5.7	5.8	5.8	1.7
s2 [Mn^III(Ls2)]	45 and 46	4.3	5.0	5.0	4.7	4.8	1.2
s3 [Mn^III(Ls3)]^1+	47	5.5	5.5	5.5	5.4	5.7	2.7
s4 [Mn^III(Ls4)]^1+	48	4.1	4.0	3.1	4.4	3.5	2.3
s5 [Mn^II(Ls5)2]	49	11.2	4.0	10.1	9.7	9.7	7.9
s6 [Mn^II(Ls6)2]	50	10.7	10.2	10.4	11.3	11.4	6.4
s7 [Mn^II(Ls7)2]	50	9.4	10.0	10.3	11.6	11.6	9.2
s8 [Fe^III(Ls8)]^1+	51	9.8	5.2	5.3	6.6	7.2	2.9
s9 [Fe^III(Ls9a)(Ls9b)2]^1+	52	11.5	12.4	12.6	13.4	13.8	4.0
s10 [Fe^III(Ls10)2]^1+	53	10.7	8.5	8.6	9.0	9.5	3.1
s11 [Fe^II(Ls11)2(NCS)2]	54	6.1	7.4	7.4	3.5	3.6	4.3
s12 [Fe(Ls12)4(NCS)2]	55	8.5	9.3	9.4	5.9	6.2	5.4
s13 [Fe^II(Ls13)2]^2+	56	9.3	14.0	14.0	8.5	8.2	5.3
s14 [Fe^II(Ls14a)(Ls14b)]	57	9.3	12.7	12.6	9.5	9.3	4.0
s15 [Fe^II(Ls15)2(NCS)2]	58	5.0	5.8	5.8	3.1	2.8	1.7
s16 [Co^II(Ls16)2]^2+	59	3.0	9.5	9.6	2.1	2.3	2.0
s17 [Co^II(Ls17)(py)2]	60	2.2	7.8	7.8	3.0	2.8	1.2
s18 [Co^II(Ls18)2]^2+	61	2.1	8.1	8.7	0.6	1.3	1.6
s19 [Co^II(Ls19)2]	62	3.8	15.1	15.1	6.8	7.1	1.5
s20 [Co^II(Ls20)2]^2+	63	6.6	10.4	10.3	5.9	5.7	1.7

---

Results from Trickey and co-workers were also published for these systems with the r²SCAN functional with a different computer code.^16,31,32 For meta-GGA functionals, two sets of values are shown in Table 1, one using the optimized geometry with the PBE (Perdew–Burke–Ernzerhof) functional³⁸ including dispersion with the many-body methodology³⁹ and the other optimizing the geometries with the same meta-GGA functionals without dispersion. It has been reported that the inclusion of the dispersion term in some meta-GGA functionals overestimates, due to a double-counting problem, these dispersion effects.⁴⁰ Due to the lack of thermodynamic data for all compounds, it is not easy to make a comparison. For example, one of the most studied spin-crossover systems s11 has experimental enthalpy and entropy values 2.06 kcal mol⁻¹ and 11.66 cal mol⁻¹·K⁻¹,⁴¹ respectively. The difference of thermal correction to the energy between high- and low-spin states is practically negligible. Thus, if energy and enthalpy differences are comparable, that would imply that the KTBM24 results are the closest among the employed functionals (see Table 1).

To make a comparison between experimental data and theoretical results for all the systems, the transition temperature has been used, which is the experimentally available data (see Table S3†) for all the systems studied. At this temperature, the free energy of the system at high-spin and low-spin states is the same. Therefore, if we calculate the thermal correction (E^therm in eqn (1), which is the value to be added to the energy to obtain the free energy) of each of the states, the difference between them must be equal to the expected high- and low-spin energy splitting that would reproduce the experimental transition temperature (see eqn (3)).

G_LS = E_LS + E^therm_LS; G_HS = E_HS + E^therm_HS. (1)

The thermal correction E^therm term contains all the contributions that must be added to the energy to obtain the free energy: thermal corrections to the translational, rotational and electronic energy, the zero-point correction and translational, rotational and electronic entropies.

At the transition temperature T_1/2

G_LS = G_HS, (2)

and consequently,

E_HS − E_LS = E^therm_LS − E^therm_HS. (3)

Moreover, considering that the DFT functionals provide reliable values of the thermal E^therm corrections mainly coming from zero-point energy and entropic terms, such an approach can provide a reasonable estimation of the energy difference between high- and low-spin states based on the experimental T_1/2. Details about the calculated values of this difference in the thermal correction for the free energy are given in Table S3.† If we take as reference such estimation from the experimental T_1/2, the smallest mean average error for KTBM24 and KTBM24//PBE + MB is 3.2 kcal mol⁻¹, while the hybrid TPSSh and the two r²SCAN options, have values of 3.5 and 5.5 kcal mol⁻¹, respectively. If we consider a qualitative criterion of the number of cases with the high- and low-spin energy difference above 10 kcal mol⁻¹ (see Table 1 and Fig. 3), the KTBM24 functional has the least number of cases, even below the TPSSh hybrid functional.

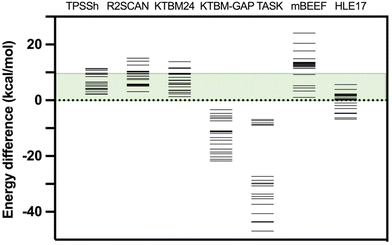Fig. 3 High- and low-spin energy differences for the test case with different exchange–correlation functionals. The green energy range indicates the region where the energy difference (below 10 kcal mol⁻¹) can be compensated by the entropy in a common spin-crossover compound. TPSSh results were previously published.¹⁵ For the six non-hybrid meta-GGA functionals, the same PBE-MB optimized geometry was employed.

The metal bond distances to the atoms of the first coordination sphere have been collected as the ESI.† The optimized structures with the three functionals, PBE + MB, r²SCAN and KTBM24, show very similar values with a mean average error around 0.012 Å between them. No clear trend is observed; mostly the PBE-MB distances are in general slightly longer than those with the meta-GGA functionals. Comparison with the experimental data (also in the ESI†) shows larger differences probably due to packing effects. It is important to keep in mind that experimental data correspond to the structures solved with single-crystal X-ray diffraction, while the DFT optimized structures are for the isolated molecules. The comparison between experimental and calculated metal–ligand bond distances shows that in low-spin structures the difference is very small. However, in high-spin systems, especially in metallocene molecules, the distance differences are larger. In the manganocene molecules, the high spin system structures are the cases with the largest discrepancy with respect to the distance values obtained in the optimizations with the DFT calculations, which is probably due to the rotation of the cyclopentadienyl ligand and long metal–ligand distances.

Additionally, a series of changes have been considered in the calculations with the KTBM24 functional, such as replacing the correlation part of the SCAN functional with that of the r²SCAN functional, which does not provide improved results (see Table 2). Also, both the quality of the grid and the quality of the base have been improved and the results remain practically unchanged (see Table 2). The inclusion of a many-body dispersion term does not improve the results as it tends to over-stabilize the low spin state as previously reported by Trickey et al.³² Finally, it has been considered an option proposed in the original paper of Kovács et al.³⁷ specifically designed for the band gap of solid state systems (KTBM_GAP functional, see Table S2†) being the best functional of the KTBM family to reproduce experimental band gaps.³⁷ However, this functional gives values with a large overestimation of the stability of the high-spin state (see Table S4† and Fig. 3). Other meta-GGA functionals also specially designed to reproduce band gap values such as TASK (Thilo Aschebrock–Stephan Kümmel),⁶⁴ mBEEF (Bayesian Error Estimation Functional)⁶⁵ and HLE17 (High Local Exchange)⁶⁶ have been tested for this problem (see Table S4† and Fig. 3).

Table 2 High- and low-spin state energy differences (in kcal mol⁻¹, positive values indicate a low-spin ground state). If two functionals are indicated, the first one was employed for the energy values and the second one to optimize the geometry. MB indicates the inclusion of many-body dispersion in the geometry optimization. See ligand formulas in the caption of Fig. 1. The first column is the reference value using KTBM24/PBE + MB approach using the FHI-aims code with radial_mutiplier = 2 for the grid the tight basis set. The next columns correspond to replace the SCAN correlation functional by the r²SCAN one, increasing the grid size with radial_multiplier = 4, improving the basis set quality with the very tight basis set and the addition of the many-body dispersion to the KTBM24 functional

Molecular system	Ref.	KTBM24//PBE + MB	KTBM24-r^2SCAN//PBE + MB	KTBM24//PBE + MB grid rm4	KTBM24//PBE + MB (very tight)	KTBM24 + MB//PBE + MB
s1 [Cr^II(Ls1)2I2]	44	5.8	7.2	5.8	5.7	8.8
s2 [Mn^III(Ls2)]	45 and 46	4.8	5.6	4.8	4.8	4.8
s3 [Mn^III(Ls3)]^1+	47	5.7	6.8	5.7	5.6	5.6
s4 [Mn^III(Ls4)]^1+	48	3.5	4.8	3.6	3.5	3.5
s5 [Mn^II(Ls5)2]	49	9.7	12.9	9.7	9.7	9.7
s6 [Mn^II(Ls6)2]	50	11.4	14.3	11.4	11.4	14.2
s7 [Mn^II(Ls7)2]	50	11.6	14.3	11.6	11.6	15.3
s8 [Fe^III(Ls8)]^1+	51	7.2	9.9	7.2	7.4	9.8
s9 [Fe^III(Ls9a)(Ls9b)2]^+1	52	13.8	16.3	13.9	13.9	18.3
s10 [Fe^III(Ls10)2]^1+	53	9.5	12.3	9.5	9.6	13.9
s11 [Fe^II(Ls11)2(NCS)2]	54	3.6	5.8	3.7	3.7	6.4
s12 [Fe(Ls12)4(NCS)2]	55	6.2	8.9	6.2	6.2	12.3
s13 [Fe^II(Ls13)2]^2+	56	8.2	10.6	8.2	8.2	12.8
s14 [Fe^II(Ls14a)(Ls14b)]	57	9.3	12.2	9.3	9.3	14.7
s15 [Fe^II(Ls15)2(NCS)2]	58	2.8	4.2	2.8	2.9	3.3
s16 [Co^II(Ls16)2]^2+	59	2.3	3.0	2.3	2.2	4.7
s17 [Co^II(Ls17)(py)2]	60	2.8	3.6	2.8	2.2	3.9
s18 [Co^II(Ls18)2]^2+	61	1.3	2.0	1.3	1.8	3.6
s19 [Co^II(Ls19)2]	62	7.1	9.2	7.2	7.4	10.1
s20 [Co^II(Ls20)2]^2+	63	5.7	7.0	5.7	5.7	8.1

---

A similar behaviour is found with the TASK functional, providing results always with the high-spin state as the lowest energy state. This problem is partially solved with the HLE17 functional, but still in quite a few cases a high-spin ground state is found. While with the mBEEF functional, it again provides in all cases a correct description of the nature of the ground state, but with very large high- and low-spin energy differences overestimating the stability of the systems in the low-spin state. These results indicate that these functionals especially dedicated to reproduce band gaps are not suitable to calculate the spin energetics of transition metal compounds.

3. Computational details

DFT calculations of high- and low-spin energy differences were carried out with the all-electron FHI-aims computer code using a numerical local orbital basis set (tight basis) and including scalar relativistic effects.⁴² This approach allows for full-potential calculations at a low computational cost without using any a priori approximations for the potential, such as pseudopotentials or frozen cores. The geometry optimizations were performed using the molecular structures using the PBE, r²SCAN³⁰ and KTBM24³⁷ exchange–correlation functionals including in some cases many-body dispersion effects⁵³ (xyz files of the optimized structures are in the ESI†). All the calculations were performed using non-periodic molecular structures. Despite that usually, the spin-crossover properties are determined in the solid state, comparison of the high- and low-spin energy differences obtained from the calculations of non-periodic molecular structures or from the solid state with PBC shows differences in the order of 2–3 kcal mol⁻¹,^14–16 so the use of molecular structures is a good approximation. The calculations with the two meta-GGA functionals were performed by using the Libxc 6.2 library of exchange–correlation functionals.⁴³ It is well-known the influence of the grid size for some meta-GGA functionals;^35,36 thus, the usual number of radial points in FHI-aims, controlled by the radial multiplier parameter equal 2 has been increased until 4 in the results of Table 2. However, in this case, such an influence seems to be practically negligible as well as the quality of the basis set using a very tight basis set (Table 2).

Additional calculations to estimate the thermal energy correction were performed using the Gaussian16 code with the hybrid B3LYP²³ and hybrid meta-GGA TPSSh functionals using 6-311G^67,68 and def2-TZVP⁶⁹ basis sets, respectively (see Table S3†). For the B3LYP calculations, also the D3 approach⁷⁰ was employed to calculate the dispersion contributions. The B3LYP results will be employed because that approach was benchmarked as the best to reproduce the vibrational frequencies, such a term being the main contributor to the thermal energy differences through the zero-point correction and entropic terms.⁷¹ Thus, such B3LYP values were included in the last column of Table 1 for the difference of the thermal correction for the high- and low-spin states to compare with the calculated energy differences.

4. Conclusions

In summary, several meta-GGA functionals have been employed to calculate the energy differences between high- and low-spin states for a test case of 20 molecules. Such energy differences are very challenging from the computational point of view because most of the theoretical methods fail not only in a quantitative approach, but also in predicting the right ground spin state and reasonable high- and low-spin energy differences. Previously, it was reported that the hybrid meta-GGA TPSSh functional provided a good estimation of such energy differences with the right ground state for the whole set of calculated systems. Among the non-hybrid functionals, the meta-GGA r²SCAN functional is the one that provides accuracy close to TPSSh, but still somewhat overestimates the stability of the low-spin state. Within the family of KTBM + SCAN exchange–correlation functionals, studied in this paper, some of them, for instance the KTBM14 and KTBM19 exchange functionals show slightly better results than the r²SCAN functional. However, the KTBM24 functional is the best in both qualitative criteria considered. When analysing values outside the range to have spin transitions below room temperature (entropy can compensate energy differences below 10 kcal mol⁻¹, see Fig. 3), it shows fewer cases, behaving even better than the hybrid TPSSh functional. And when comparing with the energy differences estimated from the experimental transition temperatures, it is the one with the smallest mean average error, 3.2 kcal mol⁻¹. It is worth noting the almost negligible dependence of the results on the grid size using the KTBM24 functional. We have analysed the performance of band gap-dedicated meta-GGA functionals (KTBM_GAP, TASK, mBEEF and HLE17, see Fig. 3), but only mBEEF does not provide wrong ground spin-states, but over-stabilizes the low-spin state. To conclude, the lack of exact-type exchange contributions in the meta-GGA KTBM24 functional makes it an excellent method for accurate spin energetics studies in large molecular transition metal systems or extended materials with periodic boundary conditions. However, there is still room for the development of new functionals to reach the “chemical accuracy” in the field of spin energetics.

Author contributions

S. G. C. and E. R. performed the DFT calculations. The manuscript was written by S. G. C. and E. R.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

Financial support from Ministerio de Ciencia, Innovación y Universidades (PID2021-122464NB-I00, TED2021-129593B-I00 and Maria de Maeztu CEX2021-001202-M) is acknowledged. We also acknowledge the Generalitat de Catalunya for the 2021-SGR-00286 grant and E.R. for an ICREA Academia grant. We thank CSUC and BSC supercomputer centres for the computational resources.

References

1. S. Song, M. C. Kim, E. Sim, A. Benali, O. Heinonen and K. Burke, J. Chem. Theor. Comput., 2018, 14, 2304.
2. S. Ye and F. Neese, Inorg. Chem., 2010, 49, 772.
3. M. Reimann and M. Kaupp, J. Chem. Theor. Comput., 2022, 18, 7442.
4. J. Cirera and E. Ruiz, Comments Inorg. Chem., 2019, 39, 216.
5. J. Cirera, M. Via-Nadal and E. Ruiz, Inorg. Chem., 2018, 57, 14097.
6. D. Mejia-Rodriguez and S. B. Trickey, Phys. Rev. A, 2017, 96, 052512.
7. A. Römer, L. Hasecke, P. Blöchl and R. A. Mata, Molecules, 2020, 25, 5176.
8. Q. M. Phung, M. Feldt, J. N. Harvey and K. Pierloot, J. Chem. Theor. Comput., 2018, 14, 2446.
9. K. Pierloot, Q. M. Phung and A. Domingo, J. Chem. Theor. Comput., 2017, 13, 537.
10. L. A. Mariano, B. Vlaisavljevich and R. Poloni, J. Chem. Theor. Comput., 2021, 17, 2807.
11. S. J. Stoneburner, D. G. Truhlar and L. Gagliardi, J. Phys. Chem. A, 2020, 124, 1187.
12. L. A. Mariano, B. Vlaisavljevich and R. Poloni, J. Chem. Theor. Comput., 2020, 16, 6755.
13. M. A. Halcrow, Spin–Crossover Materials, Wiley, 2013.
14. S. Lebègue, S. Pillet and J. G. Ángyán, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 024433.
15. J. Cirera and E. Ruiz, J. Phys. Chem. A, 2020, 124, 5053.
16. L. Bondi, S. Brooker and F. Totti, J. Mater. Chem. C, 2021, 9, 14256.
17. L. Hedin, Phys. Rev., 1965, 139, A796.
18. J. Harl and G. Kresse, Phys. Rev. Lett., 2009, 103, 056401.
19. P. Nozières and D. Pines, Phys. Rev., 1958, 111, 442.
20. X. Ren, P. Rinke, V. Blum, J. Wieferink, A. Tkatchenko, A. Sanfilippo, K. Reuter and M. Scheffler, New J. Phys., 2012, 14, 053020.
21. J. McClain, Q. Sun, G. K.-L. Chan and T. C. Berkelbach, J. Chem. Theor. Comput., 2017, 13, 1209.
22. V. N. Staroverov, G. E. Scuseria, J. Tao and J. P. Perdew, J. Chem. Phys., 2003, 119, 12129.
23. A. D. Becke, J. Chem. Phys., 1993, 98, 5648.
24. H. Paulsen, L. Duelund, H. Winkler, H. Toftlund and H. X. Trautwein, Inorg. Chem., 2001, 40, 2201.
25. S. V. Levchenko, X. Ren, J. Wieferink, R. Johanni, P. Rinke, V. Blum and M. Scheffler, Comput. Phys. Commun., 2015, 192, 60.
26. D. Mejia-Rodriguez and S. B. Trickey, Phys. Rev. B, 2018, 98, 115161.
27. J. M. Tao, J. P. Perdew, V. N. Staroverov and G. E. Scuseria, Phys. Rev. Lett., 2003, 91, 146401.
28. J. P. Perdew, J. Tao, V. N. Staroverov and G. E. Scuseria, J. Chem. Phys., 2004, 120, 6898.
29. J. Sun, A. Ruzsinszky and J. P. Perdew, Phys. Rev. Lett., 2015, 115, 036402.
30. J. W. Furness, A. D. Kaplan, J. Ning, J. P. Perdew and J. Sun, J. Phys. Chem. Lett., 2020, 11, 8208.
31. D. Mejía-Rodríguez, A. Albavera-Mata, E. Fonseca, D.-T. Chen, H. P. Cheng, R. G. Hennig and S. B. Trickey, Comput. Mater. Sci., 2022, 206, 111161.
32. D. Mejía-Rodríguez and S. B. Trickey, J. Phys. Chem. A, 2020, 124, 9889.
33. R. Díaz-Torres, T. Boonprab, S. Gómez-Coca, E. Ruiz, G. Chastanet, P. Harding and D. J. Harding, Inorg. Chem. Front., 2022, 9, 5317.
34. S.-G. Wu, L.-F. Wang, Z.-Y. Ruan, S.-N. Du, S. Gómez-Coca, Z.-P. Ni, E. Ruiz, X.-M. Chen and M.-L. Tong, J. Am. Chem. Soc., 2022, 144, 14888.
35. J. W. Furness, A. D. Kaplan, J. Ning, J. P. Perdew and J. Sun, J. Chem. Phys., 2022, 156, 034109.
36. A. P. Bartók and J. R. Yates, J. Chem. Phys., 2019, 150, 161101.
37. P. Kovács, F. Tran, P. Blaha and G. K. H. Madsen, J. Chem. Phys., 2022, 157, 094110.
38. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
39. A. Tkatchenko, R. A. DiStasio, R. Car and M. Scheffler, Phys. Rev. Lett., 2012, 108, 236402.
40. M. Kothakonda, A. D. Kaplan, E. B. Isaacs, C. J. Bartel, J. W. Furness, J. Ning, C. Wolverton, J. P. Perdew and J. Sun, ACS Mater. Au, 2023, 3, 102.
41. M. Sorai and S. Seki, J. Phys. Chem. Solids, 1974, 35, 555.
42. V. Blum, R. Gehrke, F. Hanke, P. Havu, V. Havu, X. Ren, K. Reuter and M. Scheffler, Comput. Phys. Commun., 2009, 180, 2175.
43. S. Lehtola, C. Steigemann, M. J. T. Oliveira and M. A. L. Marques, Software X, 2018, 7, 1.
44. D. M. Halepoto, D. G. L. Holt, L. F. Larkworthy, G. J. Leigh, D. C. Povey and G. W. Smith, J. Chem. Soc., Chem. Commun., 1989, 1322.
45. P. G. Sim and E. Sinn, J. Am. Chem. Soc., 1981, 103, 241.
46. P. Guionneau, M. Marchivie, Y. Garcia, J. A. K. Howard and D. Chasseau, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 214408.
47. K. Pandurangan, B. Gildea, C. Murray, C. J. Harding, H. Mueller-Bunz and G. G. Morgan, Chem. – Eur. J., 2012, 18, 2021.
48. P. N. Martinho, B. Gildea, M. M. Harris, T. Lemma, A. D. Naik, H. Mueller-Bunz, T. E. Keyes, Y. Garcia and G. G. Morgan, Angew. Chem., Int. Ed., 2012, 51, 12597.
49. M. E. Switzer, R. Wang, M. F. Rettig and A. H. Maki, J. Am. Chem. Soc., 1974, 96, 7669.
50. M. D. Walter, C. D. Sofield, C. H. Booth and R. A. Andersen, Organometallics, 2009, 28, 2005.
51. E. V. Dose, K. M. M. Murphy and L. J. Wilson, Inorg. Chem., 1976, 15, 2622.
52. Y. Maeda, H. Oshio, K. Toriumi and Y. Takashima, J. Chem. Soc., Dalton Trans., 1991, 1227.
53. A. Tissot, R. Bertoni, E. Collet, L. Toupet and M.-L. Boillot, J. Mater. Chem., 2011, 21, 18347.
54. B. Gallois, J. A. Real, C. Hauw and J. Zarembowitch, Inorg. Chem., 1990, 29, 1152.
55. C. Roux, J. Zarembowitch, B. Gallois, T. Granier and R. Claude, Inorg. Chem., 1994, 33, 2273.
56. C. Carbonera, C. A. Kilner, J.-F. Letard and M. A. Halcrow, Dalton Trans., 2007, 1284.
57. J. A. Real, M. C. Muñoz, J. Faus and X. Solans, Inorg. Chem., 1997, 36, 3008.
58. C.-F. Sheu, K. Chen, S.-M. Chen, Y.-S. Wen, G.-H. Lee, J.-M. Chen, J.-F. Lee, B.-M. Cheng, H.-S. Sheu, N. Yasuda, Y. Ozawa, K. Toriumi and Y. Wang, Chem. – Eur. J., 2009, 15, 2384.
59. B. N. Figgis, E. S. Kucharski and A. H. White, Aust. J. Chem., 1983, 36, 1527.
60. J. Zarembowitch and O. Kahn, Inorg. Chem., 1984, 23, 589.
61. A. B. Gaspar, M. C. Muñoz, V. Niel and J. A. Real, Inorg. Chem., 2001, 40, 9.
62. R. A. Taylor, A. J. Lough and M. T. Lemaire, J. Mater. Chem. C, 2016, 4, 455.
63. S. Hayami, M. Nakaya, H. Ohmagari, A. S. Alao, M. Nakamura, R. Ohtani, R. Yamaguchi, T. Kuroda-Sowa and J. K. Clegg, Dalton Trans., 2015, 44, 9345.
64. T. Aschebrock and S. Kümmel, Phys. Rev. Res., 2019, 1, 033082.
65. J. Wellendorff, K. T. Lundgaard, A. Møgelhøj, V. Petzold, D. D. Landis, J. K. Nørskov, T. Bligaard and K. W. Jacobsen, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 235149.
66. P. Verma and D. G. Truhlar, J. Phys. Chem. C, 2017, 121, 7144.
67. K. Raghavachari and G. W. Trucks, J. Chem. Phys., 1989, 91, 1062.
68. A. D. McLean and G. S. Chandler, J. Chem. Phys., 1980, 72, 5639.
69. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297.
70. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
71. A. P. Scott and L. Radom, J. Phys. Chem., 1996, 100, 16502.

---

Footnote

† Electronic supplementary information (ESI) available: Tables with additional high- and low-spin energy differences. Normalized training weights for the KBTM meta-GGA family of exchange functionals. Calculated electronic energies to reproduce the experimental transition temperatures. A text file containing xyz coordinates with the optimized structures and an excel file with the calculated and experimental bond distances. See DOI: https://doi.org/10.1039/d4dt00975d

---