Substituted fullerenes as a promising capping ligand towards stabilization of exohedral Dy(III) based single-ion magnets: a theoretical study†
Kusum
Kumari
and
Saurabh Kumar
Singh
 *
*
Computational Inorganic Chemistry Group, Department of Chemistry, Indian Institute of Technology Hyderabad, Kandi, Sangareddy, Telangana-502284, India. E-mail: sksingh@chy.iith.ac.in
First published on 27th August 2024
Abstract
Organometallic dysprosocenium-based molecular magnets are the forefront runners in offering giant magnetic anisotropy and blocking temperatures close to the boiling point of liquid nitrogen. Attaining linearity in the organometallic dysprosocenium complexes is the key to generating giant magnetic anisotropy and blocking barriers. In the present study, we have unravelled the coordination ability of the substituted fullerene (C55X5)− (where X = CCH3, B, and N) generated by fencing around the five-membered ring of fullerene towards stabilizing a new family of exohedral dysprosium organometallic complexes showcasing giant magnetic anisotropy and blockade barriers. Eight exohedral mononuclear dysprosium organometallic complexes, namely [Dy(η5-C55X5)(η4-C4H4)] (1), [Dy(η5-C55X5)(η5-Cp)]+ (2), [Dy(η5-C55X5)(η5-Cp*)]+ (3), [Dy(η5-C55X5)(η6-C6H6)]2+ (4), [Dy(η5-C55X5)(η8-C8H8)] (5), [Dy(η5-C55X5)2]+ (6) (where X = CCH3), [Dy(η5-C55B5)2]+ (7) and [Dy(η5-C55N5)2]+ (8), were studied using scalar relativistic density functional theory (SR-DFT) and the complete active space self-consistent field (CASSCF) methodology to shed light on the structure, stability, bonding and single-ion magnetic properties. SR-DFT calculations predict complexes 1–8 to be highly stable, with a strictly linear geometry around the Dy(III) ion in complexes 6–8. Energy Decomposition Analysis (EDA) predicts the following order for interaction energy (ΔEint value): 5 > 1 > 2 ≈ 3 > 6 > 7 > 8 > 4, with sizable 4f-ligand covalency in all the complexes. CASSCF calculations on complexes 1–8 predict stabilization of mJ |±15/2〉 as the ground state for all the complexes except for 5, with the following trend in the Ucal values: 6 (1573 cm−1) ≈ 3 (1569 cm−1) > 1 (1538 cm−1) > 8 (1347 cm−1) > 2 (1305 cm−1) > 7 (1284 cm−1) > 4 (1125 cm−1) > 5 (108 cm−1). Ab initio ligand field theory (AILFT) analysis provides a rationale for Ucal ordering, where π-type 4f-ligand interactions in complexes 1–4 and 6–8 offer giant barrier height while the large (C8H8)2− rings generate δ-type interaction in 5, which diminishes the axiality in the ligand field. Our detailed finding suggests that the exohedral organometallic dysprosocenium complexes are more linear compared to bent [DyCp*2]+ cations and display a giant barrier height exceeding 1500 cm−1 with negligible quantum tunnelling of magnetization (QTM) – a new approach to design highly anisotropic dysprosium organometallic complexes.
Introduction
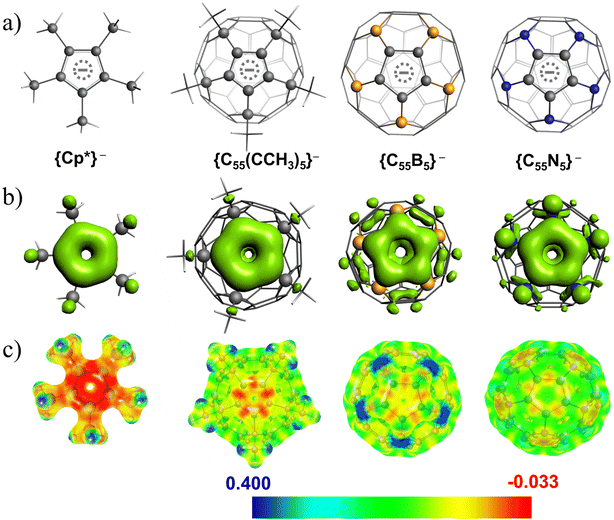
Single Molecule Magnets (SMMs) have garnered significant attention in the scientific community over the past few decades due to their unique property of displaying molecular hysteresis stemming from the intrinsic barrier height for magnetization reversal.1–5 As a result, these molecules hold immense promise for various technological applications, including molecular qubits,6–8 high-density data storage devices,9–12 and spintronics.13,14 Extensive research spanning over three decades on designing molecule-based magnets has identified that mononuclear transition metal15 and lanthanide complexes1 are much more appealing candidates for designing highly anisotropic SMMs compared to polynuclear complexes,16 thanks to the giant and tuneable magnetic anisotropy at the mononuclear level.17 Due to the unquenched orbital angular momentum associated with 4f-ions, the trivalent lanthanide ions naturally become more appealing candidates for designing SMMs with giant barrier heights.1 In particular, trivalent Dy(III) ions are highly efficient in stabilizing SMMs with a giant magnetic relaxation barrier >2000 K and blocking temperatures close to the boiling point of liquid nitrogen.18 To achieve Ising type anisotropy in Dy(III) complexes, a robust axial ligand field and extremely weak/negligible equatorial ligand field around a Dy(III) ion is required to stabilize the largest mJ |±15/2〉 as the ground state.19–24 In this context, organometallic sandwiched [DyCp2]+ based cations show remarkable SMM properties, as the strong π-type interaction between the 4f orbitals of Dy(III) and π-lobes of the monoanionic cyclopentadienyl (Cp) ligands generates a strong axial ligand field which generates a giant barrier height for magnetization reversal.18,25–27 Mills and co-workers have reported the [Dy(Cpttt)2][B(C6F5)4] (where Cpttt = (C5H2tBu3-1,2,4) and tBu = C(CH3)3) complex where the ∠Cp–Dy–Cp bond angle is reported to be 152.6° and displays a magnetic hysteresis at 60 K.25 One common strategy to maximize the anisotropy in the [DyCp2]+ family of complexes is to achieve strict linearity around the Dy(III) ion, i.e. maintaining the ∠Cp–Dy–Cp bond angle at ∼180°. Bulking up the Cp ligand is a popular approach where the enhanced steric interaction can offer linearity in the ∠Cp–Dy–Cp bond angle, resulting in a large barrier height. Numerous attempts have been made to isolate linear dysprosocenium cations; however, the maximum ∠Cp–Dy–Cp bond angle of 162.5° is observed in the groundbreaking report of the [DyCpip5Cp*] [B(C6F5)4] (where Cpip5 = penta-iso-propylcyclopentadienyl; Cp* = pentamethylcyclopentadienyl) complex showing the largest TB value of 80 K.18 Another promising strategy is introducing heteroatoms (B, Ge, P, N, and Pb) to functionalize the Cp rings,26,27,27,28 which is also a key to increasing the barrier height as both the electrostatics and covalency can help in tweaking the magnetic anisotropy. Some notable work includes the report on the [Dy(BC4Ph5)2]− complex,26 where boron substitution in the Cp ring generates stronger electrostatics resulting in a high TB value of 65 K. Another key example is the report on [(CpiPr5)Dy(CpPEt4)]+, where the presence of CpPEt4 (tetraethylphospholyl) ligands results in a high TB value of 70 K for this complex.28 As an alternative to (Cp)− ligands, computational observations predict that the cyclobutadiene dianion (C4H4)2− ligands29 are even more promising to achieve a large barrier height; however, these [Dy(C4H4)2]− family complexes are yet to be synthesized.30 Other strategies include synthesizing highly symmetric environment Dy(III) complexes with axially compressed Dy–ligand bonds over the equatorial Dy–ligand bonds, resulting in giant magnetic anisotropy.21,22,31–36 Numerous homoleptic and heteroleptic lanthanide sandwich complexes with larger rings have been reported in the literature, and a near linear geometry around the Dy(III) ion displays weak SMM behaviour.37–39 The larger ring size introduces adverse ligand field effects, generating an unfavourable equatorial ligand field, which diminishes the SMM behaviour even in a linear geometry.19 Recent theoretical studies indicate that the magnetic relaxation rate in lanthanide complexes strongly depends on the spin–phonon coupling,40 and hence, restricting the flexibility of the molecule or offering a rigid environment may help remove low-lying vibrational modes,41 which eventually helps to prevent fast magnetization reversal.Considering the dominance of substituted Cp ligands18,25 in isolating the top-performing Dy(III) based SIMs, it is worthwhile to investigate new possibilities and directions in organometallic chemistry. Besides adding bulky substituents to the Cp ligands or substituting them with heteroatoms, another possibility is to explore the spherical fullerenes and their substituted analogues to design Dy(III) based SMMs, as fullerenes are capable of trapping the metal ions inside the cage (endohedral metallofullerenes or EMFs)42,43 and outside the cage (exohedral metallofullerenes).44–48 In particular, significant progress has been made in endohedral metallofullerenes,42,43,49–53 where encapsulation of lanthanides shows peculiar bonding and magnetic properties. Popov et al. have conducted pioneering work on the structure, stability, and cluster cage interactions in several cluster metallofullerenes of carbides, sulfides, and nitrides that exhibit peculiar single-ion magnetic characteristics.49,50,54–57 Using computational tools, Rajaraman and coworkers have thoroughly investigated the role of the fullerene environment on the magnetic properties of Co(II) and Ln(III) based endohedral metallofullerenes.58–60 In addition to lanthanides, there have been a handful of reports where the actinides have been encapsulated inside C80/C82/C84 cages and thoroughly investigated to probe the electronic structure and bonding.51–53 In contrast, the chemistry of exohedral metallofullerenes is somewhat limited as stabilizing highly symmetric sandwich complexes are very rare due to spherically delocalized distribution of 60-π electrons across 90 C–C bonds, leading to a considerable reduction in the π-electron density per C–C bond compared to localized C–C double bonds.61,62 However, a few successful attempts have been made to disrupt the 60-π electron conjugation by saturating five α positions around a 5-membered ring of C60, creating a fence around the (Cp)− ring of fullerene to yield (C55(CCH3)5)−, which can mimic the (Cp) ligands.44 In this context, Nakamura and co-workers have reported a series of air-stable exohedral metallofullerene complexes with the general formula [TM(C60Me5)Cp] (where TM = Fe(II), Ru(II) and Cp = cyclopentadienyl anion) which mimics ferrocene and its analogues.44,63,64 Numerous theoretical reports suggest that all these transition metal-based exohedral fullerene complexes are highly stable in nature; however, the strength of the metal–ligand interactions is relatively weak compared to that of the ferrocene analogue.47,65 Nakajima and coworkers have characterized the Lnn–C60 multinuclear clusters using photoelectron spectroscopy, which shows that the Eu(II) and Ho(III) ions sit at the exohedral position in the cluster.66,67 Since the structural and bonding motifs of the substituted fullerenes (C55(CCH3)5)− closely resemble those of the (Cp)− ligands (see Fig. 1), the bulky (C55(CCH3)5)− ligands have more potential to offer higher axiality while developing Dy(III) based organometallic sandwiched SIMs. In one of the seminal works, Rajaraman and co-workers have explored structural and magnetic properties in Dy(III) based corannulene complexes in the endo- and exohedral fashion.68 Despite having ample experimental evidence of transition metal-based exohedral fullerenes,44,63,69 to the best of our knowledge, there are no reports available in the literature that describe the complexation, geometry, electronic structure, and single-ion behaviour in lanthanide-based exohedral fullerene complexes.
Computational tools are indispensable in predicting the geometry, electronic structure, and magnetic properties of mononuclear and polynuclear open-shell metal complexes.29 Both the scalar relativistic density functional theory (SR-DFT) and multireference-based complete active space self-consistent (CASSCF) methods are the main workhorses to study the electronic structure and single-ion magnetic behaviour in the mononuclear transition metal and lanthanide complexes. Particularly in molecular magnetism, computational tools play a profound role in predicting SIM performance, magnetic relaxation, and spin–phonon coupling.29,41,70–73 Considering the potential of substituted fullerenes as η5-donor ligands that can mimic the (Cp)− ligands,44,63 we aim to explore the capabilities of three (η5-C55X5)− ligands (where X = CCH3, N or B) in stabilizing Dy(III) based SIMs as an alternative to the [DyCp2]+ family of complexes. Except for (η5-C55(CCH3)5)− ligands,44,64 the (η5-C55B5)−/(η5-C55N5)− ligands produced by exchanging five α-carbon atoms of fullerenes are purely hypothetical and have been investigated to assess the role of orbital interactions offered by B/N atoms compared to the CCH3 group in stabilizing exohedral Dy(III) complexes.74 In the present manuscript, we have studied eight exohedral metallofullerene complexes of the Dy(III) ion with the general formula [Dy(η5-C55X5)(CmHm)] (m = 4, 5, 6, 8 and X = CCH3) and [Dy(η5-C55X5)2]+ (where X = CCH3, N or B) (see Scheme 1). Using SR-DFT calculations, we shed light on the thermodynamic stability and the nature of interaction energy in all the complexes. Bonding analysis was carried out using energy decomposition analysis (EDA) with a natural orbital for the chemical valence (EDA-NOCV)75 approach and quantum theory of atoms in molecules (QTAIM) analysis.76 Next, we performed CASSCF calculations on all the complexes to compute the single-ion anisotropy and relevant spin Hamiltonian (SH) parameters to analyze the SIM behaviour. Finally, we performed the magnetic relaxation analysis to shed light on the nature of QTM and Orbach relaxations.
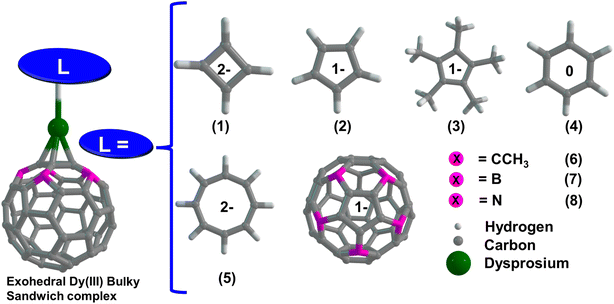 | ||
| Scheme 1 Schematic representation of complexes 1–8, with different ligands at axial positions. Color code: Dy (green), N (blue), B (pink), C (grey), and H (white). | ||
Computational methodology
Geometry optimizations were carried out in the ORCA 5.0.3 code.77,78 Geometry optimization was carried out using SR-DFT calculations at the BP8629 level of theory. Scalar relativity was accounted for using the Douglas–Kroll–Hess (DKH) approximation as implemented in the ORCA code.79 Here, we employed segmented all-electron relativistic contracted (SARC) triple zeta basis set SARC-DKH-TZVP80 for the Dy atom and DKH-adapted version of def2-SVP basis sets81 for all other atoms. The dispersion interaction is addressed using Grimme's dispersion correction with the Becke–Johnson (D3BJ) scheme82,83 as implemented in the ORCA. Vibrational frequency calculations on the DFT-optimized structures of complexes 1–8 show no negative frequency, which validates the stationary points as the local minimum. A tight SCF convergence criterion (1 × 10−8Eh) was used for energy minimization. We used “slowconv” criteria and large integration grid settings (GRID9 for Dy) to achieve smooth energy convergence. Our geometry optimization methodology is highly effective in predicting the structure of open-shell mononuclear transition metal lanthanides and actinide complexes.22,29,84 The reaction energetics are presented as formation energy (ΔE), enthalpy (ΔH), and free energy (ΔG), incorporating electronic energies along with corrections for zero-point vibrational energy. Eqn (1)–(3) have been employed to calculate ΔE, ΔH, and ΔG at 298.15K.| ΔE = Ecomplex − EDy(III) − E(C55X5) − E(CmHm) | (1) |
| ΔH = Hcomplex − HDy(III) − H(C55X5) − H(CmHm) | (2) |
| ΔG = Gcomplex − GDy(III) − G(C55X5) − G(CmHm) | (3) |
| ΔEint = ΔEelstat + ΔEPauli + ΔEorb + ΔEdisp | (4) |
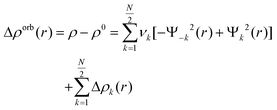 | (5) |
This includes charge transfer, electron pair bonding, and polarization. This systematic breakdown of physical components provides informative and effective insight into bonding, particularly in systems with clear σ/π separation.
Electronic and magnetic properties for complexes 1–8 were carried out using the complete-active space self-consistent field (CASSCF) method90 in the ORCA code. Here, we have used an active space of CAS(9,7), i.e. nine active electrons (f9 configurations) in seven active 4f orbitals and computed all the 21 sextet states emerging from the 6H, 6F, and 6P configurations. These 21 sextets states are good enough for the 6H15/2 SOC spectrum and the magnetic properties of Dy(III) based SIMs.91–96 Spin–orbit calculations were carried out using 21 sextet states with spin–orbit mean field (SOMF-IX) operator and second-order Douglas–Kroll–Hess (DKH2) method79 with a “picturechange 2” option as implemented in ORCA. In addition, we have performed CASSCF calculations, including all 21 sextets, 224 quartets, and 490 doublet roots, and calculations suggest that only 21 sextet roots are sufficient to compute the energy span of eight low-lying KDs in Dy(III) complexes (see Table S18† for details). Next, we utilized a standalone SINGLE_ANISO module97 for the g-values, wavefunction decompositions, crystal field parameters, and transition magnetic moments between the KDs. In addition to ab initio constructed magnetic relaxation based on the average value of transition magnetic moments, we have also computed the effective demagnetization barriers proposed by Aravena et al.70 to analyze the Orbach relaxation process and to predict the blocking temperature.98 This method utilizes the energy of the eight Kramers doublets and the magnetic transition dipole moment related to the transition between the respective KDs (i.e., +1 → −1) from the CAS(9,7) calculations. This method involves the use of eqn (6),
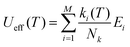 | (6) |
Here, M denotes the number of KDs, ki denotes the demagnetization rates of the KDs of energies Ei, and Nk is a normalization factor for ki as shown in eqn (7):
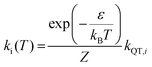 | (7) |
Results and discussion
Here, we have examined eight exohedral metallofullerene complexes named [Dy(η5-C55X5)(η4-C4H4)] (1), [Dy(η5-C55X5)(η5-Cp)]+ (2), [Dy(η5-C55X5)(η5-Cp*)]+ (3) [Dy(η5-C55X5)(η6-C6H6)]2+ (4), [Dy(η5-C55X5)(η8-C8H8)] (5), [Dy(η5-C55X5)2]+ (6) [Dy(η5-C55B5)2]+ (7) and [Dy(η5-C55N5)2]+ (8) (where X = CCH3) for our study. DFT optimization of complexes 1–8 was carried out in the gas phase without symmetry constraints (see the Computational methodology section for details). DFT-optimized coordinates are provided in the ESI.† In complexes 1–5, the computed average Dy–Lcent (Lcent = bond distance between Dy and centroid of the CmHm ring) bond distances decrease as the ring size increases (see Table S1†). In complexes 1–4, we have observed a stabilization of the bent geometry with ∠Lcent–Dy–Lcent of approximately ∼157°, 145°, 161°, and 153°, respectively. The presence of the Cp* ligand in 3 offers higher steric repulsion than in 2 (Cp ligands), resulting in a large ∠Lcent–Dy–Lcent bond angle for 3. Moreover, we compared the structural parameters of complexes 2 and 3 with the DFT optimized geometry of non-bucky analogues [DyCp2]+ (2a) and [DyCp*2]+ (3a) complexes, which suggests that the bulkiness of substituted (C55X5)− cages (X = CCH3) naturally offers more linearity in the ∠Lcent–Dy–Lcent bond angle, which is the key for maximizing the axiality in the Dy(III) based sandwiched complexes (see Table S1†). The DFT optimized geometry of complex 5 nicely matches the previously reported X-ray crystal structure of the [Cp*DyCOT] complex,99 highlighting the goodness of our computational methodology in reproducing heteroleptic organometallic sandwiched complexes. In complexes 6–8, we observed that the avg. Dy–Lcent (C55X5)− bond distance is 2.351, 2.284, and 2.389 Å, respectively, and the ∠Lcent–Dy–Lcent bond angle is close to 180°, highlighting the importance of the steric effect caused by the (C55X5)− ring which forces a linear geometry around the Dy(III) ion. Structural analysis of all the complexes reveals that the average Dy–Lcent (C55X5)− bond distances calculated from the centroid of the ring range between 2.284 and 2.389 Å, which is slightly larger than the average Dy–Cp/Dy–Cp* bond distance in complexes 2–3, indicating a comparatively weaker bonding in complexes 6–8. DFT optimization predicts the stabilization of staggered D5d local symmetry around the Dy(III) ion in complexes 6–8. The detailed structural parameters for all the complexes are provided in Table S1.† In addition, we optimized the geometry of Cp* and (C55X5)− ligands, and we observed that the highest occupied molecular orbitals (HOMOs) are mainly the π-electron clouds on the five-membered ring of the ligands. It is evident from the observed HOMOs of (C55X5)− rings (where X = B/N) that the π-conjugation in fullerenes is not completely broken when α-C atoms are replaced by B/N atoms. In contrast, for the (C55(CCH3)5)− ring, the sum of orbital densities of HOMO and HOMO−1 nicely resembles the Cp* ligands as the sp3 hybridized α-C carbon completely breaks the π-conjugation in the (C55(CCH3)5)− ring, making them electron-rich donors compared to B/N analogues (see Fig. 1). The computed molecular electrostatic potential of (C55X5)− ligands reveals that the five-membered rings are relatively electron deficient in nature compared to the Cp* ligands, which has direct consequences on metal–ligand interactions.Interaction energy and thermodynamics
To compute the interaction energies (IE) among the fragments in metallocenes, we designated the metal cation Dy(III) as a Y fragment, while the CmHm ring and (C55X5)− were identified as X and X′ fragments, respectively. The interaction energy was determined using eqn (8):| IEtotal = EXYX′free − (EXfrozen + EYfrozen + EX′frozen) | (8) |
Here EXYX′free, is the energy of the optimized geometry of the XYX′ complex (1–8), whereas EXfrozen + EYfrozen + EX′frozen are the energies of X, Y, and X′ frozen components in the optimized geometry of the XYX′ complex, respectively.
Table 1 shows that the interaction between the Dy(III) center and the two ligands ((CmHm) and (C55X5)−) is favorable, showing sizable interaction energy values ranging between ∼700 and 1200 kcal mol−1. Since the energy of the Dy(III) ion and (C55X5)− remains constant throughout the series in complexes 1–5, the key factor devising overall interaction energy is the EX and the EXYX′ component, which is the energy of the (CmHm) fragment and the total energy of the complexes respectively. The highest interaction (IETotal) is observed for complexes 1 and 5, which feature dianionic (C4H4)2− and (C8H8)2− rings, while the lowest interaction is observed for complex 4, possessing neutral (C6H6) as the X fragment. An intermediate value of IETotal is observed for complexes 2, 3, 6, 7, and 8, which possess monoanionic (CmHm) rings. The observed trend indicates that the IETotal value strongly depends on the strength of the electrostatic interaction between fragments (vide infra). A nearly identical value of IETotal is obtained for complexes 2 and 3, which suggests that the Cp and Cp* rings interact almost similarly with the other components. Among complexes 6–8, where both the X and X′ components are substituted fullerenes (C55X5)−, we observed the following trend in the IETotal value 6 > 7 ≈ 8, with the IETotal in 6 nearly ∼50 kcal mol−1 higher than 7 and 8. In addition, we have computed thermodynamic parameters at 298.15 K to predict the formation energy of these complexes, and the computed change in the free energies is highly exothermic for all the complexes, which is in line with IETotal analysis (see Tables S3 and S4†).
| Complex | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| E X(Eh) | −154.4 | −193.5 | −390.0 | −232.2 | −309.4 | −2485.6 | −2219.8 | −2369.3 |
| E Y(Eh) | −12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 148.3 148.3 |
−12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 148.3 148.3 |
−12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 148.3 148.3 |
−12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 148.3 148.3 |
−12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 148.3 148.3 |
−12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 148.3 148.3 |
−12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 148.3 148.3 |
−12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 148.3 148.3 |
| E X′(Eh) | −2485.6 | −2485.6 | −2485.6 | −2485.6 | −2485.6 | −2485.6 | −2219.8 | −2369.3 |
| E XYX′(Eh) | −14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 790.2 790.2 |
−14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 828.9 828.9 |
−15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 025.5 025.5 |
−14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 867.2 867.2 |
−14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 945.2 945.2 |
−17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 121.0 121.0 |
−16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 589.2 589.2 |
−16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 888.2 888.2 |
| IETotal(Eh) | −1.9 | −1.5 | −1.5 | −1.1 | −1.9 | −1.4 | −1.3 | −1.3 |
| IETotal(kcal mol−1) | −1211.2 | −923.1 | −933.1 | −690.2 | −1177.7 | −895.1 | −834.9 | −823.6 |
Next, we performed EDA analysis by fragmenting complexes 1–8 into two fragments, Dy(III) as fragment 1 carrying a tri positive charge, whereas the other two rings ((CmHm)2−/1−/0 and (C55X5)−) as fragment 2.100 This fragmentation scheme allowed us to understand the nature and strength of the binding interaction between the corresponding fragments. EDA analysis predicts a negative value of the total interaction energy (ΔEint) for all the complexes, which aligns with interaction energy analysis and thermodynamic calculation (see Table 2). EDA calculations predict the following trend in the ΔEint value: 5 > 1 > 3 ≈ 2 > 6 > 7 > 8 > 4, with the most considerable ΔEint value observed for 5 while the smallest ΔEint value is reported for 4. The decomposition of the interaction energy suggests that both the orbital interactions (ΔEorb) and the electrostatic interaction (ΔEelstat) are the most significant contributors to the total interaction energy (ΔEint), with the former one being relatively more dominant compared to the ΔEelstat values. We observed the following trend in the ΔEelstat value: 5 > 1 > 2 ≈ 3 > 6 > 7 > 8 > 4, which agrees with the trend observed for the ΔEint value, indicating that the ΔEelstat components control the overall interaction energy in complexes 1–8.
| Energy | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| ΔEPauli | 192.1 | 208.7 | 225.2 | 207.6 | 253.8 | 186.0 | 183.5 | 158.5 |
| ΔEelstat | −709.0 | −610.0 | −604.9 | −353.0 | −755.6 | −512.4 | −440.3 | −408.8 |
| ΔEorb | −700.8 | −623.3 | −653.9 | −608.5 | −761.5 | −623.5 | −656.6 | −639.9 |
| ΔEdisp | −7.4 | −7.1 | 19.0 | −7.1 | −7.2 | −10.8 | −4.9 | −6.9 |
| ΔEint | −1225.0 | −1031.7 | −1042.6 | −761.0 | −1270.5 | −960.7 | −918.4 | −897.0 |
| ΔEorb(1) | −282.6 | −262.2 | −269.1 | −311.4 | −227.4 | −232.8 | −249.9 | −238.4 |
| ΔEorb(2) | −216.5 | −237.9 | −231.2 | −265.4 | −206.2 | −233.4 | −249.8 | −292.6 |
| Total | −499.1 | −500.1 | −500.3 | −576.8 | −433.6 | −466.2 | −499.8 | −531.0 |
| % ΔEorb | 71.2 | 80.2 | 76.5 | 94.8 | 56.9 | 74.8 | 76.1 | 83.0 |
| ΔEint = ΔEelstat + ΔEPauli + ΔEorb + ΔEdisp | ||||||||
The orbital interaction is the most vital contributor to the overall interaction energy with the following trend in ΔEorb values: 5 > 1 > 7 > 3 > 8 > 2 ≈ 6 > 4. The most substantial orbital interaction is observed in complexes 1 (∼701 kcal mol−1) and 5 (∼762 kcal mol−1) due to the strong interaction between the Dy(III) orbitals (4f and 5d) with the π-cloud of the (C4H4)2− and (C8H8)2− ligands. Due to similar ligand scaffolds in complexes 2 and 3, we observed nearly similar ΔEorb values for these complexes. The weakest ΔEorb value of ∼609 kcal mol−1 is observed for complex 4. It is important to note here that, unlike trends observed in ΔEelstat values, the variation in the ΔEorb value is close to 20% within the studied complexes, which manifests the weak lanthanide-ligand covalency.
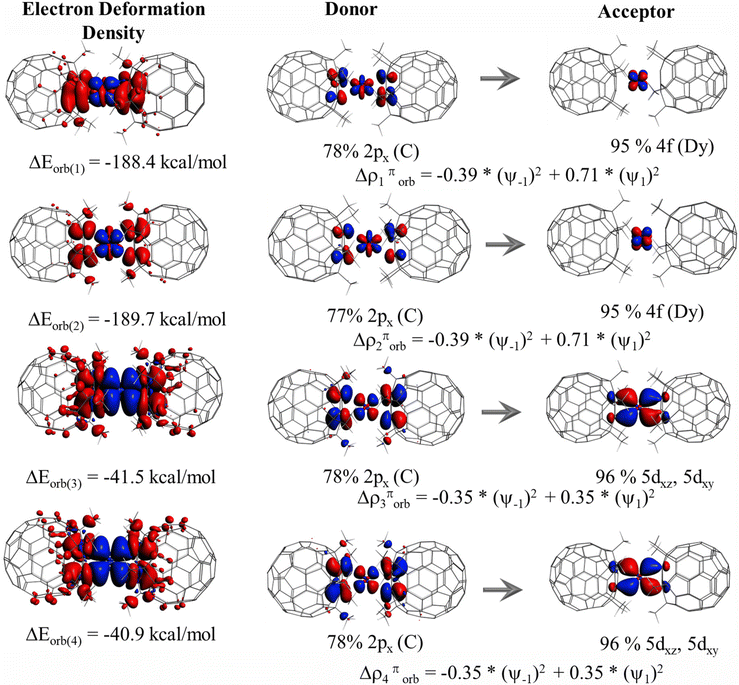
To further decompose the origin of orbital interactions, we have performed an ETS-NOCV75,100,101 analysis on complexes 1–8. In the ETS-NOCV technique, orbital interaction energy (ΔEorb) is broken down into contributions from each NOCV (donor–acceptor) pair, which can be linked to specific bonding types between fragments, such as σ and π bonding. Each interaction ΔEorb(i) is assigned a numerical energy value through visual inspection of NOCVs. NOCVs can be used to visually explore ΔEorb, represented by the eigenfunctions (Ψi) of the density difference between molecular and promolecular densities. Each pair of NOCVs corresponds to two orbitals with equal and opposite eigenvalues(νi). As a molecule forms from a promolecule, electron density transfers through channels described by these NOCV pairs. The magnitude of NOCV eigenvalues indicates the importance of each pair in bond formation. The first four deformation densities (Δρi) corresponding to the NOCV pairs for complexes 1–8 are depicted in Table S7,† starting with the pair with the greatest eigenvalue. Red areas of Δρi show charge depletion, whereas blue areas indicate charge accumulation upon bond formation. From deformation densities, it is evident that the red region is mainly located on the coordinating ligands while the blue region is located on the Dy(III) ion, suggesting an electron flow from the ligand to metal orbitals. Based on the visual inspection of the NOCVs, the ΔEorb(1) and ΔEorb(2) have the highest magnitude in complexes 1–8, which contribute around ∼70–80% of the total ΔEorb value (see Table 2). A closer inspection of NOCV pairs corresponding to ΔEorb(1) and ΔEorb(2) suggests that the giant orbital interaction energy arises due to π-type interaction, where electron flow occurs predominantly from the 2px orbital of the coordinating ligand (π-cloud) to the 4f orbital of the Dy(III) ion. This indicates the presence of sizable 4f-ligand covalency in all the studied complexes. On the other hand, the ΔEorb(3) and ΔEorb(4) correspond to the electron flow from the 2px orbitals of the coordinating ligand (π-cloud) to the 5dyz/5dxz orbital of the Dy(III) ion and roughly contribute ∼10–30% of the total ΔEorb value. Due to the difference in X and X′ ligands in complexes 1–5, we observed different ΔEorb(1) and ΔEorb(2) values, while complexes 6–8 show nearly similar values. In complex 6, the ΔEorb(1) and ΔEorb(2) values are ∼−188 kcal mol−1 and −189 kcal mol−1, which contribute around ∼74.8% of the total ΔEorb value (see Fig. 2). The ΔEorb(3) and ΔEorb(4) values are ∼−41 and −40 kcal mol−1, which corresponds to the electron flow from the 2px orbitals of the coordinating ligand (π-cloud) to the 5dyz/5dxz orbital of the Dy(III) ion, indicating 5d-covalency in the studied complexes(see Fig. 2). NPA analysis of the fragments also shows a prominent gain in the 5d orbitals (+0.30 a.u.) and 4f orbitals (+0.11 a.u.) upon complexation, confirming the participation of 4f and 5d orbitals in the bonding (see Table S8†).
EDA computed dispersion interactions are stabilizing in nature and contribute ∼1–2% of the total interaction energy. The highest dispersion interaction (ΔEdisp) is observed in complexes 3 (∼9 kcal mol−1) and 6 (∼11 kcal mol−1) due to the presence of the methyl group in the Cp* and the (C55(CCH3)5)− ligands, resulting in sizable non-covalent interaction. To further probe this, we performed a non-covalent interaction (NCI) analysis,102,103 which offers a way to present non-covalent interactions in real space. In complexes 1–5, the presence of –CH3 groups in (C55(CCH3)5)− fragments results in sizeable van der Waals (vdW) interaction between the fragments, which is visible in the NCI plots. The most considerable dispersion interaction for 6 (10.8 kcal mol−1) results from strong vdW interactions between the two bulky (C55(CCH3)5)− ligands (see Fig. 3). Replacement of CH3 groups with B/N atoms significantly reduces the non-covalent interactions in 7 and 8, resulting in weaker ΔEint values for these complexes compared to 6.
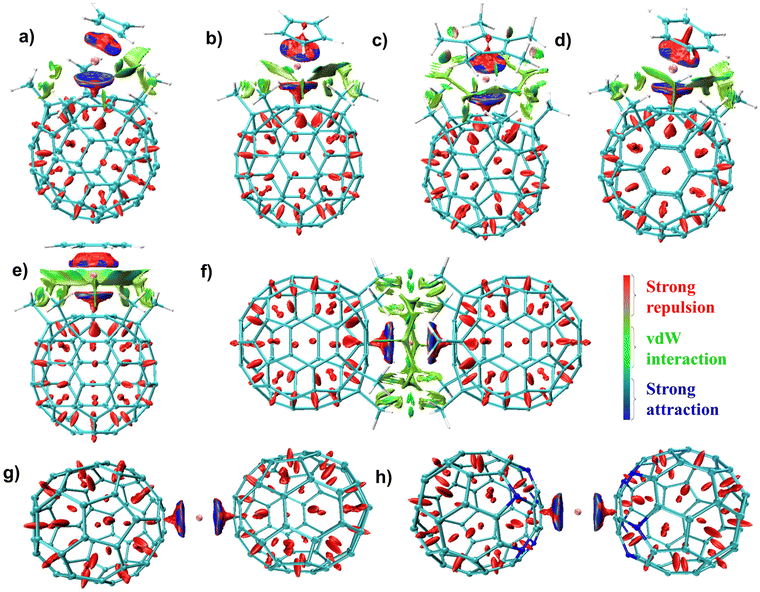 | ||
| Fig. 3 (a)–(h) Non-covalent interaction (NCI) plots for complexes 1–8. The isosurfaces are colour-coded based on the sign of the Laplacian (ρ) at a contour value of 0.05 a.u. Blue color denotes strong attraction (−ve ρ), green indicates vdW interactions (ρ ∼ 0), and red indicates repulsive interaction (+ve ρ). Images were generated using Multiwfn104 and VMD software.105 | ||
Next, we performed the QTAIM analysis76,106 for all the complexes to further quantify the nature of the bond between the Dy and ligands (see Table S9† and Fig. 4). QTAIM divides molecular electron density into separate regions using surfaces where ∇ρ(r)·n(r) = 0. Each region or basin, usually corresponds to an atom. Critical points such as bond critical points (BCPs) occur where bond paths intersect interatomic surfaces. BCPs are represented in red, and ring critical points (RCPs) in green. The values of (–G/V)BCP > 1 at the critical points signify ionic or non-covalent bonding, where local kinetic energy prevails over potential energy. On the other hand, values ranging from 0.5 to 1 indicate partial covalency.107 Based on Table S9,† it is apparent that all eight complexes in our study have |G/V|BCP values below 1, indicating the presence of partial covalency. Typically, electron densities ρ(r) exceeding 0.2 atomic units (a.u.) with ∇2ρ(r) < 0 are characteristic of covalent bonds, while those below 0.1 a.u. with ∇2ρ(r) > 0 suggest a more ionic bonding nature.108 In all cases, we observe ρ(r) less than 0.05 a.u (<0.1 a.u.) and ∇2ρ(r) ∼ 0.1(>0), suggestive of ionic bonding. To conclude, the Dy–Cligand bonds in complexes 1–8 are predominantly ionic in nature since ρ(r) is a more reliable parameter to quantify the nature of bonds.109,110 The computed average electron density ρ(r) suggests that the nature of bonding in hybrid bucky complexes (1–5) is nearly similar to di-bucky analogues (6–8), where the former ones are marginally more ionic in nature.
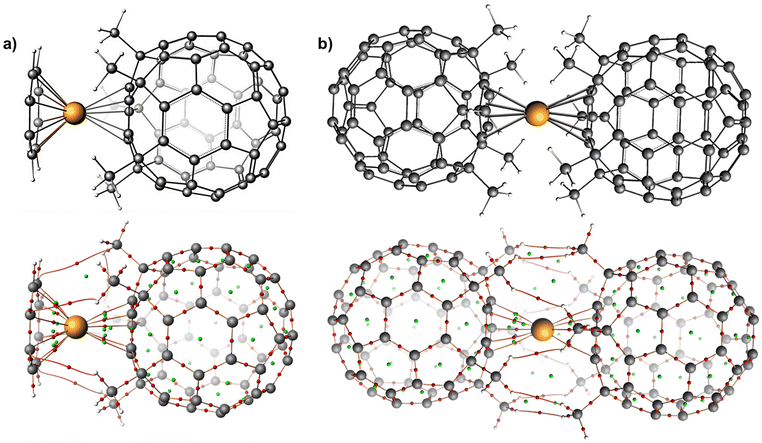 | ||
| Fig. 4 PBE0-D3(BJ)/TZP computed QTAIM topology maps for (a) complex 5 (b) complex 6. Colour code: Dy (orange), C (grey), H (white). | ||
Magnetic anisotropy analysis in complexes 1–8
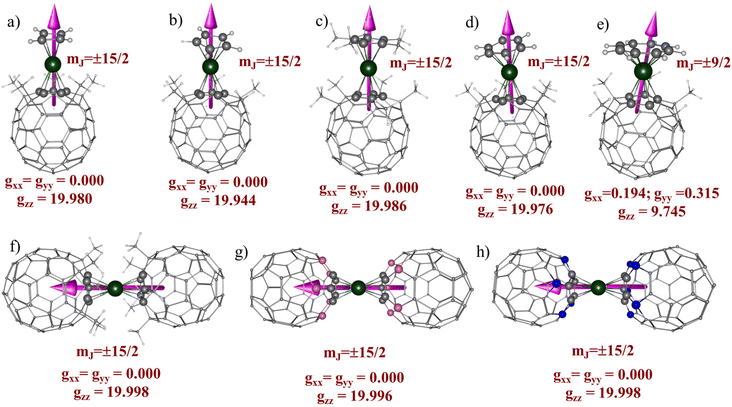
CASSCF calculations predict stabilization of mJ |±15/2〉 for all the complexes except for 5, where the ligand field stabilizes mJ |±9/2〉 as the ground state (see Fig. 5). In complex 1, the Dy(III) ion is sandwiched between the cyclobutadiene dianion (C4H4)2− ligand and the (C55(CCH3)5)− ligand with a bent ∠Lcent–Dy–Lcent angle of 156.9° degree. CASSCF calculations predict the span of the eight low-lying KDs derived from the 6H15/2 ground multiplet over an energy range of approximately 1649.2 cm−1, with the first excited KD at approximately 487.4 cm−1 for complex 1. The computed ground state g-values are highly axial in nature (gzz = 19.980) with extremely weak transverse components (gxx = gyy = 1 × 10−4) (see Table S10†). This is further explained by wavefunction decomposition analysis showing 99% mJ |±15/2〉 as the ground state with no mixing from the other excited KDs (see Table S15†). The principal z-axis of the g-tensor passes through the centre of the (C4H4)2− ligand. Analysis of the g-tensor orientation of all eight KDs suggests that the gzz orientation up to the 6th KD is nearly collinear (≤10 degrees), indicating that magnetization can be blocked up to this KD. The gzz orientation of the 7th KD deviates by an angle of 94.3° from the ground state KD, indicating that magnetization reversal is likely to occur via this state. The CASSCF computed Ucal value is 1538.6 cm−1 (2154.0 K) for 1 (see Table 3). The computed transverse magnetic moment between the ground state KDs is negligible (2.43 × 10−7μB), indicating complete quenching of QTM within the ground state KDs. Moreover, the computed transverse magnetic moment between the ground and excited KDs is always significantly higher than the values obtained within the KDs, highlighting that the thermally activated Orbach process is more dominant until the 7th KD as the QTM values are minimal. Due to the lack of linearity in the ∠Lcent–Dy–Lcent angle of 1, we have not observed the complete blockade of magnetization up to the 7th KD.| KD | g xx | g yy | g zz | θ (°) | k QTM | U cal (cm−1) | U eff (cm−1) | T B (K) | |
|---|---|---|---|---|---|---|---|---|---|
| 1 | KD1 | 0.000 | 0.000 | 19.980 | — | 2.43 × 10−7 | 1538.6 | 1501.0 | 53.6 |
| KD7 | 3.227 | 4.480 | 7.803 | 94.3 | 2.04 × 10 | ||||
| 2 | KD1 | 0.000 | 0.000 | 19.944 | — | 1.46 × 10−6 | 1305.0 | 1338.0 | 47.7 |
| KD7 | 8.519 | 8.157 | 2.690 | 0.6 | 2.78 × 10 | ||||
| 2a | KD1 | 0.000 | 0.000 | 19.890 | — | 4.53 × 10−6 | 1111.2 | 1181.0 | 42.2 |
| KD6 | 4.089 | 4.876 | 11.240 | 90.9 | 2.69 × 10 | ||||
| 3 | KD1 | 0.000 | 0.000 | 19.986 | — | 6.55 × 10−8 | 1569.5 | 1627.5 | 58.1 |
| KD7 | 2.742 | 3.097 | 3.619 | 10.4 | 9.77 × 10−1 | ||||
| 3a | KD1 | 0.000 | 0.000 | 19.970 | — | 6.02 × 10−7 | 1551.5 | 1589 | 56.8 |
| KD7 | 7.945 | 6.819 | 3.024 | 0.5 | 2.46 × 10 | ||||
| 4 | KD1 | 0.000 | 0.000 | 19.976 | — | 1.71 × 10−7 | 1124.8 | 1133.0 | 40.5 |
| KD7 | 3.309 | 3.384 | 7.521 | 82.4 | 1.87 × 10 | ||||
| 5 | KD1 | 0.194 | 0.315 | 9.745 | — | 8.48 × 10−2 | 108.4 | 95.2 | 3.4 |
| KD6 | 4.750 | 6.936 | 9.358 | 99.2 | 2.63 × 10 | ||||
| 6 | KD1 | 0.000 | 0.000 | 19.998 | — | 3.99 × 10−9 | 1573.7 | 1533.0 | 54.8 |
| KD8 | 11.607 | 9.451 | 1.188 | 0.5 | 3.51 × 10 | ||||
| 7 | KD1 | 0.000 | 0.000 | 19.996 | — | 2.37 × 10−7 | 1284.1 | 1235.0 | 44.1 |
| KD8 | 11.322 | 9.789 | 1.212 | 0.4 | 3.52 × 10 | ||||
| 8 | KD1 | 0.000 | 0.000 | 19.998 | — | 8.99 × 10−8 | 1347.0 | 1314.0 | 46.9 |
| KD8 | 11.189 | 9.907 | 1.201 | 0.4 | 3.51 × 10 |
Next, we analyzed the magnetic anisotropy in complexes 2 and 3 (see Tables S10 and S12†), which only differ with respect to Cp/Cp* ligands. As a result of the bulky effect of the Cp* ligand, we observed a relatively more linear ∠Lcent–Dy–Lcent angle in 3 (160.8°) compared to 2 (145.2°). The energies of eight low-lying KDs span over an energy range of 1423.5 and 1675.4 cm−1 for complexes 2 and 3, respectively. The energy span of 2 is shrunk by ∼15% compared to 3 due to the large bent angle, which decreases the axial ligand field strength. The computed g-values are highly axial in nature gzz = 19.944 and gxx = gyy = 1 × 10−4 (gzz = 19.986, gxx = gyy = 1 × 10−4) with a negligible transverse component in the g-values for 2(3). The principal z-axis of the g-tensor passes through the centroid of the Cp/Cp* rings in 2 and 3, respectively. The wavefunction decomposition analysis reveals stabilization of pure mJ |±15/2〉 as the ground state for 2 and 3 (see Table S15†). Consequently, the computed transverse magnetic moment between the ground state KDs is extremely weak (1.46 × 10−6μB (2) and 6.55 × 10−8μB (3)), which directly indicates that ground state QTM is quenched in both the complexes (see Table 3). For 3, the transverse magnetic moment between the ground state KD is two orders smaller than 2, indicating a stronger axial ligand field offered by the Cp* ligand helps to quench the ground state QTM. The ab initio computed blockade barrier suggests magnetization blockade up to the 6th KD, and magnetization relaxation is likely to occur via the 7th KD, which is mainly mJ |±3/2〉 in nature. The computed Ucal values are 1305.0 and 1569.5 cm−1 for 2 and 3, respectively. The presence of the electron-donating –CH3 group (see the computed NPA charges in Table S6†) in the Cp* ligand and the relatively small bent angles increases the metal–ligand interaction (π-type), which results in a higher Ucal value for 3. Interestingly, the calculated Ucal value of 3 is comparable to that of 1, which possesses a dianionic (C4H4)2− ligand. The effects of π-type interactions are well captured by the AILFT111 computed f-orbital splitting pattern, which displays a preferential destabilization of the fxz2/fyz2 orbitals compared to other 4f orbitals. For complexes 1–3, we observed the following splitting pattern fxz2/fyz2 > fz3 > fz(x2−y2)/fxyz > fx(x2−3y2)/fy(3x2−y2), with relatively stronger splitting for 3 (see Fig. S1†), which indicates that the relatively large ∠Lcent–Dy–Lcent angle in 3 dramatically increases the axial ligand field splitting and takes precedence over the electrostatic effects provided by the dianionic (C4H4)2− ligand.
Next, we compared the single-ion magnetic properties of 2 and 3 with their non-bucky analogues [DyCp2]+ (2a) and [DyCp*2]+ (3a) to assess the effect of bulky fullerenes. The first noticeable effect is witnessed in the structural parameters, where 2 (145°) and 3 (160°) show a larger ∠Lcent–Dy–Lcent angle than complexes 2a (129°) and 3a (148°), suggesting that the bulkiness offered by substituted fullerenes naturally offers more linearity (see Table S1†). For 2a, the span of eight low-lying KDs and Ucal value is shrunk by 7.0% and 14.9%, respectively, compared to 2, indicating a strong axial ligand field in 2. A fair comparison can be made between 3 and 3a where one of the X′ ligands is different. For 3a, the Ucal values and the span of the eight low-lying KDs are 1551.5 cm−1 and 1668.5 cm−1, respectively, nearly similar to what was observed for complex 3 (see Tables S11 and S12†). The similarity in the span of eight low-lying KDs hints that the strength of the ligand field is nearly similar for both 3 and 3a despite having a larger ∠Lcent–Dy–Lcent angle in 3. The only noticeable difference is observed in the computed kQTM values, which are ∼10× times smaller for complex 3 (kQTM = 6.55 × 10−8) than 3a (kQTM = 6.02 × 10−7). To further understand the origin of similarity in the span of eight low-lying KDs, we investigated the electronic effects of ligands by analyzing CASSCF computed Mulliken charges. In complex 3a, we observed that each Cp* ring carries a charge of ∼−1.17 a.u, which is significantly higher compared to the −0.38 a.u charges on the coordinated five-membered ring of (C55(CCH3)5)− ligand in 3 (see Fig. S2†). CASSCF computed Mulliken charge distribution in 3 resembles the DFT computed NPA charges (see Table S6 and Fig. S3†). Our charge analysis suggests that the abruption of π-conjugation by substituting α-carbons largely compensates the negative charges on the coordinated atoms of the five-member ring, leading to a weaker electrostatic field in the (C55(CCH3)5)− ligand compared to Cp* ligands. Our previous work on organometallic sandwiched complexes suggests that electrostatic effects are much weaker than the structural parameters, and the ∠Lcent–Dy–Lcent angle is the critical parameter to attain giant Ucal value in these complexes.29 Despite having a large ∠Lcent–Dy–Lcent angle in 3, a relatively more electron-deficient five-membered ring of the (C55(CCH3)5)− ligand compared to the Cp* ligand competes with the structural benefits, resulting in no substantial increase in the Ucal values compared to 3a. Both electronic and structural effects oppose each other in complex 3 and 3a, resulting in similar Ucal values (see Fig. S2†). Recent studies indicate that high-temperature magnetic relaxation in [Dy(Cpttt)2]+ complexes is induced by Cp–H bending modes, where strong spin–vibronic coupling leads to faster relaxation despite having large Ueff values.25,40,41,112 In this context, rigid frameworks offered by the substituted fullerene ligands offer a way to reduce these vibrational motions, which in turn reduces the resonance between the vibronic and electronic states and, hence, pave the way to slower the magnetic relaxation in Dy(III) based exohedral complexes.
For complex 4, we observed the stabilization of mJ |±15/2〉 as the ground state with Ising type anisotropy, gzz = 19.976, gxx = gyy = 1 × 10−4. Compared to complexes 3(2), the energy span of eight KDs is narrowed by 28% (16%) for 4, which arises due to the weak electrostatic interaction between the Dy(III) ion and the neutral C6H6 ring. For complex 4, the magnetic relaxation occurs via the 7th excited KD, resulting in a Ucal value of 1124 cm−1 with an extremely weak ground state kQTM value of 1.71 × 10−7μB. As observed earlier,29 the nature of Dy(III) and ligand interactions remains π-type with the following splitting pattern: fxz2/fyz2 > fz3 > fz(x2−y2)/fxyz > fx(x2−3y2)/fy(3x2−y2), resulting in a high axiality in complex 4, despite having the neutral C6H6 ligand (see Fig. S1†).
On the other hand, in complex 5, the ligand field stabilizes mJ |±9/2〉 primarily as the ground state (39% |±9/2〉 + 27% |±5/2〉 + 15% |±11/2〉), which is strongly mixed with other KDs (see Table S15†). The computed ground state g-values are axial with a sizable transverse component (gzz = 9.744, gxx = 0.193, gyy = 0.314), a typical manifestation of a low mJ state. As a result, we have noticed a giant kQTM value of 1.71 × 10−2μB in complex 5, which indicates strong QTM to be operative within the ground state. Analysis of the g-tensor orientation and blockade barrier predicts that the magnetic relaxation is likely to occur via the 6th KD through a thermally activated process, which sets the Ucal value of 108.4 cm−1. Moreover, we observed the following orbital ordering, fz(x2−y2)/fxyz > fx(x2−3y2)/fy(3x2−y2) > fxz2/fyz2 > fz2 in 5, which differs from what we observed for complexes 1–4. Although the (C8H8)2− ligand is dianionic, similar to the (C4H4)2− ligand in 1, the large ring size of the (C8H8)2− ring changes the 4f-ligand bonding interaction from π-type to δ-type, which generates an unfavourable equatorial ligand field and stabilizes the mJ |±9/2〉 ground state.29,113
Next, we analyzed the magnetic anisotropy and SIM behaviour in complexes 6–8, where the Dy(III) ion is sandwiched between two (C55X5)− ligands (where X = CCH3, B, and N). DFT optimization predicts a perfect linear arrangement around the Dy(III) ion where both the (C55X5)− ligands are arranged in a staggered fashion (D5d). As a result of the strict linearity around the Dy(III) ion in complexes 6–8, we observed stabilization of pure mJ |±15/2〉 as the ground state with negligible mixing with other excited states. CASSCF computed g-values for complexes 6–8 are highly anisotropic in nature and show an Ising type feature (gxx = gyy ≈ 1 × 10−4 and gzz = 19.998(6), gxx = gyy ≈ 1 × 10−4 and gzz = 19.996(7) and gxx = gyy ≈ 1 × 10−4 and gzz = 19.998(8)). The eight low-lying KDs span over an energy range of 1573.7, 1284.1, and 1347.0 cm−1 for complexes 6–8, respectively. For complexes 6–8, the principal z-axis of the g-tensor passes with the highest C5 symmetry axis, which passes through the center of the attached (C55X5)− ligands. Due to higher order symmetry, the orientation of all eight KDs is perfectly collinear with each other, resulting in the magnetization blockade up to the 7th KD, which enables the magnetic relaxation via the 8th KD (mJ |±1/2〉). The computed Ucal values are the same as the energy span of low-lying KDs in the following order: Ucal (6) > Ucal (8) > Ucal (7), with the largest Ucal value reported for complex 6. As the local structural parameters of complexes 6–8 are similar, the observed differences in Ucal might be due to the differences in the electronic effects. As observed in the EDA analysis, the accumulation of negative charges around the Cp ring and α-C atoms in 6 generates more electrostatic interaction from the axial direction, which helps to maximize the splitting of the 6H15/2 state. In contrast, a relatively weaker ligand field is generated in complexes 7 and 8 where the α-C atoms are substituted by B and N atoms, resulting in relatively smaller Ucal values. The ground state transverse magnetic moment is 3.99 × 10−9μB, 2.37 × 10−7μB, and 8.99 × 10−8μB for complexes 6, 7, and 8, respectively, indicating complete quenching of the QTM within the ground state. Our single-ion analysis suggests that all three complexes (6–8) are potentially good candidates for the isolation of Dy(III) based SIM; however, 6 shows an exceptionally giant barrier height and extremely weak ground state kQTM values. The computed Ucal value of 6 is even more significant than the Ucal value observed for the [DyCp*2]+ (3a) complex, which makes them highly promising for SMM designing. When comparing the kQTM values of complex 3a with complex 6, we observed that the kQTM value of 6 (kQTM = 3.99 × 10−9μB) is approximately 150× smaller than that of complex 3a (kQTM = 6.02 × 10−7μB), which is attributed solely to the strict linearity found in complex 6. The computed ab initio blockade barrier for complexes 6–8 is depicted in Fig. 6. Although the (C55X5)− (where X = CCH3, N or B) ligands offer a relatively weak electrostatic field compared to the Cp* ligand, the strict linearity offered by the (C55(CCH3)5)− ligand in complexes 6–8, makes them promising candidates for designing new-generation of exohedral substituted fullerenes based organometallic Dy(III) SMMs.
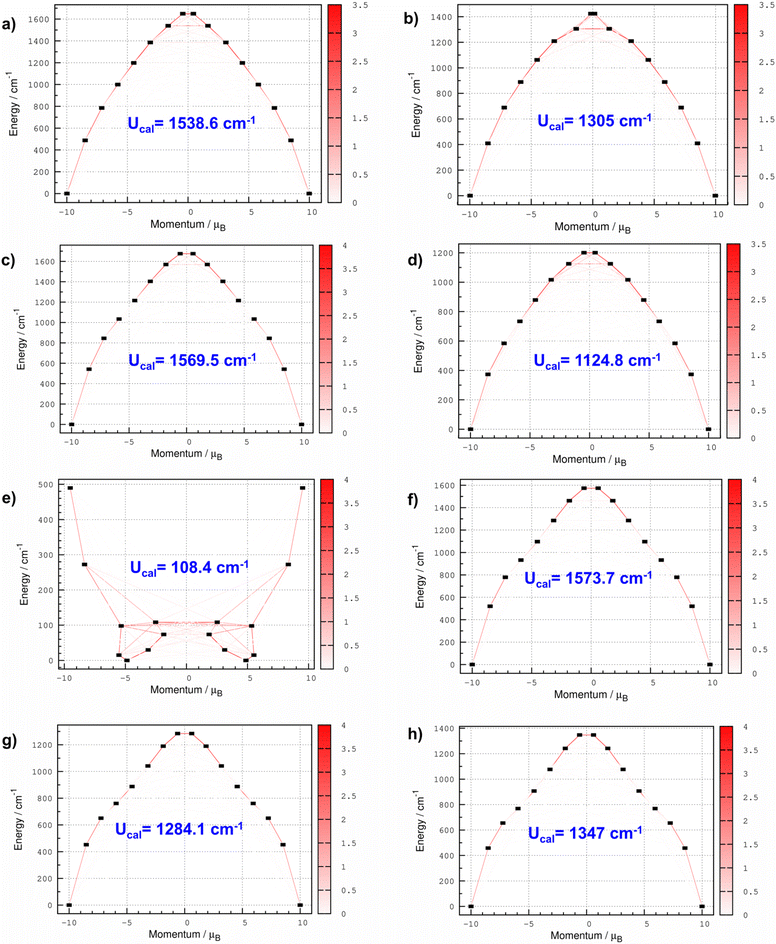 | ||
| Fig. 6 (a)–(h) SINGLE_ANISO computed magnetization blockade barriers for complexes 1–8, respectively. | ||
Next, we computed the temperature-dependent effective demagnetization barrier (Ueff) and the relative contribution from each KD, which helped us to understand the Orbach relaxation (see Fig. 7, S4, and Table S16†). For all the studied complexes, we observed that the ab initio blockade barrier nicely matches the demagnetization barrier, indicating that all these complexes are highly symmetric and exhibit negligible QTM values. From 0 K to 300 K, the temperature dependence of both Ueff and the contributions from various KDs for complexes 1–8 is illustrated in Fig. 7 and S4.† The entire temperature range can be divided into three regions: (I) the initial temperature region, (II) the region where Ueff rises sharply, and (III) the region where Ueff saturates. Within region I, the Ueff remains nearly zero since all the populations are in the mJ |±15/2〉 ground state, which is blocked due to the minimal kQTM value (∼10−6–10−9μB) except for complex 5 (∼10−2μB). This region continues up to 50 K, which indicates that the QTM is completely blocked at this temperature, and other relaxation processes, such as Orbach/Raman relaxation, must be considered in this region. In region II, a rapid temperature increase causes a rapid population growth of other excited KDs. As temperature increases beyond 50 K, the Ueff value increases by climbing to the higher excited KDs with sequential absorption of the thermally available phonons for all the complexes except 5. In region III, Ueff saturates, and the Orbach regime is reached for all the complexes at room temperature. Among complexes 1–8, complex 3 shows the largest Ueff value of 1627.5 cm−1, while complex 5 shows the smallest Ueff value of ∼95.2 cm−1. We observed the following Ueff values: 1533 cm−1, 1235 cm−1, and 1314 cm−1 for complexes 6–8, respectively, which agrees with the trends observed from ab initio calculations. In complex 6, the saturation in Ueff emerges from three KDs (KD8 81% + KD7 12% + KD6 4%) (see Table S16†), indicating that thermal-assisted quantum tunnelling of magnetization (TA-QTM) is completely blocked at lower KDs, a typical manifestation of ideal Dy(III) based SIM in complete axial ligand field. SINGLE_ANISO computed energy of KD8 is 1573.7 cm−1, nearly the same as the saturated Ueff value of 1533 cm−1. A careful analysis of temperature dependence data reveals a slight hump in region II of complex 6, which might be due to the similar strength of kQTM values of KD3 and KD4 (3.12 × 10−3 and 3.03 × 10−3), indicating a probable path for thermally assisted QTM. The wave function decomposition analysis shows significant mixing between the KD3(78.5% |±11/2〉 + 17.5% |±9/2〉) and KD4(77.6% |±9/2〉 + 20% |±11/2〉) which is the cause for the similar superposition of the kQTM values. It is important to note that the computed Ueff and TB values obtained from eqn (6) and (7) do not consider the Raman mechanism for magnetic relaxation. Hence, the computed Ueff and TB values must be viewed as an upper limit as the presence of Raman relaxation can further lower Ueff and TB significantly.98
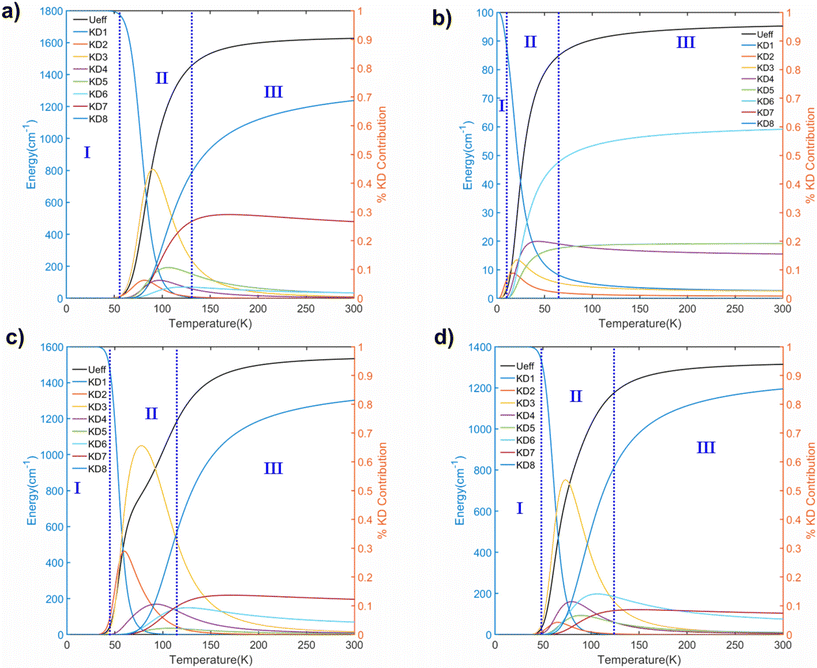 | ||
| Fig. 7 Temperature dependence of calculated Ueff, along with the relative contribution of each Kramers doublet to the relaxation, calculated as ki(T)/Nk for (a) 3, (b) 5, (c) 6, and (d) 8. | ||
Conclusion
To this end, for the first time, we have successfully explored the capability of substituted fullerenes as (Cp)− mimicking ligands towards stabilizing novel Dy(III) exohedral substituted fullerene complexes, which are relevant for designing a new generation of organometallic SIMs. DFT-optimized structural parameters reveal that complexes 1–4 possess a bent geometry while complexes 5–8 possess a linear geometry around the Dy(III) ion. The bulkiness of two (C55X5)− ligands leads to a strictly linear geometry in complexes 6–8, which is otherwise a non-trivial task to achieve by bulking the Cp ligand. Thermodynamic and interaction energy analysis at the SR-DFT level of theory predicts that these Dy(III) exohedral substituted fullerene complexes 1–8 are highly stable in nature. EDA analysis predicts stabilization in terms of interaction energy in the following order: 5 > 1 > 2 ≈ 3 > 6 > 7 > 8 > 4, and the decomposed interaction energy suggests that both the electrostatic and orbital interactions are the most dominant contributors in all these complexes. The total interaction energy trend is consistent with the observed trend in ΔEelstat values, suggesting that electrostatic interactions regulate the overall interaction energy. Among complexes 6–8, where the Dy(III) ion is sandwiched between the two (C55X5)− ligands, the interaction energy is relatively weaker compared to that of [DyCp*2] cations (3a), suggesting that the (C55X5)− ligands are relatively electron deficient compared to the Cp* ligands. NPA charge analysis and ETS-NOCV deformation density analysis predict a charge flow from the π-lobes of the ligands to 4f and vacant 5d orbitals of the Dy(III) ions, indicating the importance of both 4f/5d orbitals in bonding. Due to highly symmetric structures, CASSCF calculations predict the stabilization of mJ |±15/2〉 as the ground state for all the complexes except for 5, with the following trend in the Ucal values: 6 (1573 cm−1) ≈ 3 (1569 cm−1) > 1 (1538 cm−1) > 8 (1347 cm−1) > 2 (1305 cm−1) > 7 (1284 cm−1) > 4 (1125 cm−1) > 5 (108 cm−1). The π-type 4f-ligand interaction in complexes 1–4 helps to generate a giant axial ligand field, while the δ-type interaction between 4f and the (C8H8)2− ligand diminishes the axial ligand field and SMM behaviour. CASSCF calculations predict a giant magnetization barrier with strictly no QTM within the ground states (kQTM = 10−7–10−9) for complexes 6–8. Due to structural similarity in complexes 6–8, the observed trend in the Ucal values is solely controlled by the ligand's electronic effects, which are nicely captured in the computed NPA charges and MEPs. Substitution at the α-carbon strongly affects the electronic properties of (C55X5)− (where X = CCH3, B, and N) ligands, which is key in tuning the SIM behaviour in these complexes. Among the studied substituted fullerene ligands, the sp3 hybridized α-C carbon in the (C55(CCH3)5)− ring makes the five-membered ring electron-rich compared to B/N analogues which significantly increases the barrier height in 6 compared to those in 7 and 8. Effective demagnetization barrier analysis clearly shows that Ueff is zero below 50 K for all the complexes with the dominant contribution arising from the KD8, highlighting that highly symmetric environments completely quench the TA-QTM at lower KDs and allow Orbach relaxation to take place via the highest KD in all the complexes. Replacing Cp* with (C55X5)− ligands offers a viable way to isolate stable linear exohedral Dy(III) organometallic sandwiched complexes with Ucal exceeding 1500 cm−1, which is close to the values reported for [DyCp*2]+ cations. Our detailed findings predict substituted fullerenes as promising capping ligands for designing the next generation of stable linear Dy(III) based exohedral single-ion magnets displaying giant barrier height with negligible QTM in the ground state.Data availability
The data supporting this article have been included as part of the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
SKS acknowledges the Science and Engineering Research Board (CRG/2023/002936) and IIT Hyderabad for generous funding. KK acknowledges PMRF. SKS and KK acknowledge PARAM Seva Computing Facility under the National Supercomputing Mission at IIT Hyderabad.References
- D. N. Woodruff, R. E. P. Winpenny and R. A. Layfield, Chem. Rev., 2013, 113, 5110–5148 CrossRef CAS PubMed.
- J. Lu, M. Guo and J. Tang, Chem. – Asian J., 2017, 12, 2772–2779 CrossRef CAS PubMed.
- A. Z. Lekuona, J. M. Seco and E. Colacio, Coord. Chem. Rev., 2021, 441, 213984 CrossRef.
- J. L. Liu, Y. C. Chen and M. L. Tong, Chem. Soc. Rev., 2018, 47, 2431–2453 RSC.
- N. F. Chilton, Inorg. Chem., 2015, 54, 2097–2099 CrossRef CAS PubMed.
- Y. S. Ding, Y. F. Deng and Y. Z. Zheng, Magnetochemistry, 2016, 2, 40 CrossRef.
- M. Shiddiq, D. Komijani, Y. Duan, A. G. Ariño, E. Coronado and S. Hill, Nature, 2016, 531, 348–351 CrossRef CAS PubMed.
- R. E. P. Winpenny, Angew. Chem., Int. Ed., 2008, 47, 7992–7994 CrossRef CAS PubMed.
- A. Candini, S. Klyatskaya, M. Ruben, W. Wernsdorfer and M. Affronte, Nano Lett., 2011, 11, 2634–2639 CrossRef CAS.
- M. N. Leuenberger and D. Loss, Nature, 2001, 410, 789–793 CrossRef CAS PubMed.
- A. G. Ariño, F. Luis, S. Hill and E. Coronado, Nat. Chem., 2019, 11, 301–309 CrossRef.
- A. Ardavan and S. J. Blundell, J. Mater. Chem., 2009, 19, 1754–1760 RSC.
- L. Bogani and W. Wernsdorfer, Nat. Mater., 2008, 7, 179–186 CrossRef CAS PubMed.
- R. Vincent, S. Klyatskaya, M. Ruben, W. Wernsdorfer and F. Balestro, Nature, 2012, 488, 357–360 CrossRef CAS PubMed.
- S. G. Coca, E. Cremades, N. A. Alcalde and E. Ruiz, J. Am. Chem. Soc., 2013, 135, 7010–7018 CrossRef PubMed.
- E. Ruiz, J. Cirera, J. Cano, S. Alvarez, C. Loose and J. Kortus, Chem. Commun., 2007, 52–54 Search PubMed.
- S. G. Coca, D. Aravena, R. Morales and E. Ruiz, Coord. Chem. Rev., 2015, , 289–290, 379–392 CrossRef.
- F. S. Guo, B. M. Day, Y. C. Chen, M. L. Tong, A. Mansikkamäki and R. A. Layfield, Science, 2018, 362, 1400–1403 CrossRef CAS PubMed.
- L. Ungur, J. J. Le Roy, I. Korobkov, M. Murugesu and L. F. Chibotaru, Angew. Chem., Int. Ed., 2014, 53, 4413–4417 CrossRef CAS PubMed.
- P. Zhang, L. Zhang, C. Wang, S. Xue, S.-Y. Lin and J. Tang, J. Am. Chem. Soc., 2014, 136, 4484–4487 CrossRef CAS PubMed.
- M. Li, J. Han, H. Wu, Y. Du, Y. Liu, Y. Chen and S. Chen, Dalton Trans., 2022, 51, 16964–16972 RSC.
- S. Moorthy, I. Tarannum, K. Kumari and S. K. Singh, Dalton Trans., 2024, 53, 12073–12079 RSC.
- J. D. Rinehart and J. R. Long, Chem. Sci., 2011, 2, 2078 RSC.
- S. Lee and T. Ogawa, Chem. Lett., 2017, 46, 10–18 CrossRef CAS.
- C. A. P. Goodwin, F. Ortu, D. Reta, N. F. Chilton and D. P. Mills, Nature, 2017, 548, 439–442 CrossRef CAS.
- A. H. Vincent, Y. L. Whyatt, N. F. Chilton and J. R. Long, J. Am. Chem. Soc., 2023, 145, 1572–1579 CrossRef CAS PubMed.
- J. C. Vanjak, B. O. Wilkins, V. Vieru, N. S. Bhuvanesh, J. H. Reibenspies, C. D. Martin, L. F. Chibotaru and M. Nippe, J. Am. Chem. Soc., 2022, 144, 17743–17747 CrossRef CAS PubMed.
- F. S. Guo, M. He, G. Z. Huang, S. R. Giblin, D. Billington, F. W. Heinemann, M. L. Tong, A. Mansikkamäki and R. A. Layfield, Inorg. Chem., 2022, 61, 6017–6025 CrossRef CAS PubMed.
- I. Tarannum, S. Moorthy and S. K. Singh, Dalton Trans., 2023, 52, 15576–15589 RSC.
- J. P. Durrant, B. M. Day, J. Tang, A. Mansikkamäki and R. A. Layfield, Angew. Chem., 2022, 134, e202200525 CrossRef.
- J. Acharya, N. Ahmed, J. F. Gonzalez, P. Kumar, O. Cador, S. K. Singh, F. Pointillart and V. Chandrasekhar, Dalton Trans., 2020, 49, 13110–13122 RSC.
- P. Kalita, N. Ahmed, S. Moorthy, V. Béreau, A. K. Bar, P. Kumar, P. Nayak, J.-P. Sutter, S. K. Singh and V. Chandrasekhar, Dalton Trans., 2023, 52, 2804–2815 Search PubMed.
- A. B. Canaj, S. Dey, C. Wilson, O. Céspedes, G. Rajaraman and M. Murrie, Chem. Commun., 2020, 56, 12037–12040 RSC.
- Y. C. Chen, J. L. Liu, L. Ungur, J. Liu, Q. W. Li, L. F. Wang, Z. P. Ni, L. F. Chibotaru, X. M. Chen and M. L. Tong, J. Am. Chem. Soc., 2016, 138, 2829–2837 CrossRef CAS PubMed.
- S. Bala, G. Z. Huang, Z. Y. Ruan, S. G. Wu, Y. Liu, L. F. Wang, J. L. Liu and M. L. Tong, Chem. Commun., 2019, 55, 9939–9942 RSC.
- A. B. Canaj, S. Dey, E. R. Martí, C. Wilson, G. Rajaraman and M. Murrie, Angew. Chem., Int. Ed., 2019, 58, 14146–14151 CrossRef CAS PubMed.
- M. Tricoire, L. Münzfeld, J. Moutet, N. Mahieu, L. La Droitte, E. Moreno-Pineda, F. Gendron, J. D. Hilgar, J. D. Rinehart, M. Ruben, B. Le Guennic, O. Cador, P. W. Roesky and G. Nocton, Chem. – Eur. J., 2021, 27, 13558–13567 CrossRef CAS PubMed.
- M. D. Korzyński, M. Bernhardt, V. Romankov, J. Dreiser, G. Matmon, F. Pointillart, B. L. Guennic, O. Cador and C. Copéret, Chem. Sci., 2022, 13, 10574–10580 RSC.
- M. Jeletic, P.-H. Lin, J. J. Le Roy, I. Korobkov, S. I. Gorelsky and M. Murugesu, J. Am. Chem. Soc., 2011, 133, 19286–19289 CrossRef CAS PubMed.
- D. Reta, J. G. C. Kragskow and N. F. Chilton, J. Am. Chem. Soc., 2021, 143, 5943–5950 CrossRef CAS PubMed.
- A. Mattioni, J. K. Staab, W. J. A. Blackmore, D. Reta, J. Iles-Smith, A. Nazir and N. F. Chilton, Nat. Commun., 2024, 15, 485 CrossRef CAS PubMed.
- A. A. Popov, S. Yang and L. Dunsch, Chem. Rev., 2013, 113, 5989–6113 CrossRef CAS PubMed.
- L. Spree and A. A. Popov, Dalton Trans., 2019, 48, 2861–2871 RSC.
- M. Toganoh, Y. Matsuo and E. Nakamura, J. Am. Chem. Soc., 2003, 125, 13974–13975 CrossRef CAS PubMed.
- E. D. Jemmis, M. Manoharan and P. K. Sharma, Organometallics, 2000, 19, 1879–1887 CrossRef CAS.
- L. Zhu, T. Zhang, M. Yi and J. Wang, J. Phys. Chem. A, 2010, 114, 9398–9403 CrossRef CAS PubMed.
- S. Hokmi, S. Salehzadeh and Y. Gholiee, J. Comput. Chem., 2021, 42, 1354–1363 CrossRef CAS PubMed.
- S. Anila and C. H. Suresh, Phys. Chem. Chem. Phys., 2021, 23, 3646–3655 RSC.
- L. Dunsch, S. Yang, L. Zhang, A. Svitova, S. Oswald and A. A. Popov, J. Am. Chem. Soc., 2010, 132, 5413–5421 CrossRef CAS PubMed.
- W. Xiang, X. Jiang, Y. R. Yao, J. Xin, H. Jin, R. Guan, Q. Zhang, M. Chen, S. Y. Xie, A. A. Popov and S. Yang, J. Am. Chem. Soc., 2022, 144, 21587–21595 CrossRef CAS PubMed.
- Y. Shen, X. Yu, Q. Meng, Y. R. Yao, J. Autschbach and N. Chen, Chem. Sci., 2022, 13, 12980–12986 RSC.
- X. Zhang, W. Li, L. Feng, X. Chen, A. Hansen, S. Grimme, S. Fortier, D. C. Sergentu, T. J. Duignan, J. Autschbach, S. Wang, Y. Wang, G. Velkos, A. A. Popov, N. Aghdassi, S. Duhm, X. Li, J. Li, L. Echegoyen, W. H. E. Schwarz and N. Chen, Nat. Commun., 2018, 9, 2753 CrossRef.
- J. Zhuang, L. Abella, D. C. Sergentu, Y. R. Yao, M. Jin, W. Yang, X. Zhang, X. Li, D. Zhang, Y. Zhao, X. Li, S. Wang, L. Echegoyen, J. Autschbach and N. Chen, J. Am. Chem. Soc., 2019, 141, 20249–20260 CrossRef CAS PubMed.
- A. A. Popov and L. Dunsch, J. Am. Chem. Soc., 2007, 129, 11835–11849 CrossRef CAS PubMed.
- F. Liu, D. S. Krylov, L. Spree, S. M. Avdoshenko, N. A. Samoylova, M. Rosenkranz, A. Kostanyan, T. Greber, A. U. B. Wolter, B. Büchner and A. A. Popov, Nat. Commun., 2017, 8, 16098 CrossRef CAS PubMed.
- A. A. Popov and L. Dunsch, Chem. – Eur. J., 2009, 15, 9707–9729 CrossRef CAS PubMed.
- G. Velkos, W. Yang, Y.-R. Yao, S. M. Sudarkova, F. Liu, S. M. Avdoshenko, N. Chen and A. A. Popov, Chem. Commun., 2022, 58, 7164–7167 RSC.
- M. K. Singh and G. Rajaraman, Chem. Commun., 2016, 52, 14047–14050 RSC.
- M. K. Singh, P. Shukla, M. Khatua and G. Rajaraman, Chem. – Eur. J., 2020, 26, 464–477 CrossRef CAS PubMed.
- S. Dey and G. Rajaraman, Chem. Sci., 2021, 12, 14207–14216 RSC.
- P. W. Fowler and A. Ceulemans, J. Phys. Chem., 1995, 99, 508–510 CrossRef CAS.
- A. L. Balch and M. M. Olmstead, Chem. Rev., 1998, 98, 2123–2166 CrossRef CAS PubMed.
- Y. Matsuo, Y. Kuninobu, S. Ito and E. Nakamura, Chem. Lett., 2004, 33, 68–69 CrossRef CAS.
- M. Sawamura, Y. Kuninobu, M. Toganoh, Y. Matsuo, M. Yamanaka and E. Nakamura, J. Am. Chem. Soc., 2002, 124, 9354–9355 CrossRef CAS PubMed.
- S. Hokmi, S. Salehzadeh and Y. Gholiee, New J. Chem., 2022, 46, 2678–2686 RSC.
- J. Suzumura, N. Hosoya, S. Nagao, M. Mitsui and A. Nakajima, J. Chem. Phys., 2004, 121, 2649–2654 CrossRef CAS PubMed.
- S. Nagao, Y. Negishi, A. Kato, Y. Nakamura, A. Nakajima and K. Kaya, J. Phys. Chem. A, 1999, 103, 8909–8914 CrossRef CAS.
- T. Sharma, M. K. Singh, R. Gupta, M. Khatua and G. Rajaraman, Chem. Sci., 2021, 12, 11506–11514 RSC.
- E. Nakamura, J. Organomet. Chem., 2004, 689, 4630–4635 CrossRef CAS.
- D. Aravena, J. Phys. Chem. Lett., 2018, 9, 5327–5333 CrossRef CAS PubMed.
- A. Lunghi, F. Totti, R. Sessoli and S. Sanvito, Nat. Commun., 2017, 8, 14620 CrossRef.
- A. Lunghi, F. Totti, S. Sanvito and R. Sessoli, Chem. Sci., 2017, 8, 6051–6059 RSC.
- A. Lunghi and S. Sanvito, Sci. Adv., 2019, 5, eaax7163 CrossRef CAS.
- Y. C. Liu, Y. H. Kan, S. X. Wu, G. C. Yang, L. Zhao, M. Zhang, W. Guan and Z. M. Su, J. Phys. Chem. A, 2008, 112, 8086–8092 CrossRef CAS PubMed.
- L. Zhao, M. von Hopffgarten, D. M. Andrada and G. Frenking, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1345 Search PubMed.
- F. C. Guzmán and R. F. W. Bader, Coord. Chem. Rev., 2005, 249, 633–662 CrossRef.
- F. Neese, F. Wennmohs, U. Becker and C. Riplinger, J. Chem. Phys., 2020, 152, 224108 CrossRef CAS PubMed.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12, e1606 Search PubMed.
- T. Nakajima and K. Hirao, Chem. Rev., 2012, 112, 385–402 CrossRef CAS PubMed.
- D. A. Pantazis and F. Neese, J. Chem. Theory Comput., 2009, 5, 2229–2238 CrossRef CAS PubMed.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- S. K. Singh, J. Eng, M. Atanasov and F. Neese, Coord. Chem. Rev., 2017, 344, 2–5 CrossRef CAS.
- M. Betzinger, C. Friedrich and S. Blügel, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 195117 CrossRef.
- G. te Velde, F. M. Bickelhaupt, E. J. Baerends, C. Fonseca Guerra, S. J. A. van Gisbergen, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931–967 CrossRef CAS.
- E. Van Lenthe and E. J. Baerends, J. Comput. Chem., 2003, 24, 1142–1156 CrossRef CAS PubMed.
- M. A. Watson, N. C. Handy and A. J. Cohen, J. Chem. Phys., 2003, 119, 6475–6481 CrossRef CAS.
- E. V. Lenthe, E. J. Baerends and J. G. Snijders, J. Chem. Phys., 1994, 101, 9783–9792 CrossRef.
- B. O. Roos, P. R. Taylor and P. E. M. Sigbahn, Chem. Phys., 1980, 48, 157–173 CrossRef CAS.
- K. Bernot, J. Luzon, L. Bogani, M. Etienne, C. Sangregorio, M. Shanmugam, A. Caneschi, R. Sessoli and D. Gatteschi, J. Am. Chem. Soc., 2009, 131, 5573–5579 CrossRef CAS PubMed.
- G. Cucinotta, M. Perfetti, J. Luzon, M. Etienne, P.-E. Car, A. Caneschi, G. Calvez, K. Bernot and R. Sessoli, Angew. Chem., Int. Ed., 2012, 51, 1606–1610 CrossRef CAS PubMed.
- M. Briganti, G. F. Garcia, J. Jung, R. Sessoli, B. L. Guennic and F. Totti, Chem. Sci., 2019, 10, 7233–7245 RSC.
- M. S. Norre, C. Gao, S. Dey, S. K. Gupta, A. Borah, R. Murugavel, G. Rajaraman and J. Overgaard, Inorg. Chem., 2020, 59, 717–729 CrossRef CAS PubMed.
- P. Kalita, K. Kumari, P. Kumar, V. Kumar, S. K. Singh, G. Rogez and V. Chandrasekhar, Dalton Trans., 2024, 53, 10521–10535 RSC.
- D. Shao, W. J. Tang, Z. Ruan, X. Yang, L. Shi, X. Q. Wei, Z. Tian, K. Kumari and S. K. Singh, Inorg. Chem. Front., 2022, 9, 6147–6157 RSC.
- L. F. Chibotaru and L. Ungur, J. Chem. Phys., 2012, 137, 064112 CrossRef CAS PubMed.
- A. C. Alvarez, Y. Gil, L. Llanos and D. Aravena, Inorg. Chem. Front., 2020, 7, 2478–2486 RSC.
- S. D. Jiang, S. S. Liu, L. N. Zhou, B. W. Wang, Z. M. Wang and S. Gao, Inorg. Chem., 2012, 51, 3079–3087 CrossRef CAS PubMed.
- A. C. Parambil and A. Mansikkamäki, J. Organomet. Chem., 2024, 1007, 123024 CrossRef.
- M. Mitoraj and A. Michalak, J. Mol. Model., 2007, 13, 347–355 CrossRef CAS PubMed.
- E. R. Johnson, S. Keinan, P. M. Sánchez, J. C. García, A. J. Cohen and W. Yang, J. Am. Chem. Soc., 2010, 132, 6498–6506 CrossRef CAS PubMed.
- A. Otero-de-la-Roza, E. R. Johnson and J. C. García, Phys. Chem. Chem. Phys., 2012, 14, 12165–12172 RSC.
- T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graph., 1996, 14, 33–38 CrossRef CAS PubMed.
- R. F. Bader, Acc. Chem. Res., 1985, 18, 9–15 CrossRef CAS.
- M. Ziółkowski, S. J. Grabowski and J. Leszczynski, J. Phys. Chem. A, 2006, 110, 6514–6521 CrossRef PubMed.
- D. Cremer and E. Kraka, Angew. Chem., Int. Ed. Engl., 1984, 23, 627–628 CrossRef.
- N. Kaltsoyannis, Inorg. Chem., 2013, 52, 3407–3413 CrossRef CAS PubMed.
- S. Cooper and N. Kaltsoyannis, Dalton Trans., 2021, 50, 1478–1485 RSC.
- J. Jung, M. Atanasov and F. Neese, Inorg. Chem., 2017, 56, 8802–8816 CrossRef CAS PubMed.
- S. Dey, T. Sharma and G. Rajaraman, Chem. Sci., 2024, 15, 6465–6477 RSC.
- K. R. Meihaus and J. R. Long, J. Am. Chem. Soc., 2013, 135, 17952–17957 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4dt02090a |
| This journal is © The Royal Society of Chemistry 2024 |